A&A 451, 339-344 (2006)
DOI: 10.1051/0004-6361:20054588
The 2005 Draconid outburst
M. Campbell-Brown1, 2 -
J. Vaubaillon1, 2, 3 -
P. Brown1, 2 -
R. J. Weryk1 -
R. Arlt2
1 - University of Western Ontario, Department of Physics and Astronomy,
London ON N6A 3K7, Canada
2 -
International Meteor Organization, PF 600118, 14401 Potsdam, Germany
3 -
Institut de Mécanique Céleste et de Calcul des Éphémérides, Observatoire de Paris, 77 avenue Denfert-Rochereau, 75014 Paris, France
Received 24 November 2005 / Accepted 24 January 2006
Abstract
Aims. We report the flux profile and mean orbit for meteoroids associated with an unexpected activity outburst from the Draconid meteor shower on 8 October, 2005. The primary aim is to define the characteristics of the outburst and establish the age of the associated meteoroids.
Methods. Radar data from the outburst are used to define the flux profile and mass distribution for Draconid meteoroids at small meteoroid masses, while visual data are used to define the ZHR profile at larger masses. The radar recorded both single station and orbital data permitting orbits for many individual Draconid radar echoes as well as determination of a mean shower radiant.
Results. The peak activity was centered at 16.1 hrs UT, (
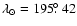 (J2000) solar longitude) with noticeably heightened radar activity lasting for a total of more than three hours. Based on the distribution of amplitudes for underdense Draconid echoes, the mean mass distribution index at masses of 10-6 kg was found to be
(J2000) solar longitude) with noticeably heightened radar activity lasting for a total of more than three hours. Based on the distribution of amplitudes for underdense Draconid echoes, the mean mass distribution index at masses of 10-6 kg was found to be
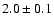 .
The equivalent hourly-binned radar ZHR was in excess of 150, while visual observations in the same intervals produced ZHRs of 40. The apparent radiant of the outburst was
.
The equivalent hourly-binned radar ZHR was in excess of 150, while visual observations in the same intervals produced ZHRs of 40. The apparent radiant of the outburst was
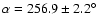 ,
,
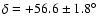 .
Numerical modelling of radar-sized Draconids show that a significant number of meteoroids from the 1946 perihelion passage of 21P/Giacobini-Zinner encountered the Earth over the interval
.
Numerical modelling of radar-sized Draconids show that a significant number of meteoroids from the 1946 perihelion passage of 21P/Giacobini-Zinner encountered the Earth over the interval
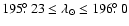 in 2005, centred about
in 2005, centred about
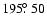
Conclusions. The shower was rich in faint meteors, and therefore showed higher activity in radar data than in visual data alone. The duration of the outburst was very similar to past returns, while the mean radar stream orbit was somewhat different than previous measurements (the radiant differed by 6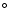 in right ascension and 2
in right ascension and 2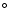 in declination) and also from the expected distribution of orbital elements for modelled 1946 meteoroids encountered in 2005.
in declination) and also from the expected distribution of orbital elements for modelled 1946 meteoroids encountered in 2005.
Key words: meteors, meteoroids - comets: individual: 21P/Giacobini-Zinner
The Draconid meteor shower (sometimes also referred to as the Giacobinids from the parent comet 21P/Giacobini-Zinner) ranks among the most spectacular of the periodic meteor showers. The shower produced strong storms (ZHRs approaching 10 000) in 1933 and 1946, with lesser activity in 1952 and 1926 and moderately strong showers in 1985 and 1998 (ZHRs more than 500) (Koseki 1990; Arlt 1998; Kronk 1988). Based on the comet encounter geometry in 2005, the Earth passed through the stream 92 days after 21P reached perihelion and 0.043 AU inside the comet orbit. This geometry is only slightly poorer (later than the comet and farther from the stream) than occurred in 1985, when peak zenithal hourly rates (ZHRs) exceeded 500. Predictions based on numerical simulations appropriate for visual-sized meteoroids (mm-sized or larger) of the 2005 shower (http://www.imcce.fr/) did not reveal direct encounters from dust released during any recent passages of 21P; hence no substantial outburst was expected.
Beginning at 14.5 UT on October 8, 2005 and lasting until at least 18 UT, radar activity from the Draconids considerably above background was noted at multiple frequencies by the Canadian Meteor Orbit Radar (CMOR). The peak flux occurred at
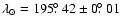 ,
corresponding to 16.1 UT. This is very similar to the comet's nodal longitude of
,
corresponding to 16.1 UT. This is very similar to the comet's nodal longitude of
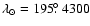 (epoch Aug. 18.0 2005) (http://cfa-www.harvard.edu/iau/Ephemerides/Comets/0021P.html). This strong radar enhancement was accompanied by a more modest increase in visual activity. Here we report analysis of the radar record of this outburst and associated visual activity. We also present refined numerical simulations of the shower appropriate for smaller, radar-sized particles, and identify the outburst as most probably belonging to meteoroids released during the 1946 perihelion passage of 21P/Giacobini-Zinner.
(epoch Aug. 18.0 2005) (http://cfa-www.harvard.edu/iau/Ephemerides/Comets/0021P.html). This strong radar enhancement was accompanied by a more modest increase in visual activity. Here we report analysis of the radar record of this outburst and associated visual activity. We also present refined numerical simulations of the shower appropriate for smaller, radar-sized particles, and identify the outburst as most probably belonging to meteoroids released during the 1946 perihelion passage of 21P/Giacobini-Zinner.
Radar data from the Draconids was recorded simultaneously at 17.450 MHz, 29.850 MHz and 38.150 MHz by the Canadian Meteor Orbit Radar (CMOR) located at 43.26N, 80.77W. CMOR operates at 6 kW peak power at all three frequencies and simultaneously records echoes using a five antenna interferometric layout (cf. Hocking et al. 2001, for more details). Echoes are detected along a great circle at 90 degrees to the meteor radiant. The transmit and receive antennas both have all-sky beams, though echoes within 20 degrees of the horizon are rejected from the analysis. Details of the CMOR system and analysis/reduction techniques can be found in Jones et al. (2005). The effective detection limit for CMOR is near an equivalent meteor magnitude of +8 (a limiting mass of approximately
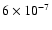 kg). One difference between earlier work and the present study is that all raw data from all three frequencies were saved and examined after the outburst and all underdense echoes (masses less than about 10-5 kg) examined in detail. Heavy daytime interference prevented usable results from being garnered from 17.450 MHz data. All subsequent analyses refer mainly to 29.850 MHz observations as this system produced all orbital information and was more sensitive to Draconids than 38.150 MHz owing to its longer wavelength and higher output power on the day of the outburst. Additionally, corrections for the non-coplanar antenna geometry were applied to reduce systematic interferometric variations (of order one to two degrees) in radiant positions noted in earlier data. The errors in echo phases from the receiver antennas was measured a few weeks after the outburst, and the largest drift in antenna phase was found to be 8 degrees, which would correspond to an error in radiant location of order one degree. Most of the antenna phases had drifted less than four degrees from previously measured values, so it is estimated that the maximum error from antenna phases is of order one degree in radiant positions. It was possible to determine orbits from three-station time delay measurements for 81 Draconids. Deceleration corrections for these orbits were applied based on comparisons of CMOR radar data of major showers with photographic data (Brown et al. 2005); in the present case it is probable that these corrections are smaller than is needed for the highly friable Draconids (cf. Jacchia et al. 1950).
kg). One difference between earlier work and the present study is that all raw data from all three frequencies were saved and examined after the outburst and all underdense echoes (masses less than about 10-5 kg) examined in detail. Heavy daytime interference prevented usable results from being garnered from 17.450 MHz data. All subsequent analyses refer mainly to 29.850 MHz observations as this system produced all orbital information and was more sensitive to Draconids than 38.150 MHz owing to its longer wavelength and higher output power on the day of the outburst. Additionally, corrections for the non-coplanar antenna geometry were applied to reduce systematic interferometric variations (of order one to two degrees) in radiant positions noted in earlier data. The errors in echo phases from the receiver antennas was measured a few weeks after the outburst, and the largest drift in antenna phase was found to be 8 degrees, which would correspond to an error in radiant location of order one degree. Most of the antenna phases had drifted less than four degrees from previously measured values, so it is estimated that the maximum error from antenna phases is of order one degree in radiant positions. It was possible to determine orbits from three-station time delay measurements for 81 Draconids. Deceleration corrections for these orbits were applied based on comparisons of CMOR radar data of major showers with photographic data (Brown et al. 2005); in the present case it is probable that these corrections are smaller than is needed for the highly friable Draconids (cf. Jacchia et al. 1950).
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{4588fig1.eps}
\end{figure}](/articles/aa/full/2006/19/aa4588-05/Timg13.gif) |
Figure 1:
The flux of Draconid meteors in intervals of
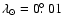 ,
equivalent to 15 min bins ( top) to a limiting mass of 10-6 kg. The solid circles with error bars are 2005 data while the open squares represent the flux from the shower in 2003 in the same solar longitude interval. The low activity in 2003 effectively delineates the magnitude of the sporadic background contamination. The collecting area for the Draconid radiant in 2005 (thick solid line) and 2003 (thin solid line) during the same interval is also shown ( bottom). Only those hourly intervals having a mean Draconid collecting area greater than 130 km2 are shown. The interval shown corresponds to 13.4-18.9 UT on October 8, 2005. ,
equivalent to 15 min bins ( top) to a limiting mass of 10-6 kg. The solid circles with error bars are 2005 data while the open squares represent the flux from the shower in 2003 in the same solar longitude interval. The low activity in 2003 effectively delineates the magnitude of the sporadic background contamination. The collecting area for the Draconid radiant in 2005 (thick solid line) and 2003 (thin solid line) during the same interval is also shown ( bottom). Only those hourly intervals having a mean Draconid collecting area greater than 130 km2 are shown. The interval shown corresponds to 13.4-18.9 UT on October 8, 2005. |
| Open with DEXTER |
The flux of Draconids was calculated from the observed echo rate and the computed collecting area appropriate to the Draconid radiant, which was measured at apparent coordinates
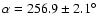 ,
,
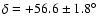 from single station radiant mapping (Jones & Jones 2006). The radar collecting area is that of a strip covering the ablation heights of meteors along the echo line. The collecting area for the Draconid radiant has two minima, one when the radiant is low in the sky (and the echo line is close to overhead), and the second when the radiant is high in the sky (and the echo line falls below the 20 degree limit). Rates from the times when the collecting area was under 130 km2 (one half the maximum) have been rejected from the analysis, since small fluctuations in background rate produce large changes in flux and ZHR. The details of the method used to compute the collecting area are given in Brown & Jones (1995). As shown in Fig. 1, the change in the collecting area during the outburst is small (except after 17.5 UT when the area drops considerably). Indeed, the effective collecting area of the radar to Draconid meteors remains between 210-260 km2 from 14-17.5 UT. Thus the fluxes derived in this interval do not suffer from artifacts of large corrections produced by severe changes in the viewing geometry and are considered robust. We assume a mass index of s=2.0 throughout, as calculated using all single station echoes consistent with the Draconid radiant. The individual Draconid echoes are identified by their proximity to the echo line of the Draconid radiant; we consider any meteor echo within 5
from single station radiant mapping (Jones & Jones 2006). The radar collecting area is that of a strip covering the ablation heights of meteors along the echo line. The collecting area for the Draconid radiant has two minima, one when the radiant is low in the sky (and the echo line is close to overhead), and the second when the radiant is high in the sky (and the echo line falls below the 20 degree limit). Rates from the times when the collecting area was under 130 km2 (one half the maximum) have been rejected from the analysis, since small fluctuations in background rate produce large changes in flux and ZHR. The details of the method used to compute the collecting area are given in Brown & Jones (1995). As shown in Fig. 1, the change in the collecting area during the outburst is small (except after 17.5 UT when the area drops considerably). Indeed, the effective collecting area of the radar to Draconid meteors remains between 210-260 km2 from 14-17.5 UT. Thus the fluxes derived in this interval do not suffer from artifacts of large corrections produced by severe changes in the viewing geometry and are considered robust. We assume a mass index of s=2.0 throughout, as calculated using all single station echoes consistent with the Draconid radiant. The individual Draconid echoes are identified by their proximity to the echo line of the Draconid radiant; we consider any meteor echo within 5 of the line to be a probable Draconid. To correct for sporadic contamination, we determined all echoes consistent with the Draconid radiant on Oct. 7 and Oct. 9, 2005 and subtracted this background from the rates on Oct. 8.
of the line to be a probable Draconid. To correct for sporadic contamination, we determined all echoes consistent with the Draconid radiant on Oct. 7 and Oct. 9, 2005 and subtracted this background from the rates on Oct. 8.
The raw flux computed from the rate divided by the collecting area is further corrected for the initial trail radius effect (cf. Campbell-Brown & Jones 2003), which is a factor of 2.2 at 20 km s-1. It is then scaled to a reference limiting magnitude of +6.5 mag using a mass index of 2.0; in this correction the power of the radar, measured on the day of observation, is also taken into account. This magnitude limit corresponds to Draconids of mass
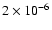 kg.
kg.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{4588fig2.eps}\end{figure}](/articles/aa/full/2006/19/aa4588-05/Timg16.gif) |
Figure 2:
Flux ( top) and equivalent Zenithal Hourly Rate ( bottom) of Draconid meteors from 2002-2005 centered about the date of maximum. Only those hourly intervals having a mean Draconid collecting area greater than 130 km2 are shown. |
| Open with DEXTER |
Figure 2 shows the computed flux at hourly intervals over the solar longitude interval 194-196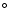 for 2005 (12 UT Oct. 7-12 UT Oct. 9) and also 2002-2004 for comparison. It is clear that no detectable activity occurred in 2002-2004 while the 2005 increase in activity is very apparent. Also shown is an equivalent visual ZHR computed from the radar flux following the technique described in Brown & Rendtel (1996).
Figure 1 shows the flux profile for 2005 and 2003 at 15 min intervals. The peak activity occurs near
for 2005 (12 UT Oct. 7-12 UT Oct. 9) and also 2002-2004 for comparison. It is clear that no detectable activity occurred in 2002-2004 while the 2005 increase in activity is very apparent. Also shown is an equivalent visual ZHR computed from the radar flux following the technique described in Brown & Rendtel (1996).
Figure 1 shows the flux profile for 2005 and 2003 at 15 min intervals. The peak activity occurs near
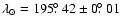 and the full-width to half maximum is approximately 0.1 degrees of solar longitude. The total time interval during which the shower was significantly above the background ranged from
and the full-width to half maximum is approximately 0.1 degrees of solar longitude. The total time interval during which the shower was significantly above the background ranged from
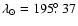 to later than
to later than
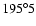 ,
a total duration of more than 3 hours. This is very similar to the durations of past outbursts (e.g. Nagasawa et al. 1985; Lindblad 1987). The end of the outburst activity likely occurs after the radar sensitivity to the Draconid radiant is zero.
,
a total duration of more than 3 hours. This is very similar to the durations of past outbursts (e.g. Nagasawa et al. 1985; Lindblad 1987). The end of the outburst activity likely occurs after the radar sensitivity to the Draconid radiant is zero.
In addition to measuring single-station flux, CMOR has the capability to measure individual orbits for a sub-set of all detected echoes. The orbits are determined using the observed echo time-delays (relative to the main station) as recorded at two remote sites located 6 and 8 km from the main site (cf. Jones et al. 2005, for more details). The measured time delays (which result from reflections at different points along the trail) together with the interferometry at the main site produce a unique trajectory solution and velocity estimate for echoes with geometries permitting specular reflection to be seen from all three sites.
In all, 81 Draconid orbits were measured during the outburst. These orbits were selected for having geocentric radiants within 15 degrees of the radiant centre. The centroid of the outburst radiant was
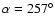 ,
,
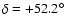 based on a plot of the geocentric radiants for all 3568 orbits measured on October 8, 2005. Additionally, orbits were selected assuming a measured velocity within 3.5 km s-1 of the nominal 23 km s-1 Draconid velocity (Fujiwara et al. 2001; Jacchia et al. 1950). For comparison in 2003 and 2004 these same criteria produced a total of 5 and 8 orbits respectively.
The large difference is due to the fact that the Draconid radiant is near the antapex direction of the Earth's motion and few sporadic meteoroids have radiants in this area. As such, we are unusually confident that essentially all detected orbits in this region are related to the Draconids. Table 1 shows the mean elements derived from 48 orbits selected as the highest quality from visual examination of the radar returns of all 81 echoes producing orbits.
based on a plot of the geocentric radiants for all 3568 orbits measured on October 8, 2005. Additionally, orbits were selected assuming a measured velocity within 3.5 km s-1 of the nominal 23 km s-1 Draconid velocity (Fujiwara et al. 2001; Jacchia et al. 1950). For comparison in 2003 and 2004 these same criteria produced a total of 5 and 8 orbits respectively.
The large difference is due to the fact that the Draconid radiant is near the antapex direction of the Earth's motion and few sporadic meteoroids have radiants in this area. As such, we are unusually confident that essentially all detected orbits in this region are related to the Draconids. Table 1 shows the mean elements derived from 48 orbits selected as the highest quality from visual examination of the radar returns of all 81 echoes producing orbits.
Table 1:
Average and standard deviation of the orbital elements for the 2005 Draconid outburst based on 48 radar orbits.
The 2005 Draconids were observed visually by 24 observers located in Asia, Europe, and North America. The total of 136 Draconid
meteors recorded during 60 hours of effective observing time were used to construct a ZHR profile of the shower (Fig. 3). The method employed here is described in Vaubaillon et al. (2005c). Three quarters of the 80 observing intervals were recorded under favorable sky conditions with limiting stellar magnitudes of better than +5.5. Much of this data does, however, suffer from the low altitude of the radiant; when Asian observers saw the activity peak it was very low (<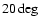 ). However, the average ZHR at solar longitude
). However, the average ZHR at solar longitude
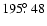 is derived from European observations where the radiant was very high in the sky. The ZHR of 24 is thus reliable and can be understood as a lower limit for the visual activity of the peak rate.
is derived from European observations where the radiant was very high in the sky. The ZHR of 24 is thus reliable and can be understood as a lower limit for the visual activity of the peak rate.
The ZHR computations are based on a population index of r=3, based on the population index derived for the 1985 and 1998 outbursts (Koseki 1990; Arlt 1998). While suitable for a ZHR graph, the number of visually recorded Draconids is too small to derive a meaningful population index profile for 2005.
The flux density profile of the 2005 Draconids was derived according to the method given in Koschack & Rendtel (1990).
We obtain a maximum flux density of 0.035 particles
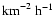 producing meteors of magnitude +6.5 or brighter. This is equivalent to a number density of almost 500 particles in a cube with sides of length 1000 km. Although this is several times more than the density in the Perseid stream, the low entry velocity of the Draconids in the Earth's atmosphere results in a poor visual display compared to the Perseids (or other fast showers), despite the high number densities.
producing meteors of magnitude +6.5 or brighter. This is equivalent to a number density of almost 500 particles in a cube with sides of length 1000 km. Although this is several times more than the density in the Perseid stream, the low entry velocity of the Draconids in the Earth's atmosphere results in a poor visual display compared to the Perseids (or other fast showers), despite the high number densities.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4588fig3.ps}
\end{figure}](/articles/aa/full/2006/19/aa4588-05/Timg31.gif) |
Figure 3:
ZHR profile of the 2005 Draconids from visual records. |
| Open with DEXTER |
4 Modelling the Draconids
Following the method developed by Vaubaillon et al. (2005b), we model the ejection of meteoroids from comet 21P/Giacobini-Zinner.
The ejection velocity is computed according to the model developed by Crifo & Rodionov (1997), which is itself based on the dirty
snowball model of Whipple (1950).
The radius of the comet was taken as  2.0 km, from the latest estimate of this parameter by Mueller (1992).
We note however that previous studies provided a smaller radius (
2.0 km, from the latest estimate of this parameter by Mueller (1992).
We note however that previous studies provided a smaller radius ( 1.3 km; see Landaberry et al. 1991; Sekanina 1985),
for an assumed Bond albedo of 0.04. The simulation of the whole stream involves 61 perihelion passages, from 1596 to 2005.
The orbital elements of the comet were provided by P. Rocher (personal communication, see also http://www.imcce.fr/en/ephemerides/donnees/comets/FICH/CIA0013.php)
and are provided in Table 2. The comet's orbit is largely stable during this time span.
1.3 km; see Landaberry et al. 1991; Sekanina 1985),
for an assumed Bond albedo of 0.04. The simulation of the whole stream involves 61 perihelion passages, from 1596 to 2005.
The orbital elements of the comet were provided by P. Rocher (personal communication, see also http://www.imcce.fr/en/ephemerides/donnees/comets/FICH/CIA0013.php)
and are provided in Table 2. The comet's orbit is largely stable during this time span.
Table 2:
Orbital elements of comet 21P/Giacobini-Zinner.
The model takes into account the radiation pressure and the Poynting-Robertson drag. The main effect of the former is to broaden the orbits of the particles, compared to that of the comet (i.e.
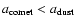 ), and depends on
), and depends on
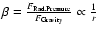 ,
with r the radius of the particle. The smaller the radius, the larger
,
with r the radius of the particle. The smaller the radius, the larger 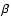 and the larger
and the larger
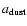 .
Therefore the position of a particle depends on its radius, as well as the ejection velocity (again the smaller the particle the higher the ejection velocity). Figure 4 highlights this fact: only the particles smaller than 100 microns are able to reach the Earth. The other ones (from 100 microns to 10 mm) are generally not spread out enough to cause enhanced activity.
.
Therefore the position of a particle depends on its radius, as well as the ejection velocity (again the smaller the particle the higher the ejection velocity). Figure 4 highlights this fact: only the particles smaller than 100 microns are able to reach the Earth. The other ones (from 100 microns to 10 mm) are generally not spread out enough to cause enhanced activity.
For the ejected grains, the model uses six bins of varying mass. Prior to this study, (following Vaubaillon et al. 2005a), six size bins of Draconid particles were chosen in the range 0.5 to 10 mm. This mass range corresponds to Draconids of visual magnitude. No substantial numbers of meteoroids from any past perihelion passage of 21P/Giacobini-Zinner were found to intersect the Earth, leading to the original predictions that no enhanced activity would occur for the Draconids in 2005.
After the high activity noted by radar, smaller meteoroids, more appropriate to radar observations, in the size range 0.05 to 0.1 mm
were included in the same simulations.
Ten thousand (104) particles were simulated per size bin, for a total of
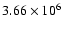 particles.
The program was run on 5 to 50 parallel processors of an IBM SP4 located at CINES (France).
The reason for taking an extra size bin is explained by the results shown in Fig. 4: only the smallest particles are able to reach Earth in 2005, corresponding approximately to those detectable in the radio-meteor size range.
The 2005 Draconids outburst is therefore found to be of the same nature
as the predicted (but unobserved) 2003
particles.
The program was run on 5 to 50 parallel processors of an IBM SP4 located at CINES (France).
The reason for taking an extra size bin is explained by the results shown in Fig. 4: only the smallest particles are able to reach Earth in 2005, corresponding approximately to those detectable in the radio-meteor size range.
The 2005 Draconids outburst is therefore found to be of the same nature
as the predicted (but unobserved) 2003 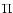 -Puppids (Vaubaillon & Colas 2005), namely very rich in fainter meteors only.
The difference between the position of the particle size bins comes from the initial conditions of the particles
(higher ejection velocity for smaller particles) and the non-gravitational forces acting on them.
The radiation pressure is especially relevant in this case, making the critical difference between intersecting (high beta values) and non-intersecting (low beta values).
This makes the evolution of the different sized populations of particles very different.
-Puppids (Vaubaillon & Colas 2005), namely very rich in fainter meteors only.
The difference between the position of the particle size bins comes from the initial conditions of the particles
(higher ejection velocity for smaller particles) and the non-gravitational forces acting on them.
The radiation pressure is especially relevant in this case, making the critical difference between intersecting (high beta values) and non-intersecting (low beta values).
This makes the evolution of the different sized populations of particles very different.
![\begin{figure}
\par\includegraphics[width=8.1cm,height=6.7cm,clip]{4588fig4.eps}...
...*{4mm} \includegraphics[width=7.4cm,height=6.7cm,clip]{4588fig5.eps}\end{figure}](/articles/aa/full/2006/19/aa4588-05/Timg39.gif) |
Figure 4:
Nodes of meteoroids ejected by comet 21P/Giacobini-Zinner encountering the Earth in 2005. Left: particles in the size range 0.5 to 10 mm.
Right: particles in the size range 0.05 to 0.1 mm.
The labels indicate the year of the perihelion return of the comet during which the particles were ejected.
No visual-sized meteoroids intersect the Earth ( left), in contrast to the smaller particles ( right).
The trail intersecting the Earth here was released during the 1946 perihelion return of the comet. |
| Open with DEXTER |
The extent of the sub-trail composed of the smallest particle
is larger than for the larger ones, causing a difference in the effect of the planetary perturbation (especially by Jupiter).
In Fig. 4, it can be seen that the 2005 Draconid outburst was due to the encounter of the Earth and
the trail ejected by 21P/Giacobini-Zinner in 1946 and composed of particles of order 100 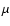 m.
The time of maximum derived from 21 test particles located within
m.
The time of maximum derived from 21 test particles located within
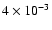 AU of the Earth centred about the 1946 streamlet (cf. Vaubaillon et al. 2005b, for a description of the technique) is the 8th of October,
AU of the Earth centred about the 1946 streamlet (cf. Vaubaillon et al. 2005b, for a description of the technique) is the 8th of October, 
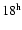 UT, 2005.
As can be seen on the figure, only a few simulated particles reach the planet; hence the 2 h
discrepancy with the observations may be an artifact of small number statistics.
This also makes a the computation of the level of the shower hard.
Considering
UT, 2005.
As can be seen on the figure, only a few simulated particles reach the planet; hence the 2 h
discrepancy with the observations may be an artifact of small number statistics.
This also makes a the computation of the level of the shower hard.
Considering
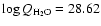 (the rate of water emission from the nucleus; cf. Ahearn et al. 1995) and
(the rate of water emission from the nucleus; cf. Ahearn et al. 1995) and
![$[Af\rho]=[0.2;0.5]$](/articles/aa/full/2006/19/aa4588-05/img44.gif) m (
m (![$[Af\rho]$](/articles/aa/full/2006/19/aa4588-05/img45.gif) is a measure of the comet activity) (typical values for this kind of comet: the values are assumed here due to lack of measuremeants of these quantities for 21P/Giacobini-Zinner), we find an equivalent ZHR within the range 80-220. These values are within the range found by the radar observations (see Fig. 2).
is a measure of the comet activity) (typical values for this kind of comet: the values are assumed here due to lack of measuremeants of these quantities for 21P/Giacobini-Zinner), we find an equivalent ZHR within the range 80-220. These values are within the range found by the radar observations (see Fig. 2).
The outburst of Draconids described here is similar qualitatively to the circumstances surrounding the 1952 outburst when the shower enhancement was detected by radar only and the peak echo rate was of the order of 180 per hour (Davies & Lovell 1955). Our equivalent (raw) hourly Draconid rate was 135 centred about the maximum in 2005. For comparison, the hourly echo rate was 15 in the equivalent period on Oct. 7, 2005. As well, the radar observations of the descending branch in 1952 (and in 2005) was truncated due to the high elevation of the radiant (and correspondingly low radar sensitivity for such a geometry). Thus the durations of the two outbursts may also have been similar. However, the differences in equipment and reduction techniques do not permit an absolute quantitative comparison between 1952 and 2005, despite the superficial similarity in recorded echo rates.
The detailed flux profile shown in Fig. 1 has several interesting features. First, notable fluctuations are apparent in the rates; similar fluctuations in Draconid outburst/storm activity curves have been noticed previously, most reliably during the 1946 storm (Kresak & Slancikova 1975). In particular, the peak 15 min bin at
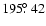 is followed by two intervals of more than 2
is followed by two intervals of more than 2 activity decrease. It is most probable that this is a statistical fluctuation; without an independent flux profile from other stations it is not possible to establish this as a true feature of the 2005 outburst as was done with fluctuations in the 1946 storm. If the single point representing the peak is a fluctuation, then the secondary peak at
activity decrease. It is most probable that this is a statistical fluctuation; without an independent flux profile from other stations it is not possible to establish this as a true feature of the 2005 outburst as was done with fluctuations in the 1946 storm. If the single point representing the peak is a fluctuation, then the secondary peak at
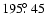 might imply an even later maximum, much closer (within
might imply an even later maximum, much closer (within  1 h) to the simulation maximum at
1 h) to the simulation maximum at
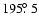 .
.
Secondly, there is a very slow apparent drop in activity after the maximum. Following Jenniskens (1995), the B factor representing the logarithmic slope of the ascending branch of the profile is found to be
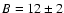 ,
in good agreement with the ascending slopes found for the 1998 outburst (B=11, Arlt (1998) and for the 1985 outburst (
,
in good agreement with the ascending slopes found for the 1998 outburst (B=11, Arlt (1998) and for the 1985 outburst (
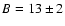 ,
Jenniskens 1995). This is shallower than found for the storms of 1933 or 1946 (Jenniskens 1995). Unfortunately, the rapidly changing radar collecting area for the Draconid radiant in the latter portion of the descending branch of the activity and the truncation of the final segment of that branch due to the high elevation of the radiant make determination of the descending slope unreliable. We suggest this very slow change in activity is an artifact of the changing geometry, rather than a reflection of the true relative change in stream flux over this interval (which was likely smaller than shown).
,
Jenniskens 1995). This is shallower than found for the storms of 1933 or 1946 (Jenniskens 1995). Unfortunately, the rapidly changing radar collecting area for the Draconid radiant in the latter portion of the descending branch of the activity and the truncation of the final segment of that branch due to the high elevation of the radiant make determination of the descending slope unreliable. We suggest this very slow change in activity is an artifact of the changing geometry, rather than a reflection of the true relative change in stream flux over this interval (which was likely smaller than shown).
The computed mean orbit of the outburst is puzzling (Table 1). From the median orbital elements of the 21 simulated Draconids encountered by the Earth from the 1946 ejection epoch, a theoretical radiant of
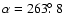 ,
,
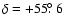 is expected. While the declination differs by only about one degree, the right ascension differs by six degrees; in absolute terms the two radiant locations are separated by about four degrees. This is a large variation and not easily understood. We believe our geocentric radiant position is reliable; measurements of the Orionid radiant in 2005 at the time of peak agreed with literature values to approximately one degree. The single station radiant positions for 29 MHz yielded an apparent radiant at
is expected. While the declination differs by only about one degree, the right ascension differs by six degrees; in absolute terms the two radiant locations are separated by about four degrees. This is a large variation and not easily understood. We believe our geocentric radiant position is reliable; measurements of the Orionid radiant in 2005 at the time of peak agreed with literature values to approximately one degree. The single station radiant positions for 29 MHz yielded an apparent radiant at
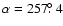 ,
,
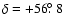 while the independent single-station radiant position measured at 38 MHz was
while the independent single-station radiant position measured at 38 MHz was
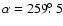 ,
,
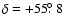 .
Some of this difference may be attributable to the large difference in the total number of Draconid echoes recorded by 29 MHz as compared to 38 MHz (66% more Draconid echoes on 29 than 38). Corrections for zenithal attraction will also decrease the
.
Some of this difference may be attributable to the large difference in the total number of Draconid echoes recorded by 29 MHz as compared to 38 MHz (66% more Draconid echoes on 29 than 38). Corrections for zenithal attraction will also decrease the 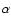 for both measurements, bringing them into better agreement with the geocentric radiant average found from the orbital measurements. Hence, while some fraction of this difference may be due to drifts in the system phases, it cannot account for the full discrepancy in radiant position. There is no obvious physical effect (fragmentation, strong deceleration) which would move the radiant systematically in this way. The several degree difference remains a puzzle and the deviation from the nominal theoretical radiant (which is very similar for almost all ejection epochs from 21P/Giacobini-Zinner) hints at potentially an origin for the stream particles perhaps related to an unusual outburst from the comet or a highly perturbed portion of the stream. Additional observations of the radiant of the 2005 outburst would be helpful in resolving this issue.
for both measurements, bringing them into better agreement with the geocentric radiant average found from the orbital measurements. Hence, while some fraction of this difference may be due to drifts in the system phases, it cannot account for the full discrepancy in radiant position. There is no obvious physical effect (fragmentation, strong deceleration) which would move the radiant systematically in this way. The several degree difference remains a puzzle and the deviation from the nominal theoretical radiant (which is very similar for almost all ejection epochs from 21P/Giacobini-Zinner) hints at potentially an origin for the stream particles perhaps related to an unusual outburst from the comet or a highly perturbed portion of the stream. Additional observations of the radiant of the 2005 outburst would be helpful in resolving this issue.
The geocentric velocity for the Draconids is also almost 1 km s-1 below the theoretically derived value (19.90 km s-1 observed compared to 20.86 km s-1 theoretical for the 1946 streamlet). Here the difference is much more likely to be undercorrection for deceleration, the original deceleration correction having been derived from a fit to other showers, none of which share the extreme fragility of Draconid meteoroids (Jacchia et al. 1950).
An outburst of the Draconid meteor shower was detected visually and by radar, which was centred about
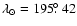 in 2005. Peak fluxes in 15 min bins approached 0.20 meteoroids km-2 h-1 to a limiting mass of 1 mg. The outburst lasted for three hours, based on radar data. A weaker enhancement of visual activity with a peak ZHR of 40 was recorded near the same time interval. The difference in apparent strength of the outburst at visual and radar meteoroid masses is real. Our modelling suggests that ejecta from the 1946 passage of 21P/Giacobini-Zinner is responsible for the outburst and that the ejecta reaching Earth from this epoch is primarily smaller (radar-sized) particles, explaining the apparent differences in observed strength between the two techniques. These results underscore the importance of modelling meteoroids in a wide range of masses when attempting to predict shower activity.
in 2005. Peak fluxes in 15 min bins approached 0.20 meteoroids km-2 h-1 to a limiting mass of 1 mg. The outburst lasted for three hours, based on radar data. A weaker enhancement of visual activity with a peak ZHR of 40 was recorded near the same time interval. The difference in apparent strength of the outburst at visual and radar meteoroid masses is real. Our modelling suggests that ejecta from the 1946 passage of 21P/Giacobini-Zinner is responsible for the outburst and that the ejecta reaching Earth from this epoch is primarily smaller (radar-sized) particles, explaining the apparent differences in observed strength between the two techniques. These results underscore the importance of modelling meteoroids in a wide range of masses when attempting to predict shower activity.
A several degree difference in the mean radiant position observed by the radar for the outburst compared to the expected theoretical radiant position from the 1946 ejecta (and small differences in the corresponding angular elements of the mean orbit as a result) are not fully understood. It is possible this may reflect an origin different from the 1946 ejecta, perhaps related to an outburst of the comet or a strongly perturbed older trail.
Once the observations and modelling are well understood, these shower observations will make possible an improved model of particle ejection from comets and the evolution of meteoroid streams.
Acknowledgements
We are grateful to the CINES (Montpelier, France) for computer time. M.C.B. and P.B. thank the Natural Sciences and Engineering Research Council of Canada for funding support. Thanks to the visual observers who reported to the IMO: R. Balciunas, J. Chang-gui, R. Chen, N. Dankova, A. Dubietis, B. Gao, R. Gray, Y. Hu, C. Johannink, V. Kiryakova, J. Lacorne, M. Liang, X. Liu, J. Ma, V. Mäkelä, P. Martin, M. Maslov, A. McBeath, K. Miskotte, M. Nissinen, R. Pomohaci, J. Rendtel, S. Slavova, V. Velkov. Thanks also to J. Baggaley for helpful comments and suggestions at the review stage.
- Ahearn, M. F.,
Millis, R. L., Schleicher, D. G., Osip, D. J., & Birch,
P. V. 1995, Icarus, 118, 223 [NASA ADS] [CrossRef] (In the text)
- Arlt, R. 1998,
JIMO, 26, 256 [NASA ADS]
- Brown, P., &
Jones, J. 1995, EM&P, 68, 223 [NASA ADS] (In the text)
- Brown, P., &
Rendtel, J. 1996, Icarus, 124, 414 [NASA ADS] [CrossRef] (In the text)
- Brown, P., Jones,
J., Weryk, R. J., & Campbell-Brown, M. D. 2005, EM&P
(In the text)
-
Campbell-Brown, M., & Jones, J. 2003, MNRAS, 343, 775 [NASA ADS] [CrossRef] (In the text)
- Crifo, J. F.,
& Rodionov, A. V. 1997, Icarus, 127, 319 [NASA ADS] [CrossRef] (In the text)
- Davies,
J. G., & Lovell, A. C. B. 1955, MNRAS, 115,
23 [NASA ADS] (In the text)
- Fujiwara,
Y., Ueda, M., Sugimoto, M., et al. 2001, Proc. Meteoroids
2001, ed. B. Warmbein, 123
- Jacchia, L.
G., Kopal, Z., & Millman, P. M. 1950, AJ, 111, 104 [NASA ADS] [CrossRef] (In the text)
-
Jenniskens, P. 1995, A&A, 295, 206 [NASA ADS] (In the text)
- Jones, J., Brown,
P., Ellis, K., et al. 2005, P&SS, 53, 413 [NASA ADS] (In the text)
- Jones, J. W.,
& Jones 2006, MNRAS, (Meteor radiant activity mapping using
single-station radar observations), in press
(In the text)
- Kresak, L.,
& Slancikova, J. 1975, Bulletin of the Astronomical Institutes
of Czechoslovakia, 26, 327 [NASA ADS] (In the text)
- Hocking, W.
K., Fuller, B., & Vandepeer, B. 2001, JASTP, 63, 155 (In the text)
- Koschack,
R., & Rendtel, J. 1990, JIMO, 18, 44 (In the text)
- Koseki, M.
1990, Icarus, 88, 122 [NASA ADS] [CrossRef]
- Kronk, G. 1988,
Meteor Showers: A Descriptive Catalog (NJ: Enslow Publishers)
-
Landaberry, S. J. C., Singh, P. D., & deFreitas Pacheon, J. A.
1991, A&A, 246, 597 [NASA ADS]
- Lindblad,
B. A. 1987, A&A, 187, 928 [NASA ADS]
- Mueller, B.
E. A. 1992, Asteroids, Comets and Meteors, 1991, 425
(In the text)
- Nagasawa,
K., Kozai, Y., & Bortle, J. 1985, IAUC, 4124, 3 [NASA ADS]
- Sekanina,
Z. 1985, AJ, 90, 827 [NASA ADS] [CrossRef]
-
Vaubaillon, J., & Colas, F. 2005, A&A, 431, 1139 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Vaubaillon, J., Colas, F., & Jorda, L. 2005a, A&A, 439,
761 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Vaubaillon, J., Colas, F., & Jorda, L. 2005b, A&A, 439,
751 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Vaubaillon, J., Arlt, R., Shenov, S., Dubrovski, S., & Sato, M.
2005c, MNRAS, 362, 1463 [NASA ADS] [CrossRef] (In the text)
- Whipple, F.
L. 1950, ApJ, 111, 375 [NASA ADS] [CrossRef]
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{4588fig1.eps}
\end{figure}](/articles/aa/full/2006/19/aa4588-05/Timg13.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{4588fig2.eps}\end{figure}](/articles/aa/full/2006/19/aa4588-05/Timg16.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4588fig3.ps}
\end{figure}](/articles/aa/full/2006/19/aa4588-05/Timg31.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,height=6.7cm,clip]{4588fig4.eps}...
...*{4mm} \includegraphics[width=7.4cm,height=6.7cm,clip]{4588fig5.eps}\end{figure}](/articles/aa/full/2006/19/aa4588-05/Timg39.gif)