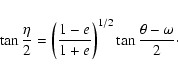A&A 451, 9-18 (2006)
DOI: 10.1051/0004-6361:20054233
Gamma-ray absorption in massive X-ray binaries
G. Dubus1,2
1 - Laboratoire Leprince-Ringuet, UMR 7638 CNRS, École Polytechnique, 91128 Palaiseau, France
2 -
Institut d'Astrophysique de Paris, UMR 7095 CNRS, Université Pierre & Marie Curie, 98bis boulevard Arago, 75014 Paris, France
Received 21 September 2005 / Accepted 5 January 2006
Abstract
Context. Gamma-ray emission in the TeV (1012 eV) range has been detected by HESS from two X-ray binaries: PSR B1259-63 and LS 5039. In both, the early-type star provides large numbers of target photons for pair-production with TeV  -rays. This results in a modulation of the
-rays. This results in a modulation of the  -ray flux as the relative positions of the
-ray flux as the relative positions of the  -ray source and companion star change with orbital phase for the observer.
-ray source and companion star change with orbital phase for the observer.
Aims. The extent to which this variable absorption can provide useful diagnostics for the location and nature of  -ray emission is examined.
-ray emission is examined.
Methods. The absorption spectrum and transmitted flux are calculated by integrating the
 cross-section along the line-of-sight, taking into account the orbit, the spectrum and the finite size of the companion star in LS 5039, PSR B1259-63 and LSI +61
cross-section along the line-of-sight, taking into account the orbit, the spectrum and the finite size of the companion star in LS 5039, PSR B1259-63 and LSI +61
 303, a system similar to LS 5039 but still undetected at TeV energies.
303, a system similar to LS 5039 but still undetected at TeV energies.
Results. In LS 5039, emission close to a black hole or a neutron star primary is considered. In both cases, the transmitted flux >250 GeV drops by an order-of-magnitude near periastron ( = 0). A black hole yields a clear spectral signature in the average spectrum at
= 0). A black hole yields a clear spectral signature in the average spectrum at 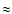 400 GeV. A neutron star yields more variability, with the spectral feature moving from 200 GeV (
400 GeV. A neutron star yields more variability, with the spectral feature moving from 200 GeV (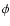 = 0.1) to 3 TeV (
= 0.1) to 3 TeV (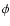 = 0.7). Only 20% of the flux is absorbed at
= 0.7). Only 20% of the flux is absorbed at 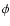 = 0.7, allowing for an almost direct view of the intrinsic spectrum. Low variability will require emission on large scales, more than 0.7 AU away to have <50% absorption in a jet. In LSI +61
= 0.7, allowing for an almost direct view of the intrinsic spectrum. Low variability will require emission on large scales, more than 0.7 AU away to have <50% absorption in a jet. In LSI +61
 303, significant absorption (up to 90% of the 100 GeV flux) is predicted only slightly before periastron, accompanied by a spectral hardening above 1 TeV. In PSR B1259-63, although 40% of the flux is absorbed before periastron, the large variability seen by HESS is due to the
303, significant absorption (up to 90% of the 100 GeV flux) is predicted only slightly before periastron, accompanied by a spectral hardening above 1 TeV. In PSR B1259-63, although 40% of the flux is absorbed before periastron, the large variability seen by HESS is due to the  -ray emission process.
-ray emission process.
Conclusions. The predictions made here are essential to distinguish variability in the emission of  -rays from that due to absorption. A modulation would provide a novel way to constrain the
-rays from that due to absorption. A modulation would provide a novel way to constrain the  -ray source. Its absence would imply that
-ray source. Its absence would imply that  -ray emission occurs on large scales.
-ray emission occurs on large scales.
Key words: radiation mechanisms: non-thermal - stars: individual: LS 5039 - stars: individual: LSI +61
 303 - stars: pulsars: individual: PSR B1259-63 - gamma rays: theory - X-rays: binaries
303 - stars: pulsars: individual: PSR B1259-63 - gamma rays: theory - X-rays: binaries
Massive X-ray binaries, composed of a neutron star or black hole in orbit around an early-type star, have long been recognized as possible  -ray emitters (Weekes 1992). Recently, the HESS collaboration has reported very high energy (VHE)
-ray emitters (Weekes 1992). Recently, the HESS collaboration has reported very high energy (VHE)  -ray emission in the TeV (1012 eV) range from two such systems. The first, PSR B1259-63 (=SS 2883) is a 47.7 ms radio pulsar in a 3.4 yr orbit around a B2Ve star. Variable
-ray emission in the TeV (1012 eV) range from two such systems. The first, PSR B1259-63 (=SS 2883) is a 47.7 ms radio pulsar in a 3.4 yr orbit around a B2Ve star. Variable  -ray emission was detected by HESS during periastron passage (Aharonian et al. 2005c). Here, the relativistic pulsar wind is confined by the stellar wind from the massive companion. Particles at the termination shock produce the non-thermal emission (Tavani et al. 1994). The second, LS 5039 (=RX J1826.2-1450), is a tight 4-day binary composed of an O6V star and an unknown compact object. Resolved radio emission from the source is thought to arise from a weakly relativistic jet with
-ray emission was detected by HESS during periastron passage (Aharonian et al. 2005c). Here, the relativistic pulsar wind is confined by the stellar wind from the massive companion. Particles at the termination shock produce the non-thermal emission (Tavani et al. 1994). The second, LS 5039 (=RX J1826.2-1450), is a tight 4-day binary composed of an O6V star and an unknown compact object. Resolved radio emission from the source is thought to arise from a weakly relativistic jet with
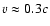 ;
LS 5039 has also been associated with the EGRET source 3EG 1824-1514 (Paredes et al. 2000). This suggests LS 5039 might be a scaled-down analogue of extragalactic blazars. The VHE emission is hard (power law photon index
;
LS 5039 has also been associated with the EGRET source 3EG 1824-1514 (Paredes et al. 2000). This suggests LS 5039 might be a scaled-down analogue of extragalactic blazars. The VHE emission is hard (power law photon index 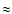 -2) and continuously detected over a timespan of 3 months in 2004 (Aharonian et al. 2005b).
-2) and continuously detected over a timespan of 3 months in 2004 (Aharonian et al. 2005b).
The large stellar luminosity (2 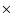
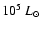 in LS 5039) provides an abundant source of seed photons for inverse Compton scattering with high energy particles. At the same time, the dense radiation field can absorb very high energy
in LS 5039) provides an abundant source of seed photons for inverse Compton scattering with high energy particles. At the same time, the dense radiation field can absorb very high energy  -ray emission through pair production
-ray emission through pair production
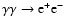 (Gould & Schréder 1967). With stellar effective temperatures in the 20 000-40 000 K range, the typical target photon energy is a few eV which is in the energy range for pair production with TeV photons. The cross-section maximum occurs close to the threshold energy and has an amplitude
(Gould & Schréder 1967). With stellar effective temperatures in the 20 000-40 000 K range, the typical target photon energy is a few eV which is in the energy range for pair production with TeV photons. The cross-section maximum occurs close to the threshold energy and has an amplitude
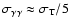 where
where
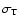 is the Thomson cross-section. The star luminosity is very high (
1038-1039 erg s-1) for radii
is the Thomson cross-section. The star luminosity is very high (
1038-1039 erg s-1) for radii 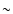
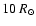 .
At a distance
.
At a distance 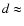 0.1 AU corresponding to periastron in LS 5039 (see Sect. 3), the stellar radiation density in 3.5 eV photons is
0.1 AU corresponding to periastron in LS 5039 (see Sect. 3), the stellar radiation density in 3.5 eV photons is
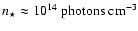 .
A rough estimate of the
.
A rough estimate of the  -ray opacity is
-ray opacity is
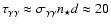 .
The detection of VHE photons from LS 5039 is therefore intriguing.
.
The detection of VHE photons from LS 5039 is therefore intriguing.
The
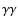 opacity depends strongly on the geometry. The opacity can be greatly reduced compared to the simple estimate above because line-of-sight
opacity depends strongly on the geometry. The opacity can be greatly reduced compared to the simple estimate above because line-of-sight  -rays travel in an anisotropic radiation field. Diffusion in the wind is too small to significantly isotropize radiation (Böttcher & Dermer 2005). The absorption will vary depending upon the relative location of the source of
-rays travel in an anisotropic radiation field. Diffusion in the wind is too small to significantly isotropize radiation (Böttcher & Dermer 2005). The absorption will vary depending upon the relative location of the source of  -rays, the companion star and the observer. In binary systems, the orbit and companion star type can be constrained by optical observations. If
-rays, the companion star and the observer. In binary systems, the orbit and companion star type can be constrained by optical observations. If  -ray emission is isotropic and close to the compact object, absorption will be periodically modulated in a predictable way (Moskalenko 1995; Protheroe & Stanev 1987). Contrast this situation with that in blazars, where the sources of radiation (accretion disc, broad line region) that can absorb
-ray emission is isotropic and close to the compact object, absorption will be periodically modulated in a predictable way (Moskalenko 1995; Protheroe & Stanev 1987). Contrast this situation with that in blazars, where the sources of radiation (accretion disc, broad line region) that can absorb  -rays close to their production site are poorly known. A generic overview of
-rays close to their production site are poorly known. A generic overview of
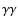 absorption in binaries is presented in Sect. 2.
absorption in binaries is presented in Sect. 2.
The effects of  -ray absorption are predicted in Sects. 3 and 4 for LS 5039, PSR B1259-63 and LSI +61
-ray absorption are predicted in Sects. 3 and 4 for LS 5039, PSR B1259-63 and LSI +61
 303 (=V615 Cas), a system very similar to LS 5039. Comparisons with existing or future observations (will) provide useful diagnostics of the location of
303 (=V615 Cas), a system very similar to LS 5039. Comparisons with existing or future observations (will) provide useful diagnostics of the location of  -ray emission and its nature. Böttcher & Dermer (2005) present calculations for LS 5039, focusing on emission from a black hole jet, and assuming e=0 and a point source approximation for the star. Here, expected differences in absorption lightcurves and spectra for
-ray emission and its nature. Böttcher & Dermer (2005) present calculations for LS 5039, focusing on emission from a black hole jet, and assuming e=0 and a point source approximation for the star. Here, expected differences in absorption lightcurves and spectra for  -ray emission close to a black hole or a neutron star primary are examined for LS 5039 and LSI +61
-ray emission close to a black hole or a neutron star primary are examined for LS 5039 and LSI +61
 303 using the measured orbits and taking into account the finite star size. Expectations if emission arises from a jet are considered in Sect. 5. In this work, the
303 using the measured orbits and taking into account the finite star size. Expectations if emission arises from a jet are considered in Sect. 5. In this work, the
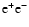 pairs created by absorption are assumed to escape the system or radiate at much lower frequencies. Possible caveats when the pairs radiate back in
pairs created by absorption are assumed to escape the system or radiate at much lower frequencies. Possible caveats when the pairs radiate back in  -rays and initiate an electromagnetic cascade are discussed in Sect. 6.
-rays and initiate an electromagnetic cascade are discussed in Sect. 6.
![\begin{figure}
\par\includegraphics[width=15.25cm,clip]{4233fi1}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg30.gif) |
Figure 1:
Gamma-ray absorption map around a massive star. The grey-scale at each location corresponds to the integrated
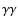 absorption seen by a VHE photon emitted at this location and travelling in the plane of this figure towards an observer located at infinity to the right. The plotted value is exp
absorption seen by a VHE photon emitted at this location and travelling in the plane of this figure towards an observer located at infinity to the right. The plotted value is exp
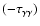 ,
on a linear scale with black corresponding to high absorption and white to low absorption. Absorption is shown for VHE photons with energies of 30 GeV, 300 GeV, 3 TeV and 30 TeV. Full lines are contours corresponding to 99%, 90% (white), 50%, 10% and 1% (black) of the emitted flux being absorbed. The star is located at the origin, has a 10 ,
on a linear scale with black corresponding to high absorption and white to low absorption. Absorption is shown for VHE photons with energies of 30 GeV, 300 GeV, 3 TeV and 30 TeV. Full lines are contours corresponding to 99%, 90% (white), 50%, 10% and 1% (black) of the emitted flux being absorbed. The star is located at the origin, has a 10 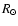 radius and an effective temperature of 40 000 K. The orbit of the binary system LS 5039 is (partially) shown as a dotted line for illustrative purposes. Here, the binary would be seen edge-on (i = 90
radius and an effective temperature of 40 000 K. The orbit of the binary system LS 5039 is (partially) shown as a dotted line for illustrative purposes. Here, the binary would be seen edge-on (i = 90 )
by the observer at right. Gamma-rays emitted close to the compact object towards this observer are more or less absorbed according to orbital phase, with maximum absorption occurring after periastron (marked by a cross). The resulting flux modulation would be close to that shown in Fig. 2 for the case of i = 60 )
by the observer at right. Gamma-rays emitted close to the compact object towards this observer are more or less absorbed according to orbital phase, with maximum absorption occurring after periastron (marked by a cross). The resulting flux modulation would be close to that shown in Fig. 2 for the case of i = 60 . . |
| Open with DEXTER |
The absorption of a  -ray of energy E on a star photon of energy
-ray of energy E on a star photon of energy 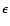 occurs above an energy threshold given by (Gould & Schréder 1967)
occurs above an energy threshold given by (Gould & Schréder 1967)
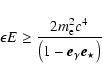 |
(1) |
where
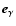 is a unit vector along the direction of propagation of the
is a unit vector along the direction of propagation of the  -ray;
-ray;
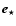 is the unit vector along the direction of propagation of the star photon (see Appendix, Fig. A.1). Absorption can only occur when the target (stellar) photons are at an angle to the
is the unit vector along the direction of propagation of the star photon (see Appendix, Fig. A.1). Absorption can only occur when the target (stellar) photons are at an angle to the  -ray and the minimum
-ray and the minimum
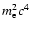 occurs for head-on collisions.
occurs for head-on collisions.
The cross-section maximum occurs close to the threshold, a useful feature for quick estimates but one that errs as the angular dependence has a significant effect. For instance,  -rays propagating directly away from the source of target photons are not absorbed (the energy threshold given by Eq. (1) is infinite). The decrease in the radiation field density when integrating over the photon path also reduces the total opacity. The opacity seen by a
-rays propagating directly away from the source of target photons are not absorbed (the energy threshold given by Eq. (1) is infinite). The decrease in the radiation field density when integrating over the photon path also reduces the total opacity. The opacity seen by a  -ray of given energy will therefore depend strongly on its emission location with respect to the star in the binary.
-ray of given energy will therefore depend strongly on its emission location with respect to the star in the binary.
The opacity depends also on the spectrum of target photons. High energy  -rays are able to interact with the stellar Rayleigh-Jeans tail while lower energy
-rays are able to interact with the stellar Rayleigh-Jeans tail while lower energy  -rays interact with the exponentially decreasing Wien part. At periastron, the compact object in LS 5039 is only
-rays interact with the exponentially decreasing Wien part. At periastron, the compact object in LS 5039 is only 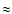 1
1 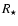 away from the surface of the star (Fig. 1). The finite size of the star can change results from a point source approximation (e.g. Moskalenko 1995), notably by giving a non-zero opacity for a radially outgoing
away from the surface of the star (Fig. 1). The finite size of the star can change results from a point source approximation (e.g. Moskalenko 1995), notably by giving a non-zero opacity for a radially outgoing  -ray. All these effects can be accurately computed (Appendix).
-ray. All these effects can be accurately computed (Appendix).
A map of absorption around a star is shown in Fig. 1 for various  -ray energies. The star has an effective temperature
-ray energies. The star has an effective temperature
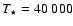 K and radius
K and radius
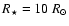 ,
appropriate for the O6.5V star in LS 5039 (Sect. 3). The grey scale represents the amount of flux absorption exp
,
appropriate for the O6.5V star in LS 5039 (Sect. 3). The grey scale represents the amount of flux absorption exp
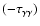 depending upon location of
depending upon location of  -ray emission. The
-ray emission. The  -rays are emitted in the plane of the figure, towards an observer situated at infinity to the right. Note that the solution has cylindrical symmetry about the line-of-sight to the star center.
-rays are emitted in the plane of the figure, towards an observer situated at infinity to the right. Note that the solution has cylindrical symmetry about the line-of-sight to the star center.
At low energies, the opacity is small until the  -ray has an energy above the minimum threshold for head-on interaction with stellar photons
-ray has an energy above the minimum threshold for head-on interaction with stellar photons 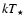 .
The opacity then rises quickly as the target radiation density initially increases exponentially. At progressively larger
.
The opacity then rises quickly as the target radiation density initially increases exponentially. At progressively larger  -ray energies, the dominant effect in setting the opacity becomes the angular dependence (top panels).
-ray energies, the dominant effect in setting the opacity becomes the angular dependence (top panels).
At a given  -ray energy, there is a cone pointing outwards close to the star for which
-ray energy, there is a cone pointing outwards close to the star for which
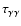 is reduced. The opening angle roughly corresponds to the threshold for interaction with stellar photons at the Wien cutoff. Keeping
is reduced. The opening angle roughly corresponds to the threshold for interaction with stellar photons at the Wien cutoff. Keeping
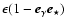 constant in Eq. (1) and starting on the x-axis,
constant in Eq. (1) and starting on the x-axis,  -rays interact with an exponentially increasing density of stellar photons as the angle increases. However, because of the finite size of the star, the absorption can still be high in this cone if the
-rays interact with an exponentially increasing density of stellar photons as the angle increases. However, because of the finite size of the star, the absorption can still be high in this cone if the  -ray is emitted close to the star. For example, >50% of the 3 TeV photons emitted outwards <0.5
-ray is emitted close to the star. For example, >50% of the 3 TeV photons emitted outwards <0.5 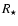 away from the star are still absorbed (bottom left panel of Fig. 1).
away from the star are still absorbed (bottom left panel of Fig. 1).
As the energy of the  -ray further increases (bottom panels), the dominant effect in modifying the opacity is the decrease in radiation density since the interaction now occurs with Rayleigh-Jeans photons. The decrease in opacity is then roughly independent of location. The situation is slightly more complex on-axis as the angular dependence is always important there.
-ray further increases (bottom panels), the dominant effect in modifying the opacity is the decrease in radiation density since the interaction now occurs with Rayleigh-Jeans photons. The decrease in opacity is then roughly independent of location. The situation is slightly more complex on-axis as the angular dependence is always important there.
The existence of a cone with low  -ray opacity shows that VHE emission can occur close to the massive star without significant absorption. However, this configuration is variable as the binary aspect changes for the observer. Assuming isotropic emission close to the compact object, in a small region compared to the binary size, the resulting absorption lightcurve at a given energy depends on the orbital parameters (orbital period
-ray opacity shows that VHE emission can occur close to the massive star without significant absorption. However, this configuration is variable as the binary aspect changes for the observer. Assuming isotropic emission close to the compact object, in a small region compared to the binary size, the resulting absorption lightcurve at a given energy depends on the orbital parameters (orbital period
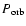 ,
total mass M, eccentricity e, periastron longitude
,
total mass M, eccentricity e, periastron longitude 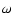 and inclination i, see Appendix). Knowledge of the orbital parameters obtained, for example, via pulsar timing or radial velocity studies, leads to constraints on the physics of VHE emission by comparing expected and observed lightcurves.
and inclination i, see Appendix). Knowledge of the orbital parameters obtained, for example, via pulsar timing or radial velocity studies, leads to constraints on the physics of VHE emission by comparing expected and observed lightcurves.
The case for which absorption is invariant of orbital phase is for a face-on, circular (i=e=0). An inclined, circular orbit results in absorbed flux lightcurves which are symmetric with respect to the orbital phase of superior or inferior conjuction. The changing orbital separation in an eccentric orbit varies the absorption even with i=0 .
Eccentric orbits typically result in
.
Eccentric orbits typically result in  -ray lightcurves with a flux dip at periastron.
-ray lightcurves with a flux dip at periastron.
The maps in Fig. 1 show that the extinction depends on
location but also on energy. Pure  -ray absorption produces an absorption trough in the spectrum that, if measured, can provide
important diagnostics for emission processes (Böttcher & Dermer 2005). The
location of maximum absorption changes as the compact object revolves
around the massive star, providing further diagnostic power. The
trough is quite wide, becoming obvious only for data covering a large
span in energies. For temperatures typical of massive stars, this span
is
-ray absorption produces an absorption trough in the spectrum that, if measured, can provide
important diagnostics for emission processes (Böttcher & Dermer 2005). The
location of maximum absorption changes as the compact object revolves
around the massive star, providing further diagnostic power. The
trough is quite wide, becoming obvious only for data covering a large
span in energies. For temperatures typical of massive stars, this span
is 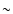 30 GeV-30 TeV (Sect. 3). The emitted
30 GeV-30 TeV (Sect. 3). The emitted  -ray spectrum is
softened by absorption in data limited to the low energy end
(
-ray spectrum is
softened by absorption in data limited to the low energy end
(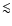 300 GeV) while it is hardened at high energies
(
300 GeV) while it is hardened at high energies
(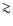 300 GeV). In contrast, the spectral energy distribution of the
extragalactic background light results in a softening at TeV energies
of the emitted
300 GeV). In contrast, the spectral energy distribution of the
extragalactic background light results in a softening at TeV energies
of the emitted  -ray spectrum from blazars
(Stecker et al. 1992). Gamma-ray absorption by Galactic background radiation
is negligible for X-ray binaries.
-ray spectrum from blazars
(Stecker et al. 1992). Gamma-ray absorption by Galactic background radiation
is negligible for X-ray binaries.
The origin of the VHE emission detected by HESS from LS 5039 has yet to be established. An intriguing possibility is that the emission occurs in a relativistic jet as in blazars. Resolved radio emission in LS 5039, attributed to a mildly relativistic jet, constitutes a strong argument in favour of this possibility. Alternatively, the VHE emission could be a result of the interaction of a pulsar relativistic wind with the stellar wind from the massive star, as in PSR B1259-63 (Tavani et al. 1994; Maraschi & Treves 1981). The similarity in spectral energy distributions between LS 5039 and PSR B1259-63 argues in favour of this interpretation.
Can the expected  -ray absorption be used to investigate the origin of the
-ray absorption be used to investigate the origin of the  -ray emission? The star temperature and radius derived from optical spectroscopy are
-ray emission? The star temperature and radius derived from optical spectroscopy are
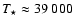 K and
K and
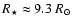 (Casares et al. 2005a, thereafter C05). The star mass is
(Casares et al. 2005a, thereafter C05). The star mass is 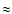
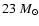 .
Radial velocity studies provide a good determination of
.
Radial velocity studies provide a good determination of
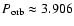 days, eccentricity
days, eccentricity
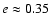 and periastron angle
and periastron angle
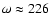
 .
The orbital solution of C05, which includes data from McSwain et al. (2004) whilst adding better phase coverage, supersedes previous determinations. By assuming that the secondary is pseudo-synchronized (in co-rotation at periastron), C05 find
.
The orbital solution of C05, which includes data from McSwain et al. (2004) whilst adding better phase coverage, supersedes previous determinations. By assuming that the secondary is pseudo-synchronized (in co-rotation at periastron), C05 find
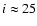
 and a compact object mass 3.7
and a compact object mass 3.7 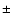
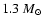 .
Whether the star has had time to pseudo-synchronize in this young, massive X-ray binary is not clear, and a neutron star cannot be firmly ruled out yet. Taking into account the mass function and the more conservative constraints on the system inclination i derived by C05, two orbital solutions are adopted here to illustrate the possible extremes: one with i=60
.
Whether the star has had time to pseudo-synchronize in this young, massive X-ray binary is not clear, and a neutron star cannot be firmly ruled out yet. Taking into account the mass function and the more conservative constraints on the system inclination i derived by C05, two orbital solutions are adopted here to illustrate the possible extremes: one with i=60 ,
corresponding to a canonical 1.4
,
corresponding to a canonical 1.4 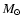 neutron star; and one with i=20
neutron star; and one with i=20 ,
implying a 4.5
,
implying a 4.5 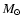 black hole.
black hole.
Hereafter, the  -ray emission is assumed constant, isotropic and occuring in a small region (compared to the binary separation) close to the compact object. Pairs created by the absorption of
-ray emission is assumed constant, isotropic and occuring in a small region (compared to the binary separation) close to the compact object. Pairs created by the absorption of  -rays are further assumed to escape freely or to radiate their energy at frequencies below those of interest. These assumptions are examined in Sects. 5 and 6. The aims are to investigate (1) how much absorption occurs and at what phases; (2) expected observational signatures; (3) whether a black hole or a neutron star primary can be distinguished.
-rays are further assumed to escape freely or to radiate their energy at frequencies below those of interest. These assumptions are examined in Sects. 5 and 6. The aims are to investigate (1) how much absorption occurs and at what phases; (2) expected observational signatures; (3) whether a black hole or a neutron star primary can be distinguished.
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{4233fi2a}\vspace*{5mm}
\includegraphics[width=7.55cm,clip]{4233fi2b}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg54.gif) |
Figure 2:
Modulation of the  -ray transmission
exp -ray transmission
exp
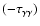 with orbital phase in LS 5039 for two values of the system inclination i. A canonical neutron star corresponds to i=60
with orbital phase in LS 5039 for two values of the system inclination i. A canonical neutron star corresponds to i=60 while i=20
while i=20 implies a
implies a
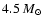 black hole. Isotropic
black hole. Isotropic  -ray emission is assumed to
occur at the location of the compact object. The solid line is for
100 GeV photons (HESS threshold), dashed is for 1 TeV and dotted
for 10 TeV photons. Periastron passage is at -ray emission is assumed to
occur at the location of the compact object. The solid line is for
100 GeV photons (HESS threshold), dashed is for 1 TeV and dotted
for 10 TeV photons. Periastron passage is at  . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{4233fi3}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg55.gif) |
Figure 3:
HESS observed lightcurve of LS 5039 in 2004 (points with error bars, Aharonian et al. 2005b), folded on the orbital period using the ephemeris of C05. The expected lightcurve caused by absorption is plotted as a solid line for i=60 and as a dashed line for i=20
and as a dashed line for i=20 .
Here, the lightcurves are integrated above 250 GeV and normalized to their maximum (Fig. 2 showed the absorption for given energy). The orbital phase of the peak and the duration of strong absorption (>90%) are different between emission close to a black hole (i=20 .
Here, the lightcurves are integrated above 250 GeV and normalized to their maximum (Fig. 2 showed the absorption for given energy). The orbital phase of the peak and the duration of strong absorption (>90%) are different between emission close to a black hole (i=20 )
and close to a neutron star (i=60 )
and close to a neutron star (i=60 ). ). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{4233fi4a}\vspace*{5mm}
\includegraphics[width=7.35cm,clip]{4233fi4b}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg56.gif) |
Figure 4:
Spectrum of  -ray absorption at selected orbital phases -ray absorption at selected orbital phases 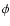 for two inclinations i of LS 5039 (see Fig. 2). The absorption spectrum varies little for i=20
for two inclinations i of LS 5039 (see Fig. 2). The absorption spectrum varies little for i=20 .
The line-like absorption feature may therefore be easier to detect for low inclinations, despite the stronger absorption near periastron for i=60 .
The line-like absorption feature may therefore be easier to detect for low inclinations, despite the stronger absorption near periastron for i=60 .
In the latter case, although spectral variations will be easier to detect, the large differences in absorption spectrum can swamp out the line feature in a phase-averaged spectrum. An almost absorption-free view of the intrinsic spectrum is expected at flux maximum for i=60 .
In the latter case, although spectral variations will be easier to detect, the large differences in absorption spectrum can swamp out the line feature in a phase-averaged spectrum. An almost absorption-free view of the intrinsic spectrum is expected at flux maximum for i=60 . . |
| Open with DEXTER |
The orbital variation of  -ray absorption at various energies
is shown in Fig. 2 for i=20
-ray absorption at various energies
is shown in Fig. 2 for i=20 and i=60
and i=60 .
In
both cases, significant absorption in the 0.1-1 TeV band is predicted
at periastron. The opacity reaches
.
In
both cases, significant absorption in the 0.1-1 TeV band is predicted
at periastron. The opacity reaches
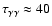 at
phase
at
phase
 for 200 GeV photons (i=60
for 200 GeV photons (i=60 ). However, the
opacity is smaller than unity over a large fraction of the orbit. VHE
). However, the
opacity is smaller than unity over a large fraction of the orbit. VHE  -rays escape because of the anisotropy of the target radiation field. The minimum absorption (peak flux) occurs at
-rays escape because of the anisotropy of the target radiation field. The minimum absorption (peak flux) occurs at
 when the compact object is far from the star and close to the observer.
when the compact object is far from the star and close to the observer.
A non-detection of the periodic variation by HESS would suggest that
 -ray emission occurs far from the companion star. Indeed, the
available HESS lightcurve from 2004 is statistically constant at the
15% confidence level (Aharonian et al. 2005b). A periodogram shows no peak
with more than 2
-ray emission occurs far from the companion star. Indeed, the
available HESS lightcurve from 2004 is statistically constant at the
15% confidence level (Aharonian et al. 2005b). A periodogram shows no peak
with more than 2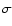 significance (Aharonian et al. 2005b). However, only
14 nightly flux averages over 120 days are available. Future
observations will allow firmer conclusions to be drawn.
significance (Aharonian et al. 2005b). However, only
14 nightly flux averages over 120 days are available. Future
observations will allow firmer conclusions to be drawn.
The amplitude and asymetry of the variation decrease with
inclination. However, these differences may be difficult to
distinguish when comparing to observations of lightcurves integrated above the instrumental enegy threshold. The absorbed
fluxes for the two inclinations are plotted in Fig. 3
along with the HESS 2004 lightcurve from Aharonian et al. (2005b). The
intrinsic spectrum was assumed to be a power law
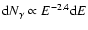 ,
which was integrated after absorption above the same
threshold as the HESS data (250 GeV) to yield the expected flux
variations. The average expected photon index is consistent in both
cases with the HESS measurement (-2.12
,
which was integrated after absorption above the same
threshold as the HESS data (250 GeV) to yield the expected flux
variations. The average expected photon index is consistent in both
cases with the HESS measurement (-2.12 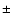 0.15,
Aharonian et al. 2005b). For an inclination of 20
0.15,
Aharonian et al. 2005b). For an inclination of 20 (black hole), the
average fraction of the intrinsic flux that is absorbed above 250 GeV
is 89%. For i=60
(black hole), the
average fraction of the intrinsic flux that is absorbed above 250 GeV
is 89%. For i=60 (neutron star), the fraction is 64%. In
Fig. 3, the observed and expected lightcurves are
renormalised to their maximum. The length of the absorption "eclipse''
is longer and the peak flux occurs later in phase for a high inclination.
(neutron star), the fraction is 64%. In
Fig. 3, the observed and expected lightcurves are
renormalised to their maximum. The length of the absorption "eclipse''
is longer and the peak flux occurs later in phase for a high inclination.
The average absorption is greater for low inclinations as the angle between the star, emission location and observer (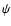 ,
Fig. A.1) stays close to 90
,
Fig. A.1) stays close to 90 .
Therefore, spectral signatures of
.
Therefore, spectral signatures of
 absorption should be easier to see in a phase-average spectrum if emission occurs close to a black hole.
absorption should be easier to see in a phase-average spectrum if emission occurs close to a black hole.
The absorption spectra expected at various orbital phases, and for the two inclinations considered, are shown in Fig. 4. There is a clear absorption at all orbital phase with limited spectral changes in the i=20 case (black hole). The shape is roughly independent of phase with maximum absorption occuring around 400 GeV. In contrast, the energy of maximum absorption changes dramatically in the i=60
case (black hole). The shape is roughly independent of phase with maximum absorption occuring around 400 GeV. In contrast, the energy of maximum absorption changes dramatically in the i=60 case, shifting from 0.2-0.3 TeV to 2-3 TeV when going from orbital phase
case, shifting from 0.2-0.3 TeV to 2-3 TeV when going from orbital phase 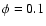 to
to 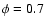 .
Hence, more dramatic changes are expected in phase-binned spectra if the inclination is high.
.
Hence, more dramatic changes are expected in phase-binned spectra if the inclination is high.
The 2004 HESS spectrum covers the 0.3-3 TeV range. Weighting by the integrated flux, the phase-averaged absorption for i=20 would produce a hardening of almost 0.5 of the intrinsic photon index between 0.3-3 TeV, assuming power-law emission at the source. Of course, a single power-law fit would not be an adequate description for a high S/N spectrum of the absorbed
would produce a hardening of almost 0.5 of the intrinsic photon index between 0.3-3 TeV, assuming power-law emission at the source. Of course, a single power-law fit would not be an adequate description for a high S/N spectrum of the absorbed  -rays. When i=60
-rays. When i=60 ,
the amplitude of the variations in absorption is greater, but the phase-averaged hardening is slight,
,
the amplitude of the variations in absorption is greater, but the phase-averaged hardening is slight, 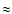 0.1 in photon index. Spectral changes are complex in this case, depending upon energy threshold. Above a few TeV, the overall effect is a spectral hardening at low fluxes compared to high fluxes. With a threshold at a few 0.1 TeV, the spectrum may appear to soften at high fluxes as the absorption trough moves to more than a TeV and more low energy photons are detected. For a neutron star, the orbital phase at which the flux peaks provides an almost direct view of the intrinsic spectrum, with at most
0.1 in photon index. Spectral changes are complex in this case, depending upon energy threshold. Above a few TeV, the overall effect is a spectral hardening at low fluxes compared to high fluxes. With a threshold at a few 0.1 TeV, the spectrum may appear to soften at high fluxes as the absorption trough moves to more than a TeV and more low energy photons are detected. For a neutron star, the orbital phase at which the flux peaks provides an almost direct view of the intrinsic spectrum, with at most 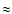 20% absorption at 2-3 TeV. The intrinsic spectrum is always significantly absorbed (
20% absorption at 2-3 TeV. The intrinsic spectrum is always significantly absorbed (
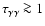 )
in the black hole case.
)
in the black hole case.
Absorption in LSI +61
 303 and PSR B1259-63 is investigated here under identical assumptions as LS 5039 for the gamma-ray emission (constant, isotropic, close to compact object). PSR B1259-63 has been detected by HESS near periastron. Inaccessible to HESS (but accessible to MAGIC and VERITAS), LSI +61
303 and PSR B1259-63 is investigated here under identical assumptions as LS 5039 for the gamma-ray emission (constant, isotropic, close to compact object). PSR B1259-63 has been detected by HESS near periastron. Inaccessible to HESS (but accessible to MAGIC and VERITAS), LSI +61
 303 has yet to be detected by ground-based Cherenkov telescopes.
303 has yet to be detected by ground-based Cherenkov telescopes.
LSI +61
 303 is a massive X-ray binary with a very similar spectral energy distribution to LS 5039. It also has resolved radio emission. LSI +61
303 is a massive X-ray binary with a very similar spectral energy distribution to LS 5039. It also has resolved radio emission. LSI +61
 303 has long been associated to hard
303 has long been associated to hard  -ray emission with possible counterparts seen by Cos-B and EGRET. This prompted Maraschi & Treves (1981) to propose that high energy emission in LSI +61
-ray emission with possible counterparts seen by Cos-B and EGRET. This prompted Maraschi & Treves (1981) to propose that high energy emission in LSI +61
 303 is powered by an interacting pulsar wind. Jet models have been proposed by Bosch-Ramon & Paredes (2004) and Romero et al. (2005). The B0V star has
303 is powered by an interacting pulsar wind. Jet models have been proposed by Bosch-Ramon & Paredes (2004) and Romero et al. (2005). The B0V star has
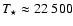 K and
K and
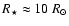 .
Recently, Casares et al. (2005b) have updated the orbital parameters from optical spectroscopy, finding
.
Recently, Casares et al. (2005b) have updated the orbital parameters from optical spectroscopy, finding
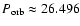 days,
days,
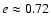 ,
,
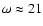
 .
Radial velocity studies are insufficient to rule out a neutron star. As with LS 5039, two cases are studied, representing extremes compatible with observations; one with i=60
.
Radial velocity studies are insufficient to rule out a neutron star. As with LS 5039, two cases are studied, representing extremes compatible with observations; one with i=60 for a 1.4
for a 1.4 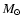 neutron star, and one with i=20
neutron star, and one with i=20 for a 4
for a 4 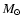 black hole.
black hole.
The absorption lightcurve is shown for both cases in Fig. 5. The orbit is wider than in LS 5039 so that the variation in  -rays absorption occurs essentially only close to periastron. The distance to the star is then
-rays absorption occurs essentially only close to periastron. The distance to the star is then 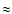 0.1 AU, as with LS 5039. The stellar luminosity is lower in LSI +61
0.1 AU, as with LS 5039. The stellar luminosity is lower in LSI +61
 303 than in LS 5039, so that not all the
303 than in LS 5039, so that not all the  -rays are absorbed at periastron despite the similar distance. At apastron the orbital separation is
-rays are absorbed at periastron despite the similar distance. At apastron the orbital separation is 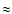 0.7 AU but there is still some absorption, around
0.7 AU but there is still some absorption, around 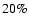 of the 1 TeV flux, because the compact object is behind the star when projecting the orbit onto the sky.
of the 1 TeV flux, because the compact object is behind the star when projecting the orbit onto the sky.
The amplitude of the variations is greater at high inclinations, as in LS 5039. The spectral changes expected close to periastron for i=60 are dramatic, with peak emission that follows the minimum within a few days. Figure 5 shows the strong hardening of the spectrum above 1 TeV with lower fluxes. The absorption feature outside of periastron is a 20% effect. LSI +61
are dramatic, with peak emission that follows the minimum within a few days. Figure 5 shows the strong hardening of the spectrum above 1 TeV with lower fluxes. The absorption feature outside of periastron is a 20% effect. LSI +61
 303 suffers less absorption for most of its orbit so should be more easily detected at VHE energies than LS 5039, if the same processes are indeed at work in the two.
303 suffers less absorption for most of its orbit so should be more easily detected at VHE energies than LS 5039, if the same processes are indeed at work in the two.
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{4233fi5a}\vspace*{5mm}
\includegraphics[width=7.55cm,clip]{4233fi5b}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg72.gif) |
Figure 5:
Modulation of the  -ray transmission with orbital phase
in LSI +61 -ray transmission with orbital phase
in LSI +61
 303 for i=20 303 for i=20 (4
(4 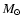 black hole) and i=60
black hole) and i=60 (1.4
(1.4 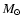 neutron star). The solid line is for 100 GeV photons, dashed is for 1 TeV and dotted for 10 TeV photons. Significant absorption occurs only slightly before periastron (
neutron star). The solid line is for 100 GeV photons, dashed is for 1 TeV and dotted for 10 TeV photons. Significant absorption occurs only slightly before periastron (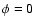 )
in both cases. As with LS 5039, a higher inclination leads to a larger amplitude of absorption. )
in both cases. As with LS 5039, a higher inclination leads to a larger amplitude of absorption. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{4233fi6}
\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg73.gif) |
Figure 6:
LSI +61
 303 absorption spectrum at orbital phases 303 absorption spectrum at orbital phases 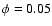 ,
0.5 and 0.95 assuming i=60 ,
0.5 and 0.95 assuming i=60 (see bottom panel of Fig. 5). There is a dramatic spectral change within a couple of days of periastron.
(see bottom panel of Fig. 5). There is a dramatic spectral change within a couple of days of periastron. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{4233fi7}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg74.gif) |
Figure 7:
Modulation caused by  -ray absorption around periastron in PSR B1259-63. The data points are the HESS integrated lightcurve above 380 GeV measured during the 2004 periastron passage (Aharonian et al. 2005c). The data are renormalised to the maximum 10-7 m-2 s-1. The solid line is the integrated flux above the same threshold after absorption, assuming constant power law emission wih a photon index of -2.8. Absorption plays a minor role in the observed variability. -ray absorption around periastron in PSR B1259-63. The data points are the HESS integrated lightcurve above 380 GeV measured during the 2004 periastron passage (Aharonian et al. 2005c). The data are renormalised to the maximum 10-7 m-2 s-1. The solid line is the integrated flux above the same threshold after absorption, assuming constant power law emission wih a photon index of -2.8. Absorption plays a minor role in the observed variability. |
| Open with DEXTER |
Pulsar timing in PSR B1259-63 allows an accurate determination of orbital parameters:
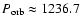 days,
days,
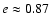 ,
(star)
,
(star)
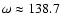
 ,
,
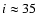
 .
The star has
.
The star has
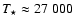 K and
K and
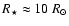 for a total luminosity of 5.8
for a total luminosity of 5.8 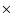
 (Johnston et al. 1994). Figure 7 shows the expected lightcurve around periastron passage, taking only absorption into account. The
(Johnston et al. 1994). Figure 7 shows the expected lightcurve around periastron passage, taking only absorption into account. The  -rays are emitted at the pulsar location with a power law spectrum
-rays are emitted at the pulsar location with a power law spectrum
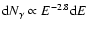 .
The pulsar is
.
The pulsar is 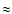 1013 cm at its closest to the Be star, further away than LS 5039 or LSI +61
1013 cm at its closest to the Be star, further away than LS 5039 or LSI +61
 303. Although the pulsar is
303. Although the pulsar is 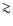 20
20 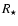 away from the star, there is still some absorption because of the orbital orientation; photons emitted at
away from the star, there is still some absorption because of the orbital orientation; photons emitted at
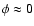 must travel near the star on their way to the observer.
must travel near the star on their way to the observer.
Maximum absorption occurs slightly before periastron, with up to 40% of the  -rays above the HESS threshold (380 GeV) being absorbed. The measured HESS lightcurve has a greater amplitude with a minimum occuring later than expected. Absorption is clearly not sufficient to explain the observations and some of the variability must be intrinsic. A likely possibility is the angle-dependence in the inverse Compton interactions producing the TeV emission (Kirk et al. 1999). VHE emission would not be isotropic. Models should be compared to absorption corrected fluxes. Finally, hardening by absorption of the 0.3-3 TeV spectrum is at most 0.2 in photon index, too small to be measured by HESS.
-rays above the HESS threshold (380 GeV) being absorbed. The measured HESS lightcurve has a greater amplitude with a minimum occuring later than expected. Absorption is clearly not sufficient to explain the observations and some of the variability must be intrinsic. A likely possibility is the angle-dependence in the inverse Compton interactions producing the TeV emission (Kirk et al. 1999). VHE emission would not be isotropic. Models should be compared to absorption corrected fluxes. Finally, hardening by absorption of the 0.3-3 TeV spectrum is at most 0.2 in photon index, too small to be measured by HESS.
Are there good reasons to expect that  -rays are emitted at the location of the compact object? For a binary plerion like PSR B1259-63, most of the VHE emission should occur close to the pulsar wind termination shock (Kirk et al. 1999; Tavani et al. 1994). The overall geometry is set by the stagnation point
-rays are emitted at the location of the compact object? For a binary plerion like PSR B1259-63, most of the VHE emission should occur close to the pulsar wind termination shock (Kirk et al. 1999; Tavani et al. 1994). The overall geometry is set by the stagnation point 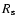 ,
the point on the orbital axis where ram pressure from the stellar and pulsar wind balance (Maraschi & Treves 1981). For LS 5039,
,
the point on the orbital axis where ram pressure from the stellar and pulsar wind balance (Maraschi & Treves 1981). For LS 5039,
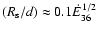 where d is the orbital separation (0.1-0.2 AU in LS 5039) and
where d is the orbital separation (0.1-0.2 AU in LS 5039) and
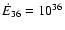 erg s-1 is the pulsar spindown power (taken equal to that measured in PSR B1259-63). The assumed stellar wind has a mass loss rate of
erg s-1 is the pulsar spindown power (taken equal to that measured in PSR B1259-63). The assumed stellar wind has a mass loss rate of
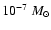 yr-1 and a coasting speed
yr-1 and a coasting speed
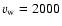 km s-1, appropriate to LS 5039 (C05). The stagnation point in PSR B1259-63 is also at about a tenth of the orbital separation (Tavani et al. 1994). VHE emission in this case can be expected to occur on a small scale compared to the orbital separation, close to the pulsar.
km s-1, appropriate to LS 5039 (C05). The stagnation point in PSR B1259-63 is also at about a tenth of the orbital separation (Tavani et al. 1994). VHE emission in this case can be expected to occur on a small scale compared to the orbital separation, close to the pulsar.
There is no such certainty with a black hole (or neutron star) jet. Jet models for the  -ray emission have been proposed for both LS 5039 and LSI +61
-ray emission have been proposed for both LS 5039 and LSI +61
 303 (Paredes et al. 2005; Bosch-Ramon & Paredes 2004; Romero et al. 2005). Although the gravitational potential energy reservoir that can be tapped is largest close to the black hole, most of the energy may not be radiated there if it is carried by protons or Poynting flux (Sikora et al. 2005). Shocks or reconnection can convert kinetic or electromagnetic energy into radiation progressively over large distances, up to a termination shock with the ISM. There is evidence for X-ray synchrotron emission on parsec scales from high energy electrons in the relativistic jet of XTE J1550-564 (Corbel et al. 2002).
303 (Paredes et al. 2005; Bosch-Ramon & Paredes 2004; Romero et al. 2005). Although the gravitational potential energy reservoir that can be tapped is largest close to the black hole, most of the energy may not be radiated there if it is carried by protons or Poynting flux (Sikora et al. 2005). Shocks or reconnection can convert kinetic or electromagnetic energy into radiation progressively over large distances, up to a termination shock with the ISM. There is evidence for X-ray synchrotron emission on parsec scales from high energy electrons in the relativistic jet of XTE J1550-564 (Corbel et al. 2002).
The change in flux absorption with height above the orbital plane in LS 5039 is shown in Fig. 8. The inclination is 20 and the black hole is at periastron. Absorption decreases to less than 50% at all energies when emission occurs more than
and the black hole is at periastron. Absorption decreases to less than 50% at all energies when emission occurs more than  0.7 AU away from the plane, as discussed in Aharonian et al. (2005b,a) and Böttcher & Dermer (2005). The same calculation for LSI +61
0.7 AU away from the plane, as discussed in Aharonian et al. (2005b,a) and Böttcher & Dermer (2005). The same calculation for LSI +61
 303 yields a distance of
303 yields a distance of  0.1 AU. If VHE emission can be independently linked to a relativistic jet, a lack of temporal or spectral absorption signatures will imply emission at large distances.
0.1 AU. If VHE emission can be independently linked to a relativistic jet, a lack of temporal or spectral absorption signatures will imply emission at large distances.
Unlike TeV blazars, the target photon field here is external to the jet and
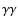 absorption will not be reduced by relativistic aberration. At a given energy, the dependence of the opacity with height is set by the companion light, providing constraints on models as in Blandford & Levinson (1995) where the jet is structured by the
absorption will not be reduced by relativistic aberration. At a given energy, the dependence of the opacity with height is set by the companion light, providing constraints on models as in Blandford & Levinson (1995) where the jet is structured by the  -photosphere.
-photosphere.
The height at which
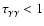 in LS 5039 corresponds to roughly 107 gravitational radii
in LS 5039 corresponds to roughly 107 gravitational radii 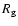 for a stellar mass black hole. In blazars, VHE emission is often proposed to occur in the broad line region at parsec-scales, i.e. about
for a stellar mass black hole. In blazars, VHE emission is often proposed to occur in the broad line region at parsec-scales, i.e. about
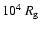 for a
for a
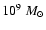 black hole. In the internal shock model, the distance of first interaction is
black hole. In the internal shock model, the distance of first interaction is 
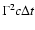 where
where 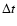 is the observed timescale and
is the observed timescale and 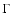 is the typical bulk Lorentz factor of ejecta (Spada et al. 2001). Assuming LS 5039 is a genuine microblazar with scaled-down physics, then
is the typical bulk Lorentz factor of ejecta (Spada et al. 2001). Assuming LS 5039 is a genuine microblazar with scaled-down physics, then 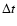 would be reduced with black hole mass. For the given emission distances, the conclusion would be that
would be reduced with black hole mass. For the given emission distances, the conclusion would be that 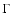 in LS 5039 is at least the same, if not higher than in blazars.
in LS 5039 is at least the same, if not higher than in blazars.
Could ejections in LS 5039 have
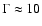 ,
as inferred in blazars from opacity arguments and
,
as inferred in blazars from opacity arguments and  -ray modelling (Ghisellini et al. 1998; Dondi & Ghisellini 1995)? Emission from a jet will be deboosted if viewed at an angle larger than
-ray modelling (Ghisellini et al. 1998; Dondi & Ghisellini 1995)? Emission from a jet will be deboosted if viewed at an angle larger than 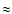 25
25 for
for 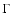 = 10. The system inclination required for a black hole primary is close to this value. In this case, emission from a jet perpendicular to the orbital plane would not be boosted. This might fit with the weak X-ray to
= 10. The system inclination required for a black hole primary is close to this value. In this case, emission from a jet perpendicular to the orbital plane would not be boosted. This might fit with the weak X-ray to  -ray luminosity observed (
-ray luminosity observed (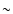 1034 erg s-1). Then, LS 5039 would not be a genuine microblazar with the jet along the line-of-sight.
1034 erg s-1). Then, LS 5039 would not be a genuine microblazar with the jet along the line-of-sight.
Current VLBI radio observations of LS 5039 only indicate a mildly relativistic outflow with 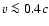 (Paredes et al. 2000). Yet, the Lorentz factors of TeV blazars deduced from
(Paredes et al. 2000). Yet, the Lorentz factors of TeV blazars deduced from
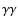 absorption are known to be much greater than those measured at larger distances by VLBI observations (Piner & Edwards 2004). In both cases, there would be a puzzling discrepancy between the high
absorption are known to be much greater than those measured at larger distances by VLBI observations (Piner & Edwards 2004). In both cases, there would be a puzzling discrepancy between the high  inferred from
inferred from  -ray studies and the low
-ray studies and the low  measured on larger scales in radio.
measured on larger scales in radio.
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{4233fi8}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg97.gif) |
Figure 8:
Variation in transmitted flux with height z above the plane in LS 5039. The assumed jet is perpendicular to the orbital plane, the inclination is 20 and the black hole is at periastron. The absorption is shown for 100 GeV and 10 TeV photons. The curve for 1 TeV photons would be indistinguishable from the 100 GeV curve in this plot. VHE photons emitted a few AU away from the black hole suffer little absorption. For comparison purposes, the orbital separation in LS 5039 varies between 0.1 and 0.2 AU.
and the black hole is at periastron. The absorption is shown for 100 GeV and 10 TeV photons. The curve for 1 TeV photons would be indistinguishable from the 100 GeV curve in this plot. VHE photons emitted a few AU away from the black hole suffer little absorption. For comparison purposes, the orbital separation in LS 5039 varies between 0.1 and 0.2 AU. |
| Open with DEXTER |
The
 pairs created by absorption can boost stellar photons to very high energies via inverse Compton interactions. These
pairs created by absorption can boost stellar photons to very high energies via inverse Compton interactions. These  -rays can in turn be absorbed and a cascade follows. The initial pair created by absorption of a 1 TeV photon has a Lorentz factor
-rays can in turn be absorbed and a cascade follows. The initial pair created by absorption of a 1 TeV photon has a Lorentz factor
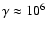 .
In LS 5039, their inverse Compton interaction with stellar photons occurs in the Klein-Nishina regime on a timescale
.
In LS 5039, their inverse Compton interaction with stellar photons occurs in the Klein-Nishina regime on a timescale
![$t_{\rm KN}\approx8\gamma_6 d_{0.1}^2 \left[\ln \gamma_6 +1.2 \right]~{\rm seconds}$](/articles/aa/full/2006/19/aa4233-05/img99.gif) (Blumenthal & Gould 1970), with d0.1 = 0.1 AU. Hence, the typical distance travelled by the pair before a photon is boosted to high energies is small enough compared to the binary size to start a cascade. However, the cascade will be quenched if the pair loses energy preferentially to another emission process that does not re-emit VHE
(Blumenthal & Gould 1970), with d0.1 = 0.1 AU. Hence, the typical distance travelled by the pair before a photon is boosted to high energies is small enough compared to the binary size to start a cascade. However, the cascade will be quenched if the pair loses energy preferentially to another emission process that does not re-emit VHE  -rays (e.g. synchrotron; Aharonian et al. 2005a; Bednarek 1997).
-rays (e.g. synchrotron; Aharonian et al. 2005a; Bednarek 1997).
The cascade reduces the effective
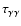 ,
since absorbed
,
since absorbed  -rays are partly re-radiated (at lower energies). If
-rays are partly re-radiated (at lower energies). If
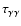 is very high, energy initially radiated in the absorbed band is degraded to frequencies below the pair production threshold (
is very high, energy initially radiated in the absorbed band is degraded to frequencies below the pair production threshold ( 30 GeV in LS 5039). The pile up at these frequencies might account for the luminosity step between the EGRET (GeV energies) and HESS (TeV energies) measurements (see Fig. 1 in Aharonian et al. 2005a). Absorption of a constant spectrum in
30 GeV in LS 5039). The pile up at these frequencies might account for the luminosity step between the EGRET (GeV energies) and HESS (TeV energies) measurements (see Fig. 1 in Aharonian et al. 2005a). Absorption of a constant spectrum in 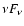 from GeV to TeV energies cannot account for this difference. Such a spectrum would, on average, only be absorbed by a factor 3-10 above 250 GeV (Sect. 3.1) when the luminosity jump is
from GeV to TeV energies cannot account for this difference. Such a spectrum would, on average, only be absorbed by a factor 3-10 above 250 GeV (Sect. 3.1) when the luminosity jump is 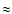 30. Taking into account the photons degraded to lower energies by the cascade would raise the absorption step. Orbital variability would then even be expected at energies below the interaction threshold (
30. Taking into account the photons degraded to lower energies by the cascade would raise the absorption step. Orbital variability would then even be expected at energies below the interaction threshold (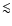 30 GeV, hence in the EGRET or GLAST range), in antiphase with the absorption lightcurves. Bednarek (1997) called this "
30 GeV, hence in the EGRET or GLAST range), in antiphase with the absorption lightcurves. Bednarek (1997) called this " -ray focusing by soft radiation''.
-ray focusing by soft radiation''.
Angular effects must be considered for
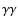 opacities of a few. The estimate of the Klein-Nishina interaction timescale assumes an isotropic photon bath. Just as the
opacities of a few. The estimate of the Klein-Nishina interaction timescale assumes an isotropic photon bath. Just as the
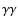 absorption is changed by the geometry, the pair motion with respect to the star will change the inverse Compton opacity. Maximum boost will be achieved for head-on collisions with stellar photons. Because of momentum conservation, the cascade should tend to develop along the direction where the initial photon was emitted. However, the cascade is effectively isotropized as the gyroradius is small compared to the interaction length (Bednarek 1997). Radiation can then be redistributed at other orbital phases.
absorption is changed by the geometry, the pair motion with respect to the star will change the inverse Compton opacity. Maximum boost will be achieved for head-on collisions with stellar photons. Because of momentum conservation, the cascade should tend to develop along the direction where the initial photon was emitted. However, the cascade is effectively isotropized as the gyroradius is small compared to the interaction length (Bednarek 1997). Radiation can then be redistributed at other orbital phases.
A quantitative description of these effects is feasible by Monte-Carlo methods (Sierpowska & Bednarek 2005; Bednarek 2000,1997) but is beyond the scope of this work. A model of the intrinsic spectrum should be considered before doing this. Cascades will probably be important only when the
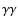 opacity is high and the source behind the star in the plane of the sky. This ensures maximum energy boost and maximum density of stellar photons along the initial development of the cascade. This is the case at periastron in LS 5039 but not in LSI +61
opacity is high and the source behind the star in the plane of the sky. This ensures maximum energy boost and maximum density of stellar photons along the initial development of the cascade. This is the case at periastron in LS 5039 but not in LSI +61
 303 (source close to front of the star at maximum absorption) and even less in PSR B1259-63 (low
303 (source close to front of the star at maximum absorption) and even less in PSR B1259-63 (low
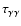 ). The amplitude of flux variations will be smaller, though perhaps not noticeably so on a linear scale and with energy thresholds
). The amplitude of flux variations will be smaller, though perhaps not noticeably so on a linear scale and with energy thresholds 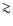 100 GeV, which are usually at or above the energy of maximum absorption (e.g. compare the Cen X-3 lightcurves above 300 GeV with and without cascade in Bednarek 2000). The absorption spectrum around periastron will be softened. The changes will be small when
100 GeV, which are usually at or above the energy of maximum absorption (e.g. compare the Cen X-3 lightcurves above 300 GeV with and without cascade in Bednarek 2000). The absorption spectrum around periastron will be softened. The changes will be small when
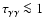 .
Qualitative differences in absorption at TeV energies for a neutron star or black hole case should therefore remain.
.
Qualitative differences in absorption at TeV energies for a neutron star or black hole case should therefore remain.
The intense stellar radiation field in massive X-ray binaries provides a novel way of investigating very high energy processes around compact objects. Because of the dependence of the
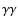 cross-section on angle, the anisotropy of the field has a strong effect on the opacity to very high energy
cross-section on angle, the anisotropy of the field has a strong effect on the opacity to very high energy  -rays
-rays 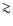 10 GeV. The orbital orientation to the observer and location of emission are crucial in determining the absorption. In PSR B1259-63 this leads to significant absorption before periastron, although the pulsar is >
10 GeV. The orbital orientation to the observer and location of emission are crucial in determining the absorption. In PSR B1259-63 this leads to significant absorption before periastron, although the pulsar is >
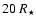 from its stellar companion.
from its stellar companion.
The changing radiation field modulates the gamma-rays in a predictable fashion. The result is a controlled, repeatable experiment that can help pinpoint the location of emission. Comparing the predictions to observations is essential to single out the variability at the source from that due to absorption in the binary. In LS 5039, the binary separation is only 2-4 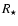 yet absorption can be much smaller than implied by simple estimates. Indeed, absorption of
yet absorption can be much smaller than implied by simple estimates. Indeed, absorption of  -rays emitted close to a neutron star (implying a high inclination) is negligible at inferior conjunction. The spectrum above 1 TeV is considerably hardened near periastron in LS 5039 and LSI +61
-rays emitted close to a neutron star (implying a high inclination) is negligible at inferior conjunction. The spectrum above 1 TeV is considerably hardened near periastron in LS 5039 and LSI +61
 303. LSI +61
303. LSI +61
 303 is largely absorption-free which should ease its detection at high energies by MAGIC or VERITAS, if similar processes are at work in both sources.
303 is largely absorption-free which should ease its detection at high energies by MAGIC or VERITAS, if similar processes are at work in both sources.
The detection of an orbital modulation of the TeV flux in LS 5039 would imply emission within the system, either from a pulsar wind termination shock or from the inner region of a jet. If the primary is a black hole, the inclination will be 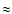 20
20 and the absorption spectrum has a break at
and the absorption spectrum has a break at 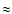 400 GeV with limited orbital spectral changes. For a neutron star, the inclination is
400 GeV with limited orbital spectral changes. For a neutron star, the inclination is 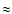 60
60 and the break is expected to change from 0.2 to 2 TeV from low to high fluxes. The absence of orbital variations or spectral signatures in VHE observations of LS 5039 would suggest emission occurring in regions of low
and the break is expected to change from 0.2 to 2 TeV from low to high fluxes. The absence of orbital variations or spectral signatures in VHE observations of LS 5039 would suggest emission occurring in regions of low
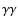 opacity. Jet emission at large distances compared to the system scale would be the prime candidate.
opacity. Jet emission at large distances compared to the system scale would be the prime candidate.
Acknowledgements
I thank B. Giebel, P. Bruel, J.-P. Lasota, V. Bosch-Ramon and M. Ribo for their helpful comments on this work and the organisers of the KITP "Physics of Astrophysical Outflows and Accretion Disks'' program where part of this work was completed. This research was supported in part by NSF grant No. PHY99-07949.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{4233fi9}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg103.gif) |
Figure A.1:
Geometry for absorption of a  -ray at a location P due to -ray at a location P due to
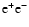 pair creation with stellar photons emitted at S. The pair creation with stellar photons emitted at S. The  -ray is emitted at I and l is the length of the -ray is emitted at I and l is the length of the  -ray path to P. The (x, z) plane is defined by the star center and -ray path to P. The (x, z) plane is defined by the star center and  -ray path. -ray path. |
The differential absorption opacity seen by a  -ray of energy E located at a position P and travelling in the direction
-ray of energy E located at a position P and travelling in the direction
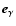 due to photons of energy
due to photons of energy 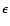 emitted at S along
emitted at S along
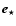 is (Gould & Schréder 1967)
is (Gould & Schréder 1967)
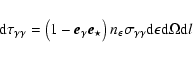 |
(A.1) |
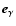 and
and
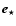 are unit vectors in the directions of propagation;
are unit vectors in the directions of propagation;
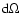 is the solid angle of the surface emitting the
is the solid angle of the surface emitting the
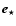 photons;
photons;
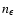 is the radiation density in photons cm-3 erg-1 sr-1.
is the radiation density in photons cm-3 erg-1 sr-1.
The
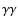 interaction cross-section
interaction cross-section
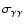 depends only on s, defined as (Gould & Schréder 1967)
depends only on s, defined as (Gould & Schréder 1967)
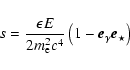 |
(A.2) |
and the photons interact only if s>1. The variable s can be rewritten as s =
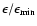 where
where
 is the threshold for interaction at
is the threshold for interaction at  -ray energy E (Eq. (1)).
-ray energy E (Eq. (1)).
The massive star dominates the radiative output in LS 5039, LSI +61
 303 and PSR B1259-63 so that any other source of radiation for pair-production with TeV
303 and PSR B1259-63 so that any other source of radiation for pair-production with TeV  -rays is neglected. The star has a radius
-rays is neglected. The star has a radius 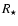 and is assumed to have a blackbody radiation density with a temperature
and is assumed to have a blackbody radiation density with a temperature 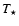
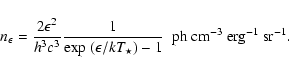 |
(A.3) |
Orienting the coordinate system so that the  -ray path is in the (x, z) plane (Fig. A.1), then the location and direction of the
-ray path is in the (x, z) plane (Fig. A.1), then the location and direction of the  -ray are given by the angle
-ray are given by the angle 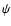 and distance d to the star center and
and distance d to the star center and
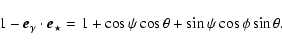 |
(A.4) |
The solid angle of the star surface element emitting photons along
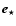 is
is
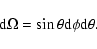 |
(A.5) |
The length l of the  -ray path since its emission at a distance d0 and at an angle
-ray path since its emission at a distance d0 and at an angle 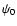 (point I in Fig. A.1 with
(point I in Fig. A.1 with 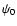 = 0 for a
= 0 for a  -ray travelling directly towards the center) is related to
-ray travelling directly towards the center) is related to 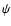 so that:
so that:
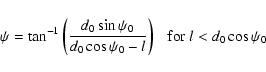 |
(A.6) |
and
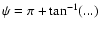 for
for
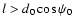 .
The distance d is related to l by
.
The distance d is related to l by
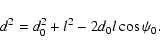 |
(A.7) |
The dependence of the differencial opacity
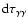 on E,
on E, 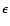 ,
,
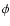 ,
,
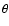 and l is now explicit. The total opacity to infinity for a
and l is now explicit. The total opacity to infinity for a  -ray of given energy E and initial location requires a quadruple integral:
-ray of given energy E and initial location requires a quadruple integral:
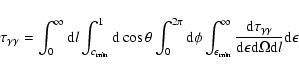 |
(A.8) |
where
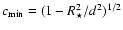 .
It is convenient to rewrite the energy integral as a definite integral on
.
It is convenient to rewrite the energy integral as a definite integral on
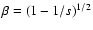 within the interval [0,1]. Similarly, the integral on l can be transformed into a definite integral on
within the interval [0,1]. Similarly, the integral on l can be transformed into a definite integral on 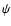 between
between
![$[\psi_0,\pi]$](/articles/aa/full/2006/19/aa4233-05/img124.gif) with the condition
with the condition
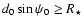 (or the
(or the  -ray hits the star). An iterated Gaussian quadrature is used to calculate the integral.
-ray hits the star). An iterated Gaussian quadrature is used to calculate the integral.
When
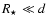 ,
an integration of Eq. (A.8) over
,
an integration of Eq. (A.8) over 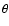 and
and 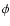 returns the point source approximation
returns the point source approximation
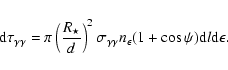 |
(A.9) |
The threshold is
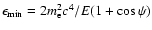 .
Numerical comparisons show the approximation works reasonably well except for
.
Numerical comparisons show the approximation works reasonably well except for
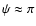 (Fig. A.2) or when
(Fig. A.2) or when
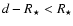 at closest approach. The full calculation is then preferable. The results presented here were derived using the exact calculation.
at closest approach. The full calculation is then preferable. The results presented here were derived using the exact calculation.
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{4233fi10}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg133.gif) |
Figure A.2:
For a  -ray emitted directly away from the star ( -ray emitted directly away from the star (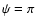 ), the point source approximation (Eq. (A.9)) predicts no absorption. The exact transmitted flux exp ), the point source approximation (Eq. (A.9)) predicts no absorption. The exact transmitted flux exp
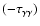 ,
calculated using Eq. (A.8) is shown here for a 1 TeV ,
calculated using Eq. (A.8) is shown here for a 1 TeV  -ray as a function of the distance of its emission point ( -ray as a function of the distance of its emission point (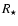 = 10 = 10 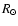 , ,
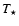 = 40 000 K). Because of the star's finite size, there is absorption even for = 40 000 K). Because of the star's finite size, there is absorption even for 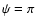 when the
when the  -ray is at distances -ray is at distances
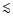 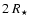 . . |
Assuming emission close to the compact object, the initial distance d0 of the  -ray to the star is simply
-ray to the star is simply
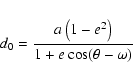 |
(A.10) |
with the semi-major axis
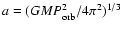 (M is the total mass), e the eccentricity,
(M is the total mass), e the eccentricity, 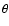 the true anomaly and
the true anomaly and 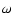 the periastron angle. The orbital phase (mean anomaly) is
the periastron angle. The orbital phase (mean anomaly) is
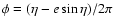 where
where 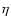 is the eccentric anomaly with
is the eccentric anomaly with
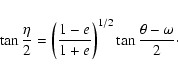 |
(A.11) |
The angle 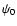 of emission to the observer (located at
of emission to the observer (located at 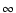 )
measured from the star, at each point of the orbit (Fig. A.1) is
)
measured from the star, at each point of the orbit (Fig. A.1) is
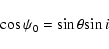 |
(A.12) |
where i is the inclination of the orbit. If emission occurs at a height z above the location of the compact object and perpendicular to the orbital plane (as in Fig. 8), then the initial distance to the star simply becomes
d=(d02+z2)1/2 and the initial angle is changed to
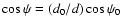 (with d0 and
(with d0 and 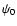 given above).
given above).
- Aharonian,
F. A., Anchordoqui, L. A., Khangulyan, D., &
Montaruli, T. 2005a [arXiv:astro-ph/0508658]
- Aharonian,
F. A., Akhperjanian, A. G., Aye, K. M., et al. 2005b,
Science, 309, 746 [NASA ADS] [CrossRef] (In the text)
- Aharonian, F. A.,
Akhperjanian, A. G., Aye, K. M., et al. 2005c, A&A, 442,
1 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Bednarek, W.
2000, A&A, 362, 646 [NASA ADS]
- Bednarek, W.
1997, A&A, 322, 523 [NASA ADS]
- Blandford,
R. D., & Levinson, A. 1995, ApJ, 441, 79 [NASA ADS] [CrossRef] (In the text)
- Blumenthal, G. R., &
Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] (In the text)
-
Bosch-Ramon, V., & Paredes, J. M. 2004, A&A, 425,
1069 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Böttcher, M.,
& Dermer, C. D. 2005, ApJ, 634, L81 [NASA ADS] [CrossRef] (In the text)
- Casares, J., Ribo,
M., Ribas, I., et al. 2005a, MNRAS, 364, 899 [NASA ADS] [CrossRef] (C05)
(In the text)
- Casares, J., Ribas,
I., Paredes, J. M., Martí, J., & Allende Prieto,
C. 2005b, MNRAS, 360, 1105 [NASA ADS] [CrossRef] (In the text)
- Corbel, S., Fender,
R. P., Tzioumis, A. K., et al. 2002, Science, 298,
196 [NASA ADS] [CrossRef] (In the text)
- Dondi, L., &
Ghisellini, G. 1995, MNRAS, 273, 583 [NASA ADS]
- Ghisellini, G.,
Celotti, A., Fossati, G., Maraschi, L., & Comastri, A. 1998,
MNRAS, 301, 451 [NASA ADS] [CrossRef]
- Gould, R. J., &
Schréder, G. P. 1967, Phys. Rev., 155, 1404 [NASA ADS] [CrossRef] (In the text)
- Gregory, P. C.,
Peracaula, M., & Taylor, A. R. 1999, ApJ, 520, 376 [NASA ADS] [CrossRef]
- Johnston, S.,
Manchester, R. N., Lyne, A. G., Nicastro, L., &
Spyromilio, J. 1994, MNRAS, 268, 430 [NASA ADS] (In the text)
- Kirk, J. G., Ball, L.,
& Skjaeraasen, O. 1999, Astroparticle Physics, 10, 31 [NASA ADS] [CrossRef] (In the text)
- McSwain, M. V.,
Gies, D. R., Huang, W., et al. 2004, ApJ, 600, 927 [NASA ADS] [CrossRef] (In the text)
- Maraschi, L., &
Treves, A. 1981, MNRAS, 194, 1 [NASA ADS]
- Moskalenko,
I. V. 1995, Space Sci. Rev., 72, 593 [NASA ADS] [CrossRef]
- Paredes, J. M.,
Martí, J., Ribó, M., & Massi, M. 2000, Science, 288,
2340 [NASA ADS] [CrossRef] (In the text)
- Paredes, J. M.,
Bosch-Ramon, V., & Romero, G. E. 2005, A&A, submitted
[arXiv:astro-ph/0509095]
- Piner, B. G., &
Edwards, P. G. 2004, ApJ, 600, 115 [NASA ADS] [CrossRef] (In the text)
- Protheroe,
R. J., & Stanev, T. 1987, ApJ, 322, 838 [NASA ADS] [CrossRef]
- Romero, G. E.,
Christiansen, H. R., & Orellana, M. 2005, ApJ, 632,
1093 [NASA ADS] [CrossRef] (In the text)
- Sierpowska, A.,
& Bednarek, W. 2005, MNRAS, 356, 711 [NASA ADS] [CrossRef]
- Sikora, M., Begelman,
M. C., Madejski, G. M., & Lasota, J.-P. 2005, ApJ,
625, 72 [NASA ADS] [CrossRef] (In the text)
- Spada, M., Ghisellini,
G., Lazzati, D., & Celotti, A. 2001, MNRAS, 325, 1559 [NASA ADS] [CrossRef] (In the text)
- Stecker, F. W.,
de Jager, O. C., & Salamon, M. H. 1992, ApJ, 390,
L49 [NASA ADS] [CrossRef] (In the text)
- Tavani, M., Arons, J.,
& Kaspi, V. M. 1994, ApJ, 433, L37 [NASA ADS] [CrossRef] (In the text)
- Weekes, T. C.
1992, Space Sci. Rev., 59, 315 [NASA ADS] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=15.25cm,clip]{4233fi1}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg30.gif)
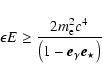
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{4233fi2a}\vspace*{5mm}
\includegraphics[width=7.55cm,clip]{4233fi2b}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg54.gif)
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{4233fi3}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg55.gif)
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{4233fi4a}\vspace*{5mm}
\includegraphics[width=7.35cm,clip]{4233fi4b}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg56.gif)
![\begin{figure}
\par\includegraphics[width=7.55cm,clip]{4233fi5a}\vspace*{5mm}
\includegraphics[width=7.55cm,clip]{4233fi5b}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg72.gif)
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{4233fi6}
\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg73.gif)
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{4233fi7}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg74.gif)
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{4233fi8}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg97.gif)
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{4233fi9}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg103.gif)
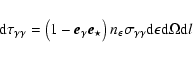
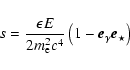
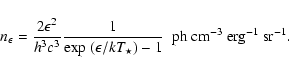
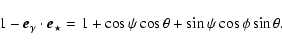
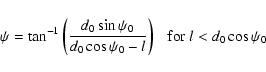
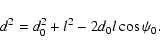
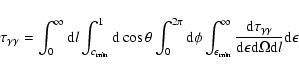
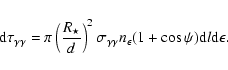
![\begin{figure}
\par\includegraphics[width=7.35cm,clip]{4233fi10}\end{figure}](/articles/aa/full/2006/19/aa4233-05/Timg133.gif)