A&A 451, 319-330 (2006)
DOI: 10.1051/0004-6361:20054171

Evolution of magnetic fields and energetics of flares in active region 8210

S. Régnier1,[*] - R. C. Canfield 2


1 - ESA Research and Scientific Support Department, SCI-SH, Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
2 - Montana State University, Physics Dept., 264 EPS Building, Bozeman, MT 59717, USA

Received 7 September 2005 / Accepted 30 January 2006

Abstract
To better understand eruptive events in the solar corona, we combine sequences of multi-wavelength observations and modelling of the coronal magnetic field of NOAA AR 8210, a highly flare-productive active region. From the photosphere to the corona, the observations give us information about the motion of magnetic elements (photospheric magnetograms), the location of flares (e.g., H$\alpha $, EUV or soft X-ray brightenings), and the type of events (H$\alpha $ blueshift events). Assuming that the evolution of the coronal magnetic field above an active region can be described by successive equilibria, we follow in time the magnetic changes of the 3D nonlinear force-free (nlff) fields reconstructed from a time series of photospheric vector magnetograms. We apply this method to AR 8210 observed on May 1, 1998 between 17:00 UT and 21:40 UT. We identify two types of horizontal photospheric motions that can drive an eruption: a clockwise rotation of the sunspot, and a fast motion of an emerging polarity. The reconstructed nlff coronal fields give us a scenario of the confined flares observed in AR 8210: the slow sunspot rotation enables the occurence of flare by a reconnection process close to a separatrix surface whereas the fast motion is associated with small-scale reconnections but no detectable flaring activity. We also study the injection rates of magnetic energy, Poynting flux and relative magnetic helicity through the photosphere and into the corona. The injection of magnetic energy by transverse photospheric motions is found to be correlated with the storage of energy in the corona and then the release by flaring activity. The magnetic helicity derived from the magnetic field and the vector potential of the nlff configuration is computed in the coronal volume. The magnetic helicity evolution shows that AR 8210 is dominated by the mutual helicity between the closed and potential fields and not by the self helicity of the closed field which characterizes the twist of confined flux bundles. We conclude that for AR 8210 the complex topology is a more important factor than the twist in the eruption process.

Key words: Sun: magnetic fields - Sun: flares - Sun: corona - Sun: evolution

1 Introduction

The structure of the Sun's corona is dominated by its magnetic field. To understand eruptive events (flares, coronal mass ejections (CMEs) or filament eruptions), we need to know the evolution of the 3D magnetic configuration (geometry and topology) of the corona. In this study, we combine observations of the solar atmosphere at various heights with models of the coronal magnetic field to determine the sources of flaring activity and the time changes of an active region before and after a flare. We focus our study on a five-hour period which is particularly interesting because (i) it precedes a major flare/CME event and (ii) it is well observed with vector magnetograms.

Most flare models (see review by Priest & Forbes 2002; Lin et al. 2003) involve magnetic reconnection processes to explain the rapid conversion of magnetic energy into kinetic energy and thermal energy (hard X-ray sources, soft X-ray flux, brightening in hot EUV lines or in H$\alpha $). In the classical CSHKP model (Hirayama 1974; Kopp & Pneuman 1976; Carmichael 1964; Sturrock 1968), the reconnection process occurs at the location of an X point in 2D, or at the location of a null point or a separator field line in 3D. In 3D topology (see Priest & Forbes 2000), the reconnection processes involved in flares do not occur only in the vicinity of a null point but can also be associated with other topological elements (e.g., fan surfaces, spine field lines). The study of the topology of coronal magnetic fields should help us to answer important questions for the energetics of flares, including (i) how is magnetic energy stored before the eruption? (ii) Is the stored magnetic energy enough to power a flare or a CME? Question (i) can be tackled by following the time evolution of the magnetic energy injected through the photosphere, and the free magnetic energy available in the corona. To answer question (ii), we need to understand the temporal and spatial relationship between observed brightenings and magnetic field changes in the corona.

Table 1: Photospheric, chromospheric and coronal observations of AR 8210 on May 1, 1998. $\Delta x$ is the pixel size, $\Delta t$ is the time between two consecutive observations.

The injection of magnetic energy into the corona through the photosphere is considered to be associated with the horizontal displacement of magnetic features on the photosphere: emergence (Nindos & Zhang 2002; Schmieder et al. 1997; Kusano et al. 2002; Ishii et al. 1998) and cancellation (Fletcher et al. 2001; Livi et al. 1989) of magnetic flux, rotation of sunspots (Lin & Chen 1989; Nightingale et al. 2002; Kucera 1982), and moving magnetic features (Moon et al. 2002; Zhang & Wang 2001). The velocity fields can be detrmined using the white light images (Nightingale et al. 2002) or by estimating the small displacements from a Local Correlation Tracking (LCT) technique (November & Simon 1988). Recently several more powerful techniques have been developed to retrieve the full photospheric velocity field from vector magnetograms (Longcope 2004; Welsch et al. 2004; Georgoulis & LaBonte 2006).

In our study, the coronal magnetic field is assumed to be in a force-free equilibrium state at the time of observation. Therefore if the photospheric distribution of vertical electric current density is known in addition to the vertical magnetic field (Sakurai 1982), the nonlinear force-free field (nlff) can be extrapolated in the corona (e.g., Mikic & McClymont 1994; Amari et al. 1997; Wheatland et al. 2000; Yan & Sakurai 2000; Wiegelmann 2004). Inside nlff magnetic configurations, a more realistic distribution of twist and shear can be considered in comparison to other assumptions commonly used to extrapolate the coronal magnetic field (potential, linear force-free fields). These nlff extrapolation methods were applied to solar active regions using one snapshot of the magnetic field (e.g., Yan & Wang 1995; Régnier et al. 2002; Bleybel et al. 2002; Régnier & Amari 2004). Here we propose to study the time evolution of an active region considering that it can be described by succesive nonlinear force-free equilibria. This assumption is justified by considering that the evolution of the active region is sufficiently slow which means that the photospheric velocities of the footpoints are small compared to characteristic speeds in the corona, such as the Alfvén velocity (Antiochos 1987).


  \begin{figure} \par\includegraphics[width=7cm,clip]{4171fg1.eps} \end{figure} Figure 1: X-ray flux measured by GOES-8 in the wavelength range 0.05-0.4 nm. Gray areas are the flaring periods. The rise (resp. decay) phase of flares are the dark (resp. light) gray areas as defined in Sect. 3.1.
Open with DEXTER

Using the above methods to estimate the velocity fields on the photosphere and the 3D coronal magnetic field, we can estimate the rate of magnetic energy injected into the corona by photospheric motions and where this energy is deposited or released in the corona. We can also derive the magnetic helicity and its evolution to understand the effects of reconnection on the connectivity of field lines. In this work, we have selected the active region 8210 (AR 8210) observed on May 1, 1998 between 17:00 UT and 21:40 UT for which we have a good set of data covering the photosphere, the chromosphere and the corona as well as a high-cadence vector magnetic field observations of good quality. AR 8210 is a well studied active region for its flaring activity on May 1st and May 2nd (Sterling & Moore 2001b; Wang et al. 2002; Pohjolainen et al. 2001; Sterling & Moore 2001a; Xia et al. 2001; Sterling et al. 2001; Warmuth et al. 2000; Thompson et al. 2000). We focus our attention on the time period shown in Fig. 1 by the evolution of the X-ray flux. We first give an overview of the AR 8210 data (see Sect. 2) we use to analyse the precursors or signatures of flaring activity (Sect. 3): X-ray flux, H$\alpha $ blueshift events (BSEs), photospheric velocity fields. In Sect. 4, we describe how to determine and analyse the 3D magnetic field of AR 8210. We then give a scenario of the magnetic field evolution during the flaring period (Sect. 5). The magnetic energy and helicity budgets are derived in Sects. 6 and 7. In Sect. 8, we discuss the implications of those processes for flaring activity and solar eruptions.


  \begin{figure} \par\mbox{\includegraphics[width=8.5cm,clip]{4171fg2a.eps}\hspace... ...ps}\hspace{4mm} \includegraphics[width=8.5cm,clip]{4171fg2d.eps} }\end{figure} Figure 2: Images of AR8210: magnetic field ( top left), H$\alpha $ ( top right), FeXII at 19.5 nm ( bottom left) and soft X-ray ( bottom right) images. We label characteristic polarities on the SOHO/MDI magnetogram (see Sect. 2.1). The strength of Bz ranges from -2500 G to 1400 G. We label the flare sites (A, B, F) as described in Sect. 3.2. Line segments in lower figures roughly indicate the position of the separatrix surfaces that we deduce directly from the EUV and soft X-ray observations.
Open with DEXTER

   
2 Data

In Table 1, we summarize the observations on May 1, 1998 we are using in this study. Between 17:00 UT and 23:00 UT, we have photospheric line-of-sight and vector magnetograms, chromospheric images and spectra, and coronal images. Those data guide the analysis presented in later sections.

   
2.1 Photospheric magnetic field

SOHO/MDI (Michelson Doppler Imager, Scherrer et al. 1995) measures the line-of-sight magnetic field strength deduced from the Zeeman splitting of the Ni I 676.8 nm line. During the period of observation, we have 1 min cadence full-disc magnetograms which allow us to study the dynamics of photospheric magnetic features. The measurement uncertainty is $\sim$20 G. In Fig. 2 top left, we have the distribution of the longitudinal magnetic field at 20:10 UT in a field-of-view of  $600''\times600''$. Basically AR 8210 is a sunspot complex of negative polarity (polarity N1) surrounded by positive polarities (P1-4). AR 8210 also includes parasitic polarities such as N2, which is a new emerged and moving negative polarity.

IVM at MSO (Imaging Vector Magnetograph/Mees Solar Observatory, Mickey et al. 1996) is a vector magnetograph measuring the full Stokes profiles of the Fe I 630.25 nm line. The four Stokes parameters, I = (I, Q, U, V), are measured inside a field-of-view of $256\times 256$ pixels with a pixel size of 1.1 $^{\prime\prime}$ square. The vector magnetograms are built with a series of 30 polarisation images obtained over 3 min (Mickey et al. 1996). To increase the signal-to-noise ratio and to suppress the effects of photospheric oscillations, we average the Stokes profiles over 15 min. In the reduction process, we take into account the cross-talk between the I and V profiles as well as scattered light using daily off-limb measurements. A detailed reduction scheme is given by LaBonte et al. (1999). To infer the magnetic field, the inversion code follows the radiative transfer of line profiles as in Landolfi & Degl'innocenti (1982) based on Unno (1956) equations and including magneto-optical effects. We then obtain the magnetic field: $B_{\rm los}$ along the line-of-sight, $B_{\rm trans}$ and $\chi$ the strength and the azimuthal angle of the transverse components (in the plane perpendicular to the line-of-sight). We perform the transformation into the disc-center heliographic system of coordinates and resolve the 180$^{\circ}$ ambiguity existing on the transverse field following Canfield et al. (1993). The resulting magnetic field in a Cartesian frame is ( Bx, By, Bz).


  \begin{figure} \par\includegraphics[width=8.2cm,clip]{4171fg3.eps} \end{figure} Figure 3: Unsigned magnetic flux for the IVM time series and the associated errors (unit of 1022 G cm2). Gray areas are the flaring periods as defined in Fig. 1.
Open with DEXTER

We have performed an analysis of the noise level for the vertical and the transverse components of the magnetic field on each of the 15 averaged magnetograms. We proceed as follows: for the vertical magnetic field we plot the distribution which can be fitted with a Gaussian profile, for the transverse field we fit the distribution with a $\chi^2$ distribution. In both cases, the estimated error is defined as the 3$\sigma$ value associated with the width ($\sigma$) of the fitted distribution (see Leka & Skumanich 1999; Leka 1999). In Fig. 3, we plot the time evolution of the photospheric unsigned magnetic flux as well as the associated errors (from the 3$\sigma$ errors on the Bz component) to show the quality of the data. The estimated formal errors on Bz range between 25 and 50 G. We observe that the variation of the magnetic flux does not exceed 10% and the errors are of 2% of the total flux. The estimated errors on the transverse components range between 40 and 90 G. By averaging the vector magnetograms over 15 min, we reduce significantly the noise. For a single magnetogram, the formal errors are $\sim$150 G or greater (see e.g. Leka & Skumanich 1999). The net magnetic flux which characterizes the imbalance of positive and negative flux is less than 15% for the IVM data, with an excess of negative flux. For the computation of the nonlinear force-free equilibria we do not take into account pixels below the estimated errors on the vertical and transverse components. Therefore the area that we consider for the computation is different from one time to another. In Fig. 4, we plot Bz in the IVM field-of-view (background image) for AR 8210 as well as the black contour representating the area of pixels used for the computation for 3 examples: typical thresholds (left), large threshold value in the transverse components (center) and large threshold value in the vertical component (right). As shown in Fig. 4, the area of valid pixels is enclosed in the black contour and the variation of area from one time to another is not significant.


  \begin{figure} \par\mbox{\includegraphics[width=2.5cm,clip]{4171fg4a.eps}\hspace... ...s}\hspace*{6mm} \includegraphics[width=2.5cm,clip]{4171fg4c.eps} }\end{figure} Figure 4: Areas inside the black contour for which the vertical component and the transverse components are above the thresholds [Bz, Bt]: at 17:13 UT ( left) with a threshold of [25 G, 46 G], at 18:01 UT ( center) with a threshold of [30 G, 90 G], and at 21:29 UT ( right) with a threshold of [55 G, 75 G].
Open with DEXTER

2.2 Chromospheric data

We use a time series of Big Bear Solar Observatory H$\alpha $ images to observe the reponse of the chromosphere to flaring activities of AR 8210 and its surroundings. Each image observed every 1 min has a field-of-view of $\sim$ $7\hbox{$^\prime$ }\times 7\hbox{$^\prime$ }$ with a pixel size of 1 $^{\prime\prime}$. In Fig. 2 top right observed on may 1, 1998 at 20:10 UT, we observed strong absorption features such as the sunspot and filaments in the neighborhood of the active region, and bright regions (plages) associated with weak magnetic field areas of the active region.In this H$\alpha $ image, we label the flare sites: A (East part of the sunspot), B (South-East positive polarity) and F (large area including A and B). The flare sites are identified by strong intensity enhancement in the BBSO images and/or by emission profiles as observed in the MCCD data.

We obtain H$\alpha $ spectroscopic data from the Mees Solar Observatory CCD (MCCD) imaging spectrograph (Penn et al. 1991). The MCCD scans were made with its standard H$\alpha $ flare setup: spectrograph camera spatial scan field of view $\sim$ $3\hbox{$^\prime$ }\times 4\hbox{$^\prime$ }$, $2\hbox{$.\!\!^{\prime\prime}$ }4$ pixels, 1.87 nm spectral range (sampled with 50 pixels), completing one scan and one H$\alpha $ monitor image each 15 s. The most important derived parameter for this study is Doppler velocity, determined from the shift of the H$\alpha $ line center (see e.g. Canfield & Reardon 1998; Des Jardins & Canfield 2003). To maximize our Doppler-velocity sensitivity, we apply to the spectra Fourier filtering, interpolation, and padding with zeros at the Nyquist frequency. We then fit the core of the H$\alpha $ line profile with a parabola. From the shifts of the minima of the fitted profiles of each pixel, we construct Doppler velocity maps; from the intensity of the minima of each profile, we construct line-center spectroheliograms. In Fig. 5, we have an example of a line center H$\alpha $ image (left) and a velocity map (right) obtained by the MCCD spectroheliograph on May 1, 1998 at 20:15:35 UT. The velocity maps are used to determine the location of blueshift events (BSEs, see Sect. 3.2). As for the BBSO image (Fig. 2 top right), we label the sites of flares as A, B and F.

2.3 EUV and soft X-ray corona

In the corona, we have access to several sets of data. The primary source of data on May 1, 1998 is the high-cadence full-disc images recorded by SOHO/EIT (Delaboudinière et al. 1995) for the Fe XII 19.5 nm line (see Table 1). We also have a time series of Yohkoh/SXT (Tsuneta et al. 1991) images recorded between 17:16 and 22:16 UT with an average time sampling of 8 min. The soft X-ray images are composite images which combine long exposure time satured images and short exposure time images. Those images are useful to have a tomography of the active region in the corona.

In Fig. 2 bottom, we highlight the coronal topology of AR 8210 which is derived from the EUV (left) and soft X-ray (right) observations: the line segments represent approximate locations of "separatrix surfaces'' dividing the active region in several connectivity domains.

  \begin{figure} \par\mbox{\includegraphics[width=4cm,clip]{4171fg5a.eps}\hspace*{4mm} \includegraphics[width=4cm,clip]{4171fg5b.eps} }\end{figure} Figure 5: Left: MCCD H$\alpha $ spectroheliogram at line center for AR 8210 at 20:15:35 UT. The sunspot, the filaments and the plages are easily identified. Right: the associated velocity map. Black (resp. white) velocities represent blueshifts (resp. redshifts). We label the flare sites (A, B, F) as described in Sect. 3.2.
Open with DEXTER

   
3 Observed flaring activity

   
3.1 X-ray flux

The X-ray flux measured by GOES-8 (see Fig. 1) shows that between 17:00 UT and 21:40 UT on May 1, there are three periods of flaring activity in AR 8210:

(1)
17:32-18:40: three consecutive flares are observed; two C-class flares and one B-class flare: a C 2.1 flare with a rise phase from 17:32 to 17:36 and a decay phase from 17:36 to >17:40, a C 2.1 flare with a rise phase from 17:40 to 17:43 and a decay phase from 17:43 to >17:51, a B9.5 flare with a rise phase from 17:51 to 17:58 and a decay phase from 17:58 to 18:40;
(2)
20:09-20:40: two consecutive flares are observed; a C 2.1 flare with a rise phase from 20:09 to 20:13 and a decay phase from 20:13 to >20:25 and a C 2.8 flare with a rise phase from 20:25 to 20:29 and a decay phase from 20:29 to 20:40;
(3)
21:15-21:35: a C 1.2 flare with a rise phase from 21:15 to 21:23 and a decay phase from 21:23 to 21:35.
(the flare classification is deduced from the X-ray flux in the 0.1-0.8 nm wavelength band). We will refer to "quiet periods'' for periods outside the above flaring activity. The EUV and X-ray full-disc images allow us to identify the sources of these activity periods in AR 8210.

   
3.2 H$\alpha $ events

Using both MCCD spectrograms and BBSO images, we first identify in the time series the locations of flare activity as indicated on the H$\alpha $ image (see Fig. 2 top right and Fig. 5 left). We observe that the H$\alpha $ intensity peaks are located at sites A and B for the event (1), at site B for the C 2.1 flare of event (2), in the large area F including sites A and B for the C 2.8 flare of event (2) and at site B for the event (3). Note that the sites A and B correspond to the areas of intensity enhancement and not simply to the peak of intensity.

Table 2: List of blueshift events (BSE) observed in AR 8210 from MCCD H$\alpha $ observations. The flare locations (A, B and F) are described in Fig. 5.

The velocity maps (see Fig. 5 right) obtained from MCCD data are used to locate BSEs in AR 8210. BSEs are often observed before or after flares in the H$\alpha $ line. Canfield & Reardon (1998) have observed BSEs with a high temporal cadence and with high spatial resolution. The authors have concluded that BSEs are related to the occurence of eruptive phenomena and are certainly the chromospheric signatures of reconnection processes in the corona. Recently, Des Jardins & Canfield (2003) have performed a statistical study of BSEs. The authors have shown that the rate of BSEs increases between 1 and 2 h before an eruptive flare (>C 6 class flares) and that there is a significant drop of the number of BSEs after flares. In Table 2, we report on 8 periods of BSEs for which we specify the start time, the time of the maximum velocity and the end time as well as the location and the relationship with the flaring activity. It appears that BSEs are at the same location as the flares (see labels in Fig. 2). The BSEs 1 and 2 occur before the flare period (1) on site A. The BSEs 3, 4, and 7 are observed during the decay phase of the three C 2.1 flares on site A. The BSE 5 is related to the rise phase of the B-class flare. The BSE 6 occurs during a time period for which no significant change of X-ray flux is observed. The BSE 8 covers the period before and after the C 2.8 flare on site F. We can already conclude that BSEs are preferentially observed after a flare at the flare site and that the duration of these events is between 5 min and 10 min.

   
3.3 Photospheric motions

To study the global evolution of the magnetic field on the photosphere, we use the long-term movie made with MDI 96 min cadence magnetograms from E30$^{\circ}$ to W30$^{\circ}$ as well as the MDI 1 min cadence movie around the time of interest. In addition to that we derive the photospheric velocity fields following Longcope (2004) using IVM vector magnetograms. We find two characteristic photospheric motions relevant for the study of the flaring activity: the rotation of the sunspot, and the emergence and the fast transverse motion of a parasitic polarity.

Estimating Photospheric Flows

Recently, Longcope (2004) has developed a new technique to estimate the photospheric velocity flow. The minimum energy fit (MEF) method is based on the vertical component of the ideal induction equation:

 \begin{displaymath}\vec \nabla_{t} \cdot (v_z \vec B_{t} - B_z \vec v_{t}) = \frac{\partial B_z}{\partial t}\cdot \end{displaymath} (1)

To solve this equation, the knowledge of the full photospheric magnetic vector provided by vector magnetograph such as IVM is needed. By minimizing a functional which resembles the kinetic energy, the vertical flow field is first derived and then the transverse velocity field on the photosphere. Longcope (2004) has tested the consistency of this technique with theoretical cases and also with solar observations. We apply this method to follow the displacement of magnetic structures in AR 8210, labeled in Fig. 2 top left.

Rotation of Sunspot

From the long-term evolution of AR 8210, we note that the main negative polarity (N1) is slowly rotating clockwise about its center. The effects of this rotation are most important in the South-East part of AR 8210 where a positive polarity (P1) is moving counter-clockwise around N1. These photospheric motions tend to increase the shear between the sunspot and the positive polarity. The transverse motions due to the sunspot rotation are not detected because the uncertainty of their measurement (at $\sim$15 min time intervals) is large (the rotation of the sunspot is just few degrees per hour, see e.g. Brown et al. 2003).

Emerging Flux

An other interesting photospheric motion is the emergence of a parasitic polarity (N2) associated with high transverse velocity field toward the South-West. We measure a transverse velocity of $\sim$0.7 km s-1. The increase of magnetic flux is estimated to be $\sim$33% in 4 h. The emergence of flux is a precursor of eruption in active region. Therefore we need to study the time evolution of this polarity to understand the disturbances created by its emergence inside a pre-existing magnetic configuration. Note that to compute the magnetic flux associated with the polarity N2, we have extracted a square of  $30\times30$ pixels of the cross-correlated time series of vector magnetograms only including negative values of Bz from N2.

In AR 8210, we have observed numerous flares, blueshift events associated with reconnection, and photospheric motions. In the following, we combine those three signatures of eruptions and the time evolution of the nonlinear force-free magnetic configurations to give a scenario of the flare process.

   
4 3D coronal magnetic configurations

4.1 Electric current density and $\alpha $ distribution

From the three components of the photospheric magnetic field ( $B_{x, {\rm phot}}, B_{y, {\rm phot}}, B_{z, {\rm {\rm phot}}}$), we can derive the distribution of the electric current density, $J_{z, {\rm {\rm phot}}}$ and the distribution of the force-free function, $\alpha_{{\rm phot}}$ as follows:

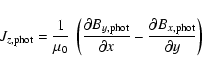\begin{displaymath}J_{z, {\rm phot}} = \frac{1}{\mu_0}~\left( \frac{\partial B_{... ...ial x} - \frac{\partial B_{x, {\rm phot}}}{\partial y} \right) \end{displaymath} (2)

and
 
                        $\displaystyle \alpha_{{\rm phot}}$ = $\displaystyle \frac{\mu_0 J_{z, {\rm phot}}}{B_{z, {\rm phot}}}$  
  = $\displaystyle \frac{1}{B_{z, {\rm phot}}}~\left( \frac{\partial B_{y, {\rm phot}}}{\partial x} - \frac{\partial B_{x, {\rm phot}}}{\partial y} \right)\cdot$ (3)

We first analyse the distributions of $\alpha_{{\rm phot}}$ which is computed for the magnetic field strength over the thresholds defined in Sect. 2.1. We study the time evolution of the mean $\alpha $ value as well as the width of the distribution at 3$\sigma$ between 17:00 UT and 21:40 UT (see Sect. 2.1) computed following Leka & Skumanich (1999). We note that the mean values of $\alpha $ are positive and less than 10-2 Mm-1. The $\alpha $ value is almost constant during the time evolution. The dispersion is between $-7\times 10^{-2}$ and  $7\times 10^{-2}$ Mm-1. According to Régnier (2001) and Régnier & Amari (2004), $\alpha $ often ranges between -1 and +1 Mm-1 with $\alpha $ values of $\pm$0.1 Mm-1 for twisted flux tubes. Therefore the $\alpha $ value and its dispersion indicate that there is only a small amount of twist in AR 8210.

In order to describe the coronal field as a nonlinear force-free equilibrium, there are several requirements on the properties of the current density distribution, $J_{z, {\rm phot}}$. The electric current should be balanced: the total electric current should be zero. The positive currents from one polarity should be equal to the negative currents in the opposite polarity. These properties can be written as follows:

 \begin{displaymath}\int_{\Sigma_+} J_{z, {\rm phot}}~{\rm d}S = \int_{\Sigma_-} J_{z, {\rm phot}}~{\rm d}S, \end{displaymath} (4)

and

 \begin{displaymath}\int_{\Sigma_+} \vert J_{z, {\rm phot}}^{\pm}\vert~{\rm d}S = \int_{\Sigma_-} \vert J_{z, {\rm phot}}^{\mp}\vert~{\rm d}S, \end{displaymath} (5)

and consequently,

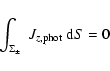\begin{displaymath}\int_{\Sigma_{\pm}}~J_{z, {\rm phot}}~{\rm d}S = 0 \end{displaymath} (6)

where $\Sigma_{+}$ (resp. $\Sigma_{-}$) is where $B_{z, {\rm phot}} > 0$(resp. $B_{z, {\rm phot}} < 0$) and  $J_{z, {\rm phot}}^{\pm}$ is only considered where $J_{z, {\rm phot}}$ is positive or negative respectively.

As an example, we study the distributions for the IVM vector magnetogram at 17:13 UT. The thresholds on the magnetic field components are 25 G for Bz and 46 G for Bt. The ratio of the area of strong field region to the area of weak field region is about 1.2. The electric current imbalance (from Eq. (4)) is 8% and from Eq. (5) the electric current imbalance is 30%.

The imbalance of electric current is plausibly due to the fact that the current in the strong-field regions is detected because the observed fields there exceed the threshold required for Jz calculations while that in weak-field regions is not detected. Note that the imbalance is negative, as one would expect, since Jz is mostly negative in the sunspot N1 where the field strength is high and then Jz well estimated.

   
4.2 nlff reconstruction

To determine the structure of the coronal field we use the nonlinear force-free approximation based on a vector potential Grad-Rubin (1958) method by using the XTRAPOL code (Amari et al. 1999,1997). The nlff field in the corona is then governed by the following equations:

\begin{displaymath}\vec \nabla \wedge \vec B = \alpha \vec B, \end{displaymath} (7)


 \begin{displaymath}\vec B \cdot \vec \nabla \alpha = 0, \end{displaymath} (8)


 \begin{displaymath}\vec \nabla \cdot \vec B = 0, \end{displaymath} (9)

where $\vec B$ is the magnetic field vector in the domain $\Omega$ above the photosphere, $\delta \Omega$, and $\alpha $ is a function of space defined as the ratio of the vertical current density, Jz and the vertical magnetic field component, Bz (see Eq. (3)). From Eq. (8), $\alpha $ is constant along a field line. In terms of the magnetic field $\vec B$, the Grad-Rubin iterative scheme can be written as follows:

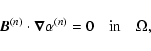\begin{displaymath}\vec B^{(n)} \cdot \vec \nabla \alpha^{(n)} = 0 \quad {\rm in} \quad \Omega, \end{displaymath} (10)


 \begin{displaymath}\alpha^{(n)}\vert _{\delta \Omega^{\pm}} = h, \end{displaymath} (11)

where $\delta \Omega^{\pm}$ is defined as the domain on the photosphere for which Bz is positive (+) or negative (-) and,

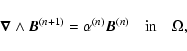\begin{displaymath}\vec \nabla \wedge \vec B^{(n+1)} = \alpha^{(n)} \vec B^{(n)} \quad {\rm in} \quad \Omega, \end{displaymath} (12)


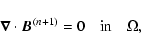\begin{displaymath}\vec \nabla \cdot \vec B^{(n+1)} = 0 \quad {\rm in} \quad \Omega, \end{displaymath} (13)


 \begin{displaymath}B_{z}^{(n+1)}\vert _{\delta \Omega} = g, \end{displaymath} (14)


 \begin{displaymath}\lim_{\vert r\vert \rightarrow \infty}~\vert\vec B\vert = 0. \end{displaymath} (15)

The boundary conditions on the photosphere are given by the distribution, g of Bz on $\delta \Omega$ (see Eq. (14)) and by the distribution h of $\alpha $ on $\delta \Omega$ for a given polarity (see Eq. (11)). We also impose that

 \begin{displaymath}B_{n} = 0 \quad {\rm on} \quad \Sigma - \delta \Omega \end{displaymath} (16)

where $\Sigma$ is the surface of the computational box, n refers to the normal component to the surface. These conditions mean that no field line can enter or leave to computational box, or in other words that the studied active region is magnetically isolated.

Practically, the boundary conditions on the photosphere are: the observed vertical component of the magnetic field, $B_{z, {\rm phot}}$ in the disc-center heliographic system of coordinates allowing the computation in cartesian coordinates, and the $\alpha_{{\rm phot}}$ distribution given by Eq. (3) in a chosen polarity (we have chosen the negative polarity which represents the sunspot N1 of the active region). In order to ensure that the entire active region is included in the field-of-view, we have created composite vector magnetograms by combining IVM magnetograms (strong-field regions) and MDI magnetograms (surrounding weak-field regions). We then compute the nonlinear force-free field for the time series of composite magnetograms using a cross-correlation technique between each magnetogram and a non-uniform grid which reduces the computational time. Those properties insure that we reconstruct the same volume of the corona. Therefore we can study the time evolution of relevant quantities as the magnetic energy or the relative magnetic helicity.

4.3 Basic topology

An interesting property of a magnetic configuration is given by its skeleton. The skeleton (Priest & Forbes 2000) corresponds to all topological elements inside a 3D magnetic field including null points, spine field lines, separatrix surfaces and separators. To analyse the evolution of AR 8210, we determine various topological elements. First we find the null points on the photosphere by determining where the magnetic field vanishes and corresponds to a local minima and for which the transverse components vanish. Around the null point, the magnetic field has three eigenvalues, $\lambda_{i} (i=1, 2, 3)$, that sum to zero to satisfy Eq. (9). An eigenvector is associated with each eigenvalue (not necessarily three perpendicular vectors). If one eigenvalue is positive (resp. negative) and the two others are negative (resp. positive), the spine is the isolated field line directed away from (resp. toward) the null and the separatrix surface consists of field lines radiating toward (resp. away from) the null. The separatrix surfaces give us the definition of the different connectivity domains that comprise AR 8210.

As shown in Fig. 6, AR 8210 exhibits a complex topology with numerous photospheric null points (triangles) and separatrix surfaces represented by the direction of the fan surfaces (green lines) and the spine (thick white lines). We only plot the topological elements inside a reduced field of view. We obtain 49 null points in the entire field of view: 26 negative nulls and 23 positive nulls. We focus our study on four nulls: PN1-3 and NN1 (PN: positive null, NN: negative null). The null points PN1-3 and their associated separatrix surface will be investigated in the next section. NN1 has a spine field line connected with surrounding negative polarities. The separatrix surface is in the same direction as the South separatrix surface shown on EUV and soft X-ray images (Fig. 2 bottom). The topology does not change dramatically during the evolution of AR 8210 (during the studied time period).

   
5 Flares, photospheric motions and magnetic reconnection

   
5.1 3D magnetic evolution associated with precursors

We now analyse the coronal magnetic changes during this time period for the emerging, moving magnetic feature, and the rotating sunspot (see Sect. 3.3). We describe small reconnection processes associated with photospheric motions. By "small'' reconnections we mean reconnection processes which do not modify the configuration of the entire active region, but for which the connectivity of field lines is modified locally.

5.1.1 Emerging flux

In terms of 3D magnetic field configurations, the emerging, moving feature is essential to understand how small reconnection processes can take place in the corona. A small negative polarity emerges in a pre-existing magnetic configuration. This pre-existing system can be depicted as two positive polarities (P3 and P4) and one large negative polarity (N1). The topology of this tripolar configuration has a separatrix surface dividing the domain into two different domains of connectivity, $\mathcal{DA}_{\rm e}$ and  $\mathcal{DB}_{\rm e}$(see Fig. 7).

Before the IVM time series, the small parasitic polarity (N2) emerges into the pre-existing magnetic topology as seen in the long-term MDI evolution. The field lines are then connected to both connectivity domains as shown in Fig. 7. During the IVM time series, the parasitic polarity moves toward the south-west. In the series of coronal field reconstructions, we see that the field lines previously connected in the domain  $\mathcal{DA}_{\rm e}$ cross the separatrix surface as the parasitic polarity moves, and then those field lines reconnect into  $\mathcal{DB}_{\rm e}$. The positive null point PN3 is located close to N2: we cannot determine if this null point was already in the pre-existing configuration or is related to the emergence of the parasitic polarity N2. The spine associated with PN3 links the two positive polarity and the footprint of the fan is well described by the separatrix surface defined on EUV and soft X-ray images (Fig. 2 bottom). The coronal field reconstructions show that the characteristic scale height of the field lines involved in this process is less than 15 Mm.

5.1.2 Rotation of sunspot

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{4171fg6.eps} \end{figure} Figure 6: Basic topological elements for AR 8210 at 17:13 UT. Red (resp. blue) triangles are positive (resp. negative) null points. Spine field lines are thick white lines and separatrix surfaces (or fan surfaces) are defined by two green vectors. Only the projection on the photospheric plane is shown. The characteristic null points are labelled PN1-3 and NN1.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8.5cm,clip]{4171fg7.eps} \end{figure} Figure 7: Area of interest extracted from AR 8210 (MDI image on the left) showing few characteristic field lines and the separatrix surface between two connectivity domains (straight line). Positive polarities are solid lines and negative polarities are dashed lines.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=8cm,clip]{4171fg8.eps} \end{figure} Figure 8: Location in AR 8210 where the effect of the sunspot rotation is stronger. The magnetic configuration is tripolar: positive polarities (P1 and P2) and one negative polarity (N1). The topology is indicated by thte separatrix surface (straight line). Few characteristic field lines are shown for the sake of clarity.
Open with DEXTER

As seen in Fig. 2, the magnetic configuration at this location can be depicted as a tripolar configuration with two positive polarities (P1 and P2) and one negative (N1). Then the topology is similar to the pre-existing configuration in the above case. The topology also includes a negative null point NN2 (Fig. 6) with a spine field line marked by the separatrix surface defined in Fig. 2. The negative polarity is rotating clockwise and the South positive polarity is moving southward. The effect is that field lines connected in domain $\mathcal{DA}_{\rm r}$ and anchored in the negative polarity move toward the separatrix surface and then reconnect in domain $\mathcal{DB}_{\rm r}$ (see Fig. 8). As for the moving feature, the same scenario of small reconnection applies. The field lines involved in the reconnection process have a characteristic height between 15 and 30 Mm (Régnier & Canfield 2004).

   
5.2 Scenario of flares

We now investigate the relationship between the small reconnections due to the sunspot rotation and the flaring activity in AR 8210 obtained in Sect. 3.

In the above sections, we have identified two sites of reconnection inside AR 8210. But only the magnetic changes associated with the rotation of the sunspot are related to the flaring activity observed in the active region. Several properties can explain the observed differences between the two sites of reconnection: the speed of transverse photospheric motions, the magnetic field strength of the magnetic field lines involved in the process, the scale height of the magnetic field lines and the topology.

For the emerging polarity, the photospheric motion is fast, the field strength is $\sim$-450 G and the height is less than 15 Mm. In terms of topology, the reconnection occurs along a separatrix surface. Assuming that a flaring activity is related to this reconnection process, the magnetic energy stored in the region of the parasitic polarity is not enough to trigger a C-class flare (or above)

The flares are related to the rotation of the sunspot and southward motion of the opposite polarity. The magnetic field strength on the photosphere is $\sim$-1500 G at the location of the flare for field lines whose height is between 15 and 30 Mm. The site of reconnection is determined by the existence of H$\alpha $ BSEs, EUV and soft X-ray enhancements and coronal magnetic field changes from a time series of nlff fields. The nature of the reconnection process is defined by the topology of the nlff field: the magnetic changes occur close to a spine field line. All these elements allow the magnetic configuration to store more magnetic energy than at the location of the emerging parasitic polarity.

   
6 Magnetic energy

The magnetic energy in a volume V associated with a magnetic configuration $\vec B$ is given by

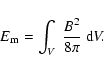\begin{displaymath}E_{\rm m} = \int_{V}~\frac{B^2}{8 \pi}~{\rm d}V. \end{displaymath} (17)

From the photospheric data, we can estimate the magnetic energy flux (or the Poynting flux) due to transverse motions (Kusano et al. 2002):

 \begin{displaymath}\left(\frac{{\rm d}E}{{\rm d}t}\right)_{t} = \int_{S}~(\vec B_{t} \cdot \vec v_{t}) \cdot B_{z}~{\rm d}S. \end{displaymath} (18)

To compute this quantity, we need the knowledge of the full photospheric magnetic field vector and the transverse components of the flow field on the photosphere derived from the MEF method (see Sect. 3.3).
  \begin{figure} \par\includegraphics[width=7.3cm,clip]{4171fg9a.eps}\par\vspace*{2mm} \includegraphics[width=7.3cm,clip]{4171fg9b.eps} \end{figure} Figure 9: Top: time evolution of magnetic energy contained in the potential field (dashed line) and in the nlff field (solid line) magnetic configurations in the coronal volume above the photosphere (unit of 1028 erg s-1). Bottom: time evolution of the rate of change of the free magnetic energy (solid line) and of the energy rate due to transverse motions (dashed line) on the photosphere (unit of 1028 erg s-1).
Open with DEXTER

From the reconstructed 3D magnetic fields, we compute the magnetic energy for the potential field, $E_{\rm pot}$, the magnetic energy for the nonlinear force-free field, $E_{\rm nlff}$, and the rate of change of the free magnetic energy given by

 \begin{displaymath}\left( \frac{{\rm d}E}{{\rm d}t} \right)_{\rm free} = \frac{{\rm d}}{{\rm d}t} (E_{\rm nlff} - E_{\rm pot} ). \end{displaymath} (19)

The characteristic value of the energy is $\sim$1033 erg. The variation is not more than $5\times 10^{31}$ erg during the time period studied with IVM vector magnetograms. The free energy budget ranges between 1 to  $5\times 10^{31}$ erg.

In Fig. 9 top, we plot the rate of change of the magnetic energy contained in the corona for the potential field (dashed line) and for the nlff field (solid line). We notice that the rate of change of the potential and nlff energies always have the same sign. We also observe that both rates are negative before the flare periods (1) and (2), for which the impulsive phase is short (<5 min), and that the energy first increases during the flares and then decreases during the decay phases. By integrating the rates of change of energy, we conclude that at the end of the time series more energy is stored in AR 8210 by $\sim$10%.

In Fig. 9 bottom, we plot the time evolution of the rates given by Eqs. (18) and (19). The rate of change of coronal energy due to transverse motions represents how the magnetic energy is injected through the photosphere into the corona. For the flare periods (1) and (2), the energy injected through the photosphere into the corona is correlated with the increase of magnetic energy in the coronal volume at the same time as the flares occur. The injection of energy is followed by a release of a comparable amount of energy during the decay phases of the flares.

The flare period (3) is somewhat different. We have an increase of the energy of the free energy budget and of the energy due to transverse motions some 20 min before the flare. We also have an increase of the nlff magnetic energy right before the flare and not during the flare as observed in two previous time periods. It seems that there is delay between the injection of energy into the corona and the response of the corona. The delay is $\sim$20 min.

   
7 Magnetic helicity

The magnetic helicity describes the complexity of a magnetic configuration in terms of topology and of linkage of field lines:

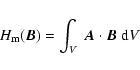\begin{displaymath}H_{\rm m}(\vec B) = \int_{V}~\vec A \cdot \vec B~{\rm d}V \end{displaymath} (20)

where $\vec B$ and $\vec A$ describe the magnetic field in the closed volume V. The helicity value depends on the gauge condition imposed on the vector potential $\vec A$. Nevertheless, a gauge-free quantity is defined as the relative magnetic helicity (helicity of the field $\vec B$ relative to a reference field):

 \begin{displaymath}\Delta H_{\rm m}(\vec B, \vec B_{\rm pot}) = \int_{V}~(\vec A + \vec A_{\rm pot}) \cdot (\vec B - \vec B_{\rm pot})~{\rm d}V \end{displaymath} (21)

given by Finn & Antonsen (1985). $\vec B$ and $\vec A$ here describe the nlff field, $\vec B_{\rm pot}$ and $\vec A_{\rm pot}$ represent the potential field as a reference field. The vector potential Grad-Rubin-like method used to determine the nlff field (see Sect. 4.2) allows us to easily compute the relative magnetic helicity.

In addition, we derive other relevant helicities. Following Berger (1999), we decompose the magnetic field into two fields:

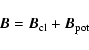\begin{displaymath}\vec B = \vec B_{\rm cl} + \vec B_{\rm pot} \end{displaymath} (22)

where $\vec B_{\rm cl}$ is a closed field with no flux through the boundaries of the computational volume, $\vec B_{\rm pot}$is the reference field (or potential field) satisfying the following properties:

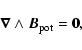\begin{displaymath}\vec \nabla \wedge \vec B_{\rm pot} = \vec 0, \end{displaymath} (23)

and the magnetic field normal to the boundaries is the same as for $\vec B$. Then two kinds of helicity can be defined: the self helicity $H_{\rm self}$ which is computed for a given magnetic field ($\vec B$, $\vec B_{\rm cl}$ or $\vec B_{\rm pot}$), and the mutual helicity $H_{\rm mut}$ between two different fields:

 \begin{displaymath}H_{\rm self}(\vec B) = \int_{V}~\vec A \cdot \vec B~{\rm d}V = H_{\rm m}(\vec B) \end{displaymath} (24)

and

 \begin{displaymath}H_{\rm mut}(\vec B_1, \vec B_2) = 2~\int_{V}~\vec A_1 \cdot \vec B_2~{\rm d}V. \end{displaymath} (25)

Equations (24) and (25) are computed using the nlff field and the potential field in the volume above the photosphere. Equation (24) is applied to both closed and potential fields. As noticed by Berger (1999), the sum of the self helicity and the mutual helicity is the relative magnetic helicity given by Eq. (21):
 
              $\displaystyle \Delta H_{\rm m}(\vec B, \vec B_{\rm pot})$ = $\displaystyle H_{\rm m}(\vec B) - H_{\rm m}(\vec B_{\rm pot})$  
  = $\displaystyle H_{\rm self}(\vec B_{\rm cl}) + H_{\rm mut}(\vec B_{\rm pot}, \vec B_{\rm cl}).$ (26)

Following Régnier et al. (2005), the self helicity of the potential field can be defined as the magnetic helicity associated with the topology of the field (no contribution of twist or writhe). The self helicity of the potential field does not vanish because the topology of the magnetic configuration of AR 8210 is complex.

In 1984, Berger & Field have derived another formula for the relative helicity given by

 \begin{displaymath}\Delta H_{\rm m} = \int_{V}~(\vec A - \vec A_{\rm pot}) \cdot (\vec B + \vec B_{\rm pot})~{\rm d}V \end{displaymath} (27)

when the boundary condition given by Eq. (16) is satisfied or when the half-space above the photosphere is considered. By computing both relative magnetic helicity given by the Finn & Antonsen and the Berger & Field formula, we show that the difference between those two quantities is never more than 5% for the entire time series. This fact means that the boundary conditions defined by the composite magnetogram (IVM + MDI) are put far enough to consider that the magnetic field vanishes at infinity required by Eq. (15).


  \begin{figure} \par\includegraphics[width=8cm,clip]{4171fg10.eps} \end{figure} Figure 10: Time evolution of magnetic helicities (unit of 1042 G2 cm4) as  $H_{\rm self}(\vec B_{\rm cl})$ (blue dot-dashed line), $H_{\rm mut}(\vec B_{\rm pot}, \vec B_{\rm cl})$ (green dashed line), $H_{\rm m}(\vec B_{\rm pot})$ or vacuum helicity (red dot-dot-dot-dashed line), $\Delta H_{\rm m}$ from the Finn-Antonsen formula (black solid line) and the sum of self and mutual helicity (stars). Gray areas are the flaring periods, dark gray areas are the impulsive phase of flares.
Open with DEXTER

In Fig. 10, we plot the time evolution of the relative magnetic helicity given by the Finn & Antonsen formula (solid line), the mutual helicity between the potential and closed fields (dashed line), the self helicity of the closed field (dot-dashed line), the vacuum helicity (dot-dot-dot-dashed line) and the sum of the mutual helicity and the self helicity (stars). As expected from Eq. (26), the sum of the self and mutual helicities (stars) follows the evolution of the relative magnetic helicity (solid line). The mutual helicity is the main contribution to the relative magnetic helicity of AR 8210. This fact means that the way the field lines crossing between each other is the essential part of the helicity and NOT the twist or the writhe inside AR 8210. That is not surprising given the complex topology of AR 8210 as shown in Figs. 2 and 6. We note that the helicity of the vacuum field is nearly constant with a positive value of $\sim$ $2.6\times 10^{41}$ G2 cm4. We consider that the vacuum helicity or helicity of the potential field is mostly related to the complex topology of AR 8210. In a simple connected domain, the self helicity of the magnetic field should be zero as no twist or writhe are inside a potential field configuration, but in cases involving separated connectivity domains the self helicity indicates the complex topology of the field (Berger & Field 1984). We note that the vacuum helicity is positive following the chirality rules of active regions (Longcope et al. 1998; Pevtsov et al. 1995), and the relative helicity is mostly negative.

Variations of magnetic helicity are expected if reconnection processes take place in a magnetic configuration (see e.g. Biskamp 1997). From Fig. 10, we note that before a flare negative relative helicity is injected in the configuration and that after a flare the relative helicity is decreasing. Again for the period (3), there is a delay of $\sim$20 min between the injection of negative helicity and the release of helicity after the flare.

   
8 Discussion and conclusions

In Sect. 5.1, we have identified two areas of interest in terms of magnetic configuration: an emerging, moving magnetic feature, and a rotating sunspot. Each of those phenomena is often seen to be a precursor of flares, CMEs and filament eruptions. In Table 3, we summarize the properties of the flaring or nonflaring activity in AR 8210 on May 1, 1998 associated with C-class flares. By combining a large dataset from the photosphere to the corona with coronal magnetic field models, we have determined the main ingredients of these flares: topology and photospheric motions.

Table 3: Summary of the properties of flare or nonflare activity in AR 8210 for the sunspot rotation and the fast moving polarity. The magnetic energy and the magnetic helicity are global quantities therefore we just mention the characteristic evolution of both quantities before and after a flare associated with BSEs. (SW = South-West)

The moving feature and the rotating sunspot are associated with the same basic magnetic configuration: three sources (two positive polarities and one negative). In this simple magnetic system, a separatrix surface divides the space into two domains of connectivity. We can compare this topology with the topological studies done by Brown & Priest (1998) and Longcope & Klapper (2002). Using a potential field method, Brown & Priest have analysed the topology of three unbalanced sources. They have found several topological states which all contain null points, separatrix surfaces and separators. In Fig. 2 of Longcope & Klapper, the same result is obtain for two negative polarities, N4 and N6, and one positive, P3. The authors have defined this topological structure as a broken fan (equivalent to two different separatrix surfaces part of the same dome). What we called a separatrix surface in Figs. 7 and 8 is the projection on the photospheric plane of the separatrix surface (including the separator field line) dividing the broken fan into two domains of connectivity. For the moving feature, the topological element dividing the domains is the fan surface. For the rotating sunspot, the spine field line has the same photospheric footprint as the separatrix surface. Those types of reconnection can be fast as shown by Parnell & Galsgaard (2004).

In both the moving feature and the sunspot rotation, the origins of reconnections lie in the photospheric motions of field lines footpoints. For the moving feature, the parasitic polarity emerges into the pre-existing three-source magnetic configuration and the fast displacement of this polarity leads to small reconnection processes. For the sunspot rotation, the field lines existing in the three-source configuration are moved toward the separatrix surface by the clockwise rotation and generate reconnections.

In this article, we have focused our study on small eruptive events which did not dramatically modify the magnetic configuration of the active region. In this study the most important ingredient is to use a good time series of vector magnetograms before and after flaring activity. A similar study can be done for M or X-class flares with the development of vector magnetic field measurements on the photosphere or in the chromosphere by Solar B/SOT (Solar Optical Telescope), SDO/HMI (Helioseismic and Magnetic Imager) or ground-based observatories (MSO, NSO/SOLIS, THEMIS, GREGOR, Huairou Observatory).

Acknowledgements
The authors would like to thank M. Berger, G. Fisher, Y. Li, D. Longcope and D. McKenzie for fruitful discussions and comment as well as Mees Solar Observatory observers who have provided us the IVM observations. S.R. research is funded by the European Commission's Human Potential Programme through the European Solar Magnetism Network. S.R. and RCC research has been supported by AFOSR under a DoD MURI grant "Understanding Solar Eruptions and Their Interplanetary Consequences''.

References

 
Copyright ESO 2006