A&A 450, 887-898 (2006)
DOI: 10.1051/0004-6361:20054107
The role of kink instability in Poynting-flux dominated jets
D. Giannios - H. C. Spruit
Max-Planck-Institute for Astrophysics, Box 1317, 85741 Garching, Germany
Received 26 August 2005 / Accepted 2 January 2006
Abstract
The role of kink instability in magnetically driven jets is explored
through numerical one-dimensional steady relativistic MHD calculations. The instability
is shown to have enough time to grow and influence the dynamics of Poynting-flux dominated
jets. In the case of AGN jets, the flow becomes kinetic flux dominated at distances 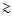
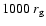 because of the rapid dissipation of Poynting flux. When applied
to GRB outflows, the model predicts more gradual Poynting dissipation and moderately magnetized
flow at distances of
because of the rapid dissipation of Poynting flux. When applied
to GRB outflows, the model predicts more gradual Poynting dissipation and moderately magnetized
flow at distances of  1016 cm where the deceleration of the ejecta due to interaction
with the external medium is expected. The energy released by the instability can power the compact
"blazar zone'' emission and the prompt emission of GRB outflows with high radiative
efficiencies.
1016 cm where the deceleration of the ejecta due to interaction
with the external medium is expected. The energy released by the instability can power the compact
"blazar zone'' emission and the prompt emission of GRB outflows with high radiative
efficiencies.
Key words: magnetohydrodynamics (MHD) - instabilities - gamma rays: bursts - quasars: general
1 Introduction
Relativistic collimated outflows have been extensively observed in active galactic nuclei
(AGN) and X-ray binaries (XRB). Gamma-ray
bursts (GRB) are also believed to be connected to ultrarelativistic and collimated outflows
to overcome the "compactness problem'' (e.g. Piran 1999) and to explain the
achromatic afterglow breaks (Rhoads 1997; Sari et al. 1999). It is also believed that
all these sources are powered by accretion of matter by a compact object.
The widely accepted mechanism for jet acceleration and collimation in the context of AGN and
XRB jets is that of magnetic driving. According to this paradigm, magnetic fields
anchored to a rotating object can launch an outflow.
The rotating object can be a star (Weber & Davis 1967; Mestel 1968), a pulsar (Michel 1969;
Goldreich & Julian 1970),
an accretion disk (Bisnovatyi-Kogan & Ruzmaikin 1976; Blandford 1976; Lovelace 1976;
Blandford & Payne 1982) or a rotating black hole (Blandford & Znajek 1977).
The material is accelerated thermally up to the sonic point and centrifugally until the
Alfvén point, defined as the point where the flow speed equals the Alfvén speed. After the
Alfvén point the inertia of mater does not allow corotation of the magnetic field. As a
result, the magnetic field lines bend, developing a strong toroidal component.
Further out the flow passes through the fast magnetosonic point where most of the energy
of the flow remains in the form of Poynting flux in the case of relativistic outflows (Michel 1969;
Goldreich & Julian 1970; Sakurai 1985; Beskin et al. 1998).
Further acceleration of the flow is not straightforward within ideal MHD. It can be shown, for
example, that a radial flow is not accelerated after the fast point (e.g. Beskin 1998).
This is a result of the fact that the magnetic pressure and tension terms of the Lorentz force
almost cancel each other (Begelman & Li 1994). A limited degree of acceleration
of the flow is possible if it has a decollimating shape (i.e. the magnetic field
diverges faster than radial; Li et al. 1992; Begelman & Li 1994).
Magnetized jets suffer from a number of instabilities. Interaction with the environment
causes instabililty of the Kelvin-Helmholtz type and kink instability causes internal rearrangement
of the field configuration.
Here we focus on kink instability, since it internally dissipates magnetic energy
associated with the Poynting flux. As demonstrated elsewhere
(Drenkhahn 2002; Drenkhahn & Spruit 2002; Spruit & Drenkhahn 2003) such
internal energy dissipation directly leads to acceleration of the flow. Dissipation
steepens the radial decrease of magnetic pressure, thereby lifting the cancellation
between outward pressure force and inward magnetic tension, and allowing the magnetic
pressure gradient to accelerate the flow.
While dissipation of magnetic energy can thus happen through kink instability in an
initially axisymmetric ("DC'') flow, it can also happen more directly by reconnection in the
outflow generated by a non-axisymmetric rotator ("AC'' flow). The two cases behave
differently in terms of the acceleration profile, and the location and amount of
radiation produced by the dissipation process. A nonaxisymmetric rotator produces
a "striped'' outflow (as in the case of a pulsar wind) with reconnectable changes of
direction of the field embedded in the flow, and energy release independent of
the opening angle of the jet. In the DC case, where energy release is instead
mediated by an instability, the rate of energy release is limited by the time it takes an
Alfvén wave to travel across the width of the jet. This makes it a sensitive function
of the jet opening angle.
The "AC'' case has been studied in detail by Drenkhahn (2002), Drenkhahn & Spruit
(2002), with application to Gamma-ray bursts. In the case of AGN and XRB, on the other
hand, the collimated jet is arguably best understood if the field in the inner
disk is of uniform polarity, resulting in an initially axisymmetric flow. Another difference
is the lower bulk Lorentz factors in the AGN/XRB case, resulting in faster energy release
(in units of the dynamical time of the central engine).
The purpose of this paper is to explore the consequences of magnetic dissipation by
internal instability in such axisymmetric (or DC) cases, and its observational signatures.
We also apply the calculations to the GRB case, where we compare the results with the AC
case studied before.
We limit ourselves to a flow with constant opening angle. That is, we leave aside the
collimation process. Kink instability is modeled by adding a sink term to the induction
equation to account for the non-ideal MHD effects arising from it.
Linear stability
theory of kink instability yields a growth time of the order
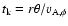 where r is the radius of the jet,
where r is the radius of the jet, 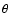 its opening angle and
its opening angle and
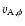 the Alfvén speed based on the
azimuthal component
the Alfvén speed based on the
azimuthal component 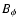 of the field. This is independent of the poloidal field
component, at least for the so-called internal kink modes (which do not disturb the outer
boundary of the field, cf. Bateman 1978 for details). For stability analysis and numerical
simulations with astrophysical applications see, e.g. Begelman (1998); Appl et al. (2000);
Lery et al. (2000); Ouyed et al. (2003); Nakamura & Meier (2004). Based on linear
theory, we would predict that the poloidal field component
can be ignored for the rate of energy release.
of the field. This is independent of the poloidal field
component, at least for the so-called internal kink modes (which do not disturb the outer
boundary of the field, cf. Bateman 1978 for details). For stability analysis and numerical
simulations with astrophysical applications see, e.g. Begelman (1998); Appl et al. (2000);
Lery et al. (2000); Ouyed et al. (2003); Nakamura & Meier (2004). Based on linear
theory, we would predict that the poloidal field component
can be ignored for the rate of energy release.
It is not clear, however, that the poloidal
component can be ignored for the nonlinear development of the instability, which is
what actually determines the energy release. As a way to explore the effect
of possible nonlinear stabilization by a poloidal component we compare two cases
in the calculations: one with energy release and field decay given by the Alfvén time
across the jet (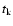 above), and one in which this rate is assumed to be reduced
by the poloidal component. This mainly affects the early phases of the acceleration of the
flow beyond the light cylinder.
above), and one in which this rate is assumed to be reduced
by the poloidal component. This mainly affects the early phases of the acceleration of the
flow beyond the light cylinder.
We find that kink instability has time to grow in the AGN and
XRB cases, dissipating energy in the toroidal component of the magnetic field while
accelerating the flow at the same time. The dissipation of magnetic energy
is almost complete and fast in the case of AGN jets, so that on parsec scales
the flow has become kinetic energy dominated, in agreement with current interpretations
of the observations (e.g. Sikora et al. 2005, where the possible effects of magnetic dissipation
are also discussed briefly).
The DC model with kink instability also produces significant flow acceleration
in the GRB case, but conversion of the Poynting flux is less effective than the AC model in
this case.
The structure of the paper is as follows. In Sect. 2 we discuss MHD instabilities
in jets and focus on the kink instability and its growth rate. The model is described in Sect. 3
including the assumptions, the dynamical equations and the parameters at the base of the flow.
In Sect. 4, we apply the model to the case of AGN jets and GRBs, while the last two sections
present the discussion and conclusions.
2 The kink instability
Magnetized outflows are subject to a variety of instabilities. These can be classified as
pressure driven, Kelvin-Helmholtz and current driven instabilities (see, e.g., Kadomtsev 1966;
Bateman 1978). Pressure driven
instabilities (Kersalé et al. 2000; Longaretti 2003) are related to the interplay between the
gas pressure and the curvature of magnetic field lines. They are relevant close to the launching region
of the outflows and may be important as long as the outflow is still subsonic. Kelvin-Helmholtz (KH)
instabilities (Ray 1981; Ferrari
et al. 1981; Bodo et al. 1989; Hardee & Rosen 1999) arise from
velocity gradients in the flow and may be important in the shearing layer between the outflow and the
external medium. KH instabilities have been extensively studied and become strongest
in the region beyond the Alfvén point but still within the fast magnetosonic point. Current driven
(CD; Eichler 1993; Spruit et al. 1997; Begelman 1998; Lyubarskii 1999; Appl et al. 2000)
instabilities have received much less attention but are the most relevant ones for
Poynting-flux dominated outflows, since they can convert the bulk Poynting flux into radiation and
kinetic energy of the flow (for the role of CD instabilities in an electromagnetic model
for GRBs see Lyutikov & Blandford 2003). Among the CD instabilities, the m=1 kink instability
is generally the most effective. In this work, we focus on the effect of the kink instability
on the dynamics of these outflows.
While magnetized outflows can be accelerated "centrifugally'' by large scale poloidal fields
(Blandford & Payne 1982; Sakurai 1985, 1987), at the radius of the light-cylinder inertial forces
become significant and the magnetic field
cannot force corotation. At this radius the strength of the toroidal and the poloidal
components are comparable. Further out, the induction equation dictates that, within ideal MHD,
the toroidal component dominates over the poloidal one since the strength of the former
scales as 1/r while that of the latter as 1/r2. This magnetic configuration of a strongly
wound-up magnetic field like this is known, however, to be highly unstable to the kink m=1 mode
from tokamak experiments (see, e.g., Bateman 1978). Linear stability analysis
has shown that the growth time of the instability is given by the Alfvén crossing time across the
outflow in a frame comoving with it (Begelman 1998; Appl et al. 2000).
The study of the non-linear evolution of the instability demands three dimensional relativistic
MHD simulations over many decades of radii and it is, therefore, not surprising that the issue is not
settled. Lery et al. (2000) and Baty & Keppens (2002) argued in favor of the dynamical importance
of the instability in reorganizing the magnetic configuration inside the jet. It has been argued,
however, that the jet creates a "backbone'' of strong poloidal field which slows
down the development of instabilities (Ouyed et al. 2003; Nakamura & Meier 2004). In view of these
works and since the growth rate of the instability is important for this study, we
consider two alternatives for the non-linear stage of the instability. In the first case, the
instability proceeds at the Alfvén crossing time across the outflow (as suggested by linear stability
analysis) and rearranges the magnetic field configuration to a more chaotic one. In this case the
instability time scale is given by the expression (in the central engine frame)
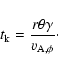 |
(1) |
We will refer to this as the "fast kink'' case.
For the second case, we reduce the dissipation rate by a suitable (but arbitrary)
function of the poloidal-to-toroidal field ratio.
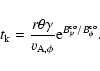 |
(2) |
We will refer to this as the "slow kink'' case. This recipe is meant only as a means
to explore the possible effect that the poloidal field component could have on the net acceleration
of the flow, if it affects the dissipation rate, and is not meant to be quantitative.
Numerical simulations of the instability
would be needed to determine which of these prescriptions (if any) of the growth time scale is
close in describing its non-linear development (see also Sect. 5).
In the last expressions,
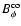 ,
,
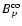 ,
are the toroidal and the poloidal
components of the magnetic field as measured by an observer comoving with the flow,
,
are the toroidal and the poloidal
components of the magnetic field as measured by an observer comoving with the flow, 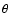 is
the jet opening angle,
is
the jet opening angle, 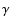 is the bulk Lorentz factor of the flow and
is the bulk Lorentz factor of the flow and
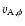 is the
is the 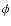 component of the Alfvén speed given by
component of the Alfvén speed given by
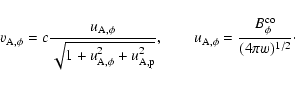 |
(3) |
Here, w is the internal enthalpy, to be defined below.
A magnetically launched outflow passes through three characteristic points where the speed of the flow
equals the speed of slow mode, the poloidal Alfvén wave and the fast mode and are called the
slow magnetosonic, the Alfvén and the fast magnetosonic points respectively. For flows where the
energy density of the magnetic field dominates that of matter, the Alfvén point lies very close
to the light-cylinder
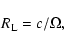 |
(4) |
where 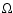 is the angular velocity of the foot point (e.g. Camenzind 1986).
At the Alfvén radius most of the centrifugal acceleration has already taken place and
the magnetic field cannot force corotation of matter. At this location, the toroidal and the poloidal
components of the magnetic field are comparable in magnitude.
Further out, the flow passes through the fast magnetosonic point at a distance
is the angular velocity of the foot point (e.g. Camenzind 1986).
At the Alfvén radius most of the centrifugal acceleration has already taken place and
the magnetic field cannot force corotation of matter. At this location, the toroidal and the poloidal
components of the magnetic field are comparable in magnitude.
Further out, the flow passes through the fast magnetosonic point at a distance 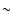 a few
a few 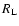 (Sakurai 1985; Li et al. 1992; Beskin et al. 1998).
At the location of the fast
magnetosonic point the speed of the four-velocity of the flow equals
(Sakurai 1985; Li et al. 1992; Beskin et al. 1998).
At the location of the fast
magnetosonic point the speed of the four-velocity of the flow equals 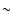
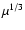 ,
where
,
where 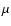 is the Michel magnetization parameter (i.e., the energy flux per unit rest mass; Michel 1969).
For Poynting-flux dominated flows (i.e.,
is the Michel magnetization parameter (i.e., the energy flux per unit rest mass; Michel 1969).
For Poynting-flux dominated flows (i.e., 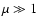 ), most of the energy is still in magnetic form at this
point since the ratio of magnetic to matter energy flux is
), most of the energy is still in magnetic form at this
point since the ratio of magnetic to matter energy flux is 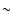
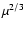 .
There is thus a choice between flows with high Lorentz factors (but inefficient
conversion of Poynting flux to kinetic energy), or efficient conversion at
the price of low terminal Lorentz factors. Better conversion within ideal MHD appears to be hard to achieve except by decollimation of the flow (Li et al. 1992;
Begelman & Li 1994; Bogovalov 2001; Daigne & Drenkhahn 2002; but see claims to the
contrary by Vlahakis & Konigl 2003a,b; Fendt & Ouyed 2004). Even with such
decollimation, the additional acceleration is rather modest (Begelman & Li 1994; Daigne &
Drenkhahn 2002).
.
There is thus a choice between flows with high Lorentz factors (but inefficient
conversion of Poynting flux to kinetic energy), or efficient conversion at
the price of low terminal Lorentz factors. Better conversion within ideal MHD appears to be hard to achieve except by decollimation of the flow (Li et al. 1992;
Begelman & Li 1994; Bogovalov 2001; Daigne & Drenkhahn 2002; but see claims to the
contrary by Vlahakis & Konigl 2003a,b; Fendt & Ouyed 2004). Even with such
decollimation, the additional acceleration is rather modest (Begelman & Li 1994; Daigne &
Drenkhahn 2002).
We set the initial conditions of our calculation at the fast magnetosonic point r0. To make
the problem tractable we make a number of simplifying assumptions. First, we limit ourselves to
a radial, static flow. Evidently, this approach does not allow us to explore the important issue
of jet collimation (see, however Sect. 5.1). Furthermore, the flow is assumed one-dimensional
by ignoring the structure of the jet in the 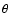 direction. Also, we ignore
the azimuthal component of the velocity. This
component is not dynamically important beyond the fast magnetosonic point (e.g. Goldreich &
Julian 1970) and can be neglected from the dynamic equations. On the other hand, the poloidal
component (taken to be radial for simplicity) still has to be taken into account when modeling
the effect of the kink instability since it influences its growth timescale (see Eqs. (1), (2)).
These simplifying assumptions minimize the number of the free parameters of the model,
allowing us to study the effect of each on the jet dynamics, as will become clear
in the next sections.
direction. Also, we ignore
the azimuthal component of the velocity. This
component is not dynamically important beyond the fast magnetosonic point (e.g. Goldreich &
Julian 1970) and can be neglected from the dynamic equations. On the other hand, the poloidal
component (taken to be radial for simplicity) still has to be taken into account when modeling
the effect of the kink instability since it influences its growth timescale (see Eqs. (1), (2)).
These simplifying assumptions minimize the number of the free parameters of the model,
allowing us to study the effect of each on the jet dynamics, as will become clear
in the next sections.
To determine the characteristics of the flow as a function of radius, one needs the conservation
equations for mass, energy and angular momentum. These equations can be brought in the form
(if, for the moment, we neglect radiative losses; e.g. Lyutikov 2001; Drenkhahn 2002)
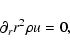 |
(5) |
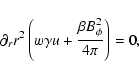 |
(6) |
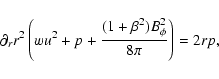 |
(7) |
where
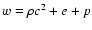 is the proper enthalpy density, e and p are the internal energy
and pressure respectively and
is the proper enthalpy density, e and p are the internal energy
and pressure respectively and
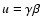 is the radial four-velocity. We still need to
assume an equation of state that will provide a relation between the pressure p
and the internal energy. Assuming an ideal gas, we take
is the radial four-velocity. We still need to
assume an equation of state that will provide a relation between the pressure p
and the internal energy. Assuming an ideal gas, we take
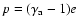 ,
where
,
where
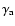 is the adiabatic index.
is the adiabatic index.
Mass conservation (5) can be integrated to yield mass flux per sterad
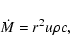 |
(8) |
while energy conservation gives the total luminosity per sterad
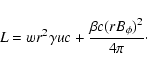 |
(9) |
The first term of the last expression corresponds to the kinetic energy flux and the second
to the Poynting flux.
A key quantity is the "magnetic content'' of the flow which we will refer
to as the magnetization parameter 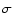 ,
defined as the ratio of the radial Poynting to matter energy flux
,
defined as the ratio of the radial Poynting to matter energy flux
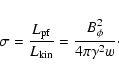 |
(10) |
For a flow to reach large asymptotic Lorentz factors (observations indicate
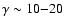 for quasars, and theoretical arguments arising from the "compactness problem'' such as Piran 1999
constrain
for quasars, and theoretical arguments arising from the "compactness problem'' such as Piran 1999
constrain
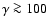 for GRBs), it must start with a high energy to mass ratio. Within
the fireball model for GRBs (Paczynski 1986; Goodman 1986)
this means that
for GRBs), it must start with a high energy to mass ratio. Within
the fireball model for GRBs (Paczynski 1986; Goodman 1986)
this means that
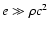 .
In this work, we focus on the opposite limit where most of the energy
is initially stored in the magnetic field (
.
In this work, we focus on the opposite limit where most of the energy
is initially stored in the magnetic field (
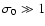 ), while we treat the flow as cold (i.e.,
), while we treat the flow as cold (i.e.,
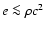 ). Obviously, there can exist an intermediate regime of a
"magnetized-fireball'' models where both
). Obviously, there can exist an intermediate regime of a
"magnetized-fireball'' models where both
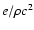 and
and
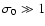 at the base of the flow.
at the base of the flow.
Finally, the strength of the radial component is given by flux conservation by the expression
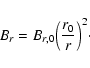 |
(11) |
For a flow that is moving radially with a bulk Lorentz factor 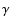 ,
the expressions that relate
the comoving components of the magnetic field to those measured in the central engine frame are
,
the expressions that relate
the comoving components of the magnetic field to those measured in the central engine frame are
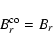 |
(12) |
and
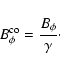 |
(13) |
The set of equations presented in the previous section is not complete. There is one more
equation needed to determine the problem at hand, which is the induction equation. For ideal MHD, the induction equation yields
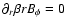 and can be integrated to give the
scaling
and can be integrated to give the
scaling
 for relativistic flows. One can immediately see that the Poynting-flux
term in Eq. (9) is approximately constant and no further acceleration of the
flow is possible within ideal MHD for a radial flow. This is a result of the fact that
the magnetic pressure and tension terms of the Lorentz force almost cancel each other (Begelman
& Li 1994).
for relativistic flows. One can immediately see that the Poynting-flux
term in Eq. (9) is approximately constant and no further acceleration of the
flow is possible within ideal MHD for a radial flow. This is a result of the fact that
the magnetic pressure and tension terms of the Lorentz force almost cancel each other (Begelman
& Li 1994).
We argue, however, that when the toroidal component of the magnetic field becomes dynamically dominant
the kink instability sets in. The instability drives its energy from 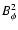 on the instability
growth time scale. This effect can be crudely modeled by the addition of one sink term on the right
hand side of the induction equation following Drenkhahn (2002), Drenkhahn & Spruit (2002)
on the instability
growth time scale. This effect can be crudely modeled by the addition of one sink term on the right
hand side of the induction equation following Drenkhahn (2002), Drenkhahn & Spruit (2002)
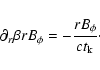 |
(14) |
The kink instability time scale is given by the expressions (2) or (1) depending on whether
the poloidal component of the magnetic field is assumed to have a stabilizing effect.
When the instability sets in, 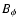 drops faster than 1/r and acceleration of the flow is
possible at the expense of its magnetic energy.
drops faster than 1/r and acceleration of the flow is
possible at the expense of its magnetic energy.
The dynamical Eqs. (6) and (7)
are derived under the assumption that no energy or momentum escape from the
outflow. This is accurate when the instability releases energy in
the optically thick region of the flow. On the the other hand,
in the optically thin regime energy and momentum may be transfered into the
radiative form that escapes and does not interact with matter. Let 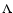 be
the emissivity of the medium in the comoving frame, that is, the energy
that is radiated away per unit time and per unit volume. If the
emission is isotropic in the comoving frame the energy and momentum
Eqs. (6), (7) including the radiative
loss terms are (Königl & Granot 2002)
be
the emissivity of the medium in the comoving frame, that is, the energy
that is radiated away per unit time and per unit volume. If the
emission is isotropic in the comoving frame the energy and momentum
Eqs. (6), (7) including the radiative
loss terms are (Königl & Granot 2002)
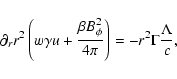 |
(15) |
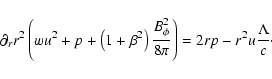 |
(16) |
The importance of the cooling term depends on the cooling time
scale. If it is short compared to the expansion time scale, the matter stays
cold during the dissipation process. In this limit, all the
dissipated energy is locally radiated away. The dissipative processes
that appear in the non-linear stage of the instability are poorly understood.
It could be the case that the released energy leads to fast moving particles
(i.e. electrons and ions) and/or to Alfvén turbulence (Thompson 1994).
Synchrotron emission is a plausible fast cooling process for the electrons. It is particularly
effective in our model, because the magnetic field strengths are high in a Poynting
flux dominated outflow. Ions, however, are, due to their higher masses, much less efficient
radiators.
The form of this cooling term we assume here is
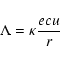 |
(17) |
where k is an adjustable cooling length parameter. The cooling
length is the distance by which the matter travels outward while the
internal energy e is lost. When
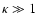 the cooling length is very short, only a small
fraction of the expansion length scale r and thus qualifies for the
description of a fast cooling flow. This, in more physical terms, corresponds to the case
where most of the energy is dissipated to fast moving (and therefore fast cooling) electrons. On the other
hand, setting
the cooling length is very short, only a small
fraction of the expansion length scale r and thus qualifies for the
description of a fast cooling flow. This, in more physical terms, corresponds to the case
where most of the energy is dissipated to fast moving (and therefore fast cooling) electrons. On the other
hand, setting
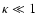 ,
the cooling length
is much longer than the expansion length and most of the energy stays in the flow
leading to more efficient adiabatic expansion. This is the case when the dissipated energy is mostly
shared among the ions.
,
the cooling length
is much longer than the expansion length and most of the energy stays in the flow
leading to more efficient adiabatic expansion. This is the case when the dissipated energy is mostly
shared among the ions.
The characteristics of the flow are determined when a number of quantities are specified at the
fast magnetosonic point r0 which is taken to be 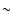 a few times the light cylinder radius
(Sakurai 1985; Begelman et al. 1994; Beskin et al. 1998),
or expressed in terms of the gravitational radius
a few times the light cylinder radius
(Sakurai 1985; Begelman et al. 1994; Beskin et al. 1998),
or expressed in terms of the gravitational radius
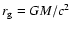 of the central engine
of the central engine
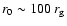 .
These quantities are the initial magnetization
.
These quantities are the initial magnetization 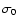 ,
the
luminosity L, the opening angle
,
the
luminosity L, the opening angle 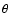 ,
the ratio
,
the ratio
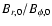 and the
cooling length scale
and the
cooling length scale 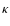 .
The quantities one has to solve for so as to determine the characteristics of the flow
are
.
The quantities one has to solve for so as to determine the characteristics of the flow
are 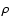 ,
e, u and
,
e, u and 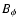 as functions or radius r. This is done by integrating
numerically the mass, energy, momentum conservation equations and the modified induction equation.
The parameters of the model determine the initial values of
as functions or radius r. This is done by integrating
numerically the mass, energy, momentum conservation equations and the modified induction equation.
The parameters of the model determine the initial values of 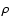 ,
e, u and
,
e, u and 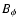 at r0.
at r0.
The initial four-velocity for our calculations is assumed to be
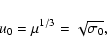 |
(18) |
in accordance with previous studies (Michel 1967; Goldreich & Julian 1970; Camenzind 1986;
Beskin et al. 1998) which show that at the fast point the ratio of Poynting to kinetic flux is 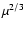 .
The flow is assumed to be cold at r0, i.e. e=0 and using the previous
expression with Eqs. (9), (10) one finds for
.
The flow is assumed to be cold at r0, i.e. e=0 and using the previous
expression with Eqs. (9), (10) one finds for 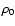 and
and
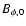
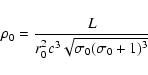 |
(19) |
and
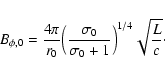 |
(20) |
The role of the different model parameters becomes
clear in the next section where the model is applied to the case of AGN jets and GRBs.
Out of the free parameters of the model, 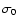 and
and 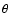 are of special
importance. The magnetization
are of special
importance. The magnetization 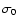 determines the "magnetic dominance'' of the flow, i.e., the speed of the flow at the
fast magnetosonic point and at a large distance from the central engine.
On the other hand, the opening angle
determines the "magnetic dominance'' of the flow, i.e., the speed of the flow at the
fast magnetosonic point and at a large distance from the central engine.
On the other hand, the opening angle 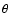 is directly related to the growth rate of the
instability (see Eqs. (1), (2)). The
instability has enough time to grow if it is faster than the expansion
time r/c. The ratio of the two time scales at the base of the flow is (using prescription (1)
for the time scale of the kink instability)
is directly related to the growth rate of the
instability (see Eqs. (1), (2)). The
instability has enough time to grow if it is faster than the expansion
time r/c. The ratio of the two time scales at the base of the flow is (using prescription (1)
for the time scale of the kink instability)
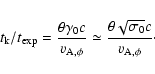 |
(21) |
If
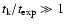 ,
the kink instability does not
have enough time to grow and the evolution is close to that predicted by ideal MHD (where
not much acceleration takes place). On the other hand, if
,
the kink instability does not
have enough time to grow and the evolution is close to that predicted by ideal MHD (where
not much acceleration takes place). On the other hand, if
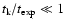 ,
the instability
grows for many e-foldings and turns almost all the magnetic energy in the flow into
radiation and kinetic flux. Keeping the opening angle fixed, this happens much more
efficiently in lower
,
the instability
grows for many e-foldings and turns almost all the magnetic energy in the flow into
radiation and kinetic flux. Keeping the opening angle fixed, this happens much more
efficiently in lower 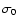 flows (provided that
flows (provided that
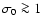 so that
the Alfvén speed is a significant fraction of the speed of light). We return to this point in the
next sections.
so that
the Alfvén speed is a significant fraction of the speed of light). We return to this point in the
next sections.
Although at first sight different, jets in AGNs (and microquasars) and GRBs probably have central
engines of similar characteristics. AGN jets are launched in the inner regions
of magnetized accretion disks (Blandford & Payne 1982), or drive their power by magnetic fields that are
threading the ergosphere of a rotating black hole (Blandford & Znajek 1977). In the case of GRBs,
the same central engine may be at work, or the energy is tapped by a millisecond magnetar
(Usov 1992; Kluzniak & Ruderman 1998; Spruit 1999). In all of these situations,
strong magnetic fields play an important role
and most of the energy is released in the form of Poynting flux![[*]](/icons/foot_motif.gif) .
.
All the above scenarios may give rise to magnetized outflows, whose evolution
depends, to a large extent, on the dominance of the magnetic energy or on the ratio
of the Poynting-flux to matter energy flux at the base of the flow.
By varying this ratio, one can apply the model to jets in both the cases of GRBs and AGNs.
Relativistic jets are commonly observed in AGNs to have bulk Lorentz factors in the range
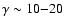 .
Such terminal Lorentz factors can be achieved for the ratio
.
Such terminal Lorentz factors can be achieved for the ratio 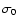 of Poynting to matter energy flux of the order of several at the fast magnetosonic
Point r0. The location of the fast point is most likely at a few light cylinder radii
(e.g. Sakurai 1985; Camenzind 1986) and is taken to be
of Poynting to matter energy flux of the order of several at the fast magnetosonic
Point r0. The location of the fast point is most likely at a few light cylinder radii
(e.g. Sakurai 1985; Camenzind 1986) and is taken to be
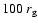 .
.
Actually, 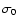 is a very important parameter of the flow. Its effect on the acceleration
of the flow is clearly seen in Fig. 1, where the bulk Lorentz factor is plotted as a function
radius r for different
is a very important parameter of the flow. Its effect on the acceleration
of the flow is clearly seen in Fig. 1, where the bulk Lorentz factor is plotted as a function
radius r for different 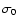 .
The rest of the parameters have the values
.
The rest of the parameters have the values
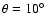 ,
,
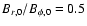 ,
while the energy released by the instability is assumed to be locally radiated
away (this is done by taking the "cooling length'' parameter
,
while the energy released by the instability is assumed to be locally radiated
away (this is done by taking the "cooling length'' parameter
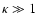 ). The results do not
depend on the luminosity L of the flow in the case of AGN jets, while r0 sets the scale
of the problem (since it is the only length scale) which means that the results can be trivially
rescaled in the case of a different choice of r0.
). The results do not
depend on the luminosity L of the flow in the case of AGN jets, while r0 sets the scale
of the problem (since it is the only length scale) which means that the results can be trivially
rescaled in the case of a different choice of r0.
The solid lines in Fig. 1 correspond to the case where Eq. (1) is used for the timescale of the kink instability (i.e., the fast kink case) and the dashed lines to the case where
the instability is slowed down by the poloidal component of the magnetic field and the time scale is given by Eq. (2) (i.e., the slow kink case).
From Fig. 1, one can see that the instability acts quickly and accelerates the flow
within 1-2 orders of magnitude in distance from the location of the fast magnetosonic point.
The acceleration is faster in the "fast kink'' case and much more gradual in the "slow kink'' one.
This is due to the fact that close to the base of the flow the ratio
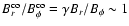 and the instability is slowed down (see Eq. (2)).
Further out, however, the toroidal component of the field also dominates in the frame comoving with the
flow and the instability proceeds faster. At larger distances, practically all the magnetic energy
has been dissipated and the terminal Lorentz factors are very similar in the slow and fast
kink cases.
and the instability is slowed down (see Eq. (2)).
Further out, however, the toroidal component of the field also dominates in the frame comoving with the
flow and the instability proceeds faster. At larger distances, practically all the magnetic energy
has been dissipated and the terminal Lorentz factors are very similar in the slow and fast
kink cases.
![\begin{figure}
\par\includegraphics[angle=270,width=7.8cm,clip]{4107fig1.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg77.gif) |
Figure 1:
The bulk Lorentz factor of the flow as a function of radius for different
values of 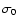 .
The black, red, blue and green curves correspond to .
The black, red, blue and green curves correspond to 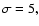 8, 10
and 25 respectively. The solid curves correspond to the case where Eq. (1) is used for the
instability growth time scale (fast kink) and the dashed to the one where Eq. (2) is used
(slow kink case).
8, 10
and 25 respectively. The solid curves correspond to the case where Eq. (1) is used for the
instability growth time scale (fast kink) and the dashed to the one where Eq. (2) is used
(slow kink case). |
| Open with DEXTER |
The acceleration of the flow and the terminal Lorentz factor depend also on what
fraction of the instability-released energy is radiated away. If the dissipative processes
that appear in the non-linear regime of the evolution of the instability lead to fast
moving electrons, then it is easy to check that they will radiate away most of this energy
through synchrotron (and/or inverse Compton) radiation on a time scale much shorter than the
expansion timescale. If, on the other hand, most of the energy is dissipated to the ions,
then most of it stays in the system as internal energy and accelerates the flow further.
To keep this study fairly general, we have calculated the bulk Lorentz factor of the
flow in the two extreme cases. In the "fast cooling'' case, all the released energy is
radiated away very efficiently, while in the "slow cooling'' case, the energy is assumed
to stay in the flow (practically this means that we set the cooling length parameter
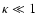 ).
).
In Fig. 2, the bulk Lorentz factor of the flow is plotted for
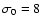 .
The red curves
correspond to the "fast cooling'' case and the black to the "slow cooling'' one. The asymptotic bulk
Lorentz factor differs substantially in these two cases, showing that a large fraction of the
energy of the flow can in principle be radiated away due to the instability-related dissipative
processes. Furthermore, the acceleration of the flow depends on the jet opening angle and is
faster for narrower jets (see green curves in Fig. 2). This is expected, since for a narrower
opening angle, the Alfvén crossing time across the jet is shorter and so is the instability growth
timescale.
.
The red curves
correspond to the "fast cooling'' case and the black to the "slow cooling'' one. The asymptotic bulk
Lorentz factor differs substantially in these two cases, showing that a large fraction of the
energy of the flow can in principle be radiated away due to the instability-related dissipative
processes. Furthermore, the acceleration of the flow depends on the jet opening angle and is
faster for narrower jets (see green curves in Fig. 2). This is expected, since for a narrower
opening angle, the Alfvén crossing time across the jet is shorter and so is the instability growth
timescale.
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig2.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg79.gif) |
Figure 2:
The bulk Lorentz factor dependence on the cooling efficiency of the flow and jet opening angles.
The solid curves correspond to the fast kink case while the dashed to the slow kink one.
The black, red and green curves correspond to fast cooling, slow cooling and jet opening angle
of 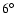 respectively. respectively. |
| Open with DEXTER |
Another quantity of special interest is the Poynting to matter energy flux ratio 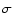 as a function of radius. While the flow is initially moderately Poynting flux
dominated, the
as a function of radius. While the flow is initially moderately Poynting flux
dominated, the 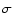 drops rapidly as a function of distance and the flow is matter-dominated
at distances
drops rapidly as a function of distance and the flow is matter-dominated
at distances
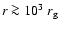 independently of the prescription of
the instability or the cooling timescales. Far enough from the fast magnetosonic point,
practically all the magnetic energy has been transfered to the matter, and the bulk
Lorentz factor saturates.
independently of the prescription of
the instability or the cooling timescales. Far enough from the fast magnetosonic point,
practically all the magnetic energy has been transfered to the matter, and the bulk
Lorentz factor saturates.
The thick lines in Fig. 3 show the ratio of the radial to the
toroidal components of the magnetic field. This ratio drops rapidly as a function of
distance showing that
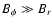 .
So, despite the fact that the
instability grows quickly from the toroidal component of the magnetic field,
this component still dominates over the radial one.
.
So, despite the fact that the
instability grows quickly from the toroidal component of the magnetic field,
this component still dominates over the radial one.
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig3.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg82.gif) |
Figure 3:
The dependence of the magnetization parameter on the radius
for the different prescriptions of radiative cooling and the instability
timescale. Notice that the flow becomes matter-dominated at distances greater than 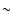 10r0. The thick lines show the ratio of the radial to the toroidal
components of the magnetic field in the flow. The dominant component is clearly the
toroidal one. 10r0. The thick lines show the ratio of the radial to the toroidal
components of the magnetic field in the flow. The dominant component is clearly the
toroidal one. |
| Open with DEXTER |
Having solved for the dynamics of the flow predicted by our modeling of
the kink instability, we turn to the implications of these findings
for observations of AGN jets. One highly debated issue is
whether the AGN jets are Poynting-flux dominated on pc and kpc scales
or not. The case-dependent arguments are reviewed in Sikora et al. (2005),
where it is shown that there is no strong observational reason to assume
Poynting-flux dominated jets on scales larger than a few pc and that the
observed emission on these scales can be understood as energy
dissipated in shocks internally in the flow (Sikora et al. 1994; Spada et al.
2001) or due to interaction of the flow with the external medium.
Our model predicts that most of the energy is in the form of kinetic
flux at distances say 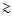
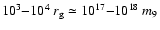 cm, where
m9 is a black hole of 109 solar masses. So, on pc scales the
magnetic fields are dynamically insignificant, in agreement with observations.
Further information on the dynamics of AGN jets comes from the shortest variability
timescale in the optical and gamma-ray bands in blazars. This timescale can
be as short as a few days, indicating that most of the non-thermal radiation comes
from a compact region of size
cm, where
m9 is a black hole of 109 solar masses. So, on pc scales the
magnetic fields are dynamically insignificant, in agreement with observations.
Further information on the dynamics of AGN jets comes from the shortest variability
timescale in the optical and gamma-ray bands in blazars. This timescale can
be as short as a few days, indicating that most of the non-thermal radiation comes
from a compact region of size
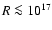 cm (the so-called blazar zone).
On the other hand, polarimetry measurements of the variable optical, infrared and mm
radiation are consistent with a toroidal magnetic field geometry on sub-pc scales
(e.g. Impey et al. 1991; Gabuzda & Sitko 1994; Nartallo et al. 1998).
cm (the so-called blazar zone).
On the other hand, polarimetry measurements of the variable optical, infrared and mm
radiation are consistent with a toroidal magnetic field geometry on sub-pc scales
(e.g. Impey et al. 1991; Gabuzda & Sitko 1994; Nartallo et al. 1998).
Since most of the magnetic energy is dissipated on these scales, it is quite
probable that the observed radiation is the result of the instability-released energy,
provided that the dissipative processes lead to wide enough particle
distributions (see also Sikora et al. 2005). However, one cannot exclude the possibility
that, within this model, the "blazar zone'' emission is a result of internal shocks.
On scales of 1017 cm, the magnetization parameter of the flow is of the order of unity
and it is interesting to study the outcome of internal shocks of moderately magnetized plasma.
The rich blazar phenomenology may indicate that both these mechanisms (i.e. magnetic
dissipation and internal shocks) are at work.
Further constraints on where the acceleration of the flow takes place come from the lack of
bulk-flow Comptonization features in the soft X-rays.
This indicates that
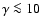 at
at 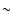
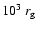 (Begelman & Sikora 1987;
Moderski et al. 2003).
This shows that the acceleration process is still going on at these distances. In view of
our results, this could in principle rule out the "fast kink'' case since the acceleration
appears to be too fast and
(Begelman & Sikora 1987;
Moderski et al. 2003).
This shows that the acceleration process is still going on at these distances. In view of
our results, this could in principle rule out the "fast kink'' case since the acceleration
appears to be too fast and
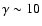 already at
already at 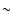
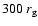 or so. At this point, however,
the uncertainties in the model are too high to make a strong statement on this issue.
If, for example, the fast point is located at a factor of, say,
or so. At this point, however,
the uncertainties in the model are too high to make a strong statement on this issue.
If, for example, the fast point is located at a factor of, say, 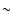 3 larger distance,
our results are compatible with the lack of soft X-ray features. Numerical simulations of the instability
are needed so that these issues can be settled (see also discussion in Sect. 5).
3 larger distance,
our results are compatible with the lack of soft X-ray features. Numerical simulations of the instability
are needed so that these issues can be settled (see also discussion in Sect. 5).
The analysis we follow so as to apply the model to GRBs is very similar
to that described in the previous sections. The only new ingredient
that has to be added is related to the very high luminosities that
characterize the GRB jets. As a result, the inner part of the flow
is optically thick to electron scattering and matter and radiation are
closely coupled. At the photospheric radius the optical depth
drops to unity and further out the flow is optically thin.
So, the high luminosity introduces a new length scale to the
problem that has to be treated in a special way described in the next section.
At the photosphere, the equation of state changes from one dominated
by radiation to one dominated by the gas pressure. To connect the
two, the radiation emitted at the photosphere has to be taken into
account. The amount of energy involved can be substantial, and
appears as an (approximate) black body component in the GRB spectrum.
It depends on the temperature of the photosphere.
The temperature at the photosphere is
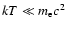 for all
parameter values used so that pairs can be neglected. The photosphere is
then simply defined as (e.g. Abramowicz et al. 1991)
for all
parameter values used so that pairs can be neglected. The photosphere is
then simply defined as (e.g. Abramowicz et al. 1991)
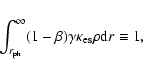 |
(22) |
where
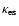 is the electron scattering opacity.
The dynamics of the flow depend on the location of the photosphere
since above the photosphere all the dissipated energy can in principle
be radiated away while this is not possible at large optical depths.
To solve Eq. (22) for
is the electron scattering opacity.
The dynamics of the flow depend on the location of the photosphere
since above the photosphere all the dissipated energy can in principle
be radiated away while this is not possible at large optical depths.
To solve Eq. (22) for
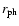 ,
we have followed an
iterative method. First, we guess a value for
,
we have followed an
iterative method. First, we guess a value for
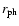 and integrate
the dynamical equations assuming no radiative losses below the photosphere
and fast cooling above it. Then we calculate the optical depth
and integrate
the dynamical equations assuming no radiative losses below the photosphere
and fast cooling above it. Then we calculate the optical depth 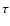 from
from
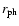 to
to 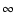 and, if
and, if 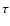 differs from unity by more than a threshold value (
differs from unity by more than a threshold value (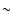 0.01 in these calculations), a new guess for
0.01 in these calculations), a new guess for
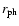 is made.
The procedure continues until the definition (22) is satisfied.
is made.
The procedure continues until the definition (22) is satisfied.
At the photosphere one has to subtract the energy and momentum carried away
by the decoupled radiation. To calculate these
quantities one needs the temperature at the photosphere.
The dimensionless temperature
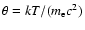 in the optically
thick region is given by the solution of
in the optically
thick region is given by the solution of
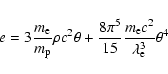 |
(23) |
where
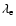 is the electron Compton wave length. The terms in Eq. (23) correspond to the matter and radiation energy density. From this solution,
we have also found that the internal energy is always dominated by radiation
(for parameters relevant for GRBs), so we take
is the electron Compton wave length. The terms in Eq. (23) correspond to the matter and radiation energy density. From this solution,
we have also found that the internal energy is always dominated by radiation
(for parameters relevant for GRBs), so we take
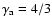 below the photosphere.
below the photosphere.
At the photosphere we calculate the temperature
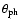 and subtract the radiation energy density of a black body
and subtract the radiation energy density of a black body
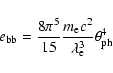 |
(24) |
from the total energy density:
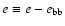 .
The
integration proceeds with an adiabatic index of
.
The
integration proceeds with an adiabatic index of
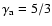 .
The
temperature
.
The
temperature
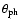 is the temperature of the emitted
black-body radiation which has a luminosity per sterad of
is the temperature of the emitted
black-body radiation which has a luminosity per sterad of
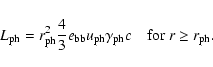 |
(25) |
The integration continues until large distances from the source (taken as 1016 cm, where
the afterglow phase starts). There, the
radiative luminosity is determined by
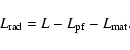 |
(26) |
This means that the radiative luminosity is the sum of the photospheric luminosity
plus the component coming from the instability-released energy above the photosphere.
The role of the photospheric component and its connection to the observed spectral
peaks of the GRB prompt emission in internal shock and slow dissipation models
(like this one) has been studied in a number of recent papers (Ryde 2005;
Rees & Mészáros 2005; Pe'er et al. 2005; Giannios 2006).
Following the procedure described in the previous section, we have
calculated the bulk Lorentz factor of the flow for different
values of 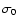 at the base of the flow and for the two
prescriptions for the timescale of the kink instability (Eqs. (1), (2)).
The fast magnetosonic point is set to R0=108 cm, the jet opening angle
to
at the base of the flow and for the two
prescriptions for the timescale of the kink instability (Eqs. (1), (2)).
The fast magnetosonic point is set to R0=108 cm, the jet opening angle
to
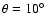 ,
the initial ratio
,
the initial ratio
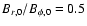 and the luminosity
of the flow
and the luminosity
of the flow
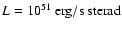 .
.
The results are given in Fig. 4, where it is shown that the flow
reaches terminal Lorentz factors
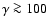 for
for
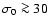 .
The solid curves correspond to the case where the timescale for the kink
instability is given by Eq. (1) (fast kink case) and the dashed to the case
where Eq. (2) is used for the timescale of the growth of the instability
(slow kink case). Notice that the initial acceleration of the flow differs
in the two cases, being much faster in the fast kink case. This is expected
since this case is characterized by rapid dissipation of magnetic
energy and acceleration from the base of the flow, while in the slow kink case
the non-negligible poloidal component of the magnetic field close to r0 slows
down the instability. The terminal Lorentz factors are, however, similar
in the two cases. Notice also that there is a discontinuity in the slope
of the curves
.
The solid curves correspond to the case where the timescale for the kink
instability is given by Eq. (1) (fast kink case) and the dashed to the case
where Eq. (2) is used for the timescale of the growth of the instability
(slow kink case). Notice that the initial acceleration of the flow differs
in the two cases, being much faster in the fast kink case. This is expected
since this case is characterized by rapid dissipation of magnetic
energy and acceleration from the base of the flow, while in the slow kink case
the non-negligible poloidal component of the magnetic field close to r0 slows
down the instability. The terminal Lorentz factors are, however, similar
in the two cases. Notice also that there is a discontinuity in the slope
of the curves 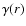 at the location of the photosphere which is a result
of our simplistic approach (for details see previous section).
at the location of the photosphere which is a result
of our simplistic approach (for details see previous section).
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig4.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg108.gif) |
Figure 4:
The bulk Lorentz factor of the flow for different 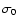 and for the fast and slow kink case. Notice that larger
values for
and for the fast and slow kink case. Notice that larger
values for 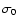 result in faster outflows.
result in faster outflows. |
| Open with DEXTER |
A second key parameter of the model is the opening angle of the jet.
For smaller opening angles, the instability timescale becomes
shorter and the flow is accelerated faster and to higher terminal
Lorentz factors as is shown in Fig. 5. This implies that
for smaller opening angles, more magnetic energy is dissipated
and the flow is less strongly magnetized at large distances.
This is clearly shown in Fig. 6, where the Poynting to
matter energy flux ratio is plotted as a function of radius r(compare the thin curve with the thick black dashed curves).
Notice that the 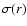 curves are discontinuous at the location of
the photosphere. This is caused by our simplified treatment at the
location of the photosphere, where we subtract the energy density
of the radiation field (see previous section) and reduce the internal
enthalpy of the flow, increasing the ratio of Poynting to matter energy
flux. More detailed radiative transfer models of the transition from optically thick
to optically thin condition, predict a rather sharp transition which
indicates that our simple approach does not introduce large
errors.
curves are discontinuous at the location of
the photosphere. This is caused by our simplified treatment at the
location of the photosphere, where we subtract the energy density
of the radiation field (see previous section) and reduce the internal
enthalpy of the flow, increasing the ratio of Poynting to matter energy
flux. More detailed radiative transfer models of the transition from optically thick
to optically thin condition, predict a rather sharp transition which
indicates that our simple approach does not introduce large
errors.
In Figs. 5 and 6 we have also plotted (see blue curves) the bulk Lorentz factor
and the magnetization 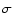 as functions of r for the "typical values'' of the
parameters of the model proposed by Drenkhahn & Spruit (2002, the "AC'' flow). In the context of that
model the magnetic field lines change direction on small scales and magnetic reconnection
dissipates magnetic energy and accelerates the flow. Notice that the non-axisymmetric model predicts
more gradual acceleration and rather higher terminal Lorentz factors (for the same
initial magnetization of the flow) than the current model. Furthermore, it is characterized by
efficient dissipation of the Poynting flux, resulting in negligible magnetization sufficiently far
from the central engine (at least in the case where the non-decayable axisymmetric component
is negligible).
as functions of r for the "typical values'' of the
parameters of the model proposed by Drenkhahn & Spruit (2002, the "AC'' flow). In the context of that
model the magnetic field lines change direction on small scales and magnetic reconnection
dissipates magnetic energy and accelerates the flow. Notice that the non-axisymmetric model predicts
more gradual acceleration and rather higher terminal Lorentz factors (for the same
initial magnetization of the flow) than the current model. Furthermore, it is characterized by
efficient dissipation of the Poynting flux, resulting in negligible magnetization sufficiently far
from the central engine (at least in the case where the non-decayable axisymmetric component
is negligible).
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig5.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg109.gif) |
Figure 5:
The bulk Lorentz factor of the flow for different jet opening angles 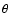 .
For smaller opening angles, the terminal Lorentz factors of the flow become
larger because of more efficient dissipation of the magnetic energy.
The blue curve corresponds to the non-axisymmetric case studied by Drenkhahn & Spruit (2002). .
For smaller opening angles, the terminal Lorentz factors of the flow become
larger because of more efficient dissipation of the magnetic energy.
The blue curve corresponds to the non-axisymmetric case studied by Drenkhahn & Spruit (2002).
|
| Open with DEXTER |
One important point deduced from Fig. 6 is that, for
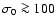 ,
the flow remains Poynting-flux dominated even at large distances away from the
source where deceleration of the outflow because of its interaction
with the interstellar medium or the stellar wind is expected, which means
that the instability is not fast enough to convert most of the
magnetic energy into bulk motion of matter. Afterglow observations
can in principle probe to the magnetic content of the ejecta through early
observations of the reverse shock emission (Fan et al. 2002; Zhang et al. 2003;
Kumar & Panaitescu 2003). Modeling of the
forward and reverse shock emission in cases where quick follow ups were possible
suggests the existence of frozen-in magnetic fields in the ejecta (Kumar & Panaitescu 2003)
that are dynamically important, with
,
the flow remains Poynting-flux dominated even at large distances away from the
source where deceleration of the outflow because of its interaction
with the interstellar medium or the stellar wind is expected, which means
that the instability is not fast enough to convert most of the
magnetic energy into bulk motion of matter. Afterglow observations
can in principle probe to the magnetic content of the ejecta through early
observations of the reverse shock emission (Fan et al. 2002; Zhang et al. 2003;
Kumar & Panaitescu 2003). Modeling of the
forward and reverse shock emission in cases where quick follow ups were possible
suggests the existence of frozen-in magnetic fields in the ejecta (Kumar & Panaitescu 2003)
that are dynamically important, with
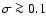 (Zhang & Kobayashi 2005).
Rapid follow-ups in the X-rays, UV and optical are now possible thanks to Swift
satellite and ground based telescopes and can test our
model which predicts a magnetization parameter of the order of unity for the
outflowing material in the afterglow region. The XRT instrument on board Swift
has already provided several early X-ray afterglows (e.g. Tagliaferri et al. 2005; Campana et al.
2005; Burrows et al. 2005). Many of these observations
indicate a slow fading component at times
102-104 s after the GRB trigger (Nowsek et al.
2005; Zhang et al. 2005; Panaitescu et al. 2005) which may be expected by the deceleration
of ejecta with
(Zhang & Kobayashi 2005).
Rapid follow-ups in the X-rays, UV and optical are now possible thanks to Swift
satellite and ground based telescopes and can test our
model which predicts a magnetization parameter of the order of unity for the
outflowing material in the afterglow region. The XRT instrument on board Swift
has already provided several early X-ray afterglows (e.g. Tagliaferri et al. 2005; Campana et al.
2005; Burrows et al. 2005). Many of these observations
indicate a slow fading component at times
102-104 s after the GRB trigger (Nowsek et al.
2005; Zhang et al. 2005; Panaitescu et al. 2005) which may be expected by the deceleration
of ejecta with
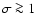 (Zhang & Kobayashi 2005; Zhang et al. 2005)
in agreement with our model predictions.
(Zhang & Kobayashi 2005; Zhang et al. 2005)
in agreement with our model predictions.
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig6.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg113.gif) |
Figure 6:
The magnetization 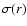 of the flow as a function of distance for
different
of the flow as a function of distance for
different 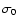 and jet opening angles. Keeping
and jet opening angles. Keeping
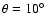 ,
the jet is
still magnetically dominated at large distance from the source for ,
the jet is
still magnetically dominated at large distance from the source for
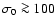 .
Smaller jet opening angles lead to lower values of .
Smaller jet opening angles lead to lower values of
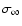 .
The blue curve corresponds to the non-axisymmetric case studied by Drenkhahn & Spruit (2002).
The discontinuity at the location of the photospheric radius is a result of the subtraction of
the radiation energy density from the internal energy of the flow. .
The blue curve corresponds to the non-axisymmetric case studied by Drenkhahn & Spruit (2002).
The discontinuity at the location of the photospheric radius is a result of the subtraction of
the radiation energy density from the internal energy of the flow.
|
| Open with DEXTER |
The ratio 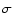 is even higher for the range of distances
is even higher for the range of distances
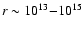 cm
where internal shocks are expected to happen in the internal shock scenario for GRBs (Rees &
Mészáros 1994; Piran 1999) and is expected the reduce their radiative efficiency.
However, allowing for non-ideal MHD effects in the shocked region, Fan et al. (2004) show that
the radiative efficiency of
cm
where internal shocks are expected to happen in the internal shock scenario for GRBs (Rees &
Mészáros 1994; Piran 1999) and is expected the reduce their radiative efficiency.
However, allowing for non-ideal MHD effects in the shocked region, Fan et al. (2004) show that
the radiative efficiency of
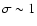 plasma may not be much lower than
the
plasma may not be much lower than
the 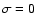 case. On the other hand, since the efficiency of internal
shocks to convert kinetic energy into gamma rays is already low (typically
of the order of a few percent; Panaitescu et al. 1999; Kumar 1999) and observations indicate
much higher radiative efficiency (Panaitescu & Kumar 2002; Lloyd & Zhang 2004), we investigate
the possibility that the energy released by the instability powers the prompt gamma-ray emission.
case. On the other hand, since the efficiency of internal
shocks to convert kinetic energy into gamma rays is already low (typically
of the order of a few percent; Panaitescu et al. 1999; Kumar 1999) and observations indicate
much higher radiative efficiency (Panaitescu & Kumar 2002; Lloyd & Zhang 2004), we investigate
the possibility that the energy released by the instability powers the prompt gamma-ray emission.
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig7.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg117.gif) |
Figure 7:
The radiative efficiency of the flow, defined as the ratio of the radiated luminosity
over the luminosity of the flow for different 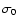 and
and 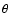 .
The black and red stars
correspond to the fast kink and slow kink cases respectively. For opening angles of .
The black and red stars
correspond to the fast kink and slow kink cases respectively. For opening angles of 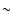 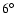 (in accordance with the values deduced by achromatic breaks of the afterglows) the efficiency
reaches values of (in accordance with the values deduced by achromatic breaks of the afterglows) the efficiency
reaches values of 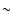 20%. The circles correspond to the non-axisymmetric case studied
by Drenkhahn & Spruit (2002). 20%. The circles correspond to the non-axisymmetric case studied
by Drenkhahn & Spruit (2002).
|
| Open with DEXTER |
In Fig. 7, we plot the
radiative efficiency - defined as the radiated luminosity
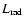 divided by the flow
luminosity L - for different values of
divided by the flow
luminosity L - for different values of 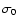 and
and 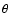 .
Fixing the angle
.
Fixing the angle 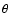 to
to 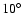 ,
one can see that the radiative efficiency peaks at
,
one can see that the radiative efficiency peaks at 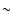 16%
for
16%
for
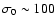 .
For smaller values of
.
For smaller values of 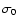 ,
most of the magnetic energy is
dissipated below the photosphere and is lost to adiabatic expansion, resulting in lower
radiative efficiencies. For larger values of
,
most of the magnetic energy is
dissipated below the photosphere and is lost to adiabatic expansion, resulting in lower
radiative efficiencies. For larger values of 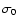 ,
the flow remains magnetically
dominated at all radii, keeping the radiative efficiency lower. Furthermore,
the "slow kink'' case has rather higher efficiencies and this comes from the
fact that dissipation happens at larger radii and therefore in optically thin
environments. So, the model can have large radiative efficiencies for
,
the flow remains magnetically
dominated at all radii, keeping the radiative efficiency lower. Furthermore,
the "slow kink'' case has rather higher efficiencies and this comes from the
fact that dissipation happens at larger radii and therefore in optically thin
environments. So, the model can have large radiative efficiencies for
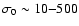 .
Notice that one also needs
.
Notice that one also needs
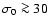 to
overcome the "compactness problem'' (e.g. Piran 1999).
to
overcome the "compactness problem'' (e.g. Piran 1999).
Fixing
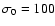 ,
one can now calculate the radiative efficiency for different
opening angles of the flow. Smaller opening angles result in more magnetic energy
dissipated (by shortening the instability timescale) and therefore
to smaller values of Poynting to matter flux at large distances. This also means
that more energy is radiated away. Although very model dependent, the opening angles
of the GRB jets can be estimated by the achromatic breaks of the afterglow lightcurves
(Rhoads 1997; Sari et al. 1999). For
,
one can now calculate the radiative efficiency for different
opening angles of the flow. Smaller opening angles result in more magnetic energy
dissipated (by shortening the instability timescale) and therefore
to smaller values of Poynting to matter flux at large distances. This also means
that more energy is radiated away. Although very model dependent, the opening angles
of the GRB jets can be estimated by the achromatic breaks of the afterglow lightcurves
(Rhoads 1997; Sari et al. 1999). For
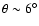 (a value typically inferred),
the efficiency is quite high and of the order of 20%.
(a value typically inferred),
the efficiency is quite high and of the order of 20%.
In Fig. 7, the radiative efficiency of the
non-axisymmetric model (Drenkhahn & Spruit 2002) is also shown for different values
of 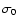 .
The non-axisymmetric model can have a higher radiative efficiency
which is close to
.
The non-axisymmetric model can have a higher radiative efficiency
which is close to 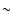
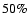 for
for
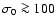 (see also Giannios & Spruit 2005,
for more detailed study on the spectra expected from this model).
(see also Giannios & Spruit 2005,
for more detailed study on the spectra expected from this model).
This work suggests that the kink instability plays a significant role in the dynamics
of magnetized outflows. The instability sets in once the toroidal component of the magnetic
field becomes dominant and drives its energy by 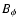 on a short time scale. The energy dissipated
by the instability accelerates the flow and turns it into kinetic flux dominated flow
for AGN jets at distance
on a short time scale. The energy dissipated
by the instability accelerates the flow and turns it into kinetic flux dominated flow
for AGN jets at distance 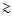
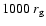 and to moderately magnetized flow for GRB jets in the
the afterglow region. If the dissipated magnetic energy is transferred to fast moving
electrons with wide enough energy distribution, then it can power the blazar zone emission
and the prompt GRB emission with high radiative efficiency.
and to moderately magnetized flow for GRB jets in the
the afterglow region. If the dissipated magnetic energy is transferred to fast moving
electrons with wide enough energy distribution, then it can power the blazar zone emission
and the prompt GRB emission with high radiative efficiency.
These results have been compared with those that are predicted by other
dissipative models (Coroniti 1990; Spruit et al. 2001; Lyubarsky & Kirk 2001;
Drenkhahn 2002; Drenkhahn & Spruit 2002). According to these models, if the magnetic field
lines change direction on small
scales, magnetic energy can be dissipated through reconnection processes. Drenkhahn (2002) and
Drenkhahn & Spruit (2002) applied this idea to GRB outflows and showed that efficient acceleration
and radiation (as high as 50%) is possible. In the context of this model, most of the magnetic energy
is dissipated, resulting in kinetic flux dominated flows at large distances where the flow starts
to be decelerated by the external medium. On the other hand, our model predicts moderately
magnetized ejecta at this region. Since the initial phase of the afterglow emission depends
on the magnetic content of the ejecta (e.g. Lyutikov 2005), these models make different
predictions about this phase and can be tested against observations.
This study assumes a radial flow and although this allowed us to minimize the number
of free parameters and clarify the role of each of them, it nevertheless leaves a number
of issues unsettled. Two important issues are these of jet collimation and of the non-linear
evolution of the kink instability. We discuss these issues in the next subsections.
The collimation of MHD outflows is usually believed to take place in the trans-Alfvénic
region because of the "hoop stress'' exerted by the toroidal component of the magnetic
field. One issue that arises is whether the same mechanism is at work in the case where
the kink instability sets in and reduces the strength of 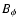 .
Our one dimensional approach cannot settle this question; 2-D calculations would be
needed if the instability is parametrized as in the present models. Time dependent, 3-D simulations will be needed if the effects of the instability are to be included realistically,
since the relevant ones are nonaxisymmetric.
Collimation of the flow can be achieved by its interaction with the environment.
This may be the collapsing star in the context of gamma-ray bursts (Woosley 1993) or a large scale
poloidal field in the case of AGN jets (Spruit et al. 1997). Another interesting possibility
is that small scale toroidal fields (probably a result of the development of the instability)
can lead to flow collimation under certain conditions (Li 2002).
.
Our one dimensional approach cannot settle this question; 2-D calculations would be
needed if the instability is parametrized as in the present models. Time dependent, 3-D simulations will be needed if the effects of the instability are to be included realistically,
since the relevant ones are nonaxisymmetric.
Collimation of the flow can be achieved by its interaction with the environment.
This may be the collapsing star in the context of gamma-ray bursts (Woosley 1993) or a large scale
poloidal field in the case of AGN jets (Spruit et al. 1997). Another interesting possibility
is that small scale toroidal fields (probably a result of the development of the instability)
can lead to flow collimation under certain conditions (Li 2002).
The linear evolution of the kink instability is rather well understood and has
been studied by linearizing the MHD equations by a number of authors (e.g. Begelman 1998;
Appl et al. 2000), which shows that the instability grows on the Alfvén crossing time across
the jet. The non-linear evolution of the instability is an issue that
cannot be solved with analytical tools and 3-dimensional RMHD simulations that
cover many decades of radii are needed to settle this issue. Preliminary numerical
investigations have been done (e.g. Lery et al. 2000; Ouyed et al. 2003; Nakamura & Meier
2004) which indicate that the kink instability is an internal mode that does not disrupt the
jet. On the other hand, whether it is able to rearrange the magnetic field configuration
internally in the flow on the short timescale implied by linear stability analysis is still
not clear.
Some intuition on this issue can be gained by this study. We have tried two different
prescriptions for the instability growth time scale, the second of which accounts for its
possible slowing down because of a strong poloidal "backbone'' in the core on the jet
(Ouyed et al. 2003). A non-negligible poloidal component can slow down the
initial growth of the instability; eventually it grows in a conical jet. This occurs
because as the jet expands, the 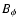 and Bp scale as 1/r and 1/r2 respectively so as to
satisfy the induction equation. This means that the toroidal component
dominates the poloidal at some point and the instability sets in. A study that assumes a cylindrical jet,
on the other hand, will not deal with the
and Bp scale as 1/r and 1/r2 respectively so as to
satisfy the induction equation. This means that the toroidal component
dominates the poloidal at some point and the instability sets in. A study that assumes a cylindrical jet,
on the other hand, will not deal with the
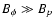 situation. Since the observed jets
do expand laterally (despite their strong collimation) by many orders in radius from their
launching region to their termination shock, we believe that it is important for numerical
investigations of the role of kink instability to allow for jet expansion to reveal the
characteristics of the non-linear development of the instability.
situation. Since the observed jets
do expand laterally (despite their strong collimation) by many orders in radius from their
launching region to their termination shock, we believe that it is important for numerical
investigations of the role of kink instability to allow for jet expansion to reveal the
characteristics of the non-linear development of the instability.
The limitations of the calculations presented here are obvious from the
parameterizations used. One may wonder to what extent these can be overcome in
numerical simulations. Since the most relevant instabilities are
nonaxisymmetric, such simulations have to be 3-dimensional. The computational expense of 3D
MHD simulations puts strong limitations on the kind of calculations that can be
done, and the realism of the conclusions that can be drawn from them. An
astrophysical jet operates over many decades in length scale, with different physics
dominating at different distances from the source.
For reasons of computational feasibility, the 3D simulations that have been
done so far use only a small range in distance, or a cylindrical geometry
(e.g. Nakamura et al. 2001; Ouyed et al. 2003; Nakamura & Meier 2004).
In the first case, the range of distance
is too narrow to follow the consequences of 3-D instabilities effectively.
In the second case, the effect of instability is limited by the boundaries.
It is well known that kink instability can saturate into a finite amplitude,
helical equilibrium when confined in a cylinder (in the astrophysical context
see e.g. Königl & Choudhuri 1986; Lyubarskii 1999).
But a computational cylinder taylored to the size of the source covers a
negligible range in length scales perpendicular to the axis, compared with an actual
jet. If, instead, the simulations were done in a spherical or conical geometry, the
continued expansion of the flow would stretch these helical configurations
perpendicular to the axis, immediately making them unstable again. This is the rationale for our
assumption that dissipation by instability will be a process that persists
for a large distance along the jet.
It may be possible to make numerical progress in, say, a conical
geometry, but limitations due to the finite range in length scales and time scales that
can be achieved will remain serious. For this reason, it is important to isolate
physical effects that can not (yet) be included realistically in simulations, and
explore them in more approximate models like the ones we have presented here.
The standard scenario for jet launching, acceleration and collimation involves
large scale magnetic fields anchored to a rotating object (e.g. Blandford & Payne 1982;
Sakurai 1985). The flow passes through
three critical points, i.e. the slow, the Alfvén and the fast point. At the fast
point the ratio of Poynting to matter energy flux is much larger than unity
in the case of relativistic jets (Michel 1967; Camenzind 1986; Beskin et al. 1998)
while further acceleration of the flow appears hard to achieve within ideal MHD except if the flow is decollimated (Li et al. 1992; Begelman & Li 1994).
In this work, we study how this picture is modified when one takes into account the
fastest growing current driven instability, i.e. the m=1 mode kink instability.
We have modeled the instability by modifying the induction equation to account for non-ideal
MHD processes and solving the relativistic MHD equations in the case of a radial flow.
The instability is driven by 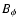 ,
dissipates Poynting flux and has been shown to be an efficient
mechanism to accelerate the flow.
,
dissipates Poynting flux and has been shown to be an efficient
mechanism to accelerate the flow.
The key parameter of the model is the ratio 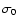 of the Poynting to matter energy flux
at the base of the flow. A large part of the AGN jet phenomenology can be understood in the
context of this model for
of the Poynting to matter energy flux
at the base of the flow. A large part of the AGN jet phenomenology can be understood in the
context of this model for
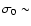 several. On sub-pc scales the flow is
Poynting-flux dominated with
several. On sub-pc scales the flow is
Poynting-flux dominated with
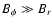 .
The flow is shown to be accelerated fast and to
become matter dominated already at
.
The flow is shown to be accelerated fast and to
become matter dominated already at  pc scales, while it reaches terminal bulk factors
of a few tens. The emission at the blazar zone can be a result of either internal shocks
that take place in an unsteady flow, where fast shells catch up with slower ones, converting
a small fraction of the bulk kinetic energy of the flow into radiation (Rees & Mészáros 1994;
Spada et al. 2001), or direct manifestation of the energy released by the instability.
pc scales, while it reaches terminal bulk factors
of a few tens. The emission at the blazar zone can be a result of either internal shocks
that take place in an unsteady flow, where fast shells catch up with slower ones, converting
a small fraction of the bulk kinetic energy of the flow into radiation (Rees & Mészáros 1994;
Spada et al. 2001), or direct manifestation of the energy released by the instability.
Within the same model, we propose that GRBs are a result of more Poynting
flux dominated outflows with
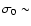 100. For these values of
100. For these values of 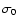 the
flow reaches terminal bulk Lorentz factors of the order of a few to several hundreds, while
it remains moderately magnetized (i.e.
the
flow reaches terminal bulk Lorentz factors of the order of a few to several hundreds, while
it remains moderately magnetized (i.e.
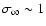 )
at the afterglow region region.
Although there is evidence for magnetized ejecta from afterglow modeling (e.g. Kumar &
Panaitescu 2003; Zhang & Kobayashi 2005), more results are anticipated from early afterglow
follow-ups that can test the model.
)
at the afterglow region region.
Although there is evidence for magnetized ejecta from afterglow modeling (e.g. Kumar &
Panaitescu 2003; Zhang & Kobayashi 2005), more results are anticipated from early afterglow
follow-ups that can test the model.
In the internal shock scenario for the prompt GRB emission, the shells collide at
typical distances of
1013-1015 cm, where the flow is moderately Poynting-flux
dominated. On the other hand, internal shock and Poynting-flux models exclude each other somewhat. If a
strong magnetic field is added to an internally-shocked outflow, the radiative efficiency
is further reduced with respect to that expected from the collision of unmagnetized shells
(e.g. Fan et al. 2004). At the same time, dissipation in a predominantly magnetic outflow by instability
(DC model) or internal reconnection (AC model) can produce radiation naturally at
very high efficiency (up to 50%).
Acknowledgements
Giannios acknowledges support from the EU FP5 Research Training Network "Gamma Ray Bursts:
An Enigma and a Tool''.
-
Abramowicz, M. A., Novikov, I. D., & Paczynski, B. 1991, ApJ,
369, 175 [NASA ADS] [CrossRef] (In the text)
- Aloy, M. A., Janka,
H.-T., & Müller, E. 2005, A&A, 436, 273 [EDP Sciences] [NASA ADS] [CrossRef]
- Appl, S., Lery, T.,
& Baty, H. 2000, A&A, 355, 818 [NASA ADS] (In the text)
- Bateman, G.
1978, MHD Instabilities (Cambridge: MIT Press)
(In the text)
- Baty, H., &
Keppens, R. 2002, ApJ, 580, 800 [NASA ADS] [CrossRef] (In the text)
- Begelman,
M. C., & Sikora, M. 1987, ApJ, 322, 650 [NASA ADS] [CrossRef] (In the text)
- Begelman,
M. C., & Li, Z.-Y. 1994, ApJ, 426, 269 [NASA ADS] [CrossRef] (In the text)
- Begelman,
M. C. 1998, ApJ, 493, 291 [NASA ADS] [CrossRef] (In the text)
- Beskin, V. S.,
Kuznetova, I. V., & Rafikov, R. R. 1998, MNRAS, 299, 341 [NASA ADS] [CrossRef] (In the text)
-
Bisnovatyi-Kogan, G. S., & Ruzmaikin, A. A. 1976, Ap&SS,
42, 401 [NASA ADS] (In the text)
-
Blandford, R. D. 1976, MNRAS, 176, 465 [NASA ADS] (In the text)
-
Blandford, R. D., & Znajek, R. L. 1977, MNRAS, 179, 433 [NASA ADS] (In the text)
-
Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] (In the text)
-
Blinnikov, S. I., Novikov, I. D., Perevodchikova, T. V., &
Polnarev, A. G. 1984, Sov. Astron. Lett., 10, 177 [NASA ADS]
- Bodo, D., Rosner,
R., Ferrari, A., & Knobloch, E. 1989, ApJ, 341, 631 [NASA ADS] [CrossRef] (In the text)
-
Bogovalov, S. V. 2001, A&A, 371, 1155 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Burrows, D.
N., Romano, P., Falcone, A., et al. 2005, Science, 309, 1833 [NASA ADS] [CrossRef] (In the text)
-
Camenzind, M. 1986, A&A, 162, 32 [NASA ADS] (In the text)
- Campana, S.,
Antonelli, L. A., Chincarini, G., et al. 2005, ApJ, 625, L23 [NASA ADS] [CrossRef] (In the text)
- Coroniti,
F. V. 1990, ApJ, 349, 538 [NASA ADS] [CrossRef] (In the text)
- Daigne, F.,
& Drenkhahn, G. 2002, A&A, 381, 1066 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Drenkhahn, G. 2002, A&A, 387, 714 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Drenkhahn, G., & Spruit, H. C. 2002, A&A, 391, 1141 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Eichler, D.
1993, ApJ, 419, 111 [NASA ADS] [CrossRef] (In the text)
- Eichler, D.,
Livio, M., Piran, T., & Schramm., D. N. 1989, Nature, 340,
126 [NASA ADS] [CrossRef]
- Fan, Y. Z., Dai, Z.
G., Huang, Y. F., & Lu, T. 2002, Chinese J. Astron. Astrophys.,
2, 449 [NASA ADS] (In the text)
- Fan, Y. Z., Wei, D.
M., & Zhang, B. 2004, MNRAS, 354, 1031 [NASA ADS] [CrossRef] (In the text)
- Fendt, C., &
Ouyed, R. 2004, ApJ, 608, 378 [NASA ADS] [CrossRef] (In the text)
- Ferrari, A.,
Trussoni, E., & Zaninetti, L. 1981, MNRAS, 196, 1051 [NASA ADS] (In the text)
- Gabuzda, D.
C., & Sitko, M. L. 1994, AJ, 107, 884 [NASA ADS] [CrossRef] (In the text)
- Giannios, D.
2006, A&A, submitted [arXiv:astro-ph/0602397]
- Giannios,
D., & Spruit, H. C. 2005, A&A, 430, 1 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Goldreich, P., & Julian, W. H. 1970, ApJ, 160, 971 [NASA ADS] [CrossRef] (In the text)
- Goodman, J.
1986, ApJ, 308, L47 [NASA ADS] [CrossRef] (In the text)
- Hardee, P. E.,
& Rosen, A. 1999, ApJ, 524, 650 [NASA ADS] [CrossRef] (In the text)
- Impey, C. D.,
Lawrence, C. R., & Tapia, S. 1991, ApJ, 375, 46 [NASA ADS] [CrossRef] (In the text)
- Janka, H.-T.,
Eberl, T., Ruffert, M., & Fryer, C. L. 1999, ApJ, 527, L39 [NASA ADS] [CrossRef]
- Jaroszynski,
M. 1993, Acta Astron., 43, 183 [NASA ADS]
-
Kadomtsev, B. B. 1966, Rev. Plasma Phys., 2, 153 [NASA ADS] (In the text)
- Kersalé,
E., Longaretti, P.-Y., & Pelletier, G. 2000, A&A, 363,
1166 [NASA ADS] (In the text)
- Kluzniak, W., &
Ruderman, M. 1998, ApJ, 505, L113 [NASA ADS] [CrossRef] (In the text)
- Königl, A.,
& Choundury, A. R. 1985, ApJ, 289, 173 [NASA ADS] [CrossRef]
- Königl, A.,
& Granot, J. 2002, ApJ, 574, 134 [NASA ADS] [CrossRef] (In the text)
- Kumar, P. 1999,
ApJ, 523, 113 [NASA ADS] [CrossRef] (In the text)
- Kumar, P., &
Panaitescu, A. 2003, MNRAS, 346, 905 [NASA ADS] [CrossRef] (In the text)
- Lery, T, Baty, H.,
& Appl, S. 2000, A&A, 355, 1201 [NASA ADS] (In the text)
- Li, L.-X. 2002, ApJ,
564, 108 [NASA ADS] [CrossRef] (In the text)
- Li, Z.-Y., Begelman, M.
C., & Chiuch, T. 1992, ApJ, 384, 567 [NASA ADS] [CrossRef] (In the text)
- Lloyd-Ronning, N.
M., & Zhang, B. 2004, ApJ, 613, 477 [NASA ADS] [CrossRef] (In the text)
-
Longaretti, P.-Y. 2003, Phys. Lett. A, 320, 215 [NASA ADS] [CrossRef] (In the text)
- Lovelace,
R. V. E. 1976, Nature, 262, 649 [NASA ADS] [CrossRef] (In the text)
-
Lyubarskii, Yu. E. 1999, MNRAS, 308, 1006 [NASA ADS] [CrossRef] (In the text)
-
Lyubarsky, Y., & Kirk, J. G. 2001, ApJ, 547, 437 [NASA ADS] [CrossRef] (In the text)
- Lyutikov,
M. 2001, Phys. Fluids, 14, 963 [NASA ADS] [CrossRef] (In the text)
- Lyutikov,
M., & Blandford, R. D. 2003
[arXiv:astro-ph/0312347]
(In the text)
- Lyutikov,
M. 2005 [arXiv:astro-ph/0512342]
(In the text)
-
MacFadyen, A., & Woosley, S. E. 1999, ApJ, 524, 262 [NASA ADS] [CrossRef]
- Mestel, L.
1968, MNRAS, 138, 359 [NASA ADS] (In the text)
- Michel, F. C.
1969, ApJ, 158, 727 [NASA ADS] [CrossRef] (In the text)
-
Mochkovitch, R., Hernanz, M., Isern, J., & Martin, X. 1993,
Nature, 361, 236 [NASA ADS] [CrossRef]
- Moderski,
R., Sikora, M., & Bla
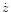 ejowski, M. 2003, A&A, 406, 855 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
ejowski, M. 2003, A&A, 406, 855 [EDP Sciences] [NASA ADS] [CrossRef] (In the text) - Nakamura,
M., Uchida, Y., & Hirose, S. 2001, New Astron., 6, 61 [NASA ADS] (In the text)
- Nakamura,
M., & Meier, D. L. 2004, ApJ, 617, 123 [NASA ADS] [CrossRef] (In the text)
- Nartallo,
R., Gear, W. K., Murray, A. G., et al. 1998, MNRAS, 297, 667 [NASA ADS] [CrossRef] (In the text)
- Nousek, J. A.,
Kouveliotou, C., Grupe, D., et al. 2005, ApJ, submitted
[arXiv:astro-ph/0508332]
- Ouyed, R.,
Clarke, D. A., & Pudritz, R. E. 2003, ApJ, 582, 292 [NASA ADS] [CrossRef] (In the text)
- Paczynski, B.
1986, ApJ, 308, L43 [NASA ADS] [CrossRef] (In the text)
-
Panaitescu, A., Spada, M., & Mészáros, P. 1999, ApJ,
522, 105 [NASA ADS] [CrossRef] (In the text)
-
Panaitescu, A., & Kumar, P., 2002, ApJ, 571, 779 [NASA ADS] [CrossRef] (In the text)
-
Panaitescu, A., Mészáros, P., Gehrels, N., Burrows. D.,
& Nousek, J. 2005, MNRAS, in press
[arXiv:astro-ph/0508340]
(In the text)
- Pe'er, A., Rees, M. J.,
& Mészáros, P. 2005, ApJ, 635, 476 [NASA ADS] [CrossRef] (In the text)
- Piran, T. 1999,
Phys. Rep., 314, 575 [NASA ADS] [CrossRef] (In the text)
- Ray, T. P. 1981,
MNRAS, 196, 195 [NASA ADS] (In the text)
- Rees, M. J., &
Mészáros, P. 1994, ApJ, 430, L93 [NASA ADS] [CrossRef] (In the text)
- Rees, M. J., &
Mészáros, P. 2005, ApJ, 628, 847 [NASA ADS] [CrossRef] (In the text)
- Rhoads, J. E.
1997, 487, L1
(In the text)
- Ryde, F. 2005, ApJ,
625, L95 [NASA ADS] [CrossRef] (In the text)
- Sakurai, T.
1985, A&A, 152, 121 [NASA ADS] (In the text)
- Sakurai, T.
1987, PASJ, 39, 821 [NASA ADS] (In the text)
- Sari, R., Piran,
T., & Halpern, J. P. 1999, ApJ, 519, L17 [NASA ADS] [CrossRef] (In the text)
- Sikora, M.,
Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 153 [NASA ADS] [CrossRef] (In the text)
- Sikora, M.,
Begelman, M. C., Madejski, M. G., & Lasota, J.-P. 2005, ApJ,
625, 72 [NASA ADS] [CrossRef] (In the text)
- Spada, M.,
Ghiselini, G., Lazzati, D., & Celloti, A. 2001, MNRAS, 325,
1559 [NASA ADS] [CrossRef] (In the text)
- Spruit, H. C.
1999, A&A, 341, L1 [NASA ADS] (In the text)
- Spruit, H. C.,
Foglizzo, T., & Stehle, R. 1997, MNRAS, 288, 333 [NASA ADS] (In the text)
- Spruit, H. C.,
Daigne, F., & Drenkhahn, G. 2001, A&A, 369, 694 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Spruit, H. C.,
& Drenkhahn, G. 2003, Magnetically powered prompt radiation and
flow acceleration in GRB, in Proceedings "Gamma Ray Bursts in the
Afterglow Era, Third Workshop'', Rome, Sep. 2002, 357
[arXiv:astro-ph/0302468]
(In the text)
-
Tagliaferri, G., Goad, M., Chincarini, G., et al. 2005, Nature,
436, 985 [NASA ADS] [CrossRef] (In the text)
- Thompson,
C. 1994, MNRAS, 270, 480 [NASA ADS] (In the text)
- Usov, V. V. 1992,
Nature, 357, 472 [NASA ADS] [CrossRef] (In the text)
- Vlahakis,
N., & Königl 2003a, ApJ, 596, 1080 [NASA ADS] [CrossRef] (In the text)
- Vlahakis,
N., & Königl 2003b, ApJ, 596, 1104 [NASA ADS] [CrossRef]
- Weber, E. J.,
& Davis, L. 1967, ApJ, 148, 217 [NASA ADS] [CrossRef] (In the text)
- Woosley, S.
E. 1993, ApJ, 405, 273 [NASA ADS] [CrossRef] (In the text)
- Zhang, B.,
Kobayashi, S., & Mészáros, P. 2003, ApJ, 595,
950 [NASA ADS] [CrossRef] (In the text)
- Zhang, B., &
Kobayashi, S. 2005, ApJ, 628, 315 [NASA ADS] [CrossRef] (In the text)
- Zhang, B., Fan,
Y. Z., Dyks, J., et al. 2005, ApJ, in press
[arXiv:astro-ph/0508321]
(In the text)
Copyright ESO 2006
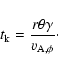
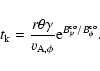
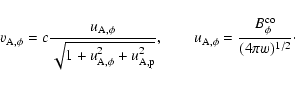
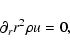
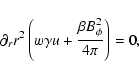
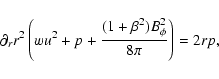
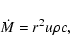
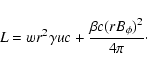
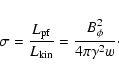
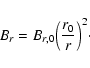
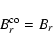
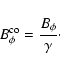
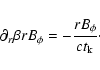
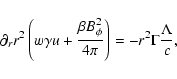
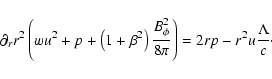
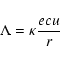
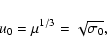
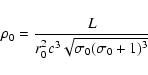
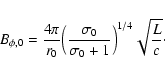
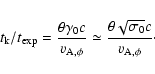
![\begin{figure}
\par\includegraphics[angle=270,width=7.8cm,clip]{4107fig1.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg77.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig2.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg79.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig3.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg82.gif)
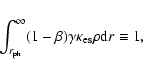
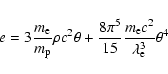
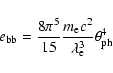
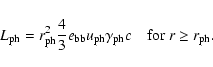
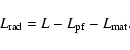
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig4.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg108.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig5.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg109.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig6.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg113.gif)
![\begin{figure}
\par\includegraphics[angle=270,width=7.5cm,clip]{4107fig7.ps}
\end{figure}](/articles/aa/full/2006/18/aa4107-05/Timg117.gif)