A&A 450, 645-654 (2006)
DOI: 10.1051/0004-6361:20054089
Landessternwarte Heidelberg, Königstuhl, 69117 Heidelberg, Germany
Received 23 August 2005 / Accepted 19 December 2005
Abstract
Context. In the first paper of this series, we presented hydrodynamical simulations with radiative cooling of jet models with parameters representative of the symbiotic system MWC 560. These were jet simulations of a pulsed, initially underdense jet in a high-density ambient medium. They were stopped when the jet reached a length of 50 AU. There, however, a transition of the initially underdense jet towards an overdense jet should occur, which should result in changed kinematics. A few minor differences between the models and the observations were thought to be solved by a model with an increased jet density during the pulses which was calculated only with purely hydrodynamical means in the former paper.
Aims. Therefore, we describe two hydrodynamical simulations with cooling beyond this density balance, one with the same parameters as model i in Paper I (now called model i![]() ), which was presented there with and without cooling, and the second with higher gas densities in the jet pulses (model iv
), which was presented there with and without cooling, and the second with higher gas densities in the jet pulses (model iv![]() ).
).
Methods. Hydrodynamical simulations, with a further approximated cooling treatment compared to Paper I, were used to be able to enlarge the computational domain.
Results. The transition causes changes in the expansion of the cocoon and therefore the morphology of the jet, e.g. a larger radial width of the jet knots. We investigate the radiation properties of the jets, the bremsstrahlung and optical emissivities, integrated emission maps, and synthetic absorption line profiles.
Conclusions. The conclusion that the high observed velocities in CH Cygni, R Aquarii, and MWC 560 favor the models with cooling is unchanged by the transition. The observed parallel features in R Aquarii can be produced by the internal knots or by a variable dense radiative shell of shocked ambient medium. The absorption line profiles show that the real parameters in MWC 560 are closer to model iv![]() than to model i
than to model i![]() .
.
Key words: ISM: jets and outflows - binaries: symbiotic - line: profiles - hydrodynamics - methods: numerical
The emergence of jets is a very common phenomenon in a variety of astrophysical objects, and it occurs in systems of very different size and mass scales. Jets are observed in active galactic nuclei (AGN) in which they are formed around supermassive black holes, in X-ray binaries with stellar black holes or neutron stars, in young stellar objects (YSO), in supersoft X-ray sources and in symbiotic stars. Symbiotic systems consist of a red giant undergoing strong mass loss and a white dwarf. More than one hundred symbiotic stars are known, but only about ten systems show jet emission. The most famous systems are R Aquarii, CH Cygni, and MWC 560.
R Aquarii, with a distance of about 200 pc, is one of the nearest symbiotic stars and a well known jet source. The jet has been extensively observed in the optical, at radio wavelengths, and with X-ray observations (e.g. Kellogg et al. 2001; Hollis et al. 1985a; Paresce & Hack 1994; Solf & Ulrich 1985; Hollis et al. 1985b). It shows a rich morphology, e.g. a series of parallel features in the jet and the counter-jet, extending a few hundred AU each. In 1984/85 CH Cygni showed a strong radio outburst, during which a double-sided jet with multiple components was ejected (Taylor et al. 1986). This event allowed an accurate measurement of the jet velocity near 1500 km s-1. In HST observations (Eyres et al. 2002), arcs can be detected that also could be produced by episodic ejection events. While the first two objects are seen at high inclinations, the jet axis in MWC 560 is practically parallel to the line of sight. This special orientation provides an opportunity to observe the outflowing gas as line absorption in the source spectrum. With such observations the radial velocity and the column density of the outflowing jet gas close to the source can be investigated in great detail. In particular we can probe the acceleration and evolution of individual outflow components with spectroscopic monitoring programs, as described in Schmid et al. (2001).
In Stute et al. (2005, hereafter Paper I), we presented hydrodynamical simulations with and without cooling of jets with parameters that were intended to represent those in MWC 560. In a grid of eight simulations we investigated the influence of different jet pulse parameters. Due to the high computational costs of simulations including cooling, this grid was restricted to adiabatic simulations. Only one model simulation was performed that included a treatment of radiative cooling.
The adiabatic jet models showed some quantitative differences for
the different pulse parameters. In comparison with the model including cooling,
huge differences were present. Those concern, e.g., a significantly higher
bow-shock velocity and a well-defined periodic shock structure with
high-density, low-temperature knots separated by hot, low-density beam
sections in the radiative model. The expansion velocity of CH Cyg was shown to
agree very closely with the jet model with cooling. The situation in R Aqr was
less clear. The observationally derived proper motion was more in the range of
the gas motion of the adiabatic models, although the origin of the observed
emission has not been confirmed yet. The small jet opening angle of
15![]() favored a jet with cooling more. We showed that the adiabatic jet
models are not able to produce low temperature regions, which are, however,
necessary to explain strong absorptions from low ionization species in the
spectra of MWC 560 as Ca II, but the cooling of the jet gas still did
not seem efficient enough. This should be achieved by another model with
higher gas densities in the jet outflow. The basic structure of the observed
jet absorptions in MWC 560 was reproduced, including the mean velocity, the
velocity width and temporal evolution of the highest velocity components,
but not their strengths. Again, another model with higher gas densities
should solve this.
favored a jet with cooling more. We showed that the adiabatic jet
models are not able to produce low temperature regions, which are, however,
necessary to explain strong absorptions from low ionization species in the
spectra of MWC 560 as Ca II, but the cooling of the jet gas still did
not seem efficient enough. This should be achieved by another model with
higher gas densities in the jet outflow. The basic structure of the observed
jet absorptions in MWC 560 was reproduced, including the mean velocity, the
velocity width and temporal evolution of the highest velocity components,
but not their strengths. Again, another model with higher gas densities
should solve this.
A drawback of our former simulations was the fact that they were stopped when the jet reached a length of 50 AU. This is unsatisfactory from an observational point of view, as the observed extents of the jet in R Aquarii and CH Cygni are much larger, as well as from the theoretical viewpoint. At this point, the density of the environment has decreased down to the density in the jet nozzle. A transition of the initially underdense jet towards an overdense jet should occur, which should result in changed kinematics. Underdense jets decelerate more than overdense jets, because the position of the jet head can be basically derived from a balance of the ram pressures of jet and external medium and because the relative importance of ram and thermal pressure should also change. As the kinematics of the models was one of the results of the former models, which were compared with the observations, it should be tested whether simulations with larger spatial scales lead to new insights into the physics of jets in symbiotic stars.
Therefore, we performed two hydrodynamical simulations with cooling beyond this density balance, one with the same parameters as model i in Paper I, which was presented both with and without cooling, and the second with higher gas densities in the jet pulses. Due to constraints set by the available computer resources, we were forced to approximate the former treatment of radiative cooling again.
In Sect. 2, we briefly describe the changes of our model with respect to Paper I. After a validating of the approximated cooling treatment in Sect. 3, we investigate the global and internal structure of the jet (Sect. 4) and its consequences on the emission (Sect. 5.1). Then synthetic absorption line profiles are calculated in Sect. 5.2. Finally a summary and a discussion are given.
The general capabilities of the code NIRVANA_CP have already been described
in detail in Paper I. The code was written by Ziegler & Yorke (1997) and modified by
Thiele (2000) to calculate radiative losses due to non-equilibrium cooling by
line emission. It solves the equations of ideal hydrodynamics with an
additional cooling term in the energy equation
![]() and a
network of rate equations:
and a
network of rate equations:
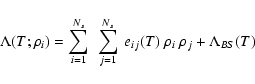 |
(2) |
Table 1:
Parameters of the jet pulses: the model number, the density of the
pulse in the nozzle
![]() in cm-3, the velocity of the
pulse in the nozzle
in cm-3, the velocity of the
pulse in the nozzle
![]() in cm s-1, the mass outflow during
the pulse
in cm s-1, the mass outflow during
the pulse ![]() in g s-1 and in
in g s-1 and in
![]() yr-1, and the
kinetic jet luminosity during the pulse in erg s-1.
yr-1, and the
kinetic jet luminosity during the pulse in erg s-1.
Due to constraints set by the available computer resources, our former
simulation with cooling, presented in Paper I, included a simpler treatment of
radiative effects. Instead of the full explicit cooling function
![]() for all species, we considered only cooling by
hydrogen, together with a general non-equilibrium (NEQ) cooling function
for all species, we considered only cooling by
hydrogen, together with a general non-equilibrium (NEQ) cooling function
![]() adapted from Sutherland & Dopita (1993) to account for the cooling by the
heavier elements. This cooling function was derived by calculating
several atomic processes as electron collision ionization, radiative and
dielectronic recombination, line radiation, and Compton heating
in the temperature range between 104 and 108.5 K. For hydrogen
we solved the atomic network of H I, H II, and e- and
calculated the cooling due to collisional ionization of H I and due to
collisional excitation of hydrogen line emission.
adapted from Sutherland & Dopita (1993) to account for the cooling by the
heavier elements. This cooling function was derived by calculating
several atomic processes as electron collision ionization, radiative and
dielectronic recombination, line radiation, and Compton heating
in the temperature range between 104 and 108.5 K. For hydrogen
we solved the atomic network of H I, H II, and e- and
calculated the cooling due to collisional ionization of H I and due to
collisional excitation of hydrogen line emission.
To perform the simulations beyond density balance with cooling, we were forced
to simplify the treatment of cooling again. We neglected the atomic
network with its rate equations and used the ionization fractions
of hydrogen as a function of temperature given by Sutherland & Dopita (1993), calculated
by using the recombination, collisional ionization, and charge transfer rates.
We included Bremsstrahlung and the general cooling function calculated with
these partial densities. In NEQ models the ionization fraction could be higher
than in the case of collisional ionization equilibrium (CIE), due to the slow
process of recombination of hydrogenic and helium-like ions. Only at
temperatures of about 105 K, however, is the CIE cooling timescale smaller
than the equilibration timescale for those ions (Sutherland & Dopita 1993), leading to
the difference between the CIE and the NEQ cooling curve used. As hydrogen is
(almost) completely ionized at temperatures higher than 20 000 K, the
differences in the ionization fractions are almost negligible in the
temperature range of the cooling curve. Small differences should only occur in
low temperature regions of the jet.
![\begin{figure}
\par\mbox{\includegraphics[width=8cm]{4089fi1a.ps} \includegraphi...
...idth=8cm]{4089fi1e.ps} \includegraphics[width=8cm]{4089fi1f.ps} }
\end{figure}](/articles/aa/full/2006/17/aa4089-05/Timg37.gif) |
Figure 1:
Comparison of temperature ( top), density
( middle), and
ionization fraction ( bottom) plots of the old model i ( left)
and model i |
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=8cm]{4089fi2a.ps} \includegraphi...
...idth=8cm]{4089fi2g.ps} \includegraphics[width=8cm]{4089fi2h.ps} }
\end{figure}](/articles/aa/full/2006/17/aa4089-05/Timg38.gif) |
Figure 2:
|
| Open with DEXTER | |
![\begin{figure}
\par\mbox{\includegraphics[width=8cm]{4089fi3a.ps} \includegraphi...
...idth=8cm]{4089fi3g.ps} \includegraphics[width=8cm]{4089fi3h.ps} }
\end{figure}](/articles/aa/full/2006/17/aa4089-05/Timg40.gif) |
Figure 3:
As Fig. 2, continued. The radiative cooling lowers the
temperature of the region of higher densities. Superposed on it, the whole
feature moves towards lower densities and lower temperatures, consistent
with adiabatic expansion. The slope of the path is approximately
|
| Open with DEXTER | |
The geometrical model is taken over without changes, except for the dimensions of the computational domain. We choose a two-dimensional slice of the full domain and assume axisymmetry. In these new simulations, the dimension in axial direction is doubled to 100 AU to be able to study the jet propagation after density compensation. The resolution remains unchanged as 20 grid cells per AU (jet beam radius).
The hot component is located in the origin of the coordinate frame, therefore
the companion is expanded into a "Red Giant Ring''. In the 2D integration
domain, only half of the cross-section of this ring on this slice is included.
The binary separation in the models is chosen to 4 AU which is of the order of
the estimated separations of 3.3-5.2 AU. The density of the red giant is set
to
![]() g cm-3 and its radius to 1 AU.
g cm-3 and its radius to 1 AU.
Surrounding the red giant, a stellar wind is implemented. The wind has a
constant velocity of v=10 km s-1, a gas temperature of T=50 K, and a
mass loss of 10-6
![]() yr-1. The density of the red
giant wind at the surface of the star is then
yr-1. The density of the red
giant wind at the surface of the star is then
![]() g cm-3.
The density of the external medium is given by a
g cm-3.
The density of the external medium is given by a
![]() -law for a
spherical wind where
-law for a
spherical wind where
![]() is the distance from the center of the
red giant. The density of the red giant wind near the jet nozzle is about
200 times higher than the initial jet density. At a distance of 50 AU from the
symbiotic system, i.e. at the end of the integration domain of the former
simulations, the wind density is about equal to the jet density at the nozzle.
is the distance from the center of the
red giant. The density of the red giant wind near the jet nozzle is about
200 times higher than the initial jet density. At a distance of 50 AU from the
symbiotic system, i.e. at the end of the integration domain of the former
simulations, the wind density is about equal to the jet density at the nozzle.
To account for the counter-jet and the other part of the jet, respectively, the boundary conditions in the equatorial plane and on the jet axis are set to reflection symmetry. On the other boundaries, outflow conditions are chosen.
The jet is produced within a thin jet nozzle with a radius of 1 AU. The
initial velocity of the jet is chosen to 1000 km s-1 or 0.578 AU d-1
and its density is set to
![]() g cm-3 (equal to a
hydrogen number density of
g cm-3 (equal to a
hydrogen number density of
![]() cm-3). These parameters lead to
a density contrast
cm-3). These parameters lead to
a density contrast ![]() of
of
![]() ,
a Mach number of
,
a Mach number of
![]() in the nozzle and a mass loss rate of
in the nozzle and a mass loss rate of
![]()
![]() yr-1. Repeatedly each seventh day, the velocity and
density values in the nozzle are changed to simulate the jet pulses which are
seen in the observations of MWC 560.
yr-1. Repeatedly each seventh day, the velocity and
density values in the nozzle are changed to simulate the jet pulses which are
seen in the observations of MWC 560.
The pulse parameters of the first simulation were chosen as in the old model i
with cooling of Paper I. The nomenclature is now model i![]() - mention of the
cooling will be omitted hereafter. A second simulation with parameters as
in the adiabatic model iv - the model with the highest density pulses - was
also performed and is now named model iv
- mention of the
cooling will be omitted hereafter. A second simulation with parameters as
in the adiabatic model iv - the model with the highest density pulses - was
also performed and is now named model iv![]() .
.
Table 1 lists the main parameters of the models: the
model number, the density of the pulse in the nozzle
![]() in cm-3, the velocity of the pulse in the nozzle
in cm-3, the velocity of the pulse in the nozzle
![]() in cm s-1, the mass loss during the pulse
in cm s-1, the mass loss during the pulse ![]() in g s-1 and in
in g s-1 and in
![]() yr-1, and the kinetic jet luminosity during
the pulse in erg s-1. Each pulse lasts for one day.
yr-1, and the kinetic jet luminosity during
the pulse in erg s-1. Each pulse lasts for one day.
By the aforementioned simplifications of the cooling treatment, we achieved a reduction in the required computational time by a factor of 8-10 with respect to the old simulation with cooling. This was a necessary condition to be able to enlarge the computational domain. Before investigating the new simulations, however, we now have to validate the ability of our approximated cooling treatment to describe the real properties inside jets of symbiotic stars.
The first way is a comparison of the plots of density, temperature, and -
more important - the ionization fraction
![]() ,
the variables
that determine the observable emission. In Fig. 1 we show
temperature, density, and ionization fraction plots from models i and i
,
the variables
that determine the observable emission. In Fig. 1 we show
temperature, density, and ionization fraction plots from models i and i![]() at day 74, the last simulated time step in the old run. Apart from the slight
differences in the internal structure, such as in the shapes of vortices, the
overall results for the bow-shock sizes of the jets, positions of the internal
shocks, and density values are identical in both simulations. Therefore the
previously derived properties, such as the jet structure, the bow-shock
geometry and evolution, the internal jet structure, and pulse evolution are
consistent in both simulations. The same also holds for the temperature.
As mentioned in Sect. 2, the recombination time,
thus the equilibration timescale, is larger than the cooling timescale
at smaller temperatures (104-105 K), which leads to an underestimation
of the ionization fraction in those jet regions - the holes in Fig. 1. As these parts are also of low density, the effects on the
cooling and the jet emission should be small. This result seems to legitimate
the use of a simplified treatment of the cooling inside jets in symbiotic
stars and makes it possible to enlarge the numerical investigations with
reduced computational constraints.
at day 74, the last simulated time step in the old run. Apart from the slight
differences in the internal structure, such as in the shapes of vortices, the
overall results for the bow-shock sizes of the jets, positions of the internal
shocks, and density values are identical in both simulations. Therefore the
previously derived properties, such as the jet structure, the bow-shock
geometry and evolution, the internal jet structure, and pulse evolution are
consistent in both simulations. The same also holds for the temperature.
As mentioned in Sect. 2, the recombination time,
thus the equilibration timescale, is larger than the cooling timescale
at smaller temperatures (104-105 K), which leads to an underestimation
of the ionization fraction in those jet regions - the holes in Fig. 1. As these parts are also of low density, the effects on the
cooling and the jet emission should be small. This result seems to legitimate
the use of a simplified treatment of the cooling inside jets in symbiotic
stars and makes it possible to enlarge the numerical investigations with
reduced computational constraints.
In a two-dimensional histogram of the density and the temperature as given in Figs. 2 and 3, one can compare the results of both runs in greater detail. They show the physical conditions of the gas irrespective of their position.
The bright bar at very low temperatures and at densities between 10-16
and 10-14 g cm-3 consists of the external medium and the internal
dense knots build up the line at T = 104 K. Each new pulse becomes visible
as an arc in the ![]() -plane with its tip at
-plane with its tip at
![]() g cm-3
and
T=107.5 K. On the third day after the pulse, this tip spreads out
along a line of constant temperature between densities of
g cm-3
and
T=107.5 K. On the third day after the pulse, this tip spreads out
along a line of constant temperature between densities of
![]() g cm-3. Then the radiative cooling comes into play by lowering the
temperature of the region of higher densities. Superposed on the radiative
cooling, the whole feature moves towards lower densities and lower
temperatures. The slope of the path is approximately
g cm-3. Then the radiative cooling comes into play by lowering the
temperature of the region of higher densities. Superposed on the radiative
cooling, the whole feature moves towards lower densities and lower
temperatures. The slope of the path is approximately
![]() ,
consistent with an adiabatic
expansion.
,
consistent with an adiabatic
expansion.
The density and temperature maps were very similar (Fig. 1), and
the statistical investigation also shows no qualitative differences. The shape
and position of the pulse structure, of the jet knots, the jet beam, and the
external medium in the ![]() -plane are identical in both runs. Both cooling
approaches are therefore similar and seem to be equally reasonable physically;
the practical differences, however, are huge as mentioned before.
-plane are identical in both runs. Both cooling
approaches are therefore similar and seem to be equally reasonable physically;
the practical differences, however, are huge as mentioned before.
One result of the small-scale simulation with cooling presented in Paper I was that the radial extent of the lateral jet bow-shock in model i remained constant, which was a significant difference to the adiabatic models where both the radial and the axial extent increased with a constant aspect ratio up to an axial extent of about 35-50 AU, depending on the model parameters.
At the beginning, the radial extent of the jet in model i![]() and the cross
section of the jet stay constant as in model i. This again leads to a faster
propagation velocity than in the adiabatic jet, which even accelerates (Fig. 4). The radial extent and, therefore, the jet head area are not
able to compensate for the decreasing local density contrast as in the
simulations without cooling. After day 70, however, the axial velocity
suddenly seems to remain constant. The radial extent and the jet head area
grow and the acceleration stops. This is a new behavior not seen in model i as
only 74 days were simulated in that run. The then constant
velocity of the jet head is about 740 km s-1.
and the cross
section of the jet stay constant as in model i. This again leads to a faster
propagation velocity than in the adiabatic jet, which even accelerates (Fig. 4). The radial extent and, therefore, the jet head area are not
able to compensate for the decreasing local density contrast as in the
simulations without cooling. After day 70, however, the axial velocity
suddenly seems to remain constant. The radial extent and the jet head area
grow and the acceleration stops. This is a new behavior not seen in model i as
only 74 days were simulated in that run. The then constant
velocity of the jet head is about 740 km s-1.
The aspect ratio r / z decreases noticeably in the first 20 days due to the constant radial extent r. After 70 days the aspect ratio itself remains constant, as seen in the initial phase of the adiabatic models. First, it is surprising that this transition, which is naively expected due to the density balance of the jet and its surrounding medium at a distance of 50 AU, already occurs on day 70 when the jet has propagated only 20 AU. When investigating slices of density along the jet axis, however, one realizes that this transition is indeed caused by a density balance (Fig. 5).
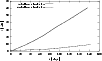 |
Figure 4:
Size of the bow-shock in axial and radial direction for model i |
| Open with DEXTER | |
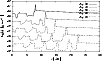 |
Figure 5:
Slices of density along the jet axis for model i |
| Open with DEXTER | |
After day 70, the density of the first internal shock behind the bow-shock is larger than the local density of the surrounding medium. As this first internal shock hits the bow-shock region and therefore continues to drive the propagation of the entire jet, this balance, i.e. the transition from an initially underdense to an overdense jet, leads to the substantial change in kinematics described above. The same scenario also holds for model iv, the velocity of the jet head is about 700 km s-1.
As in the old model i with cooling, the propagation of all pulses again can be traced until their merger with the jet head. Each new pulse is instantaneously slowed down from 2000 km s-1 to about 1200 km s-1 within the first two days. The distance between the internal shocks created by the periodic velocity pulses stays constant. The very simple, periodic jet structure in the axial cuts of the Mach number, axial velocity, density, pressure, and temperature - showing knots and the jet beam - remains unaffected in this large scale simulation by the aforementioned transition.
A difference between model i![]() and the former model i with cooling is the
radial extent of these knots (Fig. 6). The whole width of the jet,
however, is again taken by the jet beam, i.e. by unshocked jet material. A
cocoon of shocked jet matter is only a very small shell close to the contact
discontinuity, and a backflow is again absent. Therefore the basic composition
of the jet is not changed, only the dimensions. While in model i with cooling,
the knots had a radius of 1 AU, their extent is now a few AU. The density
level in the knots, however, is lowered by a factor of ten. Therefore the
total mass of each knot could be constant during this spreading process, which
could be triggered by a trough in the pressure profile at an intermediate jet
length. There also, the temperature and the sound speed are reduced, leading
to large Mach numbers.
and the former model i with cooling is the
radial extent of these knots (Fig. 6). The whole width of the jet,
however, is again taken by the jet beam, i.e. by unshocked jet material. A
cocoon of shocked jet matter is only a very small shell close to the contact
discontinuity, and a backflow is again absent. Therefore the basic composition
of the jet is not changed, only the dimensions. While in model i with cooling,
the knots had a radius of 1 AU, their extent is now a few AU. The density
level in the knots, however, is lowered by a factor of ten. Therefore the
total mass of each knot could be constant during this spreading process, which
could be triggered by a trough in the pressure profile at an intermediate jet
length. There also, the temperature and the sound speed are reduced, leading
to large Mach numbers.
The axial velocity component stays nearly constant inside the jet, but is slightly enhanced at radii of 5 AU compared to the jet axis. This leads to a slow overtaking of the radial extensions of the jet pulses. The radial velocity component shows negative velocities, i.e. towards the axis, at larger distances near the jet axis. This seems to be another result of this overtaking, leading to an eddy-like structure near the jet head.
Another feature in the radial velocity is the linear, Hubble-like increase
at lower distances from the jet axis. This is often seen in Planetary Nebulae
(e.g. Corradi et al. 2001) and can be explained by a fast wind traveling
into a self-similar 1/r2 density profile (e.g. Koo & McKee 1992).
As the radial velocities are still of the order of a few hundred km s-1, a radial radiative dense shell of shocked ambient medium is
present.
![\begin{figure}
\mbox{\includegraphics[width=8cm]{4089fi6a.ps} \includegraphics[...
...idth=8cm]{4089fi6e.ps} \includegraphics[width=8cm]{4089fi6f.ps} }
\end{figure}](/articles/aa/full/2006/17/aa4089-05/Timg56.gif) |
Figure 6:
Logarithm of density for model i |
| Open with DEXTER | |
![\begin{figure}
\mbox{ \includegraphics[width=8cm]{4089fi7a.ps} \includegraphics...
...idth=8cm]{4089fi7k.ps} \includegraphics[width=8cm]{4089fi7l.ps} }
\end{figure}](/articles/aa/full/2006/17/aa4089-05/Timg57.gif) |
Figure 7:
Radiative properties of model i |
| Open with DEXTER | |
In model iv![]() ,
the internal knots are also extended in radial size, but are no
longer pronounced as in model i
,
the internal knots are also extended in radial size, but are no
longer pronounced as in model i![]() along the full width of the jet. Instead
of the clear crescent form in model i
along the full width of the jet. Instead
of the clear crescent form in model i![]() ,
the structure of the knots is now more
complicated. Furthermore, they are drifting away from the jet axis while
traveling and do not hit the jet head, but the lateral shock, leading to a
sharp step. Therefore the pulses are not able to transfer the full momentum
to the propagation of the jet head.
,
the structure of the knots is now more
complicated. Furthermore, they are drifting away from the jet axis while
traveling and do not hit the jet head, but the lateral shock, leading to a
sharp step. Therefore the pulses are not able to transfer the full momentum
to the propagation of the jet head.
Using the density and pressure data in each grid cell of model i![]() ,
we can
calculate the temperature, the ionization fraction
,
we can
calculate the temperature, the ionization fraction
![]() ,
and
then the total emissivity due to bremsstrahlung using the formula
,
and
then the total emissivity due to bremsstrahlung using the formula
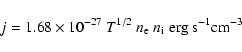 |
(3) |
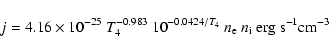 |
(4) |
with T4 the temperature in units of 104 K. Both emissivities are plotted in the first two rows of Fig. 7.
These emissivities are then rotated and integrated along a line of sight that is perpendicular to the jet axis. Assuming a distance of 200 pc to the observer, emission maps are created (Fig. 7, rows 3 and 5). The emission above a detection threshold of 10-15 erg s-1 cm-2 is also given.
In the emissivity plots, the knots with high density and lower temperature can be well detected because of their emission which is higher than that of the jet beam with its low density and higher temperature. The distinctness of these structures in the cocoon increases downstream towards the jet head and allows them to be detected more easily. After creating emission maps, however, the emission of the knots is blended by a strong emission of the dense radiative shell of shocked ambient medium.
The parts above the threshold show several distinct features that are created not by the knots, but by emission variations in this shell. As axisymmetry was assumed, these features are rings around the jet, observed as stripes at high inclinations.
In Paper I, the calculations of the jet absorption profiles have been
presented in detail. Again, we start with a normalized continuum emission and
a Gaussian emission line profile:
The parameters depending on the different hydrodynamical models are the
velocity projected onto the line of sight vj, the mass density ![]() ,
and
,
and ![]() the relative number density with respect to hydrogen
the relative number density with respect to hydrogen
![]() of the absorbing atom in the lower level k of the
investigated line transition. The velocity is binned for the calculation of
the absorption. The size of the bins
of the absorbing atom in the lower level k of the
investigated line transition. The velocity is binned for the calculation of
the absorption. The size of the bins ![]() can be interpreted as a
measure of the kinetic motion and turbulence in one grid cell. This absorption
dispersion helps to smooth the effects of the limited spatial resolution of
the numerical models. The absorption calculation through the jet region is
then repeated for all possible light paths from the emission region to the
observer. The arithmetic mean of the individual absorption line profiles from
each path is then taken as the resulting spectrum.
can be interpreted as a
measure of the kinetic motion and turbulence in one grid cell. This absorption
dispersion helps to smooth the effects of the limited spatial resolution of
the numerical models. The absorption calculation through the jet region is
then repeated for all possible light paths from the emission region to the
observer. The arithmetic mean of the individual absorption line profiles from
each path is then taken as the resulting spectrum.
In Paper I, we described that the high-velocity components in the synthetic
absorption line profiles are not as pronounced as in the observed ones. Now,
our model iv![]() could be a solution to that problem, since both ways of
increasing the absorption in the high velocity components - higher pulse
density and the cooling treatment - are now present. The parameters are now
chosen as in the best-fit model in Paper I:
could be a solution to that problem, since both ways of
increasing the absorption in the high velocity components - higher pulse
density and the cooling treatment - are now present. The parameters are now
chosen as in the best-fit model in Paper I:
![]() ,
,
![]() km s-1,
km s-1,
![]() Å,
fkl=0.69,
Å,
fkl=0.69,
![]() for
the Ca II K transition,
for
the Ca II K transition,
![]() km s-1,
km s-1, ![]() ,
and
,
and
![]() AU.
AU.
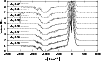 |
Figure 8:
Sequence of absorption line profiles for eight consecutive days
for model i |
| Open with DEXTER | |
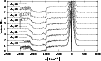 |
Figure 9:
Sequence of absorption line profiles for eight consecutive days of
model iv |
| Open with DEXTER | |
In Figs. 8, 9, the sequences of eight
consecutive nights of the two large-scale models i![]() and iv
and iv![]() are shown. In the
first case, the extension of model i
are shown. In the
first case, the extension of model i![]() to longer propagation times and
larger lengths create only slight differences compared to Fig. 26 (bottom) in
Paper I. The position of the main absorption trough, the
shape of its boundaries, the presence, persistence, and depth of the high
velocity component are all very similar to those in the former model i with
cooling. The absorption in the center of the emission line is
created by the ambient medium in front of the jet.
to longer propagation times and
larger lengths create only slight differences compared to Fig. 26 (bottom) in
Paper I. The position of the main absorption trough, the
shape of its boundaries, the presence, persistence, and depth of the high
velocity component are all very similar to those in the former model i with
cooling. The absorption in the center of the emission line is
created by the ambient medium in front of the jet.
The model iv![]() with increased jet pulse densities, however, creates clearly
visible differences. The stable absorption trough is shifted towards higher
velocities, from -1050 km s-1 up to -1300 km s-1, and its width is
increased from about 200 km s-1 to 500 km s-1. In the high velocity
component, several deep absorptions are present in contrast to the few
moderate ones in model i
with increased jet pulse densities, however, creates clearly
visible differences. The stable absorption trough is shifted towards higher
velocities, from -1050 km s-1 up to -1300 km s-1, and its width is
increased from about 200 km s-1 to 500 km s-1. In the high velocity
component, several deep absorptions are present in contrast to the few
moderate ones in model i![]() .
.
In this paper, we present results of two new hydrodynamical simulations, including radiative cooling. They were started due to a drawback in our former simulations presented in Paper I (Stute et al. 2005), which were stopped close to density balance of the jet and the ambient medium. As underdense and overdense jets behave in different ways and as the kinematics of the jets was a main result in Paper I, we expected new insights.
Another point is that a few minor differences between the models and the
observations were thought to be solved by a model with an increased jet density
during the pulses - model iv![]() - which was calculated only with purely
hydrodynamical means in the former grid of simulations. Therefore, we
performed two hydrodynamical simulations with an approximated cooling
treatment beyond this density balance, one with the same parameters as model i
in Paper I, which was presented there with and without cooling, and the second
with higher gas densities in the jet pulses, as in model iv.
- which was calculated only with purely
hydrodynamical means in the former grid of simulations. Therefore, we
performed two hydrodynamical simulations with an approximated cooling
treatment beyond this density balance, one with the same parameters as model i
in Paper I, which was presented there with and without cooling, and the second
with higher gas densities in the jet pulses, as in model iv.
Since in the new cooling treatment ionization fractions of collisional ionization equilibrium (CIE) were used and not self-consistent general non-equilibrium (NEQ) rate equations, we discussed the possible effects of underestimating the ionization fraction of hydrogen and validated this cooling treatment by comparing density and temperature values of the gas parcels in the jet, as well as by showing plots of the ionization fraction itself. We saw that the differences are only very small.
In Paper I, the jet in model i with cooling had a constant cross section over
the simulated 74 days. This led to an accelerated motion with high velocities
of 730 km s-1, while the velocity of the adiabatic jet was only about
200 km s-1. The extended model i![]() in this paper now shows that after the
first 70 days the transition from an underdense to an overdense jet lets the
cross section inflate and therefore compensate for the density profile of the
external medium. The acceleration is stopped and the jet then has a constant
velocity of about 740 km s-1. Thus, the transition results in a
completely different motion. The conclusion that the high observed velocities
in CH Cygni, R Aquarii, and MWC 560 favor the models with cooling is unchanged
by the transition.
in this paper now shows that after the
first 70 days the transition from an underdense to an overdense jet lets the
cross section inflate and therefore compensate for the density profile of the
external medium. The acceleration is stopped and the jet then has a constant
velocity of about 740 km s-1. Thus, the transition results in a
completely different motion. The conclusion that the high observed velocities
in CH Cygni, R Aquarii, and MWC 560 favor the models with cooling is unchanged
by the transition.
The radial inflation mentioned above also changes the internal structure of the
jet. The width of the internal knots is also increased, as the basic
composition of the jets is not affected. The cocoon of shocked jet matter is
again confined to a small shell close to the contact discontinuity and the
whole jet lobe is filled with unshocked jet material. In model i![]() ,
these knots
are very pronounced along their width, while their structure is not intact in
model iv
,
these knots
are very pronounced along their width, while their structure is not intact in
model iv![]() .
.
These knots are the locations of enhanced bremsstrahlung and optical
emissivity, which is therefore again more pronounced in model i![]() .
These knots
could be identified with the observed parallel features in R Aquarii
(Paresce & Hack 1994). After rotating the emissivity plots and integrating them, however,
other features become more prominent. The internal knots are blended by the
emission of the dense radiative shell of shocked ambient medium. As they are
spatially variable, parallel rings of enhanced emission are created by the
rotation and also look similar to the observations, if one keeps in mind that
axisymmetry was assumed in our model. Without that, the shapes of the features
on the shell should be different.
.
These knots
could be identified with the observed parallel features in R Aquarii
(Paresce & Hack 1994). After rotating the emissivity plots and integrating them, however,
other features become more prominent. The internal knots are blended by the
emission of the dense radiative shell of shocked ambient medium. As they are
spatially variable, parallel rings of enhanced emission are created by the
rotation and also look similar to the observations, if one keeps in mind that
axisymmetry was assumed in our model. Without that, the shapes of the features
on the shell should be different.
The observed length of the jet in R Aquarii is several hundred AU, thus much larger than in our simulations. At larger distances from the source, however, the density of the ambient medium drops by another order of magnitude, making it likely that the relative contribution of the emission of the knots will increase.
Concerning the absorption line profiles, no large differences between the
former model i with cooling and the recent model i![]() are visible. This means
that the influence of the age of the jet on the profiles should only be
marginal. In model iv
are visible. This means
that the influence of the age of the jet on the profiles should only be
marginal. In model iv![]() ,
however, differences arise. The stable absorption
trough is shifted toward higher velocities, from -1050 km s-1 up to
-1300 km s-1, and its width is increased from about 200 km s-1 to
500 km s-1. In the high velocity component, several deep absorptions are
present in contrast to the few moderate ones in model i
,
however, differences arise. The stable absorption
trough is shifted toward higher velocities, from -1050 km s-1 up to
-1300 km s-1, and its width is increased from about 200 km s-1 to
500 km s-1. In the high velocity component, several deep absorptions are
present in contrast to the few moderate ones in model i![]() .
.
Both results highly increase the ability of the model to reproduce the
observed absorption line profiles (see Fig. 1 in Paper I or Schmid et al. 2001). We
can say here that the real parameters in MWC 560 are closer to model iv![]() than
to model i
than
to model i![]() .
.
As the pulse structure was not changed, the line widths of the high velocity components are again quite narrow. This could perhaps be improved by using a sinusoidal or Gaussian pulse profile, instead of the rectangular steps in velocity and density, and also a spatial velocity and density profile, instead of the constant values within the jet nozzle.
Acknowledgements
The author wants to thank the High Performance Computing Center Stuttgart for allowing him to perform the expensive computations, and H. M. Schmid and M. Camenzind for fruitful discussions. We acknowledge the constructive comments and suggestions by the referee.