A&A 450, 83-86 (2006)
DOI: 10.1051/0004-6361:20054531
Galaxy peculiar motions under a diffusive-stochastic regime
A. L. B. Ribeiro
-
M. A. Falcão
Laboratório de Astrofísica Teórica e Observacional,
Departamento de Ciências Exatas
e Tecnológicas, Universidade Estadual de Santa Cruz - 45650-000, Ilhéus, Brazil
Received 16 November 2005 / Accepted 5 January 2006
Abstract
Context. To investigate peculiar large scale motions under a diffusive-stochastic fluid description.
Aims. Our basic aims are to find the profile of the pairwise galaxy velocity distribution using the dynamical fluid equation and to constrain the profile with current observational data.
Methods. We rewrite the fluid equation for the galaxy fluid using a coarse-grained approach. Then, we solve the equation to find the theoretical velocity probability distribution. Next, we study the mode correlations in the Fourier space and find the profile to be compared with current observational data.
Results. The theoretical profile for the mode correlations is a Lorentzian, which is in good agreement with data. Also, our model allowed us to constrain, for the first time, the viscosity parameter of the cosmic fluid as 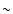 3.35
3.35
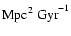 .
.
Conclusions. We find evidence that galaxy peculiar motions can be described as a fluid under a linear diffusive-stochastic regime at scales larger than 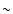 5 h-1 Mpc.
5 h-1 Mpc.
Key words: cosmology: large-scale structure of Universe - hydrodynamics
The galaxy motion has two components: the velocity
due to the Hubble flow plus the velocity that describes the motion
with respect to the background. This second component
is known as peculiar velocity
and corresponds to the difference between the predicted expansion
velocity of a galaxy and its observed velocity:
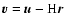 (where H is the Hubble constant). Using comoving
coordinates,
(where H is the Hubble constant). Using comoving
coordinates,
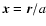 ,
and the conformal time,
,
and the conformal time, 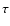 ,
we have the hydrodynamical equation for the cosmic fluid
,
we have the hydrodynamical equation for the cosmic fluid
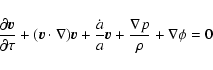 |
(1) |
where 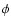 is
gravitational potential and a is the scale factor (see, for instance, Coles & Lucchin 1995).
is
gravitational potential and a is the scale factor (see, for instance, Coles & Lucchin 1995).
On scales of 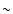 1 h-1 Mpc, galaxy clustering is highly
nonlinear and the peculiar field should be taken as an incoherent
and random field. On the other hand, on scales larger than
1 h-1 Mpc, galaxy clustering is highly
nonlinear and the peculiar field should be taken as an incoherent
and random field. On the other hand, on scales larger than 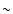 5 h-1 Mpc,
the velocity field is irrotational and one can expect
the linear perturbation theory to be a good guide to study the
peculiar velocity field through a systematic comparison
with observational data (e.g. Davis 1998). But
most of information now available
on peculiar velocities is indirectly obtained from
extensive galaxy redshift
surveys: LCRS (Las Campanas Redshift Survey), SDSS (Sloan Digital Sky
Survey) and 2dF (2 degree Field). These surveys just probe
the positions of galaxies in the redshift space, which are not
necessarily the same in the physical space, since mass concentrations
distort the structures in the redshift space (e.g. Kaiser 1986).
As a result, measurements of the galaxy two-point
correlation function are contaminated by such distortions and
what we really measure is the redshift-space correlation function
(Juszkiewicz et al. 2000).
5 h-1 Mpc,
the velocity field is irrotational and one can expect
the linear perturbation theory to be a good guide to study the
peculiar velocity field through a systematic comparison
with observational data (e.g. Davis 1998). But
most of information now available
on peculiar velocities is indirectly obtained from
extensive galaxy redshift
surveys: LCRS (Las Campanas Redshift Survey), SDSS (Sloan Digital Sky
Survey) and 2dF (2 degree Field). These surveys just probe
the positions of galaxies in the redshift space, which are not
necessarily the same in the physical space, since mass concentrations
distort the structures in the redshift space (e.g. Kaiser 1986).
As a result, measurements of the galaxy two-point
correlation function are contaminated by such distortions and
what we really measure is the redshift-space correlation function
(Juszkiewicz et al. 2000).
Alternatively, one can study the
anisotropies created by the peculiar velocities in the redshift-space correlation
function (Peebles 1980). To do that, one should split the
redshift-space correlation function in two dimensions, where the
axes correspond to the directions parallel and perpendicular to the
line-of-sight separation of a galaxy pair. The resultant correlation
function is anisotropic since the peculiar velocities distort the
correlation function along the line-of-sight. These anisotropies
can be used to estimate the peculiar velocity dispersion of galaxies
at different scales. Using this method,
several works based on numerical data and survey analysis
find that the paiwise galaxy peculiar velocity distribution has an
approximated exponential
with the pairwise velocity dispersion probably in the
range
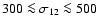 km s-1
(Davis & Peebles 1983; Marzke et al.
1995; Guzzo et al. 1997; Ratcliffe et al. 1998; Peacock 2001). Note that this approach only gets the
second moment of the distribution and the exponential
is just a fitting function. A more robust method extracts the Fourier
transform of the velocity distribution from the Fourier transform
of galaxy-galaxy correlation function in the redshift space using
a deconvolution procedure. In this case, the method returns the
entire distribution function, not only its dispersion (Landy et al. 1998).
Applying this method to large surveys (LCRS, SDSS and 2dF), it was
found that, in all cases, the velocity distribution is well characterized
by an exponential or, equivalently, a Lorentzian in the Fourier space with
width given by the
pairwise velocity dispersion around 300
km s-1
(Davis & Peebles 1983; Marzke et al.
1995; Guzzo et al. 1997; Ratcliffe et al. 1998; Peacock 2001). Note that this approach only gets the
second moment of the distribution and the exponential
is just a fitting function. A more robust method extracts the Fourier
transform of the velocity distribution from the Fourier transform
of galaxy-galaxy correlation function in the redshift space using
a deconvolution procedure. In this case, the method returns the
entire distribution function, not only its dispersion (Landy et al. 1998).
Applying this method to large surveys (LCRS, SDSS and 2dF), it was
found that, in all cases, the velocity distribution is well characterized
by an exponential or, equivalently, a Lorentzian in the Fourier space with
width given by the
pairwise velocity dispersion around 300
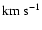 (Landy 2002).
Although the present knowledge indicates a Lorentzian for the
pairwise velocity distribution function of galaxies, it is not
simple to relate hydrodynamics to this result, through Eq. (1).
In the next section, we show that such a profile is
expected in hydrodynamical scenarios under a diffusive-stochastic regime.
(Landy 2002).
Although the present knowledge indicates a Lorentzian for the
pairwise velocity distribution function of galaxies, it is not
simple to relate hydrodynamics to this result, through Eq. (1).
In the next section, we show that such a profile is
expected in hydrodynamical scenarios under a diffusive-stochastic regime.
Structure formation in the universe can be
described in the context of fluid dynamics. The usual approach is to
perturb and linearize the hydrodynamics equations to follow the
evolution of perturbations until the modes enter into the nonlinear
regime. In this approach, let us to
change the time variable from 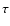 to b (the growing mode of
the linear theory) and rescaling the peculiar velocity
and the potential gravitational as
to b (the growing mode of
the linear theory) and rescaling the peculiar velocity
and the potential gravitational as
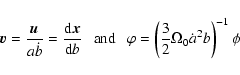 |
(2) |
so we can rewrite Eq. (1) as
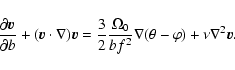 |
(3) |
where
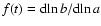 ,
,
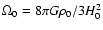 and we have neglected the thermal pressure,
added an ad hoc diffusion term
and taken the velocity field as the gradient of a velocity
potential (
and we have neglected the thermal pressure,
added an ad hoc diffusion term
and taken the velocity field as the gradient of a velocity
potential (
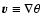 )
as long as the motion is linear and streams of
particles do not cross. Assuming that over the mildly nonlinear regime the
gravitational potential is approximately equal to the velocity
potential, we finally get
)
as long as the motion is linear and streams of
particles do not cross. Assuming that over the mildly nonlinear regime the
gravitational potential is approximately equal to the velocity
potential, we finally get
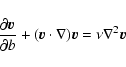 |
(4) |
which is known as the adhesion approximation, that corresponds to
a fluid under a nonlinear diffusion regime
(Gurbatov et al. 1989). In the context of coarse-grained
hydrodynamics, where galaxy clustering is
taken into account as mesoscopic structures,
it was recently shown how to physically introduce
the diffusion term in the fluid equation (Ribeiro & Peixoto de Faria 2005).
In this case, due to the granular kinetics,
the dynamics is also driven by a noise term
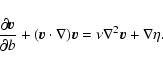 |
(5) |
Now, let us rewrite the fluid equation as
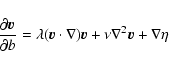 |
(6) |
where we have introduced the parameter 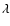 to
control the level of nonlinearity in the problem. In the case
of very small
to
control the level of nonlinearity in the problem. In the case
of very small 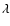 (i.e. taking the
fluid on scales larger than
(i.e. taking the
fluid on scales larger than  5 h-1 Mpc),
we have the Edwards-Wilkinson (EW) equation
5 h-1 Mpc),
we have the Edwards-Wilkinson (EW) equation
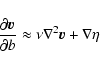 |
(7) |
which describes the diffusive-stochastic regime of
the fluid, i.e., a linear diffusion driven by a noise term (Edwards &
Wilkinson 1982).
The EW equation (or the associated Fokker-Planck equation) has
probability distribution for the wavenumber modes vk given by
![\begin{displaymath}P({v}_k,b) \propto \prod_k \exp{ \left[-{\nu\over \Delta^G}{1...
...rm e}^{-\nu k^2b}\vert^2\over{1-{\rm e}^{-2\nu k^2b}}}\right]}
\end{displaymath}](/articles/aa/full/2006/16/aa4531-05/img28.gif) |
(8) |
(see Edwards Wilkinson 1982), where vk0 is
the initial value for b=0, L is the
length scale and
we have assumed a Gaussian amplitude distribution for the
noise term 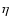
![\begin{displaymath}P(\eta)=\exp{\left[-{1\over 2\Delta^G}\int \eta(xb)^2\;{\rm d}x\;{\rm d}b\right]}
\end{displaymath}](/articles/aa/full/2006/16/aa4531-05/img30.gif) |
(9) |
with short-range correlations according to
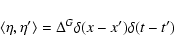 |
(10) |
where 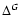 is the noise strength parameter (Fogedby 2005).
Note that, for
is the noise strength parameter (Fogedby 2005).
Note that, for
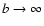 ,
P(vk,b) approaches the
stationary Gaussian distribution
,
P(vk,b) approaches the
stationary Gaussian distribution
![\begin{displaymath}P_{\rm st}({v})\propto \exp{\left[ -{\nu\over \Delta^G}\int {v}(x)^2\;{\rm d}x\right]}.
\end{displaymath}](/articles/aa/full/2006/16/aa4531-05/img34.gif) |
(11) |
At the same time, mode correlations in the k-space
have Lorentzian line shape characteristic of a conserved diffusive
mode
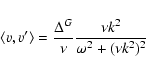 |
(12) |
with hydrodynamical linewidth 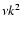 vanishing in the
long wave length limit. In terms of physical quantities, we can get the linewidth
by making
vanishing in the
long wave length limit. In terms of physical quantities, we can get the linewidth
by making
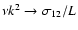 .
The slope of the correlation function for the diffusive mode should be
compared to the Fourier transform of the galaxy pairwise velocity
distribution function. Taking values of
.
The slope of the correlation function for the diffusive mode should be
compared to the Fourier transform of the galaxy pairwise velocity
distribution function. Taking values of
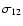 from several
works (see Table 1), we obtain the mean value:
from several
works (see Table 1), we obtain the mean value:
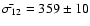 km
km
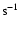 (with
(with
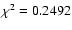 ); and a typical
scale L of
); and a typical
scale L of 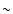 300 Mpc. Using these values in Eq. (12)
we plot the behaviour of
300 Mpc. Using these values in Eq. (12)
we plot the behaviour of
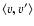 in Fig. 1.
This figure should be compared with Fig. 1 of Landy (2002), which allows us
to identify a good agreement between
the correlations of the diffusive-stochastic regime
with the galaxy pairwise velocity distribution in SDSS data.
In addition, our model allow us to constrain
the viscosity parameter for the cosmic fluid:
in Fig. 1.
This figure should be compared with Fig. 1 of Landy (2002), which allows us
to identify a good agreement between
the correlations of the diffusive-stochastic regime
with the galaxy pairwise velocity distribution in SDSS data.
In addition, our model allow us to constrain
the viscosity parameter for the cosmic fluid:
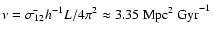 (where we have assumed
(where we have assumed
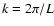 and h=0.7).
and h=0.7).
Table 1:
Pairwise peculiar velocity dispersion (
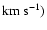 .
.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4531fig1.eps}
\end{figure}](/articles/aa/full/2006/16/aa4531-05/Timg48.gif) |
Figure 1:
Lorentzian envelope for the
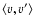 correlation with Gaussian strengh parameter
correlation with Gaussian strengh parameter
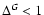 . .
|
| Open with DEXTER |
In continuity of the work of Ribeiro & Peixoto de Faria (2005), we explore
the possibility of describing the galaxy motions in the Universe
as a cosmic fluid under a diffusive-stochastic regime.
The idea is to assume the viscosity and noise terms as natural
developments in the coarse-grained large scale description.
The good correspondence
between the diffusive-stochastic modes and galaxy pairwise velocity
distribution functions (based on several redshift surveys) reinforces
the idea of this regime as a good
approximation to the cosmic fluid up to large scales.
At the same time, an important missing point in the model is about neglecting
the nonlinear term in Eq. (7). Although we should not expect
intense nonlinear effects on scales larger than 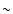 8 h-1 Mpc,
it is important to verify this assumption
according to the relative importance
of the terms in the fluid equation. As an example, we
write the observational expression for
the peculiar velocity,
v=cz - H0d, and define the large scale Reynolds number as
8 h-1 Mpc,
it is important to verify this assumption
according to the relative importance
of the terms in the fluid equation. As an example, we
write the observational expression for
the peculiar velocity,
v=cz - H0d, and define the large scale Reynolds number as
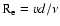 ,
where d means the distance or the scale L. Using these definitions,
we ran 500 Monte Carlo simulations of
,
where d means the distance or the scale L. Using these definitions,
we ran 500 Monte Carlo simulations of 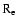 for
300<v<600
for
300<v<600
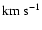 .
This range of peculiar velocity
is representative of local galaxy motions. For instance, the Milk Way
is infalling towards the Virgo cluster at
.
This range of peculiar velocity
is representative of local galaxy motions. For instance, the Milk Way
is infalling towards the Virgo cluster at 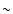 300
300
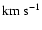 ,
while Virgo is infalling towards Hydra-Centaurus cluster at
,
while Virgo is infalling towards Hydra-Centaurus cluster at
 300
300
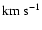 ,
producing a resultant peculiar velocity
of the local galaxy distribution of
,
producing a resultant peculiar velocity
of the local galaxy distribution of  600
600
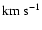 towards
Hydra-Centaurus. In Fig. 2, we show the behaviour of R
towards
Hydra-Centaurus. In Fig. 2, we show the behaviour of R for
different values of
for
different values of 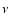 .
The Reynolds number is a measure of the
relative importance between the nonlinear and the difusive terms. For the
value of
.
The Reynolds number is a measure of the
relative importance between the nonlinear and the difusive terms. For the
value of 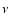 we found based on observational data, only at
very small scales we have
we found based on observational data, only at
very small scales we have
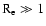 ,
giving support to our
approximation on scales
,
giving support to our
approximation on scales 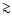 5 h-1 Mpc.
As an illustration, we also plot in this figure
simulations for smaller values of
5 h-1 Mpc.
As an illustration, we also plot in this figure
simulations for smaller values of 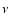 .
These points indicate
that nonlinear effects could be expected on larger scales only
for observationally unjustified small values of the viscosity term.
Our conclusion is that, for the
current available data,
the diffusive-stochastic regime seems to be a good approximation
and should drive the cosmic fluid
at most scales of astrophysical interest. At smaller scales, nonlinearity
gets importance and the fluid is probably driven by a noisy Burgers equation
(Buchert et al. 1999).
All this suggests a scenario where at different scales we have
different dynamical descriptions for the cosmic fluid. A detailed analysis
of specific solutions for the Edwards-Wilkinson to noisy-Burgers regime transition
with appropriate boundary conditions will be presented
in a forthcoming paper.
.
These points indicate
that nonlinear effects could be expected on larger scales only
for observationally unjustified small values of the viscosity term.
Our conclusion is that, for the
current available data,
the diffusive-stochastic regime seems to be a good approximation
and should drive the cosmic fluid
at most scales of astrophysical interest. At smaller scales, nonlinearity
gets importance and the fluid is probably driven by a noisy Burgers equation
(Buchert et al. 1999).
All this suggests a scenario where at different scales we have
different dynamical descriptions for the cosmic fluid. A detailed analysis
of specific solutions for the Edwards-Wilkinson to noisy-Burgers regime transition
with appropriate boundary conditions will be presented
in a forthcoming paper.
![\begin{figure}
\par\includegraphics[width=8cm]{4531fig2.eps}
\end{figure}](/articles/aa/full/2006/16/aa4531-05/Timg55.gif) |
Figure 2:
Reynolds Number for 500 Monte Carlo
realizations of Bulk Flows with
300<v<600
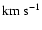 .
Filled squares means .
Filled squares means 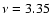 ;
open squares means ;
open squares means 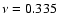 ;
and filled triangles means ;
and filled triangles means
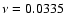
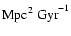 . .
|
| Open with DEXTER |
Acknowledgements
This work has the finantial support of CNPq
(under grants 470185/2003-1 and 306843/2004-8) and UESC
(under grant 220.1300.357).
- Coles, P., & Lucchin
1995, in Cosmology: The Origin and Evolution of Cosmic Structure
(John Wiley & Sons Ltd.)
(In the text)
- Buchert, T.,
Dominguez, A., & Pérez-Mercader, J. 1999, A&A, 349,
343 [NASA ADS] (In the text)
- Davis, M. 1998, PNAS,
95, 78 [NASA ADS] [CrossRef] (In the text)
- Davis, M., &
Peebles, P. J. E. 1983, ApJ, 490, 63 [NASA ADS] [CrossRef] (In the text)
- Edwards, S. F., &
Wilkinson, D. R. 1982, Proc. R. Soc. London A, 381, 17 [NASA ADS] (In the text)
- Fogedby, H. 2005,
Phys. Rev. Lett., 94, 19570 (In the text)
- Gurbatov, S. N.,
Saichev, A. L., & Shandarin, S. 1989, MNRAS, 236, 385 [NASA ADS] (In the text)
- Guzzo, L., Fisher, K.,
Strauss, M., Giovanelli, R., & Haynes, M. 1997, ApJ, 489,
37 [NASA ADS] [CrossRef] (In the text)
- Juszkiewicz, R.,
Ferreira, P., Feldman, H., Jaffe, A., & Davis, M. 2000,
Science, 287, 109 [NASA ADS] [CrossRef] (In the text)
- Kaiser, N. 1986, MNRAS,
219, 785 [NASA ADS] (In the text)
- Landy, S. 2002, ApJ,
567, 1 [NASA ADS] [CrossRef] (In the text)
- Landy, S., Szalay, A.,
& Broadhurst, T. 1998, ApJ, 494, 133 [NASA ADS] [CrossRef] (In the text)
- Marzke, R., Geller, M.,
da Costa, L. N., & Huchra, J. 1995, AJ, 110, 477 [NASA ADS] [CrossRef] (In the text)
- Peacock, J. A., Cok,
S., Norberg, P., et al. 2001, Nature, 410, 169 [NASA ADS] [CrossRef] (In the text)
- Peebles, P. J. E.
1980, The Large-Scale Structure of the Universe, (Princeton:
Princeton University Press)
(In the text)
- Ratcliffe, A.,
Shanks, T., Parker, Q., & Fong, R. 1998, MNRAS, 296, 191 [NASA ADS] [CrossRef] (In the text)
- Ribeiro, A. L. B.,
& Peixoto de Faria, J. G. 2005, Phys. Rev. D, 71, 67302 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
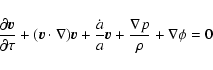
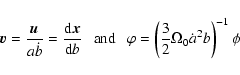
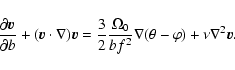
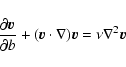
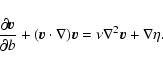
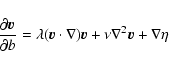
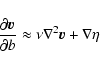
![\begin{displaymath}P({v}_k,b) \propto \prod_k \exp{ \left[-{\nu\over \Delta^G}{1...
...rm e}^{-\nu k^2b}\vert^2\over{1-{\rm e}^{-2\nu k^2b}}}\right]}
\end{displaymath}](/articles/aa/full/2006/16/aa4531-05/img28.gif)
![\begin{displaymath}P(\eta)=\exp{\left[-{1\over 2\Delta^G}\int \eta(xb)^2\;{\rm d}x\;{\rm d}b\right]}
\end{displaymath}](/articles/aa/full/2006/16/aa4531-05/img30.gif)
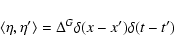
![\begin{displaymath}P_{\rm st}({v})\propto \exp{\left[ -{\nu\over \Delta^G}\int {v}(x)^2\;{\rm d}x\right]}.
\end{displaymath}](/articles/aa/full/2006/16/aa4531-05/img34.gif)
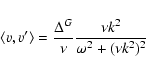
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{4531fig1.eps}
\end{figure}](/articles/aa/full/2006/16/aa4531-05/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=8cm]{4531fig2.eps}
\end{figure}](/articles/aa/full/2006/16/aa4531-05/Timg55.gif)