A&A 450, 359-364 (2006)
DOI: 10.1051/0004-6361:20054386
M. Bárta - M. Karlický
Astronomical Institute of the Academy of Sciences of the Czech Republic, Fricova 298, 25165 Ondrejov, Czech Republic
Received 9 August 2005 / Accepted 29 November 2005
Abstract
Aims. We present a new method for high-resolution structural analysis of the solar corona.
Methods. The relationship between the spectral features of various types of solar radio bursts and the physical properties of their sources have been extensively studied by many authors. On the other hand, it is plausible to accept that the spectral properties of the solar radio radiation received on the Earth are - besides the physics of the radio source - influenced by an inter-laying medium that radio waves propagate through. In particular, the regular structures in the solar corona - such as coronal waves, oscillations in shock fronts, the fine structures of coronal loops, streamer current sheets, etc. - might efficiently filter transferred radio radiation just as (broad-band) X-rays are filtered by a periodic atomic structure of crystals; the difference is only in the spatial scale. Using the wave optics methods, we investigate the prospective influence of considered coronal structures on the propagating radio waves originating in an external remote source.
Results. Preliminary results have shown that the resulting modelled radio emission may recall the spectra of observed zebra patterns for the simple 1D density structure considered here and for a reasonable set of parameters. Conversely, it is suggested that the spectra of the zebra patterns might be used for an analysis of those coronal structures that made these traces on the radiation by methods similar to those used in crystallography. The possibility of the presence of such regular small scale structures in the solar corona is demonstrated. For completeness, a brief review of contemporary models of the zebra patterns is provided.
Key words: waves - Sun: corona - Sun: radio radiation
It is a well-known fact of solid state physics that a periodic structure of the crystal grid strongly influences wave modes propagating through it. The most important consequences are the Bragg reflections of X-rays on crystals and the belt structure of energetic spectra of electrons in solids, caused by the influence of the periodic potential on the Schrödinger waves accompanying electrons (see Kittel 1976). In the case of the periodic grid, the mode propagation is constrained very strictly. For example, for a given direction the Bragg reflections occur only for sharply defined wavenumber (and its multiples); for electrons in solids, some energies (and therefore also frequencies of the corresponding Schrödinger probability waves) are completely forbidden. Nevertheless, much less regular structures also influence the dynamics of the wave passing through them: in quantum mechanics even a simple potential heap (or a well) works as a frequency filter for probability waves. It leads to the known dependence of the transmission/reflection probability of corresponding particle on its energy, usually exhibiting several maxima and minima. From another point of view, a similar principle is also used for the interference filters in optics (square-shaped "heaps'' and "wells'' of the refractive index).
Inspired by these ideas we made a first preliminary attempt to study the influence of various coronal structures such as coronal waves, oscillations in shock fronts, or the fine filamentary structure of coronal loops on the propagating, externally generated radio waves. Since the sizes of the anticipated coronal structures may be comparable to the local radio wavelength, the wave optics approach needs to be used (see, e.g. Mc Lean & Labrum 1985). This approach also takes into account the phases of radio waves involved in the process. Considered phase-coherent effects are essential in interaction between propagating waves and the structure, exactly as in the above-mentioned case of the wave propagation in solids. Therefore, basically the same principles of wave dynamics are applied, now in the context of solar radio radiation, the only difference being in spatial scales.
Considerations of propagation effects to observed radio radiation are, of course, not new. Up to now, the influence of inhomogeneities on the propagation of the radio radiation in the solar corona was extensively studied in connection with radio-wave scattering (e.g. Steinberg et al. 1971; Riddle 1972). In these studies randomly distributed density inhomogeneities and the theory based on the geometric optics were considered. Furthermore, Bougeret & Steinberg (1977) invoked a fibrous density structure to account for the source sizes and directivity of the type I radio bursts. Because we considere even smaller inhomogeneities in the present study than in the previous studies, the wave optics approach is necessary. We would like to emphasise that the wave optics approach used here for the first time introduces completely new effects on frequency-selective wave propagation and consequently on the formation of the observed spectrum.
A propagation of the electromagnetic (radio) wave as described by the electric
field intensity
![]() in unmagnetised stationary inhomogeneous
plasmas, is governed by the equation (e.g. Chen 1984)
in unmagnetised stationary inhomogeneous
plasmas, is governed by the equation (e.g. Chen 1984)
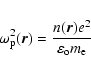
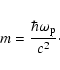
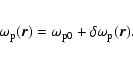
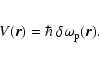
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{4386fig1.eps}\end{figure}](/articles/aa/full/2006/16/aa4386-05/Timg14.gif) |
Figure 1:
The 1D electron density structure (expressed in the scale of
the corresponding
plasma frequency) in the form of a finite series of periodically
repeating square-shaped
wells of depth
|
| Open with DEXTER | |
Although the Schrödinger Eq. (2) has been extensively
studied and many methods for its numerical solution developed, an analytical solution is available only for a few cases of the potential
![]() .
In this preliminary study the influence of the simple 1D density structure represented by a finite series of periodical square-shaped density
wells of depth
.
In this preliminary study the influence of the simple 1D density structure represented by a finite series of periodical square-shaped density
wells of depth
![]() and period 2a (see
Fig. 1) on a propagating radio wave is investigated, since the
analytical solution is available (cf. Kronig-Penney model of
solids, Kittel 1976). The studied density structure was chosen to
roughly simulate the presence of the plane density wave in the solar
corona. A slightly
modified situation with a density drop behind the structure was
studied, too, as a better approximation of shock-front oscillations.
In the introduced quantum representation of the problem under study, a photon of
the radio radiation with the angular frequency
and period 2a (see
Fig. 1) on a propagating radio wave is investigated, since the
analytical solution is available (cf. Kronig-Penney model of
solids, Kittel 1976). The studied density structure was chosen to
roughly simulate the presence of the plane density wave in the solar
corona. A slightly
modified situation with a density drop behind the structure was
studied, too, as a better approximation of shock-front oscillations.
In the introduced quantum representation of the problem under study, a photon of
the radio radiation with the angular frequency ![]() travels freely until a limited interaction area - the density structure - is reached. In the
interaction area an exact form of the wave-packet is complicated; nevertheless
as a result, the photon is either transmitted through the structure with
probability
travels freely until a limited interaction area - the density structure - is reached. In the
interaction area an exact form of the wave-packet is complicated; nevertheless
as a result, the photon is either transmitted through the structure with
probability ![]() or reflected back with probability
or reflected back with probability
![]() .
Hence, the influence of the density structure on
spectral properties of incidental radio radiation coming from the source
reduces into the transmission/reflection given by the frequency dependence of
the transmission coefficient
.
Hence, the influence of the density structure on
spectral properties of incidental radio radiation coming from the source
reduces into the transmission/reflection given by the frequency dependence of
the transmission coefficient ![]() .
In order to find the transmission
probability T we look for such a solution of Eq. (2) which
fulfils the boundary conditions in the form of a superposition of incident and
reflected waves
.
In order to find the transmission
probability T we look for such a solution of Eq. (2) which
fulfils the boundary conditions in the form of a superposition of incident and
reflected waves
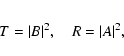
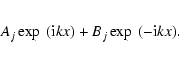
At this point it is worth mentioning that this solution can also be easily
generalised for the original
Klein-Gordon Eq. (1), if the exact dispersion relation for
electromagnetic waves in unmagnetised plasmas is used for calculations of the
wave numbers k and k'. In the present context the relation takes the form
of the relativistic energy conservation law
The influence of the density structure described above on the radio wave propagation was studied for several sets of parameters. Above all, there are two possibilities for how the density structure can influence the spectrum of propagating radiation depending on the ray paths: either the received radiation is transmitted through the structure or it is a result of the reflection on it. Corresponding ray paths are schematically pictured in Fig. 2.
![\begin{figure}
\par\includegraphics[width=6.2cm,clip]{4386fig2.eps}\end{figure}](/articles/aa/full/2006/16/aa4386-05/Timg31.gif) |
Figure 2: Two alternative ray paths leading to a modulation in the frequency: a) the filtration via transmission through (regular) density structure, b) the Bragg-like reflections on (regular) density structure. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14cm,clip]{4386fig3.eps}\end{figure}](/articles/aa/full/2006/16/aa4386-05/Timg32.gif) |
Figure 3: The transmission coefficient T for the single density well as a function of the frequency of an incident wave for the parameters given in the text. Two approximations are compared. Left: calculation based on solution of the approximate Eq. (2); right: calculation based on exact solution of Eq. (1). |
| Open with DEXTER | |
The results of our analysis of the radio waves propagating through the single
density well are shown in Fig. 3. It shows the dependence of
the transmission coefficient on the incident wave frequency
![]() in the dm range of radio waves. The background plasma
frequency
in the dm range of radio waves. The background plasma
frequency
![]() ,
variations of the plasma frequency
,
variations of the plasma frequency
![]() ,
and the period
,
and the period
![]() are used in this case. Two approximations are
compared here: the left part shows the calculated transmission
coefficient, based on the solution of (approximate) Schrödinger Eq. (2), while
the same quantity calculated directly from the Klein-Gordon Eq. (1) - i.e. using the dispersion relation (7) is displayed in the right part. As can be seen, the results are qualitatively the same, exhibiting only minor differences in positions of maxima and minima.
Figure 4 shows the reflection coefficient R=1-T as a function of
the frequency of incident wave for the case of reflection on the structure in
the form of a series of 50 density wells with the final density drop. The
background plasma frequency
are used in this case. Two approximations are
compared here: the left part shows the calculated transmission
coefficient, based on the solution of (approximate) Schrödinger Eq. (2), while
the same quantity calculated directly from the Klein-Gordon Eq. (1) - i.e. using the dispersion relation (7) is displayed in the right part. As can be seen, the results are qualitatively the same, exhibiting only minor differences in positions of maxima and minima.
Figure 4 shows the reflection coefficient R=1-T as a function of
the frequency of incident wave for the case of reflection on the structure in
the form of a series of 50 density wells with the final density drop. The
background plasma frequency
![]() ,
variations of
the plasma frequency
,
variations of
the plasma frequency
![]() ,
and
structure period
,
and
structure period
![]() are used. It can be seen that the
modulation is deeper for the rather extended interval of frequencies,
despite the depth of density wells is much smaller than in the previously studied case of
the single well. Also, peaks of the reflection coefficient are much
sharper.
are used. It can be seen that the
modulation is deeper for the rather extended interval of frequencies,
despite the depth of density wells is much smaller than in the previously studied case of
the single well. Also, peaks of the reflection coefficient are much
sharper.
To see the influence of structures on propagating radio waves directly
let us suppose now that a broad-band radio emission generated in the external remote
source with the spectral flux density of the Gaussian form
![\begin{eqnarray*}F(f)=\exp\left[-\frac{(f-f_{\rm c})^2}{2\Delta f^2}\right]
\end{eqnarray*}](/articles/aa/full/2006/16/aa4386-05/img40.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{4386fig4.eps}\end{figure}](/articles/aa/full/2006/16/aa4386-05/Timg43.gif) |
Figure 4: The reflection coefficient R=1-T for the series of 50 density wells finished by the density drop as a function of the frequency of an incident wave. See text for parameters. |
| Open with DEXTER | |
Should the results described in the previous section be not only of academic
interest without any application, the presence of fine coronal structures of
considered scales (meters to tenths of meters) is required. Besides various
short-length wave modes in coronal plasmas, one can consider the wavefronts of
coronal shocks. It is known that the shock wavefront density profile exhibits
a steep rise followed by damped oscillations around the up-stream enhanced
density value. The profile in the case of ion-sound shock was theoretically
described by Sagdeev (1966), and later on the description was
generalised for MHD shocks, too. A sample of density profile in the ion-sound shock modelled
using Sagdeev approach is shown in Fig. 5. Predicted profiles
were really observed in the laboratory (Taylor et al. 1970), as well as
in the space
plasma (Bale et al. 2003). Observations of the Cluster spacecraft were
used to estimate the scale of oscillations for the quasi-perpendicular
MHD shock
(Earth's bow shock), and it was found that for Mach numbers ![]() the
characteristic period is approximately given by the ion inertial scale
the
characteristic period is approximately given by the ion inertial scale
![]() ,
c being the speed of light and
,
c being the speed of light and
![]() the ion plasma frequency (Bale et al. 2003). In coronal
conditions, for the case modelled in Fig. 3 and
the ion plasma frequency (Bale et al. 2003). In coronal
conditions, for the case modelled in Fig. 3 and
![]() GHz, it gives the ion inertial scale
GHz, it gives the ion inertial scale
![]() m. This is consistent with the period of considered
structure (8 m).
m. This is consistent with the period of considered
structure (8 m).
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{4386fig5.eps}\end{figure}](/articles/aa/full/2006/16/aa4386-05/Timg49.gif) |
Figure 5: The theoretically predicted density profile around the ion-sound shock wavefront in the shock reference frame calculated using the Sagdeev potential approach (Sagdeev 1966). The whole structure moves to left relative to ambient plasma at the speed given by Mach number M=1.2. |
| Open with DEXTER | |
As shown by high-resolution observations made by the TRACE spacecraft, the solar corona shows fibrous structures up to the resolution limits. However, the real scales of these fine structures can be several orders of magnitude smaller than observed now. Therefore both the transient phenomena with periodic spatial structures as waves and the quasi-stationary periodic fine structures formed in magnetic loops, in streamer current sheets, and CMEs could have phase-coherent effects on propagating radio waves leading to interference patterns in the observed radio spectra.
![\begin{figure}
\par\includegraphics[width=6.7cm,clip]{4386fig6.eps}\end{figure}](/articles/aa/full/2006/16/aa4386-05/Timg50.gif) |
Figure 6: Spectrum of the broad-band continuum of an originally Gaussian spectral profile after the filtration via transmission through the single density well. See text for parameters. |
| Open with DEXTER | |
The zebra-type burst can be considered an interesting example of a pattern possibly caused by the phase-coherent effects and also found in solar radio spectra. Comparing the modelled radio flux in Fig. 6 with the spectrum of zebra pattern observed in May 2, 1998 (Fig. 7) in the dm range by the Ondrejov radiospectrograph (Jiricka et al. 1993) makes the similarities apparent. Hence it seems that the interaction of radio waves propagating through the considered coronal structures could account for modulation in frequency, which is the main feature of zebra patterns. Also, background continua frequently accompanying the zebra patterns and the temporal correlation of their intensity with that of the zebra lines (Aurass et al. 2003) may be explained naturally by these effects. In this interpretation the pattern represents a trace created by the structure under consideration on the spectrum of transferred radio radiation. Conversely, the coronal fine structures can be studied in the frame of this interpretation by analysing the zebra pattern spectra in the same way as crystalline structure of solids is studied via the diffraction patterns of X-rays transferred through the crystal.
Nevertheless, it should be noted here that many alternative interpretations of zebras exist, as this type of the radio burst has already attracted attention for many years. The existing models of the zebra pattern explain the observed spectra as a consequence of physical processes in the radio source (specific emission mechanism, eigen-modes of resonator-like source) and can be basically divided into the three following classes: 1) models based on the double plasma resonance (DPR) and subsequent transformation of generated plasma (upper-hybrid in fact) waves into the electromagnetic mode (Zheleznyakov & Zlotnik 1975; Ledenev et al. 2001; Zlotnik et al. 2003), 2) models involving the non-linear coupling of Bernstein modes (Altyntsev et al. 2005, and references therein), and 3) the model based on the eigen-modes of plasma waves trapped in a resonator-like structure formed by local plasma inhomogeneity (LaBelle et al. 2003).
| |
Figure 7: The zebra pattern observed on May 2, 1998 in the decimetric range by the Ondrejov radiospectrograph. The dynamic spectrum ( left) and frequency profile at 14:29:27.3 UT ( right) are shown. |
| Open with DEXTER | |
It is not easy to discriminate among the proposed models. Nevertheless, a new combined approach gave the first promising results based on the spectral, as well as positional, measurements in the metric range simultaneously with SOHO and TRACE observations. Besides the characteristic modulated spectrum, other features associated with the zebra burst were found. Chernov et al. (1998) have presented the event lasting almost 3 h and exhibiting "zebra patterns'' at times of the observation of three separated sources. It can agree with the considered interpretation of the zebra burst as an "interference'' pattern, too. In the case of the reflection, it gives the possibility of observing at least two separated sources (one of them the zebra source) that are correlated in time. However, stationary fine density structures are required, rather than the transient waves and shock fronts that were mostly considered for simplicity here. Furthermore, Aurass et al. (2003) show a good correlation between the inclination of a single zebra stripe to the heliographic observing frequency level in the dynamic spectrogram and the speed of the simultaneously observed projected source motion at this frequency. Besides other effects explaining this feature in terms of the DPR model of Zlotnik et al. (2003), one can imagine that the time-dependent inclination of the reflecting regular coronal fine structure may lead both to the frequency drift of zebra lines (due to the change of transmission/reflection coefficient frequency dependence) and to the apparent source motion. Since the coronal density structures are confined by the magnetic field, this issue also possibly addresses the directivity of source motion with respect to the magnetic field (Aurass et al. 2003). Nevertheless, this question requires further detailed study in the framework of a much better approximation involving a wave optics approach to the radio wave propagation in a general 3D structure.
Although the suggested interpretation has at least the potential to explain above-mentioned observational features, they can also be interpreted in framework of other models. Nevertheless, there are some specific properties of our model that can help to distinguish proposed effect observationally. First, a radio source and the periodic structure, where an interaction occurs, are spatially separated. This fact can provide a test based on the temporal correlation between the intensity variations of zebra lines and accompanying continuum. The possibly found temporal lag might be interpreted as a light-time effect or a phase delay due to the propagation of reflected/transmitted radio waves through the region of a different refractive index. Further, as can be seen in Fig. 3, the frequencies of emission lines are not exactly equidistant, but - as in the case of solid crystals - instead form a sequence characteristic for each density structure. Careful analysis of observed zebra patterns containing many emission lines can thus be used as a test of the applicability of considered effects; and in the positive case, even the density structure that made the trace on the spectrum can be determined.
Formation of solar radio spectra is not a simple process. Besides peculiarities connected with the generation of radio emission in the solar corona, the spectrum certainly can be influenced by propagation effects, too. As implications of source physics to observed radio spectra have already been studied by many authors, we concentrated on the possible influence of coronal fine structures on the spectrum of the radio radiation transferred through them. Inspired by the effects that the periodic structure of the crystals of solids has on propagation of the X-ray radiation, we studied the interaction of regular structures, such as various kinds of waves in the corona with propagating radio waves, using the methods of wave optics for the first time. In order to simplify the problem, the supposed wave-like structures in the corona were simulated by a series of regularly spaced square-shaped density variations in the direction of wave propagation throughout this preliminary study. In this 1D configuration even an analytical solution is available. It was shown that such structures can efficiently filter propagating radio radiation via transmission through or reflection on them, even for reasonably small density variations (8% in plasma frequency, Fig. 4).
As demonstrated, the resulting radio flux as received by ground-based radiospectrographs may recall observed zebra patterns for the 1D density structure used within this study and a reasonable set of model parameters. Conversely, the possibility opens for studying the regular structures in the solar corona via an analysis of the zebra (or zebra-like) spectral patterns by methods of the structural analysis of solids. Nevertheless, many alternative models of the zebra pattern exist and discrimination among them requires careful analysis of combined observational data. Moreover, a detailed study of zebra patterns spectra reveals their sub-classes (see, e.g. Jiricka et al. 2001), which could be generated by different processes. There is still a question as to whether some other spectral patterns caused by phase-coherent wave interaction with coronal structures could also be found. The answer requires further study of radio wave propagation through regular structures other than the simple 1D periodic pattern analysed here for the sake of simplicity. Also, generalisation towards the time-dependent density pattern is desirable for direct comparison of the modelled and observed dynamics of radio spectra.
The main purpose of the present paper was to emphasise a new aspect of the formation of radio spectra and of its applicable consequences. It is a first attempt to analyse the effects of regular coronal structures on resulting radio spectra in the framework of a wave optics approach, so many questions remain open. First, the square-shaped density variations are crude approximations of real density profiles. On the other hand, it is well known from the structural analysis of solids that, while the periodicity of the grid is a crucial property for ensuring the frequency selectivity for the transmission/reflection of propagating wave modes, the detailed shape of electron density profile only influences the relative amplitude of the Bragg-reflected X-rays (Kittel 1976). A further question is how the results will be affected when studying a real 3D case. One can imagine thatthe wavelength of the assumed wave (density structure) in the corona changes slowly along the wavefront. Will it smooth the frequency filtering out completely or will there be some preferred direction of propagation, e.g. due to a wavefront curvature, which would be able to concentrate waves of given wavelengths in a specified direction? Again finding inspiration in solid state analysis, there is hope that some frequency modulation could even be conserved for the radiation affected by such quasi-regular structures. Indeed, polycrystalline materials and even glasses, where regularities in the structure persist on very small scales, still show X-ray diffraction lines, however diffuse in the latter case. Nevertheless, a final answer to these questions requires much better approximation of the problem, namely numerical analysis of the radio-wave propagation in a general 3D structure in the corona in the framework of wave optics.
Acknowledgements
This work was supported by the project AV0Z10030501 and by the grants A3003202 and 1QS300120506 of the Academy of Sciences of the Czech Republic. Authors would like to thank an anonymous referee for useful comments that improved the paper.