A&A 449, 1209-1218 (2006)
DOI: 10.1051/0004-6361:20054482
J. Leenaarts1 - R. J. Rutten1,2 - P. Sütterlin1 - M. Carlsson2,3 - H. Uitenbroek4
1 - Sterrekundig Instituut, Utrecht University, Postbus 80 000,
3508 TA Utrecht, The Netherlands
2 -
Institute of Theoretical Astrophysics, University of Oslo,
PO Box 1029, Blindern, 0315 Oslo, Norway
3 -
Center of Mathematics for Applications, University of Oslo,
PO Box 1053, Blindern, 0316 Oslo, Norway
4 -
NSO/Sacramento Peak, PO Box 62, Sunspot, NM 88349-0062, USA
Received 7 November 2005 / Accepted 17 December 2005
Abstract
High-resolution solar images taken in the blue wing of the
Balmer H ![]() line with the Dutch Open Telescope show
intergranular magnetic elements as strikingly bright features,
similar to, but with appreciably larger contrast over the
surrounding granulation than their more familiar manifestation as
G-band bright points. Part of this prominent appearance is due to
low granular contrast, without granule/lane brightness reversal as,
e.g., in the wings of Ca II H & K. We use 1D and 2D radiative
transfer modeling and 3D solar convection and magnetoconvection
simulations to reproduce and explain the H
line with the Dutch Open Telescope show
intergranular magnetic elements as strikingly bright features,
similar to, but with appreciably larger contrast over the
surrounding granulation than their more familiar manifestation as
G-band bright points. Part of this prominent appearance is due to
low granular contrast, without granule/lane brightness reversal as,
e.g., in the wings of Ca II H & K. We use 1D and 2D radiative
transfer modeling and 3D solar convection and magnetoconvection
simulations to reproduce and explain the H ![]() wing images. We
find that the blue H
wing images. We
find that the blue H ![]() wing obeys near-LTE line formation. It
appears particularly bright in magnetic elements through low
temperature gradients. The granulation observed in the blue wing of
H
wing obeys near-LTE line formation. It
appears particularly bright in magnetic elements through low
temperature gradients. The granulation observed in the blue wing of
H ![]() has low contrast because of the lack of H
has low contrast because of the lack of H ![]() opacity in
the upper photosphere, Doppler cancellation, and
large opacity sensitivity to temperature working against
source function sensitivity. We conclude that the blue H
opacity in
the upper photosphere, Doppler cancellation, and
large opacity sensitivity to temperature working against
source function sensitivity. We conclude that the blue H ![]() wing represents a promising proxy
magnetometer to locate and track isolated intermittent magnetic elements, a better one than the
G band and the wings of Ca II H & K although less sharp at given aperture.
wing represents a promising proxy
magnetometer to locate and track isolated intermittent magnetic elements, a better one than the
G band and the wings of Ca II H & K although less sharp at given aperture.
Key words: Sun: magnetic fields - Sun: granulation - Sun: photosphere - Sun: chromosphere
The Dutch Open Telescope (DOT) on La Palma was equipped with a tunable
Lyot filter for the Balmer H ![]() line at 656.3 nm during the autumn
of 2004. High-resolution images taken in the blue wing of
H
line at 656.3 nm during the autumn
of 2004. High-resolution images taken in the blue wing of
H ![]() were found to display strikingly intense small-scale
brightenings at the locations where intergranular magnetic elements
cause the more familiar "G-band bright points'' in the CH band around
430.5 nm. Figures 1 and 2 below show examples.
Figure 3 demonstrates the potential of these
H
were found to display strikingly intense small-scale
brightenings at the locations where intergranular magnetic elements
cause the more familiar "G-band bright points'' in the CH band around
430.5 nm. Figures 1 and 2 below show examples.
Figure 3 demonstrates the potential of these
H ![]() bright points for tracking intermittent magnetic elements
over long durations. In this paper we reproduce and explain their
formation using numerical simulations of various nature. We
necessarily elaborate on the formation of the H
bright points for tracking intermittent magnetic elements
over long durations. In this paper we reproduce and explain their
formation using numerical simulations of various nature. We
necessarily elaborate on the formation of the H ![]() wings in some detail.
wings in some detail.
G-band bright points![]() have been a major observational diagnostic of
small magnetic elements in intergranular lanes in the two decades following Muller & Roudier (1984). A brief review is given in the introduction to Paper IV of this series (de Wijn et al. 2005). The upshot is that G-band bright points remain a very useful proxy to
chart small intergranular magnetic elements, be it not with strict one-to-one correspondence between brightness and magnetic flux density (cf. Berger & Title (2001); Berger et al. 2004),
and that they derive their brightness primarily from deeper-than-outside radiation escape, sampling temperatures that are cooler than outside at equal geometrical height but hotter at equal
optical depth. The latter excess is probably due to radiative
hot-wall heating in the absence of convective heating, as proposed
already by Spruit (1976). Magnetomechanical energy dissipation appears unimportant throughout the photosphere (Sheminova et al. 2005).
have been a major observational diagnostic of
small magnetic elements in intergranular lanes in the two decades following Muller & Roudier (1984). A brief review is given in the introduction to Paper IV of this series (de Wijn et al. 2005). The upshot is that G-band bright points remain a very useful proxy to
chart small intergranular magnetic elements, be it not with strict one-to-one correspondence between brightness and magnetic flux density (cf. Berger & Title (2001); Berger et al. 2004),
and that they derive their brightness primarily from deeper-than-outside radiation escape, sampling temperatures that are cooler than outside at equal geometrical height but hotter at equal
optical depth. The latter excess is probably due to radiative
hot-wall heating in the absence of convective heating, as proposed
already by Spruit (1976). Magnetomechanical energy dissipation appears unimportant throughout the photosphere (Sheminova et al. 2005).
![\begin{figure}
\par\includegraphics[width=16.1cm,clip]{AA4482-f1} \end{figure}](/articles/aa/full/2006/15/aa4482-05/Timg9.gif) |
Figure 1:
DOT images of a quiet-Sun area below a quiescent filament.
Top left: G band. Top right: Ca II H core.
Bottom left: blue H |
| Open with DEXTER | |
The G band provides the sharpest magnetic-element proxy imagery so
far, in particular at the Swedish 1-m Solar Telescope (SST, see Wiehr et al. 2004; Berger et al. 2004; Rouppe van der Voort et al. 2005) and so remains the workhorse of high-resolution magnetic-element studies (e.g., Sánchez Almeida et al. 2004).
Nevertheless, the G band is less suited to track isolated magnetic
elements with time than other diagnostics, in particular Ca II H & K and, as we show in this paper, the blue wing of H ![]() .
.
The sketch in Fig. 8 of Rutten (1999) illustrates why Ca II H & K provide stabler magnetic-element proxies than the G band. Small intergranular magnetic structures vary much in cross-section and shape while being deformed by granular buffeting. In the LTE-formed G band they sometimes display bright hot walls, but only intermittently. G-band bright points may therefore transform, weaken, diffuse, or vanish while the magnetic flux itself is more stably present - although at varying concentration. Granular buffeting is indeed observed to act in this manner in the plage regions described by Rouppe van der Voort et al. (2005), breaking areas with high magnetic flux density such as G-band sheets ("ribbons'') into strings of bright points and deforming the "flowers'' marking small flux concentrations.
In contrast, the H & K line cores display magnetic-element brightness
more continuously, mainly through some as yet unidentified
chromospheric magnetomechanical heating process that produces
line-center emission peaks. They produce bright features in
Ca II H & K filtergrams akin to above G-band bright points, at
larger contrast with their surroundings but much less sharply (see
Fig. 1 for examples). These Ca II H & K bright
points![]() tend to be present more consistently than the underlying photospheric
G-band bright points. They are considerably less sharp because of
resonance scattering within the solar atmosphere and through
morphology change between photosphere and chromosphere, possibly
including upward magnetic-element spreading as in idealized
magnetostatic fluxtubes. They are therefore not easily resolved in
crowded plage and network areas. However, in less crowded quiet-Sun
network and especially in internetwork regions, Ca II H & K provide
better diagnostics than the G band to track isolated magnetic elements
with time. This property was used in Paper IV of this series by de Wijn et al. (2005)
to establish the considerable longevity of internetwork field concentrations.
tend to be present more consistently than the underlying photospheric
G-band bright points. They are considerably less sharp because of
resonance scattering within the solar atmosphere and through
morphology change between photosphere and chromosphere, possibly
including upward magnetic-element spreading as in idealized
magnetostatic fluxtubes. They are therefore not easily resolved in
crowded plage and network areas. However, in less crowded quiet-Sun
network and especially in internetwork regions, Ca II H & K provide
better diagnostics than the G band to track isolated magnetic elements
with time. This property was used in Paper IV of this series by de Wijn et al. (2005)
to establish the considerable longevity of internetwork field concentrations.
In this paper we show that H ![]() -wing bright points provide
even better recognizability (at given angular resolution) than
Ca II H & K bright points, but through a different mechanism.
They derive high contrast primarily from specific H
-wing bright points provide
even better recognizability (at given angular resolution) than
Ca II H & K bright points, but through a different mechanism.
They derive high contrast primarily from specific H ![]() line
formation properties within the photosphere. In
Sect. 2 we display pertinent observations. In
Sect. 3 we first use 2D radiative transfer
modeling in a 3D MHD simulation snapshot slice to model photospheric
H
line
formation properties within the photosphere. In
Sect. 2 we display pertinent observations. In
Sect. 3 we first use 2D radiative transfer
modeling in a 3D MHD simulation snapshot slice to model photospheric
H ![]() wing formation in magnetic elements. Additional 1D modeling
using a standard solar model atmosphere is added to explain some
H
wing formation in magnetic elements. Additional 1D modeling
using a standard solar model atmosphere is added to explain some
H ![]() properties. We then use the full 3D snapshot of the MHD simulation to compare computed with observed magnetic-element brightness contrast in the blue H
properties. We then use the full 3D snapshot of the MHD simulation to compare computed with observed magnetic-element brightness contrast in the blue H ![]() wing.
wing.
The data used here were obtained with the Dutch Open Telescope (Rutten et al. 2004b)
on La Palma on October 6, 2004 during campaign JOP178. The target was
the gap in a quiescent filament seen in the bottom-right panel of
Fig. 1, at solar coordinates S16 E11.
Polarimetry of this region with THEMIS![]() shows that the clusters of magnetic elements at left and right in the field of view had opposite polarity. A tomographic
multi-wavelength image sequence was recorded during excellent seeing
from 08:47 UT until 09:42 UT with the DOT's multi-wavelength speckle
imaging system (Bettonvil et al. 2003). The latter had just been extended with the Lyot filter for H
shows that the clusters of magnetic elements at left and right in the field of view had opposite polarity. A tomographic
multi-wavelength image sequence was recorded during excellent seeing
from 08:47 UT until 09:42 UT with the DOT's multi-wavelength speckle
imaging system (Bettonvil et al. 2003). The latter had just been extended with the Lyot filter for H ![]() previously used at the Ottawa River Solar Observatory (Gaizauskas 1976).
It transmits a tunable band of 0.025 nm FWHM. Between the successive speckle bursts it was switched sequentially between H
previously used at the Ottawa River Solar Observatory (Gaizauskas 1976).
It transmits a tunable band of 0.025 nm FWHM. Between the successive speckle bursts it was switched sequentially between H ![]() line center and the blue H
line center and the blue H ![]() wing at
wing at
![]() nm.
These wavelength settings were made precise through an initial imaging scan through the whole profile. The four other DOT cameras registered the same field in the G band, blue continuum, red
continuum, and Ca II H line center (passband 0.128 nm). The burst cadence was 30 s at 100 frames/burst with five-camera synchronization.
nm.
These wavelength settings were made precise through an initial imaging scan through the whole profile. The four other DOT cameras registered the same field in the G band, blue continuum, red
continuum, and Ca II H line center (passband 0.128 nm). The burst cadence was 30 s at 100 frames/burst with five-camera synchronization.
The speckle-masking reconstruction and other reduction steps are summarized in Rutten et al. (2004b). The resulting image sequences were spatially aligned and corrected for
remaining quality variations by equalization of the average radial power spectrum![]() .
.
Figure 1 shows sample images covering the full field of view. The first panel shows the familiar G-band scene of granulation with intergranular clusters of tiny bright points which mark magnetic elements. The second panel shows the same scene in the core of Ca II H. The filter is wide enough to include part of the inner wings which show the reversed granulation analyzed in Papers II and III of this series (Rutten et al. 2004a; Leenaarts & Wedemeyer-Böhm 2005). It appears as a bright mesh pattern on which acoustic H2V grains are superimposed. The magnetic elements causing G-band bright points appear quite bright in Ca II H but very unsharp, with bright aureoles of diffuse emission around them.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{AA4482-f2} \end{figure}](/articles/aa/full/2006/15/aa4482-05/Timg10.gif) |
Figure 2:
Cut-out image magnifications corresponding to the righthand
rectangle in Fig. 1. The four images
were taken simultaneously. Top left: G band. Top
right: Ca II H line center. Bottom left: near-H |
| Open with DEXTER | |
The third panel of Fig. 1 shows the same scene
in the blue wing of H ![]() ,
the fourth panel does so in H
,
the fourth panel does so in H ![]() line center. The filament is prominent in the latter but transparent in the H
line center. The filament is prominent in the latter but transparent in the H ![]() wing. The dark streaks in the
blue-wing image are part of the elongated H
wing. The dark streaks in the
blue-wing image are part of the elongated H ![]() mottles seen at
line center. The latter do not connect the two regions of opposite
polarity across the filament gap, but curve away avoiding the neutral
line marked by the filament. Some mottle endings are likely to appear
extra dark in the blue-wing image through Doppler blueshift.
mottles seen at
line center. The latter do not connect the two regions of opposite
polarity across the filament gap, but curve away avoiding the neutral
line marked by the filament. Some mottle endings are likely to appear
extra dark in the blue-wing image through Doppler blueshift.
Apart from the dark mottle endings, the H ![]() blue-wing image
shows a greyish background of non-reversed granulation at low
contrast, plus strikingly bright points. In the network areas these
are concentrated into clusters from which the dark mottle endings
emanate. The Ca II H image also shows bright point but less
sharp and (as we show below) with different morphology. It also shows
short streaks emanating from these. The H
blue-wing image
shows a greyish background of non-reversed granulation at low
contrast, plus strikingly bright points. In the network areas these
are concentrated into clusters from which the dark mottle endings
emanate. The Ca II H image also shows bright point but less
sharp and (as we show below) with different morphology. It also shows
short streaks emanating from these. The H ![]() line center also
shows bright points near the mottle endings, but with yet larger
difference in morphology. The chromospheric features
in these images are discussed further in Rutten (2006).
line center also
shows bright points near the mottle endings, but with yet larger
difference in morphology. The chromospheric features
in these images are discussed further in Rutten (2006).
The G-band image serves to identify all H ![]() -wing bright points as
G-band bright points. They are sharper in the G band but stand out
much clearer in the H
-wing bright points as
G-band bright points. They are sharper in the G band but stand out
much clearer in the H ![]() wing. Comparison of the four images
immediately establishes H
wing. Comparison of the four images
immediately establishes H ![]() -wing bright points as excellent
magnetic-element markers, less sharp but much brighter than their
G-band counterparts while much sharper than their Ca II H counterparts.
-wing bright points as excellent
magnetic-element markers, less sharp but much brighter than their
G-band counterparts while much sharper than their Ca II H counterparts.
Figure 2 shows a similar comparison for the righthand subfield outlined in Fig. 1, at large magnification. The G-band subfield in the upper-left panel shows strings of bright points marking magnetic flux in the lower-right part of the panel. They are sharp but have rather low contrast compared with their surroundings. Their sizes are close enough to the resolution limit that they are apt to vanish through cancellation against the surrounding intergranular darkness when diminishing in size or brightness (Title & Berger 1996).
The upper-right Ca II H panel shows enhanced emission at the site of G-band bright points, but diffuse and not one-to-one. The reverse granulation in the remainder of the image also represents a vague rather than a one-to-one contrast reversal.
The red continuum image at the lower left has appreciably lower resolution and lower contrast than the G-band image due to the increase of diffraction with wavelength, smaller Planck function sensitivity to temperature, and lack of magnetic-element brightness enhancement as occurs in the G band. Some granules are appreciably brighter than the brightest magnetic elements.
For H ![]() one might expect similar loss of bright-point visibility
as in the neighboring red continuum, or lack of spatial matching as in Ca II H. However, the lower-right panel of Fig. 2 showing the same subfield in the blue
H
one might expect similar loss of bright-point visibility
as in the neighboring red continuum, or lack of spatial matching as in Ca II H. However, the lower-right panel of Fig. 2 showing the same subfield in the blue
H ![]() -wing displays all bright points seen in the G-band image at
larger contrast. In particular, the bright point at
(x,y) =
(66.7,42.2) stands out only in H
-wing displays all bright points seen in the G-band image at
larger contrast. In particular, the bright point at
(x,y) =
(66.7,42.2) stands out only in H ![]() .
All other structures in
H
.
All other structures in
H ![]() that are as bright or brighter match the morphology of G-band
bright points closely, although less sharply. In the lower-right
part of the subfield they make up the strings of bright beads called
"filigree'' by Dunn & Zirker (1973). These authors also proposed to call the individual elements "crinkles'' in view of their appearance - conform this image, but
resolved into G-band bright points in the upper-left image, and those
are likely to resolve at yet higher resolution into the flowers and
ribbons of Berger et al. (2004) and Rouppe van der Voort et al. (2005).
The background contrast in the H
that are as bright or brighter match the morphology of G-band
bright points closely, although less sharply. In the lower-right
part of the subfield they make up the strings of bright beads called
"filigree'' by Dunn & Zirker (1973). These authors also proposed to call the individual elements "crinkles'' in view of their appearance - conform this image, but
resolved into G-band bright points in the upper-left image, and those
are likely to resolve at yet higher resolution into the flowers and
ribbons of Berger et al. (2004) and Rouppe van der Voort et al. (2005).
The background contrast in the H ![]() wing, consisting of normal rather
than reversed granulation, is exceptionally small except where dark
mottle endings occur.
wing, consisting of normal rather
than reversed granulation, is exceptionally small except where dark
mottle endings occur.
The upper-right part of the H ![]() -wing image in
Fig. 2 also shows a long chain of less bright
beads in a dark lane. The G-band displays only greyish small-scale
structure there. Sometimes such structure represents speckle
reconstruction artifacts caused by DOT camera defects. However,
inspection of the temporal evolution of this area shows that the
brighter beads in the chain possess, while migrating around,
longevities of well over ten minutes. These indicate magnetic nature.
-wing image in
Fig. 2 also shows a long chain of less bright
beads in a dark lane. The G-band displays only greyish small-scale
structure there. Sometimes such structure represents speckle
reconstruction artifacts caused by DOT camera defects. However,
inspection of the temporal evolution of this area shows that the
brighter beads in the chain possess, while migrating around,
longevities of well over ten minutes. These indicate magnetic nature.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{AA4482-f3} \end{figure}](/articles/aa/full/2006/15/aa4482-05/Timg12.gif) |
Figure 3:
Cut-out image magnifications and time slices corresponding to the
lefthand outline sampling quiet network in
Fig. 1, from left to right for the G band,
Ca II H, and the H |
| Open with DEXTER | |
The large H ![]() brightness of G-band bright points, the low
contrast of the granular background in H
brightness of G-band bright points, the low
contrast of the granular background in H ![]() ,
and the above
indication that H
,
and the above
indication that H ![]() is a sensitive magnetic-feature finder
suggest that the H
is a sensitive magnetic-feature finder
suggest that the H ![]() wing is an even better indicator to locate
and follow long-lived isolated magnetic elements than Ca II H & K.
Figure 3 confirms this expectation. The G-band time
slice shows only intermittent bright-point presence. The wiggles are
probably small co-registration errors. Instead, both the H
wing is an even better indicator to locate
and follow long-lived isolated magnetic elements than Ca II H & K.
Figure 3 confirms this expectation. The G-band time
slice shows only intermittent bright-point presence. The wiggles are
probably small co-registration errors. Instead, both the H ![]() wing and the Ca II H core show much clearer brightness streaks betraying long-duration magnetic presence. Of these two, H
wing and the Ca II H core show much clearer brightness streaks betraying long-duration magnetic presence. Of these two, H ![]() is
the better proxy for locating and tracking such magnetic elements.
The lefthand bright point in the H
is
the better proxy for locating and tracking such magnetic elements.
The lefthand bright point in the H ![]() image is not identifiable as a magnetic element in the other two images, but the H
image is not identifiable as a magnetic element in the other two images, but the H ![]() time slice clearly marks it as one. A few minutes later it
merges with the righthand one by migration in x. The joint trail ends
later when the feature migrated in y off the cut location, but it
actually existed until the end of the image sequence.
time slice clearly marks it as one. A few minutes later it
merges with the righthand one by migration in x. The joint trail ends
later when the feature migrated in y off the cut location, but it
actually existed until the end of the image sequence.
The surroundings of the H ![]() streak roughly reflect the granulation
seen in the G-band panel but at lower contrast. The Ca II H time-slice
background is instead dominated by three-minute acoustic oscillations
superimposed on reversed granulation. The bright point at t=45 min
is likely an acoustic grain.
streak roughly reflect the granulation
seen in the G-band panel but at lower contrast. The Ca II H time-slice
background is instead dominated by three-minute acoustic oscillations
superimposed on reversed granulation. The bright point at t=45 min
is likely an acoustic grain.
In order to explain the high visibility of magnetic elements in the
blue wing of H ![]() we use a single time-step snapshot of a three-dimensional (3D) magneto-hydrodynamics simulation by Stein & Nordlund with a code incorporating an LTE equation of state including partial ionization and multi-group LTE radiative transfer
(Stein & Nordlund 1998). The same snapshot was used by Carlsson et al. (2004)
to analyse G-band bright point formation towards the solar limb.
we use a single time-step snapshot of a three-dimensional (3D) magneto-hydrodynamics simulation by Stein & Nordlund with a code incorporating an LTE equation of state including partial ionization and multi-group LTE radiative transfer
(Stein & Nordlund 1998). The same snapshot was used by Carlsson et al. (2004)
to analyse G-band bright point formation towards the solar limb.
The extent of the simulation is 6 Mm in both horizontal directions and
from -2.5 Mm below
![]() to 0.5 Mm above
it. The horizontal resolution is 23.6 km. The vertical resolution
varies from 35 km in the lower layers to 15 km in the upper
layers. The simulation was started with a homogeneous vertical
magnetic field of 250 G.
to 0.5 Mm above
it. The horizontal resolution is 23.6 km. The vertical resolution
varies from 35 km in the lower layers to 15 km in the upper
layers. The simulation was started with a homogeneous vertical
magnetic field of 250 G.
We evaluated the emergent intensity in the H ![]() wing that originates from this snapshot using the RH code of Uitenbroek (2001) to compute radiative transfer in the snapshot in a variety of ways. It permits LTE or NLTE radiative transfer modeling in 2D or 3D geometry with partial or complete frequency redistribution. We used it here to perform H
wing that originates from this snapshot using the RH code of Uitenbroek (2001) to compute radiative transfer in the snapshot in a variety of ways. It permits LTE or NLTE radiative transfer modeling in 2D or 3D geometry with partial or complete frequency redistribution. We used it here to perform H ![]() modeling both in 2D admitting departures from LTE and in 3D assuming LTE. We also present 1D results using the
FAL-C model of Fontenla et al. (1993) for explanatory purposes.
modeling both in 2D admitting departures from LTE and in 3D assuming LTE. We also present 1D results using the
FAL-C model of Fontenla et al. (1993) for explanatory purposes.
![\begin{figure}
\par\includegraphics[width=16.4cm,clip]{AA4482-f4} \end{figure}](/articles/aa/full/2006/15/aa4482-05/Timg14.gif) |
Figure 4:
NLTE H |
| Open with DEXTER | |
In the 2D NLTE modeling we took a 2D slice from the snapshot, reducing
the horizontal resolution by a factor of two to increase the numerical
stability of the radiative transfer computations. We added the upper
part of the FAL-C model to its top. This results in a 2D atmosphere
slice of 127 points in x and 135 points in z, with a horizontal
extent of 6000 km and extending from -450 km below to 2150 km above
![]() .
We used a 5-level-plus-continuum hydrogen atom to
compute NLTE radiative transfer with partial frequency redistribution (PRD) through this model atmosphere in the H
.
We used a 5-level-plus-continuum hydrogen atom to
compute NLTE radiative transfer with partial frequency redistribution (PRD) through this model atmosphere in the H ![]() line, with 3 ray angles per octant. Inspection showed that PRD effects are only important above 500 km, well above the formation height of the
H
line, with 3 ray angles per octant. Inspection showed that PRD effects are only important above 500 km, well above the formation height of the
H ![]() wing and therefore negligible for the discussion here. We
then adopted complete frequency redistribution (CRD) to compute a NLTE solution with 10 rays per octant. The latter increase is needed to account for the large horizontal variations in the lower atmosphere.
wing and therefore negligible for the discussion here. We
then adopted complete frequency redistribution (CRD) to compute a NLTE solution with 10 rays per octant. The latter increase is needed to account for the large horizontal variations in the lower atmosphere.
The results of the 2D NLTE modeling (shown in Fig. 4
and discussed below) demonstrated that departures from LTE are small
for the formation of the H ![]() intensity at
intensity at
![]() nm. This permitted us to perform 3D modeling with the complete
snapshot assuming LTE, a feasible computing task. For this modeling
we used the full 3D simulation snapshot without adding a chromosphere
on top. In both the 2D and the 3D modeling we took Dopplershifts from
the flow velocities into account in the line profile computation. We
used a Voigt profile for the H
nm. This permitted us to perform 3D modeling with the complete
snapshot assuming LTE, a feasible computing task. For this modeling
we used the full 3D simulation snapshot without adding a chromosphere
on top. In both the 2D and the 3D modeling we took Dopplershifts from
the flow velocities into account in the line profile computation. We
used a Voigt profile for the H ![]() line. In the damping wings it
represents an approximation for the actual Holtsmark distribution.
line. In the damping wings it
represents an approximation for the actual Holtsmark distribution.
Figure 4 shows details of the formation of H ![]() wing bright points as computed from the 2D NLTE simulation. The first panel shows the absolute value of the vector magnetic field throughout the vertical slice. It contains three fluxtube-like magnetic elements
with kilogauss field strength, one weaker-field one near x=3.2 Mm,
and a subsurface magnetic concentration at x = 4.5 Mm. Panel 2
shows the temperature against height. All magnetic elements display
marked isotherm dips: they are appreciably cooler inside than outside
at the heights of interest. The latter are specified by the
superimposed curves marking the mean height of formation along columns for the
H
wing bright points as computed from the 2D NLTE simulation. The first panel shows the absolute value of the vector magnetic field throughout the vertical slice. It contains three fluxtube-like magnetic elements
with kilogauss field strength, one weaker-field one near x=3.2 Mm,
and a subsurface magnetic concentration at x = 4.5 Mm. Panel 2
shows the temperature against height. All magnetic elements display
marked isotherm dips: they are appreciably cooler inside than outside
at the heights of interest. The latter are specified by the
superimposed curves marking the mean height of formation along columns for the
H ![]() wing and its background continuum. The upper curve
corresponds to the vertical line-wing intensity contribution functions
shown in panel 5 and represents these very well. Both curves dip
deeply within the magnetic elements due to low gas density (panel 4)
where magnetic pressure is appreciable.
wing and its background continuum. The upper curve
corresponds to the vertical line-wing intensity contribution functions
shown in panel 5 and represents these very well. Both curves dip
deeply within the magnetic elements due to low gas density (panel 4)
where magnetic pressure is appreciable.
The bottom row panels display various quantities not versus
geometrical height but as a function of the radial optical depth in
the H ![]() wing, a format introduced by Carlsson et al. (2004)
which displays atmospheric stratifications "as seen'' by the
vertically emergent radiation. The two mean height of formation
curves change correspondingly. The upper one becomes virtually flat
near
wing, a format introduced by Carlsson et al. (2004)
which displays atmospheric stratifications "as seen'' by the
vertically emergent radiation. The two mean height of formation
curves change correspondingly. The upper one becomes virtually flat
near ![]() .
The lower one displays large spatial variations in its
offset from the upper one, as set by the n2 lower level
population (panel 6) with low population producing small separation.
Panel 3 is strikingly different from panel 2 by showing large upward
isotherm humps instead of dips at the magnetic element locations. The
difference between the two representations results primarily from the
substantial variations in vertical gas density stratification between
columns. These are shown in panel 4. Comparison of panels 4 and 5
shows that the upward tails of the H
.
The lower one displays large spatial variations in its
offset from the upper one, as set by the n2 lower level
population (panel 6) with low population producing small separation.
Panel 3 is strikingly different from panel 2 by showing large upward
isotherm humps instead of dips at the magnetic element locations. The
difference between the two representations results primarily from the
substantial variations in vertical gas density stratification between
columns. These are shown in panel 4. Comparison of panels 4 and 5
shows that the upward tails of the H ![]() -wing contribution functions
decay appreciably faster than the density stratifications, making the
contribution functions unusually narrow in vertical extent. This is
discussed further in Sect. 3.2. Panel 6 shows the
fractional hydrogen population occupying the n = 2 lower level of
H
-wing contribution functions
decay appreciably faster than the density stratifications, making the
contribution functions unusually narrow in vertical extent. This is
discussed further in Sect. 3.2. Panel 6 shows the
fractional hydrogen population occupying the n = 2 lower level of
H ![]() on columnar optical depth scales. It is remarkably similar
to panel 3 because the high excitation energy of this level makes its
population very sensitive to the temperature (also discussed further
in Sect. 3.2).
on columnar optical depth scales. It is remarkably similar
to panel 3 because the high excitation energy of this level makes its
population very sensitive to the temperature (also discussed further
in Sect. 3.2).
Panels 1 to 6 illustrate the formation mechanism of the H ![]() -wing
bright points. It is similar to G-band bright point formation. The
relatively low gas density in magnetic elements (panel 4) results in
appreciable Wilson depressions in the mean height of formation (panel 5 and the superimposed curves). Although the magnetic-element insides are cooler than their surroundings at any geometrical height (panel 2), panel 3 shows that they already have higher temperature at
-wing
bright points. It is similar to G-band bright point formation. The
relatively low gas density in magnetic elements (panel 4) results in
appreciable Wilson depressions in the mean height of formation (panel 5 and the superimposed curves). Although the magnetic-element insides are cooler than their surroundings at any geometrical height (panel 2), panel 3 shows that they already have higher temperature at ![]() compared with the surrounding granules. This lateral
temperature excess increases towards smaller
compared with the surrounding granules. This lateral
temperature excess increases towards smaller ![]() thanks to flatter
thanks to flatter
![]() temperature gradients (panel 3).
Its weighting into the outer tail of the intensity contribution
functions causes enhanced brightness in magnetic elements.
temperature gradients (panel 3).
Its weighting into the outer tail of the intensity contribution
functions causes enhanced brightness in magnetic elements.
The flatter
![]() temperature gradients within magnetic
elements also cause flatter
temperature gradients within magnetic
elements also cause flatter
![]() population
gradients (panel 6). One would expect correspondingly higher
formation and loss of brightness contrast, but the sensitivity of
collisional H
population
gradients (panel 6). One would expect correspondingly higher
formation and loss of brightness contrast, but the sensitivity of
collisional H ![]() broadening to the gas density compensates for
these increases. The low density inside magnetic elements reduces the
broadening and with it the relative amount of line extinction in the
damping wings, increasing the Wilson depression between outside and
inside sampling. A test computation assuming height-independent wing
shape of an artificial line with similar height of formation indeed
gave a decrease of 5-10% in the emergent intensity within the
magnetic elements.
broadening to the gas density compensates for
these increases. The low density inside magnetic elements reduces the
broadening and with it the relative amount of line extinction in the
damping wings, increasing the Wilson depression between outside and
inside sampling. A test computation assuming height-independent wing
shape of an artificial line with similar height of formation indeed
gave a decrease of 5-10% in the emergent intensity within the
magnetic elements.
The remaining panels in the third column of Fig. 4
serve to evaluate the importance of departures from LTE in H ![]() wing formation. Panels 7 and 8 show NLTE population departure coefficients for the n = 2 and n = 3 lower and upper levels of H
wing formation. Panels 7 and 8 show NLTE population departure coefficients for the n = 2 and n = 3 lower and upper levels of H ![]() .
The lower-level values are everywhere near unity
demonstrating that the line opacity obeys LTE very closely.
.
The lower-level values are everywhere near unity
demonstrating that the line opacity obeys LTE very closely.
The upper-level populations (panel 8) virtually equal the LTE value up to the upper height of formation curve. Higher up this level becomes appreciably overpopulated, probably due to radiative overionization in the Balmer continuum causing closure recombination into the n = 3level (cf. explanation in Rutten & Carlsson 1994). This overpopulation results in slight S>B source function excess within the magnetic elements and above the granules, as shown in panel 9. The largest S/B excesses occur at smaller optical depth for the magnetic elements than for the granules.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{AA4482-f5} \end{figure}](/articles/aa/full/2006/15/aa4482-05/Timg18.gif) |
Figure 5:
H |
| Open with DEXTER | |
Figure 5 shows the H ![]() wing intensities that
result from 2D radiative transfer computation for the simulation slice
of Fig. 4. The upper panel is for monochromatic
computation at
wing intensities that
result from 2D radiative transfer computation for the simulation slice
of Fig. 4. The upper panel is for monochromatic
computation at
![]() nm. The solid curve represents
the computed NLTE intensities, the grey curves LTE intensities. The
latter are everywhere smaller than the NLTE values, but only
marginally. The differences are largest for granules, in which the
S/B excesses in panel 9 of Fig. 4 occur at larger
optical depth than in the magnetic elements. However, they remain far
smaller than the variations due to the magnetic elements.
nm. The solid curve represents
the computed NLTE intensities, the grey curves LTE intensities. The
latter are everywhere smaller than the NLTE values, but only
marginally. The differences are largest for granules, in which the
S/B excesses in panel 9 of Fig. 4 occur at larger
optical depth than in the magnetic elements. However, they remain far
smaller than the variations due to the magnetic elements.
The dashed curve in the upper panel of Fig. 5
shows the emergent continuum intensity. Its shape is roughly the
reverse of the
![]() curve in
Fig. 4. The magnetic elements are at most slightly
brighter than the granules, in good agreement with the red continuum
image in Fig. 2. The H
curve in
Fig. 4. The magnetic elements are at most slightly
brighter than the granules, in good agreement with the red continuum
image in Fig. 2. The H ![]() intensities are
appreciably lower everywhere, but much more so within granules: in
H
intensities are
appreciably lower everywhere, but much more so within granules: in
H ![]() the magnetic elements gain large excess brightness.
Comparison with panel 1 of Fig. 4 shows that all strong-field
magnetic elements stand out through marked H
the magnetic elements gain large excess brightness.
Comparison with panel 1 of Fig. 4 shows that all strong-field
magnetic elements stand out through marked H ![]() -wing intensity increase.
-wing intensity increase.
The lower panel of Fig. 5 shows the computed NLTE
and LTE intensities after spectral integration over the DOT H ![]() filter passband. It shows similar behavior as the monochromatic
intensities in the upper panel. Thus, the simulation produces
H
filter passband. It shows similar behavior as the monochromatic
intensities in the upper panel. Thus, the simulation produces
H ![]() wing bright points at least qualitatively comparable to our
observations. On average, the spectrally integrated NLTE intensity is
7% brighter than for LTE due to the S/B excesses shown in
Fig. 4. The relative brightness increase from LTE to
NLTE is generally larger within the granules since their S/B excesses peak at larger optical depth (panel 9 of Fig. 4). It is also larger within granules than for
the monochromatic case (upper panel) because addition of intensity
closer to line center implies contribution from higher layers, for
which the corresponding mean contribution curve in panel 9 of
Fig. 4 cuts closer through the granular S/B peaks.
wing bright points at least qualitatively comparable to our
observations. On average, the spectrally integrated NLTE intensity is
7% brighter than for LTE due to the S/B excesses shown in
Fig. 4. The relative brightness increase from LTE to
NLTE is generally larger within the granules since their S/B excesses peak at larger optical depth (panel 9 of Fig. 4). It is also larger within granules than for
the monochromatic case (upper panel) because addition of intensity
closer to line center implies contribution from higher layers, for
which the corresponding mean contribution curve in panel 9 of
Fig. 4 cuts closer through the granular S/B peaks.
![\begin{figure}
\par\includegraphics[width=17.2cm,clip]{AA4482-f6}\end{figure}](/articles/aa/full/2006/15/aa4482-05/Timg20.gif) |
Figure 6:
Illustration explaining the difference between H |
| Open with DEXTER | |
Solar images taken in the wings of Ca II H & K show reversed granulation, a pattern comparable to the granulation seen in the continuum but with reversed brightness modulation. It is also seen in the center panel of Fig. 1 due to the width of the DOT Ca II H filter. It is primarily caused by convection flow reversals occurring between 0.2 Mm and 0.6 Mm above continuum optical depth unity (Rutten et al. 2004a; Leenaarts & Wedemeyer-Böhm 2005).
In contrast, our H ![]() wing images show no reversed granulation
(Fig. 1). The explanation is that the large
excitation energy (10.2 eV) of the n = 2 lower level causes large
temperature sensitivity of the line opacity. In Boltzmann equilibrium
the relative temperature sensitivity of the population density n of
a level with excitation energy
wing images show no reversed granulation
(Fig. 1). The explanation is that the large
excitation energy (10.2 eV) of the n = 2 lower level causes large
temperature sensitivity of the line opacity. In Boltzmann equilibrium
the relative temperature sensitivity of the population density n of
a level with excitation energy ![]() and partition function Zis
and partition function Zis
![]() .
The population sensitivity to temperature therefore scales with the
excitation energy, since Z varies only slightly with temperature.
Figure 6 illustrates the profound effect of this large
sensitivity by comparing the formation of Ca II H and H
.
The population sensitivity to temperature therefore scales with the
excitation energy, since Z varies only slightly with temperature.
Figure 6 illustrates the profound effect of this large
sensitivity by comparing the formation of Ca II H and H ![]() in the
FALC model of Fontenla et al. (1993).
Its temperature and density stratifications are shown in the first panel. The lower-left panel shows the fractional population
in the
FALC model of Fontenla et al. (1993).
Its temperature and density stratifications are shown in the first panel. The lower-left panel shows the fractional population
![]() of the lower level of each line. Due to its
temperature sensitivity the hydrogen n=2 population drops
dramatically around the temperature minimum. In contrast, the lower
level of Ca II H is almost insensitive to temperature through being
the ground state of the dominant calcium ionization stage. Only at
chromospheric levels occurs depopulation through Ca II ionization to Ca III.
of the lower level of each line. Due to its
temperature sensitivity the hydrogen n=2 population drops
dramatically around the temperature minimum. In contrast, the lower
level of Ca II H is almost insensitive to temperature through being
the ground state of the dominant calcium ionization stage. Only at
chromospheric levels occurs depopulation through Ca II ionization to Ca III.
The two center panels show the striking resulting H ![]() - Ca II H differences in line-center extinction
- Ca II H differences in line-center extinction ![]() and optical depth
and optical depth ![]() .
Neglecting stimulated emission, the first reflects the product of gas density (first panel) and fractional population; the
second the buildup of its inward integration. The H
.
Neglecting stimulated emission, the first reflects the product of gas density (first panel) and fractional population; the
second the buildup of its inward integration. The H ![]() extinction
shows a pronounced minimum at the temperature minimum which produces a nearly flat plateau in its optical depth buildup around z=500 km.
In contrast, Ca II H has almost linear dependence between extinction
and density and regular optical depth buildup.
extinction
shows a pronounced minimum at the temperature minimum which produces a nearly flat plateau in its optical depth buildup around z=500 km.
In contrast, Ca II H has almost linear dependence between extinction
and density and regular optical depth buildup.
The lack of optical depth buildup around the temperature minimum for
H ![]() translates into a lack of intensity contribution since the
term
translates into a lack of intensity contribution since the
term
![]() vanishes in the decomposition
vanishes in the decomposition
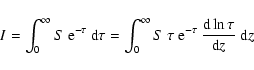 |
(1) |
In contrast, the Ca II H & K wings represent excellent diagnostics to
scan smoothly through the whole photosphere by tuning the passband
(lower rightmost panel of Fig. 6). The inner wings
sampled by the DOT Ca II H filter originate in upper-photosphere
layers where convection reversal causes reversed granulation. The
H ![]() wing misses these layers altogether. However, the outer
H
wing misses these layers altogether. However, the outer
H ![]() wing provides relatively narrow contribution functions to
sample the low photosphere.
wing provides relatively narrow contribution functions to
sample the low photosphere.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{AA4482-f7} \end{figure}](/articles/aa/full/2006/15/aa4482-05/Timg27.gif) |
Figure 7:
Demonstration of the H |
| Open with DEXTER | |
Our blue-wing H ![]() images (e.g., the one in
Fig. 1) show granulation but at very low contrast
due to multiple reasons. First: at red wavelengths the Planck
function temperature sensitivity is smaller than in the G band.
Second: the wider point spread function due to increased diffraction
decreases the small-scale contrast. Third: the granular
velocity-intensity correlation contributes Doppler cancellation of the
contrast in blueward line wings. Intergranular downflows
Doppler-shift the blue wing redward through the filter passband so
that intergranular darkening is compensated by deeper-down
higher-temperature sampling. Similarly, granular upflows shift a deeper part of the line into the blue-wing passband and so offset granular brightening by higher-up lower-temperature sampling. This
compensation works best in lines with steep wings, for example the
Ba II 455.4 nm line illustrated in Fig. 6 of Sütterlin et al. (2001),
and so has much larger effect in the H
images (e.g., the one in
Fig. 1) show granulation but at very low contrast
due to multiple reasons. First: at red wavelengths the Planck
function temperature sensitivity is smaller than in the G band.
Second: the wider point spread function due to increased diffraction
decreases the small-scale contrast. Third: the granular
velocity-intensity correlation contributes Doppler cancellation of the
contrast in blueward line wings. Intergranular downflows
Doppler-shift the blue wing redward through the filter passband so
that intergranular darkening is compensated by deeper-down
higher-temperature sampling. Similarly, granular upflows shift a deeper part of the line into the blue-wing passband and so offset granular brightening by higher-up lower-temperature sampling. This
compensation works best in lines with steep wings, for example the
Ba II 455.4 nm line illustrated in Fig. 6 of Sütterlin et al. (2001),
and so has much larger effect in the H ![]() wings than in the
extended wings of H & K (where it reverses sign with the granulation).
wings than in the
extended wings of H & K (where it reverses sign with the granulation).
A fourth effect elaborated here is decreased brightness response to
temperature due to the large H ![]() opacity sensitivity to
temperature. Spectral features that are formed in LTE without such
sensitivity, such as the wings of Ca II H & K, brighten through source
function increase where or when the temperature in the line-forming
region increases. For high-excitation lines the opacity increase
produced by temperature increase leads to higher-up line formation.
When the temperature decreases outward, as is normally the case in the
photosphere, the higher-up sampling implies darkening which offsets
the local source function increase. A cartoon illustration of this
compensation is given in Fig. 4 of Leenaarts et al. (2005).
A model illustration is given here in Fig. 7. It
compares LTE intensities in the H
opacity sensitivity to
temperature. Spectral features that are formed in LTE without such
sensitivity, such as the wings of Ca II H & K, brighten through source
function increase where or when the temperature in the line-forming
region increases. For high-excitation lines the opacity increase
produced by temperature increase leads to higher-up line formation.
When the temperature decreases outward, as is normally the case in the
photosphere, the higher-up sampling implies darkening which offsets
the local source function increase. A cartoon illustration of this
compensation is given in Fig. 4 of Leenaarts et al. (2005).
A model illustration is given here in Fig. 7. It
compares LTE intensities in the H ![]() wing computed from a granulation simulation with those computed using a fake H
wing computed from a granulation simulation with those computed using a fake H ![]() line having the same opacity but with its lower level at only 1 eV instead of 10.2 eV. The snapshot was taken from the radiation-hydrodynamics granulation simulation by Wedemeyer et al. (2004). The rms intensity variation in the lefthand granulation scene is much smaller than at right.
line having the same opacity but with its lower level at only 1 eV instead of 10.2 eV. The snapshot was taken from the radiation-hydrodynamics granulation simulation by Wedemeyer et al. (2004). The rms intensity variation in the lefthand granulation scene is much smaller than at right.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{AA4482-f8} \end{figure}](/articles/aa/full/2006/15/aa4482-05/Timg28.gif) |
Figure 8:
Results from the 3D MHD simulation. Top left: computed
intensity in the H |
| Open with DEXTER | |
Our finding in Sect. 3.1 that LTE formation is a good
assumption for the H ![]() wing in the photosphere allows us to
compute emergent wing intensities from the full 3D MHD simulation
snapshot. The results are shown in Fig. 8.
wing in the photosphere allows us to
compute emergent wing intensities from the full 3D MHD simulation
snapshot. The results are shown in Fig. 8.
The first panel shows the emergent intensity in the H ![]() wing
after spectral application of the DOT filter transmission. The top
right panel shows the magnetic field strength at the surface. The
brightest features in the computed H
wing
after spectral application of the DOT filter transmission. The top
right panel shows the magnetic field strength at the surface. The
brightest features in the computed H ![]() scene correspond to
magnetic field strengths above 1 kG.
scene correspond to
magnetic field strengths above 1 kG.
The lower panels show the simulated H ![]() wing and red continuum
scenes convoluted with a point spread function corresponding to the
DOT diameter of 45 cm. In addition, for the artificial H
wing and red continuum
scenes convoluted with a point spread function corresponding to the
DOT diameter of 45 cm. In addition, for the artificial H ![]() image
the brightness scale was clipped to cover similar range as the real
DOT H
image
the brightness scale was clipped to cover similar range as the real
DOT H ![]() image in Fig. 2. It looks much
like the latter, showing low-contrast granulation, barely visible
intergranular lanes, and magnetic elements in chains of roundish
brightness enhancements. The artificial red-continuum image in the
lower-right panel shows the same morphology but with the magnetic
elements about as bright as the granules, also in good agreement with
the corresponding DOT image in Fig. 2.
image in Fig. 2. It looks much
like the latter, showing low-contrast granulation, barely visible
intergranular lanes, and magnetic elements in chains of roundish
brightness enhancements. The artificial red-continuum image in the
lower-right panel shows the same morphology but with the magnetic
elements about as bright as the granules, also in good agreement with
the corresponding DOT image in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{AA4482-f9} \end{figure}](/articles/aa/full/2006/15/aa4482-05/Timg29.gif) |
Figure 9:
Top: H |
| Open with DEXTER | |
Figure 9 compares observed and computed H ![]() profiles and brightness contrasts, with spatial separation of bright points and granulation. Emergent-intensity H
profiles and brightness contrasts, with spatial separation of bright points and granulation. Emergent-intensity H ![]() profiles were
computed along each column of the 3D simulation assuming LTE. The
spatial separation was obtained by applying a brightness mask to the
artificial H
profiles were
computed along each column of the 3D simulation assuming LTE. The
spatial separation was obtained by applying a brightness mask to the
artificial H ![]() wing image at lower left in Fig. 8,
labeling every pixel that has
wing image at lower left in Fig. 8,
labeling every pixel that has
![]() as
belonging to a bright point, and defining all other pixels to
represent granulation. This threshold is the
as
belonging to a bright point, and defining all other pixels to
represent granulation. This threshold is the ![]() level of the
rms intensity variation in all H
level of the
rms intensity variation in all H ![]() wing images in our DOT sequence.
wing images in our DOT sequence.
The upper panel of Fig. 9 shows emergent H ![]() profiles spatially averaged over the whole simulation snapshot and spatially averaged over the magnetic elements alone. For comparison, the solar disk-center profile from the NSO Fourier Transform
Spectrometer atlas produced by J.W. Brault and calibrated by
Neckel & Labs (1984) is overlaid. The graph shows excellent agreement between the NSO atlas
and the simulated full-field average along the extended blue wing.
However, in the inner wing the simulation produces slightly higher
intensity, contrary to the expected NLTE correction indicated by
Fig. 5. This excess is not caused by the
relatively large number of bright points in the simulation since the
profile that results from spatial averaging over the granules alone
differs only marginally from the full-field average. We suspect that
the computed inner-wing excess is due to the neglect of dark
structures in the high layers sampled by the outer H
profiles spatially averaged over the whole simulation snapshot and spatially averaged over the magnetic elements alone. For comparison, the solar disk-center profile from the NSO Fourier Transform
Spectrometer atlas produced by J.W. Brault and calibrated by
Neckel & Labs (1984) is overlaid. The graph shows excellent agreement between the NSO atlas
and the simulated full-field average along the extended blue wing.
However, in the inner wing the simulation produces slightly higher
intensity, contrary to the expected NLTE correction indicated by
Fig. 5. This excess is not caused by the
relatively large number of bright points in the simulation since the
profile that results from spatial averaging over the granules alone
differs only marginally from the full-field average. We suspect that
the computed inner-wing excess is due to the neglect of dark
structures in the high layers sampled by the outer H ![]() formation
peak that are not accounted for in the 3D simulation. H
formation
peak that are not accounted for in the 3D simulation. H ![]() line-center movies, including the one sampled in Fig. 1, indicate that the upper peak samples
low-intensity chromospheric mottles and fibrils nearly everywhere,
often with large Dopplershifts. Some of these contribute considerable
darkness in the blue wing, especially near network (Fig. 1).
line-center movies, including the one sampled in Fig. 1, indicate that the upper peak samples
low-intensity chromospheric mottles and fibrils nearly everywhere,
often with large Dopplershifts. Some of these contribute considerable
darkness in the blue wing, especially near network (Fig. 1).
The dash-dotted upper curve in the upper panel of Fig. 9 holds for the spatial average over the computed bright points. Note that it is appreciably higher than the full-field average throughout the whole line profile, even though the magnetic elements in Fig. 4 are at all heights cooler than their surroundings at equal geometrical height and the 3D simulation has no chromosphere. This once again illustrates that excess brightness originating in the upper photosphere does not necessarily imply magnetomechanical heating (cf. the similar conclusion from Ca II H spectrometry in Sheminova et al. 2005).
The lower panel of Fig. 9 shows two curves specifying
the ratio of the average bright point intensity to the average granule
intensity against wavelength, one for the full-resolution simulation
scene (upper curve) and one for the DOT-like spatially smeared
simulation scene. The latter has lower contrast, as expected. The
sharp drop in the contrast curves lies slightly to the red of 656.2 nm
where the corresponding ![]() height jumps abruptly from the
deep photosphere to higher layers (Fig. 6). In the
simulation these have small lateral temperature variation. In
reality,
height jumps abruptly from the
deep photosphere to higher layers (Fig. 6). In the
simulation these have small lateral temperature variation. In
reality, ![]() lies in the mottled chromosphere where LTE computation and the simulation are certainly invalid.
lies in the mottled chromosphere where LTE computation and the simulation are certainly invalid.
Finally, we compare the average brightness of the H ![]() bright
points in the observations with the simulation curves. Applying the
brightness mask to the observed image sequence and to the smeared
passband-integrated H
bright
points in the observations with the simulation curves. Applying the
brightness mask to the observed image sequence and to the smeared
passband-integrated H ![]() wing simulation delivers
wing simulation delivers
![]() for the
observations and
for the
observations and
![]() for the simulation. The observed value is shown by
the asterisk in Fig. 9 and indeed lies above the peak
in the dotted simulation curve. Thus, the LTE simulation produces
smaller bright point contrast than is actually observed. The
differences between the NLTE and LTE curves in the lower panel of
Fig. 5 indicate that departures from LTE
reduce the computed contrast and so increase the discrepancy. In
addition, proper accounting for the broad scattering wings of the
point-spread function which are not present in our Airy-function
simulation smearing is likely to increase the discrepancy further.
for the simulation. The observed value is shown by
the asterisk in Fig. 9 and indeed lies above the peak
in the dotted simulation curve. Thus, the LTE simulation produces
smaller bright point contrast than is actually observed. The
differences between the NLTE and LTE curves in the lower panel of
Fig. 5 indicate that departures from LTE
reduce the computed contrast and so increase the discrepancy. In
addition, proper accounting for the broad scattering wings of the
point-spread function which are not present in our Airy-function
simulation smearing is likely to increase the discrepancy further.
As noted above we are not the first to describe bright points in the wing of H ![]() .
The often reprinted "filigree'' image from the Sacramento Peak Vacuum Tower Telescope in Fig. 1 of Dunn & Zirker (1973) has an H
.
The often reprinted "filigree'' image from the Sacramento Peak Vacuum Tower Telescope in Fig. 1 of Dunn & Zirker (1973) has an H ![]() panel at
panel at
![]() Å that shows
them particularly well. But it was a surprise how much promise they
possess as a diagnostic to locate intermittent magnetic elements and
track these with time (Fig. 3). They are less sharp
than G-band bright points but they show the same morphology with much
better contrast over their surroundings. On the other hand, they are
sharper than Ca II H & K line-center bright points, and they do
not suffer from the contamination by reversed granulation that affects
the H & K wings nor from bright-point morphology change as in the H & K cores (Fig. 2).
Å that shows
them particularly well. But it was a surprise how much promise they
possess as a diagnostic to locate intermittent magnetic elements and
track these with time (Fig. 3). They are less sharp
than G-band bright points but they show the same morphology with much
better contrast over their surroundings. On the other hand, they are
sharper than Ca II H & K line-center bright points, and they do
not suffer from the contamination by reversed granulation that affects
the H & K wings nor from bright-point morphology change as in the H & K cores (Fig. 2).
Similarly to G-band bright points which are exceptionally bright
through the addition of CH opacity and from partial CH destruction in
magnetic elements (Carlsson et al. 2004), H ![]() -wing bright points are exceptionally bright through the addition of Balmer-line opacity and the reduction of collisional
damping in magnetic elements. The particular flatness of the granular
background pattern in the blue H
-wing bright points are exceptionally bright through the addition of Balmer-line opacity and the reduction of collisional
damping in magnetic elements. The particular flatness of the granular
background pattern in the blue H ![]() wing derives from Doppler
cancellation and large lower-level excitation energy (Figs. 6 and 7).
wing derives from Doppler
cancellation and large lower-level excitation energy (Figs. 6 and 7).
Our 3D LTE simulation reproduces the H ![]() wing bright points quite
well (Fig. 8) but does not fully match their average
brightness contrast (Fig. 9). Our 2D NLTE simulation
indicates that departures from LTE worsen this discrepancy
(Fig. 5). An obvious speculation is to attribute
the deficit to absence of chromospheric heating in our modeling. The
Ca II H & K lines display similarly raised wings from photospheric
Wilson-depression sampling of magnetic elements that are cooler than
their surroundings, but they also display high emission peaks in
their line cores above magnetic elements that must be
attributed to magnetomechanical heating (cf. Sheminova et al. 2005).
The H
wing bright points quite
well (Fig. 8) but does not fully match their average
brightness contrast (Fig. 9). Our 2D NLTE simulation
indicates that departures from LTE worsen this discrepancy
(Fig. 5). An obvious speculation is to attribute
the deficit to absence of chromospheric heating in our modeling. The
Ca II H & K lines display similarly raised wings from photospheric
Wilson-depression sampling of magnetic elements that are cooler than
their surroundings, but they also display high emission peaks in
their line cores above magnetic elements that must be
attributed to magnetomechanical heating (cf. Sheminova et al. 2005).
The H ![]() case differs. A chromospheric component would likely be
formed at similar height as the Ca II H & K peaks, in fact with less
contribution from the upper photosphere (Fig. 6). For
such chromospheric formation the spatial morphology would differ
because magnetic elements are not ramrod straight. However, the
H
case differs. A chromospheric component would likely be
formed at similar height as the Ca II H & K peaks, in fact with less
contribution from the upper photosphere (Fig. 6). For
such chromospheric formation the spatial morphology would differ
because magnetic elements are not ramrod straight. However, the
H ![]() bright-point morphology in Fig. 2
tracks the G-band morphology closely, whereas the Ca II H bright point
morphology differs appreciably. This difference indicates that
H
bright-point morphology in Fig. 2
tracks the G-band morphology closely, whereas the Ca II H bright point
morphology differs appreciably. This difference indicates that
H ![]() bright points at
bright points at
![]() nm from line
center are predominantly photospheric. Closer to line center they are
likely to be obscured by overlying chromospheric structures.
The bright points at the mottle foots in the line-center image
in Fig. 1 indeed differ yet more from the
G-band bright point morphology than the Ca II H bright points (cf. Rutten 2006).
nm from line
center are predominantly photospheric. Closer to line center they are
likely to be obscured by overlying chromospheric structures.
The bright points at the mottle foots in the line-center image
in Fig. 1 indeed differ yet more from the
G-band bright point morphology than the Ca II H bright points (cf. Rutten 2006).
Are their other spectral features that may be similarly useful? In
principle one searches for considerable photospheric line opacity
which partially vanishes in low-density fluxtubes through e.g., atomic
ionization, molecular dissociation, or profile narrowing in damping
wings. The Mg I b1 wing was presented already by Beckers (1976)
as a good filigree diagnostic. High excitation helps by
flattening the granular background contrast, as explained in
Fig. 6. Steep line wings (on the blue side) additionally
loose granular contrast through Doppler cancellation,
as in Ba II 455.4 nm (Sütterlin et al. 2001).
The CN band shortward of 388.34 nm was presented as a promising
alternative to the G band by Rutten et al. (2001)
and more recently by Zakharov et al. (2005).
However, the latter's specification implies that their passband hardly
reached the CN bandhead and was dominated instead by the blue wing of H ![]() (upper level n=8) plus some Fe I lines. Their reported bright-point contrast was therefore not due to CN, but may be due to H
(upper level n=8) plus some Fe I lines. Their reported bright-point contrast was therefore not due to CN, but may be due to H ![]() wing formation akin to H
wing formation akin to H ![]() wing formation. The same
point is made in the recent study of Uitenbroek & Tritschler (2005)
who used the same snapshot of the MHD simulation used here to predict
bright point brightnesses in the CN band. They conclude that the CN contrast is unlikely to be markedly better than in the G band.
wing formation. The same
point is made in the recent study of Uitenbroek & Tritschler (2005)
who used the same snapshot of the MHD simulation used here to predict
bright point brightnesses in the CN band. They conclude that the CN contrast is unlikely to be markedly better than in the G band.
We suggest that another promising spectral feature is the blue
wing of H ![]() at 486.1 nm. It should produce bright points in
similar fashion to H
at 486.1 nm. It should produce bright points in
similar fashion to H ![]() while offering larger Planck function
contrast and sharper imaging from smaller diffraction. The Irkutsk
Lyot filter described by Sütterlin et al. (2001)
can be tuned to H
while offering larger Planck function
contrast and sharper imaging from smaller diffraction. The Irkutsk
Lyot filter described by Sütterlin et al. (2001)
can be tuned to H ![]() and is being installed on the DOT.
We aim to present simulated H
and is being installed on the DOT.
We aim to present simulated H ![]() bright-point formation in another paper.
bright-point formation in another paper.
Acknowledgements
We are deeply indebted to V. Gaizauskas concerning the Hfilter. Its installation on the DOT involved the Instrumentele Groep Fysica of Utrecht University. We thank the referee for improvements to the paper. The DOT is operated by Utrecht University at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias and is presently funded by the Department of Physics and Astronomy of Utrecht University, the Netherlands Organisation for Scientific Research NWO, the Netherlands Graduate School for Astronomy NOVA, and SOZOU. The DOT efforts and the Utrecht-Oslo collaboration are part of the European Solar Magnetism Network funded by the EC under contract HPRN-CT-2002-00313. This research made much use of NASA's Astrophysics Data System literature server.