A&A 449, 821-826 (2006)
DOI: 10.1051/0004-6361:20054451
Ø. Olsen
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029 Blindern, 0315 Oslo, Norway
Received 31 October 2005 / Accepted 6 December 2005
Abstract
Aims. In this work I seek to derive analytical expressions for the widths of mean motion resonances in uniformly rotating second degree and order gravity fields.
Methods. A Deprit perturbation series is used to derive Hamiltonians valid close to mean motion resonances. These expressions are reduced to the Hamiltonian of a pendulum through canonical transformations.
Results. Analytical expressions for the orbital resonance widths in uniformly rotating second degree and order gravity field are derived and tested against numerical simulations. The widths of these mean motion resonances are independent of the rotation rate and the mass of the central body. The general stability of retrograde orbits are explained by the overlap criteria.
Key words: celestial mechanics - minor planets, asteroids
I first state the potential of the problem. Then I show how to express the Hamiltonian in the uniformly rotating body-fixed frame and give a series expansion for this potential in the Delaunay elements. Following this, I use a perturbation theory to study orbits without any assumptions about resonance, and I explain why many orbits are shape stable. Finally, I derive a simple analytical model for the trajectories close to resonances.
The coordinates are body-fixed such that the principal moments of
inertia are ordered as
![]() with axes x, yand z. For simplicity I assume the body to be a tri-axial
ellipsoid. Then the second degree potential (Heiskanen & Moritz
1967) is
with axes x, yand z. For simplicity I assume the body to be a tri-axial
ellipsoid. Then the second degree potential (Heiskanen & Moritz
1967) is
The orbits are perturbed by a first order Hamiltonian, F1 = V1,
which also must be expressed in terms of the Delaunay variables. The
relations
| FC20 | = | 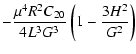 |
|
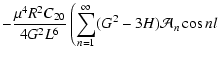 |
(8) | ||
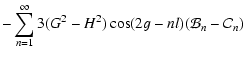 |
|||
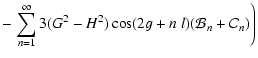 |
In this paper I'll use a Deprit perturbation series (Lichtenberg &
Lieberman 1992) to
first order. I first introduce a time ![]() associated with the
reference orbit through the equations
associated with the
reference orbit through the equations
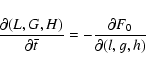 |
(10) |
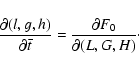 |
(11) |
Sufficiently far from resonances, the orbits are on average similar to
orbits in gravity fields without a second degree field. In other words
the orbits' size and shape are
constant on average. This theory confirms the results of
Hu & Scheeres (2001). The orientation parameters ![]() and
and
![]() changes linearly with time, while the inclination is constant
on average. Before I can procede to define sufficiently far from
resonances, I must derive a Hamiltonian valid at a nth degree
primary resonance.
changes linearly with time, while the inclination is constant
on average. Before I can procede to define sufficiently far from
resonances, I must derive a Hamiltonian valid at a nth degree
primary resonance.
| |
= | 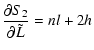 |
|
| = | 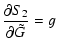 |
||
| = | 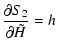 |
(19) | |
| L | = | 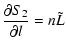 |
|
| G | = | 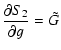 |
|
| H | = | 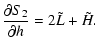 |
 |
(20) | ||
| (21) | |||
| (22) | |||
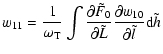 |
(23) |
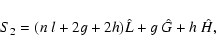 |
(26) |
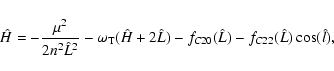 |
(28) |
Stochastic regions exist around the separatrix (Lichtenberg & Lieberman 1992) and global stochasticity may be expected when separatrices from different resonances start to overlap. The stability of retrograde orbits are therefore explained by the oscillation width's dependence on the inclination. Also, orbits around slow rotators are also expected to be more stable than orbits around similarly shaped fast rotators, since the resonances are further apart and not because they are weaker. A resonance's strength depends neither on the semi-major axis of the orbit nor on the angular rotational velocity of the central object.
From Eq. (33) it is evident that one of the
ignored terms in Eq. (24) may dominate the
Hamiltonian at certain inclinations. Using the same procedure for
these two terms, the two different expressions
I performed numerical experiments to test the resonance widths given by
Eqs. (33)-(35). For numerical analyses in this paper I used
the Burlisch Stoer (Press et al. 1996a) method to integrate the
equations of
motions in cartesian coordinates. The equations of motion were
integrated in non-rotating coordinates, and they were derived from
Eqs. (1) and (2) by replacing the angle
![]() with
with
![]() .
.
| |
Figure 1: Resonance widths for a set of prograde orbits in the gravity field of asteroid Castalia. The color coding depicts the relative change in the mean semi-major axis as a function of mean semi-major axis and eccentricity. The horizontal coordinate represents the semi-major axis in kilometers. Dark gray tones represent a decrease in the semi-major axis, whilst light tones represents an increase. The angular coordinates where chosen to select orbits close the stable fixed point of Eq. (31). |
| Open with DEXTER | |
![\begin{figure}
\par {\includegraphics[width=8.8cm,clip]{4451fig2.eps} }\end{figure}](/articles/aa/full/2006/14/aa4451-05/Timg100.gif) |
Figure 2: A closeup of the 6:2 resonance. |
| Open with DEXTER | |
The numerical experiments were performed by integrating a number of orbits with different initial semi-major axes and eccentricities. The initial values of the inclination, mean anomaly, argument of periapse and ascending node were constant within each experiment. Each orbit was integrated over a given time, and initial and final average values were computed for the semi-major axes and eccentricities. The averaging was done over a time corresponding to five times the period of the initial orbit.
The asteroid Castalia was used for the first three experiments. Initial
circular equatorial orbits around Castalia were studied by
Hu & Scheeres (2004). The gravitational constant, reference
radius, rotational
period and the coefficients C20 and C22 were taken from
Scheeres et al. (1996), and the integration time was set
to 2000 times the
rotational period of the asteroid. Two of these experiments were
performed on prograde orbits with an inclination of 60 degrees. The
initial semi-major axis was varied from 1.0 km to 2.25 km using a
step size of
![]() ,
and the eccentricity was varied from
0 to 0.5 with a step size of
,
and the eccentricity was varied from
0 to 0.5 with a step size of
![]() .
The selected
initial mean anomaly, argument of periapse and the ascending node were
based on the pendulum Eq. (31). The stable fixed
point is at
.
The selected
initial mean anomaly, argument of periapse and the ascending node were
based on the pendulum Eq. (31). The stable fixed
point is at
![]() for an inclination of 60 degrees. The
transformation from mean to instantaneous elements is periodic and
with an amplitude proportional to the perturbing Hamiltonian. Any
combination of l, g and h such that
for an inclination of 60 degrees. The
transformation from mean to instantaneous elements is periodic and
with an amplitude proportional to the perturbing Hamiltonian. Any
combination of l, g and h such that
![]() ,
will give a value
,
will give a value
![]() .
In the first two
experiments I used
.
In the first two
experiments I used
![]() and
n l + 2 g + 2 h =
0. The results from these two experiments are displayed in
Figs. 1 and 3. I repeated the first
experiment with a smaller range and stepsize to produce a
closeup of the 6:2 resonance, which is shown in
Fig. 2.
and
n l + 2 g + 2 h =
0. The results from these two experiments are displayed in
Figs. 1 and 3. I repeated the first
experiment with a smaller range and stepsize to produce a
closeup of the 6:2 resonance, which is shown in
Fig. 2.
The gray level indicate the relative change between the mean of the final and the initial semi-major axes. Light gray tones indicate an increase in the semi-major axis while dark tones indicate a decrease. The coordinates of each point are the numerically computed mean initial semi-major axis in kilometers and eccentricity for each orbit. The resonances' locations and widths were computed using Eqs. (29) and (33) and are drawn as black lines. These figures span the resonances 4:2 through 9:2 at respectively 1.26 km and 2.18 km. The white area at small semi-major axes and eccentricities are caused by the averaging process. Several orbits ended either up on an escape trajectory or passed below the reference radius. These orbits are not plotted.
A set of retrograde orbits was tested in the third experiment. Since
retrograde orbits are more stable than prograde orbits, I chose to
study orbits closer to the asteroid. The initial semi-major
axis was varied from 0.55 km to 1.8, while the interval of
eccentricities remained the same. I used an inclination of 150 degrees and
![]() .
The results are shown in
Fig. 4 together with the computed widths of
the resonances given by Eqs. (33) and
(34). Trajectories below the reference radius is the
cause of the white area in the upper left part of Fig. 4.
.
The results are shown in
Fig. 4 together with the computed widths of
the resonances given by Eqs. (33) and
(34). Trajectories below the reference radius is the
cause of the white area in the upper left part of Fig. 4.
| |
Figure 3: Resonance widths for orbits close to the unstable fixed point of Eq. (31) in the the gravity field of Castalia. |
| Open with DEXTER | |
There are two families of stable orbits. The first family consists of
orbits which are not inside any resonance. These orbits are described
by Eqs. (12) and (14), and the condition
sufficiently far away from resonances is given by the formulas for
resonances' widths and loactions. The second family of
stable orbits are orbits close to the center of the resonance. These
orbits require a combination of angular coordinates which put them
close to the stable fixed point of the pendulum equation. They are
the spikes within each resonance shown in
Fig. 1. Orbits with
![]() and which
start at
the left within a resonance, migrate to the right and vice
versa. When
and which
start at
the left within a resonance, migrate to the right and vice
versa. When
![]() the effect is reversed and resonances
pushes the orbits away from the center of the resonances. Orbits in
regions where the separatrices from different resonances overlap are
unstable as expected from Lichtenberg &
Lieberman (1992).
the effect is reversed and resonances
pushes the orbits away from the center of the resonances. Orbits in
regions where the separatrices from different resonances overlap are
unstable as expected from Lichtenberg &
Lieberman (1992).
| |
Figure 4: Resonance widths for a set of retrograde orbits around Castalia. This figure covers the resonances 2:2 through 6:2. |
| Open with DEXTER | |
Reasonable strong resonances are present between every n:2 and n+1:2resonance. These are not explained by a first order perturbation
theory, but a second order theory would involve an integral
(Lichtenberg & Lieberman 1992) of the form
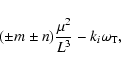 |
(37) |
Figure 2 and the overlap criteria explain why most orbits within any resonance are unstable. As the secondary resonances emerge within a primary resonace, they soon start to overlap and destroy the possibility of stable orbits. The secondary resonances are proportional to R4/r6 as opposed to R2/r3 for the primary resonances. They are therefore less important for orbits further away from the asteroid, and regions covered by a single primary resonances will become increasingly stable.
The disagreement between theory and experiment close to the asteroid
is caused mainly by the Taylor expansion of fC22 in Eq. (30).
It introduces the partial derivative of the
eccentricity with respect to the L, which leads to negative powers of
the eccentricity. fC22' and fC22'' may therefore be
non-negligible even when combined with small excursions of
![]() .
Retaining fC22 will complicate the analysis and
most likely introduce separatrices which are not symmetric around the
stable fixed points. On the other hand, the computed locations are
reasonable good as is demonstrated by the 2:2 resonance. Its nominal
position given by Eq. (17), is 0.80 km. This compares
to the computed location of 0.86 km at zero eccentricity.
.
Retaining fC22 will complicate the analysis and
most likely introduce separatrices which are not symmetric around the
stable fixed points. On the other hand, the computed locations are
reasonable good as is demonstrated by the 2:2 resonance. Its nominal
position given by Eq. (17), is 0.80 km. This compares
to the computed location of 0.86 km at zero eccentricity.
I chose the asteroid Itokawa in the final numerical
experiment. This asteroid is a slow rotator as opposed to Castalia,
and it can be used to double check the resonance widths' independence
of the rotational speed of the central body. Scheeres
et al. (2004) provide up to date information for this
asteroid. The initial
inclination was 60 degrees and I used the stable fixed point to
select initial angular coordinates. Figure 5
confirms the previous results and shows resonances from 2:2,
synchronous orbits, and up. No stable orbits were found at the 1:2resonance using this selection algorithm.
| |
Figure 5: Resonance widths for the asteroid Itokawa. |
| Open with DEXTER | |
A study of mean motion resonances in uniformly rotating second degree and order gravity field is presented. The mean motion resonances are an important factor when studying the stability of orbits in such a gravity field. Surprisingly, the widths of these mean motion resonances are independent of the rotation rate and the mass of the central body. Using the overlap criteria, stability in slowly rotating gravity fields is explained by the distance between the resonances and not by the strength of a particular resonance. On the other hand, the widths are strongly dependent on both eccentricity an inclination with resonance widths for retrograde orbits being much smaller than those for prograde orbits. Finally, the evolution of orbits within a resonance is not fully understood and warrants a closer study. A second order perturbation theory is probably necessary.