A&A 449, 461-474 (2006)
DOI: 10.1051/0004-6361:20054408

Internal dynamics of the radio halo cluster Abell 2744

W. Boschin^1,2 - M. Girardi^2,3 - M. Spolaor² - R. Barrena⁴

1 - Fundación Galileo Galilei - INAF, C/Alvarez de Abreu 70, 38700 Santa Cruz de La Palma, Canary Islands, Spain
2 - Dipartimento di Astronomia, Università degli Studi di Trieste, via Tiepolo 11, 34131 Trieste, Italy
3 - INAF - Osservatorio Astronomico di Trieste, via Tiepolo 11, 34131 Trieste, Italy
4 - Instituto de Astrofisica de Canarias, C/Via Lactea s/n, 38200 La Laguna, Tenerife, Canary Islands, Spain

Received 25 October 2005 / Accepted 15 November 2005

Abstract
Aims. We present a detailed dynamical analysis of the rich galaxy cluster A2744, containing a powerful diffuse radio halo.
Methods. Our analysis is based on redshift data for 102 galaxies, part of them recovered from unexplored spectra in the ESO archive. We combine galaxy velocity and position information to select the cluster members and determine global dynamical properties of the cluster. We use a variety of statistical tests to detect possible substructures.
Results. We find that A2744 appears as a well isolated peak in the redshift space at $\left<z\right>=0.306$, which includes 85 galaxies recognized as cluster members. We compute the line-of-sight (LOS) velocity dispersion of galaxies, $\sigma_{\rm V}=1767_{-99}^{+121}$ km s^-1, which is significantly larger than what is expected in the case of a relaxed cluster with an observed X-ray temperature of 8 keV. We find evidence that this cluster is far from dynamical equilibrium, as shown by the non-Gaussian nature of the velocity distribution, the presence of a velocity gradient and a significant substructure. Our analysis shows the presence of two galaxy clumps of different mean LOS velocities $\Delta V \sim 4000$ km s^-1. We detect a main, low-velocity clump with $\sigma_{\rm V}\sim 1200{-}1300$ km s$^{-1} \;$and a secondary, high-velocity clump with $\sigma_{\rm V}= 500{-}800$ km s^-1and located in the S-SW cluster region. We estimate a cluster mass within 1 Mpc$\;$of $1.4{-}2.4\times 10^{15}~M_{\odot}$, depending on the model adopted to describe the cluster dynamics.
Conclusions. Our results suggest a merging scenario of two clumps with a mass ratio of 3:1 and a LOS impact velocity of $\Delta V_{\rm rf} \sim 3000$ km s^-1, likely observed just after the core passage. The merging is occuring roughly in the NS direction with the axis close to the LOS. This scenario agrees with that proposed on the basis of recent Chandra results in its general lines although suggesting a somewhat more advanced merging phase. Our conclusions support the view of the connection between extended radio emission and energetic merging phenomena in galaxy clusters.

Key words: galaxies: clusters: general - galaxies: clusters: individual: Abell 2744 - galaxies: distances and redshifts - intergalactic medium - cosmology: observations

1 Introduction

Clusters of galaxies are now recognized to be not simple relaxed, but rather evolving via merging processes in a hierarchical fashion from poor groups to rich clusters. Much progress has been made in recent years in the observations of the signatures of the merging processes (see Feretti et al. 2002, for a general review). The presence of substructures is indicative of a cluster in an early phase of the process of dynamical relaxation or of secondary infall of clumps into already virialized clusters. The attempts to measure the substructure occurrence rate for a large sample of galaxies give values of about $50\%$ in both optical and X-ray data (e.g., Geller & Beers 1982; Mohr et al. 1996; Girardi et al. 1997; Kriessler & Beers 1997; Jones & Forman 1999; Schuecker et al. 2001).

A new aspect of these investigations is the possible connection of cluster mergers with the presence of extended, diffuse radio sources, halos and relics. The synchrotron radio emission of halos and relics demonstrates the existence of large-scale cluster magnetic fields, of the order of 0.1-1 $\mu$G, and of widespread relativistic particles of energy density 10 ^-14-10^-13 erg cm^-3. The difficulty in explaining radio halos arises from the combination of their large size, more than 1  h₅₀^-1 Mpc, and the short synchrotron lifetime of relativistic electrons (e.g., Giovannini & Feretti 2002). Cluster mergers were suggested to provide the large amount of energy necessary for electron reacceleration and magnetic field amplification (Feretti 1999; Feretti 2002; Sarazin 2002). However, the question is still debated since diffuse radio sources are quite uncommon and only recently can we study these phenomena on the basis of sufficient statistics (${\sim}30$ clusters up to $z\sim 0.3$, e.g., Giovannini et al. 1999; see also Giovannini & Feretti 2002; and Feretti 2005).

Growing evidence of a connection between diffuse radio emission and cluster merging is based on X-ray data (e.g., Böhringer & Schuecker 2002; Buote 2002). Studies based on a large number of clusters have found a significant relation between the radio and the X-ray surface brightness (Govoni et al. 2001a,b) and connections between the presence of radio halos/relics and an irregular and bimodal X-ray surface brightness distribution (Schuecker et al. 2001). New unprecedented insights into merging processes in radio clusters are offered by Chandra and XMM-Newton observations (e.g., Markevitch & Vikhlinin 2001; Markevitch et al. 1992; Fujita et al. 2004; Henry et al. 2004; Kempner & David 2004).

Optical data are a powerful way to investigate the presence and the dynamics of cluster mergers (e.g., Girardi & Biviano 2002), too. The spatial and kinematical analysis of member galaxies allows us to detect and measure the amount of substructure and to identify and analyze possible pre-merging clumps or merger remnants. This optical information is complementary to X-ray information since galaxies and ICM react on different time scales during a merger (see numerical simulations by Roettiger et al. 1997). Unfortunately, to date optical data has been lacking or poorly exploited. The sparse literature concerns few individual clusters (e.g., Colless & Dunn 1996; Gómez et al. 2000; Barrena et al. 2002; Mercurio et al. 2003; Boschin et al. 2004).

Abell cluster 2744, also known as AC 118, is a rich, X-ray luminous, hot cluster at moderate redshift: richness class =3 (Abell et al. 1989); $L_{\rm X}(0.1{-}2.4$ keV $) = 22.05 \times~ 10^{44} \ h_{50}^{-2}$ erg s^-1 (Ebeling et al. 1996); $T_{\rm X}=7.75_{-0.53}^{+0.59}$ (Allen 1998); z = 0.308(Couch & Newell 1984). Abell (1958) classified the spatial distribution of its galaxies as "regular'', but it has no dominant bright galaxy or galaxies, so its Bautz-Morgan class is III (Bautz & Morgan 1970). Moreover, A2744 is known for an excess of blue galaxies (Couch & Newell 1984), commonly known as Butcher-Oemler effect (Butcher & Oemler 1978). Moreover, A2744 hosts one of the most luminous known radio halos which covers the central cluster region with a radius of ${\sim }1$  h^-1₅₀ Mpc, as well as a large radio-relic at a distance of about 2  h^-1₅₀ Mpc$\;$NE of the cluster center (Giovannini et al. 1999; Govoni et al. 2001a,b).

The first indirect suggestion for a complex internal structure in A2744 came from the high value of the LOS velocity dispersion of member galaxies, $\sigma_{\rm V}\sim 1900$ km s$^{-1} \;$(Couch & Sharples 1987). Another suggestion came from the discrepancy between the gravitational shear amplitude and the velocity dispersion (Smail et al. 1997) and between the X-ray mass and strong lensing mass (Allen 1998). More direct evidences was found in subsequent years. In their study of internal dynamics of a large cluster sample, Girardi & Mezzetti (2001, hereafter GM01) found two peaks in the velocity distribution of A2744, but these peaks are so strongly superimposed that the authors questioned their separation and classified A2744 as a cluster with uncertain dynamics. ROSAT-PSPC data showed a subcluster 2.5$^\prime$ NW of the cluster center (Govoni et al. 2001b), where the galaxy distribution seems to show an overdensity (Andreon 2001, based on deep K-band photometry). This NW subcluster is also evident in XMM-Newton data analyzed by Zhang et al. (2004), who measure a negative temperature gradient moving from the center to the outskirts of the cluster. Finally, the recent paper by Kempner & David (2004, hereafter KD04) used Chandra X-ray data to show strong evidence for an ongoing major merger, detecting two secondary X-ray peaks in the central cluster region. In particular, they identified these peaks with the cool cores of two subclusters merging in the NS direction, close to the LOS and suggested that the merging is responsible for the radio halo.

In view of the above Chandra X-ray results and the availability of unexplored spectroscopic data in the ESO archive we study the internal dynamics of A2744 analyzing data of its member galaxies.

This paper is organized as follows. We present the new redshift data and the galaxy catalog in Sect. 2. We analyze the internal dynamics and detect substructures in Sects. 3 and 4, and the 2D galaxy distribution in Sect. 5. We discuss the dynamical status of A2744 in Sect. 6 and summarize our results in Sect. 7.

Unless otherwise stated, we give errors at the 68% confidence level (hereafter c.l.). Throughout the paper, we assume a flat cosmology with $\Omega_{\rm m}=0.3$, $\Omega_{\Lambda}=0.7$, and H₀=70 km s$^{-1} \;$ Mpc^-1. For this cosmological model, 1 arcmin corresponds to 271 kpc at the cluster redshift.

2 Redshift data and galaxy catalog

We considered multi-object spectroscopic data stored in ESO archive acquired using NTT-EMMI in 1998 (2 MOS masks) and 1999 (another 2 MOS masks).

Reduction of spectroscopic data was carried out with IRAF. Radial velocities were determined using the cross-correlation technique (Tonry & Davis 1979) implemented in the RVSAO package (developed at the Smithsonian Astrophysical Observatory Telescope Data Center). Each spectrum was correlated against six templates for a variety of galaxy spectral types: E, S0, Sa, Sb, Sc, Ir (Kennicutt 1992). The template producing the highest value of $\cal R$, i.e., the parameter given by the task XCSAO and related to the signal-to-noise of the correlation peak, was chosen. In two cases of galaxies with emission lines, we took the EMSAO redshift as a more reliable estimate of the redshift.

We succeeded in obtaining 78 galaxy redshifts.

	Figure 1: NTT R-band image of A2744 (north at the top and east to the left) taken from the ESO archive (see also Busarello et al. 2002). Galaxies with successful velocity measurements are labeled as in Table 1. Circles and boxes indicate cluster member and non member galaxies, respectively.
Open with DEXTER

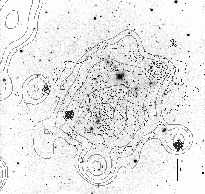Figure 2: NTT R-band image of the cluster A2744 with, superimposed, the contour levels of the Chandra archival image ID 2212 (thin black contours; built considering X-ray photons in the energy range 0.5-2.0 keV) and of a VLA radio image at 1.4 GHz (thick gray contours; courtesy of F. Govoni, see Govoni et al. 2001b). The X-ray image shows the central and the NW peaks, as well as the north and south secondary peaks (see also KD04). The radio image shows the powerful radio halo and (partially) the NE relic. Crosses indicate the position of the three peaks detected in the 2D galaxy distribution of the likely cluster members according to the photometric redshifts (see our Fig. 13). North is at the top and east to the left.

Open with DEXTER

Multiple redshift determinations were available for a few galaxies: a double determination for seven galaxies, a triple determination for one galaxy, and a quadruple determination for one galaxy. This allowed us to obtain a more rigorous estimate for the redshift errors since the nominal errors as given by the cross-correlation are known to be smaller than the true errors (e.g., Malumuth et al. 1992; Bardelli et al. 1994; Ellingson & Yee 1994; Quintana et al. 2000). Thus, we fitted the first determination vs. the second one by using a straight line and considering errors in both coordinates (e.g., Press et al. 1992). The fitted line agrees with the one to one relation, but, when using the nominal cross-correlation errors, the small value of $\chi^2$-probability indicates a poor fit, suggesting that the errors are underestimated. Only when nominal errors are multiplied by a factor of ${\sim}2.3$ can the observed scatter be explained. Therefore, hereafter it is assumed that the true errors are larger than the nominal cross-correlation errors by a factor of 2.3. The same value was obtained by Boschin et al. (2004) for another cluster at moderate redshift.

Table 1 lists new radial velocity ${V_{\rm NTT}}=cz_{\odot}$determinations we obtained for 66 galaxies (see also Fig. 1). The median error in radial velocity $\Delta V_{\rm NTT}$ is ${\sim}90$ km s^-1. For the nine galaxies with multiple redshift determinations, we considered the average of the determinations and the corresponding error. Two galaxies (ID76 and 90) show the presence of emission lines (OIIIb and H$\alpha$ in our spectra). The galaxy ID90 also exhibits a powerful X-ray emission (see Fig. 2).

We then considered the published redshifts, i.e. 40 galaxy redshifts by Couch & Sharples (1987, $\Delta V=100$ km s^-1) and 40 galaxy redshifts by Couch et al. (1998, $\Delta V=90$ km s^-1). These galaxies belong to the catalog of Couch & Newell (1984) and are numbered with the prefix "CN''. Four galaxies are listed in both the studies (CN219, CN258, CN310, CN360). We cross-matched our galaxies with those of the above authors: 14/30 galaxies of Couch & Sharples (1987)/Couch et al. (1998) were matched. For common galaxies we repeated the straight line fitting-procedure above separately for each study. We found that the fitted lines agree with the one to one relation and that adopted errors are able to explain the observed scatters. We added to our sample 26/10 galaxies coming from Couch & Sharples (1987)/Couch et al. (1998). For the galaxies with redshift determinations from NTT data and these authors, we considered the average of the determinations and the corresponding error.

Our final spectroscopic catalog consists of 102 galaxies sampling ${\sim} 5\hbox{$^\prime$ }\times 8\hbox{$^\prime$ }$ in the central cluster region (see Table 1 and Fig. 1). It covers the region with strong X-ray emission (with the exception of the NW peak) and the region with the extended radio halo, but not the region with the radio relic toward the NE (see Fig. 2).

Table 1 lists the velocity catalog (see also Fig. 1): identification number of each galaxy, ID (Col. 1); right ascension and declination, $\alpha$ and $\delta$ (J2000, Col. 2); heliocentric radial velocities obtained in this paper from NTT data, ${V_{\rm NTT}}=cz_{\odot}$ (in km s^-1, Col. 3) with assumed errors, $\Delta V_{\rm NTT}$, i.e., the nominal ones given by the cross-correlation technique multiplied by 2.3 (Col. 4); heliocentric radial velocities V of the final catalog with assumed errors $\Delta V$ (Cols. 5 and 6); CN number for galaxies with previous redshift determination by Couch & Sharples (1987) and/or Couch et al. (1998) in Col. 7.

3 Analysis of the whole system

3.1 Member selection

The identification of cluster members proceeds in two steps, following a procedure already used for nearby and medium-redshift clusters (Fadda et al. 1996; Girardi et al. 1996; GM01).

First, we perform the cluster-member selection in velocity space by using only redshift information. We apply the adaptive-kernel method (Pisani 1993, 1996) to find the significant (${>}99\%$c.l.) peaks in the velocity distribution. This procedure detects A2744 as a well isolated peak at z=0.305 assigning 89 galaxies considered as candidate cluster members (see Fig. 3). Of the non-member galaxies, seven and six are foreground and background galaxies, respectively.

	Figure 3: Redshift galaxy distribution. The solid-line histogram refers to galaxies assigned to the cluster peak according to the adaptive-kernel reconstruction method.
Open with DEXTER

All the galaxies assigned to the A2744 peak are analyzed in the second step, which uses both position and velocity information. We apply the procedure of the "shifting gapper'' by Fadda et al. (1996). This procedure rejects galaxies that are too far in velocity from the main body of galaxies and within a fixed bin that shifts along the distance from the cluster center. The procedure is iterated until the number of cluster members converges to a stable value. Following Fadda et al. (1996) we use a gap of 1000 km s$^{-1} \;$- in the cluster rest-frame - and a bin of 0.6 Mpc, or large enough to include 15 galaxies. As for the cluster center we consider the position of the most significant peak in the galaxy distribution as obtained by the 2D adaptive-kernel analysis [ ${\rm RA}=00^{{\rm h}}14^{{\rm m}}21\hbox{$.\!\!^{\rm s}$ }04$, ${\rm Dec}=-30\ensuremath{{\rm ^\circ}} 23\hbox{$^\prime$ }52\hbox{$.\!\!^{\prime\prime}$ }4$ (J2000.0), see Sect. 5]. This center is very close to the brightest cluster galaxy in the central cluster region (ID53/CN1) which is also the center of the cluster potential well according to the weak lensing analysis by Smail et al. (1997). The shifting-gapper procedure rejects four galaxies as non-members (see Fig. 4): two of them are obvious interlopers since dist ${\sim}5000$ km s$^{-1} \;$from the main body of galaxies; the other two are emission line galaxies (ID12 and ID76).

Our following analysis is thus based on 85 cluster members.

Figure 4: Left panel: rest-frame velocity vs. projected clustercentric distance for the 89 galaxies in the main peak (Fig. 3); the application of the "shifting gapper'' method rejects four galaxies (crosses) selecting 85 cluster members (circles). Right panel: velocity distribution of the 85 member galaxies. Velocities of the two brightest galaxies in the central cluster region (ID53/CN1 and ID70/CN2) are indicated.

Open with DEXTER

3.2 Global properties

By applying the biweight estimator to cluster members (Beers et al. 1990), we compute a mean cluster redshift of $\left<z\right>=0.3061\pm 0.0006$ ( $\left<V\right>=91754\pm 192)$. We estimate the LOS velocity dispersion, $\sigma _{\rm V}$, by using the biweight estimator and applying the cosmological correction and the standard correction for velocity errors (Danese et al. 1980). We obtain $\sigma_{\rm V}=1767_{-99}^{+121}$ km s^-1, where errors are estimated with a bootstrap technique.

To evaluate the robustness of the $\sigma _{\rm V}$ estimate we analyze the integral velocity dispersion profile (Fig. 5). The value of the integral $\sigma _{\rm V}$ sharply varies in the internal cluster region. A similar behaviour is shown by the mean velocity $\left<V \right>$ suggesting that a mix of galaxy clumps at different redshifts is the likely cause of the high value of the velocity dispersion rather than individual contaminating field-galaxies. A robust value of $\sigma _{\rm V}$ is reached in the external cluster regions where the integral profile flattens, as found for most nearby clusters (e.g., Fadda et al. 1996).

Figure 5: Differential (big squares) and integral (small points) profiles of mean velocity ( upper panel) and LOS velocity dispersion ( lower panel). As for the mean velocity/velocity dispersion, results for seven/four annuli from the cluster center, each of 0.15/0.3 Mpc, are shown. For the integral profiles, the mean and dispersion at a given (projected) radius from the cluster center is estimated by considering all galaxies within that radius. The error bootstrap bands at the $68\%$ c.l. are shown. In the lower panel, the horizontal line represents the X-ray temperature with the respective 90 per cent errors transformed in $\sigma _{\rm V}$ assuming the density-energy equipartition between gas and galaxies, i.e. $\beta _{\rm spec}=1$(see text).

Open with DEXTER

If A2744 is in dynamical equilibrium (but see Sects. 3.3, 4, and 6.1) one can compute global virial quantities. Following the prescriptions of GM01, we assume for the radius of the quasi-virialized region $R_{\rm vir}=0.17\times \sigma_{\rm V}/H(z) = 3.7$ Mpc$\;$- see their Eq. (1) after introducing the scaling with H(z) (see also Eq. (8) of Carlberg et al. 1997, for R₂₀₀). Thus the cluster is sampled out to a radius of $R_{\rm out}=0.35\times R_{\rm vir}$. Although the cluster is not sampled out to $R_{\rm vir}$, we can compute the virial mass within $R_{\rm vir}$ following GM01. We apply the standard estimate (Limber & Mathews 1960) with the surface term correction: $M=3\pi/2 \cdot \sigma_{\rm V}^2 R_{\rm PV}/G-C$ (The & White 1986; Girardi et al. 1998), where $\sigma _{\rm V}$ is the observed global velocity dispersion; the radius $R_{\rm PV}$, equal to two times the (projected) harmonic radius, is obtained assuming a King-like distribution, with parameters typical of nearby/medium-redshift clusters ( $R_{\rm PV}=2.72\pm0.68$); the surface term correction C is chosen to be equal to the $20\%$ of the mass, a typical value for clusters (see Carlberg et al. 1997; Girardi et al. 1998). We obtain $M({<}R_{\rm vir}=3.7 \;{\rm Mpc})=(7.4_{-2.0}^{+2.1})\times 10^{15}~M_{\odot}$.

3.3 Velocity distribution

We analyze the velocity distribution to look for possible deviations from a Gaussian that could provide important signatures of complex dynamics. For the following tests the null hypothesis is that the velocity distribution is a single Gaussian.

We estimate three shape estimators, i.e. the kurtosis, the skewness, and the scaled tail index (see, e.g., Beers et al. 1991). The value of kurtosis (-0.85) shows evidence that the velocity distribution differs from a Gaussian, being lighter-tailed, with a c.l. of ${\sim} 95{-}99\%$ c.l. (see Table 2 of Bird & Beers 1993). The W-test (Shapiro & Wilk 1965) rejects the null hypothesis of a Gaussian parent distribution at the $96.5\%$c.l.

We then investigate the presence of gaps in the distribution. A weighted gap in the space of the ordered velocities is defined as the difference between two contiguous velocities, weighted by the location of these velocities with respect to the middle of the data. We obtain values for these gaps relative to their average size, precisely the midmean of the weighted-gap distribution. We look for normalized gaps larger than 2.25 since in random sampling of a Gaussian distribution they arise at most in about $3\%$ of the cases, independent of the sample size (Wainer and Schacht 1978; see also Beers et al. 1991). One significant gap (3.074) in the ordered velocity dataset is detected (see Fig. 6). From low to high velocities the dataset is divided in two subsets containing 61 and 24 galaxies.

	Figure 6: Velocity distribution of radial velocities for the 85 cluster members. Lower panel: stripe density plot where the arrow indicates the position of the significant gap. The gap lies between 92 936 and 93 445 km s-1. Upper panel: velocity histogram with a binning of 500 km s$^{-1} \;$with the Gaussians corresponding to KMMa and KMMb in Table 2.
Open with DEXTER

3.4 Velocity field

The cluster velocity field may be influenced by the presence of internal substructures, possible cluster rotation, and the presence of other structures on larger scales, such as nearby clusters, surrounding superclusters, and filaments. Each asymmetry effect could produce a velocity gradient in the cluster velocity field.

We estimate the direction of the velocity gradient performing a multiple linear regression fit to the observed velocities with respect to the galaxy positions in the plane of the sky (see also den Hartog & Katgert 1996; Girardi et al. 1996). We find a position angle on the celestial sphere of ${\rm PA}=211_{-31}^{+19}$ degrees (measured counter-clock-wise from north), i.e. higher-velocity galaxies lie in the south-west region of the cluster, in agreement with the visual impression of the galaxy distribution in Fig. 7. To assess the significance of this velocity gradient we perform 1000 Monte Carlo simulations by randomly shuffling the galaxy velocities and for each simulation we determine the coefficient of multiple determination (RC², see e.g., NAG Fortran Workstation Handbook 1986). We define the significance of the velocity gradient as the fraction of times in which the RC² of the simulated data is smaller than the observed RC². We find that the velocity gradient is significant at the $98.2\%$ c.l.

	Figure 7: Spatial distribution on the sky of the 85 member galaxies: the larger the circle, the smaller the radial velocity. The plot is centered on the cluster center. The arrow indicates the position angle of the cluster gradient. Crosses indicate the position of X-ray peaks, i.e. the main cluster and the NW subcluster, and the north and south secondary peaks (see Fig. 2; and KD04).
Open with DEXTER

4 Detecting substructures

The existence of correlations between positions and velocities of cluster galaxies is a characteristic of real substructures. We use three different approaches to detect substructures in A2744 combining velocity and position information.

4.1 KMM analysis

As a first approach, we attempt to separate in subsystems the whole cluster starting from the velocity distribution. The adaptive-kernel method used in Sect. 3, which has the advantage of not requiring any a priori shape for the subsystem research, is not able to distinguish two peaks in the velocity distribution (see Fig. 9, in the next section). However, it finds a peak at ${\sim}90~850$ km s$^{-1} \;$and an asymmetry at higher velocities, which suggests a hidden peak at 94 000-95 000 km s^-1. To detect subsets in the velocity distribution we then resort to the Kaye's mixture model (KMM) test (Ashman et al. 1994).

The KMM algorithm fits a user-specified number of Gaussian distributions to a dataset and assesses the improvement of that fit over a single Gaussian. In addition, it provides the maximum-likelihood estimate of the unknown n-mode Gaussians and an assignment of objects into groups. KMM is most appropriate in situations where theoretical and/or empirical arguments indicate that a Gaussian model is reasonable. The Gaussian is valid in the case of cluster velocity distributions, where gravitational interactions drive the system toward a relaxed configuration with a Gaussian velocity distribution. However, one of the major uncertainties of this method is the optimal choice of the number of groups for the partition. Moreover, only in mixture models with equal covariance matrices for all components (homoscedastic case; i.e., each group has the same velocity dispersion) the algorithm converges, while this is not always true for the heteroscedastic case (i.e., groups have different velocity dispersion, see Ashman et al. 1994, for further details).

Our analysis of significant gaps suggests the presence of two Gaussians. We present the results for the heteroscedastic KMM case which we verify to be likely the corrected ipothesis. We use the results of the gap analysis to determine the first guess and we fit two velocity groups around the guess mean velocities of $90\times10^3$and $95\times10^3$ km s^-1. The algorithm fits a two-group partition at the $97.5\%$ c.l., as obtained from the likelihood ratio test.

Using the KMM algorithm, we assign member galaxies to individual groups (66/19 for the low/high velocity group). For both the groups, we find that the Gaussian hypothesis of the velocity distribution is acceptable, according to the W-test. Moreover, the two groups appear spatially segregated at the $98.7\%$ c.l. according to the 2D Kolmogorov-Smirnov test - hereafter 2DKS-test (Fasano & Franceschini 1987, as implemented by Press et al. 1992). Table 2 shows the properties of the corresponding groups KMMa and KMMb. Figure 8 shows that the galaxies of the high-velocity group populate mainly the SW cluster region. Moreover, only one (ID70/CN2) of the eight red bright galaxies belongs to the high-velocity group, where the red bright galaxies are those with $R\le 19$ mag and V-R>0.8 (see also Sect. 5).

	Figure 8: Spatial distribution on the sky of the 85 member galaxies. Open and solid triangles indicate KMMa and KMMb groups ( left panel) and KMM3Da and KMM3Db groups ( right panel). Circles indicate the nine red bright galaxies (see text). The plot is centered on the cluster center. Crosses indicate the position of X-ray peaks.
Open with DEXTER

Table 2: Results of kinematical and spatial analysis.

Figure 9: The velocity galaxy density, as provided by the adaptive-kernel reconstruction method for the whole cluster (thick-dotted line), the region within 0.4 Mpc$\;$of the cluster center (thick-solid line) and the region outside 0.4 Mpc$\;$(dotted line). Units on the y-axis are normalized to the density of the highest peak in the whole cluster. The plot also shows the velocity density for the galaxies with Dressler-Schectman deviations (see Sect. 4.3) $\delta _{i}>1.6$, 1.7, and 1.8 (thick-dashed, dashed and thin-dashed lines, respectively).

Open with DEXTER

The Gaussian model for the 2D galaxy distribution is poorly supported by theoretical and/or empirical arguments and, however, our galaxy catalog is not complete down to a magnitude limit. However, since the 3D diagnostics is in general the most sensitive indicator of the presence of substructure (e.g., Pinkney et al. 1996), we apply the 3D version of the KMM software simultaneously using galaxy velocity and positions. We use the galaxy assignment obtained in the 1D analysis to determine the first guess of the 3D analysis. The algorithm fits a two-group partition at the $97.7\%$ c.l. The results for the two groups (KMM3Da, KMM3Db) are shown in Table 2 and Fig. 8. The groups resulting from the 3D analysis are similar to those resulting from the 1D analysis for the difference in mean velocity and spatial distribution. The only remark is that the 3D high-velocity group (KMM3Db) is a more important structure with respect to the 1D high-velocity group (KMMb), as indicated by the larger velocity dispersion and the presence of three red bright galaxies.

4.2 Analysis of different spatial regions

In a second approach, we analyze the kinematical properties of galaxy populations located in different spatial regions of the cluster.

We consider the internal region within 0.4 Mpc$\;$of the cluster center containing 35 galaxies. This central region allows the inclusion of both secondary X-ray peaks and the exclusion of the NW X-ray subcluster. The velocity distribution of the central cluster region shows the presence of two significant peaks, in agreement with the 1D adaptive-kernel method results (see Fig. 9): the main peak at $V\sim 90~600$ km s$^{-1} \;$and the secondary, with a relative density of ${\gtrsim} 50\%$, at $V\sim 94~900$ km s^-1. The overlap between the two peaks in the galaxy assignment concerns only 2/35 galaxies and the velocity separation is high ( ${\sim} 4500$ km s^-1); thus, following the criteria of Fadda et al. (1996), the two peaks are well separable.

As for the external region, we divide it in a north and a south region - or alternatively in an east and a west region - with respect to the cluster center. We also consider the NW sector for its proximity to the NW X-ray subcluster.

Table 2 lists the properties of these subsamples. Here we point out interesting results.

The two peaks in the central region differ in mean velocity (at ${>}99.99\%$ c.l. according to the means-test; Press et al. 1992) and both have a different mean velocity (at ${>}99.9\%$ c.l.) and significantly smaller velocity dispersions than the whole sample (at $99.9\%$ c.l. according to the F-test; Press et al. 1992). The galaxies of the two peaks are not spatially segregated according to the 2DKS-test. The south external region has an high mean velocity, different from that of the north external region at the $98.5\%$ c.l.

The above analysis confirms the presence of the two subsystems found by the KMM method, with a secondary important high-velocity clump in the south region, partially LOS aligned with the main clump in the central cluster region. This LOS alignment is the most likely cause of the very high value of the velocity dispersion in the central cluster region (see Fig. 5).

4.3 Dressler & Schectman analysis

Finally, we combine galaxy velocity and position information to compute the $\Delta$-statistics devised by Dressler & Schectman (1988). This test is sensitive to spatially compact subsystems that have either an average velocity that differs from the cluster mean, or a velocity dispersion that differs from the global one, or both. The subsystem which must be examined is not determined a priori as in Sect. 4.2, but, for each ith galaxy, the test considers the subsample formed by this galaxy and the ten nearest neighbours and computes a parameter, $\delta _{i}$, which gives the deviation of the local kinematical parameters (velocity and velocity dispersion) from the global cluster parameters. In the case of A2744 we find $\Delta=130$ for the value of the parameter which gives the cumulative deviation. To compute the significance of the substructure we run 1000 Monte Carlo simulations, randomly shuffling the galaxy velocities, and obtain a value of $98.9\%$.

Figure 10: Spatial distribution of cluster members, each marked by a circle: the larger the circle, the larger is the deviation $\delta _{i}$ of the local parameters from the global cluster parameters, i.e. there is more evidence for substructure (according to the Dressler & Schectman test, see text). The boldface circles indicate those with $\delta _{i} \ge 1.7$ (see text). The plot is centered on the cluster center.

Open with DEXTER

Figure 10 shows the distribution on the sky of all galaxies, each marked by a circle: the larger the circle, the larger the deviation $\delta _{i}$ of the local parameters from the global cluster parameters, i.e. the higher the evidence for substructure. This figure provides information on the positions of substructures: some galaxies with low velocity are the likely cause of large values of $\delta _{i}$ in the N-NE region.

	Figure 11: The distribution of $\delta _{i}$ deviations of the Dressler-Schectman analysis for the 85 member galaxies. The solid line represents the observations, the dashed line the distribution for the galaxies of simulated clusters, normalized to the observed number.
Open with DEXTER

To obtain further information, we resort to the technique developed by Biviano et al. (2002), who used the individual $\delta _{i}$-values of the Dressler & Schectman method. The critical point is to determine the value of $\delta _{i}$ that optimally indicates galaxies belonging to substructure. To this aim we consider the $\delta _{i}$-values of all 1000 Monte Carlo simulations already used to determine the significance of the substructure (see above). The resulting distribution of $\delta _{i}$ is compared to the observed one. We find a difference at $P=99.98\%$ c.l. according to the KS-test. The "simulated'' distribution is normalized to produce the observed number of galaxies and compared to the observed distribution in Fig. 11: the latter shows a tail at large values. This tail is populated by galaxies that presumably are in substructures. For the selection of galaxies within substructures we choose the threshold value of $\delta_{\rm th}=1.7$, since after the rejection of the values $\delta_{i}>\delta_{\rm th}$, the observed and simulated $\delta _{i}$-distributions are still different at $P\sim 99\%$. With this choice, 28 galaxies of the cluster are assigned to substructure. They are located in the NE region, in the center and in the SW region (see Fig. 10). Moreover, their velocity distribution shows two significant peaks at ${\sim} 90~000$ km s$^{-1} \;$and ${\sim} 94~000$ km s$^{-1} \;$(see Fig. 9). The results of the kinematical analysis of the two galaxy-groups assigned to the two velocity peaks are listed in Table 2. The values of the velocities of the two peaks suggest us that the Dressler-Schectman test detects (part of) the same two galaxy-structures already detected in the above sections.

The two peaks in the velocity distribution are also found with a less conservative threshold value for substructure galaxies (e.g., 36 galaxies with $\delta_{i}> \delta_{\rm th}=1.6$, $P\sim 95\%$), while with a more conservative threshold only the ${\sim} 90~000$ km s$^{-1} \;$peak is detected (see Fig. 9).

5 2D galaxy distribution

By applying the 2D adaptive-kernel method to the position of A2744 galaxy members we find two very significant peaks ( ${>}99.99\%$): the densest peak (hereafter CG peak) with 43 galaxies lies on the cluster center and the secondary (hereafter NG peak) with 33 galaxies lies to the north and slightly NW [ ${\rm RA}=00^{{\rm h}}14^{{\rm m}}17\hbox{$.\!\!^{\rm s}$ }3$ ${\rm Dec}=-30\ensuremath{{\rm ^\circ}} 21\hbox{$^\prime$ }42\ensuremath{{\rm ^\prime}}\hskip -0.1em\ensuremath{{\rm ^\prime}}$ (J2000.0), see Fig. 12].

Unfortunately our galaxy catalog has two limits that could bias the above result: the small extension covered by spectroscopical data and the magnitude incompleteness. To overcome these limits we consider the catalog presented by Busarello et al. (2002). These authors present photometric V-, R-, and I-band data in a catalog of 1206 sources, where the galaxy sample is complete to R=22.3 mag, and give photometric redshifts for 459 sources for which additional U- and K-band photometry is available.

	Figure 12: Spatial distribution on the sky and relative isodensity contour map of 85 cluster members (spectroscopically confirmed), obtained with the adaptive-kernel method. The plot is centered on the cluster center. Crosses and stars indicate the position of the galaxy and X-ray peaks, respectively.
Open with DEXTER

Following the cluster member definition of Busarello et al. (2002), we select all galaxies, i.e. sources with stellar index ${\le} 0.9$, having photometric redshift such that the associated $68\%$ percentile interval $\Delta z_{68}$ overlaps the range $z \in [0.24,0.38]$. We obtain a catalog of 320 objects. Figure 13 shows the result of the 2D adaptive-kernel method. We confirm the presence of the peaks found with the spectroscopic members: 113 galaxies are assigned to the CG peak and 81 to the NG peak. Moreover, there is the presence of another significant peak (hereafter NWG peak) with 37 galaxies at the position of the NW X-ray peak [ ${\rm RA}=00^{{\rm h}}14^{{\rm m}}08\hbox{$.\!\!^{\rm s}$ }96$ ${\rm Dec}=-30\ensuremath{{\rm ^\circ}} 21\hbox{$^\prime$ }59\hbox{$.\!\!^{\prime\prime}$ }6$ (J2000.0)].

	Figure 13: Spatial distribution on the sky and relative isodensity contour map of 320 likely cluster members (according to the photometric redshifts by Busarello et al. 2002), obtained with the adaptive-kernel method. The plots are centered on the cluster center. Crosses and stars indicate the position of the galaxy and X-ray peaks, respectively.
Open with DEXTER

	Figure 14: V-R vs. R diagram for spectroscopically determined cluster galaxies. The solid line gives the best-fit color-magnitude relation; the dashed lines are drawn at $\pm$0.1 mag from the relation.
Open with DEXTER

Finally, we also consider the whole photometric galaxy catalog by Busarello et al. (2002) after a selection through the color-magnitude relation, which indicates early-type galaxy locus. Specifically, out of the R-magnitude complete catalog we select 316 likely cluster members considering galaxies within 0.1 mag from the ${V}-{R}=1.248-0.018\cdot {R}$ relation, obtained by using a 2 sigma-clipping fitting procedure to our spectroscopic catalog of member galaxies (see Fig. 14). Several peaks are shown in Fig. 15, but there are only three peaks with significance greater than the $99.99\%$ c.l.; they are those already detected above: the central, the N, and the NW peaks (56, 40, and 22 galaxies, respectively).

	Figure 15: Spatial distribution on the sky and relative isodensity contour map of 316 likely cluster members (according to the color-magnitude relation) with $R\le 22.3$, obtained with the adaptive-kernel method. The plots are centered on the cluster center. The stars indicate the position of the X-ray peaks. Crosses and stars indicate the position of the galaxy and X-ray peaks, respectively.
Open with DEXTER

6 Discussion

We analyze the internal dynamics of A2744 on the basis of spectroscopic data for 102 galaxies in a cluster region of ${\sim} 5\hbox{$^\prime$ }\times 8\hbox{$^\prime$ }$ (i.e., within a radius of ${\sim} 1.3$ Mpc$\;$from the cluster center). In particular, we present new redshifts for 66 galaxies, as recovered from spectra stored in the ESO archive. These redshifts have allowed us to expand our knowledge with respect to previous published redshifts, mainly in the northern cluster region.

The value we obtain for the LOS velocity dispersion ( $\sigma_{\rm V}\sim 1800$ km s^-1, see also Couch & Sharples 1987; and GM01) is very high for clusters (see Fadda et al. 1996; Mazure et al. 1996; GM01). This global value of $\sigma _{\rm V}$ is inconsistent with the average value of $T_{\rm X} \sim 8$ keV coming from the X-ray analysis when assuming the equipartition of mass density between gas and galaxies (i.e. $\beta_{\rm spec} =2.4^{+0.5}_{-0.4}$ to be compared with $\beta _{\rm spec}=1$, see also Fig. 5).

This suggests that the cluster is far from dynamical equilibrium. Indeed, we do find significant signatures of the young dynamical status of A2744: the non-Gaussian nature of the velocity distribution, the presence of a velocity gradient and the detection of significant substructure according to the Dressler-Schectman test.

6.1 Clump detection

In their study of the internal dynamics of a large cluster sample, GM01 found two peaks in the velocity distribution of A2744 separated by ${\sim} 4000$ km s$^{-1} \;$and having $\sigma_{\rm V}\sim 1100$ and 700 km s^-1, respectively. However, these peaks were so strongly superimposed that the authors questioned their separation and classified A2744 as a cluster with uncertain dynamics. The present analysis, performed ad hoc for A2744, supercedes the GM01 results. The presence of two well separated peaks ( $\Delta V \sim 4000$ km s^-1) characterizes the central cluster region, while the external cluster region is well described by a one-peak velocity distribution. The presence of two galaxy populations having very different mean velocities in the central cluster region explains the high value of the LOS velocity dispersion found there and the sharp change in the mean velocity (see Fig. 5). Our result also explains the strong mass discrepancy between X-ray and lensing mass estimates in central cluster regions ( $M_{\rm arc}/M_{\rm X}>3$, Allen 1998). In fact, substructure and LOS alignments of material toward the cluster core likely enhances the mass determined from the lensing data (e.g., Bartelmann & Steinmetz 1996).

As for the identification of A2744 subsystems, using the KMM technique we find that a bimodal distribution is a significantly better description in the velocity space, as well as in the position-velocity space, and we assign the galaxies to two groups. The velocity difference is $\Delta V \sim 4000$ km s$^{-1} \;$in agreement with that of the two peaks detected in the central region. Accordingly, the galaxies belonging to substructure, as detected through the Dressler-Schectman test, split into two populations of different velocity. All our results indicate the presence of two galaxy-clumps, one at $\left<V\right>=90~000{-}91~000$ km s$^{-1} \;$and the other at $\left<V\right>=94~000{-}95~000$ km s^-1.

The KMM analysis indicates that the low-velocity clump is the main one (with $\sigma_{\rm V}\sim 1200{-}1300$ km s^-1) and that the high-velocity clump is the secondary one (with $\sigma_{\rm V}= 500{-}800$ km s^-1). The value of $\sigma_{\rm V}\sim 1200{-}1300$ km s$^{-1} \;$of the main clump corresponds to $T_{\rm X}\sim 9$ keV, in agreement with the average X-ray temperature (Allen 1998). According to the KMM results, the relative importance of the secondary clump is largely uncertain. Since our analysis of the central cluster region within 0.4 Mpc$\;$supports an high relative importance, hereafter we consider only the 3D KMM results. Following the same procedure of Sect. 3.2, the values of $\sigma _{\rm V}$ for the two clumps allow us to compute virial masses separately, assuming that each of the two clumps are virialized systems. We obtain $M_{\rm a}({<}R_{\rm vir,a}=2.4 \;{\rm Mpc})=(2.2_{-0.6}^{+0.7})\times 10^{15}~M_{\odot}$ and $M_{\rm b}({<}R_{\rm vir,b}=1.7 \;{\rm Mpc})=(0.8_{-0.3}^{+0.4})\times 10^{15}~M_{\odot}$ for the 3D KMM case.

6.2 Cluster mass estimate

In Sect. 3.2 we give the mass estimate assuming the whole cluster as virialized, $M({<}R_{\rm vir}=3.7 \;{\rm Mpc})=(7.4_{-2.0}^{+2.1})\times 10^{15}~M_{\odot}$. Since the system is not virialized, but likely formed by bound structures, this estimate might overestimate the true cluster mass even by a factor two. The crude addition of the mass of the two clumps gives a value that is less than half, i.e. ${\sim} 3\times 10^{15}~M_{\odot}$. However, this should be considered an underestimate of the true cluster mass since it does not consider the NW external subcluster as well as other infalling minor groups. To obtain a more meaningful mass estimate we use both the one-clump and two-clump approaches to compute the mass values within a radius of 1 Mpc, which is well sampled by the spectroscopic data. In the case of the two-clump approach we consider the global cluster geometry as formed by the two clumps at the cluster redshift assuming the center of A2744 for both the clumps (see the following section). To rescale the mass within 1 Mpc, we assume that each system is described by a King-like mass distribution (see Sect. 3.2) or, alternatively, by a NFW profile where the mass-dependent concentration parameter is taken from Navarro et al. (1997) and rescaled by the factor 1+z (Bullock et al. 2001; Dolag et al. 2004). We obtain $M({<}R=1 \;{\rm Mpc})=1.8 {-} 2.4 \times 10^{15}$  $M_{\odot} \;$in the one-clump assumption and $M({<}R=1 \;{\rm Mpc})=1.4{-}1.5 \times 10^{15}$  $M_{\odot} \;$in the two-clump assumption. Such values are comparable to those of very massive clusters at lower redshifts (e.g., Girardi et al. 1998; GM01).

6.3 Merging scenario

As discussed in the above section, we detect two clumps with the mass ratio of about 3:1 and with a velocity separation of $\Delta V_{\rm rf} \sim 3000$ km s$^{-1} \;$in the cluster rest-frame. Cosmological simulations suggest that high impact velocities might be occurring in cluster mergers (e.g., Crone & Geller 1995). The value of a relative velocity of ${\sim} 3000$ km s$^{-1} \;$is predicted by N-body numerical simulations of Pinkney et al. (1996) and is likely associated with the phase of the core passage in a cluster-cluster merging (see their Fig. 1 for a merging with a 3:1 mass ratio). In particular, the extremely large LOS component of the velocity indicates that the merging axis is close to the LOS.

From the observation of the cool wakes in the Chandra image, KD04 deduced that the merger is not occurring entirely along the LOS, but must have at least a small transverse component. However, analyzing the galaxy distribution they found no conclusive evidence for a spatial segregation (i.e. only at the ${\gtrsim}90\%$ c.l.). Likely due to our larger spectroscopic sample, we find definitive evidence for spatial segregation as shown by the velocity gradient, the segregation of KMM groups, and the analysis of the south external region ($98{-}99\%$ c.l.). All our results agree in displacing the high-velocity group to the S-SW region.

Although the two clumps are spatially segregated, their 2D structure (i.e. the position of the respective centers and cores) is not obvious. KD04 pointed out this difficulty as due to the small sampled cluster region. In spite of the advantage of using a somewhat larger spectroscopic sample and the much more extended 2D sample of likely members, we do not reach a definitive conclusion.

Apart from the NW peak (see below), our 2D analysis of the galaxy distribution (Sect. 5) detects two significant peaks: the main peak in the central cluster region (CG peak) and the secondary peak ${\sim} 2\hbox{$^\prime$ }$ toward N-NW (NG peak). The brightest red cluster galaxies, which generally lie in cluster cores, are located in the same overdense regions. The segregation between the gas and galaxy subclustering is extremely severe. The main X-ray peak lies between CG and NG peaks, much closer to the CG peak and there is no spatial correspondence between X-ray secondary peaks and 2D galaxy peaks.

As for the CG peak, the presence of two galaxy populations having different mean velocities suggests that the cores of the two clumps might be aligned along the LOS. However, the strong spatial segregation of the two clumps suggests that they have not preserved their original structure, but that one or likely both clumps are strongly affected by the merger. In fact, the CG peak is not at the center of the 2D distribution of the high-velocity clump, but rather at the border. A few galaxies, in particular the most luminous/massive and thus the most affected by dynamical friction, might be slowed down by the interaction between the two clumps, while the other galaxies pass by. The presence in the CG peak of two very luminous galaxies differing in velocity by 4500 km s$^{-1} \;$(ID53/CN1 and ID70/CN2) supports our hypothesis: they might be the tracers of the two cores destined to oscillate around the mean velocity for a long time (i.e., several 10⁹ yr as suggested by numerical simulations; see, e.g., Nakamura et al. 1995). In fact, an high velocity difference between two dominant galaxies is often suggestive of an energetic cluster merger (e.g., Burns et al. 1995) and indeed this process is thought to be the cause of the formation of dumbbell galaxies in a few merging clusters (e.g., Beers et al. 1992; Flores et al. 2000). Galaxies that are not slowed down by cluster merging (collisionless galaxies) are likely those causing the velocity gradient, i.e.  galaxies of the high-velocity clump located in the S-SW region and galaxies of the low-velocity clump located in the N-NE region. Since the intracluster medium is not relaxed, as shown by the presence of the two secondary X-ray peaks, we suggest an early merging phase. If we are observing the merging just after the first core passage, the low-velocity clump is moving north and the high-velocity clump is moving south.

In the above scenario the identification of the north secondary X-ray peak (XN) with the gas core of the low-velocity clump and of the south secondary X-ray peak (XS) with the gas core of the high-velocity clump - see KD04 - is still meaningful, in spite of the segregation between the gas and galaxy subclustering. In fact, observations agree with the fact that (collisionless) galaxies, as detected at the north and south cluster regions, precede the (collisional) intracluster medium.

In summary, we suggest that the two galaxy clumps are in an advanced phase of merging, just after the core passage, but still far from having formed a dynamically relaxed cluster. We agree with the merging scenario proposed by KD04 in its general lines although propose a somewhat more advanced merging phase (see their Sect. 5.1). In fact, they assume that the gas has not yet decoupled from the dark matter and galaxies, while we find a strong segregation between the gas and galaxy subclustering. Moreover, we agree with KD04 about the importance of merging and the high velocity of the impact, thus supporting their hypothesis that this merger in the central cluster region is responsible for the powerful radio halo.

Indeed, the cluster structure described by our analysis is also more complex than that suggested by Chandra data. The NG peak shown by our 2D analysis, which has no counterpart in the X-ray distribution, represents an additional feature in the above scenario. The galaxies located around this peak have kinematical properties similar to those of the low-velocity clump. However, we discard the hypothesis that the NG peak represents the undisturbed core of the low-velocity main clump due to its large distance from the main X-ray peak, likely tracing the potential well of the just forming cluster. About the nature of the NG peak, we propose two alternatives, both possible in the above main merging scenario. It might be a relic of a previous merging involving the main clump (some galaxy structures might be detectable in the host cluster for a long time, see González-Casado et al. 1994) or a part of the core of the main clump that survived the ongoing merging. The second hypothesis is supported by its location along the direction of the ridge A shown by the smoothed X-ray surface brightness image of KD04, i.e. the ridge hosting the north secondary X-ray peak (see their Fig. 2; and Fig. 2 in this paper).

As for the external cluster region, our 2D analysis finds a NW peak (NWG peak) in the galaxy distribution corresponding to the NW X-ray peak. The galaxy peak is somewhat farther east than the X-ray peak, in agreement with the NW clump moving from west to east (KD04) and that collisionless faint galaxies precede the collisional intracluster medium during the interaction. The presence of an ongoing merging in the ${\sim}$NS direction and a future merging in the ${\sim}$WE direction suggests that A2744 lies in the intersection of filaments (e.g., cluster A521 analyzed by Arnaud et al. 2000), which is the natural place of rich cluster formation (e.g., Katz & White 1993). Spectral observations of galaxies in a large field around A2744 would provide new insights into this issue.

7 Summary and conclusions

We present the results of the dynamical analysis of the rich, X-ray luminous and hot cluster of galaxies A2744, containing a powerful diffuse radio halo. The X-ray emission is known to have two secondary cores in the central region and a peak in the NW external region (Govoni et al. 2001b; KD04). GM01 found two peaks in the velocity distribution, but these peaks were so strongly superimposed that the authors questioned their separation and classified A2744 as a cluster with uncertain dynamics. The present analysis, performed ad hoc for A2744, supercedes the GM01 results.

Our analysis is based on velocities and positions of 102 galaxies in a cluster region of ${\sim} 5\hbox{$^\prime$ }\times 8\hbox{$^\prime$ }$ (i.e., within a radius of ${\sim} 1.3$ Mpc$\;$from the cluster center). In particular, we present new redshifts for 66 galaxies, as recovered from spectra stored in the ESO archive.

We find that A2744 appears as a well isolated peak in the redshift space at $\left<z\right>=0.306$, which includes 85 galaxies recognized as cluster members. We compute the LOS velocity dispersion of galaxies, $\sigma_{\rm V}=1767_{-99}^{+121}$ km s^-1, which is significantly larger than what is expected in the case of a relaxed cluster with an observed X-ray temperature of 8 keV.

We find evidence that this cluster is far from dynamical equilibrium, as shown by:

• the non-Gaussian nature of the velocity distribution according to different tests;

• the presence of a velocity gradient at the ${>}98\%$ c.l.;

• the presence of significant substructures at the ${\sim}99\%$ c.l.

To detect and analyze possible subsystems we use different methods coupling galaxy position and velocity information: the KMM method, the kinematical analysis of galaxy population located in different spatial regions, and Dressler & Schectman statistics.

Our analysis shows the presence of two galaxy clumps with:

• a difference in the mean velocities of $\Delta V \sim 4000$ km s^-1;

• a value of $\sigma_{\rm V}\sim 1200{-}1300$ km s$^{-1} \;$for the main, low-velocity clump and a value of $\sigma_{\rm V}= 500{-}800$ km s$^{-1} \;$for the secondary, high-velocity clump;

• a remarked spatial segregation, with the galaxies of the high velocity clump mainly populating the S-SW cluster region.

Our results suggest a merging scenario of two clumps with a mass ratio of 3:1 and an high LOS impact velocity of $\Delta V_{\rm rf} \sim 3000$ km s^-1, likely observed just after the core passage. The merging axis, close to the LOS, is roughly along the NS direction. This scenario supports recent Chandra results (KD04) although suggests a somewhat more advanced merging phase. For the final product of the merger we estimate a mass within 1 Mpc$\;$of 1.4-2.4 $\times 10^{15}~M_{\odot}$, depending on the model adopted to describe the cluster dynamics. Such values are comparable to those of very massive clusters at lower redshifts.

Our conclusion supports the view of the connection between extended radio emission and energetic merging phenomena in galaxy clusters.

Acknowledgements

We thank Federica Govoni for the VLA radio contour levels she kindly provided us. We thank the referee, Florence Durret, for her useful suggestions.
This publication is based on observations made with the NTT telescope at the La Silla observatory (proposal IDs: 62.O-0369(A), 63.O-0257(B) and 64.O-0236(B)). Data are stored in the public ESO archive. This publication also makes use of data obtained from the Chandra data archive at the NASA Chandra X-ray center (http://asc.harvard.edu/cda/).

References

• Abell, G. O. 1958, ApJS, 3, 211 [NASA ADS] [CrossRef] (In the text)
• Abell, G. O., Corwin, H. G. Jr., & Olowin, R. P. 1989, ApJS, 70, 1 [NASA ADS] [CrossRef] (In the text)
• Allen, S. W. 1998, MNRAS, 296, 392 [NASA ADS] [CrossRef] (In the text)
• Andreon, S. 2001, ApJ, 547, 623 [NASA ADS] [CrossRef] (In the text)
• Arnaud, M., Maurogordato, S., Slezak, E., & Rho, J. 2000, A&A, 355, 461 [NASA ADS] (In the text)
• Ashman, K. M., Bird, C. M., & Zepf, S. E. 1994, AJ, 108, 2348 [NASA ADS] [CrossRef] (In the text)
• Bardelli, S., Zucca, E., Vettolani, G., et al. 1994, MNRAS, 267, 665 [NASA ADS] (In the text)
• Barrena, R., Biviano, A., Ramella, M., Falco, E. E., & Seitz, S. 2002, A&A, 386, 816 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Bartelmann, M., & Steinmetz, M. 1996, MNRAS, 283, 431 [NASA ADS] (In the text)
• Bautz, L. P., & Morgan, W. W. 1970, ApJ, 162, 149 [NASA ADS] [CrossRef] (In the text)
• Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [NASA ADS] [CrossRef] (In the text)
• Beers, T. C., Forman, W., Huchra, J. P., Jones, C., & Gebhardt, K. 1991, AJ, 102, 1581 [NASA ADS] [CrossRef] (In the text)
• Beers, T. C., Gebhardt, K., Huchra, J. P., et al. 1992, ApJ, 400, 410 [NASA ADS] [CrossRef] (In the text)
• Bird, C. M., & Beers, T. C. 1993, AJ, 105, 1596 [NASA ADS] [CrossRef] (In the text)
• Biviano, A., Katgert, P., Thomas, T., & Adami, C. 2002, A&A, 387, 8 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Böhringer, H., & Schuecker, P. 2002, in Merging Processes in Galaxy Clusters, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.), in press: Observational signatures and statistics of galaxy cluster mergers (In the text)
• Boschin, W., Girardi, M., Barrena, R., et al. 2004, A&A, 416, 839 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Bullock, J. S., Kolatt, T. S., Sigad, Y., et al. 2001, MNRAS, 321, 559 [NASA ADS] [CrossRef] (In the text)
• Buote, D. A. 2002, in Merging Processes in Galaxy Clusters, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.), in press: Optical Analysis of Cluster Mergers (In the text)
• Burns, J. O., Roettiger, K., Pinkney, J., et al. 1995, ApJ, 446, 583 [NASA ADS] [CrossRef] (In the text)
• Busarello, G., Merluzzi, P., La Barbera, F., Massarotti, M., & Capaccioli, M. 2002, A&A, 389, 787 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Butcher, H., & Oemler, A. Jr. 1978, ApJ, 219, 18 [NASA ADS] [CrossRef] (In the text)
• Carlberg, R. G., Yee, H. K. C., & Ellingson, E., et al. 1997, ApJ, 476, L7 [NASA ADS] [CrossRef] (In the text)
• Colless, M., & Dunn, A. M. 1996, ApJ, 458, 435 [NASA ADS] [CrossRef] (In the text)
• Couch, W. J., Barger, A. J., Smail, I., Ellis, R. S., & Sharples, R. M. 1998, ApJ, 497, 188 [NASA ADS] [CrossRef] (In the text)
• Couch, W. J., & Newell, E. B. 1984, ApJS, 56, 143 [NASA ADS] [CrossRef] (In the text)
• Couch, W. J., & Sharples, R. M. 1987, MNRAS, 229, 423 [NASA ADS] (In the text)
• Crone, M. M., & Geller, M. J. 1995, AJ, 110, 21 [NASA ADS] [CrossRef] (In the text)
• Danese, L., De Zotti, C., & di Tullio, G. 1980, A&A, 82, 322 [NASA ADS] (In the text)
• den Hartog, R., & Katgert, P. 1996, MNRAS, 279, 349 [NASA ADS] (In the text)
• Dolag, K., Bartelmann, M., Perrotta, F., et al. 2004, A&A, 416, 853 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Dressler, A., & Shectman, S. A. 1988, AJ, 95, 985 [NASA ADS] [CrossRef] (In the text)
• Ebeling, H., Voges, W., Böhringer, H., et al. 1996, MNRAS, 281, 799 [NASA ADS] (In the text)
• Ellingson, E., & Yee, H. K. C. 1994, ApJS, 92, 33 [NASA ADS] [CrossRef] (In the text)
• Fadda, D., Girardi, M., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1996, ApJ, 473, 670 [NASA ADS] [CrossRef] (In the text)
• Fasano, G., & Franceschini, A. 1987, MNRAS, 225, 155 [NASA ADS] (In the text)
• Feretti, L. 1999, MPE Report, 271 (In the text)
• Feretti, L. 2002, The Universe at Low Radio Frequencies, held 30 Nov.-4 Dec. 1999, Pune, India, ed. A. Pramesh Rao, G. Swarup, & Gopal-Krishna, 2002, Proc. IAU Symp., 199, 133 (In the text)
• Feretti, L. 2005, X-Ray and Radio Connections, ed. L. O. Sjouwerman, & K. K. Dyer, Published electronically by NRAO, http://www.aoc.nrao.edu/events/xraydio, held 3-6 February 2004 in Santa Fe, New Mexico, USA (In the text)
• Feretti, L., Gioia, I. M., & Giovannini, G. 2002, Merging Processes in Galaxy Clusters (The Netherlands: Kluwer Ac. Pub.) (In the text)
• Flores, R. A., Quintana, H., & Way, M. J. 2000, ApJ, 532, 206 [NASA ADS] [CrossRef] (In the text)
• Fujita, Y., Sarazin, C. L., Reiprich, T. H., et al. 2004, ApJ, 616, 157 [NASA ADS] [CrossRef] (In the text)
• Geller, M. J., & Beers, T. C. 1982, PASP, 94, 421 [NASA ADS] [CrossRef] (In the text)
• Giovannini, G., & Feretti, L. 2002, in Merging Processes in Galaxy Clusters, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.), Diffuse Radio Sources and Cluster Mergers (In the text)
• Giovannini, G., Tordi, M., & Feretti, L. 1999, New Astron., 4, 141 [NASA ADS] (In the text)
• Girardi, M., & Biviano, A. 2002, in Merging Processes in Galaxy Clusters, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.), Optical Analysis of Cluster Mergers (In the text)
• Girardi, M., Biviano, A., Giuricin, G., Mardirossian, F., & Mezzetti, M. 1993, ApJ, 404, 38 [NASA ADS] [CrossRef]
• Girardi, M., Fadda, D., Giuricin, G. et al. 1996, ApJ, 457, 61 [NASA ADS] [CrossRef] (In the text)
• Girardi, M., Escalera, E., Fadda, D., et al. 1997, ApJ, 482, 41 [NASA ADS] [CrossRef] (In the text)
• Girardi, M., Giuricin, G., Mardirossian, F., Mezzetti, M., & Boschin, W. 1998, ApJ, 505, 74 [NASA ADS] [CrossRef] (In the text)
• Girardi, M., & Mezzetti, M. 2001, ApJ, 548, 79 [NASA ADS] [CrossRef] (GM01) (In the text)
• Gómez, P. L., Hughes, J. P., & Birkinshaw, M. 2000, ApJ, 540, 726 [NASA ADS] [CrossRef] (In the text)
• González-Casado, G., Mamon, G., & Salvador-Solé, E. 1994, ApJ, 433, L61 [NASA ADS] [CrossRef] (In the text)
• Govoni, F., Ensslin, T. A., Feretti, L., & Giovannini, G. 2001a, A&A, 369, 441 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Govoni, F., Feretti, L., Giovannini, G., et al. 2001b, A&A, 376, 803 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Henry, J. P., Finoguenov, A., & Briel, U. G. 2004, ApJ, 615, 181 [NASA ADS] [CrossRef] (In the text)
• Jones, C., & Forman, W. 1999, ApJ, 511, 65 [NASA ADS] [CrossRef] (In the text)
• Katz, N., & White, S. D. M. 1993, ApJ, 412, 455 [NASA ADS] [CrossRef] (In the text)
• Kempner, J. C., & David, L. P. 2004, MNRAS, 349, 385 [NASA ADS] [CrossRef] (KD04) (In the text)
• Kennicutt, R. C. 1992, ApJS, 79, 225 [NASA ADS] (In the text)
• Kriessler, J. R., & Beers, T. C. 1997, AJ, 113, 80 [NASA ADS] [CrossRef] (In the text)
• Limber, D. N., & Mathews, W. G. 1960, ApJ, 132, 286 [NASA ADS] [CrossRef] (In the text)
• Malumuth, E. M., Kriss, G. A., Dixon, W., Ferguson, H. C., & Ritchie, C. 1992, AJ, 104, 495 [NASA ADS] [CrossRef] (In the text)
• Markevitch, A., Gonzalez, A. H., David, L., et al. 2002, ApJ, 567, 27 [NASA ADS] [CrossRef] (In the text)
• Markevitch, M., & Vikhlinin, A. 2001, ApJ, 563, 95 [NASA ADS] [CrossRef] (In the text)
• Mazure, A., Katgert, P., den Hartog, P., et al. 1996, A&A, 310, 31 [NASA ADS] (In the text)
• Mercurio, A., Girardi, M., Boschin, W., Merluzzi, P., & Busarello, G. 2003, A&A, 397, 431 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Mohr, J. J., Geller, M. J., Fabricant, D. G., et al. 1996, ApJ, 470, 724 [NASA ADS] [CrossRef] (In the text)
• NAG Fortran Workstation Handbook, 1986 (Downers Grove, IL: Numerical Algorithms Group) (In the text)
• Nakamura, F. E., Hattori, M., & Mineshige, S. 1995, A&A, 302, 649 [NASA ADS] (In the text)
• Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] (In the text)
• Pinkney, J., Roettiger, K., Burns, J. O., & Bird, C. M. 1996, ApJS, 104, 1 [NASA ADS] [CrossRef] (In the text)
• Pisani, A. 1993, MNRAS, 265, 706 [NASA ADS] (In the text)
• Pisani, A. 1996, MNRAS, 278, 697 [NASA ADS] (In the text)
• Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, in Numerical Recipes, Second Edition (Cambridge University Press) (In the text)
• Quintana, H., Carrasco, E. R., & Reisenegger, A. 2000 AJ, 120, 511 (In the text)
• Roettiger, K., Loken, C., & Burns, J. O. 1997, ApJS, 109, 307 [NASA ADS] [CrossRef] (In the text)
• Sarazin, C. L. 2002, in Merging Processes in Galaxy Clusters, ed. L. Feretti, I. M. Gioia, & G. Giovannini (The Netherlands: Kluwer Ac. Pub.), The Physics of Cluster Mergers (In the text)
• Schuecker, P., Böhringer, H., Reiprich, T. H., & Feretti, L. 2001, A&A, 378, 408 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Shapiro, S. S., & Wilk, M. B. 1965, Biometrika, 52, 591 (In the text)
• Smail, I., Ellis, R. S., Dressler, A., et al. 1997, ApJ, 479, 70 [NASA ADS] [CrossRef] (In the text)
• The, L. S., & White, S. D. M. 1986, AJ, 92, 1248 [NASA ADS] [CrossRef] (In the text)
• Tonry, J., & Davis, M. 1979, ApJ, 1511 (In the text)
• Wainer, H., & Schacht, S. 1978, Psychometrika, 43, 203 (In the text)
• Zhang, Y.-Y., Finoguenov, A., Böhringer, H., et al. 2004, A&A, 413, 49 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)