A&A 449, 791-803 (2006)
DOI: 10.1051/0004-6361:20054262
W. T. Thompson
L-3 Communications GSI, NASA Goddard Space Flight Center, Code 612.1, Greenbelt, MD 20771, USA
Received 27 September 2005 / Accepted 11 December 2005
Abstract
A set of formal systems for describing the coordinates of solar image data is
proposed. These systems build on current practice in applying coordinates to
solar image data. Both heliographic and heliocentric coordinates are
discussed. A distinction is also drawn between heliocentric and
helioprojective coordinates, where the latter takes the observer's exact
geometry into account. The extension of these coordinate systems to
observations made from non-terrestial viewpoints is discussed, such as from the
upcoming STEREO mission. A formal system for incorporation of these
coordinates into FITS files, based on the FITS World Coordinate System, is
described, together with examples.
Key words: standards - Sun: general - techniques: image processing - astronomical data bases: miscellaneous - methods: data analysis
Solar research is becoming increasingly more sophisticated. Advances in solar instrumentation have led to increases in spatial resolution, and will continue to do so. Future space missions will view the Sun from different perspectives than the current view from ground-based observatories, or satellites in Earth orbit. Both of these advances will require more careful attention to the coordinate systems used for solar image data. In fact, some taste of this has already occured with the Solar and Heliospheric Observatory (SOHO) satellite (Domingo et al. 1995), which views the Sun from the inner Lagrange point between Earth and the Sun. The Sun appears approximately 1% bigger from SOHO than it does from Earth, requiring adjustment whenever SOHO images are compared with data from ground-based observatories, or satellites in low Earth orbit.
Although there is widespread agreement on the coordinate systems to be used for interplanetary space (Russell 1971; Fränz & Harper 2002; Hapgood 1992) no formal structure exists for solar image coordinates, except for the well-established heliographic coordinate systems. In particular, there is no agreement on how these coordinates should appear in FITS headers, with potential confusion when data from one observatory is compared to data from another. This document outlines the various possible coordinate systems which may be used for solar image data, and to show how these coordinate systems relate to the World Coordinate System (WCS) formalism used in FITS files. In devising the coordinate systems outlined below, attention is given to current practice within the solar imaging community.
Normal coordinate systems used for extra-solar observations - such as right ascension and declination, or galactic longitude and latitude - only need to worry about two spatial dimensions. The same can be said for normal cartography of a planet such as Earth. However, to properly treat the complete range of solar phenomena, from the interior out into the corona, a complete three-dimensional coordinate system is required. Unfortunately, not all the information necessary to determine the full three-dimensional position of a solar feature is usually available. Therefore, in developing coordinate systems for solar data, one must take into account that one of the axes of the coordinate system may be missing.
Also, since the Sun is a gaseous body, there are no fixed points of reference on the Sun. What's more, different parts of the Sun rotate at different rates. The rotation rate depends not only on latitude, but also on how deeply the magnetic field lines of a given feature are anchored in the photosphere. Thus, for example, active regions follow different differential rotation laws than smaller-scale magnetic features at the same latitudes.
For the above reasons, attention will be given to coordinate systems which take the observer's viewing geometry into consideration. Some coordinate systems will be rotating with respect to other coordinate systems, and in all the coordinate systems, at least some part of the Sun will be moving relative to that coordinate system. For those reasons, the coordinate system should not really be considered complete without also taking time into account. In the discussion which follows, all coordinates will assume a given observation time t.
With solar imaging instrumentation now planned for spacecraft which will operate at large distances away from the Earth-Sun line, such as STEREO (Socker et al. 1996), consideration must also be given as to how the viewpoint of the instrument should be taken into account in the coordinate system. This is discussed in Sect. 9.1.
Two different styles of including coordinate information within FITS files will be considered here. The first is the coordinate system from the original FITS specification, while the second is the more modern World Coordinate System. The latter allows for much more flexibility in the types of coordinate systems which can be expressed, as well as in describing how the instrument coordinate axes map into real-world coordinates. For those reasons, we will concentrate on the World Coordinate System implementations of the coordinate systems. However, the older system will also be considered where appropriate.
In the original FITS paper (Wells et al. 1981), the coordinates of a data array were specified with the following keywords in the FITS header:
In the simple case of linear coordinates with no rotation, the transformation from pixel to real world coordinates is then
- CRPIXn:
- Reference pixel to subtract from the pixel coordinates along axis n. Note that CRPIXn follows the Fortran convention of counting from 1 to N, instead of from 0 to N-1 as is done in some programming languages.
- CRVALn:
- Coordinate value of the reference pixel along axis n.
- CDELTn:
- Pixel spacing along axis n.
- CROTAn:
- Rotation angle, in degrees, to apply to axis n. The exact method of applying the rotation angle was not specified in the original paper, but commonly used conventions have developed over the years, as discussed in Sect. 8.
- CTYPEn:
- A string value labeling each coordinate axis. A common system, used by the SOHO spacecraft, labels the westward axis as SOLARX and the northward axis as SOLARY.
The World Coordinate System (WCS) (Greisen & Calabretta 2002; Calabretta & Greisen 2002) is a system for describing
the coordinates of a FITS array, and includes a system of describing various
map projections for spherical coordinates![]() . In simplified form,
the keywords CRPIXn, CRVALn, CDELTn are retained from
the original specification, combined with the following additional or modified
keywords:
. In simplified form,
the keywords CRPIXn, CRVALn, CDELTn are retained from
the original specification, combined with the following additional or modified
keywords:
For spherical coordinates, some care must be taken in the selection of the reference pixel, depending on the projection being used.
- PCi_j:
- A coordinate transformation matrix, describing the conversion from pixel coordinate axes j into intermediate pixel coordinates i. This transformation matrix replaces the older CROTAn keyword, which is deprecated in the WCS formalism. As well as rotations, the PC matrix can also encode other transformations, such as skew. (There is also an optional form of the WCS formalism in which both the PCi_j and CDELTi keywords are combined into a single CDi_j matrix.)
- CTYPEi:
- For spherical coordinates, the first four characters express the coordinate type, while the second four characters express the map projection used.
- PVi_m:
- Additional parameters required in some coordinate systems.
- CUNITi:
- The units of the coordinates along axis i.
- LONPOLE, LATPOLE:
- Angles used for spherical coordinate transformations. These keywords have default values which depend on the map projection used.
It is a requirement in FITS files, and in WCS in particular, that all angles must be in degrees. (However, see Sect. 9.2.) For simplicity, in the following, all trigonometric functions are assumed to have their arguments in degrees, while the inverse functions are assumed to return values in degrees.
It is possible in WCS to have more than one coordinate system for any given data set. An alternate coordinate system would be expressed using all the above keywords followed by one of the letters "A'' to "Z'', e.g. CRPIX1A, PC1_1A, etc. The keywords WCSNAMEa can be used to label each alternative coordinate system - see Figs. 4 and 5.
Modified versions of the above keywords for use in binary tables and pixel lists are listed in Greisen & Calabretta (2002) and in Calabretta & Greisen (2002).
The well-known heliographic![]() coordinate system expresses the latitude
coordinate system expresses the latitude ![]() and longitude
and longitude ![]() of a feature on the solar surface, and can be extended to three dimensions by adding the radial distance r from the center of the Sun. The rotational axis used to define the coordinate system is based on the original work of Carrington (1863). Seidelmann et al. (2002) lists the right ascension
and declination of the solar north pole as
of a feature on the solar surface, and can be extended to three dimensions by adding the radial distance r from the center of the Sun. The rotational axis used to define the coordinate system is based on the original work of Carrington (1863). Seidelmann et al. (2002) lists the right ascension
and declination of the solar north pole as
![]() ,
,
![]() .
There are two basic variations on the
heliographic system, which we will refer to as Stonyhurst and Carrington
heliographic. Both use the same solar rotational axis, and differ only in the
definition of longitude.
.
There are two basic variations on the
heliographic system, which we will refer to as Stonyhurst and Carrington
heliographic. Both use the same solar rotational axis, and differ only in the
definition of longitude.
There are several limitations to the use of heliographic coordinates when used with two-dimensional image data:
![\begin{figure}
\par\includegraphics[angle=90,width=7.65cm,clip]{4262fig1.ps}\end{figure}](/articles/aa/full/2006/14/aa4262-05/Timg14.gif) |
Figure 1: A diagram of the Sun, showing lines of constant Stonyhurst heliographic longitude and latitude on the solar disk. The origin of the coordinate system is at the intersection of the solar equator and the (terrestrial) observer's central meridian. This representation is also known as a Stonyhurst grid. |
| Open with DEXTER | |
An alternative to the r coordinate is the height
![]() relative to the solar surface, where h is positive above the surface and
negative below the surface.
relative to the solar surface, where h is positive above the surface and
negative below the surface.
It should be noted that Stonyhurst heliographic coordinates are closely related
to Heliocentric Earth Equatorial (HEEQ) coordinates (Hapgood 1992).
Conversion between these two systems are given by the equations![]()
| r | = | ||
| = | (1) | ||
| = |
| |
= | ||
| = | (2) | ||
| = |
The Carrington coordinate system is a variation of the heliographic system
which rotates at an approximation to the mean solar rotational rate, as
originally used by Carrington (1863). The sidereal period of the Carrington
system is 25.38 days, which translates into a mean synodic period of
27.2753 days (Stix 1989). Seidelmann et al. (2002) gives the angle of the prime
meridian from the ascending node as
![]() at J2000.0. Each time
the Carrington prime meridian coincides with the central meridian as seen from
Earth, which happens once each 27.21 to 27.34 days, depending on where Earth is
in its orbit, marks the beginning of a new "Carrington rotation''. These
rotations are numbered sequentially, with Carrington rotation number 1
commencing on 9 November 1853. The start date and time of each Carrington
rotation (also known as the "synodic rotation number'') is published in the
Astronomical Almanac. For example, Carrington rotation
number 1900 began on 2 September 1995.
at J2000.0. Each time
the Carrington prime meridian coincides with the central meridian as seen from
Earth, which happens once each 27.21 to 27.34 days, depending on where Earth is
in its orbit, marks the beginning of a new "Carrington rotation''. These
rotations are numbered sequentially, with Carrington rotation number 1
commencing on 9 November 1853. The start date and time of each Carrington
rotation (also known as the "synodic rotation number'') is published in the
Astronomical Almanac. For example, Carrington rotation
number 1900 began on 2 September 1995.
Carrington longitude is offset from Stonyhurst longitude by a time-dependent
scalar value. In other words, at any given time t, the relationship between
Stonyhurst longitude ![]() and Carrington longitude
and Carrington longitude
![]() is given
by the equation
is given
by the equation
| (3) |
Heliocentric coordinates express the true spatial position of a feature in physical units from the center of the Sun. There are a number of well-established heliocentric coordinate systems used in space physics (Hapgood 1992). Examples include Heliocentric Aries Ecliptic (HAE), Heliocentric Earth Ecliptic (HEE), and Heliocentric Earth Equatorial (HEEQ). Each of these coordinate systems consists of three mutually perpendicular axes, X, Y, and Z, which together form a right-handed coordinate system. For example, the HEE system has an X axis pointing along the Sun-Earth line, and a Z axis pointing along the ecliptic north pole. (A precise definition of the ecliptic can be found in Lieske et al. 1977.) In this work, we will define additional heliocentric coordinate systems oriented specifically towards solar image data.
No solar observation from a single perspective can truly be said to be in heliocentric coordinates as defined below. Lines of sight from the observer to the Sun are not truly parallel to each other, so that translating image position into a physical distance will depend to some extent on where the feature is along the line of sight. Also, no attempt is made to distinguish the various possible map projections - e.g. whether one is measuring an angular distance, the sine of the angle, or the tangent of the angle. However, for many cases, these distinctions are unimportant, and heliocentric coordinates as defined here are often very useful. They also serve as a basis for the helioprojective coordinate systems discussed later.
No matter what perspective an observer has, the heliocentric coordinate systems discussed below will have axes defined relative to that observer. Thus, unlike the heliographic case, an observation made from a non-terrestrial platform will measure coordinates which will be different from those measured from Earth. Hence, at least for non-terrestrial observations, information must also be provided about the observers position to properly define the coordinate system (see Sect. 9.1).
The class of observer-dependent heliocentric coordinate systems discussed in this report falls into two subcategories: heliocentric-cartesian and heliocentric-radial.
This is a true (x,y,z) Cartesian coordinate system, with each of the axes
being perpendicular to each other, and with all lines of constant x (or yor z) being parallel to each other. The z axis is defined to be parallel
to the observer-Sun line, pointing toward the observer. The y axis is
defined to be perpendicular to z and in the plane containing both the z axis and the solar North pole axis, with y increasing towards solar North.
The x axis is defined to be perpendicular to both y and z, with xincreasing towards solar West. Thus, it is a right-handed coordinate system.
Each axis is expressed as either a physical distance in meters, or relative to ![]() .
The heliocentric-cartesian coordinate system is demonstrated in Fig. 2.
.
The heliocentric-cartesian coordinate system is demonstrated in Fig. 2.
![\begin{figure}
\par\includegraphics[angle=90,width=6.55cm,clip]{4262fig2.ps}\end{figure}](/articles/aa/full/2006/14/aa4262-05/Timg34.gif) |
Figure 2: A diagram of the Sun, with lines of constant heliocentric-cartesian position (x,y) overlayed. The z axis points out of the page. |
| Open with DEXTER | |
Heliocentric-cartesian coordinates are also known as heliocentric (or
heliographic) Radial-Tangential-Normal (HGRTN) coordinates (Fränz & Harper 2002), except
with different nomenclature. The heliocentric-cartesian axes x, y, z are
equivalent to the HGRTN axes
![]() ,
,
![]() ,
and
,
and
![]() respectively.
respectively.
Heliocentric-radial coordinates share the same z axis as
heliocentric-cartesian coordinates, but replace (x,y) with
![]() .
The parameter
.
The parameter ![]() is the radial distance from the z axis, and is also
known as the impact parameter. It is expressed either as a physical distance
or relative to
is the radial distance from the z axis, and is also
known as the impact parameter. It is expressed either as a physical distance
or relative to ![]() .
Surfaces of constant
.
Surfaces of constant ![]() form cylinders. The
position angle
form cylinders. The
position angle ![]() is measured in degrees counterclockwise from the
projection of the solar North pole. This coordinate system is demonstrated in
Fig. 3.
is measured in degrees counterclockwise from the
projection of the solar North pole. This coordinate system is demonstrated in
Fig. 3.
![\begin{figure}
\par\includegraphics[angle=90,width=8.35cm,clip]{4262fig3.ps}\end{figure}](/articles/aa/full/2006/14/aa4262-05/Timg39.gif) |
Figure 3:
A diagram of the Sun demonstrating heliocentric-radial coordinates, with
lines of constant impact parameter |
| Open with DEXTER | |
Data taken from a single perspective can only approximate true heliocentric coordinates. A more precise rendition of coordinates should recognize that observations are projected against the celestial sphere. This class of coordinate systems, which we will call helioprojective, mimics the heliocentric coordinate systems discussed above, replacing physical distances with angles. Although there's a one-to-one correspondence between the heliocentric parameters and the helioprojective parameters, the latter is really an observer-centric system. When the observer is on or just above Earth, these can be described as geocentric coordinate systems.
All projective angles discussed here have an origin at disk center. This is the apparent disk center as seen by the observer, without any corrections made for light travel time or aberrations. Such considerations do not play a role in these solar-specific coordinate systems.
Because helioprojective coordinates are ultimately spherical in nature, the
full map-projection aspects of WCS come into play. Thus, one must take into
account exactly what map projections are used in taking the data.
In essence, helioprojective coordinates are celestial spherical coordinates
that use the Sun to define their pole and origin, and which can be extended
from disk center out into the corona, and ultimately over the full
![]() steradian sky.
steradian sky.
This is the projected equivalent of heliocentric-cartesian coordinates, where
the distance parameters x and y are replaced with the angles ![]() and
and ![]() ,
where
,
where ![]() is the longitude, and
is the longitude, and ![]() is the latitude.
Close to the Sun, where the small angle approximation holds, the
heliocentric-cartesian and helioprojective-cartesian are related through the
equations
is the latitude.
Close to the Sun, where the small angle approximation holds, the
heliocentric-cartesian and helioprojective-cartesian are related through the
equations
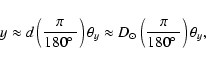
The helioprojective equivalent of z is ![]() ,
defined as
,
defined as
| (5) |
Note that, unlike usual celestial coordinate systems, helioprojective-cartesian coordinates are left-handed. This is handled through the sign of the CDELTi keyword.
This is the helioprojective equivalent of heliocentric-radial, where the
impact parameter ![]() is replaced with the angle
is replaced with the angle
![]() .
Again, this
is a spherical coordinate system, and the map projection rules come into play.
Close to the Sun, where the small-angle approximation holds, the
heliocentric-radial and helioprojective-radial impact parameters are
related through the equation
.
Again, this
is a spherical coordinate system, and the map projection rules come into play.
Close to the Sun, where the small-angle approximation holds, the
heliocentric-radial and helioprojective-radial impact parameters are
related through the equation
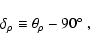 |
(7) |
A variation on radial coordinates involves replacing either ![]() or
or
![]() with the cosine of the angle between the surface normal and the
line of sight to the observer. This parameter,
with the cosine of the angle between the surface normal and the
line of sight to the observer. This parameter, ![]() ,
varies between 1 at disk
center to 0 at the limb. Because this describes spatial positions at the Sun's
surface, it has the same limitations as heliographic coordinates. (See
Sect. 2.)
,
varies between 1 at disk
center to 0 at the limb. Because this describes spatial positions at the Sun's
surface, it has the same limitations as heliographic coordinates. (See
Sect. 2.)
The conversion between heliocentric coordinates and ![]() is quite simple
is quite simple
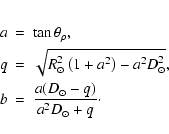
When
![]() ,
the distinction between
Eqs. (8) and (9) is negligible. Only when
,
the distinction between
Eqs. (8) and (9) is negligible. Only when ![]() is within 8 solar radii does the error grow to 0.1%, and at 1 AU the
approximation is good to almost six significant figures. Thus, for most
applications, Eq. (9) can be simplified to
is within 8 solar radii does the error grow to 0.1%, and at 1 AU the
approximation is good to almost six significant figures. Thus, for most
applications, Eq. (9) can be simplified to
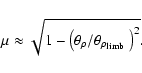 |
(10) |
Table 1 lists all the coordinate parameters referred to in this document, together with their units and WCS labels, where appropriate. The WCS labels are designed to be used in CTYPEi declarations, e.g. CTYPE1='HPLN-TAN'. They also serve as the basis for a family of keywords establishing the viewer's location (see Sect. 9.1). Spherical coordinates, i.e. heliographic or helioprojective, are always in pairs of the form xxLN/xxLT, for longitude and latitude, which is why some quantities in Table 1 have synonyms.
Table 1:
A complete list of all coordinate parameters referred to in this document.
Also included is the associated WCS label where appropriate, and the units in
which the parameters are expressed. Parameters given in meters can also be
expressed as relative to the solar radius ![]() .
.
Map projections do not enter into heliocentric coordinates, and therefore the axis labels will simply be the appropriate four-letter designation as given in Table 1. The CUNITi keyword will give the units of the coordinate values. Some examples of valid entries for CUNITi are
See Greisen & Calabretta (2002) for more information.CUNIT1 = 'm ' /meter CUNIT1 = 'km ' /kilometer CUNIT1 = 'Mm ' /megameter CUNIT1 = 'solRad ' /solar radius
The heliographic and helioprojective coordinate systems, however, are spherical in nature, and therefore are subject to the map projection formalism described in Calabretta & Greisen (2002). Some of the more common projections used are discussed below, although solar data can potentially be in any of the projections discussed in Calabretta & Greisen (2002).
One common observing method is where a solar image is focused onto a flat focal plane, such as a CCD detector. The data can then be described as being in helioprojective-cartesian coordinates. In this case, the gnomonic projection, or TAN, comes into play. The TAN projection has its native north pole at the reference pixel, and distance away from the pole increases as the tangent of the colatitude. Use of the TAN projection will place the following requirements on the WCS keywords:
The TAN projection can also be used with helioprojective-radial coordinates. The coordinate axes should be defined so that the associated parameter is locally increasing. There is, however, an ambiguity in the helioprojective-radial case when the reference pixel is disk center. At disk center,
- CRPIXj:
- Will express the pixel coordinates of the on-axis point. Often, the center of the array, or solar disk center, is a reasonable approximation.
- CDELTi:
- The detector plate scale at the reference pixel, in degrees.
- CTYPEi:
- The values for the
coordinate axes will be 'HPLN-TAN' and 'HPLT-TAN' respectively.
- CRVALi:
- The coordinates of the reference pixel, in degrees.
- LONPOLE:
- Normally 180
. See Calabretta & Greisen (2002) for a complete discussion.
We pay particular attention to the TAN projection in this paper, because we anticipate that it will be the workhorse projection for helioprojective coordinates. However, other projections can be used, depending on how the data were generated. For example, one would use a cylindrical projection for data resampled as a polar plot.
The heliographic coordinates of a solar image, e.g. from a CCD detector, can be described as a perspective zenithal projection, or AZP. The keywords in this case would be
- CRPIXj:
- Normally, the pixel coordinates of disk center, even if that's outside the array. (However, see Calabretta & Greisen (2002) for a discussion of slant zenithal projections.)
- CDELTi:
- The size of the reference pixel, in heliographic degrees. For the simple case where the reference pixel is disk center, this will be
times the helioprojective plate scale described in the previous section. At a distance of 1 AU, this renormalization factor is approximately 213.9. See Sect. 7.4.4 of Calabretta & Greisen (2002) for a more complete explanation.
- CTYPEi:
- The CTYPEi keyword for the longitude dimension will be either 'HGLN-AZP' or 'CRLN-AZP', depending on whether Stonyhurst or Carrington heliographic longitudes are used, while the value for the latitude dimension will be either 'HGLT-AZP' or 'CRLT-AZP' respectively.
- PVi_1:
- This keyword will contain the value
(note the minus sign), where i is the index of the latitude coordinate axis. At a distance of 1 AU, this is approximately -214.9.
- CRVALi:
- These will specify the latitude and longitude of the reference (disk center) pixel in degrees. Thus, together with the PVi_1 keyword, the information about the observer's position is complete.
- LONPOLE:
- Unless one is looking straight down along one of the poles, this should normally be 180
.
A special case of the AZP projection is when ![]() is large enough to
be considered to be infinitely far away. This is known as the SIN
projection and is implemented in FITS headers as follows:
is large enough to
be considered to be infinitely far away. This is known as the SIN
projection and is implemented in FITS headers as follows:
For most cases, the AZP projection is preferable to the SIN projection, but the latter can be a useful approximation when not all the information for the AZP projection is available.
- CRPIXj:
- The pixel coordinates of disk center, even if that's outside the array.
- CDELTi:
- The plate scale to be used for the SIN projection is
times the plate scale in solar radii per pixel.
- CTYPEi:
- The CTYPEi keyword for the longitude dimension will be either 'HGLN-SIN' or 'CRLN-SIN', while the value for the latitude dimension will be either 'HGLT-SIN' or 'CRLT-SIN' respectively.
- PVi_1:
- Set to 0, where i is the latitude axis.
- PVi_2:
- Set to 0, where i is the latitude axis.
- CRVALi:
- These will specify the latitude and longitude of the reference (disk center) pixel in degrees.
- LONPOLE:
- Same as for the AZP projection.
Cylindrical projections are well suited for synoptic maps, where observations are made over a period of time to build up a complete rotation's worth of data. Either Stonyhurst or Carrington heliographic coordinates can be used. The simplest kind of cylindrical projection is plate carrée (CAR), where both the longitude and latitude values are equally spaced in degrees. In order for the cylindrical axis to be aligned with the solar rotation axis, the reference pixel must be on the equator. Otherwise, the values of CRPIXj, CRVALi, and CDELTi are straightforward. The CTYPEi keyword for the longitude dimension will be either 'HGLN-CAR' or 'CRLN-CAR', while the value for the latitude dimension will be either 'HGLT-CAR' or 'CRLT-CAR' respectively. The default value of LONPOLE is zero.
We reserve the additional keyword CAR_ROT to associate the appropriate Carrington rotation number with the observation. For example, a synoptic map covering the period beginning on 2 September 1995 would have CAR_ROT = 1900. For a map containing data beginning within one Carrington rotation and ending within the next, the value of CAR_ROT will be associated with the reference pixel given by the CRPIXj keywords.
Care should be used in the formulation and use of synoptic maps, which are generally built up from data taken over a period of weeks. Because the Sun rotates differentially, the Carrington longitude of any feature will evolve over time, regardless of any evolution of the feature itself. The observation time will vary from one part of the map to another, and will depend on how the map was constructed. The general problem of mapping synoptic coordinates into instantaneous spatial coordinates is too complex for the present work. Synoptic map data providers are encouraged to document in the FITS header how the map was constructed.
Another use of the plate carrée projection is when making maps of the corona, where one axis is position angle, and the other is the radial distance from disk center. This can be naturally handled either as heliocentric coordinates in physical units (HCPA/SOLI), or as angular helioprojective-radial coordinates in the plate carrée projection (HRLN-CAR/HRLT-CAR).
Another commonly used projection for synoptic maps is cylindrical equal area (CEA), where the latitude pixels are equally spaced in the sine of the angle. In its simplest form, the keywords for the latitude axis i are
 |
Figure 4: Sample FITS header, demonstrating heliocentric-cartesian, helioprojective-cartesian, Stonyhurst heliographic, and helioprojective-radial coordinates for the same array. For simplicity, not all FITS keywords are shown. |
| Open with DEXTER | |
Figure 4 shows a sample header for a hypothetical instrument with a plate scale of 3.6 arcsec/pixel (0.001 degrees/pixel), observing from 1 AU. The detector is a 1024 ![]() 1024 CCD, with the Sun centered in the CCD.
Four different coordinate systems are shown: heliocentric-cartesian,
helioprojective-cartesian, Stonyhurst heliographic, and helioprojective-radial.
Note that the pixel scale for the heliographic coordinates is
1024 CCD, with the Sun centered in the CCD.
Four different coordinate systems are shown: heliocentric-cartesian,
helioprojective-cartesian, Stonyhurst heliographic, and helioprojective-radial.
Note that the pixel scale for the heliographic coordinates is
![]() times the pixel scale for the
helioprojective coordinates (see Sect. 5.2). The pixel scale for heliocentric-cartesian is in
solar radii based on a solar diameter of 0.533 degrees at 1 AU.
Although omitted in the FITS header here to save space, the default value of LONPOLE = 180
times the pixel scale for the
helioprojective coordinates (see Sect. 5.2). The pixel scale for heliocentric-cartesian is in
solar radii based on a solar diameter of 0.533 degrees at 1 AU.
Although omitted in the FITS header here to save space, the default value of LONPOLE = 180![]() is used in both the helioprojective and heliographic coordinate systems. In general, it's recommended that all keywords be included in the header, even when they take
default values.
is used in both the helioprojective and heliographic coordinate systems. In general, it's recommended that all keywords be included in the header, even when they take
default values.
As noted earlier, a special case of the use of the helioprojective-radial
coordinate system is when the reference pixel is disk center. This case is
illustrated
as section "C'' in Fig. 4.
Note that CDELT1C is the negative of the value CDELT1A shown in
Fig. 4, because the ![]() unit vector as defined points toward
the East limb. Consult Calabretta & Greisen (2002) for more information
about how the parameters are used to define the coordinate system.
unit vector as defined points toward
the East limb. Consult Calabretta & Greisen (2002) for more information
about how the parameters are used to define the coordinate system.
A more complicated example of helioprojective-radial coordinates
is demonstrated in Fig. 5. In this example, a scanning slit spectrometer,
operating in the extreme ultraviolet, is used to scan the corona. The slit is oriented
tangential to the limb, and is scanned outward along a radial at position angle -45![]() ,
starting at 18 arcmin (
,
starting at 18 arcmin (
![]() )
from disk center.
(For simplicity, we assume here that the radial steps go as the tangent of the
angle
)
from disk center.
(For simplicity, we assume here that the radial steps go as the tangent of the
angle
![]() ,
which may only be an approximation for a real
spectrograph. The projection to be used for any instrument will depend on its
design.) Note that the position angle
,
which may only be an approximation for a real
spectrograph. The projection to be used for any instrument will depend on its
design.) Note that the position angle ![]() is denoted as 'HRLN-TAN' because it
is here part of the helioprojective coordinate system. When used as part of a heliocentric coordinate system, it simply denoted as 'HCPA'. Note also
that
is denoted as 'HRLN-TAN' because it
is here part of the helioprojective coordinate system. When used as part of a heliocentric coordinate system, it simply denoted as 'HCPA'. Note also
that
![]() is used instead of
is used instead of
![]() ,
so the radial position is
given as
,
so the radial position is
given as
![]() rather than
rather than
![]() .
Although not included in
the FITS header, the default value of LONPOLE = 180
.
Although not included in
the FITS header, the default value of LONPOLE = 180![]() is used in
both helioprojective coordinate systems.
is used in
both helioprojective coordinate systems.
 |
Figure 5: Sample FITS header, demonstrating helioprojective-radial, and helioprojective-cartesian coordinates for the same array. See text for details. For simplicity, not all FITS keywords are shown. |
| Open with DEXTER | |
The following equations describe the conversion from one coordinate system into
another, and are intended to demonstrate the relationships between the
coordinate systems. Other coordinate conversions not shown below can be
derived from those shown. Where appropriate, the assumptions to be made when
one of the dimensions is missing is discussed. When converting between
heliocentric and helioprojective coordinates, if all three spatial dimensions
are not present, and no additional constraints (such as ![]() )
can
be applied, then the small angle approximation may be used instead. (See
Eqs. (4) and (6).)
)
can
be applied, then the small angle approximation may be used instead. (See
Eqs. (4) and (6).)
Between Stonyhurst heliographic and heliocentric-cartesian:
| x | = | ||
| y | = | (11) | |
| z | = |
| (12) | |||
Between heliocentric-cartesian and heliocentric-radial:
| (13) | |||
| z = z, |
| (14) | |||
| z = z. |
| x | = | ||
| y | = | (15) | |
| z | = |
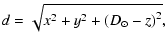 |
|||
| (16) | |||
| |
= | ||
| = | (17) | ||
| z | = |
| (18) | |||
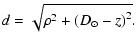 |
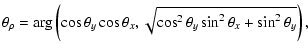 |
|||
| (19) | |||
| d = d, |
| (20) | |||
| d = d. |
The simplest relationship between the solar imaging coordinate systems
discussed above and the coordinate systems used in space physics is that
between Heliocentric Cartesian coordinates and Heliocentric Earth Equatorial
(HEEQ) coordinates (Hapgood 1992). In HEEQ coordinates, the
![]() axis is aligned with the solar North rotation pole, while the
axis is aligned with the solar North rotation pole, while the
![]() axis points toward the intersection between the solar equator
and the solar central meridian as seen from Earth. The conversion between
Heliocentric Cartesian (x,y,z) as seen from Earth, and Heliocentric Earth
Equatorial
axis points toward the intersection between the solar equator
and the solar central meridian as seen from Earth. The conversion between
Heliocentric Cartesian (x,y,z) as seen from Earth, and Heliocentric Earth
Equatorial
![]() is then
is then
| |
= | ||
| = | x, | (21) | |
| = |
| x | = | ||
| y | = | (22) | |
| z | = |
Solar astronomers have not traditionally used spherical trigonometry for image coordinates, except in the heliographic case. Instead, it's more common to work in pseudo-angles representing the plate scale of the instrument. These pseudo-angles vary as the tangent of the actual angles. This is identical to working in the gnomonic (TAN) projection. Close to the Sun, the pseudo-angles are approximately equal to their real angle counterparts. (From 1 AU, on the solar disk, they're the same to at least five significant figures.)
We define the pseudo-angles
![]() ,
,
![]() ,
and
,
and ![]() to be
the projection of a feature onto the z=0 plane, expressed as angles. Given
this definition,
the relationship between the pseudo-angle
to be
the projection of a feature onto the z=0 plane, expressed as angles. Given
this definition,
the relationship between the pseudo-angle
![]() and the actual angle
and the actual angle
![]() is fairly simple,
is fairly simple,
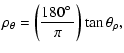 |
(23) | ||
| (24) |
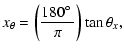 |
(25) | ||
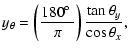 |
| |
= | (26) | |
| = | ![$\displaystyle \tan^{-1} \left[\left(\frac{\pi}{180\hbox{$^\circ$ }}\right)
\frac{y_\theta}{\sqrt{1+(\pi x_\theta/180\hbox{$^\circ$ })^2}} \right].$](/articles/aa/full/2006/14/aa4262-05/img130.gif) |
Although the conversion between pseudo-angles and true angles is not
necessarily simple, pseudo-angles are much easier to deal with than true
angles, and act more like heliocentric coordinates. For example, in
pseudo-angles, the relationships between helioprojective-cartesian and
helioprojective radial coordinates are the same as their heliocentric
counterparts:
| (28) | |||
| x' | = | ||
| y' | = | (29) | |
| = |
For a disk-centered solar telescope, using the TAN projection, the
pseudo-angles
![]() are equal to the intermediate coordinates
calculated from the FITS keywords if the spherical corrections of the TAN projection are not applied, e.g. as calculated by older non-WCS software. The
differences from the real angles
are equal to the intermediate coordinates
calculated from the FITS keywords if the spherical corrections of the TAN projection are not applied, e.g. as calculated by older non-WCS software. The
differences from the real angles
![]() scale as
scale as
![]() ,
and are about 7 milliseconds of arc at the limb, as seen from 1 AU. When the
telescope axis is not disk-centered, additional differences of comparable
magnitude will be incurred.
,
and are about 7 milliseconds of arc at the limb, as seen from 1 AU. When the
telescope axis is not disk-centered, additional differences of comparable
magnitude will be incurred.
The situation is somewhat different with helioprojective-radial coordinates
when the TAN projection is used near the Sun. Because of the high
level of curvature, one cannot simply calculate the intermediate coordinates
from CRPIXj, CRVALi, etc. Instead, one must either calculate
![]() using the full WCS spherical formalism, or calculate
using the full WCS spherical formalism, or calculate
![]() based on Eq. (27).
based on Eq. (27).
Over the last few years, an informal standard has been developing for solar image coordinates in FITS files, using the older FITS keywords rather than the newer WCS formalism. This system has the following characteristics:
Although we encourage the eventual adoption of a WCS-based system, FITS readers
should also be written to parse files using the older coordinate system
described above, as an implicit helioprojective-cartesian system. This format
is acceptable for simple two-dimensional solar images. FITS files using this
older system should include the keywords CRPIXj, CRVALi, CDELTi, CTYPEi, CUNITi, and optionally CROTAi if the
image is rotated. When CROTAi is included, then the conversion from
pixel coordinates (i,j) to spatial coordinates (x,y) should be done via the
following equations (Calabretta & Greisen 2002).
| |
= | ||
| x | = | (30) | |
| y | = |
| (31) | |||
| (32) | |||
Table 2: Comparison of the FITS coordinate keywords in the old and new system, for helioprojective-cartesian coordinates in the TAN projection. The phrase "exactly the same'' assumes that the same units are used in both cases. See Sect. 9.2 for a discussion of angular units. Although CUNITi did not appear in the original Wells et al. (1981) paper, it has been commonly used.
There has also recently been growing usage of some metadata keywords for solar
images, such as XCEN, YCEN, and ANGLE. Although these are
very useful keywords for cataloging sets of observations, they should never be considered as substitutes for the standard FITS coordinate system
keywords. However, these can also be incorporated by making the identifications
| |
= | ||
| = | |||
| = | (33) | ||
| = | |||
| = |
As mentioned earlier, some of the coordinate systems mentioned here are oriented with one of the coordinate axes pointing toward the observer. Therefore, information should be placed in the FITS header to specify the viewer's location. This is done by using the labels listed in Table 1 followed by the characters "_OBS''. Since there's no standard mechanism for specifying what units that the value of a keyword in the header takes, all distance keywords will have the units meters, while angular keywords are in degrees. In principal, any standard coordinate system could be used to specify the position of the observer, but it is recommended that at least the keywords DSUN_OBS, HGLN_OBS, and HGLT_OBS be included to specify the Stonyhurst heliographic coordinates of the observer. For example, a FITS header might include the lines
If the observer's position is not specified, then it should be assumed that the observation was made from Earth, or from low Earth orbit.DSUN_OBS= 1.507E+11 HGLN_OBS= 0.0 HGLT_OBS= 7.25
The observer's position can also be specified in any of the standard space physics coordinate systems (Russell 1971; Fränz & Harper 2002; Hapgood 1992). Table 3 lists these coordinate systems, together with their associated WCS labels. Like the other keywords discussed in this document, the observer's position would be specified in the header by appending the characters "_OBS'', e.g. HEQX_OBS, HEQY_OBS, HEQZ_OBS. In keeping with WCS standards, the values of these keywords would be in meters.
Table 3: Standard space physics coordinate systems from Russell (1971), Hapgood (1992), and Fränz & Harper (2002), together with their associated WCS labels for CTYPEi declarations.
It has long been standard in FITS files that angular measurements be expressed in degrees (Calabretta & Greisen 2002; Wells et al. 1981). However, it is also common in solar observations to express the coordinates in arcseconds from disk center. This possibility was presaged in Sect. 7.2, where helioprojective-cartesian pseudo-angles can be calculated from the FITS header parameters without resorting to spherical coordinate calculations, which is not the case for helioprojective-radial coordinates. Thus, only for the limited case where the coordinate axes are HPLN-TAN and HPLT-TAN, and where the coordinates are all relatively close to the Sun, it can be appropriate to express the coordinates in units other than degrees. Although strongly discouraged, the World Coordinate System (Greisen & Calabretta 2002) does allow for this possibility through the CUNITi keyword, which can take on the values given in Table 4. For example, if units of arcseconds is desired for a two dimensional image array, then this could be specified by setting
This allows for compatibility with other proposed standards for solar image data, which have generally called for coordinates to be expressed in arcseconds. Note that the value of the CUNITi keyword only applies to the keywords CRVALi, and CDELTi (or CDi_j). All other angular keywords, such as LONPOLE, CROTAi, etc., must be in degrees.CTYPE1 = 'HPLN-TAN' CUNIT1 = 'arcsec ' CTYPE2 = 'HPLT-TAN' CUNIT2 = 'arcsec '
Table 4: Alternate angular units.
The coordinate systems presented here have the following characteristics:

Although this proposal treats solar images as a spherical coordinate system, FITS files written in helioprojective-cartesian coordinates with the TAN projection are compatible with older non-WCS software to a high degree of accuracy. Also, files using the older non-WCS system can be treated as being implicitly helioprojective-cartesian with the TAN projection.
However, the spherical coordinate map projection capabilities of the World Coordinate System offer a large amount of flexibility in dealing with data which are not cast in straightforward Cartesian terms. With the appropriate map projections, one can handle not only images, but also synoptic maps in the heliographic system, and maps of the corona in radial distance and position angle.
Acknowledgements
I would like to thank Craig DeForrest for originally pointing out the need for this work, and Mark Calabretta for reviewing early drafts of the manuscript, and for helping with details concerning the World Coordinate System. Many others, too numerous to mention, have provided valuable comments. I would also like to thank the reviewer for many helpful comments which have made this a better paper. This work was supported by NASA Contract NAS5-32350.
Although a complete description of the specification of date and time in FITS files is beyond the scope of this document, we wish to bring the reader's attention to the revised specification for dates in FITS files, which was adopted by the IAU Fits Working Group (IAU-FWG) in November 1997 (Hanisch et al. 2001). This applies not only to the keyword DATE-OBS, but all keywords starting with the letters "DATE''. Such keywords can take one of two forms. When only the date is required, these keywords can take the form "CCYY-MM-DD'', where "CCYY'' is the century and year (i.e. the four-digit year), "MM'' is the two-digit month, and "DD'' is the two-digit day-of-month. For example,
The time can also be included, separated from the year by the letter "T''. In that case, the date keywords take the form "CCYY-MM-DDThh:mm:ss[.sss...]'', where "hh'', "mm'', and "ss'' are the hours, minutes, and seconds respectively, and where the seconds can be expanded to an arbitrary fraction. For example,DATE-OBS= '2000-03-27'
Unless otherwise specified, the dates and times are assumed to be in Coordinated Universal Time (UTC) (except for DATE itself, where no assumptions are made).DATE-OBS= '2000-03-27T22:01:41.123'
Before the IAU-FWG adopted the above convention, the SOHO project adopted a similar convention, using the keyword DATE_OBS in place of DATE-OBS to avoid conflict with the previous standard. Although the standard adopted by SOHO and later by the IAU-FWG are both ultimately based upon ISO-8601 (ISO 1988), the SOHO DATE_OBS keyword was based upon a recommendation by the Consultative Committee for Space Data Systems (CCSDS 1990) which was less restrictive than what the IAU-FWG finally adopted. The SOHO keyword differs from the IAU-FWG specification in the following ways:
The SOHO project adopted the non-standard DATE_OBS keyword to address Y2K issues which the FITS committees had not yet addressed, and to allow for the specification of time as well as date. Now that the FITS standard addresses these same issues, one should consider the SOHO DATE_OBS keyword to be deprecated in favor of the standard DATE-OBS keyword. For backwards compatibility, both forms are acceptable, but DATE-OBS is to be preferred.