A&A 449, 509-518 (2006)
DOI: 10.1051/0004-6361:20042190
S. Harfst1,2 - Ch. Theis1,3 - G. Hensler3
1 - Institut für Theoretische Physik und Astrophysik,
Universität Kiel, 24098 Kiel, Germany
2 - Centre for Astrophysics and Supercomputing, Swinburne
University, Hawthorn,
Victoria 3122, Australia
3 - Institut für Astronomie, Universität Wien,
Türkenschanzstr. 17, 1180 Wien, Austria
Received 15 October 2004 / Accepted 11 November 2005
Abstract
We present a new particle code for modelling the
evolution of galaxies. The code is based on a multi-phase
description for the interstellar medium (ISM). We include
star formation (SF), stellar feedback by massive stars and
planetary nebulae, phase transitions, and interactions between
gas clouds and ambient diffuse gas, namely condensation,
evaporation, drag, and energy dissipation. The last is
realised by radiative cooling and inelastic cloud-cloud
collisions. We present new schemes for SF and stellar
feedback that include a consistent calculation of the star-formation
efficiency (SFE) based on ISM properties, as well as
a detailed redistribution of the feedback energy into the
different ISM phases.
As a first test we show a model of the evolution of a present day Milky-Way-type galaxy.
Though the model exhibits a quasi-stationary behaviour in global properties like mass
fractions or surface densities, the evolution of the ISM is
strongly variable locally depending on the local SF and
stellar feedback. We start only with two distinct phases, but
a three-phase ISM is formed soon and consists of cold molecular
clouds, a warm gas disk, and a hot gaseous halo. Hot gas is
also found in bubbles in the disk accompanied by type II
supernovae explosions. The volume-filling factor of the
hot gas in the disk is ![]()
![]() .
The mass spectrum of the
clouds follows a power-law with an index of
.
The mass spectrum of the
clouds follows a power-law with an index of
![]() .
The star-formation rate (SFR) is
.
The star-formation rate (SFR) is ![]()
![]() on average, decreasing slowly with time due to gas
consumption. In order to maintain a constant SFR, gas
replenishment, e.g. by infall, of the order
on average, decreasing slowly with time due to gas
consumption. In order to maintain a constant SFR, gas
replenishment, e.g. by infall, of the order
![]() is required. Our model is in fair agreement with Kennicutt's
(1998, ApJ, 498, 541) SF law including the cut-off at
is required. Our model is in fair agreement with Kennicutt's
(1998, ApJ, 498, 541) SF law including the cut-off at ![]()
![]() .
Models with a constant SFE, i.e. no feedback on the SF, fail
to reproduce Kennicutt's law.
.
Models with a constant SFE, i.e. no feedback on the SF, fail
to reproduce Kennicutt's law.
We performed a parameter study varying the particle
resolution, feedback energy, cloud radius, SF time scale, and
metallicity. In most these cases the evolution of the model
galaxy was not significantly different to our reference
model. Increasing the feedback energy by a factor of 4-5 lowers the SF rate by
![]()
![]() ,
while decreasing
the metallicity by a factor of
,
while decreasing
the metallicity by a factor of ![]() 100 increases the mass
fraction of the hot gas from about 10% to 30%.
100 increases the mass
fraction of the hot gas from about 10% to 30%.
Key words: methods: N-body simulations - ISM: evolution - Galaxy: evolution - galaxies: ISM - galaxies: kinematics and dynamics
The treatment of the interstellar medium (ISM) is a crucial part in modelling galaxies due to the importance of dissipation, star formation (SF), and feedback. Single-phase TREE-SPH models suffer from over-cooling (Thacker et al. 2000; Pearce et al. 1999) because the multi-phase structure of the ISM is not resolved. As a result, baryonic matter loses angular momentum to the dark matter (DM) halos, and the disks formed in these simulations are too concentrated. Also, SF is overly efficient. On the other hand, a multi-phase ISM is a pre-requisite for the classical grid-based chemo-dynamical (CD) models (Burkert et al. 1992; Samland et al. 1997; Samland & Gerhard 2003; Theis et al. 1992), but they lack the geometrical flexibility of a (3d-)particle code.
An approach to including a multi-phase treatment of the ISM in a particle code has been presented by Semelin & Combes (2002), who combined smoothed particles hydrodynamics (SPH) with a sticky particle method (Noguchi 1988; Carlberg 1984; Combes & Gerin 1985; Palous et al. 1993; Theis & Hensler 1993). In their multi-phase ISM code, sticky particles are used to describe a cold, dense cloudy medium, while the diffuse ISM is modelled by SPH. Stars form from cold gas, and feedback processes include the heating of cold gas by supernovae and stellar mass loss (including metal enrichment). Cooling leads to a phase transition from warm to cold gas. The main advantage of this approach is the dynamical treatment of the cloud component: clouds are assumed to move on ballistic orbits and to dissipate kinetic energy in collisions.
The main purpose of this paper is to present a new extended TREE-SPH code with a multi-phase description of the ISM adopted from CD models. As in Semelin & Combes (2002), this is achieved by a combination of a sticky particle scheme and SPH. However, we use a different sticky particle scheme based on an individual treatment of single clouds. Advantages of this scheme are the build-up of a cloud mass spectrum, the individual handling of cloud collisions, and the localised treatment of phase transitions between clouds and the ambient diffuse gas. Furthermore, we apply a refined SF recipe suggested by Elmegreen & Efremov (1997, hereafter EE97). This scheme considers star formation within individual clouds including local feedback processes. As a result the star-formation efficiency is locally variable depending on the cloud mass and ambient ISM pressure.
A detailed description of the model including all the processes is given in Sect. 2. Details on the numerical treatment can be found in Sect. 3. The code is then applied to an isolated Milky-Way-type galaxy (Sect. 4), and the results (including a short parameter study) are discussed in Sect. 5. Conclusions and future applications of this code are finally presented in Sect. 6.
![\begin{figure}
\par\includegraphics[width=5.5cm,clip]{2190fig1.eps}\end{figure}](/articles/aa/full/2006/14/aa2190-04/Timg25.gif) |
Figure 1: The network of processes connecting the different gaseous and stellar components. Clouds are the sites of SF. Stars return mass and inject energy into the multi-phase ISM. The two gas phases exchange mass and momentum by means of condensation or evaporation (C/E) and drag. The energy dissipation is due to radiative cooling and cloud-cloud collisions. |
| Open with DEXTER | |
We use particles to describe all galactic components. Each particle is assigned a special type representing either stars, clouds, (diffuse) gas, or DM. The different components are connected by a network of processes including SF, stellar feedback, cooling, cloud-cloud collisions, condensation, evaporation, and drag, as shown schematically in Fig. 1.
Each star particle represents a cluster of stars formed at the same
time. The initial stellar mass distribution is given by the
multi-power law IMF of Kroupa et al. (1993) with the lower and upper
mass limits of
![]() and
and
![]() ,
respectively.
,
respectively.
The stellar life times (depending on stellar mass and metallicity) are
approximated according to Raiteri et al. (1996) to give reasonable fits to
the Padova evolutionary tracks (Bertelli et al. 1994; Alongi et al. 1993; Bressan et al. 1993) in the mass
range from
![]() to
to
![]() and for metallicities Z = 7
and for metallicities Z = 7 ![]() 10-5-0.03.
10-5-0.03.
We assume that stars with masses above
![]() end their lives as
type II supernovae (SNII), and stars from
end their lives as
type II supernovae (SNII), and stars from
![]() end as planetary
nebulae (PNe). The mass fractions of these stars are
end as planetary
nebulae (PNe). The mass fractions of these stars are ![]() and
and ![]() ,
respectively. The life times of the high mass stars range from
,
respectively. The life times of the high mass stars range from
![]() to
to
![]() .
The stellar feedback is described below.
.
The stellar feedback is described below.
The cloud particles describe a cold, clumpy phase of the ISM, i.e. the molecular clouds, which are also the sites of SF. The radius
![]() of an individual cloud is given by the following relation
based on observations (Rivolo & Solomon 1988):
of an individual cloud is given by the following relation
based on observations (Rivolo & Solomon 1988):
The giant molecular clouds represented by cloud particles consist of
gas at different densities and temperatures. Since we do not resolve
this structure, we do not define a temperature or pressure for
individual clouds. However, we assume that the clouds are influenced
by the pressure of the surrounding ISM (see
Sect. 2.6). Radiative cooling within clouds is not
taken into account. However, we allow for dissipation of kinetic
energy in cloud-cloud collisions using the dissipation scheme of
Theis & Hensler (1993). Two clouds undergo a complete inelastic collision if
they physically collide within the next time step. Additionally,
their orbital angular momentum must also be less than the break-up spin of
the final cloud, and the cloud mass must not exceed a critical mass
limit (here:
![]() ). In case of a sticky collision, the two cloud particles are replaced by one particle keeping the centre-of-mass data of the former two clouds.
). In case of a sticky collision, the two cloud particles are replaced by one particle keeping the centre-of-mass data of the former two clouds.
In a first approximation, the diffuse gas can be described as
continuous self-gravitating fluid. We model this component using an SPH approach. The gas is assumed to obey the ideal equation of state
with adiabatic index
![]() :
:
The diffuse gas can have temperatures from a few
![]() up to
several
up to
several
![]() .
In the following, we will also distinguish
between warm and hot gas, meaning gas at temperatures below or
above
.
In the following, we will also distinguish
between warm and hot gas, meaning gas at temperatures below or
above
![]() ,
respectively.
,
respectively.
In our code DM can be modelled either with particles (live halo) or as a static potential. In this work we focus on the late evolution of an isolated galaxy where a static DM potential is a reasonable approximation. We use the potential from Kuijken & Dubinski (1995), which is a flattened, isothermal potential with a core and a finite extent.
The ISM is treated as two dynamically independent gas phases. This
approach has been successfully applied in chemo-dynamical models
(Samland et al. 1997; Theis et al. 1992). The two gas phases are linked by the
processes of condensation/evaporation and a drag force. Following
Cowie et al. (1981), the mass exchange rate by condensation and evaporation
for an individual cloud particle is calculated from![]()
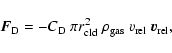 |
(5) |
The treatment of SF is usually based on the
Schmidt Law (Schmidt 1959)
Though the standard approach for SF works well for isolated galaxies, it has difficulties reproducing observations of interacting galaxies (Mihos et al. 1993,1992). Barnes (2004) suggested a second shock-induced SF mode, but this introduces another free parameter in the SF recipe.
| |
Figure 2: The SF scheme: (t0) inactive cloud (no SF); (t1) an embedded star cluster formed with a local SF efficiency; (t2) the cloud fragmented by SNII energy input. |
| Open with DEXTER | |
Different to such an approach, we apply a single SF law, but with a temporally and spatially variable SFE using a model suggested by EE97. They assign each molecular cloud an individual SFE controlled by the local ISM properties (mass of the molecular cloud, pressure of ambient diffuse gas) and the stellar feedback. According to EE97, the star formation is most efficient for massive clouds embedded in a high pressure ambient medium. A pre-requisite of using the EE97 SFE scheme is a multi-phase treatment of the ISM as proposed in this paper.
The main concept of our SF implementation is that stars form in clouds
and that clouds are destroyed by stellar feedback,
thereby self-regulating the SF (Fig. 2). Each cloud is
assumed to form stars only after a time of inactivity
![]() (t0 in Fig. 2), because not all gas in clouds is dense
or unstable enough for immediate SF. Once the SF process has started,
an embedded star cluster is formed (t1) instantaneously
(t0 in Fig. 2), because not all gas in clouds is dense
or unstable enough for immediate SF. Once the SF process has started,
an embedded star cluster is formed (t1) instantaneously![]() .
.
Following EE97 we use a variable SF efficiency ![]() depending on local properties of the ISM. A typical SFE (cloud mass
of
depending on local properties of the ISM. A typical SFE (cloud mass
of
![]() and pressure typical for solar vicinity) is
between 5% and 10% (see Fig. 4 in EE97). For details
of the implementation see Appendix A.
and pressure typical for solar vicinity) is
between 5% and 10% (see Fig. 4 in EE97). For details
of the implementation see Appendix A.
The only free parameter in our SF recipe is
![]() .
It can be
interpreted as a global SF time scale: assuming an SFE of
.
It can be
interpreted as a global SF time scale: assuming an SFE of
![]() ,
a total mass
,
a total mass
![]() in clouds of a few
in clouds of a few
![]() and
and
![]() of a few
of a few
![]() ,
we get a global
,
we get a global
![]() of
of ![]()
![]() .
.
Once the SFE has been determined, the energy released by SNII in
each time step can be computed from the chosen IMF and stellar life
times (Sect. 2.1). We assume
![]() for the energy released per SNII event.
for the energy released per SNII event.
This energy injection disrupts the cloud into smaller fragments (t2 in Fig. 2) leaving a new stellar particle. The time
for disruption
![]() (
=t2 - t1) is determined
from the energy input: in our model the energy input of the SNII
drives an expanding shell into the cloud, where the cloud mass
accumulates. The expansion of the SN shell can be
calculated from a self-similar solution (Brown et al. 1995; Theis et al. 1998). Assuming
a spherical cloud with a 1/r-density profile in agreement with the
mass-radius relation (Eq. (1)), we get
(
=t2 - t1) is determined
from the energy input: in our model the energy input of the SNII
drives an expanding shell into the cloud, where the cloud mass
accumulates. The expansion of the SN shell can be
calculated from a self-similar solution (Brown et al. 1995; Theis et al. 1998). Assuming
a spherical cloud with a 1/r-density profile in agreement with the
mass-radius relation (Eq. (1)), we get
It is assumed that the cloud is disrupted when the shell radius
reaches the cloud radius. The fragments are then placed symmetrically
on the shell with velocities corresponding to the expansion velocity
at
![]() .
The energy not consumed by cloud disruption, i.e. the energy of SNII exploding after
.
The energy not consumed by cloud disruption, i.e. the energy of SNII exploding after
![]() ,
is returned as thermal feedback to the hot gas phase.
Depending on cloud mass and SF efficiency, the fragmentation uses about 0.1-5% of the total SNII energy, of which
,
is returned as thermal feedback to the hot gas phase.
Depending on cloud mass and SF efficiency, the fragmentation uses about 0.1-5% of the total SNII energy, of which ![]()
![]() ends up as the kinetic energy of the fragments.
ends up as the kinetic energy of the fragments.
The mass returned by SNII is also added to the surrounding
gas. It is determined from the IMF and stellar life times assuming
that the mass ejected per SNII event
![]() is given by (Raiteri et al. 1996)
is given by (Raiteri et al. 1996)
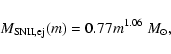 |
(9) |
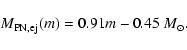 |
(10) |
In our code the gravitational force on a particle can be calculated as
a combination of the self-gravity of the N-body system and an external
force. External forces - if applied - usually mimic a static
dark-matter halo. Self-gravity is calculated using a tree scheme. We
have included two different tree schemes: the widely used one of
Barnes & Hut (1986) and a new tree algorithm proposed by Dehnen (2002). An advantage of the Dehnen-TREE is that it conserves momentum by construction. Additionally, an error control is included and the CPU scaling is basically linear with the number of particles. In our
implementation, the Dehnen-TREE is more than an order of magnitude
faster than the Barnes&Hut-TREE. Hence, we mainly apply the
Dehnen-TREE here. For easy comparison with other N-body solvers, we
realise gravitational softening by a Plummer potential with a softening length
![]() .
.
We used the SPH formalism to compute the hydrodynamics of the diffuse gas and a sticky particle scheme for the clouds. Details of our SPH implementation are given in Appendix B. The dynamics of the clouds are described by the sticky particle scheme of Theis & Hensler (1993), according to whom clouds move on ballistic orbits unless they undergo inelastic collisions. The treatment of cloud-cloud collisions is described in Sect. 2.2.
The time integration of the system is done with a leap-frog
scheme. Individual time steps are used for each particle. The time
step for an SPH particle p is chosen to satisfy a modified form of
the Courant condition (for details see Appendix B).
The time step of all other particles is based on dynamical criteria
calculated by
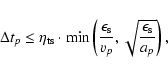 |
(11) |
The largest individual time step
![]() also defines the system
time step
also defines the system
time step
![]() ,
which is further limited not to exceed
,
which is further limited not to exceed
![]()
![]() .
Individual particle time steps are chosen to be a power-of-two subdivision of
.
Individual particle time steps are chosen to be a power-of-two subdivision of
![]() (Aarseth 1985).
(Aarseth 1985).
Several processes included in our model lead to an exchange of mass between particles or the creation or removal of particles. These processes are introduced in such a way that matter and momentum are conserved.
The mass exchange by condensation and evaporation is calculated
after each system time step
![]() .
The transferred mass
.
The transferred mass
![]() is added to the cloud. The same mass is subtracted from the surrounding SPH particles taking the weighting
from the kernel function into account. In addition, the
velocity of particles gaining mass (i.e. clouds in the case of
condensation and SPH particles for evaporation) is changed in
order to conserve momentum. The mass exchange from stars to SPH particles (SNII) and clouds (PNe) is done in a similar way.
is added to the cloud. The same mass is subtracted from the surrounding SPH particles taking the weighting
from the kernel function into account. In addition, the
velocity of particles gaining mass (i.e. clouds in the case of
condensation and SPH particles for evaporation) is changed in
order to conserve momentum. The mass exchange from stars to SPH particles (SNII) and clouds (PNe) is done in a similar way.
Whenever an SF process occurs, the star-forming cloud is removed from
the simulation. Instead a new star particle of the mass
![]() is added at the same position with the same velocity. Furthermore, the clouds formed in expanding shells are
created by adding four new cloud particles carrying the remaining
mass. Their positions and velocities are chosen according to
Eqs. (7) and (8) thereby conserving mass and momentum.
is added at the same position with the same velocity. Furthermore, the clouds formed in expanding shells are
created by adding four new cloud particles carrying the remaining
mass. Their positions and velocities are chosen according to
Eqs. (7) and (8) thereby conserving mass and momentum.
Our model allows particles to be created, merged and changed in
mass. A few constraints are used for the sake of numerical accuracy
and particle numbers. In order to prevent the formation of too many low mass star particles,
a lower mass limit
![]() and a lower
pressure limit
and a lower
pressure limit
![]() for SF are introduced.
The maximum mass for clouds is given by
for SF are introduced.
The maximum mass for clouds is given by
![]() (Sect. 2.2) but a lower mass limit for clouds
(Sect. 2.2) but a lower mass limit for clouds
![]() is also set to
is also set to
| (12) |
The SPH particles can change their mass due to condensation and
evaporation. An upper mass limit is introduced to avoid SPH particles
getting too massive. Whenever an SPH particle reaches this
limit, it is split into four new particles. The new equal mass
particles have the same center of mass, velocity, angular momentum, and
specific energy as the particle they replace. A lower mass limit
is also used where the mass of an SPH particle is distributed to the
neighbouring particles. The upper and lower mass limits are set to
![]() and
and
![]() ,
respectively, where
,
respectively, where
![]() is the SPH particle mass at the beginning of the simulation.
is the SPH particle mass at the beginning of the simulation.
We have tested our code thoroughly. Energy and angular momentum conservation is better than 1% for a pure N-body simulation following the evolution of a disk galaxy over many rotational periods. We tested our SPH implementation with the standard Evrard-test (Evrard 1988) and find that energy conservation is within 3%. In a full model, angular momentum is conserved within 3%.
A galaxy that is similar to the present-day Milky Way was set up using the galaxy-building package described by Kuijken & Dubinski (1995, hereafter KD95). The models of KD95 consist of three components: the baryonic disk and bulge and a DM halo. A distribution function for each component yields a unique density for a given potential. By solving the Boltzmann equation for the combined system, the galaxy can be set up in a self-consistent way. By construction these models are in virial equilibrium, and KD95 have also demonstrated that their models are stable over many rotation periods.
We choose model A of KD95 as a reference model
(Table 1). The scale length of the disk is
![]() ,
and the total mass of the galaxy is
2.47
,
and the total mass of the galaxy is
2.47 ![]()
![]() .
The mass and radius of the disk are set to
0.34
.
The mass and radius of the disk are set to
0.34 ![]()
![]() and
and
![]() .
The corresponding parameters
for the bulge are
.
The corresponding parameters
for the bulge are
![]() and
and
![]() and for the
DM halo
and for the
DM halo
![]() and
and
![]() ,
respectively. The
particle numbers for disk and bulge,
,
respectively. The
particle numbers for disk and bulge,
![]() and
and
![]() ,
are chosen to have particles of nearly equal mass. The
DM halo is added as a static potential. The disk is initially in
rotational equilibrium with a small fraction of disordered motion
superimposed. This results in a Toomre parameter
,
are chosen to have particles of nearly equal mass. The
DM halo is added as a static potential. The disk is initially in
rotational equilibrium with a small fraction of disordered motion
superimposed. This results in a Toomre parameter
![]() exceeding 1.9 all over the disk. Thus,
according to Polyachenko et al. (1997), the disk is stable against all axisymmetric
and non-axisymmetric perturbations.
exceeding 1.9 all over the disk. Thus,
according to Polyachenko et al. (1997), the disk is stable against all axisymmetric
and non-axisymmetric perturbations.
Table 1: Properties of the initial disk galaxy model.
A cloudy gas phase is added by treating every fifth particle from the
stellar disk as a cloud. The total mass in clouds is
![]()
![]()
![]() ,
and each cloud is randomly assigned a time of inactivity
,
and each cloud is randomly assigned a time of inactivity
![]() between 0 and
between 0 and
![]() .
Initially, all clouds have the same mass (
.
Initially, all clouds have the same mass (![]()
![]() ), but a mass spectrum is built up within the first Gyr of evolution.
), but a mass spectrum is built up within the first Gyr of evolution.
Finally, a diffuse gas component with a total mass of
![]()
![]()
![]() is added. This is more difficult
because no simple equilibrium state exists for this gas phase: it is
not only affected by the gravitational potential but also by cooling
and heating processes. The latter varies locally and temporally so
that the diffuse gas can only reach a dynamical equilibrium, as is also
revealed in high-resolution simulations of the ISM
(de Avillez & Breitschwerdt 2004). Testing different initial setups, it turned out to be most
efficient to start far from equilibrium (for the diffuse component only).
Then, the diffuse gas phase relaxes on a few dynamical
time scales to a quasi-equilibrium state. In detail, we started with a slowly rotating homogeneous gaseous halo with a radius of
is added. This is more difficult
because no simple equilibrium state exists for this gas phase: it is
not only affected by the gravitational potential but also by cooling
and heating processes. The latter varies locally and temporally so
that the diffuse gas can only reach a dynamical equilibrium, as is also
revealed in high-resolution simulations of the ISM
(de Avillez & Breitschwerdt 2004). Testing different initial setups, it turned out to be most
efficient to start far from equilibrium (for the diffuse component only).
Then, the diffuse gas phase relaxes on a few dynamical
time scales to a quasi-equilibrium state. In detail, we started with a slowly rotating homogeneous gaseous halo with a radius of
![]() and a temperature of
and a temperature of
![]() ,
which relaxed to a quasi-equilibrium within a few 100 Myr.
,
which relaxed to a quasi-equilibrium within a few 100 Myr.
Since we do not follow the chemical evolution of the galaxy, we apply
solar abundances where a metallicity is needed. In order to treat the
feedback of "old'' star particles, each star particle is assigned an age. For the bulge stars the age is
![]() and for disk stars
and for disk stars
![]() .
.
| |
Figure 3:
The evolution of stellar surface density
(at
|
| Open with DEXTER | |
| |
Figure 4:
The evolution of cloud surface density (at
|
| Open with DEXTER | |
Starting from these initial conditions, the galaxy model is evolved for
![]() with all processes switched on. After an initial phase (
with all processes switched on. After an initial phase (
![]() )
dominated by the collapse of the gaseous halo, the galaxy reaches a quasi-equilibrium defined by the interplay of the
gravitational potential, radiative cooling, heating by SNII, and
condensation and evaporation. When the equilibrium is reached, the
diffuse gas phase has formed a warm disk and a hot halo component.
Their mass ratio of about 7 remains nearly constant for the rest of
the simulation. The equilibrium state reached is almost
independent of the intial setup of the gas halo; i.e. the following
evolution is not influenced by our choice.
)
dominated by the collapse of the gaseous halo, the galaxy reaches a quasi-equilibrium defined by the interplay of the
gravitational potential, radiative cooling, heating by SNII, and
condensation and evaporation. When the equilibrium is reached, the
diffuse gas phase has formed a warm disk and a hot halo component.
Their mass ratio of about 7 remains nearly constant for the rest of
the simulation. The equilibrium state reached is almost
independent of the intial setup of the gas halo; i.e. the following
evolution is not influenced by our choice.
Snapshots of the evolution of the Milky Way model can be seen in
Figs. 3 to 6. The stellar surface density plots in
Fig. 3 demonstrate the stability of the disk during the
![]() evolution. Profiles of the surface density show that the
radial mass distribution does not change except for the central
evolution. Profiles of the surface density show that the
radial mass distribution does not change except for the central
![]() where the surface density is increased by up to a factor of 5, caused by the dissipation-induced infall of clouds that later form stars. Face-on views show weak transient spiral patterns, e.g. at
where the surface density is increased by up to a factor of 5, caused by the dissipation-induced infall of clouds that later form stars. Face-on views show weak transient spiral patterns, e.g. at
![]() .
Edge-on views reveal a thickening of the
disk. Throughout the disk the 95%-mass height
.
Edge-on views reveal a thickening of the
disk. Throughout the disk the 95%-mass height
![]() increases by 47% from
increases by 47% from
![]() to about
to about
![]() .
Only in the
central
.
Only in the
central
![]() can no thickening be seen.
can no thickening be seen.
![\begin{figure}
\par\includegraphics[angle=90,width=7.65cm,clip]{2190fig5.ps} \end{figure}](/articles/aa/full/2006/14/aa2190-04/Timg140.gif) |
Figure 5:
The of evolution of gas density (at
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=7.55cm,clip]{2190fig6.ps} \end{figure}](/articles/aa/full/2006/14/aa2190-04/Timg142.gif) |
Figure 6:
The evolution of gas temperature (at
|
| Open with DEXTER | |
The evolution of the cloudy phase (Fig. 4) is influenced by
dissipation and SF. The depletion of the cloudy medium by SF decreases
its mean surface density. Due to inelastic cloud-cloud collisions, the
clouds also show a less smooth distribution. As a consequence a mass
flow towards the centre increases its central surface density. The
radial profiles reveal that the surface density has decreased mostly
around
![]() ,
while it it almost unchanged beyond
,
while it it almost unchanged beyond
![]() .
The cloud
disk shows a thickening only outside of
.
The cloud
disk shows a thickening only outside of
![]() where the increase of
where the increase of
![]() is very similar to that of the stellar disk. Inside that radius no thickening can be seen. In fact, due to dissipation
is very similar to that of the stellar disk. Inside that radius no thickening can be seen. In fact, due to dissipation
![]() is even reduced inside
is even reduced inside
![]() by a factor of 2-3.
by a factor of 2-3.
The diffuse gas (Fig. 5) starts from a homogeneous
distribution that collapses in less than
![]() to form a disk. Initially, the gaseous disk is only a few kpc in diameter but it slowly grows in size. After
to form a disk. Initially, the gaseous disk is only a few kpc in diameter but it slowly grows in size. After
![]() it has reached a diameter of
it has reached a diameter of
![]() ,
while at 2 gyr the diameter is
,
while at 2 gyr the diameter is ![]()
![]() ,
which is comparable to
that of the stellar disk. At the same time the mass of the gaseous
disk is nearly constant. It has particle densities of
,
which is comparable to
that of the stellar disk. At the same time the mass of the gaseous
disk is nearly constant. It has particle densities of
![]() and temperatures (Fig. 6) of less than
and temperatures (Fig. 6) of less than
![]() .
Towards the centre the gas reaches higher temperatures of up to several
.
Towards the centre the gas reaches higher temperatures of up to several
![]() .
Some diffuse gas remains in the halo
at densities of
.
Some diffuse gas remains in the halo
at densities of ![]()
![]() and less, while its
temperature is in the range of
and less, while its
temperature is in the range of
![]() .
During the
initial collapse, the diffuse gas gains a significant amount of angular
momentum transferred from the clouds by the drag force. For this
reason the gaseous disk rotates with a rotation velocity of
.
During the
initial collapse, the diffuse gas gains a significant amount of angular
momentum transferred from the clouds by the drag force. For this
reason the gaseous disk rotates with a rotation velocity of
![]()
![]() .
Transient spiral patterns are also observed in the
gas disk. Stellar feedback induces the emergence of bubbles of hot gas. These bubbles have diameters of up to
.
Transient spiral patterns are also observed in the
gas disk. Stellar feedback induces the emergence of bubbles of hot gas. These bubbles have diameters of up to
![]() and they cool within a few
and they cool within a few
![]() .
The volume-filling factor of the hot gas (
.
The volume-filling factor of the hot gas (
![]() )
in the disk is 30-40%.
)
in the disk is 30-40%.
The velocity dispersion of the stars increases with time. At
![]() the heating rate is about
the heating rate is about
![]() ,
and it is nearly constant
over the whole disk. In order to see how much heating is caused by
unphysical two-body relaxation (which stems from the inability to
resolve individual stars numerically), we compared the result with a pure N-body simulation and found that the heating rate in our full model is about 30% higher than in the pure N-body calculation. The velocity dispersion of the clouds decreases at
,
and it is nearly constant
over the whole disk. In order to see how much heating is caused by
unphysical two-body relaxation (which stems from the inability to
resolve individual stars numerically), we compared the result with a pure N-body simulation and found that the heating rate in our full model is about 30% higher than in the pure N-body calculation. The velocity dispersion of the clouds decreases at
![]() due
to the energy dissipation by cloud-cloud collisions. As a result
younger stars are born with a smaller velocity dispersion. This means
that a part of the observed "heating'' in the age-velocity-relation
might indeed be due to cooling as suggested by Rocha-Pinto et al. (2004).
due
to the energy dissipation by cloud-cloud collisions. As a result
younger stars are born with a smaller velocity dispersion. This means
that a part of the observed "heating'' in the age-velocity-relation
might indeed be due to cooling as suggested by Rocha-Pinto et al. (2004).
![\begin{figure}
\par\includegraphics[angle=90,width=7.85cm,clip]{2190fig7.ps} \end{figure}](/articles/aa/full/2006/14/aa2190-04/Timg157.gif) |
Figure 7:
The evolution of the SFR with time (full line). The
SFR decreases with time due to consumption of cloud mass. The
average SFR (dashed line) is |
| Open with DEXTER | |
| |
Figure 8: The evolution of SF efficiency. SFE is up to 0.4 in the centre of the galaxy. The average over the whole disk is about 0.06. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=90,width=7.65cm,clip]{2190fig9.ps} \end{figure}](/articles/aa/full/2006/14/aa2190-04/Timg159.gif) |
Figure 9:
The open diamonds show the SFR per
|
| Open with DEXTER | |
The average SFR is ![]()
![]() (Fig. 7). Over the
(Fig. 7). Over the
![]() of evolution the SFR decreases slowly from
of evolution the SFR decreases slowly from ![]()
![]() to
to ![]()
![]() .
A simple analytic model
indicates that this is due to the consumption of the clouds. The mean SFE is roughly constant at a level of
.
A simple analytic model
indicates that this is due to the consumption of the clouds. The mean SFE is roughly constant at a level of
![]() .
The maximum values of the local SFE are highest in the centre with
.
The maximum values of the local SFE are highest in the centre with
![]() (Fig. 8). It can be seen in Fig. 9 that the SFR also compares well to a recent determination of the Schmidt law by Kennicutt (1998), who has also shown that the SF law in disk galaxies steepens abruptly below a threshold gas density of
(Fig. 8). It can be seen in Fig. 9 that the SFR also compares well to a recent determination of the Schmidt law by Kennicutt (1998), who has also shown that the SF law in disk galaxies steepens abruptly below a threshold gas density of
![]()
![]() .
We also find in our simulations that the SF law steepens for lower gas densities. This agrees with 1d CD models of the settling of a gas disk, which show a similar threshold for the formation of a thin disk (Burkert et al. 1992). Excluding the data below
.
We also find in our simulations that the SF law steepens for lower gas densities. This agrees with 1d CD models of the settling of a gas disk, which show a similar threshold for the formation of a thin disk (Burkert et al. 1992). Excluding the data below
![]() ,
we obtain a least-square fit of our data to Eq. (6) with
,
we obtain a least-square fit of our data to Eq. (6) with
![]()
![]() 0.1, which is in fair agreement with
0.1, which is in fair agreement with
![]()
![]() 0.15 of Kennicutt (1998).
0.15 of Kennicutt (1998).
The mass exchange by condensation and evaporation
reaches a quasi-equilibrium after ![]()
![]() .
Before, evaporation
is the dominant process due to the heating of the diffuse gas induced
by the initial collapse of this component. In the later evolution, the
condensation rate decreases from
.
Before, evaporation
is the dominant process due to the heating of the diffuse gas induced
by the initial collapse of this component. In the later evolution, the
condensation rate decreases from ![]()
![]() to
to
![]() .
The evaporation rate is slightly lower after
.
The evaporation rate is slightly lower after
![]() due to the decreasing SN rate, resulting in a reduced heating of the diffuse ISM.
due to the decreasing SN rate, resulting in a reduced heating of the diffuse ISM.
The total cloud mass slowly decreases, showing the depletion by SF. The total mass of the diffuse gas remains almost constant. A detailed look shows that more than half of the
diffuse gas (65%) is located in the disk (
![]() and
and
![]() ), while the rest is in the halo.
), while the rest is in the halo.
In the initial model all clouds have the same mass. However, due to fragmentation and coalescence, a stationary cloud mass spectrum is built up within
![]() (Fig. 10). This mass spectrum can be fitted by a power-law with index
(Fig. 10). This mass spectrum can be fitted by a power-law with index
![]() with an uncertainty of 0.2. Once the mass spectrum is established it remains unchanged until the end of the simulation.
with an uncertainty of 0.2. Once the mass spectrum is established it remains unchanged until the end of the simulation.
![\begin{figure}
\par\includegraphics[angle=90,width=8.1cm,clip]{2190fi10.ps} \end{figure}](/articles/aa/full/2006/14/aa2190-04/Timg172.gif) |
Figure 10:
The cloud mass spectrum. The different lines correspond to
the mass spectrum after
|
| Open with DEXTER | |
In the previous section we presented a model for a Milky-Way-type galaxy. Since our description depends on several phase transitions and exchange processes, we want to discuss their influence in this section, looking at SF, cloud mass spectrum, and metallicities.
The model has a number of parameters that can be chosen within the constraints of related observations or theory. We therefore performed simulations to investigate the influence of some of those parameters using the model presented in Sect. 4.2 as a reference. We find that most models do not deviate much from the reference model.
The mean SFR is ![]()
![]() in most models with a mean SF efficiency of
in most models with a mean SF efficiency of ![]()
![]() .
However, the SFR decreases in all models from a few to below one solar mass per year. Observations, on the other hand, reveal a much more constant SF history (Rocha-Pinto et al. 2000). The
decrease in the SFR can be reproduced in an analytic model taking the
depletion of the cloudy medium by SF into account. An explanation for
the discrepancy might be that our simulation does not include any
infall to sustain a constant SFR. An infall rate of the order of
.
However, the SFR decreases in all models from a few to below one solar mass per year. Observations, on the other hand, reveal a much more constant SF history (Rocha-Pinto et al. 2000). The
decrease in the SFR can be reproduced in an analytic model taking the
depletion of the cloudy medium by SF into account. An explanation for
the discrepancy might be that our simulation does not include any
infall to sustain a constant SFR. An infall rate of the order of
![]()
![]() would be sufficient for this, provided the
infalling gas can be used in the SF process. The necessary infall rate
could be provided by high velocity clouds (Wakker et al. 1999; Blitz et al. 1999).
would be sufficient for this, provided the
infalling gas can be used in the SF process. The necessary infall rate
could be provided by high velocity clouds (Wakker et al. 1999; Blitz et al. 1999).
The SF law agrees well with observations. Our data can be
fitted to Eq. (6) with
![]() ,
which is well
within the observed range of
n=1.4-2.0 (Kennicutt 1998; Wong & Blitz 2002; Boissier et al. 2003). It
should be noted that this result is widely independent of the choice
of our model parameters. Only models with a constant SF efficiency
show a different behaviour with n=1.2. Köppen et al. (1995) have shown that
stellar feedback leads to a self-regulated SF following a Schmidt-type
law, and our simulations confirm this result. We conclude that the
observed index n of the SF law is a consequence of the
self-regulation process that is enabled by allowing for a variable SFE.
,
which is well
within the observed range of
n=1.4-2.0 (Kennicutt 1998; Wong & Blitz 2002; Boissier et al. 2003). It
should be noted that this result is widely independent of the choice
of our model parameters. Only models with a constant SF efficiency
show a different behaviour with n=1.2. Köppen et al. (1995) have shown that
stellar feedback leads to a self-regulated SF following a Schmidt-type
law, and our simulations confirm this result. We conclude that the
observed index n of the SF law is a consequence of the
self-regulation process that is enabled by allowing for a variable SFE.
The cloud mass function in our reference model has a slope of
![]() .
In most observations the mass spectrum is shallower with
.
In most observations the mass spectrum is shallower with
![]() (e.g. Sanders et al. 1985), although there are a few observations
with higher values, e.g.
(e.g. Sanders et al. 1985), although there are a few observations
with higher values, e.g.
![]() (e.g. Brand & Wouterloot 1995). Taking the uncertainties in both our model and observations into account we are able to resolve the cloudy
phase of the ISM; i.e. each cloud particle in our simulation
represents an individual molecular cloud.
(e.g. Brand & Wouterloot 1995). Taking the uncertainties in both our model and observations into account we are able to resolve the cloudy
phase of the ISM; i.e. each cloud particle in our simulation
represents an individual molecular cloud.
Theoretical models of coagulation by Field & Saslaw (1965) also predict
![]() .
These models include a fragmentation by SF, but (different to
our model) SF occurs only when clouds reach a maximum mass. The
resulting fragments are then added to the lowest mass bin. In a more
similar model, which also takes a mass-radius relation
(Eq. (1)) into account, Elmegreen (1989) found a mass spectrum with
.
These models include a fragmentation by SF, but (different to
our model) SF occurs only when clouds reach a maximum mass. The
resulting fragments are then added to the lowest mass bin. In a more
similar model, which also takes a mass-radius relation
(Eq. (1)) into account, Elmegreen (1989) found a mass spectrum with
![]() ,
showing that our simulations can reproduce these results.
,
showing that our simulations can reproduce these results.
We compared two models with metallicities
![]() and
and
![]() .
The change of metallicity is only moderate and
does not affect the dynamical evolution of the galaxy
significantly. This result verifies that using a constant metallicity is a valid approximation on short time scales. Using a simple estimate we find that for
.
The change of metallicity is only moderate and
does not affect the dynamical evolution of the galaxy
significantly. This result verifies that using a constant metallicity is a valid approximation on short time scales. Using a simple estimate we find that for
![]() the expected
change in metallicity would be of the order
the expected
change in metallicity would be of the order
![]() ,
i.e. well within the range given by the two test models. Therefore, a model that includes stellar yields would not change
the results, as long as the late evolution (i.e. the last few Gyr) of
galaxies is simulated. However, stellar yields would have to be included
when the early formation stages are considered.
,
i.e. well within the range given by the two test models. Therefore, a model that includes stellar yields would not change
the results, as long as the late evolution (i.e. the last few Gyr) of
galaxies is simulated. However, stellar yields would have to be included
when the early formation stages are considered.
The ISM in our models can be divided into three phases: molecular
clouds and diffuse components that can be either warm or hot. The
total gas mass fraction after
![]() of evolution is about
of evolution is about ![]() in
all our models. The ratio of the mass of clouds to the mass of diffuse
gas is mainly determined by condensation and evaporation. If the
evaporation rate is higher, for example due to higher feedback energy,
this ratio is closer to unity. Between
in
all our models. The ratio of the mass of clouds to the mass of diffuse
gas is mainly determined by condensation and evaporation. If the
evaporation rate is higher, for example due to higher feedback energy,
this ratio is closer to unity. Between ![]() and
and ![]() of the diffuse gas is found
in the warm gaseous disk, while only
of the diffuse gas is found
in the warm gaseous disk, while only ![]()
![]() remain in the halo in a hot
gas phase. In the low-metallicity model this fraction is larger by a factor of 2 due to less efficient cooling. Samland & Gerhard (2003) have also presented a model of a disk galaxy, where the ratio of cloud and diffuse gas mass is 3, which is comparable to our results. They
also find a hot gaseous halo. In a similar calculation, Semelin & Combes (2002)
find equal masses in clouds and gas independent of the feedback energy,
but their models do not include phase transitions between the gas
phases by condensation and evaporation.
remain in the halo in a hot
gas phase. In the low-metallicity model this fraction is larger by a factor of 2 due to less efficient cooling. Samland & Gerhard (2003) have also presented a model of a disk galaxy, where the ratio of cloud and diffuse gas mass is 3, which is comparable to our results. They
also find a hot gaseous halo. In a similar calculation, Semelin & Combes (2002)
find equal masses in clouds and gas independent of the feedback energy,
but their models do not include phase transitions between the gas
phases by condensation and evaporation.
We found a filling factor f of 0.3-0.4 for the hot gas in the
disk. McKee & Ostriker (1977) predicted 0.7, a higher value, but our value agrees
better with the more recent findings of Norman & Ikeuchi (1989), who
predicted a filling factor of about 0.2. Furthermore, three-dimensional
simulations of a region of the galactic disk by de Avillez (2000)
show a filling factor for gas with
![]() of
of ![]() 0.4 in
good agreement with our results. We find an increase of 0.2 in f if the energy injection by SNII is higher by a factor 4, which is comparable to the results of de Avillez & Breitschwerdt (2004).
0.4 in
good agreement with our results. We find an increase of 0.2 in f if the energy injection by SNII is higher by a factor 4, which is comparable to the results of de Avillez & Breitschwerdt (2004).
One shortcoming in our treatment of the ISM is the lack of a detailed cooling below
![]() .
As a consequence, we do not allow clouds to form directly by thermal
instabilities. However, due to low mean densities and the turbulent
state of the diffuse gas, we expect the formation of clouds in
expanding SN shells (which is included) to be much more important.
Again, a more sophisticated treatment of thermal instabilities would
be required for modelling the early evolution of (gas rich) galaxies.
.
As a consequence, we do not allow clouds to form directly by thermal
instabilities. However, due to low mean densities and the turbulent
state of the diffuse gas, we expect the formation of clouds in
expanding SN shells (which is included) to be much more important.
Again, a more sophisticated treatment of thermal instabilities would
be required for modelling the early evolution of (gas rich) galaxies.
So far, in all presented models the DM halo is treated as a static potential. A static halo is reasonable for the case of the late evolution of an isolated galaxy. However, DM particles have to be used, e.g., for interacting galaxies or early galactic evolution. In one model we therefore used a DM halo made of particles in order to test how a live halo changes our results. The DM halo was modelled with 105 particles, thus DM particles are twice as massive as the initial masses of star particles. As expected we do not find significant changes in the evolution when using a live DM halo. The CPU-time needed in this run is higher by a factor of 2 (10 cpu-days instead of 5).
We have presented a new particle-based code for modelling the evolution of galaxies. In addition to the collisionless stellar and DM components, it incorporated a multi-phase description of the ISM combining standard SPH with a sticky particle method to describe diffuse warm/hot gas and cold molecular clouds, respectively. We included a new description for SF with a local SF efficiency, depending on the local pressure of the ISM and the mass of star-forming clouds. Stellar life times and an IMF are taken into account, along with SNII and PNe. The gas phases can mix by means of condensation and evaporation, and clouds are subject to a drag force.
We use this description to model
![]() of evolution for a Milky-Way-type galaxy. Overall, the evolution of our model galaxy is quite stable. Furthermore, a parameter study showed that the evolution does not change significantly when varying model parameters like
feedback energy, cloud radius, SF time scale or metallicity in a reasonable range.
of evolution for a Milky-Way-type galaxy. Overall, the evolution of our model galaxy is quite stable. Furthermore, a parameter study showed that the evolution does not change significantly when varying model parameters like
feedback energy, cloud radius, SF time scale or metallicity in a reasonable range.
Our models produced an SF law with an index n=1.7 that agrees well
with observations. For models with a constant SF efficiency ![]() ,
the index is with n=1.2 smaller than observations suggest. We
conclude, in agreement with Köppen et al. (1995), that the SF law is the
result of a self-regulation process enabled by our new
treatment of SF. The average SFR is also comparable to
observations. Over time the SFR decreases by a factor of 4-8 because
we have not included any gas infall. To get a more constant SFR, a gas
infall should be taken into account at a rate of
,
the index is with n=1.2 smaller than observations suggest. We
conclude, in agreement with Köppen et al. (1995), that the SF law is the
result of a self-regulation process enabled by our new
treatment of SF. The average SFR is also comparable to
observations. Over time the SFR decreases by a factor of 4-8 because
we have not included any gas infall. To get a more constant SFR, a gas
infall should be taken into account at a rate of
![]()
![]() .
The cloud mass spectrum in our models (with
.
The cloud mass spectrum in our models (with
![]() )
is a little bit steeper than most observations
suggest. Nonetheless, each cloud particle in our code essentially
represents an individual molecular cloud.
)
is a little bit steeper than most observations
suggest. Nonetheless, each cloud particle in our code essentially
represents an individual molecular cloud.
In all models most (85%) of the diffuse gas forms a warm (![]()
![]() )
rotating disk. A hot gaseous halo with temperatures of
)
rotating disk. A hot gaseous halo with temperatures of
![]() and densities of
and densities of
![]() has been built up. Hot gas is also found in the disk in bubbles accompanied by SNII. The filling factor of the hot disk gas is about 0.4, comparing well to observations as well as models of the ISM. This result could be used to find more realistic conditions for the initial model.
has been built up. Hot gas is also found in the disk in bubbles accompanied by SNII. The filling factor of the hot disk gas is about 0.4, comparing well to observations as well as models of the ISM. This result could be used to find more realistic conditions for the initial model.
In a next step we will apply our model to interacting galaxies in order to follow the evolution of the ISM and the SF history in perturbed galactic systems. The chemical evolution should be embedded to allow for a more detailed confrontation with observations.
Acknowledgements
The authors would like to thank P. Berczik for fruitful discussions and the anonymous referee for her/his helpful comments that improved this manuscript. We thank W. Dehnen (falcON), K. Kujken & J. Dubinski (GalactICS), and P. Teuben (NEMO) for making their software publicly available. This work was supported by the German Deutsche Forschungsgemeinschaft, DFG project number TH 511/2. S. Harfst is grateful for financial support from the Australian Department of Education, Science and Training (DEST).
Elmegreen & Efremov (1997) derived an implicit relation between cloud mass
![]() ,
pressure
,
pressure
![]() and SFE
and SFE ![]() (
(
![]() )
)
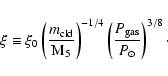 |
(A.3) |
In each SF event Eqs. (A.1) and (A.2) are solved
numerically to determine ![]() .
The resulting SFE is highest for
high-mass clouds in a high-pressure environment. Typical SFE are
between 5% and 10%.
.
The resulting SFE is highest for
high-mass clouds in a high-pressure environment. Typical SFE are
between 5% and 10%.
The idea of SPH is that a fluid is represented by N particles.
Any physical property A of the fluid at the position
![]() is evaluated by means of a locally weighted average:
is evaluated by means of a locally weighted average:
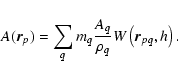 |
(B.1) |
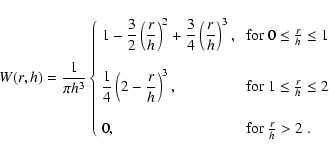 |
(B.2) |
The equation of motion of an SPH particle p is given by
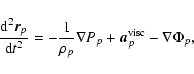 |
(B.3) |
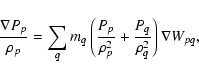 |
(B.4) |
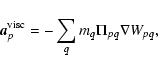 |
(B.5) |
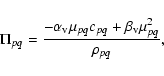 |
(B.6) |
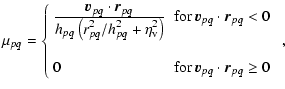 |
(B.7) |
The time integration is done by a leap-frog integrator.
Individual time steps are used for each particle. The time
step for an SPH particle p is chosen to satisfy a modified form of
the Courant condition as suggested by Monaghan (1992)
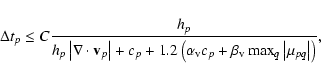 |
(B.9) |
Because cooling time scales are usually much shorter than the
dynamical times, impractically short time steps might occur.
Therefore, Eq. (B.8) is often solved semi-implicitly.
However, we chose a different approach: a fourth-order Runge-Kutta scheme is used to
integrate the cooling function beforehand with a sufficiently small
time step, and a look-up table with times and temperatures is
created. The number density
![]() is fixed to one value for this, but
cooling times scale linearly with
is fixed to one value for this, but
cooling times scale linearly with
![]() and can be easily
rescaled. Starting from a given temperature, the new temperature after
a (rescaled) time step is then simply looked up on the table. This
provides a fast way to compute the change in temperature, i.e. the
cooling rate, for any given temperature, density, and time step. The
cooling rate
and can be easily
rescaled. Starting from a given temperature, the new temperature after
a (rescaled) time step is then simply looked up on the table. This
provides a fast way to compute the change in temperature, i.e. the
cooling rate, for any given temperature, density, and time step. The
cooling rate ![]() for each particle is updated at each individual
time step.
for each particle is updated at each individual
time step.
A more detailed description of the SPH method can be found in Monaghan (1992).