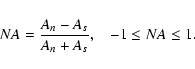A&A 449, L1-L4 (2006)
DOI: 10.1051/0004-6361:200600013

Phase asynchrony of the north-south sunspot activity

N. V. Zolotova - D. I. Ponyavin

Institute of Physics, Saint-Petersburg State University, Russia

Received 28 November 2005 / Accepted 24 January 2006

Abstract
Aims. Northern and Southern sunspot activities demonstrate striking synchronous behavior during a solar cycle. But sometimes synchronization fails and the north-south asymmetry occurs. The problem is the origin of the north-south asymmetry and its quasi-regular oscillations.
Methods. We employed Cross-Recurrence Plot analysis to extract synchronization between the Northern and Southern sunspot activities.
Results. By using Cross-Recurrence Plot technique and extracting line of synchronization we found that the north-south sunspot asymmetry is due to phase asynchrony between Northern and Southern hemispheric activities.

Key words: recurrence plots - sunspot areas - north-south asymmetry - synchronization

1 Introduction

Sunspots are the most famous and typical manifestations of solar activity. The widely known feature of the solar activity is the 11-year sunspot cycle.

Solar cycle appears near-synchronously in both hemispheres, but sometimes strange difference just occurs between the Northern and Southern sunspot activities. This is so called north-south asymmetry, which is a measure of such difference. Asymmetry can be calculated as difference between indices A_n and A_s of solar activity AA = A_n - A_s. This is definition of absolute asymmetry index. Newton & Milsom (1955) proposed a normalized measure of sunspot asymmetry:

$$NA =\frac{A_{n}-A_{s}}{A_{n}+A_{s}}, \hspace{0.3cm} -1 \leq NA \leq 1.$$ (1)

Swinson et al. (1986) reported northern excess of sunspot activity about two years after sunspot minimum. In addition they found a 22-yr periodicity in the normalized asymmetry (NA).

Carbonell et al. (1993) confirmed that the north-south asymmetry is a real feature of sunspot series and it can not be obtained from random distribution. Provided by them analysis revealed shift from south dominant at the end of 19th and the beginning of 20th centuries to north dominant during most of 20th century.

Verma (2000) applied normalized definition (NA) of sunspot asymmetry to analysis of sunspot areas, solar flares, sudden disappearing filaments, solar active prominences and others. He found that the north-south asymmetry has periodicity about 110 years. In addition he confirmed southern dominance in 22, 23 and 24 cycles as it was predicted by him earlier (Verma 1993).

Knaack et al. (2004) used Fourier and wavelet analysis to trace the temporal variations of the normalized north-south asymmetry (NA) in the magnetic flux and sunspot areas data sets. As a result there were obtained frequencies and corresponding periods for the north-south asymmetry.

However Ballester et al. (2005) had in doubt results of Knaack et al. since they used normalized index of asymmetry (NA). To avoid difficulties related with discrete Fourier transform they proposed to manipulate with time series generated by absolute measure (AA).

Recently Temmer et al. (2005) considered absolute index of the north-south asymmetry for sunspot numbers time series. They reported about near-autonomous evolution of each solar hemisphere and did not confirm a 22-yr magnetic cycle periodicity for absolute asymmetry (AA) as it was claimed by Swinson et al. (1986).

Until the present the asymmetry of sunspot activity is considered as the instantaneous dominance of one hemisphere over another. However, when viewing at the Sun it is often evident that sunspot activities in both hemispheres are shifted or delayed in time. In order to extract phase relationships between processes we need any measure that reflects shift and delay between time series.

This is difficult to do when viewing the absolute asymmetry index (AA) or normalized asymmetry index (NA), because these asymmetries reflect differences between instantaneous amplitudes of signals. Moreover analyzing these indices we can not distinguish amplitude from phase asymmetries.

Our paper is an attempt to extract phase asymmetry of the north-south solar activity using nonlinear approach.

2 Data and analysis

As a measure of solar activity historical data of sunspot areas for the Northern and Southern hemispheres were considered. We have analyzed monthly data from 1874 to 2004 year, obtained from the website of National Geophysical Data Center http://science.msfc.nasa.gov/ssl/pad/solar/sunspots.htm.

It is evident that the Sun demonstrates dissipative nonlinear behavior. Linear analysis (correlations, linear regressions, discrete Fourier transforms and etc.) is oriented toward finding linear relationships between multivariate data. When we analyze real-world processes linear approach often generates artifacts.

We have used a novel nonlinear technique to analyze multivariate time series. This is Recurrence Plot (RP) and Cross-Recurrence Plot (CRP) methodology. RP analysis was first proposed by Eckmann et al. (1987), developed later by Zbilut (1998), Marwan & Kurths (2002,2005). We have used CRP Toolbox of Marwan (http://www.agnld.uni-potsdam.de/~marwan/toolbox/), where mathematical definition of RP is:

 

$$\mbox{{\vec R}}_{i,j}^{m,\varepsilon_{i}}=\Theta(\varepsilon_{i}-\Vert{\vec x}_{i}-{\vec x}_{j}\Vert),$$

$${\vec x}_{i} \in\Re^{m}, \hspace{0.3cm} i,j=1,\ldots,N,$$ (2)

where N is number of considered states x_i; $\varepsilon_{i}$ is threshold distance, $\Vert\cdot\Vert$ is norm (e.g. the Euclidian norm), and $\Theta$ is the Heaviside function.

Visually RP is a graphical pattern of matrix $N \times N$, all elements of which either zero (white points of RP) or one (black points of RP). ${\vec R}_{i,j}$ equal one, if point j in phase space is located in predefined neighbourhood $\varepsilon$ of point i, otherwise ${\vec R}_{i,j}$ equal zero. Main diagonal is defined by values ${\vec R}_{i,i}$ always consists of ones ( ${\vec R}_{i,i} = 1$, $i = 1,\ldots,N$). For this reason it is called line of identity. Extension of RP is Cross-Recurrence Plot (Figs. 1g, h). In this case two time series (i=1,..., N_x) ( $j=1,\ldots,N_{y}$) are considered in the same phase space. Commonly $N_{x} \neq N_{y}$, then CRP is non-square matrix:

 

$$\mbox{{\bf CR}}_{i,j}^{m,\varepsilon_{i}} =\Theta(\varepsilon_{i}-\Vert{\vec x}_{i}-{\vec x}_{j}\Vert),$$

$${\vec x}_{i}, {\vec y}_{i} \in \Re^{m}, \hspace{0.3cm} i = 1,\ldots, N_{x}, j = 1,\ldots,N_{y}.$$ (3)

Depending on kind of relationships between time series the main diagonal can be broken, curved or even vanished. For this reason line of identity is replaced by line of synchronization - LOS (Figs. 1g, h). LOS contains information about temporal and amplitude shifts, time-reversions and can trace even small and smooth phase variations.

To demonstrate how informative is LOS we have tested algorithm with using three sinusoidal functions $f_{1}= \sin~(\omega_{1}t_{1}), f_{2}=\sin~(\omega_{1}t_{1} + \varphi), f_{3}=\sin~(\omega_{2}t_{1})$. We have specially considered examples without amplitude differences between time series but only shift (Fig. 1c) or difference of frequencies (Fig. 1d).

Figure 1: a) Normalized asymmetry index (NA) for f1, f2. b) The same for f1, f3. c) Sinusoidal functions $f_{1}=\sin~(\omega_{1}t_{1})$ - black curve, $f_{2}=\sin~(\omega_{1}t_{1} + \varphi$) - gray curve. d) Sinusoidal functions $f_{1}=\sin~(\omega_{1}t_{1})$- black curve, $f_{3}=\sin~(\omega_{2}t_{1})$ - gray curve. e) Line of Synchronization (LOS) extracted from Cross-Recurrence Plots for f1, f2. f) The same for f1, f3. g) Cross-Recurrence Plot for f1, f2. Thick line is Line of Synchronization. h) The same for f1, f3.

Open with DEXTER

Plots of normalized asymmetry indices are presented in Figs. 1a, b. It is easy to see that NA reveals local amplitude differences. Even in such simple cases NA measure has sufficiently complex behaviour hiding information about phase relationships. It is quite evident that NA behavior will be more fanciful in case of the real data analysis.

Recurrence plots are used to reveal non-stationarity of a series as well as to indicate the degree of aperiodicity. RP are two-dimensional representations of high dimensional phase space trajectories (Figs. 1g, h). Diagonal lines in the recurrent patterns display synchronization of time series. If diagonal line is parallel to main diagonal (from lower-left to upper-right corner), time series are synchronized in shifting time (Fig. 1g). Those diagonal lines directed from lower-right to upper-left give evidence of time-reversed processes. If diagonal lines lie angularly to the main diagonal, there is frequency difference or delay in time (Fig. 1h).

Figures 1e, f display LOS extracted from CRP analysis. By means of them it is possible recognize the value of constant shift (Fig. 1g) or value of frequency difference $\omega_{2}=2\omega_{1}$ (Fig. 1h), and which of time series lead.

In the more common nonstationary case, the local slope of LOS changes, revealing phase variations (Marwan & Kurths 2005).

It is evident that the NA and LOS measures differ significantly: whereas NA is a quantitative measure of amplitude differences, the LOS is a measure of phase synchronization. That is a reason why NA and LOS do not have cross-correlate.

Figure 2: a) Normalized asymmetry index (thin gray curve) for monthly sunspot areas for Northern and Southern hemispheres. Bold black curve is one-year moving average versus time. b) Black curve is one-year moving average of monthly mean sunspot areas for Northern hemisphere. The same but gray color is for Southern hemisphere. c) Line of Synchronization extracted from the Cross-Recurrence Plot. d) Cross-Recurrence Plot of monthly sunspot areas of Northern and Southern hemispheres with following parameters: dimension: 1; delay: 1; threshold: 10%, fixed amount of neighbors.

Open with DEXTER

3 Results and discussion

We early demonstrated that CRP technique can be applied to nonlinear analysis of sunspot activity (Ponyavin & Zolotova 2004). In the present paper we extract the LOS from recurrence plots as a measure of phase asynchrony between solar hemispheres.

In this work we have used monthly means of sunspot areas for the Northern and Southern hemispheres from 1874 to 2004. Figure 2b shows moving one-year averages: black curve corresponding to Northern hemisphere and gray curve - to Southern hemisphere.

The CRP is displayed in Fig. 2d. Black solid line is line of synchronization. LOS lies practically near the main diagonal, marking the high level of synchronization between time series. The noise around the plot reveals stochastic component existed in the sunspot data. Quasi 11-year periodicity is evident at the CRP panel demonstrating slight similarities of the solar cycles.

Figure 2c illustrates the LOS extracted from CRP analysis. At the top panel of the figure plot of the normalized asymmetry index (thin gray curve) and its moving one-year average are displayed (bold black curve).

Using sunspot areas (Fig. 2b) it is possible to determine leading hemisphere even by eye. However, NA plot does not reflect a phase asymmetry. This is especially clear during the transition from the 19th to 20th cycle, where NA $\geq$ 0 on the interval from middle of the 19th cycle to the middle of 20th cycle. Behaviour of the LOS has qualitatively another character than NA. Here change of sign reflects change of leading role between the Northern and Southern hemispheres. LOS $\geq$ 0 means the north leading, LOS $\leq$ 0 means the south leading. Between the 19th and 20th cycles LOS exhibits remarkable change from the negative to positive value. It corresponds to delay in the beginning of sunspot activity for Southern hemisphere with respect to the Northern hemisphere. Moreover asynchronization in this period is the highest (up to 3 years).

As it was mentioned above LOS and NA do not have to correlate. For example, from about 1935 to 1965 year LOS $\leq$ 0, however NA demonstrates many reversals of its sign. It means that when one of the processes leads in phase, that is not the same for amplitude leading.

Within the whole analyzed period (130 years) the LOS demonstrates non-random quasi-regular behavior. Due to the phase asyncronization the north-south asymmetry of sunspot activity is observed. Thus we have new measure, which reveals the origin of sunspot asymmetry.

4 Conclusions

We have examined sunspot activity with using monthly sunspot areas from 1874 to 2004 respectively for Northernand Southern hemispheres. We infer, that classical definition of asymmetry shows instantaneous amplitude dominance of Northern hemisphere over Southern and vice versa. The normalized asymmetry is uselessness in determining phase relationships between time series.

For this reason we have carried out nonlinear Cross-Recurrence Plot analysis with a view to recover the line of synchronization. Analysis of LOS demonstrates phase relationships between time series. Applying to the sunspot data the LOS reveals the leading role of hemispheres in sunspot activities. Moreover LOS exhibits non-random quasi-regular behavior.

The biggest deviations of LOS from the mean occur between the 19th and 20th cycles. During this time the north-south asymmetry shows its maximum. LOS has remarkable change of sign, thereby emphasizing the alteration of the north-south sunspot asymmetry and asynchrony. Asynchronization in this period is the highest: more than 3 years.

To conclude such nonlinear approach allows us to determine asymmetry of Northern and Southern sunspot activities as effect of phase asynchronization.

References

• Ballester, J. L., Oliver, R., & Carbonell, M. 2005, A&A, 431, L5 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Carbonell, M., Oliver, R., & Ballester, J. L. 1993, A&A, 274, 497 [NASA ADS] (In the text)
• Eckmann, J.-P., Kamphorst, S. O., & Ruelle, D. 1987, Europhys. Lett., 4, 973 [NASA ADS] (In the text)
• Knaack, R., Stenflo, J. O., & Berdyugina, S. V. 2004, A&A, 418, L17 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Marwan, N., & Kurths, J. 2002, Phys. Lett. A, 302, 299 [NASA ADS] [CrossRef] (In the text)
• Marwan., N., & Kurths, J. 2005, Phys. Lett. A, 336, 349 [NASA ADS] [CrossRef]
• Newton, H. W., & Milsom, A. S. 1955, MNRAS, 115, 398 [NASA ADS] (In the text)
• Ponyavin, D. I., & Zolotova, N. V. 2004, in Multi-Wavelength Investigations of Solar Activity, ed. A. V. Stepanov, E. E. Benevolenskaya, & A. G. Kosovichev (Cambridge Univ. Press), Proc. IAU, 223, 141 (In the text)
• Swinson, D. B., Koyama, H., & Saito, T. 1986, Sol. Phys., 106, 35 [NASA ADS] [CrossRef] (In the text)
• Temmer, M., Ryb $\acute{\rm a}$k, J., Bend $\acute{\rm\i}$k, P., et al. 2005, A&A, in press (In the text)
• Verma, V. K. 1993, ApJ, 403, 797 [NASA ADS] [CrossRef] (In the text)
• Verma, V. K. 2000, JApA, 21, 173 [NASA ADS] (In the text)
• Zbilut, J. P., Giulian, A., & Webber Jr., C. L. 1998, Phys. Lett. A, 246, 122 [NASA ADS] [CrossRef] (In the text)