A&A 449, 223-242 (2006)
DOI: 10.1051/0004-6361:20054279
A detailed spectral and morphological study of the gamma-ray
supernova remnant RX J1713.7-3946 with HESS
F. Aharonian1 - A. G. Akhperjanian2 - A. R. Bazer-Bachi3 - M. Beilicke4 - W. Benbow1 - D. Berge1 - K. Bernlöhr1,5 - C. Boisson6 - O. Bolz1 - V. Borrel3 - I. Braun1 - F. Breitling5 - A. M. Brown7 - P. M. Chadwick7 - L.-M. Chounet8 - R. Cornils4 - L. Costamante1,20 - B. Degrange8 - H. J. Dickinson7 - A. Djannati-Ataï9 - L. O'C. Drury10 - G. Dubus8 - D. Emmanoulopoulos11 - P. Espigat9 - F. Feinstein12 - G. Fontaine8 - Y. Fuchs13 - S. Funk1 - Y. A. Gallant12 - B. Giebels8 - J. F. Glicenstein14 - P. Goret14 - C. Hadjichristidis7 - D. Hauser1 - M. Hauser11 - G. Heinzelmann4 - G. Henri13 - G. Hermann1 - J. A. Hinton1,11 - W. Hofmann1 - M. Holleran15 - D. Horns1 - A. Jacholkowska12 - O. C. de Jager15 - B. Khélifi1 - S. Klages1 - Nu. Komin5 - A. Konopelko5 - I. J. Latham7 - R. Le Gallou7 - A. Lemière9 - M. Lemoine-Goumard8 - T. Lohse5 - J. M. Martin6 - O. Martineau-Huynh16 - A. Marcowith3 - C. Masterson1,20 - T. J. L. McComb7 - M. de Naurois16 - D. Nedbal17 - S. J. Nolan7 - A. Noutsos7 - K. J. Orford7 - J. L. Osborne7 - M. Ouchrif16,20 - M. Panter1 - G. Pelletier13 - S. Pita9 - G. Pühlhofer11 - M. Punch9 - B. C. Raubenheimer15 - M. Raue4 - S. M. Rayner7 - A. Reimer18 - O. Reimer18 - J. Ripken4 - L. Rob17 - L. Rolland16 - G. Rowell1 - V. Sahakian2 - L. Saugé13 - S. Schlenker5 - R. Schlickeiser18 - C. Schuster18 - U. Schwanke5 - M. Siewert18 - H. Sol6 - D. Spangler7 - R. Steenkamp19 - C. Stegmann5 - G. Superina8 - J.-P. Tavernet16 - R. Terrier9 - C. G. Théoret9 - M. Tluczykont8,20 - C. van Eldik1 - G. Vasileiadis12 - C. Venter15 - P. Vincent16 - H. J. Völk1 - S. J. Wagner11
1 - Max-Planck-Institut für Kernphysik, PO Box 103980, 69029
Heidelberg, Germany
2 -
Yerevan Physics Institute, 2 Alikhanian Brothers St., 375036 Yerevan,
Armenia
3 -
Centre d'Étude Spatiale des Rayonnements, CNRS/UPS, 9 Av. du Colonel Roche, BP
4346, 31029 Toulouse Cedex 4, France
4 -
Universität Hamburg, Institut für Experimentalphysik, Luruper Chaussee
149, 22761 Hamburg, Germany
5 -
Institut für Physik, Humboldt-Universität zu Berlin, Newtonstr. 15,
12489 Berlin, Germany
6 -
LUTH, UMR 8102 du CNRS, Observatoire de Paris, Section de Meudon, 92195 Meudon Cedex,
France
7 -
University of Durham, Department of Physics, South Road, Durham DH1 3LE,
UK
8 -
Laboratoire Leprince-Ringuet, IN2P3/CNRS, École Polytechnique, 91128 Palaiseau, France
9 -
APC, 11 place Marcelin Berthelot, 75231 Paris Cedex 05, France
![[*]](/icons/foot_motif.gif)
10 -
Dublin Institute for Advanced Studies, 5 Merrion Square, Dublin 2,
Ireland
11 -
Landessternwarte, Königstuhl, 69117 Heidelberg, Germany
12 -
Laboratoire de Physique Théorique et Astroparticules, IN2P3/CNRS,
Université Montpellier II, CC 70, Place Eugène Bataillon, 34095
Montpellier Cedex 5, France
13 -
Laboratoire d'Astrophysique de Grenoble, INSU/CNRS, Université Joseph Fourier, BP
53, 38041 Grenoble Cedex 9, France
14 -
DAPNIA/DSM/CEA, CE Saclay, 91191 Gif-sur-Yvette Cedex, France
15 -
Unit for Space Physics, North-West University, Potchefstroom 2520,
South Africa
16 -
Laboratoire de Physique Nucléaire et de Hautes Énergies, IN2P3/CNRS, Universités
Paris VI & VII, 4 place Jussieu, 75252 Paris Cedex 5, France
17 -
Institute of Particle and Nuclear Physics, Charles University,
V Holesovickach 2, 180 00 Prague 8, Czech Republic
18 -
Institut für Theoretische Physik, Lehrstuhl IV: Weltraum und
Astrophysik, Ruhr-Universität Bochum, 44780 Bochum, Germany
19 -
University of Namibia, Private Bag 13301, Windhoek, Namibia
20 -
European Associated Laboratory for Gamma-Ray Astronomy, jointly
supported by CNRS and MPG
Received 29 September 2005 / Accepted 12 November 2005
Abstract
Aims. We present results from deep observations of the Galactic shell-type supernova remnant (SNR) RX J1713.7-3946 (also known as G347.3-0.5) conducted with the complete HESS array in 2004.
Methods. Detailed morphological and spatially resolved spectral studies reveal the very-high-energy (VHE - Energies
E > 100 GeV) gamma-ray aspects of this object with unprecedented precision. Since this is the first in-depth analysis of an extended VHE gamma-ray source, we present a thorough discussion of our methodology and investigations of possible sources of systematic errors.
Results. Gamma rays are detected throughout the whole SNR. The emission is found to resemble a shell structure with increased fluxes from the western and northwestern parts. The differential gamma-ray spectrum of the whole SNR is measured over more than two orders of magnitude, from 190 GeV to 40 TeV, and is rather hard with indications for a deviation from a pure power law at high energies. Spectra have also been determined for spatially separated regions of RX J1713.7-3946. The flux values vary by more than a factor of two, but no significant change in spectral shape is found. There is a striking correlation between the X-ray and the gamma-ray image. Radial profiles in both wavelength regimes reveal the same shape almost everywhere in the region of the SNR.
Conclusions. The VHE gamma-ray emission of RX J1713.7-3946 is phenomenologically discussed for two scenarios, one where the gamma rays are produced by VHE electrons via Inverse Compton scattering and one where the gamma rays are due to neutral pion decay from proton-proton interactions. In conjunction with multi-wavelength considerations, the latter case is favoured. However, no decisive conclusions can yet be drawn regarding the parent particle population dominantly responsible for the gamma-ray emission from RX J1713.7-3946.
Key words: acceleration of particles - ISM: cosmic rays - gamma rays:
observations - ISM: supernova remnants - ISM: individual objects: RX J1713.7-3946
(G347.3-0.5)
It is commonly believed that the only sources capable of supplying
enough energy output to power the flux of Galactic cosmic rays are
supernova explosions (e.g., Ginzburg & Syrovatskii 1964). At the present time
there are two main arguments for this hypothesis: firstly, estimates
of the power required to sustain the observed nuclear Galactic
cosmic-ray population show that about 10% of the mechanical energy
released by the population of Galactic supernovae would suffice, or,
in other words, that supernova remnants could be the sources of the
Galactic cosmic rays if the average acceleration efficiency in a remnant is about 10%. Secondly, a rather well developed theoretical framework for the acceleration mechanism, diffusive shock
acceleration (for reviews see e.g., Malkov & O'C Drury 2001; Blandford & Eichler 1987; Jones & Ellison 1991), exists and it indeed predicts acceleration efficiencies in excess of 10%.
The best way of proving unequivocally the existence of
very-high-energy (VHE) particles, electrons or hadrons, in the
shells of supernova remnants (SNRs) is the detection of VHE (about
100 GeV up to a few tens of TeV) gamma rays produced either via
Inverse Compton (IC) scattering of VHE electrons off ambient photons
or in interactions of nucleonic cosmic rays with ambient matter. As
was argued already in Drury et al. (1994), a system of imaging atmospheric
Cherenkov telescopes with a large field of view provides the most
powerful measurement technique for extended nearby SNRs at these
very high energies. One should note that there exist two other
experimental approaches to trace VHE cosmic rays, the detection of
X-rays, which suggests the presence of VHE electrons (Koyama et al. 1995), and of high-energy neutrinos, which probe exclusively nuclear particles.
A prime candidate for gamma-ray observations is the SNR RX J1713.7-3946, in
particular because of its close association with dense molecular
clouds along the line of sight (Fukui et al. 2003; Moriguchi et al. 2005),
which might suggest a scenario of a supernova shell overtaking dense
molecular clouds, leading to a detectable VHE gamma-ray signal from
hadronic interactions, as described in Aharonian et al. (1994). RX J1713.7-3946, situated
in the Galactic plane, constellation Scorpius, was discovered in
soft X-rays in 1996 in the ROSAT all-sky
survey (Pfeffermann & Aschenbach 1996). It is roughly
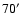 in diameter
and exhibits bright X-ray emission dominantly from its western
shell. ASCA observations revealed that the X-ray emission is a pure
non-thermal continuum without detectable line
emission (Koyama et al. 1997; Slane et al. 1999). X-ray observations have also been
conducted with Chandra and XMM with their superior angular
resolution. Chandra observed a small region in the bright
northwestern part of the
SNR (Lazendic et al. 2004; Uchiyama et al. 2003). Despite distinct brightness
variations within this small field, the corresponding X-ray spectra
were all found to be well described by power-law models with similar
absorbing column densities and photon indices, albeit with rather
large statistical uncertainties. XMM covered the remnant almost
completely in five pointings (Cassam-Chenaï et al. 2004; Hiraga et al. 2005). Also on
this much larger scale, a highly inhomogeneous and complex
morphology was found in the western part of the SNR with two narrow
rims resembling a double-shell structure running from north to
south. The (non-thermal) X-ray spectra, when fit with a power law,
exhibit strong variations in photon index across the remnant
in diameter
and exhibits bright X-ray emission dominantly from its western
shell. ASCA observations revealed that the X-ray emission is a pure
non-thermal continuum without detectable line
emission (Koyama et al. 1997; Slane et al. 1999). X-ray observations have also been
conducted with Chandra and XMM with their superior angular
resolution. Chandra observed a small region in the bright
northwestern part of the
SNR (Lazendic et al. 2004; Uchiyama et al. 2003). Despite distinct brightness
variations within this small field, the corresponding X-ray spectra
were all found to be well described by power-law models with similar
absorbing column densities and photon indices, albeit with rather
large statistical uncertainties. XMM covered the remnant almost
completely in five pointings (Cassam-Chenaï et al. 2004; Hiraga et al. 2005). Also on
this much larger scale, a highly inhomogeneous and complex
morphology was found in the western part of the SNR with two narrow
rims resembling a double-shell structure running from north to
south. The (non-thermal) X-ray spectra, when fit with a power law,
exhibit strong variations in photon index across the remnant
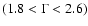 and the hydrogen column density
and the hydrogen column density
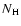 was
found to vary significantly (0.4
was
found to vary significantly (0.4 
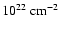
 1.1
1.1 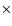
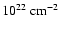 ). The spectra of the central and the western parts differ clearly at low energies, possibly indicating an increase in column density of
). The spectra of the central and the western parts differ clearly at low energies, possibly indicating an increase in column density of
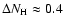
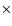
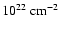 towards the west. Furthermore, a positive correlation between X-ray
brightness and absorption was interpreted as being due to the shock
front of RX J1713.7-3946 impacting a molecular cloud in the west which was
assumed to be responsible for the absorption. Further support for
this scenario is lent by CO line emission observations with the
NANTEN telescope (Fukui et al. 2003; Moriguchi et al. 2005), which suggest that
the SNR is interacting with molecular clouds in this region at a distance of 1 kpc from the Solar System. The non-thermal X-ray emission is possibly associated with interactions between the cloud and the western part of the SNR shell.
towards the west. Furthermore, a positive correlation between X-ray
brightness and absorption was interpreted as being due to the shock
front of RX J1713.7-3946 impacting a molecular cloud in the west which was
assumed to be responsible for the absorption. Further support for
this scenario is lent by CO line emission observations with the
NANTEN telescope (Fukui et al. 2003; Moriguchi et al. 2005), which suggest that
the SNR is interacting with molecular clouds in this region at a distance of 1 kpc from the Solar System. The non-thermal X-ray emission is possibly associated with interactions between the cloud and the western part of the SNR shell.
Age and distance of the SNR are under debate and have been revised
quite a few times. Initially, Koyama et al. (1997) had derived a distance
of 1 kpc and correspondingly an age of about 1000 years from the
column density towards the source as estimated from ASCA X-ray
observations. Slane et al. (1999) on the other hand have derived a larger
distance of 6 kpc (corresponding to an age of about 10 000 years)
based on the possible association of RX J1713.7-3946 with a molecular cloud in
this region and the H II region G347.6+0.2 to its
northwest. Both the latest XMM and NANTEN findings are consistent
with the remnant being closer, at 1 kpc, which might support the
hypothesis of Wang et al. (1997), that RX J1713.7-3946 is the remnant of a AD393
guest star which, according to historical records, appeared in the
tail of constellation Scorpius, close to the actual position of
RX J1713.7-3946. The high surface brightness of this object, both in VHE gamma rays and non-thermal X-rays, suggests that it is close to the evolutionary phase where the shocks are most powerful. While hardly a conclusive argument, this implies that the remnant is observed at
the sweep-up time when the ejecta are interacting with approximately
their own mass of swept-up ambient material and the energy flux
through the shocks (both forward and reverse) peaks. Normally this
would be at an age of a few hundred to a thousand years, which
indeed supports the closer distance estimate.
The radio emission of RX J1713.7-3946 is very faint (Lazendic et al. 2004) which
puts it into a peculiar class of shell-type SNRs with dominantly
non-thermal X-ray and only very faint radio emission. The only other
known object of this type is RX J0852.0-4622
(G266.2-1.2) (Slane et al. 2001; Aschenbach 1998).
RX J1713.7-3946 was detected in VHE gamma rays by the CANGAROO collaboration
in 1998 (Muraishi et al. 2000) and re-observed by CANGAROO-II in 2000 and
2001 (Enomoto et al. 2002). Recently HESS, a new array of imaging
atmospheric Cherenkov telescopes operating in Namibia, has confirmed
the detection (Aharonian et al. 2004b). This was the first independent
confirmation of VHE gamma-ray emission from an SNR shell. Furthermore, the HESS measurement provided the first ever resolved gamma-ray image at very high energies. The complex
morphology of RX J1713.7-3946 was clearly unraveled. Together with the HESS detection of RX J0852.0-4622 (Aharonian et al. 2005a) there are currently two spatially resolved VHE gamma-ray SNRs with a shell-like structure which agrees well with that seen in
X-rays. These two objects may well be the brightest SNRs in the VHE gamma-ray domain in the whole sky; anything equally bright in the Northern sky would have been clearly seen in the Milagro
survey (Atkins et al. 2004), and the HESS Galactic plane survey (Aharonian et al. 2006) reveals no SNRs brighter than RX J1713.7-3946 or RX J0852.0-4622 in the region covered.
The interpretation of the gamma-ray emission mechanisms for RX J1713.7-3946
has been the subject of debate. From their flux level, the CANGAROO
collaboration interpreted in Muraishi et al. (2000) the gamma rays as IC emission, whereas in Enomoto et al. (2002), after re-observations with CANGAROO-II, neutral pion decay was put forward as an explanation instead. The proposed model was then heavily disputed by
Reimer & Pohl (2002) and Butt et al. (2002) because of its conflict in the
GeV regime with the flux of the nearby EGRET source 3EG 1714-3857 (Hartman et al. 1999). Further attempts to model the broadband spectrum of RX J1713.7-3946 were
undertaken (e.g., Pannuti et al. 2003; Lazendic et al. 2004; Ellison et al. 2001; Uchiyama et al. 2003). However,
they did not result in unequivocal conclusions concerning the
acceleration mechanisms of the highest-energy particles or the
origin of the VHE gamma rays from this source.
Here we report on follow-up observations of RX J1713.7-3946 with the complete
HESS telescope array, conducted in 2004. The large field of view
together with the high sensitivity of the system enable us to
undertake for the first time detailed morphological studies in VHE gamma rays and measure spectral parameters in different regions of the SNR.
The paper is organised as follows: in Sect. 2
we present the data set and illustrate the performance of HESS for
observations of extended gamma-ray sources. We explain in detail the
analysis methods applied here in order to extract images and
spectra. In Sect. 3 the results of spectral and
morphological studies are presented along with systematic tests that
have been performed in order to assure the validity of the
analysis. Section 4 presents
multi-wavelength data of RX J1713.7-3946 and its surroundings aiming at
putting our measurement at TeV energies into the context of the
available data as preparation for a broadband modelling of the
spectral energy distribution (SED) in Sect. 5. We
discuss two scenarios for the generation of VHE gamma rays, a purely
electronic and a purely hadronic one. The results are finally
summarised in Sect. 6.
2 Data processing
Observations of RX J1713.7-3946 were conducted between April and July 2004
with the High Energy Stereoscopic System (HESS), a system of four
imaging atmospheric Cherenkov
telescopes (Hofmann 2003; Hinton 2004) situated in the
Khomas Highland of Namibia, at
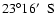
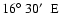 ,
1800 m above sea
level. Each of the 13-m-diameter
telescopes (Bernlöhr et al. 2003; Cornils et al. 2003) has a tessellated
Davies-Cotton mirror of
,
1800 m above sea
level. Each of the 13-m-diameter
telescopes (Bernlöhr et al. 2003; Cornils et al. 2003) has a tessellated
Davies-Cotton mirror of
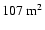 area and is equipped with
a 960-photomultiplier-tube camera (Vincent et al. 2003) covering
a large field of view of
area and is equipped with
a 960-photomultiplier-tube camera (Vincent et al. 2003) covering
a large field of view of
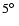 diameter. During stereoscopic
observations, an array-level hardware trigger requires each shower
to be detected by at least two telescopes simultaneously allowing
for efficient suppression of the vast number of hadronic and muonic
background events (Funk et al. 2004). The point source
sensitivity reaches
diameter. During stereoscopic
observations, an array-level hardware trigger requires each shower
to be detected by at least two telescopes simultaneously allowing
for efficient suppression of the vast number of hadronic and muonic
background events (Funk et al. 2004). The point source
sensitivity reaches 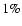 of the flux of the Crab nebula for long
exposures (
of the flux of the Crab nebula for long
exposures ( 25 h).
25 h).
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{4279_f1.eps} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg76.gif) |
Figure 1:
X-ray image of RX J1713.7-3946 (colour scale and thin grey contour
lines, 1-3 keV, from Uchiyama et al. 2002). The superimposed thick white
contours indicate the 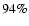 and
and 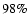 levels of the
detection-efficiency weighted HESS exposure, given by the
product of relative detection efficiency and the observation
time. It can be seen that the relative gamma-ray detection
efficiency between the centre region and the edges of the SNR
differs only by
levels of the
detection-efficiency weighted HESS exposure, given by the
product of relative detection efficiency and the observation
time. It can be seen that the relative gamma-ray detection
efficiency between the centre region and the edges of the SNR
differs only by  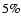 . . |
| Open with DEXTER |
The observations were mostly performed in wobble mode
around the SNR centre. In this mode the telescopes were positioned
such that the centre of the SNR was offset 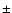
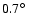 in
declination or right ascension away from the pointing direction of
the telescope system, changing to the next position every 28 min. Towards the end of the observation campaign, pure on-source pointings in which the centre of the SNR was coincident with the system centre were additionally performed. In each of the five pointings the SNR RX J1713.7-3946, roughly
in
declination or right ascension away from the pointing direction of
the telescope system, changing to the next position every 28 min. Towards the end of the observation campaign, pure on-source pointings in which the centre of the SNR was coincident with the system centre were additionally performed. In each of the five pointings the SNR RX J1713.7-3946, roughly
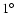 in diameter, was fully
contained in the
in diameter, was fully
contained in the 
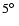 field of view of the system. The
resulting effective exposure distribution (the product of the
detection efficiency and the exposure) is illustrated in
Fig. 1, where the ASCA X-ray
measurement (Uchiyama et al. 2002) is shown (colour scale and thin contour
lines) with superimposed white, almost circular contours indicating
the
field of view of the system. The
resulting effective exposure distribution (the product of the
detection efficiency and the exposure) is illustrated in
Fig. 1, where the ASCA X-ray
measurement (Uchiyama et al. 2002) is shown (colour scale and thin contour
lines) with superimposed white, almost circular contours indicating
the 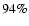 and
and 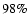 levels of the effective exposure. The
observation strategy for this data set combined with the detector
efficiency results in a very flat plateau in the region of the SNR;
from the centre to the boundaries the relative gamma-ray detection
efficiency decreases by only about
levels of the effective exposure. The
observation strategy for this data set combined with the detector
efficiency results in a very flat plateau in the region of the SNR;
from the centre to the boundaries the relative gamma-ray detection
efficiency decreases by only about 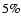 ,
which is a great advantage
compared to ASCA, for example. Not only is the SNR fully contained
in all of the five pointing positions, but one can also disregard
for most purposes the modest change in relative detection efficiency
from one region of the SNR to another.
,
which is a great advantage
compared to ASCA, for example. Not only is the SNR fully contained
in all of the five pointing positions, but one can also disregard
for most purposes the modest change in relative detection efficiency
from one region of the SNR to another.
![\begin{figure}
\par\includegraphics[width=15.25cm,clip]{4279_f2.eps} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg77.gif) |
Figure 2:
Left hand side: squared angular distance between
reconstructed and true direction for a Monte Carlo gamma-ray point
source (point-spread function). A cut on the minimum size
of images of 200 photo-electrons was applied. The simulated gamma
rays followed a power law in energy with a photon index of 2. The
zenith angle distribution and offset of the source with respect to
the telescope optical axis was matched to the actual data set of
RX J1713.7-3946. The solid circles are the Monte Carlo histogram, the fit of
a double Gaussian (dashed line) describes the point-spread
function reasonably well. Indicated is the 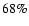 containment
radius of containment
radius of
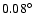 (obtained from the fit), which is taken as
the resolution of the data set. Right hand side:
(obtained from the fit), which is taken as
the resolution of the data set. Right hand side: 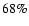 containment radii of the point-spread function determined from simulations as function of the offset between the source direction and telescope pointing. Shown are simulations for containment radii of the point-spread function determined from simulations as function of the offset between the source direction and telescope pointing. Shown are simulations for
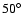 (triangles) and
(triangles) and
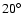 zenith angle (circles) for two different
size cuts (80 and 200 photo-electrons). The maximum offset of the
actual data set of
zenith angle (circles) for two different
size cuts (80 and 200 photo-electrons). The maximum offset of the
actual data set of
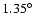 ,
given by the wobble displacement
of ,
given by the wobble displacement
of
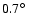 and the approximate radius of the SNR of
and the approximate radius of the SNR of
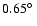 ,
is indicated by the arrow. ,
is indicated by the arrow. |
| Open with DEXTER |
The data comprise a total exposure time of 40 h. Rejecting
data taken under bad weather conditions, 36 h of observation
time corresponding to 33 h of live time remain for the
analysis. The zenith angle of observations ranged from
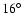 to
to
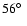 with a mean of
with a mean of
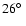 ;
it should be noted that about
;
it should be noted that about 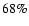 of the data were taken at small zenith angles
between
of the data were taken at small zenith angles
between
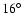 to
to
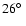 .
The energy threshold (defined by the
peak gamma-ray detection rate for a given source spectrum after all
gamma-ray selection cuts) of the system increases with zenith
angle. For the observations presented here, assuming a spectrum
appropriate for RX J1713.7-3946, the threshold was
.
The energy threshold (defined by the
peak gamma-ray detection rate for a given source spectrum after all
gamma-ray selection cuts) of the system increases with zenith
angle. For the observations presented here, assuming a spectrum
appropriate for RX J1713.7-3946, the threshold was  180 GeV at
180 GeV at
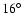 ,
,
 340 GeV at
340 GeV at
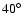 ,
and
,
and  840 GeV at
840 GeV at
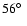 .
.
The analysis technique applied here is described in detail in
Aharonian et al. (2005b). After calibration of the
data (Aharonian et al. 2004a), tail-cuts image cleaning is applied and the
shower images in each telescope are parametrised in terms of their
centre of gravity and second moments (Hillas 1985). Stereoscopic
event reconstruction based on the intersection of image axes yields
the shower direction, providing a resolution of 
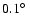 for individual gamma rays. Given the geometry of the shower, cuts
(optimised on Monte Carlo gamma-ray simulations and OFF
source data, i.e. data without gamma-ray signal) are applied to
select gamma-ray candidates and to suppress the vast hadronic
background. The gamma-ray energy is estimated from the image
intensity and the reconstructed shower geometry yielding a resolution of
for individual gamma rays. Given the geometry of the shower, cuts
(optimised on Monte Carlo gamma-ray simulations and OFF
source data, i.e. data without gamma-ray signal) are applied to
select gamma-ray candidates and to suppress the vast hadronic
background. The gamma-ray energy is estimated from the image
intensity and the reconstructed shower geometry yielding a resolution of 
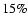 .
There is one main difference between a point-source and an extended-source analysis. In the latter case,
the cut on the squared distance of events to the assumed source
location is greatly increased in order to reflect the large source
extension. In that case the energy resolution worsens slightly (to
.
There is one main difference between a point-source and an extended-source analysis. In the latter case,
the cut on the squared distance of events to the assumed source
location is greatly increased in order to reflect the large source
extension. In that case the energy resolution worsens slightly (to 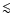
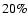 for a source of the size of RX J1713.7-3946) since an increased
number of badly reconstructed events are included in the analysis.
for a source of the size of RX J1713.7-3946) since an increased
number of badly reconstructed events are included in the analysis.
2.4 HESS performance for extended sources
The large field of view of the HESS telescope system of 
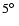 diameter provides reasonable sensitivity for point sources at an angular distance up to
diameter provides reasonable sensitivity for point sources at an angular distance up to
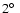 from the pointing direction of the telescope system (the point-source off-axis sensitivity derived
from Monte Carlo simulations has been confirmed via observations of
the Crab nebula, see Aharonian et al. 2005c). Given the source diameter of
up to
from the pointing direction of the telescope system (the point-source off-axis sensitivity derived
from Monte Carlo simulations has been confirmed via observations of
the Crab nebula, see Aharonian et al. 2005c). Given the source diameter of
up to
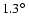 and the offsets of
and the offsets of
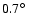 between the centre of
the SNR and the telescope pointing direction during observations, it
is important that the gamma-ray point-spread function is well
behaved and does not broaden significantly with increasing offset
from the pointing direction. Figure 2 (left) shows the
squared angular difference
between the centre of
the SNR and the telescope pointing direction during observations, it
is important that the gamma-ray point-spread function is well
behaved and does not broaden significantly with increasing offset
from the pointing direction. Figure 2 (left) shows the
squared angular difference 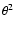 between the reconstructed and
the true direction of a simulated point source. The initial
simulations have been generated at a number of fixed zenith angles
between
between the reconstructed and
the true direction of a simulated point source. The initial
simulations have been generated at a number of fixed zenith angles
between
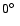 and
and
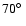 .
Taking then the zenith angle
distribution of the actual data set and forming from that the
weighted sum of the simulated
.
Taking then the zenith angle
distribution of the actual data set and forming from that the
weighted sum of the simulated 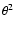 distributions one obtains a resolution (taken as the
distributions one obtains a resolution (taken as the 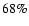 containment radius) of
containment radius) of
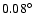 .
This is an order of magnitude smaller than the source
diameter, which implies that in terms of angular resolution HESS
is well suited for morphological studies of RX J1713.7-3946. The right hand
side of Fig. 2 illustrates the dependence of the angular
resolution on the offset between source position and pointing
direction for two representative zenith angles of
.
This is an order of magnitude smaller than the source
diameter, which implies that in terms of angular resolution HESS
is well suited for morphological studies of RX J1713.7-3946. The right hand
side of Fig. 2 illustrates the dependence of the angular
resolution on the offset between source position and pointing
direction for two representative zenith angles of
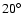 and
and
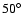 ,
for two different cuts on the minimum camera image size of 80 and 200 photo-electrons. It can be seen that the application
of a higher cut on the image size improves the direction
reconstruction by about
,
for two different cuts on the minimum camera image size of 80 and 200 photo-electrons. It can be seen that the application
of a higher cut on the image size improves the direction
reconstruction by about 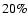 since only well defined camera images
are used in the shower reconstruction, reducing fluctuation
effects. However, the improved resolution is achieved at the expense
of an increased energy threshold. In any case, for offsets smaller
than
since only well defined camera images
are used in the shower reconstruction, reducing fluctuation
effects. However, the improved resolution is achieved at the expense
of an increased energy threshold. In any case, for offsets smaller
than
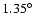 ,
which is the maximum offset under which parts of
the SNR were observed, the resolution changes only slowly with
offset and worsens by less than
,
which is the maximum offset under which parts of
the SNR were observed, the resolution changes only slowly with
offset and worsens by less than 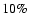 .
It was furthermore
demonstrated with observations of the point-like source
PKS 2155-304 (Aharonian et al. 2005b), that simulated
point-spread functions agree well with data distributions and are
thus well understood.
.
It was furthermore
demonstrated with observations of the point-like source
PKS 2155-304 (Aharonian et al. 2005b), that simulated
point-spread functions agree well with data distributions and are
thus well understood.
The effective gamma-ray detection area depends on trigger conditions
and analysis cuts. Well above the trigger threshold of the system,
it is of the order of the area of the Cherenkov light pool (emitted
by the secondary particle shower) on the ground. Typical effective
area curves as a function of the offset angle between the gamma-ray
source and the pointing direction of the system are shown in
Fig. 3 for a zenith angle of
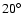 .
The
effective areas were determined from Monte Carlo simulations of a gamma-ray point source, accounting for the large extension of RX J1713.7-3946 by increasing the cut on the maximum distance to the assumed source position.
Since for an extended source like RX J1713.7-3946 the flux has to be
integrated over a larger solid angle than for point sources, the
sensitivity of the system is reduced due to an increased background
level. For moderate zenith angles and an integration region of
.
The
effective areas were determined from Monte Carlo simulations of a gamma-ray point source, accounting for the large extension of RX J1713.7-3946 by increasing the cut on the maximum distance to the assumed source position.
Since for an extended source like RX J1713.7-3946 the flux has to be
integrated over a larger solid angle than for point sources, the
sensitivity of the system is reduced due to an increased background
level. For moderate zenith angles and an integration region of
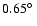 radius around a gamma-ray source at
radius around a gamma-ray source at
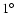 offset from the pointing direction (matched to the data set described here), simulations reveal that, for a source like RX J1713.7-3946, the sensitivity
drops roughly by a factor of four as compared to a point-source analysis.
offset from the pointing direction (matched to the data set described here), simulations reveal that, for a source like RX J1713.7-3946, the sensitivity
drops roughly by a factor of four as compared to a point-source analysis.
![\begin{figure}
\par\includegraphics[width=7.75cm,clip]{4279_f3.eps} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg88.gif) |
Figure 3:
Effective detection area A for a moderate zenith angle
of
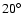 as a function of offset angle
as a function of offset angle 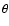 between the
source location and the pointing direction of the system. Plotted
are values at three representative energy values of 0.2 TeV (near
the post-cut trigger threshold), 1 TeV, and 10 TeV. The markers at
between the
source location and the pointing direction of the system. Plotted
are values at three representative energy values of 0.2 TeV (near
the post-cut trigger threshold), 1 TeV, and 10 TeV. The markers at
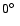 , ,
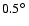 , ,
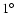 , ,
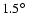 ,
and ,
and
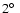 represent the offset values for which simulations are available, in between two simulated offsets effective area values are interpolated linearly.
represent the offset values for which simulations are available, in between two simulated offsets effective area values are interpolated linearly. |
| Open with DEXTER |
2.5 Analysis details
The following section explains briefly the analysis applied to
extract gamma-ray images and spectra of RX J1713.7-3946 from the data.
2.5.1 Morphology
![\begin{figure}
\par\includegraphics[width=8.25cm,clip]{4279_f4} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg89.gif) |
Figure 4:
As illustration of the good match between data and
background model, the data set of RX J1713.7-3946 ( upper panel) is
compared to the high statistics data set of
PKS 2155-304 ( lower panel) which appears as a point
source for HESS. Shown are
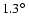 and
and
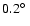 slices
along the RA axis through the centre of RX J1713.7-3946 and
PKS 2155-304, respectively, for the data (black) and
the background model (green). The good match both in shape and
absolute level between the two curves illustrates the validity
of the approach. The steps in the distributions (in the case of
RX J1713.7-3946 at
slices
along the RA axis through the centre of RX J1713.7-3946 and
PKS 2155-304, respectively, for the data (black) and
the background model (green). The good match both in shape and
absolute level between the two curves illustrates the validity
of the approach. The steps in the distributions (in the case of
RX J1713.7-3946 at 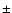
 and
and 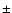
 )
are artefacts of the
analysis: the usable range in the field of view of every
observation was restricted to a radius of )
are artefacts of the
analysis: the usable range in the field of view of every
observation was restricted to a radius of
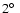 (out of
(out of
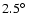 physical camera radius) around the camera centre to allow only for well reconstructed events with good camera
acceptance, and the figure combines data from different
pointings.
physical camera radius) around the camera centre to allow only for well reconstructed events with good camera
acceptance, and the figure combines data from different
pointings. |
| Open with DEXTER |
The gamma-ray images shown throughout the paper represent, unless
otherwise stated, gamma-ray excess counts with background
subtracted. For the generation of these images a cut of 200 photo-electrons on the minimum camera image size in each telescope is applied to select a subset of events with superior angular
resolution (see also Fig. 2 and Sect. 2.4). The background was estimated using about 160 h of HESS observations without any or only
very faint gamma-ray sources in the field of view. All the events in
these reference observations passing gamma-ray cuts are assumed to
be gamma-ray like background events and are used to estimate the
background for the given data set. For that purpose the set of OFF
runs has been divided into distinct zenith angle bands to account
for the dependance of the system's gamma-ray acceptance on
observation altitude. Besides that, the acceptance depends only on
the angular distance between shower and pointing direction and is to
a very good approximation radially symmetric with respect to the
pointing direction. Therefore, a radial 1D lookup (number of
background events as a function of squared distance to the pointing
centre) can be used in each zenith angle band for the background
estimation. Given an observation at a certain zenith angle, a model
background is created by selecting the 1D radial lookup from the
zenith-angle band that matches the zenith angle of the
observation. A 2D background map of the sky is then created by
rotating the corresponding 1D lookup. Finally, the overall
background map is created as the exposure weighted sum of the
individual maps. A global normalisation factor 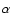 is
calculated as ratio of the number of events in the data to the
number of events in the background model, excluding regions that
emit gamma rays. Figure 4 illustrates the validity of
the approach for two HESS data sets, RX J1713.7-3946 (upper panel) and
PKS 2155-304 (lower panel), the latter being a point
source for HESS. Shown are slices along right ascension through the
source centres. Overlaid on both data curves are the normalised
background models of the whole data sets. In both cases, at
different regions in the sky, for an extended and a point-like
gamma-ray source, there is clearly a good match between model and
data in regions outside the gamma-ray sources.
is
calculated as ratio of the number of events in the data to the
number of events in the background model, excluding regions that
emit gamma rays. Figure 4 illustrates the validity of
the approach for two HESS data sets, RX J1713.7-3946 (upper panel) and
PKS 2155-304 (lower panel), the latter being a point
source for HESS. Shown are slices along right ascension through the
source centres. Overlaid on both data curves are the normalised
background models of the whole data sets. In both cases, at
different regions in the sky, for an extended and a point-like
gamma-ray source, there is clearly a good match between model and
data in regions outside the gamma-ray sources.
Images of the gamma-ray excess are obtained by subtracting the
normalised background model from the data in each bin i of the 2D map:
Subsequently, these images are smoothed with a Gaussian to reduce
statistical fluctuations.
Typically the standard deviation for the smoothing is matched to the
resolution of the data set, namely 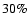 -
-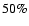 of the
of the 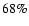 containment radius of the point-spread function. Here, for the data
of RX J1713.7-3946, a smoothing radius of
containment radius of the point-spread function. Here, for the data
of RX J1713.7-3946, a smoothing radius of
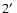 is used. The resulting
count maps are in units of integrated excess counts per Gaussian
sigma of the smoothing function.
is used. The resulting
count maps are in units of integrated excess counts per Gaussian
sigma of the smoothing function.
No correction for the falloff of detection efficiency towards the
edges of the field of view is applied because in the region of
interest, around the SNR RX J1713.7-3946, the variation in gamma-ray acceptance
is negligible (see Fig. 1).
2.5.2 Spectral analysis
For the spectral analysis, the HESS standard cut on the image size
of 80 photo-electrons is applied to the data. To obtain a spectrum
of a certain region in the sky, all events with reconstructed
direction in that particular region are considered as ON events. A
complication arises for the background estimation. The gamma-ray
acceptance and therefore the background level depend strongly on
energy; one cannot, as for the image generation, simply use a 1D radial lookup (which is integrated over all energies) as a background estimate. Instead, the acceptance lookups would have to be generated in energy bins which in practice is difficult to
handle. Another approach was applied here for the spectral analysis:
background (OFF) events were selected from the same field of view,
from the same data run, by selecting regions of the same size and
form as the ON region, but displaced on a circle around the pointing
direction of the system. The circle is chosen such that the OFF regions are at exactly the same offset (that is, at the same angular distance to the pointing direction) as the ON region. A minimum
distance between the ON and OFF regions of
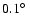 is required to
avoid gamma-ray contamination. Furthermore, known gamma-ray sources
in the field of view not associated with the test region are
excluded from the OFF regions. This approach ensures that background
events are taken at the same zenith and offset angles, which is
crucial because of the dependence of the effective detection areas
upon these two quantities, and it uses more or less the same region
of sky, with similar night-sky-background noise. For an object of
the size of RX J1713.7-3946 this results in one ON and OFF region, the latter
being simply the reflection of the former at the system centre. This
is illustrated in Fig. 5, where the OFF regions
used for each observation position are drawn.
is required to
avoid gamma-ray contamination. Furthermore, known gamma-ray sources
in the field of view not associated with the test region are
excluded from the OFF regions. This approach ensures that background
events are taken at the same zenith and offset angles, which is
crucial because of the dependence of the effective detection areas
upon these two quantities, and it uses more or less the same region
of sky, with similar night-sky-background noise. For an object of
the size of RX J1713.7-3946 this results in one ON and OFF region, the latter
being simply the reflection of the former at the system centre. This
is illustrated in Fig. 5, where the OFF regions
used for each observation position are drawn.
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{4279_f5} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg94.gif) |
Figure 5:
Count map of gamma-ray candidates for the region around
RX J1713.7-3946. A size cut of 200 photo-electrons on the camera images was
applied. The bins are uncorrelated and the background is not
subtracted. The white dashed circle indicates the region used to
extract the spectrum of the whole SNR (the ON region),
the red circles indicate the OFF regions, the regions used for
background estimation for the spectrum in each of the four wobble
observation positions, which are marked as yellow circles. The
dashed red circle to the north of the SNR indicates an OFF region
that was not used in the spectral analysis because it contains a gamma-ray source discovered in the HESS Galactic plane survey (Aharonian et al. 2006). |
| Open with DEXTER |
After the geometrical selection, in order to obtain a differential
gamma-ray flux
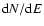 in units of
in units of
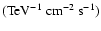 ,
ON and OFF events (
,
ON and OFF events (
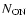 and
and
 )
are binned logarithmically in energy and divided by the mean effective area and
the exposure time in each bin. The energy dependent effective area
is determined for each data run, for the corresponding zenith
)
are binned logarithmically in energy and divided by the mean effective area and
the exposure time in each bin. The energy dependent effective area
is determined for each data run, for the corresponding zenith
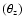 and offset
and offset 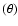 angle range, multiplied by the live time of the run and added up. Then, for each
energy bin i, the bin entries are divided by the width (
angle range, multiplied by the live time of the run and added up. Then, for each
energy bin i, the bin entries are divided by the width (
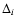 )
of that bin to obtain a differential flux value. The differential flux results from subtracting the
differential OFF- from the ON-flux histogram:
)
of that bin to obtain a differential flux value. The differential flux results from subtracting the
differential OFF- from the ON-flux histogram:
The normalisation factor
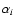 is determined from
the ratio of the areas of the ON and OFF regions used during
analysis of the whole data set and takes the exposure of the
different observations into account.
is determined from
the ratio of the areas of the ON and OFF regions used during
analysis of the whole data set and takes the exposure of the
different observations into account.
An alternative approach is the event-by-event usage of the effective
area, which served as a systematic check. Rather than determining a mean effective area for the whole data set, each event is weighted with the inverse of the effective area, taking the event zenith angle, offset and energy.
A complication arises from the dependence of the effective detection
area on zenith angle and offset. The Monte Carlo effective areas are
generated at certain discrete zenith angles and offsets. When
generating the mean effective area corresponding to a certain zenith
angle and offset range, the effective area is interpolated linearly
between the simulation values (see Fig. 3, where the
markers indicate values available from simulations and the lines are
the linear interpolations).
3 Results
With the HESS data set, the morphology of RX J1713.7-3946 and its spectrum
are resolved with high precision. Given that this is the first in
depth analysis of such an extended source in VHE gamma rays, we
present in the following first selected examples of extensive
systematic tests that were performed in order to assure the
stability of the analysis and then discuss the results.
3.1 Morphology
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{4279_f6} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg104.gif) |
Figure 6:
Correlation between the standard calibration, event
reconstruction, and background reduction method (Method 1) and an alternative, completely independent approach (Method 2, see main text for more details). The black
solid and white dashed lines run through the origin with a slope
of 1. A linear correlation is clearly visible, deviations from the
line originate from different cut efficiencies of the two methods. |
| Open with DEXTER |
When analysing the morphology of an extended source, one aims for
the best possible resolution with, at the same time, sufficient
event statistics. In order to explore image structures and their
stability, the data set was analysed using the same calibration and
analysis software, but applying different sets of cuts (like
accepting only three- and four-telescope events and events with
image amplitudes larger than 80, 200, and 400 photo-electrons),
which resulted in different resolutions and different event
statistics. Another important issue is the appropriate modelling and
subtraction of the background. As a systematic test, alternative
background models have been applied and the results compared. First,
a set of OFF runs, taken at the same zenith angles with very similar
night-sky noise as the ON runs, has been used. Furthermore, the
morphology was cross-checked using a completely independent
calibration and analysis approach, not only for the reconstruction
of the shower geometry but also for background estimation. Rather
than using standard (Hillas) parameters for image parametrisation
and reconstructing shower geometry based on these parameters, this
approach is based on a 3D modelling of Cherenkov photon emission
during the shower development in the atmosphere assuming rotational
symmetry, thereby predicting pixel amplitudes (for more
details, see Lemoine-Goumard & de Naurois 2005). A comparison of the two analysis
methods is shown in Fig. 6; plotted is the
correlation of gamma-ray excess counts for the sky region around
RX J1713.7-3946. A linear correlation is clearly apparent illustrating the good
agreement of the two independent methods.
With the systematic tests mentioned above it could be shown that the
main features of the gamma-ray morphology are stable when analysed
with different cuts, different background models as well as with
independently determined calibration coefficients and alternative
analysis methods.
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{4279_f7} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg105.gif) |
Figure 7:
Gamma-ray image of RX J1713.7-3946. The linear colour scale is in
units of excess counts (see Sect. 2.5.1
for a description of image generation). The white contour lines
indicate the significance of the different features, the levels
are linearly spaced and correspond to 5, 10, and 15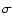 ,
respectively. The significance of each point has been calculated
assuming a point source at that position, integrating events
within a circle of ,
respectively. The significance of each point has been calculated
assuming a point source at that position, integrating events
within a circle of
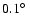 radius. In the lower left hand
corner a simulated point source is shown as it would appear in
this particular data set (taking the point-spread function and the
smoothing into account) along with a black circle of
radius. In the lower left hand
corner a simulated point source is shown as it would appear in
this particular data set (taking the point-spread function and the
smoothing into account) along with a black circle of
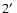 radius denoting the
radius denoting the 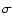 of the Gaussian the image is smoothed with.
of the Gaussian the image is smoothed with. |
| Open with DEXTER |
Figure 7 shows a
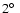
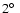 field
of view around RX J1713.7-3946. A cut on the image size at 200 photo-electrons
was applied resulting in a superior resolution of
field
of view around RX J1713.7-3946. A cut on the image size at 200 photo-electrons
was applied resulting in a superior resolution of
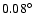 (see
Fig. 2). The corresponding energy range is
(see
Fig. 2). The corresponding energy range is  300 GeV to
300 GeV to  40 TeV. This image of RX J1713.7-3946 confirms with much higher statistics the 2003 HESS measurement, shown for example in Fig. 1 of Aharonian et al. (2004b). There is no evidence for time
variability, as expected for an object of the size of RX J1713.7-3946. The
overall gamma-ray appearance resembles a shell morphology with
bright emission regions in the western and northwestern part where
the SNR is believed to impact molecular
clouds (Fukui et al. 2003; Moriguchi et al. 2005). It is worth noting that
there is a possible gamma-ray void in the central-southeastern
region. The cumulative significance for the whole SNR is about
40 TeV. This image of RX J1713.7-3946 confirms with much higher statistics the 2003 HESS measurement, shown for example in Fig. 1 of Aharonian et al. (2004b). There is no evidence for time
variability, as expected for an object of the size of RX J1713.7-3946. The
overall gamma-ray appearance resembles a shell morphology with
bright emission regions in the western and northwestern part where
the SNR is believed to impact molecular
clouds (Fukui et al. 2003; Moriguchi et al. 2005). It is worth noting that
there is a possible gamma-ray void in the central-southeastern
region. The cumulative significance for the whole SNR is about 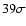 with these hard cuts, which corresponds to an excess of
with these hard cuts, which corresponds to an excess of  7700 events from the region of RX J1713.7-3946. Drawn as white lines in Fig. 7 are in addition the contours of significance of the gamma-ray signal (levels correspond to 5, 10,
and 15
7700 events from the region of RX J1713.7-3946. Drawn as white lines in Fig. 7 are in addition the contours of significance of the gamma-ray signal (levels correspond to 5, 10,
and 15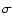 ). The significance has been calculated considering
events that fall within an angle of
). The significance has been calculated considering
events that fall within an angle of
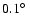 of each trial source
position. Thus, the contours quantify the significance for each
point as if there was a point source at that position. The
background estimate was derived from OFF runs as described in
Sect. 2.5.1. The brightest parts of the SNR
exceed
of each trial source
position. Thus, the contours quantify the significance for each
point as if there was a point source at that position. The
background estimate was derived from OFF runs as described in
Sect. 2.5.1. The brightest parts of the SNR
exceed 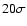 .
Except for the void structure, where the
significance just exceeds
.
Except for the void structure, where the
significance just exceeds 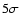 ,
most of the remaining emission
regions are well above
,
most of the remaining emission
regions are well above 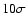 .
.
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{4279_f8} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg110.gif) |
Figure 8:
Shown is a simple geometrical model for the emission from
a thick sphere matched to the dimensions and relative fluxes of
RX J1713.7-3946. Left: 2D projection of a thick and spherical
radiating shell,
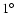 in diameter, smoothed with the HESS point-spread function. Adapted empirically to match the radial shape of the HESS data set, the dimensions of the geometrical
sphere are 5.5 pc for the inner and 10 pc for the outer boundary
if one assumes a distance of 1 kpc to the source, the presumed
distance to RX J1713.7-3946. The emissivity in the northern, western, and
southwestern part is a factor of two higher than in the southeast
and east. Right: radial profile from the geometrical
model compared to the HESS data profile of RX J1713.7-3946. The centre
coordinates used for the data plot are
in diameter, smoothed with the HESS point-spread function. Adapted empirically to match the radial shape of the HESS data set, the dimensions of the geometrical
sphere are 5.5 pc for the inner and 10 pc for the outer boundary
if one assumes a distance of 1 kpc to the source, the presumed
distance to RX J1713.7-3946. The emissivity in the northern, western, and
southwestern part is a factor of two higher than in the southeast
and east. Right: radial profile from the geometrical
model compared to the HESS data profile of RX J1713.7-3946. The centre
coordinates used for the data plot are
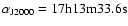 , ,
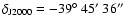 .
The geometrical model profile has been
scaled to the same area as the data profile. .
The geometrical model profile has been
scaled to the same area as the data profile. |
| Open with DEXTER |
From the gamma-ray image presented here it is clear that the
emission regions cannot be distributed homogeneously in the
sphere RX J1713.7-3946. The image is neither rotational symmetric nor
does it exhibit a shallow peak towards the centre. Instead, a shell
seems to be apparent in the northern, and western to southwestern
part. Apart from that, there is more or less uniform emission found
in the rest of the SNR with a slight flux increase towards the
southeastern boundary. This resembles very much the image one would
expect from a thick spherical shell radiating gamma rays with
enhanced emission on one side, as is illustrated in
Fig. 8 where a geometrical model of a thick
radiating sphere is presented. The good match in shape between the
data and the toy-model profile lends support to the assumption that
indeed it is the shell of RX J1713.7-3946 which radiates gamma rays.
![\begin{figure}
\par\includegraphics[width=16.35cm,clip]{4279_f9} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg114.gif) |
Figure 9:
Morphology of RX J1713.7-3946 as it appears at different
energies. Shown from left to right are gamma-ray excess images
with energies of
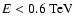 , ,
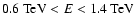 ,
and ,
and
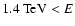 .
Drawn additionally as white lines are
contours of significance, linearly spaced at 5, 10, 15 .
Drawn additionally as white lines are
contours of significance, linearly spaced at 5, 10, 15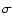 (as in Fig. 7). Note the increase in the
signal-to-noise ratio with increasing energy. The energy bands
were chosen such that each band represents about a third of the
full data set (taking events after cuts). Furthermore, all three
images were smoothed with a Gaussian of
(as in Fig. 7). Note the increase in the
signal-to-noise ratio with increasing energy. The energy bands
were chosen such that each band represents about a third of the
full data set (taking events after cuts). Furthermore, all three
images were smoothed with a Gaussian of
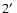 ,
which makes
them directly comparable to each other, and to
Fig. 7. The resolution in each energy band
is indicated in the lower left hand corner of the images; the
three data subsets have comparable resolutions of ,
which makes
them directly comparable to each other, and to
Fig. 7. The resolution in each energy band
is indicated in the lower left hand corner of the images; the
three data subsets have comparable resolutions of 
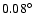 (the resolution of the intermediate energy band is about
(the resolution of the intermediate energy band is about 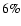 better). This might be counter-intuitive, given that
at larger energies camera images get bigger and fluctuation
effects become negligible thereby improving the energy and
direction resolution. However, in this case that effect is
compensated by the increasing mean zenith angle of the
large-energy events.
better). This might be counter-intuitive, given that
at larger energies camera images get bigger and fluctuation
effects become negligible thereby improving the energy and
direction resolution. However, in this case that effect is
compensated by the increasing mean zenith angle of the
large-energy events. |
| Open with DEXTER |
Figure 9 shows three images of RX J1713.7-3946 in three distinct energy bands,
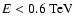 ,
,
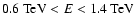 ,
and
,
and
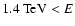 (left to right). The energy ranges were
chosen such that each band represents a third of the data set. Note
that the angular resolution of all three images is roughly the same
which makes them readily comparable. The signal-to-noise ratio of
the low-energy image is evidently smaller. The shell-like morphology
of the SNR is slightly blurred by fluctuations. Correspondingly, the
significance contours indicate that only the bright northwestern
half is significant in this energy band. In contrast, the whole
remnant sticks out significantly in the two higher-energy
bands. Most of the northwestern parts exceed
(left to right). The energy ranges were
chosen such that each band represents a third of the data set. Note
that the angular resolution of all three images is roughly the same
which makes them readily comparable. The signal-to-noise ratio of
the low-energy image is evidently smaller. The shell-like morphology
of the SNR is slightly blurred by fluctuations. Correspondingly, the
significance contours indicate that only the bright northwestern
half is significant in this energy band. In contrast, the whole
remnant sticks out significantly in the two higher-energy
bands. Most of the northwestern parts exceed 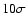 ,
the
brightest spots even exceed
,
the
brightest spots even exceed 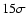 for energies beyond 1.4 TeV.
for energies beyond 1.4 TeV.
From the visual impression the remnant does seem to emit gamma rays
more uniformly with increasing energy. However, within errors, the
radial shape appears to be the same in all three energy bands, as
seen from the radial excess profiles around the centre of the SNR
shown in Fig. 10. The morphology
does not change significantly with energy. This is qualitatively
compatible with the results of the spatially resolved spectral
analysis (see Sect. 3.2).
3.2 Energy spectra
The energy spectrum of RX J1713.7-3946 was measured with HESS over a large
energy range. Systematic tests on the shape and characteristics of
the energy spectrum of the whole SNR included application of a slightly different spectral analysis technique, different background models, analysis in distinct data subsets like small and large zenith angles and the five observation positions, analysis applying
different cuts on image intensity and telescope multiplicity,
investigation of the influence of the exact binning, of the energy
estimation and the fit to the effective area histograms obtained
from simulations. Furthermore, the results were cross-checked with
the independent calibration and analysis scheme mentioned in
Sect. 3.1. Representative examples for these
systematic tests are shown in Fig. 11, where the
spectrum of the whole SNR is plotted using the standard background
estimation from the same field of view, compared to a completely
independent background estimation based on OFF runs, and to the
independent analysis chain (Lemoine-Goumard & de Naurois 2005). The three spectra are
found to be well compatible with each other.
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{4279_f10} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg116.gif) |
Figure 10:
Radial profiles around the centre of the SNR
(
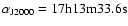 , ,
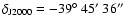 )
in
the three energy bands plotted in Fig. 9,
generated from the raw (that is, not smoothed) gamma-ray excess
images. The intermediate and high-energy band images have improved
signal-to-noise ratios. The radial profiles from these energy bands
have been scaled such that they have the same area as the low-energy
profile (scaling factors are )
in
the three energy bands plotted in Fig. 9,
generated from the raw (that is, not smoothed) gamma-ray excess
images. The intermediate and high-energy band images have improved
signal-to-noise ratios. The radial profiles from these energy bands
have been scaled such that they have the same area as the low-energy
profile (scaling factors are  0.87 and 0.87 and  0.65,
respectively), to enable direct comparisons. 0.65,
respectively), to enable direct comparisons. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4279_f11} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg117.gif) |
Figure 11:
Shown are three spectra that were produced to explore the
systematic uncertainties. The alternative spectra (blue squares
and red triangles) were scaled by factors of 10-2 and 10-4, respectively, for presentation reasons. Upper set: standard analysis and standard background modelling using a background position from the same field of view, with the exact
same shape and distance to the pointing direction as the signal
region, but opposite to it, on the other side of the pointing
direction. Middle set: alternative spectral analysis
technique (event-wise effective area weighting, see
Sect. 2.5.2) with an independent
background estimate taken from OFF runs. The background regions in
the OFF data were again selected such that they have the same
shape and distance to the pointing direction as the signal region
in the RX J1713.7-3946 observations. Lower set: spectrum produced
applying an independent analysis chain. The background was
determined similarly as for the upper set. A third spectral
analysis technique was applied here, described in
Piron et al. (2001). Plotted as black line on top of all three spectra
to guide the eye is the best fit of a power law with energy
dependent photon index to the spectrum shown in the upper set (see
Table 1 for details). The error bars on the
spectral points denote 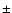 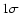 statistical errors.
statistical errors. |
| Open with DEXTER |
In order to obtain a quantitative estimate for the systematic error
on each flux point, the background estimation, the spectral analysis
technique (event-wise effective area weighting or average effective
area determination per data run) and the absolute energy scale of
the experiment were considered as dominant contributions. For the
background modelling, an uncertainty of
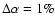 ,
,
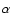 being the background normalisation factor, was derived from
the RX J1713.7-3946 data set by comparing the standard analysis to the
analysis using an independent background model derived from OFF runs, as mentioned above. It should be noted that the 1% variation found in the total number of background counts is compatible with being due to a statistical variation and thus must be regarded as an upper limit. Taking the systematic uncertainty due to the background
level and the two spectral analysis techniques, an energy dependent
systematic error was obtained by analysing the data set six times -
scaling
being the background normalisation factor, was derived from
the RX J1713.7-3946 data set by comparing the standard analysis to the
analysis using an independent background model derived from OFF runs, as mentioned above. It should be noted that the 1% variation found in the total number of background counts is compatible with being due to a statistical variation and thus must be regarded as an upper limit. Taking the systematic uncertainty due to the background
level and the two spectral analysis techniques, an energy dependent
systematic error was obtained by analysing the data set six times -
scaling 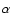 by (
1 + [-1,0,+1]
by (
1 + [-1,0,+1] 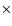
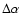 )
and
applying both analysis techniques. The rms of the resulting six flux
points in each energy bin was taken as the systematic
uncertainty. The uncertainty in the energy scale is a global
uncertainty which might cause a shift of the whole spectrum to lower
or larger energies. It is due to uncertainties in the atmospheric
transmission models used in
simulations (see Funk et al. 2004) and uncertainties in
the light collection efficiencies of the telescopes. The combined
error is estimated to be
)
and
applying both analysis techniques. The rms of the resulting six flux
points in each energy bin was taken as the systematic
uncertainty. The uncertainty in the energy scale is a global
uncertainty which might cause a shift of the whole spectrum to lower
or larger energies. It is due to uncertainties in the atmospheric
transmission models used in
simulations (see Funk et al. 2004) and uncertainties in
the light collection efficiencies of the telescopes. The combined
error is estimated to be 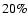 .
.
When fitting a power law with index 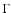 to the spectrum, the
systematic error on the integral flux obtained from the fit function
is conservatively estimated to be
to the spectrum, the
systematic error on the integral flux obtained from the fit function
is conservatively estimated to be 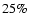 ,
on the fit index it is
,
on the fit index it is
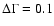 .
.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{4279_f12} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg123.gif) |
Figure 12:
Differential gamma-ray energy spectrum of RX J1713.7-3946, for the
whole region of the SNR (solid black circles). The best fit of a power law with energy dependent photon index is plotted as black line. For comparison the HESS 2003 data points are also shown
(blue open circles). Note the vast increase in energy coverage due
to the increased sensitivity of the complete telescope array. The
spectrum ranges now from 190 GeV to 40 TeV, spanning more than two decades in energy. The data points reported by the CANGAROO-II collaboration (Enomoto et al. 2002) for the northwestern part of the
remnant are also shown as red triangles, the corresponding best
fit result as dashed red line. Error bars are 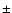 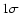 statistical errors. statistical errors. |
| Open with DEXTER |
The spectrum of the whole SNR was determined by integrating events
within
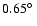 radius around the centre of the SNR,
radius around the centre of the SNR,
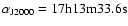 ,
,
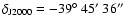 .
OFF events were selected from a reflected region in the same field of view (see Sect. 2.5.2 for explanation and
Fig. 5 for illustration). To ensure optimum match
in the offset distributions of ON and OFF events, runs taken
directly on the source, where no appropriate OFF region can be
selected in the same field of view, were discarded from the spectral
analysis. Accordingly, the total live time reduced slightly to 30.5 h. A size cut of 80 photo-electrons was applied for the spectral analysis. This results in a cumulative significance of
.
OFF events were selected from a reflected region in the same field of view (see Sect. 2.5.2 for explanation and
Fig. 5 for illustration). To ensure optimum match
in the offset distributions of ON and OFF events, runs taken
directly on the source, where no appropriate OFF region can be
selected in the same field of view, were discarded from the spectral
analysis. Accordingly, the total live time reduced slightly to 30.5 h. A size cut of 80 photo-electrons was applied for the spectral analysis. This results in a cumulative significance of  corresponding to
corresponding to  15 400 excess events (normalisation factor
15 400 excess events (normalisation factor
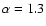 ).
).
Table 1:
Fit results for different spectral models. The
differential flux normalisation I0 and the integral flux above 1 TeV
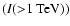 are given in units of
are given in units of
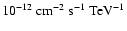 and
and
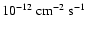 ,
respectively. The power-law fit is clearly an inappropriate description of the data, a power law with an exponential cutoff
(row 2), a power law with an energy dependent photon index (row 3), and a broken power law (row 4; in the formula, the parameter S = 0.4 describes the sharpness of the transition from
,
respectively. The power-law fit is clearly an inappropriate description of the data, a power law with an exponential cutoff
(row 2), a power law with an energy dependent photon index (row 3), and a broken power law (row 4; in the formula, the parameter S = 0.4 describes the sharpness of the transition from 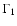 to
to 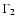 and it is fixed in the fit) are equally likely descriptions of the HESS data. Note that when fitting a broken power law to the data, some of the fit parameters are highly correlated.
and it is fixed in the fit) are equally likely descriptions of the HESS data. Note that when fitting a broken power law to the data, some of the fit parameters are highly correlated.
The resulting spectrum of the whole SNR is shown in
Fig. 12. The data is in excellent agreement with the
previous measurement in 2003, which covered the energy range from
1 TeV to 10 TeV. The latest data span more than two orders of
magnitude in energy, from 190 GeV to 40 TeV. The best fit of a power law with energy dependent photon index is plotted (the exact formula is given below). It describes the data reasonably
well. Table 1 summarises fits of different spectral
shapes to the data. Three alternative shapes have been used: a power
law with an exponential cutoff
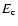 ,
,
a power law with an energy dependent exponent,
and a broken power law (transition from 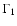 to
to 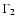 at
break energy
at
break energy
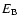 ,
S quantifies the sharpness of the
transition),
,
S quantifies the sharpness of the
transition),
In all cases, I0 is the differential flux normalisation, the
energies E are normalised at 1 TeV and photon indices are
specified with 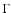 .
.
All three alternative shapes describe the data significantly better
than the pure power law. However, among the alternative spectral
shapes, none is significantly favoured over the others. At the
highest energies, above 10 TeV, there is still a significant
gamma-ray flux in excess of  .
It should be noted, though,
that in order to draw strong conclusions about the high-energy shape
of the spectrum, more data with better statistics at the high-energy
end of the spectrum are needed.
.
It should be noted, though,
that in order to draw strong conclusions about the high-energy shape
of the spectrum, more data with better statistics at the high-energy
end of the spectrum are needed.
The spectrum reported by the CANGAROO-II
collaboration (Enomoto et al. 2002) for the northwest part of the SNR is
also shown in Fig. 12. From a power-law fit to the
data they quoted a photon index
 and a differential flux normalisation at 1 TeV
and a differential flux normalisation at 1 TeV

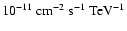 .
The difference between the two spectra is somewhat larger than the quoted errors of the measurements. However,
the CANGAROO-II spectrum is only for a part of the remnant. Moreover
we note that the CANGAROO-II collaboration has recently revised
their systematic errors upwards. For example, the Galactic Centre
photon index, which was initially given as 4.6
.
The difference between the two spectra is somewhat larger than the quoted errors of the measurements. However,
the CANGAROO-II spectrum is only for a part of the remnant. Moreover
we note that the CANGAROO-II collaboration has recently revised
their systematic errors upwards. For example, the Galactic Centre
photon index, which was initially given as 4.6 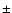 0.5 (Tsuchiya et al. 2004), was recently quoted as
4.6-1.2+5.0 (Katagiri et al. 2005).
0.5 (Tsuchiya et al. 2004), was recently quoted as
4.6-1.2+5.0 (Katagiri et al. 2005).
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{4279_f13} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg158.gif) |
Figure 13:
HESS energy spectrum of RX J1713.7-3946. Plotted are the HESS points with their 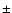 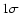 statistical errors in an energy flux diagram. The three curves (specified in
Table 1) are the best fit results of a power law
with an exponential cutoff, a power law with energy dependent
photon index, and a broken power law, extrapolated to 1 GeV to
enable comparisons with the EGRET upper limit in the range of
1-10 GeV. The shaded grey band represents the systematic
uncertainty on the measurement, originating from the uncertainty
on the background estimation. The blue arrow indicates the 20% systematic uncertainty on the energy scale, which might shift the whole curve in the given direction. statistical errors in an energy flux diagram. The three curves (specified in
Table 1) are the best fit results of a power law
with an exponential cutoff, a power law with energy dependent
photon index, and a broken power law, extrapolated to 1 GeV to
enable comparisons with the EGRET upper limit in the range of
1-10 GeV. The shaded grey band represents the systematic
uncertainty on the measurement, originating from the uncertainty
on the background estimation. The blue arrow indicates the 20% systematic uncertainty on the energy scale, which might shift the whole curve in the given direction. |
| Open with DEXTER |
Figure 13 illustrates the three spectral
shapes that were found to describe the data reasonably well. The
three curves are extrapolated to 1 GeV to compare them with the
EGRET upper limit on the energy flux of 4.9 
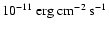 ,
ranging from 1 GeV to 10 GeV, centred at 2.9 GeV. The limit was determined
at the HESS position of RX J1713.7-3946 by modelling and subtracting the
known EGRET source 3EG 1714-3857 (Hartman et al. 1999),
assuming that 3EG 1714-3857 is not linked to the
gamma-ray emission of RX J1713.7-3946. Since the HESS location is in close
vicinity of 3EG 1714-3857 (actually it is overlapping),
this procedure could only be carried out successfully above 1 GeV. The systematic error band for the HESS data was obtained as described above. It is centred on the mean value of the three fit
curves and represents the systematic error due to background
uncertainties only. The energy scale is an energy independent
uncertainty; its scale and the direction the curve is shifted to are
marked with a blue arrow at one representative position (at 15 TeV). It is worth noting that the systematic uncertainty on the background has a considerable impact on the first few flux points
because of the smaller signal-to-noise ratio (as compared to points
at higher energies). For the spectrum shown here the systematic
uncertainty is
,
ranging from 1 GeV to 10 GeV, centred at 2.9 GeV. The limit was determined
at the HESS position of RX J1713.7-3946 by modelling and subtracting the
known EGRET source 3EG 1714-3857 (Hartman et al. 1999),
assuming that 3EG 1714-3857 is not linked to the
gamma-ray emission of RX J1713.7-3946. Since the HESS location is in close
vicinity of 3EG 1714-3857 (actually it is overlapping),
this procedure could only be carried out successfully above 1 GeV. The systematic error band for the HESS data was obtained as described above. It is centred on the mean value of the three fit
curves and represents the systematic error due to background
uncertainties only. The energy scale is an energy independent
uncertainty; its scale and the direction the curve is shifted to are
marked with a blue arrow at one representative position (at 15 TeV). It is worth noting that the systematic uncertainty on the background has a considerable impact on the first few flux points
because of the smaller signal-to-noise ratio (as compared to points
at higher energies). For the spectrum shown here the systematic
uncertainty is 
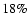 for the two lowest-energy points; it
decreases rapidly with increasing energy being well below
for the two lowest-energy points; it
decreases rapidly with increasing energy being well below 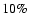 at 350 GeV.
at 350 GeV.
![\begin{figure}
\par\includegraphics[width=15.9cm,clip]{4279_f14} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg161.gif) |
Figure 14:
The image illustrates the results of the spatially
resolved spectral analysis. Left part: shown in red are
gamma-ray excess contours from Fig. 7,
linearly spaced at 30, 60, and 90 counts. Superimposed are the
14 boxes (each
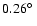 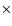
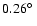 in dimension) for
which spectra were obtained independently. The dashed line is
the
in dimension) for
which spectra were obtained independently. The dashed line is
the
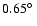 radius circle that was used to integrate events
to produce a spectrum of the whole SNR. The photon index
obtained from a power-law fit in each region is colour coded in
bins of 0.1. The ranges of the fits to the spectra have been
restricted to a maximum of 8 TeV (see Table 2). Right part: plotted is the integral flux above 1 TeV against the photon index, for the 14 regions the SNR was
sub-divided in. The error bars are radius circle that was used to integrate events
to produce a spectrum of the whole SNR. The photon index
obtained from a power-law fit in each region is colour coded in
bins of 0.1. The ranges of the fits to the spectra have been
restricted to a maximum of 8 TeV (see Table 2). Right part: plotted is the integral flux above 1 TeV against the photon index, for the 14 regions the SNR was
sub-divided in. The error bars are 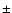 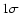 statistical
errors. Note that systematic errors of 25% on the flux and 0.1
on the photon index are to be assigned to each data point additionally. statistical
errors. Note that systematic errors of 25% on the flux and 0.1
on the photon index are to be assigned to each data point additionally. |
| Open with DEXTER |
Table 2:
Fit results for distinct regions of the SNR. Given are
for each region the photon index resulting from a power-law fit,
the best-fit 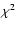 and the number of degrees of freedom (d.o.f.), the integral flux above 1 TeV and the significance of the excess events in units of standard deviation
and the number of degrees of freedom (d.o.f.), the integral flux above 1 TeV and the significance of the excess events in units of standard deviation 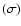 .
The
background for each region was determined from the same field of
view, as described in Sect. 2.5.2, for
each region separately, and hence the background estimates for
different regions are not independent. The first row is the fit
result of the whole SNR for comparison. For the whole table, the
upper fit range was restricted to 8 TeV to avoid biases due to
the deviation from a power law at high energies.
.
The
background for each region was determined from the same field of
view, as described in Sect. 2.5.2, for
each region separately, and hence the background estimates for
different regions are not independent. The first row is the fit
result of the whole SNR for comparison. For the whole table, the
upper fit range was restricted to 8 TeV to avoid biases due to
the deviation from a power law at high energies.
The results of the spatially resolved spectral analysis are shown in
Fig. 14. It shows the distribution of photon
indices over the SNR resulting from a power-law fit. The spectra
were determined in rectangular regions, denoted 1-14, each
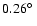
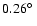 in dimension. The fit range was limited
to 8 TeV to account for (and avoid when fitting) the deviation from
a power law seen in the spectrum of the whole
remnant. Table 2 summarises the fit results. There
is a significant flux variation over the SNR. From the brightest
region in the northwest to a relatively dim one in the central part,
the flux varies by more than a factor of two. There is no
significant difference in spectral shape apparent, the photon
indices agree with each other within statistical and systematic
errors. The distribution of photon indices has a mean value of 2.09
with a root-mean-square of 0.07. This is well compatible with the
spectrum of the whole SNR when the fit range is also restricted to
maximum 8 TeV for consistency (first row in
Table 2). If one adds up the integral fluxes above
1 TeV of the individual regions, a flux of 15.1
in dimension. The fit range was limited
to 8 TeV to account for (and avoid when fitting) the deviation from
a power law seen in the spectrum of the whole
remnant. Table 2 summarises the fit results. There
is a significant flux variation over the SNR. From the brightest
region in the northwest to a relatively dim one in the central part,
the flux varies by more than a factor of two. There is no
significant difference in spectral shape apparent, the photon
indices agree with each other within statistical and systematic
errors. The distribution of photon indices has a mean value of 2.09
with a root-mean-square of 0.07. This is well compatible with the
spectrum of the whole SNR when the fit range is also restricted to
maximum 8 TeV for consistency (first row in
Table 2). If one adds up the integral fluxes above
1 TeV of the individual regions, a flux of 15.1 
 is obtained, 5% less than the flux of the whole SNR (with the restriction of the fit range). This
is in excellent agreement with expectations; the boxes as they are
plotted in Fig. 14 cover the region of RX J1713.7-3946 with significant gamma-ray excess almost completely.
is obtained, 5% less than the flux of the whole SNR (with the restriction of the fit range). This
is in excellent agreement with expectations; the boxes as they are
plotted in Fig. 14 cover the region of RX J1713.7-3946 with significant gamma-ray excess almost completely.
As can be seen from Fig. 14, right part,
there is no correlation of the gamma-ray flux and the photon index
visible in the data. This, together with the absence of any change
in the spectral shape, is a remarkable difference between the
gamma-ray and X-ray data. The spectral variation in X-rays was found
to be much larger (see Cassam-Chenaï et al. 2004).
4.1 Comparison with X-rays
There is a striking similarity between the X-ray and the gamma-ray
image of RX J1713.7-3946, as they are shown in Fig. 15 for the
1-5 keV X-ray band. The overall morphology appears to be very
similar, the brightest spots in both images are distributed on the
shell, especially in the west. For a detailed comparison one must
take into account the slightly better resolution of ASCA compared to HESS. For that purpose, the ASCA image was smoothed beyond the point-spread function of the instrument in order to match the HESS resolution. The smoothing radius was determined empirically by smoothing the ASCA point-spread function and comparing it with the HESS point-spread function. An optimum match was obtained for a smoothing radius of
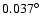 .
Furthermore, both images in Fig. 15 are corrected for relative detector acceptance. The X-ray-bright central point source 1WGA J1713.4-3949, which was argued to be the compact relic of the supernova progenitor (see for example Cassam-Chenaï et al. 2004), was removed from the X-ray image for the purpose of comparison with gamma rays.
.
Furthermore, both images in Fig. 15 are corrected for relative detector acceptance. The X-ray-bright central point source 1WGA J1713.4-3949, which was argued to be the compact relic of the supernova progenitor (see for example Cassam-Chenaï et al. 2004), was removed from the X-ray image for the purpose of comparison with gamma rays.
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{4279_f15} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg194.gif) |
Figure 15:
ASCA X-ray (1-5 keV band, Uchiyama 2005) image
of RX J1713.7-3946, overlaid with contours of the smoothed,
acceptance-corrected HESS gamma-ray image. The coloured contour
levels are labelled and linearly spaced at 30, 60, and 90 counts. Drawn as gray thin lines are eight wedge-shaped regions for which the radial profiles are compared to each other in
Fig. 16. Note that in the ASCA image, most
of the regions (faint solid lines) do not reach as far as in the
HESS image (faint dashed lines), accounting for the limited
field of view of ASCA, whose coverage did not always extend to the
boundaries of the SNR. As explained in the main text, the ASCA image was smoothed to match the HESS point-spread function to enable comparison of the two images. |
| Open with DEXTER |
After degradation of ASCA's resolution, the data were compared to
each other in eight wedge-shaped regions as they are drawn in
Fig. 15. In each wedge, radial profiles, that is,
the number of counts per unit solid angle as function of distance to
the centre, were determined. To account for the differences in the
absolute count level the X-ray images were scaled by a normalisation
factor, which has been calculated as the ratio of TeV counts,
integrated in a rectangle encompassing the SNR (and within the ASCA field of view), to keV counts, integrated in the same rectangle. The result is shown in Fig. 16 for all eight
wedges. The overall good agreement in shape of the profiles is
clearly visible, differences appear only at a few places, for
example in region 4 and 7. For a quantitative statement on the
compatibility of the two data sets, however, one would have to model
and subtract the contribution from Galactic diffuse X-ray emission
in the ASCA image, which amounts presumably to 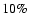 or less in the
X-ray bright parts of the SNR, but might increase to
or less in the
X-ray bright parts of the SNR, but might increase to 
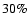 in the faint parts in the east.
in the faint parts in the east.
The interesting question of the boundaries of the SNR and if they
are the same in X-rays and gamma rays can unfortunately not be
addressed with the ASCA data set due to limited sky coverage.
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{4279_f16} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg195.gif) |
Figure 16:
Radial profiles for the eight regions marked in
Fig. 15. Plotted are HESS excess counts per unit
solid angle (solid circles) as a function of distance r in
degrees to the centre of the SNR, compared to soft (1-5 keV) and
hard (5-10 keV) X-ray data. All data were corrected for relative
acceptance. There is a very good general agreement between the keV
and TeV data sets. The most pronounced differences appear in
regions 4, where the TeV flux drops almost to zero at 
 from the centre, and 7, where a pronounced peak appears in the 1-5 keV X-ray data, which repeats neither in the 5-10 keV X-ray nor the TeV data. Note that the X-ray emission includes diffuse Galactic X-ray emission.
from the centre, and 7, where a pronounced peak appears in the 1-5 keV X-ray data, which repeats neither in the 5-10 keV X-ray nor the TeV data. Note that the X-ray emission includes diffuse Galactic X-ray emission. |
| Open with DEXTER |
4.2 CO and radio observations
![\begin{figure}
\par\includegraphics[width=16.05cm,clip]{4279_f17} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg201.gif) |
Figure 17:
Left panel: shown are the intensity distribution
of CO (J = 1-0) emission (Fukui et al. 2003) (linear colour
scale in units of
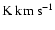 ,
truncated at a value of 23 to highlight important features),
derived by integrating the CO spectra in the velocity range from ,
truncated at a value of 23 to highlight important features),
derived by integrating the CO spectra in the velocity range from
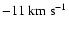 to
to
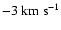 (which corresponds to
(which corresponds to
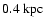 to
to
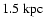 in space). Overlaid are
coloured contours of the HESS gamma-ray excess image. The levels
are labelled and linearly spaced at 30, 60, and 90 counts. Note
that the image is shown in Galactic coordinates. Right
panel: azimuth profile plot, that is, number of counts as a function of the azimuthal angle, integrated in a
in space). Overlaid are
coloured contours of the HESS gamma-ray excess image. The levels
are labelled and linearly spaced at 30, 60, and 90 counts. Note
that the image is shown in Galactic coordinates. Right
panel: azimuth profile plot, that is, number of counts as a function of the azimuthal angle, integrated in a
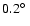 -wide ring covering the shell of RX J1713.7-3946 (dashed yellow circle in the left-hand panel). Plotted are the HESS gamma-ray and the NANTEN data set. -wide ring covering the shell of RX J1713.7-3946 (dashed yellow circle in the left-hand panel). Plotted are the HESS gamma-ray and the NANTEN data set. |
| Open with DEXTER |
CO data at 2.6 mm wavelength of RX J1713.7-3946 and its surroundings were
taken with the 4-m, mm and sub-mm telescope NANTEN in
2003 (Fukui et al. 2003). Based on positional coincidences of CO
and X-ray peaks and (in velocity space) shifted CO peaks,
Fukui et al. (2003) concluded that the SNR blast wave is
interacting with molecular clouds situated on its western side at a distance of 
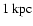 .
Further possible support for this scenario was recently published in Moriguchi et al. (2005), where
high gas excitations are reported for this part, which could arise
from heating of the molecular gas by the shock wave. The CO intensity distribution in the corresponding velocity interval is shown in Fig. 17, together with HESS gamma-ray
excess contours. One notes that in the central and southeastern part
of the SNR the CO emission becomes very faint or is completely
absent. Apart from that, there are local CO maxima that coincide
with TeV-bright parts on the western side of the SNR. The azimuth
profile plotted on the right-hand side of Fig. 17
illustrates a global agreement between the two measurements, regions
with low gamma-ray flux reveal also low CO intensity, but there is
no exact proportionality between the two measurements for the shell
region of RX J1713.7-3946. Taking the peak values, one notes that they are
shifted with respect to each other and that the gamma-ray flux
varies by a factor of about three, whereas the CO intensity drops by
roughly a factor of 100 in the central-southeastern part.
.
Further possible support for this scenario was recently published in Moriguchi et al. (2005), where
high gas excitations are reported for this part, which could arise
from heating of the molecular gas by the shock wave. The CO intensity distribution in the corresponding velocity interval is shown in Fig. 17, together with HESS gamma-ray
excess contours. One notes that in the central and southeastern part
of the SNR the CO emission becomes very faint or is completely
absent. Apart from that, there are local CO maxima that coincide
with TeV-bright parts on the western side of the SNR. The azimuth
profile plotted on the right-hand side of Fig. 17
illustrates a global agreement between the two measurements, regions
with low gamma-ray flux reveal also low CO intensity, but there is
no exact proportionality between the two measurements for the shell
region of RX J1713.7-3946. Taking the peak values, one notes that they are
shifted with respect to each other and that the gamma-ray flux
varies by a factor of about three, whereas the CO intensity drops by
roughly a factor of 100 in the central-southeastern part.
Figure 18 shows a comparison of the 1.4 GHz radio
image obtained with ATCA (Lazendic et al. 2004) and the HESS gamma-ray
excess contours. The SNR is very faint in the radio band, there are
two faint arc-like structures of emission to the west of RX J1713.7-3946,
almost perpendicular to each other, one of them directly coincident
with the brightest TeV emission region. There is no notable
resemblance between the two wavelength regimes. Spectral analysis of
the X-ray- and TeV-bright northwestern part of the SNR shell yields
a spectral index of 0.50 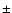 0.40, derived from two flux values
taken at 1.4 GHz and 2.5 GHz. This measurement is used further down
when comparing the HESS spectral data to broadband models.
0.40, derived from two flux values
taken at 1.4 GHz and 2.5 GHz. This measurement is used further down
when comparing the HESS spectral data to broadband models.
5 Possible emission processes
One of the key issues in the interpretation of the observed
gamma-ray emission is the identification of the particle population
responsible for the generation of the gamma rays. The close
correlation between X-rays and gamma rays might indicate an
electronic origin; models of supernova remnants as Galactic
cosmic-ray sources, on the other hand, suggest that primarily a hadronic component from pion decays exists. To identify the different contributions, the wide-band electromagnetic spectra from
radio to multi-TeV gamma-rays must be compared to model calculations.
In the literature, different schemes are employed to model broadband
emission from SNRs. Phenomenologically oriented
models (Aharonian & Atoyan 1999; Mastichiadis & de Jager 1996) start by ad hoc assuming
particle acceleration spectra - usually as power laws with a cutoff - to derive particle spectra taking into account energy losses and then calculate the electromagnetic spectrum with additional
assumptions concerning the local magnetic field, the radiation
fields which serve as target for the IC process, and the gas
density. Spectral parameters are either taken from acceleration
models, resulting in a spectral index around 2, or determined from
data. More sophisticated gamma-ray models account for the non-linear
effects arising from the interaction of the accelerated particles
with the shocked supernova shell, which result in deviations from
pure power laws, with spectra flattening at higher
energies (Baring et al. 1999; Berezhko & Völk 1997).
The original discovery paper of VHE gamma-ray emission from
RX J1713.7-3946 (Muraishi et al. 2000) claimed electrons as the likely source particle
population. However, it soon became evident that a consistent
modelling of the spectra is hard to achieve in simple one-zone
models. Apart from the choice of the electron spectrum, the only
free parameter is the magnetic field strength, which controls the
spacing of the synchrotron and IC peaks in the SED together with
their relative intensities and - one should add - the amount of
radiative cooling of the accelerated component. Enomoto et al. (2002) noted
that for modest magnetic fields - B equal to a few 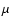 G - the
measured intensity ratios are reproduced but the gamma-ray spectra
are much too hard. Using higher fields, one can match the gamma-ray
spectra at the expense of dramatically increased X-ray yields. While
the HESS data differ from the CANGAROO-II data both in terms of
the region covered and the exact values for flux and index, this
conclusion for the electronic scenario remains basically valid. The
agreement can be improved by introducing an additional parameter to
decouple the X-ray intensity and the spectral shape, namely the
magnetic field filling factor which allows the X-ray flux to be
tuned without change of the spectra. With very small filling factors
of 0.001 (Pannuti et al. 2003) to 0.01 (Lazendic et al. 2004), difficult to
justify physically, the X-ray and the CANGAROO-II gamma-ray spectra
can be described for magnetic fields around 10
G - the
measured intensity ratios are reproduced but the gamma-ray spectra
are much too hard. Using higher fields, one can match the gamma-ray
spectra at the expense of dramatically increased X-ray yields. While
the HESS data differ from the CANGAROO-II data both in terms of
the region covered and the exact values for flux and index, this
conclusion for the electronic scenario remains basically valid. The
agreement can be improved by introducing an additional parameter to
decouple the X-ray intensity and the spectral shape, namely the
magnetic field filling factor which allows the X-ray flux to be
tuned without change of the spectra. With very small filling factors
of 0.001 (Pannuti et al. 2003) to 0.01 (Lazendic et al. 2004), difficult to
justify physically, the X-ray and the CANGAROO-II gamma-ray spectra
can be described for magnetic fields around 10 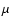 G to 15
G to 15 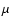 G
in the emitting region. This latter approach is not followed here.
G
in the emitting region. This latter approach is not followed here.
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{4279_f18} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg205.gif) |
Figure 18:
1.4 GHz ATCA radio image (Lazendic et al. 2004, courtesy of
P. Slane). The linear colour scale is in units of
 .
Overlaid are coloured contour lines of the HESS gamma-ray excess image. .
Overlaid are coloured contour lines of the HESS gamma-ray excess image. |
| Open with DEXTER |
The validity of electronic models could be judged more easily if the
magnetic field values in the remnant were known. For typical shock
compression ratios around 4 and pre-shock interstellar fields of a few 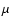 G, fields of 10
G, fields of 10 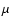 G to 15
G to 15 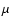 G are at the lower limit of the expected range; mechanisms of dynamical field amplification in non-linear shocks (Bell 2004; Lucek & Bell 2000; Bell & Lucek 2001) will
generally result in higher fields. The narrow filaments visible in
many high-resolution X-ray images of SNRs (see,
e.g., Bamba et al. 2005) have been pointed out to provide means to probe
magnetic fields (Vink & Laming 2003; Berezhko et al. 2003): only relatively high
fields can result in sufficiently rapid cooling of electrons to make
such filamentary features possible and visible. On the basis of the
structures seen in Chandra images in the northwest of
RX J1713.7-3946 (Uchiyama et al. 2003), Völk et al. (2005) have argued that
fields between 58
G are at the lower limit of the expected range; mechanisms of dynamical field amplification in non-linear shocks (Bell 2004; Lucek & Bell 2000; Bell & Lucek 2001) will
generally result in higher fields. The narrow filaments visible in
many high-resolution X-ray images of SNRs (see,
e.g., Bamba et al. 2005) have been pointed out to provide means to probe
magnetic fields (Vink & Laming 2003; Berezhko et al. 2003): only relatively high
fields can result in sufficiently rapid cooling of electrons to make
such filamentary features possible and visible. On the basis of the
structures seen in Chandra images in the northwest of
RX J1713.7-3946 (Uchiyama et al. 2003), Völk et al. (2005) have argued that
fields between 58 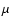 G and a few 100
G and a few 100 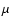 G might be possible,
depending on the detailed assumptions about the remnant's
morphology
G might be possible,
depending on the detailed assumptions about the remnant's
morphology![[*]](/icons/foot_motif.gif) . Such high fields - likely to be present throughout the remnant - would rule out a leptonic origin of VHE gamma rays right away.
. Such high fields - likely to be present throughout the remnant - would rule out a leptonic origin of VHE gamma rays right away.
On the basis of the difficulty of accommodating broadband spectra in
a single-zone electronic model, Enomoto et al. (2002) proposed RX J1713.7-3946 as the
first well-identified proton accelerator. This interpretation was
criticised by Butt et al. (2002) and Reimer & Pohl (2002) since the
CANGAROO-II spectra, extrapolated to lower energies, would violate
the flux level of the nearby EGRET source
3EG 1714-3857 (Hartman et al. 1999), which, if not associated
with RX J1713.7-3946, must then be considered as upper limit on the GeV emission. However, the EGRET limit can be circumvented by reducing the amount of low-energy protons compared to the E-2 spectrum. This can be achieved by the ad hoc assumption of a spectral break, or - for the CANGAROO-II data - by assuming a flatter overall spectrum with a photon index smaller than 2.
A very detailed modelling is beyond the scope of this paper; the
models presented in the following serve mainly to illustrate that
spectra and energetics can be reproduced with plausible input parameters.
In Fig. 19 the synchrotron and IC emission from
relativistic electrons are modelled within the framework of a one-zone model in which the electron acceleration and gamma-ray emission take place in the same region. It is assumed that the
primary electrons follow a power law with index
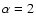 and
with an exponential cutoff E0,
and
with an exponential cutoff E0,
and that they are produced continuously over a fixed time interval T inside a region with given homogeneous distributions of magnetic field strength B and ambient gas density n. The energy
distribution of the electrons is then calculated taking into account
energy losses due to IC and synchrotron emission, Bremsstrahlung and
ionisation as well as losses due to Bohm diffusion. The broadband
energy distribution of the source is calculated for an age of T =
1000 years, an average gas density of
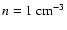 ,
and
a distance to the source of
,
and
a distance to the source of
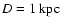 .
For the IC emission, canonical interstellar values for the seed photon densities were considered:
.
For the IC emission, canonical interstellar values for the seed photon densities were considered:
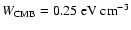 for the cosmic microwave background (CMB),
for the cosmic microwave background (CMB),
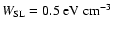 for optical star light and
for optical star light and
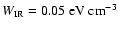 for infrared
background light. The absolute electron production rate, Q0, is
determined from the constraint of matching the observed X-ray flux
level. Figure 19 shows the resulting model curves,
together with measurements in various wavelength regimes, for three different average magnetic field values. From the absolute levels it is evident that a magnetic field around
for infrared
background light. The absolute electron production rate, Q0, is
determined from the constraint of matching the observed X-ray flux
level. Figure 19 shows the resulting model curves,
together with measurements in various wavelength regimes, for three different average magnetic field values. From the absolute levels it is evident that a magnetic field around
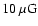 is required in order to explain both the X-ray and gamma-ray flux
levels. On the other hand one notes that such a model with the above
mentioned parameters does not provide a reasonable description of
the HESS data. The IC peak appears too narrow to reproduce the
flat TeV emission. The detailed inclusion of non-linear acceleration
effects should not change the situation very much. They are expected
to steepen the synchrotron SED above the radio range. Synchrotron
cooling of the accelerated electrons then tends to produce a flat-topped synchrotron and accordingly IC maximum. It is, however, a long way to flatten the IC spectrum so extensively at low energies as to achieve agreement with the HESS spectrum.
is required in order to explain both the X-ray and gamma-ray flux
levels. On the other hand one notes that such a model with the above
mentioned parameters does not provide a reasonable description of
the HESS data. The IC peak appears too narrow to reproduce the
flat TeV emission. The detailed inclusion of non-linear acceleration
effects should not change the situation very much. They are expected
to steepen the synchrotron SED above the radio range. Synchrotron
cooling of the accelerated electrons then tends to produce a flat-topped synchrotron and accordingly IC maximum. It is, however, a long way to flatten the IC spectrum so extensively at low energies as to achieve agreement with the HESS spectrum.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4279_f19} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg221.gif) |
Figure 19:
Broadband SED of RX J1713.7-3946. The ATCA radio data and ASCA X-ray
data (Hiraga 2005) for the whole SNR are indicated, along
with the HESS measurement and the EGRET upper limit. Note that
the radio flux was determined in Lazendic et al. (2004) for the
northwest part of the shell only and was scaled up by a factor of
two here to account for the whole SNR. The synchrotron and IC spectra were modelled assuming a source distance of 1 kpc, an age T of 1000 years, a density n of
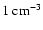 ,
and a production rate of relativistic electrons by the acceleration mechanism in the form of a power law of index ,
and a production rate of relativistic electrons by the acceleration mechanism in the form of a power law of index
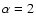 and an exponential cutoff of
and an exponential cutoff of
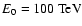 .
Shown are three curves for three values of the mean magnetic field: .
Shown are three curves for three values of the mean magnetic field:
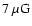 , ,
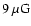 ,
and ,
and
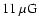 ,
to demonstrate the required range of the B field strength for this scenario. The electron luminosity is adopted such that the observed X-ray flux level is well matched. For the three magnetic field values the luminosity ,
to demonstrate the required range of the B field strength for this scenario. The electron luminosity is adopted such that the observed X-ray flux level is well matched. For the three magnetic field values the luminosity
 is
is
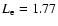 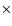
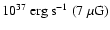 , ,
 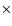
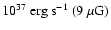 ,
and ,
and
 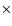
 . . |
| Open with DEXTER |
Obviously, the simple model presented here served basically to
underline the main arguments. Nevertheless, the conclusion that a power-law production spectrum fails to simultaneously account for the radio, X-ray and gamma-ray data appears to be a generic and
stable feature; additional parameters are required to decouple
either the TeV and X-ray/radio fluxes - such as a
filling factor -
or the X-ray and radio spectra - such as an ad-hoc spectral break,
which for the given source age and magnetic field can not be
justified as an effect of radiative cooling.
Assuming alternatively that nuclear cosmic-ray particles,
accelerated at the SNR shock, dominantly produce VHE gamma rays,
theoretically the most plausible differential energy spectrum of
accelerated nuclei is a concave
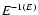 -type spectrum, due
to nonlinear back coupling, with a cutoff at gamma-ray energy
-type spectrum, due
to nonlinear back coupling, with a cutoff at gamma-ray energy 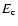 ,
where
,
where  is decreasing towards higher energies (just below the TeV energy range) to a value between 1.5 and 2,
before the spectrum is steepening again in the cutoff region. In the
test-particle approximation one expects
is decreasing towards higher energies (just below the TeV energy range) to a value between 1.5 and 2,
before the spectrum is steepening again in the cutoff region. In the
test-particle approximation one expects
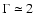 .
The
HESS spectrum is indeed compatible with such a scenario. Figure 20 shows a
.
The
HESS spectrum is indeed compatible with such a scenario. Figure 20 shows a  representation of the HESS data, together with the best-fit curve of a power law with an exponential cutoff (see Sect. 3.2, Table 1), extrapolated to
small energies. Compared to that a curve is plotted which takes the
kinematics of the production process of gamma rays, pp
representation of the HESS data, together with the best-fit curve of a power law with an exponential cutoff (see Sect. 3.2, Table 1), extrapolated to
small energies. Compared to that a curve is plotted which takes the
kinematics of the production process of gamma rays, pp
 ,
into account. The power law
spectrum continues to smaller energies with an index of
,
into account. The power law
spectrum continues to smaller energies with an index of  2,
as expected in the test-particle limit, until the suppression of
gamma rays due to
2,
as expected in the test-particle limit, until the suppression of
gamma rays due to  -decay kinematics is encountered and the
curve is turning down. Note that already the extrapolation of the
HESS spectrum is well below the EGRET upper limit from the
position of RX J1713.7-3946, introduced in Sect. 3.2. Taking
into account non-linear effects would harden the gamma-ray spectrum
even more.
-decay kinematics is encountered and the
curve is turning down. Note that already the extrapolation of the
HESS spectrum is well below the EGRET upper limit from the
position of RX J1713.7-3946, introduced in Sect. 3.2. Taking
into account non-linear effects would harden the gamma-ray spectrum
even more.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4279_f20} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg227.gif) |
Figure 20:
HESS data points plotted in an energy flux
diagram. The shaded grey band is the systematic error band for
this measurement (see Sect. 3.2). The black
curve is the best fit of a power law with exponential cutoff to
the data, extrapolated to lower energies. The dashed blue curves
is the same function, but it takes the  kinematics into
account. The EGRET upper limit from 1 GeV to 10 GeV is plotted
as red arrow. kinematics into
account. The EGRET upper limit from 1 GeV to 10 GeV is plotted
as red arrow. |
| Open with DEXTER |
One should mention at this point that on the theory side other
mechanisms to suppress contributions from low-energy (E around
10 GeV) protons have been considered (e.g., Malkov et al. 2005). When
the particles upstream of the shock hit a dense target with a spatial gradient, such as a dense molecular cloud, the gamma-ray emission of low-energy protons might also be suppressed due to the
energy dependence of the diffusion length. In a more general
context, such mechanisms - an accelerator of finite lifetime
interacting with a target at a distance where diffusion time scales
are comparable to the source lifetime - have been studied by
Aharonian & Atoyan (1996). Such arguments, however, need to be reassessed
when the exact location of the clouds with respect to the shock
front is known.
To calculate the energetics in a hadronic scenario, the mean target
gas density available for gamma-ray production in the region of
RX J1713.7-3946 is a key question. The CO image shown in
Fig. 17, left-hand side, reveals a hole in the CO emission and accordingly in the molecular hydrogen distribution in the central and eastern part of the SNR. In contrast, the TeV emission fills the whole region of the SNR (see
Fig. 7). As is shown on the right-hand side of
Fig. 17, there is no exact correlation between VHE gamma rays and CO intensity. From this one can conclude that in all
likelihood cosmic rays do not penetrate the clouds uniformly. The
bulk of the VHE gamma rays is not linked to the molecular clouds but
must be due to interactions with a different target. Indeed, the
rather good spherical shape of the remnant together with the fact
that the X-ray and gamma-ray emission only varies by a factor of two
to four across the remnant lends further support to the scenario
that the SNR is running into a more or less uniform and probably
low-density environment. Although it seems to be beginning to
interact with the dense clouds to the west, the ones that are seen
by NANTEN, VHE gamma rays are dominantly produced in cosmic-ray
interactions with rather uniform ambient gas. One possible scenario
is that the SNR is the result of a core-collapse supernova explosion
that occurred into a wind bubble of a massive progenitor star. An SNR shock expanding into the bubble, with an ambient density much lower than that suggested by an average molecular cloud scenario, could explain the relative uniformity of the gamma-ray emission,
compared to the large density variations in the clouds which likely
surround the remnant (for a theoretical treatment of such
configurations, see Berezhko & Völk 2000).
The local target density is a crucial parameter in this
scenario. With the NANTEN measurement of the void in the central
part of the SNR one might constrain the local density in that
region. The sensitivity of the final NANTEN data set as quoted in
Fukui et al. (2003) corresponds to a molecular column density of
8.3 
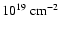 assuming the conventional
conversion relation from CO intensity to
assuming the conventional
conversion relation from CO intensity to 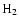 column
density (
column
density (
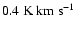 ). Taking the
diameter of the SNR as
). Taking the
diameter of the SNR as 
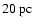 for
for
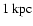 distance, one can deduce an upper limit on the molecular hydrogen column density of
distance, one can deduce an upper limit on the molecular hydrogen column density of 
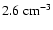 in parts of the SNR without detectable CO emission. The other
existing constraint was inferred in Cassam-Chenaï et al. (2004) from XMM data,
based on the lack of thermal X-ray emission. By fitting the spectra
with an absorbed power-law model and adding a thermal component, an upper limit on the mean gas temperature and, important here, the mean hydrogen number density of the ambient pre-shock medium of
in parts of the SNR without detectable CO emission. The other
existing constraint was inferred in Cassam-Chenaï et al. (2004) from XMM data,
based on the lack of thermal X-ray emission. By fitting the spectra
with an absorbed power-law model and adding a thermal component, an upper limit on the mean gas temperature and, important here, the mean hydrogen number density of the ambient pre-shock medium of
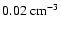 was obtained. One should note, though, that
this value is likely to be too low - if the shocks are strongly
modified by the accelerated particles, the shock heating is
substantially reduced and the data would be consistent with higher
densities.
was obtained. One should note, though, that
this value is likely to be too low - if the shocks are strongly
modified by the accelerated particles, the shock heating is
substantially reduced and the data would be consistent with higher
densities.
Assuming for now a mean target gas density of
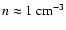 ,
uniformly spread throughout the remnant, in
accordance with the NANTEN, but not the XMM limit, one can calculate
the proton energetics implied by the gamma-ray flux measured from 0.2 to 40 TeV. The total energy in accelerated protons from about 2-400 TeV, required to provide the observed flux, can be
estimated as
,
uniformly spread throughout the remnant, in
accordance with the NANTEN, but not the XMM limit, one can calculate
the proton energetics implied by the gamma-ray flux measured from 0.2 to 40 TeV. The total energy in accelerated protons from about 2-400 TeV, required to provide the observed flux, can be
estimated as
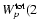 -
-
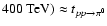
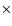
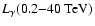 ,
where
,
where
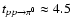
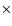
 is the characteristic cooling time of protons through the
is the characteristic cooling time of protons through the  production channel,
production channel,
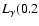 -
-
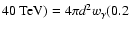 -
-
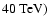 is the luminosity of the source in gamma
rays between 0.2 and 40 TeV, and
is the luminosity of the source in gamma
rays between 0.2 and 40 TeV, and
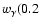 -
-
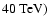 is the gamma-ray energy flux for the corresponding energy
range. Assuming then that the proton spectrum with spectral index
is the gamma-ray energy flux for the corresponding energy
range. Assuming then that the proton spectrum with spectral index
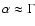 continues down to 1 GeV, the total energy in
protons can be estimated and compared to the total assumed
mechanical explosion energy of the supernova of
continues down to 1 GeV, the total energy in
protons can be estimated and compared to the total assumed
mechanical explosion energy of the supernova of
 .
These calculations reveal very similar values for the three spectral shapes given in
Fig. 20 in the gamma-ray energy range between 0.2
and 40 TeV: for the gamma-ray energy flux one obtains
.
These calculations reveal very similar values for the three spectral shapes given in
Fig. 20 in the gamma-ray energy range between 0.2
and 40 TeV: for the gamma-ray energy flux one obtains
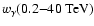
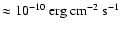 ,
the
gamma-ray luminosity is
,
the
gamma-ray luminosity is
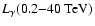
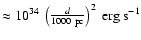 ,
and the corresponding energy content of protons is
,
and the corresponding energy content of protons is
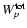 (2-400
(2-400
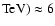
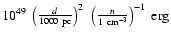 .
The
resulting total energy in protons, after extrapolating the proton
spectrum to 1 GeV and using
.
The
resulting total energy in protons, after extrapolating the proton
spectrum to 1 GeV and using
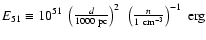 ,
is then
,
is then
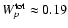
 E51 for a power law with
exponential cutoff,
E51 for a power law with
exponential cutoff,
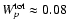
 E51 for a power law with energy dependent index, and
E51 for a power law with energy dependent index, and
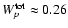
 E51 for a broken power law. These numbers
are consistent with the notion of an SNR origin of Galactic cosmic
rays involving the canonical
E51 for a broken power law. These numbers
are consistent with the notion of an SNR origin of Galactic cosmic
rays involving the canonical 
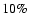 conversion efficiency of
the total supernova explosion energy. The HESS gamma-ray flux
level is close to what was predicted in Drury et al. (1994) from nearby
young SNRs for ambient densities of
conversion efficiency of
the total supernova explosion energy. The HESS gamma-ray flux
level is close to what was predicted in Drury et al. (1994) from nearby
young SNRs for ambient densities of
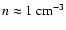 .
One should keep in mind though that the order
of magnitude uncertainties in the measurements of the distance to
the source d and of the local gas density n feed directly into
these estimates.
.
One should keep in mind though that the order
of magnitude uncertainties in the measurements of the distance to
the source d and of the local gas density n feed directly into
these estimates.
5.3 Discussion and conclusions
The models and ideas presented in this section were aiming at
exploring the possibilities available in explaining the observed VHE emission in purely electronic and purely hadronic scenarios. It is found that in the hadronic scenario, assuming gamma rays to stem from 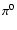 decays, the extrapolation of the HESS spectrum to
lower gamma-ray energies leads to a picture that is consistent with
the low-energy EGRET data. Furthermore, the spectral shape is well
compatible with cosmic-ray acceleration theory. The energy
requirements implied by the gamma-ray flux are in agreement with
expectations from cosmic-ray acceleration in shell-type SNRs in our
Galaxy, if one assumes a local target gas density of
decays, the extrapolation of the HESS spectrum to
lower gamma-ray energies leads to a picture that is consistent with
the low-energy EGRET data. Furthermore, the spectral shape is well
compatible with cosmic-ray acceleration theory. The energy
requirements implied by the gamma-ray flux are in agreement with
expectations from cosmic-ray acceleration in shell-type SNRs in our
Galaxy, if one assumes a local target gas density of
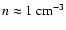 and takes the currently preferred distance
estimate of 1 kpc. Unfortunately both of these parameters are not
very well measured. The distance estimate, which factors
quadratically into the energetics calculation, has uncertainties in
the order of at least 30%. For the local target density there exist
only upper limits, since from comparisons with CO data it turns out
that gamma rays are most likely not exclusively linked to the dense
molecular clouds surrounding the SNR. These clouds, however, obscure
the measurement of the actual local target material available for
gamma-ray production. Only towards the interior and the southeast of
the SNR, where there is a hole in the molecular column density,
is there hope to actually measure and constrain the
density. Existing estimates in these regions are the NANTEN upper
limit of
and takes the currently preferred distance
estimate of 1 kpc. Unfortunately both of these parameters are not
very well measured. The distance estimate, which factors
quadratically into the energetics calculation, has uncertainties in
the order of at least 30%. For the local target density there exist
only upper limits, since from comparisons with CO data it turns out
that gamma rays are most likely not exclusively linked to the dense
molecular clouds surrounding the SNR. These clouds, however, obscure
the measurement of the actual local target material available for
gamma-ray production. Only towards the interior and the southeast of
the SNR, where there is a hole in the molecular column density,
is there hope to actually measure and constrain the
density. Existing estimates in these regions are the NANTEN upper
limit of
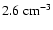 ,
which does not cause any problem
with the assumption made above, and the XMM upper limit of
,
which does not cause any problem
with the assumption made above, and the XMM upper limit of
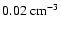 which, if correct, would seriously challenge
the idea of a hadronic scenario of gamma-ray production at least for
this object.
which, if correct, would seriously challenge
the idea of a hadronic scenario of gamma-ray production at least for
this object.
In the electronic scenario, on the other hand, the data are not
easily reproduced taking only IC emission into account. The very low
magnetic field of 
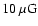 ,
fixed by the ratio of
synchrotron to IC flux, exceeds typical interstellar values only
slightly and is difficult to reconcile with the paradigm of the
diffusive shock acceleration of cosmic rays at supernova shock waves
which predicts strong field amplifications in the region of the
shock (Bell 2004; Lucek & Bell 2000; Bell & Lucek 2001). In the case of RX J1713.7-3946 it
was indeed considered possible by Völk et al. (2005) that the
magnetic field strength at the SNR shock front significantly exceeds
typical interstellar values.
,
fixed by the ratio of
synchrotron to IC flux, exceeds typical interstellar values only
slightly and is difficult to reconcile with the paradigm of the
diffusive shock acceleration of cosmic rays at supernova shock waves
which predicts strong field amplifications in the region of the
shock (Bell 2004; Lucek & Bell 2000; Bell & Lucek 2001). In the case of RX J1713.7-3946 it
was indeed considered possible by Völk et al. (2005) that the
magnetic field strength at the SNR shock front significantly exceeds
typical interstellar values.
Complete understanding of gamma-ray emission processes can only be
achieved by taking a broadband approach and using all the available
measurements in the different wavelength regimes. In
Sect. 4 the TeV data set was compared to
X-ray, radio and CO emission measurements of the region surrounding
RX J1713.7-3946. While there is no obvious resemblance with the radio image, it
turns out that there is a striking spatial correlation between the
ASCA X-ray and the HESS gamma-ray data. Most of the emission
regions seem to exhibit exactly the same morphology in both
wavelength regimes. At first sight this supports the idea that
X-rays and gamma rays are produced by the same particle population,
namely electrons. Assuming a constant magnetic field throughout the
remnant (not the most likely configuration), the intensity (and
spectrum) of both synchrotron and IC radiation trace the density
(and the spectrum) of electrons, giving rise to the observed
correlation. If the VHE gamma rays were due to non-thermal
Bremsstrahlung of electrons, which is correlated with gas density,
the observed correlation could be due to a magnetic field and gas
density correlation. However, as can be seen from
Fig. 19, Bremsstrahlung dominates over IC radiation
only for very large values of
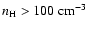 ,
which
are not compatible with the CO measurements from the centre of the
SNR, as mentioned above. But even given such a high density it is
questionable if density, field strength and electron spectra can be
fine-tuned such that the experimental results are approximately
reproduced. Another difficulty for an electronic interpretation
arises from the observation by Cassam-Chenaï et al. (2004) that the X-ray
spectra are steeper in the presumed shock front in the west, where
the blast wave probably impacts the molecular cloud, than in the
southeast, where the front propagates into a low density medium. It
is very difficult to explain why the spectral shape in X-rays, but
not in gamma rays, changes significantly in distinct regions of the
shock, if they stem from the same particle population. If on the
other hand gamma rays originate dominantly from nucleonic cosmic
rays, a spatial correlation between X-rays and gamma rays is not
automatically ensured either. There are two possible scenarios. The
correlation could point to a common acceleration process
accelerating both electrons and protons - indeed expected in the
theory of diffusive shock acceleration - such that the spatial
distributions are to first order the same and only differ because of
the different loss processes. The second alternative is a correlated
enhancement of magnetic field and local gas density.
,
which
are not compatible with the CO measurements from the centre of the
SNR, as mentioned above. But even given such a high density it is
questionable if density, field strength and electron spectra can be
fine-tuned such that the experimental results are approximately
reproduced. Another difficulty for an electronic interpretation
arises from the observation by Cassam-Chenaï et al. (2004) that the X-ray
spectra are steeper in the presumed shock front in the west, where
the blast wave probably impacts the molecular cloud, than in the
southeast, where the front propagates into a low density medium. It
is very difficult to explain why the spectral shape in X-rays, but
not in gamma rays, changes significantly in distinct regions of the
shock, if they stem from the same particle population. If on the
other hand gamma rays originate dominantly from nucleonic cosmic
rays, a spatial correlation between X-rays and gamma rays is not
automatically ensured either. There are two possible scenarios. The
correlation could point to a common acceleration process
accelerating both electrons and protons - indeed expected in the
theory of diffusive shock acceleration - such that the spatial
distributions are to first order the same and only differ because of
the different loss processes. The second alternative is a correlated
enhancement of magnetic field and local gas density.
Another possibility of course is that the VHE gamma rays are a roughly equal mixture of two components, produced by both electrons and protons. However, this scenario seems unlikely since the energy-independent gamma-ray morphology and the absence of
variations in spectral shape would again require fine-tuning of
parameters like the magnetic field B and the ambient density n.
We conclude that the straightforward and simplest approaches in both
scenarios lead to problems and one has difficulties in finding
unequivocal evidence for either of them when using all the available
broadband data. Nevertheless, the shape of the gamma-ray spectrum
favours a hadronic scenario.
6 Summary
The VHE gamma-ray emission of RX J1713.7-3946 was measured with unprecedented
precision with HESS. The accuracy of the measurement is now
approaching the level of X-ray measurements of this source, with the
distinct advantage that HESS covers the whole SNR within its field
of view. With the 2004 data, a close spatial correlation between
X-rays and gamma rays was found. The overall gamma-ray energy
spectrum was measured over more than two decades. There are
indications for a deviation from a pure power-law spectrum. The data
seem to be reasonably well described by a power law with an
exponential cutoff and a power law with energy dependent photon
index, as well as a broken power law. At the current stage further
investigations about the shape of the spectrum at the highest
energies accessible to HESS are hampered by the limited event
statistics. The large data set has allowed for a spatially resolved
spectral study. No significant variation in the gamma-ray spectral
shape over the SNR is found. The flux varies by more than a factor
of two across the SNR. The northern and western parts of the shell,
where the SNR is believed to impact molecular clouds, are
significantly brighter than the remaining parts.
We presented broadband modelling ideas and discussed RX J1713.7-3946 in terms
of the available data from all wavelength bands including the HESS
gamma-ray signal. Two scenarios were addressed, one where gamma rays
originate from electrons and one where they originate from
protons. In both cases the large uncertainties on crucial parameters
like the magnetic field strength and the effective ambient density,
which are not directly accessible to measurements, hamper decisive
conclusions. Nevertheless, the proton scenario is favoured because
of the shape of the gamma-ray spectrum. From the theory side, the
remaining challenge is the connection of the different particle
species, VHE electrons and nuclei, in a consistent broadband model
of RX J1713.7-3946. Experimentally, with the current gamma-ray data set, more
precise measurements of the surrounding molecular clouds are clearly
needed in order to link emission regions of VHE gamma rays to
regions of known density.
Acknowledgements
The support of the Namibian authorities and of the University of
Namibia in facilitating the construction and operation of
HESS is gratefully acknowledged, as is the support by the
German Ministry for Education and Research (BMBF), the Max Planck
Society, the French Ministry for Research, the CNRS-IN2P3 and the
Astroparticle Interdisciplinary Programme of the CNRS, the
U.K. Particle Physics and Astronomy Research Council (PPARC), the
IPNP of the Charles University, the South African Department of
Science and Technology and National Research Foundation, and by
the University of Namibia. We appreciate the excellent work of the
technical support staff in Berlin, Durham, Hamburg, Heidelberg,
Palaiseau, Paris, Saclay, and in Namibia in the construction and
operation of the equipment. We also thank Y. Uchiyama for
supplying the ASCA X-ray data and assisting with the comparisons
with the HESS data, and Y. Moriguchi and Y. Fukui for supplying
the NANTEN data.
- Aharonian,
F. A., & Atoyan, A. M. 1996, A&A, 309, 917 [NASA ADS] (In the text)
- Aharonian,
F. A., & Atoyan, A. M. 1999, A&A, 351, 330 [NASA ADS]
- Aharonian, F. A., Drury,
L. O., & Voelk, H. J. 1994, A&A, 285, 645 [NASA ADS] (In the text)
- Aharonian,
F. A., Akhperjanian, A. G., Aye, K.-M., et al., HESS
Collaboration, 2004a, APh, 22, 109 [NASA ADS] (In the text)
- Aharonian,
F. A., Akhperjanian, A. G., Aye, K.-M., et al., HESS
Collaboration, 2004b, Nature, 432, 75 [NASA ADS] [CrossRef] (In the text)
- Aharonian,
F. A., Akhperjanian, A. G., Bazer-Bachi, A. R.,
et al., HESS Collaboration, 2005a, A&A, 437, L7 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Aharonian,
F. A., Akhperjanian, A. G., Aye, K.-M., et al., HESS
Collaboration, 2005b, A&A, 430, 865 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Aharonian,
F. A., Akhperjanian, A. G., Aye, K.-M., et al., HESS
Collaboration, 2005c, in preparation
(In the text)
-
Aharonian, F. A., Akhperjanian, A. G., Aye, K.-M.,
et al., HESS Collaboration, 2006, ApJ, 636, 777 [NASA ADS] [CrossRef] (In the text)
-
Aschenbach, B. 1998, Nature, 396, 141 [NASA ADS] [CrossRef]
- Atkins,
R., Benbow, W., Berley, D., et al. 2004, ApJ, 608, 680 [NASA ADS] [CrossRef] (In the text)
- Bamba, A.,
Yamazaki, R., Yoshida, T., Terasawa, T., & Koyama, K. 2005,
ApJ, 621, 793 [NASA ADS] [CrossRef] (In the text)
- Baring, M. G.,
Ellison, D. C., Reynolds, S. P., Grenier, I. A.,
& Goret, P. 1999, ApJ, 513, 311 [NASA ADS] [CrossRef]
- Bell, A. R.
2004, MNRAS, 353, 550 [NASA ADS] [CrossRef]
- Bell, A. R.,
& Lucek, S. G. 2001, MNRAS, 321, 433 [NASA ADS] [CrossRef]
- Berezhko,
E. G., & Völk, H. J. 1997, APh, 7, 183 [NASA ADS]
- Berezhko,
E. G., & Völk, H. J. 2000, A&A, 357,
283 [NASA ADS] (In the text)
- Berezhko,
E. G., Ksenofontov, L. T., & Völk, H. J.
2003, A&A, 412, L11 [EDP Sciences] [NASA ADS] [CrossRef]
- Bernlöhr, K., Carrol, O.,
Cornils, R., et al. 2003, APh, 20, 111 [NASA ADS]
- Blandford, R.,
& Eichler, D. 1987, Phys. Rep., 154, 1 [NASA ADS] [CrossRef]
- Butt, Y. M., Torres,
D. F., Romero, G. E., Dame, T. M., & Combi,
J. A. 2002, Nature, 418, 499 [NASA ADS] (In the text)
-
Cassam-Chenaï, G., Decourchelle, A., Ballet, J., et al.
2004, A&A, 427, 199 [EDP Sciences] [NASA ADS] [CrossRef]
- Cornils, R.,
Gillessen, S., Jung, I., et al. 2003, APh, 20, 129 [NASA ADS]
- Drury, L. O., Aharonian,
F. A., & Völk, H. J. 1994, A&A, 287,
959 [NASA ADS] (In the text)
- Ellison, D. C.,
Slane, P., & Gaensler, B. M. 2001, ApJ, 563, 191 [NASA ADS] [CrossRef]
- Enomoto, R., Tanimori,
T., Naito, T., et al. 2002, Nature, 416, 823 [NASA ADS] [CrossRef] (In the text)
- Fukui,
Y., Moriguchi, Y., Tamura, K., et al. 2003, PASJ, 55, L61 [NASA ADS]
-
Funk, S., Hermann, G., Hinton, J., et al. 2004, APh, 22,
285 [NASA ADS] (In the text)
- Ginzburg,
V. L., & Syrovatskii, S. I. 1964, The Origin of
Cosmic Rays (New York: Macmillan)
(In the text)
- Hartman,
R. C., Bertsch, D. L., Bloom, S. D., et al.
1999, ApJS, 123, 79 [NASA ADS] [CrossRef] (In the text)
- Hillas, A. M.
1985, in Proc. 19th ICRC, 445
(In the text)
- Hinton,
J. A. (HESS Collaboration) 2004, New Astron. Rev., 48, 331
- Hiraga,
J. S. 2005, private communication
(In the text)
- Hiraga,
J. S., Uchiyama, Y., Takahashi, T., & Aharonian,
F. A. 2005, A&A, 431, 953 [EDP Sciences] [NASA ADS] [CrossRef]
-
Hofmann, W. (HESS Collaboration) 2003, in Proc. 28th ICRC,
2811
- Jones, F. C., &
Ellison, D. C. 1991, Space Sci. Rev., 58, 259 [NASA ADS] [CrossRef]
-
Katagiri, H., Enomoto, R., Ksenofontov, L. T., et al.
2005, ApJ, 619, L163 [NASA ADS] [CrossRef] (In the text)
- Koyama, K., Petre,
R., Gotthelf, E. V., et al. 1995, Nature, 378, 255 [NASA ADS] [CrossRef] (In the text)
- Koyama, K., Kinugasa,
K., Matsuzaki, K., et al. 1997, PASJ, 49, L7 [NASA ADS]
- Lazendic,
J. S., Slane, P. O., Gaensler, B. M., et al.
2004, ApJ, 602, 271 [NASA ADS] [CrossRef]
-
Lemoine-Goumard, M., & de Naurois, M. (HESS Collaboration)
2005, in High Energy Gamma-Ray Astronomy, AIP Conf. Proc., 745,
703
(In the text)
- Lucek,
S. G., & Bell, A. R. 2000, MNRAS, 314, 65 [NASA ADS] [CrossRef]
- Malkov,
M. A., & O'C Drury, L. 2001, Reports of Progress in
Physics, 64, 429 [NASA ADS]
- Malkov, M. A.,
Diamond, P. H., & Sagdeev, R. Z. 2005, ApJ, 624,
L37 [NASA ADS] [CrossRef] (In the text)
-
Mastichiadis, A., & de Jager, O. C. 1996, A&A, 311,
L5 [NASA ADS]
- Moriguchi, Y.,
Tamura, K., Tawara, Y., et al. 2005, ApJ, 631, 947 [NASA ADS] [CrossRef]
- Muraishi, H., Tanimori,
T., Yanagita, S., et al. 2000, A&A, 354, L57 [NASA ADS] (In the text)
- Pannuti, T. G.,
Allen, G. E., Houck, J. C., & Sturner, S. J.
2003, ApJ, 593, 377 [NASA ADS] [CrossRef]
- Pfeffermann,
E., & Aschenbach, B. 1996, in Roentgenstrahlung from the
Universe, 267
(In the text)
- Piron, F., Djannati-Atai,
A., Punch, M., et al. 2001, A&A, 374, 895 [EDP Sciences] [NASA ADS] (In the text)
- Reimer, O.,
& Pohl, M. 2002, A&A, 390, L43 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Slane, P., Gaensler,
B. M., Dame, T. M., et al. 1999, ApJ, 525, 357 [NASA ADS] [CrossRef]
- Slane, P.,
Hughes, J. P., Edgar, R. J., et al. 2001, ApJ, 548,
814 [NASA ADS] [CrossRef]
- Tsuchiya, K.,
Enomoto, R., Ksenofontov, L. T., et al. 2004, ApJ, 606,
L115 [NASA ADS] [CrossRef] (In the text)
-
Uchiyama, Y. 2005, private communication
(In the text)
- Uchiyama, Y., Takahashi,
T., & Aharonian, F. A. 2002, PASJ, 54, L73 [NASA ADS] (In the text)
-
Uchiyama, Y., Aharonian, F. A., & Takahashi, T. 2003,
A&A, 400, 567 [EDP Sciences] [NASA ADS] [CrossRef]
-
Vincent, P., et al. (HESS Collaboration) 2003, in Proc. 28th
ICRC, 2887
(In the text)
- Vink, J., &
Laming, J. M. 2003, ApJ, 584, 758 [NASA ADS] [CrossRef]
- Völk,
H. J., Berezhko, E. G., & Ksenofontov, L. T.
2005, A&A, 433, 229 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Wang, Z. R., Qu,
Q.-Y., & Chen, Y. 1997, A&A, 318, L59 [NASA ADS] (In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=8.5cm,clip]{4279_f1.eps} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg76.gif)
![\begin{figure}
\par\includegraphics[width=15.25cm,clip]{4279_f2.eps} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg77.gif)
![\begin{figure}
\par\includegraphics[width=7.75cm,clip]{4279_f3.eps} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=8.25cm,clip]{4279_f4} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg89.gif)
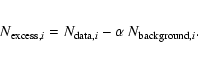
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{4279_f5} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg94.gif)
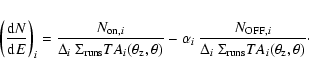
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{4279_f6} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg104.gif)
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{4279_f7} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg105.gif)
![\begin{figure}
\par\includegraphics[width=16.35cm,clip]{4279_f9} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg114.gif)
![\begin{figure}
\par\includegraphics[width=7.65cm,clip]{4279_f10} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg116.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{4279_f11} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg117.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{4279_f12} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg123.gif)
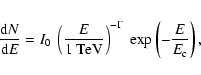
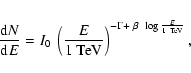
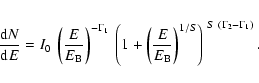
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{4279_f13} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg158.gif)
![\begin{figure}
\par\includegraphics[width=15.9cm,clip]{4279_f14} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg161.gif)
![\begin{figure}
\par\includegraphics[width=8.45cm,clip]{4279_f15} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg194.gif)
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{4279_f16} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg195.gif)
![\begin{figure}
\par\includegraphics[width=16.05cm,clip]{4279_f17} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg201.gif)
![\begin{figure}
\par\includegraphics[width=8.1cm,clip]{4279_f18} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg205.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4279_f19} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg221.gif)
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{4279_f20} \end{figure}](/articles/aa/full/2006/13/aa4279-05/Timg227.gif)