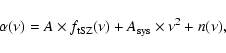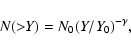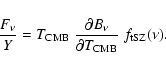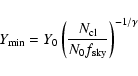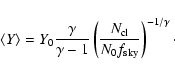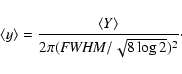A&A 449, 41-48 (2006)
DOI: 10.1051/0004-6361:20053680
Spectral indications of thermal Sunyaev-Zel'dovich effect in ARCHEOPS and
WMAP data
C. Hernández-Monteagudo1,2 - J. F. Macías-Pérez3 -
M. Tristram3 - F.-X. Désert4
1 -
Department of Physics & Astronomy, University of Pennsylvania,
209 South 33rd Str., Philadelphia, PA 19106, USA
2 -
Max-Planck-Institut für Astrophysik,
Karl-Schwarzschild-Str.1, Postfach 1317, 85741 Garching,
Germany
3 -
Laboratoire de Physique Subatomique et Cosmologie, 53 Av. des Martyrs, 38026 Grenoble Cedex, France
4 -
Laboratoire d'Astrophysique, Obs. de Grenoble, BP 53, 38041 Grenoble Cedex 9, France
Received 22 June 2005 / Accepted 21 November 2005
Abstract
In this paper, we present a joint cross-correlation
analysis of the A RCHEOPS CMB maps at 143 and 217 GHz and the
WMAP CMB maps at 41, 61 and 94 GHz with sky templates of projected
galaxy density constructed from the 2MASS Extended Source catalog.
These templates have been divided in patches sorted in decreasing
galaxy density with a fixed number of pixels (we considered patches
having 32, 64 and 128 pixels) and the cross correlation has been
performed independently for each of these patches. We find that the
densest patch shows a strong temperature decrement in the Q, V, Wbands of WMAP and in the 143 GHz channel of A RCHEOPS, but not in the 217 GHz channel. Furthermore, we find that the spectral
behavior of the amplitude of this decrement is compatible with that
expected for the non-relativistic thermal Sunyaev-Zel'dovich effect,
and is incompatible (at 4.5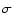 level) with the null hypothesis of
having only CMB, noise and a dust component (
level) with the null hypothesis of
having only CMB, noise and a dust component (
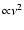 )
in those
pixels. We find that the first 32-pixel sized patch samples the cores
of 11 known massive nearby galaxy clusters. Under the assumption that
the decrement found in this patch is due entirely to the thermal
Sunyaev-Zel'dovich effect, we obtain an average comptonization
parameter for those sources of
)
in those
pixels. We find that the first 32-pixel sized patch samples the cores
of 11 known massive nearby galaxy clusters. Under the assumption that
the decrement found in this patch is due entirely to the thermal
Sunyaev-Zel'dovich effect, we obtain an average comptonization
parameter for those sources of
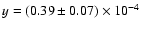 at
13 arcmin angular scales. This value is compatible at 1-
at
13 arcmin angular scales. This value is compatible at 1-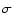 with
the expectation,
with
the expectation,
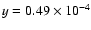 ,
from a model of the
cluster flux number counts based on the standard
,
from a model of the
cluster flux number counts based on the standard  -CDM
cosmology (Xue & Wu 2001). The observed value of y is slightly diluted
when computed for the first patch of 64 and 128 pixels, presumably due
to the inclusion of less massive clusters, and the dilution factor
inferred is also compatible with the quoted model.
-CDM
cosmology (Xue & Wu 2001). The observed value of y is slightly diluted
when computed for the first patch of 64 and 128 pixels, presumably due
to the inclusion of less massive clusters, and the dilution factor
inferred is also compatible with the quoted model.
Key words: cosmology: cosmic microwave background - Galaxy: globular clusters: general
1 Introduction
The thermal Sunyaev-Zel'dovich effect (hereafter tSZ, Sunyaev & Zel'dovich 1980)
constitutes a unique tool to explore the presence of baryons in the
Universe. It arises as a consequence of the distortion that the black
body spectrum of the Cosmic Microwave Background (CMB) radiation
experiences when it encounters a hot electron plasma. In this Compton
scattering, electrons transfer energy to the CMB radiation, generating
an excess of high energy photons and a deficit in the low energy
tail of the distribution. This photon reallocation translates into a
frequency dependent change of the brightness temperature of the CMB,
which, in the non-relativistic limit, has a very simple form,
(
![$f_{\rm tSZ}(x) = x /\tanh~ [x/2] - 4$](/articles/aa/full/2006/13/aa3680-05/img8.gif) ,
with
,
with
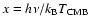 the
adimensional frequency in terms of the CMB temperature monopole
the
adimensional frequency in terms of the CMB temperature monopole
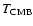 ). The amplitude of this distortion is proportional to the
electron pressure integrated along the line of sight (
). The amplitude of this distortion is proportional to the
electron pressure integrated along the line of sight (
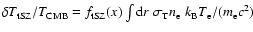 ,
with
,
with
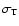 the Thomson cross section and
the Thomson cross section and 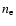 ,
,
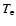 and
and
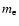 the electron number density, temperature and mass,
respectively); and this makes this effect particularly sensitive to
collapsed or collapsing structures containing hot electrons, such as
clusters and superclusters of galaxies (see Birkinshaw 1999, for a
extensive review).
the electron number density, temperature and mass,
respectively); and this makes this effect particularly sensitive to
collapsed or collapsing structures containing hot electrons, such as
clusters and superclusters of galaxies (see Birkinshaw 1999, for a
extensive review).
In addition to the intrinsic energy inhomogeneities of CMB radiation
generated during inflation, there are further temperature anisotropies
introduced in the CMB during recombination, which are mainly caused by
two physical processes. These processes are the last Doppler
kick exerted by electrons via Thomson scattering just before
recombining, and the subsequent gravitational redshift experienced by
CMB photons as they climb the potential wells generated by the
inhomogeneities in the matter distribution (Sachs & Wolfe effect,
e.g. Hu & Sugiyama 1995). While all this happens at
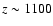 ,
a similar
scenario can take place at much lower redshifts: as the first stars
reionise the universe, new free electrons are produced which again
scatter CMB photons, partially blurring primordial anisotropies
generated during recombination and introducing new ones at much larger
angular scales. Also, if
,
a similar
scenario can take place at much lower redshifts: as the first stars
reionise the universe, new free electrons are produced which again
scatter CMB photons, partially blurring primordial anisotropies
generated during recombination and introducing new ones at much larger
angular scales. Also, if
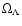 is non-zero, the decay of
gravitational potentials in linear scales introduces a net blueshift
in the CMB radiation at late epochs (z < 2), which is known as the
Integrated Sachs Wolfe effect, (ISW Sachs & Wolfe 1967). Despite the fact that
most of these phenomena introduce temperature fluctuations of
amplitudes larger than the tSZ effect, the particular frequency
dependence of the latter should enable its separation. Whereas the
first generation of CMB experiments like COBE (Smoot et al. 1991) and Tenerife
(Gutiérrez et al. 2000) aimed to simply detect the largest CMB temperature
anisotropies in the big angular scales, experiments like, e.g.,
Boomerang (Mauskopf et al. 2000), VSA (Rubiño-Martín et al. 2003), A RCHEOPS (Benoît et al. 2002)
and WMAP (Bennett et al. 2003) have already reached the sensitivity and angular
resolution levels required to probe relatively weak signals like the
tSZ effect.
is non-zero, the decay of
gravitational potentials in linear scales introduces a net blueshift
in the CMB radiation at late epochs (z < 2), which is known as the
Integrated Sachs Wolfe effect, (ISW Sachs & Wolfe 1967). Despite the fact that
most of these phenomena introduce temperature fluctuations of
amplitudes larger than the tSZ effect, the particular frequency
dependence of the latter should enable its separation. Whereas the
first generation of CMB experiments like COBE (Smoot et al. 1991) and Tenerife
(Gutiérrez et al. 2000) aimed to simply detect the largest CMB temperature
anisotropies in the big angular scales, experiments like, e.g.,
Boomerang (Mauskopf et al. 2000), VSA (Rubiño-Martín et al. 2003), A RCHEOPS (Benoît et al. 2002)
and WMAP (Bennett et al. 2003) have already reached the sensitivity and angular
resolution levels required to probe relatively weak signals like the
tSZ effect.
In this work we perform a combined analysis of A RCHEOPS and WMAP
CMB data, searching for spectral signatures of the tSZ effect.
Previous works (Afshordi et al. 2004; Hernández-Monteagudo & Rubiño-Martín 2004; Fosalba et al. 2003; Fosalba & Gaztanaga 2004; Myers et al. 2004; Bennett et al. 2003; Hernández-Monteagudo et al. 2004) have claimed the detection of tSZ in WMAP
data at different significance levels. However, all those studies were
exclusively based on spatial cross-correlations of large scale
structure catalogues with CMB data. In this work, we take advantage
of the frequency coverage provided by the combination of A
RCHEOPS and WMAP experiments in order to include an analysis of the
frequency behavior of a signal which is spatially correlated with
regions hosting large galaxy overdensities.
The sketch of the paper is as follows: in Sect. 2
we summarize the outcome of the A RCHEOPS and WMAP experiments,
whose data products are analyzed as explained in
Sect. 3. Section 4 shows our results,
which are compared with those obtained from WMAP data. Their
implications are discussed in Sect. 5. Finally, we
conclude in Sect. 6.
2 The ARCHEOPS and WMAP data set
The A RCHEOPS (Benoît et al. 2002)![[*]](/icons/foot_motif.gif) experiment was designed to obtain a
large sky coverage of CMB temperature anisotropies in a single balloon
flight at millimeter and submillimeter wavelengths. A RCHEOPS is
a precursor to the P LANCK HFI instrument (Lamarre et al. 2003), using
the same optical design and the same technology for the detectors,
spider-web bolometers, and their cooling 0.1 K dilution fridge. The
instrument consists of a 1.5 m aperture diameter telescope and an
array of 21 photometric pixels operating at 4 frequency bands centered
at 143, 217, 353 and 545 GHz. The two low frequencies are dedicated to
CMB studies while high frequency bands are sensitive to foregrounds,
essentially to interstellar dust and atmospheric emission.
Observations are carried out by spinning the payload around its
vertical axis at 2 rpm. Thus the telescope produces circular scans at
a fixed elevation of
experiment was designed to obtain a
large sky coverage of CMB temperature anisotropies in a single balloon
flight at millimeter and submillimeter wavelengths. A RCHEOPS is
a precursor to the P LANCK HFI instrument (Lamarre et al. 2003), using
the same optical design and the same technology for the detectors,
spider-web bolometers, and their cooling 0.1 K dilution fridge. The
instrument consists of a 1.5 m aperture diameter telescope and an
array of 21 photometric pixels operating at 4 frequency bands centered
at 143, 217, 353 and 545 GHz. The two low frequencies are dedicated to
CMB studies while high frequency bands are sensitive to foregrounds,
essentially to interstellar dust and atmospheric emission.
Observations are carried out by spinning the payload around its
vertical axis at 2 rpm. Thus the telescope produces circular scans at
a fixed elevation of 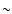 41 deg. The data were taken during the
Arctic night of February 7, 2002 after the instrument was launched by
CNES from the Esrange base near Kiruna (Sweden). The entire data set
covers
41 deg. The data were taken during the
Arctic night of February 7, 2002 after the instrument was launched by
CNES from the Esrange base near Kiruna (Sweden). The entire data set
covers 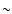 30% of the sky in 12 h of night observations.
30% of the sky in 12 h of night observations.
For the purpose of this paper, we concentrate in the low frequency
channels at 143 and 217 GHz. Maps for each of the bolometers have been
produced from the A RCHEOPS processed and foreground cleaned
timelines, using the Mirage optimal map making code (Yvon & Mayet 2005) as
discussed in (Tristram et al. 2005).
The maps for the 4 most sensitive bolometers at 143 GHz were combined
into a single map at 143 GHz and equally the two most sensitive
bolometer maps were combined at 217 GHz. The CMB dipole is the prime
calibrator of the instrument. The absolute calibration error against
the dipole as measured by COBE/DMR (Fixsen et al. 1994) and confirmed by
WMAP (Bennett et al. 2003) is estimated to be 4% and 8% in temperature
at 143 GHz and 217 GHz respectively. These errors are dominated by
systematic effects. The noise contribution in the combined maps at
143 and 217 GHz was computed using Monte Carlo simulations. For each
bolometer, by using the power spectrum of the noise in the time domain
data set, we produced fake timelines of A RCHEOPS noise. These
were processed and projected into maps following the same procedures
used for the A RCHEOPS data themselves as described before.
The WMAP satellite mission was designed to measure the CMB temperature
and polarization anisotropies in 5 frequency bands, 23, 33, 41, 61 and
94 GHz with a full sky coverage. The satellite was launched in June 2001 and its first results after the first year of observations
(Bennett et al. 2003) included the CMB temperature and temperature-polarization
cross-correlation power spectra, as well as full sky temperature maps
for each of the frequency bands. In this paper we consider only data
from the high frequency channels, Q [41 GHz], V [61 GHz] and W [94 GHz], since only for these bands there are foreground clean maps
available at the LAMBDA site http://lambda.gsfc.nasa.gov/
3 The statistical analysis
In this section we outline the correlation analysis performed on
ARCHEOPS and WMAP data and the 2MASS Extended Source Catalog (XSC,
Jarrett et al. 2003) on the sky region covered by A RCHEOPS. This
analysis is essentially identical to that applied in (Hernández-Monteagudo et al. 2004),
paper to which we refer for a more detailed description of the
statistical method. It consists of a pixel-to-pixel comparison of the CMB data with a template of the large scale structure built
from the 2MASS XSC catalog.
The 2MASS XSC catalog contains approximately 1.6 million galaxies
detected in the infrared filters I, J and K, and covers the whole
celestial sphere. Those frequencies are particularly insensitive to
dust absorption, and for this reason this catalog can trace the
extragalactic structure at very low galactic latitudes. The galaxy
templates built from it take into account the spatial distribution of
the galaxies and the instrumental beam of the CMB experiment. By using
the HEALPix![[*]](/icons/foot_motif.gif) (Górski et al. 1999) tessellation of
the sky, we built a map with the same resolution parameter (
(Górski et al. 1999) tessellation of
the sky, we built a map with the same resolution parameter (
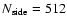 )
than the one used in A RCHEOPS and WMAP data. Every pixel
was assigned a value equal to the number of galaxies present in such
pixel. The resulting map was then convolved with a window function
corresponding to the instrumental beam of each of the detectors taken
into consideration. For A RCHEOPS, the resulting templates were
then weighted by their noise levels and co-added per frequency band,
in such a way that we ended up with two different galaxy templates
corresponding to the 143 GHz and 217 GHz bands. For WMAP, we produced
templates for the Q, V and W bands.
)
than the one used in A RCHEOPS and WMAP data. Every pixel
was assigned a value equal to the number of galaxies present in such
pixel. The resulting map was then convolved with a window function
corresponding to the instrumental beam of each of the detectors taken
into consideration. For A RCHEOPS, the resulting templates were
then weighted by their noise levels and co-added per frequency band,
in such a way that we ended up with two different galaxy templates
corresponding to the 143 GHz and 217 GHz bands. For WMAP, we produced
templates for the Q, V and W bands.
In the next step, we sorted the pixels of each template in terms of
its amplitude, so that first pixels would have higher
galaxy densities. These pixels were grouped in patches of varying
sizes (32, 64 or 128 pixels per patch), and again patches were sorted
in such a way that first patches contained larger projected galaxy
densities. Next, we analyzed each of these patches separately,
by comparing them to the corresponding patches in the
A RCHEOPS and WMAP CMB
maps on a pixel-to-pixel basis.
As explained in e.g. (Hernández-Monteagudo & Rubiño-Martín 2004), it is possible to estimate the
contribution of a given spatial template (M) on a total measured
temperature map (T), which is the result of the addition of several
components:
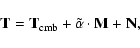 |
(1) |
namely CMB (
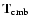 ), instrumental noise (
), instrumental noise (
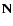 )
and some signal
coming from the extragalactic template (
)
and some signal
coming from the extragalactic template (
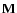 ). The contribution of
). The contribution of
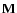 is parametrized by
is parametrized by
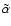 ,
and an optimal value of it
(optimal in terms of the temperature model given in
Eq. (1)), together with its formal error bar, is given by
,
and an optimal value of it
(optimal in terms of the temperature model given in
Eq. (1)), together with its formal error bar, is given by
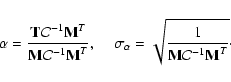 |
(2) |
The matrix 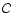 is the covariance matrix of T, which must
contain the correlation matrices of both the CMB and noise components.
For the small scales we are probing here (the pixel has a size of
is the covariance matrix of T, which must
contain the correlation matrices of both the CMB and noise components.
For the small scales we are probing here (the pixel has a size of
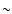 7 arcmin), the noise is the main contributor to the covariance
matrix
7 arcmin), the noise is the main contributor to the covariance
matrix![[*]](/icons/foot_motif.gif) . In our case, this matrix
must be evaluated only for the pixels belonging to the patch
under analysis. Since our patches are relatively small, the inversion
of this matrix poses no numerical problem.
. In our case, this matrix
must be evaluated only for the pixels belonging to the patch
under analysis. Since our patches are relatively small, the inversion
of this matrix poses no numerical problem.
Therefore, for every patch a value of 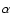 and
and
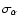 was obtained. However, uncertainties in the determination of the noise
amplitude may bias our determination of
was obtained. However, uncertainties in the determination of the noise
amplitude may bias our determination of
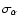 ,
and for
this reason we computed a different estimate of the uncertainty of
,
and for
this reason we computed a different estimate of the uncertainty of 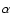 ,
namely the rms variation of this parameter for all
available patches, which will be denoted as
,
namely the rms variation of this parameter for all
available patches, which will be denoted as
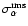 .
We remark the fact that, according to
Eq. (2), an error in the noise normalization does not
affect the estimates of
.
We remark the fact that, according to
Eq. (2), an error in the noise normalization does not
affect the estimates of 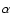 ,
but only those of
,
but only those of
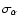 .
When comparing
.
When comparing
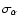 with
with
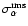 ,
we
found that for the 143 GHz channel of A RCHEOPS, the latter was
about a 40% larger than the former, and hence we decided to adopt it
in order to quote conservative estimates of statistical
significance. For the 217 GHz case no such bias was found, and we
decided to use again
,
we
found that for the 143 GHz channel of A RCHEOPS, the latter was
about a 40% larger than the former, and hence we decided to adopt it
in order to quote conservative estimates of statistical
significance. For the 217 GHz case no such bias was found, and we
decided to use again
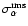 .
.
4 Combined results for ARCHEOPS and WMAP
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{figures/3680f1.ps}
\end{figure}](/articles/aa/full/2006/13/aa3680-05/Timg29.gif) |
Figure 1:
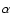 's obtained by means of
Eq. (2) from A RCHEOPS and WMAP data in the
fraction of the sky covered by the former experiment. In panels
a)- c), filled circles, crosses and diamonds refer to the W, V and Q bands respectively. In panels d)- f), the 143 GHz and 217 GHz channel
results are given by filled circles and diamonds, respectively. The
colored bands display the 2- 's obtained by means of
Eq. (2) from A RCHEOPS and WMAP data in the
fraction of the sky covered by the former experiment. In panels
a)- c), filled circles, crosses and diamonds refer to the W, V and Q bands respectively. In panels d)- f), the 143 GHz and 217 GHz channel
results are given by filled circles and diamonds, respectively. The
colored bands display the 2-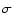 confidence limit for the
confidence limit for the
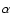 's: dark grey for filled circles, intermediate grey for
crosses, and light grey for diamonds. Our analysis are focused on
the first patch, hosting the highest projected galaxy density. 's: dark grey for filled circles, intermediate grey for
crosses, and light grey for diamonds. Our analysis are focused on
the first patch, hosting the highest projected galaxy density. |
| Open with DEXTER |
In Fig. 1 we plot the recovered 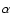 's versus
the patch index. Results are grouped in six different panels: top and
bottom panels refer to WMAP and A RCHEOPS experiments,
respectively, whereas left, middle and right panels display results
for patches of 32, 64 and 128 pixels, respectively. For
ARCHEOPS, filled circles and diamonds refer to 143 GHz and 217 GHz
respectively, whereas for WMAP those symbols correspond to the W and
the Q channels, being the results of the V band given by the crosses.
Dark and light grey colored bands limit the 2-
's versus
the patch index. Results are grouped in six different panels: top and
bottom panels refer to WMAP and A RCHEOPS experiments,
respectively, whereas left, middle and right panels display results
for patches of 32, 64 and 128 pixels, respectively. For
ARCHEOPS, filled circles and diamonds refer to 143 GHz and 217 GHz
respectively, whereas for WMAP those symbols correspond to the W and
the Q channels, being the results of the V band given by the crosses.
Dark and light grey colored bands limit the 2-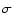 confidence
levels for filled circles and diamonds, respectively, while the
moderately dark bands refer to the V band (crosses) in the case of
WMAP.
As explained above, for the 143 GHz and 217 GHz channels the amplitude
of the shaded regions was computed from the typical dispersion of the
values obtained for
confidence
levels for filled circles and diamonds, respectively, while the
moderately dark bands refer to the V band (crosses) in the case of
WMAP.
As explained above, for the 143 GHz and 217 GHz channels the amplitude
of the shaded regions was computed from the typical dispersion of the
values obtained for 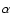 in patches where the tSZ contribution is
expected to be negligible, i.e., in patches with indexes between 40
and 300. We have found that for the 143 GHz channel the first patch
contains an unusual negative
in patches where the tSZ contribution is
expected to be negligible, i.e., in patches with indexes between 40
and 300. We have found that for the 143 GHz channel the first patch
contains an unusual negative 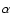 while at 217 GHz seems to be
compatible with zero. This patch, in the case it contains 64 pixels,
hosts the central pixels of 20 different ACO clusters of galaxies,
COMA among them. Out of them, 11 (COMA again included) are already
sampled by the 32 densest pixels.
Its statistical significance is slightly bigger for patches with 64 pixels (>2.5-
while at 217 GHz seems to be
compatible with zero. This patch, in the case it contains 64 pixels,
hosts the central pixels of 20 different ACO clusters of galaxies,
COMA among them. Out of them, 11 (COMA again included) are already
sampled by the 32 densest pixels.
Its statistical significance is slightly bigger for patches with 64 pixels (>2.5-
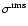 ), since it contains the first two very negative patches of 32 pixels each, (see Fig. 1d). In Fig. 1e, from the first 300
patches, very few of them (
), since it contains the first two very negative patches of 32 pixels each, (see Fig. 1d). In Fig. 1e, from the first 300
patches, very few of them (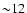 )
depart from zero by an amount
similar to that of the first patch; and such number is very close to
what one expects under Gaussian statistics at 2.5-
)
depart from zero by an amount
similar to that of the first patch; and such number is very close to
what one expects under Gaussian statistics at 2.5-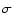 level of
significance. This peculiar behavior of the first (or first two)
patch(es) disappears at 217 GHz (see diamonds): in no case the
diamonds corresponding to the first two patches trespass the
2-
level of
significance. This peculiar behavior of the first (or first two)
patch(es) disappears at 217 GHz (see diamonds): in no case the
diamonds corresponding to the first two patches trespass the
2-
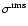 limit. This picture is consistent with part of the
signal being generated by the tSZ effect, since such component is
negative at 143 GHz and becomes zero at 217 GHz.
limit. This picture is consistent with part of the
signal being generated by the tSZ effect, since such component is
negative at 143 GHz and becomes zero at 217 GHz.
In order to interpret the results from WMAP, one musts keep in mind
that the Q and V bands have remarkably larger beams than the W band:
while the A RCHEOPS' and W band's Point Spread Functions are
similar in size (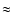 13 arcmin), the beams of the Q and V bands
have an average (linear) size of
13 arcmin), the beams of the Q and V bands
have an average (linear) size of 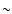 31 and 21 arcmin respectively.
This, in terms of tSZ flux, corresponds to factors
31 and 21 arcmin respectively.
This, in terms of tSZ flux, corresponds to factors 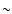 5.7 and 2.6
smaller in the Q and V band for point-like objects. On the other hand,
it is clear from Fig. 1 that WMAP has a much lower
noise level when compared to A RCHEOPS, (approx. a factor of 3.5). As one looks at the top panels in Fig. 1, one
finds that for the first patch of both 32 and 64 pixel size, the Wband gives a decrement about 4-
5.7 and 2.6
smaller in the Q and V band for point-like objects. On the other hand,
it is clear from Fig. 1 that WMAP has a much lower
noise level when compared to A RCHEOPS, (approx. a factor of 3.5). As one looks at the top panels in Fig. 1, one
finds that for the first patch of both 32 and 64 pixel size, the Wband gives a decrement about 4-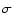 away from zero, (which however
is not found for the second patch of 32 pixel size). This statistical
singularity of the first patch decreases remarkably in the Q and Vbands, but still remains close to the 2-
away from zero, (which however
is not found for the second patch of 32 pixel size). This statistical
singularity of the first patch decreases remarkably in the Q and Vbands, but still remains close to the 2-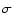 level. However, due
to the argument on beam dilution on bands Q and V with respect to W,
we still find the amplitudes given by the three bands of WMAP
consistent with being (at least partially) generated by unresolved
objects causing a temperature decrement.
level. However, due
to the argument on beam dilution on bands Q and V with respect to W,
we still find the amplitudes given by the three bands of WMAP
consistent with being (at least partially) generated by unresolved
objects causing a temperature decrement.
It also worth to remark that, if the first patch contains pixels which
do not contribute considerably to the tSZ decrement, the
significance of the overall 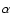 obtained for that patch will
diminish accordingly. This is our explanation for the decreasing
significance of the values of
obtained for that patch will
diminish accordingly. This is our explanation for the decreasing
significance of the values of 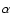 in the first patch for a size
of 128 pixels when compared to a size of 64 pixels.
in the first patch for a size
of 128 pixels when compared to a size of 64 pixels.
5 Discussion
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figures/3680f2.ps}
\end{figure}](/articles/aa/full/2006/13/aa3680-05/Timg33.gif) |
Figure 2:
tSZ fitted amplitude, A, as a function of patch number. We only observe a significant temperature decrement
(A > 0) in patch number 1. |
| Open with DEXTER |
As discussed in the previous section, Fig. 1 indicates
a significant temperature decrement
in patch 1 for both the A RCHEOPS and WMAP data sets which seems
to be compatible with the tSZ effect. For a better assessment of this
result we have compared, via a linear fit, the observed spectral
dependency of the correlation coefficients 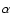 in each of the
patches to the following model
in each of the
patches to the following model
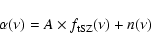 |
(3) |
where A is global calibration factor which is estimated from the
fit,
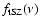 represents the spectral behavior of the
tSZ-induced change in brightness temperature and
represents the spectral behavior of the
tSZ-induced change in brightness temperature and 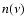 is the
instrumental noise in
is the
instrumental noise in
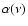 .
For this model if the signal
observed is compatible with the tSZ effect we expect a temperature
decrement and A to be significantly positive, otherwise we expect no
correlation and therefore A to be compatible with zero. We must
remark that, due to the different size of the beams for every channel,
we had to rescale the
.
For this model if the signal
observed is compatible with the tSZ effect we expect a temperature
decrement and A to be significantly positive, otherwise we expect no
correlation and therefore A to be compatible with zero. We must
remark that, due to the different size of the beams for every channel,
we had to rescale the 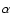 's to a common reference beam size of 13 arcmin. When doing this, we assumed that the signal was generated by
unresolved sources, and hence we scaled the
's to a common reference beam size of 13 arcmin. When doing this, we assumed that the signal was generated by
unresolved sources, and hence we scaled the 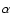 's as the ratio of
the area of the beam with the reference one.
's as the ratio of
the area of the beam with the reference one.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{figures/3680f3.ps}\par\includegraphics[width=7.8cm,clip]{figures/3680f4.ps}
\end{figure}](/articles/aa/full/2006/13/aa3680-05/Timg38.gif) |
Figure 3:
The 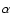 correlation coefficient in CMB temperature
units as function of frequency in GHz for patch 1 ( top panel) and
patch 201 ( bottom panel) of the 32 pixel patches. The diamonds are
the WMAP data points and the stars the A RCHEOPS one. In red,
we overplot the best-fit tSZ computed as discussed in the text.
correlation coefficient in CMB temperature
units as function of frequency in GHz for patch 1 ( top panel) and
patch 201 ( bottom panel) of the 32 pixel patches. The diamonds are
the WMAP data points and the stars the A RCHEOPS one. In red,
we overplot the best-fit tSZ computed as discussed in the text. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figures/3680f5.ps}\par\includegraphics[width=7.6cm,clip]{figures/3680f6.ps}
\end{figure}](/articles/aa/full/2006/13/aa3680-05/Timg39.gif) |
Figure 4:
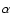 correlation coefficient in CMB temperature units
as function of frequency in GHz for patch 1 ( top panel) and patch 201
( bottom panel) of the 64 pixel patches. The diamonds are the WMAP data
points and the stars the A RCHEOPS one. In red, we overplot the
best-fit tSZ computed as discussed in the text.
correlation coefficient in CMB temperature units
as function of frequency in GHz for patch 1 ( top panel) and patch 201
( bottom panel) of the 64 pixel patches. The diamonds are the WMAP data
points and the stars the A RCHEOPS one. In red, we overplot the
best-fit tSZ computed as discussed in the text. |
| Open with DEXTER |
The main results of the fitting procedure described before are shown
in Fig. 2 where we trace the fitted amplitude, A, of the
tSZ signal as a function of the patch number for patches of 32 pixels.
We observe that only for patch number 1, where most massive clusters
might be, there is a significant temperature decrement (A>0). For
a closer look to the fits, Figs. 3-5 represent the 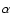 coefficient in CMB temperature
units as function of frequency in GHz for the 32, 64 and 128 pixel
patches respectively. The top plot corresponds to patch 1 and the
bottom one to a patch containing an average value of the projected
galaxy density (patch 201). In the three figures we observe that the
correlation coefficients found for the patch 1 are consistent which
what we expect for tSZ emission with A values of
coefficient in CMB temperature
units as function of frequency in GHz for the 32, 64 and 128 pixel
patches respectively. The top plot corresponds to patch 1 and the
bottom one to a patch containing an average value of the projected
galaxy density (patch 201). In the three figures we observe that the
correlation coefficients found for the patch 1 are consistent which
what we expect for tSZ emission with A values of
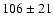
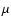 K,
K, 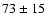
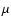 K and
K and 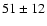
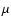 K respectively.
Notice as well that there is good agreement between the model and the
data with reduced
K respectively.
Notice as well that there is good agreement between the model and the
data with reduced 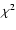 values of 2/4, 2.6/4 and 2/4 for
patches containing 32, 64 and 128 pixels respectively. For the null
hypothesis (A=0
values of 2/4, 2.6/4 and 2/4 for
patches containing 32, 64 and 128 pixels respectively. For the null
hypothesis (A=0 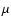 K), the reduced
K), the reduced 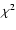 values are 28/5, 26/5 and 20/5. We interpret these results as a spectral indication
of the measurement of a tSZ signal in patch 1. However, for all other
patches we find A compatible with zero, showing that the data are in
good agreement with the null hypothesis. For example, for patch 201
the A values are
values are 28/5, 26/5 and 20/5. We interpret these results as a spectral indication
of the measurement of a tSZ signal in patch 1. However, for all other
patches we find A compatible with zero, showing that the data are in
good agreement with the null hypothesis. For example, for patch 201
the A values are
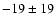
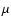 K,
K, 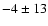
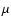 K and
K and 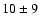
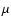 K with reduced
K with reduced 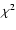 values of 2.2/4, 1.2/4 and 1.3/4respectively.
We consider these results compatible with a no
detection of tSZ signal in patch 201.
values of 2.2/4, 1.2/4 and 1.3/4respectively.
We consider these results compatible with a no
detection of tSZ signal in patch 201.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figures/3680f7.ps}\par\includegraphics[width=7.6cm,clip]{figures/3680f8.ps}
\end{figure}](/articles/aa/full/2006/13/aa3680-05/Timg48.gif) |
Figure 5:
The 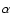 correlation
coefficient in CMB temperature units as function of frequency in GHz
for patch 1 ( top panel) and patch 201 ( bottom panel) of the 128
pixel patches. The diamonds are the WMAP data points and the stars
the A RCHEOPS one. In red, we over plot the best-fit tSZ
computed as discussed in the text.
correlation
coefficient in CMB temperature units as function of frequency in GHz
for patch 1 ( top panel) and patch 201 ( bottom panel) of the 128
pixel patches. The diamonds are the WMAP data points and the stars
the A RCHEOPS one. In red, we over plot the best-fit tSZ
computed as discussed in the text. |
| Open with DEXTER |
The uncertainties for the total amplitude of the tSZ signal, A,
presented above do not account for systematic errors on the
ARCHEOPS data. These are dominated by residuals from atmospheric and
Galactic dust emissions which in a first order approximation increase
as 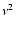 in the A RCHEOPS frequency range. To account for those
contributions we have recomputed the total amplitude for the tSZ
signal adding an extra term in the fitted function as follows:
in the A RCHEOPS frequency range. To account for those
contributions we have recomputed the total amplitude for the tSZ
signal adding an extra term in the fitted function as follows:
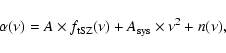 |
(4) |
where
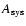 is computed only from the A RCHEOPS data. For
patch 1 we obtain A values of
is computed only from the A RCHEOPS data. For
patch 1 we obtain A values of
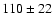
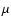 K,
K, 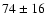
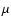 K and
K and 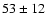
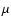 K, and
K, and
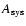 values of
values of
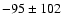
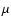 K,
K,
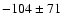
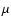 K and
K and
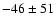
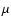 K for patches of 32, 64 and 128 pixels respectively. From these results we conclude
that the A coefficients are not significantly affected at 1-
K for patches of 32, 64 and 128 pixels respectively. From these results we conclude
that the A coefficients are not significantly affected at 1-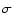 level by systematic effects present in the A RCHEOPS data.
level by systematic effects present in the A RCHEOPS data.
We have repeated the previous analyses using WMAP data only.
The results obtained are fully compatible within the error bars with
those obtained using Archeops and WMAP data combined. The error bars
for the WMAP only case are about 10% larger. One must keep present
that the WMAP data point at 94 GHz has a significantly smaller error
bar than all other points and that hence it dominates the fit.
It is interesting to check whether pixels in patch 1 correspond to
potential sources of tSZ or not. For the 32-pixel-size patches, patch
1 includes COMA, A0576, A0671, A0952, A1795, A2061, A2065, A2244,
A2245, A2249, A2255. Since these are massive and relatively nearby
galaxy clusters, it is reasonable to expect some signature of the tSZ
effect. It might occur, however, that our evidence for tSZ
signal is mainly caused by COMA, which is a nearby very massive
cluster whose tSZ signature has been studied extensively
(Battistelli et al. 2003). We have repeated our analyses after masking out all
pixels lying within a radius of 2.5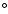 from COMA cluster's center
and found that our tSZ amplitudes decreased typically by a 10%-15%, but still being statistically significant. This demonstrates
that the presence of COMA is not critical to our results. Using the
quoted values for the A parameter we infer the following estimate
for the average Compton parameter in the source quoted above:
from COMA cluster's center
and found that our tSZ amplitudes decreased typically by a 10%-15%, but still being statistically significant. This demonstrates
that the presence of COMA is not critical to our results. Using the
quoted values for the A parameter we infer the following estimate
for the average Compton parameter in the source quoted above:
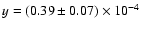 .
In the case of 64-pixel-size patches
we have roughly the same clusters and we expect therefore the signal
to be diluted,
.
In the case of 64-pixel-size patches
we have roughly the same clusters and we expect therefore the signal
to be diluted,
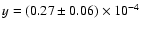 .
Finally for 128 pixel-size patches, patch 1 includes the following 27 clusters: COMA,
A0077, A0104, A0272, A0376, A0407, A0576, A0671, A0952, A1035, A1185,
A1235, A1377, A1767, A1795, A1800, A2034, A2061, A2065, A2069, A2142,
A2151, A2199, A2244, A2245, A2249, A2255. We deduce for them
.
Finally for 128 pixel-size patches, patch 1 includes the following 27 clusters: COMA,
A0077, A0104, A0272, A0376, A0407, A0576, A0671, A0952, A1035, A1185,
A1235, A1377, A1767, A1795, A1800, A2034, A2061, A2065, A2069, A2142,
A2151, A2199, A2244, A2245, A2249, A2255. We deduce for them
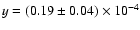 .
Since we have scaled the
.
Since we have scaled the 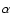 's
to the beam-size of the 143 GHz channel of A RCHEOPS, these
quoted values of y are associated to a (linear) angular scale on the
sky of
's
to the beam-size of the 143 GHz channel of A RCHEOPS, these
quoted values of y are associated to a (linear) angular scale on the
sky of  13 arcmin. For the above results we have assumed the
CMB temperature to be
13 arcmin. For the above results we have assumed the
CMB temperature to be
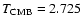 K (Mather et al. 1999).
K (Mather et al. 1999).
We now try to relate the observed average tSZ decrement
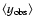 to the high end of the SZ number counts. We make 2
hypotheses: 1) that the Archeops beam encloses most of the integrated
tSZ effect in clusters and 2) that the 2MASS survey is a perfect
tracer of the tSZ effect. We will come back to these hypotheses at the
end.
to the high end of the SZ number counts. We make 2
hypotheses: 1) that the Archeops beam encloses most of the integrated
tSZ effect in clusters and 2) that the 2MASS survey is a perfect
tracer of the tSZ effect. We will come back to these hypotheses at the
end.
The correlation analysis, that is presented in the previous section,
can be recast in stating that the
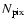 brightest clusters of
galaxies have an average integrated
brightest clusters of
galaxies have an average integrated
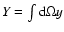 parameter equal
to
parameter equal
to
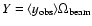 where
where
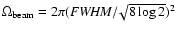 is the Archeops beam solid angle if
is the Archeops beam solid angle if
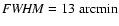 .
The integrated Compton parameter can
be directly related to the SZ flux number counts which has been the
issue of a great number of studies (e.g. Barbosa et al. 1996; Bartelmann et al. 2001; Bartlett et al. 1994; Aghanim et al. 1997) from which we select (Xue & Wu 2001) and
(Benson et al. 2002).
.
The integrated Compton parameter can
be directly related to the SZ flux number counts which has been the
issue of a great number of studies (e.g. Barbosa et al. 1996; Bartelmann et al. 2001; Bartlett et al. 1994; Aghanim et al. 1997) from which we select (Xue & Wu 2001) and
(Benson et al. 2002).
Following (Xue & Wu 2001) there are three possible models for which the
number counts of clusters over the whole sphere can be parametrized in
terms of Y as follows,
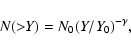 |
(5) |
where we fiducially consider
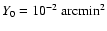
For Model 1 (M1), deduced from the cosmological 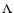 CDM matter
power spectrum, N0=29 and
CDM matter
power spectrum, N0=29 and
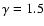 .
For Model 2 (M2), a
non-evolving X-ray luminosity function is used to correct the counts
and gives a larger N0=635 with the same exponent. Note that
(Rubiño-Martín & Sunyaev 2003) also find this exponent when studying the number counts of
high flux galaxy clusters). Finally Model 3 (M3), an evolving X-ray
luminosity function is used instead, giving N0=350 with a flatter
exponent
.
For Model 2 (M2), a
non-evolving X-ray luminosity function is used to correct the counts
and gives a larger N0=635 with the same exponent. Note that
(Rubiño-Martín & Sunyaev 2003) also find this exponent when studying the number counts of
high flux galaxy clusters). Finally Model 3 (M3), an evolving X-ray
luminosity function is used instead, giving N0=350 with a flatter
exponent
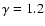 .
The conversion from flux in Jansky units to the
Compton frequency-independent quantity Y is obtained via
.
The conversion from flux in Jansky units to the
Compton frequency-independent quantity Y is obtained via
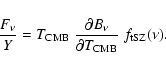 |
(6) |
For example, the fiducial value
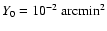 is equivalent to 0.75
and 0.91 Jy at 90 and 143 GHz (resp.).
is equivalent to 0.75
and 0.91 Jy at 90 and 143 GHz (resp.).
Table 1:
Expected average Compton parameter,
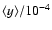 ,
in patch 1, as a function of the number of pixels in the patch
for the four number counts models discussed in the text, M1, M2 and M3 Xue & Wu (2001) and B Benson et al. (2002).
,
in patch 1, as a function of the number of pixels in the patch
for the four number counts models discussed in the text, M1, M2 and M3 Xue & Wu (2001) and B Benson et al. (2002).
From the above formulas, we deduce the lower limit
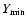 in the
number counts for the first
in the
number counts for the first
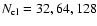 brightest clusters
as
brightest clusters
as
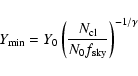 |
(7) |
where
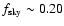 is the effective sky fraction used in the
Archeops-WMAP tSZ cross analysis. The average Y value of these
clusters is then
is the effective sky fraction used in the
Archeops-WMAP tSZ cross analysis. The average Y value of these
clusters is then
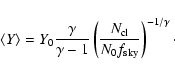 |
(8) |
We deduce the average Compton parameter for those clusters
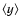 as
as
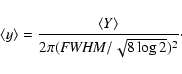 |
(9) |
For the previous three models, expected values for
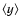 are between
are between
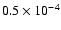 and
and
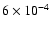 .
The value
expected from basic principles (M1),
.
The value
expected from basic principles (M1),
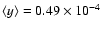 ,
is quite close to the observed value
,
is quite close to the observed value
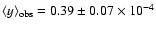 .
The observed value should
however be corrected up-wards. Non-linearities in the relation
between the 2-MASS density field and the Y parameter introduce an
efficiency which is difficult to estimate, although we note that as
discussed above most of the brightest pixels in the density map
constructed from the 2-MASS survey are associated to well-known
clusters of galaxies. If we considered that only identified clusters
(11) are present in the first patch of 32 pixels, the above expected
values should be multiplied by a factor of two. Extension of the
bright clusters beyond the fiducial beam of 13 arcmin (like Coma) may
produce a differential effect with the observing beam at different
frequencies, as well as a bias in the number counts.
.
The observed value should
however be corrected up-wards. Non-linearities in the relation
between the 2-MASS density field and the Y parameter introduce an
efficiency which is difficult to estimate, although we note that as
discussed above most of the brightest pixels in the density map
constructed from the 2-MASS survey are associated to well-known
clusters of galaxies. If we considered that only identified clusters
(11) are present in the first patch of 32 pixels, the above expected
values should be multiplied by a factor of two. Extension of the
bright clusters beyond the fiducial beam of 13 arcmin (like Coma) may
produce a differential effect with the observing beam at different
frequencies, as well as a bias in the number counts.
We also note that the dependence of
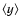 with the
number of pixels taken in the analysis (32, 64 or 128) follows quite
well the Model 1 prediction as shown in Table 1. We have
also cross-checked the (Xue & Wu 2001) modeling with that from
(Benson et al. 2002). This alternative model produces an intermediate value
between models M1 and M2 and is marginally compatible with the
observations.
with the
number of pixels taken in the analysis (32, 64 or 128) follows quite
well the Model 1 prediction as shown in Table 1. We have
also cross-checked the (Xue & Wu 2001) modeling with that from
(Benson et al. 2002). This alternative model produces an intermediate value
between models M1 and M2 and is marginally compatible with the
observations.
6 Conclusion
In this paper we have presented a joint cross-correlation analysis of
the A RCHEOPS and WMAP data sets with a template of galaxy
density constructed from the 2MASS XSC galaxy catalog. We have first
divided the 2MASS sky density map in patches of equal number of pixels
and sorted these patches in terms of decreasing projected galaxy
density. For each of these patches we have performed a
cross-correlation analysis with the A RCHEOPS data at 143 and 217
GHz and with the WMAP data for the Q, V and W bands. For patches
containing the densest 32, 64 and 128 pixels (patch 1), the
correlation test pointed to a prominent temperature decrement in
WMAP's Q, V and W bands and in the 143 GHz band of A RCHEOPS, but
not at 217 GHz, as would be expected for tSZ-induced temperature
fluctuations. All the other patches failed to show a
similar behavior.
To corroborate these results, for each of the patches we have compared
the cross-correlation coefficients to a model of the tSZ frequency
pattern, in which we fix the spectral behavior and fit for a global
amplitude parameter A. For the first patch and the three sizes
considered (32, 64 and 128 pixels), we obtain non zero A values at
more than 4.5-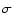 level with good agreement between the model and
the data, and negligible contribution from systematic residuals in the
Archeops data. For all other pixels having smaller projected galaxy
density, we fail to detect any signature of tSZ effect.
level with good agreement between the model and
the data, and negligible contribution from systematic residuals in the
Archeops data. For all other pixels having smaller projected galaxy
density, we fail to detect any signature of tSZ effect.
From these results, we conclude that there is clear indication of tSZ
effect for patch 1 in the A RCHEOPS and WMAP data sets. This is
not surprising, since patch 1 contains pixels centered in massive and
relatively nearby galaxy clusters. Assuming the signal observed is
tSZ, we infer, for the 32-pixels case, an average value for the
comptonization parameter of
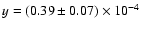 in all
those clusters at an angular scale of
in all
those clusters at an angular scale of 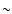 13 arcmin. This value
is compatible at 1.5-
13 arcmin. This value
is compatible at 1.5-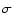 level with the expectations,
level with the expectations,
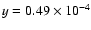 (cf. Table 1), from a model of the cluster
flux number counts based on the standard
(cf. Table 1), from a model of the cluster
flux number counts based on the standard 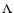 -CDM model, M1,
assuming the measured y is due to the contribution from the 32
brightest clusters. For 64 and 128-pixeles patches the tSZ signal is
diluted, probably due to the contribution of relatively not so massive
clusters. Note that the dilution observed is also compatible with the
one expected from the model M1 (cf. Table 1).
-CDM model, M1,
assuming the measured y is due to the contribution from the 32
brightest clusters. For 64 and 128-pixeles patches the tSZ signal is
diluted, probably due to the contribution of relatively not so massive
clusters. Note that the dilution observed is also compatible with the
one expected from the model M1 (cf. Table 1).
Acknowledgements
We acknowledge the Archeops collaboration for the use of the
proprietary Archeops data and for fruitful comments and careful
reading of this manuscript. We acknowledge very useful comments by
J.A. Rubiño-Martín. C.H.M. acknowledges the financial support
from the European Community through the Human Potential Programme
under contract HPRN-CT-2002-00124 (CMBNET). C.H.M. is currently
supported by NASA grants ADP03-0000-0092 and ADP04-0000-0093. We
acknowledge the use of the Legacy Archive for Microwave Background
Data Analysis (LAMBDA, http://lambda.gsfc.nasa.gov). Support
for LAMBDA is provided by the NASA Office of Space Science. This
publication makes use of data products from the Two Micron All Sky
Survey, which is a joint project of the University of Massachusetts
and the Infrared Processing and Analysis Center/California Institute
of Technology, funded by the National Aeronautics and Space
Administration and the National Science Foundation. Some of the
results in this paper have been derived using the HEALPix package,
(Górski et al. 1999).
- Afshordi, N., Lin,
Y.-T., & Sanderson, A. J. R. 2005, ApJ, 629, 1A [NASA ADS]
- Aghanim, N., De Luca,
A., Bouchet, F. R., Gispert, R., & Puget, J. L. 1997, A&A,
325, 9 [NASA ADS]
- Amblard, A., &
Hamilton, J. C. 2004, A&A, 417, 1189 [EDP Sciences] [NASA ADS] [CrossRef]
- Barbosa, D.,
Bartlett, J. G., Blanchard, A., & Oukbir, J. 1996, A&A,
314, 13 [NASA ADS]
- Barkats, D.,
Bischoff, C., Farese, P., et al. 2005, ApJ, 619, 127 [NASA ADS] [CrossRef]
- Bartelmann, M.
2001, A&A, 370, 754 [EDP Sciences] [NASA ADS] [CrossRef]
- Bartlett, J. G.,
& Silk, J. 1994, ApJ, 423, 12 [NASA ADS] [CrossRef]
- Battistelly, E. S., De
Petris, M., Lamagna, L., et al. 2003, ApJ, 598, L75 [NASA ADS] [CrossRef] (In the text)
- Bennett, C. L.,
Hinshaw, G., Banday, A., et al. 1993, ApJ, 414, L77 [NASA ADS] [CrossRef]
- Bennett, C. L.,
Halpern, M., Hinshaw, G., et al. 2003, ApJ, 148, 1 [NASA ADS] [CrossRef] (In the text)
- Benoît, A.,
Ade, P., Amblard, A., et al. 2002, APh, 17, 101 [NASA ADS] (In the text)
- Benoît,
A., Ade, P., Amblard, A., et al. 2003a, A&A, 399, L19 [EDP Sciences] [NASA ADS] [CrossRef]
-
Benoît, A., Ade, P., Amblard, A., et al. 2003b, A&A,
399, L25 [EDP Sciences] [NASA ADS] [CrossRef]
- Benson, A. J.,
Reichardt, Ch., & Kamionkowski, M. 2002, MNRAS, 331, 71 [NASA ADS] [CrossRef] (In the text)
- de Bernardis, P., Ade,
P. A. R., Bock, J. J., et al. 2000, Nature,
404, 955 [NASA ADS] [CrossRef]
- Birkinshaw, M. 1999,
PhR, 310, 97 [NASA ADS] (In the text)
- Fixsen, D. J.,
Cheng, E. S., Cottingham, D. A., et al. 1994, ApJ,
420, 445 [NASA ADS] [CrossRef] (In the text)
- Fosalba, P.,
Gaztañaga, E., Castander, F. J., et al. 2003, ApJ, 597,
L89 [NASA ADS] [CrossRef]
- Fosalba, M. , &
Gaztanaga, E. 2004, MNRAS, 350, L37 [NASA ADS] [CrossRef]
-
Górski K. M., Hivon E., &
Wandelt, B. D. 1999, in Proceedings of the MPA/ESO
Cosmology Conference, Evolution of Large-Scale Structure, ed. A. J.
Banday, R. S. Sheth, & L. Da Costa, PrintPartners Ipskamp, NL,
37 (also [arXiv:astro-ph/9812350])
(In the text)
- Gutiérrez,
C. M., Rebolo, R., Watson, R. A., et al. 2000, ApJ,
529, 47 [NASA ADS] [CrossRef] (In the text)
- Halverson, N. W.,
Leitch, E. M., Pryke, C., et al. 2002, ApJ, 568, 38 [NASA ADS] [CrossRef]
- Hanany, S., Ade, P.,
Balbi, A., et al. 2000, ApJ, 545, L5 [NASA ADS] [CrossRef]
-
Hernández-Monteagudo, C., & Rubiño-Martín,
J. A. 2004, MNRAS, 347, 403 [NASA ADS] [CrossRef]
-
Hernández-Monteagudo, C., Genova-Santos, R., &
Atrio-Barandela, F. 2004, ApJ, 613, L89 [NASA ADS] [CrossRef]
- Hinshaw, G., Spergel,
D. N., Verde, L., et al. 2003, ApJ, 148, 135 [NASA ADS] [CrossRef]
- Hu, W., & Sugiyama,
N. 1995, PhRvD, 51, 2599 [NASA ADS] (In the text)
- Jarrett, T. H.,
Chester, T., Cutri, R., Schneider, S. E., & Huchra,
J. P. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] (In the text)
- Lamarre, J. M.,
Puget, J. L., Bouchet, F., et al. 2003, NewAR, 47,
1017L [NASA ADS] (In the text)
- Lee, A. T., Ade,
P., Balbi, A., et al. 2001, ApJ, 561, L1 [NASA ADS] [CrossRef]
- Leitch, E., Kovac,
J., Halverson, N., et al. 2005, ApJ, 624, 10 [NASA ADS] [CrossRef]
- Lineweaver, C. H.,
Barbosa, D., Blanchard, A., et al. 1997, A&A, 322,
365 [NASA ADS]
- Mather, J. C., Fixsen,
D. J., Shafer, R. A., et al. 1999, ApJ, 512, 511 [NASA ADS] [CrossRef] (In the text)
- Mauskopf, P. D., Ade,
P. A. R., de Bernardis, P., et al. 2000, ApJ, 536, L59 [NASA ADS] [CrossRef] (In the text)
- Miller, A. D.,
Caldwell, R., Devlin, M. J., et al. 1999, ApJ, 524,
L1 [NASA ADS] [CrossRef]
- Myers, A. D.,
Shanks, T., Outram, P. J., Frith, W. J., &
Wolfendale, A. W. 2004, MNRAS, 347, L67 [NASA ADS] [CrossRef]
- Netterfield,
C. B., Devlin, M. J., Jarolik, N., et al. 1997, ApJ,
474, 47 [NASA ADS] [CrossRef]
- Netterfield, C. B.,
Ade, P. A. R., Bock, J. J., et al. 2002, ApJ,
571, 604 [NASA ADS] [CrossRef]
- Readhead, A., Myers,
S., Pearson, T., et al. 2004, Science, 306, 836 [NASA ADS] [CrossRef]
[arXiv:astro-ph/0409569]
- Rubiño-Martín,
J. A., & Sunyaev, R. A. 2003, MNRAS, 344, 1155 [NASA ADS] [CrossRef] (In the text)
- Rubiño-Martín,
J. A., Rebolo, R., Carreira, P., et al. 2003, MNRAS, 341,
1084 [NASA ADS] [CrossRef] (In the text)
- Sachs, R. K., &
Wolfe, A. M. 1967, ApJ, 147, 73 [NASA ADS] [CrossRef] (In the text)
- Sievers, J. L., Bond,
J. R., Cartwright, J. K., et al. 2003, ApJ, 591,
599 [NASA ADS] [CrossRef]
- Smoot, G. F., Bennett,
C. L., Kogut, A., et al. 1991, ApJ, 371, L1 [NASA ADS] [CrossRef] (In the text)
- Spergel,
D. N., Verde, L., Peiris, H. V., et al. 2003, ApJ,
148, 175 [NASA ADS] [CrossRef]
- Sunyaev,
R. A., & Zel'dovich, I. B. 1980, ARA&A, 18,
537 [NASA ADS] (In the text)
- Tristram,
M., Patanchon, G., Macías-Peréz, J. F., et al.
2005, A&A, 436, 785 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Xue, Y.-J., & Wu, X.-P.
2001, ApJ, 552, 2 [CrossRef], 452
(In the text)
- Yvon, D., & Mayet,
F. 2005, A&A, 436, 729 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
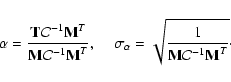
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{figures/3680f1.ps}
\end{figure}](/articles/aa/full/2006/13/aa3680-05/Timg29.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figures/3680f2.ps}
\end{figure}](/articles/aa/full/2006/13/aa3680-05/Timg33.gif)
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{figures/3680f3.ps}\par\includegraphics[width=7.8cm,clip]{figures/3680f4.ps}
\end{figure}](/articles/aa/full/2006/13/aa3680-05/Timg38.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figures/3680f5.ps}\par\includegraphics[width=7.6cm,clip]{figures/3680f6.ps}
\end{figure}](/articles/aa/full/2006/13/aa3680-05/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{figures/3680f7.ps}\par\includegraphics[width=7.6cm,clip]{figures/3680f8.ps}
\end{figure}](/articles/aa/full/2006/13/aa3680-05/Timg48.gif)