A&A 448, 861-871 (2006)
DOI: 10.1051/0004-6361:20053644
Log-parabolic spectra and particle acceleration in blazars
III. SSC emission in the TeV band from Mkn 501
E. Massaro1 - A. Tramacere1 - M. Perri2 - P. Giommi2
- G. Tosti3
1 - Dipartimento di Fisica, Università La Sapienza, Piazzale A. Moro 2,
00185 Roma, Italy
2 - ASI Science Data Center, ESRIN, 00044 Frascati, Italy
3 - Dipartimento di Fisica, Università di Perugia, via A. Pascoli,
Perugia, Italy
Received 16 June 2005 / Accepted 11 October 2005
Abstract
Curved broad-band spectral distributions of non-thermal sources like
blazars are described well by a log-parabolic law where the second
degree term measures the curvature.
Log-parabolic energy spectra can be obtained for relativistic electrons
by means of a statistical acceleration mechanism whose probability of
acceleration depends on energy.
In this paper we compute the spectra radiated by an electron population via synchrotron
and Synchro-Self Compton processes to derive the relations between
the log-parabolic parameters.
These spectra were obtained by means of an accurate numerical code
that takes the proper spectral distributions for single particle
emission into account.
We found that the ratio between the curvature parameters of the synchrotron spectrum
to that of the electrons is equal to 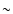 0.2 instead of 0.25, the value foreseen
in the
0.2 instead of 0.25, the value foreseen
in the 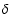 -approximation.
Inverse Compton spectra are also intrinsically curved and can be approximated
by a log-parabola only in limited ranges.
The curvature parameter, estimated around the SED peak, may vary from a lower value than
that of the synchrotron spectrum up to that of emitting electrons depending on
whether the scattering is in the Thomson or in the Klein-Nishina regime.
We applied this analysis to computing the synchro-self Compton emission from the BL Lac
object Mkn 501 during the large flare of April 1997. We fit simultaneous BeppoSAX
and CAT data and reproduced intensities and spectral curvatures of both components
with good accuracy.
The large curvature observed in the TeV range was found to be mainly
intrinsic, and therefore did not require a large pair production absorption against the
extragalactic background. We regard this finding as an indication that the Universe is
more transparent at these energies than previously assumed by several models found
in the literature.
This conclusion is supported by recent detection of two relatively
high redshift blazars with HESS.
-approximation.
Inverse Compton spectra are also intrinsically curved and can be approximated
by a log-parabola only in limited ranges.
The curvature parameter, estimated around the SED peak, may vary from a lower value than
that of the synchrotron spectrum up to that of emitting electrons depending on
whether the scattering is in the Thomson or in the Klein-Nishina regime.
We applied this analysis to computing the synchro-self Compton emission from the BL Lac
object Mkn 501 during the large flare of April 1997. We fit simultaneous BeppoSAX
and CAT data and reproduced intensities and spectral curvatures of both components
with good accuracy.
The large curvature observed in the TeV range was found to be mainly
intrinsic, and therefore did not require a large pair production absorption against the
extragalactic background. We regard this finding as an indication that the Universe is
more transparent at these energies than previously assumed by several models found
in the literature.
This conclusion is supported by recent detection of two relatively
high redshift blazars with HESS.
Key words: radiation mechanisms: non-thermal - galaxies: active - BL Lacertae objects: general - BL Lacertae objects: individual: Mkn 501
The spectral energy distributions (SEDs) of blazars, and particularly of
BL Lac objects, are characterised by a double-peak structure.
The peak at lower energies is generally explained by synchrotron radiation
from relativistic electrons in a jet that is closely aligned to the line of sight,
while the high frequency bump is produced by inverse Compton scattering
from the same electron population interacting either with the synchrotron
photons (SSC, Synchrotron-Self Compton models, see e.g. Marscher & Gear
1985) or with other photons that originated in the local environment
(ERC, External Radiation Compton models, see e.g. Sikora et al. 1994).
For the so-called Low-energy peaked BL Lac (LBL) objects, the frequency
of the first peak is in the Infrared-Optical region, while it is in
the UV-X ray range for the High-energy peaked BL Lac (HBL) (Padovani &
Giommi 1995).
The shape of these bumps is characterised in the Log
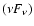 vs.
vs.
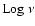 plot by a rather smooth curvature extending through several
frequency decades.
A very simple and successful analytical function that can model the shape
of these broad peaks is a parabola in the logarithms of the variables
(hereafter log-parabola).
This function has only three spectral parameters, and was used by Landau et al. (1986) to fit the broad band spectra of some bright BL Lac objects from
radio to UV.
Sambruna et al. (1996) also used a log-parabola to fit
blazars' SED to estimate peak frequencies and luminosities without, however,
attributing a physical meaning to this shape.
In two previous papers (Massaro et al. 2004a,b, hereafter Paper I
and Paper II, respectively) we used the log-parabolic model to fit the
BeppoSAX broad band X-ray spectra of the BL Lac objects Mkn 421 and
Mkn 501 and studied the relations between the spectral parameters and the
luminosity.
We also showed that, under simple approximations, a log-parabolic
synchrotron spectrum can be obtained by a relativistic electron population
having a similar energy distribution, and then derived the main relations
between their parameters.
Furthermore, in Paper I we proposed a simple explanation for the log-parabolic
energy distribution of the electrons as resulting from a statistical
mechanism where the acceleration probability decreases with the particle
energy.
plot by a rather smooth curvature extending through several
frequency decades.
A very simple and successful analytical function that can model the shape
of these broad peaks is a parabola in the logarithms of the variables
(hereafter log-parabola).
This function has only three spectral parameters, and was used by Landau et al. (1986) to fit the broad band spectra of some bright BL Lac objects from
radio to UV.
Sambruna et al. (1996) also used a log-parabola to fit
blazars' SED to estimate peak frequencies and luminosities without, however,
attributing a physical meaning to this shape.
In two previous papers (Massaro et al. 2004a,b, hereafter Paper I
and Paper II, respectively) we used the log-parabolic model to fit the
BeppoSAX broad band X-ray spectra of the BL Lac objects Mkn 421 and
Mkn 501 and studied the relations between the spectral parameters and the
luminosity.
We also showed that, under simple approximations, a log-parabolic
synchrotron spectrum can be obtained by a relativistic electron population
having a similar energy distribution, and then derived the main relations
between their parameters.
Furthermore, in Paper I we proposed a simple explanation for the log-parabolic
energy distribution of the electrons as resulting from a statistical
mechanism where the acceleration probability decreases with the particle
energy.
Curved spectra in non-thermal sources have already been studied in the past
and generally were related to the radiative ageing of the emitting electrons
that have a single power law injection spectrum.
The well-known solution by Kardashev (1962) predicts a change in the
electron spectral index by a unity (0.5 for the synchrotron
spectrum) around a break energy, whose value decreases with time.
Probably for this reason, curved spectra have been modelled by means of
rather complex functions like a double broken power law (Kataoka et al. 1999)
or a continuous combination of two power laws after releasing the condition
on the difference of spectral indices (see the discussion in Fossati et al. 2000).
A similar spectrum is generally used in the spectral modelling
of gamma-ray bursts (Band et al. 1993).
On the same basis, Sohn et al. (2003) more recently introduced a
spectral-curvature parameter, defined as the difference between two
spectral indices in different frequency intervals, to study the evolution
of synchrotron sources.
As we will show later, this parameter is strongly dependent on the chosen
frequency range and cannot be univocally related to the actual curved
shapes.
In this paper we stress the advantages of using a log-parabolic law
to model curved spectra over broad frequency ranges and present the
results of an accurate study of the spectral distributions of the
synchrotron radiation (hereafter SR) and of the inverse Compton (hereafter
IC) scattered photons by a population of relativistic electrons with
such energy spectrum.
We study, in particular, the relations between the parameters of SR spectra
and those of the electrons and show that they are generally
approximated well by simple power behaviours and that they provide useful
information on the electron spectrum.
The relations with the IC spectrum are not so simple depending upon whether the
majority of scatterings is in the Thomson or in the Klein-Nishina regime.
In any case, our calculations indicate a good way to properly model
the observed spectra.
We also consider the case in which the probability of statistical
acceleration is constant below a critical energy, thus producing a power
law spectrum that turns into a log-parabola above this energy.
In the last part of the paper, we apply our model to the large flare
from Mkn 501 observed in April 1997.
This is a unique event in which the SR and IC components were
observed simultaneously over energy bands that were broad enough to
study the spectral curvature.
We use the BeppoSAX data already analysed in
Paper II together with those in the TeV band obtained by the CAT
experiment (Djannati-Atai et al. 1999). Our approach of studying
both the SR and IC spectral curvatures is useful for evaluating the
relevance of the intergalactic absorption due to pair production
from photon-photon interactions. In particular, we discuss the
possibility that the observed TeV curvature is mainly intrinsic, as
it implies rather low absorption and the possibility of detecting
sources at larger distances than usually estimated.
The log-parabolic model is one of the simplest ways to represent curved
spectra when these show mild and nearly symmetric curvature around the
maximum instead of a sharp high-energy cut-off like that of an exponential.
In the following, we summarise the main properties of log-parabolic
spectra, while for details we refer to
Papers I and II. This law has only one more parameter than a simple power law
and can be written as:
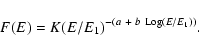 |
(1) |
The energy dependent photon index is
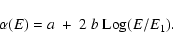 |
(2) |
With
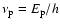 we also indicate the peak frequency
of the SED where
we also indicate the peak frequency
of the SED where 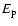 is related to the spectral parameters
of Eq. (1) as follows:
is related to the spectral parameters
of Eq. (1) as follows:
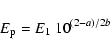 |
(3) |
and
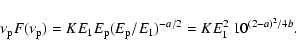 |
(4) |
It is useful to note that the above formulae must be used
when working with photon spectra, as is usual in X and  -ray
astronomy.
Energy spectra are obtained by multiplying Eq. (1) by E, and the
corresponding spectral index is therefore increased by unity.
In the following, we indicate the energy index with
-ray
astronomy.
Energy spectra are obtained by multiplying Eq. (1) by E, and the
corresponding spectral index is therefore increased by unity.
In the following, we indicate the energy index with
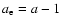 to avoid confusion.
In this case the peak frequency becomes:
to avoid confusion.
In this case the peak frequency becomes:
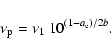 |
(3') |
An advantage of the log-parabolic model compared to other curved
spectral laws is that the curvature around the peak is characterised only
by the parameter b, while in other models, like the continuous combination
of two power laws, it is a function of more parameters.
Note also that the estimate of b is independent of the particular spectral
representation adopted for the data.
The same property does not hold for the spectral-curvature parameter
(SCP) defined by Sohn et al. (2003).
Unlike b, this quantity depends upon the energy
(frequency) interval chosen to estimate the spectral indices at high
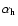 and low
and low
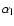 frequencies.
The relation between b and SCP can be obtained by evaluating
frequencies.
The relation between b and SCP can be obtained by evaluating 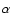 in
two energy ranges
in
two energy ranges 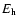 (high) and
(high) and 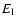 (low) from Eq. (2):
(low) from Eq. (2):
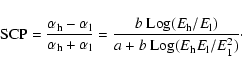 |
(5) |
For flat spectrum sources with a close to zero, SCP becomes
practically independent of b.
One limit of the log-parabolic model, however, is that it can represent
only distributions symmetrically decreasing with respect to the
peak frequency.
However, it is not difficult to modify Eq. (1) to take into account a possible
asymmetry with respect to 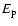 .
For instance, one can use two different values of b for energies lower
and higher than
.
For instance, one can use two different values of b for energies lower
and higher than 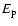 ,
where the two branches continuously match.
An interesting possibility, which can be simply explained in terms of
the energy dependence of the particle acceleration probability (see next
section), is that the low energy segment of the spectrum follows a single
power law with photon index
,
where the two branches continuously match.
An interesting possibility, which can be simply explained in terms of
the energy dependence of the particle acceleration probability (see next
section), is that the low energy segment of the spectrum follows a single
power law with photon index 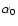 and that the log-parabolic
bending becomes apparent only above a critical value
and that the log-parabolic
bending becomes apparent only above a critical value 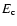 .
This behaviour can be described by the following model that takes into
account the continuity conditions on the flux and on
.
This behaviour can be described by the following model that takes into
account the continuity conditions on the flux and on 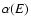 at
at 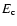 :
:
In Paper I we showed that a log-parabolic distribution is not only
a simple mathematical tool for spectral modelling, but that it also relates to the
physics of the statistical acceleration process under some simple hypotheses.
In the following, we extend the considerations of Paper I.
The results, useful to derive some relations between the acceleration
parameters, should not be considered as a complete theory of energy-dependent
acceleration.
To confirm the main findings of this approach, more detailed analytical
and numerical calculations are necessary, but such a detailed theoretical
approach is beyond the purpose of the present paper.
The energy spectrum of particles accelerated by some statistical mechanism,
e.g. a shock wave or a strong perturbation moving down a jet, is given by
a power law (Bell 1978; Blandford & Ostriker 1978; Michel 1981).
In Paper I we showed that a log-parabolic
energy spectrum is obtained when the condition that the acceleration probability
p is independent of energy is released and that its value
at the step i satisfies a power law relation as:
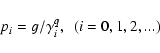 |
(7) |
where g and q are positive constants.
Such a situation can occur, for instance, when particles are confined
by a magnetic field with a confinement efficiency that decreases for an
increasing gyration radius.
In Paper I (Sect. 6.1) we found that the integral energy distribution of
accelerated particles is given by a log-parabolic law:
![\begin{displaymath}N({>}\gamma) = N_0 (\gamma/\gamma_0)^{-[s - 1 + r~ {\rm Log} (\gamma/\gamma_0)]} ,
\end{displaymath}](/articles/aa/full/2006/12/aa3644-05/img32.gif) |
(8) |
with
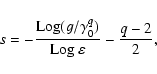 |
(9) |
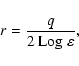 |
(10) |
where 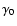 is the minimum Lorentz factor in Eq. (7).
As already discussed in Paper I the differential energy distribution
is the minimum Lorentz factor in Eq. (7).
As already discussed in Paper I the differential energy distribution
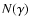 is not an exact log-parabolic law, but differs from it
only by a logarithmic term and can be approximated well by
a log-parabola with a very similar curvature over an energy range of
several decades.
is not an exact log-parabolic law, but differs from it
only by a logarithmic term and can be approximated well by
a log-parabola with a very similar curvature over an energy range of
several decades.
Shock wave acceleration is not the only statistical mechanism active in
non-thermal sources.
For instance, electron acceleration can occur in magnetohydrodynamical
turbulence in which regions of magnetic field reconnection can develop
in a very stochastic way.
Recently, Nodes et al. (2004) presented the results of the numerical
simulations of a relativistic particle acceleration in a three-dimensional
turbulent electromagnetic field configuration, also taking their SR into account.
These authors found energy spectral distributions that where significantly
flatter than s=2 and, in a few cases, characterised by a steepening
spectral index at high energies.
We verified that over sufficiently wide energy ranges, the spectra given by
Nodes et al. (2004) are represented well by a log-parabolic law or by
a combination of a power law and a parabola. The resulting curvature
parameters are generally small, but probably the curvature depends
on the distribution and size of the acceleration regions, so one
can expect that, under different assumptions, it could be higher.
Nodes et al. (2004) computed the emerging SR spectra, which show an appreciable curvature
over a few decade frequency range.
Statistical acceleration is not the only way to obtain curved electron
spectra. Energy distributions showing a rather mild
curvature have also been obtained in blazar physics.
To model the SED of MeV blazars, Sikora et al. (2002) assumed that
electrons are accelerated via a two-step process with a broken
power-law energy distribution as injection.
When the cooling effects are taken into account, the resulting electron
spectrum (see, for instance, Fig. 6 in their paper) can be described well
by a log-parabola over a range that is wider than three decades,
as we verified (in this case we found r=0.44).
The assumption of Eq. (7) about the energy dependence of the
acceleration probability can be modified to take other
escape processes into account.
For instance, one can assume that the acceleration probability is constant
for low energies and that it begins to decrease above a critical Lorentz factor
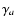 (see, for instance Eq. (23) in Paper I).
An approximate expression for the energy distribution of accelerated
particles under this condition
for
(see, for instance Eq. (23) in Paper I).
An approximate expression for the energy distribution of accelerated
particles under this condition
for
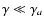 should follow a power law with spectral
index
should follow a power law with spectral
index
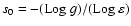 ,
while for
,
while for
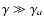 it will approximate a log-parabolic spectrum like Eq. (8):
it will approximate a log-parabolic spectrum like Eq. (8):
where for the sake of simplicity we take
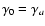 .
In addition to the power law and log-parabolic segments, we can also expect
a sharp high-energy cutoff that appears when losses make the acceleration
process highly inefficient.
.
In addition to the power law and log-parabolic segments, we can also expect
a sharp high-energy cutoff that appears when losses make the acceleration
process highly inefficient.
It is important to know the relations between the spectral parameters
a and b of the emitted radiation and those of the electron population,
namely s and r.
The spectral distribution
of the SR by relativistic electrons having a log-parabolic energy
distribution cannot be computed analitically.
For our purpose, however, the relations between the spectral parameters
can be derived under the usual 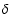 -approximation and the
assumption that the electrons are isotropically distributed in a
homogeneous randomly oriented magnetic field with an average
intensity B
-approximation and the
assumption that the electrons are isotropically distributed in a
homogeneous randomly oriented magnetic field with an average
intensity B
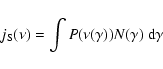 |
(12) |
where 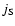 is the synchrotron emissivity,
is the synchrotron emissivity, 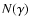 the electron
density, and the power radiated by a single particle is
the electron
density, and the power radiated by a single particle is
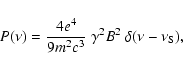 |
(13) |
and
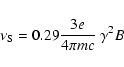 |
(14) |
is the SR peak frequency for a single particle.
We then obtain (see Paper I):
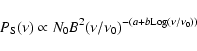 |
(15) |
with
| a |
= |
(s-1)/2 |
|
| b |
= |
r/4 . |
(16) |
Note that the parameter a, as defined above,
does not coincide with the one defined in Eq. (2), because the
former is the energy index at the frequency 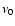 ,
whereas the
latter is the photon index at the energy E1, not necessarily
corresponding to
,
whereas the
latter is the photon index at the energy E1, not necessarily
corresponding to 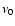 .
It is not difficult to verify that these two parameters differ for an
additional constant, whose value depends on
.
It is not difficult to verify that these two parameters differ for an
additional constant, whose value depends on 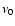 and
and
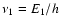 .
In Paper I we noted that
one can expect a and b to show a linear correlation,
which was indeed found for Mkn 421.
We stress that such correlation is not a general
result that can be applied to any sample of sources.
It also depends upon the
values of q, g, and
.
In Paper I we noted that
one can expect a and b to show a linear correlation,
which was indeed found for Mkn 421.
We stress that such correlation is not a general
result that can be applied to any sample of sources.
It also depends upon the
values of q, g, and 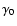 ,
which can be different from source
to source, and the dispersions of their distribution functions can introduce
a significant amount of scatter in the data that could destroy the correlation.
Reasonably, one has to expect that the linear correlation between
a and b can be found only when the physical conditions in the
acceleration region are quite similar.
The absence of correlation found by Perlman et al. (2005) in their
sample, therefore, does not imply that curved spectra in blazars
are not originated by energy-dependent statistical acceleration.
,
which can be different from source
to source, and the dispersions of their distribution functions can introduce
a significant amount of scatter in the data that could destroy the correlation.
Reasonably, one has to expect that the linear correlation between
a and b can be found only when the physical conditions in the
acceleration region are quite similar.
The absence of correlation found by Perlman et al. (2005) in their
sample, therefore, does not imply that curved spectra in blazars
are not originated by energy-dependent statistical acceleration.
The relation between r and b given above (Eq. (16)) is not exact:
one can expect that a precise calculation of the spectral curvature
of the emitted radiation must give a b value smaller than in the
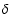 approximation and that, for high values of r, b can be
greater than unity (depending on the frequency interval used around
the peak in which it is estimated) because of the exponential cutoff
by the SR spectrum radiated by a single particle.
approximation and that, for high values of r, b can be
greater than unity (depending on the frequency interval used around
the peak in which it is estimated) because of the exponential cutoff
by the SR spectrum radiated by a single particle.
To compute the relations between the spectral parameters numerically
and to study the spectral evolution of the emitting particles,
as reported in the next subsection, we applied a time-dependent
numerical code (Tramacere & Tosti 2003; see
Tramacere 2002, for a detailed description of the code).
This code uses a numerical
integration routine that applies a modified Simpson rule ensuring
good convergence in short computing times.
In particular, this code includes an accurate evaluation of the synchrotron
frequency distribution (hereafter SFD):
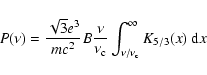 |
(17) |
where
K5/3(x) is a modified Bessel function of the second type
and
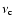 the synchrotron critical frequency (Blumenthal
& Gould 1970; Rybicki & Lightman 1979).
Note that while the maximum of
the synchrotron critical frequency (Blumenthal
& Gould 1970; Rybicki & Lightman 1979).
Note that while the maximum of 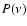 is at 0.29
is at 0.29
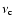 ,
the peak in the corresponding
SED
,
the peak in the corresponding
SED
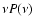 is at the frequency
is at the frequency
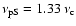 .
.
![\begin{figure}
\par\includegraphics[width=6cm,clip]{3644fg1.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg57.gif) |
Figure 1:
Synchrotron spectra emitted by an electron population
with log-parabolic (dashed lines) and power-law log-parabolic
energy distributions (Eq. (11)) (solid lines), computed for r values in the interval 0.50-1.20. Spectra were shifted
on the vertical scale to avoidconfusion.
|
| Open with DEXTER |
We calculated the SR spectra and SEDs from Eq. (12) using a log-parabolic
distribution without (LP) and with a low-energy power law branch (LPPL)
(Eq. (11)) and the frequency distribution of Eq. (17).
All the calculations in this and in the following subsections are
performed in the co-moving frame, so relativistic beaming
effects were not included.
Figure 1 shows some examples of the resulting SEDs.
In these computations we assumed a uniform magnetic field B=0.14 G,
and the spectral parameters for the electrons were
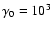 ,
s=s0=1.2 (Eq. (11)), while r values were increased from 0.5 to 1.20 by
steps of 0.05.
The electron density and the size of the emission region were taken
to be equal to the typical values used in blazar modelling.
In these conditions the synchrotron self-absorption is important
at frequencies lower than
,
s=s0=1.2 (Eq. (11)), while r values were increased from 0.5 to 1.20 by
steps of 0.05.
The electron density and the size of the emission region were taken
to be equal to the typical values used in blazar modelling.
In these conditions the synchrotron self-absorption is important
at frequencies lower than 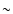 1010 Hz.
Note in Fig. 1 that at low frequencies both spectral sets tend to a
power law: in the LP case the spectral index corresponds to the SFD
asymptotic behaviour (
1010 Hz.
Note in Fig. 1 that at low frequencies both spectral sets tend to a
power law: in the LP case the spectral index corresponds to the SFD
asymptotic behaviour (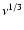 ), while in the other case it has
the energy spectral index
), while in the other case it has
the energy spectral index
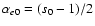 .
At high frequencies the log parabolic behaviour is very evident with a
peak frequency decreasing for higher values of r, as expected from
Eq. (3) since b is also increasing with r.
.
At high frequencies the log parabolic behaviour is very evident with a
peak frequency decreasing for higher values of r, as expected from
Eq. (3) since b is also increasing with r.
We first verified that the peak frequency in the SED of the SR component
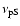 is proportional to the Lorentz factor
is proportional to the Lorentz factor
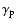 at which
the electron distribution
at which
the electron distribution
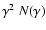 has its maximum.
Applying the same formulae of Sect. 2, we have
has its maximum.
Applying the same formulae of Sect. 2, we have
from which we have:
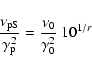 |
(18) |
where we assumed
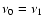 for the sake of simplicity.
In Fig. 2 we plotted the resulting
for the sake of simplicity.
In Fig. 2 we plotted the resulting
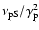 vs. 1/rfor both LP and LPPL cases: points of the two sets are coincident
in the whole range of interest and only for 1/r < 0.3 a small
deviation from the linear trend of the LPPL model is evident.
The slope of the best fit line (for 1/r > 0.3) is equal to
0.97, very close to unity as in Eq. (18).
Note also that the linear extrapolation to large values of
r (
vs. 1/rfor both LP and LPPL cases: points of the two sets are coincident
in the whole range of interest and only for 1/r < 0.3 a small
deviation from the linear trend of the LPPL model is evident.
The slope of the best fit line (for 1/r > 0.3) is equal to
0.97, very close to unity as in Eq. (18).
Note also that the linear extrapolation to large values of
r (
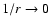 )
gives
for the
)
gives
for the
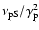 ratio a value very close to
1.33
ratio a value very close to
1.33
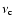 ,
consistent with the theory expectation.
,
consistent with the theory expectation.
![\begin{figure}
\par\includegraphics[width=5.7cm,clip]{3644fg2.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg68.gif) |
Figure 2:
The relation between the peak frequencies of the synchrotron
SED and those of the energy spectrum of the emitting electrons
computed using the SFD (Eq. (17)) for the LP and LPPL cases (see text).
The abscissa is the inverse of the electron spectrum curvature
to show the linear trend expected from Eq. (18).
The dashed line is the best fit computed for 1/r >0.33.
Note the small deviations of LPPL points from the best fit line
at low values of 1/r.
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5.75cm,clip]{3644fg3.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg69.gif) |
Figure 3:
The relation between the log-parabolic curvature parameters
of the electron energy distribution r and those of the
synchrotron radiation computed applying the 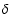 approximation
(crosses) and the SFD. The two LP point sets correspond to
log-parabolic electron spectra with b evaluated by a best
fit around the SED peak (filled circle) and on the high
frequency branch (diamonds). LPPL points (open squares)
correspond to a combined log-parabolic power law distribution.
Dashed lines are linear best fits used for the calculation of
the b/r ratio.
approximation
(crosses) and the SFD. The two LP point sets correspond to
log-parabolic electron spectra with b evaluated by a best
fit around the SED peak (filled circle) and on the high
frequency branch (diamonds). LPPL points (open squares)
correspond to a combined log-parabolic power law distribution.
Dashed lines are linear best fits used for the calculation of
the b/r ratio.
|
| Open with DEXTER |
We also used the spectra of Fig. 1 to study the relation between
r and b under different conditions.
The estimate of b is not simple because the radiation spectra
do not have an exact log-parabolic shape.
One can expect that this estimate is more accurate considering only
the SED branches at frequencies higher than the peak: a quadratic best
fit of the spectra of Fig. 1 confirms the linear relation between b
and r, but the coefficient is equal to 0.22, slightly lower than
the value found under the 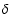 approximation (Eq. (16)).
We also computed b considering a frequency interval centred at the
peak frequency and spanning approximately two decades.
The results are shown in Fig. 3.
The relation between b and r was linear with very good accuracy,
but the coefficient decreased to 0.18, as expected because of the
smaller curvature of the low frequency branches.
The last result does not change if the low energy electron spectrum
follows a power law instead of a log-parabola (open squares in Fig. 3):
the b/r ratio in this case was found equal to 0.19.
We also verified our results by computing the spectra using the
approximation (Eq. (16)).
We also computed b considering a frequency interval centred at the
peak frequency and spanning approximately two decades.
The results are shown in Fig. 3.
The relation between b and r was linear with very good accuracy,
but the coefficient decreased to 0.18, as expected because of the
smaller curvature of the low frequency branches.
The last result does not change if the low energy electron spectrum
follows a power law instead of a log-parabola (open squares in Fig. 3):
the b/r ratio in this case was found equal to 0.19.
We also verified our results by computing the spectra using the 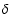 approximation and found
b/r=0.2508, in very good agreement with the
theory.
An approximate rule derived from this analysis indicates that it is
convenient to take the value of the ratio equal to 0.2, within an
accuracy of 10%.
The resulting r estimate can then be used as the input value for a more
refined modelling of the SED.
approximation and found
b/r=0.2508, in very good agreement with the
theory.
An approximate rule derived from this analysis indicates that it is
convenient to take the value of the ratio equal to 0.2, within an
accuracy of 10%.
The resulting r estimate can then be used as the input value for a more
refined modelling of the SED.
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{3644fg4.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg70.gif) |
Figure 4:
Time evolution of the SR spectrum ( upper panel) and of the
corresponding spectrum of electrons, multiplied by the square
of the Lorentz, under SR losses.
The injection spectrum was a log-parabola with
s=1.2 and r=0.7, corresponding to a peak energy of
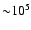 .
Spectra are plotted for equal time steps of .
Spectra are plotted for equal time steps of 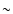 0.4 cooling times.
Note the decrease in the peak energy and the deviation
from a log-parabola due to difference in cooling time with 0.4 cooling times.
Note the decrease in the peak energy and the deviation
from a log-parabola due to difference in cooling time with 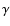 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{3644fg5.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg71.gif) |
Figure 5:
Time evolution of the log-parabolic curvature parameters
r of the electron spectrum ( upper line) and b of the SR SED
( lower line) computed
by means of a best fit around the peak. Solid lines are linear
best fits to the computed values.
|
| Open with DEXTER |
We also studied the evolution of spectral curvature due only to synchrotron
cooling. Of course, this study cannot be performed in general because
the solution of the time-dependent continuity equation is a function of
the assumed time evolution of the injection rate of emitting electrons
and of several other parameters like the mean residence time of particles
inside the emitting volume.
We studied, therefore, the simplest case of a pure radiative SR cooling
in a homogeneous and steady magnetic field without leakage and with a
log-parabolic initial spectrum.
The time evolution of SR and electron spectra are shown
in the two panels of Fig. 4, where the decrease in both the peak
frequency and intensity with time is very evident.
Although radiation losses modify the spectral shape, it remains
approximately log-parabolic, though with larger curvature parameters.
These variations are shown in Fig. 5, where we plotted the r and b
values, measured in energy/frequency intervals centered approximately at
the distribution peaks, as a function of time, measured in
units of the cooling time for the peak energy of the initial electron
spectrum, taken as
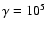 and corresponding to
and corresponding to
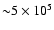 s
with a magnetic field B=0.1 G.
It is worth noting that the change in time of r and b is described well
by linear relations. The observation of a decrease in
s
with a magnetic field B=0.1 G.
It is worth noting that the change in time of r and b is described well
by linear relations. The observation of a decrease in
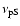 associated with an increasing curvature during the dimming phase of
an outburst is an indication of a radiative cooling evolution.
Our calculations also show that the changes of SR peak frequency and b
are correlated according to a power law as shown in the plot of Fig. 6.
associated with an increasing curvature during the dimming phase of
an outburst is an indication of a radiative cooling evolution.
Our calculations also show that the changes of SR peak frequency and b
are correlated according to a power law as shown in the plot of Fig. 6.
We stress, however, that the estimate of b may not be simple when
working with observational data because the position of the peak
may be far from the centre of the detector frequency range, and the
uncertainty on the interstellar and intrinsic absorption may be
non-negligible, particularly in the soft X-ray band.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3644fg6.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg74.gif) |
Figure 6:
The relation between the peak frequency and the curvature parameter b
of the SR spectra plotted in the upper panel of Fig. 4. The dashed line is
the best fit to the computed values.
|
| Open with DEXTER |
We computed the spectral distribution of the SSC emission from
a relativistic electron population with a log-parabolic energy
spectrum in the framework of a homogeneous one-zone model in which
the seed photons are isotropic in the bulk frame of the
electrons.
Our goal is to estimate the relations between the main spectral
parameters: the peak frequencies of the SR and IC components and their
curvatures indicated in the following by bS and bC, respectively.
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{3644fg7.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg75.gif) |
Figure 7:
The SR and SSC spectral energy distributions emitted by an electron
population with power-law log-parabolic distributions (Eq. (11)),
computed for r values in the interval 0.50-1.20.
Upper panel: spectra for
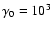 ;
lower panel: spectra
for ;
lower panel: spectra
for
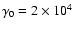 . .
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=5.9cm,clip]{3644fg8.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg76.gif) |
Figure 8:
Dependence of the peak frequencies upon the particle characteristic energies
in the SED of a single zone SSC model.
Upper panel: frequency of SSC peak vs. electron Lorentz factors of the
peaks for r values in the interval 0.50-1.90, the three curves
correspond to
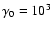 (filled circles),
(filled circles),
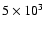 (open cicrcles),
104 (crosses).
Lower panel: ratio between the peak frequencies of IC and SR components
for the same values of the spectral parameters.
(open cicrcles),
104 (crosses).
Lower panel: ratio between the peak frequencies of IC and SR components
for the same values of the spectral parameters.
|
| Open with DEXTER |
The IC emissivity is given by (Jones 1968; Blumenthal & Gould 1970;
Band & Grindlay 1985)
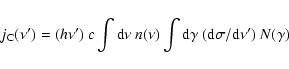 |
(19) |
where 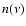 is the density of SR photons,
is the density of SR photons, 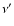 the frequency of scattered
photons, and the differential Klein-Nishina cross section is:
the frequency of scattered
photons, and the differential Klein-Nishina cross section is:
![$\displaystyle \frac{{\rm d}\sigma}{{\rm d}\nu'} = \frac{3 \sigma_{\rm T}}{16\ga...
...[4(h\nu/m_{\rm e}c^2)\gamma \eta]^2}{1+4(h
\nu/m_{\rm e}c^2)\gamma\eta}\Bigg]{}$](/articles/aa/full/2006/12/aa3644-05/img80.gif) |
|
|
(20) |
with
![\begin{displaymath}0 \leq \eta = \frac{\nu'}{4 \gamma^2 \nu [1-(h \nu'/m_{\rm e}c^2)]} \leq 1
\end{displaymath}](/articles/aa/full/2006/12/aa3644-05/img81.gif) |
(21) |
and
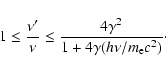 |
(22) |
Figure 7 shows two sets of resulting spectral distributions of both SR and IC
components for values of r ranging from 0.5 to 1.2 and 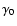 equal
to 103 (upper panel) and
equal
to 103 (upper panel) and
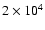 (lower panel).
The upper cut-off of the energy electron spectrum was fixed at
(lower panel).
The upper cut-off of the energy electron spectrum was fixed at
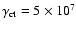 .
In the upper panel of Fig. 8, we plotted the peak frequency of the IC component
.
In the upper panel of Fig. 8, we plotted the peak frequency of the IC component
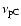 vs.
vs.
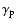 for
for
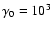 ,
,
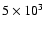 , 104 and r ranging from 0.5 to 1.9.
These curves are useful for understanding at which electron peak energy the
IC emission is dominated by the Thomson or the Klein-Nishina regime.
We stress that this does not imply that the largest contribution to
the emission around
, 104 and r ranging from 0.5 to 1.9.
These curves are useful for understanding at which electron peak energy the
IC emission is dominated by the Thomson or the Klein-Nishina regime.
We stress that this does not imply that the largest contribution to
the emission around
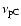 is due to electrons exactly at
is due to electrons exactly at
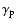 .
We computed these energies and found that, for the highest value of
.
We computed these energies and found that, for the highest value of
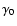 ,
the difference is on the order of a few percent, while for the
lowest
,
the difference is on the order of a few percent, while for the
lowest 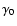 and r=1.7 the greatest contribution to the IC peak
is produced by electrons having
and r=1.7 the greatest contribution to the IC peak
is produced by electrons having
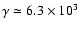 ,
while
,
while
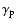 is at
is at
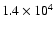 .
It is of course impossible to derive a simple rule because of the number of
parameters involved.
Figure 8 (upper panel) shows that as
.
It is of course impossible to derive a simple rule because of the number of
parameters involved.
Figure 8 (upper panel) shows that as
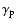 increases, the corresponding
increases, the corresponding
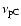 grows slower and slower indicating that the Klein-Nishina suppression
becomes more efficient.
A second way to show the relation between SR and IC components is given in the
lower panel of Fig. 8, where we plotted the ratio
grows slower and slower indicating that the Klein-Nishina suppression
becomes more efficient.
A second way to show the relation between SR and IC components is given in the
lower panel of Fig. 8, where we plotted the ratio
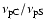 vs.
vs.
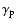 :
this ratio increases until the Thomson scattering is dominant and
reaches the maximum at the transition to the Klein-Nishina regime.
:
this ratio increases until the Thomson scattering is dominant and
reaches the maximum at the transition to the Klein-Nishina regime.
The IC spectra show an evident curvature that is not univocally related
to the r as in the SR case. Spectral curvature, in fact, depends on several
parameters in a complex way.
The spectral shape is generally different from a log-parabola, and it can be
approximated by this function only in a limited frequency interval.
Consequently, the estimate of the curvature parameter
depends on the postion and amplitude of this interval.
In particular, the curvature depends on the intrinsic electron spectral curvature,
the energy of SR photons, and on the energy of the electrons that mostly contribute
to the emission in the selected interval.
These energies, in fact, determine if the scatterings happen in the Thomson limit
or in the Klein-Nishina regime.
We obtained spectra with a curvature less pronounced than
SR only for
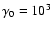 (i.e. for dominant Thomson scattering) and b
evaluated in an interval around the peak.
In all the other cases, higher b values of IC spectrum resulted.
Figure 9 shows some examples: the curvature parameter
b of the IC spectrum, computed in a single zone SSC model, was evaluated in
three adjacent frequency intervals, each having an amplitude of about
a decade starting from the peak frequency.
When the main contribution to IC emission comes from Thomson scatterings, the curvature
is closer to that of SR (solid line), and it approaches that of the electron spectrum
(dashed-dotted line) when the fraction of interactions in the Klein-Nishina regime
increases.
The two panels correspond to
(i.e. for dominant Thomson scattering) and b
evaluated in an interval around the peak.
In all the other cases, higher b values of IC spectrum resulted.
Figure 9 shows some examples: the curvature parameter
b of the IC spectrum, computed in a single zone SSC model, was evaluated in
three adjacent frequency intervals, each having an amplitude of about
a decade starting from the peak frequency.
When the main contribution to IC emission comes from Thomson scatterings, the curvature
is closer to that of SR (solid line), and it approaches that of the electron spectrum
(dashed-dotted line) when the fraction of interactions in the Klein-Nishina regime
increases.
The two panels correspond to 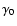 values differing by a factor of 20.
In the upper panel, IC emission is dominated by Thomson scattering in the two first
intervals, while in the lower panel the curvature approaches that of the electrons
because the majority of interactions are in the Klein-Nishina regime.
This property is really useful because a simultaneous measure of the
curvature parameters of SR and IC emissions can help to
discriminate between the two regimes of Compton scattering and to constrain
the spectral parameters of emitting electrons.
values differing by a factor of 20.
In the upper panel, IC emission is dominated by Thomson scattering in the two first
intervals, while in the lower panel the curvature approaches that of the electrons
because the majority of interactions are in the Klein-Nishina regime.
This property is really useful because a simultaneous measure of the
curvature parameters of SR and IC emissions can help to
discriminate between the two regimes of Compton scattering and to constrain
the spectral parameters of emitting electrons.
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{3644fg9.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg88.gif) |
Figure 9:
The curvature parameter b of the IC spectrum for a single zone SSC model
plotted against the electron spectral curvature r.
Dashed-dotted lines are the curvature parameters for the electrons and solid lines
for SR component.
Dashed lines correspond to IC curvatures evaluated in three adjacent frequency
intervals with an amplitude of about a decade selected starting from
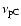 :
lowest lines correspond to the intervals closest to the peaks and the highest ones
to those at the highest frequencies.
The upper panel shows b values computed for :
lowest lines correspond to the intervals closest to the peaks and the highest ones
to those at the highest frequencies.
The upper panel shows b values computed for
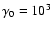 and lower panel those
for
and lower panel those
for
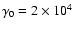 .
Note that when the largest contribution to IC emission is from Thomson scatterings
( upper panel), curvatures are closer to those of SR, while in the Klein-Nishina regime
( lower panel) b values result very close to r. .
Note that when the largest contribution to IC emission is from Thomson scatterings
( upper panel), curvatures are closer to those of SR, while in the Klein-Nishina regime
( lower panel) b values result very close to r.
|
| Open with DEXTER |
In Paper II we presented the results of analysing all BeppoSAX
observations of the nearby HBL object Mkn 501 using log-parabolic
spectral models.
In the case of this source, we did not detect significant variations
of the X-ray flux during the individual pointings, but large luminosity
changes were found between the three observations of April 1997
(on the 7, 11, and 16) for which simultaneous TeV data, obtained
with the CAT Cerenkov telescope, are available (Djannati-Atai et al. 1999).
The TeV data showed a remarkable spectral curvature modelled by these
authors by means of a log-parabolic law: best fit b values were higher
than 0.4, while those measured in the X rays are in the range 0.12-0.17
(see Paper II).
Krennich et al. (1999) observed Mkn 501 from February to June 1997
with the Whipple telescope and found a high curvature of the TeV spectra
as well.
Table 1:
Model parameters for the 1997 April flare of Mkn 501.
In Sect. 4 we discussed the relations between the parameters of
log-parabolic spectra for a SSC emission and showed that SSC emission
model can give high frequency spectra with a b value ranging from
that of the SR component to that of the electron spectrum depending on
whether the scattering occurs in the Thomson or in the Klein-Nishina regime.
From the calculations of Sect. 3, we know that an SR b value of about 0.15
corresponds to
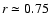 ,
and therefore a curvature of the IC component
as that measured in the TeV range can be expected.
,
and therefore a curvature of the IC component
as that measured in the TeV range can be expected.
In Paper II we also presented a two component-model to describe the
spectral evolution of the April 1997 X-ray outburst of Mkn 501.
We assumed that the components had the same curvature (b=0.18) and differ
for the peak energy and their relative intensity.
In this way we explained the nearly constant flux observed at lower energies
than 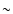 1 keV, while that around 100 keV changed by more
than one order of magnitude, and the slight decrease of b in the
higher states was interpreted as the effect of the sum of two
log-parabolic distributions peaked at different energies.
1 keV, while that around 100 keV changed by more
than one order of magnitude, and the slight decrease of b in the
higher states was interpreted as the effect of the sum of two
log-parabolic distributions peaked at different energies.
An important effect to be considered when computing the spectral
curvature in the TeV range is the absorption of the most energetic
photons due to pair production against the infrared extragalactic background
light (EBL). Dwek & Krennich (2005) have recently studied twelve
EBL models and computed the corresponding intrinsic spectra
of Mkn 501. These authors found that the majority of EBL models give
intrinsic emitted spectra showing an unphysical rise at high
TeV energies and that only the lowest intensity EBL models are acceptable.
We applied our radiation code to searching for the geometrical and
physical parameters of the emitting region that can reproduce the observed
intensities and spectral shapes, also taking EBL absorption into account.
To compare the model with the data, we need to introduce a relativistic
beaming factor 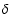 ,
which does not affect the spectral shape,
but which changes observed frequencies and fluxes by
,
which does not affect the spectral shape,
but which changes observed frequencies and fluxes by
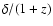 and
and
![$[\delta/(1+z)]^3$](/articles/aa/full/2006/12/aa3644-05/img98.gif) ,
respectively, where z=0.034 is the source redshift.
In the following we assume
,
respectively, where z=0.034 is the source redshift.
In the following we assume 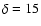 ,
in agreement with other models
for Mkn 501 (see e.g. Kataoka et al. 1999).
,
in agreement with other models
for Mkn 501 (see e.g. Kataoka et al. 1999).
We first considered a single-zone SSC model and tried to reproduce the
two extreme states of the large outburst of April 1997, i.e.
the low state on April 7 and the high state on April 16.
The spectrum of the emitting electrons was chosen with a curvature
parameter r=b/
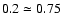 following the relation found in Sect. 4.1,
and the parameter s was fixed to 1.2.
Note that this value of r is consistent with the general behaviour
presented in Fig. 9.
The TeV curvature measured around the peak was about 0.4 for the low state
and 0.45 for the high state (Djannati-Atai et al. 1999) and, for
following the relation found in Sect. 4.1,
and the parameter s was fixed to 1.2.
Note that this value of r is consistent with the general behaviour
presented in Fig. 9.
The TeV curvature measured around the peak was about 0.4 for the low state
and 0.45 for the high state (Djannati-Atai et al. 1999) and, for
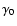 on the order of 104 and even higher, we expect a value of
r in the range 0.5-0.8.
The values of the other parameters, given in Table 1, were chosen
to achieve a satisfactory agreement between the data and the model.
It is interesting to note the behaviour of the two correlated parameters
on the order of 104 and even higher, we expect a value of
r in the range 0.5-0.8.
The values of the other parameters, given in Table 1, were chosen
to achieve a satisfactory agreement between the data and the model.
It is interesting to note the behaviour of the two correlated parameters
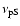 (the peak frequency in the synchrotron SED) and
(the peak frequency in the synchrotron SED) and
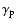 (the value of
(the value of 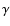 of the electrons that contribute
mostly to synchrotron peak emission).
In fact the
of the electrons that contribute
mostly to synchrotron peak emission).
In fact the
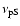 grows during the flare by a factor of 11
compared to the initial value while, according to Eq. (14),
grows during the flare by a factor of 11
compared to the initial value while, according to Eq. (14),
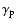 changes as the square root of
changes as the square root of
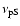 growing rate.
Spectral distributions of Fig. 10 show that the SR follows the X-ray data
accurately in both the spectral shape and peak
evolution. The TeV spectra in the two states were computed using the SSC
code described in Sect. 4.2: in the upper panel of Fig. 10 we considered
the EBL absorption for the LLL model by Dwek & Krennich (2005),
while in the lower panel this absorption was neglected. In both cases
TeV data were well fitted in both the peak position and spectral curvature.
This suggests that this curvature could be partly intrinsic rather than
produced entirely by EBL absorption. The LLL model could then be
considered an upper limit to the extragalactic background.
growing rate.
Spectral distributions of Fig. 10 show that the SR follows the X-ray data
accurately in both the spectral shape and peak
evolution. The TeV spectra in the two states were computed using the SSC
code described in Sect. 4.2: in the upper panel of Fig. 10 we considered
the EBL absorption for the LLL model by Dwek & Krennich (2005),
while in the lower panel this absorption was neglected. In both cases
TeV data were well fitted in both the peak position and spectral curvature.
This suggests that this curvature could be partly intrinsic rather than
produced entirely by EBL absorption. The LLL model could then be
considered an upper limit to the extragalactic background.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3644fg10.ps} \end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg101.gif) |
Figure 10:
Two spectral energy distributions of Mkn 501 during the low and high states
observed on 7 and 16 April 1997, respectively. X-ray points are from Paper II,
TeV points are simultaneous CAT data (Djannati-Atai et al. 1999) and soolid lines
are the spectra computed in a 1-zone SSC model for the SR and IC components.
In the upper panel IC, spectra have been absorbed (dashed lines) by interaction with
infrared EBL photons according to the LLL model by Dwek & Krennich (2005).
In the lower panel EBL absorption was neglected.
|
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3644fg11.ps} \end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg102.gif) |
Figure 11:
Two spectral energy distributions of Mkn 501 during the high states
observed on 7, 11 April 1997 ( upper panel) and 7, 16 April 1997 ( lower panel).
X-ray points are from Paper II,
and TeV points are simultaneous CAT data (Djannati-Atai et al. 1999).
Thin solid lines are the spectra computed in a 2-zone SSC model
for the SR and IC components, dashed lines are the spectra of the high-energy
flaring component, and the thick solid line is that of a slowly evolving component.
|
| Open with DEXTER |
As proposed in Paper II we considered a two-zone SSC model.
A first zone (Z1) is responsible for the "slowly'' variable emission,
whereas the second zone (Z2) is the source of the high-energy flare:
the observed fluxes are then the sum of these two contributions. We used
the April 7 emission as representative of the "slowly'' variable state (Z1) and
added the flaring component (Z2) to match the April 11 and 16 high states.
In this way the stability of the flux at energies 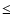 1 keV is
easily explained by the fact that the emission from Z2 is negligible when compared
with that of Z1.
The results of these calculations are represented in the SEDs of Fig. 11.
We met some difficulty in obtaining a solution capable of modelling
the observed spectral curvature mostly in the highest state.
In fact, to deplete the SR from Z2 below
1 keV is
easily explained by the fact that the emission from Z2 is negligible when compared
with that of Z1.
The results of these calculations are represented in the SEDs of Fig. 11.
We met some difficulty in obtaining a solution capable of modelling
the observed spectral curvature mostly in the highest state.
In fact, to deplete the SR from Z2 below 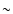 1 keV,
we need an electron population with a very low emissivity in
this band. This can be obtained only by introducing a low energy
cut-off, with the consequence of a high curvature of the low
energy portion of IC spectra at TeV energies.
The values of parameters for this 2-zone SSC model are also given
in Table 1.
1 keV,
we need an electron population with a very low emissivity in
this band. This can be obtained only by introducing a low energy
cut-off, with the consequence of a high curvature of the low
energy portion of IC spectra at TeV energies.
The values of parameters for this 2-zone SSC model are also given
in Table 1.
These results can be used to obtain some information on the
acceleration process. According to Eq. (10) we can derive the
energy gain as a function of r:
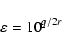 |
(23) |
which, given that
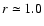 ,
gives
,
gives
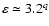 .
This implies that, unless q is very small, the energy gain
is about a factor 3. Consequently, the
number of steps to increase the energy up to
.
This implies that, unless q is very small, the energy gain
is about a factor 3. Consequently, the
number of steps to increase the energy up to
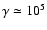 is around 10.
The acceleration must therefore be efficient and should probably
occur for rather short times.
is around 10.
The acceleration must therefore be efficient and should probably
occur for rather short times.
It is interesting to compare our SEDs of the 1997 flare of Mkn 501 with
those calculated by other authors who adopted different physical
models.
Generally, there is no explicit evaluation of a spectral curvature
parameter for both SR and IC components and consequently the electron
energy distributions are assumed to be power laws with exponential
cut-off (Konopelko et al. 2003; Krawczynski 2002) or a broken power
law (Katarzynski 2001).
To reproduce the spectral curvature in IC spectra, these authors
need to introduce a heavy contribution from EBL interaction with
TeV photons.
We stress that in our analysis the SR curvature is intrinsic, and we
do not need break or cut-off to reproduce it. More interestingly,
the IC curvature is also intrinsic and can be reproduced both using
and neglecting the TeV photon absorption by EBL photons.
In particular in the, in case of large flares where the peaks of
SR and IC components increase their energy, models with break or cut-off
do not predict intrinsically curved IC spectra, and so the spectral shape
observed at TeV and the IC peak frequency are mainly modulated by what
EBL model is chosen.
Note also that EBL attenuation could consistently modulate the position
of the IC peak because its optical depth varies with the energy and
redshift.
Observations of SR and IC components in objects with different redshifts
and the study of the variations of their peak frequencies would be very
useful for more accurate modelling of the EBL spectrum.
It is interesting to compare the values of the main model parameters.
As a further point Konopelko et al. (2003) and Krawczynski et al. (2002)
used 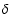 values of 50 and 45, respectively, while Katarzynski et al. (2001) used 14, very close to our choice.
values of 50 and 45, respectively, while Katarzynski et al. (2001) used 14, very close to our choice.
Over the past decade, broad-band observations of blazars have clearly shown that their
non-thermal SEDs are characterised by mildly curved shapes that can be
approximated by simple power laws only in frequency intervals that generally
not wider than a single decade.
Starting from the first paper by Landau et al. (1986), we verified that
a log-parabolic law is instead able to represent blazars' SEDs over several
frequency decades.
An advantage of this law is that it has only three free parameters.
Furthermore, we have shown that for statistical acceleration mechanisms in which
the acceleration probability is a decreasing function of the particle
energy, as in Eq. (7), the resulting spectrum follows a log-parabolic law.
Spectral properties of the SR can be derived easily only by using
the 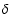 -function approximation.
-function approximation.
To find the exact relations between the spectral parameters of the energy
distribution of the relativistic electrons and of their SR, we
used a precise numerical code specifically developed for blazar
applications. The main results can be summarised as follows:
-
the SR spectrum is log-parabolic with a curvature parameter approximately equal
to the electron curvature parameter multiplied by 0.2;
-
spectral evolution due to SR cooling maintains a log-parabolic
distribution whose curvature parameter increases linearly with time;
-
the IC SED around the peak can be approximately described by a log-parabola
having a curvature parameter that ranges from values lower than the SR spectrum up to
that of the electron distribution, depending upon whether the photon scattering is
in the Thomson or Klein-Nishina regime.
The difference between the SR and IC curvatures can be used to
discriminate between the two regimes.
We applied our code to the calculation of the SR and IC spectra of Mkn 501
when it was simultaneously observed by BeppoSAX (Paper II) and CAT (Djannati-Atai et al. 1999) during the large outburst of April 1997. We estimated the
spectral parameters of the emitting electrons from X-ray data and then
computed the IC spectrum in the TeV band, taking the absorption
from pair production against EBL into account.
Our results showed that the curvature at high energy is mostly
intrinsic and larger than in the X-ray range, which shows that the IC
scattering is taking place in the Klein-Nishina regime.
This finding suggests that intergalactic absorption of TeV photons may
be small, as shown by Dwek & Krennich (2005):
their LLL spectrum could be a satisfactory description of EBL, but we
cannot exclude that it has an even lower intensity.
This interpretation agrees with a previous work by
Krawczynski et al. (2000), where the low intensity DEBRA model
(Malkan & Stecker 1998) was favored over another model of higher intensity.
It is also supported by a recent paper by Aharonian et al. (2005a), who
used HESS data to find that in the time-averaged observations of Mkn 421,
the cutoff energy of the IC spectrum is at  3.1 TeV, lower than that found
in Mkn 501 (about 6.2 TeV).
Considering the nearly equal redshifts of the these
two blazars, they conclude that the cutoff is not due to EBL attenuation but
is intrinsic to the sources, in agreement with our conclusion about
the IC curvature.
We conclude (i) that the extragalactic space is probably more
transparent to TeV photons than previously assumed and (ii) that a larger
number of blazars at higher redshifts than previously thought
could be detected in this range.
3.1 TeV, lower than that found
in Mkn 501 (about 6.2 TeV).
Considering the nearly equal redshifts of the these
two blazars, they conclude that the cutoff is not due to EBL attenuation but
is intrinsic to the sources, in agreement with our conclusion about
the IC curvature.
We conclude (i) that the extragalactic space is probably more
transparent to TeV photons than previously assumed and (ii) that a larger
number of blazars at higher redshifts than previously thought
could be detected in this range.
The same conclusion has been reached very recently by Aharonian et al. (2005b), who report the detection of
the blazar 1ES 1101-232 at z = 0.186 (by HESS in the TeV band).
An important consequence of the intrinsic curvature of TeV
spectra is that it can be variable in time and possibly related to the X-ray
curvature.
As a final remark, we stress the relevance of the simultaneous broad-band
observations that are necessary to obtain a reliable estimate of
curvature parameters for both components.
Acknowledgements
We acknowledge the helpful comments and suggestions of the referee,
A. Djannati-Atai. This work was financially supported for the
ASDC by the Italian Space Agency (ASI) and for the Physics
Dept. by Università di Roma La Sapienza.
- Aharonian,
F., Akhperjanian, A. G., Aye, K.-M., et al. 2005, A&A, 437,
95 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Aharonian,
F., Akhperjanian, A. G., et al. 2005, Nature, submitted
[arXiv:astro-ph/0508073]
(In the text)
- Band, D., Matteson, J.,
Ford, L., et al. 1993, ApJ, 413, 281 [NASA ADS] [CrossRef] (In the text)
- Bell, A. R. 1978,
MNRAS, 182, 147 [NASA ADS] (In the text)
- Blanford, R.
D., & Ostriker, J. P. 1978, ApJ, 221, L29 [NASA ADS] [CrossRef] (In the text)
- Blumenthal,
G. R., & Gould, R. J. 1970, Rev. Mod. Phys., 42, 237 [NASA ADS] [CrossRef] (In the text)
-
Djannati-Atai, A., Piron, F., Barrau, A., et al. 1999, A&A,
350, 17 [NASA ADS] (In the text)
- Dwek, E., &
Krennich, F. 2005, ApJ, 618, 657 [NASA ADS] [CrossRef] (In the text)
- Kardashev, N.
1962, Soviet Astron., 6, 317 [NASA ADS] (In the text)
- Kataoka, J.,
Mattox, J. R., Quinn, J., et al. 1999, ApJ, 514, 138 [NASA ADS] [CrossRef] (In the text)
-
Katarzyñski, K., Sol, H., & Kus, A. 2001, A&A, 367,
809 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Konopelko,
A., Mastichiadis, A., Kirk, J., et al. 2003, ApJ, 597, 851 [NASA ADS] [CrossRef] (In the text)
-
Krawczynski, H., Coppi, P. S., Maccarone, T., & Aharonian, F.
A. 2000, A&A, 353, 97 [NASA ADS] (In the text)
-
Krawczynski, H., Coppi, P. S., & Aharonian, F. 2002, MNRAS,
336, 721 [NASA ADS] [CrossRef] (In the text)
- Krennich, F.,
Biller, S. D., Bond, I. H., et al. 1999, ApJ, 511, 149 [NASA ADS] [CrossRef] (In the text)
- Landau, R.,
Golisch, B., Jones, T. J., et al. 1986, ApJ, 308, 78 [NASA ADS] [CrossRef] (In the text)
- Malkan, M. A.,
& Stecker, F. W. 1998, ApJ, 496, 13 [NASA ADS] [CrossRef] (In the text)
- Marscher, A. P.,
& Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef]
- Massaro, E.,
Perri, M., Giommi, P., & Nesci, R. 2004a, A&A, 413, 489 [EDP Sciences] [NASA ADS] [CrossRef]
(Paper I)
(In the text)
- Massaro, E.,
Perri, M., Giommi, P., et al. 2004b, A&A, 422, 103 [EDP Sciences] [NASA ADS] [CrossRef] (Paper
II)
- Michel, F. C. 1981,
ApJ, 247, 664 [NASA ADS] [CrossRef] (In the text)
- Padovani, P.,
& Giommi, P. 1995, ApJ, 111, 222 (In the text)
- Nodes, C., Birk, G.
T., Gritschneder, M., & Lesch, H. 2004, A&A, 423, 13 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Perri, M., Massaro,
E., Giommi, P., et al. 2003, A&A, 407, 453 [EDP Sciences] [NASA ADS] [CrossRef]
- Perlman, E. S.,
Madejski, G., et al. 2005, ApJ (in press)
[arXiv:astro-ph/0502298]
(In the text)
-
Piranomonte, S., Giommi, P., Verrecchia, F., & Perri, M. 2002,
in Blazar Astrophysics with BeppoSAX and other Observatories, ed.
P. Giommi, E. Massaro, & G. Palumbo (ASI Special Publ.),
51
- Sambruna, R.,
Maraschi, L., & Urry, M. C. 1996, ApJ, 463, 444 [NASA ADS] [CrossRef] (In the text)
- Sikora, M.,
Begelman, M. C., & Rees, M. J. 1994, ApJ, 421, 123 [NASA ADS] (In the text)
- Sikora, M.,
Blazejowski, M., Moderski, R., et al. 2002, ApJ, 577, 78 [NASA ADS] [CrossRef] (In the text)
- Sohn, B. W., Klein, U.,
& Mack, K.-H. 2003, A&A, 404, 133 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Tavecchio,
F., Maraschi, L., Pian, E., et al. 2001, ApJ, 554, 725 [NASA ADS] [CrossRef]
- Tramacere, A.
2002, Laurea thesis, Univ. of Perugia
(In the text)
- Tramacere,
A., & Tosti, G. 2003, New AR, 47, 697 [NASA ADS] (In the text)
Copyright ESO 2006
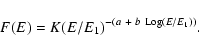
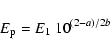
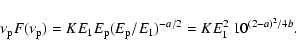
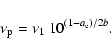
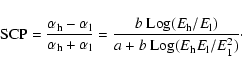
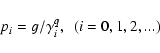
![\begin{displaymath}N({>}\gamma) = N_0 (\gamma/\gamma_0)^{-[s - 1 + r~ {\rm Log} (\gamma/\gamma_0)]} ,
\end{displaymath}](/articles/aa/full/2006/12/aa3644-05/img32.gif)
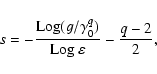
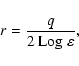
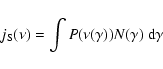
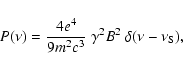
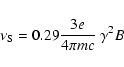
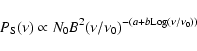
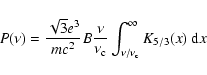
![\begin{figure}
\par\includegraphics[width=6cm,clip]{3644fg1.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg57.gif)
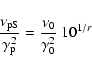
![\begin{figure}
\par\includegraphics[width=5.7cm,clip]{3644fg2.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg68.gif)
![\begin{figure}
\par\includegraphics[width=5.75cm,clip]{3644fg3.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg69.gif)
![\begin{figure}
\par\includegraphics[width=6.9cm,clip]{3644fg4.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg70.gif)
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{3644fg5.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg71.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3644fg6.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg74.gif)
![\begin{figure}
\par\includegraphics[width=7.1cm,clip]{3644fg7.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg75.gif)
![\begin{figure}
\par\includegraphics[width=5.9cm,clip]{3644fg8.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg76.gif)
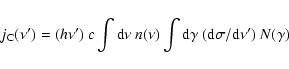
![$\displaystyle \frac{{\rm d}\sigma}{{\rm d}\nu'} = \frac{3 \sigma_{\rm T}}{16\ga...
...[4(h\nu/m_{\rm e}c^2)\gamma \eta]^2}{1+4(h
\nu/m_{\rm e}c^2)\gamma\eta}\Bigg]{}$](/articles/aa/full/2006/12/aa3644-05/img80.gif)
![\begin{displaymath}0 \leq \eta = \frac{\nu'}{4 \gamma^2 \nu [1-(h \nu'/m_{\rm e}c^2)]} \leq 1
\end{displaymath}](/articles/aa/full/2006/12/aa3644-05/img81.gif)
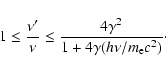
![\begin{figure}
\par\includegraphics[width=6.5cm,clip]{3644fg9.ps}\end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg88.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3644fg10.ps} \end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg101.gif)
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3644fg11.ps} \end{figure}](/articles/aa/full/2006/12/aa3644-05/Timg102.gif)