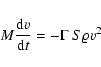A&A 448, 1185-1190 (2006)
DOI: 10.1051/0004-6361:20042156

The Pecina-Ceplecha functional as a tool to evaluate physical parameters of fireball bodies from observational data

V. V. Kalenichenko

Astronomical Observatory of Kyiv Tarass Shevchenko University, 3 Observatorna St., 04053 Kyiv, Ukraine

Received 11 October 2004 / Accepted 8 July 2005

Abstract
Aims. We have investigated the sum of squares of differences between the theoretical and observed values of distances along the fireball path (the Pecina-Ceplecha functional) as a tool to evaluate physical parameters of fireball bodies from observational data.
Methods. Using the functional to solve the fireball inverse problem, we verify its dependence of body disruption processes or gas flow conditions along the fireball path. We evaluate the functional directly after the numerical integration of the differential equations of motion and ablation for a single fireball-generating body and for a progressively disrupted one in the Earth's atmosphere. We use a continuous-flow gas-dynamic model of interaction of the body with the atmosphere by the action of radiative and convective heating. We have minimized the functional varying the values of model parameters and tested the functional on the model fireballs and on those of the Prairie network.
Results. A systematic course of the residuals with time obtained applying the functional to the observations of fireballs results not from a gross fragmentation, i.e. a sudden, instantaneous breakup of the fireball-generating body, but from the variability of the coefficient of heat transfer to the body along its path.
Conclusions. Methods based on application of the functional may be a useful supplement to the locally-ballistic method of solving this problem as the actual values of the parameters sought for usually fall in between the two solutions.

Key words: radiative transfer - meteors, meteoroids

1 Introduction

Integrating the single-body differential equations of motion and ablation for a fireball-generating body in the Earth's atmosphere may yield analytical expressions for the distance and time along the trajectory as functions of the velocity, air density and a constant coefficient of ablation, as Pecina & Ceplecha (1983) had demonstrated. By fitting these integrals to the observed distances and times the authors obtain the values of velocities along the entire trajectory and a value of the mean coefficient of ablation. This method of evaluating physical parameters of fireballs will be referred to as the Pecina-Ceplecha method (PC method). The method is based on the application of a functional such as the sum of squares of differences between the theoretical and observed values of the directly observed distance l. We define it as the Pecina-Ceplecha functional (PCF).

As shown from the papers of Pecina & Ceplecha (1983) and Ceplecha et al. (1993), the analytical integral expressions for the PCF and its further modifications are very unwieldy and extremely tedious for the numerical solution because they need an incomparably greater body of computations than the direct evaluation of the PCF after the numerical solution of the reasonably simple initial equations. It seems that the accumulation of round-off errors may be much large in first case as well.

As may be seen from p. 616 in the paper of Ceplecha et al. (1993), two assumptions are made by the PC method. The first is, that the problem should be made linear and the second is, that the increments of the unknown parameters are small. Both assumptions are not necessary for the problem solution.

2 Definition of the problem

The set of the initial differential equations for the problem, as can be seen for example from pp. 25 and 26 in the meteor physics of Bronshten (1981), is

$$% M\frac{{\rm d}v}{{\rm d}t}=-\Gamma ~S\varrho v^{2}$$ (1)

and

$$% \frac{{\rm d}M}{{\rm d}t}=-\frac{\Lambda}{2Q}S\varrho v^{3},$$ (2)

where t is the time, M is the mass and S is the area of the body's maximum cross-section perpendicular to the direction of motion; v is its velocity; $\varrho$ is the density of the atmosphere; $\Gamma$ and $\Lambda$ are the drag and heat-transfer coefficients, respectively; Q is the specific disruption energy (the energy needed for the ablation of a unit-mass). In the gas dynamics it is usual to represent the Eq. (1) in the form

$$% M\frac{{\rm d}v}{{\rm d}t}=-0.5C_{x}S\varrho v^{2},$$ (3)

as can be seen for example from p. 160 in the firebal aerodynamics of Stulov et al. (1995) and from the paper of ReVelle (1979). The drag coefficient C_x is designated C_d by Stulov et al. (1995) and C_D by ReVelle (1979). Thus $C_{x}=2\Gamma$.

As can be seen from the papers of Kalenichenko (1992, 2000), we transform this set usually to the form

$$% D\frac{{\rm d}v}{{\rm d}t}=-0.5C_{x}\varrho v^{2}$$ (4)

and

$$% \frac{{\rm d}D}{{\rm d}t}=-\frac{\Lambda}{6Q}\varrho v^{3},$$ (5)

where D=M/S. This transformation is possible if $S={\rm const.}$ or the body preserves its shape during its destruction. In the last-mentioned case there are $M=\kappa~D^{3}$ and $S=\kappa~D^{2}$, where $\kappa = {\rm const}$. The coefficients C_x, $\Lambda$, and Q in Eqs. (3)-(5) may be assumed to be variable, and the set of Eqs. (4), (5) thus gives a rather general presentation for the fireball process.

The coefficient $\Gamma$ (see Eq. (1)) is varied from values close to unity by the free-molecular flow to ones close to 0.5 by the continuous flow, as can be seen for example from p. 62 in the book of Bronshten (1981). Thus generally we have $1\leq C_{x}<2$. But it is well known, as for example Grigorian (1979) and especially for the Pribram, Lost City and Innisfree fireballs ReVelle (1979) had demonstraded, that C_x is close to unity for variously shaped bodies in the hypersonic gas flow over a wide range of the flow regimes close to the continuous one. Fireball-generating bodies undergo most decelerations in deep layers of the Earth's atmosphere for the flow regime close to the continuous one. Thus we consider C_x=1 in the following computations. Also we will assume that the body maintains its shape during the destruction.

To solve the problem, we add the equation of variation of $\varrho$in a co-moving reference frame

$$% \frac{{\rm d}\varrho}{{\rm d}t}=\frac{\varrho v \cos{z}}{H}$$ (6)

and the equation for the corresponding variation of altitude h above the Earth's surface

$$% \frac{{\rm d}h}{{\rm d}t}=-v \cos{z},$$ (7)

where z is the angle at which the body enters the atmosphere measured from the vertical and is the zenith distance of the fireball radiant, H is the parameter of the isothermal atmosphere in the Earth gravitation field (the height of a homogeneous atmosphere) to our Eqs. (4) and (5).

From Eqs. (4) and (5) we obtain

$$% \frac{{\rm d}D}{D}=\frac{\sigma}{3} ~v{\rm d}v,$$ (8)

where

$$% \sigma=\frac{\Lambda}{C_{x} ~Q}$$ (9)

is the ablation factor for the body.

If we assume $\sigma={\rm const.}$ in Eq. (8) then we obtain a very important integral

$$% \ln D = {\rm const.} + \sigma~ \frac{v^{2}}{6}\cdot$$ (10)

Substituting this integral into (4) and integrating the equation jointly with (6) and (7) we, as well as Pecina & Ceplecha (1983), can obtain in the following the aforementioned analytical expressions for the distance and time along the fireball path. But the question arises as to whether there is a need to analytically integrate these equations exactly. The initial Eqs. (4), (6) and (7) with $\sigma={\rm const.}$, along with their joint numerical integrating, are very simple, whereas the analytical expressions obtained with the same assumptions are too unwieldy. Thus we shall use the fundamental idea of the PC method in the following manner. In the set of equations considered above we will replace Eq. (5) by integral (10) in the form

$$% D = D_{0} \exp{\left(\sigma~ \frac{v^{2}-v_{0}^{2}}{6} \right)},$$ (11)

where D₀ and v₀ are the initial values of D and v. After numerically integrating the set of Eqs. (4), (6), (7) and (11) we will compare the observed values of h with the restored ones and try to fit them by varying $\sigma$, D₀ and v₀. This will be referred to as the constant-ablation method (CA method).

3 Model testing of the problem

When the PC method was applied to observations of the Prairie Network (PN) and European Network fireballs, a systematic course of the residuals with time was interpreted by Ceplecha et al. (1993) as the result of gross-fragmentation, i.e. a sudden, instantaneous breakage of the fireball-generating body. This interpretation is somewhat doubtful. The conditions of interaction between the fireball body and hypersonic gas flow may vary over a wide range along the trajectory length, as, specifically, ReVelle (1979) and Stulov et al. (1995) had demonstrated. Thus, the ablation coefficient may be not constant, and the systematic course of residuals can be caused, conceivably, by other reasons.

It is known, as be shown, specifically, from the paper of Kalenichenko (2003), that the coefficient $\Lambda$ in the Eqs. (2), (5) and (9) can be presented as

$$% \Lambda=C_{\rm H}+C_{\rm c},$$ (12)

where $C_{\rm H}$ and $C_{\rm c}$ are the radiative heat-transfer coefficient and gas-kinetic one respectively. By modeling of the Lost City, Pribram and Innisfree fireballs ReVelle (1979) found that both $C_{\rm H}$ and $\sigma$ can be changed by about an order of magnitude. According to investigations of Kalenichenko (2003, 2004) $C_{\rm H}$ can increase by about two orders of magnitude from the free-molecular flow to the continuous one and thereafter decrease more than three orders of magnitude as the velocity is decreased. According to Kalenichenko (1976) the value of $C_{\rm c}$decrease monotonically going from the free-molecular flow to the continuous one. Those can be shown from p. 102 in Bronshten (1981) as well. As shown for example from p. 76 in Stulov et al. (1995), by the continuous flow it is possible that  $C_{\rm c}\ll C_{\rm H}$. The variability of $C_{\rm H}$ and $C_{\rm c}$ implies the variability of $\sigma$. For this reason the variability of $\sigma$ along the fireball path is certain.

As Kalenichenko (2000) had demonstrated, the evaluation of the physical parameters of fireball bodies from observational data should be treated as an inverse problem because these parameters are inaccessible to immediate measurements (some inverse problem statements can be seen for example from Goncharsky et al. (1985) as well). Thus we have no way of testing any method of solving an inverse problem other than to solve the corresponding direct problem, that is, to compute the "observational'' fireball data from predetermined physical parameters of the fireball-generating body according to some model of the event. Thereafter we can use the tested method to evaluate "unobserved'' physical parameters of the fireball and compare the results with the predetermined values.

As an example we will consider a model fireball generated by the entry of a large body into the Earth atmosphere. Let the body be interacting with the atmosphere according to the continuous-flow gas-dynamic model by the action of radiative and convective heating by Stulov et al. (1995). As an adjunct to the locally-ballistic method (LB method) of the fireball physics inverse problem solution according to Kalenichenko (1992, 1997, 1999, 2000), this model (RC model) closely represents a fireball event and, moreover, it predicts the value of the terminal mass of an observed meteoroid, specifically, the ones of Lost City and Innisfree, as it is evident from Kalenichenko (1993a,b).

Using the RC model we start computing the heat-transfer coefficient $\Lambda$ for the Eq. (5) and progress to numerical integration of the set of Eqs. (4)-(7) according to Kalenichenko (1993a). We use the fourth-order Runge-Kutta method. As known, specifically, from Hamming (1962), that the distinctive property of this method is that it contain no estimation of the solution accuracy for each step and thus there is a possibility for the verification the step size. An other peculiarity of the method is the accumulation of round-off errors by the each subsequent integration step. Thus the solution accuracy sometimes cannot be increased as a whole by the further fragmentation of the integration step $\Delta~t$. We obtained realistic results for all cases of model or observational data by $\Delta~t=0.05$ s. We consider the model of progressive fragmentation of a fireball-generating body according to Kalenichenko (1993b) as well. In this way we obtain the model fireball whose data on the times, altitudes above the Earth's surface and distances along the path we will consider in the following as the "observational data''. In addition as predetermined data we obtain the values of D and v along the path that we shall consider as "true'' values for our model fireball. Now we can solve the inverse problem and test the results, estimating D and v from the model "observational data'' and comparing them with the corresponding predetermined values. In what follows we will consider the coefficient of linear regression according to (10) along the observational fireball path as an "effective'' value of $\sigma$.

As is seen from the set of Eqs. (4)-(7) (see Kalenichenko 1993a, as well), for its conclusive integrating we should assign initial values to D, v, and z (D₀, v₀ and z₀ respectively). Moreover we should set the value of Q. The value of $\varrho$ can be obtained, for each predetermined h, from the approximation of the mean standard atmosphere model CIRA (1972) according to Kalenichenko (1992).

For the sake of simplicity of model computations we shall only consider the vertical entry of the fireball body. Thus we can avoid computing the variability of z along the fireball path because of the Earth's curvature, as in this case z=0 everywhere.

Varying D₀ and v₀ and interrupting computations at different values of the terminal velocity $v_{\rm e}$ we can obtain a sufficiently large set of the "observed'' data on model fireballs for single bodies and for disrupted ones according to the aforementioned fragmentation model. To these "observed'' data we have applied the CA method. In addition to general considerations we have considered a special case using the predetermined model values of D₀ and v₀ and varying only the $\sigma$ value for minimizing PCF. As we expected, in both cases the systematic course of distance residuals with time occurs even for a single body without fragmentation (see Fig. 1). Thus the restored values of $v_{\rm e}$ and $D_{\rm e}$ be underestimated (see Figs. 2 and 3). The course of distance residuals with time and underestimations of $v_{\rm e}$ and $D_{\rm e}$do not disappear in the case of a progressively disrupted body, even if the instants of its fragmentation are known (see Figs. 4-6).

	Figure 1: The distance residuals for the single body. The long dashes correspond to the CA solution with known D0 and the short ones correspond to the complete CA method solution.
Open with DEXTER

	Figure 2: The velocity recovery for a single body. The solid curve corresponds to the actual model. For other designations see Fig. 1.
Open with DEXTER

	Figure 3: The D recovery for a single body. The dots correspond to the LB method solution. For other designations see above.
Open with DEXTER

	Figure 4: The distance residuals for the body progressively disrupted into 8 fragments. The dots and dashes correspond to the CA solution with known both D0 and fragmentation instants.
Open with DEXTER

	Figure 5: The velocity recovery for the body progressively disrupted into 8 fragments.
Open with DEXTER

	Figure 6: The D recovery for the body progressively disrupted into 8 fragments.
Open with DEXTER

Notice that, as it is evident from Pecina & Ceplecha (1983) and Ceplecha et al. (1993), an incentive for the elaboration of the gross-fragmentation model was a systematic course of residuals between the theoretical and observational values of l with time. We understand "a systematic course'' as an increase of the absolute values of residuals from the beginning point to the terminal one of the fireball path. Thus the point of great change of residuals may be at the end of the trajectory used the initial PC method of Pecina & Ceplecha (1983) as well. If this is the case the initial PC method and our CA method may be equivalent. It should be emphasized that we have obtained no systematic course of residuals using the CA method for model fireballs of $\sigma={\rm const.}$ (this is a very good test for the above mentioned methods).

Comparing Figs. 3 and 6 it is easy to see that the recovery of D along the fireball path using both CA and LB methods is better for the case of a progressively disrupted body.

4 Elaboration of the fireball observational data by two methods

We modify the CA method to elaborate observational fireball data so as to take into account the curvature of the Earth's surface. Contrary to the LB method, in this case it is necessary, because otherwise the results may be very distorted. We compare the two methods elaborating the PN fireballs and reconstructing the predetermined parameters for the aforementioned set of model fireballs.

	Figure 7: Distributions of the v0 residuals. The solid curve without symbols corresponds to differences between the results for the PN fireballs obtained by the CA and LB methods, rhombi and squares correspond to the recovery of the model v0 data by the CA and LB method.
Open with DEXTER

	Figure 8: Distributions of the D0 residuals. For symbols see Fig. 7.
Open with DEXTER

	Figure 9: Distributions of the $v_{\rm e}$ residuals. For symbols see Fig. 7.
Open with DEXTER

	Figure 10: Distributions of the $D_{\rm e}$ residuals. For symbols see Fig. 7.
Open with DEXTER

	Figure 11: Distributions of the $\sigma$ residuals. For symbols see Fig. 7.
Open with DEXTER

Both of the methods have estimated v₀ (Fig. 7) and D₀ (Fig. 8) most precisely among the other quantities. The values of $v_{\rm e}$ (Fig. 9) and $D_{\rm e}$(Fig. 10) may be underestimated by the CA method. Usually the actual quantities sought for fall in between the two solutions (see especially Figs. 8 and 11).

This raises the question as to the apparent elimination of the aforementioned systematic course of the distance residuals with time due to application of the original PC method of Ceplecha et al. (1993) with the gross-fragmentation model. The fact that the points of great change of residuals were observed at any parts of the fireball path is a peculiarity of this method. This is because that this method is able really to eliminate the systematic course of residuals. But, as noted above, many simplifying assumptions are performed by the analytical realization of this method. First, the problem is made linear by writing it for small increments of the parameters. Second, the assumption of the same value of the shape-density coefficient before and after gross-fragmentation is doubtful. Both of these simplifications can essentially perturb the PCF. This concern is supported by the time dependencies of the residuals in the papers Ceplecha et al. (1993, 2000) in the case of both theoretical models and solutions for the observational fireball data. It is easy to verify that in all submitted cases the values of v₀ are estimated with errors of about 0.1-0.2 km s^-1, as it can be shown from Fig. 1 in the paper Ceplecha et al. (2000), thus being much higher than the errors of the CA method (compare Fig. 7).

The procedure of the gross-fragmentation point location (by minimizing the PCF as well) is an inverse problem. Specifically, this procedure is insoluble (at least by classical statistical methods) unless the point of the change is predetermined or set with some prior probability, as Poirier (1976) had demonstrated. Thus the elimination of the systematic course of the distance residuals with time by varying the apparent gross-fragmentation point along the fireball path does not imply that the point was located with due significance. These doubts may be addressed using a model testing of the PC method.

Acknowledgements

We thank very much to Tamara Redjuk for the english text editing, to Pavlo Kozak, Anatoly Kasantsev, Volodymyr Marchenko, Jury Babenko, Valery Kleschonok, Vassyl Danylevsky, George Kovalchuk, Yakiv Pavlenko and Pavlo Tytarenko for the substantial help in the software installation.

References

• Bronshten, V. A. 1981, Fizika meteornykch javlenij [Physics of the meteor events, in Russian] (Moscow: Nauka), 416 (In the text)
• Ceplecha, Z., Spurny, P., Borovicka, J., & Keclikova, J. 1993, A&A, 279, 615 [NASA ADS] (In the text)
• Ceplecha, Z., Borovicka, J., & Spurny, P. 2000, A&A, 357, 1115 [NASA ADS] (In the text)
• CIRA 1972, Cospar International Reference Atmosphere (Berlin: Akademie-Verlag, Berlin), 450 (In the text)
• Goncharsky, A. V., Cherepashchuk, A. M., & Yagola, A. G. 1985, Nekorrektnyje zadachi astrofiziki [The Incorrect Astrophysical Problems, in Russian] (Moscow: Nauka), 352 (In the text)
• Grigorian, S. S. 1979, Kosmicheskie issledovanija [Cosmic Research, in Russian] 17, 875 (In the text)
• Hamming, R. W. 1962, Numerical methods for scientists and engineers (New York, San Francisco, Toronto, London: MC Graw-Hill Book Company, Inc.) (in Russian translation: Nauka, Moskow, 1972, 400) (In the text)
• Kalenichenko, V. V. 1976, Vestnik Kievskogo universiteta, serija astronomii [Messenger of the Kiev university, astronomical series] (in Russian), 18, 56 (In the text)
• Kalenichenko, V. V. 1992, Kinematika i Fizika Nebes. Tel [Kinematics and Physics of Celestial Bodies] (in Russian) 8, 69 (In the text)
• Kalenichenko, V. V. 1993a, Kinematika i Fizika Nebes. Tel, 9, 43 [NASA ADS] (In the text)
• Kalenichenko, V. V. 1993b, Kinematika i Fizika Nebes. Tel, 6, 47 (In the text)
• Kalenichenko, V. V. 1996, Kinematika i Fizika Nebes. Tel, 12, 55
• Kalenichenko, V. V. 1997, Kinematika i Fizika Nebes. Tel, 13, 34 (In the text)
• Kalenichenko, V. V. 1999, Kinematika i Fizika Nebes. Tel, 15, 123 (In the text)
• Kalenichenko, V. V. 2000, Ap&SS, 274, (3) 489 (In the text)
• Kalenichenko, V. V. 2003, Kinematika i Fizika Nebes. Tel [Kinematics and Physics of Celestial Bodies] (in Russian), 19, 159 [NASA ADS] (In the text)
• Kalenichenko, V. V. 2004, Kinematika i Fizika Nebes. Tel, 20, 157 [NASA ADS] (In the text)
• Pecina, P., & Ceplecha, Z. 1983, Bull. Astron. Inst. Czech., 34, 102 [NASA ADS] (In the text)
• Poirier, D. J. 1976, The econometrics of structural change (Amsterdam, New York, Oxford: North-Holland Publishing Company) (in Russian translation: Finansy i statistika, Moskow, 1981, 183) (In the text)
• ReVelle, D. O. 1979, J. Atmospheric and Terrestrial Physics, 41, 453 [NASA ADS] (In the text)
• Stulov, V. P., Mirsky, V. N., & Visly, A. I. 1995, Aerodinamika bolidov. [The Aerodynamics of Fireballs, in Russian] (Moscow: Nauka), 240 (In the text)