A&A 448, 633-639 (2006)
DOI: 10.1051/0004-6361:20053884
Moving shadows on the dusty disks of young stars
L. V. Tambovtseva1,2 -
V. P. Grinin1,2,3 - G. Weigelt2
1 - Main Astronomical Observatory Pulkovo, Pulkovskoe shosse 65, St. Petersburg 196140, Russia
2 -
Max-Planck-Institute für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
3 -
Crimean Astrophysical Observatory, Crimea, Nauchny, Ukraine
Received 22 July 2005 / Accepted 25 October 2005
Abstract
We investigate the formation of moving shadows on the
circumbinary (CB) disk of young binary systems. Moving shadows can
be created by a dusty disk wind of the secondary component. The
densest parts of the dusty disk wind and the associated common
envelope can be optically thick and may block the stellar
radiation inside a certain solid angle, resulting in the
appearance of a moving shadow zone. Its shape and size depends on
the mass loss rate, the disk wind velocity, and optical properties
of the dust. Our calculations show that the shadow zone is
observable if the mass loss rate
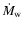 is greater than
10
is greater than
10
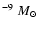 per year. This shadow resembles a clock hand.
If the orbit is an elliptical, the properties of this clock hand
will change during the orbital motion of the secondary.
per year. This shadow resembles a clock hand.
If the orbit is an elliptical, the properties of this clock hand
will change during the orbital motion of the secondary.
Key words: accretion, accretion disks - stars: formation - binaries: close - circumstellar matter - stars: pre-main sequence
1 Introduction
During the last decade, high-resolution images of the dust
environment of young stellar objects (YSOs) (e.g., Burrow et al. 1996; Koresko 1998; Padgett et al. 1999; Stapelfeldt et al. 1999)
have stimulated numerous theoretical investigations. Most of the
model images are calculated for the case of a single young star
(e.g., Whitney & Hartmann 1992, 1993; Wolf et al. 2003; Grosso et
al. 2003; Hodapp et al. 2004). The observed images show different
types of asymmetries. For example, Duchêne et al. (2004),
Krist et al. (2002), and Itoh et al. (2002) report on images of
the circumbinary disk of GG Tau (HBC 54; IRAS 04296+1725). The
images show a ring-shaped CB disk with a small gap that could be a
shadow caused by material between the stars and the ring. Roberge
et al. (2004) present the first spatially resolved spectrum of
scattered light from the TW Hydrae protoplanetary disk. The radial
profile of the integrated disk brightness showed an azimuthal
asymmetry that was not seen in the previous coronagraphic images.
In this paper, we investigate the formation of moving shadows on
the CB disks of young binaries. Our analysis is based on the
results of our previous papers (Grinin & Tambovtseva 2002;
GT2002; Grinin et al. 2004; GTS2004), in which
we investigated the effect of a common envelope, created by a
dusty disk wind of the secondary, on the optical variability of
the system. It is shown that the densest part of the common
envelope may be optically thick and may periodically obscure the
main component. Furthermore, this dusty disk wind can cause a
moving shadow on the surfaces of the CB disk. We calculated the CB
disk images for several disk wind models, and the results are
compared with observations of YSOs.
2 Modeling
The hydrodynamic (SPH) simulations reported by Artymowicz & Lubow
(1996) (AL96) show that in young binaries, the mass accretion rate
from the CB disk onto the low-mass companion can exceed the mass
accretion onto the main component. Bate & Bonnell (1997) and
Rozycka & Laphlin (1997) then confirmed this conclusion.
According to them, the mass accretion rate ratio
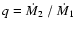 strongly depends on the specific angular
momentum ja of the accreting matter and can exceed one order of
magnitude in systems where the mass ratio
strongly depends on the specific angular
momentum ja of the accreting matter and can exceed one order of
magnitude in systems where the mass ratio
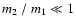 ,
if
ja is greater than the orbital specific angular momentum of the
secondary.
,
if
ja is greater than the orbital specific angular momentum of the
secondary.
The accretion activity in young binaries is a periodic function of
time (AL96), and the accretion is maximum near the apoastron
passage. The amplitude of modulation of the mass accretion rate
onto components
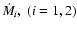 depends on eccentricity e(AL96) and also on the viscosity (Rozyczka & Laughlin 1997).
One might expect that the mass loss rates caused by the disk winds
depends on eccentricity e(AL96) and also on the viscosity (Rozyczka & Laughlin 1997).
One might expect that the mass loss rates caused by the disk winds
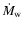 on the components will also vary periodically. However,
this is not the case. Due to the large hydrodynamic time scale
on the components will also vary periodically. However,
this is not the case. Due to the large hydrodynamic time scale
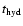 ,
which is much greater than the orbital period, the
orbital variations of
,
which is much greater than the orbital period, the
orbital variations of
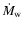 will be very weak (GTS2004).
Therefore, we only consider systems with constant mass loss rates.
will be very weak (GTS2004).
Therefore, we only consider systems with constant mass loss rates.
2.1 The disk wind parameters
The main source
of information for the velocity field in disk winds of young stars
are observations of forbidden lines ([OI] 6300 Å and some
others) in the spectra of young stars (Hartigan et al. 1995; Hirth et al. 1997) and the results of theoretical modeling (e.g.,
Goodson et al. 1999). According to Hartigan et al. (1995) and
Hirth et al. (1997), the typical radial velocities of the
low-velocity component of disk winds in the region of the
forbidden line formation (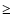 1 AU) range from about 5 km s-1 to a few tens of kilometers per second. In a binary
system with a star of one solar mass as the main component, these
characteristic velocities are on the order of the Keplerian
velocity of the secondary's orbital motion, for semimajor axes in
the range of
1 AU) range from about 5 km s-1 to a few tens of kilometers per second. In a binary
system with a star of one solar mass as the main component, these
characteristic velocities are on the order of the Keplerian
velocity of the secondary's orbital motion, for semimajor axes in
the range of 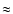 1 to 10 AU.
1 to 10 AU.
We consider the disk wind of the secondary to be an axially
symmetric bipolar outflow in its own coordinate
system![[*]](/icons/foot_motif.gif) . The outflow is
assumed to be isotropic within the wind ejection angle range from
. The outflow is
assumed to be isotropic within the wind ejection angle range from
 to
to
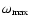 ,
where the wind ejection angle is
the angle between the disk symmetry axis and the direction in
which wind particles are ejected from the accretion disk of the
secondary. For simplicity, we assume that the wind density and
velocity do not depend on the latitude within the above angle
range. We assume that the ejection angle range lies between about 40 to 60 degrees. In this range the main part of the low-velocity
component of the disk wind is formed (Goodson et al. 1999).
According to the numerical results of these authors, the
low-velocity component provides the biggest contribution (about
80%) to the mass loss rate of the disk wind. Therefore, the
high-velocity component is not important in the models considered
below.
,
where the wind ejection angle is
the angle between the disk symmetry axis and the direction in
which wind particles are ejected from the accretion disk of the
secondary. For simplicity, we assume that the wind density and
velocity do not depend on the latitude within the above angle
range. We assume that the ejection angle range lies between about 40 to 60 degrees. In this range the main part of the low-velocity
component of the disk wind is formed (Goodson et al. 1999).
According to the numerical results of these authors, the
low-velocity component provides the biggest contribution (about
80%) to the mass loss rate of the disk wind. Therefore, the
high-velocity component is not important in the models considered
below.
Safier (1993) introduced a generalized version of the Blandford
& Payne (1982) self-similar wind model and argued that the
disk-driven outflow had enough momentum to lift dust grains from
the disk surface. He showed that the largest (millimeter-sized)
dust grains are not lifted up by the outflow. Following Safier
(1993) and Garcia et al. (2001), we assume that the disk wind
contains both gas and dust components and that they have a
"standard'' proportion, as in the interstellar medium (100:1). We
also assume that the dust component of the wind consists of a
mixture of dust particles similar to those in the circumstellar
(CS) disks of TTSs (Men'shchikov et al. 1999). According to this
paper, the absorption coefficient of such a mixture is equal to
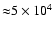 cm2 g-1 per unit of the dust mass at
the wavelength of 5500 Å (V band). In accordance, the absorption
coefficient per unit of the gas and dust mixture is
cm2 g-1 per unit of the dust mass at
the wavelength of 5500 Å (V band). In accordance, the absorption
coefficient per unit of the gas and dust mixture is
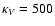 cm2 g-1.
cm2 g-1.
We calculate the trajectories of the
particles that are ejected by the low-mass companion during its
orbital motion along its eccentric orbit in the gravitational
field of the primary. In all models we considered the primary with
the one solar mass and the semimajor axis equal to 3 AU. As in our
previous papers (see e.g. GT2002), we used the ballistic
approximation for which the motion of each particle is independent
of the others. The radial and azimuthal velocity components 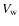 and
and 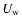 are the input parameters of the modeling (GT2002). The
distribution of the initially isotropic particles (in the
secondary rest frame) becomes anisotropic because of the orbital
motion of the wind-ejecting secondary. The motion of each particle
was calculated until it escaped the system or when the particle
reached the equatorial plane of the binary. A steady-state mass
distribution in the central part of the common envelope is
obtained after about ten orbital periods. A sketch illustrating
the geometry of the model is shown in Fig. 1.
are the input parameters of the modeling (GT2002). The
distribution of the initially isotropic particles (in the
secondary rest frame) becomes anisotropic because of the orbital
motion of the wind-ejecting secondary. The motion of each particle
was calculated until it escaped the system or when the particle
reached the equatorial plane of the binary. A steady-state mass
distribution in the central part of the common envelope is
obtained after about ten orbital periods. A sketch illustrating
the geometry of the model is shown in Fig. 1.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3884fig1.eps}\end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg22.gif) |
Figure 1:
Illustration of the geometry of the model. An asterisk
indicates the location of the primary. The secondary is not seen
because of the disk wind above and below the circumsecondary disk.
The drawing is not to scale. |
| Open with DEXTER |
To model CB disk images, we use a simple model of a flared passive
disk. This approximation cannot be used for the innermost regions
of the CB disk, where the gravity perturbations caused by the
orbital motion of the components are strong and produce density
waves (Lin & Papaloizou 1993; Lubow & Artymowicz 2000). However,
it is a good approximation for the outer regions of a CB disk
where the binary system can be considered as a single star with a
mass equal to the total mass of the system. Figure 2 shows a
schematic picture of the flared disk model, in which the surface
and midplane are shown as dashed lines. An arbitrary point O on
the disk surface has a height h and a projected radial distance
r in the midplane. The distance between the center of the star
and a point O is
d2=r2+h2. There 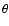 is the angle
between the midplane and the line through O and the center, and
is the angle
between the midplane and the line through O and the center, and
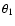 is the angle between the midplane and the tangential
line to the disk surface at point O.
is the angle between the midplane and the tangential
line to the disk surface at point O.
Figure 2 shows that
We used a commonly accepted representation of
the disk scale height
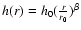 ,
where h0was assumed to be equal to 0.1 r0, the inner radius r0 is
assumed to be three-times the semimajor axis of the elliptic
binary orbits, and
,
where h0was assumed to be equal to 0.1 r0, the inner radius r0 is
assumed to be three-times the semimajor axis of the elliptic
binary orbits, and 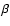 is a free parameter. In our
calculations, we used
is a free parameter. In our
calculations, we used 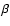 = 9/8 and 5/4 (Kenyon & Hartmann
1987; D'Alessio et al. 1999).
= 9/8 and 5/4 (Kenyon & Hartmann
1987; D'Alessio et al. 1999).
Equation (1) can be rewritten as:
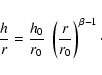 |
(1) |
Then we obtain
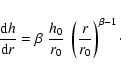 |
(2) |
The radiation flux at the point O on the disk surface can be
described as:
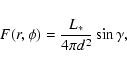 |
(3) |
where L* is the luminosity of the star. Taking into account
that part of the radiation flux will be occulted by the common
envelope created by the disk wind of the secondary companion, we
obtain
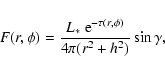 |
(4) |
where 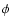 is an azimuthal angle, and
is an azimuthal angle, and
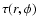 is the
optical thickness of the common envelope on the way between the
main component and the point
is the
optical thickness of the common envelope on the way between the
main component and the point 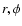 on the disk. A detailed
description of the calculations of the common envelope's optical
properties is given in GT2002.
on the disk. A detailed
description of the calculations of the common envelope's optical
properties is given in GT2002.
The scattered radiation from the disk surface is assumed to be
proportional to 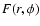 .
This is a good approximation if the
free-path length of photons in the disk is small compared to the
size of the shadow. In the CS disks of the pre-main-sequence
stars, this condition holds everywhere except at the periphery of
the disks. We did not take the forward scattering of the stellar
radiation by the disk wind into account since the albedo of dust
particles is low,
.
This is a good approximation if the
free-path length of photons in the disk is small compared to the
size of the shadow. In the CS disks of the pre-main-sequence
stars, this condition holds everywhere except at the periphery of
the disks. We did not take the forward scattering of the stellar
radiation by the disk wind into account since the albedo of dust
particles is low, 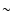 0.4-0.5 (Natta & Whitney 2000). In
order to demonstrate its possible effect on the contrast in the
shadow, we calculated the scattered light for one of the wind
models in the single scattering approximation.
0.4-0.5 (Natta & Whitney 2000). In
order to demonstrate its possible effect on the contrast in the
shadow, we calculated the scattered light for one of the wind
models in the single scattering approximation.
Using this approach for accretion disks and the phase-dependent
density distribution obtained earlier for the common envelopes
(GT2002; GTS2004), we calculated disk images seen face-on for
several disk wind models.
3 Results and discussion
Table 1 presents the parameters of our models:
eccentricity of the orbit, two velocity components of the wind
(radial 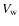 and tangential
and tangential 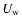 )
in units of the Keplerian
velocity of the secondary in the periastron, and the wind ejection
angle
)
in units of the Keplerian
velocity of the secondary in the periastron, and the wind ejection
angle 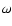 in degrees.
in degrees.
Table 1:
The model's parameters.
Figure 3 shows, as an example, the matter distribution in the
common envelope for model 1. Deviations from the axial symmetry,
which are caused by the vector summing of the wind and orbital
velocities mentioned above, are clearly seen in the XZ and YZ
images, as well as the asymmetric spiral structure of the pole-on
(XY) image. The secondary is at the point X = 0.5 and Y = 0. All
distances are given in the units of the semimajor axis.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3884fig3.eps}\end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg39.gif) |
Figure 3:
Matter distribution in the common
envelope in the XZ and XY plane for model 1. The semimajor axis of
the binary coincides with the X-axis. The low-mass companion is at
point with coordinates X = 0.5; Y = 0. |
| Open with DEXTER |
In Figs. 4-7, we present our calculated intensity distributions
for models 2-4 in the assumption that the disk surface
isotropically irradiates an incident light. All brightness
contours are given in arbitrary units (the contours are spaced by
a factor of 0.2). The coordinates X and Y are expressed in
units of the orbital semimajor axis. Figure 4 shows the isophotes
computed for model 2. The disk flaring parameter
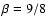 .
We
plotted three maps with different mass loss rates:
.
We
plotted three maps with different mass loss rates:
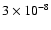 ,
10-8, and
,
10-8, and
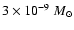 per year. One
can see that a noticeable shadow appears on the disk surface if
the mass loss rate is significant enough (
per year. One
can see that a noticeable shadow appears on the disk surface if
the mass loss rate is significant enough (
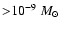 per year). Figure 5 shows the pole-on view of the disk with a
shadow for two different parameters
per year). Figure 5 shows the pole-on view of the disk with a
shadow for two different parameters 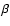 .
Evidently, more
flared disks show wider shadows at the disk periphery. The centers
of the images are masked with filled circles since the central
regions of the common envelopes can cause additional scattering
(GTS2004), which is not taken into consideration in the present
paper; but this scattering does not influence the shadow
formation.
.
Evidently, more
flared disks show wider shadows at the disk periphery. The centers
of the images are masked with filled circles since the central
regions of the common envelopes can cause additional scattering
(GTS2004), which is not taken into consideration in the present
paper; but this scattering does not influence the shadow
formation.
![\begin{figure}
\par\includegraphics[width=2.9cm,clip]{3884fig4.eps} \end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg44.gif) |
Figure 4:
Theoretical brightness map for model 2:
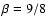 .
From top to bottom: .
From top to bottom:
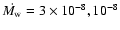 ,
and ,
and
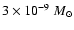 per year. The numbers on the curves mark
the intensities in the logarithmic scale, and the contours are
spaced by a factor of 0.2.
per year. The numbers on the curves mark
the intensities in the logarithmic scale, and the contours are
spaced by a factor of 0.2. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=7.2cm,clip]{3884fig5.eps} \end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg46.gif) |
Figure 5:
Theoretical brightness maps for model 2:
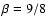 ( left),
( left),
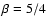 ( right),
( right),
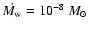 per year.
per year. |
| Open with DEXTER |
A more interesting situation is obtained in binary systems with
elliptic orbits (Figs. 6 and 7 corresponding to models 3 and 4).
In this case, the shape of the shadow on the disk will change
during the orbital motion: at the moment of the apoastron passage,
the shadow will be narrower and fainter than in the periastron. In
the periastron, the shadow can be much more extended (right
columns of Figs. 6, 7); in Figs. 6 and 7, we show the disk with a
cut outer region to represent its inner part better.
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{3884fig6.eps} \end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg48.gif) |
Figure 6:
Theoretical brightness maps for model 3:
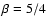 ,
( left) apoastron, ( right) periastron; from top to
bottom: ,
( left) apoastron, ( right) periastron; from top to
bottom:
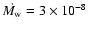 ,
10-8 and ,
10-8 and
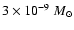 per year.
per year. |
| Open with DEXTER |
As an example, Fig. 8a illustrates the decrease in the shadow's
intensity with the distance from the star calculated for model 3.
Both intensity profiles are given at the distances of 30 and 300
AU. The mass loss rate due to the wind is
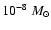 yr-1. This case is shown when the secondary component is in
the apoastron. Intensities are normalized to their maximum values
calculated out of the shadow (in the bright regions). The shadow
profile has a double-peaked form, which is also seen on the most
images presented in Figs. 4-7. It is caused by a specific wind
geometry: the particles are ejected within a cone limited by
angles of 40 and 60 degrees.
yr-1. This case is shown when the secondary component is in
the apoastron. Intensities are normalized to their maximum values
calculated out of the shadow (in the bright regions). The shadow
profile has a double-peaked form, which is also seen on the most
images presented in Figs. 4-7. It is caused by a specific wind
geometry: the particles are ejected within a cone limited by
angles of 40 and 60 degrees.
Since the dust opacity depends on the wavelength, the contrast is
also sensitive to the wavelength. Figure 8b shows an azimuthal
intensity profiles of the CB disk for the disk wind model 3 in the
two bands: V and H. The cut is made at the distance of 30 AU from
the star. Opacity in the H band is less than in the V band by
about one order of magnitude. Therefore, a contrast between
shadowed and bright parts of the CB disk dramatically decreases to
the longer wavelengths. This means that in the near infrared the
wind shadow can be detected for greater mass loss rates (
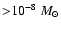 yr-1).
yr-1).
![\begin{figure}
\par\includegraphics[angle=-90,width=6cm,clip]{3884fig8.eps}\end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg52.gif) |
Figure 8:
a) Azimuthal profile intensity of the
circumbinary disk in the V band at distances of 30 AU (solid) and
300 AU (dashed) (model 3). b) V band (solid) and H band
(dashed) azimuthal profile intensity of the circumbinary disk in
the same model at 30 AU from the star. The mass loss rate
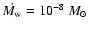 yr-1. All values are normalized
to the corresponding maximum intensities taken far from a shadow. yr-1. All values are normalized
to the corresponding maximum intensities taken far from a shadow. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[angle=-90,width=6.8cm,clip]{3884fig9.eps}\end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg53.gif) |
Figure 9:
Azimuthal variability of the CB disk intensity profile at
300 AU from the star for the two positions of the secondary
companion in model 3: a periastron (solid line) and an apoastron
(dashed line). The mass loss rate
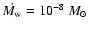 yr-1. All values are normalized to the corresponding maximum
intensities taken far from a shadow. yr-1. All values are normalized to the corresponding maximum
intensities taken far from a shadow. |
| Open with DEXTER |
Figure 9 demonstrates changes in the shadow's shape and depth
during the orbital period depending on the position of the
secondary on the orbit. For a better representation we combine
shadow profiles for the periastron and the apoastron positions.
One can see that the "periastron shadow'' is wider and deeper than
the "apoastron'' one, which is due to the fact that the particle
concentration in the disk wind decreases with the distance from
the source of the wind. For the same reason a contrast of the
shadow from the disk wind will decrease with increase in the
semimajor axis of the orbit. The results show that a shadow on the
CB disk of a young binary system resembles a clock hand. In the
case of an elliptical orbit, the properties of this clock hand,
including its shape, can change during the orbital motion of a
secondary (Fig. 10). If the masses (and luminosity) of the
companions are similar, their disk winds can form two shadows that
are located opposite each other.
![\begin{figure}
\par\includegraphics[width=8.8cm,clip]{3884fg10.eps}\end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg54.gif) |
Figure 10:
Shadow motion. a) periastron,
c) apoastron, b), d) phasesbetween
periastron and apoastron. |
| Open with DEXTER |
For model 3 we calculated a radiation scattered by the disk wind
for the optically semi-transparent case (
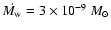 yr-1). In the single scattering approximation
that is valid if the optical depth of the wind is small compared
to unity (
yr-1). In the single scattering approximation
that is valid if the optical depth of the wind is small compared
to unity (
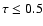 ), the flux of the scattered radiation
), the flux of the scattered radiation
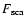 from the whole disk wind falling on the disk surface at
a given point can be written as
from the whole disk wind falling on the disk surface at
a given point can be written as
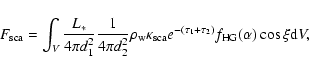 |
(5) |
where d1 is the distance from the star to the arbitrary point
in the wind, d2 the distance from this point to that on the
disk, 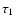 and
and 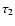 are optical depths along d1 and
d2,
are optical depths along d1 and
d2,
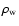 is the mass density,
is the mass density,
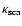 a scattering
opacity in cm2 per gram,
a scattering
opacity in cm2 per gram,
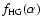 the
Henyey-Greenstein phase function (
the
Henyey-Greenstein phase function (
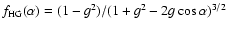 ), g the asymmetry factor,
), g the asymmetry factor, 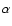 the
scattering angle, and
the
scattering angle, and 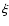 the angle between a direction of the
scattered radiation from the arbitrary point in the wind to a
given point on the CB-disk and a normal to the disk surface at
this point. Integration is carried out over a whole wind volume V. Calculations were made for the V-band with the disk flaring
parameter
the angle between a direction of the
scattered radiation from the arbitrary point in the wind to a
given point on the CB-disk and a normal to the disk surface at
this point. Integration is carried out over a whole wind volume V. Calculations were made for the V-band with the disk flaring
parameter
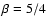 ,
g =0.5; the albedo was taken to be
equal to 0.5 to determine
,
g =0.5; the albedo was taken to be
equal to 0.5 to determine
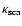 .
Figure 11 shows an
azimuthal behavior of the CB disk intensity at the distances of 30 AU (a) and 150 AU (b) from the primary with and without the
scattered radiation from the disk wind. This case is considered
when the secondary is in the periastron. One can see that a shape
and a depth of the shadow do not significantly depend on the
radiation scattered by the disk wind; its contribution to the disk
surface intensity at 30 AU is about 5% in the bright region and 14% in the shadow zone. Analogous ratios at 150 AU are
.
Figure 11 shows an
azimuthal behavior of the CB disk intensity at the distances of 30 AU (a) and 150 AU (b) from the primary with and without the
scattered radiation from the disk wind. This case is considered
when the secondary is in the periastron. One can see that a shape
and a depth of the shadow do not significantly depend on the
radiation scattered by the disk wind; its contribution to the disk
surface intensity at 30 AU is about 5% in the bright region and 14% in the shadow zone. Analogous ratios at 150 AU are 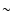 2%
and 5%, respectively. For the optically thicker winds, a major
part of the stellar radiation will be absorbed and the fraction of
the scattered radiation will be even less because of the low
albedo of the dust. As seen from Fig. 11, an effect of scattering
by the wind also leads to a small brightening of the disk surface
around the shadow.
2%
and 5%, respectively. For the optically thicker winds, a major
part of the stellar radiation will be absorbed and the fraction of
the scattered radiation will be even less because of the low
albedo of the dust. As seen from Fig. 11, an effect of scattering
by the wind also leads to a small brightening of the disk surface
around the shadow.
In some cases, CS disks around companions may produce their own
shadows on the outer CB disk. But accretion disks are
geometrically thin (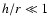 ). Besides, they are rather compact
(Artymowicz & Lubow 1994). The noticeable shadows they cause may
be seen only under specific conditions, such as when the primary
is an AA Tau-like star. The inner part of the accretion disk
around this star is warped due to interaction with the stellar
magnetosphere formed by an inclined magnetic dipole (Bouvier et
al. 2003; Terquem & Papaloizou 2000). The shadows from such a
warped disk will also be moving but with a period close to that of
the star rotation.
). Besides, they are rather compact
(Artymowicz & Lubow 1994). The noticeable shadows they cause may
be seen only under specific conditions, such as when the primary
is an AA Tau-like star. The inner part of the accretion disk
around this star is warped due to interaction with the stellar
magnetosphere formed by an inclined magnetic dipole (Bouvier et
al. 2003; Terquem & Papaloizou 2000). The shadows from such a
warped disk will also be moving but with a period close to that of
the star rotation.
![\begin{figure}
\par\includegraphics[angle=-90,width=6cm,clip]{3884fg11.eps}\end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg68.gif) |
Figure 11:
Azimuthal profile of the CB disk intensity without
(solid) and with (dashed) radiation scattered by the disk wind for
model 3 at the distances of 30 AU a) and 150 AU
b) from the star. The secondary is in the periastron.
The mass loss rate
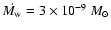 yr-1. The curves are scaled to the corresponding maximum
intensities of the CB disk without scattered radiation. yr-1. The curves are scaled to the corresponding maximum
intensities of the CB disk without scattered radiation. |
| Open with DEXTER |
The asymmetry of disks and outflows of several young objects were
explained by shadow effects. One of them is the T Tau star GG
Tau, which is a well-studied multiple system consisting of two
binaries: GG Tau A and GG Tau B, while GG Tau A's CB disk was
spatially resolved in the several wavelengths. The HST (Silber et
al. 2000; Krist et al. 2002) and Subaru images (Itoh et al. 2002)
show a narrow gap in GG Tau A's CB disk. The origin of this gap is
a matter of debate. Krist et al. (2002) assume that the gap could
be a shadow caused by a dust structure between the disc and the
primary component. However, this shadow is not located on the line
through the two binary components, but in a direction that is
nearly perpendicular to this line. Therefore, we cannot conclude
that this gap is caused by the disk wind of the secondary.
Another possibility is that the gap is the shadow of an opaque CS
dust cloud. Such clouds exist in the vicinity of young stars and
can be responsible for their brightness variability. This
mechanism can explain the variability of the UX Ori type stars (e.g., Grinin 2000). However, if this mechanism were the cause of GG
Tau A's disk gap, then the gap position should change during the
orbital motion of the CS dust cloud. Since GG Tau A's disk gap did
not change for several years, the origin of GG Tau A's disk gap is
still a mystery.
HH 30. One of the most spectacular asymmetric objects is
the reflection nebula of the jet object HH 30 (Stapelfeldt et al.
1999). Asymmetry was present in 1998, but was absent in the 1994
and 1995 images. Wood & Whitney (1998) consider the possibility
that such asymmetry could be caused by a variable, asymmetric
illumination of the CS disk by a rotating T Tauri star with spots
on its surface. Cool spots could be the result of a large-scale
magnetic field, and hot spots could be caused by accretion
activity controlled by the stellar magnetic field. If the spots
are asymmetrically distributed around the stellar axis, the
rotation of the star leads to a variable illumination of the
surrounding CS matter and can produce the changing asymmetric
image shapes. Stapelfeld et al. (1999) consider this model for the
interpretation of HH 30's variable asymmetry. Another possible
explanation discussed by Stapelfeldt et al. (1999) is a variable
CS extinction of the direct stellar radiation caused by opaque
dust clouds. If HH 30 is a close binary, a dusty disk wind of the
secondary could play the role of such an eclipsing cloud. Other
young objects with very asymmetric inner disk-outflow environments
are, for example, R Mon (e.g., Weigelt et al. 2002) and S 140 IRS 3 (Preibisch et al. 2001).
4 Conclusion
The main properties of the model considered in this
paper can be summarized as follows:
- The densest parts of the dusty disk wind and associated
common envelope can be optically thick and may block the stellar
radiation inside a certain solid angle. This results in the
appearance of a moving shadow zone whose shape and size depend on
the mass loss rate, disk wind parameters, and the optical
properties of the dust. The shadow zone is observable if the mass
loss rate is higher than 10
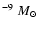 per year in the
visible and higher than 10
per year in the
visible and higher than 10
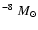 per year in the
near-infrared. The shadow of the disk wind is a permanent feature
of a CB disk. In the case of an elliptic orbit, the shadow on the
CB disk changes its shape during the orbital motion of the
secondary. The shadow is less extended and fainter during the
apoastron phase.
per year in the
near-infrared. The shadow of the disk wind is a permanent feature
of a CB disk. In the case of an elliptic orbit, the shadow on the
CB disk changes its shape during the orbital motion of the
secondary. The shadow is less extended and fainter during the
apoastron phase.
- Detection of moving shadows on the disks of young stars can
provide new information for studies of young binary systems. Such
observations might also be very interesting for studying the disk
winds themselves. The pole-on orientation of the disks is most
suitable for such observations, but shadows can also be observed
on disks seen edge-on. Optical imaging monitoring on long and
short timescales would be very interesting when seeking moving
shadows. If a shadow is caused by the disk wind of a secondary, it
will change its position on the time scale equal to the orbital
period of a system (in years).
Acknowledgements
V.G. and L.T. acknowledge the kind hospitality
of the Max-Planck-Institute für Radioastronomie, where part of
this work has been done. We are grateful to the anonymous referee
for useful comments and suggestions. This project was supported in
part by the grant of the Russian Academy of Sciences
"Non-stationary phenomena in Astronomy'' and the grant INTAS 03-51-6311.
- Artymowicz,
P., & Lubow, S. H. 1994, ApJ, 421, 651 [NASA ADS] [CrossRef] (In the text)
- Artymowicz,
P., & Lubow, S. H. 1996, ApJ, 467, L77 [NASA ADS] [CrossRef]
- Bate, M. R., &
Bonnel, I. A. 1997, MNRAS, 285, 33 [NASA ADS] (In the text)
- Blandford, R.
D., & Payne, D. G. 1982, MNRAS, 199, 883 [NASA ADS] (In the text)
- Bouvier, J.,
Grankin, K. N., Alencar, S. H. P., et al. 2003, A&A, 409,
169 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Burrows, C. J.,
Stapelfeldt, K. R., Watson, A. M., et al. 1996, ApJ, 473, 437 [NASA ADS] [CrossRef] (In the text)
- D'Alessio, P.,
Calvet, N., Hartmann, L., Lizzons, S., & Cantó, J. 1999,
ApJ, 527, 893 [NASA ADS] [CrossRef] (In the text)
- Duchêne, G.,
McCabe, C., Ghez, A. M., & Macintosh, B. A. 2004, ApJ, 606,
969 [NASA ADS] [CrossRef] (In the text)
- Garcia, P. J. V.,
Ferreira, J., Cabri, S., & Binette, L. 2001, A&A, 377,
589 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Goodson, A. P.,
Böhm, K. H., & Winglee, R. 1999, ApJ, 524, 142 [NASA ADS] [CrossRef] (In the text)
- Grinin, V. P. 2000,
in Disks Planetesimals, and Planets, ed. F. Garz'on, C. Eiroa, D.
de Winter, & T. J. Mahoney (San Francisco: ASP), ASP Conf.
Ser., 219, 216
(In the text)
- Grinin, V. P.,
& Tambovtseva, L. V. 2002, Astron. Lett., 28, 601 [NASA ADS] [CrossRef] (In the text)
- Grinin, V. P.,
Tambovtseva, L. V., & Sotnikova, N. Ya. 2004, Astron. Lett.,
30, 694 [NASA ADS] [CrossRef] (In the text)
- Grosso, N., Alves,
J., Wood, K., et al. 2003, ApJ, 586, 296 [NASA ADS] [CrossRef] (In the text)
- Hartigan, P.,
Edwards, S., & Ghandour, L. 1995, ApJ, 452, 736 [NASA ADS] [CrossRef] (In the text)
- Hirth, G. A., Mundt,
R., & Solf, J. 1997, A&AS, 126, 437 [EDP Sciences] [NASA ADS] (In the text)
- Hodapp, K. W.,
Walker, C. H., Reipurth, B., et al. 2004, ApJ, 601, L79 [NASA ADS] [CrossRef] (In the text)
- Itoh, Y., Tamura, M.,
Hayashi, S. S., et al. 2002, PASJ, 54, 963 [NASA ADS] (In the text)
- Kenyon, S. J.,
& Hartmann, L. 1987, ApJ, 323, 714 [NASA ADS] [CrossRef]
- Koresko, C. D.
1998, ApJ, 507, L145 [NASA ADS] [CrossRef] (In the text)
- Krist, J. E.,
Stapelfeldt, K. R., & Watson, A. M. 2002, ApJ, 570, 785 [NASA ADS] [CrossRef] (In the text)
- Lin, D. N. C., &
Papaloizou, J. C. B. 1993, in Protostars and Planets III, ed. E. H.
Levy, & J. I. Lunine (Tucson: Univ. Arizona Press), 749
(In the text)
- Lubow, S. H., &
Artymowicz, P. 2000, in Protostars and Planets IV, ed. V. Mannings,
A. P. Boss, & S. S. Russel (Tucson: Univ. Arizona Press),
731
(In the text)
- Men'shchikov,
A. B., Henning, T., & Fisher, O. 1999, ApJ, 519, 257 [NASA ADS] [CrossRef] (In the text)
- Natta, A., &
Whitney, B. A. 2000, A&A, 364, 633 [NASA ADS] (In the text)
- Padgett, D.,
Brandner, W., Stapelfeldt, K. R., et al. 1999, AJ, 117, 1490 [NASA ADS] [CrossRef] (In the text)
- Preibisch,
T., Balega, Yu. Yu., Schertl, D., Smith, M. D., & Weigelt, G.
2001, A&A, 378, 539 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Roberge, A.,
Weinberger, A. J., & Malumuth, E. M. 2004
[arXiv:astro-ph/0410251]
(In the text)
- Rózyczka, M.,
& Laughlin, G. 1997, in ASP Conf. Ser., 121, 792
(In the text)
- Safier, P. N. 1993,
ApJ, 408, 115 [NASA ADS] [CrossRef] (In the text)
- Silber, J.,
Gledhill, T., Duchêne, G., & Ménard, F. 2000, ApJ,
536, L89 [NASA ADS] [CrossRef] (In the text)
- Stapelfeld,
K. R., Watson, A. M., Krist, J. E., et al. 1999, ApJ, 516, L95 [NASA ADS] [CrossRef] (In the text)
- Terquem, C.,
& Papaloizou, J. C. B. 2000, A&A, 360, 1031 [NASA ADS] (In the text)
- Weigelt, G.,
Balega, Yu. Yu., Hofmann, K.-H., & Preibisch, T. 2002, A&A,
392, 937 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Whitney, B. A.,
& Hartmann, L. 1992, ApJ, 395, 529 [NASA ADS] [CrossRef] (In the text)
- Whitney, B. A.,
& Hartmann, L. 1993, ApJ, 402, 605 [NASA ADS] [CrossRef] (In the text)
- Wolf, S., Padgett, D.
L., & Stapelfeld, K. R. 2003, ApJ, 588, 373 [NASA ADS] [CrossRef] (In the text)
- Wood, K., &
Whitney, B. 1998, ApJ, 506, L43 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
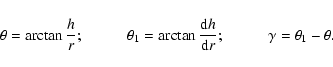
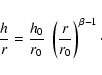
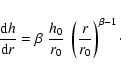
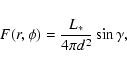
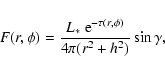
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3884fig3.eps}\end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{3884fig6.eps} \end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg48.gif)
![\begin{figure}
\par\includegraphics[width=6.8cm,clip]{3884fig7.eps}\end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg49.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=6cm,clip]{3884fig8.eps}\end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg52.gif)
![\begin{figure}
\par\includegraphics[angle=-90,width=6.8cm,clip]{3884fig9.eps}\end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg53.gif)
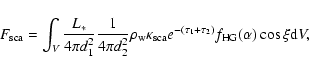
![\begin{figure}
\par\includegraphics[angle=-90,width=6cm,clip]{3884fg11.eps}\end{figure}](/articles/aa/full/2006/11/aa3884-05/Timg68.gif)