Institut d'Astronomie et d'Astrophysique, Université Libre de Bruxelles, CP 226, 1050 Brussels, Belgium

Abstract
We present new computations of the evolution of solar metallicity stars in the mass range 9 - 12 $M_{\odot }$ . This first paper of a series focuses on the propagation of the carbon burning flame front and provides a detailed analysis of the structural evolution up to the formation of the neon-oxygen core. Our calculations which do not include overshooting indicate that off-center carbon ignition is restricted to a small mass range between 9.0 and 11.3 $M_{\odot }$ . The chemical imprints of the first and second dredge-ups on the surface composition are analyzed and compared to "standard'' less massive stars. It results that, aside from being more luminous and slightly bluer in the HR diagram, massive AGB stars are almost indistinguishable from their lower mass counterparts, as far as the chemical composition is concerned. During the second dredge-up, we note however that the envelope penetrates deeper into the He burning shell than lower mass stars. Our simulations indicate that above $\sim$ 11.0 $M_{\odot }$ , the depth of the second dredge up is considerably reduced, marking the transition between low and massive stars. We also investigate the effects of the nuclear uncertainties associated with $^{12}{\rm {C}}$ + $^{12}{\rm {C}}$ reactions and show that it has a little impact on the core composition. Finally we describe the nucleosynthesis and chemical structure of the newly formed neon-oxygen core.

Key words: stars: evolution - nuclear reactions, nucleosynthesis, abundances - stars: AGB and post-AGB

1 Introduction

The evolution of stars in the mass range $\sim$ 9 - 12 $M_{\odot }$ is characterized by the off-center ignition of carbon in conditions of partial degeneracy, followed by the development of a flame that will transform the CO core into a degenerate neon-oxygen (NeO) mixture. However, the fate of these objects is still subject to large uncertainties mainly associated with our poor knowledge of the mass loss rate which is critical in this transition mass range. Massive intermediate mass stars can either enter the super-AGB (SAGB) phase where recurrent thermal instabilities develop in the helium burning shell as in standard thermally pulsing AGB stars and end as NeO white dwarfs or, if the NeO core mass exceeds $\sim$ 1.37 $M_{\odot }$ (Nomoto 1987), electron captures can induce core collapse and a supernovae explosion ensues (e.g., Miyaji et al. 1980; Nomoto 1987; Gutierrez et al. 1996).

In the late 60's and early 70's, Rakavy et al. (1967), Beaudet & Salpeter (1969) and Boozer et al. (1973) considered the evolution of CO stars in the mass range 1.03-1.44 $M_{\odot }$ and showed that stars with this typical core mass should ignite carbon off-center at relatively low density ( $\la$ 10⁷ g cm^-3). Then Barkat et al. (1974) computed the first consistent evolution of a 8 $M_{\odot }$ star from the main sequence up to the formation a OSi core and pointed out the possibility that these stars could be the progenitors of pulsars. Then, a large wealth of efforts was dedicated to pursue the advanced and final stages of the evolution of the NeO core in the regime of electron-captures and oxygen burning (e.g. Miyaji et al. 1980; Hillebrandt et al. 1984; Ray et al. 1984; Burrows & Lattimer 1985), and the field is still active (e.g. Isern et al. 1991; Gutierrez et al. 1996; Wanajo et al. 2003). In the 80's, Nomoto and collaborators (Hillebrandt et al. 1984; Nomoto 1984, 1987; Miyaji & Nomoto 1987; Hashimoto et al. 1993) explored in more detail the mass range 9 - 12 $M_{\odot }$ , investigating the evolution of 2.4 $M_{\odot }$ and 2.6 $M_{\odot }$ "helium balls'' up to the first stages of core cooling after central carbon exhaustion and the evolution of a 2.2 $M_{\odot }$ "helium ball'' from central helium burning to the shock bounce following core collapse. These works demonstrated the fundamental role of electron captures prior to the supernova explosion and gave a very good estimate of the critical core mass above which collapse must occur. More recently, Garcia-Berro and collaborators (Garcia-Berro & Iben 1994; Ritossa et al. 1996; Garcia-Berro et al. 1997; Iben et al. 1997; Ritossa et al. 1999) followed the evolution of a 9 and 10 $M_{\odot }$ model ( $Z=Z_{\odot}$ ) from main sequence up to the first thermal pulses of SAGB phase, and the evolution of a 10.5 $M_{\odot }$ and 11 $M_{\odot }$ star ( $Z=Z_{\odot}$ ) up to the activation of electron captures. These studies, based on consistent evolutionary models give a detailed analysis of the structural evolution with a first description of the deflagration during the off-center carbon burning phase. In parallel, binary evolution provided additional paths to the formation of NeO white dwarf (e.g. Iben & Tutukov 1985; Dominguez et al. 1993; Gil-Pons & Garcia-Berro 2002).

Previous studies have revealed the complex physics involved in the modeling of massive AGB stars with the propagation of a deflagration front (Timmes et al. 1994; Garcia-Berro et al. 1997) and with the apparition of the URCA process during the pre-supernovae evolution of the most massive NeO cores (e.g. Ritossa et al. 1999). However little is known about their nucleosynthesis and a lot of speculations/uncertainties surround the production of s-elements during thermally pulsing super-AGB phase (Ritossa et al. 1999) and of r-elements (Wheeler et al. 1998; Wanajo et al. 2003) during the supernovae explosion. Their contribution of SAGB stars to the galactic chemical evolution remains also largely unknown.

This paper is the first of a series intended to better understand the final evolution of massive AGB stars. In the present study, we focus on the carbon burning phase of solar metallicity stars in the mass range 9 - 12 $M_{\odot }$ . In Sect. 2, we describe the stellar evolution code and the specific numerical adaptations needed for these computations. In Sect. 3, we give a brief overview of the evolution prior to carbon ignition. In Sect. 4 we explain in details the propagation of a representative carbon burning flame, give a comparative study of the flame characteristics in the different stars and describe in Sect. 5 the chemical composition of the resulting NeO core. In Sect. 6 we discuss the second dredge-up characteristics and conclude in Sect. 7.

2 Stellar evolution code

2.1 Input physics

STAREVOL (v2.70) is a lagrangian implicit stellar evolution code. The independent variables are the mass coordinate M_r and time t. The integration variables are $\ln ~T$ , the logarithm of the temperature, $\ln~ r$ , the logarithm of the radius, $\ln~f$ a new variable related to the degeneracy parameter (see below), the lagrangian velocity u and the luminosity L_r. The equations of the stellar structure are solved iteratively by a relaxation method. The difference equations are second order accurate in space and first order in time. The nucleosynthesis equations are solved after the structure has converged and the resolution method follows Wagoner (1969).

At low-temperature (T < 8000 K), the atomic and molecular opacities are given by Alexander & Fergusson (1994). Between $8000 \le T \le 5\times 10^8$ K, we use the OPAL tables (Iglesias & Rogers 1996) and at higher temperatures radiative opacities were computed using the analytical fits compiled by Timmes et al. (2000). Conductive opacities are computed from a modified version of the Iben (1975) fits to the Hubbard & Lampe (1969) tables for non-relativistic electrons, from Itoh et al. (1983) and Mitake et al. (1984) for relativistic electrons and from formula of Itoh et al. (1983) as well as Raikh & Yakovlev (1982) for solid plasmas. Finally, opacity tables are available for different mixtures which allows us to take into account CO enrichments.

The nuclear reaction rates have been updated and new nuclear tables built by NETGEN, the NETwork GENerator tool available at http://astropc0.ulb.ac.be. By default we use the NACRE rates (Angulo et al. 1997) for charged induced reactions, Bao et al. (2000) for neutron capture reactions, Horiguchi et al. (1996) for experimental beta decay rates and Caughlan & Fowler (1988) otherwise. Our network includes 52 species up to $^{37}{\rm {Cl}}$ (see Fig. 1) and all relevant $\alpha$ , p, $\gamma$ , n, $\beta$ reactions plus the $^{12}{\rm {C}}$ + $^{12}{\rm {C}}$ and $^{12}{\rm {C}}$ + $^{16}{\rm {O}}$ reactions. In particular, the energetics is correctly accounted for up to the end of neon burning and the nucleosynthesis of light elements with $Z \le 17$ is followed accurately. The neutron abundance is computed using a fake neutron sink nucleus as described in Jorissen & Arnould (1989). In the regime of electron captures, relevant for the evolution toward the supernova stage, we included the following elements (Nomoto 1987; Ritossa et al. 1999): $^{20}{\rm {F}}$ , $^{23}{\rm {Ne}}$ , $^{24}{\rm {Na}}$ , $^{25}{\rm {Na}}$ and $^{27}{\rm {Mg}}$ . We use the analytical formula of Graboske et al. (1973) to compute the screening factors.

The neutrino energy loss rates are computed according to Itoh et al. (1996) and take into account the effects of plasma, pair, bremsstrahlung, recombination, and photo neutrino emission.

The equation of state (EOS) is based on the principle of Helmholtz free energy minimization and is described in detail in Siess et al. (2000). Briefly, we adopt the formalism developed by Eggleton et al. (1973) and expanded by Pols et al. (1995). In this approach, the new independent variable $\ln~f$ , which is intimately related to the degeneracy parameter, is used instead of the density $\rho$ . This change of variable allows a smooth, accurate and analytic derivation of the thermodynamic quantities in regimes of arbitrary ionization and degeneracy. The plasma is described by three components photons, ions and electrons, coupled only through the photoionization and photo-dissociation processes. Effects of pressure ionization and Coulomb shielding have been incorporated by means of analytical fits to the non-ideal terms in the Helmholtz free energy. The analytical expression for the Coulomb interaction (Pols et al. 1995) allows a smooth transition between the regime of weak correlation where the Debye-Hückel approximation is recovered and the regime of strong interactions where it reproduces the Monte-Carlo simulations of Slattery et al. (1980). In practice, this expression provides a confident treatment of Coulomb interactions up to an interaction parameter $\Gamma \sim 300$ . Note that up to the formation of the NeO core, this parameter remains small (typically $\Gamma < 0.1$ ) so if the Coulomb interactions play a role, they only become relevant after the completion of the carbon burning phase when the density is sufficiently high. The fit to the pressure ionization has been derived from the MHD EOS (Mihalas et al. 1988) for a mixture X = 0.70 and Z = 0.02. According to Pols et al. (1995), this correction also reproduces the expected behavior for the pressure ionization of He. However, in the later stage of evolution to overcome the limitation of this prescription, we impose the matter to be fully ionized when $T > 4\times 10^8$ K or when X+Y < 10^-2. In any case, we always assume that species other than hydrogen and helium are fully ionized.

The treatment of convection is based on the standard mixing length theory and the constant $\alpha_{\rm MLT} = 1.75$ results from solar fitting models. The Schwarzschild criterion for convection is used to define the convective boundaries and an instantaneous mixing of the chemical species is performed inside each convective zone at each iteration during the convergence process. Our models are standard in the sense that no extra mixing processes due to rotation or overshooting are included.

The mass loss rate for these objects is rather unknown since they are intermediate between the AGB and massive stars. In these computations, we arbitrarily choose Vassiliadis & Wood (1993) prescription.

The atmosphere is treated in the grey approximation and integrated up to an optical depth $\tau \simeq 5\times 10^{-3}$ . Finally the initial solar composition is taken from Grevesse et al. (1996).

2.2 Numerical treatment of the flame propagation

As already pointed out by Timmes et al. (1994), an accurate description of the flame propagation requires fine and adapted spatial and temporal discretizations otherwise the characteristics of the phenomenon can be missed. If these conditions are not fulfilled, the flame will not propagate properly and may artificially die out. Our numerical method predicts the location of the flame front at the end of the current timestep so we can guess where the spatial resolution will be needed.

Our algorithm is as follows: first we constrain the time step so that the flame front moves by no more than a certain fraction of the so-called precursor flame width $\Delta r_{\rm pf}$ which corresponds to the distance between the base of the carbon burning convective zone (CBCZ) and the minimum in the luminosity profile below it (Fig. 2). We estimate the theoretical flame speed $v_{\rm theo}$ from the values computed by Timmes et al. (1994). This quantity is tabulated as a function of the chemical composition, density and temperature at the base of the CBCZ. Once $v_{\rm theo}$ is known, the time step $\Delta t$ is chosen so that $\Delta t = \alpha \Delta r_{\rm pf}/ {\rm max}(v_{\rm theo},v_{\rm real})$ , where $v_{\rm real}$ is the effective flame speed calculated from the computed models and $\alpha$ a factor of the order of $\sim$ 0.1-0.5. This method limits $\Delta t$ to values ranging between $5\times 10^{-5} {\rm yr}\la \Delta t \la 40$ yr.

$\begin{figure} \par\includegraphics[width=8.6cm,clip]{3043fig2.ps} \end{figure}$	Figure 2: Luminosity profile at the base of the convective carbon burning zone (hashed area). The precursor flame width $\Delta r_{\rm pf}$ represents the distance between the base of the convective region and the minimum in the luminosity profile below it.
Open with DEXTER

Spatially, the problem is to account for the thinness of the precursor flame (at most a few kilometers, compared to the gigantic size of the overall stellar structure). In this region, the luminosity profile L_rvaries strongly and we impose that between two adjacent grid points the relative difference (L_i+1-L_i)/ L_i never exceeds 10%. In addition we do not allow for shell removal in the precursor flame and add the constraint that the shell underneath the CBCZ must be split into two whenever the predicted advance of the flame front $\Delta r_{\rm theo} = v_{\rm theo} \times \Delta t$ is smaller than $2 \times \Delta r_{\rm cbcz}^{\rm base}$ (where $\Delta r_{\rm cbcz}^{\rm base}$ is the width of the shell underneath the carbon burning convective zone).

This algorithm ensures that the precursor flame is described by $\sim$ 50 grid points. The typical extent of a shell is rather extreme $10^{-2}~ {\rm km}\la \Delta r \la 5$ km and $\sim$ 5000 models are needed to follow the propagation of the flame to the center.

$\begin{figure} \par\includegraphics[width=8.6cm,clip]{3043fig3.ps} \end{figure}$	Figure 3: HR diagram of selected models up to the super-AGB phase. By increasing luminosity and effective temperature, the tracks correspond to masses equal to 6.0, 9.0, 10, 11, 12 and 15 $M_{\odot }$ . The 6 and 15 $M_{\odot }$ tracks are not part of this study but were added for comparison.
Open with DEXTER

3 Evolution prior to carbon ignition

Figure 3 shows the evolution of selected models in the HR diagram. Compared to an intermediate 6 $M_{\odot }$ star, these tracks are significantly more luminous and bluer which could, in principle, make them distinguishable from their lower mass counterparts. However, the probability of observing these stars is reduced due to their shorter lifetime (Table 1).

Prior to carbon ignition, the evolution of the internal structure is very similar to that of standard intermediate mass stars: central H and He burning takes place in a convective core, the mass of which increases with the initial stellar mass ( $M_{\rm ini}$ ). The duration of the burning phases is also a smoothly decreasing function of $M_{\rm ini}$ (Table 1).

After central hydrogen exhaustion, all our models experience the first dredge up (1DUP). As shown in Table 2, the hydrogen mass fraction decreases to the benefit of helium and the surface abundances exhibit the chemical signatures of the operation of the incomplete CN and ON1 cycles: $^{12}{\rm {C}}$ and $^{16}{\rm {O}}$ are depleted while $^{17}{\rm {O}}$ , $^{13}{\rm {C}}$ and $^{14}{\rm {N}}$ are increased. The surface enrichments of $^{23}{\rm {Na}}$ and to a lower extent of $^{21}{\rm {Ne}}$ concomitant to a decrease in $^{22}{\rm {Ne}}$ witness the marginal activation of the NeNa cycle in the H burning shell. Finally, we note that $^{25}{\rm {Mg}}$ mass fraction is slightly reduced to the benefit of $^{26}{\rm {Mg}}$ as a consequence of the activation of $^{25}{\rm {Mg}}$ ( $p,\gamma$ ) $^{26}{\rm {Mg}}$ , the most rapid reaction of the MgAl cycle at low temperature. The number ratios $^{12}{\rm {C}}$ / $^{13}{\rm {C}}$ and $^{12}{\rm {C}}$ / $^{16}{\rm {O}}$ decrease from 90 to 20 and from 0.475 to 0.319, respectively.

The chemical signatures of the first dredge-up are the same in the $9 {-} 12~M_{\odot}$ models as in the standard 6 $M_{\odot }$ star. However, for the elements involved in the NeNa chains, the variations can be as large as a factor of 5. In particular the relative $^{26}{\rm {Mg}}$ enrichment and $^{25}{\rm {Mg}}$ depletion are respectively a factor of 2 and 5 larger in a $12~M_{\odot}$ model as compared to a 6 $M_{\odot }$ model. But in the end, these differences are very small and as far as the chemical composition is concerned, these stars are almost indistinguishable from their lower mass counterparts.

Near central helium exhaustion, the $^{12}{\rm {C}}$ ( $\alpha,\gamma$ ) $^{16}{\rm {O}}$ reaction takes over the nuclear energy production in the convective core. The activation of this reaction decreases the C/O ratio which final value remains highly dependent on the adopted reaction rate for $^{12}{\rm {C}}$ ( $\alpha,\gamma$ ) and also on the efficiency (semiconvection, overshooting) and duration of convective mixing in the late stage of He-core burning when the central He mass fraction drops below $\sim$ 0.1 (see e.g. Straniero et al. 2003, for a detailed discussion). The higher temperature found in the core of more massive stars favors the production oxygen but this effects is partially compensated by the shorter duration of this phase in these objects. The final C/O ratio is thus hard to guess but our models indicate that as the initial mass increases more carbon is burnt and the C/O ratio decreases (Table 1). We note however that above $\ga$ 11 $M_{\odot }$ , the C/O ratio drops as carbon ignites at the center.

4 Carbon burning phase

In stars that develop degenerate CO cores, following central helium exhaustion, the temperature maximum moves outward as a consequence of plasma neutrino emission. Eventually, the peak temperature reaches $\sim$ $7\times 10^8$ K and carbon ignites off-center. The large deposition of nuclear energy favored by the strong dependence of the carbon burning rates on temperature and the "mild'' response of the structure owing to the partial degeneracy ( $\eta \simeq 2.5{-}3$ ) leads to an accumulation of heat at the ignition point. There, the temperature gradient becomes steeper and convection sets in. Figure 4 shows the evolution of the internal structure and of relevant quantities of a representative 9.5 $M_{\odot }$ model. In all our models in the mass range 9 - 11 $M_{\odot }$ , carbon burning always proceeds in two steps characterized by a first convective zone, which we refer to as the carbon flash, followed by the development of a the flame which propagates all the way to the center. In case of the 11.3 $M_{\odot }$ , carbon ignites so close to the center that only one convective episode occurs.

Table 1: Selected features of the evolution of massive intermediate-mass stars prior to carbon ignition. The quantities shown are: the maximum extent of the convective core during the central hydrogen ( $M_{\rm HB}$ ) and helium ( $M_{\rm HeB}$ ) burning phases, the mass coordinate of the base of the convective envelope at its deepest extent during the first dredge-up ( $M_{\rm 1DUP}$ ), the mass of the CO core at carbon ignition ( $M_{\rm COi}$ ), the durations of central hydrogen ( $\Delta t_{\rm HB}$ ) and helium ( $\Delta t_{\rm HeB}$ ) burning phases, the time elapsed between the end of central helium burning and carbon ignition ( $\Delta t_{\rm HeB-CB}$ ) and the central $^{12}{\rm {C}}$ and $^{16}{\rm {O}}$ mass fractions at the end of He core burning. Masses are in solar unit ( $M_{\odot }$ ), times in years (yr). $M_{\rm COi}$ is defined as the mass coordinate of maximum nuclear energy production in the He burning shell.

Table 2: Surface abundances mass fractions at the end of the first dredge-up.

To understand why the first convective zone quenches and does not reach the center, a close study of the evolution of the structure in the vicinity of the peak temperature is required.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{3043fig4.ps} \end{figure}$

Figure 4: Evolutionary features of a representative 9.5 $M_{\odot }$ model. The top panel shows the evolution of the central temperature ( $T_{\rm c}$ : dotted), maximum temperature ( $T_{\rm max}$ : solid) and central density ( $\rho _{\rm c}$ : dash). The middle panel displays the different luminosities associated with neutrino emission ( $L_\nu$ : long-dash), with the nuclear burning of H ( $L_{\rm H}$ : short-dash), He ( $L_{\rm He}$ : dotted) and C ( $L_{\rm C}$ : solid) and the surface luminosity L. In the Kippenhahn diagram (bottom panel), the different solid lines correspond to iso-mass contours equal to 0.001, 0.03, 0.2, 0.5, 0.8 and 1.0 $M_{\odot }$ . Convective regions are represented by hatched areas.

Open with DEXTER

4.1 Carbon ignition and flame propagation

Similarly to the occurrence of thermal pulses in AGB stars, the carbon flash does not develop at the locus of maximum temperature ( $M_{T_{\rm max}}$ ) but slightly above that location. The reason simply arises from the fact that convection can only establish if the luminosity L_r is larger than a critical value defined by

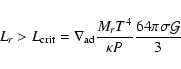
As the temperature increases, carbon is depleted. It results that the nuclear energy production rate ( $\varepsilon _{\rm nuc}$ ) is not maximum at the peak temperature but at a mass coordinate located slightly below $T_{\rm max}$ where the density is larger (Fig. 5). The deposition of thermal energy below $M_{T_{\rm max}}$ heats the material and drags the peak temperature toward the center.

On the other hand, the distance between $M_{T_{\rm max}}$ and the base of the carbon burning convective zone ( $M_{\rm CZ}$ ) is primarily determined by the nuclear energy production in this region. The luminosity at $M_{\rm CZ}$ can be approximated by

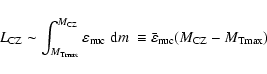
$\begin{displaymath}L_{\rm CZ} \sim \int_{M_{\rm Tmax}}^{M_{\rm CZ}} \varepsilon_... ... m\ \equiv \bar \varepsilon_{\rm nuc} (M_{\rm CZ}-M_{\rm Tmax})\end{displaymath}$

The advance of the convective zone thus depends on the nuclear energy production on both sides of $M_{T_{\rm max}}$ : below this limit it is responsible for the inward advance of the peak temperature and above it determines the location of the convective boundary. During the early development of the convective flash, because of the large increase in $\varepsilon _{\rm nuc}$ , both $M_{T_{\rm max}}$ and $M_{\rm CZ}$ are dragged to the center (Fig. 6).

As degeneracy is lifted, pressure rises and starts pushing the overlying layers. The core expands and its density decreases. As a result, the nuclear energy production rate below $M_{T_{\rm max}}$ , which indirectly drives the advance of convective zone, begins to decline and moves away from $M_{T_{\rm max}}$ (Fig. 7) in regions where both $^{12}{\rm {C}}$ and the density are higher. Core expansion induces two important consequences associated with the decrease in $\varepsilon _{\rm nuc}$ . First, it slows down the advance of $M_{T_{\rm max}}$ toward the center and second it contributes to increase ( $M_{\rm CZ}$ - $M_{T_{\rm max}}$ ).

Eventually, the distance $\Delta m$ traveled by $M_{T_{\rm max}}$ during a time interval becomes smaller than the corresponding increase in ( $M_{\rm CZ}$ - $M_{T_{\rm max}}$ ) and the convective zone starts to retreat. Then, the combined effects of a decreasing temperature at the base of the instability ( $T_{\rm max}$ in Fig. 4) and the stopping of fuel injection by growing convection contribute to accelerate the fall of the nuclear energy production in the flash. This process is irreversible and leads to the disappearance of convection $\sim$ 850 yr after it appears. Below the flash, in the radiative shells left by the receding convective zone, carbon is efficient depleted and the nuclear energy production die out (Fig. 7). The peak temperature is now driven by the nuclear energy production at the base of the convective zone and moves upward. The flash finally quenches and core contraction rapidly leads to the re-ignition of carbon at a lower mass coordinate.

$\begin{figure} \par\includegraphics[width=8.8cm,clip]{3043fig5.ps} \end{figure}$	Figure 5: Profiles of $^{12}{\rm {C}}$ mass fraction, temperature (T), nuclear energy production rate ( $\varepsilon _{\rm nuc}$ ) and density ( $\rho$ ) 150 days before the onset of the convective flash, in the 9.5 $M_{\odot }$ model. The vertical line indicates the location of the maximum temperature ( $M_{T_{\rm max}}$ ).
Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{3043fig6.ps} \end{figure}$	Figure 6: Evolution of the nuclear energy production rate ( bottom), temperature ( mid) and carbon mass fraction ( top panel) during the activation of the carbon flash in the 9.5 $M_{\odot }$ model. The profiles are shown 29 (solid), 46 (dot), 52 (long-dash), 56 (short-dash) and 58 (dot short-dash) yr after the onset of the flash, respectively.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{3043fig7.ps} \end{figure}$

Figure 7: Evolution of the temperature, $^{12}{\rm {C}}$ mass fraction, neutrino energy loss rate ( $\varepsilon _{\nu }$ ) and nuclear energy production rate ( $\varepsilon _{\rm nuc}$ ) during the retreat of the flash convective zone in the 9.5 $M_{\odot }$ model. The solid lines shows the profiles at the time of the deepest extent of the flash (63 yr after the onset of the instability) and the evolution proceeds through the dotted, short-dash, long-dash and dot-dash lines which were taken 1.7, 4.3, 8.8 and 16.8 years after the starting model (solid line), respectively.

Open with DEXTER

Concerning the evolution of the second convective zone, the initial conditions are substantially different. In the flash, the $^{12}{\rm {C}}$ abundance is initially rather high (at the end of the helium burning phase its mass fraction is between $\sim$ 0.25-0.30, see Table 1) and is kept high as the instability grows in mass. Conversely, when the flame develops, it grows in regions previously occupied by the flash where carbon had been efficiently depleted (in the flame at the time of C re-ignition, $X({}^{12}{\rm {C}}) \la 0.08$ ). It results that the nuclear energy production rate (proportional to the square of $X_{^{12}\rm C}$ ) and subsequent core expansion are significantly reduced. As a consequence, the peak of $\varepsilon _{\rm nuc}$ below $M_{T_{\rm max}}$ is maintained and is able to drive the burning front to the center. Finally a steady state is achieved where almost all the energy deposited at the base of the convective flame is instantaneously carried away by neutrinos (Timmes et al. 1994).

During the flame propagation, the luminosities are constant (Fig. 4) and the carbon burning region seems to be decoupled from the rest the star. No indication of the presence of the flame can be attested from the evolution of $T_{\rm c}$ , $\rho _{\rm c}$ or L for instance. The evolution of the temperature profiles after the onset of the flame (Fig. 8) clearly shows the establishment of a steady state where all the quantities seem to be simply translated in mass. However, as the flame deepens, the density increases and modifies the opacity profile behind the flame front, resulting in variations of the outer convective flame boundary. Ahead of the convective flame, $^{12}{\rm {C}}$ is abundant and $\varepsilon_{\rm nuc} \gg \varepsilon_\nu$ . In this region, matter is heated and the modifications to the temperature profile induce the advance of flame. To summarize, contrary to the first and violent carbon flash, the energy released at the onset of the convective flame does not induced substantial modifications to the thermodynamics of the core mainly because $L_{\rm C}$ is considerably reduced. The energy production rate below the convective zone is thus weakly affected and remains at anytime much larger than what is produced in the convective flame. As a consequence, the radiative burning of $^{12}{\rm {C}}$ ahead of the convective flame drives the peak temperature to the center and, since $\bar \varepsilon_{\rm nuc}$ varies little, ( $M_{\rm CZ}$ - $M_{T_{\rm max}}$ ) remains almost constant and convection moves to the center.

$\begin{figure} \par\includegraphics[width=12cm,clip]{3043fig8.ps} \end{figure}$	Figure 8: Profiles evolution during the development and propagation of the convective flame in the 9.5 $M_{\odot }$ model. The lines correspond, in the time unit for Fig. 4, to ages equal to 3414 (solid), 3462 (dot), 3604 (short-dash), 5188 (long-dash), 6857 (dot-sort-dash) and 7927 (dot-long-dash) yr, respectively. The flame front is located at the carbon discontinuity.
Open with DEXTER

The succession of two convective episodes, a flash and a flame, is sensitive to the adopted neutrino energy loss rate. As an illustrative tests, we run a series of computations characterized by a neutrino energy loss rate $\varepsilon _{\nu }$ five times larger and smaller. Although these variations are not realistic, they provide hints concerning the role of the neutrino losses in this process. If $\varepsilon _{\nu }$ is lower, less energy escapes the convective instability and this additional heat is further used to expand the structure. As a result, the flame quenches rapidly and in our tests we note that 3 flashes occur before a convective flame forms and propagates to the center. At this point, the carbon burning proceeds in a very similar way to the helium flash in low mass stars through the development of successive instabilities. Conversely, if the neutrino loss rate is increased, the carbon burning zone suffers less expansion and a unique convective zone appears that propagates as a convectively bound flame to the center.

4.2 Evolution as a function of initial mass

The general evolution of our 9 - 11.3 $M_{\odot }$ model stars during carbon burning phase is similar to the evolution of the 9.5 $M_{\odot }$ star described above. In all our models, carbon ignites off center and the first convective zone appears when the peak temperature reaches $T_{\rm max} \sim 6.9\times 10^8$ K. The corresponding density and degeneracy are typically $\rho(T_{\rm max})\sim 1.6\times 10^6$ g cm^-3 and $\eta(T_{\rm max})\sim 2.7$ .

As Table 3 shows, the carbon flash ignites closer to the center and is less powerful as the stellar mass increases. This is a direct consequence of the decreasing core degeneracy with increasing stellar mass. In the limit of no degeneracy, carbon ignites quietly at the center as in massive stars. This takes places in our simulations for M = 11.5 $M_{\odot }$ . The duration of the flash convective zone ( $\Delta t^1$ ) is strongly correlated to the carbon mass fraction in the instability ( ${}^{12}{\rm {C}}_{\rm max}$ ) and presents a maximum around 10.5 $M_{\odot }$ . This duration depends on the amount of fuel available and on the rate at which it is depleted which are function of the extent of the convective zone, of the carbon mass fraction initially present in the core and of the temperature in the flash. On one hand, the carbon abundance in the core tends to increase with decreasing mass (Sect. 3) but on the other hand, it is more effectively depleted during the flash of lower mass stars where higher temperatures are reached and where the extent of the convective zone is smaller ( $\Delta m_{\rm max}$ in Table 3). The duration of the convective zones is thus the result of the competing effects of burning speed and fuel enrichment. Our models indicate a maximum around 10.5 $M_{\odot }$ .

The flame develops near the $^{12}{\rm {C}}$ discontinuity left at the deepest penetration of the flash convective zone. Table 3 indicates that its duration ( $\Delta t^2$ ) is a decreasing function of stellar mass. This is mainly due to the fact that in more massive stars, the temperature in the precursor flame is higher and the flame speed, which scales as $X({}^{12}{\rm {C}})\sqrt{\rho}~T^{14}$ (Timmes et al. 1994) is faster. We also note from Table 3 that the flame, although igniting deeper in mass ( $m^2_{\rm C}$ ), is located at relatively large radii from the center ( $r^2_{\rm C}$ ), comparable to that of the flash. Typical flame speeds during the stationary descent of the convective zone increases from $\sim$ $1.5\times 10^{-3}$ cm s^-1 to $\sim$ $2.2\times 10^{-2}$ cm s^-1 as the star initial mass increases between 9 and 11.0 $M_{\odot }$ .

During the major part of the descent, the flame speed compares nicely with the predictions of Timmes et al. (1994). The best agreement is reached in the 11.0 $M_{\odot }$ star and the largest discrepancy is found in the 9.0 $M_{\odot }$ star where the flame speed is within a factor $\sim$ 2.5 of the theoretical value. As already outlined by García-Berro et al. (1997), in their model Timmes et al. (1994) neglect the gravothermal term in the energy equation which, in our simulations, represents a non negligible contribution. This simplification certainly explains the observed differences.

4.3 Comparison with previous works

The comparisons are mostly based on the simulations of Garcia-Berro and collaborators who provide a detailed description of stellar models in the same mass range. The results are globally in good agreement. In particular, off center carbon ignition starts in a 9 $M_{\odot }$ in both studies and ends near the same mass: 11 $M_{\odot }$ compared to 11.3 $M_{\odot }$ in our simulations. The morphology of the convective episodes (flashes and flames) are also very comparable. The evolution of the central temperature and density are very similar except that our models evolves systematically slower. Several explanations can be put forward to explain these rather small differences. First Garcia-Berro et al. did not take into account mass loss but our tests indicate that suppressing mass loss barely affects our results since it really becomes efficient later, during the SAGB phase. Second, and most importantly, are the differences in the input physics. In particular, they use nuclear reaction rates which date back to Caughlan & Fowler (1964) and Fowler & Hoyle (1964)! It is thus conceivable that the main reasons for the discrepancies found in the burning lifetimes find their origin in the adopted nuclear rates. Up to the end of C burning, the plasma remains weakly correlated with $\Gamma < 0.1$ . So if the degeneracy is treated correctly, the differences in the equation of state should not be too important at this stage.

In the HR-diagrams, their tracks are also slightly different but this can be easily explained by their use of analytical fits to the opacity in comparison with our use of recent OPAL tables and also because their initial composition is slightly more helium rich than what is given by Grevesse et al. (1996).

However, the value of the transition mass between stars that ignite or not carbon, usually refered to as $M_{{\rm up}}$ , can differ substantially from one simulation to the next. For solar metallicity stars, $M_{{\rm up}}$ ranges between $\sim$ 6 - 9 $M_{\odot }$ (for low values: Bertelli et al. 1985; Bressan et al. 1993; Umeda & Nomoto 1999; Bono et al. 2000; and for high values of $M_{{\rm up}}$ : Becker & Iben 1979, 1980; Maeder & Meynet 1989; Garcia-Berro et al. 1997; Poelarends & Langer 2005). This critical value depends directly on the properties of the He and CO cores which in turn are highly dependent on the mixing prescription (semiconvection, overshooting, rotational mixing...), on the He content (e.g. Bono et al. 2000) and as we noticed on the numerical resolution at the He core interface which needs to be relatively high. In particular, including overshooting can significantly decrease the value of $M_{{\rm up}}$ from $\sim$ 9 to 6 $M_{\odot }$ (Bertelli et al. 1985; Bressan et al. 1993). In view of these results and considering the fact that our models do not include any extra mixing beyond any convective boundaries, our value of $M_{{\rm up}}$ = 9 $M_{\odot }$ should be considered as an upper limit.

Table 3: Selected properties of the convective carbon burning zones as a function of the initial stellar mass. The superscripts 1 and 2 refer to the flash and flame, respectively. The quantities shown are the time (t) when convection sets in, the radius ( $r_{\rm C}$ ) and mass ( $m_{\rm C}$ ) coordinates where it develops, the duration $\Delta t$ of the convective episode, the maximum carbon luminosity $L_{\rm C}$ , the mass covered by the instability ( $\Delta m_{\rm max}$ ) and, at the time of peak luminosity, the carbon mass fraction ( $\rm ^{12}C_{max}$ ) in the convective zone.

4.4 Effect of carbon burning rates uncertainties

Carbon burning proceeds mainly through $^{12}{\rm {C}}$ ( $^{12}{\rm {C}}$ , $\alpha$ ) $^{20}{\rm {Ne}}$ and $^{12}{\rm {C}}$ ( $^{12}{\rm {C}}$ , p) $^{23}{\rm {Na}}$ reactions, the rates of which remain relatively uncertain, in particular because of the possible presence of low-energy resonances (Cussons et al. 2003). This effect comes on top of the large uncertainties already affecting $^{12}{\rm {C}}$ ( $\alpha,\gamma$ ) $^{16}{\rm {O}}$ which primarily determines the carbon content inside the white dwarf. Since we restrict our analysis to the carbon burning phase we only consider the $^{12}{\rm {C}}$ + $^{12}{\rm {C}}$ rates. We have run a series of test models increasing or decreasing both rates by a factor of 2 or 5. The main results are that for lower carbon burning rates, the onset of the convective instability is delayed and consequently the mass coordinate of the ignition point increases. For instance, for a rate twice as large (small), the flash is triggered 650 yr earlier (latter) than in the reference model and the mass coordinate $m^1_{\rm C}$ is shifted by -(+)0.06 $M_{\odot }$ . For lower rates, the peak carbon flash luminosity ( $L^1_{\rm C}$ ) is larger since higher temperatures are reached at the time of ignition. The duration of the first convective zone is also reduced because the higher flash luminosity produces a larger expansion and a more efficient quenching of the instability. Concerning the flame, it also starts at a higher mass coordinate, last longer and is hotter when the rates are reduced. The effects on the core composition mainly concern the $^{12}{\rm {C}}$ profile in the region of the carbon flash where a stronger depletion is observed at higher rates. However, where the flame passes through, the chemical changes are modest and, for the most abundant species, never exceed $\sim$ $10\%$ . In conclusion, the effects of $^{12}{\rm {C}}$ + $^{12}{\rm {C}}$ rates on the structure and evolution of the core are weak.

5 Core nucleosynthesis and the formation of the NeO white dwarf

5.1 Central nucleosynthesis

Our analysis of stellar nucleosynthesis is based on the representative 9.5 $M_{\odot }$ star and the slight differences present in other mass models do not affect the general trends depicted here.

At helium ignition, the second most abundant element in the core is $^{14}{\rm {N}}$ (1.3%) which will be entirely converted into $^{22}{\rm {Ne}}$ after two successive $\alpha$ captures. During the entire core He burning phase, the temperature remains too low for an efficient production of neutrons by $^{22}{\rm {Ne}}$ ( $\alpha$ , n) $^{25}{\rm {Mg}}$ . The neutron density never exceeds $N_{n} \la 10^5$ cm^-3 and at He exhaustion the neutron exposure remains lower than $\sim$ 0.015 mbar^-1. Therefore no s-process nucleosynthesis is expected to take place at this stage. We note however a slight production of $^{25}{\rm {Mg}}$ , $^{26}{\rm {Mg}}$ and $^{17}{\rm {O}}$ as a result of neutron capture reactions. At central helium exhaustion, the core is mainly composed of $^{16}{\rm {O}}$ (63%), $^{12}{\rm {C}}$ (34%) and $^{22}{\rm {Ne}}$ (1.2%) and helium burning proceeds radiatively in a shell surrounding the inert core.

Eventually, the increasing temperature reaches $\sim$ $6.9 \times 10^8$ K and carbon ignites. The highest nuclear fluxes come from $^{12}{\rm {C}}$ ( $^{12}{\rm {C}}$ , $\alpha$ ) $^{20}{\rm {Ne}}$ and $^{12}{\rm {C}}$ ( $^{12}{\rm {C}}$ , p) $^{23}{\rm {Na}}$ followed by $^{16}{\rm {O}}$ ( $\alpha,\gamma$ ) $^{20}{\rm {Ne}}$ . These reactions will convert the CO core into a NeO core and will supply protons and $\alpha$ particles for a richer nucleosynthesis.

Ahead of the flame where the temperature is maximum ( $T > 8.5\times 10^8$ K), the $\alpha$ particles that are not captured by $^{16}{\rm {O}}$ will participate to the complete destruction of $^{22}{\rm {Ne}}$ by ( $\alpha$ , n) and ( $\alpha,\gamma$ ) reactions. Some $^{25}{\rm {Mg}}$ is therefore produced. Locally a neutron density of $\sim$ $2\times 10^9$ cm^-3 can be achieved but the irradiation is too short for a noticeable production of s-elements. The released neutrons that are not captured by the iron seeds react with the abundant $^{16}{\rm {O}}$ and to a lower extent with $^{20}{\rm {Ne}}$ , $^{23}{\rm {Na}}$ and $^{25}{\rm {Mg}}$ , leading the production of $^{17}{\rm {O}}$ , $^{21}{\rm {Ne}}$ , $^{24}{\rm {Mg}}$ and $^{26}{\rm {Mg}}$ . The protons, mainly produced by $^{12}{\rm {C}}$ ( $^{12}{\rm {C}}$ , p) $^{23}{\rm {Na}}$ also participate to the production of $^{20}{\rm {Ne}}$ and $^{24}{\rm {Mg}}$ by (p, $\alpha$ ) and ( $p,\gamma$ ) reactions on $^{23}{\rm {Na}}$ , and to the synthesis of $^{27}{\rm {Al}}$ by ( $p,\gamma$ ) reactions on $^{26}{\rm {Mg}}$ . Note also that the chain of reactions $^{17}{\rm {O}}$ (p, $\alpha$ ) $^{14}{\rm {N}}$ ( $\alpha,\gamma$ ) $^{18}{\rm {F}}$ ( $\beta^+$ ) $^{18}{\rm {O}}$ ( $\alpha,\gamma$ ) contribute to the recycling of $^{22}{\rm {Ne}}$ which mass fraction remains always larger than 0.008. These elements are then engulfed in the convective flame where the same nucleosynthesis takes place. However, due to the lower temperature in the convective flame, the neutron density never exceeds 10⁶ cm^-3 in this region.

After the flame has reached the center, the convective zone disappears and carbon burning proceeds radiatively. Due to the exhaustion of combustible and increasing neutrino energy losses, the maximum temperature moves outward. When it reaches the chemical discontinuity left at the mass coordinate corresponding to the maximum extend of the flame, a third carbon flash of milder magnitude ( $L_{\rm C} \sim 1.2\times 10^6$ $L_\odot$ ) develops followed by a series of instabilities of decreasing strength until a NeO core of 1.108 $M_{\odot }$ is formed.

5.2 The NeO white dwarf

The central composition of the NeO white dwarf of our 9.5 $M_{\odot }$ model is showed in the lower right panel of Fig. 9. The core is mainly composed of $^{16}{\rm {O}}$ ( $\sim$ 55-60%) and $^{20}{\rm {Ne}}$ ( $\sim$ 28-32%). The main trace elements are $^{23}{\rm {Na}}$ ( $\sim$ 5.5%), $^{24}{\rm {Mg}}$ ( $\sim$ 3.3%), $^{25}{\rm {Mg}}$ ( $\sim$ 1.5%), $^{22}{\rm {Ne}}$ ( $\sim$ 0.7%), $^{26}{\rm {Mg}}$ ( $\sim$ 0.9%), $^{21}{\rm {Ne}}$ ( $\sim$ 0.8%), $^{27}{\rm {Al}}$ ( $\sim$ 0.7%) and some unburnt $^{12}{\rm {C}}$ remains. Apart from $^{12}{\rm {C}}$ , the abundance profiles are very similar among our models but some features deserve additional comments:

First, $^{23}{\rm {Na}}$ is more abundant than $^{24}{\rm {Mg}}$ by a factor of $\sim$ 1.8 throughout the core in all our models. We therefore get an NeONa core rather than an NeOMg white dwarf as input model for the potential pre-supernova evolution. So far, the initial models used in the computations of electron capture induced supernova were NeOMg cores (e.g. Nomoto 1987, and references therein; Canal et al. 1992; Gutierrez et al. 1996). Since the critical density for electron capture on $^{23}{\rm {Na}}$ is lower than that on $^{24}{\rm {Mg}}$ , an NeONa core may have a different evolution through the electron capture stages. $^{16}{\rm {O}}$ may be ignited at a lower density than previously expected, leading to a disruption of the core rather than a collapse. It is therefore important to include the appropriate abundances of both $^{23}{\rm {Na}}$ and $^{24}{\rm {Mg}}$ for collapse-explosion studies.

Second, as one can see from Fig. 9, some unburnt $^{12}{\rm {C}}$ is left over. It presents an off-center peak as high as $X({}^{12}{\rm {C}}) = 0.065$ in the 9.0 $M_{\odot }$ star which decreases with increasing mass to reach $X({}^{12}{\rm {C}}) \sim 0.001$ in the 11.3 $M_{\odot }$ star. The exact shape of the remaining $^{12}{\rm {C}}$ profile depends on the details of the carbon burning flame propagation, but as a general trend, the $^{12}{\rm {C}}$ peak location moves closer to the center and is shallower as the stellar mass increases. Garcia Berro et al. (1997) pointed out that, if the star is in a binary system and accretes enough mass to reach the Chandrasekhar limit, this remaining fuel could alter the supernovae evolution from core collapse to thermonuclear disruption as a result of C and O ignitions.

The central abundances at the end of the carbon burning phase are in qualitatively good agreement with those obtained by Ritossa et al. (1996, 1999), Garcia-Berro et al. (1997) and Iben et al. (1997). The main differences concern $^{16}{\rm {O}}$ which core abundance is smaller in our models. This discrepancy is already present at the end of the core helium burning phase and is probably a consequence of the different $^{12}{\rm {C}}$ ( $\alpha,\gamma$ ) rate adopted in these studies. The higher flame front temperature achieved in our simulations also contributes to burn $^{16}{\rm {O}}$ more efficiently and to produce more $^{20}{\rm {Ne}}$ .

At the outer edge of the CO core (where $\rm C> O$ , i.e. above $M_r \ga 1.122~M_{\odot}$ in Fig. 9) our profiles differ from those of Garía-Berro et al. (1997, see their Fig. 32). In particular, we find that $^{26}{\rm {Mg}}$ is the most abundant species after C and O rather than $^{25}{\rm {Mg}}$ . This difference can be explained by the fact that the authors did not take into account neutron capture reactions beyond $^{25}{\rm {Mg}}$ from which $^{26}{\rm {Mg}}$ is made. Finally, we can not explain their absence of $^{20}{\rm {Ne}}$ which, in our models, naturally comes from the $^{16}{\rm {O}}$ ( $\alpha,\gamma$ ) $^{20}{\rm {Ne}}$ at the base of the He burning shell nor the absence of $^{22}{\rm {Ne}}$ where it is also synthesized.

$\begin{figure} \par\includegraphics[width=8cm,clip]{3043fig9.ps} \end{figure}$	Figure 9: Evolution of the chemical profiles in the interior of a 9.5 $M_{\odot }$ stellar model. The different panels correspond to snapshot taken at the end of core helium burning ( top), during the propagation of the flame ( middle) and when the NeO core is formed and the star enters the super AGB phase ( lower right). The hatched region indicates the location of convection.
Open with DEXTER

$\begin{figure} \par\includegraphics[width=12cm,clip]{3043fig10.ps} \end{figure}$	Figure 10: Kippenhahn diagrams during the carbon burning phase and second dredge-up. The short-dashed (red), dashed (blue) and dotted (green, if present) lines indicate the mass coordinate where the nuclear energy production by carbon, helium and hydrogen burning is maximum, respectively. The hashed areas represent convective regions and the stellar mass is indicated inside each panel.
Open with DEXTER

Table 4: Surface abundances mass fractions at the end of the second dredge-up.

6 Second dredge-up phase

At the end of central helium burning, the gravothermal energy released by core contraction is imparted into heating that may lead to carbon ignition and into mechanical work that will trigger the envelope expansion and the subsequent second dredge-up. In the most massive stars ( $M \ga 10.8$ $M_{\odot }$ ), the envelope stalls near the hydrogen-helium discontinuity while, in lower mass stars (our 9.0, 9.5, 10 and 10.5 $M_{\odot }$ models) it penetrates into the He burning shell during the C burning phase. These differences mainly result from evolutionary timescale considerations: in massive stars, the evolution is faster and the envelope cannot cross this discontinuity before core collapse. In addition, lower mass stars undergo a stronger contraction needed to raise the lower initial core temperature to the carbon ignition threshold. So more energy is deposited at the base of the envelope, the expansion is there stronger and the subsequent deepening enhanced. As for the bump in globular clusters, the crossing of this chemical barrier during the 2DUP provokes some structural readjustments induced by the modification of the opacity in the envelope and, in the HR diagram, the star temporarily settles at the base of the AGB.

Note that the occurrence of secondary carbon flashes can also affect the depth of the dredge-up. In particular, if the instability develops close enough to the H/He interface, the nuclear energy produced in the flash can freely escape from the core and feed the envelope. In the expanding layers above the instability, the luminosity and concomitantly $\nabla_{\rm rad}$ increase, thus favoring the penetration of the envelope in the He burning shell. This happens e.g. in our 10 and 10.5 $M_{\odot }$ models during the late carbon flashes that follow the formation of the NeO white dwarf (Fig. 10). In this case, the top of the instability is located very close to the base of the envelope ( $\la$ 0.2 $M_{\odot }$ ).

By the time the 2DUP is completed, the convective envelope has engulfed the matter processed by the hydrogen burning shell and the surface abundances of $^{12}{\rm {C}}$ , $^{13}{\rm {C}}$ , $^{15}{\rm {N}}$ , $^{16}{\rm {O}}$ and $^{17}{\rm {O}}$ decrease while $^{14}{\rm {N}}$ mass fraction rises. The marginal activation of the NeNa cycle is also apparent in the increase of $^{21}{\rm {Ne}}$ and $^{23}{\rm {Na}}$ while $^{25}{\rm {Mg}}$ is depleted to the benefit of $^{26}{\rm {Mg}}$ as a consequence of the activation of $^{25}{\rm {Mg}}$ ( $p,\gamma$ ) $^{26}{\rm {Mg}}$ . In our models with $M \la 10.5$ $M_{\odot }$ , the envelope penetrates into the He burning shell producing a surface abundance enhancement of $^{4}{\rm {He}}$ mainly, but also of $^{18}{\rm {O}}$ , $^{22}{\rm {Ne}}$ , and $^{12}{\rm {C}}$ . The surface abundances after the second dredge-up phase are summarized in Table 4.

Our models reveal an abrupt change in the depth of the 2DUP around 11.0 $M_{\odot }$ (Table 5) indicating the transition between stars that will develop massive cores subject to hydrodynamical collapse and those that will form a degenerate white dwarf. For the 11.0 and 11.3 $M_{\odot }$ , at the end of carbon burning, neon ignites off-center. It becomes the dominant source of energy in the 11.3 $M_{\odot }$ while in the 10.8 and 11.0 $M_{\odot }$ model electron captures come into play. These interesting aspects of the final evolution of massive AGB stars will be presented in a forthcoming paper.

7 Conclusion

Comparisons of our models with previous works reveal that the critical mass for degenerate off-center carbon ignition $M_{{\rm up}}$ is very similar to the previous results of Garcia-Berro et al. (1997, and reference therein) and is around 9 $M_{\odot }$ . However this values should be considered as an upper limit since no extra-mixing processes were included in our simulations. We also show that the impact of $^{12}{\rm {C}}$ + $^{12}{\rm {C}}$ rates is marginal. Concerning the evolution of the surface composition, stars in the mass range 9 -12 $M_{\odot }$ do not differ substantially from their lower mass counterpart. Their most distinguishable characteristic is their higher luminosity. We also find that the depth of the second dredge-up changes abruptly around $\sim$ 11.0 $M_{\odot }$ , marking the transition between AGB and massive stars that develop cores massive enough to collapse. However, this transition mass depends critically on the adopted mass loss rate which governs the core growth and on the mixing prescriptions which determines the NeO core mass. Their still remain a lot to explore and in first place, the effect of metallicity and of the physical parameters such as mixing and mass loss. These aspects, as well as the subsequent evolution through the TP-SAGB phase and electron capture regime, will be presented in forthcoming papers.

Table 5: At the end of the carbon burning phase, stellar mass ( $M_{\rm AGB}$ ) and masses of the NeO ( $M_{\rm NeO}$ ) and CO cores ( $M_{\rm CO}$ ), defined as the mass coordinate where $Y({}^{20}{\rm {Ne}})=Y({}^{12}{\rm {C}})$ and $Y({}^{4}{\rm {He}})=Y({}^{12}{\rm {C}})$ respectively, as a function of the initial mass $M_{\rm ini}$ . $M_{\rm 2DUP}$ corresponds to the mass coordinate of the deepest extent of the envelope during the second dredge-up.

Evolution of massive AGB stars

I. Carbon burning phase