A&A 448, 395-399 (2006)
DOI: 10.1051/0004-6361:20053332
Applicability of the discrete-dipole approximation to light-scattering
simulations of large cosmic dust aggregates
M. Köhler1 -
H. Kimura2 -
I. Mann1
1 - Institut für Planetologie, Westfälische Wilhelms-Universität,
Wilhelm-Klemm-Str. 10, 48149 Münster, Germany
2 -
Institute of Low Temperature Science, Hokkaido University,
Kita-ku Kita-19 Nishi-8, Sapporo 060-0819, Japan
Received 28 April 2005 / Accepted 11 October 2005
Abstract
Light-scattering properties of cosmic dust particles depend on the structure and composition of the particles. A common model assumption of cosmic dust particles that is
consistent with observational data is to describe them as aggregates consisting of irregularly shaped, inhomogeneous, submicron-sized monomers. It is necessary for a study of their optical properties to apply a proper light-scattering theory, in which we can fully take this shape
and structure of particles into account. Among currently available light-scattering theories, the
discrete-dipole approximation (DDA) with the lattice dispersion relation (LDR) is the best method to simulate light scattering by aggregates of such complex structures. We investigate the accuracy of the LDR-DDA method with large aggregates consisting of spherically shaped, homogeneous, identical monomers of 0.1 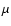 m in radius, for which rigorous solutions are known. The asymmetry parameter and single-scattering albedo of these aggregates are here computed with the LDR-DDA method
as well as the superposition T-matrix method. We find that the conditions previously given in the literature to calculate cross sections of spherical particles within
the accuracy of a few percent are also suitable for large aggregates. We discuss the required computer memory that restricts simulating the optical properties of the considered aggregates.
m in radius, for which rigorous solutions are known. The asymmetry parameter and single-scattering albedo of these aggregates are here computed with the LDR-DDA method
as well as the superposition T-matrix method. We find that the conditions previously given in the literature to calculate cross sections of spherical particles within
the accuracy of a few percent are also suitable for large aggregates. We discuss the required computer memory that restricts simulating the optical properties of the considered aggregates.
Key words: scattering - solar system: general - circumstellar matter - dust, extinction - meteors, meteoroids
Dust particles scatter, absorb, and emit electromagnetic radiation,
the amount of which is determined by their optical properties. Astronomical observations provide information about cosmic dust, but interpretation of observational results is often ambiguous due to missing data for comparison from model calculations and laboratory measurements. Modeling optical properties of dust strongly depends on the assumption
of its shape and structure as well as composition. As an approximation, we may describe cosmic dust as aggregates consisting of irregularly shaped, inhomogeneous, submicron-sized monomers. This picture is consistent with interplanetary dust particles (IDPs) collected in the stratosphere of the earth (Brownlee 1985; Jessberger et al. 2001). Similarities in the properties between IDPs and cometary dust suggest the presence of cometary dust in IDPs, though the
source of the single IDPs may not be clearly identified (see Hanner & Bradley 2004). We expect that our model of cosmic dust well describes cometary dust and presumably interstellar dust, which has been incorporated into comets during the formation of the solar system.
It is important to apply a light-scattering theory that is appropriate to the electromagnetic scattering problem of interest. Mie theory provides a rigorous solution to the light-scattering by an obstacle of a certain defined shape by expanding the scattered electromagnetic wave into spherical harmonics. While Mie theory with an effective medium approximation has
frequently been used in previous studies with porous grains, this
does not properly describe the optical properties of aggregates, especially in the case of transparent materials (Köhler & Mann 2004; Lumme & Rahola 1994). Purcell & Pennypacker (1973) developed the coupled-dipole approximation, which, following Draine (1988), is
hereafter referred to as the discrete-dipole approximation (DDA). The DDA simulates a solid particle by a finite array of polarizable elements (dipoles) and is therefore applicable for particles of
arbitrary shape, structure, size and composition. Each dipole acquires a dipole moment in response to the electric field of an incident plane wave and the electric fields generated by
the other dipoles. The electromagnetic scattering problem for an incident wave
interacting with the dipole ensemble is then solved rigorously once the location of dipoles and a prescription for their polarizabilities are specified.
Doyle (1989) derived the polarizability for a sphere from Mie theory and Okamoto (1996) applied this polarizability to DDA for an aggregate consisting of spheres that are then replaced by single dipoles. Dungey & Bohren (1991) and later Lumme & Rahola (1994) also used this polarizability but with the refractive index derived from an effective medium theory.
Initially Purcell & Pennypacker (1973) determined the polarizability of a dipole by using the Clausius-Mossotti relation, which is exact in the zero frequency limit but is not exact at finite frequencies. Draine (1988) therefore modified the Clausius-Mossotti relation so that each dipole is exposed to a radiative reaction electric field ("radiative reaction term'').
An additional non-radiative term was introduced, for example, by Hage & Greenberg (1990) whose prescription for the polarizability was adopted by Kozasa et al. (1993).
Draine & Goodman (1993) studied plane electromagnetic waves propagating and being scattered on an infinite cubic lattice of polarizable points.
They formulated the lattice dispersion relation (LDR) between the
refractive index of a solid particle and the polarizability of dipoles located in an infinite cubic lattice. This method was found to give the best numerical results (Draine & Flatau 1994).
The LDR appears to be not only valid for infinite targets but also a good choice for single spheres and two touching spheres (Flatau et al. 1993).
DDA calculations of the optical properties of aggregates consisting of spherical monomers were previously carried out: Xing & Hanner (1997) used the LDR method for aggregates consisting of a small number of large monomers, but the structures of the aggregates are not reproduceable.
Lumme & Rahola (1994) considered small aggregates consisting of small porous pseudo-spheres that do not necessarily stick together.
Wright (1987) introduced the concept of fractal aggregates in applications to cosmic dust.
Although the particles are not identical for a given procedure of construction, their properties like the fractal dimension are reproduceable.
Kozasa et al. (1992,1993) calculated the light-scattering properties of fractal aggregates with monomers of only 0.01 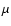 m and only in one case, for 0.03
m and only in one case, for 0.03 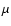 m.
West (1991) used fractal aggregates that consist of a small number of large monomers or that consist of a large number of small monomers.
What is required for a systematic study of light-scattering properties of cosmic dust is to consider large fractal aggregates with large monomer sizes (Lumme et al. 1997; Kimura 2001; Kimura & Mann 2004).
m.
West (1991) used fractal aggregates that consist of a small number of large monomers or that consist of a large number of small monomers.
What is required for a systematic study of light-scattering properties of cosmic dust is to consider large fractal aggregates with large monomer sizes (Lumme et al. 1997; Kimura 2001; Kimura & Mann 2004).
Prior to a study of light scattering by large aggregates consisting of irregularly shaped inhomogeneous grains, we first need to examine
whether the LDR-DDA method is suitable to calculate their optical
properties. To test the accuracy of the LDR-DDA method for aggregates, we carry
out LDR-DDA computations with large aggregates consisting of homogeneous spherical monomers of 0.1 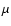 m in radius, for which we determine also exact solutions with the superposition T-matrix method (Mackowski & Mishchenko 1996). Then we seek the condition that the LDR-DDA method provides numerical solutions with a sufficient accuracy for the aggregates. With the derived condition, we present numerical results for the asymmetry parameter and single-scattering albedo of the aggregates in order to demonstrate the dependences of optical properties on the
shape, size and material of the aggregates. Finally we discuss the applicability of the LDR-DDA method to calculate optical properties of large aggregate particles consisting of irregularly shaped inhomogeneous polydisperse grains.
m in radius, for which we determine also exact solutions with the superposition T-matrix method (Mackowski & Mishchenko 1996). Then we seek the condition that the LDR-DDA method provides numerical solutions with a sufficient accuracy for the aggregates. With the derived condition, we present numerical results for the asymmetry parameter and single-scattering albedo of the aggregates in order to demonstrate the dependences of optical properties on the
shape, size and material of the aggregates. Finally we discuss the applicability of the LDR-DDA method to calculate optical properties of large aggregate particles consisting of irregularly shaped inhomogeneous polydisperse grains.
In the DDA, a solid particle is replaced by an array of Npolarizable elements
(j=1,...,N) with complex polarizabilities
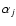 and positions
and positions
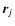 .
Each dipole has a dipole moment
.
Each dipole has a dipole moment
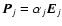 where
the electric field
where
the electric field
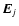 at location
at location
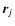 is the sum of the incident wave
is the sum of the incident wave
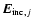 plus the electric fields resulting from the other N-1 dipoles. The electromagnetic scattering problem is then written as a system of 3N complex linear equations:
plus the electric fields resulting from the other N-1 dipoles. The electromagnetic scattering problem is then written as a system of 3N complex linear equations:
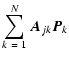 = = 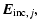 |
(1) |
where
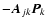 is the electric field at
is the electric field at
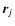 induced from the dipole
induced from the dipole
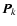 at
at
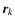 (see Draine & Flatau 1994). Once a self-consistent set of dipole moments
(see Draine & Flatau 1994). Once a self-consistent set of dipole moments
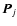 is known, it is straightforward to evaluate the asymmetry parameter g and the cross sections of extinction
is known, it is straightforward to evaluate the asymmetry parameter g and the cross sections of extinction
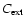 and scattering
and scattering
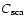 (Draine 1988). We calculate the single-scattering albedo
(Draine 1988). We calculate the single-scattering albedo
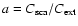 using the cross sections averaged over orientation.
using the cross sections averaged over orientation.
The LDR provides the connection between the dipole polarizability 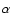 and the refractive index m, when N dipoles are located on a cubic lattice with the interdipole spacing d
(Draine & Goodman 1993). The LDR prescription for the dipole polarizabilities to terms of
order (kd)3 is given by
and the refractive index m, when N dipoles are located on a cubic lattice with the interdipole spacing d
(Draine & Goodman 1993). The LDR prescription for the dipole polarizabilities to terms of
order (kd)3 is given by
![$\displaystyle %
\alpha \!= \!
\frac{\alpha^{(0)}}{1\!+\!\left(\alpha^{(0)}/d^3\...
...right)\left({kd}\right)^2%
\!-\!\left({2/3}\right)i\left({kd}\right)^3\right]},$](/articles/aa/full/2006/10/aa3332-05/img17.gif) |
|
|
(2) |
where
b1=-1.891531,
b2=0.1648469,
b3=-1.770004 are coefficients independent of the wave number k and of the dipole spacing d, and
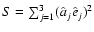 ,
,
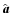 and
and
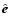 being unit vectors for the propagation direction of the incident radiation and its polarization state, respectively (see Draine & Goodman 1993).
The zeroth order polarizability
being unit vectors for the propagation direction of the incident radiation and its polarization state, respectively (see Draine & Goodman 1993).
The zeroth order polarizability
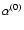 is determined by the
Clausius-Mossotti relation (Purcell & Pennypacker 1973):
is determined by the
Clausius-Mossotti relation (Purcell & Pennypacker 1973):
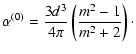 |
|
|
(3) |
The accuracy of LDR-DDA depends on the value of |m|kd where we hereafter fix the wave number
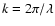 with a wavelength of
with a wavelength of
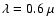 m. Two different values of the refractive index are adopted in the following numerical computations:
m. Two different values of the refractive index are adopted in the following numerical computations:
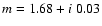 for astronomical silicate given by Laor & Draine (1993) and
for astronomical silicate given by Laor & Draine (1993) and
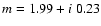 for
amorphous carbon by Rouleau & Martin (1991).
for
amorphous carbon by Rouleau & Martin (1991).
![\begin{figure}
\par\includegraphics[width=5.9cm,clip]{3332fig1.eps}\hspace*{2mm}
\includegraphics[width=5.9cm,clip]{3332fig2.eps}\end{figure}](/articles/aa/full/2006/10/aa3332-05/Timg27.gif) |
Figure 1:
Aggregates with 32 monomers consisting of an array of dipoles for
|m|kd=0.26 ( top) and |m|kd=0.6 ( bottom); left: ballistic cluster-cluster aggregates; right: ballistic particle-cluster aggregates. |
| Open with DEXTER |
Each cluster of spheres is constructed by either ballistic cluster-cluster aggregation (BCCA) or ballistic particle-cluster aggregation (BPCA) processes (see Mukai et al. 1992). We assume that constituent spheres (monomers) of aggregates are identical in composition and size with a radius of 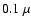 m (cf. Greenberg & Hage 1990; Mann et al. 2004).
This monomer radius is comparable to the components of collected IDPs in the stratosphere, which are mostly 0.1-0.3
m (cf. Greenberg & Hage 1990; Mann et al. 2004).
This monomer radius is comparable to the components of collected IDPs in the stratosphere, which are mostly 0.1-0.3 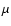 m in size (Rietmeijer 1999).
Each monomer is first replaced by single primary dipoles on the
nearest grid sites from the center of the monomers. Further dipoles are then arranged around the primary dipoles so that all the grid sites within the radius of the monomers from the
location of primary dipoles are occupied by dipoles. Once the condition for |m|kd is given, the minimum number of dipoles to properly simulate the light scattering is determined. Figure 1 shows the resulting array of dipoles at
|m|kd=0.26 and |m|kd=0.6 for BCCAs and BPCAs consisting of 32 monomers.
m in size (Rietmeijer 1999).
Each monomer is first replaced by single primary dipoles on the
nearest grid sites from the center of the monomers. Further dipoles are then arranged around the primary dipoles so that all the grid sites within the radius of the monomers from the
location of primary dipoles are occupied by dipoles. Once the condition for |m|kd is given, the minimum number of dipoles to properly simulate the light scattering is determined. Figure 1 shows the resulting array of dipoles at
|m|kd=0.26 and |m|kd=0.6 for BCCAs and BPCAs consisting of 32 monomers.
We determine the asymmetry parameter g and the single-scattering albedo a in the LDR-DDA method using the F ORTRAN code DDSCAT 6.0 given by Draine & Flatau (2003). The stabilized bi-conjugate gradient method with preconditioning is
used to iteratively solve the system of complex linear equations with
the error tolerance h=10-5. The DDSCAT code incorporates the fast-Fourier-transform method of
Temperton (1992) to accelerate iteration and to provide more accurate solutions for an array of dipoles located on a cubic lattice (Goodman et al. 1991).
We calculate first the asymmetry parameter and the cross sections of extinction and scattering in 7  7
7  7 orientations, a value for which we reach convergence in all cases. We then calculate the orientation-averaged values by numerical quadrature of the fixed-orientation values. These LDR-DDA results are compared with the rigorous solutions from the superposition T-matrix code for multi-sphere clusters in random orientations (see Mackowski & Mishchenko 1996). This is possible since we obtained orientation averaged values. The fractional errors of the asymmetry parameter and the single-scattering albedo are considered for comparison.
7 orientations, a value for which we reach convergence in all cases. We then calculate the orientation-averaged values by numerical quadrature of the fixed-orientation values. These LDR-DDA results are compared with the rigorous solutions from the superposition T-matrix code for multi-sphere clusters in random orientations (see Mackowski & Mishchenko 1996). This is possible since we obtained orientation averaged values. The fractional errors of the asymmetry parameter and the single-scattering albedo are considered for comparison.
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{3332fig3.eps}\hspace*{8mm}
\includegraphics[width=6.1cm,clip]{3332fig4.eps}\end{figure}](/articles/aa/full/2006/10/aa3332-05/Timg30.gif) |
Figure 2:
Fractional errors of the LDR-DDA method for calculations of the single-scattering albedo a. The left figure indicates the errors for ballistic cluster-cluster aggregates and the right hand figure the errors for ballistic particle-cluster aggregates. Top: aggregates of astronomical silicate; bottom: aggregates of amorphous carbon. The upper horizontal axes indicate the number of monomers, the lower axes indicate the radii of volume-equivalent spheres of the
aggregates. Note that the smallest values correspond to spherical grains, in other words, aggregates consisting of one monomer. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{3332fig5.eps}\hspace*{8mm}
\includegraphics[width=6.1cm,clip]{3332fig6.eps}\end{figure}](/articles/aa/full/2006/10/aa3332-05/Timg31.gif) |
Figure 3:
Fractional errors of the LDR-DDA method for calculations of the asymmetry parameter g. The symbols and axes are the same as Fig. 2. |
| Open with DEXTER |
In Figs. 2 and 3 we plot the fractional errors of the single-scattering albedo and the asymmetry parameter versus the
radius of spheres having the same volume as aggregates. Three different |m|kd values are chosen for aggregates composed of astronomical silicate (top panel) and of amorphous carbon (bottom panel). The left figures show the errors for BCCA particles and the right figures show the errors for BPCA particles. For the considered aggregate here, the fractional errors decrease with increasing number of dipoles as expected from the principle of the DDA.
The fractional errors of the albedo a lie within a few percent for
aggregates composed of astronomical silicate if the condition |m|kd<1 is fulfilled. For aggregates of amorphous carbon, the fractional errors are larger, but stay within 10% as long as |m|kd<1. In the case of the asymmetry parameter g even the condition |m|kd<1 results in the fractional errors up to 10% for spheres and up to 15% for small aggregates. Nevertheless, the fractional errors in g for large aggregates usually do not exceed 7%, irrespective of the shape and composition of the aggregates.
We apply the condition
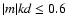 to the following numerical
calculations based on the LDR-DDA method, where the fractional errors
are expected to stay within 7%. The single-scattering albedo and asymmetry parameter for aggregates versus the radius of volume-equivalent spheres,
to the following numerical
calculations based on the LDR-DDA method, where the fractional errors
are expected to stay within 7%. The single-scattering albedo and asymmetry parameter for aggregates versus the radius of volume-equivalent spheres, 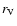 ,
are
shown in Figs. 4 and 5, respectively. The left figures show the calculated values for BCCA particles and the right figures show the calculated values for BPCA particles. There are only minor dependences of the single-scattering albedo and
asymmetry parameter on the structure of particles. Both the single-scattering albedo and the asymmetry parameter increase with aggregate radius
,
are
shown in Figs. 4 and 5, respectively. The left figures show the calculated values for BCCA particles and the right figures show the calculated values for BPCA particles. There are only minor dependences of the single-scattering albedo and
asymmetry parameter on the structure of particles. Both the single-scattering albedo and the asymmetry parameter increase with aggregate radius 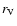 in the range of
in the range of
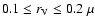 m and show only small changes at
m and show only small changes at
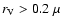 m. The single-scattering albedo is calculated as
m. The single-scattering albedo is calculated as
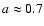 for large aggregates of amorphous carbon and about
for large aggregates of amorphous carbon and about
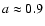 for large aggregates of astronomical silicate. The value of the asymmetry parameter is about
for large aggregates of astronomical silicate. The value of the asymmetry parameter is about
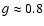 for large aggregates, nearly independent of material composition, and increases slightly with the radius of volume-equivalent spheres.
for large aggregates, nearly independent of material composition, and increases slightly with the radius of volume-equivalent spheres.
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{3332fig7.eps}\hspace*{8mm}
\includegraphics[width=6.1cm,clip]{3332fig8.eps}\end{figure}](/articles/aa/full/2006/10/aa3332-05/Timg39.gif) |
Figure 4:
The single-scattering albedo a is plotted versus the radius of volume-equivalent spheres for ballistic cluster-cluster aggregates ( left panel) and ballistic particle-cluster aggregates ( right panel). |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{3332fig9.eps}\hspace*{8mm}
\includegraphics[width=6.1cm,clip]{3332fig1a.eps}\end{figure}](/articles/aa/full/2006/10/aa3332-05/Timg40.gif) |
Figure 5:
The asymmetry parameter g is plotted versus the radius of volume-equivalent spheres for ballistic cluster-cluster aggregates ( left panel) and ballistic particle-cluster aggregates ( right panel). |
| Open with DEXTER |
Draine & Flatau (2003) suggest the requirement |m|kd<0.5 for
calculating phase functions and |m|kd<1 for calculating cross
sections in order to give sufficient accuracy for the optical
properties of single spheres and two touching spheres.
With our calculations of the asymmetry parameter and the
single-scattering albedo we find that the condition of |m|kd<1 is
in general suitable to calculate optical properties of large aggregates.
The LDR-DDA method with this condition allows us in future to calculate the optical properties of aggregates consisting of inhomogeneous, irregularly shaped, polydisperse monomers.
We cannot fully describe the spherical shape of monomers with an finite array of
dipoles and the larger the |m|kd values the more the monomer's shape deviates from spherical. Each monomer is no longer spherical at |m|kd=0.6 where we use only 19 dipoles to represent a monomer. However, small fractional errors with |m|kd=0.6 for
large aggregates imply that this nonspherical shape does not play a major role in determining the optical properties. In contrast, Xing & Hanner (1997) have shown that optical properties of aggregates consisting of spherical homogeneous
monomers deviate from those of aggregates consisting of tetrahedral shaped monomers. They carried out their DDA computations with the same wavelength
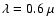 m but larger radii (
m but larger radii (
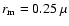 m) than used in this paper (
m) than used in this paper (
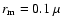 m) and they use aggregates of 4 and 10 monomers. In our study, in contrast, the shape of monomers is still similar to the spheres so that differences in the results are
small. These studies are valid for aggregates consisting of monomers of 0.1
m) and they use aggregates of 4 and 10 monomers. In our study, in contrast, the shape of monomers is still similar to the spheres so that differences in the results are
small. These studies are valid for aggregates consisting of monomers of 0.1 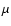 m in radius.
m in radius.
Calculations for large aggregates consisting of monomers of different shapes will be carried out in a future work. The present study shows that the LDR-DDA method is applicable for these calculations.
However, we note the limitation of the LDR-DDA method due to its computational requirements. The memory requirements increase nearly exponentially with increasing
number of monomers for both aggregates in the range of monomer
numbers considered in this paper. Therefore, the LDR-DDA method is computationally intensive for large aggregates; substantial computer memory and computing time are
necessary to determine the light-scattering properties. For example, LDR-DDA calculations with BPCA particles of 512 spheres are performed with approximately 1.5 GB of memory. In other words, the LDR-DDA method is currently limited to the size-parameter range X < 10 with 2 GB of memory for aggregates consisting of 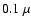 m-radius grains. Therefore,
numerical simulations of light scattering by even larger cosmic dust aggregates are still not feasible with modern personal computers.
m-radius grains. Therefore,
numerical simulations of light scattering by even larger cosmic dust aggregates are still not feasible with modern personal computers.
Acknowledgements
We would like to thank the anonymous referee for
constructive comments. We are indebted to Bruce Draine and Piotr Flatau for their DDA code,
and Daniel Mackowski, Kirk Fuller, and Michael Mishchenko for their superposition code. This research has been supported by the German Aerospace Center, DLR
(project "Rosetta: MIDAS, MIRO, MUPUS'' RD-RX-50 QP 0403), the Japanese Ministry of Education, Culture, Sports, Science and Technology MEXT under Grant-in-Aid for Scientific Research on Priority Areas "Development of Extra-Solar Planetary Science'' (#16077203).
- Bohren, C., & Hufmann, D.
1983, Absorption and Scattering of Light by Small Particles
(New York: John Wiley & Sons)
- Brownlee,
D. E. 1985, Annu. Rev. Earth Planet. Sci., 13, 147 [NASA ADS] [CrossRef]
- Doyle, W. T.
1989, Phys. Rev. B, 39, 9852 [NASA ADS] [CrossRef] (In the text)
- Draine, B. T.
1988, ApJ, 333, 848 [NASA ADS] [CrossRef] (In the text)
-
Draine, B. T., & Flatau, P. J. 1994, J. Opt. Soc. Am. A,
A11, 1491 [NASA ADS] (In the text)
-
Draine, B. T., & Flatau, P. J. 2003,
http://arxiv.org/abs/astro-ph/0300969
(In the text)
- Draine, B. T., & Goodman, J.
1993, ApJ, 405, 685 [NASA ADS] [CrossRef] (In the text)
-
Dungey, C. E., & Bohren, C. F. 1991, J. Opt. Soc. Am. A,
8, 81 [NASA ADS] (In the text)
-
Flatau, P. J., Fuller, K. A., & Mackowski, D. W. 1993,
Appl. Opt., 32, 3302 [NASA ADS] (In the text)
-
Goodman, J. J., Draine, B. T., & Flatau, P. J. 1991, Opt.
Lett., 16, 1198 [NASA ADS] (In the text)
- Greenberg, J. M., & Hage,
J. I. 1990, ApJ, 361, 260 [NASA ADS] [CrossRef]
- Hage, J. I., & Greenberg,
J. M. 1990, ApJ, 361, 251 [NASA ADS] [CrossRef] (In the text)
- Hanner, M. S., & Bradley,
J. P. 2004, in Comets II, ed. M. Festou, H. U.
Keller, & H. A. Weaver (Tucson: University of
Arizona)
(In the text)
- Jessberger, E. K., et al.
2001, in Interplanetary Dust, ed. E. Grün,
B. Å. S. Gustafson, S. F. Dermott, & H.
Fechtig (Heidelberg: Springer-Verlag), 253
- Kimura, H.
2001, J. Quant. Spec. Radiat. Transf., 70,
581 [NASA ADS]
-
Kimura, H., & Mann, I. 2004,
J. Quant. Spec. Radiat. Transf., 89, 155 [NASA ADS]
-
Köhler, M., & Mann, I. 2004,
J. Quant. Spec. Radiat. Transf., 89, 453 [NASA ADS]
-
Kozasa, T., Blum, J., & Mukai, T. 1992, A&A, 263, 423 [NASA ADS]
-
Kozasa, T., Blum, J., Okamoto, H., & Mukai, T. 1993, A&A,
276, 278 [NASA ADS] (In the text)
-
Laor, A., & Draine, B. T. 1993, ApJ, 402, 441 [NASA ADS] [CrossRef] (In the text)
-
Lumme, K., & Rahola, J. 1994, ApJ, 425, 653 [NASA ADS] [CrossRef]
-
Lumme, K., Rahola, J., & Hovenier, J. W. 1997, Icarus,
126, 455 [NASA ADS] [CrossRef]
- Mackowski, D. W., &
Mishchenko, M. I. 1996, J. Opt. Soc. Am. A, 13, 2266 [NASA ADS] (In the text)
- Mann,
I., Kimura, H., & Kolokolova, L. 2004, J. Quant. Spec. Radiat.
Transf., 89, 291 [NASA ADS]
-
Mukai, T., Ishimoto, H., Kozasa, T., Blum, J., & Greenberg,
J. M. 1992, A&A, 262, 315 [NASA ADS] (In the text)
- Okamoto, H.
1996, in Physics, Chemistry, and Dynamics of Interplanetary Dust,
ed. B. Å. S. Gustafson, & M. S. Hanner
(San Francisco: ASP), 423
(In the text)
- Purcell, E. M., &
Pennypacker, C. R. 1973, ApJ, 186, 705 [NASA ADS] [CrossRef] (In the text)
-
Rietmeijer, F. J. M. 1999, in Planetary Materials,
ed. J. J. Papike (Washington, D. C.: Mineralogical
Society of America), 2
(In the text)
- Rouleau, F., & Martin,
P. G. 1991, ApJ, 377, 526 [NASA ADS] [CrossRef] (In the text)
-
Temperton, C. 1992, SIAM J. Sci. Statistic. Comp., 13, 676 (In the text)
- West, R. A. 1991,
Appl. Opt., 30, 5316 [NASA ADS] (In the text)
- Wright, E. L.
1987, ApJ, 320, 818 [NASA ADS] [CrossRef] (In the text)
-
Xing, Z., & Hanner, M. S. 1997, A&A, 324, 805 [NASA ADS] (In the text)
Copyright ESO 2006
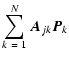 =
= ![$\displaystyle %
\alpha \!= \!
\frac{\alpha^{(0)}}{1\!+\!\left(\alpha^{(0)}/d^3\...
...right)\left({kd}\right)^2%
\!-\!\left({2/3}\right)i\left({kd}\right)^3\right]},$](/articles/aa/full/2006/10/aa3332-05/img17.gif)
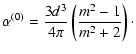
![\begin{figure}
\par\includegraphics[width=5.9cm,clip]{3332fig1.eps}\hspace*{2mm}
\includegraphics[width=5.9cm,clip]{3332fig2.eps}\end{figure}](/articles/aa/full/2006/10/aa3332-05/Timg27.gif)
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{3332fig3.eps}\hspace*{8mm}
\includegraphics[width=6.1cm,clip]{3332fig4.eps}\end{figure}](/articles/aa/full/2006/10/aa3332-05/Timg30.gif)
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{3332fig5.eps}\hspace*{8mm}
\includegraphics[width=6.1cm,clip]{3332fig6.eps}\end{figure}](/articles/aa/full/2006/10/aa3332-05/Timg31.gif)
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{3332fig7.eps}\hspace*{8mm}
\includegraphics[width=6.1cm,clip]{3332fig8.eps}\end{figure}](/articles/aa/full/2006/10/aa3332-05/Timg39.gif)
![\begin{figure}
\par\includegraphics[width=6.1cm,clip]{3332fig9.eps}\hspace*{8mm}
\includegraphics[width=6.1cm,clip]{3332fig1a.eps}\end{figure}](/articles/aa/full/2006/10/aa3332-05/Timg40.gif)