A&A 448, 23-27 (2006)
DOI: 10.1051/0004-6361:20042618

Big-bang nucleosynthesis in a Brans-Dicke cosmology with a varying ${\Lambda }$ term related to WMAP

R. Nakamura¹ - M. Hashimoto¹ - S. Gamow¹ - K. Arai²

1 - Department of Physics, Kyushu University, Fukuoka, 810-8560, Japan
2 - Department of Physics, Kumamoto University, Kumamoto, 860-8555, Japan

Received 28 December 2004 / Accepted 11 October 2005

Abstract
We investigate the big-bang nucleosynthesis in a Brans-Dicke model with a varying ${\Lambda }$ term using the Monte-Carlo method and likelihood analysis. It is found that the cosmic expansion rate differs appreciably from that of the standard model. The produced abundances of ⁴He, D, and ⁷Li are consistent with the observed ones within the uncertainties in nuclear reaction rates when the baryon to photon ratio $\eta = \left( 5.47{-}6.64 \right)$ $\times$ 10^-10, which is in agreement with the value deduced from WMAP.

Key words: nuclear reactions, nucleosynthesis, abundances - cosmology: early Universe - cosmology: cosmic microwave background

1 Introduction

The standard model of big-bang nucleosynthesis (SBBN) has succeeded in explaining the origin of the light elements ⁴He, D, and ⁷Li. Although the value of the baryon-to-photon ratio $\eta$ has been derived from the observations of the Wilkinson Microwave Anisotropy Probe (WMAP) (Bennett et al. 2003) to be $\eta^{}_{10}=6.1^{+0.3}_{-0.2}$, the value seems to be inconsistent with the results of SBBN (Coc et al. 2004). Contrary to the excellent concordance with $\eta$ of WMAP for D, the abundance of ⁴He by SBBN is rather low compared to that from WMAP. Therefore, non-standard models of BBN have been proposed with the Friedmann model modified (Steigman 2003).

For non-standard models, scalar-tensor theories have been investigated (e.g., Bergmann 1968; Wagoner 1970; Endo & Fukui 1977; Fukui et al. 2001). For a simple model with a scalar $\phi$, it is shown that a Brans-Dicke (BD) generalization of gravity with torsion includes the low-energy limit string effective field theory (Hammond 1996). Related to the cosmological constant problem, a Brans-Dicke model with a varying $\Lambda(\phi)$ term (BD${\Lambda }$) has been presented, and also investigated from the point of inflation theory (Berman 1989). Moreover, it is found that the linearized gravity can be recovered in the Randall-Sundrum brane world (Garriga & Tanaka 2000). Furthermore, scalar-tensor cosmology is constrained by a $\chi^2_{}$ test for the WMAP spectrum (Nagata et al. 2004) where the present value of the coupling parameter  $\omega_0 =\omega(\phi_0)$ is bounded to be $\omega^{}_0 > 50~(4\sigma)$ and  $\omega^{}_0 > 1000~(2\sigma)$ in the limit to BD cosmology.

BBN has been studied in BD${\Lambda }$ (Arai et al. 1987; Etoh et al. 1997). The relation between BBN and scalar-tensor gravity is investigated with the inclusion of  ${\rm e^{+}e^{-}}$ annihilation in the equation of state, where the present value of the scalar coupling has been constrained (Damour & Pichon 1999). On the other hand, it is suggested that a decaying ${\Lambda }$ modifies the evolution of the scale factor and affects the temperature $T_{\rm r}$ of the cosmic microwave background at redshift $z \le 10^4$, when the recombination begins due to the decrease in $T_{\rm r}$ (Kimura et al. 2001), while a decaying ${\Lambda }$ is found to be consistent with temperature observations of the cosmic microwave background for z < 4 (Puy 2004). Therefore, it is worthwhile to check the validity of BD${\Lambda }$ related to the recent observations. In the present paper, we investigate to what extent BBN in the BD${\Lambda }$ model can be reconciled with $\eta$ from WMAP.

In Sect. 2, the formulation for BD${\Lambda }$ is given and the evolution of the universe in BD${\Lambda }$ is shown. Our results of BBN are presented in Sect. 3 using the Monte-Carlo method (Cyburt et al. 2001), and constraints are given to the parameters inherent in BD${\Lambda }$. We examine in Sect. 4 the evolution of the scale factor and the resulting abundances taking into account the deviation from the equation of state  $p = \rho/3$ during the stage of ${\rm e^{+}e^{-}}$ annihilation. In Sect. 5, a likelihood analysis (Fields et al. 1996) is adopted to obtain the most probable values and the accompanying errors.

2 Brans-Dicke cosmology with a varying ${\Lambda }$ term

The field equations for BD${\Lambda }$ are written as follows (Arai et al. 1987):

 

$$% R_{\mu\nu} -\frac{1}{2} g_{\mu\nu} R + g_{\mu\nu} \Lambda \frac{8\pi}{\phi} T_{\mu\nu} + \frac{\omega}{\phi^2} \left(\phi_{,\mu;\nu} - \frac{1}{2} g_{\mu\nu}\phi_{,\alpha}\phi^{,\alpha}\right)$$ =

$$+ \frac{1}{\phi}\left(\phi_{,\mu;\nu} - g_{\mu\nu} \Box\phi\right),$$ (1)

$$% R-2\Lambda-2\phi\frac{\partial\Lambda}{\partial\phi}= \fra... ...}{\phi^2}\phi_{,\mu}\phi^{,\mu}-\frac{2\omega}{\phi}\Box\phi,$$ (2)

where $\omega$ is the coupling constant.

The equation of motion is obtained with use of the Friedmann-Robertson-Walker metric:

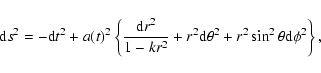$$% {\rm d}s^2 = -{\rm d}t^2 + a(t)^2\left\{ \frac{{\rm d}r^2_{... ...\rm d}\theta^2_{}+ r^2_{} \sin^2\theta {\rm d}\phi^2\right \},$$ (3)

where a(t) is the scale factor and k is the curvature constant. Let x be a scale factor normalized to its present value, i.e., x=a/a₀, then we get from the (0,0) component in Eq. (1)

$$% \left(\frac{\dot x}{x} \right)^2_{} + \frac{k}{x^2_{}}-\fr... ...}{x}\frac{\dot \phi}{\phi} = \frac{8\pi}{3}\frac{\rho}{\phi},$$ (4)

where $\rho$ is the energy density.

We assume the simplest case of the coupling between the scalar and matter fields:

$$% \Box\phi = \frac{8\pi}{2\omega + 3}\mu T_{\nu}^{\nu},$$ (5)

where $\mu$ is a constant. Assuming a perfect fluid for  $T^{}_{\mu\nu}$, Eq. (5) reduces to

$$% \frac{{\rm d}}{{\rm d}t}\left(\dot\phi x^3\right)=\frac{8\pi\mu}{2\omega+3}(\rho-3p) x^3_{},$$ (6)

where p is the pressure.

A particular solution of Eq. (2) is obtained from Eqs. (1) and (5):

$$% \Lambda =\frac{2\pi\left( \mu-1 \right)}{\phi}\rho_{{\rm m}0}x^{-3},$$ (7)

where $\rho_{m0}$ is the matter density at the present epoch.

The gravitational "constant'' G is expressed as follows

$$% G=\frac{1}{2} \left(3-\frac{2\omega+1}{2\omega+3} \mu\right) \frac{1}{\phi}\cdot$$ (8)

The radiation density $\rho_{\rm r}$ contains the contributions from photons, neutrinos, electrons and positrons at $t\le 1$ s. The total energy density is given as

 

$$% \rho = \rho^{}_{\rm m} + \rho^{}_r, \ \ \rho^{}_r =\rho_{{\rm rad}}+\rho_{\nu}+\rho_{{\rm e}^{\pm}}.$$ (9)

Here the energy density of matter varies as $\rho^{}_{\rm m}=\rho^{}_{{\rm m}0}x^{-3}_{}$. The radiation density $\rho^{}_{\rm r}=\rho^{}_{r0}x^{-4}_{}$ except ${\rm e^{+}e^{-}}$ epoch where ${\rm e^{+}e^{-}}$ annihilation changes the relation $T_{\rm r} \sim x^{-1}$. We assume that the pressure satisfies $p = \rho/3$, which is legitimate only for relativistic particles. Then, Eq. (6) is integrated to give

$$% \dot\phi = \left(\frac{8\pi\mu}{2\omega + 3}\rho^{}_{{\rm m}0}t+B\right) \frac{1}{x^3_{}},$$ (10)

where B is a constant (Arai et al. 1987). Although the relation $p = \rho/3$ does not hold during the epoch of ${\rm e^{+}e^{-}}$ annihilation, as pointed out by Damour & Pichon (1999), the inclusion of $\phi$ measures small deviation from SBBN in our interest, so that our solution (10) can reasonably describe the evolution of $\phi$ except during the annihilation epoch. We consider that B affects the evolution of x significantly from the early epoch to the present compared to the contribution from  ${\rm e^{+}e^{-}}$ annihilation. As a consequence, the neutron to proton ratio is seriously affected by the initial value of B. Considering the important contribution of  $\rho_{{\rm e}^{\pm}}$ to BBN, we examine the effects of ${\rm e^{+}e^{-}}$ annihilation in Sect. 4. Hereafter we use the normalized values: B^* = B/(10^-24 g s cm^-3) and $\eta_{10}=10^{10}\eta$. The coupled Eqs. (4), (7) and (10) can be solved numerically with the specified quantities: for macroscopic quantities, G₀ = 6.672 $\times$ 10^-8 dyn cm² g^-2, H₀=71 km s^-1 Mpc^-1 (Bennett et al. 2003), and $T^{}_{{\rm r}0}=2.725$ K (Mather et al. 1999); for microscopic quantities, the number of massless neutrino species is 3 and the half life of neutrons is 885.7 s (Hagiwara et al. 2002). Although we adopt $\omega=500$, the epoch of the appreciable growth of  $\vert\dot{G}/G\vert$ is t < 10³ s regardless of the value $\omega$ (Arai et al. 1987). Therefore, even if we adopt a value $\omega> 500$ (Will 2001), we can arrive qualitatively the same conclusion by changing the parameters $\mu$ and B^*. We impose the condition $\vert\dot{\phi}/\phi\vert^{}_{0}=\vert\dot{G}/G\vert^{}_{0}<10^{-13}_{}$ yr^-1 which is the most severe observational limit (Müller et al. 1991).

	Figure 1: Evolution of the scale factor for BD${\Lambda }$ ($\mu =0.7$, t0 =13.7 Gyr, and $\eta ^{}_{10}=6.1$) and Friedmann model.
Open with DEXTER

BD${\Lambda }$ is an extension of the original form of BD and reduces to the Friedmann model when $\phi$ = constant, $\mu = 1$ and $\omega \gg 1$. We have $\Lambda < 0$ if $\mu < 1$, and $\phi G > 0$ if both $\mu > 3$ and $\omega \gg 1$. Figure 1 shows the evolution of the scale factor for BD${\Lambda }$ with the relevant parameters in the present study and for the Friedmann model. Note that the difference in the expansion rate at t < 10 s in BD${\Lambda }$. In particular, around t=5 s, the curve x in BD${\Lambda }$ crosses that of the Friedmann model, which will have noticeable effects on BBN. Since ${\Lambda }$ is proportional to  $\rho_{{\rm m}0}$, $\mu$ affects the evolution of the scale factor around the present epoch. In our BD${\Lambda }$ model, if |B^*| increases, the expansion rate increases at t<10-100 s. The change in G between the recombination and the present epoch is less than 0.05 ($2\sigma$) from WMAP (Nagata et al. 2004), which is consistent with BD${\Lambda }$ since |(G-G₀)/G₀|<0.005 at t>1 yr.

3 Big-bang nucleosynthesis

	Figure 2: Light element abundances against $\eta$ in BD${\Lambda }$ for $\mu =0.7$ and possible values of B*.
Open with DEXTER

	Figure 3: Same as Fig. 2 but for B*=0 and various values of $\mu$.
Open with DEXTER

Changes in the expansion rate compared to the standard model affect the synthesis of light elements in the early era, because the neutron to proton ratio is sensitive to the expansion rate.

For the BBN calculation, we use the reaction rates (Cyburt et al. 2001) based on NACRE (Angulo et al. 1999). We adopt the observed abundances of ⁴He, D/H and ⁷Li/H as follows: $Y^{}_{\rm p}=0.2391$ $\pm$ 0.0020 (Luridiana et al. 2003), D/H = 2.78^+0.44_-0.38 $\times$ 10^-5 (Kirkman et al. 2003), ⁷Li/H = $\left(2.19\pm 0.28 \right)$ $\times$ 10^-10 (Bonifacio et al. 2002).

Since the results of WMAP constrain cosmological parameters, we calculate the abundance of ⁴He, D and ⁷Li paying attention to the value $\eta ^{}_{10}=6.1$. First, we carry out the BBN calculations with use of the adopted experimental values of nuclear reaction rates given in NACRE. Figure 2 illustrates ⁴He, D/H and ⁷Li/H for $\mu =0.7$. The abundance of ⁴He is very sensitive to both B^* and $\mu$; it increases if |B^*| or $\mu$ increases. On the other hand, D and ⁷Li are more sensitive to $\mu$ than B^* as seen from Fig. 3. As a result, ⁴He and D/H are consistent with $\eta$ obtained from WMAP in the range $-0.5\le\mu\le 0.8$ and $-10\le B^*\le 10$.

Next, we perform the Monte-Carlo calculations to obtain the upper and lower limits to individual abundance using the uncertainties in the nuclear reaction rates (Cyburt et al. 2001). Figure 4 illustrates ⁴He, D/H and ⁷Li/H with $2\sigma$ uncertainties for  B^*=-2.5 and $\mu =0.7$. The light-shaded areas denote the regions of observed abundances, and the dark-shaded area indicates the limit obtained from WMAP. While the obtained values of ⁴He and D are consistent with $\eta$ by WMAP, the lower limit in ⁷Li is barely consistent.

	Figure 4: Light-element abundances vs. $\eta$ in BD${\Lambda }$ for $\mu =0.7$ and B*=-2.5. Dashed lines show $\pm$$2\sigma$ uncertainties in nuclear reaction rates. The dark-shaded area indicates the constraint by WMAP and light-shaded areas denote regions of observational abundances.
Open with DEXTER

4 Effects of ${\rm e^{+}e^{-}}$ annihilation on BBN

In the previous sections, we have assumed the equation of state $p = \rho/3$ in Eq. (6) to obtain Eq. (10) at the epoch of ${\rm e^{+}e^{-}}$ annihilation. Let us discuss the effects of ${\rm e^{+}e^{-}}$ annihilation on the evolution of the scalar field and the scale factor due to the deviation from the relation $p = \rho/3$. The electron-positron pressure and energy density are written with the variable $\zeta=m^{}_{\rm e}/k^{}_{\rm B}T^{}_{\rm r}$ as follows

$$% p^{}_{\rm e} = \frac{2m_{\rm e}^{4}}{ \pi^{2}_{} \hbar^{3}_... ...\left( \frac{1}{n\zeta}\right)^{2} K_{2}\left( n\zeta \right),$$ (11)

$$% \rho^{}_{\rm e} = 3~p^{}_{\rm e} + \frac{2m_{\rm e}^{4}}{ \... ...n+1} \left( \frac{1}{n\zeta}\right) K_{1}\left(n\zeta \right),$$ (12)

where $\hbar$ is Planck's constant in units of $2\pi$, $k^{}_{\rm B}$ is Boltzmann's constant, and  $m^{}_{\rm e}$ is the electron rest mass. $K_{i}~(i=1 \mbox{ and } 2)$ are modified Bessel functions of order i(e.g. Damour & Pichon 1999). In the numerical calculations, the summations in Eqs. (11) and (12) are taken over n=1-10. We can obtain the scale factor by integrating Eq. (4) with the aid of Eq. (6). To see the effects of  ${\rm e^{+}e^{-}}$, we take the form:

$$% \dot\phi x^3= \frac{8\pi\mu}{2\omega + 3}\int^t{\left(\rho_{\rm e}-3p_{\rm e}\right)}x^3{\rm d}t +B.$$ (13)

A direct comparison is made for the evolution of the scalar field. The results are shown in Fig. 5, where the solid line indicates the case of Eq. (13) with B^*=-2.43 and $\mu =0.7$, and the broken line is the case of Eq. (10) with B^*=-2.50 and $\mu =0.7$. These sets of parameters yield the same macroscopic quantities given in Sect. 2. Although we can appreciate the slight difference at t < 10³ s, it remains small during and after the stage of BBN. The effects on the evolution of the scale factor are minor and the change in $Y_{\rm p}$ is found to be at most 0.1% compared to that obtained in Sect. 3. We can conclude that since the effects of B in the range $-10\le B^*\le 10$ is much larger then those of  ${\rm e^{+}e^{-}}$ annihilation, the deviation from the relation $p = \rho/3$ due to  ${\rm e^{+}e^{-}}$ does not change our results qualitatively. However, we note that even small differences in $Y_{\rm p}$ may affect the detailed statistical analysis combined with theoretical and observational uncertainties performed in the previous sections.

	Figure 5: Evolution of the scalar field. The solid line refers the integration of Eq. (13) with B* = -2.43, and the broken line is for Eq. (10) with B* = -2.50.
Open with DEXTER

5 Discussion and conclusions

	Figure 6: Likelihood function as a function of $\eta _{10}$ for 4He (L4), D (L2) and 7Li (L7). The vertical lines indicate the upper and lower limit to $\eta$ by WMAP.
Open with DEXTER

	Figure 7: Combined likelihood function for two  (L47) and three-elements  (L247).
Open with DEXTER

We have carried out BBN calculations in the $\mu-B^{*}$ plane and obtain the ranges $-0.5\le\mu\le 0.8$ and $-10\le B^*\le 10$ that are consistent with both the abundance observations and $\eta$ obtained from WMAP.

To evaluate the uncertainties in theory and observation, we calculate normalized likelihood distributions in BBN (Fields et al. 1996; Hashimoto et al. 2003). In Fig. 6, we show the likelihood functions for ⁴He, D and ⁷Li. The combined distributions, $L^{}_{47}=L^{}_{4}\cdot L^{}_{7}$ and $L^{}_{247}=L^{}_{2}\cdot L^{}_{4}\cdot L^{}_{7}$ are shown in Fig. 7. We obtain the 95% confidence limit of $\eta$: $5.47 \le \eta^{}_{10} \le 6.64$.

The consistency holds within $1\sigma$ errors for ⁴He and D, and $2\sigma$ for ⁴He, D and ⁷Li. Although new reaction rates recently published (Descouvemont et al. 2004) will change the errors to some extent in the likelihood analysis, our conclusion holds qualitatively.

Our previous studies (Etoh et al. 1997) showed $1<\mu<3$ if $\Lambda>0$for large values of $\omega$. In the present case, the ${\Lambda }$ term becomes negative in Eq. (7) for $\mu < 1$: this would not conflict with available observations and/or basic theory (Vilenkin 2004). Alternatively, if we consider $\Lambda=\Lambda_0 + \Lambda(\phi)$ with $\vert\Lambda(\phi_0)/\Lambda_0\vert < 0.01$, then the cosmological term becomes consistent with the present observations. Although the evolutionary path in the early universe can deviate from the Friedmann model (Arai et al. 1987), parameters in BD${\Lambda }$ must be searched in detail for values of $\omega> 500$ to obtain quantitative results of BBN. It is shown that negative energies are present in scalar-tensor theories, although it is not clear how to identify them definitely (Faraoni 2004).

To avoid the apparent inconsistency for SBBN, effects of neutrino degeneracy, changes in neutrino species or other new physical processes have been included in models (Steigman 2003). In our model, we need only a scalar field that could be related to string theory (Hammond 1996). The original BD cosmology ($\mu = 1$) would be limited severely by the more accurate observation of light elements and/or future constraints for $\eta$ as shown in the present investigation.

Acknowledgements

Data analysis was in part carried out on a general common user computer system at the Astronomical Data Analysis Center of the National Astronomical Observatory of Japan.

References

• Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] (In the text)
• Arai, K., Hashimoto, M., & Fukui, T. 1987, A&A, 179, 17 [NASA ADS] (In the text)
• Bennett, C. L., Halpern, M., & Hinshaw, G., et al. 2003, ApJS, 148, 1 [NASA ADS] [CrossRef] (In the text)
• Bergmann, P. G. 1968, Int. J. Theor. Phys., 1, 25 [CrossRef] (In the text)
• Berman, M. S. 1989, Phys. Lett. A, 142, 335 [NASA ADS] [CrossRef] (In the text)
• Bonifacio, P., Pasquini, L., Spite, F., et al. 2002, A&A, 390, 91 [EDP Sciences] [NASA ADS] (In the text)
• Brans, C., & Dicke, R. H. 1961, Phys. Rev., 124, 925 [NASA ADS] [CrossRef]
• Cardenas, R., Gonzalez, T., Leiva, Y., Martin, O., & Quiros, I. 2003, Phys. Rev. D, 67, 083501 [NASA ADS] [CrossRef]
• Coc, A., et al. 2004, in Origin of Matter and Evolution of Galaxies [arXiv:astro-ph/0401008] (In the text)
• Cyburt, R., Fields, B., & Olive, K. 2001, , 6, 215 (In the text)
• Damour, T., & Pichon, B. 1999, Phys. Rev. D, 59, 123502 [NASA ADS] [CrossRef] (In the text)
• Descouvemont, P., Adahchour, A., Angulo, C., Coc, A., & Vangioni-Flam, E. 2004, Atom. Data Nucl. Data Tabl., 88, 203 [NASA ADS] (In the text)
• Endo, M., & Fukui, T. 1977, Gen. Rel. Grav., 8, 833 [NASA ADS] [CrossRef] (In the text)
• Etoh, T., Hashimoto, M., Arai, K., & Fujimoto, S. 1997, A&A, 325, 893 [NASA ADS] (In the text)
• Faraoni, V. 2004, Phys. Rev. D, 70, 081501 [NASA ADS] [CrossRef] (In the text)
• Fields, B. D., Kainulainen, K., Olive, K. A., & Thomas, D. 1996, , 1, 77 (In the text)
• Fukui, T., Arai, K., & Hashimoto, M. 2001, Class. Quant. Grav., 18, 2087 [NASA ADS] (In the text)
• Garriga, J., & Tanaka, T. 2000, Phys. Rev. Lett., 84, 2778 [NASA ADS] [CrossRef] (In the text)
• Hagiwara, K., Hikasa, K., Nakamura, K., et al. 2002, Phys. Rev. D, 66, 010001 [NASA ADS] [CrossRef] (In the text)
• Hammond, R. T. 1996, Class. Quant. Grav. 13, L73 (In the text)
• Hashimoto, M., Kamikawa, T., & Arai, K. 2003, ApJ, 598, 13 [NASA ADS] [CrossRef] (In the text)
• Kimura, K., Hashimoto, M., Sakoda, M., & Arai, K. 2001, ApJ, 561, L19 [NASA ADS] [CrossRef] (In the text)
• Kirkman, D., Tytler, D., Suzuki, N., O'Meara, J. M., & Lubin, D. 2003, ApJS, 149, 1 [NASA ADS] [CrossRef] (In the text)
• Luridiana, V., Peimbert, A., Peimbert, M., & Cervino, M. 2003, ApJ, 592, 846 [NASA ADS] [CrossRef] (In the text)
• Mather, J. C., Fixsen, D. J., Shafer, R. A., Mosier, C., & Wilkinson, D. T. 1999, ApJ, 512, 511 [NASA ADS] [CrossRef] (In the text)
• Müller, J., Schneider, M., Soffel, M., & Ruder, H. 1991, ApJ, 382, L101 [NASA ADS] [CrossRef] (In the text)
• Nagata, R., Chiba, T., & Sugiyama, N. 2004, Phys. Rev. D, 69, 083512 [NASA ADS] [CrossRef] (In the text)
• Puy, D. 2004, A&A, 422, 1 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Steigman, G. 2003, hep-ph/0309347 (In the text)
• Vilenkin, A. 2004, in Universe or Multiverse, ed. B. J. Carr (Cambridge University Press), in press [arXiv:astro-ph/0407586] (In the text)
• Wagoner, R. V. 1970, Phys. Rev. D, 1, 3209 [NASA ADS] [CrossRef] (In the text)
• Will, C. M. 2001, Living Rev. Relativ., 4, 4 [NASA ADS] (In the text)