Contents

• The Large Magellanic Cloud: diffuse interstellar bands, atomic lines and the local environmental conditions
• 1 Introduction
• 2 Observations and data reduction procedure
• 3 Diffuse interstellar bands in the Large Magellanic Cloud
• 4 Interstellar dust in the Large Magellanic Cloud
• 5 Interstellar gas in the Large Magellanic Cloud
• 6 DIB behaviour in the LMC and comparison with the Milky Way
• 7 Summary and conclusion
• References
• 8 Online Material

A&A 447, 991-1009 (2006)
DOI: 10.1051/0004-6361:20053367

The Large Magellanic Cloud: diffuse interstellar bands, atomic lines and the local environmental conditions^,

N. L. J. Cox¹ - M. A. Cordiner² - J. Cami³ - B. H. Foing⁴ - P. J. Sarre² - L. Kaper¹ - P. Ehrenfreund⁵

1 - Astronomical Institute "Anton Pannekoek'', University of Amsterdam, Kruislaan 403, 1098 SJ, Amsterdam, The Netherlands
2 - School of Chemistry, The University of Nottingham, University Park, Nottingham NG7 2RD, UK
3 - Space Science Division, NASA Ames Research Center, Mail Stop 245-6, Moffett Field, California 94035, USA
4 - ESA/SCI-SR, ESTEC, PO Box 299, 2200 AG Noordwijk, The Netherlands
5 - Astronomy Institute, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands

Received 4 May 2005 / Accepted 19 October 2005

Abstract
The Large Magellanic Cloud (LMC) offers a unique laboratory to study the diffuse interstellar bands (DIBs) under conditions that are profoundly different from those in the Galaxy. DIB carrier abundances depend on several environmental factors, in particular the local UV radiation field. In this paper we present measurements of twelve DIBs in five lines of sight to early-type stars in the LMC, including the 30 Doradus region. From the high resolution spectra obtained with VLT/UVES we also derive environmental parameters that characterise the local interstellar medium (ISM) in the probed LMC clouds. These include the column density components (including total column density) for the atomic resonance lines of Na I, Ca II, Ti II, K I. In addition, we derive the H I column density from 21 cm line profiles, the total-to-selective visual extinction $R{_{\rm V}}$ and the gas-to-dust ratio N(H I)/$A_{\rm V}$. Furthermore, from atomic line ratios we derive the ionisation balance and relative UV field strength in these environments. We discuss the properties of the LMC ISM in the context of DIB carrier formation. The behaviour of DIBs in the LMC is compared to that of DIBs in different local environmental conditions in the Milky Way. A key result is that in most cases the diffuse band strengths are weak (up to factor 5) with respect to Galactic lines of sight of comparable reddening, . In the line of sight towards Sk -69 223 the 5780 and 5797 Å DIBs are very similar in strength and profile to those observed towards HD 144217, which is typical of an environment exposed to a strong UV field. From the velocity analysis we find that DIB carriers (towards Sk -69 243) are better correlated with the ionised species like Ca II than with neutrals (like Na I and CO). The most significant parameter that governs the behaviour of the DIB carrier is the strength of the UV field.

Key words: astrochemistry - Magellanic Clouds - ISM: clouds - ISM: lines and bands - ISM: abundances

1 Introduction

The last decade has seen considerable growth in interest in the diffuse interstellar bands (DIBs) and their origin. DIBs are observed ubiquitously in the interstellar medium (ISM) between 4000 and 10 000 Å (Herbig 1995,1993). With the advent of more powerful telescopes and sophisticated instruments it has become possible to detect DIBs towards faint objects, both in and beyond our own Galaxy. Despite fervent research for over eighty years, the identity of the DIB carriers remains until this day a mystery (Herbig 1995). Currently, much emphasis is given to complex carbonaceous gas-phase molecules, such as fullerenes (Foing & Ehrenfreund 1994), carbon chains (Maier et al. 1995) and polycyclic aromatic hydrocarbons (PAHs), as possible carriers of the DIBs (e.g. Leger & Dhendecourt 1985; Van der Zwet & Allamandola 1985).

In order to understand the formation and destruction mechanisms as well as the properties of the DIB carrier(s), it is desirable to study the DIB behaviour in a variety of environments. Studies of DIBs in external galaxies, such as the Magellanic Clouds, hold the possibility to constrain the nature of the DIB carriers. Hitherto, DIBs have been observed in only a handful of different galaxies, including the Magellanic Clouds (e.g. Morgan 1987; Ehrenfreund et al. 2002). Heckman & Lehnert (2000) demonstrated the feasibility of detecting DIBs in starburst galaxies, although even with current state of the art instrumentation this remains a difficult feat. The detection of DIBs in spectra of (bright) extra-Galactic supernovae (Rich 1987; Vladilo et al. 1987; D'Odorico et al. 1989; Sollerman et al. 2005) is very valuable but these studies are serendipitous. Until recently the only narrow DIBs observed in the LMC were those detected towards SN 1987A (Vladilo et al. 1987; Vidal-Madjar et al. 1987; and Welty et al. 1999), and R136a, the nuclear region of 30 Dor (Pettini & D'Odorico 1986). Vladilo et al. (1987) detected four DIBs conclusively, and two tentatively. Pettini & D'Odorico (1986) observed two DIBs towards R136a. Searches for broad DIBs (e.g. at 4430 Å) in the Magellanic Clouds have been carried out by Nandy et al. (1982), Houziaux et al. (1985) and Morgan (1987), but these did not result in convincing detections or constraints.

If DIB carriers are indeed carbonaceous molecules in the gas phase, then it is expected that they coexist with atomic and small molecular species in diffuse to dense interstellar clouds, and that they are thus affected by the same local physico-chemical conditions. Many investigations have been undertaken to characterise the Magellanic Cloud interstellar medium; detailed studies of interstellar atomic line profiles include those of André et al. (2004), Welty et al. (1999), Points et al. (1999), Caulet & Newell (1996), Vladilo et al. (1993), Wayte (1990), Songaila et al. (1986), Blades & Meaburn (1980), Blades (1980) and Walborn (1980). These studies provide velocity profiles for various atomic species (e.g. Ca II, Na I and Ti II), and insight in the conditions and kinematics of the interstellar medium probed by these lines of sight.

With the advent of space observatories including the International Ultraviolet Explorer (IUE), the Far Ultraviolet Spectroscopic Explorer (FUSE) and Hubble Space Telescope (HST), new spectral domains, and thus information on additional species, has become available. A large survey of the Magellanic Clouds by Danforth et al. (2002) has revealed a wealth of information on the structure of the LMC ISM and elemental abundances. Tumlinson et al. (2002) and André et al. (2004) also discuss several LMC lines of sight in great detail. The latter is of particular interest as physical parameters are derived for two LMC sightlines that are also included in our data set.

This paper presents a detailed study of the LMC targets that were highlighted by Ehrenfreund et al. (2002). The purpose of this study of diffuse interstellar bands in the Large Magellanic Cloud is to gain further insight into the physico-chemical properties of the DIB carriers (and/or their environment). The LMC, a SBm type galaxy, offers a unique laboratory where the conditions of the interstellar medium are profoundly different from those in the Galaxy. For example, it has an average metallicity one third to one quarter of that of the Milky Way (Dufour 1984), and its gas-to-dust ratio is two to four times larger (e.g. Koornneef 1982; Fitzpatrick 1986; Gordon et al. 2003). These differences have direct influences on the composition of the interstellar gas and dust. To improve our understanding of DIB carriers it is necessary to characterise the DIB behaviour, the local interstellar cloud conditions and the extinction properties of external galaxies such as the LMC. The 30 Dor (or Tarantula) nebular (i.e. H II) region is unique in the Local Group. It is often referred to as a mini-starburst, consisting of a dense cluster of OB stars producing a strong UV field, nebular emission lines, and harbouring dense clouds. We use the (atomic) line profiles of several key interstellar species (Ca II, Na I, Ti II, K I and H I) together with optical and infra red photometry to characterise the dust and gas in the local diffuse LMC medium. This study examines the relationship between the DIBs and atomic lines observed simultaneously in several LMC sightlines.

The targets and observations are discussed in Sect. 2. In Sect. 3 we present the observed DIBs and their respective strengths. Then we first derive the LMC reddening component after removal of the foreground Galactic contribution (Sect. 4.1) and the total-to-selective visual extinction ratio $R{_{\rm V}}$ (Sect. 4.2), which provides insight into the prevailing grain size and UV extinction by dust particles. In order to derive detailed information on the local environmental conditions, interstellar column density line profiles (and total column densities) for several neutral (Na I, K I, H I) and ionised (Ca II, Ti II) gas-phase elements are constructed (Sects. 5.1 and 5.2), from which the ionisation balance (Sect. 5.3) and the gas-to-dust ratio are deduced (Sect. 5.4). In the final part we discuss the behaviour of the DIBs in the context of the chemical and physical conditions of the gas and dust in the observed sightlines (Sect. 6), and explore possible implications for the nature of the DIB carriers (Sect. 7).

  
2 Observations and data reduction procedure

High resolution ( $R \approx 70~000$-100 000) spectra of four moderately reddened LMC targets and two unreddened LMC comparison stars (Fig. 1) were obtained with the Ultraviolet and Visual Echelle Spectrograph (UVES) on the Very Large Telescope (VLT) at the European Southern Observatory, Paranal, Chile. During the nights of 24 to 27 September, 2001 (ESO program 67.C-0281), 16 exposures were obtained, divided over three standard instrument set-ups, with a total integration time of approximately 300 min on each of the six LMC targets. The observations were performed under very good conditions, with a relative humidity of less than 10% and seeing between 0.4 and 0.8 arcsec. Properties of the observed targets, and the corresponding lines of sight are listed in Table 1. Three reddened targets are located in or near the LMC-2 supershell (i.e. near 30 Dor), and three targets (two unreddened, one reddened) in the outskirts of the LMC (Fig. 1).

Figure 1: The upper panel shows the location of the targets on an optical red image of the LMC. The targets observed in and near the 30 Dor star-forming region are shown in the lower panel, which is an enlargement of the rectangle shown in the upper panel. Target details are listed in Table 1. SN 1987A was extensively observed by Vladilo et al. (1987), Vidal-Madjar et al. (1987) and Welty et al. (1999). Image courtesy of Karl Gordon, based on Bothun & Thompson (1988), Kennicutt et al. (1995) and Parker et al. (1998).

The data were taken with either the 390+564 (3400-4500 Å, 4600-5600 Å and 5700-6630 Å) or 346+590 (3050-3850 Å, 4800-5750 Å and 5820-6800 Å) standard UVES settings (Kaufer et al. 2000), where the numbers indicate the central wavelength (in nm) of the blue and red arm, respectively, in order to obtain coverage of the blue and red spectral range accessible with UVES. For 4 targets the K I region was observed in the 437+860 (3800-5000 Å, 6700-8500 Å and 8700-10 300 Å) setting. The data were reduced using the UVES-pipeline (version 1.4.0) context within the MIDAS data reduction package (version 02SEPpl1.2). Selected calibration frames (ThAr arc lamp, bias and flatfield exposures) were given as input to the calibration routine ( PREP/CALDB) and corresponding output frames and tables were used to reduce the science frames with the optimal extraction routines contained in REDUCE/UVES. Typically, about 1200 arclines were identified and fitted with a polynomial for each of the CCDs and set-ups, resulting in a root mean square wavelength error of 0.003 Å in the blue and 0.008 Å in the red. The resolving power as measured from the arclines is $R \ga 60~000$, corresponding to $\la$5 km s^-1 per resolution element. The individual orders were then merged by an average method, where individual orders can be accessed for cross-check purposes.

  
2.1 Correction for telluric and stellar features

Telluric lines pollute the interstellar spectrum, in particular around the 6284 Å DIB and in general longwards of 6800 Å. Telluric correction was applied for these regions only, since it degrades the S/N of the resulting spectrum. The original spectrum was divided by the telluric standard raised to the power $\alpha$, with the initial value of $\alpha$ set to the ratio of airmass of both observations. Stellar lines in the standard spectrum can interfere with those in the target star, and were therefore, where required, removed with a spline fitted to the stellar spectrum before division of the two spectra. To improve the spectrum further it was in some instances necessary to shift the telluric standard spectrum by a small amount, typically less than one wavelength bin. Both $\alpha$ and the wavelength shift were varied iteratively until a minimum was reached for the residual telluric lines.

   

Table 1: Overview of the observed LMC targets. The targets Sk -67 5 and Sk -70 120 are comparison stars used for telluric correction and stellar line identification. Adopted values are corrected for Galactic foreground extinction (see Table 3). The final magnitudes and colour indices are on the photometric system defined by Landolt (1992). The ${\it UBV}$ optical photometry for the remainder of the LMC stars was taken from Misselt et al. (1999) and Gordon et al. (2003).

	LMC
Ska	-69 223	-69 243	-67 2	-68 135	-67 5	-70 120
HDa	38029	38268	270754	269896	268605	270196
RMCa		136	51	129	53	155
RA (J2000)	05 36 55.02	05 38 42.57	04 47 04.45	05 37 48.6	04 50 18.96	05 51 20.85
Dec (J2000)	-69 11 37.3	-69 06 03.2	-67 06 53.1	-68 55 08.0	-67 39 37.9	-70 17 08.7
B (mag)	11.70	9.63	11.304 [1]	11.36	11.22	11.54 [2]
V (mag)	11.59 [3]	9.50 [3]	11.256 $\pm$ 0.023 [1]	11.36 [2]	11.34 [4]	11.59 [1/4]
B-V (mag)	0.11 [3]	0.13 [3]	0.048 [1]	0.00 [2]	-0.12 [4]	-0.06 [1/4,5,6]
$_{\rm , tot}$ (mag)	0.27	0.40	0.21	0.22	0.10	0.10
$_{\rm , LMC}$ (mag)	0.20	0.29	0.12	0.14	0.04	0.02
Sp type (optical)	B1 Ia	O3 If	B1.5 Ia [7]	B0 Ia	B0 Ia [8]	B1.5 Ia
Sp type (uv)	WC4+OB [9]	WN4.5+OB [10]	B2 Ia[7]	ON9.7 Ia+ [11]	O9.7 Ib [8,11,12]	B1 Ia [8,11]
Notes	Edge of 30 Dor	Centre of 30 Dor	Western edge of LMC	North of 30 Dor	Standard	Standard

^a Catalogue designations: Sk = Sanduleak 1970; HD = Henry Draper; RMC = Radcliffe number (Feast et al. 1960). ^b References: ^[1] Gordon et al. (2003); ^[2] Ardeberg et al. (1972); ^[3] Feitzinger & Isserstedt (1983); ^[4] Misselt et al. (1999); ^[5] Danforth et al. (2002); ^[6] Koornneef & Code (1981); ^[7] Rousseau et al. (1978); ^[8] Fitzpatrick (1991); ^[9] Breysacher et al. (1999); ^[10] Massey & Hunter (1998); ^[11] Walborn (1977); ^[12] Walborn & Blades (1997).

 

 

Table 2: Diffuse interstellar bands investigated in this study. Equivalent widths ( EW) and associated statistical errors $\sigma _{\it EW}$ are quoted in mÅ. For non-detected DIBs upper limits are given; EW $_{\rm upper\ limit} = 3 \times \sigma _{\rm continuum} \times {\it FWHM}_{\rm DIB}$, with $\sigma _{\rm continuum}$ the noise on the adjacent continuum, and FWHM $_{\rm DIB}$ the expected full width at half maximum of the respective DIB. The values were derived by subtracting the Milky Way foreground contamination from the line of sight reddening (see Sect. 4.1 and Tables 1 and 3). The "$\times$'' signifies DIBs that were not covered by the spectral setting, and the (B) indicates possible blending with stellar or instrumental features. We have derived upper limits for DIB strengths towards the low reddened target Sk -67 5. Sk -70 120 has been used as the reference star (  = 0.0 mag).

		LMC
		Sk -69 223	Sk -69 243	Sk -67 2	Sk -68 135	Sk -67 5
$_{\rm , LMC}$		0.20	0.29	0.12	0.14	0.04
DIB	$\lambda_{\rm LMC}$	EW ( $\sigma _{\it EW}$)	EW ( $\sigma _{\it EW}$)	EW ( $\sigma _{\it EW}$)	EW ( $\sigma _{\it EW}$)	EW ( $\sigma _{\it EW}$)
4428	4431.95	<180	150 (180)	<247	<200	<200
5705	5710.23	20 (9)	25 (21)	<32	<23	<28 (B)
5780	5785.57	145 (2)	$\times$	$\times$	$\times$	$\times$
5797	5802.21	28 (6)	$\times$	$\times$	$\times$	$\times$
5849	5855.08	<8	11 (6)	10 (5)	5 (5)	<15
6196	6201.57	12 (3)	7 (3)	5 (3)	<7	<7
6203(B)	6208.67	50 (20)	25 (14)	19 (14)	17 (17)	<17
6284	6289.51	240 (21)	335 (47)	150 (29)	30 (30)	<163
6376	6381.71	5 (6)	<28	<23	<20 (B)	<17
6379	6384.96	12 (4)	15 (4)	<10	<10 (B)	<7
6613	6619.51	20 (8)	50 (14)	13 (8)	5 (3) (B)	<13

Figure 2: Normalised spectra of the 5780 and 5797 Å DIBs observed in the line of sight towards Sk -69 223, together with the low reddening standard Sk -70 120. For comparison the corresponding DIB spectra of HD 144217 ($\sigma$-type, blue) and HD 149757 ($\zeta$-type, red) are shown. The shift in wavelength is due to the receding velocity of the LMC.

   
3 Diffuse interstellar bands in the Large Magellanic Cloud

Ehrenfreund et al. (2002) reported in brief the detection of the strong $\lambda$5780, $\lambda$5797 and $\lambda$6284 DIBs towards targets in the Magellanic Clouds. Here we explore the DIB spectra in greater depth and search for "narrow'' ( ${\it FWHM} < 7$ Å) and strong (equivalent width ${\it EW} > 200$ mÅ and/or central depth $A_{\rm c} > 0.07$) DIBs as tabulated by Herbig (1995). Table 2 lists the equivalent width and central wavelength of the ten narrow and one broad DIBs recorded towards the LMC targets. Unfortunately, due to a gap in the spectral format of the used UVES standard setting (346+590), the $\lambda$5780 and $\lambda$5797 DIBs were not covered in several of the spectra. In Fig. 2 we compare the 5780 and 5797 Å DIB profiles observed in the LMC (towards Sk -69 223) with those observed in two typical Galactic lines of sight, HD149757 ($\zeta$ Oph, $\zeta$-type cloud) and HD 144217 ($\beta^1$Sco, $\sigma$-type cloud) (Krelowski & Walker 1987; Cami et al. 1997). The implications of the similarity between Sk -69 223 and HD 144217 and the properties of the respective local environments are discussed in detail in Sect. 6.3. In Fig. 3 we plot the spectral regions centred at the 6203, 6284, 6379 and 6613 Å DIBs for all observed targets.

Figure 3: Normalised and median smoothed spectra centred at the 6203, 6284, 6379 and 6613 Å DIB spectral ranges observed towards Sk -69 223, Sk -69 243, Sk -67 2, Sk -68 135, Sk -67 5 and Sk -70 120. For comparison the corresponding DIB spectra for HD 149757 (red/grey) and HD 144217 (blue/black) are shown at the bottom of each panel. The 6284 Å DIB spectra have been corrected for telluric contamination as described in Sect. 2.1. The vertical dashed lines show the Milky Way ( left) and LMC ( right) rest wavelengths of the observed DIBs. The $\Delta \lambda$ between the two lines corresponds to the $\Delta v \approx 300$ km s-1 between Milky Way and LMC components of the interstellar atomic lines. A) The sharp narrow features near 6375 Å in three of the spectra are due to a CCD defect in one of the two overlapping orders. B) The emission line at 6617 Å in Sk -68 135 is a stellar N II emission line (see e.g. Evans et al. 2004).

Figure 4: The panels of each figure show, from top to bottom, the K I, Na I, Ca II, Ti II and H I apparent column density velocity profiles for the LMC lines of sight towards Sk -69 223 ( top figure) and Sk -69 243 ( bottom figure). The velocity profile is constructed according to the method of Jenkins (1996, Sect. 5#. The H I profile is extracted from the large scale H I (21 cm) survey of the LMC by Staveley-Smith et al. (2003) and Kim et al. (2003). Johansson et al. (1994) list intensities and velocities of CO, CS, HCO+ and HCN lines towards 30 Dor. On the top panel we display the central DIB velocities, including error bars, for some observed DIBs (see also Sects. 2 and 6.2). The Na I and Ca II profiles for Sk -69 243 are in good agreement with the spectra published by Vladilo et al. (1993).

Figure 5: Apparent column density velocity profiles for K I, Na I, Ca II, Ti II and H I towards the LMC targets Sk -67 2 ( top panel) and SK -68 135 ( bottom panel). Construction of the profiles and the derivation of column densities as in Fig. 4. Although similar in reddening the column densities of the atomic species exhibit large differences. Sk -68 135 shows high column densities with respect to Sk -67 2, while its sightline produces slightly less reddening and weaker DIBs. On the top panel we display the central DIB velocities, including error bars, for some observed DIBs (see also Sects. 2 and 6.2).

Figure 6: Apparent column density velocity profiles as in Fig. 4 for the two comparison targets Sk -67 5 ( top) and Sk -70 120 ( bottom). No DIBs were observed for these targets. A tentative weak $\lambda$6203 feature is seen in spectra of Sk -67 5. Both sightlines have weak K I and Na I lines, corresponding to their low reddening. However, the Ca II and Ti II column densities are comparable to those of Sk -67 2. A notable result, not discussed in detail in this work, is the prominent intermediate velocity absorption in the 230-250 km s-1 range seen in Ca II but not in other atoms towards Sk -67 5.

Figure 7: N(Na I)/N(H I) ( a) and N(Na I)/N(Ca II) ( b) at LMC velocities. For a detailed discussion of these ratios we refer to Sects. 5.2 and 5.3. We can distinguish between cold and warm components. A higher N(Na I)/N(H I) ratio indicates a colder environment. A depletion of 7.0 dex is typical for cold dense gas, and 10.0 dex corresponds to warm low density gas (e.g. Hobbs 1974a; Ferlet et al. 1985a,b; Hobbs 1976a). Ca III could be the dominant ionisation stage. A higher N(Na I)/N(Ca II) ratio means more depletion of Ca in cold dense clouds, a lower ratio points to a warm diffuse cloud. Note that both Na I and Ca II are trace ionisation stages.

In order to measure the diffuse band central wavelengths, the observed DIB features in the LMC targets were fitted with high-quality DIB profiles using VAPID (obtained by MAC and PJS using the UCLES instrument on the Anglo-Australian Telescope in June 2004) for the single cloud lines of sight towards $\beta$ Sco ( $R \sim 60~000$, ${\it S/N} \sim 1000$). The benefit of VAPID is that it does a Monte-Carlo error analysis, whereby Poisson noise is generated and added to the datasets being fit, after which the least-squares velocity fitting is re-optimised; this process is then repeated over a hundred times to determine the $\pm$1 sigma errors. These DIB profiles, associated with very narrow atomic line components, provide a good template in the absence of DIB assignments; using Gaussian fitting would not take account of asymmetry present in some DIB profiles. We tested the effect of DIB profile variability on the result and chose the 6613 DIB which shows the most variation in profile in Galactic sightline studies (e.g. Cami et al. 2004). Using the two (extreme) single cloud profiles ($\mu$ Sgr and $\rho$ Oph; cf. the profiles of $\zeta$ Oph and $\sigma$ Sco in Walker et al. 2001) an uncertainty of only 2.5 km s^-1 is introduced in the least-squares velocity due to the difference in fine structure. Therefore we conclude that this method, which takes some account of the DIB profile shape, is preferable to fitting with a Gaussian. It is worth noting that if we had have simply applied a Gaussian fit to the observed profiles this would have resulted in less accurate central velocities, but would still have shown these DIBs to be at LMC velocities of 200 to 300 km s^-1. The template profile rest wavelengths were set using the velocity of the (narrow) K I line such that the least-squares velocity fitted to the LMC sightlines directly yielded the velocity of the DIB carriers with respect to the heliocentric rest frame (Figs. 4 to 6).

For several targets a weak Galactic component is detected; for example, Fig. 2 shows a MW $\lambda$5780 feature at $v = 0 \pm 20$ km s^-1. The equivalent width (EW) was determined by applying a straight line continuum definition and subsequent integration of the DIB profiles. The error in EW is defined as $\sigma ({\it EW}) = 2 \times \sigma_{\rm continuum} \times {\it FWHM}_{\rm DIB}$, taking $2 \times {\it FWHM}_{\rm DIB}$ as the range of integration, with FWHM adopted from Tuairisg et al. (2000) in case of a non-detection, and $\sigma _{\rm continuum}$ the statistical noise per bin of the adjacent (normalised) continuum. The upper limit for the EW of non detected DIBs is EW $_{\rm upper\ limit} = 3 \times \sigma _{\rm continuum} \times {\it FWHM}_{\rm DIB}$. The rms of the (assumed Poisson) noise distribution is fairly constant and lies typically between 0.003 and 0.010 depending on the brightness and exposure of the targets.

In the next two sections we derive various line of sight characteristics and conditions of the LMC interstellar medium. We defer a discussion of the full set of diffuse band data and a comparison between LMC and Galactic sightlines until Sect. 6.

4 Interstellar dust in the Large Magellanic Cloud

  
4.1 Disentangling LMC and MW reddening

The amount of interstellar dust in a line of sight is correlated with the amount of reddening observed for a target. The reddening of a line of sight is defined as the observed colour (B-V) minus the intrinsic colour (B-V)₀ of the observed star. Therefore, besides the B and V photometry (see Table 1), the star's intrinsic colour (B-V)₀ needs to be known. This requires an accurate determination of the spectral type of the observed star. Fitzpatrick (1991) published optical stellar spectra (3950 to 4750 Å) of the four OB supergiants in our dataset. A comparison between the new and old spectroscopic data shows excellent agreement and we therefore adopt the optical spectral classifications from Fitzpatrick (1991) and the corresponding (B-V)₀. Previous studies showed that bright LMC OB supergiants have (B-V)₀ slightly redder than expected from MW studies (Fitzpatrick & Garmany 1990; Fitzpatrick 1988). The two other targets, Sk -69 223 and Sk -69 243 are reported to be Wolf-Rayet stars of type WC4 and WN4.5, respectively. A spectrum from 3900 to 4750 Å for Sk -69 243 was previously published by Parker (1993). Our spectra of this region are identical. Bartzakos et al. (2001) obtained an intermediate resolution spectrum from 3600-6100 Å for Sk -69 223 (Brey 67) which shows both absorption and emission lines. These authors suggest that Sk -69 223 is in fact a visual binary of type WC4+OB. Inspection of our observation of Sk -69 223 in the spectral range 3950 to 4750 Å and the subsequent comparison to the spectral atlases of LMC supergiants by Fitzpatrick & Garmany (1990) and Walborn & Blades (1997) implies that this target is of type B1 Ia, i.e. it has a stellar spectrum similar to that of Sk -70 120. Surprisingly, we do not observe the previously reported strong stellar C IV emission features at 4680 and 5800 Å from which the WR status was derived. Subsequent inspection of the VLT acquisition images shows two resolved point sources at the position of Sk -69 223, separated by about 2 arcsec, with the slit superposed on the brightest component. The brighter component must therefore be the B1 supergiant, and we suspect that the fainter is in fact the WC star. The adopted intrinsic colours are listed in Table 3.

   

Table 3: Colour and extinction characteristics for the LMC lines of sight. The B and V photometric data were combined with intrinsic colours for LMC supergiants (Fitzpatrick 1988) to obtain the total for the line of sight towards the LMC targets. To derive the reddening within the LMC ( $_{\rm , LMC}$) the combined foreground contribution of both the Milky Way (MW) and intermediate velocity clouds (VC) were subtracted. All values are in magnitudes. Fitzpatrick & Savage (1984) derive $_{\rm , total} = 0.34$ mag, and $_{\rm , LMC} = 0.27$ mag for Sk -69 243, consistent with the value derived below. Smith et al. (1990) derive $_{\rm , total} = 0.39$ and 0.41 mag for Sk -69 223 and Sk -69 243, respectively.

		Sk -69 223	Sk -69 243	Sk -67 2	Sk -68 135	Sk -67 5	Sk -70 120
Sp type (UV)		WC4+OB	WN4.5+OB	B2 Ia	ON9.7 Ia	O9.7 Ib	B1 Ia
Sp type (optical)a		B1 Ia	O3 If	B1.5 Ia	B0 Ia	B0 Ia	B1.5 Ia
B-V ($\pm$0.01)		0.11	0.13	0.048	0.00	-0.12	-0.06
(B-V)0a ($\pm$0.02)		-0.16	-0.27	-0.16	-0.22	-0.22	-0.16
Reddening:
$_{\rm , total}$ (E02)		0.42	0.30	0.35	0.27	-	0.06
$_{\rm , total}$b ($\pm$0.03)		0.27	0.40	0.21	0.22	0.10	0.10
$_{\rm , FG}$c ($\pm$0.02)		0.07	0.14	0.11	0.09	0.04	0.09
$_{\rm , LMC}$c ($\pm$0.03)		0.20	0.26	0.10	0.13	0.06	0.01
$_{\rm , LMC}$d ($\pm$0.03)		0.19	0.32	0.13	0.14	0.02	0.02
Adopted
$_{\rm , LMC}$		0.20	0.29	0.12	0.14	0.04	0.02
$\sigma$		0.06	0.04	0.04	0.02	0.03	-

^a Spectral types from Table 1. (B-V)₀ adopted from Fitzpatrick (1988) for LMC supergiants of corresponding optical spectral type. Intrinsic colour for WR/WN/WC stars from Smith et al. (1990): (B-V) $_0 = -0.27 \pm 0.05$. ^b

$_{\rm , total}$ = (B-V) $_{\rm observed} - (B-V)_0$. ^c 

$_{\rm , LMC}$ = 

$_{\rm , total}$ -

$_{\rm , FG}$. The foreground reddening

$_{\rm , FG}$ (=MW + VC reddening) towards the LMC lines of sight was estimated by applying the relation N(Na I) =  $1.7 \times 10^{14}$

^1.8 (Hobbs 1974b), to the observed Na I column densities. ^d

$_{\rm , LMC}$ = 

$_{\rm , total}$ -

$_{\rm , FG}$, with

$_{\rm , FG}$ = 

$_{\rm , MW}$ + 

$_{\rm , VC} \approx 0.08$ mag.

$_{\rm , MW} \sim 0.07$ mag, estimated from the Galactic extinction map by Drimmel et al. (2003),

$_{\rm , VC} \sim 0.01$ mag, derived via N(Na I). The foreground reddening map based on H I by Staveley-Smith gives a similar value of

$_{\rm , FG} = 0.08$ mag.

In addition, before a comparison between DIB results and LMC reddening can be made, an estimate of the contamination to the total observed by the foreground Milky Way (MW) material is required. Brunet et al. (1975) derived a reddening of 0.07 mag caused by the MW foreground towards the LMC. Later, a study of the MW foreground extinction by Schwering & Israel (1991) showed variations of 0.06 to 0.17 mag on scales less than 9 $^{\prime\prime}$. From ${\it UBV}$ photometry of Galactic foreground stars Oestreicher et al. (1995) derived a Galactic foreground map with a resolution of 10 $^{\prime\prime}$. This map shows foreground values from 0.00 to 0.15 mag, with an average of 0.02 mag. We first estimate the foreground (FG) contribution by applying the relationship between MW gas and dust to the observed column density of Na I and K I at velocities v < 150 km s^-1 (see Table 5). This relationship (with large scatter) is given by Hobbs (1974a) as N(Na I) = $1.7 \times 10^{14}$ ^1.8 and N(K I) = $6.4\times 10^{12}$ ^2.0 cm^-2. The atomic interstellar line profiles are discussed in more detail in Sect. 5, where the column densities for the different atomic species due to the foreground absorption and the LMC are presented. For the LMC targets in this study the $_{\rm , FG}$ values range from 0.02 to 0.11 mag (Table 3). Sembach et al. (1993) give a slightly different relation, but the results are similar: = 0.01-0.10 mag. These values are consistent with the Galactic extinction as derived by Drimmel et al. (2003) in the direction of the LMC, as well as with the foreground reddening map derived from H I observations by Staveley-Smith et al. (2003), i.e.  = 0.06-0.08 mag. In Table 3 both foreground estimates (Na I and reddening map) are subtracted from the observed total reddening, yielding two estimates for the intrinsic LMC reddening. The final adopted LMC reddening for each line of sight is obtained by averaging the results.

In Ehrenfreund et al. (2002) we reported our first results on the DIBs in the Magellanic Clouds. In this paper we have taken a more detailed approach, using different methods, to disentangle the Galactic foreground extinction and the LMC extinction from the total observed extinction. Also, for several lines of sight more accurate photometry has become available thus altering the observed colours. Together this has resulted in values that are (in most cases) significantly lower than reported previously. For example, for Sk -67 2 the previously listed was 0.35 mag, while the extinction curve measured by Gordon et al. (2003) and Cartledge et al. (2005) yielded values of $0.15\pm0.03$ mag and $0.18\pm0.03$ mag, respectively. Our updated estimate of the LMC reddening towards Sk -67 2,  =  $0.14\pm0.02$ mag, is now in much better agreement.

  

Table 4: $R{_{\rm V}}$ values derived from optical and infrared photometry based on three different methods. The one but last column lists previously reported values for $R{_{\rm V}}$. In Col. 2 we list the comparison stars (or spectral type) adopted to compute $R{_{\rm V}}$ for the targets in Col. 1 as discussed in the main text. Together with the reddening (Col. 3) three methods were used to derive $R{_{\rm V}}$ (Cols. 5-7). The average $R{_{\rm V}}$ is given in Col. 8, and a literature value is given in Col. 9 when available. The last Col. 10 gives the spectral type of the adopted comparison target or the foreground reddening based on the Galactic extinction curve ( $R_{\rm V} = 3.1$) that is subtracted from the constructed "total'' extinction curve.

$${\begin{tabular}{lllllllrlll}\hline\hline & & & \multicolumn... ...25 & 4.29 & 4.26 (0.04) & & & B0~Ia \\ \hline \end{tabular} }$$

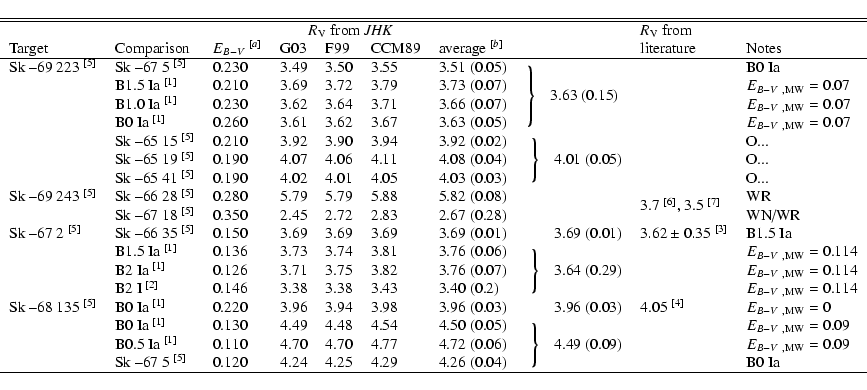
References: Intrinsic infrared colours from: ^[1] Wegner (1994); ^[2] Johnson et al. (1966). ^[3] Gordon et al. (2003); ^[4] Morgan & Nandy (1982); ^[5] 2MASS (Cutri et al. 2003); ^[6] Clayton et al. (1983); ^[7] Savage & Fitzpatrick (1984).
^[a] Colour excess derived by adopting intrinsic colours for supergiants from Wegner (1994), Schmidt-Kaler (1982), Johnson et al. (1966); ^[b] Errors in average $R{_{\rm V}}$ column are based on sigma from average of the methods G03 (Gordon et al. 2003), F99 (Fitzpatrick 1999) and CCM89 (Cardelli et al. 1989), plus the typical error on $R{_{\rm V}}$ resulting from a 0.5 spectral type mismatch (assuming same luminosity class).

  
4.2 Ratio of total to selective visual extinction ( $R{_{\rm V}}$) and the IR to UV extinction curve

The wavelength dependent dust extinction properties of the investigated lines of sight can be used to characterise the local ISM conditions. It is possible to derive the total-to-selective visual extinction ratio $R{_{\rm V}}$ from the infra red part of the extinction curve (e.g. Massa & Fitzpatrick 2003; Fitzpatrick 1999). From a single $R{_{\rm V}}$ value information can be inferred on the whole extinction curve from the infra-red to the far ultra-violet. However, it is known that the extinction curve derived from IR photometry underestimates the real far UV extinction observed in LMC lines of sight (Misselt et al. 1999; Gordon et al. 2003). The $R{_{\rm V}}$ value can therefore only be used to describe the relative contribution of large grains to the total extinction, and not so well that of the small grains that cause the far UV rise. In effect this suggests that the LMC extinction curves need a different $R{_{\rm V}}$ parametrisation.

In order to investigate the accuracy of the derived $R{_{\rm V}}$ value, we have used three different methods (Gordon et al. 2003; Fitzpatrick 1999; and Cardelli et al. 1989). All of these methods rely on the invariance of the ${\it RIJHK}$ range of the extinction curve. In deriving $R{_{\rm V}}$ the critical step is the determination of the colour excess. To correct the observed colours either an unreddened comparison star or the star's intrinsic colour is needed. In either case, it is important to know accurately the stellar surface temperature and gravity, i.e. the spectral type and luminosity class, of the target star and, if applicable, of the comparison star. In choosing an unreddened LMC comparison star the foreground Milky Way reddening is assumed to cancel out satisfactorily. Alternatively, when using intrinsic colours, it is necessary to subtract the foreground average Galactic extinction curve ( $R_{\rm V} = 3.1$), corresponding to $_{\rm , FG}$ (Table 3), from the derived extinction curve. The choices adopted for comparison, either unreddened stars or intrinsic colours, are given in Table 4. Infrared ${\it JHK}$ photometry from the 2MASS catalogue (Cutri et al. 2003) was used to obtain colours for the LMC targets and the corresponding unreddened comparison stars (see on-line Table 9 for adopted photometry). The results for $R{_{\rm V}}$ from the above methods and values previously reported are given in Table 4. Error bars can be larger than derived because reported intrinsic colours for OB supergiants can differ by up to 0.2 mag in (K-V). In Sect. 6 we show that these results do not reveal any dependence between DIB strength and $R{_{\rm V}}$ as is inferred for Galactic lines of sight by Herbig (1995).

Fitzpatrick & Savage (1984) conclude that the extinction curve observed towards 30 Dor is caused by a combination of Galactic foreground dust (equal to  = 0.06 mag), LMC foreground dust (equal to  = 0.11 mag) and 30 Dor "nebular'' dust ( = 0.17 mag). The LMC foreground component shows a strong far-UV non-linear rise, much like that observed toward Sk -67 2, while the nebular component resembles that observed for Orion stars, i.e. it shows a weak far-UV non-linear rise (per unit reddening, with respect to the average Galactic curve). Clayton et al. (1983) determine $R_{\rm V} = 3.7$ for 30 Dor. The UV extinction curve ( $R_{\rm V} = 3.62 \pm 0.35$) has also been measured for Sk -67 2 (Gordon et al. 2003) and it shows a steep, strong far-UV non-linear rise. Savage & Fitzpatrick (1984) and Fitzpatrick & Savage (1984) construct an extinction curve for the pair Sk -68 135 and Sk -67 5. This curve shows a strong far UV non-linear rise, similar to that of Sk -67 2. Fitzpatrick & Savage (1984) measured a 2200 Å bump depth (with respect to interpolated continuum) for Sk -69 243 that is twice as deep as that for Sk -68 135, which is in turn seventeen times deeper than that for Sk -67 5. The observed steep far-UV extinction is indicative of the presence of smaller particles. However, the relatively large $R{_{\rm V}}$ of 3.6 to 4.1 for these LMC sightlines, with respect to the Galactic average, $R_{\rm V} = 3.1$, points toward a LMC dust particle size distribution skewed toward larger grains. Together with the atomic data (Sect. 5) the dust extinction properties discussed above are important in characterising the composition and conditions of the local diffuse LMC ISM (e.g. the gas-to-dust ratio; Sect. 5.4) that affect the behaviour of the DIB carriers (Sect. 6).

  
5 Interstellar gas in the Large Magellanic Cloud

A useful step to gain insight into the structure and conditions of the LMC interstellar medium is to examine the interstellar line profiles produced by atomic transitions of Ti II, Ca II, Na I, K I and H I. First we discuss the conversion of the observed spectral absorption line profile to a velocity profile of the corresponding column density. From these so-called column density profiles the column density of individual components is derived by a Gaussian profile decomposition.

  
5.1 Apparent column density profiles

We chose to adopt the apparent column density method (Sembach et al. 1993; Savage & Sembach 1991) to study the gas column density velocity profiles. In this approach the column density of an atomic species is deduced according to the apparent optical depth method as described by Jenkins (1996). The most outstanding characteristic of this method is its ability to reveal unresolved saturated structure in an absorption feature. There is a vast amount of unresolved saturated structure in the strong Na I D lines observed towards the LMC targets which makes direct Voigt profile modelling difficult. The inference is that there are many cold, narrow, strong absorption components in the LMC gas whose optical depths could, from observations of a single transition, only be accurately determined using a spectroscopic resolving power approaching infinity. The presence of these clouds is revealed in moderate resolution spectra by taking the ratio of apparent optical depths of two lines with a significantly different value of $f\lambda^2$, where f is the oscillator strength and $\lambda$ is the wavelength of the transition (Morton 2003). In velocity space, unresolved saturated structure is located at velocities for which the ratio of apparent optical depths is different from the ratio of $f\lambda^2$ for the two transitions. A correction to the apparent optical depth is derived at each point in velocity space, such that an accurate estimate of the column density profile (per unit velocity) is obtained. This method is much more accurate than a traditional integrated doublet ratio or curve of growth analysis, as shown by Jenkins (1996). Where the Na I column density is very high, it is possible to use the (relatively unsaturated) Na I (UV) line at 3303.4 Å to determine an accurate Na I optical depth profile without the need for apparent optical depth correction. Due to instrumental smearing, a reconstructed optical depth profile can never give an exact representation of the column density velocity profile as the reconstructed profile will show peaks accurate only to within the Gaussian range of the instrumental point spread function. Column density velocity profiles of the interstellar atomic lines (Ti II, Ca II, Na I, K I) towards the six LMC targets are shown in Figs. 4-6, where Fig. 6 includes the data recorded towards the two standards. Optical depth reconstruction was performed for the Na I and Ca II column density profiles (using the two D lines and the H and K lines respectively), but not for Ti II (3384 Å) or K I (7699 Å), whose absorption lines were sufficiently optically thin that the effects of instrumental smearing are expected to have caused negligible degradation of their optical depth profiles.

   

Table 5: Total column density of Na I, K I, Ca II, Ti II and H I (for the Milky Way (MW), intervening high velocity clouds (VC) and Large Magellanic Cloud (LMC) components) derived from fitting the profiles with the splot task in IRAF. The column density of the individual components of the interstellar atomic line profile (as shown in Figs. 4 and 6) is given in Tables 11 to 15 (on-line only). For Sk -67 2 and Sk -68 135 the Na I D doublet is saturated and we used the Na I UV line at 3302 Å instead. The error in column density log N is about 0.02 to 0.05 dex for K I, Ca II, Ti II and about 0.03 and 0.08 dex for Na I D and Na I (UV), respectively. The apparent optical depth method picks up more unresolved structure and therefore gives slightly higher values of N than other methods (like Gaussian profile fitting). Nevertheless, the obtained column densities for Ca II and Na I (from 3302.6 Å line) agree well, within the error bars, with preliminary results obtained by Welty (private communication) for the targets Sk -69 243, Sk -68 135 and Sk -67 5.

	Sk -69 223	Sk -69 243	Sk -67 2	Sk -68 135	Sk -67 5 (STD)	Sk -70 120 (STD)
$_{\rm , LMC}$ (mag)	0.20	0.29	0.12	0.14	0.04	0.02
log N (cm-2)
LMC: ${\bf 200} < \vec{v} < {\bf 330}$ km s-1
Na I	12.59	12.84	13.49	13.25	12.49	11.30
K I	11.03b	11.24	11.65	11.51	11.09	9.70b
Ca II	12.68	12.88	12.32	12.68	12.26	12.59
Ti II	12.77	12.76	12.16	12.73	12.30	12.63
N (21 cm)a	21.58	21.60	21.31	21.55	21.21	21.02
H Ia	21.46	21.47	21.18	21.42	21.08	20.89
			21.003,4	21.441	20.891
H2		$\sim$191		$19.87\pm0.07$1	$19.44\pm0.05$1,2
H $_{\rm tot}$				21.502	21.492
Milky Way: $\vec{v} < {\bf 30}$ km s-1
Na I	12.77c	12.99c	12.44	12.26	11.80	12.01
Ca II	12.23	12.05	12.09	12.05	12.15	11.96
Ti II	12.05	11.97	12.01	11.98	11.98	12.15
Intermediate: ${\bf 30} < \vec{v} < {\bf 200}$ km s-1
Na I	-	11.48	10.89	10.75	10.74	11.12
Ca II	11.93	11.77	11.50	12.11	11.45	11.28
Ti II	-	-	11.09	11.33	-	-

References:
¹ Tumlinson et al. (2002); ² André et al. (2004); ³ Cartledge et al. (2005); ⁴ Gordon et al. (2003).
Notes: ^a LMC 21 cm column density from H I spectral line profiles provided by Staveley-Smith (Kim et al. 2003; Staveley-Smith et al. 2003). This is converted to N(H I) via N(H I) = ( $0.75\pm0.35$) $\times$ N(21 cm). For these sightlines this results in typical log N(H I) errors of +0.17 and -0.27 dex; ^b no K I data are available. K I is derived from the relation with Na I (Welty et al. 2001); ^c due to the large amount of unresolved structure in the MW gas the doublet optical depth correction method is unreliable for these targets. Using information contained in the unsaturated Na I 3303 Å line (low quality) we modelled the MW Na I lines with VAPID, including a Monte-Carlo error analysis.

  
5.2 Column density of interstellar atomic species: Magellanic Clouds, high velocity clouds and the Milky Way

The total atomic column density can be obtained by numerical integration over the full column density profile (Table 5), or by summation over the area of functions fitted to the component clouds that represent the profile. The column density profiles can be decomposed into a set of Gaussian components, for which parameters were derived using the SPLOT deblend command in IRAF. The $\chi^2$ of the fit was optimised using a minimum number of components, i.e. new components were added until the fit rms roughly matched that in the continuum of the observed spectrum. The discrete fit components may not necessarily represent individual clouds, but perhaps "cloud systems''. Fitting of individual clouds is very difficult due to the limited spectral resolution and S/N. Due to the presence of unresolved structure, particularly in the Na I profiles, we obtain slightly higher column densities than previously quoted in the literature (see also Table 5). Unresolved saturated structure in the absorption spectra does not strongly affect the integrated Ti II, Ca II and K I column densities due to the low saturation in these lines. The Poisson noise of the data introduces statistical errors of 5 to 10% ($\sim$0.02 to $\sim$0.05 dex) on the integrated column densities. For Na I D the error bars are larger, up to 20% ($\sim$0.08 dex), due to significant line saturation. The error bars are reduced to 0.03 dex when the Na I (UV) line is used instead. The use of the apparent optical depth method and simultaneous doublet correction (Jenkins 1996) is appropriate, and certainly more accurate than profile fitting, for the achieved resolution of these data.

Tables 11 to 15 (on-line only) give the velocities, column densities and Gaussian widths for the individual components discerned in each of the six targets. Neutral hydrogen 21 cm profiles (Kim et al. 2003; Staveley-Smith et al. 2003) are shown in the bottom panels of Figs. 4-6.

When comparing the 21 cm neutral hydrogen velocity profile with that of the other atomic species it should be noted that the H I material can, in principle, be situated both in front or behind the observed star; therefore, strictly speaking, only upper limits can be inferred. The velocity integrated LMC 21 cm hydrogen column density from H I is converted to N(H I) via N(H I) = ( $0.75\pm0.35$) $\times$ N(21 cm). Tumlinson et al. (2002) obtained this relationship by calibrating the 21 cm hydrogen emission measurement to H I column densities derived from Ly$\alpha$ absorption profiles. This relation provides a conservative correction for the possible apparent presence of additional neutral hydrogen in this velocity range. In addition, since the H I and, for example, the Ti II profiles have very similar structures we will assume henceforth that, for the sightlines considered in this work, indeed most (if not all) of the H I gas is associated with the absorbing material, and that therefore the corrected N(H I) column density is a good approximation of the true H I column density in the line of sight. Further support of this assumption is given by the good agreement between N(H I) derived from H(21cm) and from Ly$\alpha$ (Gordon et al. 2003) for Sk -67 2.

 

 

Table 6: Atomic column density line ratios, titanium depletion level and electron densities for the LMC sightlines. Column density ratios are calculated for the total integrated LMC profiles (from 200 to 300 km s^-1). n_e is computed via Eq. (1) in Sect. 5.3, and for the titanium depletion (log $\delta _{\rm Ti}$) a logarithmic Ti II metallicity of 0.3 dex less than the solar abundance is assumed.

	Sk -69 223	Sk -69 243	Sk -67 2	Sk -68 135	Sk -67 5 (STD)	Sk -70 120 (STD)
$_{\rm , LMC}$ (mag)	0.20	0.29	0.12	0.14	0.04	0.02
Ca II/Ti II	0.78	1.23	1.45	0.85	0.89	0.91
Na I/K I	37	40	71	55	25	37
Na I/Ca II	0.85	0.98	14.8	3.8	1.7	$\sim$0.05
Na I/H I ( $\cdot 10^{-9}$)	1.1	2.4	19.5	6.5	2.6	<0.12
Ca II/H I ( $\cdot 10^{-9}$)	1.6	2.4	1.3	1.7	1.5	5.0
Ti II/H I ( $\cdot 10^{-9}$)	2.0	2.0	0.9	2.0	1.7	4.1
log $\delta _{\rm Ti}$	-1.38	-1.40	-1.72	-1.38	-1.47	-0.95
K I/H I ( $\cdot 10^{-9}$)	0.04	0.06	0.28	0.12	0.10	0.007
$n_{\rm e}$	0.008	0.015	0.017	0.010	0.009	0.010

The gas-phase atomic material can be roughly associated with one of three locations: (i) the MW ( -40 < v < 80 km s^-1), (ii) the intermediate velocity clouds (IVCs) ( 80 < v < 200 km s^-1) and (iii) the LMC ( 200 < v < 330 km s^-1). As already mentioned in Sect. 4.1, significant differences exist in the distribution of atomic species in the Galactic foreground material detected in sightlines towards the LMC (Fig. 13).

  
5.3 Environmental conditions within the LMC ISM: atomic abundance ratios

Atomic abundance ratios (for total LMC profiles or individual components) can be used to differentiate between warm or cold clouds, neutral or ionised regions, levels of depletion, etc. If the DIB carrier(s) are of molecular nature, each carrier has a characteristic ionisation potential. Molecules can also be depleted onto grains in denser regions or recombine when the electron densities are high. Possible DIB carriers, such as PAHs and fullerenes, show very different electronic absorption spectra according to their charge state. Therefore the ionisation balance of interstellar clouds is an important parameter in defining the local environmental conditions. From the observed atomic column density variations it is in principle possible to infer the dominant ionisation stage of a given species. Only when the atomic line absorption in a given region is sufficiently strong can one obtain reliable line ratios. Although more combinations would be possible, we discuss only those line ratios that are important in adding to our understanding of the local cloud conditions.

N(Ti II)/N(H I):

Ti II traces predominantly the neutral interstellar gas, and thus H I, but unlike H I the line of sight probed by Ti II ends at the target (see also Sect. 5.2). The ratio N(Ti II)/N(H I) sets a lower limit to the gas phase titanium abundance. An indication of the fraction of Ti left in the gas phase after grain formation and processing is given by comparison with the solar system ratio of $8.5 \times 10^{-8}$ (Albert et al. 1993). The titanium depletion with respect to hydrogen, $\delta _{\rm Ti}$, is given in Table 6. The average LMC depletion of $-1.45 \pm 0.10$ dex (for our sample) is typical for Galactic warm diffuse clouds. The exception is Sk -70 120 which has a depletion lower limit two times less than that of the other sources.

N(Na I)/N(H I):

high values are indicative of a strong radiation field that ionises H I. Alternatively, a high N(Na I)/N(H I) ratio could also be due to the formation of molecular hydrogen in dense clouds. However, this is not expected for the diffuse gaseous LMC lines of sight considered here. For our lines of sight this profile ratio is closely related to that of neutral sodium, because sodium has only a few strong narrow components, while neutral hydrogen is more widely and evenly spread in velocity space. The integrated ratios (i.e. taking into account the absolute column densities of both elements) give a measure of the relative strengths of the interstellar UV radiation field along the different lines of sight. From the line profile (lower limit; see Sect. 5.2) ratios in Fig. 7 we conclude that a (relatively) less intense UV field is present in the line of sight towards Sk -69 223 and Sk -69 243, the two sources where the strong and narrow DIBs are found. The strongest 6284 Å DIB, taking into account the difference in reddening, is observed toward Sk -67 2, which has also the highest N(Na I)/N(H I) ratio. This is consistent with the idea that the 6824 Å DIB carrier needs more UV excitation to be observed with greater strength. The general trend is that the narrow DIBs are more abundant in sources with a lower ratio of N(Na I)/N(H I) indicating the destruction / ionisation of the DIB carrier by UV photons (Sect. 7, Fig. 11).

N(Na I)/N(K I):

in contrast to the ratio Na I/H I a high value of Na I/K I indicates a modest UV field. The values of the N(Na I)/N(K I) ratio (Table 6) are consistent with the N(Na I)/N(H I) ratios for all sources just described, except for Sk -67 2. For diffuse clouds N(Na I)/N(K I) $\sim 90$(Hobbs 1974a,1976a,b; Lequeux 1975), although the most recent results show significantly lower ratios (close to the cosmic value of 15) for lower column densities (Kemp et al. 2002), possibly due to a harder radiation field. For the LMC we find ratios of N(Na I)/N(K I) ranging from 37 to 71, consistent with previously obtained column densities for three other LMC targets (Welty et al. 2005, in preparation). These results are supported by the fact that on average the effective UV field is harder in diffuse clouds, i.e. the penetration of UV photons is much deeper than in dense clouds.

N(Ca II)/N(Ti II):

Ti II is the dominant ionisation stage of Ti in H I regions and predominantly samples the warm/neutral inter-cloud gas (Joseph & Jenkins 1991). Both Ti II and Ca II are usually heavily depleted. The ratio N(Ca II)/N(Ti II) in interstellar clouds depends on the ratio of the total gas-phase abundance of Ca and Ti, N(Ca)/N(Ti), and on the ionisation degree for Ca, N(Ca II)/N(Ca). If we assume that variations in N(Ca)/N(Ti) can be neglected (with respect to variations in N(Ca II)/N(Ca), we can write, assuming an ionisation equilibrium, that

$$n_{\rm e} = \frac{\Gamma_{\rm Ca}}{\alpha_{\rm Ca}} \left[ R \frac{N(Ti {\sc II})}{N(Ca {\sc ii})} - 1 \right]^{-1},$$ (1)

with $\Gamma_{\rm Ca}/\alpha_{\rm Ca}$ = 0.1 cm^-3 (Herbig 1968, Jura 1975), and R = 10 (Stokes & Hobbs 1976). The latter study concluded that titanium is less depleted from the interstellar gas than calcium (by a factor of about 4). The observed ratio N(Ca II)/N(Ti II) at LMC line of sight velocities varies between 0.5 and 3, which would give (with Eq. (1)) an electron density $n_{\rm e}$ between 0.05 and 0.005 cm^-3. Note that the meteoritic abundance ratio for Ti/Ca is approximately 0.039. The N(Ca II)/N(Ti II) ratio, which indicates rather similar electron densities, does not seem to correlate with the DIB behaviour (Sect. 7, Fig. 11), although a ratio of unity appears to be preferred.

N(Na I)/N(Ca II):

this ratio is an important indicator of metallicity depletion. The so-called Routly-Spitzer effect (Siluk & Silk 1974; Routly & Spitzer 1952) relates the decrease of the N(Na I)/N(Ca II) ratio to the increase of the peculiar velocity of

the cloud in which the absorption is produced. This decrease results from the disruption (e.g. by shocks) of interstellar grains, and the subsequent release of Ca atoms from grains into the gas phase. The ratio N(Na I)/N(Ca II) is thus an indicator of metal depletion, where variations in this ratio are due to a difference in abundance, rather than to changes in the ionisation balance. A higher ratio indicates more dust grains, and thus more molecules. A low ratio $\sim$0.01 traces the warm diffuse medium (where calcium is not depleted). However, for colder and denser clouds two processes influence this ratio; severe depletion of calcium onto grains and a decreasing UV field, making Ca II the dominant ionisation stage of calcium in the cold medium, with ratios larger than 100 (as for example observed in the Galactic line of sight towards HD 149757, Sect. 6.3). As shown in Fig. 11 and Table 6 the largest amount of calcium in the gas phase (i.e. low ratio) corresponds to the sources showing the strongest DIBs. Depletion of calcium or change of the dominant charge state (i.e. Ca I) would indicate colder and denser regions in the line of sight, which would also affect the behaviour of DIB carrier molecules.

 

 

Table 7: Total-to-selective visual extinction $R{_{\rm V}}$, visual extinction $A_{\rm V}$ and atomic gas-to-dust ratio N(H I)/$A_{\rm V}$for the four reddened LMC lines of sight.

	Sk -69 223	Sk -69 243	Sk -67 2	Sk -68 135
$R{_{\rm V}}$	3.6 or 4.1	3.7	3.6	4.1
$A_{\rm V}$	$0.9\pm0.2$	$1.2\pm0.3$	$0.4\pm0.2$	$0.7\pm0.1$
N(H I)/$A_{\rm V}$	$3.2\pm1.0$	$2.5\pm0.6$	$4.0\pm1.4$	$3.8\pm0.5$
(1021 mag-1 cm-2)

In summary, the atomic line ratios show that (1) under the hypothesis that the relative effective strength of the UV radiation field can be derived from the integrated N(Na I)/N(H I) ratio, lines of sight towards 30 Dor (Sk -69 243 and Sk -69 223) and Sk -67 5 experience a very similar UV field, while the line of sight towards Sk -68 135 is exposed to a stronger UV field (ratio is about a factor 3 higher). The line of sight towards Sk -67 2 (near a small H II region) indicates the strongest effective UV field, with the ratio N(Na I)/N(H I) about a factor of three larger than for Sk -68 135. This is qualitatively consistent with André et al. (2004) who find a UV field strength of 3 and 3000 times the interstellar standard radiation field for Sk -67 5 and Sk -68 135, respectively. (2) The 30 Dor targets (Sk -69 243 and Sk -69 223) have a low N(Na I)/N(Ca II) ratio, indicative of a warm diffuse medium where Ca is not depleted onto grains; this ratio is about 15 times higher for Sk -67 2, indicating a more dusty environment. However, it would be more consistent with the previous result if the UV field is harsh enough to ionise enough Ca II thus resulting in a higher N(Na I)/N(Ca II) ratio. The ratio for Sk -68 135 is in between. (3) The electron density $n_{\rm e} \sim 0.011 \pm 0.008$ cm^-3 and the level of titanium depletion are similar in all sources, which is not an a priori result.

   
LMC gas-to-dust ratio: N(H I)/ $A_{\rm V}$

The gas-to-dust ratio (given as N(H I)/$A_{\rm V}$ or N(H I)/ ) is an indicator of the level of dust self shielding. We use the results for and $R{_{\rm V}}$ (Sects. 4.1 and 4.2) to calculate $A_{\rm V}$ =   $\times$ $R{_{\rm V}}$ (Table 7). We obtain N(H I)/ $A_{\rm V} \approx 3.5 \times 10^{21}$ cm^-2 (see Table 7). The gas-to-dust ratio N(H I)/$A_{\rm V}$ for the LMC and LMC-2 sample of Gordon et al. (2003) is $3.25 \pm 0.28 \times 10^{21}$ cm^-2 and $6.97 \pm 0.67 \times 10^{21}$ cm^-2, respectively, although significant differences between individual lines of sight exist.

Figure 8: K I ( top) and H I ( bottom) column density versus the reddening for a variety of Galactic sightlines and the LMC lines of sight in this work. The top panel shows that the environments that are exposed to a (relatively) strong UV field lie below the average linear regression (based on the Galactic targets), and shielded regions lie above. In the bottom panel the diagonal lines represent different gas-to-dust ratios. The upper three lines show, from top to bottom, the gas to dust ratio N(H I)/ = 19.2, 14.3, and $11.1 \times 10^{21}$ cm-2 mag-1 for the LMC-2 (Gordon et al. 2003), the plotted LMC data (dotted, linear fit) and the average LMC regions (Gordon et al. 2003), respectively. The dotted line (N(H I)/  =  $4.03 \times 10^{21}$) is a fit to the Galactic data and the dashed line the Galactic gas-to-dust ratio ( $4.8 \times 10^{21}$) by Bohlin et al. (1978). This panel shows that the shielded regions, e.g. $\zeta$-type clouds, contain more dust, while the exposed ($\sigma$-type) edge dominated environments contain less dust, and the UV dominated (Orion) sightline even less. The higher gas-to-dust ratio of the LMC is a result of an, on average, stronger/harder UV field and a lower metallicity of the gas phase ISM.

Figure 9: The 5780 Å ( top) and 5797 Å ( bottom) DIB equivalent width versus reddening. Values for the LMC DIBs are for Sk -69 223 from Tables 2, 3 and 5. Milky Way interstellar cloud lines of sight are included to illustrate different types of environment; $\times$ (Galazutdinov et al. 2004), $\square$ (Thorburn et al. 2003), $\circ$ (Herbig 1993), $\blacksquare$ (Chlewicki et al. 1986), + (Kreowski et al. 1999). The 5797 and 5780 Å DIB strengths observed towards Sk -69 223 are consistent with the Galactic relationships (dashed lines).

Figure 10: The 6284 Å ( top) and 6613 Å ( bottom) DIB equivalent width versus reddening. Values for the LMC DIBs are listed in Tables 2 and 3. Milky Way interstellar cloud lines of sight are included to illustrate different types of Galactic environment. The diffuse clouds towards HD 144217 and HD 149757 are typical examples of so-called $\sigma$ and $\zeta$ type clouds, respectively (see main text for details). The weak (W) sightlines are those that show relatively weak DIB features. The lines of sight towards the Orion stars ($\diamond$) probe an H II region (for comparison to the 30 Dor region). No large deviations are found with respect to the Galactic trend.

Our results also show that the gas-to-dust ratio for these LMC lines of sight is about twice that of the MW: N(H I)/ $_{\rm , MW} = 4.8 \times 10^{21}$ cm^-2 or N(H I)/ $A_{\rm V} = 1.55 \times 10^{21}$ cm^-2(Bohlin et al. 1978), N(H I)/ $_{\rm , 30Dor-LMC} = 19.2 \times 10^{21}$ cm^-2 and N(H I)/ $_{\rm , LMC} = 11.1 \times 10^{21}$ cm^-2 (Gordon et al. 2003). In the bottom panel of Fig. 8 the H I column density is plotted as a function of reddening. The dashed and dotted lines represent the different gas-to-dust ratios (N(H I)/ ) for both the MW and the LMC. From the plotted data we derive N(H I)/   $\sim 4.03 \times 10^{21}$ cm^-2, and N(H I)/  $\sim$  $14.3 \times 10^{21}$ cm^-2 for MW and LMC, respectively.

A good correlation with reddening is found for K I, whereas for H I all of the LMC column densities lie above the mean Galactic line (Bohlin et al. 1978), but short of the dotted line that is the predicted H I behaviour if solely determined by a 4:1 Galactic: LMC gas-to-dust ratio and assuming that the grain characteristics are identical in the two galaxies.

In Fig. 11 (panel a) we show the 6284 and 6613 Å DIB strengths as a function of the gas-to-dust ratio. No clear trend can be resolved, though the data seem to suggest a decrease in DIB strength with increasing gas-to-dust ratio. It may be that this effect is simply due to differences in the amount of reddening in the lines of sight. If real, this would imply stronger DIBs for Galactic lines of sight with lower gas-to-dust ratios and provide evidence in support of a relationship between DIB strengths, the UV field and/or metallicity.

  
6 DIB behaviour in the LMC and comparison with the Milky Way

  
6.1 DIBs and reddening (dust)

In general, the DIB strength is known to rise approximately linearly with increasing reddening, i.e. the dust column; however, at high values of scatter/dispersion becomes large (e.g. Wu et al. 1981; Herbig 1993, 1995). Possibly, DIBs correlate better with gas phase neutral or ionised atomic species, as will be discussed in Sect. 6.2. In Fig. 9 the $\lambda$5780 and $\lambda$5797 DIB equivalent widths towards LMC target Sk -69 223 are plotted versus reddening, together with Galactic line-of-sight data. The $\lambda$6284 and $\lambda$6613 DIB strengths are plotted for all LMC targets versus reddening in Fig. 10. Diffuse interstellar clouds that are often used for comparison are the single clouds towards HD 149757 ($\zeta$ Oph; a $\zeta$-type cloud) and HD 144217 ($\beta^1$Sco; a $\sigma$-type cloud). In addition, the lines of sight towards the Orion stars ($\diamond$) probe a highly ionised region, which should, in this respect, represent a reference to the 30 Dor star-forming region. Figures 9 and 10 show that the Sk -69 223 DIB strengths are in line with the corresponding Galactic correlations. The $\lambda$6613 DIB (except for Sk -68 135) is in line with the Galactic relationship between DIB strength and reddening. The $\lambda\lambda$5705, 5850, 6196, 6203, 6379 bands (not shown) are marginally weak with respect to their Galactic counterparts. This result is much more tentative due to the relatively large errors associated with the measured equivalent widths, and the possible blending of a known stellar line with the 6203 Å DIB. The $\lambda$6284 is weaker than expected from the Galactic relation (Fig. 10), and the broad $\lambda$4430 band (not shown) is an extreme case being exceptionally weak (see Table 2) in the LMC for a given amount of reddening.

The 6284 Å DIB towards Sk -67 2 has a strength (per unit reddening) comparable to that of a $\sigma$-type cloud. Towards Sk -69 223 and Sk -69 243 the 6284 Å DIB is not quite that strong, but is still significantly stronger than the 6284 DIB seen towards the $\zeta$ type cloud in the direction of HD 149757 (and also the LMC targets Sk -68 73 and Sk -68 135). A strong UV field is needed to excite the carrier of the 6284 Å DIB, which is the case in an edge dominated $\sigma$ cloud and not in a core dominated $\zeta$ cloud (Krelowski & Walker 1987). For the 6613 Å DIB the difference in strength, if any, between the $\sigma$ and $\zeta$ type clouds is less clear, for both the MW and the LMC lines of sight. The 6284 Å DIB profile in both Sk -69 223 and Sk -69 243 is very similar to the one observed towards HD 144217, while that of Sk -67 2 and Sk -68 135 is more like the one seen towards HD 149757, although these have about three times less reddening in the line of sight, and are exposed to a relatively strong UV field. We will show in Sect. 6.2 that this is consistent with the picture arising from the analysis of the interstellar atomic lines. For Sk -68 135 both the 6284 and 6613 Å DIBs are weakened by a factor 10 compared to Sk -69 243, while the reddening and the UV-bump strength are only a factor 2 smaller. Additionally, because the gas-to-dust ratio is 1.5 times higher, the inferred gas column is roughly similar for both lines of sight. On the other hand, the inferred UV field is stronger ($\times$2), the electron density is lower ($\times$1.5), and the grain disruption rate, i.e. N(Na I)/N(Ca II) (Sect. 5.3), is higher ($\times$4) towards Sk -68 135, possibly resulting in a more efficient destruction (or less efficient formation) of both the 6284 and 6613 Å DIB carriers (although not necessarily by the same mechanism).

The similarity between the line of sight conditions towards Sk -69 223 and HD 144217 is especially evident from the 5780 and 5797 Å DIB profiles (Fig. 2 and Sect. 6.3). The other DIB measurements (Fig. 3) are of insufficient quality to make a similar qualitative assessment.

Figure 11: The $\lambda$6613 and $\lambda$6284 DIB strengths are plotted against four different ratios: gas-to-dust ratio N(H I)/$A_{\rm V}$, Na I/Ca II, Ca II/Ti II, and Na I/K I (see Sect. 5.3). Panel  a) seems to indicate that a lower gas-to-dust ratio (i.e. more like that of the MW) implies stronger DIBs. For high values of Na I/Ca II the DIBs are of weak/intermediate strength (panel  b)), and for values $\leq$1 the DIBs show maximum strength. There are two types of sightlines: either Ca II is undepleted (low ratio) or depleted (high ratio) from the gas phase. As calcium is released from dust grains through disruptive processes (e.g. shocks) this could imply that the diffuse clouds towards the 30 Dor targets are in a more quiescent environment than those towards Sk -67 2 and Sk -68 135. The 6284 and 6613 Å DIBs show a maximum strength for Ca II/Ti II $\sim$1-1.5 (panel  c)). From panel  d) we see that the 6284 and 6613 Å DIBs are strong only when the Na I/K I is high enough. 6284 Å DIB strength for Sk -69 202 from Vladilo et al. (1987), atomic lines from Welty et al. (1999).

Figure 12: The 6284 Å ( top) and 6613 Å ( bottom) DIB strengths as a function of K I column density. The LMC data are obtained from Tables 2 and 4. Galactic lines of sight (from Fig. 10) are included for comparison. The two reddened targets Sk -69 223 and Sk -69 243 show DIBs that are strong with respect to the K I column density, while those for Sk -68 135 and Sk -67 2 are weak with respect to the amount of potassium when compared to the Galactic trend.

 

 

Table 8: Physical properties and conditions of the interstellar medium in the lines of sight towards the LMC target Sk -69 223 (Tables 2, 5-7) and the Galactic targets HD 144217 ($\sigma$-type) and HD 149757 ($\zeta$-type).

	Sk -69 223	HD 144217	HD 149757
(mag)	0.2	0.2	0.3
$R{_{\rm V}}$	3.6 or 4.1	4.0	3.1
$A_{\rm V}$ (mag)	0.8(0.2)	0.8	0.9
5780 DIB (mÅ)	145(2)	160	66
5797 DIB (mÅ)	28(6)	22	27
6284 DIB (mÅ)	240(21)	390	111
6613 DIB (mÅ)	20(8)	40	43
5780/5797	6	8	3
log N(Na I) (cm-2)	12.59	12.94	13.85
log N(K I) (cm-2)	11.03	11.19	11.85
log N(Ca II) (cm-2)	12.68	11.73	11.76
log N(H I) (cm-2)	21.46	21.10	20.73
N(Na I)/N(H I) ($\times$ 1010)	11	16	1318
N(K I)/N(H I) ($\times$ 1010)	0.37	1.23	13.2
N(Na I)/N(Ca II)	0.9	16.2	123
N(H I)/$A_{\rm V}$ ($\times$ 1021)	3.6	1.6	0.6

  
6.2 DIBs and atomic species (gas)

The next step is to explore the link between DIB strength and the column densities of the different neutral and ionised atomic elements investigated in Sect. 5, as well as the relation of the DIBs to the other LMC extinction properties. The 6613 Å DIB central velocity has been shown to closely follow that of the Ca II components in the MW (Sonnentrucker et al. 1999). No such distinct pattern is observed here between the 6613 Å DIB strengths and the Ca II column density. On the other hand, the coincidence of the central peak velocities of the 6613 Å DIB and the strongest Ca II components does agree with this previous finding. The observed central velocities of the 6196, 6203, 6284 and 6613 Å DIBs coincide, within the error bars, with each other and the strong atomic absorption associated with the LMC gas (Figs. 4 to 6). The broad 6284 Å DIB seems to be slightly offset toward lower velocities. For Sk -69 243 there seems to be a real dichotomy between the CO which probes dense material and the DIBs that are believed to probe diffuse material (Fig. 4 top panel of bottom figure). The DIB at 6613 Å has a central velocity corresponding to the higher velocity component in the Na I and K I profiles, while the CO central velocity corresponds with the lower velocity component. The higher velocity component in the Na I and K I profile shows the highest column densities for the warm inter-cloud region tracers Ca II and Ti II. Therefore, the 6613 Å DIB seems to be related to the warm inter-cloud material, confirming the results of Sonnentrucker et al. (1999).

In Fig. 12 we show the 6613 and 6284 Å DIB strengths versus the K I column density for the LMC lines of sight, together with a Galactic sample. For Sk -67 2 and Sk -68 135 the DIB strength is relatively weak with respect to the observed amount of Na I. This is in contrast with the earlier discussion (Fig. 10, Sect. 6.1) that for Sk -67 2 the DIB strength is the strongest observed per unit reddening. In Fig. 11 we plot LMC DIB strengths versus the column density ratios N(Na I)/N(K I), N(Ca II)/N(Ti II) and N(Na I)/N(Ca II) discussed in Sect. 5.3. We also included available data for Sk -69 202/SN 1987A (Vladilo et al. 1987; Welty et al. 1999). No clear relationship becomes apparent between any of these quantities and the DIB strengths. However, as discussed next, these different indicators are useful in characterising the local environmental conditions, and are therefore important tools when comparing different lines of sight.

  
6.3 Sk -69 223: dust, gas and DIBs

In Fig. 2 we compare the 5780 and 5797 Å DIBs observed towards Sk -69 223 with those observed towards the typical $\sigma$ and $\zeta$ type clouds, HD 144217 and HD 149757. In Table 8 we compare various line of sight properties of HD 144217 and HD 149757 with those for Sk -69 223. The similarity of the 5780 and 5797 Å profiles of HD 144217 and Sk -69 223, the similar UV field impact (via N(Na I)/N(H I)), and the large grain distribution (via $R{_{\rm V}}$) imply that either the line of sight physical conditions are comparable or the respective different line of sight conditions result in a very similar local balance of DIB carrier formation and destruction processes.

For the dense and dusty line of sight towards HD 149757 the N(Na I)/N(Ca II) ratio is high because of significant depletion of calcium onto the dust grains. The lower N(Na I)/N(Ca II) ratio of 16 for HD 144217 is typical for quiescent Galactic sightlines. In the LMC this ratio is even more reduced (except for Sk -67 2) which could be due to (1) the lower metallicity and/or (2) the stronger effective UV field. The gas-to-dust ratio for Sk -69 223 is about twice that of HD 144217.

Given the 5780/5797 ratio of $\sim$6, the conditions towards Sk -69 223 seem to correspond to a Galactic $\sigma$-type line of sight. Also, unlike the lines of sight discussed above, it is found that the $\lambda\lambda$5797, 5780, 6196 and 6203 band strengths towards Sk -69 223 all lie within the Galactic target distribution in a plot of equivalent width (EW) versus reddening (see e.g. Figs. 9 and 10). This in turn implies that the DIB equivalent width directly gives the DIB carrier column density. Since the 5780 and 5797 Å DIBs are not weaker in Sk -69 223, assuming the metallicity of the diffuse LMC ISM towards Sk -69 223 is a factor four lower than in the MW (as is generally observed for the LMC). This suggests that, relative to , the abundance of the 5780 Å DIB carrier is not affected by metallicity. In contrast, the 6613 Å DIB is about a factor two weaker, possibly due to the lower metallicity of the LMC ISM.

Figure 13: Apparent MW column density profiles of Ca II, Ti II, Na I and K I.

   
7 Summary and conclusion

With respect to other extra-Galactic interstellar environments the study of the Magellanic Clouds has clear benefits. First, observing does not depend on unpredictable astrophysical events, like supernova explosions. Second, the Magellanic Clouds, our nearest neighbours, are close enough (50 and 60 kpc, respectively) so that most of the OB population stars are bright enough to obtain high quality interstellar absorption spectra with current state of the art instrumentation (e.g. VLT/UVES). The radial velocity ensures also that the LMC interstellar lines and narrow DIBs are clearly separated from those of Galactic origin. Thirdly, the Magellanic Clouds differ in metallicity, with respect to each other and to the Milky Way.

This study has revealed a wealth of information that has been extracted from the echelle spectra covering a very broad spectral range, from the UV to the near infrared. We have studied in detail the diffuse interstellar bands that originate in an extra-Galactic diffuse medium of the LMC. We obtained equivalent widths and central peak wavelengths/velocities for eleven DIBs. In addition, as a function of velocity, we obtained detailed interstellar column density profiles for five key atomic elements.

There appears to be no direct relationship between DIB strength and $R{_{\rm V}}$, the indicator for the dust grain size distribution (Sect. 4.2). The 6613 Å DIB strength is related to reddening similar to the Galactic trend, while the 6284 Å DIB is weakened with respect to the Galactic relationship. The atomic line profiles (Sect. 5) show that the majority of the LMC gas is receding at velocities between 220 and 300 km s^-1. The neutral species show strong narrow components, corresponding to colder denser cloud components, whereas the ionised species are more widely distributed, clearly tracing the warmer diffuse inter-cloud medium. The atomic line ratios (Sect. 5.3) indicate large variations in the UV field that seem to be connected to differences in observed DIB strengths. Other indicators, like electron density and titanium depletion, do not differ among lines of sight, and their impact on the DIB strength variation in the LMC seems to be less relevant. Section 5.4 showed that the gas-to-dust ratio is between four and eight times that of the MW average. Except for the general trend of increasing DIB strength with increasing dust column (Sect. 6.1), there are no clear diagnostics, except those that probe the UV field conditions (i.e. those that are good indicators of the ionisation balance), that characterise the DIB behaviour.

Comparison of the resulting column densities revealed that the most significant difference between different LMC lines of sight is the strength, (or hardness) of the UV field. Other factors like the depletion, the total to selective visual extinction, or the gas-to-dust ratio appear to be less crucial in the formation mechanisms that govern the DIB carrier presence, although they are likely to affect the balance between DIB carrier formation and destruction processes. In order to grasp more fully the effect of the UV field on the DIB carrier, and also the impact of other parameters it is important to study DIBs in a wide variety of interstellar environmental conditions. The most obvious step would be to examine diffuse lines of sight in the Small Magellanic Cloud and other galaxies in the Local Group.

Acknowledgements

The authors thank ESO for the allocated time on the VLT and their support in obtaining the observations. They also wish to thank Dan Welty for providing new results (on atomic line column densities) prior to publication, Karl Gordon for providing the LMC optical image, and Lister Staveley-Smith for the LMC H I line profiles. We are indebted to the referee for constructive comments that have improved the paper. N.L.J.C. is supported by NOVA and PE by VI-NWO (016.023.003). M.A.C. thanks the EPSRC for a research studentship. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. We acknowledge the use of the 2MASS survey. The Australia Telescope Compact Array & Parkes telescope are part of the Australia Telescope which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO.

References

 
• Albert, C. E., Blades, J. C., Morton, D. C., et al. 1993, ApJS, 88, 81
   
• André, M. K., Le Petit, F., Sonnentrucker, P., et al. 2004, A&A, 422, 483
   
• Appenzeller, I. 1972, PASJ, 24, 483
   
• Ardeberg, A., Brunet, J. P., Maurice, E., & Prevot, L. 1972, A&AS, 6, 249
   
• Bartzakos, P., Moffat, A. F. J., & Niemela, V. S. 2001, MNRAS, 324, 18
   
• Blades, J. C. 1980, MNRAS, 190, 33
   
• Blades, J. C., & Meaburn, J. 1980, MNRAS, 190, 59P
   
• Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132
   
• Bothun, G. D., & Thompson, I. B. 1988, AJ, 96, 877
   
• Breysacher, J., Azzopardi, M., & Testor, G. 1999, A&AS, 137, 117
   
• Brunet, J. P., Imbert, N., Martin, N., et al. 1975, A&AS, 21, 109
   
• Cami, J., Sonnentrucker, P., Ehrenfreund, P., & Foing, B. H. 1997, A&A, 326, 822
   
• Cami, J., Salama, F., Jiménez-Vicente, J., Galazutdinov, G. A., & Kreowski, J. 2004, ApJ, 611, L113
   
• Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245
   
• Cartledge, S. I. B., Clayton, G. C., Gordon, K. D., et al. 2005, ArXiv Astrophysics e-prints
   
• Caulet, A., & Newell, R. 1996, ApJ, 465, 205
   
• Chlewicki, G., Van der Zwet, G. P., Van Ijzendoorn, L. J., Greenberg, J. M., & Alvarez, P. P. 1986, ApJ, 305, 455
   
• Clayton, G. C., Martin, P. G., & Thompson, I. 1983, ApJ, 265, 194
   
• Cutri, R. M., Skrutskie, M. F., Van Dyk, S., et al. 2003, VizieR Online Data Catalog, 2246, 0
   
• Danforth, C. W., Howk, J. C., Fullerton, A. W., Blair, W. P., & Sembach, K. R. 2002, ApJS, 139, 81
   
• D'Odorico, S., di Serego Alighieri, S., Pettini, M., et al. 1989, A&A, 215, 21
   
• Drimmel, R., Cabrera-Lavers, A., & López-Corredoira, M. 2003, A&A, 409, 205
   
• Dufour, R. J. 1984, in Structure and Evolution of the Magellanic Clouds, IAU Symp., 108, 353
   
• Ehrenfreund, P., Cami, J., Jiménez-Vicente, J., et al. 2002, ApJ, 576, L117
   
• Evans, C. J., Crowther, P. A., Fullerton, A. W., & Hillier, D. J. 2004, ApJ, 610, 1021
   
• Feast, M. W., Thackeray, A. D., & Wesselink, A. J. 1960, MNRAS, 121, 337
   
• Feitzinger, J. V., & Isserstedt, J. 1983, A&AS, 51, 505
   
• Ferlet, R., Dennefeld, M., & Maurice, E. 1985a, A&A, 152, 151
   
• Ferlet, R., Vidal-Madjar, A., & Gry, C. 1985b, ApJ, 298, 838
   
• Fitzpatrick, E. L. 1986, AJ, 92, 1068
   
• Fitzpatrick, E. L. 1988, ApJ, 335, 703
   
• Fitzpatrick, E. L. 1991, PASP, 103, 1123
   
• Fitzpatrick, E. L. 1999, PASP, 111, 63
   
• Fitzpatrick, E. L., & Garmany, C. D. 1990, ApJ, 363, 119
   
• Fitzpatrick, E. L., & Savage, B. D. 1984, ApJ, 279, 578
   
• Foing, B. H., & Ehrenfreund, P. 1994, Nature, 369, 296
   
• Galazutdinov, G. A., Manicò, G., Pirronello, V., & Kreowski, J. 2004, MNRAS, 355, 169
   
• Gordon, K. D., Clayton, G. C., Misselt, K. A., Landolt, A. U., & Wolff, M. J. 2003, ApJ, 594, 279
   
• Heckman, T. M., & Lehnert, M. D. 2000, ApJ, 537, 690
   
• Herbig, G. H. 1968, Z. Astrophys., 68, 243
   
• Herbig, G. H. 1993, ApJ, 407, 142
   
• Herbig, G. H. 1995, ARA&A, 33, 19
   
• Hobbs, L. M. 1974a, ApJ, 191, 381
   
• Hobbs, L. M. 1974b, ApJ, 191, 395
   
• Hobbs, L. M. 1976a, ApJ, 203, 143
   
• Hobbs, L. M. 1976b, ApJ, 206, L117
   
• Houziaux, L., Nandy, K., & Morgan, D. H. 1985, MNRAS, 215, 5
   
• Isserstedt, J. 1975, A&AS, 19, 259
   
• Jenkins, E. B. 1996, ApJ, 471, 292
   
• Johansson, L. E. B., Olofsson, H., Hjalmarson, A., Gredel, R., & Black, J. H. 1994, A&A, 291, 89
   
• Johnson, H. L., Iriarte, B., Mitchell, R. I., & Wisniewskj, W. Z. 1966, Communications of the Lunar and Planetary Laboratory, 4, 99
   
• Joseph, C. L., & Jenkins, E. B. 1991, ApJ, 368, 201
   
• Jura, M. 1975, ApJ, 200, 415
   
• Kaufer, A., D'Odorico, S., & Kaper, L. 2000, UVES User Manual
   
• Kemp, S. N., Bates, B., Beckman, J. E., et al. 2002, MNRAS, 333, 561
   
• Kennicutt, R. C., Bresolin, F., Bomans, D. J., Bothun, G. D., & Thompson, I. B. 1995, AJ, 109, 594
   
• Kim, S., Staveley-Smith, L., Dopita, M. A., et al. 2003, ApJS, 148, 473
   
• Koornneef, J. 1982, A&A, 107, 247
   
• Koornneef, J., & Code, A. D. 1981, ApJ, 247, 860
   
• Kreowski, J., Ehrenfreund, P., Foing, B. H., et al. 1999, A&A, 347, 235
   
• Krelowski, J., & Walker, G. A. H. 1987, ApJ, 312, 860
   
• Landolt, A. U. 1992, AJ, 104, 340
   
• Leger, A., & Dhendecourt, L. 1985, A&A, 146, 81
   
• Lequeux, J. 1975, A&A, 39, 257
   
• Maier, J., Freivogel, P., Fulara, J., & Lessen, D. 1995, Laboratory Studies of Highly Unsaturated Carbon Chains and the Diffuse Interstellar Bands, ASSL 202: The Diffuse Interstellar Bands, 199
   
• Massa, D., & Fitzpatrick, E. 2003, in Astrophysics of Dust
   
• Massey, P., & Hunter, D. A. 1998, ApJ, 493, 180
   
• Misselt, K. A., Clayton, G. C., & Gordon, K. D. 1999, ApJ, 515, 128
   
• Morgan, D. H. 1987, QJRAS, 28, 328
   
• Morgan, D. H., & Nandy, K. 1982, MNRAS, 199, 979
   
• Morton, D. C. 2003, ApJS, 149, 205
   
• Nandy, K., Morgan, D. H., & Houziaux, L. 1982, Ap&SS, 85, 159
   
• Oestreicher, M. O., Gochermann, J., & Schmidt-Kaler, T. 1995, A&AS, 112, 495
   
• Parker, J. W. 1993, AJ, 106, 560
   
• Parker, J. W., Hill, J. K., Cornett, R. H., et al. 1998, AJ, 116, 180
   
• Pettini, M., & D'Odorico, S. 1986, ApJ, 310, 700
   
• Points, S. D., Chu, Y. H., Kim, S., et al. 1999, ApJ, 518, 298
   
• Rich, R. M. 1987, AJ, 94, 651
   
• Rousseau, J., Martin, N., Prevot, L., et al. 1978, A&AS, 31, 243
   
• Routly, P. M., & Spitzer, L. J. 1952, ApJ, 115, 227
   
• Sanduleak, N. 1970, Contributions from the Cerro Tololo Inter-American Observatory, 89
   
• Savage, B. D., & Fitzpatrick, E. L. 1984, in Structure and Evolution of the Magellanic Clouds, IAU Symp., 108, 255
   
• Savage, B. D., & Sembach, K. R. 1991, ApJ, 379, 245
   
• Schmidt-Kaler, T. 1982, Bulletin d'Information du Centre de Données Stellaires, 23, 2
   
• Schwering, P. B. W., & Israel, F. P. 1991, A&A, 246, 231
   
• Sembach, K. R., Danks, A. C., & Savage, B. D. 1993, A&AS, 100, 107
   
• Siluk, R. S., & Silk, J. 1974, ApJ, 192, 51
   
• Smith, H. A., Beall, J. H., & Swain, M. R. 1990, AJ, 99, 273
   
• Sollerman, J., Cox, N., Mattila, S., et al. 2005, A&A, 429, 559
   
• Songaila, A., Blades, J. C., Hu, E. M., & Cowie, L. L. 1986, ApJ, 303, 198
   
• Sonnentrucker, P., Foing, B. H., Breitfellner, M., & Ehrenfreund, P. 1999, A&A, 346, 936
   
• Staveley-Smith, L., Kim, S., Calabretta, M. R., Haynes, R. F., & Kesteven, M. J. 2003, MNRAS, 339, 87
   
• Stokes, G. M., & Hobbs, L. M. 1976, ApJ, 208, L95
   
• Thorburn, J. A., Hobbs, L. M., McCall, B. J., et al. 2003, ApJ, 584, 339
   
• Tuairisg, S. Ó., Cami, J., Foing, B. H., Sonnentrucker, P., & Ehrenfreund, P. 2000, A&AS, 142, 225
   
• Tumlinson, J., Shull, J. M., Rachford, B. L., et al. 2002, ApJ, 566, 857
   
• Van der Zwet, G. P., & Allamandola, L. J. 1985, A&A, 146, 76
   
• Vidal-Madjar, A., Andreani, P., Cristiani, S., et al. 1987, A&A, 177, L17
   
• Vladilo, G., Crivellari, L., Molaro, P., & Beckman, J. E. 1987, A&A, 182, L59
   
• Vladilo, G., Molaro, P., Monai, S., et al. 1993, A&A, 274, 37
   
• Walborn, N. R. 1977, ApJ, 215, 53
   
• Walborn, N. R. 1980, ApJ, 235, L101
   
• Walborn, N. R., & Blades, J. C. 1997, ApJS, 112, 457
   
• Walker, G. A. H., Webster, A. S., Bohlender, D. A., & Kreowski, J. 2001, ApJ, 561, 272
   
• Wayte, S. R. 1990, ApJ, 355, 473
   
• Wegner, W. 1994, MNRAS, 270, 229
   
• Welty, D. E., Frisch, P. C., Sonneborn, G., & York, D. G. 1999, ApJ, 512, 636
   
• Welty, D. E., Lauroesch, J. T., Blades, J. C., Hobbs, L. M., & York, D. G. 2001, ApJ, 554, L75
   
• Wu, C.-C., York, D. G., & Snow, T. P. 1981, AJ, 86, 755
  

 

  
8 Online Material

   

Table 9: Optical and infrared photometry ( ${\it UBVJHK}$). Values for ${\it JHK}$ are from the 2MASS Point Source Catalogue (Cutri et al. 2003). The invariance of the infrared part of the extinction curve is utilised to compute $R{_{\rm V}}$ (Sect. 4.2). For all adopted methods we need colour excesses which can be derived using intrinsic colours for the corresponding spectral type, or by finding a spectral type match between the reddened and comparison target. Errors are 0.02, 0.02, and 0.04 for V, B-V, and U-B, respectively.

Target		V	B-V	U-B	Source		J	H	K		Source
		(mag)	(mag)	(mag)			(mag)	(mag)	(mag)
reddened stars:
Sk -69 223		11.59	0.11	-0.73	1		11.285 $\pm$ 0.030	11.206 $\pm$ 0.033	11.108 $\pm$ 0.035		5
Sk -69 243		9.50	0.13	-0.75	1		9.428 $\pm$ 0.056	9.354 $\pm$ 0.083	8.927 $\pm$ 0.050		5
Sk -67 2		11.260	0.080	-0.690	4		11.019 $\pm$ 0.023	11.003 $\pm$ 0.024	10.917 $\pm$ 0.019		5
Sk -68 135		11.33	0.03	-0.92	3		11.233 $\pm$ 0.021	11.237 $\pm$ 0.025	11.165 $\pm$ 0.025		5
comparison stars:
Sk -70 120		11.590	-0.060	-0.880	4		11.781 $\pm$ 0.022	11.801 $\pm$ 0.027	11.919 $\pm$ 0.036		5
Sk -67 5		11.340	-0.120	-0.950	4		11.578 $\pm$ 0.022	11.610 $\pm$ 0.024	11.619 $\pm$ 0.021		5
Sk -66 35		11.550	-0.070	-0.880	4		11.732 $\pm$ 0.027	11.725 $\pm$ 0.024	11.700 $\pm$ 0.034		9
Sk -65 15		12.140	-0.100	-0.920	4		12.420 $\pm$ 0.026	12.415 $\pm$ 0.024	12.420 $\pm$ 0.025		5
Sk -65 19		12.050	-0.080	-0.960	1		12.274 $\pm$ 0.024	12.308 $\pm$ 0.025	12.290 $\pm$ 0.026		5
Sk -65 41		12.820	-0.080	-0.810	1		13.049 $\pm$ 0.028	13.052 $\pm$ 0.030	13.054 $\pm$ 0.033		5
Sk -66 28		10.810	-0.150	-	1		11.816 $\pm$ 0.047	12.044 $\pm$ 0.058	11.765 $\pm$ 0.045		5
Sk -67 18		12.020	-0.220	-1.020	1		12.482 $\pm$ 0.029	12.553 $\pm$ 0.034	12.601 $\pm$ 0.039		5

[1] Feitzinger & Isserstedt (1983); [2] Isserstedt (1975); [3] Appenzeller (1972); [4] Gordon et al. (2003); [5] 2MASS (Cutri et al. 2003).

 

 

Table 10: Local standard of rest (LSR) velocity v (km s^-1), column density N (cm^-2) and Gaussian width g (km s^-1) for the atomic species Na I D, Ca II, Ti II, K I and H I observed toward Sk -69 223. * = not optical depth corrected due to erroneous data. The bottom two lines give the total LMC column densities for the respective atoms.

Sk -69 223
Na I D				Ca II			Ti II			H I
v	N	g		v	N	g	v	N	g	v	N	g
km s-1	1010 cm-2	km s-1		km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1019 cm-2	km s-1
-13.4	+2.57	5.4	*	-14.1	+41.5	6.4
-5.4	+45.5	5.7	*	-7.2	+36.2	5.6	-7.7	+47.6	8.3
				-2.8	+20.3	6.2	-1.0	+8.39	3.7
4.0	+41.4	8.9	*	3.1	+34.0	7.2	4.6	+56.7	7.9
9.9	+38.2	5.1	*	10.2	+36.1	5.1
25.0	+3.72	5.7	*
				42.4	+16.9	7.4	40.9	+8.87	6.3
				64.7	+10.7	9.5	61.9	+4.89	4.4
				109.4	+20.2	8.3
				161.8	+18.4	13.1
				220.6	+114.0	118.3	206.6	+8.74	7.7
239.8	+21.8	12.5								236.1	+38.5	10.2
242.2	+23.8	4.9		243.8	+75.9	17.1
247.2	+11.4	4.3		243.4	+10.2	4.8	250.9	+74.7	16.7	246.5	+56.3	10.0
256.2	+17.5	6.0		257.2	+27.1	6.0	258.0	+31.2	4.6	258.0	+104.0	10.0
267.6	+14.2	3.3					263.9	+19.5	4.8
271.1	+24.4	2.3
271.9	+145.0	5.2		274.2	+145.	9.8				273.2	+92.8	9.2
275.9	+117.0	12.2					276.1	+226.0	10.8	280.3	+35.9	7.2
283.5	+14.0	3.5		284.8	+76.3	9.0	286.3	+175.0	9.0	287.9	+28.3	9.0
				298.5	+8.12	4.6	298.2	+49.1	7.9	297.2	+24.0	18.2
N	+389.0				+456.0			+584.0			+380.0
log(N)	12.59				12.66			12.77			21.58

 

 

Table 11: Local standard of rest (LSR) velocity v (km s^-1), column density N (cm^-2) and Gaussian width g (km s^-1) for the atomic species Na I D, Ca II, Ti II, K I and H I observed toward Sk -69 243. * = Not optical depth corrected due to problematic data. The bottom two lines give the total LMC column densities for the respective atoms.

Sk -69 243
Na I D				Ca II			Ti II			K I			H I
v	N	g		v	N	g	v	N	g	v	N	g	v	N	g
km s-1	1010 cm-2	km s-1		km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1019 cm-2	km s-1
				-6.5	+36.3	14.7
0.8	+15.2	7.2	*	1.4	+22.5	6.6	0.9	+77.6	11.2
6.0	+34.2	4.9	*	6.8	+29.2	8.1	6.0	-59.3	9.9
11.0	+100.0	4.8	*				8.9	+75.5	6.6
14.5	+5.92	4.3	*	16.7	+11.6	5.7
				24.3	+13.4	3.4
				48.8	+43.8	27.1
				85.6	+2.75	3.3
				104.5	+21.2	4.6
				127.3	+8.95	7.9
				184.7	+50.4	32.4
				218.6	+31.3	13.2
228.6	+20.5	11.8		228.0	+36.9	8.2							226.5	+37.5	37.5
240.2	+6.80	4.8		236.7	+25.0	3.8	233.8	+62.7	34.4
247.8	+12.5	3.4		243.1	+27.4	7.4							244.2	+12.5	9.3
249.6	+28.6	2.2		250.4	+66.4	5.9							249.1	+107.0	24.5
252.5	+173.0	5.0		256.6	+23.8	4.2	254.2	+56.9	10.1	251.7	+8.85	4.8
264.3	+53.0	9.3		264.3	+57.7	6.7				268.5	+1.39	2.4
272.4	+308.0	7.0		273.1	+210.0	8.5				272.9	+6.44	4.4	272.4	+80.5	19.5
274.1	+19.5	3.3					275.7	+280.0	18.6				274.8	+157.0	32.6
278.7	+43.7	7.8		281.6	+47.3	5.4
292.3	+34.0	6.4		289.7	+110.0	6.6	285.1	+115.0	15.7
				295.7	+59.7	9.1	295.8	+36.1	6.0
				303.2	+15.9	4.0	303.8	+26.1	7.2
N	+699.0				+711.0			+576.0			+16.7			+395.0
log(N)	12.84				12.85			12.76			11.22			21.60

 

 

Table 12: Local standard of rest (LSR) velocity v (km s^-1), column density N (cm^-2) and Gaussian width g (km s^-1) for the atomic species Na I (D and UV), Ca II, Ti II and H I observed toward Sk -67 2. The bottom two lines give the total LMC column densities for the respective atoms.

Sk -67 2
Na I D			Na I UV			Ca II			Ti II			K I			H I
v	N	g	v	N	g	v	N	g	v	N	g	v	N	g	v	N	g
km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1019 cm-2	km s-1
									-44.7	+6.46	5.7
						-11.9	+9.11	6.7	-11.1	+21.7	14.6
-3.8	+1.21	1.5				-2.0	+18.9	11.7	-0.1	+47.0	10.7
-1.1	+23.9	5.1				-1.1	+28.9	6.3
7.2	+50.9	8.6				3.1	+17.6	4.7	7.0	+27.8	11.5
8.6	+177.0	4.3				8.8	+48.3	5.0
10.3	+21.2	1.4				42.1	+3.44	13.2
						56.6	+4.35	29.3
						86.5	+4.06	8.4
						111.9	+3.83	13.7
						133.2	+5.05	5.7
						177.9	+14.2	18.9
						201.6	+4.27	11.5
						222.9	+20.4	12.4	225.0	+9.62	8.1
						227.6	+9.26	7.5
247.3	+15.7	1.7				240.3	+37.6	12.0	239.7	+13.2	7.6				238.3	+40.2	32.6
249.2	+37.5	1.6
251.2	+95.0	2.0	250.1	+391.0	7.4							250.8	+1.22	2.7
252.8	+173.0	4.7				252.2	+35.5	6.0	253.5	+63.6	10.8	253.7	+7.58	4.1	253.6	+94.3	13.1
259.8	+84.4	2.9
261.8	+132.0	1.9	262.4	+2730.0	4.6	261.7	+71.4	9.3
263.3	+95.3	1.7				261.6	+5.32	3.0	263.3	+48.5	10.7
265.0	+29.9	1.8										263.6	+34.1	3.9
265.1	+30.7	6.4										266.0	+0.26	4.6	268.9	+67.9	19.7
271.7	+7.30	1.2				273.6	+20.7	4.8	272.7	+8.24	5.1	267.2	+1.07	3.8
275.9	+8.55	5.6				278.9	+3.59	4.3
N	+710.0			+3120.0			+208.0			+143.0			+44.2			+202.0
log(N)	12.85			13.49			12.32			12.16			11.65			21.31

 

 

Table 13: Local standard of rest (LSR) velocity v (km s^-1), column density N (cm^-2) and Gaussian width g (km s^-1) for the atomic species Na I (D and UV), Ca II, Ti II, K I and H I observed toward Sk -68 135. The bottom two lines give the total LMC column densities for the respective atoms.

Sk -68 135
Na I D			Na I UV			Ca II			Ti II			K I			H I
v	N	g	v	N	g	v	N	g	v	N	g	v	N	g	v	N	g
km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1019 cm-2	km s-1
-2.0	+9.92	3.1				-2.8	+32.3	11.2	-1.1	+41.4	10.6
4.6	+325.0	7.8				3.4	+12.4	6.1
11.0	+375.0	5.3				10.8	+67.4	5.8	8.7	+41.1	8.1
12.5	+299.0	5.1
14.2	+47.5	2.6							15.0	+13.3	5.6
						49.7	+13.7	15.5
65.4	+4.27	3.3				64.8	+25.3	6.7
						113.0	+2.98	3.5
						142.3	+26.2	8.3
						155.3	+28.1	9.8	158.8	+7.44	6.8
						181.0	+16.5	10.6
						194.2	+15.7	11.4	200.5	+14.8	12.1
						211.8	+34.2	11.7	215.7	+12.2	7.1
						230.4	+30.9	12.8	236.3	+22.5	15.4
						247.8	+82.6	13.5							241.3	+52.5	11.8
256.3	+289.0	5.8	253.7	+51.9	2.6	254.1	+65.6	4.9	257.6	+99.8	14.5	255.1	+6.30	4.8
258.9	+14.9	1.6	260.2	+522.0	6.5							259.1	+5.28	4.5	258.6	+198.0	15.9
262.2	+480.0	4.2				261.0	+150.0	9.1				263.0	+16.2	4.7
265.2	+266.0	4.3	266.4	+951.0	5.6				265.7	+241.0	13.7
266.6	+117.0	9.9										267.5	+4.26	4.3
			272.2	+230.0	4.6	274.0	+79.1	11.5	278.3	+62.3	12.3				274.1	+102.0	31.2
									281.9	+64.0	17.1
293.5	+9.73	6.8							300.9	+21.4	11.1
N	+1180.0			+1760.0			+458.0			+538.0			+32.1			+352.0
log(N)	13.07			13.24			12.66			12.73			11.51			21.55

 

 

Table 14: Local standard of rest (LSR) velocity v (km s^-1), column density N (cm^-2) and Gaussian width g (km s^-1) for the atomic species Na I D, Ca II, Ti II, K I and H I observed toward Sk -67 5. The bottom two lines give the total LMC column densities for the respective atoms.

Sk -67 5
Na I			Ca II			Ti II			K I			H I
v	N	g	v	N	g	v	N	g	v	N	g	v	N	g
km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2			1010 cm-2		km s-1	1010 cm-2	km s-1	km s-1	1019 cm-2	km s-1
			-26.0	+3.24	3.9
			-20.0	+30.9	28.9
			-21.2	+3.45	3.3
			-12.6	+6.65	7.7
			-7.3	+23.6	4.5
-2.1	+172.0	8.9	-2.6	+20.6	4.7	0.5	+16.8	8.2
4.9	+101.0	5.2	5.3	+48.9	8.1	0.2	+48.7	22.2
9.8	+234.0	5.9				9.5	+24.2	6.5
						14.2	+4.97	3.6
			30.1	+4.34	9.3
64.5	+51.6	12.1
			65.6	+6.98	4.4
			131.8	+9.09	7.4
			182.5	+6.26	12.1
			234.8	+7.09	4.2
			244.7	+17.3	3.9							249.9	+27.8	16.2
256.6	+4.94	3.5	255.7	+12.0	4.8
259.5	+3.86	2.4				260.4	+19.7	10.9
261.8	+3.36	3.0	263.1	+49.7	5.6							262.2	+66.8	17.1
266.3	+33.9	6.1				268.5	+68.1	7.2	266.6	+1.48	4.2
272.5	+57.9	5.6	272.7	+92.5	10.1				273.5	+8.81	4.5	273.1	+66.6	8.7
273.7	+125.0	4.6				278.3	+112.0	8.9	280.6	+1.89	3.1
280.4	+81.0	5.3
N	+310.0			+179.0			+200.0			+12.0			+161.0
log(N)	12.49			12.25			12.30			11.09			21.21

 

 

Table 15: Local standard of rest (LSR) velocity v (km s^-1), column density N (cm^-2) and Gaussian width g (km s^-1) for the atomic species Na I D, Ca II, Ti II and H I observed toward Sk -70 120. The bottom two lines give the total LMC column densities for the respective atoms.

Sk -70 120
Na I			Ca II			Ti II			H I
v	N	g	v	N	g	v	N	g	v	N	g
km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1010 cm-2	km s-1	km s-1	1019 cm-2	km s-1
			-17.2	+41.8	7.0	-22.7	+3.62	3.0
-6.0	+67.6	6.7	-5.9	+482.0	8.0	-5.4	+59.6	6.8
1.2	+15.2	7.6	4.3	+93.7	7.8	2.3	+76.6	30.2
8.8	+40.0	6.3	9.4	+76.2	6.6
19.6	+5.65	5.8	20.6	+51.3	8.2
			52.3	+154.0	7.4
			56.4	+5.13	2.1
			64.0	+96.4	8.1
			93.0	+47.1	10.4
			106.6	+4.52	3.3
			139.2	+10.9	5.6
			177.2	+2.78	4.7
			210.3	+23.4	31.4
			210.9	+1.54	3.5
			229.6	+21.6	19.1
			239.8	+6.69	7.4				244.7	+8.10	9.9
			254.7	+25.1	15.0
			272.1	+68.0	13.0	268.8	+43.0	8.6	271.0	+52.4	21.9
			278.9	+12.4	3.8	277.3	+31.3	7.3
			283.2	+7.23	3.2
			288.6	+6.78	4.0				289.7	+6.22	4.8
			291.8	+62.2	10.3	292.9	+130.0	13.0
			301.2	+27.6	5.7				303.5	+37.2	16.2
			306.1	+22.7	4.6	308.2	+170.0	12.7
			310.5	+44.1	6.2
			316.3	+17.0	4.9
			323.4	+39.6	6.8	319.1	+54.5	10.6
			332.0	+3.25	5.3
N				389.0			+429.0			+104.0
log(N)				12.59			12.63			21.02