A&A 447, 431-440 (2006)
DOI: 10.1051/0004-6361:20053902
Large scale correlations in galaxy clustering from the two degree field galaxy redshift survey
N. L. Vasilyev1 - Yu. V. Baryshev1 - F. Sylos Labini2,3
1 - Institute of Astronomy, St. Petersburg State University, Staryj Peterhoff, 198504
St. Petersburg, Russia
2 - ``Enrico Fermi Center'', Via Panisperna 89 A, Compendio del Viminale, 00184 Rome, Italy
3 - ``Istituto dei Sistemi Complessi'' CNR, via dei Taurini 19, 00185 Rome, Italy
Received 25 July 2005 / Accepted 5 October 2005
Abstract
We study galaxy correlations from samples extracted from the 2dFGRS final release. Statistical properties are characterized by studying the nearest neighbor probability density, the conditional density and the reduced two-point correlation function. The result is that the
conditional density has a power-law behavior in redshift space described by an exponent
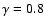
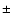 0.2 in the interval from about 1 Mpc/h, the average distance between nearest galaxies, up to about 40 Mpc/h, corresponding to radius of the largest sphere contained in the samples. These results are consistent with other studies of the conditional density and are useful to clarify the subtle role of finite-size effects on the determination of the two-point correlation function in redshift and real space.
0.2 in the interval from about 1 Mpc/h, the average distance between nearest galaxies, up to about 40 Mpc/h, corresponding to radius of the largest sphere contained in the samples. These results are consistent with other studies of the conditional density and are useful to clarify the subtle role of finite-size effects on the determination of the two-point correlation function in redshift and real space.
Key words: cosmology: observations - large-scale structure of Universe
The problem of the quantitative characterization of large scale galaxy
clustering has been intensively discussed in recent years, especially
in relation to two new galaxy surveys: the Sloan Digital Sky Survey
(SDSS - York et al. 2000) and the Two degree Field Galaxy Redshift
Survey (2dFGRS - Colless et al. 2003). These data represent a great
improvement of our knowledge of the local universe: for example the
number of measured redshifts has grown by a factor of ten with respect
to the surveys completed in the last two decades. Moreover accurate
redshift determinations and the multi-band photometry allow one a
precise characterization of many parameters and effects (e.g. K corrections) which were poorly constrained up to few years ago. It should however be noted that for some analyses, like the ones we
discuss here, a large solid angle is also required. This is still not the case for the present data, but, for instance, the final release of the SDSS will provide a large contiguous angular sky region in the very near future.
In this paper we discuss the analysis of two-point correlation
properties in the 2dFGRS sample. Up to now these data have been
mainly analyzed by studying the reduced correlation function 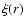 ,
in redshift and real space, and its Fourier conjugate, the power
spectrum (e.g. Norberg et al. 2001, 2002; Tegmark et al. 2002; Hawkins et al. 2003; Madgwick et al. 2003; Basilakos & Plionis 2003; Cole et al. 2005). Recently Gaztanaga et al. (2005) presented new result for the 3-point correlation function measured as a function of scale, luminosity and color using the 2dFGRS sample.
,
in redshift and real space, and its Fourier conjugate, the power
spectrum (e.g. Norberg et al. 2001, 2002; Tegmark et al. 2002; Hawkins et al. 2003; Madgwick et al. 2003; Basilakos & Plionis 2003; Cole et al. 2005). Recently Gaztanaga et al. (2005) presented new result for the 3-point correlation function measured as a function of scale, luminosity and color using the 2dFGRS sample.
In general, these statistical tools can be affected by finite-size
effects or luminosity dependent selection effects (e.g. Gabrielli et al. 2004) and, by using appropriate statistics, one may perform several tests to disentangle different biases. Finite size effects can be very important for the determination of correlation properties
in the regime of large fluctuations, which should be then clearly
identified in the studies of galaxy samples. It is well known
that at small scales, observed galaxy structures are highly irregular
and present two-point power-law correlations, in the regime of strong
clustering. However the search for the "maximum'' size of galaxy
structures and voids, beyond which the distribution becomes
essentially uniform and fluctuations can be considered small
perturbations with respect to the average density, is still an open
problem (Tikhonov & Makarov 2003; Hogg et al. 2005; Joyce et al. 2005, and see for a recent review Baryshev & Teerikorpi 2005). It is evident that from the theoretical point of view the understanding of the statistical characteristics of these structures represents the key element to be considered by a physical theory dealing with their formation.
A number of statistical methods can be used to study galaxy
distribution; the main ones involve the determination of two-point
properties although the study of the distribution function, containing
information on higher order correlations, has also been found to be a
powerful method (e.g. Sivakoff & Saslaw 2005). The primary questions
in correlation analysis of three dimensional galaxy distributions are:
(i) what is the value of the correlation exponent and (ii) what is
the scale on which the distribution becomes uniform and a crossover
to homogeneity can be clearly identified? Such a scale can be
defined, for example, to be the one beyond which conditional counts of
galaxies in three dimensional volumes of radius R grow as R3. Recently Hogg et al. (2005), by considering the properties of a deep and complete sample of luminous red galaxies extracted from the
SDSS survey, found that the transition from the strongly correlated
regime to the uniform one occurs at about 70 Mpc/h![[*]](/icons/foot_motif.gif) , which is larger than, for example, results in the CfA1 redshift survey where the transition was found at about 20 Mpc/h (Davis & Peebles 1983; see Peebles 2001, for a recent discussion). Particularly, they have measured the behavior of the
conditional density in redshift space, finding that the exponent
characterizing the power-law correlation is about
, which is larger than, for example, results in the CfA1 redshift survey where the transition was found at about 20 Mpc/h (Davis & Peebles 1983; see Peebles 2001, for a recent discussion). Particularly, they have measured the behavior of the
conditional density in redshift space, finding that the exponent
characterizing the power-law correlation is about
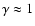 (instead of
(instead of
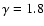 as measured by Davis & Peebles 1983) up to
20-30 Mpc/h and that this is followed by a slow crossover toward
homogeneity which is reached at about 70 Mpc/h. These results are in
good agreement with the ones presented in, e.g. Sylos Labini et al. (1998) (see Baryshev & Teerikorpi 2005 for a recent review) where the same value
as measured by Davis & Peebles 1983) up to
20-30 Mpc/h and that this is followed by a slow crossover toward
homogeneity which is reached at about 70 Mpc/h. These results are in
good agreement with the ones presented in, e.g. Sylos Labini et al. (1998) (see Baryshev & Teerikorpi 2005 for a recent review) where the same value
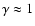 was found up to 20-30 Mpc/h and where at larger scales, with a weaker statistics, an evidence for a compatibility with the extension of such a behavior was found. In
addition Tikhonov et al. (2000) found similar results up to scales of
was found up to 20-30 Mpc/h and where at larger scales, with a weaker statistics, an evidence for a compatibility with the extension of such a behavior was found. In
addition Tikhonov et al. (2000) found similar results up to scales of  30 Mpc/h, and weaker evidence for homogeneity at scales larger than 100 Mpc/h.
30 Mpc/h, and weaker evidence for homogeneity at scales larger than 100 Mpc/h.
In this paper we present results of a correlation analysis of the
2dFGRS data studying the behavior of the conditional density and other
statistics suitable to characterize properties of distributions with
large fluctuations and control finite size effects. In Sect. 2 we
describe the procedure to construct samples which are not biased by
the luminosity selection in apparent magnitudes (the so-called volume
limited - VL - samples). In Sect. 3 we consider the nearest neighbor
probability density for the VL samples which allows us a characterization of small scales statistical properties. We then turn to the study of large scale in Sect. 4 where we discuss the estimation of the conditional density and the result obtained in the VL samples.
We discuss the relation of this statistical tool to the reduced
two-point correlation function in Sect. 5, where we compare our results
with previous estimations of the same statistics, focusing on finite
size effects and their implication for the interpretation of galaxy
correlations. In Sect. 6 we summarize our results and discuss
their relation to other studies and we draw our main conclusions.
The 2dFGRS is currently the largest completed galaxy catalog. The
Final Release (Colless et al. 2003) contains more than 220 thousand
precisely measured redshifts of the galaxies located in two strips:
about 140 thousand in the southern galactic pole (SGP), in a strip
of 
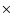
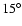 and about 70 thousand in the strip
and about 70 thousand in the strip
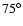
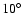 in the northern galactic pole (NGP). In
addition the survey contains 10 thousand in random fields which are
not used in this paper.
in the northern galactic pole (NGP). In
addition the survey contains 10 thousand in random fields which are
not used in this paper.
The median redshift of galaxies is
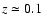 and most of the
galaxies have z<0.3. The
and most of the
galaxies have z<0.3. The 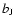 magnitude corrected for the galactic
extinction is limited to
magnitude corrected for the galactic
extinction is limited to
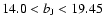 .
.
To avoid the effect of the irregular edges in the angular coordinates
due to the survey geometry, we set the following limits in right
ascension and declination in order to get a rectangular (in
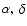 coordinates) shape on the sky:
coordinates) shape on the sky:
We select galaxies in the redshift interval
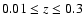 and
with the redshift quality parameter chosen such that
and
with the redshift quality parameter chosen such that 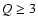 in
order to have high quality redshifts (see discussion in Hawkins et al. 2003).
in
order to have high quality redshifts (see discussion in Hawkins et al. 2003).
We do not use a correction for the redshift completeness mask and for
the fiber collision effects. Completeness varies most nearby the
survey edges which are excluded in our sample. We assume that fiber
collisions do not change sensibly the small scales correlation
properties as we set our lower cut-off to 0.5 Mpc/h which is larger
than the 0.1 Mpc/h used by Hawkins et al. (2003).
To construct VL subsamples first we compute metric distances as
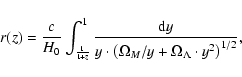 |
(1) |
where we use the standard model parameters
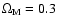 and
and
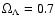 .
The absolute magnitude is
.
The absolute magnitude is
![\begin{displaymath}%
M = b_{\rm J} - 5 \cdot \log_{10}\left[r(z) \cdot (1+z)\right] - K_i(z) - 25.
\end{displaymath}](/articles/aa/full/2006/08/aa3902-05/img45.gif) |
(2) |
To calculate the K-correction Ki(z) (the index i defines the
galaxy type) we used formulas obtained by Madgwick et al. (2002):
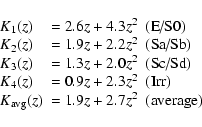 |
(3) |
where 1,2,3,4 indicies represent the spectral types of the galaxies
(in parenthesis in Eq. (3)), and the average value
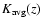 is used for the galaxies with undefined spectral type.
is used for the galaxies with undefined spectral type.
To take into account the selection effect that arises due to the
2dFGRS apparent magnitude limits
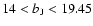 ,
one has to
consider two limits for the metric distance
,
one has to
consider two limits for the metric distance
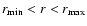 and
compute the two corresponding limits for the absolute magnitude
and
compute the two corresponding limits for the absolute magnitude
 and
and
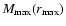 which represent the lower and upper limit for the galaxies contained in a VL sample.
which represent the lower and upper limit for the galaxies contained in a VL sample.
We select three distance intervals (50-250 Mpc/h, 100-400 Mpc/h and
150-550 Mpc/h) and compute the corresponding absolute magnitude limits
for each of two strips. Thus we get three VL subsamples for the
Northern hemisphere and three for Southern hemisphere whose main
parameters are presented Table 1. (Note
that hereafter we set h=1 unless specified). An example of the
distance-magnitude limits for the SGP400 sample (which is the largest
one considered in this paper) is shown in Fig. 1. In
Fig. 2 we show the behavior of the differential number counts
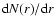 as a function of distance in different sky areas for the
sample SGP400. Particularly we put limits respectively at
as a function of distance in different sky areas for the
sample SGP400. Particularly we put limits respectively at
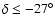 (c4),
(c4),
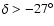 (c5),
(c5),
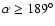 (c6) and
(c6) and
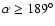 (c7). As an example we report the best fit for the sample c4, which shows an exponent
corresponding to a metric dimension larger (D=3.7) than the space
dimension. This is a purely finite-size effect corresponding to the
large fluctuations still visible at scales of the order of 100 Mpc/h.
(c7). As an example we report the best fit for the sample c4, which shows an exponent
corresponding to a metric dimension larger (D=3.7) than the space
dimension. This is a purely finite-size effect corresponding to the
large fluctuations still visible at scales of the order of 100 Mpc/h.
Table 1:
Main properties of the obtained VL samples:
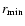 ,
,
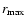 are the chosen limits for the metric distance;
are the chosen limits for the metric distance;
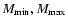 are the interval for
the absolute magnitude and
are the interval for
the absolute magnitude and 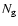 is the resulting number of galaxies
in each sample.
is the resulting number of galaxies
in each sample.
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{Fig1.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg58.gif) |
Figure 1:
The metric distance- absolute magnitude diagram for the SGP strip. The boundaries of the SGP400 subsample are shown. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig2.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg59.gif) |
Figure 2:
Differential number counts in different sky areas (defined in the text) for the SGP400 subsample. As an example we report the best fit for the sample c4, which show an exponent corresponding to a metric dimension larger than the space dimension. This is a purely finite-size effect which maybe explained by a presence of the large scale fluctuations in the studied region. |
| Open with DEXTER |
In a stochastic point process the probability
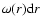 that
the nearest neighbor to a given particle lies at a distance in the
range
that
the nearest neighbor to a given particle lies at a distance in the
range
![$[r,r+{\rm d}r]$](/articles/aa/full/2006/08/aa3902-05/img61.gif) can provide a useful characterization of small scale
statistical properties. This probability density satisfies, by
definition, the condition
can provide a useful characterization of small scale
statistical properties. This probability density satisfies, by
definition, the condition
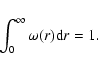 |
(4) |
According to its definition 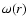 can be simply estimated as
can be simply estimated as
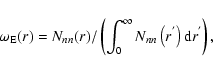 |
(5) |
where Nnn(r) is the number of points which have their nearest
neighbors in the range
![$[r,r+{\rm d}r]$](/articles/aa/full/2006/08/aa3902-05/img61.gif) .
.
The nearest neighbor probability density for a Poisson distribution
with average density
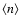 is given by (Gabrielli
et al. 2004)
is given by (Gabrielli
et al. 2004)
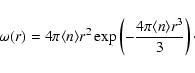 |
(6) |
In Fig. 3 we present an example of the observed 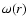 distribution in the VL SGP400, along with an artificial Poisson distribution with the same number of points in the same
three-dimensional volume. Note that the probed scales here are about
distribution in the VL SGP400, along with an artificial Poisson distribution with the same number of points in the same
three-dimensional volume. Note that the probed scales here are about
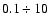 Mpc/h.
Mpc/h.
For the actual data the average distance between nearest galaxies is
smaller than for the Poisson case, and this is clear evidence for the
presence of small scale correlations. The exact analytical behavior of 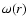 for the general case of a power-law correlated structure is unknown; an approximate relation for the simple case of a anisotropic Poisson distribution, which present a radial density
profile decaying as
for the general case of a power-law correlated structure is unknown; an approximate relation for the simple case of a anisotropic Poisson distribution, which present a radial density
profile decaying as
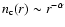 from its center with
exponent
from its center with
exponent 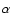 (with
(with
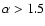 - see discussion in Gabrielli et al. 2004), is given by
- see discussion in Gabrielli et al. 2004), is given by
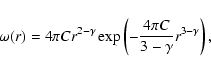 |
(7) |
where
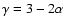 .
This is found to be a good approximation of
the actual data (see Fig. 1). In Table 2 (see below) we report the estimation of the average distance between nearest neighbors (defined as
.
This is found to be a good approximation of
the actual data (see Fig. 1). In Table 2 (see below) we report the estimation of the average distance between nearest neighbors (defined as
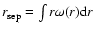 )
in the different samples (note that similar values
have been found by Peebles 2001).
)
in the different samples (note that similar values
have been found by Peebles 2001).
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{Fig3.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg74.gif) |
Figure 3:
Nearest neighbor probability density for the SGP400 sample data (squares) and for a Poisson
simulation (circles) in the same volume. The dotted lines are the best fit respectively for the anisotropic Poisson distribution (Eq. (7) with
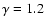 )
and for the Poisson case (Eq. (6)). )
and for the Poisson case (Eq. (6)). |
| Open with DEXTER |
In general, in a distribution of points with large fluctuations at
some scales one may determinate two-point correlations through the
estimation of the conditional density (see discussion in Gabrielli et al. 2004). We first briefly summarize the main properties of this statistical tool stressing the finite size effects and statistical errors which may enter into the estimators. Then we apply it to the
case of the VL samples extracted from the 2dFGRS, as discussed in the previous section.
The conditional density in spheres
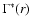 is defined for an ensemble of realizations of a given point process, as
is defined for an ensemble of realizations of a given point process, as
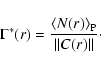 |
(8) |
This quantity measures the average number of points
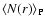 contained in a sphere of volume
contained in a sphere of volume
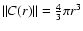 with the condition that the center of
the sphere lies on an occupied point of the distribution (and
with the condition that the center of
the sphere lies on an occupied point of the distribution (and
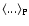 denotes the conditional ensemble average).
denotes the conditional ensemble average).
Such a quantity can be estimated in a finite sample by a volume
average (supposing stationarity of the point distribution)
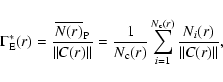 |
(9) |
where
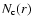 - the number of points (centers) with spheres fully
contained in the sample volume,
- the number of points (centers) with spheres fully
contained in the sample volume,
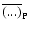 means averaging
by the sample points.
means averaging
by the sample points.
Given a sample of arbitrary geometry and a scale r at which
correlations are measured, only a subsample of the points contained in
it will satisfy the following requirement: when chosen as center of a sphere of radius r, the sphere is fully contained in the sample volume. When the average in Eq. (9) is made over such a subsample one considers the full-shell estimator of the
conditional density. Note that the number of centers
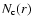 is a function of the scale r at which correlations are estimated. In fact for scales much smaller than the radius
is a function of the scale r at which correlations are estimated. In fact for scales much smaller than the radius
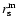 of the largest sphere fully contained in the sample volume, almost all points will
contribute to the average, while at scales comparable to the sample size only those points lying in the center of the sample volume will contribute. Thus finite-size effect can be important when one
considers the largest available scales: in this situation one cannot make a full volume averages and systematic effects, due to large fluctuations, can be important in the determination of such a statistics.
of the largest sphere fully contained in the sample volume, almost all points will
contribute to the average, while at scales comparable to the sample size only those points lying in the center of the sample volume will contribute. Thus finite-size effect can be important when one
considers the largest available scales: in this situation one cannot make a full volume averages and systematic effects, due to large fluctuations, can be important in the determination of such a statistics.
Table 2:
Characteristic scales of the VL samples:
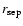 is the average separation distance
between nearest neighbor galaxies (in 2dFGRS and Poisson distribution
within the same volume and for the same number of galaxies),
is the average separation distance
between nearest neighbor galaxies (in 2dFGRS and Poisson distribution
within the same volume and for the same number of galaxies),
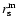 is the maximum sphere completely contained in the sample. All distances are in Mpc (H0=100 km s-1 Mpc-1).
is the maximum sphere completely contained in the sample. All distances are in Mpc (H0=100 km s-1 Mpc-1).
The scale
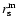 will in general be very different from the scales
will in general be very different from the scales
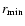 and
and
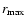 characterizing a VL sample, as it depends crucially on the sample solid angle. On the other hand the minimal scale
characterizing a VL sample, as it depends crucially on the sample solid angle. On the other hand the minimal scale
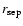 up to which correlations can be measured is given by the average distance between neighbor galaxies: clearly for
up to which correlations can be measured is given by the average distance between neighbor galaxies: clearly for
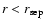 discrete shot-noise dominates estimations of any statistical quantity. Thus we will explicitly compute the scales
discrete shot-noise dominates estimations of any statistical quantity. Thus we will explicitly compute the scales
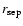 and
and
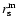 for the VL considered in what follows (see
Table 2).
for the VL considered in what follows (see
Table 2).
The conditional density in spherical shells is defined as
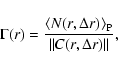 |
(10) |
where
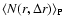 represents the ensemble
average number of points in a sphere of radius r and thickness
represents the ensemble
average number of points in a sphere of radius r and thickness 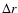 ,
of volume
,
of volume
![$\Vert C(r,\Delta{r})\Vert=\frac{4}{3}\pi[(r+\Delta{r})^{3}-r^3]$](/articles/aa/full/2006/08/aa3902-05/img86.gif) ,
around a point of distribution (and thus this is a conditional ensemble average
,
around a point of distribution (and thus this is a conditional ensemble average
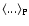 as in the previous case). Note that one can also write Eq. (10) as
as in the previous case). Note that one can also write Eq. (10) as
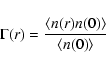 |
(11) |
where
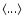 represents the (unconditional) ensemble
average and n(r) is the microscopic number density.
represents the (unconditional) ensemble
average and n(r) is the microscopic number density.
The conditional density in shells can be estimated in a finite sample
by the following volume average
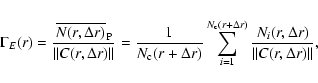 |
(12) |
where we consider again only the full-shell estimator, i.e. for which
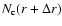 represents the number of points (centers) contained
in spherical shells fully contained in the sample volume. Analogously
to the case of
represents the number of points (centers) contained
in spherical shells fully contained in the sample volume. Analogously
to the case of
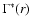 particular care should be used to
determine the scales
particular care should be used to
determine the scales
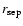 and
and
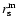 .
.
For the case where the distributions have power-law correlations and
strong fluctuations (e.g. a fractal structure) then the conditional
density in spheres behaves (in the ensemble average) as
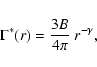 |
(13) |
while the conditional density in shells has the form
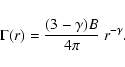 |
(14) |
where 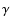 is the correlation exponent (in the case of a fractal
is the correlation exponent (in the case of a fractal
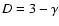 is the fractal dimension) and B is a lower cut-off
related to the smaller scale where correlations can be measured in a finite sample (i.e. to
is the fractal dimension) and B is a lower cut-off
related to the smaller scale where correlations can be measured in a finite sample (i.e. to
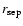 previously defined).
previously defined).
In Table 2 we show, for the different VL samples
considered, the lower and upper cut-off, previously discussed, between
which we have estimated 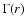 and
and
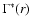 .
Note that we
have generated a Poisson distribution, for each VL sample, with the
same number of points and in the same three dimensional volume in
order to estimate the same statistical quantities in a distribution
without correlation at all. This provide us with a useful way to test
our analysis using the simplest distribution with known
properties. Note also that all our estimates have been done in redshift space: the relation with real space properties will be
discussed in Sect. 6.
.
Note that we
have generated a Poisson distribution, for each VL sample, with the
same number of points and in the same three dimensional volume in
order to estimate the same statistical quantities in a distribution
without correlation at all. This provide us with a useful way to test
our analysis using the simplest distribution with known
properties. Note also that all our estimates have been done in redshift space: the relation with real space properties will be
discussed in Sect. 6.
Figure 4 shows the behavior of the estimation of the conditional density in
spheres in the six VL samples considered. The samples with the same
luminosity and distance cuts in the NGP and SGP show approximately the
same behavior. However a difference in the amplitude is present for
all but the largest sample. The amplitude of
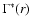 is related
to the luminosity function in the following way.
is related
to the luminosity function in the following way.
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig4.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg95.gif) |
Figure 4:
Estimation of the conditional density in spheres in the six VL samples considered
(different symbols correspond to different VL samples - see labels). The reference line has a power-law behavior with slope
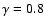 . .
|
| Open with DEXTER |
In general the joint conditional probability of finding a galaxy of
luminosity L at distance 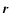 from another galaxy, i.e. the
(ensemble) conditional average number of galaxies with luminosity in
the range
from another galaxy, i.e. the
(ensemble) conditional average number of galaxies with luminosity in
the range
![$[L,L+{\rm d}L]$](/articles/aa/full/2006/08/aa3902-05/img97.gif) and in the volume element
and in the volume element
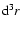 at distance rfrom an observer located in a galaxy is given by
at distance rfrom an observer located in a galaxy is given by
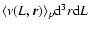 .
One can then assume that
.
One can then assume that
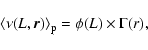 |
(15) |
where 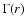 is the average conditional density and
is the average conditional density and 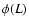 is the luminosity function such that
is the luminosity function such that
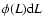 gives the probability that a randomly chosen galaxy has a luminosity in the range
gives the probability that a randomly chosen galaxy has a luminosity in the range
![$[L,L+{\rm d}L]$](/articles/aa/full/2006/08/aa3902-05/img97.gif) .
By writing Eq. (15) as a product of the
conditional space density for the luminosity function, one has
implicitly assumed that galaxy positions are independent of galaxy
luminosity. Thus from Eq. (15) it follows that the amplitude of
.
By writing Eq. (15) as a product of the
conditional space density for the luminosity function, one has
implicitly assumed that galaxy positions are independent of galaxy
luminosity. Thus from Eq. (15) it follows that the amplitude of
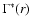 in a VL sample is given by an integral of the luminosity function over the range of absolute luminosity covered by the sample multiplied by the conditional density for all galaxies. Amplitude
variations in the same VL samples in the NGP and SGP can be due to
large local fluctuations which are not averaged out by the volume
average. Thus these differences probably can be ascribed to finite
size effects. The fact that in the deepest VL samples (i.e. the ones
cut at 550 Mpc/h), where the volume is the largest, the conditional
density does not show significant difference between the two hemispheres supports the finite-size interpretation.
in a VL sample is given by an integral of the luminosity function over the range of absolute luminosity covered by the sample multiplied by the conditional density for all galaxies. Amplitude
variations in the same VL samples in the NGP and SGP can be due to
large local fluctuations which are not averaged out by the volume
average. Thus these differences probably can be ascribed to finite
size effects. The fact that in the deepest VL samples (i.e. the ones
cut at 550 Mpc/h), where the volume is the largest, the conditional
density does not show significant difference between the two hemispheres supports the finite-size interpretation.
If one fits the behavior of the estimated
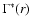 with a power-law function of the type
with a power-law function of the type
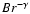 one finds that
one finds that
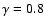
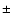 0.2. In Fig. 5
we have normalized the conditional density is spheres to the value at 10 Mpc/h. In this way it is
apparent the fact that the slope variates in the different samples:
the variation is of about 0.1. The formal statistical error for the determination of
0.2. In Fig. 5
we have normalized the conditional density is spheres to the value at 10 Mpc/h. In this way it is
apparent the fact that the slope variates in the different samples:
the variation is of about 0.1. The formal statistical error for the determination of
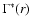 at each scale can be simply derived from the dispersion of the average
at each scale can be simply derived from the dispersion of the average
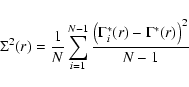 |
(16) |
where
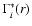 represents the determination from the
represents the determination from the 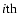 point. The corresponding error bars are too small to be plotted. However at large scales (usually the last few points)
estimators of
point. The corresponding error bars are too small to be plotted. However at large scales (usually the last few points)
estimators of
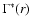 have large scatters because of the small number of points contributing to the average. Moreover in this estimation one cannot take into account systematic variations due to the fact that the volume average cannot be performed at large scales
(see discussion in Joyce et al. 1999). For these reasons the behavior for scale larger than
have large scatters because of the small number of points contributing to the average. Moreover in this estimation one cannot take into account systematic variations due to the fact that the volume average cannot be performed at large scales
(see discussion in Joyce et al. 1999). For these reasons the behavior for scale larger than 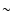 20 Mpc/h is affected by large un-averaged fluctuations.
20 Mpc/h is affected by large un-averaged fluctuations.
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig5.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg107.gif) |
Figure 5:
Conditional density in spheres normalized to the value at 10 Mpc/h.
The slope varies in the different samples. The reference line has a power-law behavior with slope
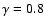 . .
|
| Open with DEXTER |
We show in Fig. 6 the behavior of the conditional
density in shells and in Fig. 7 the
conditional density in shells normalized to the value at 10 Mpc/h. It
is clear that these estimations are more affected by statistical
noise. An important parameter in this respect is represented by the
shell thickness which we take constant in a logarithmic scale.
In this case the average slope is
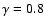
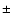 0.2 up to 30 Mpc/h.
0.2 up to 30 Mpc/h.
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig6.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg108.gif) |
Figure 6:
Estimation of the conditional density in shells for the different VL samples considered. The reference line has a power-law behavior with slope
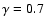 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig7.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg109.gif) |
Figure 7:
Estimation of the conditional density in shells normalized
to the value at 10 Mpc/h for the different VL samples considered. The
reference line has a power-law behavior with slope
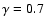 . .
|
| Open with DEXTER |
The reduced two-point correlation function 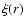 for a stochastic
point process is defined (see e.g. Peebles 1980) as
for a stochastic
point process is defined (see e.g. Peebles 1980) as
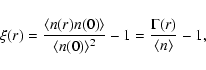 |
(17) |
where
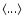 indicates the ensemble average and
indicates the ensemble average and
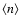 is the ensemble average number density. The last equality follows from the definition of the conditional
density (see Eq. (10)).
is the ensemble average number density. The last equality follows from the definition of the conditional
density (see Eq. (10)).
There are several estimators of 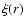 and we refer to Kerscher et al. (2000) and Gabrielli et al. (2004) for a detailed discussion of the different ones used in the literature. One may consider, for example, the Landy & Szalay (1993) (LS) estimator that is the most widespread in modern studies of correlation function for
large scale structures because it is the minimal variance estimator
for a Poisson distribution. This can be written as (Kerscher et al. 2000):
and we refer to Kerscher et al. (2000) and Gabrielli et al. (2004) for a detailed discussion of the different ones used in the literature. One may consider, for example, the Landy & Szalay (1993) (LS) estimator that is the most widespread in modern studies of correlation function for
large scale structures because it is the minimal variance estimator
for a Poisson distribution. This can be written as (Kerscher et al. 2000):
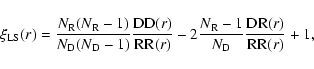 |
(18) |
where 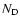 - the number of data (sample) points;
- the number of data (sample) points; 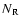 - the
number of random points homogeneously distributed in the sample
geometry;
- the
number of random points homogeneously distributed in the sample
geometry;
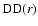 is the number data-data pairs,
is the number data-data pairs,
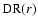 -
data-random pairs and
-
data-random pairs and
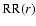 - random-random pairs. Note that in
the artificial random catalogs generated for the estimation of
Eq. (18), we have used a number of points in the range
4.5-9
- random-random pairs. Note that in
the artificial random catalogs generated for the estimation of
Eq. (18), we have used a number of points in the range
4.5-9  104. However the LS estimator can be biased by finite-size
effects in the case of strongly correlated distributions as we discuss
in what follows: we have tested that for the estimator introduced
by Davis & Peebles (1983) the situation is substantially the same.
104. However the LS estimator can be biased by finite-size
effects in the case of strongly correlated distributions as we discuss
in what follows: we have tested that for the estimator introduced
by Davis & Peebles (1983) the situation is substantially the same.
Analogously to the full-shell estimator of the conditional
density, one may define the following (full-shell)
estimator of 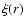 which can be induced directly from Eq. (17)
which can be induced directly from Eq. (17)
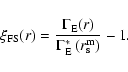 |
(19) |
where
 is the estimator of the conditional density in
shells and
is the estimator of the conditional density in
shells and
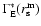 is the estimator of the conditional
density in spheres at the scale of the sample
is the estimator of the conditional
density in spheres at the scale of the sample
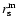 .
Although the
latter quantity is not, in general, computed through an average
because only a single point may contribute at such large scales, this
estimator, when the properties of the distribution are unknown and
likely to be characterized by strong fluctuations, has several
advantages with respect to the LS (or the one used by Davis &
Peebles 1983).
.
Although the
latter quantity is not, in general, computed through an average
because only a single point may contribute at such large scales, this
estimator, when the properties of the distribution are unknown and
likely to be characterized by strong fluctuations, has several
advantages with respect to the LS (or the one used by Davis &
Peebles 1983).
By using the full-shell estimator we are able to make a very
conservative measurement of the two-point correlation function. One
does not need to make estimations of correlations on scales larger
than
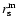 which require use of weighing schemes and special
treatment of boundary conditions. The main point is however that the
estimation of the sample density is performed on "local'' scales,
i.e. much smaller than the global scale of the sample. In addition
Eq. (19) satisfies the simple constraint
which require use of weighing schemes and special
treatment of boundary conditions. The main point is however that the
estimation of the sample density is performed on "local'' scales,
i.e. much smaller than the global scale of the sample. In addition
Eq. (19) satisfies the simple constraint
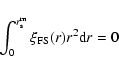 |
(20) |
which is the so-called "integral constraint''. Any estimator of 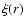 must satisfy a similar condition which comes from the fact that the average density has been estimated from the given sample. (Note that we do not use any additional correction to take into
account this particular effect: in the case of the full-shell
estimator the integral constraint has a clear effect given by
Eq. (20). For the case of the LS estimator we have not used
any correction to take into account for this constraint.) It is
however clear that Eq. (20) gives us a simple way to control
this offset, which is not the case for another estimator. The
estimation of the sample average is subject to large fluctuations
because its determination does not involve any averaging. Such
fluctuations will substantially alter the amplitude of the reduced
correlation function as we discuss below: this is a good reason to
measure statistical quantities, like
must satisfy a similar condition which comes from the fact that the average density has been estimated from the given sample. (Note that we do not use any additional correction to take into
account this particular effect: in the case of the full-shell
estimator the integral constraint has a clear effect given by
Eq. (20). For the case of the LS estimator we have not used
any correction to take into account for this constraint.) It is
however clear that Eq. (20) gives us a simple way to control
this offset, which is not the case for another estimator. The
estimation of the sample average is subject to large fluctuations
because its determination does not involve any averaging. Such
fluctuations will substantially alter the amplitude of the reduced
correlation function as we discuss below: this is a good reason to
measure statistical quantities, like 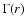 ,
which are not
affected by such fluctuations.
,
which are not
affected by such fluctuations.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{Fig8.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg121.gif) |
Figure 8:
Estimation of the two-point reduced correlation
function in the different VL samples considered by using the full
shell estimator. The reference line has a power-law behavior with
slope
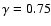 . .
|
| Open with DEXTER |
The behavior of
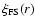 is presented in Fig. 8.
We note two main properties: the first one is that the amplitude of
is presented in Fig. 8.
We note two main properties: the first one is that the amplitude of 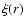 changes in different samples and the second is that the exponent in the strongly clustered regime (i.e.
changes in different samples and the second is that the exponent in the strongly clustered regime (i.e.
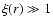 )
is about
)
is about
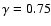 .
Both results are in qualitative agreement
with other analyses of the same samples. For example Hawkins et al. (2003) found that in the full magnitude limited sample, the redshift space value of the correlation exponent is
.
Both results are in qualitative agreement
with other analyses of the same samples. For example Hawkins et al. (2003) found that in the full magnitude limited sample, the redshift space value of the correlation exponent is
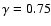 in
the range [0.1,4] Mpc/h and then
in
the range [0.1,4] Mpc/h and then
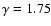 in the range [4,10] Mpc/h (see their Fig. 6). This is for example what we find in the SGP250 sample as shown in Fig. 9. The slopes measured in different VL sample may vary as shown, for example, by the SGP400 in Fig. 10. In other surveys different values of
in the range [4,10] Mpc/h (see their Fig. 6). This is for example what we find in the SGP250 sample as shown in Fig. 9. The slopes measured in different VL sample may vary as shown, for example, by the SGP400 in Fig. 10. In other surveys different values of 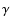 in redshift space have been found: for example in the CfA1 catalog
in redshift space have been found: for example in the CfA1 catalog
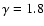 in the range
[0.1,5] Mpc/h (Davis & Peebles 1983). As discussed below we ascribe
this change of slope, like the variation of the amplitude of
in the range
[0.1,5] Mpc/h (Davis & Peebles 1983). As discussed below we ascribe
this change of slope, like the variation of the amplitude of 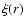 ,
to a finite size effect. For this reason, while the qualitative
behavior of the variation of the amplitude and exponent of
,
to a finite size effect. For this reason, while the qualitative
behavior of the variation of the amplitude and exponent of 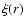 is
similar to many other estimations (e.g. Hawkins et al. 2003; Norberg
et al. 2001), the quantitative comparison depends on the sample size
and, most importantly, on the fluctuations which affect the
determination of the sample density. As these fluctuations can be
large and dependent on the specific sample considered, it is difficult
to make a more quantitative comparison between our results and others.
is
similar to many other estimations (e.g. Hawkins et al. 2003; Norberg
et al. 2001), the quantitative comparison depends on the sample size
and, most importantly, on the fluctuations which affect the
determination of the sample density. As these fluctuations can be
large and dependent on the specific sample considered, it is difficult
to make a more quantitative comparison between our results and others.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{Fig9.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg125.gif) |
Figure 9:
Estimation of the two-point reduced correlation
function in the VL sample SGP250, by using the full shell
estimator. The reference lines have a power-law behavior with slope
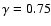 and
and
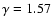 respectively.
respectively. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{Fig10.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg126.gif) |
Figure 10:
Estimation of the two-point reduced correlation
function in the VL sample SGP400, using the full shell
estimator. The reference lines have a power-law behavior with slope
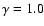 and
and
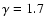 respectively.
respectively. |
| Open with DEXTER |
The zero-crossing scale
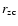 of
of 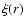 ,
shown by a sharp decay
on the scale
,
shown by a sharp decay
on the scale
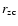 of
of
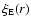 in a log-log plot, depends on the
sample size. This result again can be explained as a finite size
effect introduced by Eq. (20). This is an important feature
especially in the comparison between observations and numerical N-body
simulations (see Sylos Labini 2005 for more detail).
in a log-log plot, depends on the
sample size. This result again can be explained as a finite size
effect introduced by Eq. (20). This is an important feature
especially in the comparison between observations and numerical N-body
simulations (see Sylos Labini 2005 for more detail).
Concerning the amplitude, we note that Norberg et al. (2001) found a similar variation of the redshift-space 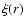 .
This is consistent with the results discussed here. The difference lies in the way these results are interpreted. While Norberg et al. (2001) ascribe the
different amplitudes to different selections in luminosity (or
spectral type, or colors, etc.), we discuss below that, given the
behavior of the conditional density, such variations can be easily
explained as a finite size effect.
.
This is consistent with the results discussed here. The difference lies in the way these results are interpreted. While Norberg et al. (2001) ascribe the
different amplitudes to different selections in luminosity (or
spectral type, or colors, etc.), we discuss below that, given the
behavior of the conditional density, such variations can be easily
explained as a finite size effect.
In order to directly show the importance of finite size effects, and
illustrate their role in a specific example, we have considered the
sample SGP400 and constructed some different subsamples. In all cases
the other boundaries in
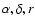 remain the same as for the
original sample while an additional cut has been imposed. The sample C1 is cut at
remain the same as for the
original sample while an additional cut has been imposed. The sample C1 is cut at 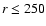 Mpc/h, C2 at
Mpc/h, C2 at 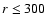 Mpc/h, C3 at
Mpc/h, C3 at 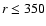 Mpc/h, C4 at
Mpc/h, C4 at
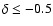 radiant, C5 at
radiant, C5 at
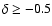 radiant, C6 at
radiant, C6 at
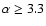 radiant, C7 at
radiant, C7 at
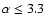 radiant and C8 at
radiant and C8 at 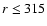 Mpc/h. Note that in these subsamples the lower cut-off remains the same as for the full SGP400, while the upper cut-off changes: in what follows we focus on how the finite size effect at large scales influence the amplitude of the
Mpc/h. Note that in these subsamples the lower cut-off remains the same as for the full SGP400, while the upper cut-off changes: in what follows we focus on how the finite size effect at large scales influence the amplitude of the 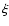 -function. The results obtained by the Landy-Szalay estimator
(Eq. (18)) are shown in Fig. 11 The amplitude of
-function. The results obtained by the Landy-Szalay estimator
(Eq. (18)) are shown in Fig. 11 The amplitude of
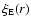 varies in the different subsamples. We refer to the amplitude variation of
varies in the different subsamples. We refer to the amplitude variation of 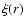 as shown by
Fig. 11 without making a detailed analysis of the power-law
exponent and the corresponding amplitude. The reason for this choice
lies in the insignificant values of formal statistical errors along
with large systematic errors (especially at large scales) due to the
finite volume and single realization. Instead of performing precise
estimations of r0 and
as shown by
Fig. 11 without making a detailed analysis of the power-law
exponent and the corresponding amplitude. The reason for this choice
lies in the insignificant values of formal statistical errors along
with large systematic errors (especially at large scales) due to the
finite volume and single realization. Instead of performing precise
estimations of r0 and 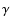 we simply demonstrate the general
behavior of the
we simply demonstrate the general
behavior of the 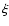 -function. This variation is due to fluctuations
in the large scale distribution of galaxies and thus they are volume
dependent effects. Therefore the amplitude of
-function. This variation is due to fluctuations
in the large scale distribution of galaxies and thus they are volume
dependent effects. Therefore the amplitude of 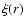 is affected by
finite-size effects as long as the distribution has not been found to
have relaxed to a uniform system. The Landy-Szalay estimator uses a sample density computed on a global sample scale, thus introducing a mixture of large scale and small scale properties in the measurement of correlations. Although the sample depth is of order of hundreds Mpc/h, finite size effects related to the presence of large scale structures can be still important. The use of the conditional density avoids both these problems.
is affected by
finite-size effects as long as the distribution has not been found to
have relaxed to a uniform system. The Landy-Szalay estimator uses a sample density computed on a global sample scale, thus introducing a mixture of large scale and small scale properties in the measurement of correlations. Although the sample depth is of order of hundreds Mpc/h, finite size effects related to the presence of large scale structures can be still important. The use of the conditional density avoids both these problems.
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{Fig11.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg139.gif) |
Figure 11:
Estimation of the two-point reduced correlation
function in the different subsamples of the SGP400 VL sample by the
Landy-Szalay estimator (Eq. (18)). The length-scale r0 varies
from 6.1 Mpc/h to 7.7 Mpc/h in the different samples. |
| Open with DEXTER |
In order to explain the amplitude and slope variation observed by the
estimation of two-properties by 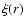 we introduce a simple
model. However one may repeat the following argument for any
distribution, and thus for any functional behavior of the conditional
density, one finds in the data. In the regime of strong clustering,
evidenced by the range of scales where
we introduce a simple
model. However one may repeat the following argument for any
distribution, and thus for any functional behavior of the conditional
density, one finds in the data. In the regime of strong clustering,
evidenced by the range of scales where 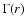 has not reached a clear flattening behavior, the determination of
has not reached a clear flattening behavior, the determination of 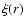 and thus of the average density, is sample size dependent.
and thus of the average density, is sample size dependent.
If the conditional density has a power-law behavior up to the size
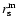 of the type
of the type
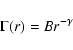 |
(21) |
with
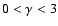 then the estimation of the sample average
through the conditional density in spheres is
then the estimation of the sample average
through the conditional density in spheres is
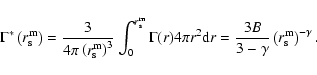 |
(22) |
Thus from Eq. (19) we find that
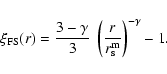 |
(23) |
Equation (23) easily takes into account both the amplitude
variation in samples of different size and the change of the slope as
a function of scale (due to the different regime of strong correlation
where the fit with a power-law is possible). From
Eq. (23) one may note that the slope depends on scale in
a continuous way: for example at r=r0 such that
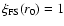 one easily derives that the local slope becomes
one easily derives that the local slope becomes 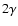 (see
Fig. 9). Hawkins et al. (2003) fitted the slope around the scale r0in the different samples (see their Table 1) with the consistent
result that the slope is 1.6.
(see
Fig. 9). Hawkins et al. (2003) fitted the slope around the scale r0in the different samples (see their Table 1) with the consistent
result that the slope is 1.6.
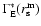 can differ from Eq. (21) in a single
sample determination: while the latter is the expectation value for
the ensemble average quantity, the former quantity is subject to
large finite size fluctuations. This implies that the scaling of the
amplitude of
can differ from Eq. (21) in a single
sample determination: while the latter is the expectation value for
the ensemble average quantity, the former quantity is subject to
large finite size fluctuations. This implies that the scaling of the
amplitude of
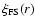 does not hold precisely in a single
measurement, while this is the expectation in an ensemble of
realizations (which is not possible to obtain in the analysis of a single sample).
does not hold precisely in a single
measurement, while this is the expectation in an ensemble of
realizations (which is not possible to obtain in the analysis of a single sample).
We have not directly measured the real space properties here. However
the same finite-size effects that perturb the redshift space reduced
two-point correlation function may affect the projected one (usually
called
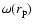 - see e.g. Davis & Peebles 1983). In general,
one may relate the real space
- see e.g. Davis & Peebles 1983). In general,
one may relate the real space
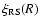 to the projected
to the projected
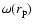 ,
where
,
where 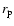 represents the projection of the redshift
space distance in a direction perpendicular to the line of sight,
through the following equation
represents the projection of the redshift
space distance in a direction perpendicular to the line of sight,
through the following equation
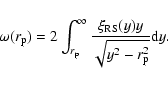 |
(24) |
Let us now consider the following situation: if the real space
conditional density has the behavior
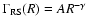 then we can repeat the argument which results in to
Eq. (23) with the result that
then we can repeat the argument which results in to
Eq. (23) with the result that
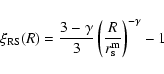 |
(25) |
where
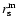 is the sample depth, as discussed. Thus the real space
is the sample depth, as discussed. Thus the real space
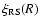 shows the same finite-size effects present in the redshift space correlation function previously discussed. If
shows the same finite-size effects present in the redshift space correlation function previously discussed. If
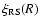 has a pure power-law behavior with
has a pure power-law behavior with 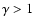 then
from Eq. (24) one gets
then
from Eq. (24) one gets
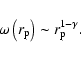 |
(26) |
In the present situation this is not the case, because the second
term in Eq. (25) gives an infinite contribution when
integrated over all space. In practice however one truncates the
integral to scales of order of
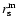 and one expects to recover
Eq. (26) only at small enough scales. Thus
and one expects to recover
Eq. (26) only at small enough scales. Thus
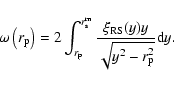 |
(27) |
The finite size effect introduced by the cut-off
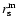 may well take
into account the observed shape of
may well take
into account the observed shape of
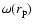 .
For example for
.
For example for
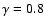 we get from Eqs. (25) and (27) the
behavior shown in Fig. 12, which is very similar to the one
measured by Hawkins et al. (2003). Hence, while in this example
we get from Eqs. (25) and (27) the
behavior shown in Fig. 12, which is very similar to the one
measured by Hawkins et al. (2003). Hence, while in this example
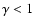 we get that
we get that
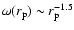 in some finite
range of scales: this is a finite size effect similar to the one
varying the estimation of the exponent of the redshift space correlation
function. Note that a similar finite-size effect may be present in
the measurement of the angular two-point correlation function (see
e.g., Montuori & Sylos Labini 1997).
While we are clearly not able to make a definitive statement about
whether the behavior of
in some finite
range of scales: this is a finite size effect similar to the one
varying the estimation of the exponent of the redshift space correlation
function. Note that a similar finite-size effect may be present in
the measurement of the angular two-point correlation function (see
e.g., Montuori & Sylos Labini 1997).
While we are clearly not able to make a definitive statement about
whether the behavior of
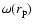 found by, for instance, Hawkins
et al. (2003), is perturbed by systematic biases, our analysis shows
that one needs to consider finite size effects explicitly also for the
computation of the real space properties.
found by, for instance, Hawkins
et al. (2003), is perturbed by systematic biases, our analysis shows
that one needs to consider finite size effects explicitly also for the
computation of the real space properties.
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig12.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg157.gif) |
Figure 12:
Behavior of
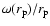 computed numerically
from Eqs. (25) and (27) with
computed numerically
from Eqs. (25) and (27) with
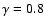 and
and
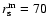 Mpc/h. The dashed line has a slope of -1.5. Mpc/h. The dashed line has a slope of -1.5. |
| Open with DEXTER |
We have studied redshift space correlation properties of six volume
limited samples extracted from the 2dFGRS. We have considered several
statistical properties. Particularly, the characterization of
small-scale properties through the nearest neighbor probability
density allow us to determine the smallest scale up to which
correlation properties can be studied in a robust way. In fact, at
scales smaller than the average distance between nearest neighbors,
typically in the range of few Mpc/h (see Table 2), discrete shot noise dominates the measurements leading to deviations from a power-law behavior. Whether
the result of Zehavi et al. (2004), who found departures from a power
law behavior in the galaxy correlation function of some samples of the
SDSS catalog can be interpreted in this way, i.e. as dominated by
nearest-neighbor correlations, is an open question, as they did not
mention the average distance between nearest neighbors in their
sample, and they performed the analysis in real space instead of
redshift space as we do here.
For the conditional average density we find that it is characterized
fairly well by a power-law behavior in the range between 0.5 and 40 Mpc/h, where the exponent is
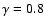
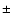 0.2. This result is very robust at small scales (r< 20 Mpc/h), as the volume average can be properly performed, and it becomes progressively weaker when the
limits of the sample (set by the radius
0.2. This result is very robust at small scales (r< 20 Mpc/h), as the volume average can be properly performed, and it becomes progressively weaker when the
limits of the sample (set by the radius
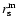 of the largest sphere
fully contained in it) are reached. Systematic noise, due to
non-averaged large fluctuations, increases when
of the largest sphere
fully contained in it) are reached. Systematic noise, due to
non-averaged large fluctuations, increases when
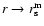 :
one way to overcome this problem is to consider larger samples. In
this respect it is useful to compare our results with the ones derived
by Hogg et al. (2005) by analyzing the largest sample ever studied for
this correlation analysis. They considered a sample of luminous red
galaxies, covering a volume of about
:
one way to overcome this problem is to consider larger samples. In
this respect it is useful to compare our results with the ones derived
by Hogg et al. (2005) by analyzing the largest sample ever studied for
this correlation analysis. They considered a sample of luminous red
galaxies, covering a volume of about 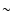 0.6 (Gpc/h)3. They
found the same power-law as we find here up to 20/30 Mpc/h. They then
detected a slow crossover toward homogeneity which is eventually
reached at 70 Mpc/h. With the data we have considered here, due to the
limited solid angle of the survey, we are not able to confirm or
disprove this result. In this respect it is worth noticing that, for
example, Sylos Labini et al. (1998) found a similar value for the
redshift space correlation exponent for the conditional density at
those scales: extending the analysis to larger scales, with
statistical tests of weaker robustness, they however found evidence
for a continuation of correlations with almost the same exponent up to
scales of the order of one hundred Mpc/h. Apparently the results by
Hogg et al. (2005) do not confirm completely such findings.
0.6 (Gpc/h)3. They
found the same power-law as we find here up to 20/30 Mpc/h. They then
detected a slow crossover toward homogeneity which is eventually
reached at 70 Mpc/h. With the data we have considered here, due to the
limited solid angle of the survey, we are not able to confirm or
disprove this result. In this respect it is worth noticing that, for
example, Sylos Labini et al. (1998) found a similar value for the
redshift space correlation exponent for the conditional density at
those scales: extending the analysis to larger scales, with
statistical tests of weaker robustness, they however found evidence
for a continuation of correlations with almost the same exponent up to
scales of the order of one hundred Mpc/h. Apparently the results by
Hogg et al. (2005) do not confirm completely such findings.
Leaving the question of the extension of the power-law behavior to
further studies, we focus now on the interpretation of small-scale
correlations. Up to the scale of a few tens of Mpc/h, the conditional
density 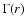 show a power-law behavior, with exponent
show a power-law behavior, with exponent
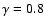
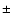 0.2 and well defined amplitude, although with some
fluctuations in different sky regions. As discussed, the amplitude of
the conditional density varies in different VL samples according to
the luminosity of the galaxies selected. This has a very simple
explanation, that brighter galaxies are less frequent than fainter
ones. One can develop an analytical formalism by considering the
effect of the galaxy luminosity function to understand this change: in
the hypothesis that space and luminosity are not correlated, usually
adopted in studies of large scale galaxy distribution, one can
quantitatively compute the amplitude of the conditional density in
different samples.
0.2 and well defined amplitude, although with some
fluctuations in different sky regions. As discussed, the amplitude of
the conditional density varies in different VL samples according to
the luminosity of the galaxies selected. This has a very simple
explanation, that brighter galaxies are less frequent than fainter
ones. One can develop an analytical formalism by considering the
effect of the galaxy luminosity function to understand this change: in
the hypothesis that space and luminosity are not correlated, usually
adopted in studies of large scale galaxy distribution, one can
quantitatively compute the amplitude of the conditional density in
different samples.
We have discussed that the results we get for the reduced two-point
correlation function, although in agreement with the ones obtained by
other groups, are affected by finite size effects. The reason is
simply that as long as the distribution presents strong fluctuations,
the study of 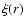 is problematic. The regime of strong
fluctuations is described by a certain functional behavior of the
conditional density
is problematic. The regime of strong
fluctuations is described by a certain functional behavior of the
conditional density 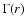 ,
in the present case a power-law
function. In this situation the estimation of the sample density is
not only affected by large (statistical) noise, but it becomes sample
size dependent, i.e. by a systematic effect. However because of the
intrinsic large fluctuations systematic and statistical noise are
entangled in the information provided by the amplitude of
,
in the present case a power-law
function. In this situation the estimation of the sample density is
not only affected by large (statistical) noise, but it becomes sample
size dependent, i.e. by a systematic effect. However because of the
intrinsic large fluctuations systematic and statistical noise are
entangled in the information provided by the amplitude of 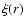 .
Thus explicit tests for systematic finite size effects are needed, and
these are provided by the analysis of the conditional density.
.
Thus explicit tests for systematic finite size effects are needed, and
these are provided by the analysis of the conditional density.
- Baryshev, Yu.,
& Teerikorpi, P. 2005, Bull. Special Astrophys. Obs., 59, in
press [arXiv:astro-ph/0505185]
(In the text)
- Basilakos, S., &
Plionis, M. 2003, ApJ, 593, L91 [NASA ADS] (In the text)
- Cole, S., et al. (The
2dFGRS team) 2005, MNRAS, in press
[arXiv:astro-ph/0501174]
(In the text)
- Colless, M., et
al. (The 2dFGRS team) 2003 [arXiv:astro-ph/0306581]
(In the text)
- Davis, M., & Peebles,
P. J. E. 1983, ApJ, 267, 46 [NASA ADS] (In the text)
- Gabrielli,
A., Sylos Labini, F., Joyce, M., & Pietronero, L. 2004,
Statistical physics for cosmic structures (Springer Verlag)
(In the text)
- Gaztanaga, E., et al.
2005 [arXiv:astro-ph/0506249]
(In the text)
- Hawkins, E.,
Maddox, S., Cole, S., et al. (The 2dFGRS team) 2003, MNRAS, 346,
78
(In the text)
- Hogg, D. W.,
Eisenstein, D., Blanton, M., et al. 2005, ApJ, 624, 54 [NASA ADS] [CrossRef] (In the text)
- Joyce, M., Montuori, M.,
& Sylos Labini, F. 1999, ApJ, 514, L5 [NASA ADS] [CrossRef] (In the text)
- Joyce, M., Sylos
Labini, F., Gabrielli, A., Montuori, M., & Pietronero, L. 2005,
A&A, 443, 11 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kerscher, M.,
Szapudi, I., & Szalay, A. S. 2000, ApJ, 535, L13 [NASA ADS] [CrossRef] (In the text)
- Landy, S. D., &
Szalay, A. 1993, ApJ, 412, 64 [NASA ADS] [CrossRef] (In the text)
- Madgwick, D.
S., Lahav, O., et al. 2002, MNRAS, 333, 133 [NASA ADS] [CrossRef] (In the text)
- Madgwick,
Hawkins, E., Lahav, O., et al. (The 2dFGRS team) 2003, MNRAS, 344,
847
(In the text)
- Montuori, M., & Sylos
Labini, F. 1997, ApJ, 487, L21 [NASA ADS] [CrossRef] (In the text)
- Norberg, E.,
Baugh, C., Hawkins, E., et al. 2001, MNRAS, 328, 64 [NASA ADS] [CrossRef] (In the text)
- Norberg, E.,
Baugh, C., Hawkins, E., et al. 2002, MNRAS, 332, 827 [NASA ADS] [CrossRef] (In the text)
- Peebles, P. J. E.
1980, The Large-Scale Structure of the Universe (Princeton Univ.
Press, Princeton, New Jersey)
(In the text)
- Peebles, P. J. E.
2001, in Historical Development of Modern Cosmology, ed. V. J.
Martinez, V. Trimble, & M. J. Pons-Borderi, ASP Conf. Ser.
[arXiv:astro-ph/0103040]
(In the text)
- Peebles, P. J.
E. 2001, ApJ, 557, 495 [NASA ADS] [CrossRef] (In the text)
- Sivakoff, G. R., &
Saslaw, W. C. 2005, ApJ, 626, 795 [NASA ADS] [CrossRef] (In the text)
- Sylos Labini, F.,
Montuori, M., & Pietronero, L. 1998, Phys. Rep., 293, 61 [NASA ADS] [CrossRef] (In the text)
- Sylos Labini, F. 2005
[arXiv:astro-ph/0507277]
(In the text)
- Tikhonov, A. V., Makarov,
D. I., & Kopylov, A. I. 2000, Bull. Spec. Astrophys. Obs., 50,
39 [NASA ADS] (In the text)
- Tikhonov, A. V., &
Makarov, D. I. 2003, Astron. Lett., 29, 289 [NASA ADS] [CrossRef] (In the text)
- York, D., Adelman,
J., Anderson, J. E., Jr., et al. 2000, AJ, 120, 1579 [NASA ADS] [CrossRef] (In the text)
- Zehavi, I.,
Weiberg, D. H., Zheng, Z., et al. 2004, ApJ, 608, 16 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006
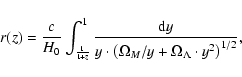
![\begin{displaymath}%
M = b_{\rm J} - 5 \cdot \log_{10}\left[r(z) \cdot (1+z)\right] - K_i(z) - 25.
\end{displaymath}](/articles/aa/full/2006/08/aa3902-05/img45.gif)
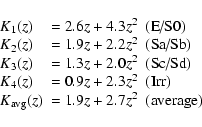
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{Fig1.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg58.gif)
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig2.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg59.gif)
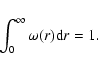
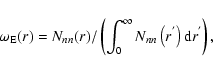
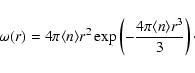
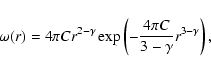
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{Fig3.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg74.gif)
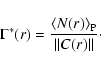
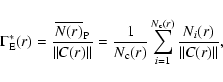
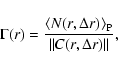
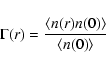
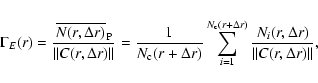
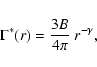
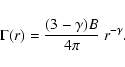
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig4.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg95.gif)
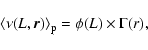
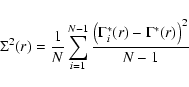
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig5.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg107.gif)
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig6.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg108.gif)
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig7.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg109.gif)
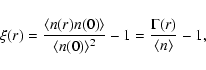
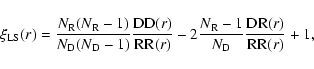
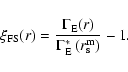
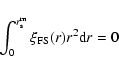
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{Fig8.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg121.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{Fig9.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg125.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{Fig10.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg126.gif)
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{Fig11.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg139.gif)
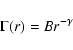
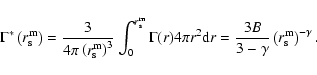
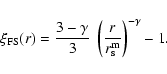
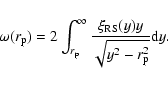
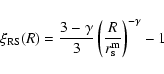
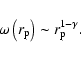
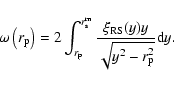
![\begin{figure}
\par\includegraphics[width=8.35cm,clip]{Fig12.eps}\end{figure}](/articles/aa/full/2006/08/aa3902-05/Timg157.gif)