A&A 447, 413-418 (2006)
DOI: 10.1051/0004-6361:20053668
1 - Centre de Physique
Théorique, CNRS - Luminy, Case
907, 13288 Marseille Cedex 9, France
2 -
Centre de Physique des Particules de
Marseille, CNRS - Luminy, Case
907, 13288 Marseille Cedex 9, France
Received 21 June 2005 / Accepted 23 September 2005
Abstract
Aims. We study the image of the transform from scale parameters to Hubble diagrams and present a lower bound on the radius of the universe today a0 and a monotonicity constraint on the Hubble diagram.
Methods. Our theoretical input is minimal: Einstein's kinematics and maximally symmetric universes.
Results. Present supernova data yield
![]() ,
i.e.
,
i.e.
![]() .
We attempt to quantify the monotonicity constraint and do not see any indication of non-monotonicity.
.
We attempt to quantify the monotonicity constraint and do not see any indication of non-monotonicity.
Key words: cosmological parameters
In a homogeneous, isotropic, expanding universe, the
apparent luminosity of a standard candle is a monotonically decreasing
function of the time of flight of emitted photons if the universe is open.
This is also true in spherical universes if the time of flight is small
enough with respect to the radius divided by the speed of light.
In principle, the (apparent) luminosity ![]() as a function of time can
be used to measure the scale factor a(t). In reality, arriving photons do
not tell us their time of flight, but only their spectral deformation,
as a function of time can
be used to measure the scale factor a(t). In reality, arriving photons do
not tell us their time of flight, but only their spectral deformation,
![]() ,
where
,
where ![]() is the frequency of
the photon. In an expanding universe
z is positive, "red shift''. If we pretend to know the scale factor a(t), we
can compute the luminosity
is the frequency of
the photon. In an expanding universe
z is positive, "red shift''. If we pretend to know the scale factor a(t), we
can compute the luminosity
![]() and confront it with the Hubble diagram. The transform
and confront it with the Hubble diagram. The transform
![]() reminds us of the Fourier transform and of
course we are interested in the inverse transform
reminds us of the Fourier transform and of
course we are interested in the inverse transform
![]() .
Therefore we must ask three questions: what is the domain of
definition of the initial transform, what is its
image, and is the transform injective? Also, should the
measured luminosity
.
Therefore we must ask three questions: what is the domain of
definition of the initial transform, what is its
image, and is the transform injective? Also, should the
measured luminosity ![]() be "far away'' from the image our working
hypotheses are made to test.
be "far away'' from the image our working
hypotheses are made to test.
We assume the kinematics of general relativity:
We also assume the comological hypotheses of maximally symmetric spaces:
![$\displaystyle c^2\hbox{\rm {d}}\tau ^2=c^2\hbox{\rm {d}}t^2-a(t)^2\left[ \hbox{...
...c x^2+k~\frac{(\vec
x\cdot \hbox{\rm {d}}\vec x)^2}{1-k\vec x^2}~ \right] \cdot$](/articles/aa/full/2006/08/aa3668-05/img17.gif) |
(1) |
From these hypotheses we can compute (see for instance Berry 1976)
the (apparent) luminosity
![]() of a standard candle in Watt
of a standard candle in Watt
![]() as a function of
emission time t
as a function of
emission time t
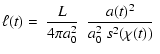 |
(2) |
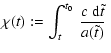 |
(3) |
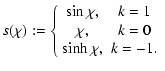 |
(4) |
From the above hypotheses, we can also compute the spectral
deformation as a function of emission time,
| (5) |
If we suppose that the scale factor is strictly
increasing with
![]() ,
then z is positive, "red shift'', and
we can invert the function
z(t). For convenience, we write t(z) for its inverse. Then the
Hubble diagram is a function
,
then z is positive, "red shift'', and
we can invert the function
z(t). For convenience, we write t(z) for its inverse. Then the
Hubble diagram is a function
![]() that, still for convenience, is written
that, still for convenience, is written
![]() ,
,
| (6) |
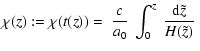 |
(7) |
The short distance divergency now is at z=0 and easy to get rid of. Let us
define the regularized luminosity
| (10) |
Let us first try to describe the image, that is, all luminosity functions
![]() that can be obtained from strictly increasing scale factors
a(t) with
that can be obtained from strictly increasing scale factors
a(t) with ![]() and with
and with
![]() .
.
We already know that
![]() comes with the short distance divergency at
z=0, which is such that
comes with the short distance divergency at
z=0, which is such that
![]() is regular there.
For open universes, there are no other singularities. In fact,
is regular there.
For open universes, there are no other singularities. In fact,
![]() is a decreasing function. For closed universes, on
the other hand,
g(z) goes through a minimum as the photons pass the equator,
is a decreasing function. For closed universes, on
the other hand,
g(z) goes through a minimum as the photons pass the equator,
![]() .
From there on, the luminosity increases again and goes to the
antipode divergency. It might happen, of course, that the equator is
masked by the horizon, in which case g(z) remains decreasing forever,
even though the universe is closed.
.
From there on, the luminosity increases again and goes to the
antipode divergency. It might happen, of course, that the equator is
masked by the horizon, in which case g(z) remains decreasing forever,
even though the universe is closed.
Let us now ask whether the transform is injective in the domain of
increasing scale factors.
If we pretend to know k, the answer is
affirmative for open universes. Indeed, solving Eq. (8) for
![]() and differentiating with respect to z yields (Esposito-Farèse
& Polarski
2001)
and differentiating with respect to z yields (Esposito-Farèse
& Polarski
2001)
| |
= | 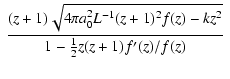 |
|
| = | 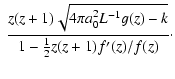 |
(11) |
Integrating the Hubble rate with respect to t gives us the
scale factor with the ambiguity of the initial condition a0. But for flat
universes, this initial condition is unphysical. By
a coordinate transformation of ![]() ,
we can set a0=1 m. This is
different for curved universes, where a0 is related to a local
observable, the curvature. In the closed case, a0 is also related to a global
observable, the
radius of the universe today. However, unless g(z) already exhibits an
increase, only a lower bound on the radius today can be reconstructed
from the luminosity,
,
we can set a0=1 m. This is
different for curved universes, where a0 is related to a local
observable, the curvature. In the closed case, a0 is also related to a global
observable, the
radius of the universe today. However, unless g(z) already exhibits an
increase, only a lower bound on the radius today can be reconstructed
from the luminosity,
If we admit that we do not know k and if the luminosity function
![]() satisfies (i)
satisfies (i)
![]() is regular at z=0; and (ii)
is regular at z=0; and (ii)
![]() is decreasing, then there are three positive functions
is decreasing, then there are three positive functions
![]() and
a(t), such that the universes with scale
factor
a-(t), k=-1, with scale factor a(t), k=0 and with scale
factors a+(t), k=1 have the same luminosity function
and
a(t), such that the universes with scale
factor
a-(t), k=-1, with scale factor a(t), k=0 and with scale
factors a+(t), k=1 have the same luminosity function ![]() .
These
three scale factors satisfy
.
These
three scale factors satisfy
Example (constant deceleration parameter):
take the scale factor,
| (15) |
| v |
= | ||
| = | (16) |
Example (constant regularized luminosity):
suppose we have measured a constant regularized luminosity
![]() .
Then the Hubble rate is
.
Then the Hubble rate is
| (17) |
| a(t) | = | ![$\displaystyle a_0(2H_0t)^{1/2} \sqrt{1-k\left[
~\frac{1-(2H_0t)^{1/2}}{a_0H_0/c}~\right] ^2},$](/articles/aa/full/2006/08/aa3668-05/img65.gif) |
|
| (18) |
| (19) |
Example (constant Hubble rate):
to have an example without a horizon, consider the scale factor
| (20) |
Example (closed universe):
suppose we have measured the luminosity:
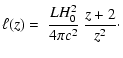 |
(21) |
Counter-example (wiggling g(z)):
suppose we have measured the luminosity, Fig. 1:
 |
Figure 1: The monotonic luminosity (22). |
| Open with DEXTER | |
 |
Figure 2: Its wiggling g(z). |
| Open with DEXTER | |
The last two examples illustrate that our constraint of monotonic g(z)is stronger than the constraint of monotonic luminosity ![]() .
.
If the scale factor is strictly decreasing, we get similar results with a
negative spectral deformation: -1<z<0, "blue shift''.
One might think that one can produce non-monotonic functions g(z)by starting from non-monotonic scale factors a(t), but this is not true. In
fact any non-monotonic scale factor produces multi-valued luminosities
in terms of the spectral deformation z. The first example is, of course,
the constant scale factor with no spectral deformation, ![]() ,
but
varying luminosity. A more generic example is shown in Fig. 3:
,
but
varying luminosity. A more generic example is shown in Fig. 3:
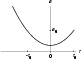 |
Figure 3: The non-monotonic scale factor (23). |
| Open with DEXTER | |
| (24) |
![$\displaystyle \chi (t) =
c\sqrt{~\frac{2}{g\alpha }~ }\left[
\arctan\left(
\sqr...
...lpha }~} t_0\right) -\arctan\left(
\sqrt{~\frac{g}{2\alpha }~} t\right)\right],$](/articles/aa/full/2006/08/aa3668-05/img88.gif) |
(25) |
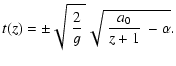 |
(26) |
 |
Figure 4: The regularized luminosity of the non-monotonic scalefactor (23) |
| Open with DEXTER | |
We use the "Gold'' sample data compiled by Riess et al. (2004) with
157 SN's, including a few at z>1.3 from the Hubble Space Telescope (HST
GOODS ACS Treasury survey). For convenience we normalize the
luminosity to the maximum absolute SN luminosity estimated by Jha et al.
(1999), Saha et al. (2001), and Gibson & Stetson
(2001),
![]() W. The Hubble rate today H0 is
taken as
W. The Hubble rate today H0 is
taken as
![]() km
km
![]() (Krauss 2001; Raux 2003).
(Krauss 2001; Raux 2003).
The regularized luminosity allows us to extract
LH02 from the Hubble diagram with small red shift, Fig. 5.
The value f(0) is extracted by a second order polynomial extrapolation
fit on the SN data up to a red shift of 0.1. By construction, the fitted
value f(0) is equal to
![]() ,
where
the error is only coming from the fit itself.
,
where
the error is only coming from the fit itself.
The first of Eqs. (9) and Eq. (12) together give the
lower bound on
a0 as
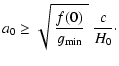 |
(27) |
| |
|||
| (28) |
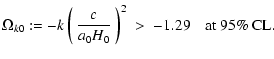 |
(29) |
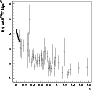 |
Figure 5: The regularized luminosity as measured today (Riess et al. 2004), with a binning of 0.02 in red shift. The full line at low red shift corresponds to a second order polynomial extrapolation fit. |
| Open with DEXTER | |
Let us compare this bound with the one obtained from the SN data but
now adding the dynamics of the
![]() cosmology fitting the
matter density
cosmology fitting the
matter density
![]() ,
the cosmological constant density
,
the cosmological constant density
![]() ,
and the nuisance normalization parameter, but without any
other input constraint:
,
and the nuisance normalization parameter, but without any
other input constraint:
![]() at 95% CL.
at 95% CL.
Including ![]() ray bursts with their high z potentially
improves our bound, but does not do so at present because of the high
uncertainty of their absolute luminosity. Also, we expect a small improvement
on our bound from SNAP data:
ray bursts with their high z potentially
improves our bound, but does not do so at present because of the high
uncertainty of their absolute luminosity. Also, we expect a small improvement
on our bound from SNAP data:
![]() ,
,
![]() at 95% CL. This improvement relies on the assumption that the central values of
the apparent luminosities will not change significantly and comes from
the reduction of the error bars, mainly due to adding more
nearby supernovae (Yèche et al. 2006).
at 95% CL. This improvement relies on the assumption that the central values of
the apparent luminosities will not change significantly and comes from
the reduction of the error bars, mainly due to adding more
nearby supernovae (Yèche et al. 2006).
Of course our bound from supernova data cannot compete with constraints from CMB anisotropy data. It has, however, the virtue of not being subject to any dynamical hypotheses, like a cosmological constant, dark matter, exotic equations of state, power spectra, inflation, etc.
![\begin{figure}
\par {\includegraphics[width=8.8cm]{3668fig6.ps}\\ [8mm]
\includegraphics[width=8.8cm]{3668fig7.ps} }
\par\end{figure}](/articles/aa/full/2006/08/aa3668-05/Timg115.gif) |
Figure 6:
Color contours: significance of wiggle detection (vertical
colour scale) as function of the
wiggle position |
| Open with DEXTER | |
We must now ask the question whether the data is compatible with a
monotonic luminosity ![]() .
We will also ask the finer question of
whether g(z) is monotonic.
.
We will also ask the finer question of
whether g(z) is monotonic.
To detect non-monotonicity in the SN data set, we assume that the
luminosity ![]() and its g(z) can be described by monotonic
functions to which we add a simple Gaussian:
and its g(z) can be described by monotonic
functions to which we add a simple Gaussian:
![$\displaystyle \ell(z,LH_0^2,p)=~\frac{LH_0^2}{4\pi c^2}~\left(
\frac{p-1}{(z+1)[1-(z+1)^{1-p}]}\right) ^2 ,$](/articles/aa/full/2006/08/aa3668-05/img119.gif) |
(32) |
Our wiggle detection
procedure
consists of scanning the plane in wiggle position
![]() and wiggle width
and wiggle width
![]() in steps of 0.01 in both directions.
In each point
in steps of 0.01 in both directions.
In each point
![]() of this plane, we
fit the normalization LH02, the power pand the wiggle amplitude
of this plane, we
fit the normalization LH02, the power pand the wiggle amplitude ![]() .
Warning: if the wiggle amplitude
.
Warning: if the wiggle amplitude ![]() is smaller than a critical
amplitude
is smaller than a critical
amplitude
![]() the modified functions (30) and (31) will still
be monotonic.
the modified functions (30) and (31) will still
be monotonic.
We could claim that ![]() ,
and all the more the luminosity g(z), is
not monotonic if the ratio between the fitted wiggle
amplitude and the associated error is greater than 5 (5
,
and all the more the luminosity g(z), is
not monotonic if the ratio between the fitted wiggle
amplitude and the associated error is greater than 5 (5![]() level
detection) and if the wiggle amplitude is greater than the critical one.
The sensitivity of the method is computed by Monte Carlo simulation. The
same SN sample as the Riess data set with the same statistical power is
simulated by assuming the
level
detection) and if the wiggle amplitude is greater than the critical one.
The sensitivity of the method is computed by Monte Carlo simulation. The
same SN sample as the Riess data set with the same statistical power is
simulated by assuming the
![]() cosmology, and a wiggle of positive or
negative amplitude is added to
cosmology, and a wiggle of positive or
negative amplitude is added to ![]() and g(z) for each
point in the (
and g(z) for each
point in the (![]() ,
,
![]() )
plane. We apply the wiggle detection
procedure to each simulation, restricted to a small grid of points
around the simulated one to speed the processing up. The significance of
the wiggle amplitude
)
plane. We apply the wiggle detection
procedure to each simulation, restricted to a small grid of points
around the simulated one to speed the processing up. The significance of
the wiggle amplitude
![]() is computed at each point, and the
smaller value from the positive or negative wiggle amplitude is retained. The
sensitivity is computed at a
is computed at each point, and the
smaller value from the positive or negative wiggle amplitude is retained. The
sensitivity is computed at a ![]() level corresponding to a
level corresponding to a ![]() confidence level exclusion limit on the wiggle magnitude
confidence level exclusion limit on the wiggle magnitude ![]() defined
by
defined
by
| (33) |
Figure 6 shows the significance of the wiggle fit
performed on the Riess data sample (color contours) for the luminosity
![]() and
g(z) with
and
g(z) with ![]() varying from 0.01 to 1.8 and
varying from 0.01 to 1.8 and
![]() from 0.01 to 2 in steps of 0.01 in both directions. The maximum
significance for both
from 0.01 to 2 in steps of 0.01 in both directions. The maximum
significance for both ![]() and g(z) is 2.4 for a wiggle at the position
and g(z) is 2.4 for a wiggle at the position
![]() ,
with width of 0.07. The wiggle magnitude is
,
with width of 0.07. The wiggle magnitude is
![]() for
luminosity
for
luminosity ![]() ,
and
,
and
![]() for g(z). The dashed lines
indicate the location of the critical wiggle magnitude
for g(z). The dashed lines
indicate the location of the critical wiggle magnitude
![]() of a
positive wiggle that breaks the monotonicity.
of a
positive wiggle that breaks the monotonicity.
No wiggle greater than this value is observed, so we conclude that no
wiggle is detected at a ![]() level using the actual SN data set. On
the same figures, the sensitivity for different values of the wiggle
magnitude is shown (plain line). Wiggles of magnitude greater than
2 are excluded at
level using the actual SN data set. On
the same figures, the sensitivity for different values of the wiggle
magnitude is shown (plain line). Wiggles of magnitude greater than
2 are excluded at ![]() CL up to a redshift of 1.6. Up to a redshift of 1,
the
CL up to a redshift of 1.6. Up to a redshift of 1,
the ![]() CL exclusion limit on the wiggle magnitude is
0.6. These two magnitudes are below the critical magnitudes;
therefore, these wiggles do not upset the monotonicity.
CL exclusion limit on the wiggle magnitude is
0.6. These two magnitudes are below the critical magnitudes;
therefore, these wiggles do not upset the monotonicity.