A&A 447, 769-781 (2006)
DOI: 10.1051/0004-6361:20034226

Calibration of the PRONAOS/SPM submillimeter photometer

F. Pajot¹ - B. Stepnik¹ - J.-M. Lamarre² - J.-P. Bernard³ - X. Dupac³⁴ - M. Giard³ - G. Lagache¹ - B. Leriche¹ - C. Meny³ - G. Recouvreur¹ - J.-C. Renault⁵ - C. Rioux¹ - I. Ristorcelli³ - G. Serra³ - J.-P. Torre⁶

1 - Institut d'Astrophysique Spatiale (IAS), Bât. 121, Université Paris-Sud 11 and CNRS (UMR8617), 91405 Orsay, France
2 - LERMA, CNRS, Observatoire de Paris, 61 av. de l'Observatoire, 75014 Paris, France
3 - Centre d'Étude Spatiale des Rayonnements, CNRS, 9 av. du Colonel Roche, BP 4346, 31028 Toulouse, France
4 - ESA-ESTEC, Astrophysics Division, Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
5 - Institut d'Astrophysique de Paris, CNRS, 98 bis bd. Arago, 75014 Paris, France
6 - Service d'Aéronomie, CNRS, BP 3, 91371 Verrières Le Buisson, France

Received 25 August 2003 / Accepted 14 October 2005

Abstract
Aims. PRONAOS is a stratospheric balloon-borne project dedicated to submillimeter astronomy. Sensitive to low emission gradients, PRONAOS allowed pointed observations in four photometric bands between 200 $\mu$m and 1.2 mm with an angular resolution of 2$^{\prime}$ to 3.5$^{\prime}$. We present here the PRONAOS calibration strategy and the accuracy achieved.
Methods. An absolute calibration scheme based on an Internal Calibration System provided original photometric data. The accurate determination of the spectral dependence of the measured fluxes is a key to the understanding of the cold universe.
Results. We demonstrate that the PRONAOS absolute photometric accuracy is 8% (1-$\sigma$) and that the channel to channel relative accuracy is 6% (1-$\sigma$). This calibration is checked against observations of Saturn. We show that the PRONAOS calibration is in good agreement with the present knowledge of the Saturn submillimeter emission. PRONAOS observations also agrees with the observations of several compact and extended sources by the COBE/DIRBE or the ISOPHOT instruments.

Key words: submillimeter - techniques: photometric - standards - balloons - planets and satellites: individual: Saturn

   
1 Introduction

Absolute calibration to the level of a few percent in the submillimeter range (100 $\mu$m to 1 mm) needs careful instrument design and characterisation. Two major physical effects make the calibration a difficult process in this range.

First, all components along the optical path radiate a submillimeter thermal emission which is several order of magnitude larger than the astrophysical signal. The total power received by the detectors is therefore dominated by a strong background emission whose control and knowledge are required to carry out the appropriate response corrections. The background emission can be dramatically reduced using appropriate techniques. The instrument is usually cooled down to very low temperatures (between a few and a few tenth of Kelvin) reducing both the thermal emission and the associated photon noise. Optical modulation such as chopping and nodding can be used to extract the astrophysical signal from the background due to the telescope and to the atmosphere. However, these techniques increase the calibration and operational complexity.

Second, the dimensions of optical components are not very large compared to the wavelength. Large diffraction effects are difficult to model or measure but need to be characterized for the determination of the optical efficiency and the far sidelobes. These two physical effects contribute to make submillimeter photometry among the least accurate astronomical measurements. The accuracy of absolute submillimeter calibrations is generally not better than 10%, and often much poorer, leading to poor photometric standards in this range. An important exception is the FIRAS instrument on the COBE satellite, which achieved an excellent absolute calibration accuracy of 3% (Fixsen et al. 1997) thanks to space conditions and the use of movable external blackbody filling the whole beam. However, FIRAS had a very small collecting optics diameter (less than 15 cm) giving a poor angular resolution (7$^{\circ}$) and this method cannot be used for a large diameter telescope with better angular resolution, such as PRONAOS .

PRONAOS ("PROgramme National d'AstrOnomie Submillimétrique'') is a stratospheric balloon borne project devoted to submillimeter astronomy. PRONAOS carries a two meter telescope and measures the submillimeter continuum emission in four large photometric bands with an angular resolution from 2$^{\prime}$ to 3.5$^{\prime}$ (FWHM). Ground and on-board blackbodies and a physical model of the telescope were used to calibrate the PRONAOS experiment. This provided an absolute calibration to point and extended sources without using any prior observations with other instruments or sky modelling. The calibration accuracy achieved for the PRONAOS experiment is 6% in relative (band to band) and 8% in absolute, as derived further in this paper. As of today, this is the best calibration accuracy obtained for a large diameter telescope observing in the submillimeter range. Such an accuracy was essential to the scientific analysis of the PRONAOS  data on the Sunyaev-Zel'dovich (SZ) effect (Lamarre et al. 1998), and on the interstellar medium emission (Ristorcelli et al. 1998; Bernard et al. 1999; Dupac et al. 2001; Stepnik et al. 2003; Dupac et al. 2002; Serra et al. 2002; Dupac et al. 2003) for which fine spectral variations and the absolute intensity of the interstellar medium emission were analysed. The absolute calibration accuracy of the PRONAOS project is one of its major strength. This paper describes the calibration scheme of the experiment and quantifies its accuracy.

The paper is organised as follows. In Sect. 2, we present the PRONAOS instrument and detail the optics, detectors and observing strategy aspects important to guaranty a good calibration. In Sect. 3, we describe the original calibration scheme developed for the PRONAOS experiment and the calibration accuracy reached for the whole experiment. In Sect. 4, we compare the point source absolute calibration of PRONAOS with a model of the Saturn planet emission (detailed in Appendix A). In Sect. 5, we compare our measurements with COBE/DIRBE observations of Galactic compact and extended sources and in Sect. 6 with ISOPHOT maps of Galactic sources.

  
2 PRONAOS instrument

  
2.1 Project overview

PRONAOS is a French project conducted by CNES, designed and built in cooperation between CNES and several CNRS laboratories. PRONAOS  is a stratospheric balloon-borne two meter telescope, devoted to submillimeter astronomy (see Fig. 1). A dedicated stellar sensor (Buisson & Durand 1990; Serra et al. 1997) allows telescope pointing with an absolute accuracy and stability of 20 $^{\prime\prime}$. PRONAOS was launched from Fort Sumner, New Mexico (USA), as part of the NSBF-NASA launch campaigns. Three flights were conducted in 1994 (FS94), 1996 (FS96) and 1999 (FS99). About 20 sources of 0.5 $^{\circ^{2}}$ were observed totalling about 30 h of observations.

The PRONAOS focal plane instrument SPM (Spectro Photomètre Multibande, Lamarre et al. 1994), has been designed to simultaneously perform sensitive measurements in four wide spectral bands at 200, 260, 360 and $580~{\rm\mu m}$ (Table 1). PRONAOS/SPM is a single beam multi-band instrument. Background emission, including the contributions of the optics, telescope and the residual atmosphere at the flight altitude is reduced using a wobbling mirror (Sect. 2.3). Beam switching on the sky is performed at a constant zenith angle, with a 6$^{\prime}$ peak-to-peak amplitude and a sampling frequency of 19.5 Hz. Thus, the measured signal is a difference between sky fluxes at +3$^{\prime}$ ("plus beam'') and -3$^{\prime}$ ("minus beam'') of the telescope axis. The Sunyaev-Zel'dovich measurements were carried using a 5 sky position sequence where the "plus beam'' successively observes on source, left, on, right, on, above, on, below, on (Lamarre et al. 1998). In order to obtain maps of extended or compact sources, the sky was scanned in an "on the fly'' mode. In all observing modes, beam switching was employed and the observations are therefore sensitive only to the emission gradients of the sky brightness and reconstruction of the astrophysical signal therefore requires deconvolution from the dual beam pattern. Note that this is also true for ground based submillimeter continuum observations.

	Figure 1: Artist view of the PRONAOS/SPM gondola in flight. The front side of the telescope is not represented in order to show the primary mirror structure and the focal plane instrument.
Open with DEXTER

Table 1: PRONAOS/SPM bands characteristics. $\lambda _{\rm eff,dust}$ is the effective wavelength for a standard 30 K dust spectrum with a $\lambda ^{-2}$ emissivity law and $\lambda _{\rm eff,SZ}$ is the effective wavelength for the Sunyaev-Zel'dovich thermal effect (Lamarre et al. 1998). The definitions of $\lambda _{\rm ref}$ and $\lambda _{\rm eff}$ are detailed in Sect. 3.1.2.

2.2 Detectors

Each channel uses one DC polarised bolometer. Bolometers of channels 1 and 2 are commercial silicon bolometers from Infrared Laboratories Inc. Channel 3 uses a composite bolometer (Leblanc et al. 1975) with a 30 $\mu$m thick diamond substrate and a monolithic doped germanium thermistor (Leblanc et al. 1977). The bolometer of channel 4 is a "spider web'' bolometer developed by Bock et al. (1995), a design used since in a number of ground based or balloon submillimeter experiments and in the HFI instrument of the forthcoming Planck satellite mission (Lamarre et al. 2000). Each bolometer is fitted into an integrating sphere (Leblanc et al. 1985; Lamarre 1977). In order to achieve the lowest possible Noise Equivalent Power (NEP), the bolometers are cooled down to 0.3 K. The detectors cooling is produced by two closed cycle ³He mini-fridges (Torre & Channin 1985) inside the liquid ⁴He cryostat (Sect. 2.3). This system provides an intrinsic NEP smaller than 10^-15 W Hz^-1/2 at 19.5 Hz, below (bands 1 and 2) or close (bands 3 and 4) to the photon noise.

  
2.3 Optical design

PRONAOS is a Cassegrain focus telescope (diameter D=2 m, equivalent focal length F=20 m). The primary mirror (M 1) is segmented, with six light-weight panels (see Fig. 1). The panels and the secondary mirror (M 2) are held by a carbon fiber structure. Moreover, position sensors and actuators support the panels and compensate for the gravity and temperature effects. This system keeps the long term surface deformations to RMS values smaller than $12~{\rm\mu m}$.

The whole telescope is embedded in a sunshade protecting the optical system from external sources of heat, such as the sun, the earth and the balloon. The sunshade limits the temperature gradients along a diameter of the primary mirror to values less than a few Kelvin which is an important characteristic for a beam switching instrument. A cone placed on the secondary mirror prevents the instrument from seeing itself through the central hole of the primary mirror.

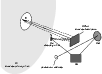	Figure 2: Design of the warm optics of the SPM instrument located behind the primary mirror M 1.
Open with DEXTER

The SPM instrument is composed of a warm and a cold optics. Both have been designed to minimize the spurious direct and diffracted thermal emission from the instrument.

The warm optics drives the radiation from the telescope into the cryostat (Fig. 2). The sky chopping is performed using a wobbling mirror (M 4) which is the optical conjugate of the telescope secondary mirror (M 2) through the M 3 mirror. The wobbling stability achieved is better than 1 $^{\prime\prime}$ on the sky. The wobbling mirror is in turn imaged by M 6 on the entrance cold stop in the cryostat. All mirrors are oversized with respect to the geometrical beam in order to limit the flux seen by diffraction from the outside of the mirrors. Special care was taken in the baffling around M 3, located in the focal plane, since it is where the field modulation takes place.

The cold optics is inside a ⁴He cryostat cooled down to 4 K at ground pressure and about 1.6 K at flight altitude pressure. The 1.6 K cold stop is the actual pupil of the optical system. At the cryostat entrance short wavelengths blocking filters ( $\lambda < 180~{\rm\mu m}$) are attached to the cryostat thermal screens. The four spectral bands are separated by three dichroics. For each channel, a short wavelength pass filter is located just in front of the field stop defining the field of view. Then, an off-axis parabolic mirror forms the image of the cold pupil on the entrance of the light cones and sends the image of the field stop at infinity. The toroidal-parabolic light cone, attached to the detector, achieves the optical matching of the beam with the bolometer.

Special attention has been given to straylight. Microwave absorbing baffles divide the different optical subsystems and allow to control the flux not coming from the optical path.

  
2.4 Optics alignment

The alignment of optics and the knowledge of the beam characteristics is essential to high sensitivity submillimeter photometry. The first step consists on aligning the telescope primary segmented mirror. The specific procedure used is described in Ristorcelli et al. (1997). The second step consists in the internal alignment of the focal instrument. Finally the instrument and telescope are aligned with respect to each other.

After an optical alignment in the visible using a HeNe laser beam, the adjustment of the SPM instrument optics is done in the submillimeter range. A dedicated modulated source is imaged on a small flat mirror (2 or 8 mm diameter) maintained at a 45$^{\circ}$ angle in the beam by a thin mount in order to minimize obscuration. This source is mounted on a two axis motorized table, and scanned across the beam. Maps representing the response of the system at different locations in the optical path are obtained and used to optimize the alignment of the different mirrors. Special care was given to the optical matching of the aperture stops (photometer cold stop, chopping mirror M 4, telescope secondary mirror M 2), taking into account the extended diffraction wings present at these wavelengths. Field stop alignment and size are also checked with the same method, and data are used to derive a first order model of the beam on the sky.

  
3 PRONAOS/SPM calibration

The PRONAOS/SPM calibration is based on ground based extensive characterisation and in-flight calibration. It only relies on measurements of blackbodies and on a physical instrument model. For this purpose, we have developed an extended absolute blackbody used on ground as a primary calibrator and an Internal Calibration System (ICS) composed of two blackbodies which is used in-flight as a secondary calibrator. The PRONAOS/SPM calibration is an absolute calibration against the ICS.

   
3.1 Spectral response

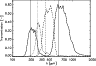	Figure 3: Measurements of the PRONAOS/SPM spectral response. The vertical lines correspond to the effective wavelength positions for each band (Sect. 3.1.2).
Open with DEXTER

3.1.1 Measurements

The spectral transmission measurement of the photometer is done on the ground. It has been measured using a Fourier transform spectrometer. Figure 3 shows the total transmission of the four PRONAOS/SPM bands. They are large bands covering the whole spectral range from 180 to $1100~{\rm\mu m}$ (Table 1).

   
3.1.2 Effective wavelengths

We refer to the PRONAOS/SPM photometric channels by the value of their reference wavelength, a rounded value close to their effective wavelength. The effective wavelength is a weighted average of the wavelength, using the product of the source spectral intensity by the transmission of the band as the weighting function:

$$\lambda_{\rm eff}=\frac{\int \lambda I({\lambda}) T_{r}(\lamb... ...rm d}\lambda}{\int I({\lambda}) T_{r}(\lambda) {\rm d}\lambda}$$ (1)

where $I({\lambda})$ is the source spectral intensity and $T_{r}(\lambda)$the photometer spectral transmission for a given band. Astronomical sources such as the dust observed in the interstellar medium have very steep spectra, such as:

$$I(\lambda) \propto \lambda^{-\beta} \times B_{\lambda}(T)$$ (2)

where $B_{\lambda}$ is the Planck function at a temperature T and $\beta$ is the spectral emissivity index. A typical spectral emissivity index is $\beta =2$ and gives a $I(\lambda) \propto \lambda^{-6}$ law for the source spectral intensity in the Rayleigh-Jeans domain. Therefore, most of the power comes from the short wavelength side of the photometric band. This is reflected in the effective wavelength values. The PRONAOS/SPM reference wavelengths $\lambda _{\rm ref}$ given in Table 1 are chosen close to the corresponding effective wavelength $\lambda _{\rm eff}$for a standard 30 K dust spectrum with a $\lambda ^{-2}$ emissivity law. The effective wavelengths for the Sunaev-Zel'dovich thermal effect were computed for band 3 and 4 only, where the effect is expected to be measurable, and the values found are noticeably different from those of dust (Table 1).

  
3.1.3 Color corrections

Wide photometric bands require color correction. The flux intensities measured using PRONAOS/SPM are computed at the reference wavelengths of Table 1. Different sources accounting for the same power measured in one PRONAOS spectral band but with different emission spectral shape will therefore have different intensities at the reference wavelengths. For example, at $200~{\rm\mu m}$ the flux intensity of a source with $T=30~\rm K$, $\beta =2$ is about 20% larger than that of a source with T=10 K, $\beta =2$. When the source spectrum is poorly known, color correction must be done iteratively: a first order correction is made assuming a given spectrum. Then, using the four PRONAOS/SPM channels, a better determination of the spectrum is obtained and the color correction is determined. This process is repeated until the correction gets smaller than 0.5%. Table 2 shows the color corrections taken into account when transforming the PRONAOS flux intensities from a $I_{\lambda} \propto \lambda^{-2} \times B_{\lambda}(T=30~\rm K)$ spectrum to a $I_{\lambda} \propto \lambda^{-\beta} \times B_{\lambda}(T)$spectrum.

Table 2: Color correction factors to be taken into account in order to transform the PRONAOS flux intensities from a (T=30 K, $\beta =2$) spectrum to a (T, $\beta$) or Rayleigh-Jeans (RJ) spectrum.

Table 3: PRONAOS/SPM transmission computed in the PRONAOS/SPM photometric bands and their 3$\sigma$ errors.

3.1.4 Errors on color correction

The PRONAOS/SPM instrument is calibrated against blackbodies. Color correction from calibration data to astronomical data, as shown in Table 2, relies on the knowledge of the spectral transmission of the photometric channels. An upper limit on the error on the color correction factors due to uncertainties on the filters transmission knowledge is determined using a simple simulation: the spectral transmission of a given channel is increased by 5% (3-$\sigma$) for $\lambda < \lambda_{\rm ref}$, a very pessimistic case. This leads to an error smaller than 1% (3$\sigma$) on the color correction factors of Table 2, the maximum error beeing obtained for Band 1, and a ( $T=10~\rm K$, $\beta =2$) spectrum.

3.2 Transmission

The PRONAOS/SPM response is obtained using the ICS, located close to the interface between the instrument and the telescope. The ICS over-illuminates the wobbling mirror (M 4). Determination of the absolute response on the sky then requires the evaluation of the telescope optical coupling with the mirror M 4 and of the sky transmission.

3.2.1 Instrument optical coupling with the sky

The optical coupling of the focal instrument with the sky is characterized by a factor combining the transmission of the telescope and the losses by diffraction. This factor is the ratio of the powers received by the instrument to (1) an extended uniform source filling the SPM instrument beam and (2) the same source filling the PRONAOS/SPM beam. Its measurement would require a very large vacuum chamber facility (>10 m) to hold both the telescope and a source simulator. Instead, we used an optical model of the telescope, developed during the design phase. This model uses classical diffraction Fresnel laws at finite distance, integrated numerically after proper use of symmetries. Straylight is computed by using a reverse propagation for the rays, starting from the exit pupil of the photometer and propagating them towards the sky. The results, shown in Table 3, take into account the presence of the secondary mirror (M 2) support spider, the transmission of the primary mirror (M 1), diffraction losses around it, the transmission of the secondary mirror, losses due to the cone on the secondary mirror (M 2), losses around the secondary mirror (M 2) and losses around the wobbling mirror (M 4). The instrument/sky coupling is the most important source of error in the PRONAOS/SPM error budget: the grid used for the numerical integration is optimized to limit the computing time and the real design is simplified in the model. This yield a 6% (3-$\sigma$) error contribution on the calibration.

   
3.2.2 Atmospheric transmission

We use the MODTRAN code (Berk et al. 1989) to compute the atmospheric transmission in the PRONAOS flight conditions. MODTRAN (MODerate-resolution TRANsmission) is a medium resolution atmospheric model (spectral resolution $\sim$1 cm^-1) derived from the program LOWTRAN (spectral resolution $\sim$20 cm^-1). These programs are commonly used by the atmospheric community and are based on the best data from laboratory spectroscopy taken in the Air Force Geophysics Laboratory database. We have used the version 7.0 of the MODTRAN program and computed the atmospheric transmission at 38 km, which is the PRONAOS/SPM flight altitude, and towards a 45$^{\circ}$ elevation direction, which is the mean elevation pointing direction of the PRONAOS/SPM observations. The results are presented in Table 3. The atmospheric absorption is almost negligible in the submillimeter range at stratospheric altitude (${<}1 \%$).

  
3.3 Beams characterisation

The calibration strategy exposed so far applies to extended sources (filling the beam) with uniform brightness. Beam characterisation is a crucial point in order to determine fluxes for point or compact sources. Straylight and beam profile are controlled by a careful design of the PRONAOS/SPM optics (Sect. 2.3). The beam profile is determined using measurements on point sources during the flight and a physical model of the optics.

  
3.3.1 Main beam profiles

Beam profiles of the focal instrument have been measured and optimised on the ground during the optics alignment phase (Sect. 2.4). The main beam profile on the sky depends on the optical quality of the telescope caracterised by its WFE (wavefront error), which value is estimated between 15 and $24~{\rm\mu m}$ RMS for the PRONAOS telescope.

Therefore, the actual beam profiles of PRONAOS/SPM were derived from point source observations. The planet Saturn has been observed using PRONAOS/SPM during flight FS96. Saturn can be considered as a point source (diameter $< 20^{\prime \prime}$) at the resolution of PRONAOS/SPM (beam FWHM $\ge 2^{\prime}$). Saturn profiles across 20$^{\prime}$ scans were measured in the four photometric channels, covering a total mapped area of $10.4^{\prime} \times 20^{\prime}$. These profiles are shown in Fig. 4. They have been used to derive the PRONAOS/SPM main beam shape for distances smaller than 6$^{\prime}$ away from the observing direction (Table 4).

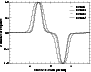	Figure 4: PRONAOS/SPM dual beam section measured on Saturn.
Open with DEXTER

  
3.3.2 Far sidelobes

For distances larger than 6$^{\prime}$, no reliable estimate of the sidelobes shape could be obtained from the Saturn observations. Therefore, the far sidelobes have been modelled using classical diffraction laws for a Cassegrain telescope. This contribution was added to the main beams to obtain the PRONAOS/SPM full beams. Integration of the full beams leads to the beam solid angles presented in Table 4.

As explained in Sect. 3.4.2, the primary PRONAOS/SPM calibration is an extended source calibration. An accurate estimate of far sidelobes is needed to be confident in the use of the ground calibration for sources measurements. Table 4 shows that far sidelobes can account for at most 3% of the total power collected for an uniform brightness source. We estimate the validity of the determination of the beams solid angles to be better than 5% (3-$\sigma$).

Table 4: Beam characteristics for the geometric optical conjugate of the cold stop (geometrical beam), the Saturn observations (main beam), and a combination of the Saturn observations and a telescope model (full beam).

  
3.4 Calibration on the internal calibration system

The Internal Calibration System (ICS) is a subsystem of the PRONAOS/SPM experiment which guaranties the absolute calibration accuracy during the flight.

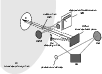	Figure 5: Optics design of the SPM instrument and the ICS as seen from the back of the telescope primary mirror (M 1).
Open with DEXTER

   
3.4.1 Principle

The ICS (Fig. 5) is composed of two blackbodies whose optical axis intersect at 90$^{\circ}$ and a reflective chopper selecting them alternately. The temperatures of the two blackbodies are respectively set to 40 $^{\circ}$C and 100 $^{\circ}$C. The modulation is done at the frequency of the internal chopper of the instrument, 19.5 Hz. The temperatures of the two blackbodies are continuously monitored during the flight using thermometers. This monitoring indicated that the blackbody temperatures are stable to better than 20 mK/h and 60 mK/h respectively. The monitoring allows to predict the amplitude of the ICS input signal with an accuracy better than 1% (3-$\sigma$) in brightness temperature. In flight, a calibration sequence is done between each astronomical sequence, typically every 30 to 60 min. This calibration signal is used to determine the response of the SPM instrument. During a calibration sequence, the wobbling of the M 4 mirror is turned off. This stops the sky modulation and allows to center the beam on the optical axis where a small mobile mirror (MC1) is placed, redirecting the signal of the ICS onto the detectors. The warm ICS signal (310-370 K) is seen against a cold background (around 50 K). However, MC1 is small compared to the beam so that the ICS signal is diluted and induces a background change limited to about 10% in brightness temperature. This change is taken into account in the calibration data processing (Sect. 3.5.2).

   
3.4.2 Calibration of the ICS

The ICS was calibrated on the ground against an absolute extended blackbody filling the SPM beam before each flight. This extended blackbody is the primary standard of the PRONAOS/SPM calibration scheme. All subsequent calibrations refer to the ICS.

The absolute extended blackbody has been designed and developed for the PRONAOS/SPM calibration. It is operated between 30 $^{\circ}$C and 50 $^{\circ}$C. It is composed of a cube of 400 mm on edge with a square aperture of 200 mm centered on one face. The inside of the cavity has a pyramidal structure surface coated with black paint. The statistical average number of reflexions of a ray in the cavity is 24 before exiting. Conservative assumptions of a minimum number of reflexions of 8 and a black paint emissivity of 0.5 give a blackbody emissivity larger than 0.98. The overall emissivity of the blackbody is taken equal to 0.99 $\pm$ 0.01 (3-$\sigma$). The opening is closed by a $10~{\rm\mu m}$ mylar to obtain an homogeneous temperature of the air inside the cavity equal to that of the walls. Homogeneity of the temperature is checked using 3 thermometers at various locations within the cavity and on the walls. The mylar is tilted at an angle of about 5$^{\circ}$ to avoid reflexion of the detector onto itself and its transmission in taken into account during the ICS calibration.

First, the absolute extended blackbody is placed in front of the focal instrument, filling entirely the SPM beam centered on the optical axis, the sky modulation by M 4 being turned off. The blackbody entrance is modulated by an oversized bow tie chopper covered with Eccosorb at ambient temperature, tilted with respect to the optical axis. The chopper temperature is permanently monitored, as well as the environment temperature. During the calibrations, the ambient and chopper temperature were close to 21 $^{\circ}$C and the absolute blackbody set to 40 $^{\circ}$C. The total error on the knowledge of this modulated signal is estimated to 3% (3-$\sigma$) in brightness temperature. Second, the bow tie chopper is stopped and a standard calibration sequence on the ICS is done. The geometrical dilution of the ICS in the beam is equal to the ratio of the measure of the signal on the absolute extended blackbody to the measure obtained on the ICS. Therefore this calibration is relevant for extended sources of uniform brightness. Corrections are made to take into account the change of background when chopping against the absolute blackbody, and the slight deviations from the Rayleigh-Jeans regime. The value of the dilution are found to be between $1.69\times 10^{-2}$ and $3.67\times 10^{-2}$ depending on the band.

During the calibration procedure, special care was given to have an equal atmospheric optical path from the input window of the photometer to the entrance of the absolute blackbody and to the entrance of the ICS. Thus the same atmospheric absorption applies for both paths. However, the atmospheric transmission varies during the calibration procedure inducing a bias estimated to 2% (3-$\sigma$). An additional source of error is the position of the mobile MC1 mirror (Sect. 3.4.1, Fig. 5) inside the beam during the calibration sequence. Gravity bendings of the MC1 support affect the position of MC1 in the beam for different zenith angle of the telescope, and due to near field diffraction the beam at the MC1 position is not flat. This effect contributes to a maximum calibration error of 5% (3-$\sigma$).

3.4.3 Calibration history during flight

History of all calibration sequences acquired during the FS2 PRONAOS flight are plotted in Fig. 6. During most of the duration of the flight, the environment conditions of the instrument were very stable and the response in the four bands showed a dispersion smaller than 6 to 12% (3$\sigma$). The scientific data reduction includes the correction to these variations.

	Figure 6: PRONAOS/SPM response variation on ICS during the 1996 flight. Response is expressed as SPM internal units vs. brightness temperature for extended sources in mK.
Open with DEXTER

3.5 Response change during flight

The response of semiconductor bolometers depends on three variable parameters: the bias current, the temperature of the thermal reference and the optical background. The bias current is optimized and fixed before the flight to get the best signal-to-noise ratio on astronomical sources. The effect of the two other parameters on the response is discussed below.

3.5.1 Response change with the bolometer reference temperature

The variation of the detector response with the temperature of the cold end of the 0.3 K ³He mini-fridge was measured on the ground. The relative variation coefficient for the four bands was found between 0.35%/mK and 0.7%/mK around 295 mK. The ³He mini-fridge temperatures during the 3 flights were very stable at the ceiling altitude (always in the range 290-300 mK, variation rate smaller than 1 mK/h). Using the calibration sequences acquired before and after each astronomical observation, there was no need to introduce any specific correction to the detector response due to detector reference temperature changes. The corresponding error is estimated to be less than 0.2% and can be neglected.

  
3.5.2 Response change with background

The background power received by the detectors is very stable at ceiling altitude during astrophysical observations, but is significantly larger during the calibration sequences (Sect. 3.4.1). The variation of response induced by this background change is determined in order to get the actual response on astrophysical sources.

We have calibrated the dependency of the response as a function of the background equivalent temperature at the entrance of the cryostat. First, the DC component of the bolometer read-out was measured at various known background levels at the cryostat input window, using a liquid Nitrogen bath and a set of 300 K geometrical occultations (0 to 100%). Then the response on a constant modulated signal was measured for various backgrounds, using the background scale provided in the previous step. These responses normalized at 293 K are represented in Fig. 7.

The absolute contribution of the ICS to the background is measured on the ground against a large liquid nitrogen bath. In flight, the total background (including the ICS) is estimated from the ICS response. Then, the contribution of the ICS is subtracted and the bolometer response variation between calibration on ICS and observations sequences is computed from Fig. 7. This correction varies from 1.09 to 1.16 for band 1 to 4. The absolute error associated to this correction is estimated to 1% (3-$\sigma$).

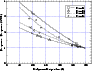	Figure 7: PRONAOS/SPM response variation with background temperature. Lines are polynomial fits to data points sets.
Open with DEXTER

3.6 Electronics linearity and stability

During the PRONAOS/SPM development phase, special attention was given to the experiment electronic design in order to guaranty linearity and stability of all the detection system. The bolometers read-out, lock-in amplification and digitization have been checked for all amplifier gains (1 to 64) and over the full dynamic range (16 bits) and do show a linearity and a stability better than 0.1%.

3.7 Final calibration accuracy

3.7.1 Calibration accuracy

Table 5 presents the different systematic error sources of the PRONAOS/SPM calibration detailed in the previous sections. In order to compute the total calibration accuracy, these possible systematic errors have been linearly added. The PRONAOS/SPM  absolute calibration accuracy is 8% at the 1-$\sigma$ level. In the band-to-band errors of Table 5, second order errors are neglected (totality of the contributions related to the absolute blackbody/chopper and to the atmospheric path length, part of the contributions related to the ICS MC1 mirror position, to the ICS monitoring, to the background response correction and to the instrument/sky coupling). Independent errors (color correction, beam solid angle) are multiplied by $\sqrt{2}$. The band-to-band calibration accuracy is 6% at the 1-$\sigma$ level. We want to emphasis here, that thanks to a careful optical design and a complete calibration procedure, these figures are up to now among the most accurate for large telescope instruments in the submillimeter range.

Table 5: PRONAOS/SPM calibration error budget: absolute and band to band relative errors

3.7.2 Measured noise

The careful design and building of the PRONAOS/SPM instrument allows to reach high sensitivities. In order to illustrate the measurement accuracy, we give in Table 6 the PRONAOS/SPM NEFD (Noise Equivalent Flux Density) measured in flight. These NEFDs are computed on empty fields observed during the PRONAOS second flight. We present the NEFD of the galactic maps and the Sunyaev-Zel'dovich measurements corresponding to two different observation modes, mapping and 5 points (Sect. 2.1). These NEFDs are very similar.

Table 6: Noise Equivalent Flux Densities of the PRONAOS/SPM  experiment measured in flight.

Table 7: Summary of the Saturn model: Rayleigh-Jeans brightness temperature of the Saturn sub-Earth point and the different contributions we have taken into account. The predictions of the model are compared with the PRONAOS/SPM observations.

  
4 Point source calibration check

Planets are usually used as primary calibrators in the submillimeter. In order to check the calibration procedure described above, we compare here the PRONAOS/SPM observation of Saturn with a detailed model of the planet's emission in the submillimeter. Due to visibility and observation planning constraints, Saturn was the only planet observed using PRONAOS/SPM.

4.1 Observations of the Saturn submillimeter emission

Saturn is a true point source for PRONAOS  (Sect. 3.3.1). The Saturn flux was derived from the maximum value in the map observed during the FS96 flight, and using the angular size of the planet (Sect. A.1) and the PRONAOS/SPM beam (Table 4). Table 7 presents the resulting fluxes in the four PRONAOS/SPM photometric channels, converted to Rayleigh-Jeans temperatures, and including the correction for the atmospheric transmission. The signal to noise ratio on the Saturn data is about 1000 in the data. Therefore, the error bars are only due to the absolute photometric accuracy of the instrument.

4.2 Model of the Saturn submillimeter emission

Large features in the submillimeter region of the Saturn spectrum require a careful spectral integration over the PRONAOS/SPM photometric bands. Moreover, in order to be consistent with the accuracy of the PRONAOS/SPM calibration, the contribution of the rings must be evaluated. We have built a model from literature data with the goal of obtaining an absolute photometric accuracy better than the PRONAOS/SPM one (i.e. 8%). The emission and the absorption spectra of the Saturn disk and rings, and the geometric configuration of the planet are taken into account. The model is detailed in Appendix A. Table 7 gives a summary of the predictions of this model in the PRONAOS/SPM channels.

4.3 Comparison of model and observations

The brightness temperature ratios between the observations and the model are respectively 0.89, 0.89, 0.91 and 0.99 for the four PRONAOS/SPM  channels (see Table 7). The differences between the model and the observation (${<}11\%$) for all channels are compatible with the combined error bars of the model (5$\%$) and the observations (8$\%$). The difference observed in the first three channels is about 10% which is larger than the absolute calibration error alone. This indicates that the model used may actually under-estimate the emission in the 500-900 $\mu$m range.

  
5 Comparison with COBE/DIRBE

We have compared several COBE/DIRBE and PRONAOS observations of selected astrophysical targets, both compact (point-like for COBE/DIRBE) and extended. The COBE/DIRBE wavelength range overlaps that of Pronaos around $200~{\rm\mu m}$, therefore this comparison provides cross-check of the PRONAOS calibration procedure for the band 1. Table 8 lists the PRONAOS observations used in these intercalibrations.

Table 8: List of the PRONAOS observations (second flight) used in the intercalibration with COBE/DIRBE and ISO/ISOPHOT .

5.1 Compact sources

In this section, we compare the DIRBE and PRONAOS observations towards M 82. Although this object is a point source for DIRBE, it is slightly resolved with PRONAOS. This is therefore a check of the PRONAOS calibration on compact objects.

The DIRBE fluxes for M 82 has been obtained using the DIRBE Point Source Photometry tool (http://cobe.gsfc.nasa.gov/cio/browser.html), which uses the time-ordered DIRBE data. The resulting fluxes are given in Table 9, from 60 to $240~{\rm\mu m}$.

The PRONAOS fluxes for M 82 were obtained using aperture photometry (e.g., Howell 1989) in the maps observed during flight FS96 (see Table 8). M 82 is a slightly extended object lying on a flat background in these maps. The quoted error has been computed outside the emission regions, the error being equal to the rms value in an empty region of the map divided by the square root of the number of pixels in the flux integration region.

Table 9: Integrated fluxes of M 82 measured by PRONAOS and DIRBE in Jy. The flux convention is $\nu \times I_{\nu } = \rm cste.$ in both cases.

We have fitted a grey body of the form

$$I_{\lambda}^{\rm fit} = \epsilon_{250~\mu {\rm m}} \times \l... ...\mu {\rm m}}\right)^{-\beta} \times B_{\lambda}(T_{\rm dust})$$ (3)

to the PRONAOS and DIRBE data. The resulting fit parameters are given in Table  10. These spectral shapes were then used to color correct the PRONAOS data (see Sect. 3.1.3) to the $\nu \times I_{\nu } = \rm cste.$ convention used in the DIRBE data. Figure 8 shows the resulting spectrum. It can be seen that the DIRBE  $140~{\rm\mu m}$ flux is inconsistent, within its error bar, with the remaining data points. This is most likely due to the DIRBE noise at this wavelength being underestimated. Note also that the DIRBE data point at $60~{\rm\mu m}$falls above the fit, which is expected since the dust emission at this wavelength is dominated by very small grains (e.g. Désert et al. 1990) which are not accounted for in the fit. The PRONAOS  fluxes were then extrapolated to the $240~{\rm\mu m}$ DIRBE wavelength using the above fit, and compared to the DIRBE fluxes at this wavelength. We obtain $I_{\rm PRONAOS~}/I_{\rm DIRBE~}= 1.05^{+0.05}_{-0.04}$. This result shows that a good agreement is obtained between the PRONAOS  calibration on compact sources and the absolute calibration of the DIRBE instrument.

	Figure 8: Spectrum of M 82 measured by PRONAOS  and DIRBE . The data in Table 10 have been iteratively color corrected in order to take into account of the actual spectral shape: $\epsilon_{250 ~{\rm \mu m}}=5.7^{+1.2}_{-1.9}~10^{-4}$, $\beta =1.94^{+0.2}_{-0.3}$, $T=35.1_{-2.5}^{+6.9}~\rm K$.
Open with DEXTER

Table 10: Fit parameters for the M 82 spectrum using PRONAOS data and PRONAOS +DIRBE data.

5.2 Extended sources

In order to check the absolute calibration of the PRONAOS instrument on extended sources, we have carried out a comparison between DIRBE and PRONAOS observations of several extended bright regions. Unlike for compact sources, this is not an easy task and it requires a good understanding of the characteristics of the two instruments. In particular the sky modulation used during the PRONAOS observations subtracts low spatial frequencies in the maps, while DIRBE measurements are sensitive to the total sky power. Simulations of PRONAOS observations taking into account the effect of the scanning strategy and sky modulation have been carried out. They have shown, provided that a linear background is subtracted from the DIRBE  data in order to account for the subtraction of the low spatial frequencies in the PRONAOS data, that an accuracy better than $5\%$can be obtained if the size of the PRONAOS map is larger than the DIRBE beam size and the source is compact at the DIRBE scale. We have therefore limited the comparison to those sources where a sufficiently large region was mapped using PRONAOS. The selected regions for this study are M 42, M 17, $\rho$-Ophiuchi and Cygnus B (see Table 8).

Figure 9: This figure illustrates the method used when comparing the PRONAOS and DIRBE  brightnesses for extended sources on the M 42 data. The grey scale shows the DIRBE  $240~{\rm\mu m}$ map and the contours represent the PRONAOS  200 $\mu$m data. The central square marks the central DIRBE pixel chosen for the comparison (see text). The triangles mark the DIRBE  pixels chosen for computing the linear background. The circle represents the DIRBE beam size at $240~{\rm\mu m}$ (55').

Open with DEXTER

We have used the DIRBE Zodi-Subtracted Mission Average (ZSMA) maps which are the most accurate. Typical noise levels on empty regions of these maps is estimated to be 0.03, 0.05, 2.5 and 1.3 MJy/sr (1-$\sigma$) at 60, 100, 140 and $240~{\rm\mu m}$ respectively.

The DIRBE brightness value is taken to be the ZSMA value at the brightest DIRBE pixel falling in the PRONAOS map. The DIRBE background at this position is estimated through a linear regression using the ZSMA values in the second concentric ring of pixels surrounding the central DIRBE pixel (see Fig. 9). This background value is subtracted from the DIRBE brightness, leading to a background subtracted value. The resulting values are shown as triangles in Fig. 10. The above ZSMA brightness errors are very small compared to the brightness of the sources considered here. The uncertainty upon the DIRBE brightness for each source is therefore dominated by that on the background subtraction method, which we computed to be about $10\%$ of the background value for each source.

The PRONAOS maps were convolved by the DIRBE beam centered on the central ZSMA pixel, leading to the brightness values in the PRONAOS  bands at 200 and $260~{\rm\mu m}$ as would have been observed by DIRBE when pointing toward the central ZSMA pixel. In this process, regions falling outside the PRONAOS map have been replaced by the DIRBE  background subtracted value at this point, extrapolated in wavelength to the pronaos bands using a grey body fit.

The contribution by the regions not covered by the pronaos map is typically $20\%$ of the final brightness. The errors were calculated from the PRONAOS noise level taking into account the number of PRONAOS pixels used and their weight in the convolution. The resulting values are shown as square symbols in Fig. 10.

Table 11 gives the ratio of the PRONAOS to DIRBE average brightnesses, as computed above, for each source. The quoted errors are the quadratic sum of the PRONAOS and DIRBE  error contribution.

	Figure 10: PRONAOS DIRBE intercalibration results on extended sources. Spectra of M 42, M 17, $\rho$-Ophiuchi and CygnusB.
Open with DEXTER

Table 11: Ratio of the PRONAOS to DIRBE  average brightnesses on extended sources. The average value is weighted using 1/$\sigma ^2$.

The comparison between the PRONAOS and DIRBE fluxes over the four extended sources above leads to a $5\%$ agreement in average and better than $10\%$ in any case. Owing to the additional difficulty of performing intercalibration on extended sources (which is reflected in the quoted error bars), this confirms the accuracy of the PRONAOS calibration summarized in Table 5.

  
6 Intercalibration with ISOPHOT 

We have carried a similar intercalibration on selected ISO/ISOPHOT observations of targets also observed using PRONAOS  (Table 8).

The ISOPHOT instrument on board ISO has performed observations at $200~~{\rm\mu m}$ with an angular resolution of 1.6 arcmin, similar to that of PRONAOS at this wavelength. Like DIRBE, ISOPHOT was not equipped with an absolute calibration device. Its calibration relied on point sources. We have selected regions which have been observed with PRONAOS and with ISOPHOT in the $200~{\rm\mu m}$ channel. We have restricted the selection to ISOPHOT observations obtained in the P22 mode where the ISOPHOT photometric calibration is the best understood and to ISOPHOT observations with a map size large enough to allow a good comparison with the PRONAOS data. As a result, only 3 ISOPHOT  observations were selected, two in M 42 and one in $\rm\rho - Ophiuchi$.

The ISOPHOT data were reduced using the PHOT Interactive Analysis (PIA, Gabriel et al. 1997) in its version 7.2.2, in order to correct for instrumental effects, remove glitches and calibrate the data. We have checked that the data do not show any residual of transient effects after treatment. The data have then been projected onto the sky, using flat field correction softwares similar to that used by Lagache and Dole (2001). The ISOPHOT maps obtained are shown in Fig. 11, along with the region observed by PRONAOS. As can be seen on the figure, only a partial overlap sometimes exist betwen the two observations which makes a direct comparison difficult. Most importantly, the beam modulation in the PRONAOS data subtracts out the lowest spatial frequencies from the sky signal, while ISOPHOT is sensitive to absolute power. This is taken into account by simulating the PRONAOS observing strategy (scanning and beam modulation) on the ISOPHOT maps at the positions observed by PRONAOS. The simulated signal produced was processed in the same way as the PRONAOS data and a linear regression analysis was performed in the regions of overlap between the ISOPHOT data and the PRONAOS data color-corrected to the $\nu I_{\nu}=\rm cste.$ convention (Fig. 12). This lead to the intercalibration factors given in Table 12.

It can be seen that the agreement between the ISOPHOT and the PRONAOS  calibration is good ($7\%$) for the two observations of the M 42 region. The origin of the $25\%$ difference between the observations of the $\rm\rho - Ophiuchi$ region remains unexplained. However, the ISOPHOT observations of M 42 and $\rm\rho - Ophiuchi$ have been obtained at different dates, and it is known that the ISOPHOT calibration has varied by about $10\%$ during the ISO observations.

	Figure 11: ISOPHOT (grey scale) and PRONAOS  $200~{\rm\mu m}$ maps (contours) of $\rho$-Ophiuchi ( left) and M 42 ( right) used for the comparison of their calibration. The PRONAOS scans positions are shown as the dashed lines.
Open with DEXTER

	Figure 12: Correlation diagrams between the ISOPHOT and PRONAOS modulated data at $200~{\rm\mu m}$ for $\rho$-Ophiuchi ( left), M 42-1 ( center) and M 42-2 ( right).
Open with DEXTER

Table 12: Ratio of the PRONAOS to ISOPHOT average brightnesses on extended sources. The average value is weighted using 1/$\sigma ^2$.

7 Conclusions

We have presented the absolute calibration of the PRONAOS/SPM  instrument. PRONAOS/SPM has observed the sky simultaneously in four submillimeter wide photometric channels using a two meter telescope carried onboard a stratospheric balloon. The PRONAOS/SPM instrument has been carefully designed to guaranty clean beam shapes, sensitive measurements and accurate photometry. An absolute photometric accuracy of 8% (1-$\sigma$) and a channel to channel relative calibration accuracy of 6% (1-$\sigma$) are obtained thanks to the absolute calibration, based on ground and in-flight measurements of controlled blackbodies and a physical model of the instrument. This original calibration scheme gives the best calibration accuracy of today's large telescope submillimeter instruments. We have validated the point source calibration accuracy of PRONAOS/SPM by comparing a detailed submillimeter emission model of the Saturn planet and the PRONAOS/SPM observations. We also checked the calibration on compact and extended astrophysical sources by cross-calibration with the DIRBE  data and a detailed comparison with ISO/ISOPHOT data.

These comparisons confirm the accuracy of the PRONAOS/SPM calibration and therefore validate the original scientific results obtained using the PRONAOS/SPM instrument.

The calibration methodology described in this paper has direct implications on the preparation of future submillimeter space missions such as Planck and Herschel.

Acknowledgements

The PRONAOS program was funded by CNES, with the support of the CNRS laboratories. We thank the CNRS technical team whose work was essential to the realisation of the SPM instrument, the CNES team for developing and operating the gondola and telescope and the NSBF team at Fort Sumner for the flight operations.

We would like to thank E. Lellouche and R. Moreno for they helpful discussions on Saturn atmosphere models.

References

• Astronomical Almanac, 1996, US Government Printing office, Washington, DC (In the text)
• Berk, A., Bernstein, L. S., & Robertson, D. C. 1989, MODTRAN: A Moderate Resolution Model for LOWTRAN 7 (GL-TR-89-0122), Air Force Geophysics Laboratory, Bedford, Mass (In the text)
• Bernard,, J.-P., Abergel, A., Ristorcelli, I., et al. 1999, A&A, 347, 640 [NASA ADS] (In the text)
• Bézard, B., Gautier, D., & Marten, A. 1986, A&A, 161, 387 [NASA ADS] (In the text)
• Bock, J. J., Chen, D., Mauskopf, P. D., & Lange, A. E. 1995, Space Sci. Rev., 74, 229 [NASA ADS] [CrossRef] (In the text)
• Buisson, F., & Durand, M. 1990, in ESA From Ground-Based to Space-Borne submillimeter Astronomy, 323 (In the text)
• Coron, N., Internal IAS, Note, 26 April 1992
• Cuzzi, J. N., Lissauer, J. J., esposito, L. W., et al. 1984, in Planetary Rings, ed. R. Greenberg, & A. Brahic (Tucson, Arizona: Univ. of Arizona Press), 72 (In the text)
• Désert, X., Boulanger, F., & Puget, J. L. 1990, A&A, 237, 215 [NASA ADS] (In the text)
• Dowling, T. E., Muhleman, D. O., & Berge, G. L. 1987, Icarus, 70, 506 [NASA ADS] [CrossRef] (In the text)
• de Parter, I., & Dickel, J. R. 1991, Icarus 94, 474 (In the text)
• Dupac, X., Giard, M., Bernard, J.-P., et al. 2001, ApJ, 553, 604 [NASA ADS] [CrossRef] (In the text)
• Dupac, X., Giard, M., Bernard, J.-P., et al. 2002, A&A, 392, 691 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Dupac, X., del Burgo, C., Bernard, J.-P., et al. 2003, MNRAS, in press (In the text)
• Epstein, E. E., Janssen, M. A., Cuzzi J. N., et al. 1980, Icarus, 41, 103 [NASA ADS] [CrossRef] (In the text)
• Esposito, L. W., Cuzzi, J. N., Holberg, J. B., et al. 1984, in Saturn, ed. T. Gehrels (Tucson, Arizona: Univ. of Arizona Press), 463 (In the text)
• Fixsen, D. J., Weiland, J. L., Brodd, S., et al. 1997, ApJ, 490, 82 [NASA ADS] (In the text)
• Gabriel, C., Acosta-Pulido, J., Heinrichsen, I., et al. 1997, Astron. Data Analysis Software and Systems VI, ASP Conf. Ser., ed. Gareth Hunt, & H. E. Payne, 125, 108 (In the text)
• Grossman, A. W. 1990, in Ph.D. Thesis, California Institute of Technology, Pasadena, California (In the text)
• Hanel, R., Conrath, B., Flasar, F. M., et al. 1982, Science, 215, 544 [NASA ADS] (In the text)
• Howell, S. B. 1989, PASP, 101, 616 [NASA ADS] [CrossRef] (In the text)
• Lagache, G., & Dole, H. 2001, A&A, 372, 702 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Lamarre, J.-M., Internal LPSP Note; 19 April 1977 (In the text)
• Lamarre, J.-M., Pajot, F., Torre, J.-P., et al. 1994, IR Phys. Techno., 35, 277 (In the text)
• Lamarre, J.-M., Giard, M., Pointecouteau, E., et al. 1998, ApJ, 507, L5 [NASA ADS] [CrossRef] (In the text)
• Lamarre, J.-M., Ade, P. A. R., Benoit, A., et al. 2000, Astrophys. Lett. Comm., 37, 161 (In the text)
• Leblanc, J., Dambier, G., Coron, N., et al., French Patent No. 7536104, 26 Nov. 1975 (In the text)
• Leblanc, J., Dambier, G., Coron, N., et al., German Patent No. 2653865; 8 June 1977; US Patent No. 4116063, 26 Sept. 1978 (In the text)
• Leblanc, J., Dambier, G., & Coron, N., CNRS French Patent No. 8508945; 13 June 1985 (In the text)
• Muhleman, D. O., & Berge, G. L. 1982, in Planetary Rings, ed. A. Brahic, UAI Coll. 75 (Toulouse, France: Cepadues-Editions), 57 (In the text)
• Mullin, T. S. 1984, in Saturn, ed. T. Gehrels (Tucson, Arizona: Univ. of Arizona Press) 931 (In the text)
• Ristorcelli, I., Lamarre, J.-M., Giard, M., et al. 1997, Exp. Astron., 7, Issue 1, 13 (In the text)
• Ristorcelli, I., Serra G., Lamarre, J.-M., et al. 1998, ApJ, 496, 267 [NASA ADS] [CrossRef] (In the text)
• Roellig, L. T, Werner, M. W., & Becklin, E. E. 1988, Icarus, 73, 574 [NASA ADS] [CrossRef] (In the text)
• Schloerb, F. P., Muhleman, D. O., & Berge, G. L. 1979, Icarus 39, 214 (In the text)
• Serra, G., Sirmain, C., Lamarre, J. M., et al. 1997, Proc. of International Conference of Space Optics (ICSO) (In the text)
• Serra, G., Giard, M., Bouchou, F., et al. 2002, Adv. Space Res., 30, 1297 [NASA ADS] (In the text)
• Stepnik, B., Abergel, A., Bernard, J.-P., et al. 2001, A&A, 398, 551 [EDP Sciences] [NASA ADS] (In the text)
• Torre, J.-P., & Chanin, G. 1985, Rev. Scient. Inst., 26, 328 (In the text)

 

  
Online Material

   
Appendix A: Model of the Saturn submillimeter emission

A.1 Disk emission

The emission spectrum of the center of the apparent Saturn disk (sub-Earth point) is taken from the Bézard et al. 1986 model. They have computed the submillimeter spectrum of Saturn in the 10-200 cm^-1 range with a spectral resolution better than 0.1 cm^-1. Figure A.1 presents the predicted temperature brightness spectrum. In order to obtain the sub-Earth temperature brightness observed by PRONAOS/SPM, we have integrated this spectrum in the PRONAOS/SPM bands (see Fig. A.1). In the four PRONAOS/SPM spectral channels, the Rayleigh-Jeans brightness temperatures obtained for the Saturn sub-point are 70.9, 79.3, 96.0 and 111.5 K ( $T_{\rm disk}$). The expected absolute accuracy of these temperatures is about 5%, as quoted in Bézard et al. (1986).

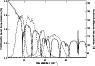Figure A.1: Spectrum of Saturn's disk (continuous line) as quoted in Bézard et al. (1986), and the transmission shape of the four PRONAOS/SPM spectral channels (dashed lines).

Then, the whole disk emission is computed from the radii dimensions of Saturn and the flux intensity variations from the center to the edge of the planet. We have used the radii at 1 bar pressure of Mullin (1984), i.e. $R_{\rm eq}=60~330$ km, $R_{\rm pol}=54~180$ km at the equator and pole respectively. The Saturn disk emission is limb darkened in the submillimeter and millimeter range. Muhleman & Berge (1982) have modelled it at 2.7 mm using the following law:

$$\begin{eqnarray*}I(\theta) = I(0) \times \cos^{\rm\alpha}(\rm\theta), \end{eqnarray*}$$

where $\theta$ is the angle between a point at the Saturn surface and the sub-Earth point, and $\alpha=0.038\pm0.02$. In their model the limb darkening is mainly due to amoniac vapour absorption in the upper atmosphere, which is also the main absorber in the submillimeter range (Bézard et al. 1986). Therefore, we have used their law to compute the average emission over the whole disk. We derive a whole disk average intensity 3.7 $\pm$ 1.8% lower than for the uniform case.

 

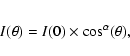
Finally, we have taken into account the dilution factor of the planet inside the PRONAOS/SPM beams (Sect. 3.3; Table 4). The apparent size of Saturn at the observing time was $19.46^{\prime\prime} \times 17.38^{\prime\prime}$, which corresponds to a solid angle of $6.24\times 10^{-9}$sr (Astronomical Almanac 1996). Note, that in our case, we do not need to correct the apparent disk size for the polar angle tilt because the tilt angle is less than 6$^{\circ}$ (Astronomical Almanac 1996), which induces a correction smaller than 0.2%.

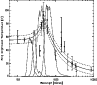Figure A.2: Brightness temperature spectrum of the Saturn rings. The black diamonds are the data collected by Esposito et al. (1984), the grey squares are the Roellig et al. (1988), Grossman et al. (1990), Dowling et al. (1987) and de Pater & Dickel (1991) data and their 1$\sigma$ error bars. The continuous lines show the analytic laws: $T_{1}=0.2 \times \left(\frac{\lambda}{20~\rm cm}\right)^{-1} + 5~\rm K$for $\lambda>480~\mu\rm m$ (de Pater & Dickel 1991) and $T_{1}=55 + \left(\frac{\lambda}{480~\mu{\rm m}}\right)^{3} \times (T_{1}(480~\mu \rm m)-55)~K$. The dashed lines are the 1$\sigma$ error bars of the models.

A.2 Effect of the rings

We have used a simple model, inspired from Schloerb et al. (1997), in order to predict the emission from the Saturn's rings. The model considers only the contribution of the A, B and C rings. The flux of the other rings is negligible because of their smaller solid angle and density (Cuzzi et al. 1984). We have assumed equal and uniform brightness temperature for the rings, and no dependence upon ring inclination because of the lack of constraining data. Saturn ring brightness temperatures have been collected by Esposito et al. (1984) and de Pater & Dickel (1991). They have shown strong variations upon wavelengths. de Pater & Dickel (1991) have modelled these variations for wavelengths above 480 $\mu$m using:

$$\begin{eqnarray*}T_{1}\rm (\lambda)=0.2 \times \left(\frac{\lambda}{20~cm}\right)^{-1} + 5~K,~\lambda \geq 480~~{\rm\mu m}. \end{eqnarray*}$$

In order to obtain an analytic expression of these variations for wavelengths under $480~{\rm\mu m}$, we have approximated the data using the following empirical law:

$$\begin{eqnarray*}T_{2}(\lambda)= a + \left(\frac{\lambda}{480~\rm\mu m}\right)^{b} \times (T_{1}(480~{\rm\mu m})-a),~\lambda < 480~\mu\rm m, \end{eqnarray*}$$

where a and b are constant parameters fitted by a $\chi^{2}$minimisation. We have found a=55 K and b=3. Figure A.2 presents the data of the ring temperature brightness spectrum quoted above, the model of de Pater & Dickel (1991), and our analytic law (continuous lines). We have estimated the errors on the brightness temperature law to about $\pm$6 K (dashed lines in Fig. A.2). Using these analytic laws and the PRONAOS/SPM spectral transmission shapes (Sect. 3.1), we have deduced the Rayleigh-Jeans brightness temperatures observed by PRONAOS/SPM towards the rings ( $T_{\rm rings}$): 29 $\pm$ 5 K, 37 $\pm$ 6 K, 53 $\pm$ 6 K, and 60 $\pm$ 6 K.

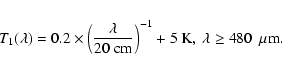
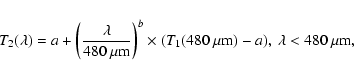
Where the rings obscure the disk, the disk emission is reduced by the ring optical depth $\tau$, which varies with the ring inclination B as

$$\begin{eqnarray*}\tau = \tau_{0} / \sin(\vert B\vert), \end{eqnarray*}$$

where $\tau_{0}$ is the optical depth normal to the ring plane (Epstein et al. 1980). The inclination B was equal to -4.6$^{\circ}$ at the observing time. We have used the optical depth value measured by Voyager II (Hanel et al. 1982), which are $\tau_{0A}=0.40\pm0.05$, $\tau_{0B}=0.8\pm0.2$ and $\tau_{0C}=0.10\pm0.03$. In addition to the direct emission of the disk and rings alone, we take into account the emission of the form $T_{\rm rings}+T_{\rm disk} \times \rm e^{-\tau}$ where the disk and rings overlap.

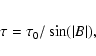
The geometry of the rings has been computed from the Astronomical Almanac (1996) ephemerid. We have found thesolid angles 4.94, 6.64, $3.33 \times 10^{-10}$ sr for the rings A, B and C, and 0.88, 1.6 and $1.2 \times 10^{-10}$ sr for the rings in front of the Saturn disk. Therefore, on one hand the whole planet brightness temperature is increased by 9.7 $\pm$ 1.7%, 11.1 $\pm$ 1.8%, 13.2 $\pm$ 1.5%, and 12.8 $\pm$ 1.2% in the four PRONAOS/SPM bands, due to the ring emission. On the other hand, the rings hide 5.9% of the disk surface and the disk flux through the rings is only 0.6 $\pm$ 0.2% of the planet brightness temperature. Therefore, the whole planet brightness temperature is also decreased by 5.3 $\pm$ 0.2% due to the ring absorption.

Note, that in our case, the angle between the Sun, Saturn, and the Earth was only 0.6$^{\circ}$ (Astronomical Almanac 1996). Therefore, no disk phase or ring shadowing was taken into account here.

A.3 Saturn integrated emission

Table 7 summarizes the contributions to the whole planet emission mentioned previously. The Rayleigh-Jeans temperatures in the PRONAOS/SPM spectral bands, obtained using the model are 71.4 $\pm$ 3.7, 81 $\pm$ 4.2, 99.9 $\pm$ 5.0 and 115.8 $\pm$ 5.8. The errors quoted are the quadratic sum of the different factors error.