A&A 447, 245-261 (2006)
DOI: 10.1051/0004-6361:20053938
J. Wilms1 - M. A. Nowak2 - K. Pottschmidt3 - G. G. Pooley4 - S. Fritz5
1 - Department of Physics, University of Warwick, Coventry, CV4 7AL, UK
2 - MIT-CXC, NE80-6077, 77 Massachusetts Ave., Cambridge, MA 02139, USA
3 - Center for Astrophysics and Space Sciences, University of
California at San Diego, La Jolla, CA 92093-0424, USA
4 - Mullard Radio Astronomy Observatory, Cavendish Laboratory, Madingley
Road, Cambridge CB3 0HE, UK
5 - Institut für Astronomie und Astrophysik, Universität
Tübingen, Sand 1, 72076 Tübingen, Germany
Received 28 July 2005 / Accepted 13 September 2005
Abstract
Continuing the observational campaign initiated by our
group, we present the long term spectral evolution of the Galactic
black hole candidate Cygnus X-1 in the X-rays and at 15 GHz. We
present ![]() 200 pointed observations taken between early 1999 and
late 2004 with the Rossi X-ray Timing Explorer and the Ryle radio
telescope. The X-ray spectra are remarkably well described by a
simple broken power law spectrum with an exponential cutoff.
Physically motivated Comptonization models, e.g., by
Titarchuk (1994, ApJ, 434, 570, compTT) and by Coppi (1999, in High Energy Processes in Accreting Black Holes, ed.
J. Poutanen, & R. Svensson (San
Francisco: ASP), ASP Conf. Ser., 161, 375, eqpair),
can reproduce this simplicity; however, the success of the
phenomenological broken power law models cautions against
"overparameterizing'' the more physical models. Broken power law
models reveal a significant linear correlation between the photon
index of the lower energy power law and the hardening of the power
law at
200 pointed observations taken between early 1999 and
late 2004 with the Rossi X-ray Timing Explorer and the Ryle radio
telescope. The X-ray spectra are remarkably well described by a
simple broken power law spectrum with an exponential cutoff.
Physically motivated Comptonization models, e.g., by
Titarchuk (1994, ApJ, 434, 570, compTT) and by Coppi (1999, in High Energy Processes in Accreting Black Holes, ed.
J. Poutanen, & R. Svensson (San
Francisco: ASP), ASP Conf. Ser., 161, 375, eqpair),
can reproduce this simplicity; however, the success of the
phenomenological broken power law models cautions against
"overparameterizing'' the more physical models. Broken power law
models reveal a significant linear correlation between the photon
index of the lower energy power law and the hardening of the power
law at ![]() 10 keV. This phenomenological soft/hard power law
correlation is partly attributable to correlations of broad band
continuum components, rather than being dominated by the weak
hardness/reflection fraction correlation present in the
Comptonization model. Specifically, the Comptonization models show
that the bolometric flux of a soft excess (e.g., disk component) is
strongly correlated with the compactness ratio of the Comptonizing
medium, with
10 keV. This phenomenological soft/hard power law
correlation is partly attributable to correlations of broad band
continuum components, rather than being dominated by the weak
hardness/reflection fraction correlation present in the
Comptonization model. Specifically, the Comptonization models show
that the bolometric flux of a soft excess (e.g., disk component) is
strongly correlated with the compactness ratio of the Comptonizing
medium, with
![]() .
Over the course of our
campaign, Cyg X-1 transited several times into the soft state, and
exhibited a large number of "failed state transitions''. The
fraction of the time spent in such low radio emission/soft X-ray
spectral states has increased from
.
Over the course of our
campaign, Cyg X-1 transited several times into the soft state, and
exhibited a large number of "failed state transitions''. The
fraction of the time spent in such low radio emission/soft X-ray
spectral states has increased from ![]() 10% in 1996-2000 to
10% in 1996-2000 to
![]() 34% since early 2000. We find that radio flares typically
occur during state transitions and failed state transitions (at
34% since early 2000. We find that radio flares typically
occur during state transitions and failed state transitions (at
![]() ), and that there is a strong
correlation between the 10-50 keV X-ray flux and the radio
luminosity of the source. We demonstrate that rather than there
being distinctly separated states, in contrast to the timing
properties the spectrum of Cyg X-1 shows variations between extremes
of properties, with clear cut examples of spectra at every
intermediate point in the observed spectral correlations.
), and that there is a strong
correlation between the 10-50 keV X-ray flux and the radio
luminosity of the source. We demonstrate that rather than there
being distinctly separated states, in contrast to the timing
properties the spectrum of Cyg X-1 shows variations between extremes
of properties, with clear cut examples of spectra at every
intermediate point in the observed spectral correlations.
Key words: stars: individual: Cyg X-1 - stars: binaries: close - X-rays: binaries - black hole physics
Observations over the last three decades have shown that Galactic BHC
exhibit distinct and very characteristic states with different
spectral shape and variability behavior, with AGN seemingly
following similar trends (McHardy et al. 2005; Jester 2005, and
therein). The state of a BHC depends on not
yet fully understood parameters (Homan et al. 2001), although it is
believed that the mass accretion rate, ![]() ,
and therefore the
luminosity of the accreting system, plays a vital role. See
McClintock & Remillard (2003) and Belloni (2004) for an extensive
discussion of these issues.
,
and therefore the
luminosity of the accreting system, plays a vital role. See
McClintock & Remillard (2003) and Belloni (2004) for an extensive
discussion of these issues.
For low accretion luminosities in the "hard state'' of Galactic black
holes, the X-ray spectrum can be described by a hard power law with
photon index
![]() and an exponential cutoff at
and an exponential cutoff at
![]() 150 keV. At low energies, most BHC show some kind of soft
excess with a characteristic temperature of a few 100 eV. This
baseline continuum is modified by a Fe K
150 keV. At low energies, most BHC show some kind of soft
excess with a characteristic temperature of a few 100 eV. This
baseline continuum is modified by a Fe K![]() emission line at
emission line at
![]() 6.4 keV and by reflection features, indicating the close
proximity of the source of hard X-rays and relatively cold material.
The hard state is furthermore characterized by strong X-ray
variability of >10% rms and by the presence of radio emission. In
systems where the radio sources have been resolved, this radio
emission has been shown to originate in an outflow that is consistent
with being mildly relativistic (
6.4 keV and by reflection features, indicating the close
proximity of the source of hard X-rays and relatively cold material.
The hard state is furthermore characterized by strong X-ray
variability of >10% rms and by the presence of radio emission. In
systems where the radio sources have been resolved, this radio
emission has been shown to originate in an outflow that is consistent
with being mildly relativistic (
![]() )
in the hard state
(Gallo et al. 2003; Stirling et al. 2001). For Cyg X-1, this outflow has recently
been shown to have a time averaged kinetic power of
)
in the hard state
(Gallo et al. 2003; Stirling et al. 2001). For Cyg X-1, this outflow has recently
been shown to have a time averaged kinetic power of
![]()
![]() to
to
![]() ,
i.e., a significant fraction of
the system's X-ray luminosity (Gallo et al. 2005).
,
i.e., a significant fraction of
the system's X-ray luminosity (Gallo et al. 2005).
In contrast to the "hard state'', the (typically) higher luminosity "soft
state'' exhibits a soft X-ray spectrum that can be well described by
thermal emission from a standard accretion disk. Where a hard spectral
component is detected, it does not show any appreciable curvature,
sometimes up to the MeV regime
(Grove et al. 1998; McConnell et al. 2000,2002). The X-ray variability
during the soft state is weak (![]() 6% rms) and no radio
emission is detected (Fender et al. 1999).
6% rms) and no radio
emission is detected (Fender et al. 1999).
While there is general agreement that the soft excess is due to
emission from an accretion disk, the interpretation of the hard
spectral component and its relationship to the reprocessing features
is still debated. The canonical interpretation of the hard state X-ray
spectrum, first proposed in the 1970s
(e.g., Thorne & Price 1975; Shapiro et al. 1976; Sunyaev & Trümper 1979) and later
elaborated upon, e.g., by Haardt & Maraschi (1991) and Haardt & Maraschi (1993),
is that the hard spectral component is caused by Comptonization, where
soft X-rays from the inner disk are Compton upscattered by hot
electrons (
![]() keV) in a predominantly thermal
electron gas, often called the "accretion disk corona'' (ADC). The
spectrum emerging from the corona has the proper power law plus
exponential cutoff shape. To explain the presence of the ADC,
magnetohydrodynamical instabilities (e.g., Balbus & Hawley 1998, and references
therein), which only work efficiently at lower
keV) in a predominantly thermal
electron gas, often called the "accretion disk corona'' (ADC). The
spectrum emerging from the corona has the proper power law plus
exponential cutoff shape. To explain the presence of the ADC,
magnetohydrodynamical instabilities (e.g., Balbus & Hawley 1998, and references
therein), which only work efficiently at lower ![]() ,
have been invoked.
,
have been invoked.
Observations limit the covering factor of the ADC with respect to the
source of soft X-rays to ![]() 1. Otherwise the ADC would fail to reach
the high coronal temperatures, inferred from the energy of the
exponential cutoff, due to efficient Compton cooling (e.g., Dove et al. 1997b; Haardt et al. 1997; Dove et al. 1997a, and
therein). Geometric models invoked to
achieve smaller ADC covering factors include patchy coronae
(Stern et al. 1995), magnetic flares
(Beloborodov 1999; Poutanen & Fabian 1999), advection dominated
accretion flows (Esin et al. 1998), ADCs with non-static or outflowing
coronae (Malzac et al. 2001; Beloborodov & Illarionov 2001), and accretion
flows with an inner geometrically thick ADC and an outer geometrically
thin and optically thick accretion disk (Dove et al. 1997b,a). In
all of these models, a fraction of the hard X-rays is scattered back
towards the disk, giving rise to fluorescence Fe K
1. Otherwise the ADC would fail to reach
the high coronal temperatures, inferred from the energy of the
exponential cutoff, due to efficient Compton cooling (e.g., Dove et al. 1997b; Haardt et al. 1997; Dove et al. 1997a, and
therein). Geometric models invoked to
achieve smaller ADC covering factors include patchy coronae
(Stern et al. 1995), magnetic flares
(Beloborodov 1999; Poutanen & Fabian 1999), advection dominated
accretion flows (Esin et al. 1998), ADCs with non-static or outflowing
coronae (Malzac et al. 2001; Beloborodov & Illarionov 2001), and accretion
flows with an inner geometrically thick ADC and an outer geometrically
thin and optically thick accretion disk (Dove et al. 1997b,a). In
all of these models, a fraction of the hard X-rays is scattered back
towards the disk, giving rise to fluorescence Fe K![]() emission
and the Compton reflection hump (Lightman & Rybicki 1979; Lightman & White 1988).
Comparisons between observations and theoretical model spectra for all
of these different geometries have been successful.
emission
and the Compton reflection hump (Lightman & Rybicki 1979; Lightman & White 1988).
Comparisons between observations and theoretical model spectra for all
of these different geometries have been successful.
With the realization of the importance of jets and their association with the hard state, the "Comptonization paradigm'' has recently been challenged. The discovery of a tight correlation between the radio and the X-ray emission on time scales of days (Pooley et al. 1999; Corbel et al. 2000; Hannikainen et al. 1998) suggests a close coupling between the X-ray and the radio emitting media (Heinz & Sunyaev 2003; Markoff et al. 2003). In addition, in a direct comparison between data and theory, jet models capable of reproducing the radio-X-ray correlations have been recently shown to describe the X-ray spectrum with a precision comparable to Comptonization models (Markoff et al. 2005). The origin of the X-rays in these models is due to a combination of synchrotron emission from the jet and synchrotron self Compton emission from the jet base. We note, however, that a small separation of the emission regions cannot be ruled out from joint radio-X-ray timing timing arguments (Gleissner et al. 2004a), furthermore, accretion models postulating a strong coupling between a Comptonizing medium and the jet are also able to explain the radio-X-ray correlation without postulating a jet origin for the X-rays (Merloni & Fabian 2002; Meier 2001).
In conclusion, all existing models suggest a complex interplay between
the energetics and emission from the accretion disk, Comptonizing
plasma, and radio jet. This interplay can be disturbed by changes in
some external parameter, such as ![]() .
These changes may lead to
state changes as well as to subtle changes in the overall source
properties, such as the so called "failed state transitions''
(Pottschmidt et al. 2000). An empirical understanding of the overall
accretion process is therefore difficult to gain from only a few
single and isolated observations, although these are very important
for determining broad band spectra or for measuring spectra with high
energy resolution (e.g., Miller et al. 2002). Monitoring campaigns
covering the characteristic time scales of these spectral changes are
required. We note that the necessity of monitoring campaigns follows
also from hysteresis effects seen in many sources, i.e., the earlier
source history is important for determining the source properties in a
given observation (Maccarone & Coppi 2003; Nowak et al. 2002; Miyamoto et al. 1995).
.
These changes may lead to
state changes as well as to subtle changes in the overall source
properties, such as the so called "failed state transitions''
(Pottschmidt et al. 2000). An empirical understanding of the overall
accretion process is therefore difficult to gain from only a few
single and isolated observations, although these are very important
for determining broad band spectra or for measuring spectra with high
energy resolution (e.g., Miller et al. 2002). Monitoring campaigns
covering the characteristic time scales of these spectral changes are
required. We note that the necessity of monitoring campaigns follows
also from hysteresis effects seen in many sources, i.e., the earlier
source history is important for determining the source properties in a
given observation (Maccarone & Coppi 2003; Nowak et al. 2002; Miyamoto et al. 1995).
Monitoring campaigns using large effective area and proportional counter energy resolution became possible in the 1990s with the Rossi X-ray Timing Explorer (RXTE). Since then, monitoring campaigns using RXTE's pointed instruments, the Proportional Counter Array (PCA; Jahoda et al. 1997) and the High Energy X-ray Timing Experiment, (HEXTE; Rothschild et al. 1998), have been performed for virtually all known persistent and transient Galactic black hole candidates. Among many others, examples for such campaigns are those on LMC X-1 and LMC X-3 (Wilms et al. 2001; Nowak et al. 2001), GX 339-4 (Kong et al. 2002; Nowak et al. 1999,2002; Homan et al. 2005; Belloni et al. 2005; Wilms et al. 1999), V1408 Aql (Nowak & Wilms 1999), 4U 1543-47 (Kalemci et al. 2005), XTE J1650-500 (Kalemci et al. 2003), 4U 1630-47 (Tomsick & Kaaret 2000), and XTE J1550-564 (Kalemci et al. 2001; Sobczak et al. 2000).
In this paper, we present results from one of the longest of these
monitoring campaigns, which was initiated by the authors in 1996 to be
performed on the prototypical hard state black hole candidate (BHC)
Cygnus X-1. Our campaign consists of biweekly, ![]() 5 ks
long RXTE pointings and simultaneous radio observations at
15 GHz (
5 ks
long RXTE pointings and simultaneous radio observations at
15 GHz (
![]() )
with the Mullard Radio Astronomy
Observatory's Ryle telescope in Cambridge, UK. Earlier papers in this
series concentrated on the evolution of X-ray time lags
(Pottschmidt et al. 2000), of the power spectrum (Pottschmidt et al. 2003b, hereafter
Paper I), the linear relationship between
the short term root mean square variability and the flux
(Gleissner et al. 2004b, hereafter Paper II), and correlations
between the soft X-rays and the radio flux (Gleissner et al. 2004a, hereafter
Paper III). Amongst others, archival data
from the campaign have also been used in the discovery of giant flares
from Cyg X-1 (Gierlinski & Zdziarski 2003), a subset of the archival
observations was also used in studies of Cyg X-1's spectral and
temporal variability (Axelsson et al. 2005; Ibragimov et al. 2005). Here, we
discuss the results obtained on the spectral evolution of Cyg X-1
throughout the RXTE monitoring campaign, starting in
Sect. 2 with a description of the changes of our
data reduction procedure with respect to Papers I
through III. In Sect. 3 we give the
results of modeling the broad band 3-200 keV X-ray spectra using
empirical spectral models as well as advanced Comptonization models
and consider the evidence for interaction between the X-ray and the
radio emission. We summarize our results in Sect. 4.
We will discuss the joint spectral-timing behavior of Cyg X-1 based on
our analyses in a future paper.
)
with the Mullard Radio Astronomy
Observatory's Ryle telescope in Cambridge, UK. Earlier papers in this
series concentrated on the evolution of X-ray time lags
(Pottschmidt et al. 2000), of the power spectrum (Pottschmidt et al. 2003b, hereafter
Paper I), the linear relationship between
the short term root mean square variability and the flux
(Gleissner et al. 2004b, hereafter Paper II), and correlations
between the soft X-rays and the radio flux (Gleissner et al. 2004a, hereafter
Paper III). Amongst others, archival data
from the campaign have also been used in the discovery of giant flares
from Cyg X-1 (Gierlinski & Zdziarski 2003), a subset of the archival
observations was also used in studies of Cyg X-1's spectral and
temporal variability (Axelsson et al. 2005; Ibragimov et al. 2005). Here, we
discuss the results obtained on the spectral evolution of Cyg X-1
throughout the RXTE monitoring campaign, starting in
Sect. 2 with a description of the changes of our
data reduction procedure with respect to Papers I
through III. In Sect. 3 we give the
results of modeling the broad band 3-200 keV X-ray spectra using
empirical spectral models as well as advanced Comptonization models
and consider the evidence for interaction between the X-ray and the
radio emission. We summarize our results in Sect. 4.
We will discuss the joint spectral-timing behavior of Cyg X-1 based on
our analyses in a future paper.
We have already given an extensive overview of the RXTE observing strategy and our data extraction in Papers I through III. Here, we only highlight the most important points pertaining to the X-ray spectral analysis, mainly centered on the RXTE calibration.
In this paper we consider 202 observations with a typical good time of
3-7 ks, for a total good time of ![]() 989 ks. We use data
from both the PCA and the HEXTE. Spectra are extracted with
HEASOFT 5.3.1 and then fit with XSPEC 11.3.1w (Arnaud 1996). For
the spectral analysis, we generated 3-25 keV PCA spectra from the
top xenon layer data and analyze spectra taken with different numbers
of proportional counter units (PCUs) separately. This choice was made
to allow the comparability with the results of the timing analysis.
For the HEXTE, data from 18-120 keV were considered.
989 ks. We use data
from both the PCA and the HEXTE. Spectra are extracted with
HEASOFT 5.3.1 and then fit with XSPEC 11.3.1w (Arnaud 1996). For
the spectral analysis, we generated 3-25 keV PCA spectra from the
top xenon layer data and analyze spectra taken with different numbers
of proportional counter units (PCUs) separately. This choice was made
to allow the comparability with the results of the timing analysis.
For the HEXTE, data from 18-120 keV were considered.
As shown in Appendix A, compared to earlier versions of the response matrices, the PCA is now in much better agreement with the HEXTE and also with other missions, in both, flux and spectral slope, with the remaining uncertainty being taken into account by a multiplicative constant that is normally very close to unity. Our reevaluation of the PCA calibration also shows that remaining calibration uncertainties can be modeled to first order by adding a systematic uncertainty of 0.5% to the data, although even with this choice some significant calibration effects are still visible in the residuals (see Appendix A). As shown in Appendix B, however, this systematic error leads to a dramatic overestimation of the range of the confidence intervals for the fit parameters. Thus, although we compute confidence intervals at the 90% level for one interesting parameter, we do not show error bars in the figures.
The good time of the observations is mainly defined by excluding times of high PCA background. Due to the requirements of X-ray timing analysis, early in the campaign very conservative constraints were chosen, i.e., data taken within 30 minutes of passages through the South Atlantic Anomaly (SAA) and during times of high particle background were discarded. While in principle improved PCA background models now allow for good results even closer to the SAA passages, for consistency reasons and in order to facilitate the comparison of spectral parameters to the results of Papers I through III, the previous limits were retained.
Electronic tables in the Flexible Image Transport System (FITS) format containing the results of the spectral fitting and the confidence intervals for all best fit parameters are available in electronic form at the CDS. In our discussion of peculiar observations below, we identify observations in a way that makes it easy to find them in these FITS files and in the RXTE archive. The abbreviated syntax used is of the type Pxxxxx/XXwhere xxxxx is the RXTE proposal ID and where XX is the number of the observation within each proposal. We also give the date and time of the observation to the closest hour and, in cases where an observation resulted in more than one spectrum because different detector combinations were used, we identify those detectors that were off.
We also find that for complex models, such as the Comptonization fits
described in Sects. 3.4 and 3.5, the
![]() -valley exhibits a large number of local minima and there are
many degeneracies between parameter combinations. Both effects result
in a significant fraction of fits converging on local
-valley exhibits a large number of local minima and there are
many degeneracies between parameter combinations. Both effects result
in a significant fraction of fits converging on local ![]() -minima.
Even when employing standard tricks, such as computing error contours,
the global minimum was not always reached. These "rogue fits'' can
be identified through outliers in one or more parameters when looking
at correlations between different spectral parameters. Where we
identified such bad fits we refit the data using a different set of
starting parameters obtained from "typical fits'' using the same
model.
-minima.
Even when employing standard tricks, such as computing error contours,
the global minimum was not always reached. These "rogue fits'' can
be identified through outliers in one or more parameters when looking
at correlations between different spectral parameters. Where we
identified such bad fits we refit the data using a different set of
starting parameters obtained from "typical fits'' using the same
model.
A potential drawback of this approach is that it effectively forces
these observations onto the correlations. Only about 20% of our
observations, however, had to be treated in this labor intensive way.
For a small fraction of these refitted observations, the
![]() of the finally adopted spectral model was found to
be larger by
of the finally adopted spectral model was found to
be larger by
![]() than the original
than the original
![]() due to degeneracies between the fitting
parameters. A typical example here are fits where the Fe K
due to degeneracies between the fitting
parameters. A typical example here are fits where the Fe K![]() line energy pegs at its (unphysical) lower bound of 6 keV, which is
often the case because of the PCA calibration uncertainty around the
Xe L-edge. In such cases we searched for better models with the Fe
line energy at
line energy pegs at its (unphysical) lower bound of 6 keV, which is
often the case because of the PCA calibration uncertainty around the
Xe L-edge. In such cases we searched for better models with the Fe
line energy at ![]() 6.4 keV and accepted the best fit parameters
from these fits, even if their
6.4 keV and accepted the best fit parameters
from these fits, even if their ![]() was slightly higher. The
number of observations for which such a strategy was required is still
small enough, and the increase of
was slightly higher. The
number of observations for which such a strategy was required is still
small enough, and the increase of ![]() was only
was only
![]() ,
such that this strategy does not influence the results listed below
and we are confident that all parameters shown in the following
reflect the physical behavior of Cyg X-1.
,
such that this strategy does not influence the results listed below
and we are confident that all parameters shown in the following
reflect the physical behavior of Cyg X-1.
In general, for all spectral fits presented here we find that for the
reduced ![]() ,
,
![]() .
Values of
.
Values of ![]() clearly larger than 1 might appear worrisome at first, however, we
stress that the signal to noise ratio of our observations is very high
and that the available spectral models are often too simple to be able
to describe all subtleties of the observations. Furthermore, given our
choice of systematics, for lower
clearly larger than 1 might appear worrisome at first, however, we
stress that the signal to noise ratio of our observations is very high
and that the available spectral models are often too simple to be able
to describe all subtleties of the observations. Furthermore, given our
choice of systematics, for lower
![]() PCA data are
completely dominated by calibration uncertainties. In principle this
would require data analysis methods that treat systematic errors in a
much more elaborate way. We stress that typical observations of
bright sources with other satellites, such as Chandra or
XMM-Newton, result in good
PCA data are
completely dominated by calibration uncertainties. In principle this
would require data analysis methods that treat systematic errors in a
much more elaborate way. We stress that typical observations of
bright sources with other satellites, such as Chandra or
XMM-Newton, result in good ![]() values despite having
significantly larger (10% or more) deviations between the data
and the model than our RXTE fits, where we typically find
that data and model deviate by <1%. These better
values despite having
significantly larger (10% or more) deviations between the data
and the model than our RXTE fits, where we typically find
that data and model deviate by <1%. These better ![]() values
from Chandra and XMM-Newton are by virtue of their
smaller effective areas and consequently larger Poisson errors which
dominates over the calibration uncertainty of these satellites. Seen
in this light, our RXTE models thus provide an overall good
description of the spectral shape of Cygnus X-1.
values
from Chandra and XMM-Newton are by virtue of their
smaller effective areas and consequently larger Poisson errors which
dominates over the calibration uncertainty of these satellites. Seen
in this light, our RXTE models thus provide an overall good
description of the spectral shape of Cygnus X-1.
![\begin{figure}
\par\includegraphics[width=11.2cm,clip]{3938fi01.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg37.gif) |
Figure 1: RXTE-ASM 2-10 keV, and radio lightcurves of Cyg X-1 from 1996 until the end of 2004. The 15 GHz data are from the Ryle telescope, the 8.3 GHz and 2.25 GHz measurements come from the National Radio Astronomy Observatory's Green Bank Interferometer. The data are rebinned to a resolution of 5.6 d to smooth out the orbital variability. |
| Open with DEXTER | |
The figure clearly shows the well known fact that Cyg X-1 transits
between two states. As will be elaborated upon below, for ASM count
rates below ![]() 45 cps, the source is in a classical hard state.
During this time radio emission is observed at a level of
45 cps, the source is in a classical hard state.
During this time radio emission is observed at a level of
![]() 12 mJy at 15 GHz. In contrast, during times when the ASM
count rate is
12 mJy at 15 GHz. In contrast, during times when the ASM
count rate is ![]() 80 cps, the source spectrum is soft, although
a hard power law component is still seen. We will call these phases
the "soft state'', although it is important to note that Cyg X-1 only
rarely reaches what one would call a classical "soft state'' in
transient BHC. During these soft states, the radio emission is
strongly reduced. We especially note that during the long soft state
of 2001/2002 there were phases where no radio emission could be
detected (mm-emission was quenched during that time as
well; Tigelaar et al. 2004).
80 cps, the source spectrum is soft, although
a hard power law component is still seen. We will call these phases
the "soft state'', although it is important to note that Cyg X-1 only
rarely reaches what one would call a classical "soft state'' in
transient BHC. During these soft states, the radio emission is
strongly reduced. We especially note that during the long soft state
of 2001/2002 there were phases where no radio emission could be
detected (mm-emission was quenched during that time as
well; Tigelaar et al. 2004).
During transitions between the hard and soft states, radio flares are observed where the radio flux can be up to a factor of two higher than during the hard state. Cyg X-1 also shows short episodes where the ASM count rate increases. We have identified these episodes with "failed state transitions'' before (Paper I), since they are characterized by the X-ray spectrum softening and by clearly changed timing properties (e.g., increased X-ray time lags; Pottschmidt et al. 2000), similar to state transitions, although the source never really settles into a soft state like behavior.
Prior to ![]() 1999, Cyg X-1 was in the hard state for most of the
time, except for rather short "failed state transitions'' and the
short soft state of 1996. From that time onwards, the frequency of the
failed state transitions increased until, from 2001 July onwards,
Cyg X-1 reached the long 2001/2002 soft state. It stayed in this phase
for almost a year until 2002 August/September where it rapidly
transited back into the hard state, with a spectrum similar to before
the soft state. Shortly after this, in 2003 June and at the turn of
2003/2004, two other short soft state episodes occured. From early
2004 onwards, the RXTE ASM count rate was generally increased
with respect to the 1997-1999 hard states and the source spectrum was
generally softer as well.
1999, Cyg X-1 was in the hard state for most of the
time, except for rather short "failed state transitions'' and the
short soft state of 1996. From that time onwards, the frequency of the
failed state transitions increased until, from 2001 July onwards,
Cyg X-1 reached the long 2001/2002 soft state. It stayed in this phase
for almost a year until 2002 August/September where it rapidly
transited back into the hard state, with a spectrum similar to before
the soft state. Shortly after this, in 2003 June and at the turn of
2003/2004, two other short soft state episodes occured. From early
2004 onwards, the RXTE ASM count rate was generally increased
with respect to the 1997-1999 hard states and the source spectrum was
generally softer as well.
We can quantify this behavior for the moment by defining the hard
state to have an orbit averaged ASM count rate of <45 cps (see
Sect. 3.3) and the soft state to have an ASM count rate
![]() 80 cps. Using these definitions, for the total time interval
from 1996-2004, Cyg X-1 spent 75% of the time in the hard state, 4%
in the soft state and 21% in between. Before MJD 51300, the source
was in the hard state for 90% of the time, in the soft state 4% of
the time, and in between for
80 cps. Using these definitions, for the total time interval
from 1996-2004, Cyg X-1 spent 75% of the time in the hard state, 4%
in the soft state and 21% in between. Before MJD 51300, the source
was in the hard state for 90% of the time, in the soft state 4% of
the time, and in between for ![]() 6% of the time. These numbers
change dramatically after MJD 51300, where the time spent in the hard
state decreased to 66%, while the soft and intermediate phases
account for 34% of all ASM data points. While these numbers are not
too precise because of our arbitrary cuts between the different states
in terms of the ASM count rate, they clearly point towards a change in
source behavior in recent years, which might have been foreshadowed by
a change in the timing properties of the source around MJD 50920 (see
Fig. 3 of Paper I). Specifically, around this time the
short time scale rms variability (i.e., the rms associated with
individual pointed observations) significantly decreased, while the
long time scale variabilty (i.e., the prevalence of failed state
transitions) increased.
6% of the time. These numbers
change dramatically after MJD 51300, where the time spent in the hard
state decreased to 66%, while the soft and intermediate phases
account for 34% of all ASM data points. While these numbers are not
too precise because of our arbitrary cuts between the different states
in terms of the ASM count rate, they clearly point towards a change in
source behavior in recent years, which might have been foreshadowed by
a change in the timing properties of the source around MJD 50920 (see
Fig. 3 of Paper I). Specifically, around this time the
short time scale rms variability (i.e., the rms associated with
individual pointed observations) significantly decreased, while the
long time scale variabilty (i.e., the prevalence of failed state
transitions) increased.
The physical reason for this change of behavior after ![]() MJD 51000
is unclear. In its simplest interpretation, the soft state occurs at
higher
MJD 51000
is unclear. In its simplest interpretation, the soft state occurs at
higher ![]() ,
and thus one could speculate that the mass accretion
rate increased around that date. As
,
and thus one could speculate that the mass accretion
rate increased around that date. As ![]() is related to the mass
loss rate of HDE 226868, in principle it is possible to measure
is related to the mass
loss rate of HDE 226868, in principle it is possible to measure ![]() from its correlation with the equivalent width (EW) of the
H
from its correlation with the equivalent width (EW) of the
H![]() line (Puls et al. 1996). The simplest picture, that a higher
mass loss rate of HDE 226868 results in a higher
line (Puls et al. 1996). The simplest picture, that a higher
mass loss rate of HDE 226868 results in a higher ![]() for the
black hole, however, is contradicted by the observations. Contrary to
expectations, the soft state H
for the
black hole, however, is contradicted by the observations. Contrary to
expectations, the soft state H![]() EW is generally lower than in
the hard state
(Brocksopp et al. 1999a; Tarasov et al. 2003; Gies et al. 2003; Voloshina et al. 1997). For single
stars, such a behavior indicates a lower mass loss rate
(Gies et al. 2003, and therein). A possible solution to this enigma is
that photoionization by the X-ray source changes the wind ionization
state (Hatchett & McCray 1977). Observationally, this effect could be the
cause of the variation of the H
EW is generally lower than in
the hard state
(Brocksopp et al. 1999a; Tarasov et al. 2003; Gies et al. 2003; Voloshina et al. 1997). For single
stars, such a behavior indicates a lower mass loss rate
(Gies et al. 2003, and therein). A possible solution to this enigma is
that photoionization by the X-ray source changes the wind ionization
state (Hatchett & McCray 1977). Observationally, this effect could be the
cause of the variation of the H![]() line profile with orbital
phase (Tarasov et al. 2003; Gies et al. 2003). To explain the relation between
the X-rays and the optical data, both teams of authors suggest that a
decrease in the mass loss rate of HDE 226868,
line profile with orbital
phase (Tarasov et al. 2003; Gies et al. 2003). To explain the relation between
the X-rays and the optical data, both teams of authors suggest that a
decrease in the mass loss rate of HDE 226868,
![]() ,
changes the properties of the accretion flow onto the black hole. A
decreased wind density results in an increase of the size of the
Strömgren sphere around the X-ray source, resulting in a lower
radiative acceleration and consequential lower terminal wind velocity,
,
changes the properties of the accretion flow onto the black hole. A
decreased wind density results in an increase of the size of the
Strömgren sphere around the X-ray source, resulting in a lower
radiative acceleration and consequential lower terminal wind velocity,
![]() .
Since the mass accretion rate is
.
Since the mass accretion rate is
![]() (Bondi & Hoyle 1944; Davidson & Ostriker 1973), an increase of
(Bondi & Hoyle 1944; Davidson & Ostriker 1973), an increase of ![]() through the
accretion disk is triggered, leading to the increase in soft X-ray
emission. The sparse optical coverage prohibits so far direct tests
whether this picture is true, although at least for one failed state
transition, Tarasov et al. (2003) find a decrease of the EW before the
flare, consistent with the above model. If this general idea is
correct, it then follows that the recent increase in soft state
activity of Cyg X-1 could be linked to episodes of lower mass loss
from HDE 226868 (Gies et al. 2003), e.g., linked to activity cycles of
the donor star.
through the
accretion disk is triggered, leading to the increase in soft X-ray
emission. The sparse optical coverage prohibits so far direct tests
whether this picture is true, although at least for one failed state
transition, Tarasov et al. (2003) find a decrease of the EW before the
flare, consistent with the above model. If this general idea is
correct, it then follows that the recent increase in soft state
activity of Cyg X-1 could be linked to episodes of lower mass loss
from HDE 226868 (Gies et al. 2003), e.g., linked to activity cycles of
the donor star.
![\begin{figure}
\par\includegraphics[width=11.2cm,clip]{3938fi02.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg43.gif) |
Figure 2: Unfolded spectrum and residuals for the Cyg X-1 observation of 1999 July 30 (P40090/14), using the broken power law model as the baseline continuum. |
| Open with DEXTER | |
Here, we use an approach already used by us earlier in a study of GX 339-4 (Nowak et al. 2002) to describe the spectral evolution of Cyg X-1 using several different spectral models. We start in Sect. 3.3 with the most simple spectral model, a broken power law with an exponential cutoff. This model gives a very good empirical description of the hard state X-ray spectral shape. We then use two different physically motivated models to find an interpretation of the empirically derived spectral shape in terms of Comptonization. In Sect. 3.4 we use the widely available Comptonization model of Titarchuk (1994, see also Titarchuk & Lyubarskij 1995; Titarchuk & Hua 1995#, compTT. We contrast the compTT results in Sect. 3.5 with the more elaborate Comptonization model eqpair (Coppi 1999,1992), which provides a good example for todays class of self consistent Comptonization models that also include the capability to generate the spectra resulting from non-thermal Comptonization.
Figure 2 shows a typical example for a broken
power law fit, illustrating that for most observations this continuum
model gives a good description of the data, with
![]() .
A similar result for broken power law fits has
been found previously, e.g., by Gierlinski et al. (1999). In general,
we find that during the hard state the goodness of the broken power
law fits as measured in terms of their
.
A similar result for broken power law fits has
been found previously, e.g., by Gierlinski et al. (1999). In general,
we find that during the hard state the goodness of the broken power
law fits as measured in terms of their
![]() surpasses
that of the compTT and eqpair fits. During the soft
state, the broken power law fits still provide a very good description
of the hard spectrum above
surpasses
that of the compTT and eqpair fits. During the soft
state, the broken power law fits still provide a very good description
of the hard spectrum above ![]() 6 keV, but fare less well below
6 keV, but fare less well below
![]() 6 keV where the accretion disk becomes important
6 keV where the accretion disk becomes important![]() . For these data, compTT and
eqpair give a better description of the spectrum.
. For these data, compTT and
eqpair give a better description of the spectrum.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3938f03a.eps}\hspace*{3mm}
\includegraphics[width=8.2cm,clip]{3938f03b.eps}\par\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg51.gif) |
Figure 3:
a) Correlation between the soft power law index,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.3cm,clip]{3938fi04.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg52.gif) |
Figure 4:
Correlation between the photon index of the soft power
law index, |
| Open with DEXTER | |
As shown in Fig. 3a, for all observations of
Cyg X-1 studied here,
![]() ,
that is, the higher energy
power law is spectrally harder than the soft one. For the majority of
our fits, the break energy of the power laws is found between 15 and
40 keV. There is a weak correlation between
,
that is, the higher energy
power law is spectrally harder than the soft one. For the majority of
our fits, the break energy of the power laws is found between 15 and
40 keV. There is a weak correlation between
![]() and
and
![]() in the sense that higher break energies also have
higher folding energies. A similar correlation exists between
in the sense that higher break energies also have
higher folding energies. A similar correlation exists between ![]() and
and
![]() (Fig. 4), where we
find that a softer continuum implies more curvature at high energies
than harder spectra. In Fig. 3 and all following
figures showing spectral parameters, we show data points from the hard
state with the filled symbolds and data from observations from the
intermediate and soft state using open symbols. To define the hard
state, we use
(Fig. 4), where we
find that a softer continuum implies more curvature at high energies
than harder spectra. In Fig. 3 and all following
figures showing spectral parameters, we show data points from the hard
state with the filled symbolds and data from observations from the
intermediate and soft state using open symbols. To define the hard
state, we use
![]() (a simplified version of the
classification of Remillard 2005), corresponding to ASM count
rates below 45
(a simplified version of the
classification of Remillard 2005), corresponding to ASM count
rates below 45
![]() .
.
The most interesting property of the broken power law fits is the
hardening of the broken power law, which can be physically interpreted
as the hardening of the underlying continuum caused by Compton
reflection off cold or mildly ionized material. As has been pointed
out by Zdziarski et al. (1999), for Seyfert galaxies and galactic black hole
binaries, there is a correlation between the power law index and the
covering factor of the reflecting medium,
![]() ,
in the sense
that softer power laws tend to show stronger reflection. Our broken
power law fits show a similar correlation: There is a strong linear
relationship between
,
in the sense
that softer power laws tend to show stronger reflection. Our broken
power law fits show a similar correlation: There is a strong linear
relationship between ![]() and
and ![]() (Fig. 3a). Correlating the soft power law index,
(Fig. 3a). Correlating the soft power law index,
![]() with the hardening of the broken power law at the break
energy,
with the hardening of the broken power law at the break
energy,
![]() ,
results in a similarly tight
correlation (Fig. 3b). As discussed, e.g., by
Zdziarski et al. (1999, and references therein), for standard power law plus
reflection fits,
,
results in a similarly tight
correlation (Fig. 3b). As discussed, e.g., by
Zdziarski et al. (1999, and references therein), for standard power law plus
reflection fits, ![]() and
and
![]() are not strictly
independent fit parameters: During
are not strictly
independent fit parameters: During ![]() minimization, softer power
law continua can be compensated to some extent by increasing
minimization, softer power
law continua can be compensated to some extent by increasing
![]() .
This behavior can lead to artificial correlations
between these two parameters. While the range of
.
This behavior can lead to artificial correlations
between these two parameters. While the range of ![]() and
and ![]() used to derive the observed
used to derive the observed ![]() -
-![]() correlation was much
larger than the systematic uncertainty caused by the non-independent
fit parameters (Zdziarski et al. 1999), for sources where
correlation was much
larger than the systematic uncertainty caused by the non-independent
fit parameters (Zdziarski et al. 1999), for sources where ![]() and
and ![]() do not vary as much, the artificial correlation is still of
some concern. In contrast, in the broken power-law fits
do not vary as much, the artificial correlation is still of
some concern. In contrast, in the broken power-law fits ![]() and
and
![]() are virtually independent and therefore artificial
correlations are not an issue for our analysis.
are virtually independent and therefore artificial
correlations are not an issue for our analysis.
Lastly, we comment on the behavior of the Fe K![]() line in the
broken power law fits. In general, we find the line at 6.4 keV, i.e.,
consistent with neutral iron, although spectra showing a larger
line in the
broken power law fits. In general, we find the line at 6.4 keV, i.e.,
consistent with neutral iron, although spectra showing a larger
![]() tend to show slightly higher line energies. In no case
does the line energy exceed 6.7 keV. This trend could indicate a
slightly higher degree of disk ionization for the softer spectra
during these episodes. The distribution of the line width,
tend to show slightly higher line energies. In no case
does the line energy exceed 6.7 keV. This trend could indicate a
slightly higher degree of disk ionization for the softer spectra
during these episodes. The distribution of the line width,
![]() ,
from all observations can be well
described by a Gaussian distribution with a mean of 0.6 keV,
consistent, e.g., with earlier BeppoSAX and RXTE
results (Frontera et al. 2001; Gilfanov et al. 1999). We performed Monte Carlo
simulations, confirming our experience that with its 18% FWHM energy
resolution at 5.9 keV the PCA can resolve lines down to
,
from all observations can be well
described by a Gaussian distribution with a mean of 0.6 keV,
consistent, e.g., with earlier BeppoSAX and RXTE
results (Frontera et al. 2001; Gilfanov et al. 1999). We performed Monte Carlo
simulations, confirming our experience that with its 18% FWHM energy
resolution at 5.9 keV the PCA can resolve lines down to
![]() keV. The fits indicate, therefore, that the Fe K
keV. The fits indicate, therefore, that the Fe K![]() line is
slightly broadened, as has been found also with higher resolution
instruments (e.g., Miller et al. 2002). Note, however, that the
line is
slightly broadened, as has been found also with higher resolution
instruments (e.g., Miller et al. 2002). Note, however, that the
![]() 5 keV calibration feature discussed in
Appendix A as well as the presence of a soft excess
can bias the line parameters towards a lower energy and larger
5 keV calibration feature discussed in
Appendix A as well as the presence of a soft excess
can bias the line parameters towards a lower energy and larger ![]() .
.
We took compTT as the baseline continuum, assuming a disk
geometry. The parameters of the continuum are the electron optical
depth,
![]() ,
and the electron temperature
,
and the electron temperature
![]() .
An
accretion disk continuum with a r-3/4 temperature profile and
inner disk temperature
.
An
accretion disk continuum with a r-3/4 temperature profile and
inner disk temperature
![]() (XSPEC model diskbb;
Mitsuda et al. 1984; Makishima et al. 1986) was added to model the soft
emission. We set the temperature of the seed photons for
Comptonization equal to
(XSPEC model diskbb;
Mitsuda et al. 1984; Makishima et al. 1986) was added to model the soft
emission. We set the temperature of the seed photons for
Comptonization equal to
![]() ,
indicating that the disk is
the source of the seed photons. Note that this approach is only
approximately justified, since the seed photon distribution assumed by
compTT is a Wien distribution and not a proper disk spectrum.
We take Compton reflection of the Comptonization continuum into
account using the Green's functions of Magdziarz & Zdziarski (1995, XSPEC model
reflect), assuming solar abundances, a neutral
reflector, an inclination of
,
indicating that the disk is
the source of the seed photons. Note that this approach is only
approximately justified, since the seed photon distribution assumed by
compTT is a Wien distribution and not a proper disk spectrum.
We take Compton reflection of the Comptonization continuum into
account using the Green's functions of Magdziarz & Zdziarski (1995, XSPEC model
reflect), assuming solar abundances, a neutral
reflector, an inclination of ![]() ,
and taking into account
absorption in the interstellar medium and the stellar wind. The
behavior of the latter is similar to that seen in the eqpair
fits, so we will defer a discussion of the behavior of the hydrogen
equivalent column,
,
and taking into account
absorption in the interstellar medium and the stellar wind. The
behavior of the latter is similar to that seen in the eqpair
fits, so we will defer a discussion of the behavior of the hydrogen
equivalent column, ![]() ,
to Sect. 3.5. All best
fit parameters, including
,
to Sect. 3.5. All best
fit parameters, including
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
the Fe line parameters, and the model normalizations,
as well as their 90% confidence intervals are available in the
electronic Table 2 (available at the CDS). The table also
includes fluxes from the model in the same standard bands as Table 1,
as well as the total bolometric flux inferred from the model. Finally,
the table also includes the total bolometric accretion disk flux.
,
the Fe line parameters, and the model normalizations,
as well as their 90% confidence intervals are available in the
electronic Table 2 (available at the CDS). The table also
includes fluxes from the model in the same standard bands as Table 1,
as well as the total bolometric flux inferred from the model. Finally,
the table also includes the total bolometric accretion disk flux.
The Fe K![]() line was again modeled by a Gaussian, but with the Fe
K
line was again modeled by a Gaussian, but with the Fe
K![]() line energy fixed at 6.4 keV (fits with the line energy
free were virtually identical). There is one clear difference between
the Fe K
line energy fixed at 6.4 keV (fits with the line energy
free were virtually identical). There is one clear difference between
the Fe K![]() parameters in the broken power law fits and the ones
found with compTT: Fe K
parameters in the broken power law fits and the ones
found with compTT: Fe K![]() line widths are greater by a
factor of
line widths are greater by a
factor of ![]() 1.55 than in the broken power law fits. Inspection of
the compTT residuals shows the PCA to have a wavy structure
at low energies around the Fe line, indicating that our choice of soft
spectral components does not adequately describe the details of the
shape of the soft continuum. In addition, we see the K
1.55 than in the broken power law fits. Inspection of
the compTT residuals shows the PCA to have a wavy structure
at low energies around the Fe line, indicating that our choice of soft
spectral components does not adequately describe the details of the
shape of the soft continuum. In addition, we see the K![]() line
width increasing almost linearly with the accretion disk flux, until
it saturates at
line
width increasing almost linearly with the accretion disk flux, until
it saturates at
![]() with a line width
of
with a line width
of ![]() 1 keV. Such a behavior is similar to that of a similarly
broad line feature (at
1 keV. Such a behavior is similar to that of a similarly
broad line feature (at ![]() 5.7 keV) seen in XTE J1908+094,
in the early and late phases of the outburst of this soft X-ray
transient (Gögüs et al. 2004). The broader Fe K
5.7 keV) seen in XTE J1908+094,
in the early and late phases of the outburst of this soft X-ray
transient (Gögüs et al. 2004). The broader Fe K![]() line width can
thus be seen as an attempt of the
line width can
thus be seen as an attempt of the ![]() -minimization procedure to
smooth out the continuum to provide a more power-law like soft
continuum. This conclusion is verified by the generally worse
-minimization procedure to
smooth out the continuum to provide a more power-law like soft
continuum. This conclusion is verified by the generally worse
![]() of the compTT fits compared to the broken power law
ones, although in general the model is still providing a good
description of the data: For hard state and intermediate state
observations,
of the compTT fits compared to the broken power law
ones, although in general the model is still providing a good
description of the data: For hard state and intermediate state
observations,
![]() ,
for soft state
observations,
,
for soft state
observations,
![]() is clearly higher, although (except
for four cases) still better than 2. Note that only in 12 out of the 202 observations is the
is clearly higher, although (except
for four cases) still better than 2. Note that only in 12 out of the 202 observations is the
![]() of the compTT
fits better than that of the broken power law fits.
of the compTT
fits better than that of the broken power law fits.
Replacing the disk component with a relativistic disk spectrum (XSPEC model diskpn, Gierlinski et al. 1999) resulted in significantly worse fits. Adding a second soft component (modeled either by a second disk spectrum or by optically thick Comptonization; Gierlinski et al. 1999) to our baseline diskbb model did not result in improving the residuals significantly either. We therefore decided to stick with our baseline model, especially since the Comptonization parameters are mainly driven by the harder spectrum.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3938fi05.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg67.gif) |
Figure 5:
Correlation between the electron temperature of
the Comptonizing plasma,
|
| Open with DEXTER | |
Figure 5 shows the correlation between the optical
depth, ![]() ,
and the temperature
,
and the temperature
![]() of the Comptonizing
plasma. Defining the Compton y parameter in the usual fashion,
of the Comptonizing
plasma. Defining the Compton y parameter in the usual fashion,
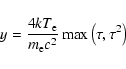 |
(1) |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3938fi06.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg74.gif) |
Figure 6: Relationship between Compton-y and the unabsorbed accretion disk flux for the compTT fits. Symbols used are the same as in Fig. 3. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.4cm,clip]{3938fi07.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg75.gif) |
Figure 7:
Correlation between y and the covering factor for reflection,
|
| Open with DEXTER | |
Since the parameter responsible for the shape of the Comptonization
spectrum is the Compton-y, we now study the relationship between the
accretion disk and the reflection parameters and y(Figs. 6 and 7). In general, the
correlations found in this way are much tighter than correlations with
respect to
![]() and
and ![]() ,
as these two parameters are
strongly coupled.
,
as these two parameters are
strongly coupled.
We compute the bolometric unabsorbed flux of the accretion disk,
![]() ,
by integrating the diskbb component of the
best fit model from 1 eV to 50 keV. The second source of soft
photons, the Wien seed photon spectrum, is not taken into account.
Comparison with the soft fluxes derived with eqpair, where
the seed photons can be taken into account (see Sect. 3.5
below), shows that not taking the Wien spectrum into account results
in the bolometric disk fluxes from compTT to be 73% of the
eqpair fluxes. After correcting the compTT fluxes
for this offset, the standard deviation of the the eqpair and
compTT ratio is found to 20%, which we take as the
systematic uncertainty of the individual fluxes caused by
extrapolating the best fit model outside of the energy range used for
fitting. This 20% systematic uncertainty of individual flux points is
much smaller than the overall variation of the disk fluxes found in
the data. Note that in the following, when quoting
,
by integrating the diskbb component of the
best fit model from 1 eV to 50 keV. The second source of soft
photons, the Wien seed photon spectrum, is not taken into account.
Comparison with the soft fluxes derived with eqpair, where
the seed photons can be taken into account (see Sect. 3.5
below), shows that not taking the Wien spectrum into account results
in the bolometric disk fluxes from compTT to be 73% of the
eqpair fluxes. After correcting the compTT fluxes
for this offset, the standard deviation of the the eqpair and
compTT ratio is found to 20%, which we take as the
systematic uncertainty of the individual fluxes caused by
extrapolating the best fit model outside of the energy range used for
fitting. This 20% systematic uncertainty of individual flux points is
much smaller than the overall variation of the disk fluxes found in
the data. Note that in the following, when quoting
![]() from compTT fits we do not apply any correction
factor, such as might be caused by ignoring the Wien seed spectrum.
from compTT fits we do not apply any correction
factor, such as might be caused by ignoring the Wien seed spectrum.
Figure 6 shows how
![]() depends on y.
There are clearly two regimes of different spectral behavior
recognizable: during the hard state (filled symbols),
depends on y.
There are clearly two regimes of different spectral behavior
recognizable: during the hard state (filled symbols),
![]() is seen to vary by almost an order of magnitude, while y remains
constant. At the same time,
is seen to vary by almost an order of magnitude, while y remains
constant. At the same time,
![]() varies only slightly
(Fig. 7). This behavior of parameters holds for disk
fluxes below
varies only slightly
(Fig. 7). This behavior of parameters holds for disk
fluxes below
![]()
![]() ,
corresponding to a threshold disk luminosity of
,
corresponding to a threshold disk luminosity of
![]() (assuming a distance of
2 kpc, see Ziókowski 2005, and references therein). Above this
threshold the intermediate or the soft state is reached. Here, y is
seen to vary strongly, the disk luminosity is far less variable than
before, and
(assuming a distance of
2 kpc, see Ziókowski 2005, and references therein). Above this
threshold the intermediate or the soft state is reached. Here, y is
seen to vary strongly, the disk luminosity is far less variable than
before, and
![]() varies strongly.
varies strongly.
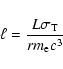 |
(2) |
Similar to the compTT fits, we model the soft excess by
adding a diskbb to the continuum. In contrast, detectors with
a lower energy threshold than the PCA often have shown the soft X-ray
spectrum in eqpair modeling to be more complex than what we
use here. The soft excess has been described by optically thick
Comptonization of 100-300 eV disk photons (Ba-u-cinska-Church et al. 1995), as
predicted for the inner regions of Shakura & Sunyaev (1973) disks
(Frontera et al. 2001; Di Salvo et al. 2001; Gierlinski et al. 1997). Our spectra have an
![]() 3 keV lower threshold, thus we cannot describe in detail this
component. Similar to the compTT fits, we find that adding a
diskbb spectrum to the eqpair continuum results in a
satisfactory description of the data. We set the inner disk
temperature to the maximum temperature of the eqpair seed
photon distribution. Modeling the soft excess with the
diskbb works better than with the diskpn, as the
shape of the diskbb model better approximates the shape of a
(saturated) Comptonization spectrum.
3 keV lower threshold, thus we cannot describe in detail this
component. Similar to the compTT fits, we find that adding a
diskbb spectrum to the eqpair continuum results in a
satisfactory description of the data. We set the inner disk
temperature to the maximum temperature of the eqpair seed
photon distribution. Modeling the soft excess with the
diskbb works better than with the diskpn, as the
shape of the diskbb model better approximates the shape of a
(saturated) Comptonization spectrum.
![\begin{figure}
\par\includegraphics[width=11.2cm,clip]{3938fi08.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg83.gif) |
Figure 8:
Spectral evolution of Cyg X-1 from 1999 until the end of
2004. Shown from top to bottom are the radio flux at 15 GHz as
measured with the Ryle telescope, the compactness ratio,
|
| Open with DEXTER | |
Absorption in the interstellar medium and in the stellar wind is taken
into account using the model of Baucinska-Church & McCammon (1992), letting the hydrogen
equivalent column vary freely. We find a dependence of ![]() with orbital phase (using the ephemeris of Brocksopp et al. 1999b),
with
with orbital phase (using the ephemeris of Brocksopp et al. 1999b),
with ![]() being higher by a factor
being higher by a factor ![]() 2 during superior
conjunction, pointing towards significant absorption in the stellar
wind of HDE 226868 (see Wen et al. 1999 for a similar conclusion
based on RXTE-ASM data). We also confirm earlier results by
Baucinska-Church et al. (2000) of a secondary maximum of
2 during superior
conjunction, pointing towards significant absorption in the stellar
wind of HDE 226868 (see Wen et al. 1999 for a similar conclusion
based on RXTE-ASM data). We also confirm earlier results by
Baucinska-Church et al. (2000) of a secondary maximum of ![]() around orbital
phase 0.6, which earlier has been identified with absorption in the
accretion stream. No other fit parameters show a significant
dependence on orbital phase.
around orbital
phase 0.6, which earlier has been identified with absorption in the
accretion stream. No other fit parameters show a significant
dependence on orbital phase.
Using this approach, our fits gave
![]() values similar
to the models discussed in Sects. 3.3
and 3.4, with only a very weak dependence of
values similar
to the models discussed in Sects. 3.3
and 3.4, with only a very weak dependence of
![]() on the source state (softer spectra tend to have
slightly worse
on the source state (softer spectra tend to have
slightly worse
![]() ). During the hard state,
). During the hard state,
![]() for the eqpair fits is generally worse
than that of the broken power law fits, while it is better during the
soft state (we attribute the latter to us not including a thermal
component in the broken power law fits). All best-fit parameters,
including
for the eqpair fits is generally worse
than that of the broken power law fits, while it is better during the
soft state (we attribute the latter to us not including a thermal
component in the broken power law fits). All best-fit parameters,
including
![]() ,
,
![]() ,
and the Fe
line parameters, and X-ray fluxes for the same bands as for the broken
powerlaw and compTT fits, as well as unabsorbed fluxes for
the accretion disk and for the broadband spectrum are contained in
Table 3, which is only available in electronic form at the CDS.
,
and the Fe
line parameters, and X-ray fluxes for the same bands as for the broken
powerlaw and compTT fits, as well as unabsorbed fluxes for
the accretion disk and for the broadband spectrum are contained in
Table 3, which is only available in electronic form at the CDS.
Figure 8 shows the evolution of energetics of the
soft and the hard spectral components. Similar to the compTT
fits, we characterize the soft flux by the unabsorbed bolometric
accretion disk flux,
![]() .
This flux is computed as the
sum of the 1 eV-50 keV fluxes of the diskpn
.
This flux is computed as the
sum of the 1 eV-50 keV fluxes of the diskpn![]() . and diskbb
spectral components of the best fit models. As discussed in
Sect. 3.4, the systematic uncertainty of these fluxes is
estimated to be 20%, much smaller than the variations observed. Not
unexpectedly, the disk flux is correlated with the binary orbit
averaged RXTE-ASM count rate. A more careful analysis of the
lightcurve reveals, however, that there the ASM does not always fully
track
. and diskbb
spectral components of the best fit models. As discussed in
Sect. 3.4, the systematic uncertainty of these fluxes is
estimated to be 20%, much smaller than the variations observed. Not
unexpectedly, the disk flux is correlated with the binary orbit
averaged RXTE-ASM count rate. A more careful analysis of the
lightcurve reveals, however, that there the ASM does not always fully
track
![]() .
For example,
.
For example,
![]() increases
significantly during the second and third of the three dominant soft
flares around MJD 51500 and remains weak during the first. We will
revisit these differences, which might be due to hysteresis effects
similar to BHC transient outbursts, below. Overall, however, the
correlation between
increases
significantly during the second and third of the three dominant soft
flares around MJD 51500 and remains weak during the first. We will
revisit these differences, which might be due to hysteresis effects
similar to BHC transient outbursts, below. Overall, however, the
correlation between
![]() and the ASM count rate is good,
with the Spearman rank correlation coefficient indicating a highly
significant correlation (
and the ASM count rate is good,
with the Spearman rank correlation coefficient indicating a highly
significant correlation (
![]() ). A linear regression gives
). A linear regression gives
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3938fi09.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg89.gif) |
Figure 9:
Relationship between the compactness ratio of the
Comptonizing medium,
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3938fi10.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg90.gif) |
Figure 10:
The bolometric luminosity of the accretion disk,
|
| Open with DEXTER | |
The hard spectral component is characterized by the compactness ratio,
![]() and the optical depth
and the optical depth ![]() of the Comptonizing medium.
Large
of the Comptonizing medium.
Large
![]() correspond to the hard state. As shown in
Fig. 9,
correspond to the hard state. As shown in
Fig. 9, ![]() increases with
increases with
![]() ,
indicating the
increased importance of the Comptonizing medium for higher
,
indicating the
increased importance of the Comptonizing medium for higher
![]() .
Consequently, low
.
Consequently, low
![]() correspond to the soft state, such that
there is an anticorrelation between
correspond to the soft state, such that
there is an anticorrelation between
![]() and the accretion disk
luminosity (Fig. 10). This anticorrelation can
be expressed as a power law dependence of the bolometric accretion
disk luminosity,
and the accretion disk
luminosity (Fig. 10). This anticorrelation can
be expressed as a power law dependence of the bolometric accretion
disk luminosity,
![]() ,
and
,
and
![]() ,
,
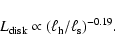 |
(4) |
We now briefly turn to the evolution of the bolometric flux of
Cyg X-1. Based on RXTE and CGRO data,
Zhang et al. (1997) claimed that the difference in bolometric luminosity
of Cyg X-1 between the 1996 hard and soft states was ![]()
![]() -70%, a statement later revisited by Zdziarski et al. (2002). Based on
a small number of observations, these authors found that the
bolometric flux of the source was higher by a factor of 3-4 in the
soft state. The availability of our broad band fits allows us to
confirm Zdziarski et al. (2002)'s earlier results: During the RXTE
campaign, the mean bolometric unabsorbed flux of Cyg X-1 was
-70%, a statement later revisited by Zdziarski et al. (2002). Based on
a small number of observations, these authors found that the
bolometric flux of the source was higher by a factor of 3-4 in the
soft state. The availability of our broad band fits allows us to
confirm Zdziarski et al. (2002)'s earlier results: During the RXTE
campaign, the mean bolometric unabsorbed flux of Cyg X-1 was
![]() ,
with a
minimum flux of
,
with a
minimum flux of
![]() measured on
2003 January 10 (observation P60090/23.14off), and a maximum flux of
measured on
2003 January 10 (observation P60090/23.14off), and a maximum flux of
![]() measured on
2002 March 25 (observation P60090/02.14off).
measured on
2002 March 25 (observation P60090/02.14off).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3938f11a.eps}\hspace*{3mm}
\includegraphics[width=7.8cm,clip]{3938f11b.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg96.gif) |
Figure 11:
Relationship between
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=11.2cm,clip]{3938fi12.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg97.gif) |
Figure 12: Unfolded spectra and residuals for the eqpair fits of the Cyg X-1 observations of 2003 January 10 (P60090/23.14off; hard spectrum) and 2003 July 29 (P60090/35.14off; soft spectrum), illustrating the typical spectral variability of the source. |
| Open with DEXTER | |
Finally, we discuss the variability of the reprocessing features,
i.e., the covering factor of the reflecting medium,
![]() ,
and
the Fe K
,
and
the Fe K![]() line. Figure 13 shows that
line. Figure 13 shows that
![]() for
for
![]() ,
indicating moderate
amounts of reflection during the hard state. There is a moderate
trend for
,
indicating moderate
amounts of reflection during the hard state. There is a moderate
trend for
![]() to decrease with increasing
to decrease with increasing
![]() (and
increasing
(and
increasing ![]() ), although this trend is somewhat weaker and less
distinct than previously claimed anti-correlations between reflection
fraction and spectral hardness (Zdziarski et al. 1999,2003, and references
therein). For our observations, the eqpair
and the compTT fits show a similar relative behavior;
however,
), although this trend is somewhat weaker and less
distinct than previously claimed anti-correlations between reflection
fraction and spectral hardness (Zdziarski et al. 1999,2003, and references
therein). For our observations, the eqpair
and the compTT fits show a similar relative behavior;
however,
![]() derived from eqpair is larger by
derived from eqpair is larger by
![]() 0.1. This slightly larger fitted covering factor is likely due
to the usage of a relativistic smeared reflection continuum in the
eqpair fits; reflection in the compTT model is
artificially reduced to minimize the sharp Fe edge in the reflection
model used with those latter fits. There may also be influences from
the different shapes of the exponential cutoff in these two models.
In the eqpair models, as the source approaches the soft state
and
0.1. This slightly larger fitted covering factor is likely due
to the usage of a relativistic smeared reflection continuum in the
eqpair fits; reflection in the compTT model is
artificially reduced to minimize the sharp Fe edge in the reflection
model used with those latter fits. There may also be influences from
the different shapes of the exponential cutoff in these two models.
In the eqpair models, as the source approaches the soft state
and
![]() decreases, there is no clear correlation with
decreases, there is no clear correlation with
![]() .
The reflection fraction varies in a seemingly
independent manner, although in general our highest fitted reflection
fractions come from the soft state. Again this is reminiscent of the
behavior already seen in the compTT fits
(Fig. 7).
.
The reflection fraction varies in a seemingly
independent manner, although in general our highest fitted reflection
fractions come from the soft state. Again this is reminiscent of the
behavior already seen in the compTT fits
(Fig. 7).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3938fi13.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg104.gif) |
Figure 13:
Correlation between the compactness ratio of the Comptonizing
medium,
|
| Open with DEXTER | |
The second indicator for reprocessing in cold material, the Fe
K![]() line, does not show a correlated behavior with any of the
spectral parameters considered here. This lack of correlation is
puzzling. Since the Fe K
line, does not show a correlated behavior with any of the
spectral parameters considered here. This lack of correlation is
puzzling. Since the Fe K![]() line is thought to be the result of
fluorescence in the accretion disk, we would expect the Fe line to
track
line is thought to be the result of
fluorescence in the accretion disk, we would expect the Fe line to
track
![]() ,
i.e., the variation of the Compton reflection
component. Similar to our fits with the broken power law or the
compTT model, there is a larger fraction of fits in which the
Fe K
,
i.e., the variation of the Compton reflection
component. Similar to our fits with the broken power law or the
compTT model, there is a larger fraction of fits in which the
Fe K![]() line has an energy that is significantly below 6.4 keV.
The residuals for these observations often show the Xe L edge
calibration feature, indicating that calibration effects might lead at
least in part of the observations to spurious Fe K
line has an energy that is significantly below 6.4 keV.
The residuals for these observations often show the Xe L edge
calibration feature, indicating that calibration effects might lead at
least in part of the observations to spurious Fe K![]() line
parameters, although we cannot exclude other effects, such as a more
complex shape of the soft excess. As already indicated above, however,
neither the addition of a Compton component (Gierlinski et al. 1999) nor
the substitution of the diskbb soft component by a
diskpn component result in a better description of the soft
excess and the Fe K
line
parameters, although we cannot exclude other effects, such as a more
complex shape of the soft excess. As already indicated above, however,
neither the addition of a Compton component (Gierlinski et al. 1999) nor
the substitution of the diskbb soft component by a
diskpn component result in a better description of the soft
excess and the Fe K![]() line.
line.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3938fi14.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg105.gif) |
Figure 14:
The power law break, |
| Open with DEXTER | |
To parameterize our data with the least possible theoretical bias, we
can use the results from the broken power law fits. As shown in
Sect. 3.3, these fits indicate the presence of two
spectral components that vary in a correlated manner as described by
the ![]() -
-![]() correlation. We show in
Fig. 14 that there is an almost linear
relation between the soft excess luminosity found from Comptonization
fits and
correlation. We show in
Fig. 14 that there is an almost linear
relation between the soft excess luminosity found from Comptonization
fits and
![]() .
In Comptonization models,
therefore, one can interpret the power law break in part as a measure
of the bolometric accretion disk luminosity, although part of the
break can also be caused by the
.
In Comptonization models,
therefore, one can interpret the power law break in part as a measure
of the bolometric accretion disk luminosity, although part of the
break can also be caused by the ![]() -
-![]() -relationship.
-relationship.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3938fi15.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg107.gif) |
Figure 15:
For power law breaks
|
| Open with DEXTER | |
Alternatively, however, in models explaining the X-ray spectra of BHC
in terms of emission from along a jet, the power law break describes
the transition from synchrotron radiation (as well as accretion disk
emission) to a synchrotron self-Compton spectrum that is modified by
Compton reflection
(Markoff & Nowak 2004; Markoff et al. 2003,2005; Nowak et al. 2005).
Figure 15 provides an important benchmark for
such models. For
![]() ,
i.e., most hard state
observations, the radio flux is seemingly independent of
,
i.e., most hard state
observations, the radio flux is seemingly independent of
![]() ,
while above that threshold strong variations of the
radio flux are observed.
,
while above that threshold strong variations of the
radio flux are observed.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3938fi16.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg109.gif) |
Figure 16:
Correlation between the 15 GHz radio flux and
the compactness ratio of the Comptonizing medium,
|
| Open with DEXTER | |
Using the Comptonization interpretation of the X-ray spectrum, we can
study how the radio emission and the Comptonizing medium interact. For
such a study the eqpair models are especially interesting,
since
![]() is a measure of the energetics of the Comptonizing
medium. We find that the radio flux is highest at intermediate
is a measure of the energetics of the Comptonizing
medium. We find that the radio flux is highest at intermediate
![]() (
(
![]() ;
Fig. 16). This behavior is a
consequence of the "failed state transitions'', where Cyg X-1 shows
characteristic flaring behavior in the radio, similar to what has also
been seen in GX 339-4 and other jet sources (Corbel et al. 2003,2000; Fender et al. 2004; Hannikainen et al. 1998, see also
Figs. 1
and 8).
Note that
;
Fig. 16). This behavior is a
consequence of the "failed state transitions'', where Cyg X-1 shows
characteristic flaring behavior in the radio, similar to what has also
been seen in GX 339-4 and other jet sources (Corbel et al. 2003,2000; Fender et al. 2004; Hannikainen et al. 1998, see also
Figs. 1
and 8).
Note that
![]() corresponds to a soft photon index of
corresponds to a soft photon index of
![]() ,
consistent with the upper limit for the hard state
,
consistent with the upper limit for the hard state
![]() as defined by Remillard (2005). Note also that there
seems to be a much tighter relationship between the radio flux and
as defined by Remillard (2005). Note also that there
seems to be a much tighter relationship between the radio flux and
![]() for the soft state compared to the scatter seen for the hard
state.
for the soft state compared to the scatter seen for the hard
state.
In general, BHC for which radio fluxes have been measured exhibit a
strong correlation between the radio and the X-ray flux
(Merloni et al. 2003; Gallo et al. 2003). For Cyg X-1, this correlation becomes
less well pronounced as the soft X-ray flux increases
(Paper III; Gallo et al. 2003). We likewise do not find a
significant relationship between the radio flux and either the
bolometric flux or the disk emission. As already described in
Paper III and by Nowak et al. (2005), however, the radio flux
correlates well with the 10-50 keV hard X-ray flux (
![]() ).
For 15 GHz fluxes above 0.1 mJy, the lowest flux at which the source
was detected during the campaign, we find that the 10-50 keV X-ray
flux, F10-50, can be found from
).
For 15 GHz fluxes above 0.1 mJy, the lowest flux at which the source
was detected during the campaign, we find that the 10-50 keV X-ray
flux, F10-50, can be found from
This result is in strong support of the idea that the hard X-ray flux
is tightly coupled to the radio, suggesting a possible physical
connection between the regions in which this radiation is produced.
Note that for many X-ray transients the radio-X-ray relationship is
found from the 2-10 keV RXTE-ASM data, which is possible
only because of the less complex soft excess in these Roche lobe
accreting systems. Overall, however, the radio behavior of Cyg X-1 as
expressed by Eq. (5) seems to be slightly different
from that of X-ray transients, where Gallo et al. (2003) and
Corbel et al. (2003) find that the radio flux, ![]() ,
and X-ray
flux,
,
and X-ray
flux, ![]() are related by
are related by
![]() .
Such a scaling is expected in various models in
which the X-ray and radio producing regions are connected, either by
the X-rays originating in a jet
(Corbel et al. 2003; Falcke & Biermann 1996; Markoff et al. 2005,2003) or by the X-rays
originating in an advection dominated type of accretion flow that is
coupled to the radio outflow (Heinz & Sunyaev 2003).
Figure 17 shows that for Cyg X-1 there are
indications that the radio-X-ray relationship is steeper than this
canonical value. Taking all observations with available radio fluxes
into account, we find
.
Such a scaling is expected in various models in
which the X-ray and radio producing regions are connected, either by
the X-rays originating in a jet
(Corbel et al. 2003; Falcke & Biermann 1996; Markoff et al. 2005,2003) or by the X-rays
originating in an advection dominated type of accretion flow that is
coupled to the radio outflow (Heinz & Sunyaev 2003).
Figure 17 shows that for Cyg X-1 there are
indications that the radio-X-ray relationship is steeper than this
canonical value. Taking all observations with available radio fluxes
into account, we find
![]() (Fig. 17, solid line). Limiting ourselves to
the hard state observations only, where the radio fluxes are best
determined, we find
(Fig. 17, solid line). Limiting ourselves to
the hard state observations only, where the radio fluxes are best
determined, we find
![]() (Fig. 17, dashed line), which, given the
uncertainty of the flux determination, can be considered as consistent
with the
(Fig. 17, dashed line), which, given the
uncertainty of the flux determination, can be considered as consistent
with the
![]() relationship. Similarly
steep radio-X-ray relationships have been seen in the black hole
candidate XTE J1908+094 (Jonker et al. 2004) and in the neutron star
system 4U 1728-34 (Migliari et al. 2003).
relationship. Similarly
steep radio-X-ray relationships have been seen in the black hole
candidate XTE J1908+094 (Jonker et al. 2004) and in the neutron star
system 4U 1728-34 (Migliari et al. 2003).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3938fi17.eps}
\end{figure}](/articles/aa/full/2006/07/aa3938-05/Timg117.gif) |
Figure 17:
Correlation between the 10-50 keV hard X-ray flux and the
15 GHz radio flux. The dotted line corresponds to the canonical
|
| Open with DEXTER | |
Acknowledgements
We thank Thomas Gleißner, Sara Benlloch, and William "Biff'' Heindl for many discussions and help with the data screening and extraction during the years it took to assemble the data from the Cyg X-1 campaign and the anonymous referee for his/her comments. This work has been partly funded by NASA contract NAS5-30720, NASA grant SV3-73016, by Deutsches Zentrum für Luft- und Raumfahrt grant 50 OR 302 and by travel funds from the Deutscher Akademischer Austauschdienst and the National Science Foundation (NSF contract INT-0233441). The Ryle telescope is supported by PPARC. This work has made use of data obtained from the High Energy Astrophysics Science Archive Research Center (HEASARC), provided by NASA's Goddard Space Flight Center. The Green Bank Interferometer was a facility of the National Science Foundation operated by the National Radio Astronomy Observatory in support of NASA High Energy Astrophysics programs. The University of Warwick Centre for Scientific Computing provided significant computing resources through its Cluster of Workstations (COW). We thank the Aspen Center for Physics for its hospitality during the final stages of the preparation of this paper.
In this Appendix we summarize our results for the spectral calibration
of the RXTE based on HEASOFT 5.3.1. As shown, e.g., by
Wilms et al. (1999), earlier HEASOFT versions exhibited a significant
difference in spectral slope of ![]() 0.05 between the PCA and HEXTE,
with PCA spectra being consistently softer than spectra derived from
HEXTE and other missions. For observations of black holes, such a
difference is especially worrisome since the apparent hardening
implied by the older calibration can mimic a Compton reflection
component. In HEASOFT 5.3.1, this discrepancy is now much smaller and
fits to RXTE observations of the Crab nebula and pulsar give
the canonical spectral shape (see Jahoda et al. 2005, for an extensive discussion
of the PCA calibration). For example, modeling the joint
PCA and HEXTE data from RXTE's Crab observation
40805-01-05-01 in 1999 we find that the joint spectrum can be
described as the sum of two power laws with photon indices
0.05 between the PCA and HEXTE,
with PCA spectra being consistently softer than spectra derived from
HEXTE and other missions. For observations of black holes, such a
difference is especially worrisome since the apparent hardening
implied by the older calibration can mimic a Compton reflection
component. In HEASOFT 5.3.1, this discrepancy is now much smaller and
fits to RXTE observations of the Crab nebula and pulsar give
the canonical spectral shape (see Jahoda et al. 2005, for an extensive discussion
of the PCA calibration). For example, modeling the joint
PCA and HEXTE data from RXTE's Crab observation
40805-01-05-01 in 1999 we find that the joint spectrum can be
described as the sum of two power laws with photon indices
![]() and
and
![]() .
The nebula flux at 1 keV is
found to be
10.3
.
The nebula flux at 1 keV is
found to be
10.3
![]() ,
or about 8% higher than the canonical value of Toor & Seward (1974), the
hard pulsar continuum contributes
0.05
,
or about 8% higher than the canonical value of Toor & Seward (1974), the
hard pulsar continuum contributes
0.05
![]() at this energy (all values given are unabsorbed fluxes, absorption in
the interstellar medium was taken into account by using the
cross-sections and abundances of Wilms et al. 2000 and by assuming a
H-equivalent column of
at this energy (all values given are unabsorbed fluxes, absorption in
the interstellar medium was taken into account by using the
cross-sections and abundances of Wilms et al. 2000 and by assuming a
H-equivalent column of
![]() as found with Chandra by Weisskopf et al. 2004).
as found with Chandra by Weisskopf et al. 2004).
In addition to the difference in spectral slope, earlier HEASOFT
versions also showed a very significant overestimate of the PCA flux
with respect to the HEXTE, with the PCA fluxes being consistently
higher by ![]() 30%. This overestimate can be taken into account in
30%. This overestimate can be taken into account in
![]() -fitting by multiplying the spectral model instrument
dependent constant. Traditionally, this normalization constant was set
to 1 for the PCA and let vary for the HEXTE. This traditional approach
is unfortunate, since it implies that the flux normalization of the
HEXTE is uncertain, while in reality it was the PCA that showed clear
deviations in flux with respect to other instruments. For consistency
with other studies, however, here we continue using the traditional
approach. For all different spectral models used in this paper, we
find that under HEASOFT 5.3.1 both instruments now agree remarkably
well, with the distribution of the constant values being consistent
with a normal distribution of mean 1.01 and standard deviation 0.03.
We still chose to include the constant in our final fits, as in
individual observations a mismatch between the PCA and the HEXTE is
possible, for example for those observations where the PCA deadtime
becomes important
-fitting by multiplying the spectral model instrument
dependent constant. Traditionally, this normalization constant was set
to 1 for the PCA and let vary for the HEXTE. This traditional approach
is unfortunate, since it implies that the flux normalization of the
HEXTE is uncertain, while in reality it was the PCA that showed clear
deviations in flux with respect to other instruments. For consistency
with other studies, however, here we continue using the traditional
approach. For all different spectral models used in this paper, we
find that under HEASOFT 5.3.1 both instruments now agree remarkably
well, with the distribution of the constant values being consistent
with a normal distribution of mean 1.01 and standard deviation 0.03.
We still chose to include the constant in our final fits, as in
individual observations a mismatch between the PCA and the HEXTE is
possible, for example for those observations where the PCA deadtime
becomes important![]() . There are only 7 observations
with constants more than 2
. There are only 7 observations
with constants more than 2![]() away from the mean. Except for the
significantly deviating normalization constant, these observations are
not remarkable in any other way, and are therefore included in our
further analysis, although the cause for the deviation is currently
unknown. We conclude, therefore, that for the overwhelming majority of
observations there is now agreement in the PCA and HEXTE derived
fluxes.
away from the mean. Except for the
significantly deviating normalization constant, these observations are
not remarkable in any other way, and are therefore included in our
further analysis, although the cause for the deviation is currently
unknown. We conclude, therefore, that for the overwhelming majority of
observations there is now agreement in the PCA and HEXTE derived
fluxes.
As shown in the previous appendix, the high signal to noise
observations from RXTE require us to take the systematic
error of the instrument into account in order to obtain reasonable
spectral parameters. In general, this is done by adding the systematic
error in quadrature to the Poisson errors estimated from the
observation. For instruments such as the PCA it can happen that the
systematic error starts dominating the overall error. As a
consequence, the standard
"
![]() ''-procedure for obtaining
confidence intervals, as outlined, e.g., by Lampton et al. (1976) or
Bevington & Robinson (1992), does not apply since it is based on the assumption
that the variance of the data points is due to a Gaussian
distribution. Since the addition of systematic errors decreases the
''-procedure for obtaining
confidence intervals, as outlined, e.g., by Lampton et al. (1976) or
Bevington & Robinson (1992), does not apply since it is based on the assumption
that the variance of the data points is due to a Gaussian
distribution. Since the addition of systematic errors decreases the
![]() sum, confidence intervals estimated using the
Lampton et al. (1976) prescription in the presence of systematic errors
are significantly larger than what is justified from statistical
grounds.
sum, confidence intervals estimated using the
Lampton et al. (1976) prescription in the presence of systematic errors
are significantly larger than what is justified from statistical
grounds.
Table B.1: Error bars for a representative observation of Cyg X-1, computed using the prescription of Lampton et al. (1976). See text for further explanation.
To study the influence of the systematic error on the confidence intervals in our observations, we have used a Monte Carlo simulation: We first determined the best fit parameters for the compTT model of observation P60090/16 (2002.10.06:15) using the Lampton et al. (1976) approach, including systematic errors. We then used this best fit model to simulate how this observation would look like if the PCA and HEXTE calibration were perfectly known. These simulated spectra were then refit without applying a systematic error and new confidence intervals were determined. The resulting 90% confidence intervals for both fits are shown in Table B.1 (Error bars at the 68% level can be obtained from the 90% confidence intervals to a sufficiently high precision by assuming that the uncertainty can be approximated by a normal distribution). Depending on the parameter, the error bars are smaller by a factor of 2 to 5, showing that the confidence interval is completely dominated by the systematic error.
Since the systematic error will affect all observations of the Cyg X-1
RXTE campaign in a similar way and since the major interest
is in determining trends in the evolution of spectral
parameters, using the overestimation of the range of the confidence
intervals determined from
individual observations would lead to misleading results. It is
better, therefore, to talk about an "ensemble average'' in
determining the errors and to take the scatter found in individual
relationships between the fit parameters of Cyg X-1 in a similar state
as an estimate their uncertainty. For this reason, we have decided to
not show the misleading individual error bars in the figures in the
main part of this paper, although they are available in the online
data accompanying this paper (Tables 1-3).