A&A 447, 389-395 (2006)
DOI: 10.1051/0004-6361:20053269

Dielectronic recombination data for dynamic finite-density plasmas

X. The hydrogen isoelectronic sequence

N. R. Badnell

Department of Physics, University of Strathclyde, Glasgow G4 0NG, UK

Received 19 April 2005 / Accepted 16 August 2005

Abstract
We have calculated total and final-state resolved partial dielectronic recombination (DR) rate coefficients for 32 H-like ions: He+ through Zn29+ plus Kr35+, Mo41+ and Xe53+. Breit-Pauli intermediate coupling calculations have been carried-out which allow for l-mixing within the He-like autoionizing complex. We discuss the comparison of these results with those of other workers, and with experiment. Fitting coefficients which describe the total DR rate coefficients are presented in this paper. A full set of partial results can be accessed from the Atomic Data and Analysis Structure (ADAS) database or from the Oak Ridge Controlled Fusion Atomic Data Center under http://www-cfadc.phy.ornl.gov/data_and_codes.

Key words: atomic data - atomic processes - plasmas

    
1 Introduction

As first noted by Burgess (1964), dielectronic recombination (DR) is the dominant electron-ion recombination process in many astrophysical and laboratory plasmas. DR rate coefficients are needed for determining both the level populations and the ionization balance of non-equilibrium plasmas over a wide range of electron densities and plasma timescales. Accurate DR rate coefficients are essential for the reliable spectral diagnosis of non-equilibrium laboratory and astrophysical plasmas.

In an effort to provide a comprehensive upgrade to the DR database available, over and above a piecemeal assemblage of detailed calculations combined with the Burgess (1965) General Formula for example, we have outlined a programme (Badnell et al. 2003) for the generation of a DR database which will meet the demands of modern plasma diagnostics. In particular, the need to describe dynamic plasmas whose physical properties change on a timescale such that metastable states are not in quasi-static equilibrium with the ground state, and to describe finite-density plasmas where the recombined electron is further collisionally re-distributed (e.g. stepwise ionization) rather than allowed to cascade back down to the ground state of the recombined ion - the coronal picture.

The rapid advancement of X-ray satellite resolving power (Chandra, XMM-Newton) places new demands upon thetheoretical modelling of photoionized plasmas. Here, the ionization balance occurs at much lower temperatures, for the same ion, compared to electron collision dominated plasmas. In particular, DR through non-dipole core excitations becomes important, viz. between terms of the ground configuration and between levels of the ground term. (This is not an issue for H-like ions of course, but it is a key feature of the overall programme.)

In some ways the DR of H-like ions is simple, viz. there is only a single $1{\rm s}~^2{\rm S}_{1/2}$initial ground level to be considered. In other ways, so often the case for collision processes involving H and H-like ions, it is a special case. In particular, the near-degeneracy of the H-like core means that l-mixing of the He-like autoionizing levels needs to be considered. For all other isoelectronic sequences that have been considered within our programme it has only been necessary to allow for configuration mixing within the core, when the captured electron is not part of the core complex. In particular, Pindzola et al. (1990) obtained up to a 50% increase in the KLn DR cross sections on going from single configuration LS-coupling to multi-configuration intermediate coupling in light ions (C and O). This effect diminishes with increasing Z, as noted by Chen (1988) for Cr and Xe.

The first comprehensive set of calculations for the DR of H-like ions was carried-out by Burgess & Tworkowski (1976)who summarized their (LS-coupling) results as an ion-dependent correction to the Burgess (1965) General Formula for total DR rate coefficients. Total DR rate coefficients were obtained by summing Breit-Pauli satellite intensities for O, Mg and Ca by Bely-Dubau et al. (1984) and Fe by Dubau et al. (1981). Nilsen (1986) carried-out relativistic calculations for Ne, Si, Ar, Ti, Fe, Zn, Kr, Mo and Xe while Karim & Bhalla (1988) carried-out Breit-Pauli calculations for Ne, Si, Ar, Ca, Ti, Fe and Ni. Based-on these detailed results[*] are a number of compendia of fits to total DR rate coefficients, and for other isoelectronic sequences, viz. Shull & Van Steenberg (1982), Arnaud & Rothenflug (1985), Mattioli (1988) and Mazzotta et al. (1998). However, it is not always clear just how they obtained their fit results for some ions. Since then, Gu (2003) has published total DR rate coefficients for Mg, Si, S, Ar, Ca, Fe and Ni using his fully-relativistic flexible atomic code. Also, Dasgupta & Whitney (2004) have studied the Z-scaling of energies and autoionization and radiative rates in intermediate coupling, with explicit calculations for total DR rate coefficients for Al, Ti, Ni, Kr and Mo. Finally, Nahar and co-workers have published R-matrix results for C, N, O and Fe (Nahar & Pradhan 1997; Nahar 1999; Nahar et al. 2000, 2001).

There were a number of DR measurements for H-like ions utilizing electron-coolers in the early 1990s, viz. Tanabe et al. (1992) and DeWitt et al. (1994) on He+, Wolf et al. (1991) on C5+, Kilgus et al. (1990) on O7+ and Kilgus et al. (1992) on S15+. Prior to these cooler measurements was an observation in the JET tokamak of H-like satellite lines in Ni (Bombarda et al. 1988).

This Paper XI completes our work on DR for the H-like through Ne-like isoelectronic sequences. Recent papers are on the N-like (Mitnik & Badnell 2004), Ne-like (Zatsarinny et al. 2004) and He-like (Bautista & Badnell 2005) sequences and they contain references to papers on earlier sequences in the series. Work is already under way on the M-shell - see Altun et al. (2006a,b) for the recently completed Na-like and Mg-like isoelectronic sequences. Furthermore, generalised collisonal-radiative calculations for dynamic finite-density plasmas have now been carried-out for carbon, oxygen and neon (Summers et al. 2006) utilising the DR data, as outlined by Badnell et al. (2003).

The full set of partial DR data in the Atomic Data and Analysis Structure (ADAS) adf09 format (Summers 2003) is available from within ADAS and from the Oak Ridge Controlled Fusion Atomic Data Center under http://www-cfadc.phy.ornl.gov/data_and_codes, both for the present and all earlier sequences.

   
2 Computational details

The partial dielectronic recombination rate coefficient  $\alpha_{i\nu}$ from an initial metastable state $\nu$into a recombined resolved finalstate i is given in the independent processes and isolated resonance approximations by (Burgess 1964)

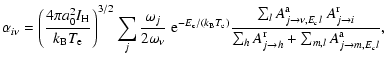$\displaystyle \alpha_{i\nu}=\left({4\pi a^2_0 I_{\rm H} \over k_{\rm B} T_{\rm ... ...{{\rm r}}_{j \rightarrow h} + \sum_{m,l} A^{{\rm a}}_{j \rightarrow m, E_cl}} ,$     (1)

where $\omega_j$ is the statistical weight of the (N+1)-electron doubly-excited resonance state j, $\omega_\nu$ is the statistical weight of the N-electron target state and the autoionization ($A^{\rm a}$) and radiative ($A^{\rm r}$) rates are in inverse seconds. Here, $E_{\rm c}$ is the energy of the continuum electron (with orbital angular momentum l), which is fixed by the position of the resonances, and $I_{\rm H}$ is the ionization potential energy of the hydrogen atom (both in the same units of energy), $k_{\rm B}$ is the Boltzman constant, $T_{\rm e}$ the electron temperature and  $(4\pi a^2_0)^{3/2}=6.6011\times10^{-24}$ cm3.

For the DR of H-like ions, we consider the following (1-2) core excitations:

$\displaystyle 1{\rm s}+ {\rm e}^- \rightarrow 2lnl' ,$     (2)

for l=0,1, l'=0-5 and n=2-1000. We allow for all possible autoionizations, following the above dielectronic capture, and for all possible stabilizing radiative transitions.

We also looked at the contribution from 1-3 core excitations for C, Fe and Xe but the 3-2 alternative autoionization pathway efficiently suppresses it. It contributes no more than 2%, 3% and 5%, respectively, to the peak of the total DR rate coefficient.

We used the code AUTOSTRUCTURE (Badnell 1986; Badnell & Pindzola 1989; Badnell 1997) to calculate multi-configuration intermediate coupling Breit-Pauli energy levels and rates. In particular, we included mixing between all configurations of the He-like autoionizing complex. Non-relativistic radial functions were used up to Zn (to enable us to generate LS- and well as intermediate coupling data) and semi-relativistic radial functions (Pindzola & Badnell 1990) for intermediate coupling data only there-on.

   
3 Comparison with experiments

3.1 He+

Measurements of velocity-averaged DR cross sections utilizing electron coolers have been made for He+ by Tanabe et al. (1992) and by DeWitt et al. (1994); both compared them with the results computed with AUTOSTRUCTURE by the present author.

The resolution of the measurement by Tanabe et al. (1992) was such that only a single broad peak consisting of DR resonances $n\la 10$ was observed. The peak result from AUTOSTRUCTURE was about 20% larger than that measured, somewhat less if not all of the 10l resonances survived the charge-state analyzer.

The resolution of the measurement by DeWitt et al. (1994) was much higher than that of Tanabe et al. (1992) and they observed peaks due to capture into n=2-5, plus a smaller contribution from higher-n that partially survived the charge-state analyzer. The results from AUTOSTRUCTURE were slightly smaller ($\sim$$10\%$) than those observed for the main peaks.


  \begin{figure} \par\includegraphics[width=8cm,clip]{fig1.eps}\end{figure} Figure 1: DR cross sections for C5+. Solid line, from the experiment by Wolf et al. (1991); dotted line, radiation damped Breit-Pauli R-matrix from Zhang et al. (1999); dashed line, present Breit-Pauli perturbation theory results, convoluted with a Gaussian of energy-dependent width corresponding to $kT_{\Vert}=0.002$ eV. Peak "a'' consists of autoionizing resonances $2{\rm s}^2~ ^1{\rm S}+ 2{\rm s}2{\rm p}^3{\rm P}$, peak "b'' of  $2{\rm p}^2~ ^1{\rm D}+ 2{\rm s}2{\rm p}^1{\rm P}$ and "c'' is  $2{\rm p}^2~ ^1{\rm S}$.
Open with DEXTER

3.2 C 5+

Measurements of DR cross sections utilizing an electron cooler have been made for C5+by Wolf et al. (1991)[*] and calculations were made in anticipation of them by Pindzola et al. (1990). However, the two sets of results were never compared directly. We show such a direct comparison in Fig. 1 utilizing the AUTOSTRUCTURE data computed as part of the present work. We see that there is good agreement between the theoretical and experimental results for both the magnitude and position of the peaks. The Breit-Pauli radiation damped R-matrix results of Zhang et al. (1999) are in good agreement both with experiment and our Breit-Pauli perturbative results for the n=2-5 resonance peaks, but appear to underestimate the higher-n contribution to the Rydberg accumulation peak somewhat. We note that it becomes increasingly demanding to resolve accurately the narrower higher-n resonances within the R-matrix method - see Gorczyca et al. (2002) for a detailed discussion. Both calculations include all possible n-values. The experiment essentially counts all that contribute significantly; field ionization by the charge-state analyzer does not occur until at least $n\approx 40$.

3.3 O7+

Measurements of DR cross sections utilizing an electron cooler have been made for O7+by Kilgus et al. (1990) and calculations were made by Pindzola et al. (1990). Comparisons between the two were made, but it is easier to view the level of agreement in the figure presented by Kilgus et al. (1990) rather than in the one shown by Pindzola et al. (1990). However, Pindzola et al. (1990) also presented a table of calculated and measured DR resonance strengths as a function of principal quantum number. They presented results from several calculations which demonstrated the importance of allowing for configuration mixing and intermediate coupling within the He-like autoionizing complex. Pindzola et al. (1990) also compared multi-configuration intermediate coupling results obtained both from Cowan's code (Cowan 1981) and AUTOSTRUCTURE. We show these latter results in Table 1 along with the current AUTOSTRUCTURE results which were obtained with Slater-Type-Orbital (STO) model potentials as opposed to the Thomas-Fermi (TF) ones used by Pindzola et al. (1990). We observe very little difference between the two sets of AUTOSTRUCTURE results, except for n=2 where the current results are closer to those obtained using the Hartree-Fock (HF) orbitals in Cowan's code; even so, the agreement with the measured value is only a little improved as we move from an underestimate to an overestimate.

3.4 S15+

Measurements of DR cross sections utilizing an electron cooler have been made for S15+by Kilgus et al. (1992) and calculations were made in anticipation of them by Pindzola et al. (1990). Kilgus et al. (1992) showed a direct graphical comparison between the results of their measurements and the multi-configuration intermediate coupling AUTOSTRUCTURE results of Pindzola et al. (1990). The level of accord is similar to that found for C5+and O7+.

Table 1: Dielectronic recombination resonance strengths (10-20 cm2 eV) for O7+.

Table 2: Fitting coefficients ci (cm3 s-1 K1.5) and Ei(K) (see Eq. (3)) for the total DR rate coefficients of H-like ions. X(Y) means $X\times 10^Y$.

Table 3: Ratio of peak temperature total DR rate coefficients of other workers to this work.

   
4 Results for rate coefficients

LS- and Breit-Pauli intermediate coupling final-state resolved partial dielectronic recombination rate coefficients for the 32 H-like ions He+ through Zn29+ plus Kr35+, Mo41+ and Xe53+ have been archived in the ADAS adf09 format (Summers 2003) at the Oak Ridge Controlled Fusion Atomic Data Center under http://www-cfadc.phy.ornl.gov/data_and_codes.

Breit-Pauli intermediate coupling total DR rate coefficients have been fitted to the following form:

 
$\displaystyle \alpha = \frac{1}{T^{3/2}} \sum_{i=1}^{3} c_i {\rm e}^{-E_i/T}.$     (3)

In this equation, T and Ei have units of Kelvin, ci units of cm3 s-1 K1.5 and the rate coefficients $\alpha$ have units of cm $^3~\rm s^{-1}$. Our fits are accurate to better than 5% for all ions over the ADAS tabulated temperature range $(10^1{-}10^7)\times Z^2$ K, where Z is the residual charge of the initial ion, or at least down to the temperature at which the rate coefficient becomes vanishingly small (<10-30 cm3 s-1) and radiative recombination completely dominates. In fact, the 5% applies only at the lowest temperatures. Over the rest of the temperature range, including that of the peak rate coefficient, the accuracy is better than 1%. The fitting coefficients ci and Ei for the 32 H-like ions are presented in Table 2.

The temperature dependence of the DR rate coefficient for H-like ions is simple and comparisons between the results of different calculations can be summarized succinctly by the ratio of the peak rate coefficients. In Table 3 we present the ratio of other workers peak DR rate coefficient to our intermediate coupling results, obtained as outlined in Sect. 2.

We note the slow variation in the ratio comparing our results with those of Burgess & Tworkowski (1976) which we have have determined allowing only for $1{\rm s}{-}2{\rm p}$ core excitations, as discussed in Sect. 2. Applying (the Burgess and Tworkowski correction to) the Burgess (1965) General Formula (GF) for higher core-excitations grossly overestimates their contribution because no allowance is made for autoionization into excited states (we will return to this point later). Burgess & Tworkowski (1976) carried-out detailed calculations in LS-coupling for 1-2 core excitations, including diagonalization of the (N+1)-electron Hamiltonian. There is close agreement at lower-Z (apart from He+) but the Burgess & Tworkowski (1976) results become increasingly larger than the present as Z increases. (However, our LS-coupling results are smaller than our intermediate coupling ones.)

The agreement with Mazzotta et al. (1998) is erratic because they recommend data from different sources. The agreement is very close for Be and B simply because the recommended data is that from AUTOSTRUCTURE due to Pindzola & Badnell (1992). It is very poor for He and Li because they used the results of Shore (1969)[*], divided by a factor of 2 because that was what was necessary to bring Shore's results for Be and B into agreement with those of Pindzola & Badnell (1992).

For C to Ni, elucidating the original data source upon which the recommended data of Mazzotta et al. (1998) is based is tricky. Mazzotta et al. (1998) reference Mattioli (1988) and Karim & Bhalla (1988). Karim & Bhalla (1988) carried-out calculations similar to ours and the agreement with our results is excellent for all of the ions that they considered. The lack of agreement with Mazzotta et al. (1998), except for Ni, either illustrates the (in-)accuracy of the fitting data given by Mazzotta et al. (1998) or the fact that they based it upon the data used by Mattioli (1988). However, Mattioli (1988) only reported (fits to) data for C, O, Ar, Ti, Cr, Fe and Ni. Mattioli's (1988) fits for C, O, Ar, Fe and Ni were taken from Arnaud & Rothenflug (1985) and those for Ti and Cr interpolated from these. Arnaud & Rothenflug's (1985) fits for O and Fe (and Mg and Ca) were derived from the results of original calculations by Bely-Dubau et al. (1984) and Dubau et al. (1981)[*], while those for C, Ar and Ni were taken from Shull & Van Steenberg (1982), but multiplied by 0.6 for Ar and Ni. Arnaud & Rothenflug's (1985) fits for Ne, Si and S were also Shull & Van Steenberg's (1982) fits, multiplied by 0.7, 0.6 and 0.6; N was taken by them unaltered. Arnaud & Rothenflug (1985) make no comment on what they used for Al. Al was not considered by Shull & Van Steenberg (1982), who gave fits for 11 H-like ions (C, N, O, Ne, Mg, Si, S, Ar, Ca, Fe, Ni), all based upon their use of the Burgess & Tworkowski (1976) formula. However, Shull & Van Steenberg (1982) included DR via $1{\rm s}{-}n{\rm p}$ core excitations for n=2-7. This caused total DR rate coefficients obtained from the Burgess & Tworkowski (1976) formula to be overestimated significantly (as we have already discussed). This overestimate was noted by Arnaud & Rothenflug (1985) on comparing the Shull & Van Steenberg (1982) totals with those obtained from summing DR satellite intensities (Dubau et al. 1981; Bely-Dubau et al. 1984) and caused them to introduce large correction factors so as to compensate.

So, it appears then that the Mazzotta et al. (1998) recommended DR data for the 23 H-like ions C through Ni can be traced back (via Mattioli 1988) to the use of the Burgess & Tworkowski (1976) formula by Shull & Van Steenberg (1982), multiplied by a correction factor due to Arnaud & Rothenflug (1985), and to estimates from summing DR satellite intensities due to Dubau et al. (1981) and Bely-Dubau et al. (1984). The rest were obtained by interpolation - total DR rate coefficients for the H-like sequence are amenable to interpolation. However, the fits that we have given are comprehensive and come direct from original calculations.

The Mazzotta et al. (1998) recommended DR results are consistently below ours for O through Fe. It is not possible to be sure about the cause of this. The results for Fe of Dubau et al. (1981) are about 10% smaller than ours at their peak. The Bely-Dubau et al. (1984) results are unpublished and the subsequent correction factor for Mg (0.56) determined by Arnaud & Rothenflug (1985) is abnormally low compared to those for O (0.81) and Ca (0.64). Together with the use of correction factors consisting of a single significant figure for other ions and interpolations for the initial uncorrected data, the net result in Table 3 is not unreasonable. The agreement of our results with those of Nilsen (1986) (except for Ne), Karim & Bhalla (1988) and Gu (2003) is excellent. Dasgupta & Whitney (2004) only provide their results in graphical form: they agree with ours to within $\sim$$5\%$ for Al, Ti, Ni and Kr but are $\sim$$15\%$ smaller for Mo.

We have already compared our partial DR cross sections for C5+ with those of the R-matrix calculations by Zhang et al. (1999). The R-matrix method gives rise to a combined DR and radiative recombination (RR) total. In the case of high resolution cross sections it is easy to separate the two - the latter is readily ignored. In the case of rate coefficients the broad Maxwellian distribution means that RR must be subtracted from the R-matrix total or added to our DR contribution so as to make the two comparable. We choose the former approach since we are focusing on DR. In Paper I (Badnell et al. 2003) we discussed why it is preferable and, at times, necessary to use perturbation theory for DR (and thus treat DR and RR separately) so as to be able to carry-out collisional-radiative modelling. Pindzola et al. (1992) demonstrate that it is an accurate approximation to neglect the quantum mechanical interference between DR and RR. Nevertheless, it is important to ensure that a meaningful RR contribution is subtracted from the R-matrix total rate coefficient so as to ensure a like-for-like comparison for DR. To do this, we fit the R-matrix total rate coefficient at lower temperatures, where DR is negligible, to the functional form of Verner & Ferland (1996). We also restrict this procedure to low-Z ions, where DR dominates the total recombination rate coefficient - for O it contributes two-thirds of the total at the temperature of the peak DR contribution.

Following the above procedure, we find that our estimates of the peak DR contribution to the total (DR+RR) rate coefficient results of Nahar & Pradhan (1997) for C and N are a factor of 2.02 and 1.54 larger than ours, respectively. That this is probably due to the neglect of radiation damping from their R-matrix photoionization cross sections can be seen from subsequent results for C and O (Nahar et al. 2000; Nahar 2000) which include radiation damping and for which the relevant ratio is 1.19 and 1.17 (they did not revise N). Nahar et al. (2001) have also calculated results for Fe, but RR contributes significantly to the total recombination rate coefficient in the vicinity of the peak DR contribution and so it is not possible to extract a meaningful comparison of the DR contribution from the Maxwellian rate coefficients. However, extensive comparisons between the Breit-Pauli results of perturbation theory and of radiation damped R-matrix calculations have been carried-out for He-like Fe - Gorczyca & Badnell (1997), Badnell et al. (1998) and Zhang et al. (1999). There, DR and RR were separated at the cross-section level and comparisons made for the KLn DR resonances for n=2-6. The conclusion of these works was that there was very close agreement between the results of perturbation theory and R-matrix calculations, to within a few percent. Indeed, for KLO and KLP the differences between R-matrix results from the two groups was greater than the difference between perturbation theory and R-matrix results from within the two groups.

   
5 Summary

We have reported-on systematic calculations of dielectronic recombination data for the H-like isoelectronic sequence as part of a programme to assemble a dielectronic recombination database suitable for modelling dynamic finite-density plasmas (Badnell et al. 2003). Calculations were carried-out in a multi-configuration intermediate-coupling Breit-Pauli approximation for all ions He+ through Zn29+, as well as for Kr35+, Mo41+, and Xe53+, using non-relativistic (up to Zn) and semi-relativistic (from Zn) radial functions. Fitting coefficients were presented for the total DR rate coefficients and the final-state resolved partial rate coefficients have been archived within ADAS in the adf09 format and are also available from the Oak Ridge Controlled Fusion Atomic Data Center under http://www-cfadc.phy.ornl.gov/data_and_codes.

We have seen (Table 3) that the published results from detailed calculations are not comprehensive and that in many cases the recommended data of Mazzotta et al. (1998) is ultimately dependent on results from the Burgess & Tworkowski (1976) formula, multipled by large correction factors due to Arnaud & Rothenflug (1985). That this is in fact unnecessary can be traced back to the use by Shull & Van Steenberg (1982) of the Burgess & Tworkowski (1976) formula beyond its original remit.

This paper completes our work on DR for the H-like through Ne-like isoelectronic sequences. Work is now in progress on M-shell ions e.g. Na-like and Mg-like (Altun et al. 2006a,b), while generalised collisonal-radiative calculations for dynamic finite-density plasmas have now been carried-out for carbon, oxygen and neon (Summers et al. 2006) utilising the DR data.

References

 
Copyright ESO 2006