A&A 447, 173-184 (2006)
DOI: 10.1051/0004-6361:20052730

3D kinematics of white dwarfs from the SPY project. II.[*],[*]

E.-M. Pauli1 - R. Napiwotzki1,2,3 - U. Heber1 - M. Altmann1,4 - M. Odenkirchen5


1 - Dr. Remeis-Sternwarte, Astronom. Institut, Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049 Bamberg, Germany
2 - Department of Physics & Astronomy, University of Leicester, University Road, Leicester LE1 7RH, UK
3 - Centre for Astrophysics Research, University of Hertfordshire, College Lane, Hatfield AL10 9AB, UK
4 - Departamento de Astronomia, Universidad de Chile, Camino Del Observatorio 1515, Las Condes, Chile
5 - Max-Planck-Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany

Received 20 January 2005 / Accepted 24 August 2005

Abstract
We present the kinematics of a sample of 398 DA white dwarfs from the SPY project (ESO SN Ia Progenitor surveY) and discuss kinematic criteria for distinguishing of thin-disk, thick-disk, and halo populations. This is the largest homogeneous sample of white dwarfs for which 3D space motions have been determined. Since the percentage of old stars among white dwarfs is higher than among main-sequence stars, they are presumably valuable tools in studies of old populations, such as the halo and the thick disk. Studies of white-dwarf kinematics can help to determine the fraction of the total mass of our Galaxy contained in the form of thick-disk and halo white dwarfs, an issue which is still under discussion. Radial velocities and spectroscopic distances obtained by the SPY project were combined with our measurements of proper motions to derive 3D space motions. Galactic orbits and further kinematic parameters were computed. We calculated individual errors of kinematic parameters by means of a Monte Carlo error propagation code. Our kinematic criteria for assigning population membership were deduced from a sample of F and G stars taken from the literature, for which chemical criteria can be used to distinguish between a thin-disk, a thick-disk and a halo star. Our kinematic population classification scheme is based on the position in the U-V-velocity diagram, the position in the Jz-eccentricity diagram, and the Galactic orbit. We combined this with age information and found seven halo and 23 thick-disk white dwarfs in this brightness limited sample. Another four rather cool white dwarfs probably also belong to the thick disk. Correspondingly 2% of the white dwarfs belong to the halo and 7% to the thick disk. The mass contribution of the thick-disk white dwarfs is found to be substantial, but is insufficient to account for the missing dark matter.

Key words: stars: white dwarfs - stars: kinematics - Galaxy: halo - Galaxy: kinematics and dynamics - Galaxy: disk

  
1 Introduction: population membership of white dwarfs

White dwarfs are the evolutionary end-products of most stars. Since they are faint objects, only the nearby objects have been detected so far; however, a large number of white dwarfs should be present in the Galaxy. Determining the contribution of white dwarfs to the total mass of the Galaxy could help to solve one of the fundamental questions in modern astronomy: what is the nature of dark matter? The fact that the rotation curves of many galaxies are not Keplerian (Rubin et al. 1978) invokes the existence of additional dark matter distributed in a near-spherical structure, the so-called heavy-halo (Ostriker & Peebles 1973). It is estimated that for the Milky Way only 10% of the total mass are present in the form of stars, gas, and dust in the Galactic disk and halo (Alcock et al. 2000). Dark matter candidates for the remaining 90% include exotic particles, cold molecular gas, and compact objects like black holes, white dwarfs, and brown dwarfs. The role of white dwarfs in the dark matter problem is still uncertain. An open issue is the fraction of white dwarfs in the thick-disk and halo populations, as well as their fraction of the total mass of the Galaxy. In this context, kinematic studies have proved a useful tool in deciding on population membership of white dwarfs.

Oppenheimer et al. (2001) have claimed to have detected cool halo white dwarfs as the main source for Galactic dark matter. Their results have been discussed controversially by many groups: e.g. Reid et al. (2001), Hansen (2001), Torres et al. (2002), and Reylé et al. (2001), who criticise the input parameters used in the Oppenheimer et al. (2001) analysis. The main problem lies in the lack of radial velocity information and poorly determined distances. Oppenheimer et al. (2001) are criticised for putting radial velocities to zero, as well as for their distance estimates.

Salim et al. (2004) have overcome some of these problems by measuring radial velocities for a subsample of those 13 white dwarfs from the Oppenheimer et al. (2001) sample that show an H $_{\rm\alpha}$ line. They also present new CCD photometry for half of the sample, in order to obtain new distance estimates. Their new results confirm those of Oppenheimer et al. (2001). But it should be kept in mind that these results are based on small number statistics. On the other hand, the velocity cut made by Oppenheimer et al. (2001) was shown to be inappropriate for a proper motion limited survey (Flynn et al. 2003; Reylé et al. 2001; Graff 2001). Moreover, Bergeron (2003) found the white dwarfs of Oppenheimer et al. (2001) to be warmer than 5000 K and therefore to most likely be too young to belong to the halo.

The common problem of the investigations discussed above is the lack of radial velocity measurements. Especially deviating conclusions derived from the white dwarfs of the Oppenheimer et al. (2001) sample demonstrate that different assumptions about the values of $v_{\rm rad}$can produce different fractions of halo and thick-disk stars and thus can affect the determination of the white dwarf halo density. Therefore a sample of white dwarfs with known radial velocity measurements is needed in order to obtain the full 3D kinematic information.

Examples of kinematics studies based on complete 3D space motions are the samples from Silvestri et al. (2002,2001). In our previous study (Pauli et al. 2003, hereafter referred to as Paper I), we presented the first homogeneous sample of white dwarfs for which complete 3D space motions were determined thanks to precise radial velocities and spectroscopic distances from high resolution spectra taken with UVES at the UT2 telescope of the ESO VLT.

Since radial velocities of white dwarfs are difficult to measure, Silvestri et al. (2002,2001) have obtained radial velocities from the spectra of the main-sequence companions of white dwarfs in common proper motion pairs. We derived white dwarf radial velocities from high resolution spectra directly and analysed a sample of 107 single DA white dwarfs in Paper I. There we demonstrated how a combination of several kinematic classification criteria allows efficient distinction of the different stellar populations. In contrast to previous studies, we not only considered the classical velocity components U, V, and W of each white dwarf, but also calculated its orbit in the Galaxy.

This allowed us to define new sophisticated criteria for classifying thin-disk, thick-disk, and halo populations by considering Galactic orbits and kinematic parameters. Another important question is how errors of the input parameters affect errors of the kinematic output parameters. An error propagation code using a Monte Carlo simulation was developed which allowed us to check the statistical significance of our results. Four halo, and seven thick-disk white dwarfs were found. Our fraction of halo white dwarfs is much smaller than the one of Oppenheimer et al. (2001), indicating that halo white dwarfs are not a major component of the dark matter in the Galaxy.

In a next step, we enlarged the sample of white dwarfs analysed. We present here a sample of 398 DA white dwarfs from the ESO SN Ia Progenitor surveY (SPY, Napiwotzki et al. 2001,2003). The SPY sample allowed us to overcome several limitations of previous investigations. When investigating DA white dwarfs, radial velocities could be measured from the shifts of the Balmer lines. Due to high resolution UVES VLT spectra, we could benefit from measurements of radial velocities of unprecedented precision (typical errors of only $2~{\rm km~s^{-1}}$) and of spectroscopic distances (relative errors of only 10%). Effective temperatures and gravities are from Koester et al. (2001) and from preliminary results of Koester (priv. comm.). The final results will be reported in a forthcoming paper (Voss et al., in preparation).

We supplemented these data with the best proper motion measurements available. Therefore we possess a very homogeneous set of radial and tangential velocity information with individual errors for each star. We refined our population classification scheme, thanks to a larger calibration sample, and applied it to 398 SPY white dwarfs.

Our publication is structured as follows: Sect. 2 deals with the input data. In Sect. 3 our kinematic analysis method is described and applied to the calibration sample and to the sample of SPY white dwarfs. Our results appear in Sect. 4 and are discussed in Sects. 5 and 6. We finish with conclusions in Sect. 7.

  
2 Kinematical data

   
2.1 Sample

Our sample consists of 398 DA white dwarfs from the SPY project. We have to stress that our stars are drawn from a brightness limited selection of known white dwarfs (see Napiwotzki et al. 2001, for details), and are not selected from proper motion surveys. Radial velocities, corrected for gravitational redshift were taken from Napiwotzki et al. (in prep.) and spectroscopic distances from Koester et al. (2001) and Voss et al. (in prep.). Radial velocities were measured using the cross-correlation technique described in Napiwotzki et al. (2001) but are still somewhat preliminary (final results to be published in a forthcoming paper). Uncertainties in the radial velocities are mostly much smaller than those of the tangential velocities computed from the proper motions (see also Paper I).

The aim of the SPY project is to detect radial velocity (RV) variable binary white dwarfs. Two spectra at different epochs were taken and checked for RV variations. Since orbital motions distort the measurement of space motions, RV variable stars were discarded from our sample. It should be noted that, while more than one spectrum is available for most SPY white dwarfs, there are 52 stars where only one spectrum exists. Of the 107 stars analysed in Paper I, only 104 are also present in this larger 398 sample. Three stars have turned out (according to information from additional spectra) to be in binary systems so were excluded from the sample. Given a binarity fraction of about $5\%$ (Napiwotzki et al. 2005), we can estimate that there may be only two or three still undetected spectroscopic binaries in the kinematically analysed sample, a negligible number. Nevertheless, in Table 8 we mark those stars with an asterisk where the radial velocity is based on only one spectrum.

2.2 Proper motions

Sources for proper motions are the USNO-B catalogue (Monet et al. 2003), the SuperCOSMOS Sky Survey (Hambly et al. 2001c,a,b), the UCAC2 catalogue (Zacharias et al. 2000), the Yale Southern Proper Motion catalogue (Girard et al. 2003), the revised NLTT catalogue (Salim & Gould 2003; Gould & Salim 2003), and the revised LHS catalogue (Bakos et al. 2002). Additional proper motions (for 202 stars) were measured using the Bonner Astrometry Software (Geffert et al. 1997), the procedure is described in Paper I.

For most programme stars, there is more than one astrometric measurement. The question is how to combine the proper motions and their errors from the different sources. If all the different measurements were completely independent of each other and if the errors followed a Gaussian distribution, average proper motions $\langle\mu\rangle$ and their errors $\langle\sigma_{\rm\mu}\rangle$would have to be weighted by the inverse variances, as:

 \begin{displaymath}\left< \mu\right> = {\left(\sum_{i=1}^{n}{\mu_{i}/{\sigma^{2}... ...bigg/ {\left(\sum_{i=1}^{n}{1/{\sigma^{2}_{\mu i}}}\right)}\ . \end{displaymath} (1)


 \begin{displaymath}\left< \sigma_{\rm\mu}\right> = {\left(\sum_{i=1}^{n}{1/{\sigma^{2}_{\mu i}}}\right)}^{-1/2}\ . \end{displaymath} (2)

We know, however, that not all measurements are independent of each other, since some of the catalogues share the same plate material. Furthermore, though we checked as far as possible whether the star found in the catalogue by the automatic search procedure using its coordinates is indeed the white dwarf, in some cases misidentifications have occurred. Comparing the proper motions of one star in different sources permits false detections to be eliminated.

To do this, we calculated the combined average and error, plus the quadratic deviation $\Delta^{2}_{\mu i}$of an individual measurement from this average:

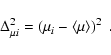\begin{displaymath}\Delta^{2}_{\mu i} = \left( \mu_{i}-\left< \mu\right> \right) ^{2}\ . \end{displaymath} (3)

If each $\Delta^{2}_{\mu i}$ is divided by the corresponding $\sigma_{\mu i}^{2}$, the sum over all i is taken and divided by the number of measurements n. We get a quantity $\Delta_{\rm check}$ that allows to check if the individual measurements are consistent with each other and, if not, to eliminate the measurement which differs from the others:

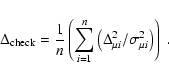\begin{displaymath}\Delta_{\rm check}= {1\over n} \left(\sum_{i=1}^{n} \left( \Delta^{2}_{\mu i}/\sigma^{2}_{\mu i} \right) \right)\ . \end{displaymath} (4)

If $\Delta_{\rm check}>1$, we checked the different catalogue values manually in order to decide which values to choose and which to eliminate. Having thus eliminated false detections the next step was to calculate the quantity $\left< \Delta_{\rm\mu}\right>$:

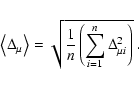\begin{displaymath}\left< \Delta_{\rm\mu}\right> = \sqrt {{1\over n} \left(\sum_{i=1}^{n} \Delta^{2}_{\mu i}\right)}\ . \end{displaymath} (5)

We adopted the weighted mean $\left< \mu\right>$ from Eq. (1) and the maximum of $\left< \sigma_{\rm\mu}\right>$and $\left< \Delta_{\rm\mu}\right>$ as the corresponding error. This enabled us to obtain a realistic error estimate, which typically lies between $5~{\rm mas~{yr}^{-1}}$ and $10~{\rm mas~{yr}^{-1}}$.

The input parameters radial velocities, spectroscopic distances, and proper motion components together with their errors, are listed for all white dwarfs in Table 8.

  
3 Revised population classification scheme

In Paper I we presented a new sophisticated population classification scheme based on the U-V-velocity diagram, the JZ-eccentricity-diagram, and the Galactic orbit. For the computation of orbits and kinematic parameters, we used the code by Odenkirchen & Brosche (1992) based on a Galactic potential by Allen & Santillan (1991). The classification scheme was based on a calibration sample of main-sequence stars. In the meantime, new spectroscopic analyses have become available which allowed us to enlarge the calibration sample and to refine our classification criteria.

  
3.1 The calibration sample

Unlike for main-sequence stars, the population membership of white dwarfs cannot be determined from spectroscopically measured metalicities. Therefore we have to rely on kinematic criteria. Those criteria have to be calibrated using a suitable calibration sample of main-sequence stars. In our case this sample consists of 291 F and G main-sequence stars from Edvardsson et al. (1993), Fuhrmann (1998), Fuhrmann (2000[*], 2004). It is important to note that the stars were selected from flux limited samples and not from proper motion surveys. Thanks to the work of Fuhrmann (2004), the number of calibration sample stars has been doubled, which makes it worthwhile revisiting the classification criteria outlined in Paper I.

For both samples a detailed abundance analysis was carried out. Fuhrmann (1998) combined abundances, ages, and 3D kinematics for population classification and found that the disk and halo populations can be distinguished best in the [Mg/Fe] versus [Fe/H] diagram. Halo and thick-disk stars can be separated by means of their [Fe/H] abundances, as they possess a higher [Mg/Fe] ratio than thin-disk stars (see also Bensby et al. 2003). In Fig. 1 the ${\rm [Mg/Fe]}$ versus ${\rm [Fe/H]}$ abundances for the 291 main-sequence stars are shown. These stars are divided into halo, thick disk, and thin disk according to their position in the diagram. The halo stars have $[{\rm Fe}/{\rm H}]<-1.05$, the thick-disk stars $-1.05\le[{\rm Fe}/{\rm H}]\le-0.3$ and $[{\rm Mg}/{\rm Fe}]\ge 0.3$, and the thin-disk stars $[{\rm Fe}/{\rm H}]>-0.3$ and $[{\rm Mg}/{\rm Fe}] \le 0.2$. Stars in the overlapping area between the thin and the thick disk (open triangles in Fig. 1) were neglected in order to ensure a clear distinction between the two disk populations.

There are four stars left to the halo border, which according to Fuhrmann (2004) belong to the metal-weak thick disk (MWTD, open boxes). As their kinematics are indeed incompatible with halo membership, we omitted them from further analysis. Also rejected was the star HD 148816, which though in the thick-disk region in the abundance diagram, clearly shows halo kinematics (not shown in the diagram).

This demonstrates that a clear distinction between halo and thick-disk stars by means of abundances is difficult, but as will be shown later, halo and thick-disk stars show very distinct kinematic properties, so that they are unlikely to be confused.

  \begin{figure} \resizebox{8.8cm}{!}{ \begin{psfrags} \psfrag{[Fe/H]}{${\rm [Fe/... ...metweak} \includegraphics[width=17cm]{2730fig1.eps} \end{psfrags}} \end{figure} Figure 1: ${\rm [Mg/Fe]}$ vs. ${\rm [Fe/H]}$ abundance diagram for the calibration sample (see text).
Open with DEXTER

  
3.2 The U - V-velocity diagram

A classical tool for kinematic investigations is the U-V-velocity diagram. In Fig. 2, U is plotted versus V for the main-sequence stars. For the thin-disk and the thick-disk stars, the mean values and standard deviations of the two velocity components were calculated. The values for the thin disk are: $\left<U_{\rm ms}\right>=3~\rm {km~s^{-1}}$, $\left<V_{\rm ms}\right>=215~\rm {km~s^{-1}}$, $\sigma_{U_{\rm ms}}=35~\rm {km~s^{-1}}$, and $\sigma_{V{\rm ms}}=24~\rm {km~s^{-1}}$. The corresponding values for the thick disk are: $\left<U_{\rm ms}\right>=-32~\rm {km~s^{-1}}$, $\left<V_{\rm ms}\right>=160~\rm {km~s^{-1}}$, $\sigma_{U_{\rm ms}}=56~\rm {km~s^{-1}}$, and $\sigma_{V{\rm ms}}=45~\rm {km~s^{-1}}$. The negative value of $\left<U_{\rm ms}\right>$ is explained in Fuhrmann (2004) as an effect of the Galactic bar. Indeed, nearly all thin-disk stars stay inside the $3\sigma _{\rm thin}$-limit, and all halo stars lie outside the $3\sigma _{\rm thick}$-limit, as can be seen from Fig. 2. In our previous paper, we used the $2\sigma-$limit of the thin and thick-disk stars for finding thick-disk stars and $\sqrt{U^2+(V-195)^2}\ge 150~\rm {km~s^{-1}}$ for finding halo stars. We replaced these by the more stringent $3\sigma-$limits of the thin and thick-disk stars to obtain a clear-cut separation.
  \begin{figure} \par\begin{psfrags} \psfrag{V(kms^-1)}{$V/{\rm km~s^{-1}}$ } \psf... ...limit} \includegraphics[width=13cm]{2730fig2.eps}\end{psfrags} \par\end{figure} Figure 2: U-V-velocity diagram for the calibration sample of main-sequence stars with $3\sigma _{\rm thin}$-, $3\sigma _{\rm thick}$-contours.
Open with DEXTER


  \begin{figure} \par\begin{psfrags} \psfrag{e}{$e$ } \psfrag{Jz(kpc km s^-1)}{$J_... ...{Region~C} \includegraphics[width=13cm]{2730fig3.eps}\end{psfrags} \end{figure} Figure 3: JZ-e-diagram for the calibration sample of main-sequence stars.
Open with DEXTER

   
3.3 The Jz - e-diagram

The U-V-plot is not the only source of information about population membership. Two important orbital parameters are the z-component of the angular momentum JZ and the eccentricity of the orbit e. Both are plotted against each other for the main-sequence stars in Fig. 3. The different populations can be distinguished well in this diagram. The thin-disk stars cluster in a V-shaped area of low eccentricity and JZ around $1800~\rm {kpc ~ km~s^{-1}}$, which we denote as region A.

In general, the thick-disk stars possess higher eccentricities e>0.27 and lower angular momenta. They can be found in region B. There is also a clump of thick-disk stars with lower eccentricity around 0.2 and higher JZ. Region B is defined such that it excludes as many thin-disk stars as possible. The price that has to be paid for this is the loss of some thick-disk stars. But this way there is a high probability of identifying only those stars as thick-disk members that really belong to the thick disk. It should be noted that region 3 in our previous paper, which seemed to be different from the thin-disk and the thick-disk regions A and B, has proven to be just an extension of the thin-disk region to higher eccentricities. Therefore it does not appear as an additional region in this revised classification scheme.

The halo stars with very high eccentricity and smaller JZ can be found in Region C, separated well from all other stars.

  
3.4 Galactic orbits

The eccentricity was extracted from the Galactic orbit of the stars. The classification can be confirmed by checking the orbits themselves. Typical orbits for thin-disk, thick-disk and halo main-sequence stars can be found in Paper I and will not be repeated here.

   
3.5 Population classification scheme

Our classification scheme (developed in Paper I) combines three different classification criteria: i) the position in U-V diagram; ii) the position in JZ-e diagram; and iii) the Galactic orbit.

We repeat some details here of the population classification scheme presented in Paper I and then describe the new refinements and changes. We classified white dwarfs as halo members if they had a value of $\sqrt{U^2+(V-195)^2}\ge 150~\rm {km~s^{-1}}$ and lay in region 4 in the JZ-e-diagram (see Paper I).

To detect thick-disk white dwarfs, first all stars either situated outside the $2\sigma$-limit in the U-V-diagram or in region 2 or 3 in the JZ-e-diagram were selected as thick-disk candidates. In a second step, each candidate was assigned a classification value c. c was defined as the sum of the individual values $c_{\rm UV}$, cJZe and $c_{\rm orb}$ corresponding to the three different criteria: position in U-V-diagram, position in JZ-e-diagram, and Galactic orbit.

We assigned $c_{\rm UV}=+1$ to a star outside the $2\sigma$-limit in the U-V-diagram, whereas one inside the $2\sigma$-limit got $c_{\rm UV}=-1$. The different regions in the JZ-e-diagram are characterised by cJZe=-1 for region 1, 0 for region 3, and +1 for region 2. The third classification value $c_{\rm orb}$ described the orbits: c=-1 for orbits of thin-disk type and c=+1 for orbits of thick-disk type. Then the sum $c=c_{\rm UV}+c_{J_{Z}e}+c_{\rm orb}$ was computed. Stars with c=+3 or c=+2 were considered as bona fide thick-disk members, and those with c=+1 as probable thick-disk members. If $c \le 0$, the star was classified as belonging to the thin disk.

The new classification scheme is more concise due to the elimination of region 3. As described in Sect. 3.2, we also sharpened the selection criterion for the U-V plane by replacing the $2\sigma$ by a $3\sigma$ limit. A star is classified as a halo candidate if it lies either outside the $3\sigma _{\rm thick}$-limit in the U-V diagram or in region C in the JZ - e diagram. Then classification values  $c_{\rm UV}$, cJZe, and  $c_{\rm orb}$are assigned to all halo candidates which take the value of +1 if the criterion favors a halo membership and -1 if not. More precisely: $c_{\rm UV}=+1$ if the star lies outside the $3\sigma _{\rm thick}$-limit, cJZe=+1 if the star lies in region C, and $c_{\rm orb}=+1$ if the star has a halo orbit. Then the sum $c=c_{\rm UV}+c_{J_{Z}e}+c_{\rm orb}$ is calculated. All of the halo candidates with $c \ge +1$are classified as halo members, the rest as thick-disk members.

All the remaining stars (not found to belong to the halo), either outside the $3\sigma _{\rm thin}$-limit in the U-V diagram or in region B in the JZ-e diagram, are classified as thick-disk candidates. Then the analogous procedure to the halo classification is applied: $c_{\rm UV}=+1$ if the star lies outside the $3\sigma _{\rm thin}$-limit, cJZe=+1 if the star lies in region B, and $c_{\rm orb}=+1$ if the star has a thick-disk orbit. In contrast to Paper I due to the elimination of region 3, there is no longer a value 0 to be assigned to cJZe; hence, we expect the number of thick-disk candidates to decrease. All of the thick-disk candidates with $c \ge +1$are assigned to the thick-disk population, the rest to the thin-disk population.

   
3.6 Consistency check for the kinematical classification criteria

In this section a consistency check of our classification scheme is performed. This is done by applying our kinematic classification criteria to our calibration main-sequence sample.

Thirty-three main-sequence stars are known to belong to the thick disk because of their abundance patterns (for reasons mentioned above we have excluded here the metal-weak thick-disk stars), and 22 of them have a kinematical classification value $c \geq +1$ and are classified as thick-disk stars. Only one of them has c=0 and is thus misclassified as a thin-disk star. This corresponds to a detection efficiency of about $67\%$ for thick-disk members. In addition to those 22 stars, six thin-disk main-sequence stars with $c \geq +1$ are misclassified as thick-disk stars, so that the total number of stars classified as thick disk is 28 indicating a contamination with thin-disk stars of about $21\%$.

   
3.7 Application to the white dwarf sample of Paper I

Furthermore, in order to be able to compare the results of Paper I with this paper, we applied the new classification scheme to the 107 white dwarfs analysed in Paper I. The fraction of halo stars is not changed by this new scheme. Due to the elimination of region 3 in the JZ - e diagram, four stars lose their thick-disk candidate status, and we end up with a total number of eight thick-disk stars compared to twelve previously. This reduces the local fraction of thick-disk white dwarfs from $11\%$ to $7.5\%$, and demonstrates the uncertainty of kinematic population classification. Even higher errors are to be expected when the population separation is based on a single criterion such as the position in U-V diagram alone, which is the case for most other kinematical studies of white dwarfs in the literature.

  
4 Kinematic population classification of the SPY white dwarfs

We calculated orbits and kinematic parameters for all 398 white dwarfs (see Table 9). The errors of e, JZ, U, V, W were computed with the Monte Carlo error propagation code described in Paper I. They can be found in Table 9 as well.

  \begin{figure} \par\begin{psfrags} \psfrag{V(kms^-1)}{$V/{\rm km~s^{-1}}$ } \psf... ... -limit} \includegraphics[width=13.2cm]{2730fig4.eps}\end{psfrags} \end{figure} Figure 4: U-V-velocity diagram for the white dwarfs with $3\sigma -{\rm thin}$ and $3\sigma -{\rm thick}$ - contours from Fig. 2, symbols with numbers are the white dwarfs mentioned in the text.
Open with DEXTER


  \begin{figure} \par\begin{psfrags} \psfrag{e}{$e$ } \psfrag{Jz(kpc km s^-1)}{$J_... ...WD~2029} \includegraphics[width=13.2cm]{2730fig5.eps}\end{psfrags} \end{figure} Figure 5: Jz-e-diagram of the white dwarfs.
Open with DEXTER

  
4.1 The U - V-velocity diagram

In Fig. 4, the U-V-velocity diagram for the white dwarfs is shown together with the $3\sigma$-limits of the thin and thick-disk stars from the calibration sample. The white dwarfs can be divided into two main groups that appear to be separated from each other: one group that is clustered mainly within the $3\sigma _{\rm thin}$-limit with some stars just outside the $3\sigma _{\rm thin}$-border and another second group with smaller V that lies outside or just inside the $3\sigma _{\rm thick}$-border. All the white dwarfs belonging to the second group are marked with the first letters of their names in Fig. 4.

The second group comprises five stars outside the $3\sigma _{\rm thick}$-limit (which qualify as halo candidates according to Sect. 3.5) HS 1527+0614, WD 0252-350, WD 1448+077, WD 1524-749, and WD 2351-365. Exceptional are WD 1448+077 and WD 1524-749, which have a negative value of V; i.e. they move on retrograde orbits. This behaviour is incompatible with disk membership and strongly suggests that they belong to the halo.

The other three white dwarfs of the second group are HE 0201-0513, WD 2029+183 and WD 2359-324. Situated inside the $3\sigma _{\rm thick}$, they do not qualify as halo candidates but we must check if they belong to the halo or to the thick disk by means of the JZ-eccentricity diagram and the orbits.

   
4.2 The Jz - e-diagram

We now move on to the JZ-eccentricity diagram of the SPY white dwarfs (Fig. 5). Again, two groups of stars can be detected: one first group starting in Region A with a high-eccentricity tail in Region B, which represents the disk population, and a second group in the right part of Region B and in Region C. Contrary to the main-sequence stars there is a gap in Region B that is not populated at all by white dwarfs. If this is real or just due to selection effects cannot be said at this point.

The second group contains all the stars discussed individually in the previous section and labeled by name in Fig. 5. HE 0201-0513, since situated in Region C, is added to the list of halo candidates. The two retrograde stars, WD 1448+077 and WD 1524-749, can be distinguished easily by their negative value of JZ.

4.3 Galactic orbits

Next we inspect the Galactic orbits of the SPY white dwarfs. We display some meridional plots of white dwarfs with thin-disk, thick-disk, or halo like orbits, respectively, in Figs. 6 to 8.

Most white dwarfs have thin-disk-like orbits, an example is WD 0310-688 (Fig. 6). Some orbits, like the one of WD 1013-010 (Fig. 7), show thick-disk characteristics. The star WD 2029+183 mentioned earlier has a thick-disk orbit. Five stars (HS 1527+0614, HE 0201-0513, WD 0252-350, WD 2351-365, and WD 2359-324) have chaotic halo orbits, as can be seen from Fig. 8 in the case of HS 1527+0614.


  \begin{figure}\resizebox{8.8cm}{!}{ \begin{psfrags} \psfrag{rho/kpc}{$\rho/{\r... ...c}{$Z/{\rm kpc}$ } \includegraphics{2730fig6.eps} \end{psfrags} } \end{figure} Figure 6: WD 0310-688: a white dwarf with a thin-disk orbit.
Open with DEXTER


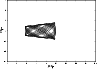  \begin{figure}\resizebox{8.8cm}{!}{ \begin{psfrags} \psfrag{rho/kpc}{$\rho/{\r... ...c}{$Z/{\rm kpc}$ } \includegraphics{2730fig7.eps} \end{psfrags} } \end{figure} Figure 7: WD 1013-010: a white dwarf with a thick-disk orbit.
Open with DEXTER


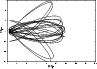  \begin{figure}\resizebox{8.8cm}{!}{ \begin{psfrags} \psfrag{rho/kpc}{$\rho/{\r... ...c}{$Z/{\rm kpc}$ } \includegraphics{2730fig8.eps} \end{psfrags} } \end{figure} Figure 8: HS 1527+0614: a white dwarf with a (chaotic) halo orbit.
Open with DEXTER

4.4 Classification

We used the population classification scheme presented in Sect. 3.5 to divide the SPY white dwarfs into the three different populations. We start with the halo candidates, e.g. with all white dwarfs that are either situated outside the $3\sigma$-limit of the thick disk in the U-V-velocity diagram or that lie in Region C in the JZ-eccentricity diagram. Six white dwarfs fulfill these conditions: all but one lie outside the $3\sigma _{\rm thick}$-limit, and all lie in Region C. Two white dwarfs, WD 1448+077 and WD 1524-749, are on retrograde orbits characterised by a negative value of V and JZ. When the classification values of the halo white dwarf candidates are added, it is found that all of them have c>1 and therefore belong to the halo population. We have mentioned before that the star WD 2359-324, though it does not fulfill the criteria for a halo candidate, has an orbit typical for a halo object. As its error-bar places it near Region C in the JZ - e diagram, we therefore decided to classify it as a halo object. This leaves us with seven halo white dwarfs. Details can be found in Table 1.

We now move on to the remaining 32 white dwarfs that lie either outside the $3\sigma$-limit of the thin disk in the U-V-velocity diagram or that lie in Region B in the JZ-eccentricity diagram. Twenty-seven of them have a classification value of c>1and are classified as thick-disk members, the remaining five are assigned a thin-disk membership (see Table 2). All the remaining white dwarfs are assumed to belong to the thin disk, leaving us with seven halo, 27 thick-disk, and 364 thin-disk out of the 398 SPY white dwarfs.

Table 1: Classification values for the halo candidates. Note that WD2359-324 is classified as a halo star despite having c=-1; see text.

Table 2: Classification values for the thick-disk candidates.

   
5 Age estimates

The seven halo and 27 thick-disk white dwarfs were assigned to the respective populations by means of purely kinematic criteria. Accordingly they must be old stars; therefore, we attempted to estimate their ages. A check to see whether their physical parameters, mass and effective temperature, are compatible with their belonging to an old population must now be made. Masses M for the white dwarfs were derived from ${\rm log}~g$ and the mass-radius relation by Wood (1995).

The halo is older than $10~{\rm Gyr}$. Bensby et al. (2003) determined a mean age for the thick disk as $11.2 \pm 4.3~{\rm Gyr}$. It is very probable that stars that are younger than $7~{\rm Gyr}$do not belong to the thick disk. Thus the main-sequence life-time (plus about $20\%$ for time spent during the giant phases and the horizontal branch), plus the time the white dwarf has cooled down until it reaches its actual $T_{\rm eff}$, has to be greater than the age of the youngest stars of the respective populations. The main-sequence life-time $\tau_{\rm ms}$ depends on the mass of the white dwarf progenitor and is approximately proportional to $\tau_{\rm ms} \propto M^{-2.5}$ (Kippenhahn & Weigert 1994). The main-sequence life-time is $\tau_{\rm ms}=10~{\rm Gyr}$ for the Sun, $7.9~{\rm Gyr}$ for a $1.1~\mbox{~$M_{\odot}$ }$ mass star, $4.3~{\rm Gyr}$ for a $1.4~\mbox{~$M_{\odot}$ }$ mass star, and $1.8~{\rm Gyr}$ for a $2~\mbox{~$M_{\odot}$ }$ mass star. Adding the $20\%$ horizontal branch plus giant phase lifetime, the total pre-white dwarf lifetimes would be $12~{\rm Gyr}$, $9.5~{\rm Gyr}$, $5.2~{\rm Gyr}$, and $2.2~{\rm Gyr}$, respectively.

The mass of the white dwarf is related to the mass of its progenitor by the initial-to-final mass relation. Until now, no definitive initial-to-final mass relation has been established; however, different estimates exist from different groups derived from theoretical considerations and from observational investigations of open clusters; see e.g. Weidemann (2000) and Schröder & Sedlmayr (2001). Unfortunately no initial-to-final mass relation for the halo and the thick disk has been derived yet, so we have to work with what is available for the thin disk and keep in mind that our age estimates are crude. According to Weidemann (2000), stars with initial masses of $1~\mbox{~$M_{\odot}$ }$, $1.1~\mbox{~$M_{\odot}$ }$, $1.4~\mbox{~$M_{\odot}$ }$, and $2~\mbox{~$M_{\odot}$ }$ would evolve into white dwarfs with masses of $0.55~\mbox{~$M_{\odot}$ }$, $0.555~\mbox{~$M_{\odot}$ }$, $0.57~\mbox{~$M_{\odot}$ }$, and $0.6~\mbox{~$M_{\odot}$ }$, respectively. The initial-to-final mass relation of Schröder & Sedlmayr (2001), on the other hand, yields white dwarf masses of $0.55~\mbox{~$M_{\odot}$ }$, $0.565~\mbox{~$M_{\odot}$ }$, $0.605~\mbox{~$M_{\odot}$ }$, and $0.67~\mbox{~$M_{\odot}$ }$.

We now estimate how long it takes for a C/O core white dwarf to cool down to $20~000~{\rm K}$, $10~000~{\rm K}$, $8000~{\rm K}$, and $5000~{\rm K}$ using the cooling tracks of Wood (1995). For a $0.5~\mbox{~$M_{\odot}$ }$ mass white dwarf, the respective cooling times would be $0.05~{\rm Gyr}$, $0.5~{\rm Gyr}$, $0.9~{\rm Gyr}$, and $4~{\rm Gyr}$. For a $0.6~\mbox{~$M_{\odot}$ }$ mass white dwarf, the corresponding values are $0.08~{\rm Gyr}$, $0.6~{\rm Gyr}$, $1.1~{\rm Gyr}$, and $6~{\rm Gyr}$. Hence, only for white dwarfs cooler than $8000~{\rm K}$ does the cooling time contribute significantly to the total age.

All the halo white dwarfs we found have masses less than $0.55~\mbox{~$M_{\odot}$ }$; i.e. their progenitors had a pre-white dwarf life-time of more than $12~{\rm Gyr}$. They are all hotter than $14~000~{\rm K}$, meaning they have all cooled less than $0.5~{\rm Gyr}$. Due to the large pre-white dwarf lifetime, their total age is perfectly compatible with halo membership. It should be noted that the low mass of WD 0252-350 of only $0.35~\mbox{~$M_{\odot}$ }$ indicates that it probably does not possess a CO core but instead a He one.

Now the masses and effective temperatures of the thick-disk white dwarfs detected in the SPY sample were likewise checked. We found that four white dwarfs WD 0255-705, WD 0352+052, WD 1013-010, and WD 1334-678 have masses which imply ages of less than $7~{\rm Gyr}$, which would make them too young to belong to the thick disk.

These four stars are the coolest in our sample of thick-disk candidates (see Table 4), with $T_{\rm eff}$ ranging from 8800 K to 10 600 K. Liebert et al. (2005) derived the mass distribution of 348 DA white dwarfs from the PG survey and found that the average gravities and masses increase with decreasing effective temperature for $T_{\rm eff} < 12~000$ K. A similar trend is found in the analysis of more than 600 DA white dwarfs from the SPY survey (Voss et al., in prep.). The physical reason is unknown, but two conjectures have been published. The high masses inferred from spectroscopy below $\approx$12 000 K may actually be due to helium being brought to the surface by the hydrogen convection zone (Bergeron et al. 1992; Liebert et al. 2005). On the other hand, Koester et al. (2005) suggest that the treatment of non-ideal effects for the level population with the Hummer-Mihalas (Hummer & Mihalas 1998) occupation probability mechanism may be insufficient for neutral perturbers that become important at lower $T_{\rm eff}$. Since these effects are unaccounted for in the model atmospheres, we may have overestimated the masses of cool DA white dwarfs ( $T_{\rm eff} < 12~000$ K).

As a result, the four cool white dwarf stars with thick-disk-like kinematics may have a lower mass and, therefore, a significantly larger age, one that is perhaps even consistent with that of the thick disk. Therefore we regard them as very likely belonging to the thick disk as well.

Table 3: Effective temperatures, surface gravities, and masses of the halo white dwarfs.

Table 4: Effective temperatures, surface gravities, and masses of the thick-disk white dwarfs. The four coolest stars have higher masses than the rest; however, the masses of the former may have been overestimated (see text).

An alternative explanation for the four cool DA stars discussed above having gained thick-disk-like orbits could be that they might be run-away stars that were born in a binary system in the thin disk and were thereafter ejected from it. Two ejection mechanisms have been suggested. The first one implies a close binary system in which the primary undergoes a supernova explosion and releases the secondary at high velocity (Davies et al. 2002). This study showed that, indeed, a large fraction of such binaries are broken up when the primary explodes as a supernova. A large number of the secondaries receive kick velocities of $100{-}200~{\rm km~ s^{-1}}$ and travel on Galactic orbits similar to those of thick-disk stars. Thus a population of white dwarfs originating in the thin disk may contribute significantly to the observed population of high-velocity white dwarfs.

Another possibility for explaining young white dwarfs with thick-disk-like kinematics was proposed by Kroupa (2002), who suggests a scenario for the thickening of galactic disks through clustered star formation. Massive star clusters may add kinematically hot components to galactic field populations.

As their masses may be overestimated, we think it is not required to invoke such run-away scenarios to explain the origin of the four cool white dwarfs discussed above. A more natural explanation would be that we have simply underestimated their ages.

We therefore classify those 23 white dwarfs where age and kinematics both indicate a thick-disk membership as bona fide thick-disk members. In addition, the four cool white dwarfs are classified as probable thick-disk stars, i.e. all 27 stars are retained as thick-disk members. This leaves us with a fraction of $2\%$ halo and $7\%$ thick-disk white dwarfs.

  
6 Discussion

We have refined and sharpened the population classification scheme developed in Paper I and applied it to a kinematical analysis of a sample of 398 DA white dwarfs from the SPY project. Combining three kinematic criteria, i.e. the position in the U-V-diagram, the position in the JZ-e-diagram, and the Galactic orbit with age estimates, we found seven halo and 23 thick-disk members.

To be able to discuss the kinematic parameters of the three different populations white dwarfs, we calculated the mean value and standard deviation of the three velocity components. Of interest are the asymmetric drift ( $V_{\rm lag}=220~{\rm km~s^{-1}}-\langle V\rangle$) for the thick-disk white dwarfs and the velocity dispersions of the white dwarfs of all three populations (Tables 5-7). For comparison, the corresponding values derived by Chiba & Beers (2000) and Soubiran et al. (2003) for main-sequence stars are also shown.

The velocity dispersions that were found for the thin-disk white dwarfs are compatible with the ones of Soubiran et al. (2003). The same is the case for the asymmetric drift and the velocity dispersions of the thick disk. Here agreement with the results of Soubiran et al. (2003) is much better than with the earlier results of Chiba & Beers (2000). There, $\sigma _{U}$ and $\sigma _{V}$ of the halo white dwarfs are similar to the values of Chiba & Beers (2000), while our $\sigma _{W}$ is much smaller. This is probably due to the fact that our local sample does not extend as far in the Z-direction as the sample of Chiba & Beers (2000) does. Also with only seven halo white dwarfs, we have to account for small number statistics. In general, the kinematic parameters of the white dwarfs of the three different populations do not differ much from those of the main-sequence samples.

Table 5: Standard deviation of U, V, W for the 361 SPY thin-disk white dwarfs, $\sigma _{U}$, $\sigma _{V}$, and $\sigma _{W}$from Soubiran et al. (2003) are shown for comparison.

Table 6: Asymmetric drift $V_{\rm lag}$ and standard deviation of U, V, W for the 27 SPY thick-disk white dwarfs, $V_{\rm lag}$, $\sigma _{U}$, $\sigma _{V}$, and $\sigma _{W}$from Soubiran et al. (2003), and Chiba & Beers (2000) are shown for comparison.

Table 7: Standard deviation of U, V, W for the seven SPY halo white dwarfs, $V_{\rm lag}$, $\sigma _{U}$, $\sigma _{V}$, and $\sigma _{W}$from Chiba & Beers (2000) shown for comparison.

We found seven halo white dwarfs in our sample, which corresponds to a fraction of $2\%$. In Paper I we found $4\%$ halo white dwarfs, a deviation possibly due to small number statistics or to a target selection effect. In our first paper, we analysed stars from the early phase of SPY. This sample contained a relatively large fraction of white dwarfs detected in proper motion surveys (Giclas et al. 1978; Luyten 1979, and references therein). Therefore an over-representation of white dwarfs with high tangential velocities is not unexpected.

Our value is lower than the one derived by Sion et al. (1988), who identified about 5% of their sample as halo white dwarfs. Liebert et al. (1989), on the other hand, obtained a percentage of 14% halo white dwarfs by classifying all stars that exceed a certain value of tangential velocity as halo members. When comparing those samples with ours, it has to be kept in mind that our selection criteria are sharper and allow us to separate thick-disk from halo stars. It is likely that a fraction of the white dwarfs classified as halo stars by Sion et al. (1988) and Liebert et al. (1989) actually belong to the thick disk. Furthermore, both samples suffer from the lack of radial velocity information.

It is difficult to compare our sample to the one of Oppenheimer et al. (2001), because the inhomogeneous sky coverage of SPY does not allow us to calculate a space density for halo white dwarfs. It has to be taken into account that our sample is a magnitude limited sample and thus biased towards high temperatures (mean temperature of 21 000 K; see also discussion in Schröder et al. 2004), whereas Oppenheimer et al. (2001) analyse much cooler white dwarfs.

Classically, halo white dwarfs are supposed to be cool stars that originated from high mass progenitors. The main contribution to the total ages of these white dwarfs is the cooling time. This work demonstrates that another class of hot, low-mass halo white dwarfs exists with low-mass progenitors that only recently have become white dwarfs so have not had much time to cool down. This makes this SPY sample complement to samples that focus on cool halo white dwarfs.

There are 27 SPY white dwarfs classified as thick-disk members out of which four are too cool to allow reliable ages to be derived. This corresponds to a local fraction of thick-disk white dwarfs of $7\%$ or $6\%$, if we reject the four cool stars. These values are somewhat lower than the $11\%$ found by Silvestri et al. (2002) but are much smaller than that of Fuhrmann (2000)[*], who predicted a fraction of 17% thick-disk white dwarfs. The differences are possibly caused by the temperature bias mentioned above. An over-representation of white dwarfs compared to low mass main-sequence stars, which would require a truncated initial mass function as suggested by Favata et al. (1997), has not been found.

The question of whether thick-disk white dwarfs contribute significantly to the total mass of the Galaxy is very important for clarifying the dark matter problem. This contribution can be estimated from the results derived above. To derive the densities of thin-disk and thick-disk white dwarfs, we used the $1/V_{\rm max}$ method (Schmidt 1968). The mass density of thick-disk over thin-disk white dwarfs ${M_{\rm thick}\over M_{\rm thin}}$ was calculated as described in Paper I. For the thick disk we adopted the values of Ojha (2001), scale length $l_{\rm0,thick}=3.7~{\rm kpc}$, and tried two extreme values of the scale height, $h_{\rm0,thick}=0.8~{\rm kpc}$ (Ojha et al. 1999) and $h_{\rm0,thick}=1.3~{\rm kpc}$ (Chen 1997). For the thin disk, we assumed $l_{\rm0,thin}=2.8~{\rm kpc}$ (Ojha 2001) and $h_{\rm0,thin}=0.25~{\rm kpc}$, in between the values of Kroupa (1992) and Haywood et al. (1997). We found ${M_{\rm thick}\over M_{\rm thin}}=0.12 \pm 0.36$ and ${M_{\rm thick}\over M_{\rm thin}}=0.19 \pm 0.57$ for thick-disk scale heights of $0.8~{\rm kpc}$and $1.3~{\rm kpc}$, respectively. Accordingly, upper limits for ${M_{\rm thick}\over M_{\rm thin}}$ are 0.48 and 0.76, respectively. Of course the errors are huge because of the poor statistics of the relatively small thick-disk sample. Nevertheless, it can be concluded that the total mass of thick-disk white dwarfs is less than $48\%$($76\%$) of the total mass of thin-disk white dwarfs. Therefore the mass contribution of the thick-disk white dwarfs must not be neglected, but it is not sufficient to account for the missing dark matter.

  
7 Conclusions

We have demonstrated how a combination of sophisticated kinematic analysis tools can distinguish halo, thick-disk, and thin-disk white dwarfs. We identified a fraction of 2% halo and 7% thick-disk white dwarfs. Most of our thick-disk and halo white dwarfs are hot and possess low masses. Our results suggest that the mass present in halo and thick-disk white dwarfs is not sufficient for explaining the missing mass of the Galaxy. But to draw definite conclusions, more data are needed. Our goal is to extend this kinematic analysis to all 1000 degenerate stars from the SPY project, in order to have a large data base for deciding on the population membership of white dwarfs and their implications for the mass and evolution of the Galaxy.

Acknowledgements
We thank D. Koester for providing us with the results of his spectral analysis prior to publication and B. Voss for prolific discussions. E.-M.P. acknowledges support by the Deutsche Forschungsgemeinschaft (grant Na 365/2-1) and is grateful to the Studienstiftung des Deutschen Volkes for a grant. M. Altmann acknowledges support from the DLR 50 QD 0102 and from FONDAP 1501 0003. R.N. is supported by a PPARC Advanced Fellowship. Thanks go to J. Pauli for interesting and fruitful discussions. This research has made use of the SIMBAD database, operated at the CDS, Strasbourg, France and of DSS images based on photographic data obtained with the UK Schmidt Telescope.

References

 
Copyright ESO 2006