A&A 446, 1157-1163 (2006)
DOI: 10.1051/0004-6361:20053672

Compton backscattered and primary X-rays from solar flares: angle dependent Green's function correction for photospheric albedo

E. P. Kontar1 - A. L. MacKinnon2 - R. A. Schwartz3 - J. C. Brown1


1 - Department of Physics and Astronomy, University of Glasgow, G12 8QQ, UK
2 - DACE, University of Glasgow, G3 6NH, UK
3 - SSAI, Science Systems & Applications, Inc., Code 612.1, NASA/GSFC, Greenbelt, MD 20771, USA

Received 21 June 2005 / Accepted 30 September 2005

Abstract
The observed hard X-ray (HXR) flux spectrum $I(\epsilon)$ from solar flares is a combination of primary bremsstrahlung photons $I_{\rm P}(\epsilon)$ with a spectrally modified component from photospheric Compton backscatter of downward primary emission. The latter can be significant, distorting or hiding the true features of the primary spectrum which are key diagnostics for acceleration and propagation of high energy electrons and of their energy budget. For the first time in solar physics, we use a Green's function approach to the backscatter spectral deconvolution problem, constructing a Green's matrix including photoelectric absorption. This approach allows spectrum-independent extraction of the primary spectrum for several HXR flares observed by the Ramaty High Energy Solar Spectroscopic Imager (RHESSI). We show that the observed and primary spectra differ very substantially for flares with hard spectra close to the disk centre. We show in particular that the energy dependent photon spectral index $\gamma (\epsilon)=-{\rm d} \log I/{\rm d} \log \epsilon$ is very different for $I_{\rm P}(\epsilon)$ and for $I(\epsilon)$ and that inferred mean source electron spectra ${\overline F}(E)$ differ greatly. Even for a forward fitting of a parametric ${\overline F}(E)$ to the data, a clear low-energy cutoff required to fit $I(\epsilon)$ essentially disappears when the fit is to $I_{\rm P}(\epsilon)$ - i.e. when albedo correction is included. The self-consistent correction for backscattered photons is thus shown to be crucial in determining the energy spectra of flare accelerated electrons, and hence their total number and energy.

Key words: Sun: flares - X-rays: general - methods: data analysis - techniques: spectroscopic - scattering

   
1 Introduction

Bremsstrahlung HXR spectra of solar flares give us direct information about the distribution of accelerated high energy electrons propagating in dense regions of the solar atmosphere. Though quite dense, the atmosphere above the X-ray bremsstrahlung producing region is optically thin, but the very dense lower photospheric layers are not and photons emitted downwards are Compton backscattered by atomic electrons there with an energy dependent efficiency. Photons of energy above ${\sim}100$ keV penetrate so deeply that they are lost to the observer, while below ${\sim}10$ keV they are mostly photoelectrically absorbed by their first scattering. The resulting spectral reflectivity thus has a broad hump in the range 10-100 keV with a maximum around 30-40 keV. At some energies and view angles the reflectivity approaches 100% so the observed spectrum may have been substantially affected by backscatter. This effect is well-known in solar physics (and more generally in X-ray astronomy - Magdziarz & Zdziarski 1995) and there have been several discussions of its influence on observed X-ray spectra (Tomblin 1969; Santangelo et al. 1973; Bai & Ramaty 1978), and on electron spectra inferred from them (Johns & Lin 1992; Alexander & Brown 2002), now that high resolution data are available. Contamination of the observed X-ray spectrum by reflected photons leads to flattening of the spectrum and underestimation of the spectral index (Bai & Ramaty 1978). This can lead to substantial underestimation of the total extrapolated electron energy in a flare. Spectral features connected with a low energy cut-off in the electron distribution, of crucial diagnostic interest for determining the acceleration mechanism and the total fast electron energy content, are hidden or substantially changed by the backscattered component (Zhang & Huang 2004). Moreover, an apparent low-energy cut-off in albedo-uncorrected electron spectrum may not be required by data from the "true'' primary (albedo corrected) spectrum.

Comptonisation of prescribed primary HXRs can be straightforwardly studied using Monte-Carlo simulations (e.g. Bai & Ramaty 1978). This technique is ideal for obtaining the reflected, and hence the total observed, photon spectrum if one knows or assumes the form of the primary X-ray spectrum (Alexander & Brown 2002). However, the primary spectrum is unknown and unlikely to be an exact power-law, as is usually assumed. Even with a power-law distribution of primary electrons a number of physical processes exist which will cause the resultant photon distribution to deviate from pure power-law form e.g. effects of nonuniform ionization (Brown 1973; Kontar et al. 2003), beam return current losses (Zharkova & Gordovskyy 2005) and others. Results obtained from Monte Carlo simulation for power-law primary photon spectra cannot be straightforwardly applied to such situations. More sophisticated parametric modelling of the primary photon spectrum, with more theoretical uncertainties and free parameters, would become necessary. Therefore, an approach independent of the primary spectrum is required.

Understanding and modelling backscatter has become even more important with the advent of high quality X-ray spectra from the Ramaty High Energy Solar Spectroscopic Imager (RHESSI) with spectral resolution as high as ${\simeq}1$ keV, in combination with uncertainties as low as a few percent (for strong flares) allowing detailed spectral analysis over a broad X-ray range (Lin et al. 2002). A correct treatment of Compton backscatter by a cold medium has also been important for understanding spectra from cosmic X-ray sources (reviewed e.g. by Svensson 1996). This led to construction (Magdziarz & Zdziarski 1995) of an analytic (piecewise continuous), angle dependent, Green's function $G(\mu,\epsilon_o,\epsilon)$ for the probability that a photon, of initial energy $\epsilon_o$ and drawn from a distribution isotropic in the downward hemisphere, incident on a plane-parallel atmosphere, is re-emitted in direction $\theta$ ( $\mu = \cos\theta$) with energy $\epsilon$. This was obtained by fitting the results of a large set of Monte Carlo calculations, and its form is guided, particularly in various limits, by analytical results such as those of Illarionov et al. (1979), Lightman et al. (1981), White et al. (1988). Representing as it does the results of Monte Carlo calculations, no assumptions of single scattering or on the form of primary spectrum are involved. The only major assumptions in the Green's function formulation are those already mentioned: plane geometry of the cold matter - this is well satisfied for the photospheric conditions and downward isotropy of the primary photon distribution.

Combined with a treatment of absorption (Morrison & McCammon 1983) with standard solar photosphere element abundances (Anders & Grevesse 1989), the Green's function formulation of Compton backscatter provides us with a powerful tool for interpreting flare hard X-ray spectra. Firstly, it allows us to calculate easily, without time consuming Monte Carlo simulations, the total observable photon spectrum for any specified primary spectrum, not just the power-law cases treated by Bai & Ramaty (1978). More importantly, because the Green's function may be used to express the observed spectrum in terms of any primary spectrum, we may use regularized inversion techniques (Craig & Brown 1986; Kontar et al. 2004, and references therein) to deconvolve the primary photon spectrum from observations. Features of this primary spectrum arise only from features of the HXR source electron distribution, not of the energy-dependence of backscattering, so it may be safely inverted (Kontar et al. 2004) to yield a meaningful source-averaged electron distribution in the sense of (Brown et al. 2003). Although the Green's function makes such model-independent inversion possible, this step is carried out here for the first time.

Sections 2, 3 describe the Green's function formulation and the incorporation of absorption respectively. Section 4 describes how to recover the primary spectrum from data, and Sect. 5 applies this to real RHESSI data. In Sect. 6 we discuss applications and implications of our work.

2 Backscattering of X-rays

As discussed in Sect. 1, downward-emitted photons will be either absorbed or scattered, and some scattered toward the observer, adding to the total flux detected. The backscattered photons will be emitted from an extended region of the photosphere, out to the horizon distance but with greatest intensity in an area of extent comparable to the altitude of the primary source (Brown et al. 1975; Bai & Ramaty 1978; Schmahl & Hurford 2004). The Green's function implemented here ignores spatial structure, however, simply summing over all photons that emerge in the correct direction. This makes it ideal for dealing with spatially unresolved spectra.

While the Green's function (Magdziarz & Zdziarski 1995) was obtained for use in studying cosmic X-ray sources, it applies to any plane-stratified slab of "cold'' material (i.e. the scattering electrons are non-relativistic). Scattering takes place only on electrons, whether free or atomic. To account for elements heavier than hydrogen the Compton cross-section is multiplied by an effective mean atomic number z=1.2. The detailed density structure of the medium is irrelevant (Tomblin 1972).

Absorption, on the other hand, does depend strongly on chemical composition, and the best estimate of photospheric abundances should be included when adding absorption to the Green's function treatment. We use standard abundances given by Anders & Grevesse (1989). The heavy elements Fe/Ni play the most important role in the range from 10 keV up to 30 keV, while lighter elements contribute below 10 keV (Morrison & McCammon 1983).

   
3 Green's function

The definition of the Green's function allows us to write the secondary, backscattered spectrum $I_{\rm S}$ for any isotropic primary spectrum $I_{\rm P}$ (both have units of photons keV-1 s-1 cm-2):

 \begin{displaymath} I_{\rm S}(\epsilon)=\int\limits_{\epsilon}^{\epsilon_{\max}}I_{\rm P} G(\mu,\epsilon,\epsilon_0){\rm d}\epsilon_0 \end{displaymath} (1)

where $G(\mu , \epsilon ,\epsilon _0)$ is the angle-dependent Green's function and $\mu =\cos (\theta)$, where $\theta$ is the heliocentric position angle of the X-ray source. The observed spectrum, at direction $\mu$, is then the sum of $I_{\rm S}$ and $I_{\rm P}$. The importance of not averaging over viewing angle may be seen from Bai & Ramaty (1978). The Green's function itself is shown in Fig. 1a - for details see Lightman & White (1988), Magdziarz & Zdziarski (1995), Ross & Fabian (1993) and references therein.

The total observed spectrum $I(\epsilon)$ is given by the sum of $I_{\rm P}$ and $I_{\rm S}$, i.e. using (1)

 \begin{displaymath} I(\epsilon)=I_{\rm P}(\epsilon)+\int\limits_{\epsilon}^{\eps... ..._{\max}} I_{\rm P}G(\mu,\epsilon,\epsilon_0){\rm d}\epsilon_0. \end{displaymath} (2)

With measured $I(\epsilon)$ the primary spectrum $I_{\rm P}$, which tells us directly about the source electrons, may be obtained via a solution of the integral Eq. (2). This is a Volterra Equation of the second kind (with $I_{\rm P}$ appearing outside as well as inside the integral, solution of which is more stable against noise in I than those of the first kind, e.g. Craig & Brown 1986). In addition, the kernel (Green's function) is peaked so that the kernel function/matrix is not too far from diagonal. Thus regularization to achieve an accurate stable solution for $I_{\rm P}$given I is less troublesome than in other inverse problems such as using $I_{\rm P}(\epsilon)$ to find the source electron spectrum following Kontar et al. (2005).

In practice measurements yield discrete quantities and the integral Eq. (2) is presented in matrix form

 \begin{displaymath} I(\epsilon_i)=I_{\rm P}(\epsilon_i)+G_{ij}(\mu)I_{\rm P}(\epsilon_j) \end{displaymath} (3)

where we have used the summation convention for repeated indices, and introduced what we may call the Green's matrix

 \begin{displaymath} G_{ij}(\mu)=\int\limits_{\epsilon_{j}}^{\epsilon_{j+1}}G(\mu,\epsilon _0,\epsilon _i) {\rm d}\epsilon _0. \end{displaymath} (4)

Note, that the integration in Eq. (4) is best performed via a change of variable to the wavelength domain $y=mc^2/\epsilon$, $y_0=mc^2/\epsilon _0$ due to sharp features in the Green's function (Fig. 1). Special care should be taken when integrating near $\Delta y=y-y_0=2$.


  \begin{figure} \par\includegraphics[width=7.5cm]{3672_f1.eps} \end{figure} Figure 1: Green's functions $G(\mu , \epsilon ,\epsilon _0)$ including Compton scattering and photoelectric absorption for three primary photon energies $\epsilon _0 =20,80,300$ keV and $\mu =0.7$( $\theta \sim 45^\circ $).
Open with DEXTER

The shape of the Green's function depends on the maximum energy of a primary photon. For primary photons with low energies $\epsilon _{0}<30$ keV, the Green's function has a rather simple structure close to a Dirac's delta function (Fig. 1) showing that backscattering is dominated by the first scattering, while the contribution from higher orders of scattering is small. In the range below ${\sim} 12$ keV photoelectric absorption dominates scattering and Compton scattering can be treated as diffuse monochromatic radiation transfer. The Green's function then can be replaced by $G(\mu, \epsilon ,\epsilon _0)\approx F(\mu,\lambda)\delta(\epsilon -\epsilon _0)$ (Chandrasekhar 1960, where the form of $F(\mu,\lambda)$ is given), $\lambda (\epsilon)=\sigma_{\rm C}(\epsilon)/(\sigma_{\rm C}(\epsilon)+\sigma_{\rm A}(\epsilon))$, $\sigma_{\rm C}(\epsilon)$, $\sigma_{\rm A}(\epsilon)$ are the total Compton and absorption cross-sections respectively. $\lambda$ gives the single-scattering albedo modified by absorption and completely controls the influence of absorption. Application to the solar case simply requires evaluation of $\lambda$ with solar photospheric abundances. In this energy range below 10 keV the total Compton scattering cross-section can be approximated by the Thompson cross-section $8\pi r_{\rm e}^2/3$. The absorption cross-section is based on the element abundances from Anders & Grevesse (1989). We use the coefficients of a piecewise polynomial fit to the numerical results given by Morrison & McCammon (1983) in the range below 10 keV and extrapolate them as $\sigma_{\rm A}(\epsilon)\sim \epsilon ^{-3}$ above 10 keV. Due to rapid decrease of the absorption cross-section $\sigma_{\rm A}\approx \sigma_{\rm C}$ around 12 keV. The generated Green's matrices (4) have uncertainty around 6% (due to the approximations used) and 1 keV energy resolution.


  \begin{figure} \par\includegraphics[width=73mm]{3672_f2.eps} \end{figure} Figure 2: Upper panel: primary (solid line), reflected (dotted line) and total (dashed line) photon spectra calculated assuming a primary spectrum $I_{\rm P}(\epsilon )\sim \epsilon ^{-3}$, and using the Green's function for a X-ray source at heliocentric angle $\theta = 45^\circ $. The lower panel shows the reflectivity, defined as the ratio of reflected to primary fluxes $R(\epsilon , \theta =45^\circ )=I_{\rm R}(\epsilon )/I_{\rm P}(\epsilon )$. The reflectivity taken from Bai & Ramaty (1978) is shown with diamonds. Two absorption edges of Fe at 7.1 keV and Ni at 8.3 keV are seen in the reflected component.
Open with DEXTER

The absorption is photo-electric in nature and below 10 keV has a complex structure with multiple absorption edges due to elements heavier than hydrogen. In consequence it is also strongly influenced by elemental abundances. Figure 2 shows the two absorption edges of Fe at 7.1 keV and Ni at 8.3 keV in the reflected component. The spectrum shows features in agreement with the study of the reflection spectra in intergalactic nuclei by Ross & Fabian (1993). Here we ignored the fluorescence of the lines which is beyond the scope of our paper.

Note that Bai & Ramaty (1978) and Zhang & Huang (2004) assumed a different absorption approximation from us based on earlier photoelectric absorption cross-sections by Fireman (1974) and photospheric abundances by Withbroe (1971). However, we should note that the difference is rather modest accounting for around 30% of reflectivity at low energies and becoming smaller at higher energies, where absorption is less important (Fig. 2). The reflectivity, and thus the contribution of Compton back-scattered photons into observed spectra is spectrum-dependent (Fig. 3). Therefore, the albedo spectrum depends on the shape of the primary spectrum (Fig. 3), - previous studies (Bai & Ramaty 1978; Alexander & Brown 2002) considered only the results for prescribed power-law primary spectra. This difference is important when one tries to infer a primary spectrum from an observed one.

We verified that we can reproduce the forward results of Bai & Ramaty (1978) by numerically evaluating Eq. (1) for the particular case $I_{\rm P} \sim \epsilon^{-\gamma}$ and the parameters described in Fig. 2. Consistency with previous treatments being established in this way, we now turn to the inverse problem - deduction of the primary spectrum from observations of the total spectrum.


  \begin{figure} \par\includegraphics[width=78mm]{3672_f2a.eps} \end{figure} Figure 3: Spectrum dependency of the reflected flux. Upper panel: primary (dashed line), reflected (solid line) and total (dotted line) photon spectra calculated for a modelled flare spectrum $I_{\rm P}(\epsilon )\sim \epsilon ^{-3}$ for $\epsilon > 45$ keV, $I_{\rm P}(\epsilon)\sim \epsilon ^{-2}+\exp(-\epsilon/1.7)$ for $\epsilon < 45$ keV. The lower panel shows the reflectivity for a X-ray source at heliocentric angle $\theta = 45^\circ $, defined as the ratio of reflected to primary fluxes $R(\epsilon , \theta =45^\circ )=I_{\rm R}(\epsilon )/I_{\rm P}(\epsilon )$ (solid line). The reflectivity assuming power-law for a primary source with spectral index 3 (dotted line) and 2 (dashed line).
Open with DEXTER

4 From observed to primary X-ray spectrum

In the absence of data noise we could immediately invert Eq. (2) to obtain $I_{\rm P}$:

 \begin{displaymath} I_{\rm P}(\epsilon_j)={\vec A}_{ij}I(\epsilon_i), \;\;\;\; {\vec A}=({\vec 1}+{\vec G}(\mu))^{-1}. \end{displaymath} (5)

The same result as Eq. (5) can be obtained solving the original system of linear Eqs. (4) using, for example, singular value decomposition. In reality, we have photon spectra contaminated by noise. If the resulting matrix has a large condition number (ratio of largest to smallest singular values), then a regularized approach should be adopted (e.g. Craig & Brown 1986; Piana et al. 2002; Kontar et al. 2004). In practice, we can incorporate the effects connected with solar albedo as a part of instrument response.

4.1 SPEX and albedo correction

For a given instrument such as RHESSI, the count flux $C(\epsilon _{i})$ is the linear composition of instrument response matrix ${\vec R}_{ij}$ and the photon flux $I(\epsilon_j)$ coming from the Sun (Schwartz et al. 2002)

 \begin{displaymath} C(\epsilon _{i})= {\vec R}_{ij} \;\; I(\epsilon_j). \end{displaymath} (6)

However, since we are interested in the flare primary spectra rather than the observed flux, we can combine Eqs. (3) and (6) to get

 \begin{displaymath} C(\epsilon _{i})= {\vec R^{\prime}}_{ij} \;\; I_p(\epsilon_j) \end{displaymath} (7)

where ${\vec R^{\prime}}_{ij}={\vec R}_{ik}({\vec 1}_{kj}+\alpha {\vec G}_{kj})$. Here we introduced a coefficient $\alpha$ that accounts for anisotropy of the source in the Eddington approximation - that is, distinct but constant specific intensities in the downward and in the upward hemispheres, in the ratio $\alpha$.

This approach has already been incorporated into the SPEX software (Schwartz et al. 2002) including the object oriented version (OSPEX). The software is publicly available as a part of Solar SoftWare (SSW).


  \begin{figure} \par\includegraphics[width=80mm]{3672_f3.eps} \end{figure} Figure 4: Temporal variation in four energy channels (4 seconds cadence) of the count rates summed over seven front RHESSI detectors for the September 17, 2002 solar flare. The vertical lines show the accumulation interval selected 5:50:48-5:51:36 UT for further spectral analysis.
Open with DEXTER

   
5 RHESSI solar flare HXR spectra

5.1 Photon spectral correction

The spectral effect of Compton back-scattering on HXRs is most pronounced for harder (flatter) spectra such as in the flare of September 17, 2002 around 05:50 UT (see Fig. 4) which we study here though quite a number of such flares have been observed: August 20, 2002 (Kasparova et al. 2005), April 25, 2002 (Kontar & Brown 2005). The location of our flare, which uniquely determines the Green's function, was in the western hemisphere at (560,-300) arcseconds corresponding to a heliocentric angle of $\theta \simeq 41^\circ$.

We consider the spectrum around flare maximum (5:50:48-5:51:36 UT) when we have enough counts over the range 3 keV up to >100 keV. We used 7 out of 9 front segments, excluding detectors 2 and 7 due to their low energy resolution at the time of observation (Smith et al. 2002). The time interval is shown in Fig. 4.

After background subtraction, spectral results are shown in Fig. 5 for both the total observed spectrum, and the primary spectrum $I_{\rm P}$ determined via the method of the previous section and using $\alpha =1$ (isotropic emission). We note how removal of backscattered photons, as expected, reduces the primary flux and steepens the spectrum in the 20-50 keV photon energy range and slightly flattens the spectrum at energies above the albedo maximum.


  \begin{figure} \par\includegraphics[width=72mm]{3672_f4.eps} \end{figure} Figure 5: Spectrum of the September 17, 2002 solar flare in the time interval 5:50:48-5:51:36 UT. The solid line shows the observed spectrum; the dash line is the primary spectrum (corrected for Compton back-scattering).
Open with DEXTER

5.2 Effect of albedo on photon spectral index

The albedo changes the spectral indices of photon spectra, both of power-law fits and of the local energy dependent spectral index defined by

 \begin{displaymath} \gamma (\epsilon)\equiv - \frac{\epsilon}{I(\epsilon)}\fra... ...n}=- \frac{{\rm d} \ln I(\epsilon)}{{\rm d} \ln \epsilon}\cdot \end{displaymath} (8)

Direct numerical calculation of any derivative gives poor results in the presence of data noise, even for data as good as that from RHESSI. Differentiation is a specific case of solving an integral equation and to obtain meaningful results in the presence of noise needs some sort of stabilization such as Tikhonov regularization, which we use here following Kontar & MacKinnon (2005). We limited our analysis to the most interesting range between 10and 40 keV, where the albedo effect is most pronounced. At the energies above 40 keV the count rate is small and thus uncertainties are large, whereas at the energies below 10 keV Fe/Ni lines affect the bremsstrahlung spectra.

Figure 6 shows the energy dependent spectral index for our flare spectrum. Both spectra (with and without albedo correction) increase toward the ends of the energy interval. At low energies this is probably due to a thermal component while at higher energies it is likely connected with softening of a nonthermal electron spectrum. The spectral index of the observed data shows a clear minimum around 15 keV, while the spectrum corrected for albedo has a rather extended minimum in the broad range 15-30 keV. The albedo correction increases the minimum value of $\gamma $ from 2.0 to 2.6. The opposite effect can be seen at higher energies: the spectral index at 40 keV decreases from 3.5 to 3.2, albedo correction making the primary spectrum harder. Qualitatively similar results have been obtained for forward modelled spectra (Bai & Ramaty 1978; Zhang & Huang 2004).


  \begin{figure} \par\includegraphics[width=65mm]{3672_f5.eps} \end{figure} Figure 6: Energy dependent photon spectral index $\gamma (\epsilon )$ of the September 17, 2002 solar flare. The solid line shows the spectral index of the observed spectrum; the dash line is the spectral index for the primary spectrum (corrected for Compton back-scattering). The confidence intervals represent the range of solutions found by allowing the incident photon spectrum to range randomly within the estimated (instrument + shot noise) errors.
Open with DEXTER

5.3 Effect of albedo on inferred source averaged electron spectra

The primary photon flux is directly connected with the mean source electron (so-called thin target) spectrum (Brown 1971; Brown et al. 2003)

  \begin{displaymath} I_{\rm P}(\epsilon) = {1 \over 4\pi R^2} ~ ~ \bar n V \int_\epsilon^\infty \bar F(E) ~ Q(\epsilon,E)~ {\rm d}E, \end{displaymath} (9)

where $Q(\epsilon, E)$ is the bremsstrahlung cross-section differential in $\epsilon$ (Haug 1997) and the density weighted mean radiation source electron flux spectrum ${\overline F}(E)$(electrons cm-2 s-1 keV-1) is defined by

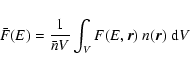\begin{displaymath}\bar F(E)= \frac{1}{\bar n V} \int_V F(E,{\vec r}) ~ n({\vec r}) ~ {\rm d}V \end{displaymath} (10)

with $F(E,{\vec r})$ and $n({\vec r})$ the local electron spectrum and source proton density at position ${\vec r}$ in radiating volume V with mean target proton density $\bar n = V^{-1}\int n({\vec r}) ~ {\rm d}V$.

Solution of Eq. (9) for ${\overline F}(E)$ is a somewhat unstable inverse problem (Craig & Brown 1986; Piana et al. 2003) and so results are strongly affected when the observed $I(\epsilon)$ is used instead of the albedo corrected $I_{\rm P}(\epsilon)$ required for correct solution of Eq. (9). ${\overline F}(E)$ is important in the study of acceleration mechanisms and of the flare electron energy budget. Of particular interest are data such as from the flare discussed above which exhibit very flat regions which may correspond to ${\overline F}(E)$with a low energy cut-off in the mean electron spectrum which would have major implications for electron acceleration and propagation, and for the energy budget (Kontar & Brown 2005).

We used standard SPEX software (Schwartz et al. 2002) to fit to the observed X-ray counts an approximate parametric ${\overline F}(E)$ comprising an isothermal plus broken power-law form with low energy cut off. The minimum $\chi ^2$ fit of the observed spectra gives emission measure $EM=8.0\times 10^{46}$ cm-3, temperature kT=1.36 keV, spectral indexes $\delta _{\rm low}=1.11$, $\delta _{\rm high}=3.01$ with break energy EB=54 keV and a low energy cut-off at 18 keV very clearly visible above the isothermal part (Fig. 7).

Next we carried out the same model fit but using the instrument response matrix corrected for albedo as described above - i.e. we repeat the process for $I_{\rm P}$ instead of I. The result shows the same tendency as we saw in the analysis of energy dependent photon spectral index. The primary photon spectrum is softer at low energies and harder at high energies. Now we find a slightly bigger emission measure $EM=9.2\times 10^{46}$ cm-3 and slightly smaller temperature kT=1.29 keV. The spectral index of energetic electrons becomes softer at low energies $\delta _{\rm low}=1.28$ and harder at high energies $\delta _{\rm high}=2.73$with the break energy at higher energies EB=59 keV. Most importantly, in contrast with the fit to the observed spectrum, the primary spectrum fit yields a much lower low energy cut-off, around 10 keV, not clearly visible above the large thermal component there (Fig. 7). Therefore, we cannot conclude that the true ${\overline F}(E)$ derived from the primary photon spectrum has a well defined low-energy cut-off.


  \begin{figure} \par\includegraphics[width=75mm]{3672_f6.eps} \end{figure} Figure 7: Mean electron flux spectra of the September, 2002 solar flare. The solid/dash lines show the spectrum without and with albedo correction.
Open with DEXTER


  \begin{figure} \par\includegraphics[width=65mm]{3672_f7.eps} \end{figure} Figure 8: Inverted mean electron flux of the August 20, 2002 solar flare for the time interval 08:25:20-08:25:40 UT. The dash line shows the spectra with albedo correction. The confidence intervals represent the range of solutions found by allowing the incident photon spectrum to range randomly within the estimated (instrument + shot noise) errors.
Open with DEXTER

Figure 8 gives a further example from the flare of August 20, 2002 (Kasparova et al. 2005). We have obtained regularized ${\bar F}(E)$ using the method of Kontar et al, 2005 starting from the total observed spectrum $I(\epsilon)$ and the albedo-corrected primary spectrum $I_{\rm P}(\epsilon)$. Note that a local maximum in ${\bar F}(E)$ at ${\sim} 40$ keV, difficult to accommodate in conventional thick-target models (Kontar & Brown 2005), is no longer required when albedo is properly accounted for.

   
6 Discussion and conclusions

We have shown how the Compton backscatter Green's function of Magdziarz & Zdziarski (1995) may be employed to deduce primary hard X-ray spectra from observations. We have applied this procedure to RHESSI data, particularly from a couple of flares with hard photon spectra. Without a treatment of albedo, spectral hardening found in some flares at photon energies of ${\sim} 40$ keV appears to require a local minimum in the mean fast electron distribution (Piana et al. 2003; Kasparova et al. 2005). These local minima are particularly interesting, since they might, if steep, (Kontar & Brown 2005) be inconsistent with the very widely used collision-dominated thick-target model for X-ray production (Brown 1971; Lin & Hudson 1976). Here we have seen that a complete treatment of albedo removes much of the spectral hardening in this photon energy range, potentially restoring the viability of the collisional thick target.

The major assumption here is the isotropy of the downward directed radiation. At the relevant photon energies here 10-100 keV, the intrinsic bremsstrahlung cross-section polar diagram has a characteristic width of about $30^\circ$ (see figure in Massone et al. 2004). Since the emitting electron angular distribution will be broadened by pitch-angle scattering (Leach & Petrosian 1981; MacKinnon & Craig 1991), the resulting hard X-ray flux might be fairly close to downward isotropic.

Inclusion of the albedo effect reduces the number of energetic electrons required for the production of the observed spectra. The total flux of energetic electrons

 \begin{displaymath}\langle vn_{\rm e} n V \rangle = \int_{E_{\rm low}}^\infty \langle \bar F(E)nV\rangle ~ {\rm d}E, \end{displaymath} (11)

where v is the average electron velocity. A thin-target fit of the observed spectrum of the September, 2002 event gives $\langle vn_{\rm e} n V\rangle = 6.2\times 10^{54}$ cm-2 s-1, 15% larger than the value obtained for the albedo corrected spectrum. This effect is more pronounced in the total energy than in total numbers, the energy flux $\langle vEn_{\rm e}nV\rangle $ being 30% overestimated when Compton back-scattering is ignored. The influence of albedo can be even more substantial, especially for a very flat spectra. For example in the August 20, 2002 flare analyzed by Kasparova et al. (2005), the apparent low energy cut-off in observed spectra was found around 44 keV, a higher value than normally assumed.

It should be also stressed here that these are rather conservative (lower limit) estimates of the albedo correction, assuming an isotropic primary X-ray source. In fact, if the electrons are strongly downward directed, the back-scattered photons could produce a several times larger contribution to the observed spectrum. This would have a major effect and clearly one must consider the albedo to get a realistic idea of the flare electron spectrum and energy budget. The capacity to account completely for the effects of albedo also restores some optimism over discussing, in terms of X-ray spectra, issues such as the lowest energies at which electron acceleration operates (see Zhang & Huang 2004), though electron transport close to the thermal speed complicates the interpretation of the X-ray spectrum there (Galloway et al. 2005).

Acknowledgements
We are grateful to Gordon Holman and Jana Kasparova for valuable discussions and to Kim Tolbert for adding our code to OSPEX package. EPK, ALM, and JCB acknowledge the financial support of a PPARC Rolling Grant. RAS is supported by contract NAS5 - 01160.

References

 
Copyright ESO 2006