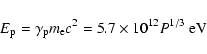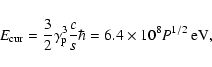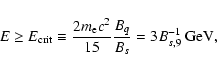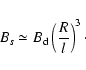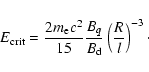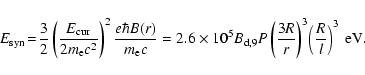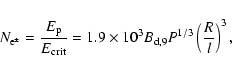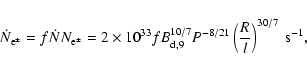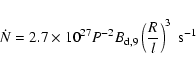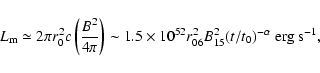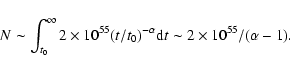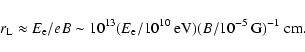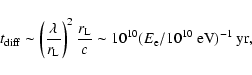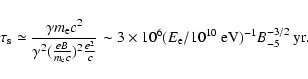A&A 446, 943-948 (2006)
DOI: 10.1051/0004-6361:20053559
Could electron-positron annihilation lines in the Galactic
center result from pulsar winds?
W. Wang1,3 - C. S. J. Pun2 - K. S. Cheng2
1 - Max-Planck-Institut für extraterrestrische Physik,
Postfach 1312, 85741 Garching, Germany
2 - Department of Physics, University of
Hong Kong, Pokfulam Road, Hong Kong, PR China
3 - National Astronomical Observatories, Chinese Academy of
Sciences, Beijing 100012, PR China
Received 2 June 2005 / Accepted 20 September 2005
Abstract
Observations of a strong and extended positron-electron
annihilation line emission in the Galactic center (GC) region by
the Spectrometer on the International Gamma-Ray Astrophysical
Laboratory (SPI/INTEGRAL) are challenging to the existing models
of positron sources in the Galaxy. In this paper, we study the
possibility that pulsar winds in the GC produce the 511 keV line.
We propose that three possible scenarios of pulsar winds may exist
as the positron sources: normal pulsars, rapidly spinning strongly
magnetized neutron stars (magnetars) in gamma-ray burst (GRB)
progenitors, a population of millisecond pulsars in the Galactic
center. These e pairs could be trapped in the region by the
magnetic field in the Galactic center, and cool through
synchrotron radiation and Coulomb interactions with the medium,
thereby becoming non-relativistic particles. The cooling
timescales are shorter than the diffuse timescale of positrons, so
low-energy positrons could annihilate directly with electrons into
511 keV photons or could form positronium before annihilation. We
find that normal pulsars cannot be a significant contributor to
the positron sources. Although magnetars in the GC could be
potential sources of positrons, their birth rate and birth
locations may pose some problems for this scenario. We believe
that the most likely candidates for positron sources in the GC may
be a population of millisecond pulsars in the GC. Our preliminary
estimations predict that the e
pairs could be trapped in the region by the
magnetic field in the Galactic center, and cool through
synchrotron radiation and Coulomb interactions with the medium,
thereby becoming non-relativistic particles. The cooling
timescales are shorter than the diffuse timescale of positrons, so
low-energy positrons could annihilate directly with electrons into
511 keV photons or could form positronium before annihilation. We
find that normal pulsars cannot be a significant contributor to
the positron sources. Although magnetars in the GC could be
potential sources of positrons, their birth rate and birth
locations may pose some problems for this scenario. We believe
that the most likely candidates for positron sources in the GC may
be a population of millisecond pulsars in the GC. Our preliminary
estimations predict that the e annihilation rate in the GC
is
annihilation rate in the GC
is
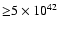 s-1, which is consistent with the
present observational constraints. Therefore, the e
s-1, which is consistent with the
present observational constraints. Therefore, the e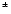 pairs
from pulsars winds can contribute significantly to the positron
sources in the Galactic center region. Furthermore, since the
diffusion length of positrons is short, we predict that the
intensity distribution of the annihilation line should follow the
distribution of millisecond pulsars, which should then correlate
to the mass distribution in the GC.
pairs
from pulsars winds can contribute significantly to the positron
sources in the Galactic center region. Furthermore, since the
diffusion length of positrons is short, we predict that the
intensity distribution of the annihilation line should follow the
distribution of millisecond pulsars, which should then correlate
to the mass distribution in the GC.
Key words: Galaxy: center - gamma-rays: theory - pulsars:
general
Since the first detection (Johnson & Haymes 1973) and subsequent
identification (Leventhal et al. 1978) of the Galactic 511 keV
annihilation line, the origin of the galactic positrons has become
a lively topic of scientific debate. With the launch of the
INTEGRAL gamma-ray observatory in 2002, the SPI board on telescope
provides a strong constraints on the morphology and intensity of
the 511 keV line emission from the Galactic center (Knödlseder et al. 2003; Jean et al. 2003). The data analyses show that the
line emitting source is diffuse, and that the line flux within
5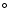 of the GC amounts to
of the GC amounts to
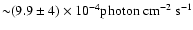 (Knödlseder et al. 2003),
corresponding to a luminosity of
(Knödlseder et al. 2003),
corresponding to a luminosity of
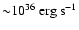 .
The high line luminosity requires that the positron injection rate
in the GC should be around
.
The high line luminosity requires that the positron injection rate
in the GC should be around
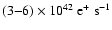 .
Recently, analyses of the observational data by SPI/INTEGRAL with
deep Galactic center region exposure (longer than 4 Ms) show that
the spatial distribution of 511 keV line appears centered on the
Galactic center (bulge component), with no contribution from a
disk component (Teegarden et al. 2005; Knödlseder et al. 2005;
Churazov et al. 2005). Analysis by Churazov et al. (2005) suggests
that the positron injection rate is up to
.
Recently, analyses of the observational data by SPI/INTEGRAL with
deep Galactic center region exposure (longer than 4 Ms) show that
the spatial distribution of 511 keV line appears centered on the
Galactic center (bulge component), with no contribution from a
disk component (Teegarden et al. 2005; Knödlseder et al. 2005;
Churazov et al. 2005). Analysis by Churazov et al. (2005) suggests
that the positron injection rate is up to
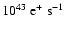 within
within
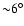 ,
and an intrinsic annihilation line
width
,
and an intrinsic annihilation line
width
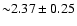 keV.
keV.
The potential positron sources include: neutron stars or black
holes (Lingenfelter & Ramaty 1983); 56Co 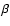 -decays in
supernova remnants (Lingenfelter & Ramaty 1979; Ellison et al. 1990); other radioactive nuclei formed by nucleosynthesis
in supernova, nova, red giants, and Wolf-Rayet stars (Ramaty et al. 1979); cosmic ray interactions with the interstellar medium
(Kozlovsky et al. 1987); pair production by gamma-ray photons
interacting with starlight photons in the interstellar medium
(Mastichiadis et al. 1991) and gamma-ray cascades
at the polar caps of pulsars (Harding & Ramaty 1987; Boulares 1989); electron-positron pairs produced by the pulsar winds (Chi et al. 1996); and probably gamma-ray bursts (GRB,
Lingenfelter & Hueter 1984). However, recent results from
SPI/INTEGRAL on the 511 keV annihilation line emission in the
Galactic center show a diffuse source with high line luminosity,
and present a challenge to the existing models of the origin of
galactic positrons. As a result, Cassé et al. (2004) argues that
normal supernova explosion in the GC cannot contribute to the
required positrons, but hypernovae (Type Ic supernovae/gamma-ray
bursts) in the Galactic center may be possible sources of galactic
positrons. In addition, annihilations of light dark matter
particles into
-decays in
supernova remnants (Lingenfelter & Ramaty 1979; Ellison et al. 1990); other radioactive nuclei formed by nucleosynthesis
in supernova, nova, red giants, and Wolf-Rayet stars (Ramaty et al. 1979); cosmic ray interactions with the interstellar medium
(Kozlovsky et al. 1987); pair production by gamma-ray photons
interacting with starlight photons in the interstellar medium
(Mastichiadis et al. 1991) and gamma-ray cascades
at the polar caps of pulsars (Harding & Ramaty 1987; Boulares 1989); electron-positron pairs produced by the pulsar winds (Chi et al. 1996); and probably gamma-ray bursts (GRB,
Lingenfelter & Hueter 1984). However, recent results from
SPI/INTEGRAL on the 511 keV annihilation line emission in the
Galactic center show a diffuse source with high line luminosity,
and present a challenge to the existing models of the origin of
galactic positrons. As a result, Cassé et al. (2004) argues that
normal supernova explosion in the GC cannot contribute to the
required positrons, but hypernovae (Type Ic supernovae/gamma-ray
bursts) in the Galactic center may be possible sources of galactic
positrons. In addition, annihilations of light dark matter
particles into
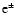 pairs (Boehm et al. 2004) have also been
suggested as the potential origin of the 511 keV line in the GC.
pairs (Boehm et al. 2004) have also been
suggested as the potential origin of the 511 keV line in the GC.
In this paper, we study the possible contribution to positrons in
the Galactic center by pulsar winds. We suggest that there are
three possibilities of pulsar winds as positron sources in the
Galactic center: normal pulsars (e.g. Crab and Vela like pulsars),
the rapidly spinning strongly magnetized neutron stars that are
possible GRB progenitors (Usov 1992), and a millisecond pulsar
population (Wang et al. 2005). In Sect. 2, we study the
possibility that electron-positron pairs can be produced by the
pulsar winds. In Sect. 3, we discuss in detail how electron-positrons
may be produced in three possible scenarios. These
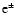 pairs
could be trapped in the Galactic center by the magnetic field. In
Sect. 4, we find that both the synchrotron cooling timescale and
energy loss timescale by Coulomb interactions in the medium are
less than the diffuse timescale of electron-positrons in the GC,
so that
pairs
could be trapped in the Galactic center by the magnetic field. In
Sect. 4, we find that both the synchrotron cooling timescale and
energy loss timescale by Coulomb interactions in the medium are
less than the diffuse timescale of electron-positrons in the GC,
so that
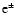 pairs will become non-relativistic, and then
annihilate into 511 keV emission lines. The summary and
discussions follow in Sect. 5.
pairs will become non-relativistic, and then
annihilate into 511 keV emission lines. The summary and
discussions follow in Sect. 5.
It is well known that relativistic particles from pulsar winds
interacting with the interstellar medium form the synchrotron wind
nebulae (see reviews by Arons 1998; Kaspi et al.
2004). Chi et al. (1996) proposed that the bulk of the
comic positrons could originate from pulsar winds. In this paper,
we consider that the electron-positron pair production occurs in
the pulsar outer-magnetospheric region, the so-called outer gap
(Cheng et al. 1986).
Zhang & Cheng (1997) have developed a self-consistent mechanism
to describe the high energy radiation from spin-powered pulsars.
In their model, relativistic charged particles from a thick outer
magnetospheric accelerator (outer gap) radiate through the
synchro-curvature radiation mechanism (Cheng & Zhang 1996) rather
than through the synchrotron and curvature mechanisms in general,
thereby producing non-thermal photons from the primary
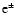 pairs along the curved magnetic field lines in the outer gap. The
criterion for the existence of the outer gap requires the
fractional size of this outer gap f<1, which is the ratio
between the mean vertical separation of the outer gap boundaries
in the plane of the rotation axis and the magnetic axis to the
light cylinder radius. There f is limited by the pair production
between the soft thermal X-rays from the neutron star surface and
the high energy gamma-ray photons emitted from the outer gap
region, and it can be approximated as
pairs along the curved magnetic field lines in the outer gap. The
criterion for the existence of the outer gap requires the
fractional size of this outer gap f<1, which is the ratio
between the mean vertical separation of the outer gap boundaries
in the plane of the rotation axis and the magnetic axis to the
light cylinder radius. There f is limited by the pair production
between the soft thermal X-rays from the neutron star surface and
the high energy gamma-ray photons emitted from the outer gap
region, and it can be approximated as
 (Zhang & Cheng 1997), where P is the
spin period, and B12 is the surface magnetic field in units
of 1012 G.
(Zhang & Cheng 1997), where P is the
spin period, and B12 is the surface magnetic field in units
of 1012 G.
The pair production mechanism is a synchrotron photon cascade in a
strong magnetic field. According to Halpern & Ruderman (1993),
each primary electron-positron from an outer gap will have an
energy
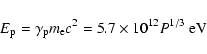 |
(1) |
before it strikes the neutron star surface, where
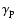 is the Lorentz factor of the primary electrons,
is the Lorentz factor of the primary electrons, 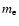 the rest
mass of the electron, and c the light speed. These primary
electron-positrons will continue to emit curvature photons with a
typical energy
the rest
mass of the electron, and c the light speed. These primary
electron-positrons will continue to emit curvature photons with a
typical energy
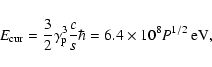 |
(2) |
where 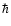 is the
Planck constant,
is the
Planck constant,
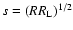 the curvature radius, R=106cm the radius of the neutron star, and
the curvature radius, R=106cm the radius of the neutron star, and
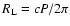 is the light
cylinder distance. These curvature photons will be converted into
secondary
is the light
cylinder distance. These curvature photons will be converted into
secondary
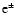 pairs in the local magnetic field when their
energy satisfies (Ruderman & Sutherland 1975)
pairs in the local magnetic field when their
energy satisfies (Ruderman & Sutherland 1975)
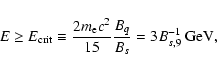 |
(3) |
where
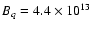 G is a critical magnetic
field, and Bs,9 is the local surface magnetic field of the
neutron star in units of 109 G.
G is a critical magnetic
field, and Bs,9 is the local surface magnetic field of the
neutron star in units of 109 G.
It has been proposed that there is a strong multipole magnetic
field near the stellar surface, although a global dipole magnetic
field gives a good description of the magnetic field far from the
star (Ruderman & Sutherland 1975; Ruderman 1991; Arons 1993). The
typical radius of curvature l of the local magnetic field is on
the order of the crust thickness of the star (i.e.
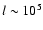 cm), which is much less than the dipole radius of curvature s of
dipole field component near stellar surface. The relation between
the local multipole magnetic field and dipole field can be given
by (Zhang & Cheng 2003)
cm), which is much less than the dipole radius of curvature s of
dipole field component near stellar surface. The relation between
the local multipole magnetic field and dipole field can be given
by (Zhang & Cheng 2003)
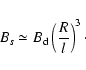 |
(4) |
Here 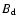 is the dipole magnetic field of a pulsar, so the
critical energy is rewritten as
is the dipole magnetic field of a pulsar, so the
critical energy is rewritten as
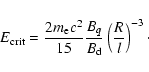 |
(5) |
The secondary
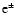 pairs will lose their energy via synchrotron
radiation with a photon energy at a distance of r
pairs will lose their energy via synchrotron
radiation with a photon energy at a distance of r
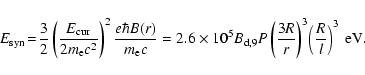 |
(6) |
We can see that generally
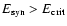 ,
so
a photon-electron cascade will start and develop until this
condition fails. At the end of a cascade, each incoming primary
electron-positron can produce, on average,
,
so
a photon-electron cascade will start and develop until this
condition fails. At the end of a cascade, each incoming primary
electron-positron can produce, on average,
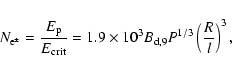 |
(7) |
and then the total pair
production rate can be estimated as
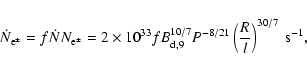 |
(8) |
where
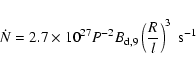 |
(9) |
is the primary electron-positrons passing
through the polar gap (Goldreich & Julian 1969).
Since these pairs are created close to the stellar surface and the
field lines are converging, only a small fraction may keep moving
toward the star and annihilate on the stellar surface. Ho (1986)
showed that the loss cone for these pairs will approach 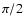 (cf. Eq. (29) of Ho 1986), in other words, most pairs will be
reflected by the magnetic mirroring effect and then move toward
the light cylinder. These particles will flow out with the pulsar
wind and be accelerated by the low-frequency electro-magnetic
wave. In theory, the maximum Lorentz factor of pulsar wind
particles could be larger than 104 (Rees & Gunn 1974; Kennel
& Coroniti 1984).
(cf. Eq. (29) of Ho 1986), in other words, most pairs will be
reflected by the magnetic mirroring effect and then move toward
the light cylinder. These particles will flow out with the pulsar
wind and be accelerated by the low-frequency electro-magnetic
wave. In theory, the maximum Lorentz factor of pulsar wind
particles could be larger than 104 (Rees & Gunn 1974; Kennel
& Coroniti 1984).
As discussed in the introduction, we consider three possibilities
of positron sources from pulsar winds in the Galactic center
region. In this section, we discuss them separately in detail.
The deep radio survey (LaRosa et al. 2000) and recent observations
in the Galactic center field targeted in the deep Chandra X-ray
surveys (Wang et al. 2002a; Muno et al. 2003) show that a few
supernova remnants are present. Detailed analyses of X-ray nebulae
G0.13-0.11, G359.89-0.08 and G359.54+0.18 (Wang et al. 2002b;
Lu et al. 2003) suggested young pulsars might lie inside
them. In the past years, young pulsars may have been actively
produced in the Galactic center region. However, because the
average proper motion velocity of normal pulsars is high (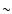 500 km s-1), few of them (
500 km s-1), few of them (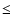 40%) lie in the GC
(Arzoumanian et al. 2002), so the number of normal
pulsars whose active timescale is
40%) lie in the GC
(Arzoumanian et al. 2002), so the number of normal
pulsars whose active timescale is 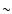 1 Myr in the GC should be
small, and the number of Crab or Vela like pulsars is around 10
(Wang et al. 2005).
1 Myr in the GC should be
small, and the number of Crab or Vela like pulsars is around 10
(Wang et al. 2005).
There is both theoretical and experimental evidence that young
pulsars can emit intense electron/positron winds. In the case of
Crab and Vela, the
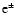 injection rates are up to
injection rates are up to
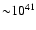 e+ s-1 and
e+ s-1 and
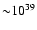 e+ s-1. Then in
the timescale of the age of Crab or Vela, the total number of
positrons is about
e+ s-1. Then in
the timescale of the age of Crab or Vela, the total number of
positrons is about
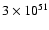 .
Assuming that the birth rate
of young pulsars is 1 per 103 years in the GC, and that the
lifetime of positrons is 1 million years (cf. the cooling time
scale estimate in Sect. 4), there will be about
.
Assuming that the birth rate
of young pulsars is 1 per 103 years in the GC, and that the
lifetime of positrons is 1 million years (cf. the cooling time
scale estimate in Sect. 4), there will be about
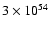 positrons in the region. On average the annihilation rate is
positrons in the region. On average the annihilation rate is
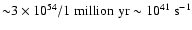 .
Therefore, our analysis suggests that the young pulsar winds could
not be a significant contributor to the positrons in the Galactic
center region.
.
Therefore, our analysis suggests that the young pulsar winds could
not be a significant contributor to the positrons in the Galactic
center region.
It has been suggested that gamma-ray bursts in the GC are
potential positron sources (Cassé et al. 2004; Parizot et al.
2005). Their models assume that the annihilation line may relate
to nucleosynthesis in the hypernova that is the GRB progenitor.
But the GRB progenitor could also be a rapidly spinning, strongly
magnetized neutron star (millisecond magnetar, see Usov 1992;
Thompson 1994), that is also a very strong
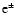 pair emitter.
The generic magnetized
pair emitter.
The generic magnetized
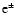 outflow from a spinning compact
object could be given by
outflow from a spinning compact
object could be given by
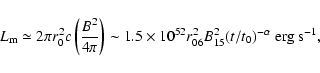 |
(10) |
where r0 is the size of the central engine,
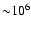 cm;
cm;
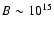 G is the magnetic field of
magnetars; t0 is a characteristic timescale after the burst,
i.e.
G is the magnetic field of
magnetars; t0 is a characteristic timescale after the burst,
i.e. 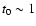 s, where we have assumed the magnetic field
decay would follow a power law and
s, where we have assumed the magnetic field
decay would follow a power law and 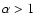 .
Assuming the
average energy of positrons is
.
Assuming the
average energy of positrons is 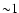 GeV, the total number of
positrons emitted by magnetars is
GeV, the total number of
positrons emitted by magnetars is
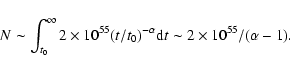 |
(11) |
If we take
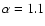 ,
the total
,
the total
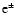 number is up to
number is up to
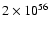 .
For other possible values of
.
For other possible values of 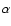 ,
the
total
,
the
total
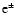 number will be reduced by a factor of several times.
On the other hand, the toroidal magnetic field of magnetars can
reach 1017 G, and part of this toroidal magnetic field energy
can also be converted into
number will be reduced by a factor of several times.
On the other hand, the toroidal magnetic field of magnetars can
reach 1017 G, and part of this toroidal magnetic field energy
can also be converted into
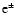 (Kluzniak & Ruderman 1998; Dai
& Lu 1998).
(Kluzniak & Ruderman 1998; Dai
& Lu 1998).
Therefore, in this model more than 1056 positrons would be
produced. Because the GRB birth rate from the present observations
is
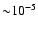 yr-1 in a galaxy (Piran 2004) after
considering the beaming effect correction, we expect the GRB rate
in the GC is about one per 106 years. Therefore, the
annihilation rate of positrons produced by the magnetar is
yr-1 in a galaxy (Piran 2004) after
considering the beaming effect correction, we expect the GRB rate
in the GC is about one per 106 years. Therefore, the
annihilation rate of positrons produced by the magnetar is
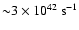 .
But more comments on the GRB rates
are required here. Observations of the long GRBs and host galaxies
are in agreement with a correlation of GRB locations with blue
regions/spirals of host galaxies (Bloom et al. 2002), which
implies that long bursts do not concentrate in the bulge region.
Theoretical studies of merging neutron stars and black holes
suggest that most short bursts may be located in the halo region
(e.g. Voss & Tauris 2003), so here we may have overestimated the
GRB rate in the Galactic center region considering the
uncertainties of the burst sites of different GRB populations.
.
But more comments on the GRB rates
are required here. Observations of the long GRBs and host galaxies
are in agreement with a correlation of GRB locations with blue
regions/spirals of host galaxies (Bloom et al. 2002), which
implies that long bursts do not concentrate in the bulge region.
Theoretical studies of merging neutron stars and black holes
suggest that most short bursts may be located in the halo region
(e.g. Voss & Tauris 2003), so here we may have overestimated the
GRB rate in the Galactic center region considering the
uncertainties of the burst sites of different GRB populations.
We have argued that millisecond pulsars could be the major
contributor to the pulsar population in the Galactic center (see
Wang et al. 2005). There may exist a population of old
neutron stars with low space velocities that have not escaped the
Galactic center (see Belczynski & Taam 2004a,b). Such
neutron stars could be recycled to millisecond periods, and could
remain in the GC through their lifetime because of their
relatively low proper motion velocity (Lyne et al. 1998;
Arzoumanian et al. 2002). Wang et al.
(2005) suggest that the millisecond pulsar population can
contribute significantly to the diffuse gamma-rays in the Galactic
center (Mayer-Hasselwander et al. 1998). In addition, the X-ray
synchrotron nebula around the millisecond pulsar B1957+20
(Stappers et al. 2003) provides evidence that millisecond pulsars
can remain active enough to emit relativistic winds. Therefore, we
propose that electron-positrons from the winds of the millisecond
pulsar population could be the possible positron sources in the
GC.
Since millisecond pulsars can lie in the GC and remain active for
1 Gyr, we believe they are continuous positron injecting sources.
For the typical parameters of millisecond pulsars, P=3 ms,
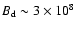 G and according to Eq. (8), we estimate the
positron injection rate
G and according to Eq. (8), we estimate the
positron injection rate
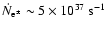 for a millisecond pulsar. Wang et al. (2005) showed that
about 6000 millisecond pulsars could contribute to the diffuse
gamma-rays in the Galactic center region covered by EGRET. Since
the present annihilation observations show that the line emission
region toward GC is about 6
for a millisecond pulsar. Wang et al. (2005) showed that
about 6000 millisecond pulsars could contribute to the diffuse
gamma-rays in the Galactic center region covered by EGRET. Since
the present annihilation observations show that the line emission
region toward GC is about 6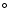 ,
which is much larger than the
EGRET observation region (1.5
,
which is much larger than the
EGRET observation region (1.5 ), a larger number of MSPs
are expected to lie in the bulge region of 6
), a larger number of MSPs
are expected to lie in the bulge region of 6 .
We do not
know the distribution of MSPs in GC, so we just scale the number
of MSPs by
.
We do not
know the distribution of MSPs in GC, so we just scale the number
of MSPs by
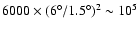 ,
where we
assume the number density of MSPs may be distributed as
,
where we
assume the number density of MSPs may be distributed as
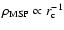 ,
where
,
where 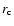 is the scaling size of GC. Based on the population analysis of Lyne et al. (1998), the
number of millisecond pulsars in the entire Galaxy may exceed
is the scaling size of GC. Based on the population analysis of Lyne et al. (1998), the
number of millisecond pulsars in the entire Galaxy may exceed
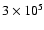 ,
so the number of millisecond pulsars in the bulge
region estimated here could be reasonable. The total positron
injection rate from the millisecond pulsar population is thus
,
so the number of millisecond pulsars in the bulge
region estimated here could be reasonable. The total positron
injection rate from the millisecond pulsar population is thus
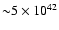 e+ s-1.
e+ s-1.
The outflowing electron-positrons could be trapped by the magnetic
field in the Galactic center. The Larmor radius (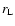 )
of a
relativistic electron with energy
)
of a
relativistic electron with energy 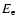 is given by
is given by
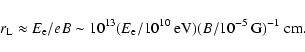 |
(12) |
The angular size of
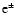 annihilation
line emission detected by SPI/INTEGRAL is several degrees
(Knödlseder et al. 2003), so we take
annihilation
line emission detected by SPI/INTEGRAL is several degrees
(Knödlseder et al. 2003), so we take
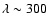 pc as the
size of the Galactic center region studied in this paper (assuming
the distance of the GC to us
pc as the
size of the Galactic center region studied in this paper (assuming
the distance of the GC to us 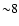 kpc). The diffuse timescale
of the electron is estimated as
kpc). The diffuse timescale
of the electron is estimated as
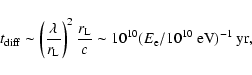 |
(13) |
where we take the average magnetic field in the GC
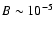 G (Uchida & Güsten 1995; LaRosa et al. 2005) and
G (Uchida & Güsten 1995; LaRosa et al. 2005) and
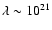 cm.
cm.
Electrons and positrons in the Galactic center will lose their
energy via synchrotron radiation and Coulomb interactions with the
medium, and then annihilate into 511 keV photons. If we assume the
injection electron-positron energy spectrum in the form
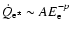 ,
where
,
where 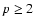 ,
then positrons
with energies higher than
,
then positrons
with energies higher than
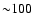 MeV will cool through
synchrotron radiation in the magnetic field, while a large number
of low energy positrons lower than
MeV will cool through
synchrotron radiation in the magnetic field, while a large number
of low energy positrons lower than
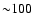 MeV lose their
energy by Coulomb interactions in the medium of the GC. The other
energy-loss processes, like inverse Compton cooling and
bremsstrahlung, are negligible. When the positrons reach an energy
around a few tens of eV, they could either annihilate directly
with electrons or form positronium by charge exchange or radiative
capture (Bussard et al. 1979). Thus the annihilation
timescales depend on the cooling timescales.
MeV lose their
energy by Coulomb interactions in the medium of the GC. The other
energy-loss processes, like inverse Compton cooling and
bremsstrahlung, are negligible. When the positrons reach an energy
around a few tens of eV, they could either annihilate directly
with electrons or form positronium by charge exchange or radiative
capture (Bussard et al. 1979). Thus the annihilation
timescales depend on the cooling timescales.
The synchrotron cooling timescale of relativistic positrons is
estimated as
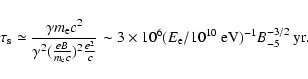 |
(14) |
We find
that the electron synchrotron timescale is lower than the
diffusion timescale for the same electron energy,
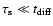 ,
so the positrons could significantly lose their energy
to become non-relativistic and stay in the Galactic center.
,
so the positrons could significantly lose their energy
to become non-relativistic and stay in the Galactic center.
The energy loss timescale of Coulomb interactions in the medium
 depends on the positron energy, the medium density, and
the degree of ionization. For the positrons with energy around
1-100 MeV, the Coulomb interaction cooling timescale is estimated
as
depends on the positron energy, the medium density, and
the degree of ionization. For the positrons with energy around
1-100 MeV, the Coulomb interaction cooling timescale is estimated
as
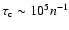 yr (within a factor of 2), and n is
the medium number density in units of cm-3. However, the
medium in GC is quite complicated, as many giant molecular clouds
(LaRosa et al. 2000) exist, as does hot gas discovered in X-rays
(Muno et al. 2004). Then the energy loss timescales could vary
from
yr (within a factor of 2), and n is
the medium number density in units of cm-3. However, the
medium in GC is quite complicated, as many giant molecular clouds
(LaRosa et al. 2000) exist, as does hot gas discovered in X-rays
(Muno et al. 2004). Then the energy loss timescales could vary
from
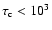 yr in the molecular clouds (
yr in the molecular clouds (
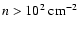 ),
),
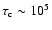 yr for the typical warm interstellar
medium (
yr for the typical warm interstellar
medium (
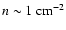 ), and
), and
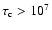 yr for the hot
gas (
yr for the hot
gas (
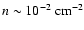 ). Analysis of the 511 keV
annihilation spectrum suggests that the dominant fraction of
positrons (
). Analysis of the 511 keV
annihilation spectrum suggests that the dominant fraction of
positrons (
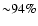 )
form positronium before annihilation,
which constrains the positron annihilation in the hot gas to a
very small fraction (<8%, see Churazov et al. 2005). Most
positron annihilations seem to lie in the warm medium, so the
cooling timescale is also much shorter than the diffusion
timescale.
)
form positronium before annihilation,
which constrains the positron annihilation in the hot gas to a
very small fraction (<8%, see Churazov et al. 2005). Most
positron annihilations seem to lie in the warm medium, so the
cooling timescale is also much shorter than the diffusion
timescale.
The origin of Galactic positrons is still a mystery at present. In
this paper, we have proposed a possible contribution to positron
sources by the pulsar winds in the region of the Galactic center.
We discussed the contributions of three possible pulsar scenarios
in the GC: normal pulsars, the rapidly spinning strongly
magnetized neutron stars in GRB progenitors (millisecond
magnetars), and a millisecond pulsar population. Electron-positron
pairs are injected into the Galactic center region from three
classes of pulsar winds, and could be trapped in this region by
the magnetic field in the Galactic center. These relativistic
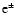 pairs will lose their energy though the synchrotron
radiation and the Coulomb interactions with the medium to become
non-relativistic. The cooling timescales are shorter than the
diffusion timescale of positrons in the magnetic field in the GC,
so positrons could form positronium by charge exchange or
radiative capture, or annihilate directly with electrons into
photons to produce the 511 keV line observed by the present
detectors. Our results have shown that normal pulsars cannot be a
significant contributor to positron sources in the GC, but the
millisecond magnetar and a millisecond pulsar population could be
potential positron sources. However, as we estimate that the
diffusion time is much longer than the cooling time, it is not
clear how the positrons produced by GRBs can spread over the
entire galactic bulge or at least do so in the range of
6
pairs will lose their energy though the synchrotron
radiation and the Coulomb interactions with the medium to become
non-relativistic. The cooling timescales are shorter than the
diffusion timescale of positrons in the magnetic field in the GC,
so positrons could form positronium by charge exchange or
radiative capture, or annihilate directly with electrons into
photons to produce the 511 keV line observed by the present
detectors. Our results have shown that normal pulsars cannot be a
significant contributor to positron sources in the GC, but the
millisecond magnetar and a millisecond pulsar population could be
potential positron sources. However, as we estimate that the
diffusion time is much longer than the cooling time, it is not
clear how the positrons produced by GRBs can spread over the
entire galactic bulge or at least do so in the range of
6 .
Parizot et al. (2005) argue that the turbulent
diffusion process is able to diffuse the positrons over the
galactic bulge in a timescale of 107 yr. However, it is still
not clear why the positrons produced by GRBs should concentrate in
the galactic bulge, and this is not supported by the observations
of GRBs and their host galaxies (e.g. long bursts in Bloom et al.
2002; short bursts in Gehrels et al. 2005). In view of the
uncertainty of the birth rate of GRBs in the GC and annihilation
lines lacking in the disk, we must have reservations about GRBs as
the significant positron sources in the GC.
.
Parizot et al. (2005) argue that the turbulent
diffusion process is able to diffuse the positrons over the
galactic bulge in a timescale of 107 yr. However, it is still
not clear why the positrons produced by GRBs should concentrate in
the galactic bulge, and this is not supported by the observations
of GRBs and their host galaxies (e.g. long bursts in Bloom et al.
2002; short bursts in Gehrels et al. 2005). In view of the
uncertainty of the birth rate of GRBs in the GC and annihilation
lines lacking in the disk, we must have reservations about GRBs as
the significant positron sources in the GC.
The predicted annihilation rate of positrons from the millisecond
pulsar population is
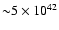 s-1 which is
consistent with observational constraints by SPI/INTEGRAL. We
therefore conclude that the
s-1 which is
consistent with observational constraints by SPI/INTEGRAL. We
therefore conclude that the
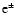 pairs from these classes of
pulsar winds are potential positron sources that can significantly
contribute to the 511 keV annihilation lines in GC.
pairs from these classes of
pulsar winds are potential positron sources that can significantly
contribute to the 511 keV annihilation lines in GC.
The important problem for positrons is determineing the
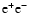 annihilation line intensity and radiation morphology in the
Galaxy. Recently, analyses of the data by SPI/INTEGRAL with deep
Galactic center region exposure show that the spatial distribution
of 511 keV line appears centered on the Galactic center (bulge
component), with no contribution from a disk component (Teegarden et al. 2005; Knödlseder et al. 2005; Churazov et al. 2005). We
suggested that the positrons produced by pulsar winds could be
trapped in the Galactic center by the magnetic field, and the
diffusion timescale is higher than the cooling timescales, so that
the positrons can annihilate into 511 keV photons before they can
escape from the Galactic center region. In the other viewpoints,
the bulge-dominated morphology of the 511 keV line may indicate
that the positron source population could be an old stellar
population. Knödlseder et al. (2005) suggest that the low-mass
X-ray binaries (LMXBs) could be the candidate sources because more
than 60% of the Galactic LMXBs are observed towards the galactic
bulge (see Grimm et al. 2002). The millisecond pulsar population
is a very old stellar population, and part of them stay in LMXBs,
but most may be isolated as radio pulsars, X-ray sources, and be
even detectable in gamma-rays. Recent radio observations find most
millisecond pulsars lie in globular clusters (see the review by
Camilo & Rasio 2005, and references therein), with few of them in
the Galactic field. If assuming the millisecond pulsar
evolutionary formation channels in globular clusters are similar
to the Galactic center region or bulge region, then we expect the
millisecond pulsar population in the GC as a significant
contributor to the positron sources. The millisecond pulsars can
stay in the Galactic center region throughout their lifetime,
which is well consistent with the 511 line emission morphology.
annihilation line intensity and radiation morphology in the
Galaxy. Recently, analyses of the data by SPI/INTEGRAL with deep
Galactic center region exposure show that the spatial distribution
of 511 keV line appears centered on the Galactic center (bulge
component), with no contribution from a disk component (Teegarden et al. 2005; Knödlseder et al. 2005; Churazov et al. 2005). We
suggested that the positrons produced by pulsar winds could be
trapped in the Galactic center by the magnetic field, and the
diffusion timescale is higher than the cooling timescales, so that
the positrons can annihilate into 511 keV photons before they can
escape from the Galactic center region. In the other viewpoints,
the bulge-dominated morphology of the 511 keV line may indicate
that the positron source population could be an old stellar
population. Knödlseder et al. (2005) suggest that the low-mass
X-ray binaries (LMXBs) could be the candidate sources because more
than 60% of the Galactic LMXBs are observed towards the galactic
bulge (see Grimm et al. 2002). The millisecond pulsar population
is a very old stellar population, and part of them stay in LMXBs,
but most may be isolated as radio pulsars, X-ray sources, and be
even detectable in gamma-rays. Recent radio observations find most
millisecond pulsars lie in globular clusters (see the review by
Camilo & Rasio 2005, and references therein), with few of them in
the Galactic field. If assuming the millisecond pulsar
evolutionary formation channels in globular clusters are similar
to the Galactic center region or bulge region, then we expect the
millisecond pulsar population in the GC as a significant
contributor to the positron sources. The millisecond pulsars can
stay in the Galactic center region throughout their lifetime,
which is well consistent with the 511 line emission morphology.
We have shown that the millisecond pulsar population in the
Galactic center could provide the major sources of positrons.
Normal pulsars could not be the main positron sources, but GRB
progenitors,i.e. millisecond magnetars, may be significant
contributors. In addition, hypernovae/GRBs could also be the
potential positron sources (Cassé et al. 2004). Thus, how could
we distinguish the model of a millisecond pulsar population from
other models, especially models related to GRBs? Firstly, we can
estimate the typical spatial diffusion scale, according to Eq. (13),
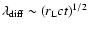 .
The average cooling
time of positrons in the GC is 106 years (Churazov et al.
2005), so the characteristic diffusion scale is about 1018 cm. Because of the low angular resolution of SPI/INTEGRAL (about 2 degrees, Vedrenne et al. 2003), we can assume that the positrons
annihilate in the same local region as their sources, i.e. the
millisecond pulsars. Therefore we predict that the spatial
intensity distribution of the annihilation lines should follow the
spatial distribution of MSPs if a millisecond population exists in
the GC. Additionally, we could assume the spatial distribution of
MSPs should follow the mass distribution of the GC though we do
not know how well they follow each other. But because the proper
motion velocity of MSPs is relatively low, we could reasonably
assume that the two distributions are quite close to each other.
Therefore, if the positron sources originate in the MSP
population, the 511 keV annihilation line intensity would follow
the mass distribution of the Galactic center region. The present
image of 511 keV line emission (see Figs. 4 and 6 in Knödlseder
et al. 2005) shows that the flux is strongest in the center and
decreases toward the outside region, possibly tracing the mass
distribution of the GC, but this needs confirmation by future high
resolution observations. The millisecond pulsar population could
naturally explain the diffuse emission morphology and does not
have the problem of the turbulent diffusion, which is required to
diffuse all these positrons to a few hundred pc. On the other
hand, for models associated with GRBs, the positron source is
initially a point-like source, so the diffuse emission of 511 keV
line needs the strong turbulent diffusion to diffuse the positrons
on to a larger scale (Parizot et al. 2005). Thus far, GRB
progenitors (either magnetars or hypernovae) are related to
massive stars and dense clouds (e.g. molecular clouds in the GC
that has a dimension of a few tens pc, LaRosa et al. 2000), the
mean density
.
The average cooling
time of positrons in the GC is 106 years (Churazov et al.
2005), so the characteristic diffusion scale is about 1018 cm. Because of the low angular resolution of SPI/INTEGRAL (about 2 degrees, Vedrenne et al. 2003), we can assume that the positrons
annihilate in the same local region as their sources, i.e. the
millisecond pulsars. Therefore we predict that the spatial
intensity distribution of the annihilation lines should follow the
spatial distribution of MSPs if a millisecond population exists in
the GC. Additionally, we could assume the spatial distribution of
MSPs should follow the mass distribution of the GC though we do
not know how well they follow each other. But because the proper
motion velocity of MSPs is relatively low, we could reasonably
assume that the two distributions are quite close to each other.
Therefore, if the positron sources originate in the MSP
population, the 511 keV annihilation line intensity would follow
the mass distribution of the Galactic center region. The present
image of 511 keV line emission (see Figs. 4 and 6 in Knödlseder
et al. 2005) shows that the flux is strongest in the center and
decreases toward the outside region, possibly tracing the mass
distribution of the GC, but this needs confirmation by future high
resolution observations. The millisecond pulsar population could
naturally explain the diffuse emission morphology and does not
have the problem of the turbulent diffusion, which is required to
diffuse all these positrons to a few hundred pc. On the other
hand, for models associated with GRBs, the positron source is
initially a point-like source, so the diffuse emission of 511 keV
line needs the strong turbulent diffusion to diffuse the positrons
on to a larger scale (Parizot et al. 2005). Thus far, GRB
progenitors (either magnetars or hypernovae) are related to
massive stars and dense clouds (e.g. molecular clouds in the GC
that has a dimension of a few tens pc, LaRosa et al. 2000), the
mean density
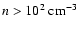 ,
and the cooling time of
positrons is less than 103 years. Thus the spatial diffusion
scale is only 1017 cm, which makes the annihilation line
emission look like a point source that is correlated with the
molecular clouds. In order to make the line emission be a diffuse
source, GRB positrons must diffuse to a hundred pc with a long
diffusion timescale > 107 years, so it requires that the mean
density in the GC is
,
and the cooling time of
positrons is less than 103 years. Thus the spatial diffusion
scale is only 1017 cm, which makes the annihilation line
emission look like a point source that is correlated with the
molecular clouds. In order to make the line emission be a diffuse
source, GRB positrons must diffuse to a hundred pc with a long
diffusion timescale > 107 years, so it requires that the mean
density in the GC is
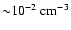 .
But this low
density seems unreasonable in the GC, and it is also not
consistent with the constraint on the medium environment from the
spectrum of 511 keV line (Churazov et al. 2005). Furthermore, if
positrons cannot diffuse to larger distances, the intensity
distribution of annihilation lines should not correlate with the
general mass distribution of the GC; instead, it should be more
correlated to the distribution of massive stars and dense
molecular clouds. Moreover, GRBs occur more likely in the disk,
where more dense molecular clouds and massive stars are located,
and in fact, the detected magnetars and soft gamma-ray repeaters
are also distributed in the disk. Giant flares from soft gamma-ray
repeaters (SGR) are also positron source candidates that are
distributed in the Galactic plane, but the 511 keV line
observations show a very weak disk component (Teegarden et al.
2005; Knödlseder et al. 2005). The 27 Dec. giant flare from SGR 1806-20 released an energy up to 1047 erg (Hurley et al.
2005), and it is thought to be a possible origin of short GRBs, so
might be considered as the 511 keV emission source in the future.
In summary, the positron source models associated with GRBs are
disputable. Our scenario of a millisecond pulsar population as
possible positron sources in the GC has some advantages of
explaining the diffuse morphology of 511 keV line emissions, and
it predicts that the line intensity distribution should follow the
mass distribution of the GC, which may be tested by future high
resolution observations.
.
But this low
density seems unreasonable in the GC, and it is also not
consistent with the constraint on the medium environment from the
spectrum of 511 keV line (Churazov et al. 2005). Furthermore, if
positrons cannot diffuse to larger distances, the intensity
distribution of annihilation lines should not correlate with the
general mass distribution of the GC; instead, it should be more
correlated to the distribution of massive stars and dense
molecular clouds. Moreover, GRBs occur more likely in the disk,
where more dense molecular clouds and massive stars are located,
and in fact, the detected magnetars and soft gamma-ray repeaters
are also distributed in the disk. Giant flares from soft gamma-ray
repeaters (SGR) are also positron source candidates that are
distributed in the Galactic plane, but the 511 keV line
observations show a very weak disk component (Teegarden et al.
2005; Knödlseder et al. 2005). The 27 Dec. giant flare from SGR 1806-20 released an energy up to 1047 erg (Hurley et al.
2005), and it is thought to be a possible origin of short GRBs, so
might be considered as the 511 keV emission source in the future.
In summary, the positron source models associated with GRBs are
disputable. Our scenario of a millisecond pulsar population as
possible positron sources in the GC has some advantages of
explaining the diffuse morphology of 511 keV line emissions, and
it predicts that the line intensity distribution should follow the
mass distribution of the GC, which may be tested by future high
resolution observations.
Acknowledgements
We are grateful to the referee for the critical comments, to R.
Diehl, Y. F. Huang and A. Strong for the discussions. This work
was supported by an RGC grant of the Hong Kong Government under
HKU 7015/05P and the National Natural Science Foundation of China
under grant 10273011 and 10573021.
- Arons, J. 1998,
preprint [arXiv:astro-ph/9809392]
(In the text)
-
Arzoumanian, Z., Chernoff, D. F., & Cordes, J. M. 2002, ApJ,
564, 333 [NASA ADS] [CrossRef] (In the text)
-
Belczynski, K., & Taam, R. E. 2004a, ApJ, 603, 690 [NASA ADS] [CrossRef] (In the text)
-
Belczynski, K., & Taam, R. E. 2004b, ApJ, submitted
[arXiv:astro-ph/0311287]
- Bloom, J. S.,
Kulkarni, S. R., & Djorgovski, S. G. 2002, AJ, 123, 1111 [NASA ADS] [CrossRef] (In the text)
- Boehm, C., et al.
2004, Phys. Rev. Lett., 92, 101301 [NASA ADS] [CrossRef] (In the text)
- Boulares, A.
1989, ApJ, 342, 807 [NASA ADS] [CrossRef] (In the text)
- Bussard, R. W.,
Ramaty, R., & Drachman, R. J. 1979, ApJ, 471, 673 (In the text)
- Camilo, F., &
Rasio, F. A. 2005, preprint [arXiv:astro-ph/0501226]
(In the text)
- Cassé, M.,
Cordier, B., Paul, J., & Schanne, S. 2004, ApJ, 602, L17 [NASA ADS] [CrossRef] (In the text)
- Cheng, K. S., Ho, C.,
& Ruderman, M. A. 1986, ApJ, 300, 500 [NASA ADS] [CrossRef] (In the text)
- Cheng, K. S., et al.
1990, J. Phys. G: Nucl. Part. Phys., 16, 1115 [NASA ADS] [CrossRef]
- Cheng, K. S., &
Zhang, L. 1996, ApJ, 463, 271 [NASA ADS] [CrossRef] (In the text)
- Chevalier, R.
A. 2000, ApJ, 539, L45 [NASA ADS] [CrossRef]
- Chi, X., Cheng, K. S.,
& Young, E. C. M. 1996, ApJ, 459, L83 [NASA ADS] (In the text)
- Churazov, E.,
Sunyaev, R., Sazonov, S., Revnivtsev, M., & Varshalovich, D.
2005, MNRAS, 357, 1377 [NASA ADS] [CrossRef] (In the text)
- Dai, Z. G., & Lu, T.
1998, Phys. Rev. Lett., 81, 4301 [NASA ADS] [CrossRef] (In the text)
- Ellison, D. C.,
Frank, J. C., & Ramaty, R. 1990, in Proc. 21st Int. Cosmic-Ray
Conf., ed. R. J. Protheroe (Adelaide: Univ. Adelaide), 4
(In the text)
- Gehrels, N., et
al. 2005 [arXiv:astro-ph/0505630]
(In the text)
- Goldreich,
P., & Julian, W. H. 1969, ApJ, 157, 859 [NASA ADS] (In the text)
- Grimm, H. J.,
Gilfanov, M., & Sunyaev, R. 2002, A&A, 391, 923 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Halpern, J. P.,
& Ruderman, M. 1993, ApJ, 415, 286 [NASA ADS] [CrossRef] (In the text)
- Harding, A. K.,
& Ramaty, R. 1987, in Proc. 20th Int. Cosmic-Ray Conf. (Moscow:
Nauka), 2
(In the text)
- Ho, C. 1986, MNRAS, 221,
523 [NASA ADS] (In the text)
- Hurley, K., Boggs,
S. E., Smith, D. M., et al. 2005, Nature, 434, 1098 [NASA ADS] [CrossRef] (In the text)
- Jean, K.,
Knödlseder, J., Lonjou, V., et al. 2003, A&A, 407,
L55 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Johnson, W. N.,
& Haymes, R. C. 1973, ApJ, 184, 103 [NASA ADS] [CrossRef] (In the text)
- Kaspi, V. M.,
Roberts, M. S. E., & Harding, A. K. 2004, preprint
[arXiv:astro-ph/0402136]
(In the text)
- Kennel, C. F.,
& Coroniti, F. V. 1984, ApJ, 283, 694 [NASA ADS] [CrossRef] (In the text)
- Kluzniak, W.,
& Ruderman, M. 1998, ApJ, 508, L113 [NASA ADS] [CrossRef] (In the text)
-
Knödlseder, J., Lonjou, V., Jean, P., et al. 2003, A&A,
411, L457 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
-
Knödlseder, J., Jean, P., Lonjou, V., et al. 2005, A&A,
441, 513 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Kozlovsky,
B., Lingenfelter, R. E., & Ramaty, R. 1987, ApJ, 316, 801 [NASA ADS] [CrossRef] (In the text)
- LaRosa, T. N.,
Kassim, N. E., Lazio, T. J. W., & Hyman, S. D. 2000, AJ, 119,
207 [NASA ADS] [CrossRef] (In the text)
- LaRosa, T. N., et
al. 2005, preprint [arXiv:astro-ph/0505244]
(In the text)
- Leventhal,
M., MacCallum, C. J., & Stang, P. D. 1978, ApJ, 225, L11 [NASA ADS] [CrossRef] (In the text)
-
Lingenfelter, R. E., & Ramaty, R. 1979, in Proc. 16th Int.
Cosmic-Ray Conf., ed. S. Miyake (Tokyo: Tokyo Univ. Press), 1
(In the text)
-
Lingenfelter, R. E., & Ramaty, R. 1983, in Positron-Electron
Pairs in Astrophysics, ed. M. L. Burn, A. K. Harding, & R.
Ramaty, AIP Conf. Proc., 267
(In the text)
-
Lingenfelter, R. E., & Hueter, G. J. 1984, in High-Energy
Transients in Astrophysics, ed. S. E. Woosley, AIP Conf. Proc.,
558
(In the text)
- Lu, F., Wang, Q. D., &
Lang, C. 2003, AJ, 126, 319 [NASA ADS] [CrossRef] (In the text)
- Lyne, A. G.,
Manchester, R. N., Lorimer, D. R., et al. 1998, MNRAS, 295,
743 [NASA ADS] [CrossRef] (In the text)
-
Mastichiadis, A., Protheroe, R. J., & Stephen, S. A. 1991, in
Proc. 22d Int. Cosmic-Ray Conf., ed. D. O'Sullivan (Dublin: Dublin
Institute), 2
(In the text)
- Mayer-Hasselwander,
H. A., et al. 1998, A&A, 335, 161 [NASA ADS] (In the text)
- Muno, M. P., Baganoff,
F. K., Bautz, M. W., et al. 2003, ApJ, 589, 225 [NASA ADS] [CrossRef] (In the text)
- Muno, M. P., Baganoff,
F. K., Bautz, M. W., et al. 2004, ApJ, 613, 326 [NASA ADS] [CrossRef] (In the text)
- Parizot, E.,
Cassé, M., Lehoucq, R., & Paul, J. 2005, A&A, 432,
889 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Piran, T. 2004, Rev.
Mod. Phys., 76, 1143 [NASA ADS] [CrossRef] (In the text)
- Ramaty, R.,
Kozlovsky, B., & Lingenfelter, R. E. 1979, ApJS, 40, 487 [NASA ADS] [CrossRef] (In the text)
- Rees, M. J., &
Gunn, J. E. 1974, MNRAS, 167, 1 [NASA ADS] (In the text)
- Ruderman, M.
A., & Sutherland, P. 1975, ApJ, 196, 57 [NASA ADS] (In the text)
- Ruderman, M. A.
1991, ApJ, 366, 261 [NASA ADS] [CrossRef] (In the text)
- Stappers, B.
W., Gaensler, B. M., Kaspi, V. M., van der Klis, M., & Lewin,
W. H. G. 2003, Science, 299, 1372 [NASA ADS] [CrossRef] (In the text)
- Teegarden, B.
J., Watanabe, K., Jean, P., et al. 2005, ApJ, 621, 296 [NASA ADS] [CrossRef] (In the text)
- Thompson, C.
1994, Mon. N. Royal Astron. Soc., 270, 480 [NASA ADS] (In the text)
- Uchida, K. I.,
& Güsten 1995, A&A, 298, 473 [NASA ADS] (In the text)
- Usov, V. V. 1992,
Nature, 357, 472 [NASA ADS] [CrossRef] (In the text)
- Vedrenne, G.,
Roques, J.-P., Schönfelder, V., et al. 2003, A&A, 411,
L63 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Voss, R., & Tauris,
T. M. 2003, MNRAS, 342, 1169 [NASA ADS] [CrossRef] (In the text)
- Wang, Q. D.,
Gotthelf, E. V., & Lang, C. 2002a, Nature, 415, 148 [NASA ADS] [CrossRef]
- Wang, Q. D., Lu, F.,
& Lang, C. 2002b, ApJ, 581, 1148 [NASA ADS] [CrossRef] (In the text)
- Wang, W., Jiang, Z. J.,
& Cheng, K. S. 2005, MNRAS, 358, 263 [NASA ADS] [CrossRef] (In the text)
- Zhang, L., &
Cheng, K. S. 1997, ApJ, 487, 370 [NASA ADS] [CrossRef] (In the text)
- Zhang, L., &
Cheng, K. S. 2003, A&A, 398, 639 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2006