A&A 446, 1191-1204 (2006)
DOI: 10.1051/0004-6361:20053246
J.-L. Starck1,2 - Y. Moudden1 - P. Abrial1 - M. Nguyen3
1 - DAPNIA/SEDI-SAP, Service d'Astrophysique, CEA-Saclay,
91191 Gif-sur-Yvette Cedex, France
2 -
Department of Statistics, Sequoia Hall, 390 Serra Mall,
Stanford University, Stanford, CA 94305, USA
3 -
Laboratoire Traitement de l'Image et du Signal,
CNRS UMR 8051/ENSEA/Université de Cergy-Pontoise,
ENSEA, 6 avenue du ponceau, 95014 Cergy, France
Received 15 April 2005 / Accepted 8 September 2005
Abstract
We present in this paper new multiscale transforms on the sphere, namely the isotropic
undecimated wavelet transform, the pyramidal wavelet transform,
the ridgelet transform and the curvelet transform. All of these transforms can be inverted
i.e. we can exactly reconstruct the original data from its coefficients in either representation.
Several applications are described.
We show how these transforms can be used in denoising and especially in a Combined Filtering Method,
which uses both the wavelet and the curvelet transforms,
thus benefiting from the advantages of both transforms.
An application to component separation from multichannel data mapped to the sphere is also
described in which we take advantage of moving to a wavelet representation.
Key words: cosmic microwave background - methods: data analysis - methods: statistical
The most popular wavelet algorithm in astrophysical applications is the so-called "à trous algorithm''. It is an isotropic undecimated wavelet transform in which the scaling function used is a Box-Spline of order three. The isotropy of the wavelet function makes this decomposition optimal for the detection of isotropic objects. The non decimation makes the decomposition redundant (the number of coefficients in the decomposition is equal to the number of samples in the data multiplied by the number of scales) and allows us to avoid Gibbs aliasing after reconstruction in image restoration applications, as generally occurs with orthogonal or bi-orthogonal wavelet transforms. The choice of a B3-spline is motivated by the fact that we want an analyzing function close to a Gaussian, but verifying the dilation equation, which is required in order to have a fast transformation. One last property of this algorithm is to provide a very straightforward reconstruction. Indeed, the sum of all the wavelet scales and of the coarsest resolution image reproduces exactly the original image.
When analyzing data that contains anisotropic features, wavelets are no longer optimal and this has motivated the development of new multiscale decompositions such as the ridgelet and the curvelet transforms (Starck et al. 2002a; Donoho & Duncan 2000). In Starck et al. (Starck et al. 2004), it has been shown that the curvelet transform could be useful for the detection and the discrimination of non Gaussianity in CMB data. In this area, further insight will come from the analysis of full-sky data mapped to the sphere thus requiring the development of a curvelet transform on the sphere.
The goal of this paper is to extend existing 2D multiscale decompositions, namely the ridgelet transform, the curvelet transform and the isotropic wavelet transform, which work on flat images to multiscale methods on the sphere. In Sect. 2, we present a new isotropic wavelet transform on the sphere which has similar properties to the à trous algorithm and therefore should be very useful for data denoising and deconvolution. This algorithm is directly derived from the FFT-based wavelet transform proposed in Starck et al. (1994) for aperture synthesis image restoration, and is relatively close to the Freeden & Maier (Freeden & Schneider 1998) method, except that it features the same straightforward reconstruction as the à trous algorithm (i.e. the sum of the scales reproduces the original data). This new wavelet transform also can be easily extended to a pyramidal wavelet transform, hence with reduced redundancy, a possibility which may be very important for larger data sets such as expected from the future Planck-Surveyor experiment. In Sect. 3, we show how this new decomposition can be used to derive a curvelet transform on the sphere. Section 4 describes how these new transforms can be used in denoising applications and introduces the Combined Filtering Method, which allows us to filter data on the sphere using both the Wavelet and the Curvelet transforms. In Sect. 5, we show that the independent component analysis method wSMICA (Moudden et al. 2005), which was designed for 2D data, can be extended to data on the sphere.
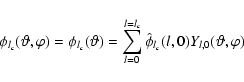 |
(1) |
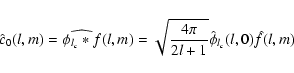 |
(2) |
A sequence of smoother approximations of f on
a dyadic resolution scale can be obtained using the scaling function
![]() as follows
as follows
| (3) |
| |
= | 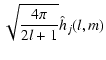 |
|
| = | 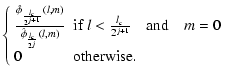 |
(4) |
![\begin{figure}
\par\includegraphics[width=12.8cm,height=5.2cm,bb=68 597 557 713,clip]{fig_sphere_filterbank.ps}\end{figure}](/articles/aa/full/2006/06/aa3246-05/Timg28.gif) |
Figure 1:
On the left, the scaling function
|
| Open with DEXTER | |
Given an axisymmetric wavelet function
![]() ,
we can derive in the same way a
high pass filter gj on each scale j:
,
we can derive in the same way a
high pass filter gj on each scale j:
| |
= | 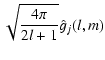 |
|
| = | 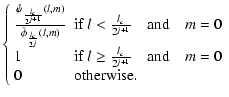 |
(5) |
Just as with the à trous algorithm, the wavelet coefficients can be defined as the difference between two consecutive resolutions,
![]() ,
which in fact corresponds to making the following specific choice for the wavelet function
,
which in fact corresponds to making the following specific choice for the wavelet function
![]() :
:
| (6) |
| |
= | 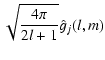 |
|
| = | 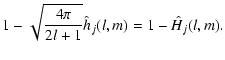 |
(7) |
Any function with a cut-off frequency is a possible candidate. We retained here
a B-spline function of order 3. It is very close to a Gaussian function and converges
rapidly to 0:
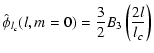 |
(8) |
In Fig. 1 the chosen scaling function derived from a B-spline of degree 3, and its resulting wavelet function, are plotted in frequency space.
The numerical algorithm for the undecimated wavelet transform on the sphere is:
 |
Figure 2:
On the left, the filter
|
| Open with DEXTER | |
 |
Figure 3: WMAP data and its wavelet transform on the sphere using five resolution levels (4 wavelet scales and the coarse scale). The sum of these five maps reproduces exactly the original data ( top left). Top: original data and the first wavelet scale. Middle: the second and third wavelet scales. Bottom: the fourth wavelet scale and the last smoothed array. |
| Open with DEXTER | |
If the wavelet is the difference between two resolutions, Step 5 in the above UWTS algorithm can be replaced by the following simple subtraction
wj+1 = cj - cj+1. In this case, the reconstruction of an image from its wavelet coefficients
![]() is straightforward:
is straightforward:
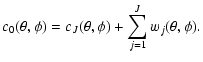 |
(9) |
| (10) |
| (11) |
 |
Figure 4: Backprojection of a wavelet coefficient at different scales. Each map is obtained by setting all but one of the wavelet coefficients to zero, and applying an inverse wavelet transform. Depending on the scale and the position of the non zero wavelet coefficient, the reconstructed image presents an isotropic feature with a given size. |
| Open with DEXTER | |
Figure 3 shows the WMAP data (top left) and its undecimated wavelet decomposition on the sphere using five resolution levels. Figures 3 middle left, middle right and bottom left show respectively the four wavelet scales. Figure 3 bottom right shows the last smoothed array. Figure 4 shows the backprojection of a wavelet coefficient at different scales and positions.
 |
Figure 5: WMAP data ( top left) and its pyramidal wavelet transform on the sphere using five resolution levels (4 wavelet scales and the coarse scale). The original map can be reconstructed exactly from the pyramidal wavelet coefficients. Top: original data and the first wavelet scale. Middle: the second and third wavelet scales. Bottom: the fourth wavelet scale and the last smoothed array. The number of pixels is divided by four at each resolution level, which can be helpful when the data set is large. |
| Open with DEXTER | |
In the previous algorithm, no downsampling is performed and each scale of the wavelet decomposition has the same number of pixels as the original data set. Therefore, the number of pixels in the decomposition is equal to the number of pixels in the data multiplied by the number of scales. For applications such as PLANCK data restoration, we may prefer to introduce some decimation in the decomposition so as to reduce the required memory size and the computation time. This can be done easily by using a specific property of the chosen scaling function. Indeed, since we are considering here a scaling function with an initial cut-off lc in spherical harmonic multipole number l, and since the actual cut-off is reduced by a factor of two at each step, the number of significant spherical harmonic coefficients is then reduced by a factor of four after each convolution with the low pass filter h. Therefore, we need fewer pixels in the direct space when we compute the inverse spherical harmonic transform. Using the Healpix pixelization scheme (Górski et al. 2002), this can be done easily by dividing by 2 the nside parameter when resorting to the inverse spherical harmonic transform routine.
Figure 5 shows WMAP data (top left) and its pyramidal wavelet transform using five scales. As the scale number increases (i.e. the resolution decreases), the pixel size becomes larger. Figures 5 top right, middle left, middle right and bottom left show respectively the four wavelet scales. Figure 5 bottom right shows the last smoothed array.
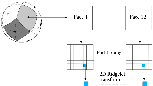 |
Figure 6: Flowgraph of the ridgelet transform on the sphere. |
| Open with DEXTER | |
The 2D curvelet transform, proposed in Donoho & Duncan (2000), Starck et al. (2002a, 2003a) enables the
directional analysis of an image in different scales.
The fundamental property of the curvelet transform is to
analyze the data with functions of length of about
2-j/2 for the jth sub-band
[2j, 2j+1] of the
two dimensional wavelet transform.
Following the implementation described in Starck et al. (2002a) and Starck et al. (2003a), the data first undergoes an isotropic undecimated wavelet transform (i.e. à trous algorithm). Each scale j is then decomposed into smoothly overlapping blocks of
side-length Bj pixels in such a way that the overlap between two
vertically adjacent blocks is a rectangular array of size
![]() .
Finally, the ridgelet transform (Candès & Donoho 1999) is applied on each individual block which amounts to applying a 1-dimensional wavelet transform to the slices of its Radon transform. More details on the implementation of the digital curvelet transform
can be found in Starck et al. (2002a, 2003a).
It has been shown that the curvelet transform could be very useful for the
detection and the discrimination of sources of non-Gaussianity in CMB (Starck et al. 2003b).
The curvelet transform is also redundant, with a redundancy factor of 16J+1 whenever J scales
are employed. Its complexity scales like that of the ridgelet transform that is as
.
Finally, the ridgelet transform (Candès & Donoho 1999) is applied on each individual block which amounts to applying a 1-dimensional wavelet transform to the slices of its Radon transform. More details on the implementation of the digital curvelet transform
can be found in Starck et al. (2002a, 2003a).
It has been shown that the curvelet transform could be very useful for the
detection and the discrimination of sources of non-Gaussianity in CMB (Starck et al. 2003b).
The curvelet transform is also redundant, with a redundancy factor of 16J+1 whenever J scales
are employed. Its complexity scales like that of the ridgelet transform that is as
![]() .
This method is best for the detection of anisotropic structures and smooth curves and edges of different lengths.
.
This method is best for the detection of anisotropic structures and smooth curves and edges of different lengths.
Figure 6 shows the flowgraph of the ridgelet transform on the sphere and Fig. 7 shows the backprojection of a ridgelet coefficient at different scales and orientations.
 |
Figure 7: Backprojection of a ridgelet coefficient at different scales and orientations. Each map is obtained by setting all but one of the ridgelet coefficients to zero, and applying an inverse ridgelet transform. Depending on the scale and the position of the non zero ridgelet coefficient, the reconstructed image presents a feature with a given width and a given orientation. |
| Open with DEXTER | |
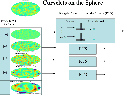 |
Figure 8: Flowgraph of the curvelet transform on the sphere. |
| Open with DEXTER | |
The CTS is very redundant, which may be a problem in handling huge data sets such as the future PLANCK data. The redundancy can be reduced by substituting, in the curvelet transform algorithm, the pyramidal wavelet transform to the undecimated wavelet transform. The second step which consists in applying the ridgelet transform on the wavelet scale is unchanged. The pyramidal curvelet transform algorithm is:
| (14) |
![\begin{figure}
\par\includegraphics[width=10.5cm,height=9cm,clip]{fig_back_cur_sphere.ps}\end{figure}](/articles/aa/full/2006/06/aa3246-05/Timg85.gif) |
Figure 9: Backprojection of a curvelet coefficient at different scales and orientations. Each map is obtained by setting all but one of the curvelet coefficients to zero, and applying an inverse curvelet transform. Depending on the scale and the position of the non zero curvelet coefficient, the reconstructed image presents a feature with a given width, length and orientation. |
| Open with DEXTER | |
 |
Figure 10: Denoising. Upper left and right: simulated synchrotron image and same image with an additive Gaussian noise (i.e. simulated data). Middle: pyramidal wavelet filtering and residual. Bottom: pyramidal curvelet filtering and residual. On such data, displaying very anisotropic features, the residual with curvelet denoising is cleaner than with the wavelet denoising. |
| Open with DEXTER | |
Figure 10 describes the setting and the results of a simulated denoising experiment:
upper left, the original simulated map of the synchrotron emission (renormalized between 0 and 255);
upper right, the same image plus additive Gaussian noise (![]() ); middle, the pyramidal wavelet
filtered image and the residual (i.e. noisy data minus filtered data); bottom, the
pyramidal curvelet transform filtered image and the residual. A
); middle, the pyramidal wavelet
filtered image and the residual (i.e. noisy data minus filtered data); bottom, the
pyramidal curvelet transform filtered image and the residual. A
![]() detection threshold
was used in both cases. On such data, displaying very anisotropic features, using curvelets produces
better results than the wavelets.
detection threshold
was used in both cases. On such data, displaying very anisotropic features, using curvelets produces
better results than the wavelets.
| |
Figure 11: Denoising. Combined Filtering Method (pyramidal wavelet and pyramidal curvelet) and residual. |
| Open with DEXTER | |
 |
Figure 12: Combined Filtering Method, face 6 in the Healpix representation of the image shown in Fig. 11. From top to bottom and left to right, respectively the a) original image face, b) the noisy image, c) the combined filtered image, d) the combined filtering residual, e) the wavelet filtering residual and f) the curvelet filtering residual. |
| Open with DEXTER | |
The residual images for both the wavelet and curvelet transforms shown in Fig. 10 show that wavelets do not restore long features with high fidelity while curvelets are seriously challenged by isotropic or small features. Each transform has its own area of expertise and this complementarity is of great potential. The Combined Filtering Method (CFM) (Starck et al. 2001) allows us to benefit from the advantages of both transforms. This iterative method detects the significant coefficients in both the wavelet domain and the curvelet domain and guarantees that the reconstructed map will take into account any pattern detected as significant by either of the transforms. A full description of the algorithm is given in Appendix A. Figure 11 shows the CFM denoised image and its residual. Figure 12 shows one face (face 6) of the following Healpix images: upper left, original image; upper right, noisy image; middle left, restored image after denoising by the combined transform; middle right, the residual; bottom left and right, the residual using respectively the curvelet and the wavelet denoising method. The results are reported in Table 1. The residual is much better when the combined filtering is applied, and no feature can be detected any longer by eye in the residual. Neither with the wavelet filtering nor with the curvelet filtering could such a clean residual be obtained.
Blind Source Separation (BSS) is a problem that occurs in multi-dimensional data processing.
The goal is to recover unobserved signals, images or sources S from
mixtures X of these sources observed typically at the output of an array of m sensors.
A simple mixture model would be linear and instantaneous with additive noise as in:
Algorithms for blind component separation and mixing matrix estimation depend on the a priori model used for the probability distributions of the sources (Cardoso 2001) although rather coarse assumptions can be made (Cardoso 1998; Hyvärinen et al. 2001). In a first set of techniques, source separation is achieved in a noise-less setting, based on the non-Gaussianity of all but possibly one of the components. Most mainstream ICA techniques belong to this category: JADE (Cardoso 1999), FastICA, Infomax (Hyvärinen et al. 2001). In a second set of blind techniques, the components are modeled as Gaussian processes and, in a given representation (Fourier, wavelet, etc.), separation requires that the sources have diverse, i.e. non proportional, variance profiles. The Spectral Matching ICA method (SMICA) (Delabrouille et al. 2003; Moudden et al. 2005) considers in this sense the case of mixed stationary Gaussian components in a noisy context: moving to a Fourier representation, the point is that colored components can be separated based on the diversity of their power spectra.
Table 1: Table of error standard deviations and SNR values after filtering the synchrotron noisy map (Gaussian white noise - sigma = 5 ) by the wavelet, the curvelet and the combined filtering method. Images are available at http://jstarck.free.fr/mrs.html.
SMICA, which was designed to address some of the general problems raised by Cosmic Microwave Background data analysis, has already shown significant success for CMB spectral estimation in multidetector experiments (Delabrouille et al. 2003; Patanchon et al. 2004). However, SMICA suffers from the non locality of the Fourier transform which has undesired effects when dealing with non-stationary components or noise, or with incomplete data maps. The latter is a common issue in astrophysical data analysis: either the instrument scanned only a fraction of the sky or some regions of the sky were masked due to localized strong astrophysical sources of contamination (compact radio-sources or galaxies, strong emitting regions in the galactic plane). A simple way to overcome these effects is to move instead to a wavelet representation so as to benefit from the localization property of wavelet filters, which leads to wSMICA (Moudden et al. 2005). The wSMICA method uses an undecimated à trous algorithm with the cubic box-spline (Starck & Murtagh 2002) as the scaling function. This transform has several favorable properties for astrophysical data analysis. In particular, it is a shift invariant transform, the wavelet coefficient maps on each scale are the same size as the initial image, and the wavelet and scaling functions have small compact supports in the initial representation. All of these allow missing patches in the data maps to be handled easily.
 |
Figure 13:
Left: zero mean templates for CMB (
|
| Open with DEXTER | |
Table 2: Entries of A, the mixing matrix used in our simulations.
Table 3: Nominal noise standard deviations in the six channels of the Planck HFI.
Extending SMICA to deal with multichannel data mapped to the sphere is straightforward (Delabrouille et al. 2003). The idea is simply to substitute the spherical harmonics transform for the Fourier transform used in the SMICA method. Then, data covariance matrices are estimated in this representation over intervals in multipole number l. However SMICA on spherical maps still suffers from the non locality of the spherical harmonics transform whenever the data to be processed is non stationary, incomplete, or partly masked.Moving to a wavelet representation allows one to overcome these effects: wSMICA can be easily implemented for data mapped to the sphere by substituting the UWTS described in Sect. 2 to the undecimated à trous algorithm used in the previous section. In the linear mixture model (15), X now stands for an array of observed spherical maps, S is now an array of spherical source maps to be recovered and N is an array of spherical noise maps. The mixing matrix A achieves a pixelwise linear mixing of the source maps. Applying the above UWTS on both sides of (15) does not affect the mixing matrix A so that, assuming independent source and noise processes, the covariance matrix of the observations at scale j is again structured as in (16). Source separation follows from minimizing the covariance matching criterion (23) in this spherical wavelet representation. A full description is given in Appendix B.
The simulated CMB, galactic dust and Sunyaev Zel'dovich (SZ) maps used, shown on the left-hand side of Fig. 13, were obtained as described in Delabrouille et al. (2003). The problem of instrumental point spread functions is not addressed here, and all maps are assumed to have the same resolution. The high level foreground emission from the galactic plane region was removed using the Kp2 mask from the WMAP team website![]() . These three incomplete maps were mixed using the matrix in Table 2, in order to simulate observations in the six channels of the Planck high frequency instrument (HFI).
. These three incomplete maps were mixed using the matrix in Table 2, in order to simulate observations in the six channels of the Planck high frequency instrument (HFI).
Gaussian instrumental noise was added in each channel according to model (15). The relative noise standard deviations between channels were set according to the nominal values of the Planck HFI given in Table 3.
The synthetic observations were decomposed into six scales using the isotropic UWTS and wSMICA was used to obtain estimates of the mixing matrix and of the initial source templates. The resulting component maps estimated using wSMICA, for nominal noise levels, are shown on the right-hand side of Fig. 13 where the quality of the reconstruction can be visually assessed by comparison to the initial components. The component separation was also performed with SMICA based on Fourier statistics computed in the same six dyadic bands imposed by our choice of wavelet
transform, and with JADE. In Fig. 14, the performances of SMICA, wSMICA and JADE are compared in the particular case of CMB map estimation, in terms of the relative standard deviation of the reconstruction error, MQE, defined by
![\begin{figure}
\par\includegraphics[width=8cm,clip]{resultats_aa}\end{figure}](/articles/aa/full/2006/06/aa3246-05/Timg114.gif) |
Figure 14: Relative reconstruction error defined by (17) of the CMB component map using SMICA, wSMICA and JADE as a function of the instrumental noise level in dB relative to the nominal values in Table 3. The zero dB noise level corresponds to the expected noise in the future PLANCK mission. |
| Open with DEXTER | |
We have introduced new multiscale decompositions on the sphere, the wavelet transform, the ridgelet transform and the curvelet transform. It was shown in Starck et al. (2004) that combining the statistics of wavelet coefficients and curvelet coefficients of flat maps leads to a powerful analysis of the non-Gaussianity in the CMB. Using the new decompositions proposed here, it is now possible to perform such a study on data mapped to the sphere such as from the WMAP or PLANCK experiments. For the denoising application, we have shown that the Combined Filtering Method allows us to significantly improve the result compared to a standard hard thresholding in a given transformation. Using the isotropic UWTS and statistics in this representation also allows us to properly treat incomplete or non-stationary data on the sphere which cannot be done in the non-local Fourier representation. This is clearly illustrated by the results obtained with wSMICA which achieves component separation in the wavelet domain thus reducing the negative impact that gaps have on the performance of source separation using the initial SMICA algorithm in the spherical harmonics representation. Further results are available at http://jstarck.free.fr/mrs.hmtl
as well as information about the IDL code for the described transformations based on the Healpix package (Górski et al. 2002).
Acknowledgements
We wish to thank David Donoho, Jacques Delabrouille, Jean-François Cardoso and Vicent Martinez for useful discussions.
In general, suppose that we are given K linear transforms
![]() and let
and let ![]() be the coefficient sequence of an
object x after applying the transform Tk, i.e.
be the coefficient sequence of an
object x after applying the transform Tk, i.e.
![]() .
We will assume that for each transform Tk, a
reconstruction rule is available that we will denote by T-1k, although this is
clearly an abuse of notation. T will denote the block
diagonal matrix with Tk as building blocks and
.
We will assume that for each transform Tk, a
reconstruction rule is available that we will denote by T-1k, although this is
clearly an abuse of notation. T will denote the block
diagonal matrix with Tk as building blocks and ![]() the
amalgamation of the
the
amalgamation of the ![]() .
.
A hard thresholding rule associated with the transform Tk synthesizes
an estimate
![]() via the formula
via the formula
Given data y of the form
![]() ,
where s is the image
we wish to recover and z is standard white noise, we propose to solve
the following optimization problem (Starck et al. 2001):
,
where s is the image
we wish to recover and z is standard white noise, we propose to solve
the following optimization problem (Starck et al. 2001):
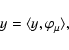
We propose to solve (19) using the method of hybrid steepest descent (HSD) (Yamada 2001). HSD consists of building the sequence
| (21) |
The combined filtering algorithm is:
A detailed derivation of SMICA and wSMICA can be found in Delabrouille et al. (2003) and Moudden et al. (2005). Details are given here showing how the Isotropic Undecimated Wavelet Transform on the Sphere described in Sect. 2 above can be used to extend SMICA to work in the wavelet domain on spherical data maps. We will refer to this extension as wSMICA-S.
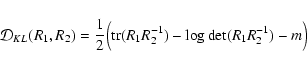 |
(24) |
In dealing with non stationary data or incomplete data, an
attractive feature of wavelet filters over the spherical harmonic transform is
that they are well localized in the initial representation. Provided the wavelet filter
response on scale j is short enough compared to
data size and gap widths, most of the samples in the filtered
signal will then be unaffected by the presence of gaps.
Using exclusively these samples yields an estimated covariance matrix
![]() which is not biased by the missing data. Writing the wavelet decomposition on J scales of X as
which is not biased by the missing data. Writing the wavelet decomposition on J scales of X as
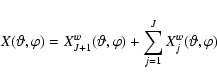 |
(25) |
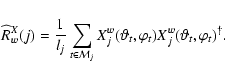 |
(26) |
As a result of applying wSMICA-S, power densities in each scale are estimated
for the sources and detector noise along with the estimated mixing matrix. These are
used in reconstructing the source maps via Wiener filtering in
each scale: a coefficient
![]() is used to reconstruct the maps according to
is used to reconstruct the maps according to