A&A 446, L13-L16 (2006)
DOI: 10.1051/0004-6361:200500226

Reviving Dead Zones in accretion disks by Rossby vortices at their boundaries

P. Varnière1,2 - M. Tagger3


1 - Department of Physics & Astronomy, Rochester University, Rochester NY 14627-0171, USA
2 - LAOG, Université J. Fourier, UMR 5571, France
3 - Service d'Astrophysique (UMR Astroparticules et cosmologie) CEA/Saclay, 91191 Gif-sur-Yvette, France

Received 10 September 2005 / Accepted 13 December 2005

Abstract
Models of the accretion disks of Young Stellar Objects show that they should not be ionized at a few AU from the star, and thus not subject to the MHD turbulence believed to cause accretion. This has been suggested to create a "Dead Zone'' where accretion remains unexplained. Here we show that the existence of the Dead Zone self-consistently creates a density profile favorable to the Rossby Wave Instability of Lovelace et al. (1999, ApJ, 513, 805). This instability will create and sustain Rossby vortices in the disk which could lead to enhanced planet formation.

Key words: accretion disks - instabilities - planetary systems: formation

1 Introduction

The existence of a Dead Zone in the accretion disk of Young Stellar Objects (YSO) was first proposed by Gammie (1996); he found that the inner region of the disk is ionized by collisions, and the outer region by cosmic rays. On the other hand there exists an intermediate region, dubbed a Dead Zone, where the ionization remains so low that the gas is not coupled to magnetic fields. This creates a problem since accretion is widely believed to result from MHD instabilities, such as the Magneto-Rotational Instability (Balbus & Hawley 1991). The Dead Zone should thus inhibit accretion in a significant portion of the disk. More recent studies (for example D'Alessio et al. 1998; Reyes-Ruiz 2001; Matsumura & Pudritz 2005) have put constraints on the position and extent of the Dead Zone depending on the heating mechanisms and disk properties, and related them to observations. Various estimates have been given for the extent of the Dead Zone, which is typically found to range between 1 and 5 AU from the star.

In the present paper we discuss the consequences on the disk dynamics of the presence of such a zone, where the transport of matter and angular momentum (which we will represent by a turbulent viscosity) is significantly lower than elsewhere in the disk. In particular we show that an important role could be played by the Rossby Wave Instability (RWI), introduced by Lovelace et al. (1999) as a possible means of transporting angular momentum in non-magnetized disks. This instability requires locally an extremum of a certain quantity, which we will discuss below.

Here we show that the existence of a Dead Zone naturally generates such an extremum at its boundaries. The RWI naturally generates Rossby vortices. We relate this to the observation by several authors (Barge & Sommeria 1995; Chavanis 2000; Johansen et al. 2004), that vortices can speed up planet formation, by allowing planetesimals to accumulate in their center without following the viscous accretion. As shown in Barge & Sommeria (1995), this might solve a problem encountered in present views of planet formation, where planetesimals accrete to the central star on a viscous time scale, before they have had time to form a planet. We also show that the instability extends across the Dead Zone as spiral waves, which can maintain a significant accretion rate despite the absence of locally generated turbulence.

2 Rossby waves instability

In 1999 Lovelace et al. (see also Li et al. 2000, 2001), elaborating on previous work by Lovelace & Hohlfeld (1978), found a non-axisymmetric instability (Rossby Wave Instability, or RWI) occurring in unmagnetized disks, when there is a local extremum in the radial profile of a quantity $\cal L$.

$\displaystyle {\cal L} = {\cal F}(r) S^{2/\Gamma}(r) = \frac{\Sigma \Omega}{\kappa^{2}} \frac{p}{\Sigma^{\Gamma}}\cdot$     (1)

Where $\Sigma$ is the surface density, $\Omega$ the rotation frequency, $\kappa$ the epicyclic frequency and $\Gamma$ is the adiabatic index. With $\Gamma =1$, $\cal L$ reduces to the inverse of the vortensity responsible for the corotation resonance of the Papaloizou-Pringle instability (Papaloizou & Pringle 1985; Goldreich et al. 1986; Papaloizou & Lin 1989). Numerical simulations by Li et al. (2000) confirmed that a bump or jump in the surface density $\Sigma$ or the pressure p can cause the instability, and studied its consequences. Here we show how such a bump in the radial density profile can naturally result from the presence of a Dead Zone in the disk of a young stellar object (YSO).

3 Numerical model of the Dead Zone/ instability criterion

3.1 Modeling the Dead Zone

The Dead Zone is a limited region in the disk where the gas is not well coupled with the magnetic field, because the ionization is too low. If we make the assumption, as in Gammie (1996), that turbulent accretion is due to MHD instabilities such as the Magneto-Rotational Instability (MRI, Balbus & Hawley 1991), we can model that region by a drop of the turbulent (MRI-generated) transport.

We represent accretion in the disk by a turbulent viscosity (Shakura & Sunyaev 1973) which drops in the region of the dead zone, where MHD instabilities are inactive. We include this viscosity profile in the 2D non-linear hydrodynamic code developed by Masset (2002), Masset & Papaloizou (2003). This is an Eulerian polar grid code with a staggered mesh and an artificial second order viscous pressure to stabilize the shocks (see also Stone & Norman 1992). The code uses the FARGO algorithm which significantly accelerates computations in a differentially rotating disk. The simulation are done using standard boundary conditions, namely accretion is allowed through the inner boundary by using open boundary conditions and we assume the disk to be larger by allowing mass to flow in from the outer boundary. An axisymmetric, steady-state solution, which implies $\nu\Sigma= \rm const$., would give an artificially huge overdensity in the Dead Zone. Since the instability would cancel this condition, we rather start from a simple power-law density profile that is allowed to evolve self-consistently during the simulations. Reaching a true steady state in these conditions would require prohibitive computation time and we rather concentrate in this paper on the development of the instability and a discussion of its consequences.

The runs we present here are done with a resolution of Nr = 150 and $N_\theta = 450$ grid points. We performed two types of simulations: in the first one, which allows only a limited resolution, the physical size of the grid spans radii between .25 AU and 10 AU, and the Dead Zone extends from 1 to 5 AU. In the second one, for higher resolution, and since we are mainly interested in what happens at the boundaries of the Dead Zone, we use a grid spanning from .25 to 4 AU, with a Dead Zone extending from .5 to 1 AU.

In both cases the disk aspect ratio H/r = 0.04 where H, the vertical scale height of the disk, is uniform and constant. The sound speed of the gas is set from the disk aspect ratio. The initial density profile is $\Sigma(r) = 10^{-5} \left({r / R_{{\rm min}}}\right)^{-1}$ where $R_{{\rm min}}$ is the radius of the inner edge of the grid. Matter is allowed to flow in from the outer boundary, by accretion from the outer regions of the disk not included in the simulation.

In order to model the Dead Zone we use an arctangent drop in the radial viscosity profile:

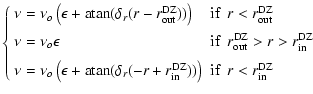$\displaystyle \left\{ \begin{array}{lll} \nu = \nu_o \left( \epsilon + {\rm ata... ...in}}))\right) &\mbox{if}& r<r^{{\rm DZ}}_{{\rm in}}\nonumber \end{array}\right.$      

where $\epsilon$ represents a residual viscosity in the Dead Zone, and  $\delta_{r}$ defines the steepness of the viscosity profile at the edges of the Dead Zone. All the runs presented here are done with $\epsilon$ and  $\delta_{r}$ equal to 10-5 and 50 respectively, giving the profiles shown in Fig. 1. We did runs with $\epsilon$ varying from 10-2 to 10-5 to confirm the behaviour with a less steep Dead-Zone.
  \begin{figure} \par\includegraphics[width=8.8cm,clip]{alpha_profile3.eps} \end{figure} Figure 1: Profile of the $\alpha $-viscosity implemented to represent a Dead Zone between 1 and 5 AU with $(\epsilon , \delta _{r}) = (10^{-5}, 50)$.
Open with DEXTER

3.2 Evolution of the RWI criterion

With the prescribed viscosity profile, viscous accretion occurs in the outer region of the simulation but is far slower in the Dead Zone. As a result, gas accumulates near the outer edge of this zone, and naturally produces in less than a hundred orbits at that radius the extremum of $\cal L$ required by the RWI (see Fig. 2 of the low resolution run) If we now look at the inner edge of the Dead Zone, the opposite happens, namely the matter in the Dead-Zone is accreted slower than that in the inner region, therefore creating a dip inward from the Dead-Zone, also producing a favorable profile of $\cal L$


  \begin{figure} \par\mbox{\epsfig{file=density_1_5AU_accretion.eps,width=5cm}\epsfig{file=RWI_5AU.eps,width=5cm} } \end{figure} Figure 2: Left: plot of $\cal L$ a t=0 and once the vortices have formed. Right: plot of the density in the disk at t = 100 years, with the velocity field superimposed. The velocity field shows the vortex at 5 AU. There is also one at 1 AU, not visible here.
Open with DEXTER

3.3 Formation of vortices

Once the threshold for the instability is reached we see Rossby vortices developing in the disk (there was still enough of the initial random perturbation to seed the instability).

  \begin{figure} \par\includegraphics[width=8.8cm,clip]{out1_disk_several} \end{figure} Figure 3: Zoom of the first 2 inner AU of the simulation at t=0, 100, 200, 300 years, showing the density. One sees three vortices forming, later evolving to two vortices, near the outer edge of the Dead Zone.
Open with DEXTER

Figure 3 shows a surface density plot of the disk at t=0,100,200,300 years. We first see three vortices forming, but later only two of them surviving. These vortices are anticyclonic, and it is known (Barge & Sommeria 1995; Chavanis 2000; de la Fuente Marcos & Barge 2001; Johansen et al. 2004) that this can cause an accumulation of dust and enhanced formation of planetesimals. Barge & Sommeria (1995), computed the amount of mass captured by a vortex depending on its distance to the star. Using our Dead Zone extending from 1 to 5 AU we see that the vortex at the inner edge of the Dead Zone will be able to capture $0.6~M_{\oplus}$ in 500 years (=500 orbits). From the same calculation the vortex at the outer edge of the Dead Zone will accumulate $16~M_{\oplus}$ in $6\times 10^{3}$ years (=500 orbits). Those values, obtained in the case of a standard model nebula (Cuzzi et al. 1993) and using dust simulations, are given here as an indication for the timescale/captured mass to expect from such vortices.

3.4 Accretion through the Dead Zone


  \begin{figure} \par\includegraphics[width=8cm,clip]{accretion_density_out5_2} \end{figure} Figure 4: This figure shows the density profile at t=100 (formation of the vortices) and 400 years: this shows that the spiral waves, seen in Fig. 2 to extend from the vortices, cause accretion across the Dead Zone.
Open with DEXTER

These simulations do not allow to follow the evolution of the vortices with enough precision. Therefore we focus our simulation box on either of the boundaries by putting it at the radius of r = 1 AU. This allows us to have a much better resolution at the location of the vortices. Figure 4 shows the evolution of the density profile in the region around the outer edge of the Dead Zone between t=100 years, when the RWI appears, and t=400 years. This shows that accretion proceeds across the Dead Zone, despite the low viscosity. This can be attributed to the spiral waves generated by the vortices, and seen in Fig. 3 to extend across the Dead Zone. The generation of these waves corresponds to an exchange of energy and angular momentum between the vortices and the gas of the Dead Zone. We did not attempt to quantify this accretion, since this would require reaching a steady state which we can not obtain reliably with our present simulations, for a number of reasons: first, because of the 2D nature of the code we use; second, because on longer timescales the dynamics of the vortices will be influenced by the accumulated dust, and a two-phase code following separately both gas and dust would be required; finally, we also note that even a weak self-gravity would significantly enhance the coupling between the vortices and the spiral waves.

4 Conclusion

Although the Dead Zone is not turbulent, we have shown that it naturally results in conditions supporting the development of the Rossby Wave Instability. The differential mass accretion creates a high density bump/ring at the boundaries of the Dead Zone and trigger the RWI. The vortices, in turn, survive long enough to be significant for dust accretion and enhanced planet formation. They also generate spiral waves, resulting in significant accretion across the Dead Zone.

Further studies will be needed to quantify these effects. This will require, in particular, a gas/dust/planetesimal code able to run on long time scales, and probably also the inclusion of self-gravity.

Acknowledgements
P.V. is supported by NSF grants AST-9702484, AST-0098442, NASA grant NAG5-8428, HST grant, DOE grant DE-FG02-00ER54600, the Laboratory for Laser Energetics.

We thanks F. Masset for the code and fruitful discussion. P.V. thanks P. Barge and the OAMP for the month long stay at Marseille where part of this work was done.

References

 
Copyright ESO 2006