A&A 446, L5-L8 (2006)
DOI: 10.1051/0004-6361:200500225
A new method for determining mass-to-light ratios of nearly face-on spiral
galaxies
TaoHu
1 -
Qiu-He Peng1,2,3 -
Ying-He Zhao1
1 - Department of Astronomy, Nanjing University, Nanjing 210093, PR China
2 - Joint Astrophysics Center of Chinese Academy of Science-Peking
University, Beijing 100871, PR China
3 - The Open Laboratory of Cosmic Ray and High Energy
Astrophysics, Chinese Academy of Science
Received 12 August 2005 / Accepted 8 December 2005
Abstract
Aims. This letter gives a new method for determining mass-to-light ratios of nearly face-on spiral galaxies.
Methods. The method is based on the effective thickness of the galactic disk, the distribution of the vertical velocity dispersion, and the surface brightness of a spiral galaxy.
Results. As examples, the results of the determination of NGC 1566 and NGC 5247 in B-band are presented, and their mass-to-light ratios are
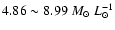 and
and
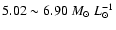 respective.
respective.
Key words: galaxy: disk - galaxies: fundamental parameters - galaxies: spiral -
galaxies: structure - galaxies: individual: NGC 1566, NGC 5247
1 Introduction
Van der Kruit & Searle (1981a,b) investigated surface
photometry of edge-on spiral galaxies, they fitted the z distribution of light at each r of the disk by a model of a
locally isothermal sheet. Let 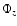 denote the gravitational
force in the z-direction as a function of z,
denote the gravitational
force in the z-direction as a function of z, 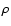 the space
density of matter and
the space
density of matter and
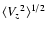 the
dispersion in the velocities in the z-direction. From the case
Poisson's and Liouville's equations, it could be reduced to
the
dispersion in the velocities in the z-direction. From the case
Poisson's and Liouville's equations, it could be reduced to
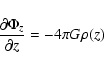 |
(1) |
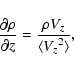 |
(2) |
with
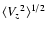 independent of z-direction,
and the solution is (Camm 1950; Spitzer 1942)
independent of z-direction,
and the solution is (Camm 1950; Spitzer 1942)
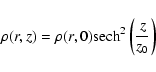 |
(3) |
with
![\begin{displaymath}z_0=\frac{{\langle
V_z}^2\rangle ^{1/2}}{[2\pi G\rho (r,0)]^{1/2}},
\end{displaymath}](/articles/aa/full/2006/05/aahh121/img18.gif) |
(4) |
z0 is effective thickness of a galactic disk (H=z0/2 is
scale height of a galactic disk).
By integrating Eq. (3), we have the total surface density of
disk
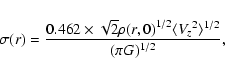 |
(5) |
so Eq. (4) can be reduced to
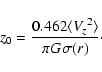 |
(6) |
Van der Kruit & Freeman (1986) pointed out that the
mass-to-light ratio (
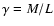 )
of old disk is approximately
constant, in good approximation independent of position along the
radius. When a spiral galaxy is nearly face-on, the total surface
density can be taken as
)
of old disk is approximately
constant, in good approximation independent of position along the
radius. When a spiral galaxy is nearly face-on, the total surface
density can be taken as
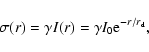 |
(7) |
with I(r) the surface brightness and 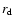 the scale
length of galactic disk. Therefore, from Eqs. (6) and (7), we can find
the scale
length of galactic disk. Therefore, from Eqs. (6) and (7), we can find
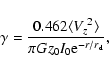 |
(8) |
if we obtain the parameters z0, Vz, I0, and  ,
mass-to-light ratio
,
mass-to-light ratio 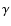 could be calculated by Eq. (8).
could be calculated by Eq. (8).
Van der Kruit & Searle (1981a) proposed a method to determine
the scale heights of edge-on disk galaxies. It is based on
measuring surface brightness that is distributed with exponential
function of radius. A method for determining the scale heights of
spiral galaxies observed non-edge-on was proposed by Peng (1988)
on the basis of the asymptotic expression of the perturbed
gravitational potential. Zhao et al. (2004)
re-investigate the method based on the rigorous expression of the
perturbed gravitational potential. We have already obtained
perturbed gravitational potential for such a logarithmic density
disturbance via the Poisson's equation for the galactic disk with
finite thickness (Peng et al. 1978, 1979), the perturbed
gravitational potential may be expressed
where
here, 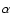 is thickness factor of a spiral galactic disk,
is thickness factor of a spiral galactic disk,
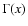 and Jm(x) are the usual Gamma and Bessel functions,
respective. For an infinitely thin disk (
and Jm(x) are the usual Gamma and Bessel functions,
respective. For an infinitely thin disk (
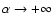 ), the Eq. (9) has a simplified form as same as the
expression given by Kalnajs (1971)
), the Eq. (9) has a simplified form as same as the
expression given by Kalnajs (1971)
The ratio (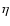 )
of the amplitude for the
perturbed gravitational potential for a disk galaxy with finite
thickness to that of an infinitely thin disk at the forbidden
radius r0 is (Zhao et al. 2004)
)
of the amplitude for the
perturbed gravitational potential for a disk galaxy with finite
thickness to that of an infinitely thin disk at the forbidden
radius r0 is (Zhao et al. 2004)
![\begin{displaymath}\eta=\frac{V_\alpha(\alpha,m,\Lambda,r_0)}{V_{\alpha\rightarr...
...,r_0)}={\rm Re}[g(\Lambda,m;\alpha
r_0)]\sqrt{m^2+\Lambda^2},
\end{displaymath}](/articles/aa/full/2006/05/aahh121/img39.gif) |
(12) |
it can be obtained the effective thickness (
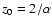 )
through Eq. (12) by determining the winding parameter (
)
through Eq. (12) by determining the winding parameter (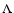 ), the number of spiral arms (m), and the forbidden
radius (A spiral arm can not extend to the forbidden region with
radius r0 to the galactic center.).
), the number of spiral arms (m), and the forbidden
radius (A spiral arm can not extend to the forbidden region with
radius r0 to the galactic center.). 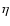 was assumed to be 0.5 based on the comparison between z0 and r0 which have
been observed and measured for Milky Way and Andromeda Nebula (M 31). In fact, we use the same values of the parameters of 71 spiral galaxies given by Ma et al. (1998) to calculate the factor
was assumed to be 0.5 based on the comparison between z0 and r0 which have
been observed and measured for Milky Way and Andromeda Nebula (M 31). In fact, we use the same values of the parameters of 71 spiral galaxies given by Ma et al. (1998) to calculate the factor 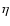 by Eq. (12), and obtain the average
by Eq. (12), and obtain the average
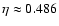 .
In this paper, we take the average value of 0.5 and 0.486, i.e.,
.
In this paper, we take the average value of 0.5 and 0.486, i.e.,
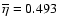 .
.
It is well known that spiral arms can be represented by equiangular spirals
on the galactic disk. In Fig. 1, we determine the inclinations
and the winding parameters of the spiral galaxies NGC 1566 and
NGC 5247 (B-band) by fitting the curves of spiral arms in their
images, i.e., it is the optimum inclination of a spiral galaxy,
which is corresponding to the best fitted spiral curves.
![\begin{figure}
\par\includegraphics[width=3cm,clip]{Hh121_f1a.eps}\hspace*{1.3cm}
\includegraphics[width=3cm,clip]{Hh121_f1b.eps}
\end{figure}](/articles/aa/full/2006/05/aahh121/Timg43.gif) |
Figure 1:
Images of NGC 1566 and NGC 5247 in B-band with superposed fitted curves of spiral arms. |
| Open with DEXTER |
NGC 1566 and NGC 5247 were investigated based on studying the
surface photometric and spectroscopic by Bottema (1992) and Van der Kruit & Freeman (1986), respectively. The parameters Vz,
I0, and 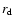 we need are listed in Table 1 in this
paper. As shown in Table 1 Col. 5, the vertical velocity
dispersion Vz of NGC 1566 was obtained from Table 4 Col. 4 in
Bottema's paper (1992) and NGC 5247 from Table 1 Col. 4 in Van der Kruit & Freeman (1986), it only needs to get Vz,r at the
radius r in the galactic disk. However, we have obtained the
effective thickness z0, the vertical velocity dispersion Vz,r, and the surface brightness I(r) at radius r, the
only unknown parameter is mass-to-light ratio
we need are listed in Table 1 in this
paper. As shown in Table 1 Col. 5, the vertical velocity
dispersion Vz of NGC 1566 was obtained from Table 4 Col. 4 in
Bottema's paper (1992) and NGC 5247 from Table 1 Col. 4 in Van der Kruit & Freeman (1986), it only needs to get Vz,r at the
radius r in the galactic disk. However, we have obtained the
effective thickness z0, the vertical velocity dispersion Vz,r, and the surface brightness I(r) at radius r, the
only unknown parameter is mass-to-light ratio 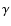 in Eq. (8).
in Eq. (8).
On the basis of the method proposed in this paper, we obtain the
effective thicknesses (z0) of NGC 1566 and NGC 5247 by Eq. (12) and their mass-to-light ratios (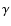 )
by Eq. (8).
The main results are listed in Table 2,
)
by Eq. (8).
The main results are listed in Table 2, 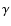 listed in Col. 8 and z0 in Col. 7.
listed in Col. 8 and z0 in Col. 7.
Table 1:
Vz and parameters of surface brightness of NGC 1566 and NGC 5247 (B-band).
Table 2:
The effective thicknesses and the mass-to-light ratios of NGC 1566 and NGC 5247 (B-band).
![\begin{figure}
\par\subfigure[]{\includegraphics[width=3.2cm,clip]{Hh121_f2a.eps...
...
\subfigure[]{\includegraphics[width=3.1cm,clip]{Hh121_f2d.eps} }
\end{figure}](/articles/aa/full/2006/05/aahh121/Timg52.gif) |
Figure 2:
Panel a) shows
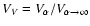 with different z0
with different z0
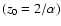 .
VV is the
ratio for the amplitude of the gravitational potential
perturbation of a disk with finite thickness to that of an
infinitely thin disk. The curves from top down correspond to .
VV is the
ratio for the amplitude of the gravitational potential
perturbation of a disk with finite thickness to that of an
infinitely thin disk. The curves from top down correspond to
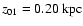
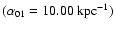 , ,
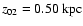
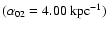 ,
and ,
and
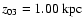
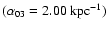 ,
respectively. Panels b)- d) are three panels for NGC 1566 to
illustrate the changes of z0 with r0, ,
respectively. Panels b)- d) are three panels for NGC 1566 to
illustrate the changes of z0 with r0,  ,
and m,
respectively. ,
and m,
respectively. |
| Open with DEXTER |
- 1.
- As shown in Fig. 2 with four panels
(Figs. 2a-d), Fig. 2a is displayed the
radial dependence of
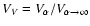 by Eqs. (9) and (11), it is noted that VV is the
ratio for the amplitude of the gravitational potential
perturbation of a disk with finite thickness to that of an
infinitely thin disk. As an example, we choose a sample with two
spiral arms and winding parameter
by Eqs. (9) and (11), it is noted that VV is the
ratio for the amplitude of the gravitational potential
perturbation of a disk with finite thickness to that of an
infinitely thin disk. As an example, we choose a sample with two
spiral arms and winding parameter
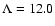 .
The curves from
the top to bottom denote the galactic disk with different
effective thicknesses correspond to
.
The curves from
the top to bottom denote the galactic disk with different
effective thicknesses correspond to
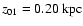
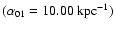 ,
,
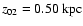
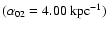 ,
and
,
and
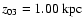
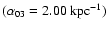 ,
respectively. In Fig. 2a, it is
shown that the amplitude of gravitational perturbation for a disk
with finite thickness is weaker than that of an infinitely thin
disk, and the thicker the galactic disk is, the weaker the
amplitude of the gravitational potential perturbation becomes.
When it is close to the center of the disk (
,
respectively. In Fig. 2a, it is
shown that the amplitude of gravitational perturbation for a disk
with finite thickness is weaker than that of an infinitely thin
disk, and the thicker the galactic disk is, the weaker the
amplitude of the gravitational potential perturbation becomes.
When it is close to the center of the disk (
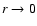 ),
the decrease of the amplitude of gravitational potential
perturbation becomes even faster, the amplitude is too weak to
stir up the self-consistent density waves due to the physical
concept of density waves suggested by Lindblad, spiral arms would
disappear in the forbidden region with radius r0 to the
galactic center. When
),
the decrease of the amplitude of gravitational potential
perturbation becomes even faster, the amplitude is too weak to
stir up the self-consistent density waves due to the physical
concept of density waves suggested by Lindblad, spiral arms would
disappear in the forbidden region with radius r0 to the
galactic center. When
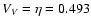 as shown in Fig. 2a, the
thicker the galactic disk is, the larger the forbidden radius
becomes (
r03>r02>r01).
as shown in Fig. 2a, the
thicker the galactic disk is, the larger the forbidden radius
becomes (
r03>r02>r01).
- 2.
- Figures 2b-d are three panels for NGC 1566. z0 is obtained
by calculating Eq. (12). Figure 2b shows the effective thickness
z0 changes with r0, keeping the other two parameters m and
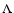 constant at their adopted values in Table 2. We could
note that z0 becomes thicker as the the forbidden radius r0is increased, it is in agreement with the conclusion obtained from
Fig. 2a (when
constant at their adopted values in Table 2. We could
note that z0 becomes thicker as the the forbidden radius r0is increased, it is in agreement with the conclusion obtained from
Fig. 2a (when
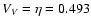 ,
the thicker the galactic disk is,
the larger the forbidden radius r0 becomes.).
,
the thicker the galactic disk is,
the larger the forbidden radius r0 becomes.).
Figure 2c is shown the change of z0 with 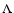 ,
keeping mand r0 constant. We can learn from Peng (1988) and Ma et al.
(1998) that
,
keeping mand r0 constant. We can learn from Peng (1988) and Ma et al.
(1998) that
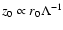 ,
for the spiral
galaxies with the same or similar value of z0, the forbidden
radii r0 become larger as
,
for the spiral
galaxies with the same or similar value of z0, the forbidden
radii r0 become larger as 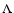 be increased, it shows some
correlations with Hubble sequence. As displayed in Fig. 2c, r0is kept constant at the value in Table 2, z0 becomes thinner as
be increased, it shows some
correlations with Hubble sequence. As displayed in Fig. 2c, r0is kept constant at the value in Table 2, z0 becomes thinner as 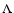 becomes larger, it is in agreement with the method for
determining the thickness of a spiral galactic disk by Peng (1988)
and Ma et al. (1998).
becomes larger, it is in agreement with the method for
determining the thickness of a spiral galactic disk by Peng (1988)
and Ma et al. (1998).
Figure 2d shows the dependence of z0 on the parameter m, keeping
r0 and 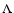 constant. It is noted that the larger the
number of spiral arms (m) becomes, the narrower the gap of the
spiral arms is. It is similar to the result of
constant. It is noted that the larger the
number of spiral arms (m) becomes, the narrower the gap of the
spiral arms is. It is similar to the result of 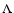 increased, when
increased, when 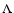 is increased, the gap of the spiral arms
becomes smaller. As shown in Fig. 2d, z0 becomes thinner as mbecomes larger.
is increased, the gap of the spiral arms
becomes smaller. As shown in Fig. 2d, z0 becomes thinner as mbecomes larger.
- 3.
- The mass-to-light ratios of NGC 1566 and NGC 5247 in
B-band given by Bottema (1992) and Van der Kruit & Freeman (1986)
respectively are both
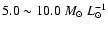 .
As shown in Table 2 Col. 8 in this paper, we obtain the
mass-to-light ratios of NGC 1566 and NGC 5247 are
.
As shown in Table 2 Col. 8 in this paper, we obtain the
mass-to-light ratios of NGC 1566 and NGC 5247 are
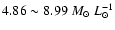 and
and
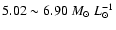 ,
respective.
,
respective.
- 4.
- Van de Kruit & Searle (1981a) and de Grijs & Van de Kruit (1996) found that, for scale heights
of edge-on spirals, H=z0/2 is in good approximation
independent of position along the major axis, but Kent et al.
(1991), de Grijs & Peletier (1997) noted that the scale height
seems to increase with radius along the major axis, it seems to
occur more often in early type galaxies than in later type. Shaw
& Gilmore (1990) found that the radial variation of scale
heights is within
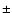
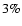 ,
with no dependence on color or model
type. Here, we presume scale height to be approximately constant
along the axis of the galactic disk, and for Eq. (8), it is
obvious that mass-to-light ratio is approximately constant too, in
agreement with Van der Kruit & Freeman (1986).
,
with no dependence on color or model
type. Here, we presume scale height to be approximately constant
along the axis of the galactic disk, and for Eq. (8), it is
obvious that mass-to-light ratio is approximately constant too, in
agreement with Van der Kruit & Freeman (1986).
Acknowledgements
We are very grateful to the referee for the careful and useful reviews of
this paper, the insightful comments and suggestions have improved
this paper very much. The images of NGC 1566 and NGC 5247 in B-band
are both got from the NASA/IPAC Extragalactic Database (NED),
which is operated by the Jet Propulsion Laboratory, California
Institute of Technology, under contract with NASA. The image of
NGC 1566 is obtained with the 2.5 m telescope at LCO, with the image
size
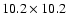 arcmin, and the image of NGC 5247 is got
with the 0.9 m telescope at CTIO, with the image size
arcmin, and the image of NGC 5247 is got
with the 0.9 m telescope at CTIO, with the image size
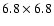 arcmin. This research is supported by Chinese National Science
Foundation No. 10573011, No.10273006, and the Doctoral Program
Foundation of State Education Commission of China.
arcmin. This research is supported by Chinese National Science
Foundation No. 10573011, No.10273006, and the Doctoral Program
Foundation of State Education Commission of China.
- Bottema, R.
1992, A&A, 257, 69 [NASA ADS] (In the text)
- Camm, G. L. 1950,
MNRAS, 110, 305 [NASA ADS] (In the text)
- de Grijs, R.,
& Van der Kruit, P. C. 1996, A&AS, 117, 19 [NASA ADS] (In the text)
- de Grijs, R.,
& Peletier, R. F. 1997, A&A, 320, L21 [NASA ADS] (In the text)
- Kalnajs, A.
J. 1971, ApJ, 166, 275 [NASA ADS] [CrossRef] (In the text)
- Kent, S. M., &
Dame, T. M. 1991, ApJ, 378, 131 [NASA ADS] [CrossRef] (In the text)
- Ma, J., Peng, Q. H.,
& Gu, Q. S. 1998, A&AS, 130, 449 [EDP Sciences] [NASA ADS] (In the text)
- Peng, Q. H. 1988,
A&A, 206, 18 [NASA ADS] (In the text)
- Peng, Q. H., Huang,
K. L., Huang, J. H., Li, X. G., & Su, H. J. 1978, Acta Astron.
Sinica, 19, 182 [NASA ADS] (In the text)
- Peng, Q. H., Li, X.
G., Su, H. J., Huang, K. L., & Huang, J. H. 1979, Sci. Sinica,
XXII, 925
(In the text)
- Shaw, M. A., &
Gilmore, G. 1990, MNRAS, 242, 59 [NASA ADS] (In the text)
- Spitzer, L.
1942, ApJ, 95, 329 [NASA ADS] [CrossRef] (In the text)
- Van der Kruit,
P. C., & Searle, L. 1981a, A&A, 95, 105 [NASA ADS] (In the text)
- Van der Kruit,
P. C., & Searle, L. 1981b, A&A, 95, 116 [NASA ADS]
- Van der Kruit, P.
C., & Freeman, K. C. 1986, ApJ, 303, 556 [NASA ADS] [CrossRef] (In the text)
- Zhao, Y. H., Peng,
Q. H., & Wang, L. 2004, Chjaa, 1, 51 [NASA ADS] (In the text)
Copyright ESO 2006
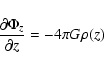
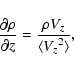
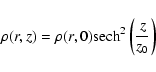
![\begin{displaymath}z_0=\frac{{\langle
V_z}^2\rangle ^{1/2}}{[2\pi G\rho (r,0)]^{1/2}},
\end{displaymath}](/articles/aa/full/2006/05/aahh121/img18.gif)
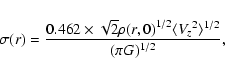
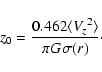
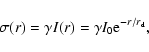
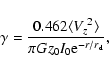
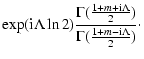
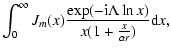
![\begin{displaymath}\eta=\frac{V_\alpha(\alpha,m,\Lambda,r_0)}{V_{\alpha\rightarr...
...,r_0)}={\rm Re}[g(\Lambda,m;\alpha
r_0)]\sqrt{m^2+\Lambda^2},
\end{displaymath}](/articles/aa/full/2006/05/aahh121/img39.gif)
![\begin{figure}
\par\subfigure[]{\includegraphics[width=3.2cm,clip]{Hh121_f2a.eps...
...
\subfigure[]{\includegraphics[width=3.1cm,clip]{Hh121_f2d.eps} }
\end{figure}](/articles/aa/full/2006/05/aahh121/Timg52.gif)