A&A 446, 403-415 (2006)
DOI: 10.1051/0004-6361:20042540
The Hanle effect in a random medium
H. Frisch
Laboratoire Cassiopée (CNRS, UMR 6202), Observatoire de
la Côte d'Azur, BP 4229, 06304 Nice Cedex 4,
France
Received 15 December 2004 / Accepted 21 September 2005
Abstract
This paper considers the Hanle effect produced by a
turbulent magnetic field. To overcome the simplified microturbulent
treatment whereby the Hanle phase matrix is locally averaged over some
magnetic field distribution, we consider a turbulent magnetic field
with a finite correlation length. We assume that the magnetic field
along each individual photon path can be represented by a
Kubo-Anderson process (KAP) and study the stationary solution as time
goes to infinity. A KAP is a discontinuous Markov process. The random
magnetic field is characterized by a correlation length and a
distribution function of the magnetic field vector; both can be chosen
arbitrarily. The microturbulent limit is recovered when the
correlation length goes to zero. A non-stochastic integral equation of
the Wiener-Hopf type is obtained for a mean conditional source
vector. This integral equation yields explicit expressions for the
mean Stokes parameters, provided one makes physically realistic
approximations, namely neglect the effect of the magnetic field on
Stokes I, keep only the contributions from I and Q in the
source terms for Stokes Q and Stokes U and solve the
integral equation for Q with a two-scattering approximation. The
final expressions involve mean values and
correlation functions of some of the elements of the Hanle phase
matrix and show the dependence on the correlation length of the random
magnetic field.
The combined effects of a turbulent velocity field and a turbulent
magnetic field with finite correlation lengths is also studied. The
velocity field is represented by a KAP with the same correlation
length as the magnetic field. Some of the velocity field effects
are treated with an effective medium approximation
as in Frisch & Frisch (1976, MNRAS, 175, 157). Explicit expressions are
obtained for the mean Stokes parameters. They can account for
correlations between velocity field and magnetic field fluctuations.
Key words: line: formation - polarization - magnetic fields -
turbulence - radiative transfer
1 Introduction
The Hanle effect is a powerful diagnostic tool for the measurement of
weak magnetic fields, deterministic or turbulent (Stenflo 1978;
Sahal-Bréchot #Sahal-Br&; Stenflo 1982). Contrary
to the Zeeman effect, the Hanle effect leaves a signature on the
polarization even for an isotropically distributed random field with
zero mean. The work of Stenflo and followers is based on the
assumption that the magnetic field is microturbulent, namely that it has a
correlation scale much smaller than a photon mean-free path around
line center. One can then average the Hanle phase matrix over
the distribution of the random magnetic field. If the latter is
isotropically distributed, the Hanle
problem reduces to a resonance polarization problem with a modified
(smaller) polarization parameter (Stenflo 1982,
1994). All the determinations of solar turbulent magnetic fields have been
carried out so far with this particular microturbulent magnetic field
model (Faurobert-Scholl 1993, 1996; Faurobert et al. 2001; Trujillo Bueno at al. 2004; Bommier et al. 2005).
The diagnostic method is based on a comparison between the observed
Stokes parameters and the Stokes parameters given by an atmospheric
model with zero magnetic field. The magnetic field determination is
therefore fairly sensitive to the atmospheric parameters and in
particular to the assumed turbulent velocity field which influences the
width and depth of the Stokes parameters profiles (Stenflo
1994). Nearly all determinations of the turbulent magnetic field in
the quiet regions of the solar photosphere have been carried out with
a turbulent velocity represented by a mixture of microturbulence and
macroturbulence, each one being modeled by a Gaussian distribution.
The micro and macroturbulent root mean square (rms) velocities are
deduced from the frequency profiles of Stokes I, the microturbulent
rms from the line width and the macroturbulent rms from the line
center intensity. The sensitivity of the magnetic field determination
to the choices of the micro and macro rms is discussed in Bommier
et al. (2005). Recently Trujillo Bueno et al. (2004) have determined
the mean magnetic field strength in the quiet sun, using a 3D
hydrodynamical numerical simulation of the solar surface
convection. The turbulent magnetic field is treated as usual with a
microturbulent approximation.
To overcome the micro/macro turbulent approximation, we consider here
the effects of random magnetic and velocity fields in which turbulent
fluctuations have a wide range of wave numbers. This is actually the
standard situation in stellar atmospheres because of the very large
kinetic and magnetic Reynolds numbers. Our goal is to obtain mean
values for the observable Stokes parameters. Our approach is largely
inspired by the work carried out in the seventies on the broadening of
spectral lines by a turbulent velocity with a finite correlation
length. Several velocity field models with a finite correlation
length were introduced to address this question. A detailed review can
be found in Mihalas (1978). For the present investigation, we have
chosen Kubo-Anderson processes (KAP) to model
the random magnetic and velocity fields. We
note here that Landi Degl'Innocenti (1994) (see also
Landi Degl'Innocenti & Landolfi 2004, henceforth LL04) has used a KAP
to study the Zeeman effect by a turbulent magnetic field.
A KAP is a step-wise stationary Markov process. It takes constant but
random values on intervals of random length. It is characterized by a
distribution function and a correlation length. The former gives the
random values of the Markov process and the latter the mean distance
between the jumps from one value to another. The
Markov property is essential to obtain explicit expressions for
mean quantities. A KAP has an exponential covariance. The
microturbulent limit is recovered when the correlation length goes to
zero and the macroturbulent limit when the correlation length goes to
infinity.
The distribution of the magnetic field vector in the upper layers of
the quiet photosphere is not well known nor are the correlations
between magnetic field and velocity fields fluctuations. For
isotropic turbulence, symmetry arguments give that these correlations
are zero when the magnetic field is treated as a pseudo-vector (Domke
& Pavlov 1979). In the usual magnetic field determinations based on a
microturbulent description of the magnetic field associated with a
micro/macro description of the velocity field, the magnetic field and
velocity field fluctuations are fully decoupled. The method that we
describe here shows how treat magnetic fields and velocity fields with
a finite correlation length and can handle correlations between the
magnetic field and velocity field fluctuations.
For spectral lines formed by multiple scatterings of photons,
i.e. under non-LTE conditions, it is not possible, even with a Markov
model, to obtain closed equations for mean quantities because the
photons can return several time to the same turbulent element (Gail et al. 1975; Magnan 1975; Frisch & Frisch 1976, henceforth FF76). A way
out of this difficulty is to assume a random process in time instead
of a random process in space and then consider the stationary solution
as time goes to infinity. This method was introduced in FF76 and
worked out in Froeschlé & Frisch (#Froeschl&, henceforth FF80). The
results of these papers are generalized here to treat the Hanle effect
with random magnetic fields and velocity fields.
The outline of the paper is the following. In Sect. 2,
we recall the transfer equation for the Hanle effect. In
Sects. 3 to 5, we assume that the magnetic
field only is random. In Sect. 3, we show how to set up
the time-dependent transfer problem, introduce the random magnetic
field model, construct a time-independent stochastic transfer equation
and establish an integral equation for a mean conditional
time-independent source vector. In Sect. 4 we
explain how the problem can be simplified by taking into account some
of the properties of the Hanle effect. In Sect. 5 we
establish explicit expressions for the mean observable Stokes
parameters. They involve the correlation length of the magnetic field
and are constructed with a two-scattering
approximation. Section 6 is devoted to the joint effects
of turbulent magnetic and velocity fields.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2540fig1.eps} %
\end{figure}](/articles/aa/full/2006/05/aa2540-04/Timg11.gif) |
Figure 1:
Reference system. Definition of 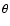 and
and 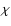 ,
the
inclination and longitude of the direction ,
the
inclination and longitude of the direction
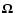 . . |
| Open with DEXTER |
2 The transfer equation for the Hanle effect
We consider a plane parallel semi-infinite atmosphere and choose the
reference system shown in Fig. 1 where z is the normal to the
atmosphere. The Hanle effect, i.e., resonance scattering in the
presence of a magnetic field, can be described by the three Stokes
parameters I, Q, U. At any point in the medium the
three-component Stokes vector
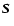 with components I, Q, U depends on z and on a direction
with components I, Q, U depends on z and on a direction
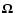 defined by its two
polar angles
defined by its two
polar angles 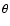 and
and 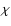 .
It also depends on a frequency
variable x. Here x is measured in Doppler width units with the
zero at line center. We also assume a two-level atom with unpolarized
ground level.
.
It also depends on a frequency
variable x. Here x is measured in Doppler width units with the
zero at line center. We also assume a two-level atom with unpolarized
ground level.
The full theory of the Hanle effect is still in a somewhat preliminary
phase, in particular when it comes to describe the frequency
redistribution at each scattering although some theoretical progress
have been made by Bommier (1997a,b; see also Landi Degl'Innocenti et al. 1997). Observations are usually analyzed with some simplifying
assumptions namely that the full redistribution matrix can be
written as a sum of terms, each of which is the product of a frequency
redistribution function r(x,x') by a scattering phase matrix
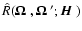 .
Here
.
Here
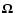 and xare the direction and
frequency of the incident beam,
and xare the direction and
frequency of the incident beam,
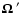 and x' the direction and
frequency of the scattered beam and
and x' the direction and
frequency of the scattered beam and
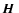 the magnetic field
vector (see e.g. Domke & Hubeny 1998; Stenflo 1994, and references
therein; Faurobert et al. 2001; Bommier et al. 2005; Holzreuter et al. 2005). For a two-level
atom model, with unpolarized ground level and a redistribution
function of the above type, each Stokes parameter can be written in the form
the magnetic field
vector (see e.g. Domke & Hubeny 1998; Stenflo 1994, and references
therein; Faurobert et al. 2001; Bommier et al. 2005; Holzreuter et al. 2005). For a two-level
atom model, with unpolarized ground level and a redistribution
function of the above type, each Stokes parameter can be written in the form
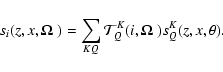 |
(1) |
Here i=0,1,2 is the index of the Stokes component, with s0=I,
s1=Q and s2=U. The indices Kand Q take the values K=0,Q=0,
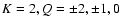 .
The
.
The
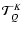 are irreducible spherical tensors for polarimetry introduced
by Landi Degl'Innocenti (1984) (see also LL04). The six
functions sKQ depend on the inclination angle
are irreducible spherical tensors for polarimetry introduced
by Landi Degl'Innocenti (1984) (see also LL04). The six
functions sKQ depend on the inclination angle 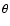 but not on
the longitude
but not on
the longitude 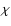 .
They are complex quantities and,
since the si are real, they satisfy the same conjugation property
as the
.
They are complex quantities and,
since the si are real, they satisfy the same conjugation property
as the
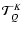 ,
namely
,
namely
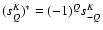 ,
where
,
where 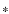 stand for complex conjugate. Using the conjugation
property, it is possible to construct six real functions :
I1=s00, I2=s20,
stand for complex conjugate. Using the conjugation
property, it is possible to construct six real functions :
I1=s00, I2=s20,
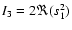 ,
,
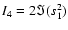 ;
;
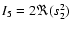 ,
,
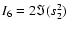 .
The Stokes parameters can then
be written as
.
The Stokes parameters can then
be written as
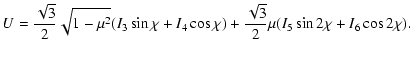 |
|
|
(4) |
A decomposition very similar to Eq. (1) was first given
for the six real functions Ii by Faurobert-Scholl (1991) with a
Fourier decomposition with respect to 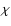 of the Stokes vector and
of the Hanle phase matrix (see also Nagendra et al. 1998, henceforth
NFF98; Frisch 1998, 1999, henceforth F99). Recently
Loskutov (2004) and Ivanov (2004) have proposed a factorization of the
phase matrix
of the Stokes vector and
of the Hanle phase matrix (see also Nagendra et al. 1998, henceforth
NFF98; Frisch 1998, 1999, henceforth F99). Recently
Loskutov (2004) and Ivanov (2004) have proposed a factorization of the
phase matrix 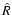 which provides a simple method for achieving the
same decomposition. Actually the simplest method to establish
Eq. (1) is to write the phase matrices
which provides a simple method for achieving the
same decomposition. Actually the simplest method to establish
Eq. (1) is to write the phase matrices
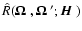 in terms of the
irreducible tensors
in terms of the
irreducible tensors
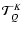 ,
using expressions given in,
e.g., LL04.
,
using expressions given in,
e.g., LL04.
Here we make the assumption that the redistribution matrix contains a
single term of the form
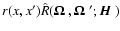 .
For simplicity we also assume
that there is no correlation between x and x', i.e. we assume
complete frequency redistribution as in Landi Degl'Innocenti et al. (1990), for example. We then have
.
For simplicity we also assume
that there is no correlation between x and x', i.e. we assume
complete frequency redistribution as in Landi Degl'Innocenti et al. (1990), for example. We then have
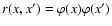 ,
where
,
where
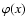 is the line absorption profile, normalized to
unity. The Ii, can be used to form a six-component vector
is the line absorption profile, normalized to
unity. The Ii, can be used to form a six-component vector
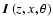 .
In the following we use this vector to represent the
polarized field and refer to it as the irreducible Stokes vector.
.
In the following we use this vector to represent the
polarized field and refer to it as the irreducible Stokes vector.
The transfer equation for
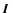 can be written as
can be written as
![$\displaystyle \mu {\partial {\mbox{\boldmath$\vec{I}$ }}\over \partial z}= -k(z...
...'){\mbox{\boldmath$\vec{I}$ }}(z,x',\mu')~{{\rm d}\mu'\over 2}~{\rm d}x'\Bigr].$](/articles/aa/full/2006/05/aa2540-04/img37.gif) |
|
|
(5) |
Here
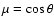 .
We have denoted k(z) the line frequency integrated
absorption coefficient per unit length. The variables z and x have
been introduced above. The vector
.
We have denoted k(z) the line frequency integrated
absorption coefficient per unit length. The variables z and x have
been introduced above. The vector
 is a given
source term. It is a six-component vector corresponding to a
decomposition similar to Eq. (1) of a primary source
term, often of thermal origin. If the latter
is unpolarized, as assumed here, only the first component G1 is non
zero.
is a given
source term. It is a six-component vector corresponding to a
decomposition similar to Eq. (1) of a primary source
term, often of thermal origin. If the latter
is unpolarized, as assumed here, only the first component G1 is non
zero.
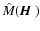 is a
is a 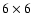 matrix which
depends on the magnetic field and
matrix which
depends on the magnetic field and 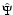 also a
also a 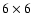 matrix. The matrix
matrix. The matrix
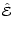 accounts for inelastic
collisions and elastic depolarizing collisions. It is a diagonal
matrix. The
accounts for inelastic
collisions and elastic depolarizing collisions. It is a diagonal
matrix. The 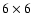 unit matrix is simply denoted by 1. More details
on these matrices are given in Sect. 4.
unit matrix is simply denoted by 1. More details
on these matrices are given in Sect. 4.
The Hanle effect acts only around the line center (Omont et al. 1973; LL04).
In the line wings, the life-time of the upper level is too short for
the magnetic field to destroy the phase coherences of the Zeeman
sub-levels. A simple way to take this property into account is to
consider that 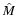 becomes equal to the identity matrix
for frequencies
becomes equal to the identity matrix
for frequencies
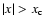 .
Typically
.
Typically
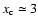 .
The results are
not very sensitive to the choice of
.
The results are
not very sensitive to the choice of 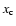 .
We explain on the final
results how this cutoff can be implemented.
.
We explain on the final
results how this cutoff can be implemented.
3 Time-dependent transfer problem
In the transfer equation, randomness comes through the matrix 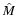 .
Proceeding as in FF76, we assume that the magnetic field
.
Proceeding as in FF76, we assume that the magnetic field
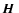 is a function of time t,
is a function of time t,
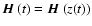 ,
where z(t) is the random position of the photon at time
t. Together with the time-dependent random magnetic field, we
must use the time-dependent transfer equation,
,
where z(t) is the random position of the photon at time
t. Together with the time-dependent random magnetic field, we
must use the time-dependent transfer equation,
![$\displaystyle {1\over c}{\partial {\mbox{\boldmath$\vec{I}$ }}(t,z,x,\mu)\over ...
...si(\mu')
{\mbox{\boldmath$\vec{I}$ }}(t,z,x',\mu')~{\rm d}\mu'~{\rm d}x'\Bigg],$](/articles/aa/full/2006/05/aa2540-04/img49.gif) |
|
|
(6) |
where c is the velocity of light. We have used the compact notation
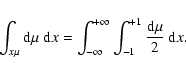 |
(7) |
In addition, we must prescribe an initial condition
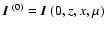 .
We assume that the primary source
.
We assume that the primary source
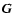 is
time-independent. Hence, Eq. (6) has a stationary
solution. We are interested in the mean value of this solution.
is
time-independent. Hence, Eq. (6) has a stationary
solution. We are interested in the mean value of this solution.
3.1 The magnetic field model
As mentioned in Sect. 1, we assume that the random
magnetic field can be represented by a KAP.
A KAP is a step-wise constant Markov process which jumps at
randomly chosen points between random step-values. The jumping points
ti are uniformly and independently distributed in
![$[-\infty,+\infty]$](/articles/aa/full/2006/05/aa2540-04/img52.gif) with a Poisson distribution of density
with a Poisson distribution of density
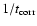 .
In each interval
ti-1< t < ti, the magnetic field
takes a constant value
.
In each interval
ti-1< t < ti, the magnetic field
takes a constant value
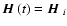 .
The
.
The
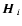 are
random variables with a probability density
are
random variables with a probability density
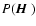 .
A KAP is
therefore characterized by a correlation time
.
A KAP is
therefore characterized by a correlation time
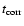 and a
probability density
and a
probability density
 .
.
This type of process was introduced in connection with nuclear
magnetic resonance (Anderson 1954; Kubo 1954). It was used to model
the stochastic Stark effect (Frisch & Brissaud 1971; Brissaud &
Frisch 1971). For
radiative transfer, it was employed to study the broadening of
spectral lines by a turbulent velocity field (Auvergne et al. 1973). The denomination KAP was introduced in this context. The
KAP, and some generalized versions, are discussed in detail in
Brissaud & Frisch (1974), a review article on the solution of linear
stochastic differential equations.
As
 is a stationary Markov random process (Wang & Uhlenbeck 1945; Barucha-Reid 1960; Papoulis 1965; Feller 1971), the transition
probability density
is a stationary Markov random process (Wang & Uhlenbeck 1945; Barucha-Reid 1960; Papoulis 1965; Feller 1971), the transition
probability density
 ,
such that
,
such that
 is the probability to find a field
is the probability to find a field
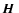 (within
(within
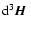 )
at time s+t, given a field
)
at time s+t, given a field
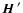 at
time s, satisfies the Kolmogorov equation
at
time s, satisfies the Kolmogorov equation
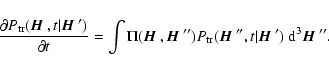 |
(8) |
Here 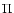 is an integral operator which defines the Markov process.
For diffusion processes, like the Brownian motion or the
Ornstein-Uhlenbeck process (Uhlenbeck & Ornstein 1930; Feller 1971),
the Kolmogorov equation is actually a second-order differential
equation. In the modern terminology, it is called a Fokker-Planck
equation. The stationary solution of the Kolmogorov equation is the
distribution
is an integral operator which defines the Markov process.
For diffusion processes, like the Brownian motion or the
Ornstein-Uhlenbeck process (Uhlenbeck & Ornstein 1930; Feller 1971),
the Kolmogorov equation is actually a second-order differential
equation. In the modern terminology, it is called a Fokker-Planck
equation. The stationary solution of the Kolmogorov equation is the
distribution
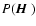 .
The transition probability satisfies
.
The transition probability satisfies
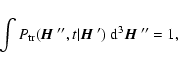 |
(9) |
with the initial condition
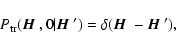 |
(10) |
where 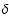 is the Dirac distribution. For a KAP,
is the Dirac distribution. For a KAP,
![\begin{displaymath}\Pi({\mbox{\boldmath$\vec{H}$ }},{\mbox{\boldmath$\vec{H}$ }'...
...ldmath$\vec{H}$ }'}) - P({\mbox{\boldmath$\vec{H}$ }})\right].
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img67.gif) |
(11) |
The solution of the Kolmogorov equation is
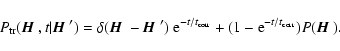 |
(12) |
The first term gives the probability that the magnetic field keeps
its initial value
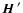 after an interval of time t and the second
term the probability that it takes a value
after an interval of time t and the second
term the probability that it takes a value
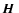 ,
with
probability
,
with
probability
 .
.
3.2 The mean conditional irreducible Stokes vector
Equation (6) is a stochastic differential equation with
Markov coefficients to which we can apply the standard technique of
solution (Frisch 1968). Symbolically, Eq. (6) can be
written as
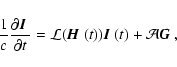 |
(13) |
where 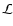 is a linear operator which depends
deterministically on the Markov process
is a linear operator which depends
deterministically on the Markov process
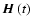 and
and
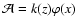 .
The crucial remark is that the joint process
.
The crucial remark is that the joint process
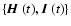 is also a Markov process. Its probability
density
is also a Markov process. Its probability
density
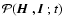 satisfies
satisfies
![\begin{displaymath}{\partial {\cal P}\over\partial t}= \Pi{\cal P} -c
\sum_{l=1}...
...}}){\mbox{\boldmath$\vec{I}$ }} + {\cal A}G_l] {\cal P}\Bigr].
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img75.gif) |
(14) |
The index l refers to the 6 components of
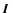 .
The first
term expresses the change between t and
.
The first
term expresses the change between t and
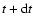 of the probability
density of the magnetic field and the following terms the change in
the probability of the components of
of the probability
density of the magnetic field and the following terms the change in
the probability of the components of
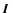 which evolve
according to Eq. (13)
which evolve
according to Eq. (13)![[*]](/icons/foot_motif.gif) . The initial condition is
. The initial condition is
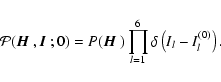 |
(15) |
We now introduce a mean conditional irreducible Stokes vector
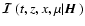 .
Each component
.
Each component
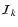 is defined for k=1 to 6 by
is defined for k=1 to 6 by
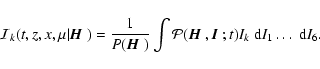 |
(16) |
We stress that
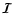 is a conditional mean. Indeed,
is a conditional mean. Indeed,
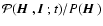 is the conditional
probability density of
is the conditional
probability density of
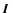 at time t, knowing
at time t, knowing
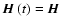 .
To obtain the
mean irreducible Stokes vector itself, it suffices to average
.
To obtain the
mean irreducible Stokes vector itself, it suffices to average
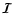 over
over
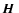 with the density
with the density
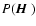 .
Here
conditional means are denoted with calligraphic uppercase letters
and means over the magnetic distribution with Roman letters.
.
Here
conditional means are denoted with calligraphic uppercase letters
and means over the magnetic distribution with Roman letters.
Equation (14), is the starting point to construct a closed
transfer equation for each
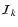 : it suffices to
multiply it by Ik and then to integrate as in
Eq. (16). The terms involving the partial derivatives
in the r.h.s. of Eq. (14) can be integrated by parts. The
integrated term is zero because of the factor
: it suffices to
multiply it by Ik and then to integrate as in
Eq. (16). The terms involving the partial derivatives
in the r.h.s. of Eq. (14) can be integrated by parts. The
integrated term is zero because of the factor  .
The
remaining integral contains only the term corresponding to l=k. One
thus obtains
.
The
remaining integral contains only the term corresponding to l=k. One
thus obtains
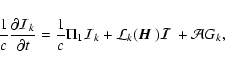 |
(17) |
where
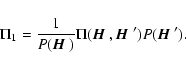 |
(18) |
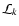 is the k-component of the operator
is the k-component of the operator 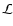 .
We
can write this result in the vectorial form
.
We
can write this result in the vectorial form
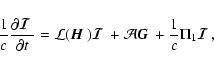 |
(19) |
where 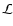 is the transfer operator. In explicit notation,
Eq. (19) can be written as
is the transfer operator. In explicit notation,
Eq. (19) can be written as
There is an initial condition
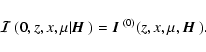 |
(21) |
3.3 Stationary transfer equation for the mean conditional
irreducible Stokes vector
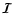
We are interested in the stationary solution only, so we set
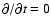 .
This solution is independent of the initial
condition
.
This solution is independent of the initial
condition
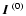 .
We introduce the line optical depth defined
as
.
We introduce the line optical depth defined
as
 .
We thus obtain for
.
We thus obtain for
 the
transfer equation
the
transfer equation
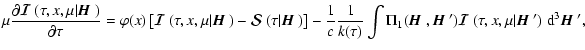 |
|
|
(22) |
where
 |
|
|
(23) |
In the following we refer to
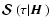 as the mean conditional source vector.
The boundary conditions are given at the surface
as the mean conditional source vector.
The boundary conditions are given at the surface 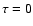 and at
infinity. We assume as usual that the radiation incident on the surface is zero
and that it tends to
and at
infinity. We assume as usual that the radiation incident on the surface is zero
and that it tends to
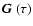 at infinity. In addition, boundedness
for
at infinity. In addition, boundedness
for
 must be assumed to ensure uniqueness of
the solution of Eq. (22).
must be assumed to ensure uniqueness of
the solution of Eq. (22).
The operator  introduced in
Eq. (11) contains a correlation time scale
introduced in
Eq. (11) contains a correlation time scale
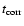 .
The
corresponding spatial correlation scale measured in optical depth
units is
.
The
corresponding spatial correlation scale measured in optical depth
units is
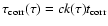 .
It is convenient to
introduce
.
It is convenient to
introduce
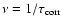 which can be interpreted as a mean
number of turbulent eddies per unit optical depth. Here we assume that
which can be interpreted as a mean
number of turbulent eddies per unit optical depth. Here we assume that
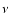 is independent of optical depth. To simplify the notation, we
redefine the operator
is independent of optical depth. To simplify the notation, we
redefine the operator 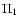 such that
such that
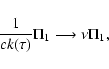 |
(24) |
with the new 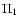 defined by
defined by
![\begin{displaymath}\Pi_1= - {1\over P({\mbox{\boldmath$\vec{H}$ }})}\left[\delta...
...\boldmath$\vec{H}$ }})\right]P({\mbox{\boldmath$\vec{H}$ }'}).
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img108.gif) |
(25) |
We observe here for future use that
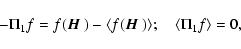 |
(26) |
for any function
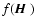 .
To obtain this result, we multiply Eq. (25) by
.
To obtain this result, we multiply Eq. (25) by
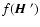 and integrate over
and integrate over
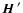 .
We note also that
.
We note also that
 |
(27) |
for all powers n of 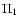 .
.
3.4 Integral equation for the mean conditional source vector
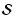
From the equation of transfer for
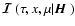 ,
we can construct an integral operator equation for
,
we can construct an integral operator equation for
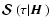 by the usual method.
Writing the operator
by the usual method.
Writing the operator 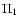 as an abstract
operator, the formal solution of Eq. (22) can be written
as
as an abstract
operator, the formal solution of Eq. (22) can be written
as
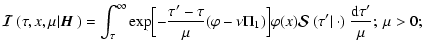 |
|
|
(28) |
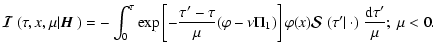 |
|
|
(29) |
The source vector
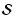 is a function of the magnetic
field, but its dependence cannot be written explicitly because of the
exponential operator. The magnetic field dependence is indicated by a
dot. Here
is a function of the magnetic
field, but its dependence cannot be written explicitly because of the
exponential operator. The magnetic field dependence is indicated by a
dot. Here 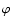 stands for
stands for
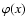 times the
operator unity. Inserting this formal solution into
Eq. (23), we obtain an operator integral equation
of the Wiener-Hopf type,
times the
operator unity. Inserting this formal solution into
Eq. (23), we obtain an operator integral equation
of the Wiener-Hopf type,
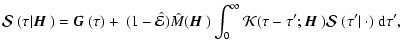 |
|
|
(30) |
where the operator 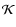 is defined by
is defined by
![$\displaystyle {\cal K}(\tau;{\mbox{\boldmath$\vec{H}$ }}) =
\int_{x\mu}^{\rm wh...
...ert\tau\vert\over
\mu}(\varphi - \nu\Pi_1)\Bigr]\varphi(x)~{\rm d}\mu~{\rm d}x.$](/articles/aa/full/2006/05/aa2540-04/img120.gif) |
|
|
(31) |
We have introduced the notation
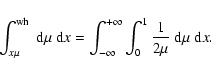 |
(32) |
Equations (22) and (30) have the structure of
ordinary vectorial transfer equations, but with an additional
independent 3D variable
 .
Attempts to solve these equations
numerically will encounter serious difficulties. The problem can be
simplified by taking advantage of some properties of the Hanle effect.
.
Attempts to solve these equations
numerically will encounter serious difficulties. The problem can be
simplified by taking advantage of some properties of the Hanle effect.
4 A simplified Hanle problem
Polarization produced by resonance scattering is always weak
since it is created by the anisotropy of the radiation field. In the
presence of a magnetic field, the polarization becomes in general even
weaker. Approximations based on this
remark have been shown to give very satisfactory results with
errors falling within the error bar of standard measurements
(Faurobert-Scholl 1991; NFF98). They will allow us to obtain an
explicit expression for the mean observable Stokes parameters. Before
we describe the approximation, we must recall the meaning of the three
matrices in Eq. (5) (see also Eq. (23)).
The matrices  ,
,
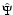 and
and
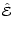 are
are 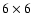 matrices with lines and columns numbered from 1 to 6. The elements of
these matrices can be found in Faurobert-Scholl (1991) (see also
NFF98; F99). Here we give only a few of them. We note also that signs
may be different from those of the above mentioned articles because
of sign differences in the elements of the vector
matrices with lines and columns numbered from 1 to 6. The elements of
these matrices can be found in Faurobert-Scholl (1991) (see also
NFF98; F99). Here we give only a few of them. We note also that signs
may be different from those of the above mentioned articles because
of sign differences in the elements of the vector
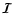 .
The first line and first
column of
.
The first line and first
column of 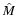 contain only zeros, except for M1,1=1 (we drop
the symbol hat when we refer to elements of these matrices). The
others 25 elements of
contain only zeros, except for M1,1=1 (we drop
the symbol hat when we refer to elements of these matrices). The
others 25 elements of 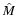 are non zero and depend on the
magnetic field (strength and direction). In
are non zero and depend on the
magnetic field (strength and direction). In
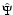 ,
only the diagonal elements and the two off diagonal
elements
,
only the diagonal elements and the two off diagonal
elements
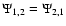 are non zero. The non zero elements
are
are non zero. The non zero elements
are
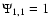 ,
,
The other non-zero elements,
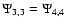 and
and
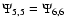 are not used here.
Henceforth we assume W2=1, value corresponding to a normal Zeeman
triplet. The matrix
are not used here.
Henceforth we assume W2=1, value corresponding to a normal Zeeman
triplet. The matrix
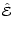 is diagonal with
is diagonal with
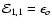 and
and
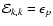 for k=2 to
6. The parameter
for k=2 to
6. The parameter
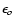 describes destruction by inelastic
collisions and
describes destruction by inelastic
collisions and
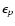 depolarization by elastic collisions. One roughly
has
depolarization by elastic collisions. One roughly
has
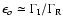 and
and
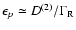 where
where
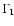 is the
inelastic collision rate,
is the
inelastic collision rate,
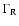 the radiative de-excitation
rate and D(2) the collisional depolarization rate. If
the radiative de-excitation
rate and D(2) the collisional depolarization rate. If
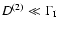 then
then
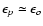 (for the full definitions
of
(for the full definitions
of
 and
and
 ,
see Frisch 1998; also
Faurobert et al. 2001; Bommier et al. 2005; LL04 Sect. 5.14).
,
see Frisch 1998; also
Faurobert et al. 2001; Bommier et al. 2005; LL04 Sect. 5.14).
In Eq. (5), the source term (inside the square bracket)
can be written as
 ,
where
,
where
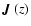 is a 6-component
vector. Numerical solutions of Eq. (5) (see NFF98) show
that J2 is roughly ten times smaller than J1 and that the other
Jk with
is a 6-component
vector. Numerical solutions of Eq. (5) (see NFF98) show
that J2 is roughly ten times smaller than J1 and that the other
Jk with
 are roughly ten times smaller than J2. To
evaluate the source function, it is actually sufficient to keep the
two first columns in the matrix
are roughly ten times smaller than J2. To
evaluate the source function, it is actually sufficient to keep the
two first columns in the matrix  and set all the other
elements to zero (in the first column, only the element M1,1 is
not zero). With this approximation we keep in the source terms the
contributions from the Q=0 components, s00=I1 and s20=I2,
only. The transfer equations for the Ik take thus much simpler
forms.
and set all the other
elements to zero (in the first column, only the element M1,1 is
not zero). With this approximation we keep in the source terms the
contributions from the Q=0 components, s00=I1 and s20=I2,
only. The transfer equations for the Ik take thus much simpler
forms.
The transfer equation for I1 becomes the usual scalar one,
![$\displaystyle \mu{\partial I_1(\tau,x,\mu)\over \partial\tau} =
\varphi(x) I_1(...
...o)\int_{x'\mu'}
\varphi(x')I_1(\tau,x',\mu')~{\rm d}\mu'~{\rm d}x' + G_1\Bigr].$](/articles/aa/full/2006/05/aa2540-04/img143.gif) |
|
|
(34) |
It contains no random elements, hence I1 is not random.
The transfer equation for I2 is
![\begin{displaymath}\mu{\partial I_2(\tau,x,\mu)\over \partial\tau} =
\varphi(x) \bigl[I_2(\tau,x,\mu) - S_2(\tau)\bigr],
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img144.gif) |
(35) |
where
![$\displaystyle S_2(\tau)= (1-\epsilon_p)M_{2,2}({\mbox{\boldmath$\vec{H}$ }})
\l...
...int_{x\mu}\Psi_{2,2}(\mu)\varphi(x)
I_2(\tau,x,\mu)~{\rm d}\mu~{\rm d}x\right],$](/articles/aa/full/2006/05/aa2540-04/img145.gif) |
|
|
(36) |
with
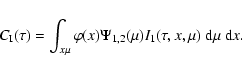 |
(37) |
The definition of
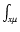 is given in Eq. (32).
Since I1 is non random,
is given in Eq. (32).
Since I1 is non random, 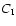 is non random either. It plays
the role of a primary source term for the Stokes parameter Q. Actually
is non random either. It plays
the role of a primary source term for the Stokes parameter Q. Actually
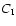 is the dominant term in the component
is the dominant term in the component
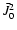 of the
frequency averaged irreducible tensor of the radiation field
of the
frequency averaged irreducible tensor of the radiation field
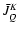 (LL04). When the radiation field is isotropic,
(LL04). When the radiation field is isotropic, 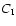 is zero. In the
equation for I2, randomness comes thus from the matrix element
M2,2. Since this equation contains a scattering term involving
I2, it presents the same kind of difficulties as
Eq. (5), but it is possible, in contrast with
Eq. (5), to make physically reasonable assumptions which
permit the calculation of the mean value of I2, as shown below.
is zero. In the
equation for I2, randomness comes thus from the matrix element
M2,2. Since this equation contains a scattering term involving
I2, it presents the same kind of difficulties as
Eq. (5), but it is possible, in contrast with
Eq. (5), to make physically reasonable assumptions which
permit the calculation of the mean value of I2, as shown below.
The transfer equations for Ik,
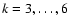 ,
are of the form
,
are of the form
![\begin{displaymath}\mu{\partial I_k(\tau,x,\mu)\over \partial\tau} =
\varphi(x) \bigl[I_k(\tau,x,\mu) - S_k(\tau)\bigr],
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img151.gif) |
(38) |
with 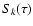 given by
Eq. (36) where M22 should be
replaced by Mk2, while the two terms in the square bracket are
unchanged. Thus, the equations for the Ik have no
scattering terms. Randomness comes from the matrix elements Mk,2 and from
I2. The solution of the transfer problem for I2 will allow
us to calculate the mean values of the Ik for k=3 to 6.
given by
Eq. (36) where M22 should be
replaced by Mk2, while the two terms in the square bracket are
unchanged. Thus, the equations for the Ik have no
scattering terms. Randomness comes from the matrix elements Mk,2 and from
I2. The solution of the transfer problem for I2 will allow
us to calculate the mean values of the Ik for k=3 to 6.
5 Mean Stokes Q and U
We show in this Section how to determine the mean values of Ik,
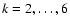 .
Equations (2) to (4) will
then give us the mean values of the Stokes parameters Q and U and
the magnetic field dependent terms in the expansion of Stokes I.
.
Equations (2) to (4) will
then give us the mean values of the Stokes parameters Q and U and
the magnetic field dependent terms in the expansion of Stokes I.
We introduce
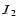 ,
the conditional mean of I2 and apply the
technique described in Sect. 3 to
Eq. (35). In Sect. 5.1, we construct
an integral equation similar to Eq. (30) for a mean
conditional source function
,
the conditional mean of I2 and apply the
technique described in Sect. 3 to
Eq. (35). In Sect. 5.1, we construct
an integral equation similar to Eq. (30) for a mean
conditional source function
 .
A Neumann
series expansion of this integral equation, limited to the two first
terms, yields an explicit expression for
.
A Neumann
series expansion of this integral equation, limited to the two first
terms, yields an explicit expression for
 as is shown in Sect. 5.2. In
Sect. 5.3, we show how to average
as is shown in Sect. 5.2. In
Sect. 5.3, we show how to average
 over the magnetic field distribution. We thus
obtain a mean source function
over the magnetic field distribution. We thus
obtain a mean source function
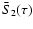 which is used in
Sect. 5.4 to calculate the mean value of
which is used in
Sect. 5.4 to calculate the mean value of
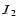 .
In Sect. 5.5, we show how to construct the mean
values of the
.
In Sect. 5.5, we show how to construct the mean
values of the
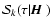 and
and
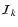 ,
for
,
for
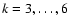 .
.
5.1 Stokes Q. Integral equation for the mean conditional
source function
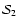
Following the procedure described in Sect. 3, we deduce
from Eqs. (22) and
(23) the transfer equation,
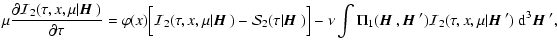 |
|
|
(39) |
where
![$\displaystyle {\cal S}_2(\tau\vert{\mbox{\boldmath$\vec{H}$ }})= (1-\epsilon_p)...
...al I}_2(\tau,x,\mu\vert{\mbox{\boldmath$\vec{H}$ }})~{\rm d}\mu~{\rm d}x\Bigg].$](/articles/aa/full/2006/05/aa2540-04/img159.gif) |
|
|
(40) |
Inserting the formal solution of Eq. (39) into
Eq. (40), we obtain for
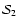 the Wiener-Hopf
integral equation
the Wiener-Hopf
integral equation
![$\displaystyle {\cal S}_2(\tau\vert{\mbox{\boldmath$\vec{H}$ }})=
(1-\epsilon_p)...
...\mbox{\boldmath$\vec{H}$ }})
{\cal S}_2(\tau'\vert~\cdot)~{\rm d}\tau' \right],$](/articles/aa/full/2006/05/aa2540-04/img160.gif) |
|
|
(41) |
where the operator
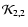 is given by
is given by
![$\displaystyle {\cal K}_{2,2}(\tau;{\mbox{\boldmath$\vec{H}$ }}) =
\int_{x\mu}^{...
...\Bigl[-{\vert\tau\vert\over
\mu}(\varphi - \nu\Pi_1)\Bigr]~{\rm d}\mu~{\rm d}x.$](/articles/aa/full/2006/05/aa2540-04/img162.gif) |
|
|
(42) |
As pointed out, solving this integral equation where
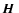 is an
independent variable will be a very laborious task. We now construct
an approximate solution by way of a Neumann series expansion.
is an
independent variable will be a very laborious task. We now construct
an approximate solution by way of a Neumann series expansion.
5.2 Neumann series expansion
The Neumann series expansion method of solution applies to
any type of integral equations. For simplicity, we present
it for the integral equation satisfied by 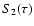 and then apply
it to Eq. (41).
and then apply
it to Eq. (41).
The formal solution of Eq. (35) yields the integral equation
![$\displaystyle S_2(\tau)= (1-\epsilon_p)M_{2,2}({\mbox{\boldmath$\vec{H}$ }})
\l...
...rm I}(\tau)
+ \int_0^\infty K_{2,2}(\tau-\tau') S_2(\tau')~{\rm d}\tau'\right],$](/articles/aa/full/2006/05/aa2540-04/img164.gif) |
|
|
(43) |
where
![\begin{displaymath}K_{2,2}(\tau)=\int_{x\mu}^{\rm wh}\varphi ^2(x)\Psi_{2,2}(\mu...
...{\vert\tau\vert\varphi(x)\over\mu}\right]~{\rm d}\mu~{\rm d}x.
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img165.gif) |
(44) |
Here
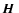 is any magnetic field, random or not.
For the component I1, one can also introduced a source function
S1 defined as S2 with
is any magnetic field, random or not.
For the component I1, one can also introduced a source function
S1 defined as S2 with
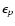 replaced by
replaced by
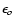 ,
M2,2 replaced by M1,1,
,
M2,2 replaced by M1,1,
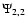 by
by
 and the primary
source term
and the primary
source term
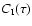 replaced by
replaced by 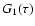 .
The source
function S1 satisfies an integral equation similar to
Eq. (43). Although the
equations for S1 and S2 look formally the
same, they have quite different behaviors because the integral of
.
The source
function S1 satisfies an integral equation similar to
Eq. (43). Although the
equations for S1 and S2 look formally the
same, they have quite different behaviors because the integral of
 over
over 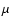 is equal to unity while the integral of
is equal to unity while the integral of
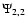 is equal to 7/10 as can be easily deduced from
Eq. (33). Therefore the integral of K2,2 over
is equal to 7/10 as can be easily deduced from
Eq. (33). Therefore the integral of K2,2 over 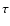 (from
(from 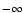 to
to 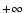 )
is also equal to 7/10 (we recall that
)
is also equal to 7/10 (we recall that
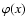 is normalized to unity). To construct the solution of
Eq. (43), it is convenient to introduce a renormalized kernel
is normalized to unity). To construct the solution of
Eq. (43), it is convenient to introduce a renormalized kernel
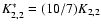 ,
normalized to unity, and an albedo for
single scattering
,
normalized to unity, and an albedo for
single scattering
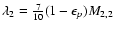 .
The Neumann series expansion for S2 can thus be written
.
The Neumann series expansion for S2 can thus be written
The term of order n gives the contribution of all the photons that
have been scattered n times after creation by the primary source
term. Its magnitude is order of
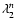 since
since
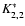 is
normalized to unity. It is easy to see that
is
normalized to unity. It is easy to see that 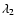 is smaller
than unity. Even if
is smaller
than unity. Even if
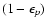 is close to unity, the two other
factors are significantly smaller than unity (M2,2 is equal to
one only if the magnetic field is zero). Hence a few terms should
suffice to properly represent the solution of the integral Eq. (43). We remark also that the accuracy of a truncated
Neumann series expansion is not directly related to the optical depth
of the line. The latter affects mainly the optical depth dependence of
is close to unity, the two other
factors are significantly smaller than unity (M2,2 is equal to
one only if the magnetic field is zero). Hence a few terms should
suffice to properly represent the solution of the integral Eq. (43). We remark also that the accuracy of a truncated
Neumann series expansion is not directly related to the optical depth
of the line. The latter affects mainly the optical depth dependence of
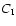 .
It is clear that a Neumann series expansion would not be
a good method to calculate I1, i.e. Stokes I, since
.
It is clear that a Neumann series expansion would not be
a good method to calculate I1, i.e. Stokes I, since
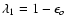 is extremely close to unity. Spectral lines
that are used to evaluate the solar turbulent magnetic field with the
Hanle effect typically have
is extremely close to unity. Spectral lines
that are used to evaluate the solar turbulent magnetic field with the
Hanle effect typically have
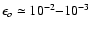 .
The
Neumann series expansion could be used to calculate Stokes I only
for a line with optical depth much smaller than unity.
.
The
Neumann series expansion could be used to calculate Stokes I only
for a line with optical depth much smaller than unity.
A fairly common approximation to evaluate Stokes Q is the single
scattering approximation, also called the last-scattering
approximation (Stenflo 1982, 1994). It amounts to keep only
the zeroth order term corresponding to n=0 in the expansion
(45) in powers of 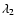 ,
i.e. to consider that the
polarization is created by photons which have been scattered only
once. It has the advantage of by-passing transfer calculations for the
polarized field. It is not restricted to optically thin lines. For
example, it works quite well for a line like Sr I 460.7 nm which
has an optical depth around 10 (Faurobert et al. 2001). This can be
explained by the fact that
,
i.e. to consider that the
polarization is created by photons which have been scattered only
once. It has the advantage of by-passing transfer calculations for the
polarized field. It is not restricted to optically thin lines. For
example, it works quite well for a line like Sr I 460.7 nm which
has an optical depth around 10 (Faurobert et al. 2001). This can be
explained by the fact that 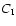 decreases fairly rapidly with
increasing values of
decreases fairly rapidly with
increasing values of 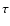 and by the fact that the single scattering
albedo is significantly smaller than unity.
and by the fact that the single scattering
albedo is significantly smaller than unity.
Here we make an approximation slightly more sophisticated than the
single scattering approximation and refer to it as
a two-scattering approximation. Namely, we keep in
Eq. (45) the zeroth order term but also the first order
term corresponding to n=1. With this approximation,
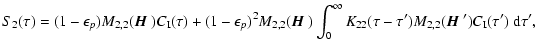 |
|
|
(46) |
where
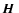 stands for
stands for
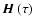 and
and
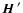 for
for
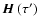 .
Here, two terms contribute to the source function
at a point of optical depth
.
Here, two terms contribute to the source function
at a point of optical depth 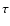 ,
a local term and a non local one
given by the integral over the whole atmosphere of the primary source
term weighted by the transport operator. Because the single scattering
albedo is smaller than unity, the non local term will be smaller than
the local one. Whereas the single scattering approximation is a local
approximation for the calculation of the polarization, our
two-scattering approximation is clearly not.
,
a local term and a non local one
given by the integral over the whole atmosphere of the primary source
term weighted by the transport operator. Because the single scattering
albedo is smaller than unity, the non local term will be smaller than
the local one. Whereas the single scattering approximation is a local
approximation for the calculation of the polarization, our
two-scattering approximation is clearly not.
5.3 Stokes Q. The mean source function
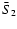
We show in this section how to calculate the mean source function
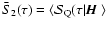 ,
where
,
where
 stand for the average over
stand for the average over
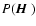 .
The two-scattering
approximation applied to Eq. (41) yields
.
The two-scattering
approximation applied to Eq. (41) yields
![$\displaystyle {\cal S}_2(\tau\vert{\mbox{\boldmath$\vec{H}$ }})=
(1-\epsilon_p)...
...mbox{\boldmath$\vec{H}$ }}) M_{2,2}(\cdot) C_{\rm I}(\tau')~{\rm d}\tau'\Bigr].$](/articles/aa/full/2006/05/aa2540-04/img191.gif) |
|
|
(47) |
Averaging the primary source term
in Eq. (47) is straightforward. To average the integral
term, we must calculate the quantity
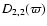 defined by
defined by
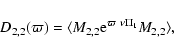 |
(48) |
where
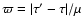 (see Eq. (42)). In the
macroturbulent (
(see Eq. (42)). In the
macroturbulent ( )
and microturbulent
(
)
and microturbulent
(
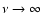 )
limits,
)
limits,
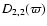 becomes equal to
becomes equal to
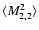 and
and
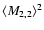 ,
respectively. We recall that in the
microturbulent limit all the random coefficients can be replaced by
their local averages over the magnetic field distribution. We now show
that for a finite non zero value of
,
respectively. We recall that in the
microturbulent limit all the random coefficients can be replaced by
their local averages over the magnetic field distribution. We now show
that for a finite non zero value of 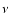 ,
,
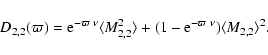 |
(49) |
Observe that this result is simply a linear combination of the
macro and microturbulent limits and is consistent with both limits.
We consider the Laplace transform of
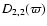 :
:
The calculation of the inverse of the operator
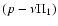 is
equivalent to the solution of the integral equation
is
equivalent to the solution of the integral equation
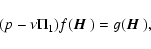 |
(51) |
with f the unknown and g given. Here p is
implicitly multiplied by the operator unity. Using
Eq. (25), this integral equation can be written as
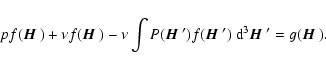 |
(52) |
We first calculate the mean value of
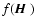 by averaging over
by averaging over
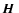 .
Inserting the result into Eq. (52),
we obtain
.
Inserting the result into Eq. (52),
we obtain
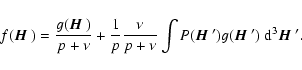 |
(53) |
Now we set
g= M2,2, multiply
by M2,2 and average over the magnetic field distribution (see
Eq. (50)). A decomposition of
![$\nu/[p (\nu+p)]$](/articles/aa/full/2006/05/aa2540-04/img207.gif) in simple fractions yields
in simple fractions yields
![\begin{displaymath}\tilde D_{2,2}(p)= {1\over p+\nu}[\langle M_{2,2}^2\rangle- \langle
M_{2,2}\rangle^2] + {1\over p}\langle M_{2,2}\rangle^2.
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img208.gif) |
(54) |
One sees immediately that
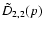 is the Laplace transform
of the result given in Eq. (49).
is the Laplace transform
of the result given in Eq. (49).
A less general but more direct method for obtaining
Eq. (49) is to expand the
exponential operator in Eq. (48). This leads to
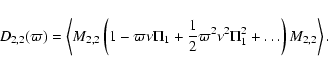 |
(55) |
Using the properties of 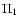 given in Eqs. (26) and
(27), we obtain
given in Eqs. (26) and
(27), we obtain
![$\displaystyle D_{2,2}(\varpi) = \langle M_{2,2}^2\rangle- \varpi \nu
~\left[\la...
...i^2 \nu ^2 \left[\langle M_{2,2}^2\rangle- \langle M_{2,2}\rangle^2\right] +...$](/articles/aa/full/2006/05/aa2540-04/img211.gif) |
|
|
(56) |
Summing all the terms, we recover the result in
Eq. (49).
So our final result for the mean source function is
This expression involves only the primary source term 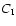 defined in Eq. (37) and the mean values of M2,2 and
M2,22.
defined in Eq. (37) and the mean values of M2,2 and
M2,22.
As already pointed out, in the microturbulent and macroturbulent
limits, the large square bracket reduces to
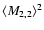 and
and
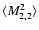 ,
respectively. For a
stationary Kubo-Anderson process m(t) of zero mean and density
,
respectively. For a
stationary Kubo-Anderson process m(t) of zero mean and density 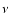 ,
the
covariance is given by (Brissaud & Frisch 1974)
,
the
covariance is given by (Brissaud & Frisch 1974)
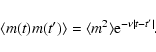 |
(58) |
Replacing m(t) by the difference
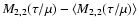 ,
we see that the square bracket, is simply the
autocorrelation function
,
we see that the square bracket, is simply the
autocorrelation function
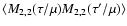 .
If we had considered
.
If we had considered
 as a random process in space and not
in time, i.e. if we had averaged Eq. (46) over the
magnetic field distribution, there would be no factor
as a random process in space and not
in time, i.e. if we had averaged Eq. (46) over the
magnetic field distribution, there would be no factor 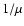 .
This
factor
.
This
factor 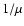 properly takes into account the number of turbulent
eddies that are crossed along the line of sight.
properly takes into account the number of turbulent
eddies that are crossed along the line of sight.
We note also that for large values of
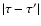 such that
such that
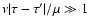 ,
the dominant factor inside the large
square bracket in Eq. (57) is
,
the dominant factor inside the large
square bracket in Eq. (57) is
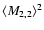 .
So, as
expected, we recover the microturbulent limit when many turbulent
eddies lie between
.
So, as
expected, we recover the microturbulent limit when many turbulent
eddies lie between 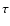 and
and 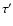 .
.
Equation (57) shows also that 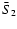 is independent of
the correlation length of the magnetic field in the standard single
scattering approximation since
is independent of
the correlation length of the magnetic field in the standard single
scattering approximation since 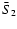 is approximated by the first
term in the r.h.s.
is approximated by the first
term in the r.h.s.
5.4 Mean Stokes Q
We are now ready to determine
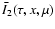 ,
the
average of the mean conditional polarization
,
the
average of the mean conditional polarization
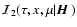 over the distribution of the magnetic
field. Averaging Eq. (39), we obtain for
over the distribution of the magnetic
field. Averaging Eq. (39), we obtain for 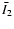 a standard
transfer equation
a standard
transfer equation
![\begin{displaymath}\mu {\partial \bar I_2(\tau,x,\mu)\over \partial
\tau}=\varphi(x)\Bigl[\bar I_2(\tau,x,\mu) - \bar S_2(\tau)\Bigr],
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img226.gif) |
(59) |
where
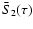 is given in Eq. (57). There is no contribution
from the term involving the operator
is given in Eq. (57). There is no contribution
from the term involving the operator 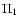 since it becomes zero
upon averaging (see Eq. (26)). The solution of
Eq. (59) is of the form shown in
Eqs. (28) and (29). For the surface value we
simply have
since it becomes zero
upon averaging (see Eq. (26)). The solution of
Eq. (59) is of the form shown in
Eqs. (28) and (29). For the surface value we
simply have
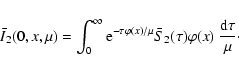 |
(60) |
This expression is consistent with the fact that there is no
randomness in the profile 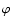 .
The mean value of the azimuthal
average of Stokes Q follows then from Eq. (3).
.
The mean value of the azimuthal
average of Stokes Q follows then from Eq. (3).
To summarize, the calculation of the mean value of
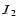 involves
only a few fairly simple steps. First one has to solve a scalar
transfer problem for I1 with, say, an accelerated Lambda iteration
method. Equation (57) gives an explicit
expression for the mean source function
involves
only a few fairly simple steps. First one has to solve a scalar
transfer problem for I1 with, say, an accelerated Lambda iteration
method. Equation (57) gives an explicit
expression for the mean source function 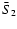 in which
in which 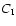 ,
the
primary source, is given by Eq. (37). It suffices then
to integrate the source function as shown in Eq. (60). Of
course a choice has to be made for the distribution of the magnetic
field.
,
the
primary source, is given by Eq. (37). It suffices then
to integrate the source function as shown in Eq. (60). Of
course a choice has to be made for the distribution of the magnetic
field.
The element M2,2 can be written as (Stenflo 1994)
![\begin{displaymath}M_{2,2}= 1- 3 \sin^2\theta_{\rm B}\gamma_{\rm B}^2
\left[{\s...
... + {\cos^2\theta_{\rm B}\over 1+ \gamma_{\rm B}^2}\right]\cdot
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img228.gif) |
(61) |
Here,
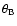 is the inclination angle of the magnetic field and
is the inclination angle of the magnetic field and
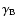 is a dimensionless parameter which depends on the
intensity of the magnetic field. Namely,
is a dimensionless parameter which depends on the
intensity of the magnetic field. Namely,
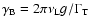 ,
with
,
with
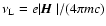 the
Larmor frequency of the electron in the magnetic field, g the
Landé factor of the upper level,
the
Larmor frequency of the electron in the magnetic field, g the
Landé factor of the upper level,
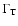 the
destruction rate of the upper level alignment (sum of the radiative,
inelastic and depolarizing destruction rates) (Bommier 1997a,b;
Faurobert et al. 2001; Bommier et al. 2005). The element M2,2does not depend on the longitude
the
destruction rate of the upper level alignment (sum of the radiative,
inelastic and depolarizing destruction rates) (Bommier 1997a,b;
Faurobert et al. 2001; Bommier et al. 2005). The element M2,2does not depend on the longitude
 of the magnetic field.
of the magnetic field.
For a magnetic field with a constant intensity, isotropically distributed
over the solid angle
(Stenflo 1982; Landi Degl'Innocenti & Landi Degl'Innocenti 1988; LL04),
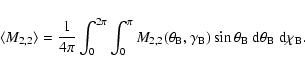 |
(62) |
A simple calculation yields
![\begin{displaymath}\langle M_{2,2} \rangle= 1-{2\over 5}\left[{\gamma_{\rm B}^2\...
...
B}^2} + {4\gamma_{\rm B}^2\over 1+4\gamma_{\rm B}^2}\right],
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img236.gif) |
(63) |
and
![\begin{displaymath}\langle M_{2,2}^2 \rangle= 1- {4\over 35}{\gamma_{\rm B}^2\ov...
...^2)\over (1+4\gamma_{\rm B}^2)^2 (1+\gamma_{\rm B}^2)}\right].
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img237.gif) |
(64) |
One can verify that
 is always positive.
is always positive.
5.5 Mean Stokes U
As shown by Eq. (4), Stokes U depends on Ik,
 ,
only. Proceeding as above, we
introduce the mean conditional components
,
only. Proceeding as above, we
introduce the mean conditional components
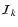 which
satisfy the transfer Eq. (39) with the mean
conditional source functions given by
which
satisfy the transfer Eq. (39) with the mean
conditional source functions given by
![$\displaystyle {\cal S}_k(\tau\vert{\mbox{\boldmath$\vec{H}$ }})=(1-\epsilon_p)M...
...{\rm 2}(\tau,x,\mu\vert{\mbox{\boldmath$\vec{H}$ }})~{\rm d}\mu~{\rm d}x\Bigg].$](/articles/aa/full/2006/05/aa2540-04/img238.gif) |
|
|
(65) |
Now we remark that the square bracket can be
expressed in terms of
 (see Eq. (40)).
We thus obtain
(see Eq. (40)).
We thus obtain
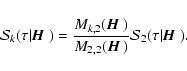 |
(66) |
Hence
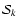 is also given by Eq. (47) where
M2,2 is replaced by Mk,2 outside the square bracket.
Averaging over the magnetic field as in Sect. 5.3, we
obtain for
is also given by Eq. (47) where
M2,2 is replaced by Mk,2 outside the square bracket.
Averaging over the magnetic field as in Sect. 5.3, we
obtain for
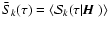 a result quite
similar to Eq. (57), namely
a result quite
similar to Eq. (57), namely
In the first term
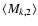 replaces
replaces
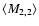 and in
the square bracket we have combinations of the macroturbulent and
microturbulent limits of the product
Mk,2M2,2.
and in
the square bracket we have combinations of the macroturbulent and
microturbulent limits of the product
Mk,2M2,2.
At the surface, the mean values
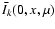 are simply given by
Eq. (60) with
are simply given by
Eq. (60) with 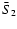 replaced by
replaced by 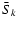 .
The Mk,2 depend linearly on
.
The Mk,2 depend linearly on
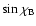 and
and
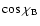 .
Hence the mean values of
.
Hence the mean values of
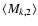 and
and
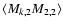 over an isotropically distributed field are zero
(see Eq. (62)) and Stokes U is zero as it should be.
The same situation holds for any axisymmetric magnetic field distribution.
over an isotropically distributed field are zero
(see Eq. (62)) and Stokes U is zero as it should be.
The same situation holds for any axisymmetric magnetic field distribution.
5.6 Line core and line wings
Since the Hanle effect acts only in the line core, the conditional source
functions
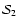 and
and
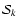 are actually function of
the frequency x. The expressions given in Eqs. (57) and
(67) must then be somewhat modified. In the first term which
serves as primary source, M22 must be set to unity and Mk2to zero when
are actually function of
the frequency x. The expressions given in Eqs. (57) and
(67) must then be somewhat modified. In the first term which
serves as primary source, M22 must be set to unity and Mk2to zero when
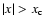 .
In the integral term, the coefficient M22must be set to unity and the coefficient Mk2 to zero when
.
In the integral term, the coefficient M22must be set to unity and the coefficient Mk2 to zero when
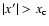 .
.
6 The Hanle effect with turbulent velocity and magnetic
fields
We now consider the joint effects of a turbulent velocity field
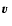 and of a turbulent magnetic field
and of a turbulent magnetic field
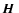 .
We assume that the
velocity field has the same statistical properties as the magnetic
field, namely that it is also a KAP with density
.
We assume that the
velocity field has the same statistical properties as the magnetic
field, namely that it is also a KAP with density 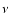 and that it has
the same jumping points as the magnetic field. We denote by
and that it has
the same jumping points as the magnetic field. We denote by
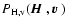 the joint probability density of
the joint probability density of
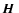 and
and
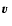 and by
and by
 and
and
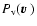 the marginal density probability of
the marginal density probability of
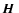 and
and
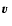 ,
respectively. An effective medium approximation will be introduced to
handle the complexity introduced by the turbulent field, otherwise the
method follows the same lines as above.
,
respectively. An effective medium approximation will be introduced to
handle the complexity introduced by the turbulent field, otherwise the
method follows the same lines as above.
The operator of the full random Markov process is
![$\displaystyle \Pi({\mbox{\boldmath$\vec{H}$ }},{\mbox{\boldmath$\vec{v}$ }};{\m...
...
P_{\rm H,v}({\mbox{\boldmath$\vec{H}$ }},{\mbox{\boldmath$\vec{v}$ }})\right].$](/articles/aa/full/2006/05/aa2540-04/img258.gif) |
|
|
(68) |
Because of the Doppler effect, the random field
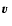 enters in the absorption profile which becomes
enters in the absorption profile which becomes
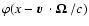 ,
with
,
with
 the
direction of propagation of the radiation. Proceeding as above, we
consider the magnetic field and
velocity field to be random processes in time. We introduce the joint
process
the
direction of propagation of the radiation. Proceeding as above, we
consider the magnetic field and
velocity field to be random processes in time. We introduce the joint
process
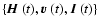 and its probability
density
and its probability
density
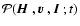 which satisfies
which satisfies
![\begin{displaymath}{\partial {\cal P}\over\partial t}= \Pi{\cal P} -c
\sum_{l=1}...
...} + {\cal A({\mbox{\boldmath$\vec{v}$ }})}G_l] {\cal P}\Bigr],
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img262.gif) |
(69) |
with the initial condition
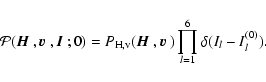 |
(70) |
We introduce the mean conditional irreducible Stokes vector
 .
Each component is defined as in
Eq. (16) with
.
Each component is defined as in
Eq. (16) with
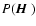 replaced by
replaced by
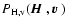 .
The stationary solution of the
time-dependent transfer equation for
.
The stationary solution of the
time-dependent transfer equation for
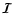 satisfies a set of equations similar to Eqs. (22) and (23) where
satisfies a set of equations similar to Eqs. (22) and (23) where
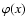 is replaced by
is replaced by
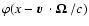 .
The integral equation corresponding to Eq. (30) is
.
The integral equation corresponding to Eq. (30) is
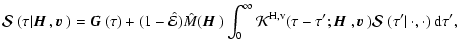 |
|
|
(71) |
where the operator
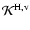 is defined by
is defined by
![$\displaystyle {\cal K}^{\rm H,v}(\tau;{\mbox{\boldmath$\vec{H}$ }},{\mbox{\bold...
...au\vert\over \mu}(\varphi -
\nu\Pi_1)\right]\varphi(\cdot)~{\rm d}\mu~{\rm d}x.$](/articles/aa/full/2006/05/aa2540-04/img267.gif) |
|
|
(72) |
As above, conditional means are denoted with calligraphic upper case
letters. The notation
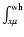 is defined in
Eq. (32). The dots indicates that
is defined in
Eq. (32). The dots indicates that 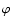 and
and
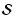 are functions of the velocity and magnetic fields
variables. In the exponential,
are functions of the velocity and magnetic fields
variables. In the exponential, 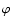 stands for
stands for
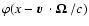 times the operator unity. The operator
times the operator unity. The operator
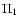 is defined by
is defined by
![$\displaystyle \Pi_1({\mbox{\boldmath$\vec{H}$ }},{\mbox{\boldmath$\vec{v}$ }}\v...
...\Bigr]P_{\rm H,v}({\mbox{\boldmath$\vec{H}$ }'},{\mbox{\boldmath$\vec{v}$ }'}).$](/articles/aa/full/2006/05/aa2540-04/img269.gif) |
|
|
(73) |
To simplify the notation, we now introduce the symbol
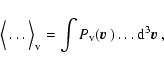 |
(74) |
the variable
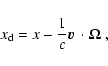 |
(75) |
and the operator
![\begin{displaymath}{\cal O}(\tau,\mu;\varphi,\Pi_1) =\exp\left[-{\vert\tau\vert\over
\mu}(\varphi(x_{\rm d}) - \nu\Pi_1)\right].
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img272.gif) |
(76) |
We also introduce
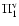 ,
the projection of
,
the projection of 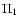 on functions
independent of the magnetic field. It can be written as
on functions
independent of the magnetic field. It can be written as
![\begin{displaymath}\Pi_1^{\rm v}= - {1\over P_{\rm v}({\mbox{\boldmath$\vec{v}$ ...
...ldmath$\vec{v}$ }})] P_{\rm v}({\mbox{\boldmath$\vec{v}$ }'}).
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img274.gif) |
(77) |
We now show how to establish explicit expressions for the mean values
of the six components of the source vector
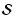 .
In
addition to approximations described in Sect. 4, an
effective medium is introduced to handle some of the random velocity
field effects.
.
In
addition to approximations described in Sect. 4, an
effective medium is introduced to handle some of the random velocity
field effects.
6.1 Stokes I; effective medium approximation
With the above assumptions, the component
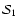 is independent
of the magnetic field and we recover the problem treated in FF76. The
integral equation for
is independent
of the magnetic field and we recover the problem treated in FF76. The
integral equation for
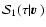 is
is
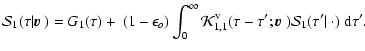 |
|
|
(78) |
Here the operator
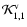 is defined as in
Eq. (72) with
is defined as in
Eq. (72) with 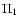 replaced by
replaced by
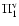 and
and
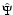 replaced by
replaced by
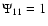 .
.
An effective source function, independent of the velocity field was
introduced in FF76 on the ground that the source function is
rather insensitive to turbulent fields (Athay 1972). This point is
discussed again below. So we make
the approximation,
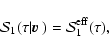 |
(79) |
and use it as an Ansatz in Eq. (78). Since the integral
term still depends on
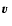 ,
we average it
over the velocity distribution (see Sect. 8 in
FF76). This procedure leads to the integral equation
,
we average it
over the velocity distribution (see Sect. 8 in
FF76). This procedure leads to the integral equation
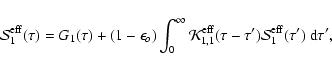 |
(80) |
with
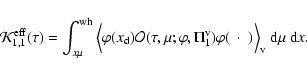 |
(81) |
A numerical method for the calculation of the effective source function
is described in FF80.
6.2 Stokes Q; mean source function
We deduce from Eq. (71) that
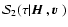 satisfies an integral equation which can be written
satisfies an integral equation which can be written
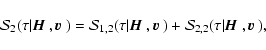 |
(82) |
where
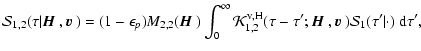 |
|
|
(83) |
plays the role of a primary source term and where
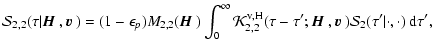 |
|
|
(84) |
is the integral term. In the single scattering approximation,
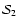 reduces to
reduces to
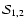 .
Here
.
Here
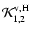 and
and
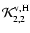 are defined as in
Eq. (72), with
are defined as in
Eq. (72), with 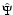 replaced by
replaced by
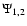 and
and
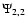 ,
respectively. The integral equation for
,
respectively. The integral equation for
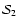 is now solved with a first order Neumann series expansion (see
Sect. 5.2) and the solution is averaged over the
magnetic and velocity field distribution to obtain the mean value
is now solved with a first order Neumann series expansion (see
Sect. 5.2) and the solution is averaged over the
magnetic and velocity field distribution to obtain the mean value
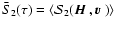 .
We first deal
with
.
We first deal
with
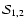 and then with
and then with
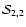 .
.
6.2.1 Evaluation and mean value of
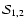
For consistency with the effective medium approximation used to
evaluate Stokes I, we replace in Eq. (83)
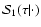 by
by
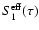 and
thus obtain
and
thus obtain
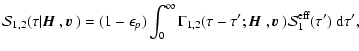 |
|
|
(85) |
with
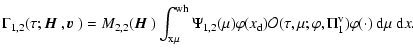 |
|
|
(86) |
Proceeding as in Sect. 5.3, we calculate the Laplace
transform of
 .
It may be written as
.
It may be written as
where  stands for
stands for
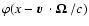 .
.
Now we remark that the integration over x plays a role somewhat
similar to an averaging over the velocity field. When 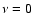 (
macroturbulent limit), an integration over x is exactly
equivalent to an integration over
(
macroturbulent limit), an integration over x is exactly
equivalent to an integration over
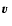 .
It is not true when
.
It is not true when
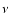 is finite. This remark, which explains
why the source function, in the scalar case, is not very
sensitive to turbulent velocities, suggests to
introduce for
is finite. This remark, which explains
why the source function, in the scalar case, is not very
sensitive to turbulent velocities, suggests to
introduce for
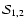 an effective medium approximation, namely
an effective medium approximation, namely
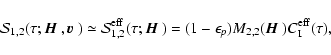 |
(88) |
with
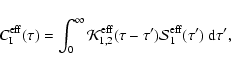 |
(89) |
and
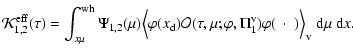 |
|
|
(90) |
In the macro and micro turbulent limits,
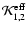 reduces to the usual deterministic K1,2 with either the frequency
profile
reduces to the usual deterministic K1,2 with either the frequency
profile 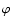 or its mean value
or its mean value
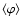 over the velocity
distribution. In these
limits the integral of K1,2 over
over the velocity
distribution. In these
limits the integral of K1,2 over
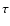 (from
(from 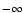 to
to  )
is zero. This property holds also
for
)
is zero. This property holds also
for
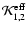 .
It is a consequence of the fact that
the integral of
.
It is a consequence of the fact that
the integral of
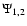 over
over 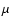 is zero.
is zero.
The effective medium approximation cannot take into account any sort
of coupling between magnetic field and velocity field fluctuations. We
show now that one can construct an approximation of
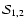 based on the macro and microturbulent limits of
based on the macro and microturbulent limits of
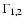 which
does not have this drawback.
which
does not have this drawback.
The inverse Laplace transform in Eq. (87) cannot be
calculated explicitely, however one can easily obtain the macro
(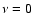 )
and microturbulent (
)
and microturbulent (
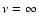 )
limits,
)
limits,
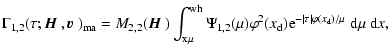 |
|
|
(91) |
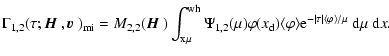 |
|
|
(92) |
Note that these limits still depend on the random values of
 and
and
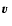 .
A numerical investigation of the effective kernel
.
A numerical investigation of the effective kernel
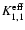 (FF80) shows that it behaves as the microturbulent limit for optical
depths larger than
(FF80) shows that it behaves as the microturbulent limit for optical
depths larger than 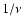 and like that the macroturbulent limit for
optical depths smaller than
and like that the macroturbulent limit for
optical depths smaller than
 with a smooth transition
between the two limits. Also the exact expression for obtained
with a smooth transition
between the two limits. Also the exact expression for obtained
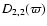 in Eq. (49) is a combination of the
macro and microturbulent limits. We propose the approximation
in Eq. (49) is a combination of the
macro and microturbulent limits. We propose the approximation
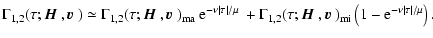 |
|
|
(93) |
It is consistent with the exact result in Eq. (49)
obtained for the pure magnetic field case. It should be possible to
improve this approximation by expanding
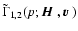 in powers of
in powers of 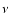 for
for 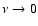 and in powers of
and in powers of 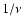 for
for
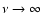 .
.
We now average
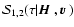 over
the joint magnetic and velocity field distribution to obtain the mean
source function in the single scattering approximation denoted here
by
over
the joint magnetic and velocity field distribution to obtain the mean
source function in the single scattering approximation denoted here
by
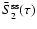 .
We consider separately each of the two
approximations constructed for
.
We consider separately each of the two
approximations constructed for
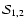 .
The effective medium
approximation leads to
.
The effective medium
approximation leads to
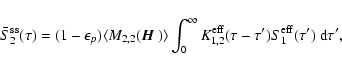 |
(94) |
where
 is defined in Eq. (90). The
second approximation, which can account for correlations between the
velocity and magnetic field distributions, yields
is defined in Eq. (90). The
second approximation, which can account for correlations between the
velocity and magnetic field distributions, yields
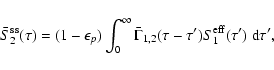 |
(95) |
where
In Eqs. (94) and (96), the average of M2,2 is
over the magnetic field distribution function
 ,
the average of
,
the average of 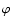 is over the velocity distribution function
is over the velocity distribution function
 and for the quantities which depend on
and for the quantities which depend on
 and
and
 ,
the averages are over the joint magnetic and
velocity distribution function
,
the averages are over the joint magnetic and
velocity distribution function
 .
It should be
noted that the second approximation reduces to an approximate version
of the first one if
.
It should be
noted that the second approximation reduces to an approximate version
of the first one if
 can be factorized as a
product
can be factorized as a
product
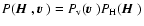 .
We note also that the integral over
.
We note also that the integral over 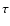 of
of
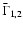 is zero, as is the integral of
is zero, as is the integral of
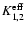 .
.
6.2.2 Evaluation and mean value of
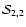
To calculate
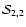 we should in principle replace in
Eq. (84)
we should in principle replace in
Eq. (84)
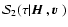 by
by
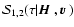 .
Here we use the approximate value
.
Here we use the approximate value
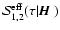 given in
Eq. (88). With the full expression the algebra would become
unnecessary complicated for a term which can be considered as a
correction to
given in
Eq. (88). With the full expression the algebra would become
unnecessary complicated for a term which can be considered as a
correction to
 since the single scattering albedo
since the single scattering albedo
 is smaller than
unity (see Sect. 5.2). We thus obtain
is smaller than
unity (see Sect. 5.2). We thus obtain
 |
|
|
(97) |
with
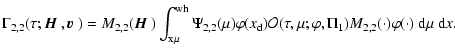 |
|
|
(98) |
We now consider the Laplace transform of
 .
To calculate the action of the operator
.
To calculate the action of the operator
![$\Bigl[p + (\varphi -
\nu\Pi_1)/\mu\Bigr]^{-1}$](/articles/aa/full/2006/05/aa2540-04/img329.gif) we proceed as in Sect. 5.3, i.e. we look for the
solution of the integral equation
we proceed as in Sect. 5.3, i.e. we look for the
solution of the integral equation
![\begin{displaymath}\left[p + (\varphi -
\nu\Pi_1)/\mu\right]f({\mbox{\boldmath...
...\mbox{\boldmath$\vec{H}$ }})g_2({\mbox{\boldmath$\vec{v}$ }}),
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img330.gif) |
(99) |
where
 and
and
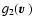 are given functions and
are given functions and
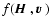 the unknown. After some simple algebra, we find
the unknown. After some simple algebra, we find
This expression is similar to Eq. (87) but is quadratic in
M2,2. Its limits for 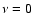 and
and
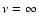 are
are
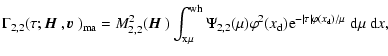 |
|
|
(101) |
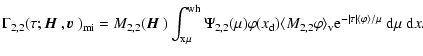 |
|
|
(102) |
With these two limits, one can construct an approximate expression for
the mean value
 with the procedure applied in
Eq. (93) to
with the procedure applied in
Eq. (93) to
 .
.
Collecting all the results, we obtain
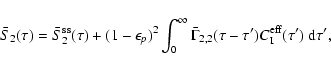 |
(103) |
where
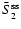 is given by Eqs. (94) or
(95) and
is given by Eqs. (94) or
(95) and
This expression takes a simpler form if the distribution function
 can be factorized since one can average
M2,2 and
can be factorized since one can average
M2,2 and  independently. If
independently. If  is not random, one
recovers the expression given for
is not random, one
recovers the expression given for 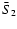 in Eq. (57).
in Eq. (57).
6.3 Stokes U. Mean source function
The expressions given in Sect. 5.5 are easily
generalized to the random velocity case. The
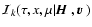 (k=3 to 6) satisfy the
transfer Eq. (39) with
(k=3 to 6) satisfy the
transfer Eq. (39) with
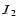 replaced by
replaced by
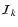 and
and
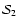 replaced by
replaced by
![\begin{displaymath}{\cal S}_k(\tau\vert{\mbox{\boldmath$\vec{H}$ }},{\mbox{\bold...
...box{\boldmath$\vec{H}$ }},{\mbox{\boldmath$\vec{v}$ }})\bigr],
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img348.gif) |
(105) |
where
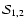 and
and
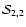 are defined in
Eqs. (83) and (84). The expression of
are defined in
Eqs. (83) and (84). The expression of
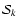 is a straightforward generalization of Eqs. (65)
and (66).
is a straightforward generalization of Eqs. (65)
and (66).
To calculate the mean value of
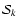 ,
we follow the procedure
described in Sect. 6.2. Replacing
,
we follow the procedure
described in Sect. 6.2. Replacing
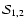 by
by
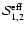 ,
we obtain
,
we obtain
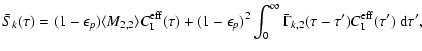 |
|
|
(106) |
where
If 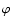 is not random, we recover the expression given in
Eq. (67).
is not random, we recover the expression given in
Eq. (67).
6.4 Mean Stokes parameters
The mean conditional six-component vector
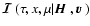 is given by
Eqs. (28) and (29) with
is given by
Eqs. (28) and (29) with
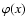 replaced
by
replaced
by
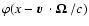 and
and
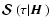 by
by
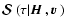 .
The averaging over the magnetic field and velocity field
distributions cannot be performed explicitly unless we replace
each component of
.
The averaging over the magnetic field and velocity field
distributions cannot be performed explicitly unless we replace
each component of
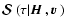 by the
mean source functions
by the
mean source functions
 ,
,
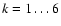 ,
constructed above (for k=1, the mean source function is
,
constructed above (for k=1, the mean source function is
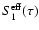 ). With this approximation, the six components of
the mean irreducible Stokes vector at
). With this approximation, the six components of
the mean irreducible Stokes vector at  can be written as
can be written as
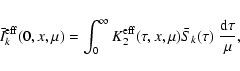 |
(108) |
with
![\begin{displaymath}K_2^{\rm eff}(\tau,x,\mu)= \Big\langle
\exp\Bigl[-{\vert\tau...
... \nu\Pi_1^{\rm v})\Bigr]
\varphi(~\cdot~)\Big\rangle_{\rm v}.
\end{displaymath}](/articles/aa/full/2006/05/aa2540-04/img359.gif) |
(109) |
The operator
 is defined in Eq. (77). The mean
source functions are given in
Eq. (80) for k=1, in Eq. (103) for k=2 and in
Eq. (106) for the other values of k.
The function
is defined in Eq. (77). The mean
source functions are given in
Eq. (80) for k=1, in Eq. (103) for k=2 and in
Eq. (106) for the other values of k.
The function
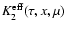 is the
effective escape probability introduced in FF76. A numerical method
for the calculation of
is the
effective escape probability introduced in FF76. A numerical method
for the calculation of
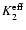 based on an exponential
representation is described in FF80. The mean values of Q and Ucan then be deduced from Eqs. (3) and (4).
based on an exponential
representation is described in FF80. The mean values of Q and Ucan then be deduced from Eqs. (3) and (4).
In this section we have treated simultaneously the effects of a
turbulent velocity field and of a turbulent magnetic field, both
represented by KAPs. The magnetic field effects were treated with the
same approximations as in the absence of velocity field. Namely, we
have neglected the effect of the magnetic field on Stokes I, the
coupling of Stokes Q with Stokes U and we have calculated the
polarization with a two-scattering approximation. For the Stokes
parameter I, we have introduced an effective source function which
takes into account finite correlation length effects of the velocity
field and allows one to
separate some of the velocity field from the magnetic field
effects. We have thus been able to construct explicit expressions for
the mean Stokes parameters Q and U which take into account finite
correlation length effects and also correlations between the magnetic
field and velocity field fluctuations. In the model we have used, the
velocity field and magnetic field have the same correlation length and
the same jumping points. It is certainly possible to release these
assumption. For instance, in Brissaud & Frisch (1971), the electronic
and ionic microfields of the stochastic Stark effect are represented
by two KAPs with different correlation lengths.
7 Concluding remarks
In this paper, we have given explicit expressions for the mean
observable Stokes parameters. We defer to a subsequent work the
numerical calculation of these mean Stokes parameters. The results
will depend on the choices made for the velocity field and magnetic
field distribution function. The current views on solar magnetic
fields (Stenflo 2004) is that 1% of the photospheric volume is filled
by kG flux tubes while 99% is filled with a small scale turbulent
field with a strength in the range of tens of Gauss. Magnetograms from the
Swedish La Palma telescope and from MDI indicate that the probability
distribution function (PDF) of the magnetic field strengths can be
well fitted by Voigt functions with dispersion (damping) wings that
extend out to kG fields (Stenflo & Holzreuter 2002, 2003). For scales
below the diffraction limit of present day telescopes (about 100 km),
numerical simulations of magneto-convection or fully developed
turbulence can provide the PDF of the magnetic field strength, but
also the distribution of the magnetic field directions and some
indications on typical correlation scales. Numerical simulations may
also provide some informations on the velocity distribution and on the
correlations between velocity and magnetic field fluctuations. We note
that our model should be able to incorporate an anisotropic
distribution of magnetic fields and also a correlation scale depending
on a mean magnetic field strength.
Acknowledgements
I have greatly benefited from discussions with Dr. V. Bommier,
M. Faurobert and J. Stenflo. This research was supported by the
Indo-French Center for the Promotion of Advanced Research
(IFCPAR 2404-2).
- Anderson,
P. W. 1954, J. Phys. Soc. Jpn 9, 316
(In the text)
- Athay, G. 1972,
Radiation Transport in Spectral Lines (Dordrecht, Holland: Reidel
Publishing Company)
(In the text)
- Auvergne,
M., Frisch, H., Frisch, U., Froeschlé, Ch., & Pouquet, A.
1973, A&A, 29, 93 [NASA ADS] (In the text)
-
Barucha-Reid, A. T. 1960, Elements of the Theory of Markov
Processes and their Applications (New York: McGraw-Hill)
(In the text)
- Bommier, V.
1997a, A&A, 328, 706 [NASA ADS] (In the text)
- Bommier, V.
1997b, A&A, 328, 726 [NASA ADS]
- Bommier, V.,
Derouich, M., Landi Degl'Innocenti, E., Molodij, G., &
Sahal-Bréchot, S. 2005, A&A, 432, 295 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Brissaud,
A., & Frisch, U. 1971, J. Quant. Spec. Radiat. Transf., 11,
1767 (In the text)
- Brissaud,
A., & Frisch, U. 1974, J. Math. Phys., 15, 524 [CrossRef] (In the text)
- Domke, H., &
Hubeny, I. 1988, ApJ, 213, 296
- Domke, H., &
Pavlov, G. G. 1979, Ap&SS, 66, 47 [NASA ADS] (In the text)
- Faurobert-Scholl, M. 1991,
A&A, 246, 469 [NASA ADS] (In the text)
- Faurobert-Scholl, M. 1993,
A&A, 268, 765 [NASA ADS] (In the text)
- Faurobert-Scholl, M. 1996, Sol.
Phys. 164, 79
(In the text)
-
Faurobert, M., Arnaud, J., Vigneau, J., & Frisch, H. 2001,
A&A, 378, 627 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Feller, W.
1971, An Introduction to probability theory and its applications,
Vol. II, Second edition (New York: John Wiley and Sons Inc.)
(In the text)
- Frisch, H.
1998, A&A, 338, 683 [NASA ADS] (In the text)
- Frisch, H.
1999, in ASSL Series 243, Solar Polarization, ed. K. N. Nagendra,
& J. O. Stenflo, 97 (F99)
(In the text)
- Frisch, H.,
& Frisch, U. 1976, MNRAS, 175, 157 [NASA ADS] (FF76)
(In the text)
- Frisch, U.
1968, in Probabilistic Methods in Applied Mathematics, ed. A. T.
Bharucha-Reid (New York: Academic Press), 75
(In the text)
- Frisch, U.,
& Brissaud, A. 1971, J. Quant. Spec. Radiat. Trans., 11,
1753 (In the text)
- Froeschlé, Ch.,
& Frisch, H. 1980, A&A, 91, 202 [NASA ADS] (FF80)
- Gail, H. P.,
Sedlmayr, E., & Traving, G. 1975, A&A, 44, 421 [NASA ADS] (In the text)
-
Holzreuter, R., Fluri, D. M., & Stenflo. J. O. 2005, A&A,
434, 713 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Ivanov, V.V.,
2004, personnal communication
(In the text)
- Kubo, R. 1954, J.
Phys. Soc. Jpn, 9, 935 (In the text)
- Landi
Degl'Innocenti, E. 1984, Sol. Phys., 91, 1 [NASA ADS] (In the text)
- Landi
Degl'Innocenti, E. 1994, in Solar Surface Magnetism, ed. R. J.
Rutten, & C. J. Schrijver, 29
- Landi
Degl'Innocenti, E., Bommier, V., & Sahal-Bréchot, S. 1990,
A&A, 235, 459 [NASA ADS] (In the text)
- Landi
Degl'Innocenti, M., & Landi Degl'Innocenti, E. 1988, A&A,
192, 374 [NASA ADS] (In the text)
- Landi
Degl'Innocenti, E., Landi Degl'Innocenti, M., & Landolfi, M.
1997, in Forum THEMIS, Publications de l'Observatoire de Paris, ed.
N. Mein, & S. Sahal-Bréchot, 59
(In the text)
- Landi
Degl'Innocenti, E., & Landolfi, M. 2004, Polarization in
Spectral Lines (Kluwer Academic Publishers) (LL04)
(In the text)
- Loskutov,
V. M. 2004, Astron. Rep., 48, 21 [NASA ADS] [CrossRef]; transl. Astron. Zhurnal, 81,
24
(In the text)
- Mihalas, D.
1978, Stellar Atmospheres, Second edition(San Francisco: W.H.
Freeman and Co.)
(In the text)
- Magnan, C.
1975, J. Quant. Spec. Radiat. Transf., 15, 979 [NASA ADS] (In the text)
- Nagendra,
K. N., Frisch, H., & Faurobert-Scholl, M. 1998, A&A, 332,
610 [NASA ADS] (NFF98)
(In the text)
- Omont, A., Smith,
E. W., & Cooper, J. 1973, ApJ, 182, 283 [NASA ADS] [CrossRef] (In the text)
- Papoulis,
A. 1965, Probability, Random Variables and Stochastic Processes
(McGraw-Hill Inc.)
(In the text)
- Sahal-Bréchot,
S. 1981, Space Sc. Rev., 29, 391
- Stenflo, J.
O. 1978, A&A, 66, 241 [NASA ADS] (In the text)
- Stenflo, J.
O. 1982, Sol. Phys., 80, 209 [NASA ADS] [CrossRef] (In the text)
- Stenflo, J.
O. 1994, Solar Magnetic Fields (Dordrecht: Kluwer)
(In the text)
- Stenflo, J.
O. 2004, Rev. Mod. Astron., 17, 269 (In the text)
- Stenflo, J.
O., & Holzreuter, R. 2002, in Magnetic Coupling of the Solar
Atmosphere, ed. H. Sawaya-Lacoste, ESA Publ. SP-505, 101
(In the text)
- Stenflo, J.
O., & Holzreuter, R. 2003, in Current Theoretical Models and
High Resolution Solar Observations: Preparing for ATST, ed. A. A.
Pevtsov, & H. Uitenbroeck, ASP Conf. Ser., 286, 169
(In the text)
-
Trujillo Bueno, J., Shchukina, N., & Asensis Ramos, A. 2004,
Nature, 430, 326 [NASA ADS] [CrossRef]
-
Uhlenbeck, G. E., & Ornstein, L. S. 1930, Phys. Rev., 36, 823 [NASA ADS] [CrossRef];
reprinted in 1954, Selected Papers in Noise and Stochastic
Processes, ed. E. Wax (New York: Dover Publications Inc.), 93
(In the text)
- Wang, M. C., &
Uhlenbeck, G. E. 1945, Rev. Mod. Phys., 17, 323 [NASA ADS] [CrossRef]; reprinted in 1954,
Selected Papers in Noise and Stochastic Processes, ed. E. Wax (New
York: Dover Publications Inc.), 113
(In the text)
Copyright ESO 2006
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2540fig1.eps} %
\end{figure}](/articles/aa/full/2006/05/aa2540-04/Timg11.gif)
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{2540fig1.eps} %
\end{figure}](/articles/aa/full/2006/05/aa2540-04/Timg11.gif)
![]() .
Here
.
Here
![]() and xare the direction and
frequency of the incident beam,
and xare the direction and
frequency of the incident beam,
![]() and x' the direction and
frequency of the scattered beam and
and x' the direction and
frequency of the scattered beam and
![]() the magnetic field
vector (see e.g. Domke & Hubeny 1998; Stenflo 1994, and references
therein; Faurobert et al. 2001; Bommier et al. 2005; Holzreuter et al. 2005). For a two-level
atom model, with unpolarized ground level and a redistribution
function of the above type, each Stokes parameter can be written in the form
the magnetic field
vector (see e.g. Domke & Hubeny 1998; Stenflo 1994, and references
therein; Faurobert et al. 2001; Bommier et al. 2005; Holzreuter et al. 2005). For a two-level
atom model, with unpolarized ground level and a redistribution
function of the above type, each Stokes parameter can be written in the form
![]() .
For simplicity we also assume
that there is no correlation between x and x', i.e. we assume
complete frequency redistribution as in Landi Degl'Innocenti et al. (1990), for example. We then have
.
For simplicity we also assume
that there is no correlation between x and x', i.e. we assume
complete frequency redistribution as in Landi Degl'Innocenti et al. (1990), for example. We then have
![]() ,
where
,
where
![]() is the line absorption profile, normalized to
unity. The Ii, can be used to form a six-component vector
is the line absorption profile, normalized to
unity. The Ii, can be used to form a six-component vector
![]() .
In the following we use this vector to represent the
polarized field and refer to it as the irreducible Stokes vector.
.
In the following we use this vector to represent the
polarized field and refer to it as the irreducible Stokes vector.
![]() can be written as
can be written as
![]() becomes equal to the identity matrix
for frequencies
becomes equal to the identity matrix
for frequencies
![]() .
Typically
.
Typically
![]() .
The results are
not very sensitive to the choice of
.
The results are
not very sensitive to the choice of ![]() .
We explain on the final
results how this cutoff can be implemented.
.
We explain on the final
results how this cutoff can be implemented.
![]() is a stationary Markov random process (Wang & Uhlenbeck 1945; Barucha-Reid 1960; Papoulis 1965; Feller 1971), the transition
probability density
is a stationary Markov random process (Wang & Uhlenbeck 1945; Barucha-Reid 1960; Papoulis 1965; Feller 1971), the transition
probability density
![]() ,
such that
,
such that
![]() is the probability to find a field
is the probability to find a field
![]() (within
(within
![]() )
at time s+t, given a field
)
at time s+t, given a field
![]() at
time s, satisfies the Kolmogorov equation
at
time s, satisfies the Kolmogorov equation
![]() : it suffices to
multiply it by Ik and then to integrate as in
Eq. (16). The terms involving the partial derivatives
in the r.h.s. of Eq. (14) can be integrated by parts. The
integrated term is zero because of the factor
: it suffices to
multiply it by Ik and then to integrate as in
Eq. (16). The terms involving the partial derivatives
in the r.h.s. of Eq. (14) can be integrated by parts. The
integrated term is zero because of the factor ![]() .
The
remaining integral contains only the term corresponding to l=k. One
thus obtains
.
The
remaining integral contains only the term corresponding to l=k. One
thus obtains
![]() .
This solution is independent of the initial
condition
.
This solution is independent of the initial
condition
![]() .
We introduce the line optical depth defined
as
.
We introduce the line optical depth defined
as
![]() .
We thus obtain for
.
We thus obtain for
![]() the
transfer equation
the
transfer equation
![]() introduced in
Eq. (11) contains a correlation time scale
introduced in
Eq. (11) contains a correlation time scale
![]() .
The
corresponding spatial correlation scale measured in optical depth
units is
.
The
corresponding spatial correlation scale measured in optical depth
units is
![]() .
It is convenient to
introduce
.
It is convenient to
introduce
![]() which can be interpreted as a mean
number of turbulent eddies per unit optical depth. Here we assume that
which can be interpreted as a mean
number of turbulent eddies per unit optical depth. Here we assume that
![]() is independent of optical depth. To simplify the notation, we
redefine the operator
is independent of optical depth. To simplify the notation, we
redefine the operator ![]() such that
such that
![]() ,
,
![]() and
and
![]() are
are ![]() matrices with lines and columns numbered from 1 to 6. The elements of
these matrices can be found in Faurobert-Scholl (1991) (see also
NFF98; F99). Here we give only a few of them. We note also that signs
may be different from those of the above mentioned articles because
of sign differences in the elements of the vector
matrices with lines and columns numbered from 1 to 6. The elements of
these matrices can be found in Faurobert-Scholl (1991) (see also
NFF98; F99). Here we give only a few of them. We note also that signs
may be different from those of the above mentioned articles because
of sign differences in the elements of the vector
![]() .
The first line and first
column of
.
The first line and first
column of ![]() contain only zeros, except for M1,1=1 (we drop
the symbol hat when we refer to elements of these matrices). The
others 25 elements of
contain only zeros, except for M1,1=1 (we drop
the symbol hat when we refer to elements of these matrices). The
others 25 elements of ![]() are non zero and depend on the
magnetic field (strength and direction). In
are non zero and depend on the
magnetic field (strength and direction). In
![]() ,
only the diagonal elements and the two off diagonal
elements
,
only the diagonal elements and the two off diagonal
elements
![]() are non zero. The non zero elements
are
are non zero. The non zero elements
are
![]() ,
,
![]() ,
where
,
where
![]() is a 6-component
vector. Numerical solutions of Eq. (5) (see NFF98) show
that J2 is roughly ten times smaller than J1 and that the other
Jk with
is a 6-component
vector. Numerical solutions of Eq. (5) (see NFF98) show
that J2 is roughly ten times smaller than J1 and that the other
Jk with
![]() are roughly ten times smaller than J2. To
evaluate the source function, it is actually sufficient to keep the
two first columns in the matrix
are roughly ten times smaller than J2. To
evaluate the source function, it is actually sufficient to keep the
two first columns in the matrix ![]() and set all the other
elements to zero (in the first column, only the element M1,1 is
not zero). With this approximation we keep in the source terms the
contributions from the Q=0 components, s00=I1 and s20=I2,
only. The transfer equations for the Ik take thus much simpler
forms.
and set all the other
elements to zero (in the first column, only the element M1,1 is
not zero). With this approximation we keep in the source terms the
contributions from the Q=0 components, s00=I1 and s20=I2,
only. The transfer equations for the Ik take thus much simpler
forms.
![]() ,
are of the form
,
are of the form
![]() .
Equations (2) to (4) will
then give us the mean values of the Stokes parameters Q and U and
the magnetic field dependent terms in the expansion of Stokes I.
.
Equations (2) to (4) will
then give us the mean values of the Stokes parameters Q and U and
the magnetic field dependent terms in the expansion of Stokes I.
![]() ,
the conditional mean of I2 and apply the
technique described in Sect. 3 to
Eq. (35). In Sect. 5.1, we construct
an integral equation similar to Eq. (30) for a mean
conditional source function
,
the conditional mean of I2 and apply the
technique described in Sect. 3 to
Eq. (35). In Sect. 5.1, we construct
an integral equation similar to Eq. (30) for a mean
conditional source function
![]() .
A Neumann
series expansion of this integral equation, limited to the two first
terms, yields an explicit expression for
.
A Neumann
series expansion of this integral equation, limited to the two first
terms, yields an explicit expression for
![]() as is shown in Sect. 5.2. In
Sect. 5.3, we show how to average
as is shown in Sect. 5.2. In
Sect. 5.3, we show how to average
![]() over the magnetic field distribution. We thus
obtain a mean source function
over the magnetic field distribution. We thus
obtain a mean source function
![]() which is used in
Sect. 5.4 to calculate the mean value of
which is used in
Sect. 5.4 to calculate the mean value of
![]() .
In Sect. 5.5, we show how to construct the mean
values of the
.
In Sect. 5.5, we show how to construct the mean
values of the
![]() and
and
![]() ,
for
,
for
![]() .
.
![]() ,
i.e. to consider that the
polarization is created by photons which have been scattered only
once. It has the advantage of by-passing transfer calculations for the
polarized field. It is not restricted to optically thin lines. For
example, it works quite well for a line like Sr I 460.7 nm which
has an optical depth around 10 (Faurobert et al. 2001). This can be
explained by the fact that
,
i.e. to consider that the
polarization is created by photons which have been scattered only
once. It has the advantage of by-passing transfer calculations for the
polarized field. It is not restricted to optically thin lines. For
example, it works quite well for a line like Sr I 460.7 nm which
has an optical depth around 10 (Faurobert et al. 2001). This can be
explained by the fact that ![]() decreases fairly rapidly with
increasing values of
decreases fairly rapidly with
increasing values of ![]() and by the fact that the single scattering
albedo is significantly smaller than unity.
and by the fact that the single scattering
albedo is significantly smaller than unity.
![]() :
:
![]() and
and
![]() ,
respectively. For a
stationary Kubo-Anderson process m(t) of zero mean and density
,
respectively. For a
stationary Kubo-Anderson process m(t) of zero mean and density ![]() ,
the
covariance is given by (Brissaud & Frisch 1974)
,
the
covariance is given by (Brissaud & Frisch 1974)
![]() such that
such that
![]() ,
the dominant factor inside the large
square bracket in Eq. (57) is
,
the dominant factor inside the large
square bracket in Eq. (57) is
![]() .
So, as
expected, we recover the microturbulent limit when many turbulent
eddies lie between
.
So, as
expected, we recover the microturbulent limit when many turbulent
eddies lie between ![]() and
and ![]() .
.
![]() is independent of
the correlation length of the magnetic field in the standard single
scattering approximation since
is independent of
the correlation length of the magnetic field in the standard single
scattering approximation since ![]() is approximated by the first
term in the r.h.s.
is approximated by the first
term in the r.h.s.
![]() involves
only a few fairly simple steps. First one has to solve a scalar
transfer problem for I1 with, say, an accelerated Lambda iteration
method. Equation (57) gives an explicit
expression for the mean source function
involves
only a few fairly simple steps. First one has to solve a scalar
transfer problem for I1 with, say, an accelerated Lambda iteration
method. Equation (57) gives an explicit
expression for the mean source function ![]() in which
in which ![]() ,
the
primary source, is given by Eq. (37). It suffices then
to integrate the source function as shown in Eq. (60). Of
course a choice has to be made for the distribution of the magnetic
field.
,
the
primary source, is given by Eq. (37). It suffices then
to integrate the source function as shown in Eq. (60). Of
course a choice has to be made for the distribution of the magnetic
field.
![]() are simply given by
Eq. (60) with
are simply given by
Eq. (60) with ![]() replaced by
replaced by ![]() .
The Mk,2 depend linearly on
.
The Mk,2 depend linearly on
![]() and
and
![]() .
Hence the mean values of
.
Hence the mean values of
![]() and
and
![]() over an isotropically distributed field are zero
(see Eq. (62)) and Stokes U is zero as it should be.
The same situation holds for any axisymmetric magnetic field distribution.
over an isotropically distributed field are zero
(see Eq. (62)) and Stokes U is zero as it should be.
The same situation holds for any axisymmetric magnetic field distribution.
![]() (
macroturbulent limit), an integration over x is exactly
equivalent to an integration over
(
macroturbulent limit), an integration over x is exactly
equivalent to an integration over
![]() .
It is not true when
.
It is not true when
![]() is finite. This remark, which explains
why the source function, in the scalar case, is not very
sensitive to turbulent velocities, suggests to
introduce for
is finite. This remark, which explains
why the source function, in the scalar case, is not very
sensitive to turbulent velocities, suggests to
introduce for
![]() an effective medium approximation, namely
an effective medium approximation, namely
![]() based on the macro and microturbulent limits of
based on the macro and microturbulent limits of
![]() which
does not have this drawback.
which
does not have this drawback.
![]() )
and microturbulent (
)
and microturbulent (
![]() )
limits,
)
limits,
![]() over
the joint magnetic and velocity field distribution to obtain the mean
source function in the single scattering approximation denoted here
by
over
the joint magnetic and velocity field distribution to obtain the mean
source function in the single scattering approximation denoted here
by
![]() .
We consider separately each of the two
approximations constructed for
.
We consider separately each of the two
approximations constructed for
![]() .
The effective medium
approximation leads to
.
The effective medium
approximation leads to
![]() (k=3 to 6) satisfy the
transfer Eq. (39) with
(k=3 to 6) satisfy the
transfer Eq. (39) with
![]() replaced by
replaced by
![]() and
and
![]() replaced by
replaced by
![]() ,
we follow the procedure
described in Sect. 6.2. Replacing
,
we follow the procedure
described in Sect. 6.2. Replacing
![]() by
by
![]() ,
we obtain
,
we obtain