A&A 446, 367-372 (2006)
DOI: 10.1051/0004-6361:20053919
M. Wernli 1 - P. Valiron 1 - A. Faure 1 - L. Wiesenfeld 1 - P. Jankowski 2 - K. Szalewicz 3
1 - Laboratoire d'Astrophysique de Grenoble, UMR 5571
CNRS-UJF, OSUG, Université Joseph Fourier, BP 53, 38041
Grenoble Cedex 9, France
2 - Department of Quantum Chemistry,
Institute of Chemistry, Nicholaus Copernicus University, Gagarina
7, 87-100 Torun, Poland
3 - Department of Physics and
Astronomy, University of Delaware, Newark, DE 19716, USA
Received 26 July 2005 / Accepted 12 September 2005
Abstract
Cross sections for the rotational (de)excitation of CO by
ground state para- and ortho-H2 are obtained using quantum
scattering calculations for collision energies between 1 and
520 cm-1. A new CO-H2 potential energy surface is employed
and its quality is assessed by comparison with explicitly correlated
CCSD(T)-R12 calculations. Rate constants for rotational levels of
CO up to 5 and temperatures in the range 5-70 K are deduced. The
new potential is found to have a strong influence on the resonance
structure of the cross sections at very low collision energies. As a
result, the present rates at 10 K differ by up to 50![]() with those
obtained by Flower (2001) on a previous, less accurate, potential
energy surface.
with those
obtained by Flower (2001) on a previous, less accurate, potential
energy surface.
Key words: molecular data - molecular processes - ISM: molecules
Since its discovery in interstellar space more than 30 years ago (Wilson et al. 1970), carbon monoxide (CO) has been extensively observed both in our own and in other galaxies. CO is indeed the second most abundant molecule in the Universe after H2 and, thanks to its dipole moment, it is the principal molecule used to map the molecular gas in galactic and extragalactic sources. CO is also currently the only molecule to have been observed at redshifts as high as z=6.42(Walter et al. 2003). Collisional excitation of rotational levels of CO occurs in a great variety of physical conditions and emission from levels with rotational quantum numbers J up to 39 have been identified in circumstellar environments (Cernicharo et al. 1996).
Hydrogen molecules are generally the most abundant colliding partners
in the interstellar medium, although collisions with H, He and
electrons can also play important roles, for example in diffuse
interstellar clouds. Rate coefficients for collisions with H2 based
on the potential energy surface (PES) of Jankowski & Szalewicz (1998, hereafter JS98),
have been calculated recently
(Flower 2001; Mengel et al. 2001). These rates were found to be in reasonable
agreement (typically within a factor of 2 at 10 K) with those computed
on older and less accurate PES (e.g. Schinke et al. 1985). However, in
contrast to previous works, Mengel et al. (2001) and Flower (2001)
found the inelastic rates with
![]() larger than those with
larger than those with
![]() for para-H2. This result reflects the crucial
importance of the PES, whose inaccuracies are one of the main sources
of error in collisional rate calculations, especially at low
temperatures (see, e.g., Balakrishnan et al. 2002). The JS98 surface has been
checked against experiment by a couple of
authors. Gottfried & McBane (2001), in particular, computed second virial
coefficients below 300 K and showed that the attractive well of the
PES was slightly too deep. A modification which consists of
multiplying the PES by a factor of 0.93 was therefore suggested by
these authors. This modification was applied by Mengel et al. (2001) and
it was indeed found to produce better agreement with measurements of
pressure broadening cross sections. On the other hand, the original
PES was found to give a very good agreement with experimental
state-to-state rotational cross sections measured near 1000 cm-1(Antonova et al. 2000). At these energies, however, only the short-range
repulsive region of the PES is probed. Finally, Flower (2001)
showed that the scaling of 0.93 has only minor influence on the
rotational rates and he employed the original PES.
for para-H2. This result reflects the crucial
importance of the PES, whose inaccuracies are one of the main sources
of error in collisional rate calculations, especially at low
temperatures (see, e.g., Balakrishnan et al. 2002). The JS98 surface has been
checked against experiment by a couple of
authors. Gottfried & McBane (2001), in particular, computed second virial
coefficients below 300 K and showed that the attractive well of the
PES was slightly too deep. A modification which consists of
multiplying the PES by a factor of 0.93 was therefore suggested by
these authors. This modification was applied by Mengel et al. (2001) and
it was indeed found to produce better agreement with measurements of
pressure broadening cross sections. On the other hand, the original
PES was found to give a very good agreement with experimental
state-to-state rotational cross sections measured near 1000 cm-1(Antonova et al. 2000). At these energies, however, only the short-range
repulsive region of the PES is probed. Finally, Flower (2001)
showed that the scaling of 0.93 has only minor influence on the
rotational rates and he employed the original PES.
Very recently, a new PES has been computed by
Jankowski & Szalewicz (2005, hereafter JS05). In contrast to the JS98 surface, which was
calculated within the symmetry-adapted perturbation theory (SAPT), the
JS05 surface has been obtained using the supermolecular approximation
based on the CCSD(T) method using correlation-consistent basis sets
complemented by bonding functions and basis set extrapolation. It
turned that the major inaccuracy of JS98 was due to the use of a
correction for the effects of the third and higher orders extracted in
an approximate way from supermolecular SCF calculations. It recently
became clear that this correction should not be used for nonpolar or
nearly nonpolar monomers. If this term is removed from JS98, the
agreement of the resulting surface with JS05 is
excellent. Jankowski & Szalewicz (2005) have employed their new PES to
calculate rovibrational energy levels of the para-H2-CO complex and
they obtained a very good agreement (better than 0.1 cm-1compared to 1 cm-1 for the JS98 surface) with the measurements by
McKellar (1998). The computed values of the second virial
coefficients also agree very well with the experimental ones. Full
details can be found in Jankowski & Szalewicz (2005). In the present paper, we
present new rate constants for the rotational excitation of CO by
H2 based on the JS05 surface. Our results are restricted to low
temperatures (T<70 K) because the new PES calculations are found to
affect the rotational cross sections only at low collision energy
(
![]() cm-1). As shown below, differences with the
results of Flower (2001) range from a few percent to 50
cm-1). As shown below, differences with the
results of Flower (2001) range from a few percent to 50![]() .
Such
effects, if not dramatic, are significant in view of the special
importance of the CO-H2 system in astrophysics. Furthermore, the
present results are of particular interest for comparisons with future
measurements planned in Rennes by Sims and collaborators
(Sims 2005).
.
Such
effects, if not dramatic, are significant in view of the special
importance of the CO-H2 system in astrophysics. Furthermore, the
present results are of particular interest for comparisons with future
measurements planned in Rennes by Sims and collaborators
(Sims 2005).
Following the conventions of JS98, the CO-H2 "rigid-body'' PES
is described by the following four Jacobi coordinates: three angles
![]() ,
,
![]() and
and ![]() and the distance R denoting the
intermolecular centre of mass separation. The angles
and the distance R denoting the
intermolecular centre of mass separation. The angles ![]() and
and
![]() are the tilt angles of H2 and CO with respect to the
intermolecular axis, and
are the tilt angles of H2 and CO with respect to the
intermolecular axis, and ![]() is the dihedral angle. In the linear
geometry, the oxygen atom points toward H2 when
is the dihedral angle. In the linear
geometry, the oxygen atom points toward H2 when
![]() .
The
JS05 surface has been obtained by averaging over the intramolecular
ground state vibration of H2, while CO was treated as rigid at its
vibrational ground-state averaged geometry. The JS05 surface has a
global depth of -93.049 cm-1 for the linear geometry with the C
atom pointing toward the H2 molecule (
.
The
JS05 surface has been obtained by averaging over the intramolecular
ground state vibration of H2, while CO was treated as rigid at its
vibrational ground-state averaged geometry. The JS05 surface has a
global depth of -93.049 cm-1 for the linear geometry with the C
atom pointing toward the H2 molecule (
![]() ,
,
![]() ,
,
![]() )
and for a centre of mass
separation
)
and for a centre of mass
separation
![]() bohrs.
The (unscaled) JS98 and JS05 surfaces are presented in
Fig. 1 and compared to independent CCSD(T)-R12 calculations
using ground-state averaged geometries for CO and H2.
bohrs.
The (unscaled) JS98 and JS05 surfaces are presented in
Fig. 1 and compared to independent CCSD(T)-R12 calculations
using ground-state averaged geometries for CO and H2.
![\begin{figure}
\includegraphics[width=8.6cm,clip]{3919fig1.eps} \end{figure}](/articles/aa/full/2006/04/aa3919-05/Timg17.gif) |
Figure 1:
H2-CO interaction energy as a function of R for three
coplanar configurations:
|
| Open with DEXTER | |
The latter calculations can be considered as high accuracy
state-of-the-art ab initio calculations. Indeed the CCSD(T)-R12
approach![]() has been shown to produce intermolecular energies with near
spectroscopic accuracy without recourse to extrapolation
(Faure et al. 2005; Müller & Kutzelnigg 2000; Halkier et al. 1999). In order to save some computing
time and to improve the numerical stability of the R12 operator, the
core orbitals were frozen
has been shown to produce intermolecular energies with near
spectroscopic accuracy without recourse to extrapolation
(Faure et al. 2005; Müller & Kutzelnigg 2000; Halkier et al. 1999). In order to save some computing
time and to improve the numerical stability of the R12 operator, the
core orbitals were frozen![]() in the
CCSD(T)-R12 calculations. We employed R12-suited basis sets including
up to g functions for C and O, and d functions for H (as developed
in Kedzuch et al. 2005; Noga & Valiron 2003). The R12 results are assumed to approach the
basis set limit within 1-2 cm-1. In particular the inclusion of
a large set of bonding functions (corresponding to the R12-suited H
set) affects the interaction by
in the
CCSD(T)-R12 calculations. We employed R12-suited basis sets including
up to g functions for C and O, and d functions for H (as developed
in Kedzuch et al. 2005; Noga & Valiron 2003). The R12 results are assumed to approach the
basis set limit within 1-2 cm-1. In particular the inclusion of
a large set of bonding functions (corresponding to the R12-suited H
set) affects the interaction by ![]() 0.5 cm-1 only at 7 bohrs separation, while the counterpoise corrections remain very
small, generally below 1 cm-1.
0.5 cm-1 only at 7 bohrs separation, while the counterpoise corrections remain very
small, generally below 1 cm-1.
Here, we can observe that the JS05 surface agree very well with the
CCSD(T)-R12 results while the JS98 surface overestimates the depth of
the CO-H2 potential well by about 10-20![]() ,
as anticipated by
Gottfried & McBane (2001). However, the JS05 surface lies slightly below the
CCSD(T)-R12 one. This agrees with the observation in JS05, based on
extrapolations involving bases up to quintuple zeta quality, that the
potential is about 1-2 cm-1 too deep in the region of the global
minimum. On the other hand, the comparison of the virial coefficients
from JS05 with experiment suggests that the exact potential is still
deeper, probably due to the effects resulting from theory levels
beyond CCSD(T). We also checked that the R12 values are recovered
within 1 cm-1 by a basis set extrapolation involving larger
(triple and quadruple zeta) sets and the popular bonding functions
proposed by Williams et al. (1995). These comparisons provides a further check
of the quality of the new CO-H2 PES and also confirm the
suspected inaccuracies of the JS98 surface.
,
as anticipated by
Gottfried & McBane (2001). However, the JS05 surface lies slightly below the
CCSD(T)-R12 one. This agrees with the observation in JS05, based on
extrapolations involving bases up to quintuple zeta quality, that the
potential is about 1-2 cm-1 too deep in the region of the global
minimum. On the other hand, the comparison of the virial coefficients
from JS05 with experiment suggests that the exact potential is still
deeper, probably due to the effects resulting from theory levels
beyond CCSD(T). We also checked that the R12 values are recovered
within 1 cm-1 by a basis set extrapolation involving larger
(triple and quadruple zeta) sets and the popular bonding functions
proposed by Williams et al. (1995). These comparisons provides a further check
of the quality of the new CO-H2 PES and also confirm the
suspected inaccuracies of the JS98 surface.
In order to interface the JS98 and JS05 surfaces with the scattering
code, the FORTRAN routines of Jankowski & Szalewicz (2005,1998)
were employed to generate a grid of 57 000 geometries. These grid
points were distributed in 19 fixed intermolecular distances R (in
the range 4-15 bohrs) via random sampling for the angular
coordinates. At each intermolecular distance, the interaction
potential V was least-squares fitted over the following angular
expansion:
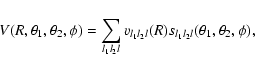 |
(1) |
| vl1 l2 l(R) | = | ||
| (2) |
We selected an initial angular expansion including all anisotropies up
to l1=10 for CO and l2=6 for H2, resulting in 142
sl1 l2
l functions. The accuracy of the angular expansion was monitored
using a self-consistent Monte Carlo error estimator (Rist et al. 2005),
which also permitted to select the most pertinent angular terms. The
resulting set was composed of 60 basis functions involving
anisotropies up to l1=7 and l2=4. A cubic spline interpolation
was finally employed over the whole intermolecular distance range and
was smoothly connected with standard extrapolations to provide
continuous expansion coefficients suitable for scattering
calculations. The final accuracy of this 60 term expansion was found
to be better than 1 cm-1 in the global minimum region of the PES
while the individual expansion coefficients were converged within
0.01 cm-1. It should be noted that the expansion does not reproduce
exactly the values of the potential energy at the grid
points![]() , in contrast to the approach
followed by Flower (2001) who used the same number (25) of angular
geometries and basis functions. The main advantage of our approach is
to guarantee the convergence of the individual expansion coefficients,
in particular in the highly anisotropic short-range part (R<6 bohrs)
of the interaction.
, in contrast to the approach
followed by Flower (2001) who used the same number (25) of angular
geometries and basis functions. The main advantage of our approach is
to guarantee the convergence of the individual expansion coefficients,
in particular in the highly anisotropic short-range part (R<6 bohrs)
of the interaction.
The MOLSCAT code (Hutson & Green 1994) was employed to perform the
rigid-rotor scattering calculations reported below. All calculations
were made using the rigid rotor approximation, with rotational
constants
![]() cm-1 and
cm-1 and
![]() cm-1. For para-H2 (j2=0), calculations were carried out at
total energies (collision plus CO rotation) ranging from 4 to
520 cm-1. Full close-coupling calculations were performed between
4 and 160 cm-1, with steps of 0.2 cm-1 in the resonance
range 4-120 cm-1, and a much coarser step of 5 cm-1between 120 and 160 cm-1. Between 160 and 520 cm-1, the
coupled-state approximation (McGuire & Kouri 1974) was shown to reproduce
full close-coupling calculations within a few percent and was thus
employed. The energy step was 20 cm-1 between 160 and
340 cm-1, and 30 cm-1 at higher energies. For ortho-H2,
the same collision energy grid was used, resulting in total energies
in the range 126-642 cm-1. The propagator used was the
log-derivative propagator (Alexander & Manolopoulos 1987). Parameters of the
integrator were tested and adjusted to ensure a typical precision of
1-2%. All the calculations with para-H2 used a
j2=0, 2basis, while the ortho-H2 calculations used only a j2=1basis. Tests of this basis were made at the highest energy, where
inclusion of the j2=3 (closed) state was found to affect cross
sections by less than one percent. At least three closed channels were
included at each energy for the CO rotational basis. At the highest
energy, we had thus a
cm-1. For para-H2 (j2=0), calculations were carried out at
total energies (collision plus CO rotation) ranging from 4 to
520 cm-1. Full close-coupling calculations were performed between
4 and 160 cm-1, with steps of 0.2 cm-1 in the resonance
range 4-120 cm-1, and a much coarser step of 5 cm-1between 120 and 160 cm-1. Between 160 and 520 cm-1, the
coupled-state approximation (McGuire & Kouri 1974) was shown to reproduce
full close-coupling calculations within a few percent and was thus
employed. The energy step was 20 cm-1 between 160 and
340 cm-1, and 30 cm-1 at higher energies. For ortho-H2,
the same collision energy grid was used, resulting in total energies
in the range 126-642 cm-1. The propagator used was the
log-derivative propagator (Alexander & Manolopoulos 1987). Parameters of the
integrator were tested and adjusted to ensure a typical precision of
1-2%. All the calculations with para-H2 used a
j2=0, 2basis, while the ortho-H2 calculations used only a j2=1basis. Tests of this basis were made at the highest energy, where
inclusion of the j2=3 (closed) state was found to affect cross
sections by less than one percent. At least three closed channels were
included at each energy for the CO rotational basis. At the highest
energy, we had thus a
![]() basis. Transitions among all
levels up to j1=5 were computed. Finally, rate constants were
calculated for temperatures ranging from 5 to 70 K by integrating the
cross sections over essentially the whole collision energy range
spanned by the corresponding Maxwell-Boltzmann distributions. The
energy grid was chosen so that the highest collision for all
transitions be about ten times larger than the highest
temperature. The accuracy of the present rates is expected to lie
between 5 and 10% at 70 K, and probably better at lower temperatures.
basis. Transitions among all
levels up to j1=5 were computed. Finally, rate constants were
calculated for temperatures ranging from 5 to 70 K by integrating the
cross sections over essentially the whole collision energy range
spanned by the corresponding Maxwell-Boltzmann distributions. The
energy grid was chosen so that the highest collision for all
transitions be about ten times larger than the highest
temperature. The accuracy of the present rates is expected to lie
between 5 and 10% at 70 K, and probably better at lower temperatures.
![\begin{figure}
\includegraphics[width=8.8cm,clip]{3919fig2.eps} \end{figure}](/articles/aa/full/2006/04/aa3919-05/Timg26.gif) |
Figure 2: Inelastic deexcitation cross sections for CO in collisions with para-H2 as a function of total energy. Both curves are the results of our calculations with the unscaled JS98 PES (dashed curves), and the JS05 PES (solid curves). |
| Open with DEXTER | |
Figure 2 clearly illustrates the fact that the resonance pattern, which is here of "shape'' rather than "Feshbach'' type as discussed by Flower (2001), strongly depends on the interaction potential. We also note that the very fine grid used at the lowest energies was necessary for a proper description of the resonances. It can be observed that the cross sections converge at higher energies (above the resonance regime), as the collision energy becomes large compared to the potential energy welldepth. As a result, rate constants are expected to differ significantly from those of Flower (2001) at very low temperatures only.
Table 1: Rotational deexcitation rates of CO in collision with para-H2 (j2=0) at three temparatures. I and F are the CO initial and final rotation states, respectively. All rates are given in units of 10-10 cm3/s. Third column recalls the rates of Flower (2001), obtained with the unscaled JS98 surface. Fourth column presents our rates obtained with the JS05 surface. In the 30 K panel, the rates obtained with our expansion of the JS98 surface are also presented.
Table 2: Rotational deexcitation rates of CO in collision with ortho-H2 (j2=1). The conventions are the same as for the para case.
We present in Tables 1 and 2 our rate constants at 10, 30 and 70 K, and those of Flower (2001) for comparison. We note that especially at 10 K, rates can vary up to 50%. These differences reflect the influence of three independent parameters: (i) the high accuracy of the new ab initio potential energy calculations, (ii) the use of a well converged expansion of the PES over the angular basis functions and (iii) the careful description of resonances. It is however not clear how to discriminate among the three effects. At 70 K (and beyond), our rates and those of Flower (2001) agree within typically 10-20 %, as anticipated from the convergence of the cross sections at high energy. We therefore conclude that the differences between our results and those of Flower (2001) are astrophysically relevant for temperatures below 70 K. Above this value, the inaccuracies of the JS98 PES have only a minor influence on the rotational rates and the results of Flower (2001) and Mengel et al. (2001) are reliable.
The para-H2 rates presented in the 30 K panel in Table 1 illustrate the respective contribution of the surface and of the subsequent angular expansion and collisional treatment. Data in Cols. 1 and 2 are based upon the same JS98 surface and the differences are ascribable to the better convergence of the angular expansion and to the finer description of the resonances. Conversely, data in Cols. 2 and 3 are based upon the same angular expansion and collisional treatment, and the differences only reflect the improvement in the surface. Depending on initial and final rotation states, various situations may occur. In some cases there is a compensation of errors for the surface (as for 2-1, 3-0, 3-2), or for the expansion and collisional treatment (as for 5-0). Collisional and surface errors may also partially cancel out, as for the 1-0 rate, or add up as for the 2-0 rate. While the detailed behaviour seems complex and irregular, in average the errors introduced by the older JS98 surface are of the same order of magnitude as the errors introduced by the limited angular expansion and energy mesh in the older work by Flower (2001).
It is interesting to note that for collisions with para-H2,
inelastic rates with
![]() are larger than those with
are larger than those with
![]() while the reverse applies for ortho-H2. The propensity to
favor even
while the reverse applies for ortho-H2. The propensity to
favor even
![]() over odd
over odd
![]() has been explained
semiclassically by McCurdy & Miller (1977) in terms of an interference effect
related to the even anisotropy of the PES. The reverse propensity can
also occur if the odd anisotropy is sufficiently large, as observed
experimentally in the case of CO-He (Carty et al. 2004). Here, the
propensity depends on the quantum state of the projectile because in
the para case (j2=0), some terms of the PES expansion (those
associated with the quadrupole of H2) vanish
identically. Therefore, the even anisotropy of the PES is larger with
ortho-H2 than with para-H2 and
has been explained
semiclassically by McCurdy & Miller (1977) in terms of an interference effect
related to the even anisotropy of the PES. The reverse propensity can
also occur if the odd anisotropy is sufficiently large, as observed
experimentally in the case of CO-He (Carty et al. 2004). Here, the
propensity depends on the quantum state of the projectile because in
the para case (j2=0), some terms of the PES expansion (those
associated with the quadrupole of H2) vanish
identically. Therefore, the even anisotropy of the PES is larger with
ortho-H2 than with para-H2 and
![]() are favored. Note,
however, that these propensity rules depend on j1,
are favored. Note,
however, that these propensity rules depend on j1,
![]() and
the temperature. Another interesting point is that the differences
with the results of Flower (2001) are generally smaller with
ortho-H2 than with para-H2. This again reflects the different
anisotropies of the PES for para and ortho-H2: in the ortho case,
cross sections are larger and scattering calculations are less
sensitive to small changes in the PES. Similar effects have also been
observed recently in the case of H2O-H2 (Dubernet et al. 2005).
and
the temperature. Another interesting point is that the differences
with the results of Flower (2001) are generally smaller with
ortho-H2 than with para-H2. This again reflects the different
anisotropies of the PES for para and ortho-H2: in the ortho case,
cross sections are larger and scattering calculations are less
sensitive to small changes in the PES. Similar effects have also been
observed recently in the case of H2O-H2 (Dubernet et al. 2005).
It is also of some interest to compare the present results with the CO-He rates obtained by Cecchi-Pestellini et al. (2002). It is generally assumed that rates with para-H2 (j2=0) should be about 50% larger than He rates owing to the smaller collisional reduced mass and the larger size of H2. We have checked that the present H2 (j2=0) rates are in fact within a factor of 1-3 of the He rates. Thus, as already shown by Phillips et al. (1996) in the case of H2O, rates for excitation by H2 are not adequately represented by scaled rates for excitation by He.
Finally, for use in astrophysical modelling, the temperature
dependence of the above transition rates k(T) have been fitted by
the analytic form used by Balakrishnan et al. (1999):
Cross sections for the rotational (de)excitation of CO by ground state
para- and ortho-H2 have been computed using quantum scattering
calculations for collision energies in the range 1-520 cm-1. A
new, highly accurate, CO-H2 potential energy surface has been
employed and it has been shown to strongly influence the resonance
structure of the cross sections in the very low collision energy
regime (
![]() cm-1). Conversely, at higher
energies, the effect of the new potential was found to be only
minor. As a result, the present rate constants are found to differ
significantly from those of Flower (2001), obtained on a previous
and less accurate potential, only for temperatures lower than
70 K. Transitions among all levels up to j1=5 only were computed as
higher states are generally not populated at the low temperatures
investigated here.
cm-1). Conversely, at higher
energies, the effect of the new potential was found to be only
minor. As a result, the present rate constants are found to differ
significantly from those of Flower (2001), obtained on a previous
and less accurate potential, only for temperatures lower than
70 K. Transitions among all levels up to j1=5 only were computed as
higher states are generally not populated at the low temperatures
investigated here.
This work illustrates the relationship between the accuracy of the potential energy surface and the accuracy of the corresponding inelastic cross sections for a simple system of astrophysical relevance. Even at low temperatures, moderate inaccuracies in the surface (in the 10-20% range) result in semi-quantitative inelastic rates with typical errors in the 20-50% range with no dramatic amplification of errors. However, this optimistic conclusion presents also a harder counterpart, as we show that in order to obtain accurate inelastic rates one has to satisfy all three conditions, i.e., use an accurate surface, a properly converged angular expansion, and a detailed description of the cross-section resonances. Consequently, the improvement of the accuracy of inelastic rates, especially at higher temperatures when the number of channels is large, represents a considerable computational effort. In this respect, the work by Flower (2001) represented an excellent compromise to achieve a typical 20% accuracy below 100 K.
This work extends the initial objectives of the "Molecular Universe'' European FP6 network (2005-2008) and participates to the current international efforts to improve the description of the underlying microscopic processes in preparation of the next generation of molecular observatories.
Acknowledgements
CCSD(T)-R12 calculations were performed on the IDRIS and CINES French national computing centers (projects no. 051141 and x2005 04 20820). MOLSCAT calculations were performed on an experimental cluster using a subset of the computer grid tools (under project Cigri of the "Action Incitative GRID'') with the valuable help from F. Roch and N. Capit. This research was supported by the CNRS national program "Physique et Chimie du Milieu Interstellaire'' and the "Centre National d'Études Spatiales''. MW was supported by the Ministère de l'Enseignement Supérieur et de la Recherche. K.S. acknowledges the NSF CHE-0239611 grant.
Table A1: Fitting coefficients of CO-para-H2 rates, following formula 3. I and F are the initial and final rotation states, respectively. The rates thus obtained are in cm3 s-1.
Table A2: Fitting coefficients of CO-ortho-H2 rates, following formula 3. I and F are the initial and final rotation states, respectively. The rates thus obtained are in cm3 s-1.