A&A 446, 267-277 (2006)
DOI: 10.1051/0004-6361:20053911
1 - Astronomy Department, 521 Campbell Hall, University of California, Berkeley, CA 94720, USA
2 -
Hamburger Sternwarte, Universität Hamburg, Gojenbergsweg 112, 21029 Hamburg, Germany
Received 25 July 2005 / Accepted 12 September 2005
Abstract
More than 600 high resolution spectra of stars with spectral
type F and later were obtained in order to search for signatures of
differential rotation in line profiles. In 147 stars the rotation
law could be measured, with 28 of them found to be differentially
rotating. Comparison to rotation laws in stars of spectral type A
reveals that differential rotation sets in at the convection
boundary in the HR-diagram; no star that is significantly hotter
than the convection boundary exhibits the signatures of differential
rotation. Four late A-/early F-type stars close to the convection
boundary and at
![]() km s-1 show
extraordinarily strong absolute shear at short rotation periods
around one day. It is suggested that this is due to their small
convection zone depth and that it is connected to a narrow range in
surface velocity; the four stars are very similar in
km s-1 show
extraordinarily strong absolute shear at short rotation periods
around one day. It is suggested that this is due to their small
convection zone depth and that it is connected to a narrow range in
surface velocity; the four stars are very similar in
![]() and
and ![]() .
Detection frequencies of differential rotation
.
Detection frequencies of differential rotation
![]() were analyzed in stars with
varying temperature and rotation velocity. Measurable differential
rotation is more frequent in late-type stars and slow rotators. The
strength of absolute shear,
were analyzed in stars with
varying temperature and rotation velocity. Measurable differential
rotation is more frequent in late-type stars and slow rotators. The
strength of absolute shear,
![]() ,
and differential
rotation
,
and differential
rotation ![]() are examined as functions of the stellar effective
temperature and rotation period. The highest values of
are examined as functions of the stellar effective
temperature and rotation period. The highest values of
![]() are found at rotation periods between two and three
days. In slower rotators, the strongest absolute shear at a given
rotation rate
are found at rotation periods between two and three
days. In slower rotators, the strongest absolute shear at a given
rotation rate
![]() is given approximately by
is given approximately by
![]() ,
i.e.,
,
i.e.,
![]() const. In faster rotators, both
const. In faster rotators, both
![]() and
and
![]() diminish less rapidly. A comparison with
differential rotation measurements in stars of later spectral type
shows that F-stars exhibit stronger shear than cooler stars do and
the upper boundary in absolute shear
diminish less rapidly. A comparison with
differential rotation measurements in stars of later spectral type
shows that F-stars exhibit stronger shear than cooler stars do and
the upper boundary in absolute shear
![]() with temperature
is consistent with the temperature-scaling law found in Doppler
Imaging measurements.
with temperature
is consistent with the temperature-scaling law found in Doppler
Imaging measurements.
Key words: stars: activity - stars: late-type - stars: rotation - stars: general
Stellar rotation rates range from those too slow to be detected by Doppler broadening up to rates at which centrifugal forces become comparable to surface gravity. Surface magnetic fields, either fossil or generated by some type of magnetic dynamo, can couple to ionized plasma and brake a star's rotation via a magneto-thermal wind. Magnetic braking is observed in stars with deep convective envelopes where magnetic dynamo processes can efficiently maintain strong magnetic fields. As a consequence, field stars of a spectral type later than F are generally slow rotators with surface velocities below 10 km s-1.
Magnetic braking requires the existence of a magnetic field, which also causes the plethora of all the effects found in stellar magnetic activity. While early magnetic braking may be due to fossil fields amplified during contraction of the protostellar cloud, magnetic activity at later phases requires a mechanism that maintains magnetic fields on longer timescales. In the Sun, a magnetic dynamo located at the interface between convective envelope and radiative core is driven by radial differential rotation. This dynamo has been identified as the main source of magnetic fields, although there is growing evidence that it is not the only source of magnetic field generation (e.g., Schrijver & Zwaan 2000) and that magnetic fields also exist in fully convective stars (Johns-Krull & Valenti 1996). The solar-type dynamo, however, has the potential to generate magnetic fields in all non-fully convective stars, as long as they show a convective envelope, and magnetic fields have been observed in a variety of slowly rotating stars (e.g., Solanki 1991; Marcy 1984; Gray 1984).
Calculations of stellar rotation laws, which describe angular velocity as a function of radius and latitude, have been carried out by Kitchatinov & Rüdiger (1999) and Küker & Rüdiger (2005) for different equatorial angular velocities. Kitchatinov & Rüdiger (1999) investigated rotation laws in a G2- and a K5-dwarf. They expect stronger latitudinal differential rotation in slower rotators, and their G2-dwarf model exhibits stronger differential rotation than the K5-dwarf does. Küker & Rüdiger (2005) calculate a solar-like model, as well as a model of an F8 main sequence star. They also come to the conclusion that differential rotation is stronger in the hotter model; the maximum differential rotation in the F8 star is roughly twice as strong as in the G2 star for the same viscosity parameter. The calculated dependence of horizontal shear on rotation rate, however, does not show a monotonic slope but has a maximum that occurs near 10 d in the F8 type star and around 25 d in the solar-type star. The strength of differential rotation depends on the choice of the viscosity parameter, which is not well constrained, but the trends in temperature and rotation are unaffected by that choice.
Observational confirmation of solar radial and latitudinal differential rotation comes from helioseismological studies that provide a detailed picture of the differentially rotating outer convection zone (e.g., Schou 1998). Such seismological studies are not yet available for any other star. Asteroseismological missions, like COROT and Kepler, may open a new window on stellar differential rotation, but its data quality may provide only a very limited picture in the near future (Gizon & Solanki 2004). In the case of the Sun, radial differential rotation manifests itself in latitudinal differential rotation that can be observed at the stellar surface, but all stars except the Sun are at distances where their surfaces cannot be adequately resolved. With the advent of large optical interferometers, more may be learned from observations of spatially resolved stellar surfaces (Domiciano de Souza et al. 2004). For now, we have to rely on indirect methods to measure the stellar rotation law.
Photometric programs that search for stellar differential rotation assume that starspots emerge at various latitudes with different rotation rates, as observed on the Sun. Hall (1991) and Donahue et al. (1996) measured photometric rotation periods and interpreted seasonal variations as the effect of differential rotation on migrating spots. Although these techniques are comparable to the successful measurements of solar differential rotation through sunspots (Balthasar et al. 1986), they still rely on a number of assumptions, e.g., the spot lifetime being longer than the observational sequence, an assumption difficult to test in stars other than the Sun (cf. Wolter et al. 2005). Photometric measurements report lower limits for differential rotation on the order of 10% of the rotation velocity (i.e. the equator rotating 10% faster than the polar regions), and differential rotation is reported to be stronger in slower rotators.
Doppler Imaging (DI) has been extensively used to determine latitudinal differential rotation where the derived maps are constructed from time-series of high-resolution spectra. Differential rotation can then be extracted from comparing two surface maps taken with time separation of a few rotation periods (e.g., Wolter et al. 2005; Donati & Collier Cameron 1997). Doppler maps can also be constructed that incorporate differential rotation during the inversion algorithm (Petit et al. 2002). Detections of differential rotation through DI have recently been compiled by Barnes et al. (2005), who also analyze dependence on stellar rotation and temperature, and then compare them to results obtained from other techniques. Their results will be discussed in Sect. 6.
The technique employed in this paper is to search for latitudinal
differential rotation in the shape of stellar absorption line
profiles. This method is applicable only to stars not dominated by
spots. From a single exposure, latitudinal solar-like differential
rotation - i.e. the equator rotating faster than polar regions - can
be derived by measuring its unambiguous fingerprints in the Fourier
domain. The foundations of the Fourier transform method (FTM) were
laid by Gray (1977,1998), and first models were done by
Bruning (1981). A detailed description of the fingerprints of
solar-like differential rotation and the first successful detections
are given in Reiners & Schmitt (2003a,2002a). The FTM is limited to
moderately rapid rotators (see Sect. 2), but the big
advantage of this method is that latitudinal differential rotation can
be measured from a single exposure. This allows the analysis of a
large sample of stars with a comparably small amount of telescope
time. Reiners & Schmitt (2003a) report on differential rotation in ten out of
a sample of 32 stars of spectral types F0-G0 with projected rotation
velocities 12 km s
![]() km s-1.
Reiners & Schmitt (2003b) investigated a sample of 70 rapid rotators with
km s-1.
Reiners & Schmitt (2003b) investigated a sample of 70 rapid rotators with
![]() km s-1 and found a much lower fraction of
differential rotators. Differential rotation has also been sought in
A-stars that have no deep convective envelopes. Reiners & Royer (2004)
report on three objects out of 76 in the range A0-F1,
60 km s
km s-1 and found a much lower fraction of
differential rotators. Differential rotation has also been sought in
A-stars that have no deep convective envelopes. Reiners & Royer (2004)
report on three objects out of 76 in the range A0-F1,
60 km s
![]() km s-1, which show
signatures of differential rotation.
km s-1, which show
signatures of differential rotation.
In the cited works, differential rotation is investigated in stars of limited spectral types and rotation velocities. In this paper, I aim to investigate all measurements of differential rotation from FTM, add new observations, and finally compare them to results from DI and theoretical predictions. Currently, more than 600 stars were observed during the course of this project, and in 147 of them the rotation law could be measured successfully.
Latitudinal differential rotation has a characteristic fingerprint in
the shape of the rotational broadening that appears in each spectral
line. Since all other line broadening mechanisms, like turbulence,
thermal, and pressure broadening, etc., also affect the shape of
spectral lines, the effects of differential rotation are very subtle.
Signatures of differential rotation and a recipe for measuring them
are presented in Reiners & Schmitt (2002a). Since the signatures are so small,
and spectral line blending is a serious issue even in stars of
moderate rotation rates at
![]() km s-1,
single lines are not measured, but instead a total broadening function
is constructed from many lines of similar intrinsic shape. This
process typically involves 15 lines in slow rotators observed at very
high resolution (Sect. 3), and 300 lines in
rapid rotators observed at lower resolution. In order to derive a
unique broadening function at the required precision, high data
quality is required. Detailed information about demands on data
quality can be found in Reiners & Schmitt (2003b,a).
km s-1,
single lines are not measured, but instead a total broadening function
is constructed from many lines of similar intrinsic shape. This
process typically involves 15 lines in slow rotators observed at very
high resolution (Sect. 3), and 300 lines in
rapid rotators observed at lower resolution. In order to derive a
unique broadening function at the required precision, high data
quality is required. Detailed information about demands on data
quality can be found in Reiners & Schmitt (2003b,a).
Interpretation of the profile's shape with rotational broadening
requires that the line profiles are not affected by starspots, stellar
winds, spectroscopic multiplicity, etc. The Fourier transform method
is therefore limited to unspotted single stars with projected rotation
velocities
![]() km s-1, and an upper limit at
km s-1, and an upper limit at
![]() km s-1 is set by gravitational
darkening. More specific information on the influence of starspots, of
very rapid rotation, and some examples of detected signatures of
differential rotation in line profiles can be found in
Reiners (2003), and Reiners & Schmitt (2003b,a,2002a).
km s-1 is set by gravitational
darkening. More specific information on the influence of starspots, of
very rapid rotation, and some examples of detected signatures of
differential rotation in line profiles can be found in
Reiners (2003), and Reiners & Schmitt (2003b,a,2002a).
From the derived broadening profile, the rotation law is determined by
measuring the first two zeros of the profile's Fourier transform,
q1 and q2. In sufficiently rapid rotators, those are direct
indicators of rotational broadening since other broadening mechanisms
(for example turbulence or instrumental broadening) do not show zeros
at such low frequencies. This is also the reason only stars with
![]() km s-1 can be studied; in slower rotators,
line broadening is dominated by turbulence and the zeros due to
rotation cannot be measured. In stars spinning fast enough to be
analyzed with FTM, approximation of net broadening by convolutions is
also justified. The important point in choosing the Fourier domain for
profile analysis is that convolutions become multiplications in
Fourier space. Thus, the fingerprints of rotational broadening
are directly visible in the observed broadening profile's Fourier
transform, and the spectra do not have to be corrected for
instrumental or for any other line broadening, as long as the targets'
rotation dominates the important frequency range.
km s-1 can be studied; in slower rotators,
line broadening is dominated by turbulence and the zeros due to
rotation cannot be measured. In stars spinning fast enough to be
analyzed with FTM, approximation of net broadening by convolutions is
also justified. The important point in choosing the Fourier domain for
profile analysis is that convolutions become multiplications in
Fourier space. Thus, the fingerprints of rotational broadening
are directly visible in the observed broadening profile's Fourier
transform, and the spectra do not have to be corrected for
instrumental or for any other line broadening, as long as the targets'
rotation dominates the important frequency range.
In the following, the stellar rotation law will be approximated in
analogy to the solar case. Differential rotation is expressed in terms
of the variable ![]() ,
with
,
with ![]() the angular velocity and lthe latitude. The rotation law is approximated by
the angular velocity and lthe latitude. The rotation law is approximated by
The role of differential rotation especially for magnetic field
generation in rapid rotators is not understood well. In the case of
the Sun, we know that its magnetic cycle is driven, at least in part,
by radial differential rotation, which itself is reflected in
latitudinal differential rotation. How (and if) magnetic dynamos
depend on the strength of differential rotation in terms of ![]() or on absolute shear
or on absolute shear
![]() has not yet been empirically
tested. Furthermore, different observing techniques measure different
quantities, and authors express their results on stellar rotation laws
in different variables. A variable frequently used is the lap time,
i.e. the time it takes the equator to lap the polar regions (or vice
versa), which is essentially the reciprocal of the shear
has not yet been empirically
tested. Furthermore, different observing techniques measure different
quantities, and authors express their results on stellar rotation laws
in different variables. A variable frequently used is the lap time,
i.e. the time it takes the equator to lap the polar regions (or vice
versa), which is essentially the reciprocal of the shear
![]() .
Differential rotation
.
Differential rotation
![]() is
the shear divided by the angular velocity. Expressing rotation
velocity in terms of rotation period P essentially means the
reciprocal of angular velocity
is
the shear divided by the angular velocity. Expressing rotation
velocity in terms of rotation period P essentially means the
reciprocal of angular velocity ![]() ,
but using
,
but using ![]() instead
of
instead
of
![]() introduces several problems, since one has to
consider whether P denotes equatorial or polar rotation period, the
latter being larger with solar-like differential rotation
(cf. Reiners & Schmitt 2003b). In this paper, I will express the rotation
law in terms of
introduces several problems, since one has to
consider whether P denotes equatorial or polar rotation period, the
latter being larger with solar-like differential rotation
(cf. Reiners & Schmitt 2003b). In this paper, I will express the rotation
law in terms of ![]() and
and
![]() ,
in order to search for
correlations with rotation velocity. The quantity measured by the FTM
is
,
in order to search for
correlations with rotation velocity. The quantity measured by the FTM
is ![]() with a fixed observational threshold of
with a fixed observational threshold of
![]() thereby limiting the detection of deviations to rigid
rotation. The uncertainty in
thereby limiting the detection of deviations to rigid
rotation. The uncertainty in ![]() measured by FTM is approximately
measured by FTM is approximately
![]() .
The perhaps more intuitive parameter for the
physical consequences of differential rotation, however, is the shear
.
The perhaps more intuitive parameter for the
physical consequences of differential rotation, however, is the shear
![]() ,
where
,
where ![]() has to be obtained from
has to be obtained from ![]() and the radius. When analyzing the rotation law in terms
of
and the radius. When analyzing the rotation law in terms
of
![]() ,
one has to keep in mind that it can never exceed
angular velocity itself, if polar and equatorial regions are not
allowed to rotate in opposite directions. In other words,
differential rotation cannot be larger than 100%.
,
one has to keep in mind that it can never exceed
angular velocity itself, if polar and equatorial regions are not
allowed to rotate in opposite directions. In other words,
differential rotation cannot be larger than 100%.
Table 1: Data used for this analysis. Spectra were taken with different high-resolution spectrographs. Detection of differential rotation requires higher resolution in slower rotators. The minimum rotation velocities required for determining the rotation law are given in Col. 4. From the 147 spectra from which differential rotation could be determined, 28 stars show signatures of differential rotation.
Data for this study have been compiled from observations carried out
at different telescopes. Observations of field stars with projected
rotation velocities higher than
![]() km s-1 have
been carried out with FEROS on the 1.5 m telescope (
R = 48 000),
ESO, La Silla, or with FOCES (
R = 40 000) on the 2.2 m at CAHA.
Slower rotating field stars were observed at higher resolution at the
CES with the 3.6 m telescope, ESO, La Silla (
R = 220 000).
Additionally, observations in open clusters were carried out with the
multi-object facility FLAMES feeding VLT's optical high-resolution
spectrograph UVES at a resolution of
R = 47 000. Details of the
spectra and instruments used are given in
Table 1. Parts of the data were published in
Reiners & Schmitt (2003b,a) and Reiners et al. (2005). For more
information about observations and data reduction, the reader is
referred to these papers. Ten of the cluster targets (FLAMES/UVES), as
well as 34 FOCES targets were not reported on in former
publications
km s-1 have
been carried out with FEROS on the 1.5 m telescope (
R = 48 000),
ESO, La Silla, or with FOCES (
R = 40 000) on the 2.2 m at CAHA.
Slower rotating field stars were observed at higher resolution at the
CES with the 3.6 m telescope, ESO, La Silla (
R = 220 000).
Additionally, observations in open clusters were carried out with the
multi-object facility FLAMES feeding VLT's optical high-resolution
spectrograph UVES at a resolution of
R = 47 000. Details of the
spectra and instruments used are given in
Table 1. Parts of the data were published in
Reiners & Schmitt (2003b,a) and Reiners et al. (2005). For more
information about observations and data reduction, the reader is
referred to these papers. Ten of the cluster targets (FLAMES/UVES), as
well as 34 FOCES targets were not reported on in former
publications![]() .
.
More than 600 stars were observed for this project during the last
four years. For this analysis, I selected the 147 stars for which the
ratio of the Fourier transform's zeros q2/q1 - the tracer of the
rotation law - is measured with a precision better than 0.1, i.e.
better than 6% in case of the typical value of
q2/q1 = 1.76.
These 147 stars exhibit broadening functions that are (i) symmetric
(to avoid contamination by starspots), and (ii) reveal rotation
velocities between
![]() km s-1 and 150 km s-1, the latter being an arbitrary threshold in order to
minimize the amount of gravity-darkened stars with
km s-1 and 150 km s-1, the latter being an arbitrary threshold in order to
minimize the amount of gravity-darkened stars with
![]() km s-1 (Reiners 2003). Depending on the spectral
resolution, the minimum rotation velocity is
km s-1 (Reiners 2003). Depending on the spectral
resolution, the minimum rotation velocity is
![]() km s-1 (CES) or 45 km s-1 (FEROS, FOCES, UVES, see
also Table 1).
km s-1 (CES) or 45 km s-1 (FEROS, FOCES, UVES, see
also Table 1).
More than 450 stars have not been used in this analysis. Their broadening functions show a whole variety of broadening profiles. Many are slow rotators, although some were reported as rapid rotators in earlier catalogues (cf. Reiners & Schmitt 2003b). A large number of spectroscopic binaries (or even triples) were found, and another large part of the sample shows spectra that are apparently distorted by starspots or other mechanisms that cause the spectra to appear asymmetric. For analyzing the rotation law from the broadening profile alone, these spectra are useless and are not considered in this work. They may be promising targets for DI techniques or other science; a catalogue of broadening profiles is in preparation.
Reiners & Royer (2004) measured the rotation law in 78 stars of spectral type A including a few early F-type stars. This sample will only be incorporated in the HR-diagram in Sect. 6.1. As will be shown there, rotation laws in A-stars are fundamentally different from those in F-stars. For this reason, I will not incorporate the A-stars in the sample analyzed for rotation- and temperature-dependencies of differential rotation. One of the stars observed during this project has recently been studied with DI, with comparison of the results given in the appendix in Sect. A.
Projected rotation velocities ![]() were derived from the first
zero q1 in the Fourier transform as explained in Reiners & Schmitt (2003b).
As mentioned there, the precision of this measurement is usually <1 km s-1, but simulations revealed a systematic uncertainty of
were derived from the first
zero q1 in the Fourier transform as explained in Reiners & Schmitt (2003b).
As mentioned there, the precision of this measurement is usually <1 km s-1, but simulations revealed a systematic uncertainty of ![]()
![]() in
in ![]() .
Thus, I chose the maximum of the
uncertainty in the intrinsic measurement and the
.
Thus, I chose the maximum of the
uncertainty in the intrinsic measurement and the ![]() limit as the
error on
limit as the
error on ![]() .
.
The typical uncertainty for the determined values of relative
differential rotation in terms of
![]() is
is
![]() (Reiners & Schmitt 2003a). In slow rotators, this
uncertainty is dominated by the noise level due to comparably sparse
sampling of the profile even at very high resolution. In fast
rotators, the profile (i.e., the zeros of the profile's Fourier
transform) can be measured with very high precision. Here the
uncertainty in
(Reiners & Schmitt 2003a). In slow rotators, this
uncertainty is dominated by the noise level due to comparably sparse
sampling of the profile even at very high resolution. In fast
rotators, the profile (i.e., the zeros of the profile's Fourier
transform) can be measured with very high precision. Here the
uncertainty in ![]() stems from poor knowledge of the limb
darkening parameter
stems from poor knowledge of the limb
darkening parameter ![]() .
For the case of a linear limb
darkening law, the value of the measured ratio of the Fourier
transform's first two zeros, q1 and q2, is in the range
1.72 <
q2/q1 < 1.85 (Dravins et al. 1990). With the very conservative estimate
that
.
For the case of a linear limb
darkening law, the value of the measured ratio of the Fourier
transform's first two zeros, q1 and q2, is in the range
1.72 <
q2/q1 < 1.85 (Dravins et al. 1990). With the very conservative estimate
that ![]() is essentially unknown (
is essentially unknown (
![]() ), every
star with
1.72 < q2/q1 < 1.85 in this analysis was considered a
rigid rotator, and
q2/q1 < 1.72 was interpreted as solar-like
differential rotation with the equator rotating faster than the polar
regions. From the measured value of q2/q1, the parameter
), every
star with
1.72 < q2/q1 < 1.85 in this analysis was considered a
rigid rotator, and
q2/q1 < 1.72 was interpreted as solar-like
differential rotation with the equator rotating faster than the polar
regions. From the measured value of q2/q1, the parameter
![]() was determined as explained above.
was determined as explained above.
Stars can exhibit ratios of q2/q1 > 1.85 as well, but this value also does not agree with rigid rotation of a homogenous stellar surface. In the investigated sample of 147 stars, eight (5%) exhibit a ratio of q2/q1 > 1.85. In contrast to solar-like differential rotation with the equator rotating more rapidly than polar regions, this case may be due to anti solar-like differential rotation with polar regions rotating faster than the equator. On the other hand, it can also be caused by a cool polar cap, which is expected to occur in rapidly rotating stars (Schrijver & Title 2001). The lower flux emerging from a cool polar cap makes the line center shallow and has the same signature as anti solar-like differential rotation. While anti solar-like differential rotation cannot be distinguished from a cool polar cap by investigating the rotation profile, the existence of a cool polar cap in rapidly rotating F-stars seems much more plausible than anti solar-like differential rotation. Differentiation between the two cases can only be achieved by measuring differential rotation independent of the line shape. For the scope of this paper, however, I will interpret stars with q2/q1 > 1.85 as rigid rotators with a cool polar cap.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{3911f1.ps}
\end{figure}](/articles/aa/full/2006/04/aa3911-05/Timg45.gif) |
Figure 1: Projected rotation velocity plotted vs. B-V for the whole sample of 147 stars. Differential rotators are plotted as filled circles. Contents of subsamples I-IV are given in Table 2. |
| Open with DEXTER | |
The observations carried out with FEROS, FOCES, UVES, and the CES are
very homogeneous in terms of data quality and the investigated
wavelength region, and only measurements that fulfill the criterion
![]() are considered. The targets have similar
spectral types, but they do not form a statistically unbiased sample.
The quality requirements discussed above make it difficult to analyze
stars in a well-defined sample. This sample certainly is severely
biased by observational and systematic effects. The most important
bias is probably due to rotational braking, by connecting spectral
type with rotational velocity in the presumably old field stars. Later
spectral types suffer from stronger magnetic braking and are expected
to be generally slower than earlier spectral types.
are considered. The targets have similar
spectral types, but they do not form a statistically unbiased sample.
The quality requirements discussed above make it difficult to analyze
stars in a well-defined sample. This sample certainly is severely
biased by observational and systematic effects. The most important
bias is probably due to rotational braking, by connecting spectral
type with rotational velocity in the presumably old field stars. Later
spectral types suffer from stronger magnetic braking and are expected
to be generally slower than earlier spectral types.
Projected rotation velocities ![]() of the sample stars are
plotted versus color B-V in Fig. 1, while
differentially rotating stars (i.e. stars with
of the sample stars are
plotted versus color B-V in Fig. 1, while
differentially rotating stars (i.e. stars with
![]() )
are
indicated by filled circles and will be discussed in detail in
Sect. 6. A clear dependence of
)
are
indicated by filled circles and will be discussed in detail in
Sect. 6. A clear dependence of ![]() on color
is apparent, as expected. In Fig. 1, the sample is
divided arbitrarily into four subsamples with projected rotation
velocities that are higher (lower) than
on color
is apparent, as expected. In Fig. 1, the sample is
divided arbitrarily into four subsamples with projected rotation
velocities that are higher (lower) than
![]() km s-1, and color redder (bluer) than B-V = 0.4. The
total numbers of stars in each subsample and the numbers of
differential rotators are given in Table 2. Most
targets occupy regions I and IV. The scarcity in region II is due to
the early F-type stars not being subject to strong magnetic braking, and
since the sample mainly consists of field stars, most stars later than
B-V = 0.4 have been decelerated into region IV and do not appear in
region III. Thus, slower rotating stars generally have a later
spectral type in the sample. This implies that the effects of
temperature and rotation velocity on the fraction of differentially
rotating stars are degenerate in this sample; slow rotation implies
late spectral type. It is therefore not possible to uniquely
distinguish between the effects of rotation and spectral type in the
investigated sample. This degeneracy has to be kept in mind when
trying to interpret rotation- and temperature-dependencies of
differential rotation in the following chapters.
km s-1, and color redder (bluer) than B-V = 0.4. The
total numbers of stars in each subsample and the numbers of
differential rotators are given in Table 2. Most
targets occupy regions I and IV. The scarcity in region II is due to
the early F-type stars not being subject to strong magnetic braking, and
since the sample mainly consists of field stars, most stars later than
B-V = 0.4 have been decelerated into region IV and do not appear in
region III. Thus, slower rotating stars generally have a later
spectral type in the sample. This implies that the effects of
temperature and rotation velocity on the fraction of differentially
rotating stars are degenerate in this sample; slow rotation implies
late spectral type. It is therefore not possible to uniquely
distinguish between the effects of rotation and spectral type in the
investigated sample. This degeneracy has to be kept in mind when
trying to interpret rotation- and temperature-dependencies of
differential rotation in the following chapters.
Table 2: Amount of differential rotators, total number of stars, and percentage of differential rotators for each subsample of Fig. 1.
![\begin{figure}
\par\includegraphics[angle=-90,width=15cm,clip]{3911f2.ps}
\end{figure}](/articles/aa/full/2006/04/aa3911-05/Timg48.gif) |
Figure 2:
HR-diagram of all currently available measurements
of latitudinal differential rotation from FTM. Stars analyzed in
this work are plotted in black, and stars from the A-star sample
in Reiners & Royer (2004) in grey. Differential rotators are indicated
by filled circles. Symbol size represents ranges of projected
rotation velocity |
| Open with DEXTER | |
As a first result of the profile analysis, I present ![]() and
the measurement of the rotation law for all 147 objects in
Appendix B. Fields stars (FEROS, FOCES, and CES
observations) are compiled in Table B.1, FLAMES/UVES
targets in Table B.2.
and
the measurement of the rotation law for all 147 objects in
Appendix B. Fields stars (FEROS, FOCES, and CES
observations) are compiled in Table B.1, FLAMES/UVES
targets in Table B.2.
In the sample of 147 stars for which the rotation law was measured, 28 (19%) exhibit signatures of solar-like differential rotation ( q2/q1 < 1.72). CES-, FEROS-, and FOCES-samples contain field stars of spectral type later than F0, with the majority of them brighter than V = 6 mag. Stars in fields of open clusters contained in the UVES-sample probably are mostly younger than the field stars, and all of them should have reached the main sequence (Stahler & Palla 2004).
All currently available measurements of the stellar rotation law from
rotation profile shape (i.e., 147 stars from this sample and 78 stars from Reiners & Royer 2004) are plotted in an HR-diagram in
Fig. 2. For the field and A-stars, effective temperature
![]() and bolometric magnitude
and bolometric magnitude
![]() were derived from
were derived from
![]() photometry taken from Hauck & Mermilliod (1998) using the program
UVBYBETA published by Moon (1985). For
photometry taken from Hauck & Mermilliod (1998) using the program
UVBYBETA published by Moon (1985). For
![]() a new
calibration by Napiwotzki et al. (1993) based on the grids of
Moon & Dworetsky (1985) was used, and the statistical error of the temperature
determination is about
a new
calibration by Napiwotzki et al. (1993) based on the grids of
Moon & Dworetsky (1985) was used, and the statistical error of the temperature
determination is about
![]() K. For three of the
field stars, no
K. For three of the
field stars, no ![]() photometry is available; all three are
rigid rotators, so no value of
photometry is available; all three are
rigid rotators, so no value of
![]() was calculated to avoid
inconsistencies. For the cluster stars, no
was calculated to avoid
inconsistencies. For the cluster stars, no ![]() data is
available, so radius and temperature are estimated from B-V color
using zero-age main sequence (ZAMS) polynomials taken from
Gray (1976), i.e., they are assumed to be young. For them,
data is
available, so radius and temperature are estimated from B-V color
using zero-age main sequence (ZAMS) polynomials taken from
Gray (1976), i.e., they are assumed to be young. For them,
![]() is calculated from
is calculated from
In Fig. 2, stars are plotted as open or filled circles
that indicate rigid (
![]() )
or differential rotation (
)
or differential rotation (
![]() ), respectively. Circle sizes display projected rotation velocities
), respectively. Circle sizes display projected rotation velocities
![]() as explained in the figure. The 147 stars given in
Tables B.1 and B.2 are plotted as
black symbols, while stars from Reiners & Royer (2004) are plotted as grey
symbols. Evolutionary main sequence tracks for
M = 1.2, 1.4, 1.6,
2.0, and
as explained in the figure. The 147 stars given in
Tables B.1 and B.2 are plotted as
black symbols, while stars from Reiners & Royer (2004) are plotted as grey
symbols. Evolutionary main sequence tracks for
M = 1.2, 1.4, 1.6,
2.0, and
![]() and the ZAMS from Siess et al. (2000) are also
shown. Near the interface of A-stars and F-stars, the "granulation
boundary'' from Gray & Nagel (1989) is indicated with dashed lines. This is
the region where line bisectors measured in slow rotators show a
reversal. For dwarfs and subgiants, the "granulation boundary''
coincides with theoretical calculations of the "convection boundary''
and thus can be identified as the region where deep envelope
convection disappears (cf. Gray & Nagel 1989). The exact region of this
boundary is not defined well and may depend on factors other than
temperature and luminosity.
and the ZAMS from Siess et al. (2000) are also
shown. Near the interface of A-stars and F-stars, the "granulation
boundary'' from Gray & Nagel (1989) is indicated with dashed lines. This is
the region where line bisectors measured in slow rotators show a
reversal. For dwarfs and subgiants, the "granulation boundary''
coincides with theoretical calculations of the "convection boundary''
and thus can be identified as the region where deep envelope
convection disappears (cf. Gray & Nagel 1989). The exact region of this
boundary is not defined well and may depend on factors other than
temperature and luminosity.
The stars shown in Fig. 2 cover a wide range in temperature on both sides of the convection boundary. Because field stars are investigated, many stars have evolved away from the ZAMS. Rotation velocity as indicated by symbol size follows the well-known behavior of magnetic braking; late type stars are generally slowed down and exhibit slower rotation velocities. The striking fact visible in Fig. 2 is that none of the differential rotators detected with FTM lies significantly on the hot side of the convection boundary - latitudinal differential rotation has only been detected in stars believed to possess a deep convective envelope.
The largest group of differential rotators can be found near the ZAMS
at all temperatures that are cooler than the convection boundary. The
convection boundary itself is also populated by differential rotators.
A few others can be found far away from the ZAMS (at masses
![]() ) to the right end of the main sequence tracks. There
is a hint that differential rotators are lacking in the region between
these few rotators and those near the ZAMS and again between them and
those near the convection boundary, although this region is occupied
by rigidly rotating stars (i.e., stars with differential rotation
weaker than the observational threshold). However, it is not clear
from the available sample whether temperature (and evolutionary stage)
or rotation velocity may be the important parameter in determining
differential rotation in F-type stars (see
Sect. 5).
) to the right end of the main sequence tracks. There
is a hint that differential rotators are lacking in the region between
these few rotators and those near the ZAMS and again between them and
those near the convection boundary, although this region is occupied
by rigidly rotating stars (i.e., stars with differential rotation
weaker than the observational threshold). However, it is not clear
from the available sample whether temperature (and evolutionary stage)
or rotation velocity may be the important parameter in determining
differential rotation in F-type stars (see
Sect. 5).
Table 3:
Four stars with extreme values of differential
rotation
![]() .
It is speculated that these objects represent a special class of targets (marked with downward arrows in Fig. 2) in a narrow region of rotation velocity and effective temperatures near the convection boundary.
.
It is speculated that these objects represent a special class of targets (marked with downward arrows in Fig. 2) in a narrow region of rotation velocity and effective temperatures near the convection boundary.
Among all the differentially rotating stars shown as filled circles in
Fig. 2, the four stars with the strongest shear
![]() are found very close to the convection boundary. This
group of rapidly rotating late A-/early F-type stars is listed in
Table 3
are found very close to the convection boundary. This
group of rapidly rotating late A-/early F-type stars is listed in
Table 3![]() . All four
exhibit very similar effective temperatures around
. All four
exhibit very similar effective temperatures around
![]() K, putting them into the region where convective envelopes are
extremely shallow. The four stars show remarkably similar projected
rotation velocities all within 10% of
K, putting them into the region where convective envelopes are
extremely shallow. The four stars show remarkably similar projected
rotation velocities all within 10% of
![]() km s-1, and all four have rotation periods shorter than P
= 2 d. Two of them, HD 6869 and Cl* IC 4665 V 102, exhibit a
shear that is as strong as
km s-1, and all four have rotation periods shorter than P
= 2 d. Two of them, HD 6869 and Cl* IC 4665 V 102, exhibit a
shear that is as strong as
![]() rad d-1 at
rotation periods that are shorter than one day. This contrasts the 34 other stars that show comparably small rotation periods but have
different temperatures or surface velocities. None of the 34 other
rapid rotators exhibits a shear
rad d-1 at
rotation periods that are shorter than one day. This contrasts the 34 other stars that show comparably small rotation periods but have
different temperatures or surface velocities. None of the 34 other
rapid rotators exhibits a shear
![]() in excess of 0.7 rad d-1, i.e. a factor of three weaker than the two
mentioned above, and only three of the 34 show
in excess of 0.7 rad d-1, i.e. a factor of three weaker than the two
mentioned above, and only three of the 34 show
![]() at
all.
at
all.
The fact that the four strongest differential rotators are found at
hot temperatures and high rotation velocities contradicts the general
trend that differential rotation is more common in slowly rotating
cool stars, which will be discussed in the following sections. All
four are very close to the convection boundary or even on its blue
side, meaning extremely shallow convective envelopes. This leads to
the suspicion that the mechanism responsible for the strong shear is
different from the one that drives the shear in stars with deeper
convection zones. This is supported by the observation that all four
stars also exhibit very similar (and comparably large) surface
velocities of about 100 km s-1. It is thus suggested that the
strong surface shear in the four stars in Table 3 is
not comparable to the rest of the sample, but is facilitated by the
high surface velocity in a particularly shallow convective envelope.
Such a mechanism could be supported by eigenmodes that are comparable
to pulsational instabilities, for example in ![]() Scu stars, but
further investigation is beyond the scope of this paper.
Scu stars, but
further investigation is beyond the scope of this paper.
![\begin{figure}
\mbox{
\resizebox{7cm}{!}{\includegraphics[angle=-90,bbllx=28,b...
...cludegraphics[bbllx=0,bblly=0,bburx=480,bbury=275]{3911f3d.ps}} }
\end{figure}](/articles/aa/full/2006/04/aa3911-05/Timg71.gif) |
Figure 3:
Upper panel: histograms of the sample in B-V ( left column)
and |
| Open with DEXTER | |
In this section, the hypothesis that the fraction of differentially
rotating stars with
![]() is independent of rotation velocity
is independent of rotation velocity ![]() and color B-V will be tested. The actual strength of
differential rotation is not taken into account, but will be
investigated in the following sections.
and color B-V will be tested. The actual strength of
differential rotation is not taken into account, but will be
investigated in the following sections.
In Fig. 1, the whole sample of 147 stars has been
divided into the four arbitrary regions mentioned in
Sect. 5 (dividing at
![]() km s-1 and B-V = 0.4). The number of stars and
differential rotators (
km s-1 and B-V = 0.4). The number of stars and
differential rotators (
![]() ,
for this sample this means stars
with
,
for this sample this means stars
with ![]() above the observational threshold of
above the observational threshold of
![]() ), and the percentage of differential rotators is given
in Table 2. The percentage of differentially rotating
stars among slow rotators in regions II and IV is higher than it is
among rapid rotators in regions I and III, respectively; a trend
towards a higher fraction of differential rotators at slower rotation
velocity is visible in both color regimes. The same is true for the
percentage of differentially rotating stars among late-type stars in
regions III and IV. A comparison to earlier type stars among regions I
and II yields a higher fraction of differentially rotating stars
towards later spectral type. I tested the hypothesis that subsamples I-IV are drawn from the same distribution with a total mean of 19%
differential rotators. Samples II and III are consistent with this
hypothesis (5 and 4 expected differential rotators, respectively). For
samples I and IV, the hypothesis can be rejected at a 99% level
(99.3%, 11 expected, and 99.6%, 8 expected for samples I and IV,
respectively). Thus, the fraction of differential rotators with
), and the percentage of differential rotators is given
in Table 2. The percentage of differentially rotating
stars among slow rotators in regions II and IV is higher than it is
among rapid rotators in regions I and III, respectively; a trend
towards a higher fraction of differential rotators at slower rotation
velocity is visible in both color regimes. The same is true for the
percentage of differentially rotating stars among late-type stars in
regions III and IV. A comparison to earlier type stars among regions I
and II yields a higher fraction of differentially rotating stars
towards later spectral type. I tested the hypothesis that subsamples I-IV are drawn from the same distribution with a total mean of 19%
differential rotators. Samples II and III are consistent with this
hypothesis (5 and 4 expected differential rotators, respectively). For
samples I and IV, the hypothesis can be rejected at a 99% level
(99.3%, 11 expected, and 99.6%, 8 expected for samples I and IV,
respectively). Thus, the fraction of differential rotators with ![]() larger than the observational threshold of
larger than the observational threshold of
![]() - which does not depend on
- which does not depend on ![]() or color - is
not constant. It is larger in slower rotators and stars of a later
spectral type.
or color - is
not constant. It is larger in slower rotators and stars of a later
spectral type.
The distribution of differential rotators in ![]() and B-V is
investigated further in Fig. 3. The upper panel shows
the total number of stars divided into five bins in B-V (left), and
seven bins in
and B-V is
investigated further in Fig. 3. The upper panel shows
the total number of stars divided into five bins in B-V (left), and
seven bins in ![]() (right). The lower panel of
Fig. 3 displays the fraction of differential rotators
(
(right). The lower panel of
Fig. 3 displays the fraction of differential rotators
(
![]() )
in the respective color/rotation bins with
)
in the respective color/rotation bins with
![]() -errors. For example, 48% of the 25 stars with projected
rotation velocities
-errors. For example, 48% of the 25 stars with projected
rotation velocities ![]() between 10 and 30 km s-1 show
signatures of differential rotation. Although some bins are sparsely
populated and have large errors, the change from color B-V = 0.4 to
B-V = 0.5 and the transition from slow rotators to stars with
between 10 and 30 km s-1 show
signatures of differential rotation. Although some bins are sparsely
populated and have large errors, the change from color B-V = 0.4 to
B-V = 0.5 and the transition from slow rotators to stars with
![]() km s-1 are significant. The trends indicated
in Table 2 stand out in the lower panel of
Fig. 3. In this sample, profiles with
km s-1 are significant. The trends indicated
in Table 2 stand out in the lower panel of
Fig. 3. In this sample, profiles with
![]() are more frequent in slow rotators, which implies that they are
more frequent in stars of later spectral type (due to the sample bias,
cf. Sect. 5).
are more frequent in slow rotators, which implies that they are
more frequent in stars of later spectral type (due to the sample bias,
cf. Sect. 5).
![\begin{figure}
\par\includegraphics[angle=-90,width=7cm,clip]{3911f4a.ps}\hspace*{4mm}
\includegraphics[angle=-90,width=7cm,clip]{3911f4b.ps}
\end{figure}](/articles/aa/full/2006/04/aa3911-05/Timg75.gif) |
Figure 4:
Differential rotation vs. projected rotation
period
|
| Open with DEXTER | |
In this and the following sections, I will investigate the strength of
differential rotation and especially the maximum strength of
differential rotation at different rotation rates. I discuss
differential rotation in terms of
![]() in
Sect. 6.4.1, and analyze the shear
in
Sect. 6.4.1, and analyze the shear
![]() in
Sect. 6.4.2. Although both quantities essentially have
the same meaning, it is instructive to look at both of them
separately. Rotation speed will be expressed as a function of
equatorial rotation period instead of rotation velocity. The rotation
period itself is not measured for the majority of stars, so I will use
in
Sect. 6.4.2. Although both quantities essentially have
the same meaning, it is instructive to look at both of them
separately. Rotation speed will be expressed as a function of
equatorial rotation period instead of rotation velocity. The rotation
period itself is not measured for the majority of stars, so I will use
![]() instead, as calculated from measured
instead, as calculated from measured ![]() and the
radius according to Eq. (3).
and the
radius according to Eq. (3).
In the left and right panels of Fig. 4, values of
differential rotation ![]() and absolute shear
and absolute shear
![]() are
plotted against projected rotation period
are
plotted against projected rotation period
![]() ,
respectively.
From the 147 stars in Table 1, only the 28 stars
with signatures of differential rotation are shown, while the other
119 objects populate the
,
respectively.
From the 147 stars in Table 1, only the 28 stars
with signatures of differential rotation are shown, while the other
119 objects populate the
![]() region at
region at
![]() .
Field stars from this
sample with available
.
Field stars from this
sample with available ![]() measurements are plotted as filled
circles, while the four cluster targets for which the ZAMS-age has
been assumed are plotted as open circles. In both panels, the three
differentially rotating stars from Reiners & Royer (2004), which have been
discussed in Sect. 6.2, are marked as crosses.
measurements are plotted as filled
circles, while the four cluster targets for which the ZAMS-age has
been assumed are plotted as open circles. In both panels, the three
differentially rotating stars from Reiners & Royer (2004), which have been
discussed in Sect. 6.2, are marked as crosses.
In the left and right panels of Fig. 4, the long
dashed lines qualitatively indicate the upper envelope of
![]() and
and
![]() ,
respectively. No fit was attempted, so the lines should only guide the
eye to clarify what will be discussed in the next sections.
,
respectively. No fit was attempted, so the lines should only guide the
eye to clarify what will be discussed in the next sections.
The advantage of using ![]() is that it is measured directly and
its detection does not depend on rotation period, hence radius, while
measuring
is that it is measured directly and
its detection does not depend on rotation period, hence radius, while
measuring
![]() does. Differential rotation
does. Differential rotation ![]() is
smaller than 0.45 for all rotation periods. While a minimum threshold
of
is
smaller than 0.45 for all rotation periods. While a minimum threshold
of
![]() applies, the
observational technique has no limitations towards high values of
applies, the
observational technique has no limitations towards high values of ![]() .
Thus, the highest detected value of differential rotation
.
Thus, the highest detected value of differential rotation
![]() is not due to
limitations of the FTM.
is not due to
limitations of the FTM.
At rotation periods between two and ten days, the targets populate the
whole region
![]() ,
while the slower
targets could not be analyzed due to the limitations of the FTM (cf.
Sect. 2). Among the rapid rotators with projected
rotation periods that are shorter than two days, the upper envelope
shows a clear decline among the F-stars (filled circles in the left
panel of Fig. 4). Except for the group of A-stars
discussed in Sect. 6.2 (listed in
Table 3), no star with a projected rotation period
less than two days shows
,
while the slower
targets could not be analyzed due to the limitations of the FTM (cf.
Sect. 2). Among the rapid rotators with projected
rotation periods that are shorter than two days, the upper envelope
shows a clear decline among the F-stars (filled circles in the left
panel of Fig. 4). Except for the group of A-stars
discussed in Sect. 6.2 (listed in
Table 3), no star with a projected rotation period
less than two days shows
![]() ,
and no star with
,
and no star with
![]() d shows
d shows
![]() .
Neglecting those four stars, the maximum
value in differential rotation,
.
Neglecting those four stars, the maximum
value in differential rotation,
![]() ,
grows from virtually zero at P = 0.5 d to
,
grows from virtually zero at P = 0.5 d to
![]() in stars slower than
P = 2 d. In slower rotators,
in stars slower than
P = 2 d. In slower rotators,
![]() remains approximately constant.
remains approximately constant.
Absolute shear (
![]() )
is shown in the right
panel of Fig. 4. Since observed values of both
)
is shown in the right
panel of Fig. 4. Since observed values of both ![]() and
and ![]() depend on inclination i, the observed absolute
shear is
depend on inclination i, the observed absolute
shear is
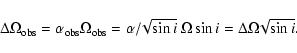 |
(4) |
As expected from Sect. 6.4.1, the F-stars form a
relatively smooth upper envelope in the maximum absolute shear
![]() ,
as observed at different rotation rates. The
slowest rotators exhibit low values of
,
as observed at different rotation rates. The
slowest rotators exhibit low values of
![]() rad d-1 at
rad d-1 at
![]() d.
d.
![]() grows towards a faster rotation rate with a maximum between two and
three days before it diminishes slightly with more rapid rotation. The
strongest differential rotation occurs at rotation periods P between
two and three days at a magnitude of
grows towards a faster rotation rate with a maximum between two and
three days before it diminishes slightly with more rapid rotation. The
strongest differential rotation occurs at rotation periods P between
two and three days at a magnitude of
![]() rad d-1 (i.e., lapping times on the order of 10 d). At
higher rotation rates in the range
rad d-1 (i.e., lapping times on the order of 10 d). At
higher rotation rates in the range
![]() ,
the maximum shear has a slope of roughly
,
the maximum shear has a slope of roughly
![]() .
This slope, however, is not constrained well due to the
large uncertainties and sparse sampling. The data are also consistent
with a plateau at
.
This slope, however, is not constrained well due to the
large uncertainties and sparse sampling. The data are also consistent
with a plateau at
![]() rad d-1 for
0.5 <
P < 3 d. At slower rotation, right from the maximum, the slope is
approximately
rad d-1 for
0.5 <
P < 3 d. At slower rotation, right from the maximum, the slope is
approximately
![]() .
.
Küker & Rüdiger (2005) recently calculated
![]() in an F8 star for
different rotation periods. Their results for
in an F8 star for
different rotation periods. Their results for
![]() (with
a viscosity coefficient
(with
a viscosity coefficient
![]() )
are displayed qualitatively in
both panels of Fig. 4 as a short-dashed line
(Fig. 6 in Küker & Rüdiger 2005). One of their results is that in their
model
)
are displayed qualitatively in
both panels of Fig. 4 as a short-dashed line
(Fig. 6 in Küker & Rüdiger 2005). One of their results is that in their
model
![]() does not follow a single scaling relation for all
periods (as was approximately the case in the calculations
by Kitchatinov & Rüdiger 1999), but that a maximum shear arises at a rotation
period of about P = 7 d in the case of the modeled F8-star.
Comparison of their calculations (right panel of
Fig. 4) to the upper envelope suggested in this work
(long-dashed line) still shows a large quantitative discrepancy. The
qualitative slopes of both curves, however, are in reasonable
agreement with each other. The theoretical curve was calculated for an
F8-star. Küker & Rüdiger (2005) also show
does not follow a single scaling relation for all
periods (as was approximately the case in the calculations
by Kitchatinov & Rüdiger 1999), but that a maximum shear arises at a rotation
period of about P = 7 d in the case of the modeled F8-star.
Comparison of their calculations (right panel of
Fig. 4) to the upper envelope suggested in this work
(long-dashed line) still shows a large quantitative discrepancy. The
qualitative slopes of both curves, however, are in reasonable
agreement with each other. The theoretical curve was calculated for an
F8-star. Küker & Rüdiger (2005) also show
![]() for a solar-type
star, where
for a solar-type
star, where
![]() is essentially moved towards higher
rotation periods and lesser shear; i.e. the short-dashed curve in the
right panel of Fig. 4 moves to the lower right for
later spectral types. Although earlier spectral types are not
calculated by Küker & Rüdiger (2005), it can be expected that
is essentially moved towards higher
rotation periods and lesser shear; i.e. the short-dashed curve in the
right panel of Fig. 4 moves to the lower right for
later spectral types. Although earlier spectral types are not
calculated by Küker & Rüdiger (2005), it can be expected that
![]() will shift towards higher shear and shorter rotation
periods in stars of an even earlier spectral type. Since most stars
investigated in this sample are earlier than F8, this would suggest
qualitative consistency between theoretical curves and the slope of
will shift towards higher shear and shorter rotation
periods in stars of an even earlier spectral type. Since most stars
investigated in this sample are earlier than F8, this would suggest
qualitative consistency between theoretical curves and the slope of
![]() shown here.
shown here.
Differential rotation measurements are now available from a variety of observational techniques (see Sect. 1), comparison of results from techniques becomes possible. However, such a comparison has to be carried out with great care. Photometrically measured periods, for example, are only sensitive to latitudes covered by spots; they reflect only parts of the rotation law and are always lower limits. Furthermore, temperature has been shown to be the dominating factor for the strength of differential rotation (Barnes et al. 2005; Kitchatinov & Rüdiger 1999; Küker & Rüdiger 2005), which has to be taken into account when analyzing the rotation dependence of differential rotation.
In the past, analyses of relations between rotation and differential
rotation have generally assumed a monotonic scaling relation between
period P (or angular velocity
![]() )
and
)
and
![]() .
Such a relation was expected from calculations by
Kitchatinov & Rüdiger (1999). As mentioned above, Küker & Rüdiger (2005) recently
presented new calculations showing that the
.
Such a relation was expected from calculations by
Kitchatinov & Rüdiger (1999). As mentioned above, Küker & Rüdiger (2005) recently
presented new calculations showing that the
![]() vs.
vs. ![]() -relation may have a temperature dependent
maximum.
-relation may have a temperature dependent
maximum.
Searching for dependence on angular velocity, Barnes et al. (2005) recently
compiled data from differential rotation measurements from DI,
photometric monitoring, and FTM. Fitting a single power law to the
compiled data, they derive
![]() ,
which is compared to the case of a G2 dwarf
calculated in Kitchatinov & Rüdiger (1999). From the latter, they cite the
theoretical G2 dwarf relation as
,
which is compared to the case of a G2 dwarf
calculated in Kitchatinov & Rüdiger (1999). From the latter, they cite the
theoretical G2 dwarf relation as
![]() ,
and claim agreement to their fit. Although the work
of Kitchatinov & Rüdiger (1999) has been superseded by Küker & Rüdiger (2005), it
should be mentioned that Kitchatinov & Rüdiger (1999) report
,
and claim agreement to their fit. Although the work
of Kitchatinov & Rüdiger (1999) has been superseded by Küker & Rüdiger (2005), it
should be mentioned that Kitchatinov & Rüdiger (1999) report
![]() ,
implying stronger shear for slower rotation
instead of weaker (note that Küker & Rüdiger 2005, also report a negative exponent
for their solar-like star model at periods less than 20 d).
In fact, the large scatter in the compilation of all measurements from
different techniques (Fig. 3 in Barnes et al. 2005) and the severe
bias due to systematic uncertainties (like the lack of small values
,
implying stronger shear for slower rotation
instead of weaker (note that Küker & Rüdiger 2005, also report a negative exponent
for their solar-like star model at periods less than 20 d).
In fact, the large scatter in the compilation of all measurements from
different techniques (Fig. 3 in Barnes et al. 2005) and the severe
bias due to systematic uncertainties (like the lack of small values
![]() in the sample measured with FTM) leads to any
conclusion about the period dependence from such a heterogeneous
sample very uncertain. The new data in this paper does not
significantly improve this situation and no analysis that improves
upon the one performed by Barnes et al. (2005) can be expected.
in the sample measured with FTM) leads to any
conclusion about the period dependence from such a heterogeneous
sample very uncertain. The new data in this paper does not
significantly improve this situation and no analysis that improves
upon the one performed by Barnes et al. (2005) can be expected.
Although the constantly growing amount of differential rotation measurements provides a relatively large sample, the results from analyzing all measurements as one sample do not yet provide convincing evidence for a unique rotation dependence of differential rotation over the whole range of rotation periods.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.8cm,clip]{3911f5.ps}
\end{figure}](/articles/aa/full/2006/04/aa3911-05/Timg101.gif) |
Figure 5:
Differential rotation
|
| Open with DEXTER | |
Effective temperature is the second parameter after rotation to govern
stellar differential rotation, since convection zone depth, as well as
convection velocity, are very sensitive to
![]() .
Küker & Rüdiger (2005) and Kitchatinov & Rüdiger (1999) report stronger differential
rotation with higher effective temperatures when comparing a
solar-type star to stars of spectral types F8 and K5. The differential
rotators in the sample of F-stars investigated here span a range in
effective temperature between 6000 K and 7150 K. As a result,
analysis of temperature effects on differential rotation is limited by
the small range of targets in
.
Küker & Rüdiger (2005) and Kitchatinov & Rüdiger (1999) report stronger differential
rotation with higher effective temperatures when comparing a
solar-type star to stars of spectral types F8 and K5. The differential
rotators in the sample of F-stars investigated here span a range in
effective temperature between 6000 K and 7150 K. As a result,
analysis of temperature effects on differential rotation is limited by
the small range of targets in
![]() ,
and is biased by the
large range in rotation periods, as discussed above. Thus, I limit the
analysis of temperature dependence to a comparison to differential
rotation in stars that are significantly cooler than
,
and is biased by the
large range in rotation periods, as discussed above. Thus, I limit the
analysis of temperature dependence to a comparison to differential
rotation in stars that are significantly cooler than
![]() K.
K.
Considering stars with effective temperatures in the range
![]() K, Barnes et al. (2005) found a power-law
dependence in their measurements of absolute shear
K, Barnes et al. (2005) found a power-law
dependence in their measurements of absolute shear
![]() on
stellar surface temperature. Their result is compared to the sample of
this work in Fig. 5. Absolute shear follows the
trend expected by Küker & Rüdiger (2005) and Kitchatinov & Rüdiger (1999) with a
stronger surface shear at higher effective temperatures. Although a
large scatter is observed in the F-star measurements, they
qualitatively follow this trend and connect to cooler stars at roughly
the expected values. In addition, the rotation rate of the F-stars is
indicated by symbol size, larger symbols displaying higher rotation
rate. Stars exhibiting a shear in excess of the expected rate for
their temperature tend to show very rapid rotation. Thus, the
investigated F-stars agree qualitatively with the temperature fit
derived by Barnes et al. (2005). A more quantitative analysis is
complicated by the large scatter among measurements of absolute shear,
which is visible also in the sample of Barnes et al. (2005). Again, it
should be noted that the values plotted for the F-star sample only
display stars for which signatures of differential rotation have been
measured. A large number of stars populate the region of weaker
surface shear or rigid rotation (
on
stellar surface temperature. Their result is compared to the sample of
this work in Fig. 5. Absolute shear follows the
trend expected by Küker & Rüdiger (2005) and Kitchatinov & Rüdiger (1999) with a
stronger surface shear at higher effective temperatures. Although a
large scatter is observed in the F-star measurements, they
qualitatively follow this trend and connect to cooler stars at roughly
the expected values. In addition, the rotation rate of the F-stars is
indicated by symbol size, larger symbols displaying higher rotation
rate. Stars exhibiting a shear in excess of the expected rate for
their temperature tend to show very rapid rotation. Thus, the
investigated F-stars agree qualitatively with the temperature fit
derived by Barnes et al. (2005). A more quantitative analysis is
complicated by the large scatter among measurements of absolute shear,
which is visible also in the sample of Barnes et al. (2005). Again, it
should be noted that the values plotted for the F-star sample only
display stars for which signatures of differential rotation have been
measured. A large number of stars populate the region of weaker
surface shear or rigid rotation (
![]() ), and the
temperature law applies only to the strongest differential rotators.
), and the
temperature law applies only to the strongest differential rotators.
The sample of stars with rotation laws measured from spectral broadening profiles with the FTM is constantly growing. In this work, 44 new observations of stars of spectral type F and later were added to the results from former publications. Currently, rotation laws have been analyzed in a homogeneous data set of 147 stars of spectral type F and later, and in a second data set in 78 stars of spectral type A. Among all these observations covering the temperature range between 5600 K and 10 000 K (including A-stars from Reiners & Royer 2004), 31 stars exhibit signatures of solar-like differential rotation. Only three of them are of spectral type A. In the HR-diagram, differential rotators appear near and on the cool side of the convection boundary. No differentially rotating star hotter than 7400 K is known, and it is obvious that the signatures of solar-like differential rotation are closely connected to the existence of deep convective envelopes.
Most differential rotators can be found near to the ZAMS at young
ages, but due to the limited sample and severe selection effects, this
needs confirmation from a less biased sample. Particularly, a number
of slower rotators with temperatures around
![]() K
are needed.
K
are needed.
Four differential rotators are very close to the convection boundary.
All four show extraordinarily strong absolute shear and exhibit
projected rotation velocities within 10% around
![]() km s-1. It is suggested that these stars form a group of
objects in which rotation velocity and convection zone depth
facilitate very strong absolute shear and that the mechanism causing
the shear is different from the later F-type stars.
km s-1. It is suggested that these stars form a group of
objects in which rotation velocity and convection zone depth
facilitate very strong absolute shear and that the mechanism causing
the shear is different from the later F-type stars.
Among the F-stars, differential rotation occurs in the whole range of
temperatures and rotation rates. The sample of 147 stars of spectral
type F and later was investigated for the dependence of differential
rotation on rotation and temperature. 28 of them (19%) exhibit
signatures of differential rotation. The distribution of differential
rotation was approached with two different strategies: (i) investigation of the fraction of stars exhibiting differential
rotation (
![]() ); and (ii) analysis of the maximum
); and (ii) analysis of the maximum ![]() and
maximum
and
maximum
![]() as a function of rotation period and
temperature. The first approach reflects the typical values of
as a function of rotation period and
temperature. The first approach reflects the typical values of
![]() and
and
![]() at any given temperature and
rotation rate, while the second focuses on the question how strong the
absolute shear can possibly be in such stars. Due to the large
uncertainties in the measurements and the high minimum threshold in
differential rotation, the mean values of
at any given temperature and
rotation rate, while the second focuses on the question how strong the
absolute shear can possibly be in such stars. Due to the large
uncertainties in the measurements and the high minimum threshold in
differential rotation, the mean values of ![]() and
and
![]() are not particularly meaningful. Furthermore, it is not clear whether
a smooth transition from stars exhibiting strong differential rotation
to "rigidly'' rotating stars (
are not particularly meaningful. Furthermore, it is not clear whether
a smooth transition from stars exhibiting strong differential rotation
to "rigidly'' rotating stars (
![]() )
or a distinction
between these two groups exists, and the mentioned approaches were
preferred for the analysis.
)
or a distinction
between these two groups exists, and the mentioned approaches were
preferred for the analysis.
In the sample, hotter stars generally rotate more rapidly, and effects
due to rotation velocity and temperature cannot be disentangled. The
distribution of differential rotators depends on color and/or rotation
rate, and the fraction of stars with differential rotation (
![]() )
increases with cooler temperature and/or slower rotation. It is
not clear what this means to the mean shear,
)
increases with cooler temperature and/or slower rotation. It is
not clear what this means to the mean shear,
![]() .
For
example, it is not inconsistent with
.
For
example, it is not inconsistent with
![]() being
constant at all rotation rates. In this case,
being
constant at all rotation rates. In this case,
![]() would be smaller in more rapidly rotating
stars, and thus a lower fraction of stars would exhibit differential
rotation
would be smaller in more rapidly rotating
stars, and thus a lower fraction of stars would exhibit differential
rotation ![]() above the observational threshold, as is observed.
above the observational threshold, as is observed.
On the other hand, the maximum observed values of differential
rotation,
![]() ,
and of the absolute shear,
,
and of the absolute shear,
![]() ,
do vary depending on the rotation rate. The
strongest absolute shear of
,
do vary depending on the rotation rate. The
strongest absolute shear of
![]() rad d-1 is
found at rotation periods between two and three days with
significantly smaller values in slower rotators. The more rapidly
rotating stars show a slight decrease in absolute shear as well,
although the sparse data are also consistent with a plateau at
rad d-1 is
found at rotation periods between two and three days with
significantly smaller values in slower rotators. The more rapidly
rotating stars show a slight decrease in absolute shear as well,
although the sparse data are also consistent with a plateau at
![]() rad d-1 for
rad d-1 for
![]() d. A
maximum in differential rotation
d. A
maximum in differential rotation
![]() has recently been
predicted by Küker & Rüdiger (2005) for an F8-star, although of lesser
strength and at a slower rotation rate, a difference that may in parts
be due to their later spectral type.
has recently been
predicted by Küker & Rüdiger (2005) for an F8-star, although of lesser
strength and at a slower rotation rate, a difference that may in parts
be due to their later spectral type.
The investigated sample does not cover a wide range in effective temperature since only very few late-type field stars rotate fast enough for the method applied. Although temperature is expected to strongly influence the strength of differential rotation, the large range in rotation rate and the connection between rotation rate and temperature in the sample makes conclusions about temperature effects insecure. The results were compared to differential rotation measurements in cooler stars and found in qualitative agreement with an extrapolation of the empirical temperature dependence that Barnes et al. (2005) found when analyzing a sample of differentially rotation measurements done with DI.
The implications of the relations discussed here for stellar magnetic activity and the nature of the dynamo working in F-type stars still remain unclear from an observational point of view. Naively, one would expect stronger magnetic activity to occur in stars with stronger differential rotation among groups of comparable temperature or rotation rate. Those stars for which X-ray measurements are available, however, do not yet exhibit such a trend, but a meaningful investigation is hampered by the limited amount of data points available (especially for comparable temperature or rotation velocity). It has been shown that qualitative conclusions can be derived from the currently available measurements of stellar rotation laws, but a more detailed investigation of the consequences on the dynamo operating in F-type stars has to wait until a statistically better-defined sample of stars is available.
Acknowledgements
I am thankful to G. Basri for carefully reading the manuscript and for very helpful discussions, and to J. Schmitt for valuable comments on an earlier version of the manuscript. I thank the referee, Dr. John Barnes, for a careful and very constructive report. A.R. has received research funding from the European Commission's Sixth Framework Programme as an Outgoing International Fellow (MOIF-CT-2004-002544).
![\begin{figure}
\par\includegraphics[angle=-90,width=7.4cm,clip]{3911fA1.ps}
\end{figure}](/articles/aa/full/2006/04/aa3911-05/Timg111.gif) |
Figure A.1: Broadening function of HD 307938. This object has also been studied with Doppler Imaging by Marsden et al. (2005). |
Recently, Marsden et al. (2005) have presented Doppler Images of
HD 307938, a young active G dwarf in IC 2602. This star was also
observed for this project in the FLAMES/UVES campaign, and I report on
the rotation law in Table B.2. Marsden et al. (2005) took
a time series over four nights detecting spectroscopic variability.
Their data is contaminated by a significant amount of sunlight
reflected by the moon, which they have carefully removed before
constructing Doppler Images. The result of Doppler Imaging is that
HD 307938 has a cool polar cap extending down to ![]()
![]() latitude, and
latitude, and
![]() km -1, which
excellently corresponds to
km -1, which
excellently corresponds to
![]() km s-1,
as derived here (on comments about uncertainties in
km s-1,
as derived here (on comments about uncertainties in ![]() ,
see
Sect. 6). They also report marginal differential
rotation of
,
see
Sect. 6). They also report marginal differential
rotation of
![]() rad d-1 with a
rad d-1 with a
![]() error. From this result, one expects a value of q2/q1that is only marginally less than 1.76, the value for rigid rotation
and the best guess for the limb darkening parameter. The cool polar
spot found on HD 307938 influences q2/q1 as well, as it enlarges
q2/q1 much more than the small deviation from rigid rotation does;
q2/q1 is thus expected to be larger than 1.76. The spectrum
secured for the analysis presented here is not contaminated by
sunlight, and the broadening function derived is shown in
Fig. A.1. The profile does not reveal large
asymmetry, although a spot may be visible around
error. From this result, one expects a value of q2/q1that is only marginally less than 1.76, the value for rigid rotation
and the best guess for the limb darkening parameter. The cool polar
spot found on HD 307938 influences q2/q1 as well, as it enlarges
q2/q1 much more than the small deviation from rigid rotation does;
q2/q1 is thus expected to be larger than 1.76. The spectrum
secured for the analysis presented here is not contaminated by
sunlight, and the broadening function derived is shown in
Fig. A.1. The profile does not reveal large
asymmetry, although a spot may be visible around
![]() km s-1. The profile is fully consistent with the
broadening functions presented in Marsden et al. (2005), who were able to
show temporal variations in the profile from lower quality data. The
profile parameter determined from FTM is
km s-1. The profile is fully consistent with the
broadening functions presented in Marsden et al. (2005), who were able to
show temporal variations in the profile from lower quality data. The
profile parameter determined from FTM is
![]() ,
indicating no signs of solar-like differential rotation that is large
enough to be detected with this method. However, the fact that
q2/q1 is slightly larger than 1.76 supports the idea that a cool
spot occupies the polar caps. Thus, the finding of marginal
differential rotation and a cool polar spot is consistent with the
result derived from FTM (besides the good consistency in
,
indicating no signs of solar-like differential rotation that is large
enough to be detected with this method. However, the fact that
q2/q1 is slightly larger than 1.76 supports the idea that a cool
spot occupies the polar caps. Thus, the finding of marginal
differential rotation and a cool polar spot is consistent with the
result derived from FTM (besides the good consistency in
![]() ). This is the first time that a direct comparison of the
results is possible, since the majority of Doppler Imaging targets
usually show spot signatures that are stronger than what can be dealt
with using FTM.
). This is the first time that a direct comparison of the
results is possible, since the majority of Doppler Imaging targets
usually show spot signatures that are stronger than what can be dealt
with using FTM.
Table B.1: Field stars with measured differential rotation.
Table B.2: Stars in cluster fields, FLAMES/UVES observations.