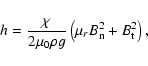A&A 446, 389-393 (2006)
DOI: 10.1051/0004-6361:20053880

Large magnetic liquid mirrors

E. F. Borra - D. Brousseau - A. Vincent

Département de physique, génie physique et optique and Centre d'Optique Photonique et Laser (COPL), Université Laval, Québec, Canada G1K 7P4

Received 21 July 2005 / Accepted 22 September 2005

Abstract
We present a new class of large liquid mirrors that use a ferrofluid covered by a reflecting layer of nanoparticles. The surface of the mirror is shaped by several concentric loops of current carrying coils. We first validate our theoretical models by comparing the theoretical predictions to interferometric measurements of a small prototype, finding agreement between data and theory. We then compute with Monte Carlo simulations models for f/2 mirrors having diameters varying between 15 and 44 m. Although much work remains to be done before a functional large mirror is actually built, our first exploration of the concept indicates that it is technologically feasible, thus warranting further work.

Key words: telescopes

1 Introduction

The end of the last century and the beginning of the present one have witnessed great improvements in optical mirror technology that have resulted in significant increases in mirror sizes up to the 10 m diameter of the Keck telescope. Telescopes having larger mirrors are currently being planned. All of these new generation telescopes would use solid primary mirrors. Polished solid surfaces, and the support systems that keep them aligned, are expensive so that cost is a major issue. Considering that costs of the order of a billion dollars are quoted for the 30 to 100 m currently planned, it is obvious that costs will soon be limiting factors. It is therefore worthwhile to begin exploring alternative technologies that could reduce costs.

Liquid mirrors offer an interesting alternative to conventional mirrors. They take advantage of the facts that liquid surfaces are very smooth, and that the support system is a simple container, to give inexpensive optical quality surfaces. For example, a rotating liquid takes the shape of a paraboloid of revolution, giving inexpensive high-quality parabolic mirrors. The performance and quality of liquid mirrors are well documented by laboratory tests (Borra et al. 1992; Girard & Borra 1997; Tremblay & Borra 2000) as well as by observations (Sica et al. 1995; Hickson & Mulrooney 1998; Cabanac et al. 1998). However, rotating liquid mirrors on earth will be limited by winds generated by the rotation of the mirror.

Liquid surfaces can be shaped with other means than rotation. For example, the surfaces of ferrofluids can be shaped with magnetic fields (Borra et al. 2004) and the surfaces of non-conducting liquids can be shaped by thermal fields (Truong et al. 2005). In this article we explore the possibilities offered by magnetically shaped liquid mirrors made of a ferrofluid coated with a reflective layer of nanoparticles.

2 Liquid mirrors shaped with magnetic fields

Magnetically shaped liquid mirrors have been considered before by Shuter & Whitehead (1994) who proposed to use magnets to reshape a classical mercury-based rotating liquid parabolic mirror into a sphere. Ragazzoni & Marchetti (1994) proposed an adaptive liquid mirror that uses an electrically conducting metallic reflecting liquid that carries a current and is shaped by a number of current carrying coils. Ragazzoni et al. (1996) also considered a large space telescope that uses a magnetically confined ferro-magnetic liquid mirror. Unfortunately, while mercury is well suited for rotating liquid mirrors, it has problems as a magnetic liquid. First, the chemistry of mercury is such that it is very difficult to obtain a stable mercury-based ferrofluid (Rosensweig 1997). Second, the high density of mercury necessitates a large deforming force and thus a strong magnetic field. To overcome the problems with mercury Borra et al. (2004) have experimented with adaptive ferrofluidic mirrors coated with colloidal particles and shaped with magnetic actuators. Ferrofluids are ordinary liquids to which one adds ferromagnetic nanoparticles coated with a chemical agent that prevents coalescence. The liquid is thus rendered ferromagnetic so that it feels a force and its surface can be shaped by an externally applied magnetic field. Ferrofluids are commercially available. It can readily be shown that the height of the surface above the undisturbed surface is given by:

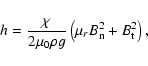$$h = \frac{\chi }{{2\mu _0 \rho g}}\left(\mu _r B_{\rm n}^2 + B_{\rm t}^2 \right),$$ (1)

where g and the Greek symbols have the usual meanings and $B_{\rm n}$ and $B_{\rm t}$ are respectively the normal and tangent components of the magnetic field.

High-performance ferrofluids are dark liquids that have low reflectivity and, consequently, must be coated with reflective layers. This can be accomplished by coating them with reflective coatings of colloidal metallic nanoparticles (Borra et al. 2004; Yockell-Lelievre et al. 2003) called MELLFs. MELLFs were originally introduced as a technique of chemical analysis of the material that coats the nanoparticles (Yogev & Efrima 1988; Gordon et al. 1989) and have been adopted and perfected in the Laval laboratory to coat liquid mirrors. The technology has steadily improved since our latest published work. We also have begun exploring techniques that would allow the sort of large-scale production needed for large mirrors and have built an automated MELLF-making machine.

The cylindrical symmetry of an astronomical mirror suggests that the field should be shaped with electric currents flowing in circular coils. We therefore computed numerically the field generated with circular coils using the Biot-Savart law. To test the accuracy of our numerical models, we computed a magnetic field generated by our program and then compared the results to interferometric measurements made on a small prototype ferrofluidic mirror subjected to that field. The coil is made of 150 windings of resin-coated 1.3 mm diameter copper wire wound on a 12.7 cm diameter aluminum core. The ferrofluid is 5 mm thick and placed in an aluminum container. Figure 1 shows a photograph of the mirror and coil in their mounts.

	Figure 1: Photograph of the mirror and coil in their mounts. The photograph gives an idea of what a real terrestrial mirror would look like.
Open with DEXTER

The accuracy of the surface will be affected by fluctuations in currents and deviations from the ideal geometry used in the computations. We computed that for this particular coil the current fluctuation needed for a $\lambda/10$ deviation is only 40 mA. Although reachable with commercial power supplies, this is a stiff stabilization requirement for a 5 A current. However, this requirement does not take into account the viscosity of the liquid which dampens the fluctuations. In practice we find experimentally that a stability of the order of a few mA is sufficient. To estimate the impact that an error in the winding would have on the surface, we assumed that a single winding (out of 150) would have a diameter of 6.61 cm instead of 6.60 cm and carry a current of 5.5 A instead of 6 A. We found that this would cause an error of 1.8 $\mu$m at a radius of 3 cm. It would thus appear that the surface is not greatly affected by winding uncertainties. This is especially true if one considers that the winding errors should average out for 150 windings.

We have tested the surface with a Mach-Zender interferometer made by the Zygo corporation. Because the interferometer is designed to test flat surfaces, we introduced in the beam a 10 cm diameter f/11 reference sphere. Figure 2 shows a block diagram of the experimental setup. Figure 3 shows the azimuthal averaged deviations from the reference surface predicted (full line) and measured (dots). We can see a good agreement between theory and experiment. We did not have data beyond 1.5 cm because the surface deviates too much from the reference sphere giving interferometric fringes too close to measure with our interferometer. The agreement between theory and measurements validates the theoretical model discussed in the following section.

	Figure 2: Block diagram of the experimental testing setup. Because the interferometer is designed to test flat surfaces, we introduced in the beam a refracting compound lens that gives a 10 cm diameter f/11 reference sphere.
Open with DEXTER

	Figure 3: Azimuthally averaged deviations from the reference surface predicted (full line) and measured (dots) for a small experiment.
Open with DEXTER

3 Extremely large magnetic mirrors

The physical properties of ferrofluids limit the maximum size of mirrors that can be made with this technology. There are two major factors that limit the diameters of magnetic liquid mirrors. One of them is the Rosensweig instability (Rosensweig 1997). This instability depends greatly on the physical parameters of the ferrofluid but one of the major suppliers of ferrofluids (Ferrotec Corp.) assured us that it is possible to synthesize a ferrofluid that has physical characteristics that do not show the instability. The other limiting factor comes from the maximum magnetization of ferrofluids. This limit is due to the maximum physical concentration of magnetite particles in the carrier fluid. At higher concentrations the surfactant surrounding each nanoparticle is inefficient and the particles begin to aggregate. Consequently, we estimate that the maximum magnetic field that can be applied to a ferrofluid is about 900 Gauss. Considering this value, we find that the maximum diameter achievable with existing ferrofluids should be about 50 m, for a numerical aperture of f/2. As we have seen in Sect. 2, the ferrofluidic surface generated by a single coil follows a spherical surface for small diameters and large f numbers; however deviations from a sphere grow rapidly with increasing radius thus making this simple geometry useless for large mirrors. To improve the situation, one can add an array of several concentric coils, each having varying radii, vertical positions and currents. We limited our computations to a maximum of 6 concentric coils.

Table 1: Parameters of selected magnetic liquid mirrors. The currents assume conducting wires only, without ferromagnetic materials. Adding ferromagnetic materials would greatly reduce them. See Sect. 4 for more details. Negative currents signify that they flow in the opposite direction.

To find optimal geometries, we carried out Monte Carlo simulations that use an adapted version of the well-known downhill simplex method in multi-dimensions described in Numerical Recipes in C (Press et al. 1989). The downhill simplex method is due to Nelder and Mead (Nelder & Mead 1965) and requires only function evaluations, not derivatives. It is not very efficient in terms of the number of function evaluations it requires but the computational burden is small and it permits to get results fast. To minimize computer time we assume that each coil is made of turns of vanishingly thin wire. The function we are optimizing is the standard deviation between the actual calculated surface and the desired one. The algorithm stops when a given number of iterations are attained or when the deviation is of the order of the machine precision. The starting points are randomly generated about the values of the radius, position and currents estimated in the manual optimization process. Our first observation is that the result of one optimization depends greatly on the number of iterations we allow the program to work with, and the values of the starting points. Finding the right combination of starting values and iteration number is a trial and error process, each optimization taking a non-negligible amount of time. Table 1 gives the results of computations for selected f/2 parabolic mirrors having diameters of 15, 30 and 44 m. We give two solutions for the 15 and 30 m to illustrate the fact that there many possible combinations of parameters. Note that the two solutions for the 15 m mirrors use 3 coils and have very different parameters. We can also see that the first 30 m uses 4 coils while the second 30 m uses 6 coils, yet the two surfaces have comparable rms values. Figure 4 shows the deviation from a perfect parabola for the 30 m mirror that uses 4 coils. The curves for the other mirrors have similar general appearances. The mirrors are not diffraction limited, having rms deviations ranging from 1.06 $\mu$m for the best 15 m mirror to 27 $\mu$m for the 44 m mirror. Smaller deviations are almost certainly obtainable with more computations but, as argued in the next section, they can reach diffraction-limited performance with auxiliary optics.

Figure 1 gives an idea of how a practical mirror would look like. We can see a central foot that holds the container with the ferrofluid. In a large mirror, the surface of the container would follow the ideal shape of the mirror within a fraction of a millimeter to minimize the quantity of ferrofluid used. The positions of the magnetic coils would have to be adjusted with a three-point mount and a centering mechanism. The outstanding difference between a large mirror and our small prototype is that it would need several coils instead of a single one. A tall tower would hold the corrector system and the detector above the mirror.

	Figure 4: Deviation from a perfect parabola computed for the 30 m mirror that uses 4 coils. The curves for the other mirrors have similar general appearances.
Open with DEXTER

4 Discussion and conclusion

What motivates this work is the consideration that the cost of the largest optical telescopes that use solid mirrors will eventually reach a limit above which society will no longer be willing to pay. It is thus worthwhile to explore alternative technologies. Furthermore, even in a context of affordability, it is worthwhile to explore new technologies that will reduce costs, thus making telescopes more affordable and allowing the astronomical community to build more of them. Considering the long times it takes to bring new technologies to practicality, exploration of radically new technology must be done well ahead of the time when it will actually be needed. This paper presents a first look at liquid mirrors that are shaped by magnetic fields.

We made a small prototype mirror to ascertain that the technique works and, by comparing the results to numerical computations, validate the theory that is used to examine the parameters of very large mirrors. Figure 3 shows that our model is in good agreement with the interferometric measurements of the prototype mirror. We then carry out Monte Carlo simulations of large ferrofluidic mirrors, finding that it should be possible to produce mirrors having diameters of several tens of meters. The surfaces obtained follow parabolas within a few microns; consequently the mirrors are not diffraction limited. We find that for the mirrors in Table 1, the PSF before correction with a secondary mirror, typically gives $50\%$of the energy within 2 to 3 arcsec diameters. However, this is not a major problem for two reasons. Firstly, it is almost certainly possible to find, with additional Monte Carlo computations other combinations of geometries that yield better surfaces. It is in the nature of Monte Carlo simulations in multidimensional space that different runs with different initial conditions yield different solutions. We obtained several combinations of geometries and currents that yielded solutions close to those that we report in Table 1. We did not carry out more extensive computations because they are very time consuming and because the purpose of this paper is to explore the concept rather than finding an optimized model. Secondly, the residual aberrations are sufficiently small and slowly varying that they could be corrected with a combination of a warped auxiliary mirror and adaptive optics. Consider for example the 44 m mirror. The errors on the mirror follow a smooth cylindrically symmetric surface having amplitude of a few tens of microns. Their radial variations vary smoothly with sinus-like variations having varying "periods'' of the order of a few meters similar to those seen in Fig. 4. Imposing a similar correction on auxiliary optics (e.g. the secondary mirror) seems technologically feasible. Furthermore, since adaptive optics would have to be used to make use of a diffraction limited mirror on Earth, they could also correct small residual errors on the wavefront along with the atmospherically induced variations. Likewise, they could correct small current variations and departures from ideal coil geometries. The errors on the 30 m (see Fig. 4) and the 15 m mirrors are sufficiently small that they could be corrected with adaptive optics system currently in use.

In our computations, we assumed that every coil is made of 2000 windings. Assuming copper wires having diameters of 2 cm and the currents given in Table 1, we find that the mirrors would necessitate 240 MWatts for the first 15 m, 1.2 MWatts for the second 15 m, 117 MWatts for the first 30 m, 332 MWatts for the second 30 m and 670 MWatts for the 44 m. These values are obviously unrealistic. However, this assumes the worse case scenario where one uses common copper wires. In practice, there are several options that can considerably decrease the power used.

Simply adding ferromagnetic material between the coils would greatly reduce power consumption. Common ferromagnetic materials have relative permeability as high as 5000, thereby reducing the power dissipated to a far more manageable 0.25 KWatts and 48 KWatts for the 15 m, 23 and 66 KWatts for the 30 m and 134 KWatts for the 44 m. Special alloys can have relative permeabilities as high as 10⁶, reducing the power requirements to negligible levels. Since the alloy would not be subjected to mechanical strains, one could certainly use brittle material having high permeability.

Superconducting wires would also dramatically decrease the power required. On the other hand they would require a cooling mechanism which would increase costs. It is beyond the scope of this article to discuss the present state of superconducting materials. Let us however note that superconducting materials are commercially available, some of them capable of sustaining large currents at liquid nitrogen temperatures. It must be noted that, because our application needs small magnetic fields, it would be possible to use the wires very near their critical temperature, unlike imaging applications which require high magnetic fields thereby limiting them to temperatures of the order of half the critical temperature. Superconductivity research is driven by practical applications such as imaging magnets and superconducting wires destined to carry the power of transmission lines. We can thus expect major advances over the next few years and the availability of superconducting wires at increasing higher temperatures. Quantum wires, wires spun from carbon nanotubes offer another promising technology that will greatly reduce the power dissipated. Quantum wires conduct much better then copper and dissipate very little electricity as heat. Unlike superconducting wires, there is no need to cool them. There are considerable research efforts, driven by use in the power grids, to bring them to practicality. Fibers as long as 100 m have already been produced.

Heat generated from the coils is a potential problem since it could deteriorate image quality. Obviously this would be a major issue with copper wires that are impractical anyway because of the power requirements quoted above. However, the few KWatts needed with mirrors that use ferromagnetic material would readily be manageable with a simple cooling system. Heat would not be an issue with superconducting wires or carbon nanotubes.

The field of view of a fixed parabolic mirror, equipped with conventional corrector design is small, of the order of a square degree (extended to 300 times as much by the rotation of the Earth), thereby limiting its usefulness; although they can yield powerful survey telescopes (Borra 2003). Conventional corrector designs would also necessitate very large and expensive optical elements. Fortunately, there are several possibilities available to increase the field of view. Innovative corrector designs can increase the field of view (Moretto & Borra 1997; Hickson 2002; Richardson & Morbey 1988). Another strategy involves the correction of off-axis aberrations by applying the correction on a projected pupil (Borra 1993). A combination of solid active mechanically deformable mirrors (Lemaitre & Wang 1995) and ferrofluidic mirrors could be used. These are, however, technologies that have not been tested for actual astronomical observations.

Another strategy involves magnetically shaping a spherical primary, instead of a parabolic one. Because a sphere remains a sphere when viewed off-axis, it allows one, with the proper corrector, to observe further off-axis than with a parabolic mirror. This consideration was the motivation to the work of Shutter & Whitehead (1994) who proposed to transform a parabolic rotating mercury liquid mirror to a spherical one. They estimated that this should enable one to access a $20\times 20$ degrees field.

Although the technology appears to be limited to diameters of the order of 50 m, if sufficiently inexpensive, it could be used to make multi-mirror systems thereby increasing the effective collective area. It is also possible that advances in ferromagnetic materials could increase performance to yield larger diameters. Magnetic mirrors could also be used for moon-based telescopes. Since the deformation is inversely proportional to g, one could make significantly larger mirrors. Finally, it could be used for a space telescope, following the suggestion of Ragazzoni et al. (1996).

The environmental impact of these large mirrors will be negligible. In particular the ferrofluid itself can be made with essentially any liquid (e.g. water or oil) containing nontoxic magnetite particles coated with nontoxic surfactant. With the appropriate liquid, there would be little evaporation of the ferrofluid that could be disposed, if needed, much as ordinary oil would be. A 50 m diameter mirror would use a layer having a thickness of the order of a millimeter and every millimeter would contribute a volume of about 30 000 liters. By comparison, the volume of the tank of a typical truck that delivers gasoline to a street gasoline pumping station is 40 000 liters.

Although the technology is not ready yet to be implemented right now in an astronomical observatory environment, all of the basic technological ingredients have been demonstrated. It could be brought to practicality with additional work.

Acknowledgements

This research was supported by the Natural Sciences and Engineering Research Council of Canada.

References

• Borra, E. F. 2003, A&A, 404, 47 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Borra, E. F. 1993, A&A, 278, 665 [NASA ADS] (In the text)
• Borra, E. F., Content, R., Girard, L., et al. 1992, ApJ, 393, 829 [NASA ADS] [CrossRef] (In the text)
• Borra, E. F., Ritcey, A. M., Bergamasco, R., et al. 2004, A&A, 419, 777 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Cabanac, R., Borra, E. F., & Beauchemin, M. 1998, ApJ, 509, 309 [NASA ADS] [CrossRef] (In the text)
• Girard, L., & Borra, E. F. 1997, Appl. Opt., 36, 25, 6278 (In the text)
• Gordon, K. C., McGarvey, J. J., & Taylor, K. P. 1989, J. Phys. Chem., 93, 6814 [CrossRef] (In the text)
• Hickson, P. 2002, MNRAS, 330, 540 [NASA ADS] [CrossRef] (In the text)
• Hickson, P., & Mulrooney, M. 1998, ApJS, 115, 35 [NASA ADS] [CrossRef] (In the text)
• Lemaitre, G. R., & Wang, M. 1995, A&AS, 114, 373 [NASA ADS] (In the text)
• Nelder, J. A., & Mead, R. 1965, Comput. J., 7, 308 (In the text)
• Moretto, G., & Borra, E. F. 1997, Appl. Opt., 36, 2114 [NASA ADS] (In the text)
• Press, W. H., Flannery, B. P., Teukolsky, S. A., & Vetterling, W. T. 1989, in Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. (Cambridge University Press) (In the text)
• Ragazzoni, R., & Marchetti, A. 1994, A&A, 283, L17 [NASA ADS] (In the text)
• Ragazzoni, R., Marchetti, A., & Claudi, R. U. 1996, A&A, 115, 175 [NASA ADS] (In the text)
• Richardson, E. H., & Morbey, C. L. 1988, in Instrumentation for Ground-Based Optical Astronomy, ed. L. B. Robinson (NY: Springer-Verlag), 270 (In the text)
• Rosensweig, R. E. 1997, Ferrohydrodynamics (Dover) (In the text)
• Shuter, W. L. H., & Whitehead, L. A. 1994, ApJ, 422, L139 [NASA ADS] (In the text)
• Sica, R. J., Sargoytchev, S., Borra, E. F., et al. 1995, Appl. Opt., 34, 6925 [NASA ADS] (In the text)
• Tremblay, G., & Borra, E. F. 2000, Appl. Opt., 39, 5651 [NASA ADS] (In the text)
• Truong, L., Borra, E. F., Bergamasco, R., et al. 2005, Appl. Opt., 44, 1595 [NASA ADS] [CrossRef] (In the text)
• Yockell-Lelievre, H., Borra, E. F., Ritcey, A., & da Silva, L. 2003, Appl. Opt., 42, 1882 [NASA ADS] (In the text)
• Yogev, D., & Efrima, S. 1988, J. Phys. Chem., 92, 5754 [CrossRef] (In the text)