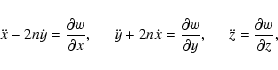 |
(1) |
A&A 446, 357-360 (2006)
DOI: 10.1051/0004-6361:20053828
C. N. Douskos - V. V. Markellos
Department of Engineering Sciences, University of Patras, 26500 Patras, Greece
Received 14 July 2005 / Accepted 26 September 2005
Abstract
The equations of motion of the three-dimensional
restricted three-body problem with oblateness are found to allow
the existence of out-of-plane equilibrium points. These points
lie in the (x-z) plane almost directly above and below the
center of each oblate primary. Their positions can be determined
numerically and are approximated by series expansions. The effects
of their existence on the topology of the zero-velocity curves
are considered and their stability is explored numerically.
Key words: celestial mechanics
The restricted three-body problem with oblateness of primaries, with or without radiation, has received attention especially in the two-dimensional case and with respect to its five coplanar equilibrium points, i.e. the collinear (or "Eulerian'') points L1, L2, L3 and the isosceles triangle (or "Lagrangian'') points L4, L5 (e.g. Sharma & Subba Rao 1976; Sharma 1987). The three-dimensional case has also been considered (e.g. Sharma & Subba Rao 1976; Oberti & Vienne 2003; Gurfil & Meltzer 2005). However, to the present authors' knowledge no mention has been made of any equilibrium points out of the plane of motion of the primaries for this problem.
In the present paper, using the equations of the three-dimensional problem given in the literature we report the existence of equilibrium points located in the (x-z) plane, above and below the center of each oblate primary. We obtain their positions both numerically and by analytical approximations in the form of power series in the oblateness coefficient. The case of oblateness of one or both primaries and the case of oblateness of one primary and radiation of the other are considered. We also consider the effects of their existence on the topology of the zero velocity curves and obtain numerical evidence indicating that these equilibrium points are unstable.
The three-dimensional restricted three-body problem with an
oblate primary m2 is described in a barycentric rotating
coordinate system by the equations of motion:
![\begin{figure}
\par\includegraphics[width=5.6cm,clip]{3828fig1.eps}
\end{figure}](/articles/aa/full/2006/04/aa3828-05/Timg15.gif) |
Figure 1:
Position of
Lz1(2) in the (x-z) plane as a function of A2 in the
interval [0,0.02], for |
| Open with DEXTER | |
The positions of the out-of-plane equilibrium points can be
found from the equations of motion by putting all velocity and
acceleration components equal to zero and solving the resulting
system,
![]() ,
numerically for
x, y, z. The second equation is satisfied for y=0, so we
must solve the remaining two equations for y=0 and
,
numerically for
x, y, z. The second equation is satisfied for y=0, so we
must solve the remaining two equations for y=0 and ![]() .
In
the case of w2, for example, we have to solve the system:
.
In
the case of w2, for example, we have to solve the system:
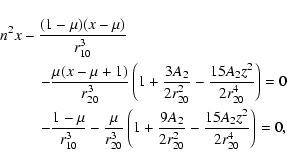 |
(7) |
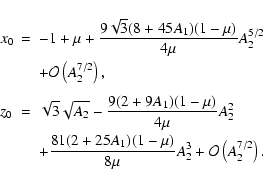 |
(8) |
Similarly, in the case of an oblate primary m2 and a radiating
primary m1 the positions of
Lz1(2) and
Lz2(2)are approximated to third-order terms in A2 by:
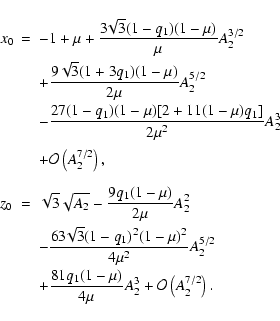 |
(9) |
In the following we consider the case when only the primary m2is oblate (![]() ,
A1=0) and the other primary is not
radiating (q1=1). In this case both the above approximations
reduce to:
,
A1=0) and the other primary is not
radiating (q1=1). In this case both the above approximations
reduce to:
![\begin{figure}
\topfigrule
\par\includegraphics[scale=0.68]{3828fig2a.eps}\hspac...
...e*{3mm}
\includegraphics[scale=0.68]{3828fig2h.eps}\par\topfigrule
\end{figure}](/articles/aa/full/2006/04/aa3828-05/Timg31.gif) |
Figure 2:
Zero-velocity curves in the (x-z) plane for |
| Open with DEXTER | |
Oblateness of primaries and the existence of the out-of-plane
equilibrium points has significant effects on the structure of the
regions allowed to motion and their boundaries, the zero-velocity
surfaces. In this section we present the zero-velocity curves in
the (x-z) plane in the case of w2. As a particular example we show in Fig. 2 the
four possible topologies of the curves in this case for ![]() .
Only the curves for Jacobi constant values corresponding
to the collinear equilibrium points and the out-of-plane point
Lz1(2)
(Lz2(2)) are shown. For clarity, in each case we also show
separately (left frame in each row) the curve corresponding to the
out-of-plane equilibrium point. These four topologies correspond
to four successive intervals of A2 values, separated by three
transition values at which a change of topology occurs. These
transitions occur when the Jacobi constant value corresponding to
the out-of-plane point coincides with one of the values
corresponding to the collinear equilibrium points. In all cases,
between the center of the oblate primary and its companion
out-of-plane equilibrium points the zero-velocity curves form
small ovals of regions not allowed to motion.
.
Only the curves for Jacobi constant values corresponding
to the collinear equilibrium points and the out-of-plane point
Lz1(2)
(Lz2(2)) are shown. For clarity, in each case we also show
separately (left frame in each row) the curve corresponding to the
out-of-plane equilibrium point. These four topologies correspond
to four successive intervals of A2 values, separated by three
transition values at which a change of topology occurs. These
transitions occur when the Jacobi constant value corresponding to
the out-of-plane point coincides with one of the values
corresponding to the collinear equilibrium points. In all cases,
between the center of the oblate primary and its companion
out-of-plane equilibrium points the zero-velocity curves form
small ovals of regions not allowed to motion.
To determine the linear stability of the out-of-plane point
Lz1(2) we transfer the origin to
(x0,0,z0) and
linearize the equations of motion, obtaining:
| (12) |
We have found that the equations of motion of the three-dimensional restricted three-body problem with oblateness given in the literature allow the existence of out-of-plane equilibrium points. These points lie in the (x-z) plane almost directly above and below the center of each oblate primary. Their positions are determined numerically and are approximated by series expansions in the oblateness coefficient. Oblateness and the existence of the out-of-plane equilibrium points is seen to have significant effects on the topology of the zero-velocity curves in the (x-z) plane. In particular, between the center of the oblate primary and its companion out-of-plane equilibrium points the zero-velocity curves form small ovals of regions not allowed to motion. Finally, numerical evidence is obtained indicating that these equilibrium points are unstable. We have not checked, however, if their existence might be due to the truncation of the potential employed in deriving the equations of motion.