A&A 446, 43-60 (2006)
DOI: 10.1051/0004-6361:20053487
G. Hütsi1,2
1 - Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1,
86740 Garching bei München, Germany
2 - Tartu Observatory, Tõravere 61602, Estonia
Received 20 May 2005 / Accepted 9 September 2005
Abstract
We study the clustering of SZ-selected galaxy clusters on a past light-cone, particularly paying attention to the possibility of constraining properties of dark energy. The prospects of detecting baryonic features in the cluster power spectrum for a wide and shallow survey like PLANCK, and for an SPT-like narrow and deep survey are discussed. It is demonstrated that these future blank sky SZ surveys will have the capability to improve over the recently announced detection of baryonic oscillations based on the SDSS Luminous Red Galaxy (LRG) sample. We carry out parameter estimation using a Fisher matrix approach taking into account the anisotropic nature of the power spectrum due to redshift space and cosmological distortions. The clustering signal which is not too sensitive to systematic uncertainties serves as a valuable piece of information that in combination with other sources of data helps in breaking degeneracies between the cosmological parameters.
Key words: galaxies: clusters: general - cosmology: theory - cosmology: large-scale structure of Universe - cosmology: cosmic microwave background
The existence of acoustic rulers in the Universe is of enormous importance since they permit us to measure the behavior of the Hubble parameter with redshift and also allow us to establish the distance-redshift relation. This is especially important now when the discovery of dark energy (DE) is introducing more questions than the answers it provides. Different areas of observational cosmology (SNe Ia e.g. SCP![]() ,
high - z SN search
,
high - z SN search![]() ; large scale structure surveys e.g. SDSS
; large scale structure surveys e.g. SDSS![]() , 2dF
, 2dF![]() ; CMB experiments) provide evidence that the expansion of our Universe has been proceeding in an accelerated fashion since
; CMB experiments) provide evidence that the expansion of our Universe has been proceeding in an accelerated fashion since
![]() (Perlmutter et al. 1999; Riess et al. 1998; Spergel et al. 2003). Currently there is no physical understanding or even a reliable model for the DE. One of the first tasks to understand the nature of DE will be the measurement of its equation of state parameter,
(Perlmutter et al. 1999; Riess et al. 1998; Spergel et al. 2003). Currently there is no physical understanding or even a reliable model for the DE. One of the first tasks to understand the nature of DE will be the measurement of its equation of state parameter,
![]() ,
and its possible evolution with time w(z). When we are equipped with a good standard ruler and are able to measure its angular behavior with redshift, we can obtain very valuable information about w(z). With the CMB data we can determine an angular diameter distance to the last scattering surface with high precision. By combining this information with the measurement of acoustic peaks in the distribution of baryons at lower redshifts
0<z<1 - 2, we will have unique information about the effective w and may even be able to determine w(z) (Hu & Haiman 2003; Blake & Glazebrook 2003; Eisenstein & Hu 1998; Linder 2003; Seo & Eisenstein 2003).
,
and its possible evolution with time w(z). When we are equipped with a good standard ruler and are able to measure its angular behavior with redshift, we can obtain very valuable information about w(z). With the CMB data we can determine an angular diameter distance to the last scattering surface with high precision. By combining this information with the measurement of acoustic peaks in the distribution of baryons at lower redshifts
0<z<1 - 2, we will have unique information about the effective w and may even be able to determine w(z) (Hu & Haiman 2003; Blake & Glazebrook 2003; Eisenstein & Hu 1998; Linder 2003; Seo & Eisenstein 2003).
It was obvious since the first publications that acoustic oscillations should also leave their imprint on the large scale structure of the Universe and thus influence e.g. the correlation function and the power spectrum of galaxies. The first successful detection of these features was presented by Eisenstein et al. (2005) who found traces of acoustic oscillations in the distribution of luminous red galaxies for which they had excellent measurements of angular positions and redshifts obtained by the SDSS collaboration.
In this paper we discuss the opportunities that will be opened by the planned blank sky deep SZ cluster surveys which will be performed in the coming years. Clusters of galaxies are especially interesting objects for the study of acoustic features in the spatial distribution of objects since it has long been known that the clustering of clusters is an order of magnitude enhanced in comparison to galaxies (Kaiser 1984; Bahcall & Soneira 1983). Therefore even with smaller statistics of clusters it is possible to get useful results.
In the next few years there will be very deep SZ cluster surveys of the restricted regions of the sky performed by several projects, e.g. APEX![]() ,
SZA
,
SZA![]() , AMI
, AMI![]() , ACT
, ACT![]() . Our analysis showed that the volume of these surveys and the number of possible cluster detections will be unfortunately insufficient for the search for the acoustic wiggles in the power spectrum. However, two planned surveys which will be carried out by the PLANCK Surveyor
. Our analysis showed that the volume of these surveys and the number of possible cluster detections will be unfortunately insufficient for the search for the acoustic wiggles in the power spectrum. However, two planned surveys which will be carried out by the PLANCK Surveyor![]() spacecraft and the South Pole Telescope
spacecraft and the South Pole Telescope![]() (SPT) have very good prospects for the detection of acoustic features. PLANCK will make a shallow blank sky cluster survey permitting one to detect up to 20 000 rich clusters of galaxies (e.g. Majumdar & Mohr 2004) with the bulk of objects at z<0.5, but will reach distances of
(SPT) have very good prospects for the detection of acoustic features. PLANCK will make a shallow blank sky cluster survey permitting one to detect up to 20 000 rich clusters of galaxies (e.g. Majumdar & Mohr 2004) with the bulk of objects at z<0.5, but will reach distances of
![]() .
In contrast the SPT survey will observe deeper, but will cover only
.
In contrast the SPT survey will observe deeper, but will cover only ![]() of the sky. This survey is expected to detect up to 30 000 clusters of galaxies (Majumdar & Mohr 2004), and many of them will be at significantly higher redshifts compared to the ones observed by PLANCK. Unfortunatelly it is not enough to measure only the SZ flux or brightness of the clusters. In order to measure the equation of state of DE we need the redshift estimate for each cluster in the sample which will be hard and time consuming work for many optical, X-ray and possibly radio astronomers. However, when this problem is solved, cosmologists will have a unique sample of clusters of galaxies with good knowledge of their angular position, redshift, and hopefully also mass. In this paper we investigate what limits to the DE equation of state might be obtained when these large experimental efforts are completed. It is obvious that in parallel other ways to measure w(z) will be implemented, but any additional and independent information will be useful. Especially important is that PLANCK and SPT surveys of clusters of galaxies will be performed in any case. Certainly, for many various purposes: (i) study of the redshift distribution of clusters; (ii) study of the properties of the clusters as a population; (iii) search for high-z clusters etc., we always need to estimate redshift. Therefore the information on the power spectrum of clusters of galaxies, acoustic wiggles and the subsequent determination of w is complementary but extremely important part of these surveys.
of the sky. This survey is expected to detect up to 30 000 clusters of galaxies (Majumdar & Mohr 2004), and many of them will be at significantly higher redshifts compared to the ones observed by PLANCK. Unfortunatelly it is not enough to measure only the SZ flux or brightness of the clusters. In order to measure the equation of state of DE we need the redshift estimate for each cluster in the sample which will be hard and time consuming work for many optical, X-ray and possibly radio astronomers. However, when this problem is solved, cosmologists will have a unique sample of clusters of galaxies with good knowledge of their angular position, redshift, and hopefully also mass. In this paper we investigate what limits to the DE equation of state might be obtained when these large experimental efforts are completed. It is obvious that in parallel other ways to measure w(z) will be implemented, but any additional and independent information will be useful. Especially important is that PLANCK and SPT surveys of clusters of galaxies will be performed in any case. Certainly, for many various purposes: (i) study of the redshift distribution of clusters; (ii) study of the properties of the clusters as a population; (iii) search for high-z clusters etc., we always need to estimate redshift. Therefore the information on the power spectrum of clusters of galaxies, acoustic wiggles and the subsequent determination of w is complementary but extremely important part of these surveys.
The structure of this paper is as follows. In Sect. 2 we describe an analytical model for a cluster power spectrum on a light-cone and calibrate it against the numerical simulations. Section 3 discusses the possibility of detecting baryonic oscillations with the forthcoming SZ surveys. In Sect. 4 we carry out parameter forecasting using a Fisher matrix approach and Sect. 5 contains our conclusions.
To calculate the power spectrum we follow the direct method of Feldman et al. (1994) (FKP), which is shown to be optimal for sufficiently large k-modes i.e. ![]() ,
where L is the typical spatial extent of a survey volume (Tegmark et al. 1998). Because FFTs are used to achieve significant speedup for Fourier sum calculations, we first have to find the density field on a grid. To this end we use the Triangular Shaped Cloud (TSC) (Hockney & Eastwood 1988) mass assignment scheme. Thus our density field is a filtered version of the underlying field, and as shown in Jing (2005), the real power spectrum P can be expressed as the following sum over aliases (correct again for the case
,
where L is the typical spatial extent of a survey volume (Tegmark et al. 1998). Because FFTs are used to achieve significant speedup for Fourier sum calculations, we first have to find the density field on a grid. To this end we use the Triangular Shaped Cloud (TSC) (Hockney & Eastwood 1988) mass assignment scheme. Thus our density field is a filtered version of the underlying field, and as shown in Jing (2005), the real power spectrum P can be expressed as the following sum over aliases (correct again for the case ![]() ):
):
When calculating the power spectrum in the above described way we assumed that the influence of selection/survey geometry effects on the power spectrum are separable. This is not the case for large scales (
![]() )
and also if too narrow (i.e.
)
and also if too narrow (i.e.
![]() )
power spectrum bins are used. In the following we always make the power spectrum binning broad enough so that the neighboring bins can be safely assumed to be uncorrelated.
)
power spectrum bins are used. In the following we always make the power spectrum binning broad enough so that the neighboring bins can be safely assumed to be uncorrelated.
The power spectrum error is estimated using the simple "mode counting'' result of FKP (see also Tegmark et al. 1998):
Then the mass within the radius r can be expressed as:
In order to convert halo mass M corresponding to the overdensity ![]() to the one corresponding to the overdensity
to the one corresponding to the overdensity ![]() we proceed as follows:
we proceed as follows:
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3487_f01.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg68.gif) |
Figure 1:
Mass conversion from
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{3487_f02.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg69.gif) |
Figure 2:
Light-cone mass functions for different redshift intervals. For clarity the curves have been shifted by the factors given in the legend. Boxes show simulation results with the applied mass conversion from
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3487_f03.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg73.gif) |
Figure 3: Upper panel: various corrections applied to reach the final power spectrum estimate. Lower panel: results of the consistency test for the "sharpening'' scheme using different grid sizes. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.4cm,clip]{3487_f04.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg75.gif) |
Figure 4:
Upper panel: power spectrum of clusters more massive than
|
| Open with DEXTER | |
In the upper panel of Fig. 3 we show various corrections needed to achieve a reliable estimate of the power spectrum of the underlying cluster distribution while the lower panel demonstrates the consistency of the applied "sharpening'' scheme. Here we have used the z=0 cluster catalog to allow for a comparison with the results presented in Colberg et al. (2000). The lower mass for the cluster selection was taken to be
![]() in order to get the total number of objects equal to
in order to get the total number of objects equal to ![]() 915 000 as was used in Colberg et al. (2000). Also we have selected a spherical volume out of the full box to test how well the geometry correction works. The results of this comparison are given in Fig. 4. We see that the Colberg et al. (2000) power spectrum agrees with our calculations at the largest scales; however, for the smaller scales it drops below our results. We suspect that their correction for the grid smoothing effect was insufficient, although in their paper they do not describe how the power spectrum was calculated. As can be seen from the figure the shape of our cluster power spectrum agrees very well with the linear theory matter power spectrum up to the scale
915 000 as was used in Colberg et al. (2000). Also we have selected a spherical volume out of the full box to test how well the geometry correction works. The results of this comparison are given in Fig. 4. We see that the Colberg et al. (2000) power spectrum agrees with our calculations at the largest scales; however, for the smaller scales it drops below our results. We suspect that their correction for the grid smoothing effect was insufficient, although in their paper they do not describe how the power spectrum was calculated. As can be seen from the figure the shape of our cluster power spectrum agrees very well with the linear theory matter power spectrum up to the scale
![]() .
Clearly with such a large number of clusters (
.
Clearly with such a large number of clusters (![]() 477 000 inside our spherical volume) baryonic oscillations are easily detectable and the corresponding "smooth'' model without them is disfavored. The theoretical matter power spectra were calculated as described in Eisenstein & Hu (1998). Using the z=0 cluster catalog we also calculate power spectra and two-point correlation functions for various lower mass cutoffs. These results are presented in Fig. 5 where the left-hand panels show power spectra divided by the smooth model without baryonic oscillations and right-hand panels the respective correlation functions. Here the uppermost power spectrum is the same as the one given in Fig. 4. Solid/dotted lines show theoretical models with/without baryonic oscillations. Correlation functions were calculated using the estimator given by Landy & Szalay (1993):
477 000 inside our spherical volume) baryonic oscillations are easily detectable and the corresponding "smooth'' model without them is disfavored. The theoretical matter power spectra were calculated as described in Eisenstein & Hu (1998). Using the z=0 cluster catalog we also calculate power spectra and two-point correlation functions for various lower mass cutoffs. These results are presented in Fig. 5 where the left-hand panels show power spectra divided by the smooth model without baryonic oscillations and right-hand panels the respective correlation functions. Here the uppermost power spectrum is the same as the one given in Fig. 4. Solid/dotted lines show theoretical models with/without baryonic oscillations. Correlation functions were calculated using the estimator given by Landy & Szalay (1993):
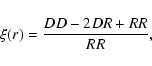 |
(16) |
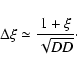 |
(17) |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{3487_f05.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg81.gif) |
Figure 5:
Power spectra ( left panels) and correlation functions
( right panels) for the lower mass cutoffs of
|
| Open with DEXTER | |
For the mass function n(M,z) and bias parameter b(M,z) we use both Press-Schechter (PS) (Press & Schechter 1974) and Sheth-Tormen (ST) (Sheth & Tormen 1999) prescriptions. It is well known that PS mass function underpredicts the number density of massive objects (Sheth & Tormen 1999). PS overestimates while ST underestimates the bias parameter for massive halos (especially at larger redshifts) (Sheth & Tormen 1999). PS underestimation of number density turns out to be approximately compensated for by its overestimation of bias parameter, and as such, we get the best agreement with the numerical light-cone power spectra using a plain PS approach. This is demonstrated in Fig. 6 where we show the light-cone power spectra for various values of lower mass cutoff
![]() .
Results in the upper panel apply for the SphereB cluster catalog (reaching redshift
.
Results in the upper panel apply for the SphereB cluster catalog (reaching redshift
![]() )
whereas the ones on the lower part of the figure correspond to the OctantB catalog (reaching
)
whereas the ones on the lower part of the figure correspond to the OctantB catalog (reaching
![]() )
of VIRGO Hubble Volume simulation outputs. We obtained the best agreement if clusters were selected using M180, but in bias calculations virial mass
)
of VIRGO Hubble Volume simulation outputs. We obtained the best agreement if clusters were selected using M180, but in bias calculations virial mass
![]() was used instead.
was used instead.
Overall the agreement between the numerical results and an analytical description is better
than ![]() .
.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{3487_f06.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg92.gif) |
Figure 6:
Upper panel: light-cone power spectra for SphereB output of VIRGO |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3487_f07.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg93.gif) |
Figure 7: Theoretical dark matter power spectra with a smooth component divided out (using transfer functions as given by Eisenstein & Hu 1998) for the WMAP "concordance'' model (solid line) and for the model used in VIRGO Hubble Volume simulations (dashed line). The numbered vertical lines show the locations of the corresponding peaks in the CMB angular power spectrum e.g. 1. corresponds to the 1st acoustic peak etc. |
| Open with DEXTER | |
Here instead of galaxies we discuss the possibility of using SZ-selected galaxy clusters for that purpose. Some calculations related to the SPT-type of SZ survey were also presented in Hu & Haiman (2003). It is clear from Figs. 4 and 7 that with wide field galaxy cluster surveys we should be especially sensitive to the scales that correspond to the 2nd and 3rd acoustic peaks in the CMB angular power spectrum.
A few advantages of using galaxy clusters compared to the galaxies are:
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3487_f08.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg107.gif) |
Figure 8: Cumulative number counts of SZ clusters for observing frequency 150 GHz. Crosses show simulation results by White et al. (2002) whereas solid/dashed lines correspond to analytical results assuming a ST/PS mass function. |
| Open with DEXTER | |
In reality the mass-observable relations are currently rather poorly known but one may argue that planned surveys with the yields of tens of thousands of galaxy clusters have significant power for "self-calibration'' (Majumdar & Mohr 2004). As also shown in Majumdar & Mohr (2004) a much better approach would be to establish these scaling laws using external mass determinations (e.g. through lensing studies) for a subset of a complete sample. For a more precise modeling of the selection effects one also has to consider scatter around these mean relations. These issues can be settled once we obtain a real sample. Moreover, the clustering as compared to the number count of objects is much less sensitive to the uncertainties in the precise knowledge of the selection effects. Here the selection effects enter when relating the clustering of tracer objects to the underlying dark matter i.e. while determining the effective bias of objects. As it turns out (see Sect. 4), future large cluster samples are able to provide a good estimate of the effective bias themselves through the redshift space distortions.
![\begin{figure}
\par\includegraphics[width=7.7cm,clip]{3487_f09.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg108.gif) |
Figure 9:
Upper panel:
|
| Open with DEXTER | |
We investigate how well we can determine the power spectrum with SZ surveys having various sensitivity limits, specifically concentrating on the range ![]() mJy. Our results for
mJy. Our results for
![]() (or equivalently for the effective volume, see Eq. (6)) and for the number of detectable clusters are given in Fig. 9. Here the upper panel assumes full sky coverage and the lower one applies for one octant of the sky. With the solid lines we have plotted the fractional accuracy
(or equivalently for the effective volume, see Eq. (6)) and for the number of detectable clusters are given in Fig. 9. Here the upper panel assumes full sky coverage and the lower one applies for one octant of the sky. With the solid lines we have plotted the fractional accuracy
![]() achieved for different lower flux limits and follow-up survey depths applying the FKP weighting scheme. The wavenumber k in the calculations was taken to be
achieved for different lower flux limits and follow-up survey depths applying the FKP weighting scheme. The wavenumber k in the calculations was taken to be
![]() ,
which is close to the first major acoustic feature in the expected matter power spectrum (see Fig. 7). The bin width
,
which is close to the first major acoustic feature in the expected matter power spectrum (see Fig. 7). The bin width
![]() is large enough so that even for the shallowest surveys reaching only
is large enough so that even for the shallowest surveys reaching only ![]() the power spectrum bins can be assumed to be independent. Here and also in the following we perform analytical calculations for the observational frequency 150 GHz and assume cosmological parameters consistent with the WMAP "concordance'' model (Spergel et al. 2003).
the power spectrum bins can be assumed to be independent. Here and also in the following we perform analytical calculations for the observational frequency 150 GHz and assume cosmological parameters consistent with the WMAP "concordance'' model (Spergel et al. 2003).
Light-cone power spectra for SZ clusters are calculated using Eq. (18) where the lower integration boundary
![]() is given by Eqs. (22) and (24). Then
is given by Eqs. (22) and (24). Then
![]() is found using Eqs. (6)-(8) and the mean underlying number density
is found using Eqs. (6)-(8) and the mean underlying number density
![]() is given by Eq. (19). Also we have taken into account the increase of the isotropized power spectrum due to linear redshift space distortions by a factor of
is given by Eq. (19). Also we have taken into account the increase of the isotropized power spectrum due to linear redshift space distortions by a factor of
![]() (Kaiser 1987), where
(Kaiser 1987), where
![]() .
.
The solid lines in Fig. 9 starting from below correspond to
![]() values of
values of ![]() ,
,
![]() ,
,
![]() in the upper panel and
in the upper panel and ![]() ,
,
![]() ,
,
![]() in the lower one. With the dashed lines we have plotted the number of clusters. Moving from the lower right to the upper left each line represents a factor of two increase in number with the starting values being 20 000 and 10 000 in upper and lower panels, respectively. The flattening out of
in the lower one. With the dashed lines we have plotted the number of clusters. Moving from the lower right to the upper left each line represents a factor of two increase in number with the starting values being 20 000 and 10 000 in upper and lower panels, respectively. The flattening out of
![]() and cluster number curves at low fluxes is due to the imposed lower mass cutoff
and cluster number curves at low fluxes is due to the imposed lower mass cutoff
![]() .
Thus below some flux limit we see all the clusters inside a specified volume that have masses above that cutoff value.
.
Thus below some flux limit we see all the clusters inside a specified volume that have masses above that cutoff value.
In general, by increasing the volume of the survey we also boost the shot noise contribution due to the decreasing number density of distant objects. As seen from the figure - in the case of FKP weighting - the accuracy of power spectrum estimate does not degrade as we move to further distances since we downweight the contribution of the far away objects in such a way as to compensate for the increase in shot noise. For too small survey volumes, on the other hand, limits on achievable accuracy are set by the growing importance of the cosmic variance. The FKP weighting scheme is not strictly optimal in our case since it was derived assuming a fixed i.e. non-evolving underlying power spectrum. Certainly, for a better scheme one should weight down the contribution of the far away objects slightly more mildly since the clustering strength of these objects is higher. This type of weighting method, which is able to handle at least the case with an evolving amplitude, is presented in Percival et al. (2004). Nevertheless in the following calculations for simplicity we still apply the FKP weight function.
The results in Fig. 9 assumed that we have a full follow-up such that we are able to obtain all the redshifts of the clusters detected by an imaging survey. Also the sample was assumed to be purely flux-selected which is rather unrealistic for real experiments e.g. for PLANCK many clusters remain undetected due to rather poor angular resolution or oppositely in the case of SPT some fraction of clusters will be "resolved out'' and a significant amount of signal will be lost. Many objects might remain undetected for these reasons.
If the systems that are left out are low mass clusters (as in the case of PLANCK) then our power spectrum estimate might actually
be almost as good as before since low mass systems are relatively weakly clustered and as such they do not contribute significantly to the total signal. This can be seen in Fig. 10 where in the upper panel we have shown the influence of changing the lower mass cutoff
![]() on
on
![]() .
On the lower panel the respective number of clusters is given. These calculations are done for two different survey types: (1) solid lines represent results for a shallow SZ survey covering the full sky and reaching redshift
.
On the lower panel the respective number of clusters is given. These calculations are done for two different survey types: (1) solid lines represent results for a shallow SZ survey covering the full sky and reaching redshift
![]() with a sensitivity limit
with a sensitivity limit
![]() mJy at 150 GHz, (2) dashed lines represent a deep survey (with no upper redshift cutoff imposed) covering 1/8 of the sky with a flux limit
mJy at 150 GHz, (2) dashed lines represent a deep survey (with no upper redshift cutoff imposed) covering 1/8 of the sky with a flux limit
![]() mJy at 150 GHz. The first might be applicable for the case of the PLANCK mission
mJy at 150 GHz. The first might be applicable for the case of the PLANCK mission![]() and the second for the SPT cluster survey. In practice the measurements will be performed in many frequency channels which helps to separate clusters from other foreground sources due to the specific frequency behavior of the thermal SZ effect. Here for simplicity we have chosen the sensitivity limits corresponding to the "weakest'' of the channels available for SZ purposes. We see that for a full sky with the 20 000 most massive clusters up to redshift
and the second for the SPT cluster survey. In practice the measurements will be performed in many frequency channels which helps to separate clusters from other foreground sources due to the specific frequency behavior of the thermal SZ effect. Here for simplicity we have chosen the sensitivity limits corresponding to the "weakest'' of the channels available for SZ purposes. We see that for a full sky with the 20 000 most massive clusters up to redshift ![]() ,
one could obtain an estimate of the power spectrum at
,
one could obtain an estimate of the power spectrum at
![]() with a fractional error below
with a fractional error below ![]() while for the one octant of the sky with less than
while for the one octant of the sky with less than ![]() 25 000 clusters we always stay above
25 000 clusters we always stay above ![]() accuracy.
accuracy.
The previously described approach where we use all the data to obtain a single combined estimate of the power spectrum is appropriate if we only intend to place constraints on
![]() .
Combining this power spectrum estimate which is sensitive to
.
Combining this power spectrum estimate which is sensitive to
![]() with the CMB constraint on
with the CMB constraint on
![]() gives us
gives us
![]() and h separately. Additionally, knowing the geometry of the Universe from CMB measurements gives us immediately an estimate of
and h separately. Additionally, knowing the geometry of the Universe from CMB measurements gives us immediately an estimate of
![]() .
Since in the majority of the DE models DE starts to dominate relatively recently, driving the Universe furthest from the plain Einstein-de Sitter behavior, the best redshift to complement the CMB data is at z=0.
.
Since in the majority of the DE models DE starts to dominate relatively recently, driving the Universe furthest from the plain Einstein-de Sitter behavior, the best redshift to complement the CMB data is at z=0.
On the other hand if our aim is to constrain the equation of state parameter w and its possible change in time it is essential to measure the power spectrum at different redshifts. This leads to the question of how to bin up the sample in redshift? Certainly there are optimal ways of combining data, but unfortunately they all depend on the way we choose to parametrize our model for DE. Recently Huterer & Starkman (2003) argued that in the absence of a theoretically well motivated parametrization one should use a stepwise function with the value wi in the ith redshift bin and let the data itself determine which combinations of wi will be well constrained. One can then reconstruct the behavior of w with the redshift as a linear combination of the "cleanest'' eigenmodes. Here we are not trying to implement that kind of general parametrization since as a first step it should be sufficient to determine an effective constant w and see whether it deviates from the currently most well motivated w=-1. Therefore, in the following we mostly investigate the case with a constant equation of state parameter w0. The redshift binning is chosen so as to get equal relative accuracies of the power spectrum in each bin. The results of this binning procedure for the above described two types of survey are given in Fig. 11 with the solid lines corresponding to the shallow one. For the shallow (deep) survey we have assumed 3 (4) redshift bins. In the inset the upper curves show the relative accuracy achievable in each redshift bin while the lower lines correspond to the full sample without any binning and so coincide with the lines shown in the upper panel of Fig. 10. This kind of redshift division is also used in the following parameter estimation section.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{3487_f10.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg129.gif) |
Figure 10:
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3487_f11.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg130.gif) |
Figure 11: "Equal accuracy'' redshift binning for different lower mass cutoffs. Solid (dashed) lines correspond to the shallow (deep) SZ survey with 3 (4) redshift bins. In the inset the upper curves show the relative accuracy achievable in each redshift bin while the lower lines correspond to the full sample without any binning. |
| Open with DEXTER | |
Since the study of the SDSS LRG sample has led to the detection of acoustic oscillations in the spatial distribution of galaxies (Eisenstein et al. 2005)![]() , it would be instructive to compare the "strength'' of this survey to the planned blank sky SZ cluster surveys like PLANCK and SPT.
In Fig. 12 we show the number density of clusters as a function of redshift for the above described two types of SZ survey. The upper group of lines corresponds to the SPT-like deep survey while the lower curves are for a wide and shallow survey like PLANCK. For each of the surveys we have varied the lower mass cutoff
, it would be instructive to compare the "strength'' of this survey to the planned blank sky SZ cluster surveys like PLANCK and SPT.
In Fig. 12 we show the number density of clusters as a function of redshift for the above described two types of SZ survey. The upper group of lines corresponds to the SPT-like deep survey while the lower curves are for a wide and shallow survey like PLANCK. For each of the surveys we have varied the lower mass cutoff
![]() so as to obtain in total 15 000, 25 000 and 35 000 clusters. These three cases are shown with solid lines. Dashed lines display the pure flux-limited surveys without any lower cutoff in the mass imposed. Using these results and also taking into account the proper biasing factors as given by the square root of Eq. (18) divided by P(k,z=0)
so as to obtain in total 15 000, 25 000 and 35 000 clusters. These three cases are shown with solid lines. Dashed lines display the pure flux-limited surveys without any lower cutoff in the mass imposed. Using these results and also taking into account the proper biasing factors as given by the square root of Eq. (18) divided by P(k,z=0)![]() we can readily obtain
we can readily obtain
![]() as given by
Eqs. (6) and (7). The results of this calculation are given in Fig. 13. Here the solid lines correspond to the PLANCK-like and dashed ones to the SPT-like surveys. Each set of lines corresponds to the detected cluster numbers (starting from above): 15 000, 25 000 and 35 000. The dash-dotted curve, showing the results for the SDSS LRG sample, is found using
Eq. (6) and the data for the effective volume given in Fig. 1 of Eisenstein et al. (2005) (again
as given by
Eqs. (6) and (7). The results of this calculation are given in Fig. 13. Here the solid lines correspond to the PLANCK-like and dashed ones to the SPT-like surveys. Each set of lines corresponds to the detected cluster numbers (starting from above): 15 000, 25 000 and 35 000. The dash-dotted curve, showing the results for the SDSS LRG sample, is found using
Eq. (6) and the data for the effective volume given in Fig. 1 of Eisenstein et al. (2005) (again
![]() was assumed). We can see that on large scales future SZ surveys have enough strength to improve the results obtained using the SDSS LRG sample. However, the SDSS LRG sample is going to double in size within a few years as the survey is completed. The achievable
was assumed). We can see that on large scales future SZ surveys have enough strength to improve the results obtained using the SDSS LRG sample. However, the SDSS LRG sample is going to double in size within a few years as the survey is completed. The achievable
![]() for this final sample is shown in Fig. 13 as a dotted line. Moreover, it seems that acoustic oscillations are able to survive at the quasilinear scales (
for this final sample is shown in Fig. 13 as a dotted line. Moreover, it seems that acoustic oscillations are able to survive at the quasilinear scales (
![]() )
(see Fig. 4) which significantly increases the amount of information available for the galaxy redshift surveys. This is also confirmed by the recent N-body simulations by Springel et al. (2005) and Seo & Eisenstein (2005). In order to fully exploit this information one needs a complete theoretical understanding of how nonlinear effects, redshift space distortions and nonlinear biasing influence these features. So far there have been only a few works studying these important issues (e.g. White 2005; Springel et al. 2005; Seo & Eisenstein 2005; Meiksin et al. 1999) and we do not have a full theoretical description of them available yet. For this reason we have not attempted to incorporate the SDSS LRG sample into our Fisher matrix parameter estimation process.
)
(see Fig. 4) which significantly increases the amount of information available for the galaxy redshift surveys. This is also confirmed by the recent N-body simulations by Springel et al. (2005) and Seo & Eisenstein (2005). In order to fully exploit this information one needs a complete theoretical understanding of how nonlinear effects, redshift space distortions and nonlinear biasing influence these features. So far there have been only a few works studying these important issues (e.g. White 2005; Springel et al. 2005; Seo & Eisenstein 2005; Meiksin et al. 1999) and we do not have a full theoretical description of them available yet. For this reason we have not attempted to incorporate the SDSS LRG sample into our Fisher matrix parameter estimation process.
![\begin{figure}
\par\includegraphics[width=7.6cm,clip]{3487_f12.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg135.gif) |
Figure 12: Comoving number density of clusters as a function of redshift for the PLANCK- (lower set of curves) and SPT-like (upper set of curves) SZ surveys. Solid lines in each set correspond to the cases with 15 000, 25 000 and 35 000 clusters. The vertical dotted line shows the applied upper limiting redshift for the PLANCK. Dashed lines represent purely flux-limited cases i.e. without any lower mass cuttoff imposed. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3487_f13.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg136.gif) |
Figure 13: Comparison of the "strength'' of the future SZ cluster surveys with respect to the SDSS LRG. Lines shown for the PLANCK- and SPT-like surveys correspond to the detected cluster numbers (starting from above): 15 000, 25 000 and 35 000. |
| Open with DEXTER | |
For the SZ surveys the spectroscopic follow-up is a crucial issue, but several other studies (such as cluster number counts) also require determination of redshifts. As these investigations will be performed anyway, the clustering study can be seen as coming essentially "for free''.
![\begin{figure}
\par\includegraphics[width=16cm,clip]{3487_f14.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg139.gif) |
Figure 14:
Upper left panel: 2D light-cone power spectrum for clusters with mass above
|
| Open with DEXTER | |
In Fig. 14 we present some examples of 2D power spectra calculated in the manner described above. The top left-hand panel shows the 2D light-cone power spectrum of clusters with a mass above
![]() (in logarithmic units) while the lower left-hand panel contains the same spectrum but with the redshift space distortion "switched off''. The contours starting from the upper right corner correspond to the values 104.8 and 104.7 for the upper and lower panel, respectively and the step size was taken
(in logarithmic units) while the lower left-hand panel contains the same spectrum but with the redshift space distortion "switched off''. The contours starting from the upper right corner correspond to the values 104.8 and 104.7 for the upper and lower panel, respectively and the step size was taken
![]() .
It is clearly seen how linear redshift-space distortion boosts power along the line of sight. The cosmological distortion (in the currently selected reference model) on the other hand works in the opposite way. Since the chosen Milne model is strongly different from the
.
It is clearly seen how linear redshift-space distortion boosts power along the line of sight. The cosmological distortion (in the currently selected reference model) on the other hand works in the opposite way. Since the chosen Milne model is strongly different from the ![]() CDM "concordance'' model the cosmological distortion is easily visible. We use Milne's model only for illustrative purposes but in the following parameter estimation part we change the reference model to the WMAP "concordance'' cosmology. On the right-hand panels of the figure we have removed the smooth component of the power spectrum revealing the series of acoustic rings. Here the continuous contours correspond to
CDM "concordance'' model the cosmological distortion is easily visible. We use Milne's model only for illustrative purposes but in the following parameter estimation part we change the reference model to the WMAP "concordance'' cosmology. On the right-hand panels of the figure we have removed the smooth component of the power spectrum revealing the series of acoustic rings. Here the continuous contours correspond to
![]() values of 0.95 and 1.05 while the dashed lines are for the values 0.97 and 1.03. It is important to note that the picture on both panels looks practically the same. This is due to the fact that cosmological and redshift-space distortions work in a different way: cosmological transformation stretches or compresses the power spectra on the plane of the figure whereas redshift distortion moves the spectra in a vertical direction. If we had smooth power spectra without any particular features then it would be extremely hard to disentangle these two types of distortions. Having the power spectra with acoustic features it is easy to isolate cosmological distortion by dividing out a smooth component. The ability to disentangle cosmological and redshift-space distortions is extremely important to extract the bias parameter from the survey in a self-consistent way. In the parameter estimation part of this section we see how much better one does with the model having acoustic oscillations as compared to the one without.
values of 0.95 and 1.05 while the dashed lines are for the values 0.97 and 1.03. It is important to note that the picture on both panels looks practically the same. This is due to the fact that cosmological and redshift-space distortions work in a different way: cosmological transformation stretches or compresses the power spectra on the plane of the figure whereas redshift distortion moves the spectra in a vertical direction. If we had smooth power spectra without any particular features then it would be extremely hard to disentangle these two types of distortions. Having the power spectra with acoustic features it is easy to isolate cosmological distortion by dividing out a smooth component. The ability to disentangle cosmological and redshift-space distortions is extremely important to extract the bias parameter from the survey in a self-consistent way. In the parameter estimation part of this section we see how much better one does with the model having acoustic oscillations as compared to the one without.
The total power spectrum measured over a broad z-interval is a weighted sum of differently distorted power spectra and so there will be some loss of acoustic features. The loss is stronger along the line of sight, as can be seen from Fig. 14. This is due to the currently chosen reference model where
![]() .
Again, this effect is strongly pronounced because Milne's model differs strongly from the WMAP "concordance'' cosmology for which our calculation was done.
.
Again, this effect is strongly pronounced because Milne's model differs strongly from the WMAP "concordance'' cosmology for which our calculation was done.
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{3487_f15.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg171.gif) |
Figure 15: Error ellipses for the PLANCK-like SZ survey including CMB priors as described in the text. Solid/dashed lines show results for 3/1 redshift bin(s). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=14.8cm,clip]{3487_f16.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg172.gif) |
Figure 16: Analog of Fig. 15 for the SPT-like survey. Solid/dashed lines show results for 4/1 redshift bin(s). |
| Open with DEXTER | |
Here we perform calculations for two types of SZ survey. The first one that should serve as a prototype for PLANCK is a shallow survey that covers the full sky with a sensitivity limit of
![]() mJy at 353 GHz
mJy at 353 GHz![]() . We also apply a lower mass cutoff of
. We also apply a lower mass cutoff of
![]() resulting in total
resulting in total ![]() 25 000 clusters up to the applied limiting redshift
25 000 clusters up to the applied limiting redshift
![]() (see Fig. 10 lower panel). The calculations are done for one redshift bin spanning
(see Fig. 10 lower panel). The calculations are done for one redshift bin spanning
![]() and also for three bins:
and also for three bins:
![]() ,
,
![]() ,
,
![]() .
The achieved
.
The achieved
![]() values at
values at
![]() are
are ![]() for the one bin case and
for the one bin case and ![]() for each of the bins in the three bin case. The other deep and rather "narrow'' survey should mimic the performance of SPT. Here we have taken
for each of the bins in the three bin case. The other deep and rather "narrow'' survey should mimic the performance of SPT. Here we have taken
![]() mJy at 150 GHz and
mJy at 150 GHz and
![]() (see Ruhl et al. 2004; Majumdar & Mohr 2004). Moreover, we assumed that the survey is capable of covering one octant of the sky and here we have not applied any high redshift cutoff. As for the PLANCK-like survey two different cases are considered here. In the first case while combining all the data to one common power spectrum we are able to achieve
(see Ruhl et al. 2004; Majumdar & Mohr 2004). Moreover, we assumed that the survey is capable of covering one octant of the sky and here we have not applied any high redshift cutoff. As for the PLANCK-like survey two different cases are considered here. In the first case while combining all the data to one common power spectrum we are able to achieve
![]() ,
whereas in the second case with the four redshift bins:
,
whereas in the second case with the four redshift bins:
![]() ,
,
![]() ,
,
![]() ,
,
![]() we find a
we find a
![]() in each redshift bin. The total number of objects detected with this type of survey would be
in each redshift bin. The total number of objects detected with this type of survey would be ![]() 27 000.
27 000.
The results in Figs. 15 and 16 present constraints for the five cosmological parameters:
![]() ,
,
![]() ,
,
![]() ,
h and w0. Here we have added priors to
,
h and w0. Here we have added priors to
![]() and
and
![]() from the CMB angular power spectrum studies, and also a prior to the bias parameters. In order to be able to compare our results to the ones given in Hu & Haiman (2003) the fractional errors of 0.01 for
from the CMB angular power spectrum studies, and also a prior to the bias parameters. In order to be able to compare our results to the ones given in Hu & Haiman (2003) the fractional errors of 0.01 for
![]() and
and
![]() (this should be achievable with the PLANCK mission (Hu 2002)) were similarly assumed. These constraints are easily "rotated'' to the frame used here since under coordinate transformations the Fisher matrix transforms as a second rank tensor. Moreover, we have restricted our calculations to the flat models only, and for the bias have assumed that one is able to describe it with a relative accuracy of
(this should be achievable with the PLANCK mission (Hu 2002)) were similarly assumed. These constraints are easily "rotated'' to the frame used here since under coordinate transformations the Fisher matrix transforms as a second rank tensor. Moreover, we have restricted our calculations to the flat models only, and for the bias have assumed that one is able to describe it with a relative accuracy of ![]() .
Finally, the joint Fisher matrix is the sum of all the Fisher matrices transformed to a common frame. All the calculations done here assume an underlying model with baryonic features in the matter power spectrum.
Figure 15 presents results for the previously described shallow survey with full sky coverage while the error ellipses in Fig. 16 apply to the deep and narrow survey. In both figures dashed lines correspond to the single and solid lines to the multiple bin case. Due to the fact that with a single bin one is able to measure the shape of the power spectrum with a higher precision than in the case of multiple bins, we see from the above figures that in general stronger constraints on
.
Finally, the joint Fisher matrix is the sum of all the Fisher matrices transformed to a common frame. All the calculations done here assume an underlying model with baryonic features in the matter power spectrum.
Figure 15 presents results for the previously described shallow survey with full sky coverage while the error ellipses in Fig. 16 apply to the deep and narrow survey. In both figures dashed lines correspond to the single and solid lines to the multiple bin case. Due to the fact that with a single bin one is able to measure the shape of the power spectrum with a higher precision than in the case of multiple bins, we see from the above figures that in general stronger constraints on
![]() are obtained. On the other hand constraints on w0 are much stronger in the multiple bin case due to the increased knowledge about the redshift derivatives. We also performed calculations taking two redshift bins and the results were already rather close to the solid curves in the figures above which can be interpreted as an indication that any further redshift slicing would not improve constraints on w0. Also one should not increase the number of redshift bins much above the maximally used values of three and four since then the wavevector bins with width
are obtained. On the other hand constraints on w0 are much stronger in the multiple bin case due to the increased knowledge about the redshift derivatives. We also performed calculations taking two redshift bins and the results were already rather close to the solid curves in the figures above which can be interpreted as an indication that any further redshift slicing would not improve constraints on w0. Also one should not increase the number of redshift bins much above the maximally used values of three and four since then the wavevector bins with width
![]() would become highly correlated and the above Fisher matrix calculation would not be meaningful.
would become highly correlated and the above Fisher matrix calculation would not be meaningful.
Probably the most interesting constraints in Figs. 15 and 16 are the ones for
![]() (or
(or
![]() since we have assumed flat models) and w0. Error ellipses in the
since we have assumed flat models) and w0. Error ellipses in the
![]() -w0 plane are also given in Fig. 17 for various different assumptions. The top panel here corresponds to the PLANCK-type and the lower one to the SPT-type of survey. The order of ellipses in the top panel starting from the bottommost one is as follows: (1) clustering signal of the model without baryonic oscillations + CMB priors, (2) (1) + prior on bias, (3) clustering signal of the "wiggly'' model, (4) (3) + CMB priors, (5) (4) + prior on bias. The only difference in the lower panel is the reversed order of (2) and (3). The inset in the lower plot displays the constraints obtainable (again starting from the bottommost ellipse) with (1) SPT, (2) PLANCK, (3) SPT + PLANCK, (4) the survey with SPT characteristics covering the full sky. For all of the cases shown in the inset we have included CMB and bias priors. The constraint ellipses for the "clustering only'' case assuming a "smooth'' model would fill almost all the plot area and for the sake of clarity we have not displayed them here. It is evident from Fig. 17 that the model with baryonic oscillations is performing much better compared to its smoothed counterpart. Adding prior information (in contrast to the "smooth'' case) does not result here in a strong improvement i.e. the clustering signal alone already has a significant constraining power.
-w0 plane are also given in Fig. 17 for various different assumptions. The top panel here corresponds to the PLANCK-type and the lower one to the SPT-type of survey. The order of ellipses in the top panel starting from the bottommost one is as follows: (1) clustering signal of the model without baryonic oscillations + CMB priors, (2) (1) + prior on bias, (3) clustering signal of the "wiggly'' model, (4) (3) + CMB priors, (5) (4) + prior on bias. The only difference in the lower panel is the reversed order of (2) and (3). The inset in the lower plot displays the constraints obtainable (again starting from the bottommost ellipse) with (1) SPT, (2) PLANCK, (3) SPT + PLANCK, (4) the survey with SPT characteristics covering the full sky. For all of the cases shown in the inset we have included CMB and bias priors. The constraint ellipses for the "clustering only'' case assuming a "smooth'' model would fill almost all the plot area and for the sake of clarity we have not displayed them here. It is evident from Fig. 17 that the model with baryonic oscillations is performing much better compared to its smoothed counterpart. Adding prior information (in contrast to the "smooth'' case) does not result here in a strong improvement i.e. the clustering signal alone already has a significant constraining power.
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{3487_f17.eps}
\end{figure}](/articles/aa/full/2006/04/aa3487-05/Timg190.gif) |
Figure 17: Upper panel: error ellipses under various assumptions for the PLANCK-like survey. Here we have shown the following cases: 1. Clustering signal of the model without baryonic oscillations + CMB priors, 2. #1 + prior on bias, 3. Clustering signal of the "wiggly'' model, 4. #3 + CMB priors, 5. #4 + prior on bias. Lower panel: as above, except for the SPT-like survey and with a changed order of the cases #2 and #3. Lower panel inset: constraints obtainable with: 1. SPT, 2. PLANCK, 3. SPT + PLANCK, 4. The survey with SPT characteristics covering the full sky. All of the cases here have CMB and bias priors added. |
| Open with DEXTER | |
Table 1 lists the principal components of the clustering analysis only i.e. no CMB and bias priors included. Also we have marginalized over bin bias parameters. This serves as a compact way of summarizing our results. The principal components are given in the form:
Table 1: Principal components as given in Eq. (36) for the "clustering only'' case for PLANCK-like, SPT-like and for the combined survey.
In the last part of the paper we carried out a Fisher matrix forecasting analysis for cosmological parameters, which add up to nine in the case of four redshift bins:
![]() ,
,
![]() ,
,
![]() ,
h, w0 plus a free bias parameter for each bin. We included prior information for
,
h, w0 plus a free bias parameter for each bin. We included prior information for
![]() and
and
![]() from CMB angular power spectrum studies and also constrained the possible values for the bias parameters. A prior on bias parameters only has a significant effect in the case of models with smooth power spectra i.e. models with acoustic oscillations have enough constraining power to give an estimate of bias parameters from the survey itself. The most interesting constraints are obtained for
from CMB angular power spectrum studies and also constrained the possible values for the bias parameters. A prior on bias parameters only has a significant effect in the case of models with smooth power spectra i.e. models with acoustic oscillations have enough constraining power to give an estimate of bias parameters from the survey itself. The most interesting constraints are obtained for
![]() and w0. Wide and rather shallow surveys like PLANCK in combination with a CMB prior on
and w0. Wide and rather shallow surveys like PLANCK in combination with a CMB prior on
![]() are able to provide strong constraints on
are able to provide strong constraints on
![]() or in the case of flat models equivalently on
or in the case of flat models equivalently on
![]() .
The constraints on w0 on the other hand are not as good as the ones obtained by deeper and narrower surveys with the characteristics of SPT due to the lack of higher redshift objects. We also give our results as the principal components of the Fisher matrix that should allow for an easy way of comparison and also for a fast way of incorporating these constraints into further parameter forecasting studies.
.
The constraints on w0 on the other hand are not as good as the ones obtained by deeper and narrower surveys with the characteristics of SPT due to the lack of higher redshift objects. We also give our results as the principal components of the Fisher matrix that should allow for an easy way of comparison and also for a fast way of incorporating these constraints into further parameter forecasting studies.
Acknowledgements
I thank Rashid Sunyaev for useful discussions and Maximilian Stritzinger for proofreading the paper. I am grateful to the anonymous referee for helpful comments and suggestions. Also I acknowledge the support provided through the European Community's Human Potential Programme under contract HPRN-CT-2002-00124, CMBNET, and the ESF grant 5347.
The simulations in this paper were carried out by the Virgo Supercomputing Consortium using computers based at the Computing Centre of the Max-Planck Society in Garching and at the Edinburgh parallel Computing Centre. The data are publicly available at http://www.mpa-garching.mpg.de/NumCos