A&A 445, 1099-1126 (2006)
DOI: 10.1051/0004-6361:20053832

Quantitative spectroscopy of BA-type supergiants^,

N. Przybilla¹ - K. Butler² - S. R. Becker^2, - R. P. Kudritzki³

1 - Dr. Remeis-Sternwarte Bamberg, Sternwartstr. 7, 96049 Bamberg, Germany
2 - Universitäts-Sternwarte München, Scheinerstraße 1, 81679 München, Germany
3 - Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822, USA

Received 15 July 2005 / Accepted 12 September 2005

Abstract
Luminous BA-type supergiants have enormous potential for modern astrophysics. They allow topics ranging from non-LTE physics and the evolution of massive stars to the chemical evolution of galaxies and cosmology to be addressed. A hybrid non-LTE technique for the quantitative spectroscopy of these stars is discussed. Thorough tests and first applications of the spectrum synthesis method are presented for the bright Galactic objects $\eta$ Leo (A0 Ib), HD 111613 (A2 Iabe), HD 92207 (A0 Iae) and $\beta$ Ori (B8 Iae), based on high-resolution and high-S/N Echelle spectra. Stellar parameters are derived from spectroscopic indicators, consistently from multiple non-LTE ionization equilibria and Stark-broadened hydrogen line profiles, and they are verified by spectrophotometry. The internal accuracy of the method allows the 1$\sigma$-uncertainties to be reduced to $\la$1-2% in  $T_{\rm eff}$ and to 0.05-0.10 dex in $\log g$. Elemental abundances are determined for over 20 chemical species, with many of the astrophysically most interesting in non-LTE (H, He, C, N, O, Mg, S, Ti, Fe). The non-LTE computations reduce random errors and remove systematic trends in the analysis. Inappropriate LTE analyses tend to systematically underestimate iron group abundances and overestimate the light and $\alpha$-process element abundances by up to factors of two to three on the mean. This is because of the different responses of these species to radiative and collisional processes in the microscopic picture, which is explained by fundamental differences of their detailed atomic structure, and not taken into account in LTE. Contrary to common assumptions, significant non-LTE abundance corrections of $\sim$0.3 dex can be found even for the weakest lines ( $W_{\lambda}\la 10$ mÅ). Non-LTE abundance uncertainties amount to typically 0.05-0.10 dex (random) and $\sim$0.10 dex (systematic 1$\sigma$-errors). Near-solar abundances are derived for the heavier elements in the sample stars, and patterns indicative of mixing with nuclear-processed matter for the light elements. These imply a blue-loop scenario for $\eta$ Leo because of first dredge-up abundance ratios, while the other three objects appear to have evolved directly from the main sequence. In the most ambitious computations several ten-thousand spectral lines are accounted for in the spectrum synthesis, permitting the accurate reproduction of the entire observed spectra from the visual to near-IR. This prerequisite for the quantitative interpretation of intermediate-resolution spectra opens up BA-type supergiants as versatile tools for extragalactic stellar astronomy beyond the Local Group. The technique presented here is also well suited to improve quantitative analyses of less extreme stars of similar spectral types.

Key words: stars: supergiants - stars: early-type - stars: atmospheres - stars: fundamental parameters - stars: abundances - stars: evolution

  
1 Introduction

Massive supergiants of late B and early A-type (BA-type supergiants, BA-SGs) are among the visually brightest normal stars in spiral and irregular galaxies. At absolute visual magnitudes up to $M_V \simeq -$9.5 they can rival with globular clusters and even dwarf spheroidal galaxies in integrated light. This makes them primary candidates for quantitative spectroscopy at large distances and makes them the centre of interest in the era of extragalactic stellar astronomy. The present generation of 8-10 m telescopes and efficient multi-object spectrographs can potentially observe individual stars in systems out to distances of the Virgo and Fornax cluster of galaxies (Kudritzki 1998, 2000). The first steps far beyond the Local Group have already been taken (Bresolin et al. 2001, 2002; Przybilla 2002).

BA-type supergiants pose a considerable challenge for quantitative spectroscopy because of their complex atmospheric physics. The large energy and momentum density of the radiation field, in combination with an extended and tenuous atmosphere, gives rise to departures from local thermodynamic equilibrium (non-LTE), and to stellar winds. Naturally, this makes BA-SGs interesting in terms of stellar atmosphere modelling and non-LTE physics, but there is more to gain from their study. They can be used as tracers for elemental abundances, as their line spectra exhibit a wide variety of chemical species, ranging from the light elements to $\alpha$-process, iron group and s-process elements. These include, but also extend the species traced by H II-regions and thus they can be used to investigate abundance patterns and gradients in other galaxies to a far greater extent than from the study of gaseous nebulae alone. In fact, stellar indicators turn out to be highly useful for independently constraining (Urbaneja et al. 2005) the recently identified systematic error budget of strong-line analyses of extragalactic metal-rich H II regions (Kennicutt et al. 2003; Garnett et al. 2004; Bresolin et al. 2004), and its impact on models of galactochemical evolution. BA-type supergiants in other galaxies allow the metallicity-dependence of stellar winds and stellar evolution to be studied. In particular, fundamental stellar parameters and light element abundances (He, CNO) help to test the most recent generation of evolution models of rotating stars with mass loss (Heger & Langer 2000; Meynet & Maeder 2000,2003,2005; Maeder & Meynet 2001) and in addition magnetic fields (Heger et al. 2005; Maeder & Meynet 2005). These make predictions about the mixing of the stellar surface layers with nuclear processed matter which can be verified observationally. Moreover, BA-SGs can act as primary indicators for the cosmological distance scale by application of the wind momentum-luminosity relationship (WLR, Puls et al. 1996; Kudritzki et al. 1999) and by the flux-weighted gravity-luminosity relationship (FGLR, Kudritzki et al. 2003; Kudritzki & Przybilla 2003). In addition to the stellar metallicity, interstellar reddening can also be accurately determined, so that BA-SGs provide significant advantages compared to classical distance indicators such as Cepheids and RR Lyrae.

Despite this immense potential, quantitative analyses of BA-SGs are scarce. Only a few single objects were studied in an early phase; several bright Galactic supergiants, preferentially among these $\alpha$ Cyg (A2 Iae) and $\eta$ Leo (Groth 1961; Przybylski 1969; Wolf 1971; Aydin 1972) and the visually brightest stars in the Magellanic Clouds (Przybylski 1968, 1971, 1972; Wolf 1972, 1973). Near-solar abundances were found in almost all cases. Surveys for the most luminous stars in the Local Group galaxies followed (Humphreys 1980, and references therein), but were not accompanied by detailed quantitative analyses. These first quantitative studies were outstanding for their time, but from the present point of view they were also restricted in accuracy by oversimplified analysis techniques/model atmospheres, inaccurate atomic data and the lower quality of the observational material (photographic plates). Non-LTE effects were completely ignored at that time, as appropriate models were just being developed (e.g. Mihalas 1978, and references therein; Kudritzki 1973).

BA-type supergiants have become an active field of research again, following the progress made in model atmosphere techniques and detector technology (CCDs), and in particular the advent of 8-10 m-class telescopes. In a pioneering study by Venn (1995a,b) over twenty (less-luminous) Galactic A-type supergiants were systematically analysed for chemical abundances, using modern LTE model atmosphere techniques, and non-LTE refinements in a few cases. These indicated near-solar abundances for the heavier elements and partial mixing with CN-cycled gas. A conflict with stellar evolution predictions was noted, as the observed high N/C ratios were realised through carbon depletion and not via the predicted nitrogen enrichment. Later, this conflict was largely resolved by Venn & Przybilla (2003). However, an analysis of helium was not conducted, and more luminous supergiants, which are of special interest for extragalactic studies, were missing in the sample. Similar applications followed on objects in other spiral and dwarf irregular galaxies (dIrrs) of the Local Group (McCarthy et al. 1995; Venn 1999; Venn et al. 2000, 2001, 2003) and the nearby Antlia-Sextans Group dIrr galaxy Sextans A (Kaufer et al. 2004). The primary aim was to obtain first measurments of heavy element abundances in these galaxies. Good agreement between stellar oxygen abundances and literature values for nebular abundances was found, with the exception of the dIrr WLM (Venn et al. 2003). The number of objects analysed is small, thus prohibiting the derivation of statistically significant further conclusions. Moreover, abundances of the mixing indicators He, C and N were not determined in almost all cases.

Parallel to this, a sample of Galactic BA-SGs were studied by Takeda & Takada-Hidai (2000, and references therein) for non-LTE effects on the light element abundance analyses which confirm the effects of mixing in the course of stellar evolution. However, a conflict with the predictions of stellar evolution models was found, because C depletion was apparently accompanied by He depletion. The authors regarded this trend not being real, but indicated potential problems with the He  I line-formation. On the other hand, stellar parameters were not independently determined in these studies, but estimated, which can result in severe systematic global errors as will be shown later. Verdugo et al. (1999b) concentrated on deriving basic stellar parameters for over 30 Galactic A-type supergiants, assuming the validity of LTE. Independently, the Galactic high-luminosity benchmark $\alpha$ Cyg was investigated for elemental abundances by Takeda et al. (1996), solving the restricted non-LTE problem, and by Albayrak (2000), using a pure LTE approach. Fundamental parameters of $\alpha$ Cyg were determined by Takeda (1994) and by Aufdenberg et al. (2002). At lower luminosity, $\eta$ Leo was the subject of a couple of such studies (Lambert et al. 1988; Lobel et al. 1992). The results from these studies mutually agree only if rather generous error margins are allowed for, implying considerable systematic uncertainties in the analysis methods. Among the late B-type supergiants the investigations focused on $\beta$ Ori (Takeda 1994; Israelian et al. 1997). A larger sample of Galactic B-type supergiants, among those a number of late B-types, was studied by McErlean et al. (1999) for basic stellar parameters and estimating elemental abundances, on the basis of unblanketed non-LTE model atmospheres and non-LTE line formation. The chemical analysis recovers values being consistent with present-day abundances from unevolved Galactic B-stars, except for the light elements, which again indicate mixing of the surface layers with material from the stellar core.

Figure 1: Spectra of the sample stars around H$\gamma$ and H$\alpha$. The major spectral features are identified, short vertical marks indicate Fe II lines. Luminosity increases from bottom to top. Likewise, H$\alpha$ develops from a pure absorption line into a P-Cygni-profile because of the strengthening stellar wind. Note the marked incoherent electron scattering wings of H$\alpha$ in the most luminous object.

Open with DEXTER

The basic stellar parameters and abundances from modern studies of individual objects can still be discrepant by up to $\sim$20% in  $T_{\rm eff}$, $\sim$0.5 dex in $\log~g$ and $\sim$1 dex in the abundances. This is most likely to be the result of an interplay of systematic errors and inconsistencies in the analysis procedure, as we will discuss in the following. In order to improve on the present status, we introduce a spectrum synthesis approach for quantitative analyses of the photospheric spectra of BA-SGs. Starting with an overview of the observations of our sample stars and the data reduction, we continue with a thorough investigation of the suitability of various present-day model atmospheres for such analyses, and their limitations. General aspects of our line-formation computations are addressed in Sect. 4, while the details are summarised in Appendix A. Our approach to stellar parameter and abundance determination is examined and tested on the sample stars in Sects. 5 and 6. The consequences of these for the evolutionary status of our BA-SG sample are briefly discussed in Sect. 7. Finally, the applicability of our technique is tested for intermediate spectral resolution in Sect. 8. At all stages we put special emphasis on identifying and eliminating sources of systematic error, which allows us to constrain all relevant parameters with unprecedented accuracy. We conclude this work with a summary of the main results.

We will address the topic of stellar winds in our sample of BA-SGs separately, completing the discussion on the analysis inventory for this class of stars. Applications to Galactic and extragalactic BA-SGs in Local Group systems and beyond will follow. Note that the technique presented and tested here in the most extreme conditions is also well suited to improve quantitative analyses of less luminous stars of similar spectral classes.

  
2 Observations and data reduction

We test our analysis technique on a few bright Galactic supergiants that roughly sample the parameter space in effective temperature and surface gravity covered by future applications. We chose the two MK standards $\eta$ Leo (HD 87737) and $\beta$ Ori (HD 34085), the brightest member of the rich southern cluster NGC 4755, HD 111613, and one of the most luminous Galactic A-type supergiants known to date, HD 92207, for this objective.

For $\eta$ Leo, HD 111613 and HD 92207, Echelle spectra using FEROS (Kaufer et al. 1999) at the ESO 1.52 m telescope in La Silla were obtained on January 21 and 23, 1999. Nearly complete wavelength coverage between 3600 and 9200 Å was achieved, with a resolving power $R =\lambda/\Delta\lambda \approx 48~000$ (with 2.2 pixels per  $\Delta\lambda$resolution element), yielding a S/N of several hundred in V in 120, 600 and 300 s exposures. A corresponding spectrum of $\beta$ Ori was adopted from Commissioning II data (#0783, 20 s exposure taken in November 1998).

Data reduction was performed using the FEROS context in the MIDAS package (order definition, bias subtraction, subtraction of scattered light, order extraction, flat-fielding, wavelength calibration, barycentric movement correction, merging of the orders), as described in the FEROS documentation (http://www.ls.eso.org/lasilla/Telescopes/2p2T/E1p5M/FEROS/docu/Ferosdocu.html). Optimum extraction of the orders with cosmic ray clipping was chosen. In the spectral region longward of $\sim$8900 Å problems with the optimum extraction arose due to the faintness of the signal. Standard extraction was therefore performed in this region. No correction for telluric lines was made. The spectral resolution is sufficiently high to trace the (broadened) stellar lines in our spectrum synthesis approach even within the terrestrial O₂ and H₂O bands in many cases, see e.g. Fig. 9 of Przybilla et al. (2001b). The spectra were normalised by fitting a spline function to carefully selected continuum points. This suffices to retain the line profiles of the Balmer lines in supergiants as these are rather weak and sampled by a single Echelle order. Finally, the spectra were shifted to the wavelength rest frame by accounting for a radial velocity  $v_{\rm rad}$as determined from cross-correlation with an appropriate synthetic spectrum. Excellent agreement with  $v_{\rm rad}$ data from the literature (see Table 2) was found. Representative parts of the spectra are displayed in Fig. 1.

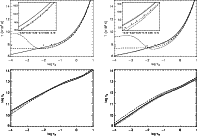Figure 2: Comparison of different model atmospheres: temperature structure ( top) and electron density ( bottom) for two supergiant models as a function of the Rosseland optical depth. On the left for the LC Ib with stellar parameters according to our model for $\eta$ Leo, on the right for the LC Iae (HD 92207), corresponding to our sample objects at lowest and highest luminosity. Full line: A TLAS9 line-blanketed LTE model (adopted for the analysis), dashed: A TLAS9 H+He LTE model without line blanketing, dashed-dotted: T LUSTY H+He non-LTE model without line blanketing, boxes: grey atmosphere. A second A TLAS9 line-blanketed LTE model is displayed in the case of the Iae object (dotted), calculated with background opacities corresponding to solar metallicity. In our final model for HD 92207 the background opacities are reduced by an empirical factor of two in metallicity, correcting at least qualitatively for neglected non-LTE effects. In the inset the formation region of weak lines is displayed enlarged.

Open with DEXTER

  
3 Model atmospheres

Model atmospheres are a crucial ingredient for solving the inverse problem of quantitative spectroscopy. Ideally, BA-SGs should be described by unified (spherically extended, hydrodynamical) non-LTE atmospheres, accounting for the effects of line blanketing. Despite the progress made in the last three decades, such model atmospheres are still not available for routine applications. In the following we investigate the suitability of existing models for our task, their robustness for the applications and their limitations. The criterion applied in the end will be their ability to reproduce the observations in a consistent way.

3.1 Comparison of contemporary model atmospheres

Two kinds of classical (plane-parallel, hydrostatic and stationary) model atmospheres are typically applied in the contemporary literature for analyses of BA-SGs: line-blanketed LTE atmospheres and non-LTE H+He models (without line-blanketing) in radiative equilibrium. First, we discuss what effects these different physical assumptions have on the model stratification and on synthetic profiles of important diagnostic lines. We therefore include also an LTE H+He model without line-blanketing and additionally a grey stratification in the comparison for two limiting cases: the least and the most luminous supergiants of our sample, $\eta$ Leo and HD 92207, of luminosity class (LC) Ib and Iae. The focus is on the photospheric line-formation depths, where the classical approximations are rather appropriate - the velocities in the plasma remain sub-sonic, the spatial extension of this region is small (only a few percent) compared to the stellar radius in most cases, and the BA-SGs photospheres retain their stability over long time scales, in contrast to their cooler progeny, the yellow supergiants, which are to be found in the instability strip of the Hertzsprung-Russell diagram, or the Luminous Blue Variables.

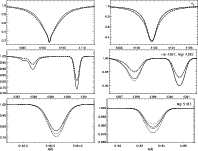Figure 3: Comparison of theoretical non-LTE profiles for several diagnostic lines, calculated on the basis of different model atmospheres for A0 supergiants of LC Ib ($\eta$ Leo, left) and Iae (HD 92207, right). Ordinate is normalised flux. The same line designations as in Fig. 2 are used, and the profiles are broadened accounting for instrumental profile, rotation and macroturbulence (see Table 2). Note that the He I and Mg I lines react sensitively to the detailed structure of the models while for the Balmer lines and the Mg II lines only the profiles of the line-blanketed and the unblanketed models can be discriminated well.

Open with DEXTER

The non-LTE models are computed using the code T LUSTY (Hubeny & Lanz 1995), the LTE models are calculated with A TLAS9 (Kurucz 1993), in the version of M. Lemke, as obtained from the CCP7 software library, and with further modifications (Przybilla et al. 2001b) where necessary. Line blanketing is accounted for by using solar metallicity opacity distribution functions (ODFs) from Kurucz (1992). For the grey temperature structure, $T^4 = \frac{3}{4}~T_{\rm eff}^4~[\tau+q(\tau)]$, exact Hopf parameters $q(\tau)$ (Mihalas 1978, p. 72) are used.

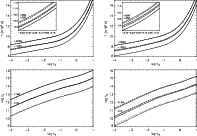Figure 4: Influence of the helium abundance on the atmospheric structure ( bottom) and effects of metallicity ( middle) and microturbulence (top set of curves) on the atmospheric line blanketing: temperature structure ( upper panels) and electron density ( lower panels). On the left the comparison is made for a LC Ib object with stellar parameters matching those of our model for $\eta$ Leo, on the right for the LC Iae (HD 92207). Only one parameter is modified each time: atmospheric helium abundance of y = 0.089 (solar value, full line) and y = 0.15 (dotted line); using ODFs with [M/H] = 0.0, -0.3, -0.7 and -1.0 dex (full, dotted, dashed, dashed-dotted lines); using ODFs with $\xi$ = 8, 4 and 2 km s-1 (full, dotted, dashed lines). In the inset, the formation region for weak lines is enlarged. For convenience, the individual sets of curves have been shifted by the factors indicated.

Open with DEXTER

In Fig. 2 we compare the model atmospheres, represented by the temperature structure and the run of electron number density $n_{\rm e}$. For the less-luminous supergiant marked differences in the line-formation region (for metal lines, typically between Rosseland optical depth $-1\la \log~\tau_{\rm R}\la 0$) occur only between the line-blanketed model, which is heated due to the backwarming effect by $\la$200 K, and the unblanketed models. In particular, it appears that non-LTE effects on the atmospheric structure are almost negligible, reducing the local temperature by $\la$50 K. The good agreement of the grey stratification and the unblanketed models indicates that Thomson scattering is largely dominating the opacity in these cases. A temperature rise occurs in the non-LTE model because of the recombination of hydrogen - it is an artefact from neglecting metal lines. The gradient of the density rise with atmospheric depth is slightly flatter in the line-blanketed model. In the case of the highly luminous supergiant, line-blanketing effects retain their importance (heating by $\la$300 K), but non-LTE also becomes significant (cooling by $\la$200 K). From the comparison with observation it is found empirically, that a model with the metal opacity reduced by a factor of 2 (despite the fact that the line analysis yields near-solar abundances) gives an overall better agreement. This is slightly cooler than the model for solar metal abundance and may be interpreted as an empirical correction for unaccounted non-LTE effects on the metal blanketing in the most luminous objects, i.e. $\beta$ Ori and HD 92207 in the present case. The local electron number density in the line-blanketed case is slightly lower than in the unblanketed models. We conclude from this comparison that at photospheric line-formation depths the importance of line blanketing outweighs non-LTE effects, with the rôle of the latter increasing towards the Eddington limit, as expected. In the outermost regions the differences between the individual models become more pronounced. However, none of the stratifications can be expected to give a realistic description of the real stellar atmosphere there, as spherical extension and velocity fields are neglected in our approach.

The results of spectral line modelling depend on the details of the atmospheric structure and different line strengths result from computations based on the different stratifications. Therefore, non-LTE line profiles for important stellar parameter indicators are compared in Fig. 3: H$\delta$ as a representative for the gravity-sensitive Balmer lines, a typical He I line, and features of Mg I/II, which are commonly used for the $T_{\rm eff}$-determination. In the case of the Balmer and the Mg II lines discrimination is only possible between the line-blanketed and the unblanketed models. Both the LTE and non-LTE H+He model structure without line blanketing result in practically the same profiles. This changes for the lines of He I and Mg I, which react sensitively to modifications of the atmospheric structure: all the different models lead to distinguishable line profiles. These differences become more pronounced at higher luminosity.

This comparison of model structures and theoretical line profiles is instructive, but the choice of the best suited model can only be made from a confrontation with observation. It is shown later that the physically most sophisticated approach available at present, LTE with line blanketing plus non-LTE line formation and appropriately chosen parameters, allows highly consistent analyses of BA-SGs to be performed. This is discussed next.

  
3.2 Effects of helium abundance and line blanketing

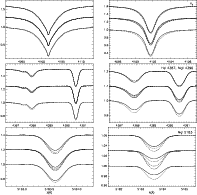Figure 5: Influence of the helium abundance ( bottom), metallicity ( middle) and microturbulence ( top set of curves) on the profiles of diagnostic lines for our models for $\eta$ Leo and HD 92207. The same designations as in Fig. 4 are used, and the profiles are broadened accounting for instrumental profile, rotation and macroturbulence. Note the strong sensitivity of the lines to these "secondary'' parameters at LC Iae.

Open with DEXTER

Helium lines become visible in main sequence stars at the transition between A- and B-types at $T_{\rm eff} \sim 10~000$ K. In supergiants this boundary is lowered to $\sim$8000 K due to stronger non-LTE effects in He I and by the commonly enhanced atmospheric helium abundance in these stars (see Sect. 6). The main effect of an helium enhancement is the increase of the mean molecular weight of the atmospheric material, affecting the pressure stratification; the decrease of the opacity and thus an effect on the temperature structure on the other hand is negligible (Kudritzki 1973). Both effects are quantified in Fig. 4, where the test is performed for solar and an enhanced abundance of y = 0.15, while all other parameters remain fixed. The relative increase in density strengthens with decreasing surface gravity. The spectrum analysis of the most luminous supergiants is distinctly influenced by helium enhancement, while farther away from the Eddington limit the effects diminish, see Fig. 5. Obviously, the He I lines are notably strengthened with increasing abundance. For higher surface gravities, the Balmer lines and the ionization equilibrium of Mg I/II are almost unaffected. On the other hand, near the Eddington limit the Balmer lines are noticeably broadened through an increased Stark effect, simulating a higher surface gravity in less careful analyses. A marked strengthening of the Mg I lines is noticed, as the ionization balance is shifted in favour of the neutral species through the increased electron density. In addition, the lines from both ionic species of magnesium are strengthened by the locally increased absorber density: the combined effects result in a higher effective temperature from Mg I/II, when helium enhancement is neglected. All studies of highly luminous BA-type supergiants (like $\alpha$ Cyg or $\beta$ Ori) to date have neglected atmospheric structure modifications due to helium enhancements, as these introduce an additional parameter into the analysis. It is shown that this is not justified: a higher precision in the stellar parameter determination is obtained in the present work by explicitly accounting for this parameter.

Line blanketing is an important factor for atmospheric analyses. However, it is not only a question of whether line blanketing is considered or not, but how it is accounted for in detail. The two important parameters to consider here are metallicity and microturbulence, which both affect the line strengths and consequently the magnitude of the line blanketing effect. In studies of supergiants so far this has been neglected. The introduction of two extra parameters further complicates the analysis procedure and requires additional iteration steps, but is rewarded in terms of accuracy.

The influence of the metallicity on the atmospheric line blanketing effect is displayed in Fig. 4. Here all parameters are kept fixed except the metallicity of the ODFs used for the model computations. A model sequence for four metallicities, spanning a range from solar to 0.1$\times$ solar abundances, is compared. In the LC Ib supergiant model, the density structure is hardly affected and the local temperatures in the line-formation region differ by less than 100 K for a change of metallicity within a factor of ten. This difference increases to $\sim$200 K close to the Eddington limit: the higher the metallicity, the stronger the backwarming and the corresponding surface cooling due to line blanketing. In addition, the density structure is also notably altered, to a larger extent as in the case of a moderately increased helium abundance. Radiative acceleration diminishes for decreasing metallicity and thus the density rises. The corresponding effects on the line profiles are summarised in Fig. 5. An appreciable effect is noticed only for the highly temperature sensitive He I and Mg I lines at LC Ib. Again, at high luminosity all the diagnostic lines are changed considerably, the extreme case being the Mg I line which is strengthened by a factor of almost three. Ignoring the metallicity effect on the line blanketing in detail will result in significantly altered stellar parameters from the analysis.

Microturbulence has a similar impact on the line blanketing. An increase in the microturbulent velocity $\xi$ strengthens the backwarming effect as does an increase in the metallicity, since a larger fraction of the radiative flux is being blocked. The resulting atmospheric structures from a test with ODFs at three different values for microturbulence, for $\xi = 2$, 4 and 8 km s^-1, and otherwise unchanged parameters are shown in Fig. 4. In both stellar models the local temperatures in the line-formation region are increased by $\sim$100 K when moving from the lowest to the highest value of $\xi$. A noticeable change of the density structure is only seen for the LC Iae model. The corresponding changes in the line profiles are displayed in Fig. 5. Similar effects are found as in the case of varied metallicity, however they are less pronounced.

The consistent treatment proposed here improves the significance of analyses, in particular for the most luminous supergiants. This also applies to the closely related line blocking, which is likewise treated in a consistent manner.

3.3 Neglected effects

Spherical extension of the stellar atmosphere is the first of a number of factors neglected in the current work. It becomes important in all cases where the atmospheric thickness is no longer negligible compared to the stellar radius. Observable quantities like the emergent flux, the colours and line equivalent widths from extended models will deviate from plane-parallel results for increasing extension $\eta$ (= atmospheric thickness/stellar radius), which can lead to a modified interpretation of the observed spectra. The expected effects on the line spectrum are (mostly) reduced equivalent widths due to extra emission from the extended outer regions and a shift in the ionisation balance. Details on the differences between spherically extended and plane-parallel hydrostatic LTE model atmospheres can be found in Fieldus et al. (1990). Note that $\eta$ will be on the order of a few percent for the photospheres of the objects investigated here (adopting atmospheric thicknesses from the A TLAS9 models and stellar radii from Table 2).

Evidence for macroscopic velocity fields, i.e. a stellar wind, in BA-SG atmospheres is manifold, most obviously from P-Cygni profiles of strong lines but also from small line asymmetries with extra absorption in the blue wing and blue-shifts of the central line wavelength in less spectacular cases. Kudritzki (1992) investigated the influence of realistic velocity fields from radiation driven winds on the formation of photospheric lines (in plane-parallel geometry). The subsonic outflow velocity field at the base of the stellar wind strengthens lines that are saturated in their cores even for the moderate mass-loss rates typically observed for BA-SGs. Desaturation of the lines due to the Doppler shifts experienced by the moving medium is the driving mechanism for this strengthening.

Velocity fields therefore counteract the proposed line weakening effects of sphericity, apparently leading to a close net cancellation for the weak line spectrum. Plane-parallel hydrostatic atmospheres thus seem a good approximation to spherical and hydrodynamic (unified) atmospheres for the modelling of BA-SGs, if one concentrates on the photospheric spectrum. In fact, first results from a comparison of classical LTE with unified non-LTE atmospheres in the BA-SG regime indicate good agreement (Santolaya-Rey et al. 1997; Puls et al. 2005; J. Puls, private communication). The situation appears to be similar in early B-supergiants (Dufton et al. 2005)

BA-type supergiants have been known as photometric and optical spectrum variables for a long time. The most comprehensive study to date in this context is that of Kaufer et al. (1996, 1997). Additional observational findings in the UV spectral region, in particular of the Mg II and Fe II resonance lines, are presented by Talavera & Gomez de Castro (1987) and Verdugo et al. (1999a). Kaufer et al. (1997) find peak-to-peak amplitude variations of the line strength of 29% on time scales of years. Unaccounted variability is therefore a potential source of inconsistencies when analysing data from different epochs, see Sect. 5 for our approach to overcome this limitation.

BA-type supergiants are slow rotators with typical observed values of $v\sin i$between 30 to 50 km s^-1 (Verdugo et al. 1999b). The modelling can therefore be treated as a 1-D problem, as rotationally induced oblateness of the stars is insignificant. Finally, magnetic fields in BA-SGs appear to be too weak to cause atmospheric inhomogeneities. For $\beta$ Ori a weak longitudinal magnetic field, on the order of 100 G was observed by Severny (1970). Little information on other objects is available.

3.4 Limits of the analyses

The spectrum synthesis technique described in the present work is applicable to a rather wide range of stellar parameters, but nevertheless it is restricted. Its scope of validity principally concentrates on BA-SGs and related objects of lower luminosity. This is mainly due to the limits posed by the underlying atmospheric models and the atomic models implemented.

From estimates, such as that presented by Kudritzki (1988, Fig.  III, 9), it is inferred that non-LTE effects on the atmospheric structure, increasing with stellar effective temperature, will inhibit analyses with the present technique of any supergiants above $\sim$20 000 K, i.e. in the early B-types. However, main sequence stars and even (sub-)giants of such spectral type are analysed with classical atmospheric models on a routine basis. For the less-luminous supergiants of mid B-type the method may still be applicable. This requires further investigation (including an extension of the model atom database to doubly-ionized species), but it can be expected to fail at higher luminosity. As Dufton et al. (2005) indicate that classical and unified non-LTE atmosphere analyses give similar results for early B-SGs, the solution for analyses of highly luminous mid-B supergiants will be to use non-LTE line-formation computations based on classical line-blanketed non-LTE (instead of LTE) model atmospheres.

The lower limit (in $T_{\rm eff}$) for the applicability of the method is determined by several factors. At $T_{\rm eff} \simeq 8000$ K helium lines disappear in the spectra of A-supergiants. Thus the helium abundance has to remain undetermined, introducing some uncertainties into the analyses. Around the same temperature convection can be expected to set in, as shown by Simon et al. (2002) for main sequence stars, who place the boundary line for convection at $T_{\rm eff} \simeq 8250$ K (however, no information is available for A-supergiants). Since the theoretical considerations of Schwarzschild (1975), which predict only a small number of giant convection cells scattered over the stellar surface, atmospheric convection in supergiants has attracted little interest until recently. Interferometric observations of the late-type supergiant $\alpha$ Ori (Young et al. 2000) can be interpreted in favour of this, further strengthened by first results from 3-D stellar convection models (Freytag et al. 2002). Again, no quantitative information on this is available for mid and late A-supergiants, resulting in a potential source of systematic error for model atmosphere and line formation computations. Furthermore, convective stellar envelopes give rise to chromospheres (see Dupree et al. (2005) for observational evidence in the cooler luminous stars), which introduce an additional source of UV irradiance, altering the non-LTE populations of the photospheric hydrogen (as compared to models without chromospheres) and potentially affecting the H^- opacity and thus the stellar continuum (Przybilla & Butler 2004b).

Figure 6: Example for the occurrence of pressure inversion in supergiants of spectral types later than $\sim$A4. The pressure stratification as a function of mass scale is displayed for two A TLAS9 models for $T_{\rm eff} = 7700$ K and $\log g = 0.42$ (the computed Eddington limit, dotted line) and 0.47 (full line). The inset compares the respective H$\delta$ profiles. A change in $\log g$ by 0.05 dex results in equivalent widths differing by a factor of 2 - an artefact of the pressure bump in the line-formation depth and its impact on the Stark broadening.

Open with DEXTER

Moreover, supergiant model atmospheres cooler than $T_{\rm eff} \sim 8200$ K are characterised by pressure inversion (and accompanying density inversion). Pressure inversion can develop close to the Eddington limit when radiative acceleration locally dominates over gravity because of an opacity bump in the hydrogen ionization zone, which is located in the photosphere at these effective temperatures. An example of the effect is shown in Fig. 6, where two A TLAS9 models close to the hotter end of the pressure inversion regime are compared. A small change of surface gravity by $\sim$10% results in a drastic change of a factor of 2 in equivalent width of the Balmer lines in this (extreme) case. Despite a general strong sensitivity of the hydrogen line equivalent widths to surface gravity close to the Eddington limit (see Sect. 5) this huge effect is an artefact of the modelling for the most part. Another possible effect of pressure inversion on line-formation computations concerns deviations from generally inferred trends in the behaviour of line strengths with stellar parameter variations. At slightly hotter temperatures the hydrogen line strengths decrease with decreasing surface gravity. In the pressure inversion regime this trend can be compensated, and even reversed, by a developing pressure bump. Naturally, pressure inversion affects all spectral features with line-formation depths coinciding with the pressure bump because of its effect on absorber densities. Systematic errors for stellar parameters from ionization equilibria and chemical abundance determinations can be expected. Pressure inversion is also discussed in the context of hydrodynamical models (Achmad et al. 1997; Asplund 1998). It is not removed by stationary mass outflow (except for very high mass-loss rates not supported by observation). It is not initiating the stellar wind either. Abolishing the assumption of stationarity provides a solution to the problem as discussed by de Jager (1998, and references therein), leading to pulsations and enhanced mass-loss in the yellow super- and hypergiants, which are located in a sparsely populated region of the empiric Hertzsprung-Russell diagram.

From these considerations we restrict ourselves to supergiant analyses at $T_{\rm eff}\ga8000$ K using the methodology presented here. In our opinion extension to studies of supergiants at cooler temperatures (of spectral types mid/late A, F, G, and of Cepheids) requires additional theoretical efforts in stellar atmosphere modelling, far beyond the scope of the present work. At lower luminosities the problems largely diminish so that the hybrid non-LTE technique provides an opportunity to improve on the accuracy of stellar analyses over a large and important part of the Hertzsprung-Russell diagram. Non-LTE model atoms for many of the astrophysically interesting chemical species are already available for studies of stars of later spectral types, as will be discussed next.

  
4 Statistical equilibrium and line formation

Table 1: Non-LTE model atoms.

Detailed quantitative analyses of stellar spectra require another ingredient besides realistic stellar model atmospheres: an accurate modelling of the line-formation process. While our restricted modelling capacities do not allow the overall problem to be solved in a completely natural fashion, i.e. simultaneously, experience tells us that we can split the task into several steps. In particular, while non-LTE effects are present in all cases, as photons are leaving the stellar atmosphere, they may be of little importance for the atmospheric structure when the main opacity sources remain close to LTE (H and He in early-type stars). Minor species - this includes trace elements as well as high-excitation levels of hydrogen and helium - behave in this way. They can be treated in a rather coarse approximation for atmospheric structure computations, while detailed non-LTE calculations may be required for the analysis of their spectra in order to use them as stellar parameter or abundance indicators. We therefore chose such a hybrid approach for our analyses: based on line-blanketed classical model atmospheres we solve the statistical equilibrium and the radiative transfer problem for individual species in great detail. The derived level occupations are then used in the formal solution to calculate the emergent flux, considering exact line-broadening. The last two steps are performed using the non-LTE line-formation package D ETAIL and S URFACE (Giddings 1981; Butler & Giddings 1985), which has undergone substantial extension and improvement over the years. In our context the inclusion of an Accelerated Lambda Iteration (ALI) scheme (Rybicki & Hummer 1991) is of primary interest, as it allows elaborate non-LTE model atoms to be used while keeping computational expenses moderate. Line blocking is taken into account via ODFs. Special care is required in computations for major line opacity sources, like iron: in order to prevent counting the line opacity twice (via the ODFs and as radiative transitions in the statistical equilibrium computations) we adopt ODFs with a metallicity reduced by a factor 2. This approximately corrects for the contribution of the element to the total line opacity.

Figure 7: Comparison of non-LTE departure coefficients bi for O I ( top) and Fe II ( bottom) in HD 92207 as a function of $\tau _{\rm R}$. Displayed are thedeparture coefficients of the ground state (thick-dotted line), ofthe ground state of the next higher ion (long-dashed line) and those of the levels from which the diagnostic spectral lines in the optical/near-IR arise (O I). In the case of Fe II the departure coefficients of all non-LTE levels are shown. The two ionic species are representative for the non-LTE behaviour of the light (including the $\alpha$-process elements) and iron group elements, see the text for further discussion.

Open with DEXTER

At the centre of our hybrid non-LTE analysis technique stand sophisticated model atoms, which comprise many of the most important elements in the astrophysical context. An overview is given in Table 1, summarising the references where the model atoms and their non-LTE behaviour were discussed in detail. In brief, they are characterised by the use of accurate atomic data, replacing approximate data as typically used in such work, by experimental data (a minority) or data from quantum-mechanical ab-initio computations (the bulk). We have profited from the efforts of the Opacity Project (OP; Seaton et al. 1994) and the IRON Project (IP; Hummer et al. 1993), as well as numerous other works from the physics literature. In particular, a major difference to previous efforts is the use of large sets of accurate data for excitations via electron collisions. Thus, not only the (non-local) radiative processes driving the plasma out of LTE are treated realistically (line blocking is considered via Kurucz (1992) ODFs), but also the competing (local) processes of thermalising collisions. These are essential to bring line analyses from different spin systems of an atom/ion into agreement. A few of the older models have been updated/extended with respect to the original publications. In the case of S II/III the fits to the original photoionization cross-sections of the OP data (neglecting resonances due to autoionizing states) have been replaced by the detailed data, and for these ions, as well as for He I and O II the features treated in the line-formation computations have been extended, as well as oscillator strengths and broadening parameters updated to more modern values, see Appendix A for further detail. In the following we will discuss some more general conclusions, which can be drawn from the analysis of such a comprehensive set of model atoms, while referring the reader to the original publications (see Table 1) for the details of individual atoms/ions.

There is a fundamental difference between the non-LTE behaviour of the light and $\alpha$-process elements on the one hand and the iron group elements on the other. The first group is characterised by a few valence electrons, which couple to only a few low-excitation states in the ground configuration that are separated by a large energy gap (several eV) from the higher excited levels. These excited states in turn show a similar structure on a smaller scale: a few (pseudo-)metastable levels are detached from the remainder by a $\sim$2 eV gap, see e.g. the Grotrian diagrams in the references given in Table 1. Collisional processes are effective in coupling levels either below or above the energy gaps, such that these are in or close to LTE relative to each other. The levels of highest excitation couple to the ground state of the next higher ionization stage via collisions. On the other hand, only a few electrons in the high-velocity tail of the Maxwell distribution are energetic enough in the atmospheres of BA-type stars to pass the first gap, and considerably more, but a minority nonetheless, the second gap. This favours strong non-LTE overpopulations of the excited (pseudo-)metastable states, as shown exemplarily for O I in Fig. 7, manifested in non-LTE departure coefficients $b_i = n_i^{\rm NLTE}/n_i^{\rm LTE} > 1$, where the n_i are non-LTE and LTE level occupation numbers, respectively. Therefore, the diagnostic lines in the optical/near-IR from the light and $\alpha$-process elements are typically subject to non-LTE strengthening.

On the other hand, the electrons in the open 3d-shell of the iron group elements give rise to numerous energetically close levels throughout the whole atomic structure. Photoionizations from the ground states of the single-ionized iron group elements are typically not very effective, as the ionization thresholds fall short of the Lyman limit where the stellar flux is negligible. The situation is different for the well populated levels a few eV above the ground state. They show the largest non-LTE depopulations (see Fig. 7 for the example of Fe II). Because of the collisional coupling the ground states also become depopulated, but to a lower degree. Nonetheless, a net overionization is established, resulting in a non-LTE overpopulation of the main ionization stage (Fe III in Fig. 7 - note that no Fe III lines are observed in the optical/near-IR for this star). Again, the highest excitation levels of the lower ionization stage couple collisionally to this and are thus also overpopulated. A continuous distribution of departure coefficients results, with the b_i of the upper levels of the transitions typically larger than those of the lower levels. Consequently, the optical/near-IR lines from the iron group elements experience non-LTE weakening. Therefore, LTE analyses of luminous BA-SGs will tend to systematically overestimate abundances of the light and $\alpha$-process elements, and to underestimate abundances of the iron group elements. These effects will be quantified in Sect. 6 where the comparison of non-LTE and LTE computations with observation is made. Note however that non-LTE computations, when performed with inaccurate atomic data, also bear the risk of introducing systematic errors to the analysis, see e.g. the discussions in Przybilla & Butler (2001, 2004a). This is because of the nature of statistical equilibrium, where (de-)population mechanisms couple all energy levels with each other. The predictive power of non-LTE computations is therefore only as good as the models atoms used.

The spectral lines treated in our non-LTE approach comprise about $\sim$70% of the observed optical/near-IR features in BA-SGs. This includes in particular most of those of large and intermediate line strength. The remainder of the observed lines is typically weak, except for several Si II and Cr II transitions. In order to achieve (near) completeness we incorporate these and another ten chemical species into our spectrum synthesis in LTE. It can be expected that this approach will introduce some systematic deficiencies, in particular for the most luminous objects, as will be indicated by the analysis in Sect. 6. However, the solution for high-resolution observations is to draw no further conclusions from these species. Interpretation of medium-resolution spectra (see Sect. 8) on the other hand would suffer more from their absence than from their less accurate treatment, as they typically contribute only small blends to the main diagnostic features.

The currently used line lists comprise several ten-thousand transitions, covering the classical blue region for spectral analyses between $\sim$4000 and 5000 Å well. At longer wavelengths a number of features are missing in our spectrum synthesis computations, mostly lines from highly-excited levels of the iron group elements. However, these are intrinsically weak (with equivalent widths  $W_{\lambda}$ $\la$ 10 mÅ) and typically isolated, so that their absence will hardly be noticed when compared to intermediate-resolution observations.

Figure 8: Impact of stellar parameter variations on non-LTE line profile fits for H$\delta$ in $\eta$ Leo ( left) and HD 92207 ( right). Spectrum synthesis for the adopted parameters (see Table 2, thick red line) and varied parameters, as indicated (thin lines), are compared to observation. A vertical shift by 0.5 units has been applied to the upper profiles. Note the decrease of the Balmer line strength in the progression from LC Ib ($\eta$ Leo) to Iae (HD 92207), and the increased sensitivity to the surface gravity parameter. In fact, the comparison indicates that for the more luminous supergiants uncertainties in the surface gravity determination become as low as 0.05 dex (dotted lines). The sensitivity to reasonable $T_{\rm eff}$-changes is almost negligible. Wind emission slightly contaminates the red wing of H$\delta$ in HD 92207.

Open with DEXTER

Where it was once a supercomputing application, comprehensive non-LTE modelling like the present can now be made on workstations or PCs. Typical running times to achieve convergence in the statistical equilibrium and radiative transfer calculations with D ETAIL range from $\sim$10 min for the most simple model atoms to a couple of hours for the Fe II model on a 3 GHz P4 CPU - for one set of parameters. The formal solution for a total of  $2{-}3\times 10^5$ frequency points with S URFACE requires $\sim$20-30 CPU min. Because of the highly iterative and interactive nature of our analysis procedure (see next two sections) the total time for a comprehensive study of one high-resolution, high-S/N spectrum, assuming excellent wavelength coverage from around the Balmer jump to $\sim$9000 Å as typically achieved by modern Echelle spectrographs, amounts to 1-2 weeks for the experienced user. This is the price to pay for overcoming the restrictions of contemporary BA-SG abundance studies and advancing them from factor 2-3 accuracy astronomy to precision astrophysics.

Future extensions of the present work will aim to provide more non-LTE model atoms, but these quite often require the necessary atomic data to be calculated first, as many data are still unavailable in present-day literature. In particular, the status of collisional data has largely to be improved. Note that the Si II ion in the silicon model atom by Becker & Butler (1990) is only rudimentary (though sufficient for their main purpose, analyses of early B-stars). Several energy levels involved in the observed transitions in BA-SGs are missing, and test calculations indicate a wide spread of the non-LTE abundances from the remaining transitions. On the basis of these findings we refrain from using the model atom for analyses in the present work, but wish to emphasise that qualitatively the correct non-LTE behaviour - line strengthening - is predicted.

  
5 Determination of stellar parameters

Stellar parameter determination for BA-SGs is complicated because of the intrinsic variability of these objects. Observational data from different epochs may therefore reflect different physical states of the stellar atmosphere, unless these are obtained (nearly) simultaneously. While we can expect the mass of a supergiant and its surface abundances to be conserved on human timescales, other stellar parameters may not. The observed variability patterns of light curves, radial velocities and line profiles can be interpreted in favour of a mix of radial and non-radial pulsations (see e.g. Kaufer et al. 1997), which may affect  $T_{\rm eff}$ and $\log g$, that in turn determine colours, the spectral energy distribution and the spectra. Even the stellar luminosity may be subject to small changes (Dorfi & Gautschy 2000). The parameter variations are not as pronounced as in other variable stars, but use of information from different epochs can potentially introduce systematic uncertainties into high-precision analyses. A solution is to derive the desired quantities from one set of observational data. Echelle spectra are the best choice, containing all information required for the derivation of stellar parameters and elemental abundances. With few exceptions, use of photometric data (from other sources) can thus be avoided. In the following we discuss the details of our spectroscopic approach for the parameter determination of BA-SGs. Spectrophotometry is only briefly considered for consistency checks. Finally, our findings are compared with previous analyses of the two well studied standards $\eta$ Leo and $\beta$ Ori.

Figure 9: Temperature determination for $\eta$ Leo using the Mg I/II non-LTE ionization equilibrium. Displayed are the observed line profiles for some of the strategic lines, Mg I $\lambda$ 5183 ( left panel) and Mg II $\lambda$ 4390 and He I $\lambda$ 4387 ( right panel), and the best non-LTE fit for stellar parameters as given in Table 2 (thick red line); theoretical profiles for varied parameters are also shown (thin lines, as indicated). A vertical shift by 0.3 units has been applied to the upper set of profiles. Note the strong sensitivity of the minor ionic species, Mg I, to parameter changes, while Mg II is virtually unaffected.

Open with DEXTER

	Figure 10: Fit diagrams of temperature- and gravity-sensitive indicators for $\eta$ Leo and $\beta$ Ori in the $T_{\rm eff}$-$\log g$-plane. The curves are parameterised by surface helium abundance y. The intersection determines  $T_{\rm eff}$ and $\log g$, with uncertainties as indicated.
Open with DEXTER

5.1 Spectroscopic indicators

The hydrogen lines are the most noticeable features in the spectra of BA-type stars. Their broadening by the linear Stark effect gives a sensitive surface gravity indicator in the mostly ionized atmospheric plasma. We employ the recent Stark broadening tables of Stehlé & Hutcheon (1999, SH), which compare well with the classically used data from Vidal et al. (1973, VCS; with extensions of the grids by Schöning & Butler, private communication) in the BA-SG regime. The SH tables have not only the advantage of being based on the more sophisticated theory but they also cover the Paschen (and Lyman) series for transitions up to principal quantum number n = 30. A detailed discussion of our hydrogen non-LTE line-formation computations for BA-SGs can be found in Przybilla & Butler (2004a), where lines of the Brackett and Pfund series were also studied. In short, it has been shown that except for the lower series members - which are affected or even dominated by the stellar wind - excellent consistency can be achieved from all available indicators, if accurate data for excitation via electron collisions are accounted for. Note that the only other study of H lines from these four series, in the prototype A-SG Deneb (Aufdenberg et al. 2002), fails in this. Their non-LTE model atmosphere and line-formation computations produce much too strong near-IR features because of inaccurate collisional data in their hydrogen model atom, as indicated by our findings. The problems are resolved using the improved effective collision strengths (P. Hauschildt, private communication).

Figure 11: Determination of projected rotational and macroturbulent velocities, exemplarily shown for three spectral regions of $\eta$ Leo including discrete and blended absorption features. The upper comparison between observation (black line) and spectrum synthesis (red line, for finally derived mean abundances) is made for $\zeta$ = 16.5 km s-1 and zero $v~\sin i$ (our finally adopted optimum values), the lower comparison is made assuming a pure rotational profile with $v~\sin i$ = 13.3 km s-1. See the text for further discussion. Line identifiers are given. The markers are vertically extended by 0.05 units.

Open with DEXTER

Our method for deriving surface gravities from the hydrogen lines deviates in a few details from the usual approach, which is based on the modelling of the H$\gamma$ and H$\delta$ line wings. The effect of variations of $\log g$ and  $T_{\rm eff}$ on the H$\delta$ profiles of $\eta$ Leo and HD 92207 are displayed in Fig. 8. We have chosen parameter offsets to our finally adopted values which we consider conservative estimates for the uncertainties of our analysis. It is clear that the internal accuracy of our modelling is higher, amounting to $\la$0.10 dex at LC Ib and as accurate as 0.05 dex at LC Iae. The temperature sensitivity is smaller, but non-negligible. Note the strong decrease of the H$\delta$ line strength in the luminosity progression. Close to the Eddington limit a modification by 0.05 dex in $\log g$ can amount to a change in  $W_{\lambda}$ of the Balmer lines by 15%. Note also that in the less luminous supergiant not only the line wings but also the entire line profile and thus also the equivalent width is accurately reproduced (which becomes important for intermediate- and low-resolution studies), indicating that the model atmosphere is sufficiently realistic over all line-formation depths. At the highest luminosities the accuracy of the spectrum synthesis degrades somewhat, because of stellar wind and sphericity effects. However, excellent agreement can be restored even for the higher Balmer lines, and for the accessible Paschen series members (see Fig. 11 in Przybilla & Butler 2004a), which are formed even deeper in the atmosphere. This also includes good reproduction of the series limits and their transition into the continua. Moreover, we also account for the effects of non-solar helium abundances on the density structure (see Sect. 3.2), which is mandatory for achieving consistent results, but which has been ignored in all BA-SG analyses so far.

In order to resolve the ambiguity in $T_{\rm eff}/\log g$ another indicator has to be applied. In a spectroscopic approach this is typically the ionization equilibrium of one chemical species. Potential ionization equilibria useful for  $T_{\rm eff}$ and $\log g$ determinations in optical/near-IR spectroscopy of BA-SGs are C I/II, N I/II, O I/II, Mg I/II, Al I/II, Al II/III, Si II/III, S II/III, Fe I/II and Fe II/III. Of these we can use only half because model atoms are currently unavailable for the rest. The lines of the minor ionic species are highly sensitive to temperature and electron density changes, while the weak lines of the major ionic species are excellent abundance indicators. A suitable set of parameters  $T_{\rm eff}/\log g$ is found in the case where both ionic species indicate the same elemental abundance within the individual error margins. However, great care has to be practised in the modelling, using carefully selected model atmospheres (see Sect. 3) and sophisticated non-LTE techniques (see Sects. 4 and 6).

An example is displayed in Fig. 9, where tests on the Mg I/II ionization balance in one of the sample objects are performed. Results from the best fit obtained in the detailed non-LTE analysis are compared with those from conservative parameter studies at an unchanged elemental abundance. The sensitivity of the predicted Mg I line strengths to changes of  $T_{\rm eff}$ and $\log g$ within the error margins is high, indicating internal uncertainties of $\Delta T_{\rm eff} < 100$ K and of $\Delta \log g \la 0.10$ dex. The profile changes by conservative parameter variation are similar to those achieved by abundance variations of the order 0.1 dex. On the other hand, no perceptible changes are seen in the Mg II line for the same parameter variations. All Mg I/II lines behave in a similar way, and the same qualitative characteristics are shared with ionization equilibria from other elements.

Both, hydrogen profiles and ionization equilibria are affected by the helium abundance, which therefore has to be simultaneously constrained as an additional parameter. Enhanced helium abundances manifest in broadened hydrogen lines and shifts in ionization equilibria - in BA-SGs the spectral lines of the minor ionization species are strengthened. Thus, parameter studies assuming a solar helium abundance will tend to derive systematically higher effective temperatures and surface gravities. In the BA-SGs the transitions of He I are typically weak. The helium abundance y (by number) can therefore be inferred from line profile fits to all available features. Typical uncertainties in the determination of stellar helium abundances amount to $\sim$10% because of the availability of excellent atomic data.

The whole process of the basic atmospheric parameter determination can be summarised in an $T_{\rm eff}{-}\log g$ diagram, which is done exemplarily for $\eta$ Leo and $\beta$ Ori in Fig. 10. The intersection of the different loci marks the appropriate set of stellar parameters. Note that these diagnostic diagrams differ from those typically found in the literature in two respects: first, the different indicators lead to consistent stellar parameters, and second, the loci are parameterised with the helium abundance, a necessary procedure to obtain the excellent agreement. When deriving the stellar parameters one can profit from the slow and rather predictable behaviour of the derived helium abundance with varying $T_{\rm eff}$/$\log g$.

The microturbulent velocity $\xi$ is determined in the usual way by forcing elemental abundances to be independent of equivalent widths. The difference to previous studies of BA-SGs is that this is done on the basis of non-LTE line-formation (see Fig. 13 and the discussion in Sect. 6). An LTE analysis would tend to find higher values in order to compensate non-LTE line strengthening. Typically, the extensive iron spectrum is used for the microturbulence analysis. Because the Fe II non-LTE computations are by far the most time-intensive, alternatives have to be considered here. The Ti II and in particular the N I spectra are excellent replacements, the latter distinguished by more accurate atomic data. Later, the iron lines can be used to verify the $\xi$-determination. Note that this is the only occasion where equivalent widths are used in the analysis process - elsewhere line profile fits are preferred.

Table 2: Basic properties and stellar parameters of the sample stars.

Good starting estimates for the microturbulent velocity in BA-SGs are $\xi = 4$, 6 and 8 km s^-1 for objects of LC Ib, Iab and Ia, respectively. After the determination of an improved value of $\xi$the model atmosphere has to be recalculated in some cases, and small corrections to $T_{\rm eff}$/$\log g$/y may become applicable. Only one iteration step is typically necessary to reestablish consistency in the atmospheric parameters. The uncertainties amount to typically $\pm$1 km s^-1. In the present study the different microturbulence indicators give a single value for $\xi$ within these error margins. This is consistent with findings from recent (LTE) work on less-luminous A-type supergiants (Venn 1995a, 1999), while older studies based on more simple model atmospheres and less accurate oscillator strengths had to invoke different values for various elemental species, or a depth-dependent $\xi$ (e.g. Rosendhal 1970; Aydin 1972).

Microturbulence also has to be considered as additional non-thermal broadening agent in the radiative transfer and statistical equilibrium computations. The Doppler width is then given by  $\Delta \lambda_{\rm D} = \lambda_0/c~(v_{\rm th}^2 + \xi^2)^{1/2}$, where $\lambda_0$ is the rest wavelength of the transition, c the speed of light and  $v_{\rm th}$ the thermal velocity of the chemical species of interest. The main effect is a broadening of the frequency bandwidth for absorption in association with a shift in line-formation depth, typically leading to a net strengthening of individual lines by different amounts, see e.g. Przybilla et al. (2000, 2001a,b) for further details.

Individual metal abundances are typically of secondary importance for the computation of model atmospheres, as elemental ratios are remarkably constant (i.e. close to solar) over a wide variety of stars, except for the chemically peculiar. We determine the stellar metallicity [M/H], which is the more important parameter, as the arithmetic mean from five elements, for which non-LTE computations can be done and which are unaffected by mixing processes: $[{\rm M/H}]\equiv([{\rm O/H}]+[{\rm Mg/H}]+[{\rm S/H}]+[{\rm Ti/H}]+[{\rm Fe/H}])/5$. High weight is thus given to the $\alpha$-process elements, which have a different nucleosynthesis history than the iron group elements, but $[\alpha$/Fe] $\sim$ 0 can be expected for these Population I objects. Because of the importance of metallicity for line blanketing a further iteration step may be required in the parameter determination.

Finally, the projected rotational velocity $v\sin i$ and the (radial-tangential) macroturbulent velocity $\zeta$ are derived from a comparison of observed line profiles with the spectrum synthesis. Single transitions as well as line blends should be used for this, as they contain some complementary information. Both quantities are treated as free parameters to obtain a best fit via convolution of the synthetic profile with rotation and macroturbulence profiles (Gray 1992a), while also accounting for a Gaussian instrumental profile. An example is shown in Fig. 11, where the comparison with observation indicates pure macroturbulence broadening for $\eta$ Leo. The theoretical profiles intersect the observed profiles if the spectral lines are broadened by rotation alone, resulting in slightly too broad line cores and insufficiently broad line wings. Typically, both parameters are non-zero, with the macroturbulent velocity amounting to less than twice the sonic velocity in the atmospheric plasma. Macroturbulence is suggested to be related to surface motions caused by (high-order) nonradial oscillations (Lucy 1976). Weak lines should be used for the $v\sin i$ and $\zeta$-determinations in supergiants in order to avoid systematic uncertainties due to asymmetries introduced by the outflowing velocity field in the strong lines.

5.2 Stellar parameters of the sample objects

We summarise the basic properties and derived stellar parameters of the sample supergiants in Table 2. The first block of information concentrates on quantities which in principle can be deduced directly, with only little modelling involved. Besides Henry-Draper catalogue numbers, alternative names, information on association membership and spectral classification and equatorial and galactic coordinates are given. Hipparcos parallaxes $\pi$ have been included for completeness, as none of the measurements is of sufficient statistical significance. The stellar distances d are therefore deduced by other means.

Figure 12: Computed (red full lines) and measured spectral energy distributions for the sample stars from the UV to the near-IR in the K-band. Overall, good to excellent agreement is obtained. Displayed are IUE spectrophotometry (full lines), Johnson (boxes), Strömgren (triangles), Walraven (filled circles) and Geneva photometry (open circles). The observations have been dereddened using colour excesses according to Table 2. A ratio RV = AV/E(B-V) = 3.1, as typical for the local ISM, is assumed for $\beta$ Ori and $\eta$ Leo. In the case of the notably reddened HD 92207 both, color excess and RV, can be determined, implying RV = 3.9. For clarity, the data for $\eta$ Leo has been shifted vertically by -3 units. IUE spectrophotometry for HD 111613 is not available. Consequently, this star has been omitted from the comparison.

Open with DEXTER

A distance modulus of 8 $.\!\!^{\rm m}$5 (viz. 500 pc) is found for the Ori OB 1 association by Blaha & Humphreys (1989). However, $\beta$ Ori shows a smaller radial velocity than the mean of the Ori OB1 association ($\sim$30 km s^-1). Therefore, the association distance gives only an upper limit, if one assumes that the star was formed near the centre of Ori OB1. During its lifetime $\beta$ Ori could have moved $\sim$100 pc from its formation site. The finally adopted distance of 360 pc is indicated by Hoffleit & Jaschek (1982), who associate $\beta$ Ori with the $\tau$ Ori R1 complex.

Recent studies of the cluster NGC 4755 found a distance modulus of  $11.6 \pm0.2$ mag, with a mean value of E(B - V) of $0.41 \pm 0.05$ mag (Sagar & Cannon 1995) and  $0.36 \pm0.02$ mag (Sanner et al. 2001). However, HD 111613 is situated at a rather large distance from the cluster centre and was not observed in either study. In a previous work (Dachs & Kaiser 1984) the object was found to be slightly behind the cluster by 0.2 mag. Consequently, this difference is accounted for in the present study, otherwise using the modern distance.

The line of sight towards the Car OB1 association coincides with a Galactic spiral arm, such that the star population in Car OB1 is distributed in depth over 2 to 3 kpc (Shobbrook & Lyngå 1994). A more decisive constraint on the distance of HD 92207 is indicated by Carraro et al. (2001), who argue that the star may be associated with the cluster NGC 3324. The star will not be gravitationally bound because of its large proper motion, but appears to be spatially close to the cluster, and may have been ejected. We therefore adopt the cluster distance modulus for HD 92207 with an increased error margin. Finally, the distance to the field star $\eta$ Leo can only be estimated, based on its spectroscopic parallax.

Galactocentric distances of the stars are calculated from the coordinates and d, using a galactocentric solar distance of $R_0 = 7.94\pm 0.42$ kpc (Eisenhauer et al. 2003). In one case an interferometrically determined true angular diameter  $\theta_{\rm D}$ (allowing for limb darkening) is available from the literature. Our measured radial velocities  $v_{\rm rad}$ (from cross-correlation with synthetic spectra) are compatible with the literature values, which in combination with proper motions  $\mu_{\alpha}$and  $\mu_{\delta}$ are used to calculate galactocentric velocities U, Vand W, assuming standard values for the solar motion (U = 10.00 km s^-1, V = 5.23 km s^-1, W = 7.17 km s^-1, Dehnen & Binney 1998) relative to the local standard of rest (220 km s^-1, Kerr & Lynden-Bell 1986).

In the second block our results from the spectroscopic stellar parameter determination are summarised. Photometric data are collected in the third block. Observed visual magnitudes and colours in the Johnson system are used to derive the colour excess E(B-V) by comparison with synthetic colours. Note that for HD 111613 and HD 92207 the derived colour excess is in excellent agreement with literature values for their parent clusters. From the distance moduli (m-M)₀ absolute visual magnitudes M_V are calculated, which are transferred to absolute bolometric magnitudes $M_{\rm bol}$ by application of bolometric corrections B.C. from the model atmosphere computations. Note also our previous comments on the photometric variability of BA-SGs, which can introduce some systematic uncertainty into our analysis, as the photometry and our spectra may reflect slightly different physical states of the stellar atmospheres. The sensitivity of the Johnson colours to $T_{\rm eff}$-changes is not high enough to use them as an alternative indicator for a precise determination of the stellar effective temperature.

Finally, we derive the physical parameters luminosity L, stellar radius R and spectroscopic mass  $M^{\rm spec}$ of the sample stars by combining atmospheric parameters and photometry. Thus the determined stellar radius of $\beta$ Ori is in good agreement with that derived from the angular diameter measurement ( $99\pm 11~R_{\odot}$). From comparison with stellar evolution computations (Meynet & Maeder 2003) zero-age main-sequence masses  $M^{\rm ZAMS}$ and evolutionary masses  $M^{\rm evol}$are determined, and the evolutionary age  $\tau_{\rm evol}$. The stars were of early-B and late-O spectral type on the main sequence. The results will be discussed in detail in Sect. 7. Note that the rather large uncertainties in the distance determination dominate the error budget of the physical parameters.

Table 3: Comparison of stellar parameters of $\eta$ Leo and $\beta$ Ori from the literature.

  
5.3 Spectrophotometry

The principal aim of the present study is a self-consistent method for the analysis of BA-type supergiants in the whole. This requires above all the reproduction of the stellar spectral energy distribution (SED). A comparison of our model fluxes for three of the sample supergiants with observation is made in Fig. 12. The observational database consists of IUE spectrophotometry (as obtained from the IUE Final Archive) and photometry in several passbands (broad-band to small-band) from the near-UV to near-IR, in the Johnson (Morel & Magnenat 1978; Ducati 2002, for HD 92207), Geneva (Rufener 1988), Strömgren (Hauck & Mermilliod 1998) and Walraven systems (de Geus et al. 1990). We have omitted HD 111613 from the comparison because crucial UV spectrophotometry is unavailable for this star. The observations have been de-reddened using a reddening law according to Cardelli et al. (1989). Overall, good to excellent agreement is found. This verifies our spectroscopic stellar parameter determination.

Use of SED information can provide an additional $T_{\rm eff}$-indicator, independent of weak spectral lines used in the ionization equilibria approach. This makes SED-fitting attractive for extragalactic applications, as it has the potential to improve on the modelling situation when only intermediate-resolution spectra are available (see Sect. 8). As the present work concentrates on the spectroscopic approach to BA-SGs analyses, we will report on a detailed investigation of this elsewhere.

  
5.4 Comparison with previous analyses

The two MK standards $\eta$ Leo and $\beta$ Ori have been analysed with model atmosphere techniques before. A comparison of our derived stellar parameters with literature values is made in Table 3. The methods used for the parameter determination are indicated and comments on the model atmospheres and the observational data are given. For the comparison we have omitted publications earlier than the 1970ies.

Good agreement of the present parameters for $\eta$ Leo with those of Venn (1995a) is found, as the methods employed are comparable. Other authors find a substantially hotter  $T_{\rm eff}$ for this star, while the values for surface gravity and microturbulence are comparable. All these values are based on less elaborate model atmospheres, with less or no line-blanketing, and they completely ignore non-LTE effects on the line formation. Note that a $T_{\rm eff}$ of 9380 K is obtained from Strömgren photometry, using the calibration of Gray (1992b).

For $\beta$ Ori basically two disjunct values for the effective temperature are found in the literature. Model atmosphere analyses so far found a systematically higher  $T_{\rm eff}$, which is likely to be due in good part to ignored/reduced line-blanketing. The measurements of surface gravity and microturbulent velocity are again similar. The other group of $T_{\rm eff}$ analyses mostly find significantly lower values than that derived in the present work, from measured total fluxes and interferometric radius determinations, or from the infrared flux method: 11 800 $\pm$ 300/11 700 $\pm$ 200 (Nandy & Schmidt 1975), 11 550 $\pm$ 170 (Code et al. 1976), 11 410 $\pm$ 330 (Beeckmans 1977), 11 780 (Underhill et al. 1979), 11 014 (Blackwell et al. 1980), 11 380 (Underhill & Doazan 1982) and 11 023/11 453 K (Glushneva 1985). These methods are prone to systematic errors from inappropriate corrections for interstellar absorption. The authors all supposed zero interstellar extinction. In fact, the only such study that accounts for a non-zero E(B-V) (Stalio et al. 1977, +0.04 vs. +0.05 as derived here) finds a temperature in excellent agreement with the present value, see Table 3. However, using LTE Fe II/III and Si II/III ionization equilibria and Balmer profiles they derive $T_{\rm eff} \ga 13~000$ K.

Table 4: Elemental abundances in the sample stars.

To conclude, effective temperatures from our approach appear to be systematically lower than from previous model atmosphere analyses and higher than from previous (spectro)photometric studies. Not only is consistency now achieved from these indicators, but also the uncertainties in the parameter determination have been markedly reduced by bringing all the indicators simultaneously into agreement. This provides a solid basis for precise metal abundance analyses, which are discussed next.

  
6 Abundance analysis

The chemical composition of the stars is deduced from the analysis of the weak line spectra of the individual elements. This is done by fitting non-LTE and LTE line profiles to the observation, as this puts tighter constraints on the modelling than is possible by reproducing equivalent widths alone. The results from the analysis of several hundred spectral lines from 30 ionization stages of 20 chemical species are summarised in Appendix A. We have also thoroughly tested the line list for suitability in abundance analyses of BA-stars on the main sequence (Przybilla 2002) and recommend it for use in future applications.

Figure 13: Elemental abundances in $\eta$ Leo from individual spectral lines of elements with non-LTE calculations, plotted as a function of equivalent width: non-LTE (solid) and LTE results (open symbols) for neutral (boxes) and single-ionized species (circles). The grey bands cover the 1$\sigma$-uncertainty ranges around the non-LTE mean values (see Table 4). Note that in the determination of these some additional spectral lines have been used in some cases, which are accessible to spectrum synthesis only. Data for the strongest O I lines has been adopted from Przybilla et al. (2000). Proper non-LTE calculations reduce the line-to-line scatter and remove systematic trends. Note that even weak lines can show considerable departures from LTE.

Open with DEXTER

A comparison of non-LTE and LTE results from the individual metal lines in $\eta$ Leo is made in Fig. 13. This supergiant shows the richest metal-line spectrum of all our sample objects. Note that a few lines from Table A.1 without measured equivalent widths had to be omitted for this, and results for a few strong O I lines have been added from Przybilla et al. (2000). By correctly accounting for non-LTE effects homogeneous abundances are derived from all the available indicators, which show little scatter around the mean value (the derived abundance). This also implies that the microturbulent velocity is correctly chosen, and it is the same for the elements under study. The non-LTE analysis thus avoids the systematic trends of abundance with line-strength in the approximation of LTE, such as for N I or O I. In other cases, like for singly ionized sulphur, titanium and iron, the non-LTE abundances are systematically shifted relative to LTE. Also the statistical scatter is reduced in non-LTE, and contrary to common assumption significant non-LTE abundance corrections are found even in the weak line limit. These can exceed 0.3 dex for lines with $W_{\lambda}\la 10$ mÅ, in particular for the more luminous objects, where the non-LTE effects are amplified. The qualitative behaviour of non-LTE and LTE abundances is similar in all the sample stars, which occurs because of the reasons discussed in Sect. 4.

Mean elemental abundances for the sample stars are given in Table 4, along with the solar standard and results from the literature on Galactic A-supergiants and their main sequence progenitors of early B-type at less than 2 kpc distance (in order to avoid artefacts introduced by the Galactic abundance gradient). Note that we prefer solar standard abundances as summarised by Grevesse & Sauval (1998) over the more recent compilation of Asplund et al. (2005) for several reasons discussed below. Non-LTE results are indicated by italics. For the sample stars statistical uncertainties (1-$\sigma$ standard deviations from the line-to-line scatter) are given, with the number of analysed lines in parenthesis. In the case of the previous studies the uncertainties denote 1-$\sigma$ standard deviations from the star-to-star scatter.

The present non-LTE analysis finds abundances compatible with the LTE study (with non-LTE corrections for a few elements) of Venn (1995a,b) on less-luminous A-SGs. This is because the objects in that study are, on the mean, far cooler and of higher surface gravity than ours, which reduces the importance of non-LTE. In such a case a tailored LTE analysis is meaningful for most elements. Consequently, we and Venn recover abundances which agree within the uncertainties with the present-day ISM abundances (which appear to be slightly sub-solar), as expected. Exceptions are the carbon and nitrogen abundances, which reflect mixing of the surface layers of the supergiants by nuclear processed material, see below.

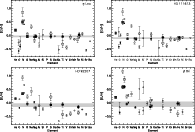Figure 14: Results from the elemental abundance analysis (relative to the solar composition) for our sample stars. Filled symbols denote non-LTE, open symbols LTE results. The symbol size codes the number of spectral lines analysed - small: 1 to 5, medium: 6 to 10, large: more than 10. Boxes: neutral, circles: single-ionized, diamonds: double-ionized species. The error bars represent 1$\sigma$-uncertainties from the line-to-line scatter. The grey shaded area marks the deduced metallicity of the objects within 1$\sigma$-errors. Non-LTE abundance analyses reveal a striking similarity to the solar abundance distribution, except for the light elements which have been affected by mixing with nuclear-processed matter.

Open with DEXTER

The B main sequence stars (B-MSs) together with H II regions define the present-day abundances in the solar neighbourhood. Consequently, mutual agreement with our results exists for the $\alpha$-process elements with non-LTE abundances. The B-star abundances of helium and nitrogen are lower and the carbon abundances higher than in the BA-SGs, indicating little to no mixing with nuclear processed matter, which is also expected. Note that the B-MSs oxygen abundances appear to be slightly lower than in our BA-SGs; this may be an effect of small number statistics. Note also that the LTE analysis by Rolleston et al. (2000) finds systematically different B-MSs abundances than the other three B-MSs studies. Little information is available for the iron-group abundances, and nothing on s-process abundances in B-MSs. BA-type supergiants and B-MSs are therefore complementary for galactochemical and stellar evolution studies: the former contain information on the heavier element abundances and mixing patterns, while the latter provide stellar present-day abundances for the light elements. Consistency can be checked on the basis of the $\alpha$-elements for which both star groups have features in common.

The comparison of our sample stars with the solar standard (Grevesse & Sauval 1998) is visualised in Fig. 14. First, we want to discuss the results from the LTE analysis, which comprises a wider variety of elements than can be done in non-LTE at present. For the least luminous supergiant of our sample, $\eta$ Leo, close to solar abundances are derived for most of the $\alpha$-process and iron group elements. The only s-process elements accessible through their resonance lines, Sr II and Ba II, appear underabundant, as are the lightest iron group elements, scandium through vanadium. Neon appears to be overabundant and a discrepancy in the Al I/II ionization equilibrium is noteworthy, while Mg I/II is on the verge of a discrepancy. Of the light elements, carbon is under- and nitrogen overabundant, with a discrepancy in the N I/II ionization balance indicated. Note that these LTE results are valid for the finally adopted parameters from the non-LTE analysis. A pure LTE study would indicate a slightly higher  $T_{\rm eff}$ from most of the ionization equilibria, implying an overall increase of the metallicity and a more pronounced N I/II discrepancy. Similar abundance patterns are found for the LC Iab supergiant HD 111613, with several of the $\alpha$-processes elements (O, Ne and S) showing a tendency to being overabundant, as also appears to be the case for carbon. For these two stars an LTE analysis appears meaningful, in the sense that abundances are derived which are expected for a young star of the Galactic thin disk, with only a few exceptions.

The situation changes drastically when considering an object of even higher luminosity, like HD 92207. Practically no element comes close to the solar standard, with the entire iron group appearing to be vastly underabundant, and the $\alpha$-process and light elements largely overabundant. An LTE analysis suggests an abundance pattern resembling $\alpha$-enhancement for this star, which is appropriate for the old halo population but not for a Population I object. This pattern is basically also derived for $\beta$ Ori. However, at the higher atmospheric temperatures features from double-ionized species appear, which suggest drastic imbalances in several ionization equilibria. No parameter combination can be found that brings all the available ionization equilibria simultaneously into agreement in LTE.

The non-LTE analysis of some of the astrophysically most interesting elements on the other hand reveals a rather homogeneous appearance of the abundance distribution in the four stars. Note that we derive absolute abundances, which depend on physical data and not on oscillator strengths (and line broadening data) tuned to match observations, as is the case in many differential studies of solar-type stars. The $\alpha$-process and iron group elements reproduce the solar abundance pattern, showing little scatter around slightly sub-solar mean metallicities (the grey bands in Fig. 14). Among the light elements, helium and nitrogen are enhanced and carbon is underabundant, which is qualitatively well understood in the framework of the evolution of rotating massive stars, see the next section for details.

The total abundance of the fusion catalysts C, N, and O in the sample stars correlates well with the stellar metallicity. Use of the solar abundances of Asplund et al. (2005) instead of the Grevesse & Sauval (1998) data as standard would imply an overabundance of CNO relative to the heavier elements in these young stars, in particular [O/Fe] > 0. This is inconsistent with other astrophysical indicators. Here, the more recent solar abundance data may imply another conflict like the recently unveiled solar model problem, i.e. the loss of accordance between helioseismological measurements and the predictions of theoretical solar models (Bahcall et al. 2005).

Note that good agreement for the available non-LTE ionization equilibria is obtained, and that the statistical scatter in the abundance determination is typically reduced with respect to LTE, amounting to 0.05 to 0.10 dex (1-$\sigma$ standard deviations). Nitrogen and oxygen are particularly good examples. This comes close to the accuracy that is usually obtained in differential analyses of solar-type stars, however on absolute terms.

The non-LTE abundance corrections vary from element to element and there is a well-known tendency for increased non-LTE corrections with luminosity (i.e. lower $\log g$), and temperature. Typically, non-LTE abundance corrections amount to a factor of two to three on the mean. In some cases, the corrections can amount to factors of several tens for individual transitions, see e.g. oxygen in Fig. 13, and in the most extreme cases they exceed a factor of a hundred. Many strong lines of Ti II and Fe II have been omitted in the present study, because of the additional computational costs and their insensitivity as abundance indicators. These also show stronger non-LTE effects as the corresponding weak-line spectra. This is also the case for the prominent Mg II $\lambda$4481 feature (Przybilla et al. 2001a).

The only exception from our general improvement due to non-LTE refinements is the Mg I/II ionization balance in HD 922207, which we attribute to small insufficiencies of our LTE model atmospheres at highest luminosity. The Mg I lines are highly sensitive to even the smallest changes in the modelling close to the Eddington limit, see the discussion in Sect. 3. In this case the N I/II ionization equilibrium is a better choice for the temperature indicator, as its behaviour is better constrained - much more accurate atomic data are available for nitrogen than for magnesium, and the ground state ionization for N I is determined by the Lyman continuum instead of the more complicated radiation field longward of the Lyman jump, which is more prone to modelling uncertainties, as in the case of Mg I.

The detailed non-LTE behaviour of the ionic species under study is well explained from their atomic structure, as discussed in Sect. 4. This allows us to estimate, at least qualitatively, the non-LTE behaviour of the large number of elements in the supergiant spectra, for which we do not have non-LTE spectrum synthesis at hand for the moment. Certainly, the entire singly-ionized iron group elements will show a similar non-LTE weakening like Ti II and Fe II, as they all are subject to non-LTE overionization. This will also be the case for Sr II and Ba II. A non-LTE strengthening of the Ne I lines was described by Sigut (1999) in B-MSs, which can be expected to occur to a similar extent also at lower  $T_{\rm eff}$ in the BA-SGs. This would imply a present-day neon abundance from the sample stars compatible with their overall metallicity close to the solar value as given by Grevesse & Sauval (1998), and agreement with the ISM abundance as derived from the Orion nebula (Esteban et al. 2004), for non-LTE abundance corrections by a factor $\sim$2. Compatibility with the value of $\log$ Ne/H + 12 = 8.27 as determined by Drake & Testa (2005) from nearby solar-like stars is possible for lower non-LTE abundance corrections. The solar value of Asplund et al. (2005) which contributes to the solar model problem could only be restored for unrealistically high non-LTE corrections by a factor $\sim$4-5 (the Ne I lines are typically weak). Note that an increase of the surface abundance of neon due to mixing with nuclear-processed matter is only expected in the Wolf-Rayet phase of the evolution of massive stars, such that BA-SGs should reflect present-day neon abundances of the ISM.

Figure 15: Comparison of our spectrum synthesis (thin red line) with the high-resolution spectrum of HD 92207 (full line). The major spectral features are identified, short vertical marks designate Fe II lines. The location of the diffuse interstellar band around 4430 Å is indicated. With few exceptions, excellent agreement between theory and observation is found (H$\gamma$ is affected by the stellar wind).

Open with DEXTER

We conclude that the derived abundance patterns from our LTE study are probably an artefact of the assumption of detailed equilibrium. It may be speculated that close to solar abundance patterns will be recovered for the four sample stars from a full non-LTE analysis. We will continue our efforts to improve the status of the modelling situation, but note that for many ionic species practically none of the required atomic data needed to construct reliable non-LTE model atoms are available at present.

Another important aspect of the non-LTE abundance analysis are constraints for the systematic uncertainties. This includes tests for the response of the spectrum synthesis to modifications of the stellar parameters as well as to variations of the atomic data that is used for assembling the non-LTE model atoms. Such tests have been done for C I/II, N I/II, O I and Mg I/II by Przybilla et al. (2000, 2001a,b) and Przybilla & Butler (2001). When we scale these results for the stellar parameter uncertainties of the present work and consider continuum placement in our high-S/N spectra to be a negligible problem we can conclude that the systematic uncertainties of our non-LTE abundance determination are of the order $\sim$0.10 dex (1-$\sigma$-error). This is from quadratic summation over all uncertainty contributors, assuming them to be independent. As this is not strictly the case for the stellar parameters (e.g. $T_{\rm eff}$/$\log g$ have to be varied simultaneously to retain consistency of a spectroscopic indicator with observation, see e.g. Fig. 10), the true systematic uncertainties may be slightly smaller. The given uncertainty has consequently to be viewed as a conservative estimate. Note that the main contribution to the systematic uncertainty of abundance determinations in BA-SGs comes from the uncertainties in the stellar parameters. The typical uncertainties in oscillator strengths, photoionization and collisional excitation cross-sections from quantummechanical ab-initio computations are of the order 10-20% and therefore contribute only little to the total error budget. Thoroughly constraining the systematic uncertainties is an extremely computationally intensive task, requiring hundreds of model runs with modified parameters, the problem thus being $\sim$2 orders of magnitude more complex than the abundance determination itself. We therefore assume the systematic abundance uncertainties for S II/III, Ti II and Fe II also to amount to $\sim$0.10 dex (1-$\sigma$-error). The atomic data used for assembling these model atoms is of similar quality (perhaps slightly lower because the atoms are more complex) than in the lighter elements. The response to stellar parameter changes can also be expected to be similar, as deduced from a few exploratory test calculations.

We omit a detailed comparison of our non-LTE abundance determination with previous work from the literature. For C I/II, N I/II, O I and Mg I/II this has been done elsewhere (Przybilla et al. 2000, 2001a,b; Przybilla & Butler 2001). The main conclusions are that in general the results from the other studies are close to our findings, or origins of the differences have been found, e.g. different stellar parameters, see Sect. 5.4. Major discrepancies were found only for N I, where the previous studies gave systematically lower nitrogen abundances, by a factor $\sim$2. This has been traced to use of approximate collision data in the previous non-LTE model atoms, but see also Venn & Przybilla (2003). Contrary to previous studies, our non-LTE analysis for these elements yields homogeneous results from all available spectral lines. Non-LTE studies of S II/III, Ti II and Fe II in BA-SGs have not been reported in the literature so far.

Figure 16: The evolutionary status of the sample stars and mixing with nuclear-processed matter. Evolutionary tracks accounting for mass-loss and rotation from Meynet & Maeder (2003) are displayed, for solar metallicity at an initial rotational velocity of 300 km s-1 (full line) and the non-rotating case (dotted line). Numbers along the tracks give the ratio of N/C (by mass, (N/C)0 is the initial value). For the sample objects (dots) the observed ratios are given. The three more massive supergiants have most likely evolved directly from the main sequence, whereas $\eta$ Leo appears to have already undergone the first dredge-up (as inferred from its high N/C ratio and also the helium enrichment) and is currently in a blue-loop phase. Uncertainties in  $\log T_{\rm eff}$ are of the order of the symbol size.

Open with DEXTER

Finally, a comparison of the high-resolution observations of the luminous Galactic supergiant HD 92207 with our spectrum synthesis is made in Fig. 15. The model can successfully reproduce the line spectrum with high accuracy over extended wavelength regions, except for a few features which are strong enough to be affected by sphericity effects and the stellar wind. An obvious example for this is H$\gamma$. Some complications in localised spectral regions occur because of interstellar absorption bands, which are not modelled. Finally, CCD defects and insufficiently corrected cosmic ray hits can render some regions useless for the analysis, e.g. near Ti II $\lambda$4501 in the present case. In high-resolution data these are easily recognised. However at intermediate resolution, in particular at low S/N, special care has to be taken to identify the artefacts and to exclude them from the analysis.

  
7 Evolutionary status

Massive stars provide the dominant contribution to the momentum and energy budget of the interstellar matter. They are the main drivers for the dynamical and chemical evolution (as sites of nucleosynthesis) of the interstellar environment, and consequently for the evolution of galaxies. Understanding the evolution of massive stars is a prerequisite for such further studies. Massive star evolution is an active field of research (see e.g. Maeder & Meynet (2000) for an overview) where the overall problem has been solved in many respects but where many details are still not conclusively explained because of the uncertainty in several free parameters of the input physics. These have to be constrained by observation. In particular quantifying the rôle of stellar winds and rotation as a function of metallicity requires further efforts, as well as transport phenomena as manifested in surface abundance anomalies, and the existence and extent of blue loops. BA-type supergiants are of special interest in this regard, as they allow these problems to be investigated beyond the Galaxy and its nearest satellites, in a much wider range of different galactic environments. In the following we wish to discuss our four sample stars in the context of their evolutionary status, putting special emphasis on areas where our analysis technique allows for an improvement on previous work.

Table 5: Surface abundance data relevant for stellar evolution.

First, reduced uncertainties in the stellar parameters (see Table 2) allow the objects to be located precisely in the Hertzsprung-Russell diagram (HRD, Fig. 16). Here, the major remaining uncertainties arise from the constraints of an indirect distance determination. Improvements on this can only be expected from future astrometric satellite missions. The objects cover a wide range in luminosity within the supergiant regime, and include two of the most luminous and massive BA-SGs analysed so far. Evolutionary and spectroscopic masses are in excellent agreement, indicating good consistency between the stellar properties inferred from the present analysis and those predicted by theory. In particular the integrated mass-loss history of these (near-)solar metallicity objects is apparently well described.

Then, additional information on the evolutionary status of the stars comes from abundance patterns of the light elements. The reaction rates for the CNO-cycle result in an accumulation of nitrogen at the cost of carbon and (to lesser extent) oxygen, with helium being the fusion product. If transport mechanisms are active throughout the stellar envelope, these fusion products may be mixed into the stellar atmosphere. The observed abundance patterns are summarised in Table 5 (by mass fraction for Y, N/C and N/O). The most sensitive indicator, the N/C ratio, is also discussed in the HRD diagram in Fig. 16. All objects show enrichments of helium and nitrogen, depletion of carbon and practically solar oxygen. The sum of the CNO abundances [CNO/H] correlates well with the stellar metallicity [M/H], consistent with the catalyst rôle of these elements in the main fusion cycle on the main sequence. The comparison with the predictions of evolution computations by Meynet & Maeder (2003) shows good qualitative agreement, while discrepancies remain in the details. In particular, helium enrichment traces the increasing N/C ratio well, while oxygen depletion obviously does not occur to the predicted extent.

In this scenario the three more luminous supergiants appear to have evolved directly from the main sequence, at initial rotational velocities larger than 300 km s^-1 ($\beta$ Ori, HD 111613) and at a lower rate, respectively, in the case of HD 92207. The high helium abundance and N/C ratio (the highest of the sample) of $\eta$ Leo on the other hand are indicative for the first dredge-up and thus a blue loop scenario for this object. Note that this classification can only be made for the individual objects with statistical significance because of the reduced abundance uncertainties. However, additional efforts are required to further improve the significance of the N/C ratios, which are currently still impaired by the remaining uncertainties in the carbon abundance determination.

  
8 Analyses at intermediate resolution

	Figure 17: Same as Fig. 15, however artifically degraded to 5 Å resolution. The excellent agreement between theory and observation is preserved. Deviations are found only for H$\gamma$, Mg II $\lambda$4481 (see text) and in the regions of the interstellar band around 4430 Å and near Ti II $\lambda$4501 (due to a CCD defect, cf. also Fig. 15.
Open with DEXTER

Figure 18: Same as Fig. 17, but artifically degraded to a $S/N \simeq 50$. The comparison with synthetic spectra for scaled abundances and modified temperatures (thin red lines, as indicated) shows that the models react sensitively to changes of the metal abundances only. Consequently, stellar parameters estimated from the spectral classification ( $T_{\rm eff}$) and from fitting of the higher Balmer lines ($\log g$) suffice to constrain the stellar metallicity to $\sim$0.2 dex. The lower set of spectra in each panel has been shifted by -0.2 units.

Open with DEXTER

In order to analyse intermediate-resolution data ( $R \simeq 1000{-}5000$) whole spectral regions have to be modelled at once, as the individual spectral features are typically no longer resolved by the instrument. The spectrum synthesis technique implemented here allows for such analyses, as practically all spectral features in BA-SGs of significant strength (more than a few mÅ) are included. In particular the spectral region between the Balmer jump and $\sim$5000 Å - the classical region for analyses of hot stars - is well covered. Thus, an estimate of the overall stellar metallicity and abundances of individual elements from several unblended lines of intermediate strength can be obtained from a comparison of the observed with synthesised spectra. The feasibility of this approach is tested in the following. Note that spectral regions containing lines of intermediate strength ( $W_{\lambda} \la 300$ mÅ) are best suited for an analysis, as these are strong enough to produce a noticeable signal even at modest S/N, but are also weak enough to be of photospheric origin. In BA-SGs several ionic species give rise to such lines, typically N I, O I, Mg II, Si II, Ti II, Cr II, Fe II and in the hotter stars He I as well. The three iron group elements hereby dominate the line spectrum, whereas He I, N I and the three $\alpha$-elements contribute only a few distinct features.

A test for the applicability of our spectrum synthesis at intermediate resolution is made in the following, based on the most luminous object of our sample, HD 92207. The transition from the high resolution comparison to intermediate resolution is made in Fig. 17, where the observed and the synthetic spectrum from Fig. 15 have been artifically degraded to 5 Å resolution. Such data can be expected e.g. from observations with FORS1 (FOcal Reducer and low-dispersion Spectrograph) at the VLT. The excellent agreement between model and observation is preserved, except for a few spectral features already discussed above (Sect. 6). However, observational data at such a high S/N will typically not be available. In order to consider a more realistic case, the observed spectrum is further degraded to a ${\it S/N} \simeq 50$ in Fig. 18. Additionally, test calculations for scaled abundances and modified effective temperature are displayed. While the surface gravity can still be determined at high accuracy from the higher Balmer lines, testing for the temperature sensitivity of the synthetic spectra becomes necessary as ionization equilibria are unavailable for a direct $T_{\rm eff}$-determination (typically, one of the ionic species shows only weak lines). Instead, empirical (metallicity-dependent) spectral type -  $T_{\rm eff}$calibrations have to be applied (see e.g. Kudritzki et al. 2003; Evans & Howarth 2003), increasing the uncertainties, or a spectrophotometric approach, which requires further investigation (see Sect. 5.3). The tests show that within a considerable $T_{\rm eff}$-interval the systematic effects on the overall spectrum synthesis are rather small. Modifications of the abundances on the other hand show a much larger effect, and we conclude that our method allows the stellar metallicity to be constrained within approximately $\pm$0.2 dex (1-$\sigma$ uncertainties). This is considerable larger than the statistical uncertainties from the high-resolution analysis but sufficient for meaningful applications in extragalactic stellar astronomy. In fact, such uncertainties are characteristic for the status of contemporary abundance work on BA-SGs in the literature. From a few features, like Fe II  $\lambda\lambda$4351, 4508 and the pure Fe II blends around 4520 and 4580 Å, even the iron abundance can be derived in this wavelength region. In a similar manner, one can use the regions around He I  $\lambda\lambda$4026 and 4471 to determine the helium abundance. More chemical species become accessible in other wavelength regions.

Note that the microturbulent velocity can also not be directly derived from intermediate resolution spectra, as the whole range from the weak lines to those of intermediate strength is not available for the analysis. However, our high resolution analyses and data from the literature indicate that microturbulence values of $\xi = 8\pm 2$ km s^-1are appropriate for BA-SGs at luminosities $\log L/L_{\odot} \ga 5.0$. We assume that this empirical finding holds for analogous objects in the galaxies beyond the Local Group, for which only the next generation of extremely large telescopes will allow for high-resolution spectroscopy and direct microturbulence determinations. Within the typical uncertainties in $\xi$, no marked systematic effects for the metallicity determination are found.

To conclude, the present spectrum synthesis technique in combination with sophisticated non-LTE model atoms allows for reliable metallicity determinations for BA-type supergiants on the basis of intermediate-resolution spectra. With suitable spectra available, abundances for several elements of general astrophysical relevance can also be obtained. This opens up BA-SGs as versatile tools for extragalactic stellar astronomy. First applications to metallicity analyses of A-type supergiants well beyond the Local Group, in the field spiral galaxy NGC 3621 and the Sculptor group spiral NGC 300, have already been discussed by Przybilla (2002) and Bresolin et al. (2001, 2002).

  
9 Summary and conclusions

We have presented a hybrid non-LTE spectrum synthesis technique for the quantitative analysis of BA-type supergiants and related objects of lower luminosity and tested it on high-quality observations of four bright Galactic objects. The statistical equilibrium and radiative transfer problem for several of the astrophysically most important elements is solved on the basis of classical line-blanketed LTE atmospheres. These have been shown to be sufficient to obtain consistent results from the available spectroscopic indicators. A prerequisite for this is that secondary atmospheric parameters such as helium abundance, metallicity and microturbulence are accounted for consistently, because of the high sensitivity of the model atmospheres and line formation to the details of the computations close to the Eddington limit. It has been shown that the stellar parameters of BA-SGs can be determined with unprecedented precision: the internal accuracy of the methods allows  $T_{\rm eff}$ to be constrained to better than 1-2% and $\log g$to 0.05-0.10 dex. Non-LTE computations with sophisticated model atoms reduce random errors and remove systematic trends in abundance analyses. The 1-$\sigma$ errors in the determination of absolute abundances amount to typically 0.05-0.10 dex and $\sim$0.10 dex for statistical and systematic uncertainties, respectively. This comes close to the accuracy that is usually achieved in differential studies of solar-type stars in the contemporary literature. Contrary to common assumption, significant non-LTE abundance corrections by a factor 2-3 can occur even for the weakest lines in BA-SGs, and considerably larger corrections for the stronger lines. Because of this, a purely LTE analysis of highly luminous supergiants fails to obtain meaningful results, while the less-luminous supergiants can in principle be addressed in such a way, if reduced accuracy can be tolerated. LTE analyses thereby tend to systematically overestimate the abundances of the light and $\alpha$-process elements, and to underestimate the abundances of the iron group species. The non-LTE analysis implies close to solar abundance for the heavier elements in the sample objects, and patterns characteristic for mixing with nuclear-processed matter in the case of the light elements. These indicate a blue-loop scenario for one of the sample stars because of first dredge-up abundance ratios, while the other objects were restricted to the blue part of the HRD. Using the full potential of our spectrum synthesis, we have shown that almost the entire visual and near-IR spectra of BA-SGs can be accurately reproduced, implying the the technique is also suitable for analyses of intermediate-resolution spectra. Thus BA-type supergiants have become a diagnostic tool for quantitative stellar spectroscopy beyond the Local Group.

Acknowledgements

We are indebted to the numerous atomic physicists making this research possible by providing the vast amounts of input data required for non-LTE modelling. It is our hope that we can stimulate further efforts by the present work - they would be most welcome. We are grateful to A. Kaufer for his help with obtaining some of the spectra at La Silla. We thank J. Puls for numerous stimulating discussions on many aspects of non-LTE modelling of hot stars and K. A. Venn for many discussions on analyses of A-type supergiants in particular. N.P. would like to acknowledge the financial support of the Max-Planck-Gesellschaft, the BMBF through grant 05AV9WM12, and by the Insitute for Astronomy, Hawaii, which made this project feasible throughout the diploma, the Ph.D. and a postdoctoral phase. This research has made use of the Simbad database, operated at CDS, Strasbourg, France.

References

• Achmad, L., Lamers, H. J. G. L. M., & Pasquini, L. 1997, A&A, 320, 196 [NASA ADS] (In the text)
• Albayrak, B. 2000, A&A, 364, 237 [NASA ADS] (In the text)
• Asplund, M. 1998, A&A, 330, 641 [NASA ADS] (In the text)
• Asplund, M., Grevesse, N., & Sauval, A. J. 2005, in Cosmic Abundances as Records of Stellar Evolution and Nucleosynthesis, ed. T. G. Barnes III, & F. N. Bash (San Francisco: ASP), 25 (In the text)
• Aufdenberg, J. P., Hauschildt, P. H., Baron, E., et al. 2002, ApJ, 570, 344 [NASA ADS] [CrossRef] (In the text)
• Aydin, C. 1972, A&A, 19, 369 [NASA ADS] (In the text)
• Bahcall, J. N., Basu, S., Pinsonneault, M., & Serenelli, A. M. 2005, ApJ, 618, 1049 [NASA ADS] [CrossRef] (In the text)
• Barnard, A. J., Cooper, L., & Shamey, L. J. 1969, A&A, 1, 28 [NASA ADS]
• Barnard, A. J., Cooper, L., & Smith, E. W. 1974, J. Quant. Spec. Radiat. Transf., 14, 1025
• Bates, D., & Damgaard, A. 1949, Phil. Trans. R. Soc. London, Ser. A, 242, 101
• Becker, S. R. 1998, in Boulder-Munich II: Properties of Hot, Luminous Stars, ed. I. D. Howarth (San Francisco: ASP), 137
• Becker, S. R., & Butler, K. 1988, A&A, 201, 232 [NASA ADS]
• Becker, S. R., & Butler, K. 1990, A&A, 235, 326 [NASA ADS] (In the text)
• Beeckmans, F. 1977, A&A, 60, 1 [NASA ADS] (In the text)
• Blackwell, D. E., Petford, A. D., & Shallis, M. J. 1980, A&A, 82, 249 [NASA ADS] (In the text)
• Blaha, C., & Humphreys, R. M. 1989, AJ, 98, 1598 [NASA ADS] [CrossRef] (In the text)
• Bresolin, F., Kudritzki, R. P., Méndez, R. H., & Przybilla, N. 2001, ApJ, 548, L159 [NASA ADS] [CrossRef] (In the text)
• Bresolin, F., Gieren, W., Kudritzki, R. P., Pietrzynski, G., & Przybilla, N. 2002, ApJ, 567, 277 [NASA ADS] [CrossRef] (In the text)
• Bresolin, F., Garnett, D. R., & Kennicutt, R. C. 2004, ApJ, 615, 228 [NASA ADS] [CrossRef] (In the text)
• Butler, K., & Giddings, J. R. 1985, in Newsletter on Analysis of Astronomical Spectra, No. 9 (London: Univ. London) (In the text)
• Butler, K., Mendoza, C., & Zeippen, C. J. 1993, J. Phys. B, 26, 4409 [NASA ADS] [CrossRef]
• Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] (In the text)
• Carraro, G., Patat, F., & Baumgardt, H. 2001, A&A, 371, 107 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Code, A. D., Davis, J., Bless, R. C., & Hanbury Brown, R. 1976, ApJ, 203, 417 [NASA ADS] [CrossRef] (In the text)
• Cowley, C. 1971, Observatory, 91, 139 [NASA ADS]
• Dachs, J., & Kaiser, D. 1984, A&AS, 58, 411 [NASA ADS] (In the text)
• Daflon, S., & Cunha, K. 2004, ApJ, 617, 1115 [NASA ADS] [CrossRef]
• Davidson, M. D., Snoek, L. C., Volten, H., & Dönszelmann, A. 1992, A&A, 255, 457 [NASA ADS]
• Dehnen, W., & Binney, J. J. 1998, MNRAS, 298, 387 [NASA ADS] [CrossRef] (In the text)
• Dimitrijevic, M. S., & Sahal-Bréchot, S. 1990, A&AS, 82, 519 [NASA ADS]
• Dimitrijevic, M. S., & Sahal-Bréchot, S. 1996, A&AS, 117, 127 [EDP Sciences] [NASA ADS]
• Dimitrijevic, M. S., & Sahal-Bréchot, S. 1997, A&AS, 122, 163 [EDP Sciences] [NASA ADS]
• Dorfi, E. A., & Gautschy, A. 2000, ApJ, 545, 982 [NASA ADS] [CrossRef] (In the text)
• Drake, J. J., & Testa, P. 2005, Nature, 436, 525 [NASA ADS] [CrossRef] (In the text)
• Ducati, J. R. 2002, Stellar Photometry in Johnson's 11-color system (Madison: University of Wisconsin), VizieR On-line Data Catalog: II/237 (In the text)
• Dufton, P. L., Ryans, R. S. I., Trundle, C., et al. 2005, A&A, 434, 1125 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Dupree, A. K., Lobel, A., Young, P. R., et al. 2005, ApJ, 622, 629 [NASA ADS] [CrossRef] (In the text)
• Eisenhauer, F., Schödel, R., Genzel, R., et al. 2003, ApJ, 597, L121 [NASA ADS] [CrossRef] (In the text)
• Esteban, C., Peimbert, M., García-Rojas, J., et al. 2004, MNRAS, 355, 229 [NASA ADS] [CrossRef] (In the text)
• Evans, C. J., & Howarth, I. D. 2003, MNRAS, 345, 1223 [NASA ADS] [CrossRef] (In the text)
• Fieldus, M. S., Lester, J. B., & Rogers, C. 1990, A&A, 230, 371 [NASA ADS] (In the text)
• Freytag, B., Steffen, M., & Dorch, B. 2002, Astron. Nachr., 323, 213 [NASA ADS] [CrossRef] (In the text)
• Fuhr, J. R., & Wiese, W. L. 1998, in CRC Handbook of Chemistry and Physics, 79th ed., ed. D. R. Lide (Boca Raton: CRC Press)
• Fuhr, J. R., Martin, G. A., & Wiese, W. L. 1988, J. Phys. & Chem. Ref. Data, Vol. 17, Suppl. 4
• Garnett, D. R., Kennicutt, R. C., & Bresolin, F. 2004, ApJ, 607, L21 [NASA ADS] [CrossRef] (In the text)
• de Geus, E. J., Lub, J., & van de Grift, E. 1990, A&AS, 85, 915 [NASA ADS] (In the text)
• Giddings, J. R. 1981, Ph.D. Thesis, Univ. London (In the text)
• Glushneva, I. N. 1985, in Calibration of Fundamental Stellar Quantities, ed. D. S. Haynes, N. E. Pasinetti, & A. G. Davis Philip (Dordrecht: D. Reidel Publishing Company), 465 (In the text)
• Gray, D. F. 1992a, Observations and Analysis of Stellar Photospheres, 2nd edition (Cambridge: Cambridge University Press) (In the text)
• Gray, R. O. 1992b, A&A, 265, 704 [NASA ADS] (In the text)
• Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] (In the text)
• Griem, H. R. 1964, Plasma Spectroscopy (New York: McGraw-Hill Book Company)
• Griem, H. R. 1974, Spectral Line Broadening by Plasmas (New York and London: Academic Press)
• Groth, H. G. 1961, ZAp, 51, 231 [NASA ADS] (In the text)
• Gummersbach, C. A., Kaufer, A., Schäfer, D. R., et al. 1998, A&A, 338, 881 [NASA ADS]
• Hanbury Brown, R., Davies, J., & Allen, L. R. 1974, MNRAS, 167, 121 [NASA ADS]
• Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [EDP Sciences] [NASA ADS] (In the text)
• Heger, A., & Langer, N. 2000, ApJ, 544, 1016 [NASA ADS] [CrossRef] (In the text)
• Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [NASA ADS] [CrossRef] (In the text)
• Hoffleit, D., & Jaschek, C. 1982, The Bright Star Catalogue, 4th edition (New Haven: Yale University Observatory) (In the text)
• Hubeny, I. 1988, Computer Physics Comm., 52, 103 [NASA ADS]
• Hubeny, I., & Lanz, T. 1995, ApJ, 439, 875 [NASA ADS] [CrossRef] (In the text)
• Hummer, D. G., Berrington, K. A., Eissner, W., et al. 1993, A&A, 279, 298 [NASA ADS] (In the text)
• Humphreys, R. M. 1980, ApJ, 241, 587 [NASA ADS] [CrossRef] (In the text)
• Husfeld, D., Butler, K., Heber, U., & Drilling, J. S. 1989, A&A, 222, 150 [NASA ADS]
• Israelian, G., Chentsov, E., & Musaev, F. 1997, MNRAS, 290, 521 [NASA ADS] (In the text)
• de Jager, C. 1998, A&A Rev., 8, 145 [NASA ADS] (In the text)
• Kaufer, A., Stahl, O., Wolf, B., et al. 1996, A&A, 305, 887 [NASA ADS] (In the text)
• Kaufer, A., Stahl, O., Wolf, B., et al. 1997, A&A, 320, 273 [NASA ADS] (In the text)
• Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, ESO Messenger, 95, 8 [NASA ADS] (In the text)
• Kaufer, A., Venn, K. A., Tolstoy, E., Pinte, C., & Kudritzki, R. P. 2004, AJ, 127, 2723 [NASA ADS] [CrossRef] (In the text)
• Kennicutt, R. C., Bresolin, F., & Garnett, D. R. 2003, ApJ, 591, 801 [NASA ADS] [CrossRef] (In the text)
• Kerr, F. J., & Lynden-Bell, D. 1986, MNRAS, 221, 1023 [NASA ADS] (In the text)
• Kilian, J. 1992, A&A, 262, 171 [NASA ADS]
• Kilian, J. 1994, A&A, 282, 867 [NASA ADS]
• Kudritzki, R.P. 1973, A&A, 28, 103 [NASA ADS] (In the text)
• Kudritzki, R. P. 1988, in Radiation in Moving Gaseous Media, ed. Y. Chmielewski, & T. Lanz (Sauverny: Geneva Observatory), 1 (In the text)
• Kudritzki, R. P. 1992, A&A, 266, 395 [NASA ADS] (In the text)
• Kudritzki, R. P. 1998, in Stellar Astrophysics for the Local Group, ed. A. Aparicio, A. Herrero, & F. Sánchez (Cambridge: Cambridge University Press), 149 (In the text)
• Kudritzki, R. P. 2000, in From Extrasolar Planets to Cosmology: The VLT Opening Symposium, ed. J. Bergeron, & A. Renzini (Berlin: Springer Verlag), 236 (In the text)
• Kudritzki, R. P., & Przybilla, N. 2003, in Stellar Candles for the Extragalactic Distance Scale, ed. D. Alloin, & W. Gieren, Lecture Notes in Physics, Vol. 635 (Berlin: Springer Verlag), 123 (In the text)
• Kudritzki, R. P., Puls, J., Lennon, D. J., et al. 1999, A&A, 350, 970 [NASA ADS] (In the text)
• Kudritzki, R. P., Bresolin, F., & Przybilla, N. 2003, ApJ, 582, L83 [NASA ADS] [CrossRef] (In the text)
• Kurucz, R. L. 1979, ApJS, 40, 1 [NASA ADS] [CrossRef]
• Kurucz, R. L. 1992, Rev. Mex. Astron. Astrofis., 23, 45 [NASA ADS] (In the text)
• Kurucz, R. L. 1993, Kurucz CD-ROM No. 13 (Cambridge, Mass.: Smithsonian Astrophysical Observatory) (In the text)
• Kurucz, R. L., & Bell, B. 1995, Kurucz CD-ROM No. 23 (Cambridge, Mass.: Smithsonian Astrophysical Observatory)
• Lambert, D. L., Hinkle, K. H., & Luck, R. E. 1988, ApJ, 333, 917 [NASA ADS] [CrossRef] (In the text)
• Lanz, T., Dimitrijevic, M. S., & Artru, M.-C. 1988, A&A, 192, 249 [NASA ADS]
• Lobel, A., Achmad, L., de Jager, C., & Nieuwenhuijzen, H. 1992, A&A, 256, 159 [NASA ADS] (In the text)
• Lucy, L. B. 1976, ApJ, 206, 499 [NASA ADS] [CrossRef] (In the text)
• Maeder, A., & Meynet, G. 2000, ARA&A, 38, 143 [NASA ADS] (In the text)
• Maeder, A., & Meynet, G. 2001, A&A, 373, 555 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Maeder, A., & Meynet, G. 2005, A&A, 440, 1041 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Martin, G. A., Fuhr, J. R., & Wiese, W. L. 1988, J. Phys. & Chem. Ref. Data, Vol. 17, Suppl. 3
• McCarthy, J. K., Lennon, D. J., Venn, K. A., et al. 1995, ApJ, 455, L135 [NASA ADS] (In the text)
• McErlean, N. D., Lennon, D. J., & Dufton, P. L. 1999, A&A, 349, 553 [NASA ADS] (In the text)
• Meynet, G., & Maeder, A. 2000, A&A, 361, 101 [NASA ADS] (In the text)
• Meynet, G., & Maeder, A. 2003, A&A, 404, 975 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Meynet, G., & Maeder, A. 2005, A&A, 429, 581 [EDP Sciences] [NASA ADS] [CrossRef]
• Mihalas, D. 1978, Stellar Atmospheres, 2nd edition (San Francisco: Freeman) (In the text)
• Morel, M., & Magnenat, P. 1978, A&AS, 34, 477 [NASA ADS] (In the text)
• Nandy, K., & Schmidt, E. G. 1975, ApJ, 198, 119 [NASA ADS] [CrossRef] (In the text)
• Nicolet, B. 1978, A&AS, 34, 1 [NASA ADS]
• Perryman, M. A. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS]
• Przybilla, N. 2002, Ph.D. Thesis, Univ. Munich (In the text)
• Przybilla, N., & Butler, K. 2001, A&A, 379, 955 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Przybilla, N., & Butler, K. 2004a, ApJ, 609, 1181 [NASA ADS] [CrossRef] (In the text)
• Przybilla, N., & Butler, K. 2004b, ApJ, 610, L61 [NASA ADS] [CrossRef] (In the text)
• Przybilla, N., Butler K., Becker S. R., Kudritzki, R. P., & Venn, K. A. 2000, A&A, 359, 1085 [NASA ADS] (In the text)
• Przybilla, N., Butler, K., Becker, S. R., & Kudritzki, R. P. 2001a, A&A, 369, 1009 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Przybilla, N., Butler, K., & Kudritzki, R. P. 2001b, A&A, 379, 936 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Przybylski, A. 1968, MNRAS, 139, 313 [NASA ADS] (In the text)
• Przybylski, A. 1969, MNRAS, 146, 71 [NASA ADS] (In the text)
• Przybylski, A. 1971, MNRAS, 152, 197 [NASA ADS] (In the text)
• Przybylski, A. 1972, MNRAS, 159, 155 [NASA ADS] (In the text)
• Puls, J., Kudritzki, R. P., Herrero, A., et al. 1996, A&A, 305, 171 [NASA ADS] (In the text)
• Puls, J., Urbaneja, M. A., Venero, R., et al. 2005, A&A, 435, 669 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Rolleston, W. R. J., Smartt, S. J., Dufton, P. L., & Ryans, R. S. I. 2000, A&A, 363, 537 [NASA ADS] (In the text)
• Rosendhal, J. D. 1970, ApJ, 160, 627 [NASA ADS] [CrossRef] (In the text)
• Rufener, F. 1988, Observations in the Geneva Photometric System 4 (Geneva: Geneva Observatory), VizieR On-line Data Catalog: II/169 (In the text)
• Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] (In the text)
• Sagar, R., & Cannon, R. D. 1995, A&AS, 111, 75 [NASA ADS] (In the text)
• Sanner, J., Brunzendorf, J., Will, J.-M., & Geffert, M. 2001, A&A, 369, 511 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
• Santolaya-Rey, A. E., Puls, J., & Herrero, A. 1997, A&A, 323, 488 [NASA ADS] (In the text)
• Seaton, M. J., Yu, Y., Mihalas, D., & Pradhan, A. K. 1994, MNRAS, 266, 805 [NASA ADS] (In the text)
• Severny, A. 1970, ApJ, 159, L73 [NASA ADS] [CrossRef] (In the text)
• Shobbrook, R. R., & Lyngå, G. 1994, MNRAS, 269, 857 [NASA ADS] (In the text)
• Sigut, T. A. A. 1999, ApJ, 519, 303 [NASA ADS] [CrossRef] (In the text)
• Simon, T., Ayres, T. R., Redfield, S., & Linsky, J. L. 2002, ApJ, 579, 800 [NASA ADS] [CrossRef] (In the text)
• Stehlé, C., & Hutcheon, R. 1999, A&AS, 140, 93 [EDP Sciences] [NASA ADS] (In the text)
• Schwarzschild, M. 1975, ApJ, 195, 137 [NASA ADS] [CrossRef] (In the text)
• Stalio, R., Selvelli, P. L., & Crivellari, L. 1977, A&A, 60, 109 [NASA ADS] (In the text)
• Takeda, Y. 1994, PASJ, 46, 181 [NASA ADS] (In the text)
• Takeda, Y., & Takada-Hidai, M. 2000, PASJ, 52, 113 [NASA ADS] (In the text)
• Takeda, Y., Takada-Hidai, M., & Kotake, J. 1996, PASJ, 48, 753 [NASA ADS] (In the text)
• Talavera, A., & Gómez de Castro, A. I. 1987, A&A, 181, 300 [NASA ADS] (In the text)
• Underhill, A., & Doazan, V. 1982, B Stars with and Without Emission Lines (Washington, DC: NASA) (In the text)
• Underhill, A. B., Divan, L., Prévot-Burnichon, M.-L., & Doazan, V. 1979, MNRAS, 189, 601 [NASA ADS] (In the text)
• Urbaneja, M. A., Herrero, A., Bresolin, F., et al. 2005, ApJ, 622, 862 [NASA ADS] [CrossRef] (In the text)
• Venn, K. A. 1995a, ApJS, 99, 659 [NASA ADS] [CrossRef] (In the text)
• Venn, K. A. 1995b, ApJ, 449, 839 [NASA ADS] [CrossRef]
• Venn, K. A. 1999, ApJ, 518, 405 [NASA ADS] [CrossRef] (In the text)
• Venn, K. A., & Przybilla, N. 2003, in CNO in the Universe, ed. C. Charbonnel, D. Schaerer, & G. Meynet (San Francisco: ASP), 20 (In the text)
• Venn, K. A., McCarthy, J. K., Lennon, D. J., et al. 2000, ApJ, 541, 610 [NASA ADS] [CrossRef] (In the text)
• Venn, K. A., Lennon, D. J., Kaufer, A., et al. 2001, ApJ, 547, 765 [NASA ADS] [CrossRef] (In the text)
• Venn, K. A., Tolstoy, E., Kaufer, A., et al. 2003, AJ, 126, 1326 [NASA ADS] [CrossRef] (In the text)
• Verdugo, E., Talavera, A., & Gómez de Castro, A. I. 1999a, A&AS, 137, 351 [EDP Sciences] [NASA ADS] (In the text)
• Verdugo, E., Talavera, A., & Gómez de Castro, A. I. 1999b, A&A, 346, 819 [NASA ADS] (In the text)
• Vidal, C. R., Cooper, J., & Smith, E. W. 1973, ApJS, 25, 37 [NASA ADS] [CrossRef] (In the text)
• Vrancken, M., Butler, K., & Becker, S. R. 1996, A&A, 311, 661 [NASA ADS]
• Wiese, W. L., Smith, M. W., & Glennon, B. M. 1966, Nat. Stand. Ref. Data Ser., Nat. Bur. Stand. (US), NSRDS-NBS 4, Vol. I
• Wiese, W. L., Smith, M. W., & Miles, B. M. 1969, Nat. Stand. Ref. Data Ser., Nat. Bur. Stand. (US), NSRDS-NBS 22, Vol. II
• Wiese, W. L., Fuhr, J. R., & Deters, T. M. 1996, J. Phys. & Chem. Ref. Mon. Data, 7
• Wolf, B. 1971, A&A, 10, 383 [NASA ADS] (In the text)
• Wolf, B. 1972, A&A, 20, 275 [NASA ADS] (In the text)
• Wolf, B. 1973, A&A, 28, 335 [NASA ADS] (In the text)
• Young, J. S., Baldwin, J. E., Boysen, R. C., et al. 2000, MNRAS, 315, 635 [NASA ADS] [CrossRef] (In the text)

 

  
Online Material

  
Appendix A: Spectral line analysis

In this appendix we provide details on our spectral line analysis, as a basis for further applications. Table A.1 summarises our line data and the results from the abundance analysis for our sample stars. It is available in electronic form only. The first columns give the line wavelength $\lambda$ (in Å), excitation energy of the lower level $\chi$ (in eV), adopted oscillator strength $\log gf$, an accuracy indicator and the source of the gf value. Most of the gf-data is retrieved from the atomic spectra database (V2.0) of the National Institute of Standards and Technology (http://physics.nist.gov/cgi-bin/AtData/main_asd). Then, for each object the measured equivalent width $W_{\lambda}$ (in mÅ) is tabulated, followed by the derived abundance $\log \varepsilon = \log {(X/{\rm H})}$ + 12. In cases with an entry for the non-LTE abundance correction $\Delta \log \varepsilon = \log \varepsilon_{\rm NLTE}- \log \varepsilon_{\rm LTE}$ this denotes the non-LTE abundance, else the LTE abundance. The equivalent widths have been measured by direct integration over the spectral lines, deviating from the usual approach of fitting the observed profiles by a Gaussian. Forhigh-S/N observations of BA-SGs as in the present study this helps to avoid systematic uncertainties, as the line profiles are potentially subject to asymmetries imposed by the velocity field at the base of the stellar wind. In some cases metal lines are situated in the wings of the Balmer lines. Then their equivalent width is measured with respect to the local continuum, indicated by "S( $W_{\lambda}$)''. Abundances are determined from a best match of the spectrum synthesis to the observed line profiles, and not the equivalent widths, see the discussion in Sect. 6. Equivalent widths are used as auxiliary diagnostics for the determination of microturbulent velocity (see e.g. Fig. 13). Spectrum synthesis also allows blended features to be used for abundance determinations, where a $W_{\lambda}$measurement is hampered. These cases are marked by a sole "S'' in Table A.1. For He I only non-LTE abundances are derived because of the potential of this major atmospheric constituent to change atmospheric structure and thus the stellar parameter determination, see Sect. 3.2. Entries in italics are disregarded when computing abundance averages (Table 4).

Table A.1: Spectral line analysis.