A&A 445, 857-867 (2006)
DOI: 10.1051/0004-6361:20053616
E. Pompei1 - R. R. de Carvalho2 - A. Iovino 3
1 - European Southern Observatory,
Alonso de Cordova 3107, Vitacura, Casilla 19001, Santiago 19, Chile
2 -
INPE/MCT,
Av. dos Astronautas 1758,
S. J. Campos, SP 12227-010, Brazil
3 -
Osservatorio Astronomico di Brera
via Brera 28, 20121 Milano, Italy
Received 11 June 2005 / Accepted 30 August 2005
Abstract
This paper presents the results of a pilot redshift survey
of 18 candidate compact groups from the distant DPOSS survey that extends to redshift ![]() 0.2
the available surveys of compact groups of galaxies, mainly
Hickson Compact Groups and Southern Compact Groups. The goal of our survey was to confirm group
membership via redshift information and to measure the characteristic
parameters of a representative, albeit small, sample of DPOSS survey
groups.
0.2
the available surveys of compact groups of galaxies, mainly
Hickson Compact Groups and Southern Compact Groups. The goal of our survey was to confirm group
membership via redshift information and to measure the characteristic
parameters of a representative, albeit small, sample of DPOSS survey
groups.
Of the 18 candidates observed, seven are found to be indeed isolated
compact groups, i.e. groups with 3 or more concordant members and with
no neighbouring known cluster, while 7 are chance
projection configurations on the sky. Three remaining candidates,
despite having 3 or more concordant member galaxies, are located in
the neighbourhood of known clusters, while another candidate turned out to be a
dense sub-condensation within Abell 0952.
The median redshift of our 7 confirmed groups is
![]() ,
to be
compared with a median redshift of 0.03 for
the local sample of compact groups by Hickson. The typical group size is
,
to be
compared with a median redshift of 0.03 for
the local sample of compact groups by Hickson. The typical group size is
![]() 50 kpc, and the median radial velocity
dispersion is 167 km s-1, while typical crossing times range from
0.005
H0-1 to 0.03
H0-1 with a median value of 0.018
H0-1, all similar to the values usually found in the
literature for such structures in the local universe. The average
mass-to-light ratio for our groups, M/LB, is 92h,
higher than the value found for nearby Hickson compact groups
but lower than that found for loose groups. Our results suggest that,
once full redshift information for its members
becomes available, the DPOSS sample will provide a reference sample to study the
properties of compact groups beyond the local universe.
50 kpc, and the median radial velocity
dispersion is 167 km s-1, while typical crossing times range from
0.005
H0-1 to 0.03
H0-1 with a median value of 0.018
H0-1, all similar to the values usually found in the
literature for such structures in the local universe. The average
mass-to-light ratio for our groups, M/LB, is 92h,
higher than the value found for nearby Hickson compact groups
but lower than that found for loose groups. Our results suggest that,
once full redshift information for its members
becomes available, the DPOSS sample will provide a reference sample to study the
properties of compact groups beyond the local universe.
Key words: galaxies: clusters: general - techniques: spectroscopic
Compact groups (hereafter CGs) are well known systems, ever since the discovery by Edouard Stephan of the first one in 1877, at a time when we did not even know about the expansion of the universe and about the existence of other galaxies outside our own. These galactic systems drew attention due to their small angular scale; their sizes are comparable to the mean distance between their member galaxies. Physically, we naively classify these systems as having low mass, high projected density, and low velocity dispersion. Galaxy-galaxy interactions (e.g. close tidal encounters) and mergers are therefore likely to dominate their evolution. Until now, however, signs of interactions in CGs selected from the Hickson catalogue, the most widely studied catalogue of such objects (Hickson 1982), were found to be uncommon and traces of mergers to be rare (Zepf 1993). When present, these features are mainly found in spiral-dominated groups.
Subsequent studies by Mendes de Oliveira
et al. (1994) showed that, while interactions (i.e. encounters
which do not disrupt the galaxies) between galaxies
in compact groups are quite common, mergers remain rare, to the level of 6![]() of
the group galaxies. Addtional studies by Proctor et al. (2004) showed that
the stellar population of the early-type member galaxies of nearby,
of
the group galaxies. Addtional studies by Proctor et al. (2004) showed that
the stellar population of the early-type member galaxies of nearby, ![]() 0.03,
compact groups is quite old.
This led to doubt the existence of compact groups as physically bound system,
but detection of diffuse intra-group matter in 75
0.03,
compact groups is quite old.
This led to doubt the existence of compact groups as physically bound system,
but detection of diffuse intra-group matter in 75![]() of HCGs (Ponman et al. 1996)
confirmed that these are indeed bound, self-gravitating
structures. The question then arises about the origin and evolution of compact groups:
how can they survive for so long?
of HCGs (Ponman et al. 1996)
confirmed that these are indeed bound, self-gravitating
structures. The question then arises about the origin and evolution of compact groups:
how can they survive for so long?
Studies of the environment of HCGs (de Carvalho et al. 1997; Ribeiro et al. 1998) have shown that compact groups can be divided into three categories, namely: real compact groups, systems composed of a core+halo structure, and sparse groups. Objects belonging to different categories have different surface density profiles, and we observe a propensity for higher activity level in lower velocity dispersion groups. These differences are also reflected in their X-ray emission: groups detected in X-ray have higher galaxy density than groups without detectable X-ray emission. Moreover early type galaxies are more centrally concentrated in X-ray emitting groups than in the non-emitting ones; and finally groups dominated by late type spirals do not show X-ray emission (Zabludoff & Mulchaey 1998).
The different properties of the group categories identified by de Carvalho et al. (1994, 1997) might be interpreted as an evolutionary scheme in which the groups form in a looser concentration of galaxies, followed by a period of strong evolution with merging episodes. They then settle into a more quiescent phase and finally end up as isolated field ellipticals (Coziol et al. 2004). However, the already cited recent studies by Proctor et al. (2004) and Mendes de Oliveira et al. (2005) find that early type galaxies in compact groups are older than field galaxies of the same type and similar to cluster galaxies. This means that formation of early type galaxies in groups by galaxy-galaxy mergers must have happened a long time ago (of the order of a few Gyrs). On the other hand, compact groups have a very short crossing time, of the order of a few percent of the Hubble time, making it unclear how groups dominated by early type galaxies are observable today, because they should have disappeared a long time ago. A different possibility might be that compact groups are quite young configurations and that we are observing different stages of an ongoing merging process at the same time. If this is true, then we might wonder what a search for compact groups at increasing redshift would produce: would we find an higher number of interacting groups than at present time? Would we find an increase in the activity of the member galaxies? Would we find changes in the group's physical characteristics, like velocity dispersion, mass, radius, and crossing time?
To achieve these goals requires a complete sample of compact groups whose
observational and statistical biases are well understood.
A new sample of 459 compact group candidates with a median expected
redshift of ![]() 0.12, i.e. 10 times higher than the typical
crossing time of present-day compact groups, has been selected with an automatic algorithm
applied to the Digitized Second Palomar Observatory Sky Survey II (herafter DPOSS II)
galaxy catalogues (Iovino et al. 2003 and de
Carvalho et al. 2005). We refer the reader to these cited papers
for detailed information on the sample, however, we report here the
selection criteria for the sake of completeness:
0.12, i.e. 10 times higher than the typical
crossing time of present-day compact groups, has been selected with an automatic algorithm
applied to the Digitized Second Palomar Observatory Sky Survey II (herafter DPOSS II)
galaxy catalogues (Iovino et al. 2003 and de
Carvalho et al. 2005). We refer the reader to these cited papers
for detailed information on the sample, however, we report here the
selection criteria for the sake of completeness:
A first step in exploiting such a sample is to define via spectroscopic follow-up how many groups are indeed bound, selecting subsamples of groups with three/four galaxies sharing the same recession velocity. In addition, the spectroscopic data allow us to estimate the dynamic characteristics of the groups and assess the level of activity in their galaxy population. Here we present the first results from a pilot study carried out at the 3.58 m New Technology Telescope (NTT) at La Silla Observatory. In the next section we describe the observation and data reduction, in Sect. 3 we present our results and in Sect. 4 our findings.
Throughout the paper, a ![]() CDM cosmology (
CDM cosmology (
![]() ;
;
![]() )
and H0=67 km s-1 Mpc-1 have
been used.
)
and H0=67 km s-1 Mpc-1 have
been used.
The targets were selected from the published DPOSS II compact group
sample by Iovino et al. (2003) on the basis of available
observational windows. They represent a fair sample of the total catalogue
published in Iovino et al.(2003); in fact a k-s test on the observed sample
and the complete DPOSS II
group catalogue shows that the two populations are the same with a probability
of 96.1![]() .
Notice also that the Iovino et al. (2003)
sample is a subset (with a few exceptions) of the larger sample of
Carvalho et al. (2005), which presents the final complete sample of DPOSS
candidate compact groups. These group galaxies were observed with the
NTT telescope and the ESO Multi Mode Instrument (hereafter EMMI) in
spectroscopic mode in the red arm, equipped with
grism
.
Notice also that the Iovino et al. (2003)
sample is a subset (with a few exceptions) of the larger sample of
Carvalho et al. (2005), which presents the final complete sample of DPOSS
candidate compact groups. These group galaxies were observed with the
NTT telescope and the ESO Multi Mode Instrument (hereafter EMMI) in
spectroscopic mode in the red arm, equipped with
grism ![]() 2 and a slit of 1.5
2 and a slit of 1.5
![]() ,
under clear/thin cirrus
conditions and grey time. The MIT/LL new red detector, a mosaic
of 2 CCDs
,
under clear/thin cirrus
conditions and grey time. The MIT/LL new red detector, a mosaic
of 2 CCDs
![]() ,
was binned by 2
in both spatial and spectral direction, with a resulting dispersion of
3.56
,
was binned by 2
in both spatial and spectral direction, with a resulting dispersion of
3.56 ![]() /pix, a spatial scale of 0.33
/pix, a spatial scale of 0.33
![]() /pix, an instrumental
resolution of 322 km s-1, and a wavelength coverage from 3800 to
11 000
/pix, an instrumental
resolution of 322 km s-1, and a wavelength coverage from 3800 to
11 000 ![]() .
When possible, two or more galaxies were placed together
in the slit, whose position angle was constrained by the location
of galaxies in the sky and almost never coincided with the
parallactic angle. Exposure times varied from 720 s to 1200 s per spectrum, and
two spectra/target were taken to ensure reliable
cosmic ray subtraction.
The full log of the observations is given in Table 1.
.
When possible, two or more galaxies were placed together
in the slit, whose position angle was constrained by the location
of galaxies in the sky and almost never coincided with the
parallactic angle. Exposure times varied from 720 s to 1200 s per spectrum, and
two spectra/target were taken to ensure reliable
cosmic ray subtraction.
The full log of the observations is given in Table 1.
Table 1: Observing log.
On-site data reduction was performed using the EMMI spectroscopic
quick look tool available at La Silla Observatory (Pompei et al. 2004) and refined later using the MIDAS data reduction package![]() . Our
steps include bias subtraction, flat-field correction, wavelength
calibration, cosmic ray filtering, sky subtraction, and correction by
atmospheric extinction, but no flux calibration, as our nights were not
all of photometric quality. Flat field correction was good up to
2
. Our
steps include bias subtraction, flat-field correction, wavelength
calibration, cosmic ray filtering, sky subtraction, and correction by
atmospheric extinction, but no flux calibration, as our nights were not
all of photometric quality. Flat field correction was good up to
2![]() ,
except in the reddest part of the spectra (redward of
8000
,
except in the reddest part of the spectra (redward of
8000 ![]() ), where fringing becomes significant (up to 4
), where fringing becomes significant (up to 4![]() from
peak-to-peak variation). As a consequence, absorption lines redward of
8000
from
peak-to-peak variation). As a consequence, absorption lines redward of
8000 ![]() were not considered for the redshift measurement. A
two-dimensional dispersion solution was obtained using the arc frames
taken in the afternoon. No arc was taken during the night, since EMMI
flexures are less than 1 pixel over the full 360 degrees instrument
rotation.
A third order polynomial was used for the dispersion direction, while
a second order one was employed to correct for the geometrical
distortion along the spatial direction. An upper limit of 0.16
were not considered for the redshift measurement. A
two-dimensional dispersion solution was obtained using the arc frames
taken in the afternoon. No arc was taken during the night, since EMMI
flexures are less than 1 pixel over the full 360 degrees instrument
rotation.
A third order polynomial was used for the dispersion direction, while
a second order one was employed to correct for the geometrical
distortion along the spatial direction. An upper limit of 0.16 ![]() was found for the rms of the wavelength solution.
was found for the rms of the wavelength solution.
Sky subtraction was performed on the two-dimensional rectified
spectrum of each target and the rms in the background of the sky
subtracted spectra varies from 5 to 10![]() ,
which is the worst for nights
with a full moon. The atmospheric absorption feature at
,
which is the worst for nights
with a full moon. The atmospheric absorption feature at ![]() 7600
7600 ![]() was not corrected and any line falling close or in it was not
considered for the redshift measurement. The two spectra available
for each galaxy
were collapsed perpendicular to the dispersion direction, in order to measure
the FWHM of the galaxy, on average 4.3
was not corrected and any line falling close or in it was not
considered for the redshift measurement. The two spectra available
for each galaxy
were collapsed perpendicular to the dispersion direction, in order to measure
the FWHM of the galaxy, on average 4.3
![]() .
To obtain the final
one-dimensional, wavelength calibrated galaxy spectrum an extraction
window of 3
.
To obtain the final
one-dimensional, wavelength calibrated galaxy spectrum an extraction
window of 3 ![]() FWHM was always used. An exception to this rule is
represented by two galaxies very close to each other: in this case the
biggest non-overlapping window has been chosen, which was never
smaller than 4.3
FWHM was always used. An exception to this rule is
represented by two galaxies very close to each other: in this case the
biggest non-overlapping window has been chosen, which was never
smaller than 4.3
![]() .
.
The two one-dimensional spectra available for each galaxy were averaged
together at the end of the reduction, giving an average S/N of ![]() 30 (grey time) or
30 (grey time) or ![]() 10-15 (almost full moon) per resolution
element at 6000
10-15 (almost full moon) per resolution
element at 6000 ![]() .
.
In some cases, nearby galaxies happened to fall in the slit together with the candidate member galaxies, so their spectra were reduced and extracted following the same procedure used for the target galaxies. Radial velocity standards from the Andersen et al. (1985) paper were observed with the same instrumental set-up used for the target galaxies; in addition to this, we also used galaxy templates with known spectral characteristics and heliocentric velocity available from the literature, i.e. M 32, NGC 7507, and NGC 4111.
The IRAF![]() packages xcsao and emsao have been used to
measure the galaxy redshifts by means of cross-correlation method
(Tonry & Davis 1979), where good results were obtained with galaxy spectra
dominated by emission lines or by absorption lines. For spectra
dominated by absorption lines, we used galaxy templates and stellar
radial velocity standards, while for emission line dominated spectra we
used a synthetic template generated by the IRAF package linespec. Starting from a list of the stronger emission lines
(H
packages xcsao and emsao have been used to
measure the galaxy redshifts by means of cross-correlation method
(Tonry & Davis 1979), where good results were obtained with galaxy spectra
dominated by emission lines or by absorption lines. For spectra
dominated by absorption lines, we used galaxy templates and stellar
radial velocity standards, while for emission line dominated spectra we
used a synthetic template generated by the IRAF package linespec. Starting from a list of the stronger emission lines
(H![]() ,
[OIII], [OI], H
,
[OIII], [OI], H![]() ,
[NII], [SII]), the package creates
a synthetic spectrum, which is then convolved with the instrumental
resolution.
,
[NII], [SII]), the package creates
a synthetic spectrum, which is then convolved with the instrumental
resolution.
Following the discussion by Kurtz & Mink (1998), we
performed visual checks of the complete galaxy sample, in order to
understand the reliability limit of the automatic redshift
determination. This is given by a confidence parameter, r,
defined for the first time in Tonry & Davis (1979), which is basically the
ratio between the height of the true peak of the correlation function
and the average peak of a spurious function (called remainder function
in Tonry & Davis). We found that all redshifts with a confidence parameter
![]() are reliable, but measurements with
are reliable, but measurements with
![]() need
to be checked by hand. Measurements with
need
to be checked by hand. Measurements with
![]() are not
reliable. All the confirmed member galaxies in our sample had
a
are not
reliable. All the confirmed member galaxies in our sample had
a
![]() .
.
In some cases emsao failed to correctly identify the emission lines, which happened each time some emission lines were contaminated by underlying absorption. When this happened, we measured the redshift by Gaussian fitting of the strongest emission lines visible and took the average of the results obtained from each line. If two or more lines were blended, the IRAF command deblend within the splot package was used.
The error quoted for the recession velocity is the quadrature sum of two terms: the first is the error in the dispersion solution and the second is the error in the velocity estimate, defined as the scatter in the measurement resulting from the use of different templates, or as the scatter given by the Gaussian fitting of different emission lines. The recession velocity errors varied between 15 and 100 km s-1, depending also on the S/N of the target spectrum.
Correction to heliocentric recession velocity values was obtained with the IRAF task rvcorrect in the package noao.rv.
After checking the literature, we found no overlapping data in the 2dF and
6dF survey, and only one of our galaxies has a published redshift in
Nasa Extragalactic Database (hereafter NED), PCG 114333+215356B. The quoted
redshift is z = 0.130 (Tovmassian
et al. 1999), while the one we measured is
![]() ,
i.e.
,
i.e. ![]() 600 km s-1 difference. On the other hand the
published value is quoted there without any errors, and addressing the
reader to a forthcoming paper on the optical spectroscopy, which at the
time of writing this article, was not yet available. Another comparison can be done
with the paper of Miller et al. (2002), where they measure redshifts
of galaxies in Abell 0952. Unfortunately, only one galaxy is common to
both samples, PGC 101345+194541A, at
600 km s-1 difference. On the other hand the
published value is quoted there without any errors, and addressing the
reader to a forthcoming paper on the optical spectroscopy, which at the
time of writing this article, was not yet available. Another comparison can be done
with the paper of Miller et al. (2002), where they measure redshifts
of galaxies in Abell 0952. Unfortunately, only one galaxy is common to
both samples, PGC 101345+194541A, at ![]() = (10:13:45.11) and
= (10:13:45.11) and
![]() = (+19:45:44.4). The two velocity measurements,
= (+19:45:44.4). The two velocity measurements,
![]() km s-1
in our case and
km s-1
in our case and
![]() km s-1 for Miller, agree within
the experimental errors.
km s-1 for Miller, agree within
the experimental errors.
Table 2, which is available only in electronic form, lists the galaxy name (Col. 1), J2000 coordinates from the DPOSS II survey (Cols. 2 and 3), heliocentric radial velocity and velocity error (Cols. 4), type of velocity measurement (from absorption lines "abs'', from emission lines "em'', from a combination of both "mix''; Col. 5), and the emission lines detected in the spectrum, if any (Col. 6).
In this section we present the results obtained in our pilot survey. We first discuss group membership and the spectral properties of the member galaxies in detail. We then discuss statistical properties of our sample more generally: velocity dispersion, crossing time, M/L ratio and typical size. While it is difficult to produce statistically significant results with only 18 groups, it is nevertheless interesting to examine the trends. We also searched the environment of each group, checking for the possible presence of a nearby known cluster, with the goal of ascertaining whether the group is really isolated or if it belongs to a larger structure.
Finally we note that sometimes other nearby galaxies, close on the sky to our target galaxy but not included as member galaxies in the original group definition, entered in our slit and happened to have a concordant velocity with other members of the group. In order to avoid a contamination of the group selection function or of the group properties, we decided in the following to calculate all the quantities taking into account only the candidate members, as shown on the finding charts on the paper from Iovino et al. (2003).
Following the paper by Hickson et al. (1992), we decided to consider
as bona fide confirmed groups all the candidates with at least
three galaxies, whose relative velocity difference was ![]()
![]() km s-1 from the median velocity of the group.
km s-1 from the median velocity of the group.
The opportunity of such a choice is confirmed by the plot in Fig. 1, which shows the distribution around the median velocity of the group for all galaxies (both concordant and discordant) and originally classified as group members. All the spectroscopically confirmed member galaxies are within 1000 km s-1 of the median velocity of the group while the discordant ones are off the scale. This result is very similar to the one found by Hickson for the HCGs catalog.
![\begin{figure}
\par\includegraphics[angle=-90,width=7.5cm,clip]{3616fig1.ps}\end{figure}](/articles/aa/full/2006/03/aa3616-05/Timg50.gif) |
Figure 1: Distribution of the difference in velocity from the median velocity of the group for all the galaxies cataloged to belong to the same group. |
| Open with DEXTER | |
Table 3: Classification of the DPOSS II compact groups and neighbouring large scale structures. n represents all galaxies which fulfilled the velocity criteria, irrespective of the original catalogue of group galaxies, while the number quoted in parentheses is the number of concordant galaxies that were originally part of the DPOSS catalog. When a (2+2) is given for n (members), it means that the candidate group is composed of two concordant pairs of galaxies.
To calculate the median group velocity and radial velocity dispersion,
we used the biweight estimators of location and scale (Beers et al. 1990), which takes all relevant cosmological effects into account.
Of a total of 18 candidate compact groups, we found 11 concordant
and 7 discordant objects, for a total of 60![]() success rate.
The radial velocities of our groups range from
cz = 23 800 to 44 586 km s-1, with a median
success rate.
The radial velocities of our groups range from
cz = 23 800 to 44 586 km s-1, with a median
![]() km s-1. These values should be
compared to the corresponding ones for the HCGs: radial velocities
range from 1380 to 41 731 km s-1, with a median
km s-1. These values should be
compared to the corresponding ones for the HCGs: radial velocities
range from 1380 to 41 731 km s-1, with a median
![]() km s-1.
km s-1.
With the redshift information of each group in hand, we first explored the group environment using NED. We decided to take all the available cluster catalogues into account, with the exception of the Zwicky one, as most of its clusters lack redshift measurements. In our analysis, we also included the DPOSS II cluster catalogue (Gal et al. 2003), which is more homogeneous and covers the same depth and area of our group survey, and whose clusters have a reliable photometric redshift estimate.
To find neighboring clusters, we adopted a search radius of
15
![]() ,
i.e.
,
i.e. ![]() 3
3
![]() bigger than the Abell radius of a
cluster placed at the distance of the our furthest group, z=0.148.
Once we have a list of possible cluster neighbours, we checked if any of
them has a measured redshift. If so, we further refined the
search using a redshift criterion by assuming that a group is close to
a cluster if the difference in redshift between the two is
bigger than the Abell radius of a
cluster placed at the distance of the our furthest group, z=0.148.
Once we have a list of possible cluster neighbours, we checked if any of
them has a measured redshift. If so, we further refined the
search using a redshift criterion by assuming that a group is close to
a cluster if the difference in redshift between the two is ![]() z< 0.01. This corresponds to a velocity difference of 3000 km s-1, one
order of magnitude above the typical dispersion of compact groups and
z< 0.01. This corresponds to a velocity difference of 3000 km s-1, one
order of magnitude above the typical dispersion of compact groups and ![]() 2.5
times wider than the biggest velocity dispersion measured for clusters
(
2.5
times wider than the biggest velocity dispersion measured for clusters
(![]() 1200 km s-1; Zabludoff et al. 1993).
1200 km s-1; Zabludoff et al. 1993).
Accordingly our candidate groups are then divided in three classes: A, B, and C. Candidate groups belonging to class A are confirmed and isolated systems; candidate groups belonging to class B are confirmed but close on the sky to larger structures to which they might be associated. Candidate groups belonging to class C are all the targets with less than 3 concordant galaxies, and thus not groups according to our definition. Of the 11 confirmed groups, we found seven that we consider class A, while four are close to a cluster. One candidate turned out to be a dense sub-condensation within Abell 0952, while the remaining three are located in the outskirts of known clusters. In Table 3 we show the group name (Col. 1), the coordinates of the centre of the group (Cols. 2, 3), the number of concordant galaxies (Col. 4), the mean redshift of the group (Col. 5), its class (Col. 6) and any neighbour that has been found (Col. 7). No cluster name means none has been found within the search radii used. It is interesting to note that there is only one candidate group with 4 discordant members, PCG 121157+134421.
We then analyzed the morphological type of the galaxies in our
candidate compact groups. Lacking good quality images, we adopted the
same criterium as in Ribeiro et al. (1998), i.e. we assumed that a
galaxy has a late morphological type if EW(H
![]()
![]()
![]() . The EW(H
. The EW(H![]() )
has been estimated on the wavelength
calibrated spectra using the IRAF task splot; to separate the
H
)
has been estimated on the wavelength
calibrated spectra using the IRAF task splot; to separate the
H![]() line from the two nearby [NII] lines, we used the
deblend task and the results are shown in Table 4 only for groups of
class A and B.
line from the two nearby [NII] lines, we used the
deblend task and the results are shown in Table 4 only for groups of
class A and B.
We assumed that a group can be considered of late morphological type if
at least 50![]() of its member galaxies have an EW(H
of its member galaxies have an EW(H
![]()
![]() ,
which gives us 5 late type groups from the 11 confirmed
targets, see Table 4.
Of the 37 galaxies belonging to the confirmed groups, 13 show
emission in H
,
which gives us 5 late type groups from the 11 confirmed
targets, see Table 4.
Of the 37 galaxies belonging to the confirmed groups, 13 show
emission in H![]() ,
for a total of 35
,
for a total of 35![]() emitters. No galaxy
shows a velocity dispersion characteristic of a Sy2, but 1 of them is
a starburst galaxy, (EW(H
emitters. No galaxy
shows a velocity dispersion characteristic of a Sy2, but 1 of them is
a starburst galaxy, (EW(H
![]()
![]() ,
Kennicutt & Kent 1983), PCG 130157+191151C, and another is an HII galaxy, PCG 130157+191151A (see below).
This percentage of emission line objects is equal to what has been
found for Southern Compact Groups and for Hickson groups, for which
the fraction of emission line galaxies is
,
Kennicutt & Kent 1983), PCG 130157+191151C, and another is an HII galaxy, PCG 130157+191151A (see below).
This percentage of emission line objects is equal to what has been
found for Southern Compact Groups and for Hickson groups, for which
the fraction of emission line galaxies is ![]() 35
35![]() of the total
(Coziol et al. 2000, 2004).
of the total
(Coziol et al. 2000, 2004).
Table 4:
Morphological classification of the member galaxies for groups of class A and B.
![]() is the morphogical type of the group as defined by the percentage of galaxies
with EW(H
is the morphogical type of the group as defined by the percentage of galaxies
with EW(H
![]()
![]() .
.
Here we give a brief description of the individual compact groups
selected for this study. The morphological characterisation of the
galaxies is based on their measured EW(H![]() ), as stated in the
previous section.
), as stated in the
previous section.
It should be noted that this group is not in the final list of DPOSS compact groups candidates in Carvalho et al. (2005). It is located on a plate whose quality was not good enough to ensure reliable star galaxy separation (explaining a posteriori why such object entered our sample).
In the following sections we discuss only the properties of the groups classified as A and B.
In Fig. 4 we show the distribution of the velocity dispersion for the observed groups, which is perfectly consistent with that of HCGs and Southern Compact Groups (hereafter SCGs, Iovino 2000), while it is smaller than the average value found for loose groups of galaxies (see for example Eke et al. 2004). The base 10 logarithm of the values measured for the confirmed groups are shown in Col. 3 of Table 5.
![\begin{figure}
\par\includegraphics[width=7.5cm,clip]{3616fig4.ps}\end{figure}](/articles/aa/full/2006/03/aa3616-05/Timg78.gif) |
Figure 4: Distribution of the observed velocity dispersion for the DPOSS groups (hatched area), Southern Compact Groups survey (SCGs, strong line) and Hickson Compact Groups (HCGs, light line). |
| Open with DEXTER | |
Table 5:
Group dynamical properties.
![]() ,
R, and
,
R, and
![]() are
expressed in logarithmic values; mass,
luminosity, and mass-to-light ratio are given in solar units. The symbols follow Hickson et al. (1992).
are
expressed in logarithmic values; mass,
luminosity, and mass-to-light ratio are given in solar units. The symbols follow Hickson et al. (1992).
To have an idea of how our groups compare to HCGs and
to SCGs, we next estimated the crossing time, defined as (Hickson et al. 1992):
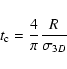 |
(1) |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3616fig5.ps}\end{figure}](/articles/aa/full/2006/03/aa3616-05/Timg104.gif) |
Figure 5: Distribution of dimensionless crossing time for the confirmed DPOSS groups (hatched area), compared to that obtained for HCGs (light line) and for SCGs (heavy line). |
| Open with DEXTER | |
Finally, we provide an estimate of the group mass and the corresponding
mass-to-light ratio in the Gunn r filter.
To estimate the mass of the groups, we assume that we can use the
virial theorem, so that the expression for the mass is:
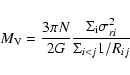 |
(2) |
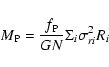 |
(3) |
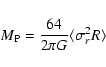 |
(4) |
We calculated both quantities, ![]() and
and
![]() ,
and found that
,
and found that ![]() is a few percent smaller than
is a few percent smaller than ![]() ,
but
of a comparable order of magnitude. The mass estimate we report in Col. 6 of
Table 5 is the average of the two estimators. Errors on the estimate of the mass
are largely dominated by the difference between the two estimators, which has been
assumed as total error.
,
but
of a comparable order of magnitude. The mass estimate we report in Col. 6 of
Table 5 is the average of the two estimators. Errors on the estimate of the mass
are largely dominated by the difference between the two estimators, which has been
assumed as total error.
To estimate the luminosities, we use the r band magnitudes of the groups
obtained by summing up all the flux of the member galaxies as measured on the
calibrated DPOSS II plates and also published in Iovino et al. (2003): these are corrected for galactic
extinction, and for k-correction, and re-scaled to absolute
value.
Two different k-corrections have been defined: one for early type
galaxies (E-Sa) and another for spirals (Sbc): the EW(H![]() )
has been used to discriminate
in this sense.
)
has been used to discriminate
in this sense.
As a reference for the solar magnitude, we used the paper by Jorgensen
(1994). From stars with a
![]() (i.e. the same colour of
the sun) it is possible to estimate a colour index
(i.e. the same colour of
the sun) it is possible to estimate a colour index
![]() .
Taking
.
Taking
![]() (Binney & Merrifield 2001), we have
(Binney & Merrifield 2001), we have
![]() .
The values for the light and the mass-to-light
ratio are shown in Cols. 7 and 8 of Table 5 respectively.
Errors on the luminosity were estimated by assuming the maximum error
on the photometric calibration of DPOSS plates, i.e. an error of 0.19 mag for an r magnitude of 19 (Gal et al. 2004).
.
The values for the light and the mass-to-light
ratio are shown in Cols. 7 and 8 of Table 5 respectively.
Errors on the luminosity were estimated by assuming the maximum error
on the photometric calibration of DPOSS plates, i.e. an error of 0.19 mag for an r magnitude of 19 (Gal et al. 2004).
The median value of the M/Lr in the sample is 47.
It should be noted, however, that Hickson used B-band luminosity, not r. If
we use the B band luminosity,
assuming the transformation (Windhorst et al. 1991),
| (5) |
In Fig. 6, we show the distribution of the physical radius for our
confirmed compact groups (classes A and B). We observe a narrow
distribution of physical sizes around ![]() 50 kpc, with the values
greater than 100 kpc given by the very elongated group PCG 130926+155358.
This very well agrees with the characteristics physical scale
for compact groups, 50 Kpc, hence we can be confident within our
small number statistics that we are indeed observing compact groups.
50 kpc, with the values
greater than 100 kpc given by the very elongated group PCG 130926+155358.
This very well agrees with the characteristics physical scale
for compact groups, 50 Kpc, hence we can be confident within our
small number statistics that we are indeed observing compact groups.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{3616fig6.ps}\end{figure}](/articles/aa/full/2006/03/aa3616-05/Timg119.gif) |
Figure 6:
Distribution of the galaxy-galaxy distance for class A and B
groups. The peak of the distribution is consistent with the
characteristic physical scale of compact groups, |
| Open with DEXTER | |
Observation and analysis of this small sample of 18 candidate groups have shown several important results of the DPOSS survey:
The Sloan survey data do not allow redshift determination for
individual group members, again due to the large separation on the
sky of the fibers used to carry on the survey: 60
![]() ,
i.e.
80 h-1 kpc at
,
i.e.
80 h-1 kpc at
![]() .
Basically, these
data are affected by the same problem as LCRS. The identification
of a group is made by assigning the same redshift of the brightest
galaxy to all galaxies within
the fiber limitation circle, or, in the best cases, a group is identified by
measuring only two redshifts.
.
Basically, these
data are affected by the same problem as LCRS. The identification
of a group is made by assigning the same redshift of the brightest
galaxy to all galaxies within
the fiber limitation circle, or, in the best cases, a group is identified by
measuring only two redshifts.
Since we have shown here that only one candidate group out of 18 has all its members with discordant redshifts, the technique used by the Sloan cannot uniquely identify a compact group. In a similar way, the 2dF survey is affected by limitation due to the fiber diameter; however, many fields have been observed more than once with the fibers in different positions, thus reducing the problem. However, the catalogue created by Merchan & Zandivarez (#Merch&) covers a wide range in redshift (0.003 to 0.25), and the mass range and crossing times also include objects that are much more like loose groups than to compact groups.
Finally, one might object that an average redshift of 0.2 is not
so very high in an epoch where discovery of z = 3 targets is common.
While this is true, it is important to keep in mind that the projected size
of a typical compact group at
![]() ,
1
,
1
![]() corresponds to 13 kpc on the sky, i.e. to a fourth of the typical radius
of a compact group (50 kpc). At
corresponds to 13 kpc on the sky, i.e. to a fourth of the typical radius
of a compact group (50 kpc). At
![]() ,
1
,
1
![]() is already twice
the size of a compact group, and at
is already twice
the size of a compact group, and at ![]() a compact group is spread
over an area of <20
a compact group is spread
over an area of <20
![]() .
To this one must add the increasing fore/background
contamination of other objects, making the task of identifying and
studying compact groups
at higher redshift quite a challenging one.
.
To this one must add the increasing fore/background
contamination of other objects, making the task of identifying and
studying compact groups
at higher redshift quite a challenging one.
Summing up, we can reasonably conclude that, of the existing
surveys of compact groups at intermediate z, the DPOSS II survey and
its spectroscopic follow-up will indeed provide, once completed, an unprecedented
database for the study of compact groups outside the local universe.
The other important question is what the properties of confirmed
DPOSS groups tell us. Having only 11 targets makes it difficult to draw firm conclusions.
However, we can point out what we would expect
if the majority of the DPOSS groups were to show the same characteristics.
The fraction of late type galaxies (
![]() )
and the crossing times
(
)
and the crossing times
(
![]() )
are similar to those measured for Hickson Compact Groups
(
)
are similar to those measured for Hickson Compact Groups
(
![]() ;
;
![]() ), while other group characteristics, like mass,
and velocity dispersion are also very similar.
), while other group characteristics, like mass,
and velocity dispersion are also very similar.
With these results in hand, we might wonder whether we have find an answer to our three questions: with increasing redshift, do we find:
This indeed looks puzzling, since a redshift of z = 0.12 corresponds to a look-back
time of 1.56 Gyr, while our compact groups should have dissolved in 0.21
Gyrs, given their median crossing time of
![]() .
This could mean that either we are looking at a different set of groups
from the one we observe in the nearby Universe, e.g. groups that have already merged by
the present time, leaving a field elliptical or a substructure within a cluster,
or there is something that stabilizes the groups extending their lifetime.
.
This could mean that either we are looking at a different set of groups
from the one we observe in the nearby Universe, e.g. groups that have already merged by
the present time, leaving a field elliptical or a substructure within a cluster,
or there is something that stabilizes the groups extending their lifetime.
This seems to agree well with numerical models that favour an early formation of a common, massive halo within which individual galaxies form (Gomez-Flechoso & Dominguez-Tenreiro 2001). This model, unlike the one proposed by Atahnassoula & Makino (1997), predicts a central concentration for the common halo, in agreement with the observations. Moreover, according to this model, the galaxy interactions perturb the global halo potential and become significant in changing the group only if they are comparable to the global field of force of the halo. This scenario seems consistent with previous findings that individual galaxy properties within the group do not correlate with the group global properties. It must be kept in mind, however, that active groups with a low velocity dispersion, like those present in the Southern Compact Group survey, are still not explained well by this scenario, so that a more detailed investigation is needed to understand the nature of compact groups completely.
Our results suggest that the DPOSS sample, once full redshift information for its members becomes available, will provide a reference sample for studying the properties of compact groups beyond the local universe.
Acknowledgements
It is a pleasure to thank the La Silla Science Operation team for their help during the observations and daytime support. R.R.dC. would like to thank Roy Gal for several insightful discussions on the subject.
This research made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
Table 2: Observed compact groups candidates from the DPOSS survey. Column 5 lists the kind of spectrum for each galaxy: abs means a spectrum which is dominated by absorption lines; em means a spectrum dominated by emission lines and mix a spectrum where both emission and absorption lines are present. The most significant emission lines have been listed for the observed galaxies.
![\begin{figure}\par\includegraphics[width=15cm,clip]{3616fig2a.ps}\end{figure}](/articles/aa/full/2006/03/aa3616-05/Timg131.gif) |
Figure 2:
Acquisition images of the concordant groups. The
orientation is explicitly given for each frame. The individual
galaxies are labelled as in the DPOSS catalogue. Galaxies labelled
with an x followed by a number are objects which fell in
the slit along the target galaxies and turned out to be
concordant with the DPOSS targets. The solid line
at the bottom of each image corresponds to 1
|
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=15cm,clip]{3616fig2b.ps}\end{figure}](/articles/aa/full/2006/03/aa3616-05/Timg132.gif) |
Figure 2: continued. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=15cm,clip]{3616fig3a.ps}\end{figure}](/articles/aa/full/2006/03/aa3616-05/Timg133.gif) |
Figure 3: Spectral atlas of the concordant member galaxies for groups of class A and B. On the x axis there is the wavelength, while on the y axis there are the number counts (ADU). The spectra have been shifted an arbitrary amount for display purpose. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=15cm,clip]{3616fig3b.ps}\end{figure}](/articles/aa/full/2006/03/aa3616-05/Timg134.gif) |
Figure 3: continued. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=15cm,clip]{3616fig3c.ps}\end{figure}](/articles/aa/full/2006/03/aa3616-05/Timg135.gif) |
Figure 3: continued. |
| Open with DEXTER | |
![\begin{figure}\par\includegraphics[width=15cm,clip]{3616fig3d.ps}\end{figure}](/articles/aa/full/2006/03/aa3616-05/Timg136.gif) |
Figure 3: continued. |
| Open with DEXTER | |