A&A 445, 1061-1067 (2006)
DOI: 10.1051/0004-6361:20053140
A. Claret
Instituto de Astrofísica de Andalucía, CSIC, Apartado 3004, 18080 Granada, Spain
Received 28 March 2005 / Accepted 12 September 2005
Abstract
The evolutionary status of the double-lined eclipsing binary EK Cep is reanalysed.
Due to problems with the empirical determination of its effective temperatures, we have
used a different approach to compare the observations with theoretical models: we
have adopted the effective temperature ratio, which is a better determined parameter
from light curve analysis, instead of their
absolute values. Such an approach is supported observationally by
the inconsistency found in the photometric distances for both components of EK Cep.
By using the effective temperature ratio, masses, radii, apsidal-motion rate and
lithium depletion, we have found that standard models are able to fit the physical
properties of EK Cep simultaneously at the same isochrone.
In the case of rotating models, we have also found acceptable solutions
without the need for a very
fast rotating core.
On the other hand, the apsidal-motion rate of EK Cep is
critically revised.
Key words: stars: binaries: eclipsing - stars: evolution - stars: rotation
The eclipsing binary system EK Cephei is a very interesting object to test evolutionary stellar models due to its intrinsic characteristics: 1) it is a double-lined eclipsing binary with accurate determination of absolute dimensions, at least concerning masses and radii; 2) its secondary component is a Pre Main-Sequence star (PMS); 3) the system presents apsidal motion with a high relativistic contribution; 4) lithium has been measured for the less massive mate and 5) an evaluation of the metallicity of the binary is also available. Often, double-lined eclipsing binaries are good candidates to probe the capability of stellar models but never with as high a number of constraints as in the case of EK Cep.
Among the characteristics of EK Cep (Table 1, see Popper 1987 and Andersen 1991),
the most important is probably
the PMS nature of the secondary since it presents low surface gravity
(Popper 1987). This was confirmed later by the lithium determination
obtained by Martín & Rebolo (1993). The theoretical interpretation
of EK Cep is thus a tractable task. Indeed, in 1995 Claret et al. made
the first attempt to explain the evolutionary status, the apsidal-motion
and the lithium depletion of this binary star. They confirmed the secondary
as a PMS star while
the more massive companion seems to be at the begining of the hydrogen-
burning phase. The theoretical apsidal-motion rate was found to be in
good
agreement with the observational data. The level of lithium depletion was also
found to be in agreement with the observations of the secondary while for the primary
Claret et al. (1995) reported no significant depletion. The radii of both components
were approximately fitted at a common age of
![]() 6 years.
To
avoid problems with effective temperature calibration, only isochrones in the
masses
6 years.
To
avoid problems with effective temperature calibration, only isochrones in the
masses![]() radii plane were used.
radii plane were used.
More recently, Yildiz (2003) also analysed the system. Some of his
results will be discussed
in the next sections. Marques et al.
(2004) used a ![]() minimization method to find the best theoretical
models. They were not able, however, to reproduce the radii for both components
simultaneosly for the same isochrone. Given that the evolutionary scenario
is neither clear nor satisfactory, we decided to reanalyse EK Cep using
a new version of our evolution code (Claret 2004) incorporating new input physics
and a different approach to the problem.
minimization method to find the best theoretical
models. They were not able, however, to reproduce the radii for both components
simultaneosly for the same isochrone. Given that the evolutionary scenario
is neither clear nor satisfactory, we decided to reanalyse EK Cep using
a new version of our evolution code (Claret 2004) incorporating new input physics
and a different approach to the problem.
Table 1: Absolute dimensions of EK Cep (solar, cgs, K units).
Our procedure to explain the evolutionary status of EK Cep is different
from that by Yildiz (2003) and by Marques et al. (2004) with regards to
the observed constraints to be used.
The effective temperatures of EK Cep and their respective error bars are
key to model
the system and the mentioned
authors used them as strong constraints to
their solutions. However, in general, effective temperatures are not a direct measurement:
they depend on a previous calibration, based on stellar atmosphere models. The involved
uncertainties are often larger than we obtain simply by interpolating in the
atmosphere grids. If we consider the uncertainties in the opacities, the plane
paralell approach and the adopted extintion law, we conclude that, in some cases,
the error estimation is too low. In the particular case of EK Cep
the situation is even worse: the mass ratio is around 0.5, and as a consequence
there is an intrinsic
difficulty in the determination of the effective temperature for the less massive component,
which is around 10 times fainter than its mate.
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm,clip]{fig1.eps}
\end{figure}](/articles/aa/full/2006/03/aa3140-05/Timg7.gif) |
Figure 1: Percent differences between the photometric distances for the individual components of detached eclipsing binaries. Note the position of EK Cep. The data are taken from Ribas et al. (1998). |
| Open with DEXTER | |
To reinforce those difficulties we plot in Fig. 1 the relative differences between the individual photometric distances for some detached eclipsing binaries taken from the work by Ribas et al. (1998). The inconsistency found for both components of EK Cep is notorious and the distances obtained for each individual component differ by around 10%. This is the largest discrepancy found in the sample. This may indicate some problems with the absolute dimensions of this binary (and with other systems too). The radii are often well measured parameters in detached eclipsing binaries and do not depend on previous calibrations. The same does not apply to the effective temperatures. As already mentioned, the effective temperatures are strongly dependent on calibrations. In the case of EK Cep this limitation may be even larger given the PMS nature of the secondary because the calibration of PMS stars does not have similar observational/theoretical support as for normal main-sequence stars. Popper (1987) reported some anomalies in the secondary of EK Cep, such as an excess of radiation in the B band or discrepancies between (B-V) and (V-R).
The determination of the effective temperature of the primary also presents
similar problems:
![]() (photometry) is about 7% larger than
(photometry) is about 7% larger than
![]() (Hipparcos).
From these results we conclude that the effective temperatures are not,
in this case, a good selection to constrain the theoretical models.
In fact, the difficulties with the effective temperatures seem to be a common general trend:
eclipsing binaries present the largest internal scattering when
used as distance indicators, as pointed out by Alves (2004). This indicates that
a serious and systematic problem may be present in the determination of the effective
temperatures of such stars.
However, even if the
effective temperatures are not well determined (mainly concerning the error bars)
they still can be used to constrain the models for EK Cep. We decided to use the effective
temperature ratio
(Hipparcos).
From these results we conclude that the effective temperatures are not,
in this case, a good selection to constrain the theoretical models.
In fact, the difficulties with the effective temperatures seem to be a common general trend:
eclipsing binaries present the largest internal scattering when
used as distance indicators, as pointed out by Alves (2004). This indicates that
a serious and systematic problem may be present in the determination of the effective
temperatures of such stars.
However, even if the
effective temperatures are not well determined (mainly concerning the error bars)
they still can be used to constrain the models for EK Cep. We decided to use the effective
temperature ratio
![]() /
/
![]() ,
instead of their absolute values, since this ratio is determined much more
accurately from the light curve analysis and is free from calibrations.
,
instead of their absolute values, since this ratio is determined much more
accurately from the light curve analysis and is free from calibrations.
In Claret et al. (1995) we did not directly use the effective temperatures in
order to avoid problems with calibrations and an acceptable solution was found for
(X, Z)=(0.705, 0.015) using the observed masses and radii as contraints. However, in the past
10 years, the
input physics of our code of stellar evolution has
changed drastically: the opacities, the nuclear network, the mass loss rates and the mass range
for which the models are computed. For radiative opacities we have adopted the
calculations by Iglesias & Rogers (1996) completed with Alexander & Ferguson (1994) results
for lower temperatures. A more elaborated nuclear network with up to 47 isotopes can also be
used for the production/destruction of light elements or when more advanced stages
of nucleosynthesis are required.
The Sun was calibrated by using
![]() .
For a more detailed description of the code, see Claret (2004). For the present study, in order
to guarantee more precise calculations we have
restricted the triangle used to define an envelope in the HR diagram to
.
For a more detailed description of the code, see Claret (2004). For the present study, in order
to guarantee more precise calculations we have
restricted the triangle used to define an envelope in the HR diagram to
![]() and
and
![]() or smaller.
or smaller.
Before computing the stellar models for both components of EK Cep it is crucial
to define clearly which observational parameters will be used as constraints. Here
we shall adopt the masses,
the radii and the effective temperature ratio, as explained above. Also, we will restrict models
around
![]() ,
as given by Martín & Rebolo (1993). The apsidal-motion and the
lithium depletion will be treated after obtaining an acceptable solution. A key
question is whether we should use rotating or non-rotating models. Given that all stars rotate,
rotating models should be preferred. However, the effects of rotation do not seem
to be important
for the present evolutionary status of EK Cep (given that no
significant oblateness in the light curves is observed (Hill & Ebbighausen 1984) which
implies that the components
are well within their
Roche lobes and they are not fast rotators). Moreover, it will be interesting to explore the
capability of standard models to predict the physical properties of EK Cep.
,
as given by Martín & Rebolo (1993). The apsidal-motion and the
lithium depletion will be treated after obtaining an acceptable solution. A key
question is whether we should use rotating or non-rotating models. Given that all stars rotate,
rotating models should be preferred. However, the effects of rotation do not seem
to be important
for the present evolutionary status of EK Cep (given that no
significant oblateness in the light curves is observed (Hill & Ebbighausen 1984) which
implies that the components
are well within their
Roche lobes and they are not fast rotators). Moreover, it will be interesting to explore the
capability of standard models to predict the physical properties of EK Cep.
As already mentioned, the primary component is at the begining of the hydrogen-burning phase.
At this stage, stars evolve with almost constant radius. This makes it
difficult to determine the stellar age. For both components of EK Cep we have found that,
for
(X, Z) = (0.7075, 0.0175),
a mixing-length parameter
![]() and
no core overshooting (because its effects are not important here), the
radii and the effective temperature ratio TR are on the same isochrone (Fig. 2).
We have used a modified
and
no core overshooting (because its effects are not important here), the
radii and the effective temperature ratio TR are on the same isochrone (Fig. 2).
We have used a modified ![]() method to obtain the present solution.
The derived age is around
method to obtain the present solution.
The derived age is around
![]() years, a value larger than that derived
in the 1995 paper. The fitting is acceptable and within the uncertainties. Similar solutions -
or more refined ones - may be found by varying slightly
the input physics of the models. The relative success of the theoretical
predictions are not only due to the models. The selection of the observational
parameters used to constrain the solutions was a key piece of information.
years, a value larger than that derived
in the 1995 paper. The fitting is acceptable and within the uncertainties. Similar solutions -
or more refined ones - may be found by varying slightly
the input physics of the models. The relative success of the theoretical
predictions are not only due to the models. The selection of the observational
parameters used to constrain the solutions was a key piece of information.
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{fig2.eps}
\end{figure}](/articles/aa/full/2006/03/aa3140-05/Timg16.gif) |
Figure 2: Theoretical standard models for EK Cep (without rotation). The upper panel shows the radius of the models as a function of the age (continuous line represents the primary and dashed line denotes the secondary). The middle panel shows the effective temperature ratio TR. The bottom panel presents the apsidal-motion constants for EK Cep. Note that there is an acceptable agreement between radii and TR for a same isochrone (vertical lines). The horizontal lines represent the error bars. |
| Open with DEXTER | |
We do not consider the solution shown in Fig. 2 as a definitive one. However,
standard models are also capable of predicting the absolute
dimensions of EK Cep without
the need to introduce a very fast rotating core (with all its problems discussed
in the next
section). Within this approach, let us investigate the apsidal-motion rate.
For clarity, we write down the basic equations, say, the Radau differential equation:
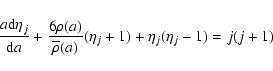 |
(1) |
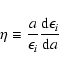 |
(2) |
and the relationship between a and r is
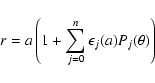 |
(3) |
where a is the mean radius of a given equipotential, ![]() is the
mass density at the distance a from the center,
is the
mass density at the distance a from the center,
![]() is the mean mass density within a sphere of radius a,
is the mean mass density within a sphere of radius a,
![]() are the Legendre polynomials and
are the Legendre polynomials and
![]() describes the amplitude of the
distortions. The kj are computed using the equation
describes the amplitude of the
distortions. The kj are computed using the equation
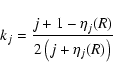 |
(4) |
where
![]() is the value at the surface of the model. Because the contributions
for j =3 and 4 are small, we retain only the term with j=2.
is the value at the surface of the model. Because the contributions
for j =3 and 4 are small, we retain only the term with j=2.
![\begin{figure}
\par\includegraphics[width=8.8cm,height=8cm,clip]{fig3.ps}
\end{figure}](/articles/aa/full/2006/03/aa3140-05/Timg26.gif) |
Figure 3:
Apsidal-motion constant k2 as a function of time for a 1.12 |
| Open with DEXTER | |
Yildiz (2003) used the Kopal (1978) approximation
to obtain the theoretical k2.
The approach is a very important point that restricts his analysis. Some time ago,
Claret & Giménez (1989) showed that if the Kopal approximation is used,
instead of the appropriate Radau differential equation, a systematic deviation is
detected. Since Kopal assumed a priori that
![]() -
where
-
where ![]() is the local density and
is the local density and
![]() is the mean density of a
given stellar configuration - the values of k2 obtained using such an approximation
will be systematically smaller than those derived from the Radau equation, i.e.,
the Kopal approach gives more centrally condensed configurations. In Fig. 3
these effects can be seen. The continuous line represents the apsidal-motion constant k2 for
a standard model for EK CepB by integrating the Radau differential equation, and the dashed
one that computed following the Kopal approach. The differences can be as high as
0.20 dex. The actual level of refinement in the apsidal-motion investigation is
almost a order of magnitud better than these differences (Claret & Willems 2002).
is the mean density of a
given stellar configuration - the values of k2 obtained using such an approximation
will be systematically smaller than those derived from the Radau equation, i.e.,
the Kopal approach gives more centrally condensed configurations. In Fig. 3
these effects can be seen. The continuous line represents the apsidal-motion constant k2 for
a standard model for EK CepB by integrating the Radau differential equation, and the dashed
one that computed following the Kopal approach. The differences can be as high as
0.20 dex. The actual level of refinement in the apsidal-motion investigation is
almost a order of magnitud better than these differences (Claret & Willems 2002).
Let us evaluate the theoretical weighted
![]() which
will be useful to compare with the observational one:
which
will be useful to compare with the observational one:
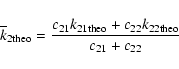 |
(5) |
![\begin{displaymath}{c_{2 i}} = \left[ \left({\Omega_{i}\over{\Omega_{K}}}\right)...
...i}\over{m_{i}}}g(e)
\right]
{\left({R_{i}\over{A}}\right)^{5}}
\end{displaymath}](/articles/aa/full/2006/03/aa3140-05/img32.gif) |
(6) |
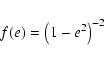 |
(7) |
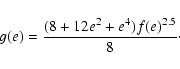 |
(8) |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{fig4.eps}
\end{figure}](/articles/aa/full/2006/03/aa3140-05/Timg39.gif) |
Figure 4: The same as for Fig. 2 but taking into account solid rotation. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{fig5.eps}
\end{figure}](/articles/aa/full/2006/03/aa3140-05/Timg40.gif) |
Figure 5: The same as for Fig. 2 but taking into account rotation with local conservation of the angular momentum. |
| Open with DEXTER | |
The observed k2 is related to the observed apsidal-motion rate:
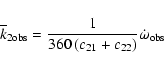 |
(9) |
where
![]() is the observed apsidal-motion constant to be compared with
its theoretical value, given by Eq. (5). Before such a comparison, the relativistic
contribution must be evaluated following Levi-Civita (1937)
is the observed apsidal-motion constant to be compared with
its theoretical value, given by Eq. (5). Before such a comparison, the relativistic
contribution must be evaluated following Levi-Civita (1937)
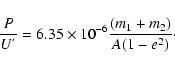 |
(10) |
Although the observed lithium depletion was not measured with high accuracy, we obtained for the secondary a depletion of 0.15 dex, approximately the same amount derived in the 1995 paper, which is within the uncertainty limits given by Martín & Rebolo (1993).
The method used here to simulate rotation differs from that used by Yildiz (2003) mainly concerning
how the differential equations are modified. A more detailed description and numerical details
can be found in Kippenhahn & Thomas (1970), Endal & Sofia (1976) and Claret (1999).
We restricted the calculation to first order theory. Thus the total potential can be
written (Kopal 1959)
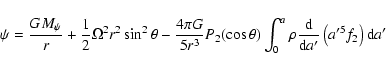 |
(11) |
where
| (12) |
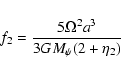 |
(13) |
![]() is the angular velocity, P2(
is the angular velocity, P2(
![]() )
is the second Legendre polynomial,
a the radius of the level surface,
)
is the second Legendre polynomial,
a the radius of the level surface, ![]() is connected with Radau's equation (Eq. (2)), and the
remaining symbols have their usual meaning.
is connected with Radau's equation (Eq. (2)), and the
remaining symbols have their usual meaning.
The differential equations of the structure are changed as follows:
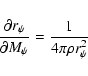 |
(14) |
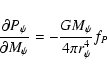 |
(15) |
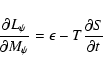 |
(16) |
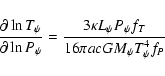 |
(17) |
and the Schwarzschild criterion is given by:
![\begin{displaymath}{\partial \ln T_{\psi}\over{\partial \ln P_{\psi}}} = {\rm mi...
...rm ad},
{\bigtriangledown_{\rm rad}}{f_{T}\over {f_P}}\right]
\end{displaymath}](/articles/aa/full/2006/03/aa3140-05/img56.gif) |
(18) |
where
![]() and
and
![]() are the spherical
adiabatic and radiative gradients.
The atmospheric factor PGM/(
are the spherical
adiabatic and radiative gradients.
The atmospheric factor PGM/(![]() R2
R2![]() )
is also changed by fP, which is
considered constant for the whole atmosphere and equal to that of the last point of the envelope.
On the other hand, the factors fP and fT are
given by
)
is also changed by fP, which is
considered constant for the whole atmosphere and equal to that of the last point of the envelope.
On the other hand, the factors fP and fT are
given by
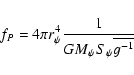 |
(19) |
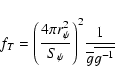 |
(20) |
To compute fP and fT one has to know the relationship between a and ![]() .
The radius of a sphere with equivalent volume is related to the radius of the level surface by
.
The radius of a sphere with equivalent volume is related to the radius of the level surface by
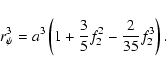 |
(21) |
Recently Yildiz (2003) proposed that rotating models could explain the physical properties of EK Cep. In that paper he concluded that only if the primary presents a rotating rapid core, can an acceptable solution be found. However, his method to introduce rotation may be not adequate because the only differential equation of the stellar structure which is changed is the hydrostatic one (Kippenhahn et al. 1970). Using such an approximation the oblatness effects are neglected.
Here we define the laws of angular momentum conservation to be adopted. We are implementing the fourth order differential equation which governs the evolution of the angular velocity (see for example, Zahn 1992) but the results are still preliminary and will not be considered here. We shall select two laws: 1) solid body rotation and 2) local conservation of angular momentum. Such laws are limits since for the first one the redistribution of the angular momentum is complete while for the second there is no redistribution. A more realistic treatment is expected to give intermediate results. Thus, both laws will serve as a good control for the calculations. We note that the transport of angular momentum due to rotationally-induced instabilities will not be considered because the related diffusion equation is coupled to the differential equation for the evolution of the angular velocity.
Case 1) The calculations of rotating models were carried out by introducing
some numerical tolerances (for example, the number of shells was larger than 4000) in order to guarantee
the conservation of the angular momentum. In order to get the rotating model displaying the observed
rotational velocity for each component of EK Cep we have used trial models until
the equatorial velocity is the same as that observed for both components. As EK Cep
is not a very distorted system, the effects of rotation are expected to be not large.
The factors fP and fT at the
surface are not very different from 1. We have used the same input physics (no core overshooting, no mass loss, etc.) as that for the standard models except for the mixing-length parameter (
![]() ).
The agreement can be considered as good (Fig. 4) and the radii and effective temperature ratio can
be fitted by the same isochone simultaneously (
).
The agreement can be considered as good (Fig. 4) and the radii and effective temperature ratio can
be fitted by the same isochone simultaneously (
![]() 6 years). Note that other solutions
are also
possible but they were not taken into account because the effective temperature ratio requirement
was not fulfilled. Solid body rotation, although it is a very simple approach,
is capable of predicting the properties of EK Cep without need for a rapidly rotating core. Moreover,
as we will see below, it is not fully incompatible with the results from helioseismology. The
theoretical individual values of k2 inferred from
the last panel of Fig. 4 give, according Eq. (1),
6 years). Note that other solutions
are also
possible but they were not taken into account because the effective temperature ratio requirement
was not fulfilled. Solid body rotation, although it is a very simple approach,
is capable of predicting the properties of EK Cep without need for a rapidly rotating core. Moreover,
as we will see below, it is not fully incompatible with the results from helioseismology. The
theoretical individual values of k2 inferred from
the last panel of Fig. 4 give, according Eq. (1),
![]() ,
which is in agreement with observations (log
,
which is in agreement with observations (log
![]() ). The depletion of lithium in the secondary component is of the same order as that for
non-rotating models and also is in agreement with the observational data
and their respective uncertainties.
). The depletion of lithium in the secondary component is of the same order as that for
non-rotating models and also is in agreement with the observational data
and their respective uncertainties.
Case 2) Other series of models were computed by assuming local conservation of the angular momentum.
The results can be seen in Fig. 5. By inferring the values of k2 in the
third panel of Fig. 5 we obtain log
![]() at an age of
at an age of
![]() years, which is also in agreement with observations. The results concerning
radii, effective temperature ratio, apsidal-motion rate and lithium depletion are very similar
regardless of whether the models were computed without rotation, with solid rotation or local
conservation of the angular momentum. This is due to the fact that the rotating models are not
considerably perturbed by rotation in this case. Probably, the best results would be obtained
from an intermediary formulation, as for example the integration the differential equation of the
transport of angular momentum. However, case 2
can be used to verify the values obtained by Yildiz (2003) with respect to
the ratio of core/envelope rotation rate. Our results differ mainly in two
aspects: first, there is no discontinuities in the angular velocities inside
any model and second, we have not detected differences as large as 65 times
between the envelope and the nucleus. The ratio of angular rotation is always
smaller (one order of magnitude) than this. If one uses
the fourth order differential equation governing the transport of angular momentum coupled with
the diffusion one, the ratio is still smaller than found in case 2.
years, which is also in agreement with observations. The results concerning
radii, effective temperature ratio, apsidal-motion rate and lithium depletion are very similar
regardless of whether the models were computed without rotation, with solid rotation or local
conservation of the angular momentum. This is due to the fact that the rotating models are not
considerably perturbed by rotation in this case. Probably, the best results would be obtained
from an intermediary formulation, as for example the integration the differential equation of the
transport of angular momentum. However, case 2
can be used to verify the values obtained by Yildiz (2003) with respect to
the ratio of core/envelope rotation rate. Our results differ mainly in two
aspects: first, there is no discontinuities in the angular velocities inside
any model and second, we have not detected differences as large as 65 times
between the envelope and the nucleus. The ratio of angular rotation is always
smaller (one order of magnitude) than this. If one uses
the fourth order differential equation governing the transport of angular momentum coupled with
the diffusion one, the ratio is still smaller than found in case 2.
As previously commented, Yildiz (2003) finds an acceptable solution only if the core - containing 52% of the total masses - rotates 65 times faster than the outer layers. The question is: is such a redistribution of angular velocity possible for EK CepA, which is a very young star? Had this component enough time to achieve such a fast core (that does not coincide necessarily with its smaller convective core)? The only observational evidence of stellar internal rotation comes from the Sun (see for example Schou et al. 1998; Chaplin et al. 1999; for a more extensive and updated review see Thompson et al. 2003). The distribution of angular velocities obtained from helioseismologic studies indicates that there are no large differences between surface and interior. Of course, there is a latitude dependence but the maximum ratio is around 1.4 times (Fig. 7 by Thomson et al. 2003). Theoretical calculations also reinforce the scenario of a rather flat distribution of angular velocities, as we have seen. Therefore, the angular velocity distribution assumed by Yildiz (nucleus rotating 65 times faster than the surface) seems to be not supported by observational and theoretical evidence. A fast rotating core, but smaller than 52% of the total mass, may be present in the primary only for much more evolved models.
The profile of internal rotation
postulated by Yildiz also yields some
difficulties. In the boundary core-envelope the drastic change
of the angular velocity (
![]() rad s-1 to
rad s-1 to
![]() rad s-1) may introduce some
kind of instability.
rad s-1) may introduce some
kind of instability.
In addition, a fast rotating nucleus would change the dynamics of the system, altering the rate of apsidal-motion. Indeed, Dicke (1970) invoked such a possibility to explain the advance of the perihelion of Mercury as due to the presence of a fast rotating core in the Sun.
Although we are able to model EK Cep without the need for a rapid rotating core, some uncertainties still remain and we do not consider the solutions presented here as definitive ones. The aim of the present paper is to show that standard stellar models (or rotating ones without the need for a very fast rotating core) are capable of fitting the observational properties of EK Cep, including radius, masses, effective temperature ratio and apsidal-motion rate. We estimate that the accuracy of our solution is around 5-10%.
The system should be reobserved both photometrically (preferently with Strömgren filters) and spectroscopically in order to reduce the observational uncertainties. But the theoretical aspects should also be worked out. Neverthless, large discrepancies between observations and theoretical prediction are found in double-lined eclipsing binaries whith a low mass ratio. This suggests that, apart from the intrinsic difficulties in determining the individual absolute dimensions for the less luminous component, some kind of physical process may occur during the formation and evolution of the system. A key question arises: is the chemical composition equally distributed between both components, as usually assumed? The distribution of light elements in the solar system indicates that there segregation between massive and not massive bodies. Can a similar physical process act also in the case of eclipsing binaries with low mass ratio? This possibility should be investigated more closely.
Acknowledgements
The author thanks J. Fernandes, I. Ribas and L. F. Miranda for many useful comments which helped to improve the manuscript. The Spanish MCYT (AYA2003-04651) is gratefully acknowledged for its support during this work.