A&A 445, 485-491 (2006)
DOI: 10.1051/0004-6361:20053686
On the structure of globular cluster systems in elliptical galaxies
K. Bekki
1 -
D. A. Forbes2
1 - School of Physics, University of New South Wales,
Sydney 2052, NSW, Australia
2 -
Centre for Astrophysics and Supercomputing,
Swinburne University of Technology, Mail H39, PO Box 218,
Hawthorn, VIC 3122, Australia
Received 23 June 2005 / Accepted 14 September 2005
Abstract
It has long been known that the radial density profiles of
globular cluster systems (GCSs) in elliptical galaxies
vary with the total luminosities of their host galaxies.
In order to elucidate the origin of this structural non-homology
in GCSs, we numerically investigate the structural properties
of GCSs in elliptical galaxies formed from a sequence of
major dissipationless galaxy merging.
We find that the radial density profiles of GCSs
in elliptical galaxies become progressively flatter as the galaxies
experience more major merger events.
The density profiles of GCSs in ellipticals are well described as power-laws
with slopes (
 )
ranging from -2.0 to -1.0.
They are flatter than,
and linearly proportional to, the slopes (
)
ranging from -2.0 to -1.0.
They are flatter than,
and linearly proportional to, the slopes (
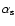 )
of the stellar density profiles
of their host galaxies.
We also find that the GCS core radii (
)
of the stellar density profiles
of their host galaxies.
We also find that the GCS core radii (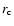 )
of the density profiles
are larger in ellipticals that experienced more mergers.
By applying a reasonable scaling relation between luminosities and sizes of galaxies
to the simulation results,
we show that
)
of the density profiles
are larger in ellipticals that experienced more mergers.
By applying a reasonable scaling relation between luminosities and sizes of galaxies
to the simulation results,
we show that
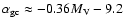 ,
,
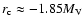 ,
and
,
and
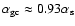 ,
where
,
where 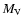 is the total V-band absolute magnitude of a galaxy.
We compare these predictions with observations
and discuss their physical meaning.
We suggest that the origin of structural non-homology of GCSs
in ellipticals can be understood in terms of the growth
of ellipticals via major dissipationless galaxy merging.
is the total V-band absolute magnitude of a galaxy.
We compare these predictions with observations
and discuss their physical meaning.
We suggest that the origin of structural non-homology of GCSs
in ellipticals can be understood in terms of the growth
of ellipticals via major dissipationless galaxy merging.
Key words: Galaxy: globular clusters: general - galaxies: star clusters -
galaxies: elliptical and lenticular, cD -
galaxies: evolution -
galaxies: interactions
The structural properties of globular cluster systems (GCSs)
in galaxies have long been suggested to
contain fossil information on the early dynamical histories
of galaxies and has accordingly been investigated both
observationally and theoretically (e.g., Harris 1986, 1991).
In particular, radial density profiles of GCSs and their
correlations with physical properties of their host galaxies
have been discussed
in terms of formation and evolution of elliptical galaxies
(e.g., Harris 1986; Zepf & Ashman 1993; Ashman & Zepf 1998;
Forbes et al. 1996, 1997;
Bekki et al. 2002, 2003).
In particular, observational studies found that the
GCSs in early-type galaxies were less centrally concentrated than
the stellar light of the host galaxy
(e.g., Harris & Racine 1979; Strom et al. 1981; Grillmair
et al. 1994; Forbes et al. 1996), and that the outer slope of the GCS
density profile correlated with the host galaxy luminosity
(e.g., Ashman & Zepf 1998; Harris 1986).
Major galaxy merging between equal-mass disk galaxies
has long been considered to be a promising formation scenario
for elliptical galaxy formation (e.g., Toomre 1977).
Although this galaxy formation scenario has been discussed in many
contexts (e.g., the color-magnitude relation),
it has not been extensively
investigated in terms of whether it can self-consistently explain
the observed properties of GCSs around ellipticals.
So far, only the observed higher specific frequency (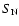 )
and
bimodal color distributions of GCSs have been discussed in terms
of hierarchical galaxy formation (Beasley et al. 2002).
It is thus unknown what implications the observed structural
properties of GCSs in ellipticals has for galaxy formation.
)
and
bimodal color distributions of GCSs have been discussed in terms
of hierarchical galaxy formation (Beasley et al. 2002).
It is thus unknown what implications the observed structural
properties of GCSs in ellipticals has for galaxy formation.
The purpose of this paper is to propose
that the radial density profiles of GCSs in elliptical galaxies
have fossil information on how often ellipticals
have experienced major merger events in their dynamical histories.
By using dissipationless N-body
simulations of major merging of galaxies,
we investigate how the structural properties of GCSs in elliptical
galaxies change as they grow by successive (gas-free) mergers.
We compare our theoretical predictions with
observations to discuss the origin of the observational
trends. We also briefly discuss the role of GC accretion.
In particular, we focus on the luminosity-dependence of
the GCS slope (
 )
which implies a "non-homology'' in the structural properties
of GCSs.
)
which implies a "non-homology'' in the structural properties
of GCSs.
We investigate the dynamical evolution of GCSs
of elliptical galaxies formed from sequential dissipationless major merging
based on numerical simulations
carried out on the GRAPE
board (Sugimoto et al. 1990) in GRAPE 5 systems.
We here stress that the roles of minor merging/accretion of GC in
shaping radial density profiles of GCSs in galaxies are not
extensively investigated in the present models.
We adopt the following merging scheme to model
elliptical galaxy formation through sequential major equal-mass disk mergers.
First an elliptical galaxy is formed by major merging
between two equal-mass disk galaxies.
We refer to the remnant elliptical galaxy as the 1st-generation
elliptical.
This 1st-generation elliptical then merges with other
1st-generation one to form the 2nd-generation
elliptical.
This sequential major merging can repeat for
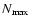 times, and the structural
properties of stellar components and GCSs are investigated
for each ith generation elliptical (
times, and the structural
properties of stellar components and GCSs are investigated
for each ith generation elliptical (
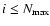 ).
The total particle number used
is 27 670 for the simulations of the 1st-generation elliptical
and 221 360 for those of the 4th-generation one (i.e.,
).
The total particle number used
is 27 670 for the simulations of the 1st-generation elliptical
and 221 360 for those of the 4th-generation one (i.e.,
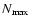 of 4).
The initial total particle number for GCs is set to be 1000,
because an order of 1000 (not 10 or 100) is necessary to make robust
predictions for the radial profiles of structure and kinematics of GCSs
in galaxies (Bekki et al. 2005).
of 4).
The initial total particle number for GCs is set to be 1000,
because an order of 1000 (not 10 or 100) is necessary to make robust
predictions for the radial profiles of structure and kinematics of GCSs
in galaxies (Bekki et al. 2005).
Since the numerical methods and techniques we employ for modeling
dynamical evolution of galaxy mergers with GCs
have already been described in detail
elsewhere (Bekki et al. 2002, 2005), we give only a brief review here.
The progenitor disk galaxies that take part in a merger
(for the 1st-generation elliptical) are assumed to
have a dark halo, a bulge, a stellar halo, a thin exponential disk,
and a GCS.
The total disk mass and size are 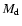 and
and 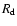 ,
respectively.
Henceforth, all masses are measured in units of
,
respectively.
Henceforth, all masses are measured in units of 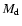 and distances in units of
and distances in units of 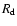 ,
unless otherwise specified.
We adopt the density distribution of the NFW
halo (Navarro et al. 1996) suggested from CDM simulations:
,
unless otherwise specified.
We adopt the density distribution of the NFW
halo (Navarro et al. 1996) suggested from CDM simulations:
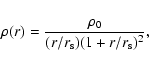 |
(1) |
where r, 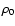 ,
and
,
and 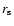 are
the spherical radius, the central density of a dark halo, and the scale
length of the halo, respectively.
The dark matter to disk mass ratio is fixed at 9 for all models.
The value of
are
the spherical radius, the central density of a dark halo, and the scale
length of the halo, respectively.
The dark matter to disk mass ratio is fixed at 9 for all models.
The value of 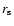 (typically
(typically 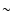 3
3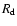 )
is chosen such that
the rotation curve of the disk is reasonably consistent with
observations for a given bulge mass.
We adopt
the R1/4 profile for the bulge with the
mass of 0.17 and a scale length of 0.04
)
is chosen such that
the rotation curve of the disk is reasonably consistent with
observations for a given bulge mass.
We adopt
the R1/4 profile for the bulge with the
mass of 0.17 and a scale length of 0.04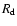 .
The radial (R) and vertical (Z) density profiles
of the disk are assumed to be
proportional to
.
The radial (R) and vertical (Z) density profiles
of the disk are assumed to be
proportional to
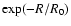 with scale length
with scale length
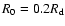 and to
and to
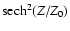 with scale length
with scale length
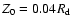 in our units, respectively.
in our units, respectively.
The GCSs in the progenitor spirals have a spherical distribution with
a density profile of
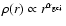 .
We adopt
.
We adopt
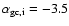 for most models (however
the dependence of the final radial profiles of GCSs in mergers
on
for most models (however
the dependence of the final radial profiles of GCSs in mergers
on
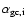 is also investigated).
The adopted density profile of
is also investigated).
The adopted density profile of
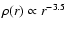 is
consistent with that observed for the Galactic GCS
(Djorgovski & Meylan 1994). The GCS of M 31 reveals a similar
surface density distribution to the Milky Way GCS
(e.g. Battistini et al. 1993). Very little is known about the
density profile of GCSs in other spirals.
The velocity dispersion of a GCS is assumed to be isotropic
which is consistent with the observations of the Galactic GCS
(e.g., Freeman 1993).
is
consistent with that observed for the Galactic GCS
(Djorgovski & Meylan 1994). The GCS of M 31 reveals a similar
surface density distribution to the Milky Way GCS
(e.g. Battistini et al. 1993). Very little is known about the
density profile of GCSs in other spirals.
The velocity dispersion of a GCS is assumed to be isotropic
which is consistent with the observations of the Galactic GCS
(e.g., Freeman 1993).
The simulations
are dissipationless so no new GCs form in the merging
process. Thus our simulations are more appropriate for relatively
gas-free mergers which may be expected to occur at some late epochs.
Recently, observational studies by Bell et al. (2005)
have demonstrated that
present day spheroidal galaxies with
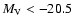 on average have undergone
between 0.5 and 1 major "dry merger'' (i.e., gas-poor mergers)
since
on average have undergone
between 0.5 and 1 major "dry merger'' (i.e., gas-poor mergers)
since 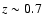 .
This observational paper thus suggests that the dissipationless
merger models adopted in the present paper can be reasonable
for elliptical galaxy formation.
Proto-GCs have been observed to form in late epoch
mergers (e.g. Whitmore & Schweizer 1995),
which implies that some fraction
of GCs in ellipticals could be quite young.
However, latest observational studies
(e.g. Cohen et al. 1998, 2003;
Forbes et al. 2001; Kuntschner et al. 2002; Beasley et al. 2004;
Strader et al. 2004; Pierce et al. 2005), in which
more reliable age estimation of GCs can be done based on
the higher resolution spectra and the improved stellar population
synthesis model,
have demonstrated that the vast bulk of GCs
in early-type galaxies are very old, i.e.
.
This observational paper thus suggests that the dissipationless
merger models adopted in the present paper can be reasonable
for elliptical galaxy formation.
Proto-GCs have been observed to form in late epoch
mergers (e.g. Whitmore & Schweizer 1995),
which implies that some fraction
of GCs in ellipticals could be quite young.
However, latest observational studies
(e.g. Cohen et al. 1998, 2003;
Forbes et al. 2001; Kuntschner et al. 2002; Beasley et al. 2004;
Strader et al. 2004; Pierce et al. 2005), in which
more reliable age estimation of GCs can be done based on
the higher resolution spectra and the improved stellar population
synthesis model,
have demonstrated that the vast bulk of GCs
in early-type galaxies are very old, i.e. 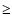 10 Gyrs.
These suggest that
pre-existing GCs dominate in old merger remnants.
10 Gyrs.
These suggest that
pre-existing GCs dominate in old merger remnants.
In all of the simulations, the orbit of the two galaxies is set to be
initially in the xy plane and the distance between
the center of mass of the two
is assumed to be 6 in our units.
The pericenter distance (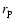 )
and the eccentricity (
)
and the eccentricity (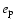 )
in a merger
are assumed to be free parameters that control
orbital energy and angular momentum of the merger.
The spin of each galaxy in a merger
is specified by two angles
)
in a merger
are assumed to be free parameters that control
orbital energy and angular momentum of the merger.
The spin of each galaxy in a merger
is specified by two angles
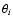 and
and
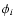 ,
where suffix i is used to identify each galaxy.
Here
,
where suffix i is used to identify each galaxy.
Here
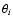 is the angle between the z axis and the vector of
the angular momentum of a galaxy, and
is the angle between the z axis and the vector of
the angular momentum of a galaxy, and
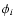 is the azimuthal angle measured from the x axis to
the projection of the angular momentum vector of a galaxy onto the xy plane.
We specifically show four
different and representative models of merger sequences with
is the azimuthal angle measured from the x axis to
the projection of the angular momentum vector of a galaxy onto the xy plane.
We specifically show four
different and representative models of merger sequences with
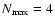 in which merger pairs take one of the following orbital configurations
(i.e., galaxy inclinations with respect to the orbital plane):
A prograde-prograde model represented by "PP''
with
in which merger pairs take one of the following orbital configurations
(i.e., galaxy inclinations with respect to the orbital plane):
A prograde-prograde model represented by "PP''
with
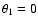 ,
,
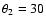 ,
,
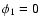 ,
,
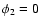 ,
,
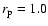 ,
and
,
and
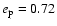 a retrograde-retrograde ("RR'')
with
a retrograde-retrograde ("RR'')
with
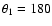 ,
,
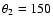 ,
,
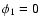 ,
,
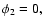
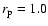 ,
and
,
and
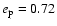 and a highly
inclined model ("HI'') with
and a highly
inclined model ("HI'') with
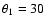 ,
,
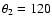 ,
,
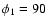 ,
and
,
and
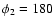 ,
,
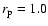 ,
,
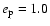 and the low orbital angular momentum model ("LA'')
with
and the low orbital angular momentum model ("LA'')
with
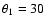 ,
,
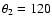 ,
,
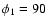 ,
and
,
and
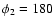 ,
,
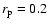 ,
,
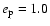 .
.
In analyzing the projected radial density profiles of GCs (
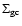 )
and stars (
)
and stars (
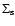 ), we assume that
they are approximated as
), we assume that
they are approximated as
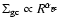 and
and
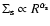 ,
where R is the projected distance from the center of a galaxy.
We derive the slopes of
,
where R is the projected distance from the center of a galaxy.
We derive the slopes of
 and
and
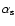 and the difference of the two
and the difference of the two
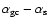 ,
for
,
for
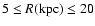 so that the derived values
can be directly compared with observations.
We determine a core radius (
so that the derived values
can be directly compared with observations.
We determine a core radius (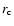 )
for the GCS
by adopting an isothermal profile of the form
)
for the GCS
by adopting an isothermal profile of the form
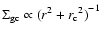 ,
which can
be directly compared to the observations of Forbes et al. (1996).
For an isothermal profile
,
which can
be directly compared to the observations of Forbes et al. (1996).
For an isothermal profile 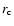
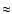
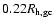 ,
where
,
where
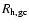 is a half-number radius of the GCS.
In order to estimate the total V-band magnitude of a merger remnant,
we assume an initial disk mass of
is a half-number radius of the GCS.
In order to estimate the total V-band magnitude of a merger remnant,
we assume an initial disk mass of
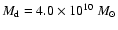 ,
an initial disk size of
,
an initial disk size of
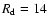 kpc and
kpc and
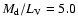 ,
where
,
where 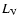 is the total V-band
luminosity of the initial disk.
The remnant's total mass is
is the total V-band
luminosity of the initial disk.
The remnant's total mass is
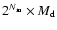 ,
where
,
where 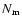 is total number of major merger events that
the remnant elliptical experienced.
is total number of major merger events that
the remnant elliptical experienced.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f1.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg74.gif) |
Figure 1:
Dependences of projected number distributions of stars (thin)
and GCs (thick) in merger remnants (i.e., elliptical galaxies)
on the total number of major
merger events (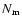 )
which an elliptical experienced during its formation.
For clarity, the density distributions are normalized to
their central values.
Thin dotted lines represent power-law slopes ( )
which an elliptical experienced during its formation.
For clarity, the density distributions are normalized to
their central values.
Thin dotted lines represent power-law slopes (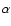 )
of )
of
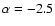 ,
-2.0, -1.5, and -1.0.
Note that the density profiles of GCSs become flatter
for larger ,
-2.0, -1.5, and -1.0.
Note that the density profiles of GCSs become flatter
for larger 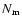 ,
i.e. more mergers. ,
i.e. more mergers. |
| Open with DEXTER |
All the calculations related to the above dissipationless evolution
have been carried out on a GRAPE
board (Sugimoto et al. 1990) in the GRAPE 5 system
at the National Astronomical Observatory of Japan.
The parameter of gravitational softening for
stellar particles is set to be fixed at 0.039 in our
units (0.68 kpc). The time integration of
the equation of motion is performed by using the 2nd-order leap-flog method.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f2.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg75.gif) |
Figure 2:
Comparison between the observed
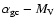 relation and the simulated one.
The observational data, represented by open circles, come from
the table in the appendix of Ashman & Zepf (1998).
Solid, dotted, short-dashed, and long-dashed lines
show the results of the HI, PP, RR, and LA models, respectively.
Note that both simulations and observations show a tendency
for flatter density profiles in brighter ellipticals. relation and the simulated one.
The observational data, represented by open circles, come from
the table in the appendix of Ashman & Zepf (1998).
Solid, dotted, short-dashed, and long-dashed lines
show the results of the HI, PP, RR, and LA models, respectively.
Note that both simulations and observations show a tendency
for flatter density profiles in brighter ellipticals. |
| Open with DEXTER |
Figure 1 plots the radial density profiles of stars and GCs
in ellipticals variation with 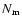 in the HI model sequence.
The reference GC profile with
in the HI model sequence.
The reference GC profile with
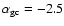 in this figure
corresponds to the Galactic GC profile (Zinn 1985) which
shows
in this figure
corresponds to the Galactic GC profile (Zinn 1985) which
shows
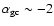 out to R=10 kpc
and
out to R=10 kpc
and
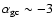 beyond R=20 kpc (Harris 1976).
This figure shows that up to
beyond R=20 kpc (Harris 1976).
This figure shows that up to
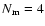 ,
the ellipticals have
positive
,
the ellipticals have
positive
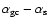 (e.g. 0.58 for
(e.g. 0.58 for
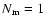 ),
and thus show flatter profiles for GCs than for field stars, which is consistent
qualitatively with observations (e.g., Harris 1986, 1991).
The reason for this is that GCs in a merger are more "puffed up''
relative to the stars after they inevitably absorb orbital angular momentum and kinetic
energy during the merger,
because most GCs are initially located in the galactic outer parts
where such absorption
is most likely to occur.
The radial density profile of a GCS in an elliptical
is always flatter in the inner region (R<20 kpc)
than in the outer one (
),
and thus show flatter profiles for GCs than for field stars, which is consistent
qualitatively with observations (e.g., Harris 1986, 1991).
The reason for this is that GCs in a merger are more "puffed up''
relative to the stars after they inevitably absorb orbital angular momentum and kinetic
energy during the merger,
because most GCs are initially located in the galactic outer parts
where such absorption
is most likely to occur.
The radial density profile of a GCS in an elliptical
is always flatter in the inner region (R<20 kpc)
than in the outer one (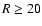 kpc). Again, qualitatively
consistent with observations (e.g., Forbes et al. 1996).
kpc). Again, qualitatively
consistent with observations (e.g., Forbes et al. 1996).
Both stellar and GC profiles in an elliptical become progressively flatter
as the elliptical experiences more major merger events
(i.e., larger 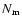 ).
For example, in the HI model
).
For example, in the HI model
 is estimated as -1.99 for
is estimated as -1.99 for
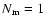 and -1.23 for
and -1.23 for
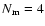 ,
which implies
that the slope
,
which implies
that the slope
 of a GCS in
an elliptical has fossil information
on how many times the elliptical has experienced dissipationless major merger
events in its formation history.
The derived slopes for
ellipticals are generally flatter than that observed
for the Galactic GCS which has
of a GCS in
an elliptical has fossil information
on how many times the elliptical has experienced dissipationless major merger
events in its formation history.
The derived slopes for
ellipticals are generally flatter than that observed
for the Galactic GCS which has
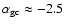 (Zinn 1985).
This suggests that major merging can transform the initially steeper
density profiles of GCSs in spirals into the flatter ones observed in
ellipticals. The general trends shown in Fig. 1 do not depend on model parameters.
(Zinn 1985).
This suggests that major merging can transform the initially steeper
density profiles of GCSs in spirals into the flatter ones observed in
ellipticals. The general trends shown in Fig. 1 do not depend on model parameters.
Figure 2 shows how
 depends on the total V-band magnitude of ellipticals
for four different sets of models (i.e., PP, RR, HI, and LA).
Irrespective of the models,
GCSs in brighter ellipticals show flatter
density profiles (i.e., larger
depends on the total V-band magnitude of ellipticals
for four different sets of models (i.e., PP, RR, HI, and LA).
Irrespective of the models,
GCSs in brighter ellipticals show flatter
density profiles (i.e., larger
 ), which is
reasonably consistent with observations.
This is due to the fact that
), which is
reasonably consistent with observations.
This is due to the fact that
 becomes larger each time a major merger occurs.
A least square fit to the simulation data shown in
Fig. 2 gives
becomes larger each time a major merger occurs.
A least square fit to the simulation data shown in
Fig. 2 gives
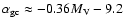 ,
which is similar to the observed relation of
,
which is similar to the observed relation of
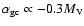 (Harris 1986).
This result suggests that the origin of the luminosity-dependent
(Harris 1986).
This result suggests that the origin of the luminosity-dependent
 (Harris 1991; Ashman & Zepf 1998) can be
understood in terms of the growth of ellipticals
via major dissipationless mergers.
It should be however noted, that the simulated range of
(Harris 1991; Ashman & Zepf 1998) can be
understood in terms of the growth of ellipticals
via major dissipationless mergers.
It should be however noted, that the simulated range of
 ,
for a given luminosity, is quite narrow so that
the present models can not simply explain the scatter
observed for
,
for a given luminosity, is quite narrow so that
the present models can not simply explain the scatter
observed for
 (in particular, for
(in particular, for
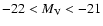 ).
).
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f3.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg84.gif) |
Figure 3:
The dependence of the GCS profile slope (
 )
and
that for the galaxy stars ( )
and
that for the galaxy stars (
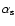 )
in 16 simulated merger remnants, i.e. elliptical galaxies.
The dotted line indicates )
in 16 simulated merger remnants, i.e. elliptical galaxies.
The dotted line indicates
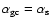 . . |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f4.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg85.gif) |
Figure 4:
Comparison between the observed
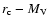 and the simulated ones.
Here and the simulated ones.
Here 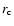 is the core radius of
a GCS's distribution.
The observational data represented by open circles come from
Forbes et al. (1996).
Solid, dotted, short-dashed, and long-dashed line
show the results of the HI, PP, RR, and LA models, respectively.
is the core radius of
a GCS's distribution.
The observational data represented by open circles come from
Forbes et al. (1996).
Solid, dotted, short-dashed, and long-dashed line
show the results of the HI, PP, RR, and LA models, respectively. |
| Open with DEXTER |
Figure 3 shows a positive correlation between
 and
and
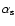 (
(
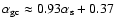 ), which means that
ellipticals with flatter distributions of stars are highly
likely to show flatter distributions of GCSs.
Figure 3 also shows that
), which means that
ellipticals with flatter distributions of stars are highly
likely to show flatter distributions of GCSs.
Figure 3 also shows that
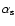 is always smaller
than
is always smaller
than
 (i.e.,
(i.e.,
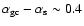 )
and thus confirms
that elliptical galaxies formed by major merging can have GCSs with
the density profiles flatter than those of stars.
The density profiles of the GCSs can be fit by a
power-law with slope
)
and thus confirms
that elliptical galaxies formed by major merging can have GCSs with
the density profiles flatter than those of stars.
The density profiles of the GCSs can be fit by a
power-law with slope
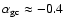 for
the inner region of
for
the inner region of
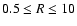 kpc.
However the shallower profiles of GCSs
in the inner regions can not be
regarded as "flat cores'' (
kpc.
However the shallower profiles of GCSs
in the inner regions can not be
regarded as "flat cores'' (
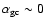 )
which
appear to be common
in the GCSs of giant ellipticals (e.g., Harris 1986, 1991;
Forbes et al. 1996).
)
which
appear to be common
in the GCSs of giant ellipticals (e.g., Harris 1986, 1991;
Forbes et al. 1996).
Figure 4 shows a clear trend of larger GCS core radii (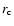 )
for brighter ellipticals, which is consistent qualitatively with
the observational results of Forbes et al. (1996) for the overall GCS.
The derived trend is due to the fact that
)
for brighter ellipticals, which is consistent qualitatively with
the observational results of Forbes et al. (1996) for the overall GCS.
The derived trend is due to the fact that 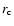 becomes larger
by a factor of
becomes larger
by a factor of 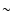 1.4 after each
major merger.
We can estimate the luminosity-dependence
of
1.4 after each
major merger.
We can estimate the luminosity-dependence
of 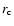 as
as
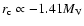 for the observational data with
for the observational data with
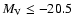 of
Forbes et al. (1996),
and as
of
Forbes et al. (1996),
and as
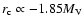 for the simulation data set shown in Fig. 4.
The derived luminosity-dependence of
for the simulation data set shown in Fig. 4.
The derived luminosity-dependence of 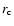 is therefore
steeper than the observed one.
is therefore
steeper than the observed one.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f5.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg94.gif) |
Figure 5:
Dependences of projected number distributions of
GCs in merger remnants (i.e., elliptical galaxies)
on the initial slope of radial density profiles of GCSs in
spirals (i.e.,
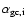 )
for the models
with )
for the models
with
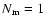 .
For clarity, the density distributions are normalized to
their central values.
Thin dotted lines represent power-law slopes ( .
For clarity, the density distributions are normalized to
their central values.
Thin dotted lines represent power-law slopes (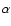 )
of )
of
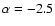 ,
-2.0, -1.5, and -1.0.
Note that there are no remarkable differences between
the three models. ,
-2.0, -1.5, and -1.0.
Note that there are no remarkable differences between
the three models. |
| Open with DEXTER |
Although we adopt the slope of the Galactic GCS as the initial
radial profile for GCSs in our progenitor spirals (i.e.,
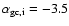 ),
our results do not depend strongly on the initial profile slope.
Figure 5 shows how the radial profiles of GCSs depend on
),
our results do not depend strongly on the initial profile slope.
Figure 5 shows how the radial profiles of GCSs depend on
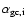 for the models with
for the models with
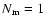 .
It is clear from this figure that there is no remarkable
difference in the profiles between the three models
for R<20 kpc: the difference of the final
.
It is clear from this figure that there is no remarkable
difference in the profiles between the three models
for R<20 kpc: the difference of the final
 between the models with
between the models with
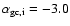 and -4.0becomes at most
and -4.0becomes at most  0.5, if we fit the profiles to
the power-law ones for R<20 kpc.
It should be also stressed that the model with
0.5, if we fit the profiles to
the power-law ones for R<20 kpc.
It should be also stressed that the model with
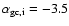 and -4.0shows a slightly steeper profile for the outer parts of the
merger remnants (R>40 kpc) compared with the model
with
and -4.0shows a slightly steeper profile for the outer parts of the
merger remnants (R>40 kpc) compared with the model
with
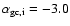 .
This tendency can be seen in other models with different
orbital configurations.
.
This tendency can be seen in other models with different
orbital configurations.
The derived weak dependence on
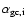 is due
to the fact that violent relaxation during major galaxy merging
can effectively wipe
out the original density distributions of GCSs for
is due
to the fact that violent relaxation during major galaxy merging
can effectively wipe
out the original density distributions of GCSs for
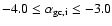 .
The resulting profiles of
.
The resulting profiles of
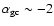 of GCSs
in merger remnants with
of GCSs
in merger remnants with
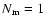 follow their dark matter halos, and furthermore
do not depend on initial orbital configurations of galaxy merging.
These results, combined with those shown in Fig. 1,
imply that the present results on the dependence of
follow their dark matter halos, and furthermore
do not depend on initial orbital configurations of galaxy merging.
These results, combined with those shown in Fig. 1,
imply that the present results on the dependence of
 on
on 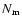 (thus on
(thus on 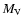 )
does not depend strongly on
)
does not depend strongly on
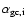 and thus can be regarded
as fairly robust.
and thus can be regarded
as fairly robust.
It is of interest to investigate whether the derived dependence
of
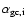 on
on 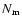 can be seen in models
with
can be seen in models
with
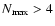 and thereby confirm that results are true
for a possible range of
and thereby confirm that results are true
for a possible range of 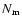 .
We note that the most massive ellipticals, with
.
We note that the most massive ellipticals, with
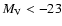 mag, are typically cD galaxies at the centres of clusters, for which accretion of GCs from
cluster member galaxies are important (e.g., Bekki et al. 2003)
and may well play a role in determining the radial profiles of
GCSs. The luminosity range (for
mag, are typically cD galaxies at the centres of clusters, for which accretion of GCs from
cluster member galaxies are important (e.g., Bekki et al. 2003)
and may well play a role in determining the radial profiles of
GCSs. The luminosity range (for
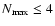 )
in the present simulations is thus appropriate for most
ellipticals but not cD galaxies.
)
in the present simulations is thus appropriate for most
ellipticals but not cD galaxies.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f6.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg100.gif) |
Figure 6:
The projected number distributions of stars (thin)
and GCs (thick) in merger remnant (i.e., elliptical galaxies)
with
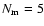 .
For clarity, the density distributions are normalized to
their central values.
Thin dotted lines represent power-law slopes ( .
For clarity, the density distributions are normalized to
their central values.
Thin dotted lines represent power-law slopes (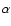 )
of )
of
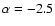 ,
-2.0, -1.5, and -1.0. ,
-2.0, -1.5, and -1.0. |
| Open with DEXTER |
Figure 6 shows the radial density profiles of stars and GCs in
the model with
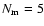 for the PR orbital configuration.
It is clear from this figure and Fig. 1 that the profile
of GCS becomes even flatter than that in the model with
for the PR orbital configuration.
It is clear from this figure and Fig. 1 that the profile
of GCS becomes even flatter than that in the model with
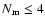 .
This result can be seen in other models with different orbital configurations.
For example,
.
This result can be seen in other models with different orbital configurations.
For example,
 is estimated as -0.77 for
the PR and -1.03 for the PP models.
These results confirm that radial density profiles of GCSs of ellipticals
formed by sequential major merging depend strongly on
is estimated as -0.77 for
the PR and -1.03 for the PP models.
These results confirm that radial density profiles of GCSs of ellipticals
formed by sequential major merging depend strongly on 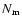 .
We note that for
.
We note that for
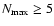 and
and
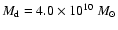 ,
the resulting merger remnant has
,
the resulting merger remnant has
 mag and thus few if any observational counterparts.
mag and thus few if any observational counterparts.
It should be noted that the spatial coverage and number of GCs
observed for the estimation of
 (e.g., Ashman & Zepf 1998)
varies from galaxy to galaxy.
The spatial coverage
of the simulation data, on the other hand, is fixed at
(e.g., Ashman & Zepf 1998)
varies from galaxy to galaxy.
The spatial coverage
of the simulation data, on the other hand, is fixed at
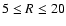 kpc
for the
kpc
for the
 estimation,
which suggests that the present compassion is not fully self-consistent.
It is accordingly important for the present study to show
how the
estimation,
which suggests that the present compassion is not fully self-consistent.
It is accordingly important for the present study to show
how the
 values depend on the spatial coverage.
It is found that
values depend on the spatial coverage.
It is found that
 is
is 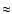 -2.0 for
-2.0 for
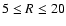 kpc,
kpc,
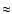 -1.6 for
-1.6 for
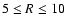 kpc,
and
kpc,
and 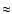 -2.4 for
-2.4 for
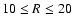 kpc in the HI model with
kpc in the HI model with
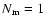 .
This result suggests that (1)
.
This result suggests that (1)
 can be larger (i.e., GCS density profiles are flatter)
if
can be larger (i.e., GCS density profiles are flatter)
if
 is derived for the inner
regions of ellipticals and (2)
is derived for the inner
regions of ellipticals and (2)
 can
be smaller (i.e., GCS density profiles are steeper)
if
can
be smaller (i.e., GCS density profiles are steeper)
if
 is derived for the outer parts of
ellipticals. Given the fact that these tendencies can be
seen in other models (PP, RR, and LA) the present results imply that
a more careful comparison between observations and
simulations is necessary in deriving physical meaning
of the GCS density profiles in ellipticals.
is derived for the outer parts of
ellipticals. Given the fact that these tendencies can be
seen in other models (PP, RR, and LA) the present results imply that
a more careful comparison between observations and
simulations is necessary in deriving physical meaning
of the GCS density profiles in ellipticals.
In the present study we suggest that sequential major merging
has the physical effect of flattening the radial density profiles of GCSs
so that the radial profiles of GCSs in ellipticals
contain fossil information about
their past merger history.
Neither of the above two points has been previously suggested
by theoretical studies.
The GCSs in ellipticals are thought to be subject to dynamical
destruction processes (e.g. Baumgardt 1998; Fall & Zhang 2001;
Vesperini et al. 2003), which are not included in this work.
However there is currently little convincing observational evidence
for destruction of GCs in ellipticals, e.g. Harris et al. (1998)
found no variation of the bright end of the GCLF with
galactocentric radius in M 87.
Vesperini et al. (2003)
also found no variation in the GCLF with radius in M 87, which
they claimed was consistent with dynamical destruction if
the GC mass function initially had a bell-shaped distribution.
To date, theoretical studies which focus on GC dynamical destruction
have not yet investigated the luminosity dependence
of the GCS density slope (
 ).
Thus it remains to be seen whether GC destruction can account for
this dependence, which is modelled here by sequential merging.
).
Thus it remains to be seen whether GC destruction can account for
this dependence, which is modelled here by sequential merging.
Destruction processes are expected to be
stronger in the galaxy inner regions and thus
play some role in determining the inner core radius of the
GCS. However it is difficult to understand how such processes could
explain the trend of 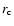 with galaxy luminosity given that destruction
processes are expected to be less efficient in the central regions
of more massive ellipticals (Murali & Weinberg 1997).
with galaxy luminosity given that destruction
processes are expected to be less efficient in the central regions
of more massive ellipticals (Murali & Weinberg 1997).
Although the present sequential merger model can qualitatively
explain some of the observed GCS structural properties, it
has the following three
disadvantages:
firstly, it remains unclear why
GCSs in some intermediate
luminosity ellipticals (
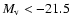 )
can show steeper (
)
can show steeper (
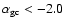 )
profiles,
which are not fully consistent with the observation
(See Fig. 2).
Secondly, the simulated core radius (
)
profiles,
which are not fully consistent with the observation
(See Fig. 2).
Secondly, the simulated core radius (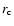 )
of a GCS
for a given luminosity is appreciably larger than the observed
one (Note that the derived luminosity-dependence of
)
of a GCS
for a given luminosity is appreciably larger than the observed
one (Note that the derived luminosity-dependence of 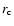 is
steeper than the observed one in Fig. 4). Thirdly, although the derived trend that
is
steeper than the observed one in Fig. 4). Thirdly, although the derived trend that
 is always larger than
is always larger than
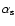 is broadly consistent with the observed trend (e.g., Harris 1991),
GCSs in some ellipticals show
is broadly consistent with the observed trend (e.g., Harris 1991),
GCSs in some ellipticals show
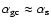 (e.g., Ashman & Zepf 1999), which
is not fully consistent with the present results.
(e.g., Ashman & Zepf 1999), which
is not fully consistent with the present results.
What additional physics is required to overcome these limitations?
As mentioned above, the inclusion of
destruction processes may be important but this is unlikely to
explain the trends with host galaxy luminosity.
The present study is dissipationless and so does not include the formation of the new GCs,
which would be formed preferentially in the central
regions of gaseous galaxy mergers
along with field star formation (e.g. Bekki et al. 2002).
A future study should investigate
the role of new GC formation in shaping the radial density profiles
of GCSs. Given our lack of understanding of the physics of GC formation, this is
a difficult task. As we have noted above, the
contribution of new GCs to the existing GCSs of ellipticals
appears to be small.
Bekki et al. (2003) showed that the strong tidal field
in galaxy clusters can strip GCs from cluster ellipticals
and consequently steepen the radial density profiles of the
remaining GCS in the donor galaxy. Consequently, the recipient
galaxy may obtain a flatter GCS profile.
Recent theoretical and numerical studies suggest that
if cosmic reionization can strongly suppress the formation
of old, metal-poor GCs in dwarfs at high redshifts (z>6),
then the radial profiles of GCSs in galaxies would be influenced
at very early epochs (Santos 2003; Bekki 2005).
Finally, the accretion of GCs via minor mergers (discussed in the next section) may
also have an important effect on some galaxies.
Thus the radial density
profiles of GCSs in galaxies could be influenced by
several physical processes associated with galaxy formation
and evolution.
Future studies should therefore seek to determine the
relative importance of each physical mechanism
in shaping the radial density profiles of GCSs.
For this purpose, it is vital that future observational studies
provide observational data on
structural, kinematical, and chemical properties of GCs
which can be compared with any theoretical predictions.
For example, systematic
observations of the radial dependence of GC luminosity functions
in ellipticals over a range of galaxy luminosities
will provide a clue as to the dominant physical processes.
Although minor galaxy merging between a spiral and a dwarf
can not form an elliptical
(e.g., Walker et al. 1996; Bekki 1998), the accretion of GCs from the dwarf
onto the spiral (e.g. Forbes et al. 2004)
can possibly change the original density profiles of the GCS
of the spiral.
Since full discussions on this matter are
obviously beyond the scope of this paper,
we here briefly discuss
how GC accretion events
can change the radial profiles of GCSs of galaxies
in a more general way.
Although the following discussions
are on GC accretion onto disk galaxies,
the basic results
can be also applied to GC accretion onto elliptical
galaxies (Bekki & Forbes 2005).
Here we model a dwarf elliptical (dE) composed of dark matter, stars,
and GCs and investigate the dynamical evolution of GCs
during its orbital evolution around the present disk galaxy
model. The full details of the dE model orbiting
a spiral like the Galaxy or M31 can be found
in Bekki & Freeman (2003),
Bekki & Chiba (2004), and Bekki & Forbes (2005).
Figure 7 shows the final distributions of stars and GCs initially
within a dE with
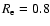 kpc,
kpc,
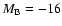 mag, and
mag, and
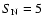 (corresponding
to 20 GCs in the dE), where
(corresponding
to 20 GCs in the dE), where 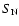 is the specific frequency
of GCs. In this model, the dE is assumed to be initially located
35 kpc from the center of the disk galaxy and have a circular
velocity of 209 km s-1 at this position.
The dE can be almost completely destroyed within
is the specific frequency
of GCs. In this model, the dE is assumed to be initially located
35 kpc from the center of the disk galaxy and have a circular
velocity of 209 km s-1 at this position.
The dE can be almost completely destroyed within 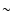 6 Gyr
of its evolution around the disk galaxy, and GCs initially within
the dE are all tidally stripped and dispersed into the halo
region of the disk galaxy. The tidal destruction of the dE
can happen well outside the disk in this model so that
most GCs of the dE can be distributed in the outer part of
the disk's halo. Consequently, the radial density profile
of the GCSs composed both of the original GCs of the disk
and of the stripped
GCs from the dE in the disk can become flattened, as shown
in Fig. 8.
6 Gyr
of its evolution around the disk galaxy, and GCs initially within
the dE are all tidally stripped and dispersed into the halo
region of the disk galaxy. The tidal destruction of the dE
can happen well outside the disk in this model so that
most GCs of the dE can be distributed in the outer part of
the disk's halo. Consequently, the radial density profile
of the GCSs composed both of the original GCs of the disk
and of the stripped
GCs from the dE in the disk can become flattened, as shown
in Fig. 8.
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f7.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg112.gif) |
Figure 7:
Final distributions of stars ( left)
and GCs ( right) projected onto the x-y plane for
the disk galaxy model after minor merging of the disk with
a dwarf elliptical galaxy (dE) with
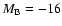 mag. GCs in
the right panel for this minor merger model are those stripped from the dE
and represented by filled squares.
The center of the disk galaxy with the initial size
of 17.5 kpc, which is not shown within
the two frames for clarity, is coincident with the center
of each frame.
Note that most GCs are located in the outer part of the disk. mag. GCs in
the right panel for this minor merger model are those stripped from the dE
and represented by filled squares.
The center of the disk galaxy with the initial size
of 17.5 kpc, which is not shown within
the two frames for clarity, is coincident with the center
of each frame.
Note that most GCs are located in the outer part of the disk. |
| Open with DEXTER |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f8.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg113.gif) |
Figure 8:
The projected number distributions
and GCs in the initial disk model ( left)
and the minor merger one ( right) where a dwarf elliptical
galaxy (dE) merges with the disk.
For clarity, the density distributions are normalized to
their central values.
Thin dotted lines represent power-law slopes (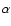 )
of )
of
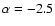 ,
-2.0, -1.5, and -1.0.
Note that the outer profile ( ,
-2.0, -1.5, and -1.0.
Note that the outer profile (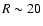 kpc) of the GCS of the disk
becomes flattened after GC accretion associated with the minor merging. kpc) of the GCS of the disk
becomes flattened after GC accretion associated with the minor merging. |
| Open with DEXTER |
These results imply that GC accretion associated with
destruction of dwarfs in disk galaxies can flatten the
radial profiles of GCSs in the disk galaxies.
These results furthermore suggest that although
minor merging can not transform disk galaxies into
ellipticals (Walker et al. 1996; Bekki 1998), the radial profiles
of GCSs in disk galaxies can be significantly changed
by minor merger events if such events are repeated
in the dynamical histories of the galaxies.
The density profiles of dark matter halos of galaxies
can be the key parameters in
the flattening of the density profiles
of GCSs by GC accretion (Bekki & Forbes 2005, in preparation).
Therefore the flattening processes
by GC accretion are unlikely to depend on morphological
types (e.g., Sp, E, and cD) of luminous components,
if all galaxies have similar dark matter profiles like
the NFW profile.
Recent numerical simulations have suggested that GC accretion
from cluster member galaxies onto the central giant
cDs in clusters of galaxies is highly likely
(e.g., Bekki et al. 2003).
The results shown in Figs. 7 and 8
therefore can suggest that GC accretion can be also responsible
for the origin of the very flat density profiles
of GCSs in cDs.
We have demonstrated that the observed
luminosity dependence of the GCS slope (
 )
can be reasonably well reproduced in elliptical galaxies
formed through sequential dissipationless major merger events.
Previous numerical simulations have already demonstrated that
the origin of structural non-homology in elliptical galaxies can be
closely associated with the dynamics of major galaxy merging
(e.g., Capelato et al. 1995; Bekki 1998; Dantas et al. 2002).
We suggest that structural non-homology seen in both the stellar
component and GCSs of ellipticals can have a common origin,
i.e. the growth of elliptical galaxies through
dissipationless major merging.
The derived
)
can be reasonably well reproduced in elliptical galaxies
formed through sequential dissipationless major merger events.
Previous numerical simulations have already demonstrated that
the origin of structural non-homology in elliptical galaxies can be
closely associated with the dynamics of major galaxy merging
(e.g., Capelato et al. 1995; Bekki 1998; Dantas et al. 2002).
We suggest that structural non-homology seen in both the stellar
component and GCSs of ellipticals can have a common origin,
i.e. the growth of elliptical galaxies through
dissipationless major merging.
The derived
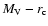 and
and
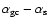 relationships
are also the direct result of this growth.
Thus the radial density profiles of GCSs in
elliptical galaxies can be regarded
as containing fossil records of their
merging histories.
Given the fact that dynamical non-homology can be closely
associated with the origin of the Fundamental Plane
(e.g., Djorgovski & Davis 1987) of elliptical galaxies,
it is an interesting observational question whether
GCSs show an analogous "Fundamental Plane''.
relationships
are also the direct result of this growth.
Thus the radial density profiles of GCSs in
elliptical galaxies can be regarded
as containing fossil records of their
merging histories.
Given the fact that dynamical non-homology can be closely
associated with the origin of the Fundamental Plane
(e.g., Djorgovski & Davis 1987) of elliptical galaxies,
it is an interesting observational question whether
GCSs show an analogous "Fundamental Plane''.
Acknowledgements
We are grateful to the referee for valuable comments,
which contribute to improve the present paper.
K.B. and DAF acknowledge financial support from the Australian
Research Council (ARC) throughout the course of this work. The
numerical simulations reported here were carried out on GRAPE
systems kindly made available by the Astronomical Data Analysis
Center (ADAC) at National Astronomical Observatory of Japan
(NAOJ).
- Ashman, K. M.,
& Zepf, S. E. 1992, ApJ, 384, 50 [NASA ADS] [CrossRef]
- Ashman, K. M.,
& Zepf, S. E. 1998, in Globular cluster systems (Cambridge, U.
K.; New York: Cambridge University Press)
(In the text)
- Battistini,
P., Bonoli, F., Casavecchia, M., et al. 1993, A&A, 272, 77 [NASA ADS] (In the text)
- Baumgardt, H.
1988, A&A, 330, 480 [NASA ADS]
- Beasley, M. A.,
Baugh, C. M., Forbes, D. A., Sharples, R. M., & Frenk, C. S.
2002, MNRAS, 333, 383 [NASA ADS] [CrossRef] (In the text)
- Beasley, M. A.,
Forbes, D. A., Brodie, J. P., & Kissler-Patig, M. 2004, MNRAS,
347, 1150 [NASA ADS] [CrossRef] (In the text)
- Bekki, K. 1998, ApJ,
496, 713 [NASA ADS] [CrossRef] (In the text)
- Bekki, K. 2005, ApJ,
626, L93 [NASA ADS] [CrossRef] (In the text)
- Bekki, K., &
Freeman, K. C. 2003, MNRAS, 346, L11 [NASA ADS] [CrossRef]
- Bekki, K., &
Chiba, M. 2004, A&A, 417, 437 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Bekki, K., &
Forbes, D. A. 2005, in preparation
- Bekki, K., Forbes, D.
A., Beasley, M. A., & Couch, W. J. 2002, MNRAS, 335, 1176 [NASA ADS] [CrossRef] (In the text)
- Bekki, K., Forbes, D.
A., Beasley, M. A., & Couch, W. J. 2003, MNRAS, 344, 1334 [NASA ADS] [CrossRef] (In the text)
- Bekki, K., Beasley,
M. A., Brodie, J. P., & Forbes, D. A. 2005, MNRAS,
submitted
- Bell, E., et al. 2005,
[arXiv:astro-ph/0506425]
(In the text)
- Capelato, H.
V., de Carvalho, R. R., & Carlberg, R. G. 1995, ApJ, 451,
525 [NASA ADS] [CrossRef] (In the text)
- Cohen, J. G.,
Blakeslee, J. P., & Ryzhov, A. 1998, ApJ, 496, 808 [NASA ADS] [CrossRef] (In the text)
- Cohen, J. G.,
Blakeslee, J. P., & Côte, P. 2003, ApJ, 592, 866 [NASA ADS] [CrossRef] (In the text)
- Dantas, C. C.,
Capelato, H. V., Ribeiro, A. L. B., & de Carvalho, R. R. 2003,
MNRAS, 340, 398 [NASA ADS] [CrossRef]
- Djorgovski,
S., & Davis, M. 1987, ApJ, 313, 59 [NASA ADS] [CrossRef] (In the text)
- Djorgovski,
S., & Meylan, G. 1994, AJ, 108, 1292 [NASA ADS] [CrossRef] (In the text)
- Fall, S. M., &
Zhang, Q. 2001, ApJ, 561, 751 [NASA ADS] [CrossRef] (In the text)
- Forbes, D. A.,
Franx, M., Illingworth, G. D., & Carollo, C. M. 1996, ApJ, 467,
126 [NASA ADS] [CrossRef] (In the text)
- Forbes, D. A.,
Brodie, J. P., & Grillmair, C. J. 1997, AJ, 113, 1652 [NASA ADS] [CrossRef] (In the text)
- Forbes, D. A.,
Beasley, M. A., Brodie, J. P., & Kissler-Patig, M. 2001, ApJ,
563, L143 [NASA ADS] [CrossRef] (In the text)
- Forbes, D. A.,
Strader, J., & Brodie, J. P. 2004, AJ, 127, 3394 [NASA ADS] [CrossRef] (In the text)
- Freeman, K. C.
1993, in the globular cluster-galaxy connection ed. G. H. Smith,
& J. P. Brodie (San Francisco: ASP), ASP Conf. Ser., 48,
27
(In the text)
- Grillmair, C.
J., Faber, S. M., Lauer, Tod R., et al. 1994, AJ, 108, 102 [NASA ADS] [CrossRef] (In the text)
- Harris, W. E. 1976,
AJ, 81, 1095 [NASA ADS] [CrossRef] (In the text)
- Harris, W. E. 1986,
AJ, 91, 822 [NASA ADS] [CrossRef] (In the text)
- Harris, W. E. 1991,
ARA&A, 29, 543 [NASA ADS] (In the text)
- Harris, W. E.,
& Racine, R. 1979, ARA&A, 17, 241 [NASA ADS] (In the text)
- Harris, W. E.,
Harris, G., & McLaughlin, D. 1998, AJ, 115, 1801 [NASA ADS] [CrossRef] (In the text)
- Kuntschner,
H., Ziegler, B. L., Sharples, R. M., Worthey, G., & Fricke, K.
J. 2002, A&A, 395, 761 [EDP Sciences] [NASA ADS] [CrossRef] (In the text)
- Murali, C., &
Weinberg, M. D. MNRAS, 288, 767
- Navarro, J. F.,
Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [NASA ADS] [CrossRef] (In the text)
- Pierce, M., Brodie,
J. P., Forbes, D. A., Beasley, M. A., & Strader, J. 2005,
MNRAS, accepted
(In the text)
- Santos, M. R. 2003,
Extragalactic Globular Cluster Systems ed. M. Kissler-Patig
(Garching: ESO), 348
(In the text)
- Strader, J.,
Brodie, J. P., & Forbes, D. A. 2004, AJ, 127, 295 [NASA ADS] [CrossRef] (In the text)
- Strom, S. E., Strom,
K. M., Wells, D. C., et al. 1981, ApJ, 245, 416 [NASA ADS] [CrossRef] (In the text)
- Sugimoto, D.,
Chikada, Y., Makino, J., et al. 1990, Nature, 345, 33 [NASA ADS] [CrossRef] (In the text)
- Toomre, A. 1977, in
The evolution of galaxies and stellar Populations ed. by B.
Tinsley, & R. Larson (New. Haven. CN: Yale Univ. Press),
401
(In the text)
- van den
Bergh, S. 2000, The Galaxies of the Local Group (Cambridge:
Cambridge Univ. Press)
- Vesperini,
E., Zepf, S. E., Kundu, A., & Ashman, K. M. 2003, ApJ, 593,
760 [NASA ADS] [CrossRef] (In the text)
- Walker, I. R.,
Mihos, J. C., & Hernquist, L. 1996, ApJ, 460, 121 [NASA ADS] [CrossRef] (In the text)
- Whitmore, B.
C., & Schweizer, F. 1995, AJ, 109, 960 [NASA ADS] [CrossRef] (In the text)
- Zepf, S. E., &
Ashman, K. M. 1993, MNRAS, 264, 611 [NASA ADS] (In the text)
- Zinn, R. 1985, ApJ,
293, 424 [NASA ADS] [CrossRef] (In the text)
Copyright ESO 2005
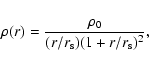
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f1.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg74.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f2.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg75.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f3.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg84.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f4.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg85.gif)
![\begin{figure}
\par\includegraphics[width=8cm,clip]{3686f5.eps}
\end{figure}](/articles/aa/full/2006/02/aa3686-05/Timg94.gif)