A&A 445, 601-616 (2006)
DOI: 10.1051/0004-6361:20053439
M. Gustafsson1 - D. Field1 - J. L. Lemaire2 - F. P. Pijpers3
1 - Department of Physics and Astronomy, University of Aarhus,
8000 Aarhus C, Denmark
2 - Observatoire de Paris &
Université de Cergy-Pontoise, LERMA & UMR
8112 du CNRS, 92195 Meudon, France
3 - Space and Atmospheric
Physics, Dept. Physics, Imperial College London, England
Received 16 May 2005 / Accepted 8 September 2005
Abstract
A statistical analysis is presented of the turbulent
velocity structure in the Orion Molecular Cloud at scales ranging
from 70 AU to
![]() AU. Results are based on IR Fabry-Perot
interferometric observations of shock and photon-excited H2 in
the K-band S(1) v=1-0 line at 2.121
AU. Results are based on IR Fabry-Perot
interferometric observations of shock and photon-excited H2 in
the K-band S(1) v=1-0 line at 2.121 ![]() m and refer to the dynamical
characteristics of warm perturbed gas. Data consist of a spatially
resolved image
with a measured velocity for each resolution limited region
(
m and refer to the dynamical
characteristics of warm perturbed gas. Data consist of a spatially
resolved image
with a measured velocity for each resolution limited region
(
![]() )
in the image. The effect of removal of apparent large
scale velocity gradients is discussed and the conclusion drawn that
these apparent gradients represent part of the turbulent cascade and
should remain within the data. Using our full data set, observations
establish that the Larson size-linewidth relation is obeyed to the
smallest scales studied here extending the range of validity of this
relationship by nearly 2
orders of magnitude. The velocity probability distribution function
(PDF) is constructed showing extended exponential wings, providing evidence of intermittency, further supported by
the skewness (third moment) and kurtosis (fourth
moment) of the velocity distribution. Variance and kurtosis of the
PDF of velocity differences are constructed as a function of
lag. The variance shows an
approximate power law dependence on lag, with exponent significantly lower
than the Kolmogorov value, and with deviations below
2000 AU which are attributed to outflows and possibly disk structures associated with low mass star
formation within OMC1. The kurtosis shows strong deviation from a
Gaussian velocity field, providing evidence of velocity correlations at small
lags. Results agree accurately with semi-empirical simulations
in Eggers & Wang (1998).
)
in the image. The effect of removal of apparent large
scale velocity gradients is discussed and the conclusion drawn that
these apparent gradients represent part of the turbulent cascade and
should remain within the data. Using our full data set, observations
establish that the Larson size-linewidth relation is obeyed to the
smallest scales studied here extending the range of validity of this
relationship by nearly 2
orders of magnitude. The velocity probability distribution function
(PDF) is constructed showing extended exponential wings, providing evidence of intermittency, further supported by
the skewness (third moment) and kurtosis (fourth
moment) of the velocity distribution. Variance and kurtosis of the
PDF of velocity differences are constructed as a function of
lag. The variance shows an
approximate power law dependence on lag, with exponent significantly lower
than the Kolmogorov value, and with deviations below
2000 AU which are attributed to outflows and possibly disk structures associated with low mass star
formation within OMC1. The kurtosis shows strong deviation from a
Gaussian velocity field, providing evidence of velocity correlations at small
lags. Results agree accurately with semi-empirical simulations
in Eggers & Wang (1998).
In addition, 170 individual H2 emitting clumps have been analysed with sizes between 500 and 2200 AU. These show considerable diversity with regard to PDFs and variance functions (related to second order structure functions) displaying a variety of shapes of the PDF and different values of the scaling exponent within a restricted spatial region. However, a region associated with an outflow from a deeply embedded O-star shows high values of the scaling exponent of the variance function, representing a strong segregation of high and low exponent clumps. Our analysis constitutes the first characterization of the turbulent velocity field at the scale of star formation and provide a dataset which models of star-forming regions should aim to reproduce.
Key words: ISM: individual objects: OMC1 - ISM: kinematics and dynamics - ISM: molecules - shock waves - turbulence - infrared: ISM
A key to understanding the mechanism of star formation is to
characterise in detail the nature of the turbulent, weakly ionized and
magnetised plasma in which stars form. Recently Gustafsson et al. 2003
(Paper I) published observational results for the vibrational emission
of H2 in the archetypal star-forming region in the Orion Molecular
Cloud, OMC1. Using a combination of Fabry-Perot interferometry and the
PUEO adaptive optics system on the Canada-France-Hawaii Telescope
(CFHT), data achieved a spatial resolution of 0
![]() 15 (70 AU at the
distance of OMC1, D=460 pc (Bally et al. 2000)), with a velocity discrimination
of 1 km s-1 in regions of high brightness. These data, limited as they
are to highly excited regions in OMC1, provide the first
opportunity to study the physical properties of a star-forming region
both in terms of its morphology and bulk gas motion at the scale of
star formation.
The aim of the present paper is to characterise the nature of the
turbulent velocity field in OMC1 for the subset of regions represented
through vibrationally excited H2. Our results should help to
provide a benchmark for comparison with MHD models of star-forming
regions.
15 (70 AU at the
distance of OMC1, D=460 pc (Bally et al. 2000)), with a velocity discrimination
of 1 km s-1 in regions of high brightness. These data, limited as they
are to highly excited regions in OMC1, provide the first
opportunity to study the physical properties of a star-forming region
both in terms of its morphology and bulk gas motion at the scale of
star formation.
The aim of the present paper is to characterise the nature of the
turbulent velocity field in OMC1 for the subset of regions represented
through vibrationally excited H2. Our results should help to
provide a benchmark for comparison with MHD models of star-forming
regions.
The importance of turbulent gas motion in regulating star formation
may be illustrated as follows. Relative bulk motions obtained from observations reported here range up to 40 km s-1 in dense gas. Since these motions are supersonic, it is evident that bulk motion must contribute more energy per unit
volume, that is, pressure, than thermal energy. Equally if a simple
scaling law is used between magnetic induction, B, and particle
density, n, whereby
![]() G, with n in
cm-3 (Troland & Heiles 1986), then the energy contained in
bulk mass motion will exceed the energy in the magnetic field, B2/2
G, with n in
cm-3 (Troland & Heiles 1986), then the energy contained in
bulk mass motion will exceed the energy in the magnetic field, B2/2![]() (in SI units), for
bulk velocities greater than 2.2 b km s-1. The constant b
lies typically between 1 and 2 (Kristensen et al. 2005). Thus in many
regions the
turbulent pressure may exceed the magnetic pressure, given that bulk motion proceeds at tens of km s-1 as mentioned above. The magnetic
pressure in turn typically exceeds the thermal pressure, the ratio of
thermal to magnetic pressure being
(in SI units), for
bulk velocities greater than 2.2 b km s-1. The constant b
lies typically between 1 and 2 (Kristensen et al. 2005). Thus in many
regions the
turbulent pressure may exceed the magnetic pressure, given that bulk motion proceeds at tens of km s-1 as mentioned above. The magnetic
pressure in turn typically exceeds the thermal pressure, the ratio of
thermal to magnetic pressure being
![]() T/b2, where T is
the gas temperature. In the above simple prescription, any anisotropy
of the magnetic field has been ignored. At all events, on
purely energetic grounds, in earlier stages of star formation,
turbulence is the controlling support mechanism against gravitational
collapse, if bulk mass motions exceed a few km s-1. This statement remains true even in the warm regions involved in the present study.
T/b2, where T is
the gas temperature. In the above simple prescription, any anisotropy
of the magnetic field has been ignored. At all events, on
purely energetic grounds, in earlier stages of star formation,
turbulence is the controlling support mechanism against gravitational
collapse, if bulk mass motions exceed a few km s-1. This statement remains true even in the warm regions involved in the present study.
Observational and computational evidence for the simple picture presented above has grown considerably in the last decade as described in recent reviews by Larson (2003) and Mac Low & Klessen (2004). Moreover the role of turbulence goes further than simply slowing the process of gravitational collapse. Simulations show that turbulence may determine the initial mass function (IMF) for star formation through turbulent fragmentation (e.g. Nordlund & Padoan 2003). It is evident that MHD models, which make such far-reaching predictions, need to be constrained by observations. The meeting of theory and observation may be achieved by recording the statistical properties of velocity fields and this standard approach is adopted here. In the present work we make only very limited comparison with published models. Rather, we present modellers with characteristic behaviour which it is their challenge to reproduce.
Several techniques have previously been used to characterize the structure of brightness and velocity in molecular clouds based largely upon CO observations, reviewed by Goodman et al. (1998) and Miesch et al. (1999). These earlier observations, tracing relatively cool and low density gas, are limited in spatial resolution and can only be used to address the physics at scales larger than roughly 0.03 pc (6000 AU). When dealing with turbulence it is assumed that most features are scale-free between the driving and dissipation scale and that the behaviour for example of the structure functions (see Sect. 4.4) can be extrapolated to the very much smaller scales of individual star formation. This is however far from certain. The high spatial resolution infrared data reported in Paper I give the opportunity to discover how structure functions develop at much smaller scales than have hitherto been probed.
In this paper we use three standard statistical measures to provide observational constraints on theories and simulations concerning gravitational collapse and star formation in a turbulent ISM. First, we test whether the observed scaling behaviour of the velocity structure, encapsulated in the size-linewidth relation or "Larson law'' (Larson 1981), holds for the smaller scales involved here (Sect. 4.2). Second, we use probability distribution functions (PDFs) of velocities (Sect. 4.3) as a probe of intermittency (Ossenkopf & Mac Low 2002; Miesch & Scalo 1995; Falgarone & Phillips 1990; Falgarone et al. 1994; Falgarone & Phillips 1991; Miesch et al. 1999). Third, we calculate the low order moments of the velocity difference PDF (Ossenkopf & Mac Low 2002; Miesch & Scalo 1995; Lis et al. 1998; Miesch et al. 1999) as a function of lag (Sect. 4.4), that is, the structure functions or functions directly related to structure functions. In addition, the high spatial resolution of the data allows us to go further than determining these quantities for the observed field as a whole. In Sect. 5 we identify 170 individual clumps in OMC1 with a mean size of 1300 AU. We calculate the individual PDFs of peak velocities and the variance functions for these clumps.
Near infrared K-band observations of the strongest H2 emission line in
Orion, v= 1-0 S(1) at 2.121 ![]() m, are used as a tracer of radial gas velocity to provide the data for the statistical analysis performed here.
The observational data are the same as those described in
Paper I and a detailed
description of the data acquisition and reduction may be found there.
In brief, OMC1 was observed using the CFHT with GriF on the night of
December 5th
2000. The GriF instrument (Clénet et al. 2002), is a combination of the
PUEO adaptive optics (AO)
system on the CFHT with interferometric spectral scanning. The
interferometer, a Queensgate ET50WF Fabry-Perot (FP), affords a
measured spectral resolution
m, are used as a tracer of radial gas velocity to provide the data for the statistical analysis performed here.
The observational data are the same as those described in
Paper I and a detailed
description of the data acquisition and reduction may be found there.
In brief, OMC1 was observed using the CFHT with GriF on the night of
December 5th
2000. The GriF instrument (Clénet et al. 2002), is a combination of the
PUEO adaptive optics (AO)
system on the CFHT with interferometric spectral scanning. The
interferometer, a Queensgate ET50WF Fabry-Perot (FP), affords a
measured spectral resolution ![]() /
/
![]() ,
that is, 150 km s-1. The detector has a field of view of 36
,
that is, 150 km s-1. The detector has a field of view of 36
![]()
![]() 36
36
![]() with a pixel scale of 0
with a pixel scale of 0
![]() 035. The region of
OMC1 observed, shown in Fig. 1, consists of four
overlapping fields
and the
entire region is centred 15
035. The region of
OMC1 observed, shown in Fig. 1, consists of four
overlapping fields
and the
entire region is centred 15
![]() N and 15
N and 15
![]() W of TCC0016
(05
W of TCC0016
(05
![]() ,
,
![]() ,
J2000).
,
J2000).
Each field has been scanned through the H2 line from a wavelength
in the far blue wing to a wavelength in the far red wing, using
step sizes between
![]() m and
m and
![]() m
(
m
(![]() km s-1), allowing adequate sampling of the
instrumental profile. To
prevent superposition of different FP orders
during scanning, a H2 v=1-0 S(1) interference filter with a
2.122
km s-1), allowing adequate sampling of the
instrumental profile. To
prevent superposition of different FP orders
during scanning, a H2 v=1-0 S(1) interference filter with a
2.122 ![]() m central wavelength and a bandwidth of 0.02
m central wavelength and a bandwidth of 0.02 ![]() m, was
inserted between the FP and the detector. For each region and
each wavelength, a single exposure of 400 s was performed.
Data reduction includes dark and bias subtraction,
flat-fielding, bad pixel rejection, image
recentering, 2D wavelength correction and
subtraction of sky background obtained from an image in the far wing of
the H2 profile.
Various reference stars for the AO were used: TCC0016
(
m, was
inserted between the FP and the detector. For each region and
each wavelength, a single exposure of 400 s was performed.
Data reduction includes dark and bias subtraction,
flat-fielding, bad pixel rejection, image
recentering, 2D wavelength correction and
subtraction of sky background obtained from an image in the far wing of
the H2 profile.
Various reference stars for the AO were used: TCC0016
(
![]() )
in the SE and SW field, Parenago 1838 (
)
in the SE and SW field, Parenago 1838 (
![]() )
in NE and Parenago 1819 (
)
in NE and Parenago 1819 (
![]() )
in NW. The FWHM of
the point-spread-function of stars in the region has been examined yielding
a spatial
resolution of 0
)
in NW. The FWHM of
the point-spread-function of stars in the region has been examined yielding
a spatial
resolution of 0
![]() 15. This near diffraction limited spatial
resolution was maintained throughout all observations.
In view of the spatial resolution of 0
15. This near diffraction limited spatial
resolution was maintained throughout all observations.
In view of the spatial resolution of 0
![]() 15, all images have been smoothed by a moving average of 3 by 3 pixels to improve S/N without significantly degrading the spatial resolution.
15, all images have been smoothed by a moving average of 3 by 3 pixels to improve S/N without significantly degrading the spatial resolution.
Radial velocities were found by choosing a specific position on the sky and taking a cut through the cube made up of the channel maps. This yielded a set of count rates as a function of wavelength constituting a line profile and a Lorentzian is fitted to the profile (Clénet et al. 2002). The position of the peak in emission gives the radial velocity. The Lorentzian form was chosen because it represents the instrumental profile of the Fabry-Perot. We note that the instrument profile is highly symmetric (Clénet et al. 2002) and thus a choice for example of a centroid rather than the peak of a Lorentzian is immaterial to an estimation of the velocity. We also note that less than 2% of profiles are double peaked: the velocity of the brighter of the two peaks is chosen when these cases are encountered (Paper I).
![\begin{figure}
\par {\includegraphics[width=8.3cm,clip]{3439fig1.ps} }
\end{figure}](/articles/aa/full/2006/02/aa3439-05/Timg32.gif) |
Figure 1:
Velocity integrated emission in the S(1) v= 1-0 H2 emission line covering the full observed field in OMC1. (0,0) marks
the position of TCC0016 05
|
| Open with DEXTER | |
Performing these operations pixel by pixel for the full field
of view results in very accurate fits for the brighter regions. Including
statistical error in the count rates, relative peak wavelengths may be
found in bright local zones to 2 to 3
parts per 106 (3![]() ,
that is, to better than
,
that is, to better than
![]() km s-1. The quality of the fit decreases with decreasing
brightness. Since an assessment of errors is important in
discussing the statistical properties of the velocity field, the
accuracy of determination of the central wavelength has been
estimated by performing a large number of fits for a range of pixel
brightness. An empirical
correspondence between brightness and error in velocity has thereby
been determined. This may be expressed as follows:
km s-1. The quality of the fit decreases with decreasing
brightness. Since an assessment of errors is important in
discussing the statistical properties of the velocity field, the
accuracy of determination of the central wavelength has been
estimated by performing a large number of fits for a range of pixel
brightness. An empirical
correspondence between brightness and error in velocity has thereby
been determined. This may be expressed as follows:
In addition to random errors in the velocity, systematic
errors may also occur in establishing velocity differences between
regions which are physically remote. This may take place due to distortions in the 2D
wavelength correction
arising from possible mechanical instabilities or drift. In this connection, observations of a
restricted part of the full field comprising two
36
![]()
![]() 36
36
![]() fields to the SE and NW were performed in
January 2003. Comparisons have been made of the velocity fields in
the 2000 data, used here, and in the 2003 data. Average velocities
have been estimated within regions of about
fields to the SE and NW were performed in
January 2003. Comparisons have been made of the velocity fields in
the 2000 data, used here, and in the 2003 data. Average velocities
have been estimated within regions of about
![]() pixels
(1
pixels
(1
![]()
![]()
![]() 75) separated by up to 60
75) separated by up to 60
![]() ,
the full
size of the image. We find that velocity differences in the 2000
data and the 2003 data agree to better than
,
the full
size of the image. We find that velocity differences in the 2000
data and the 2003 data agree to better than ![]() 1 km s-1. Since these
results were obtained using independent calibration data, they provide
a clear indication that systematic errors in velocity differences between remote regions are not present.
1 km s-1. Since these
results were obtained using independent calibration data, they provide
a clear indication that systematic errors in velocity differences between remote regions are not present.
Conversion of count rates to
absolute values of surface brightness was obtained by comparison with
calibrated data in Vannier et al. (2001). Thus the count rate
of 2.15 counts pixel-1 s-1, at the peak of emission to the SE
of TCC0016, corresponds to a velocity integrated brightness of
![]() W m-2 sr-1.
W m-2 sr-1.
The composite field observed within OMC1, shown in
Fig. 1, is 90
![]()
![]() 70
70
![]() .
This allows us to address statistical
issues involving scales ranging from 70 to
.
This allows us to address statistical
issues involving scales ranging from 70 to
![]() AU or
AU or
![]() to 0.15 pc.
to 0.15 pc.
Velocities are expressed as
![]() by assigning a mean velocity of all the data of
by assigning a mean velocity of all the data of ![]() km s-1 in the
local standard of rest
(Chrysostomou et al. 1997; O'Dell 2001; Salas et al. 1999). Since
we are essentially concerned only with the relative velocities of
regions within OMC1, the uncertainty in the value of
km s-1 in the
local standard of rest
(Chrysostomou et al. 1997; O'Dell 2001; Salas et al. 1999). Since
we are essentially concerned only with the relative velocities of
regions within OMC1, the uncertainty in the value of
![]() is not
material to our discussion.
is not
material to our discussion.
There is a wealth of data for the dense star-forming region of OMC1, even if consideration is restricted to IR observations of H2 emission. Reference to these extensive data, covering features such as the well-known "bullets'' and "fingers'' of H2 emission, and very high spatial resolution observations of H2 performed using the HST, VLT and CFHT may be found in recent work e.g. McCaughrean & Mac Low (1997); Stolovy et al. (1998); Schultz et al. (1999); Lee & Burton (2000); O'Dell (2001); Davis et al. (2001); Vannier et al. (2001); Doi et al. (2002); Gustafsson et al. (2003) (Paper I); Lacombe et al. (2004). Our account here is restricted to data specifically concerned with radial motion measured in Orion using H2 IR emission as a tracer (Chrysostomou et al. 1997; Sugai et al. 1995; Salas et al. 1999). Excitation mechanisms of H2 are however briefly considered here since these have a bearing on later discussion.
The high brightness of H2 emission in the v=1-0 S(1) line,
frequently exceeding 10-5 W m-2 sr-1, indicates that the
gas is of high column density. Since brightly emitting clumps are
typically 1
![]() to 2
to 2
![]() in angular size (1
in angular size (1
![]() pc), the inference is that number densities are also
high. The most feasible general mechanism of H2 excitation, for high
brightness, is through C-type (magnetic) shocks (Kaufman & Neufeld 1996b,a; Kristensen et al. 2003,2005; Wilgenbus et al. 2000; Smith & Brand 1990; Flower et al. 2003; Le Bourlot et al. 2002; Vannier et al. 2001; Timmermann 1998). Low
velocity shock excitation in dense gas in regions of OMC1
shown in Fig. 1, has been analysed in detail for example in
Vannier et al. (2001) and in Kristensen et al. (2003). Densities in the
post-shock gas exceed 107 cm-3. In addition, the data of Paper
I graphically illustrate the presence of shocks through
the clear spatial association of bright H2 emission with gas flows.
pc), the inference is that number densities are also
high. The most feasible general mechanism of H2 excitation, for high
brightness, is through C-type (magnetic) shocks (Kaufman & Neufeld 1996b,a; Kristensen et al. 2003,2005; Wilgenbus et al. 2000; Smith & Brand 1990; Flower et al. 2003; Le Bourlot et al. 2002; Vannier et al. 2001; Timmermann 1998). Low
velocity shock excitation in dense gas in regions of OMC1
shown in Fig. 1, has been analysed in detail for example in
Vannier et al. (2001) and in Kristensen et al. (2003). Densities in the
post-shock gas exceed 107 cm-3. In addition, the data of Paper
I graphically illustrate the presence of shocks through
the clear spatial association of bright H2 emission with gas flows.
In addition to shocks, photon induced excitation of H2, in so-called
photon dominated regions (PDRs), can play a role in yielding the
observed H2 IR emission. This has been discussed in detail in
Kristensen et al. (2003) who show that PDRs may contribute significantly
in specific regions, for example in the SE (Peak 2) region, especially at the edge
of clumps of material in this region. In strongly emitting zones,
PDRs cannot yield sufficient brightness,
even including effects of advection (Lemaire et al. 1999), high density, and the high UV flux
from ![]() Ori-C, in excess of 105 times the standard UV field (Störzer & Hollenbach 1999).
Ori-C, in excess of 105 times the standard UV field (Störzer & Hollenbach 1999).
The presence of large scale velocity differences in OMC1 has been known for many years. Sugai et al. (1995), Chrysostomou et al. (1997) and Salas et al. (1999) have all used FP interferometry in OMC1 in the IR and studied the large scale velocity structure of the hot H2component. From our observations (Paper I) we find that the gas in Peak 1 (NW of BN) is on average 10 km s-1 more blueshifted than in Peak 2 (SE of BN: Fig. 1; see also Fig. 2 in Paper I). This velocity difference has generally been viewed in the context of an outflow mechanism from the IRc2-complex and has previously been explained by an expanding shell (Scoville et al. 1982; Sugai et al. 1995), a bipolar outflow (Chrysostomou et al. 1997) or a spherical wind (Salas et al. 1999). The velocity difference could however be a manifestation of turbulent energy injected into the system and stirring of the gas in large scale vortices. Thus the nature of the velocity difference remains uncertain and in the following we will explore this question further.
As discussed in Miesch & Bally (1994), Miesch & Scalo (1995) and Miesch et al. (1999), large scale trends - such as a general velocity gradient - could dominate any statistical quantifier and give misleading results. This is due to the fact that the statistical methods lose spatial information and therefore depend on an absence of systematic trends within the data. It may therefore be argued that any large scale trends should be removed and only local velocity fluctuations studied. Ossenkopf & Mac Low (2002) however point out that large scale systematic motions may be part of the turbulent cascade if these inject energy into the system and should therefore only be removed if the turbulence studied is exclusively driven on smaller scales.
In this connection, observations of molecular clouds seem to indicate that interstellar turbulence is driven on scales larger than the clouds themselves, and arguments have been presented that supernovae explosions dominate (Mac Low & Klessen 2004). However, contributions to the continuous driving of the turbulence may also arise from protostellar outflows (Matzner & McKee 2000) and stellar winds from massive O stars (Mac Low & Klessen 2004). OMC1 is itself a region of highly active star formation. Observations ranging from X-ray (Garmire et al. 2000; Feigelson et al. 2002) to radio wavelengths (e.g. Churchwell et al. 1987; Zapata et al. 2004) reveal the presence of protostars, outflows (e.g. Genzel & Stutzki 1989), HH objects (e.g. Doi et al. 2004; O'Dell et al. 1997) and mainline OH, H2O and SiO maser emission (e.g. Greenhill et al. 2004b; Gaume et al. 1998; Menten & Reid 1995; Norris 1984), noting that maser emission of the nature observed in OMC1 is associated with the presence of O-stars. Thus, in OMC1 the turbulence could be driven locally by the powerful outflow from the BN-IRc2 complex, which contains a number of possible candidates such as source I, source n and BN itself (Greenhill et al. 2004a; Doeleman et al. 1999; Menten & Reid 1995; Shuping et al. 2004; Gezari et al. 1998). Turbulence may also be driven on smaller scales by low mass star formation.
The alternative mechanism remains, as mentioned earlier, that the larger scale dynamics is predominantly part of a turbulent cascade driven on greater scales. For this reason we test the statistical quantifiers explored in this paper with the full velocity field and also the residual velocity fluctuations resulting from removing the large scale velocity trends.
The procedure of removal of large scale gradients, or filtering, follows Miesch & Bally (1994). The removal is performed by convolving the data with a smoothing function and then subtracting the smoothed image from the original to obtain the residual image of the small scale velocity fluctuations. The residual image should then reveal any small scale structures that were superposed on the large scale trends in the original. The filtering or smoothing function used here is a two-dimensional equally weighted moving average in the form of a square box. The optimal size of the filter is the broadest possible that removes the large scale gradient but leaves all other features. The 2D autocorrelation function of a velocity map can be used for detecting velocity gradients. These show up as anticorrelations in the direction of the gradient and recorrelations in the direction at right angles (Spicker & Feitzinger 1988).
In the autocorrelation function of our velocity map
the correlation persists in the NE-SW direction and decorrelation
occur in the NW-SE direction. This indicates a large scale velocity
gradient in the NW-SE direction which is consistent with the velocity
difference between Peak 1 and 2. The widest
filter where no anticorrelated sidelobes are discernible in the
autocorrelation function of the residual image is the optimal. By calculating the autocorrelation function for filters of varying size,
the optimal filter size was found to be 14
![]()
![]() 14
14
![]() (
(
![]() AU). All further analysis has been carried out on both the
original full velocity field and on the residual image obtained from filtering with the optimal filter. This latter will be
referred to as the filtered velocity image or field. We find that it is certainly unwise to remove apparent large scale
velocity trends and that the filtered image is not representative of the dynamics in OMC1, as discussed immediately below in Sect. 4.2.
AU). All further analysis has been carried out on both the
original full velocity field and on the residual image obtained from filtering with the optimal filter. This latter will be
referred to as the filtered velocity image or field. We find that it is certainly unwise to remove apparent large scale
velocity trends and that the filtered image is not representative of the dynamics in OMC1, as discussed immediately below in Sect. 4.2.
Larson (1981) identified an empirical relation between
linewidth (or velocity dispersion) and size for molecular clouds and clumps within clouds over
scales of
![]() 0.1-100 pc. Larson obtained a power law
0.1-100 pc. Larson obtained a power law
The structure of OMC1, measured in vibrationally excited H2, reveals a very clumpy environment where the regions of bright emission are in many circumstances imposed on extended weaker emission. OMC1 is thus a case study in the difficulty of determining the physical extent of individual clumps in a turbulent environment. In order to circumvent this problem in computing a size-linewidth relation we follow the method developed by Ossenkopf & Mac Low (2002). We remind the reader at this stage that our observations of linewidth are indirect. That is, we obtain the velocity associated with any pixel from the peak of the line profile observed with the low resolution Fabry-Perot, see Sect. 2. Thus the linewidth associated with any chosen assembly of pixels is given by the velocity dispersion of these peak velocities. This is in contrast to the standard technique in radio observations in which the velocity resolution of observations is a fraction of the linewidth, and the linewidth may then be obtained directly from the measured lineshape. The technique which we use here, that of taking the peak of the line for each pixel, was also used by Ossenkopf & Mac Low (2002) (using centroid velocities). For this reason we refer below to the Larson relationship as a size-velocity dispersion relation, rather than the more familiar size-linewidth. In the present case we note that H2 emission is optically thin and there are no optical depth effects, such as those discussed in detail in Ossenkopf & Mac Low (2002).
![\begin{figure}
\par {\includegraphics[width=8cm]{3439fig2.ps} }
\end{figure}](/articles/aa/full/2006/02/aa3439-05/Timg51.gif) |
Figure 2: Larson size-linewidth relations, Eq. (2). Top: velocity dispersion as a function of size for the full velocity field. A power law fit of index 0.205 is overlaid. Centre: velocity dispersion for the filtered velocity image. Power laws of index 0.210 and -0.004 are overlaid. Bottom: velocity dispersion for the outflow region ( upper line) and Peak 1 ( lower line) with power law fits overlaid. |
| Open with DEXTER | |
The average
brightness weighted velocity
dispersion,
![]() ,
within regions of varying size, is estimated following the prescription of Ossenkopf & Mac Low (2002). We compute the
brightness weighted
probability distribution function of the peak velocities in a circular
region with a given radius and find the corresponding velocity
dispersion from a fit to a Gaussian. This is repeated throughout the map and for a number of radii, R(see Eq. (2)). For each radius the
average velocity dispersion is calculated using intensity weighting. The relation between velocity dispersion and size is shown in
Fig. 2 for both the full velocity image (upper frame) and the
filtered velocity image (centre frame). Errors shown are the statistical standard
error on the mean.
Within the errors the relation for the full velocity field is
consistent with a single power law over more than two orders of
magnitude in R with an exponent
,
within regions of varying size, is estimated following the prescription of Ossenkopf & Mac Low (2002). We compute the
brightness weighted
probability distribution function of the peak velocities in a circular
region with a given radius and find the corresponding velocity
dispersion from a fit to a Gaussian. This is repeated throughout the map and for a number of radii, R(see Eq. (2)). For each radius the
average velocity dispersion is calculated using intensity weighting. The relation between velocity dispersion and size is shown in
Fig. 2 for both the full velocity image (upper frame) and the
filtered velocity image (centre frame). Errors shown are the statistical standard
error on the mean.
Within the errors the relation for the full velocity field is
consistent with a single power law over more than two orders of
magnitude in R with an exponent
![]() ,
although there also appears to be some deviation above 8000 AU.
The value of the exponent agrees with the average value of
,
although there also appears to be some deviation above 8000 AU.
The value of the exponent agrees with the average value of
![]() that
Caselli & Myers (1995) found for massive cores in the Orion A and B clouds
at scales 0.03-1 pc. It is striking that the Larson relationship appears both to hold in this very different regime and to have a very similar exponent as for massive cores, although we are dealing here with
highly excited material.
that
Caselli & Myers (1995) found for massive cores in the Orion A and B clouds
at scales 0.03-1 pc. It is striking that the Larson relationship appears both to hold in this very different regime and to have a very similar exponent as for massive cores, although we are dealing here with
highly excited material.
The appearance of the region south-west of BN with fewer and more isolated clumps of emission, suggests that the dominating physical processes in this region are different from those in Peaks 1 and 2. In Peaks 1 and 2 the emission is more homogeneous and more spatially concentrated. All clumps with measurable radial velocities south-west of BN are blue-shifted. Nissen et al. (2005) provide clear evidence that these objects form the IR counterpart of an outflow detected in radio observations of SiO masers associated with a buried O-star within OMC1 (Greenhill et al. 2004a,b; Menten & Reid 1995; Doeleman et al. 1999; Shuping et al. 2004). For this reason we refer to this zone as the "outflow region''.
We have computed the size-velocity dispersion relation for the outflow
region and Peaks 1 and 2 separately, in each case for the full
velocity field (that is, without filtering of the data - see
Sect. 4.1). The resulting size-velocity dispersion relationships,
shown for the outflow region and Peak 1, with Peak 2 omitted
for clarity, are shown in the third frame of
Fig. 2. This illustrates that the structure adheres to
the Larson relationship in the outflow region south-west of BN but with a significantly lower slope and a somewhat higher proportionality
parameter ![]() in
in
![]() than for Peaks 1 and 2. In the latter two regions
than for Peaks 1 and 2. In the latter two regions ![]() 's and the exponents
's and the exponents ![]() are the same within observational error. The lower value of
are the same within observational error. The lower value of ![]() associated with the outflow region supports the conclusion of Caselli & Myers (1995) that lower exponents are characteristic of massive star-forming regions.
associated with the outflow region supports the conclusion of Caselli & Myers (1995) that lower exponents are characteristic of massive star-forming regions.
The relation based on the filtered velocity image in the centre frame of Fig. 2
shows that the velocity dispersion is not well
represented by a single power law. At radii smaller than ![]() 1600 AU
the relation follows a power law of index 0.210, essentially the same as for the full velocity field. This similarity of behaviour is expected since the filter applied to
remove the velocity gradient has a width of
1600 AU
the relation follows a power law of index 0.210, essentially the same as for the full velocity field. This similarity of behaviour is expected since the filter applied to
remove the velocity gradient has a width of
![]() 0 AU
(Sect. 4.1), and an equivalent radius of 3200 AU, and thus should not affect smaller scales. In contrast to the full velocity field, the
velocity dispersion for the filtered data at larger scales is
constant within observational error as a function of size, in marked contradiction to the accepted form of
the Larson relationship, with an index at scales larger than 1600 AU of
0 AU
(Sect. 4.1), and an equivalent radius of 3200 AU, and thus should not affect smaller scales. In contrast to the full velocity field, the
velocity dispersion for the filtered data at larger scales is
constant within observational error as a function of size, in marked contradiction to the accepted form of
the Larson relationship, with an index at scales larger than 1600 AU of
![]() .
In
a turbulent medium, where the velocity distribution is expected to get broader
with increasing size of the region, this is unnatural and can only be
caused if some of the turbulent velocities have been artificially
removed. We conclude that by removing the large scale gradient we have
removed some of the turbulent energy. It follows therefore that the
large scale motions in OMC1, reported both here and by a number of other
authors (Chrysostomou et al. 1997; Scoville et al. 1982; Sugai et al. 1995; Salas et al. 1999) should be seen as representing real scales of a
turbulent cascade. By implication the turbulence is driven at large
scales and this suggests that turbulence on the scale of the
map could
be either the result of an energy cascade from still greater scales or
injection of
turbulent energy by the large scale outflows associated with massive
star formation in the IRc2 region.
.
In
a turbulent medium, where the velocity distribution is expected to get broader
with increasing size of the region, this is unnatural and can only be
caused if some of the turbulent velocities have been artificially
removed. We conclude that by removing the large scale gradient we have
removed some of the turbulent energy. It follows therefore that the
large scale motions in OMC1, reported both here and by a number of other
authors (Chrysostomou et al. 1997; Scoville et al. 1982; Sugai et al. 1995; Salas et al. 1999) should be seen as representing real scales of a
turbulent cascade. By implication the turbulence is driven at large
scales and this suggests that turbulence on the scale of the
map could
be either the result of an energy cascade from still greater scales or
injection of
turbulent energy by the large scale outflows associated with massive
star formation in the IRc2 region.
This in turn implies that the turbulence in the OMC1 region does not have a strong injection of energy at scales of less than 0.1 pc
and is thus not
primarily driven on small scales, for example by low mass protostellar
outflows.
In support of this, the energy injected by a high mass
stellar outflow considerably exceeds that of the sum total of low mass outflows.
Elsewhere we have estimated (Nissen et al. 2005) that the mass outflow rate is
of the order of >10-3 ![]() /yr in the blue-shifted
outflow, SW of BN, with an average velocity of 18 km s-1. Low mass
protostellar outflow rates are typically three orders of magnitude
lower (Richer et al. 2000), with a
similar velocity. This simple argument on the basis of energetics supports
our conclusion that the injection of energy at the 0.1 pc scale of massive
stars outweighs on the global scale the energy input from low mass
stars. However, as we find in Sect. 5, locally as opposed to globally, the character of the turbulence is strongly affected by low mass protostellar outflows.
/yr in the blue-shifted
outflow, SW of BN, with an average velocity of 18 km s-1. Low mass
protostellar outflow rates are typically three orders of magnitude
lower (Richer et al. 2000), with a
similar velocity. This simple argument on the basis of energetics supports
our conclusion that the injection of energy at the 0.1 pc scale of massive
stars outweighs on the global scale the energy input from low mass
stars. However, as we find in Sect. 5, locally as opposed to globally, the character of the turbulence is strongly affected by low mass protostellar outflows.
The velocity gradient, as identified above, should consequently not be removed prior to analysis. In the following we thus mainly focus on the full velocity field containing velocities on all scales, but for completeness we have also included analysis of the filtered velocity image.
The shape of the wings of the PDF is diagnostic of
intermittency, in which, at random scales and/or time intervals, energy
is dissipated as heat in the turbulent medium. At any scale the
removal of energy must involve those elements of the medium with the
most prevalent velocities. Thus it is the velocities at the centre
of the distribution which becomes most depleted. Thus the velocity
distribution loses its initial Gaussian form, with the
centre depressed and the wings relatively enhanced.
Increasing degrees
of intermittency create a transition from Gaussian (
![]() )
to
exponential (
)
to
exponential (
![]() )
wings in a PDF.
)
wings in a PDF.
Gaussian PDFs may be found in studies of decaying supersonic
turbulence (Ossenkopf & Mac Low 2002) and incompressible turbulence
(e.g. Jayesh & Warhaft 1991; Batchelor 1956). Exponential PDFs can be
found in the literature of
simulations, e.g.
from inelastic collisions of clouds (Ricotti & Ferrara 2002) and interactions
of shells (Chappell & Scalo 2001). Further relevant theoretical studies involve
the stretched exponential form (
![]() )
where
)
where
![]() is fractional (e.g. Frisch & Sornette 1997; Eggers & Wang 1998), where
is fractional (e.g. Frisch & Sornette 1997; Eggers & Wang 1998), where
![]() reproduces the Gaussian PDF and
reproduces the Gaussian PDF and
![]() the exponential form. Fractional
the exponential form. Fractional ![]() values can arise
from random processes whose overall effect accumulate in a
multiplicative manner (see Sect. 4.4).
Other studies are concerned with wings of PDFs in the
form of power laws for example arising from stellar winds or outflows
(Silk 1995).
values can arise
from random processes whose overall effect accumulate in a
multiplicative manner (see Sect. 4.4).
Other studies are concerned with wings of PDFs in the
form of power laws for example arising from stellar winds or outflows
(Silk 1995).
Using line profile data for CO from various isotopes Falgarone & Phillips (1990,1991), Ossenkopf & Mac Low (2002); Falgarone et al. (1994) do not find simple Gaussian behaviour for most observations. However, Falgarone & Phillips (1991) showed that most of the PDFs could be represented by two Gaussians, with the wing component being about 3 times broader than the core component. The PDFs in the present work cannot be so represented. Other work uses centroid velocities, corresponding to the peak velocities used here. For example, Miesch & Scalo (1995), Miesch et al. (1999) found exponential tails in most of their PDFs, while Ossenkopf & Mac Low (2002) found that the PDFs of the Polaris Flare could be reproduced by two Gaussians as in Falgarone & Phillips (1991).
In the present work, the normalized PDF of peak velocities has been calculated by binning the velocities in intervals of 1 km s-1. The PDF can be estimated by assigning the same weight to every pixel or by weighting every velocity with the corresponding brightness in that pixel. By testing both methods we found that the chosen method of weighting does not influence the shape of the PDF significantly. Brightness weighting is less influenced by observational noise and is therefore used in the following analysis.
![\begin{figure}
\par {\includegraphics[width=7.8cm,clip]{3439fig3.ps} }
\end{figure}](/articles/aa/full/2006/02/aa3439-05/Timg65.gif) |
Figure 3:
Probability distribution functions of velocities. Top: (+) PDF for the full velocity field. ( |
| Open with DEXTER | |
Figure 3 shows the peak velocity PDF of the full
velocity field and of the filtered velocity image. The PDF of the filtered
velocity image is artificially
centered around 0 km s-1 through the action of filtering. The PDFs
are shown on a log-linear scale where a Gaussian distribution would
form a parabola and an exponential a straight line. To test
the influence of uncertainties in the
determination of velocities on the shape of the PDF, we have added
to each velocity in the original dataset a random velocity from a
Gaussian distribution with standard deviation corresponding to the
uncertainty in the velocity of
the pixel in question, as given by Eq. (1).
We created a
series of such velocity fields and calculated the PDF from each of
them. The PDFs of
velocity fields so generated are effectively indistinguishable from
the PDF of the real data set, reflecting the fact that the large
number of pixels used in the
PDF,
![]() ,
reduces the effect of the
observational noise to a negligible level. Again, since every bin of the histogram
is populated by a large number of pixels, the relative error,
,
reduces the effect of the
observational noise to a negligible level. Again, since every bin of the histogram
is populated by a large number of pixels, the relative error,
![]() ,
becomes very small, including taking account of the
effective
,
becomes very small, including taking account of the
effective ![]() pixels resolution. Except for the very least populated
bins the statistical error bars would be smaller than the symbols in
Fig. 3 and have therefore been omitted.
pixels resolution. Except for the very least populated
bins the statistical error bars would be smaller than the symbols in
Fig. 3 and have therefore been omitted.
The PDFs in Fig. 3 are clearly not well represented by
Gaussians except
in the inner core, where Gaussians are shown as dashed lines in
Fig. 3. Our data - for hot dense gas -
show a different result to the data reported for much larger
scales in Falgarone & Phillips (1991) (for cool, diffuse gas and
obtained using line profiles), where, as noted, a combination of
two Gaussians fit the
observations. The wings in the present work can be fitted by stretched exponentials (full lines). These lines are derived for the full velocity field data by fitting between +12 and -32 km s-1 and yield
![]() .
A similar fit for the filtered data yields
.
A similar fit for the filtered data yields
![]() .
.
It is clear from Fig. 3 that the PDFs are not symmetric and that the red wing displays large deviations from a smooth behaviour, especially at velocities of 50-60 km s-1, where a hump is seen in the PDF. By inspection of the velocity data we found that the hump results from a single structure in the field. This structure is the only clump of emission with velocities consistently larger than 50 km s-1 and is shown in Fig. 4 in xy-velocity space. If we ignore all pixels in this structure with velocities larger than 43 km s-1, then the PDF for the full field no longer contains a secondary hump at 55 km s-1 (diamonds in the upper frame in Fig. 3). This suggests that the structure involved is an independent entity which does not fit into the overall turbulent cascade. The nature of this dense fast moving object remains mysterious.
The shape of the PDF(s) in Fig. 3 can be further
quantified by the brightness weighted statistical moments, computed directly from the dataset as:
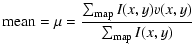 |
(3) | ||
![$\displaystyle {\rm std.~ dev.}=\sigma =\sqrt{\frac{\sum_{\rm map}
I(x,y)[v(x,y)-\mu]^2}{\sum_{\rm map} I(x,y)}}$](/articles/aa/full/2006/02/aa3439-05/img72.gif) |
(4) | ||
![$\displaystyle {\rm skewness}=\frac{\sum_{\rm map} I(x,y)[v(x,y)-\mu]^3}{\sigma^3 \sum_{\rm map} I(x,y)}$](/articles/aa/full/2006/02/aa3439-05/img73.gif) |
(5) | ||
![$\displaystyle {\rm kurtosis}=\frac{\sum_{\rm map} I(x,y)[v(x,y)-\mu]^4}{\sigma^4 \sum_{\rm map} I(x,y)}$](/articles/aa/full/2006/02/aa3439-05/img74.gif) |
(6) |
![\begin{figure}
\par {\includegraphics[width=8.5cm,clip]{3439fig4.ps} }
\end{figure}](/articles/aa/full/2006/02/aa3439-05/Timg75.gif) |
Figure 4:
The brightly emitting clump that causes the hump in
the red wing of the PDF (Fig. 3, + symbols). The xy plane is the plane of the sky, the vertical axis shows the radial
velocity
|
| Open with DEXTER | |
Table 1: Moments and stretching exponents of the peak velocity PDF for the full velocity field and the filtered velocity field
The standard deviation quantifies the spread of the PDF, the skewness is a measure of the asymmetry and the kurtosis characterizes the deviation from a Gaussian profile. A Gaussian distribution has a kurtosis of 3 and larger values imply that the PDF has relatively more prominent wings. An exponential distribution has a kurtosis of 6. The calculated values for the PDF from our present data are listed in Table 1, showing a departure from Gaussian and from pure exponential behaviour. We conclude that the data show clear evidence of intermittency. There is also a skewness towards the blue. This may arise through preferential obscuration of red-shifted flows, compared to blue-shifted, in this dusty and partly obscured region.
The PDFs presented above carry no spatial information. In order to retain some of the spatial characteristics of the velocity field and to quantify how velocities are spatially related within the medium, we now construct the probability distribution function of velocity differences between points separated by a certain distance in the plane of the sky, the lag. The resulting distributions should provide a more searching test of theoretical models than PDFs of peak or centroid velocities.
Velocity differences,
![]() ,
are used in this analysis. Here both
,
are used in this analysis. Here both ![]() and
and
![]() ,
the lag, are two-dimensional space vectors.
Previous
authors, using both observational data and theoretical models, the
latter for incompressible turbulence (Miesch & Scalo 1995; Miesch et al. 1999; Lis et al. 1998) have described how the shape of the PDF
changes with different lags. Specifically, PDFs were found to exhibit strong
non-Gaussian forms at small lags.
,
the lag, are two-dimensional space vectors.
Previous
authors, using both observational data and theoretical models, the
latter for incompressible turbulence (Miesch & Scalo 1995; Miesch et al. 1999; Lis et al. 1998) have described how the shape of the PDF
changes with different lags. Specifically, PDFs were found to exhibit strong
non-Gaussian forms at small lags.
For homogeneous, isotropic turbulence - as assumed here - the same
information can be obtained in a more compact form by investigating
the structure functions as a function of lag magnitude,
![]() .
Structure functions of order p are defined as
.
Structure functions of order p are defined as
Here we study the second order structure function, S2(L), that is the variance, and the kurtosis, S4(L)/S2(L)2 as a function of lag magnitude, L. In this manner information is obtained concerning the evolution of the PDF as a function of lag without the necessity for studying velocity difference PDFs directly. We have included a weighting function for the velocity differences, see Eqs. (8) and (9), and to avoid confusion with the traditional definition of the structure functions (Eq. (7)) we refer to Eq. (8) as the variance function and to Eq. (9) as the kurtosis function.
Both the variance and the kurtosis functions are powerful tools when comparing observations with different models of turbulence. For example, Kolmogorov turbulence predicts a power law variation of the variance function (see Eq. (8)) with lag magnitude, with a scaling exponent of 2/3, whereas Miesch et al. (1999) find values between 0.33 and 1.05 (see below). Numerical and analytical studies of driven supersonic magnetohydrodynamic turbulence find a second order structure function exponent of 0.74 (Boldyrev et al. 2002).
Constructing the variance and kurtosis functions involves combining
data from all pairs of pixels to
obtain PDFs as a function of lag magnitude,
![]() .
The variance and kurtosis of the PDF of velocity differences are then
.
The variance and kurtosis of the PDF of velocity differences are then
In the above, w is some weighting
function. An important issue is whether the velocity data should be brightness
weighted (
![]() )
in counts per second)
or equally weighted (w=1) in calculating the variance and kurtosis of the
velocity difference PDFs. In order to address this problem, we need further
to consider errors in the data. We have already removed data at the 2% level as described in Sect. 2. We now examine whether this cut-off is sufficiently low for the examination of variance and kurtosis functions. We find that a 2% cut-off is too low if we do not use intensity weighting but that it is acceptable if intensity weighting is included.
)
in counts per second)
or equally weighted (w=1) in calculating the variance and kurtosis of the
velocity difference PDFs. In order to address this problem, we need further
to consider errors in the data. We have already removed data at the 2% level as described in Sect. 2. We now examine whether this cut-off is sufficiently low for the examination of variance and kurtosis functions. We find that a 2% cut-off is too low if we do not use intensity weighting but that it is acceptable if intensity weighting is included.
In order to investigate the effect of errors, we
use equal weighting and calculate the variance
function for a
number of cut-off values in brightness.
All the variance functions can be
approximated by power laws, but we find that the scaling exponent,
![]() in
in
![]() ,
increases with increasing cut-off value before converging to a
constant value when the cut-off value reaches
,
increases with increasing cut-off value before converging to a
constant value when the cut-off value reaches ![]() of
of
![]() .
This indicates that
pixels with brightness lower than this value contribute significantly
to the random noise and that they
should be removed prior to analysis. This analysis emphasizes
that caution should always be exercised when equal
weighting is used since results may show dependence on the choice
of cut-off.
.
This indicates that
pixels with brightness lower than this value contribute significantly
to the random noise and that they
should be removed prior to analysis. This analysis emphasizes
that caution should always be exercised when equal
weighting is used since results may show dependence on the choice
of cut-off.
The brightness
weighted variance function is expected to be less influenced by
noise. We find that
the brightness weighted variance function including all pixels is
essentially the same as the equally
weighted variance function with a brightness cut-off of 9% of
![]() .
Due to the lesser influence from noise we use the
brightness weighted variance and kurtosis functions in the following.
.
Due to the lesser influence from noise we use the
brightness weighted variance and kurtosis functions in the following.
Errors in the brightness weighted variance function resulting from uncertainties in the
velocities have been calculated by using the error propagation
law and taking the 1![]() uncertainty on the velocity in each pixel
from Eq. (1). Due to the large number of pixel pairs
that goes into the calculation of the variance function the relative error is
typically 10-3 and therefore negligible.
uncertainty on the velocity in each pixel
from Eq. (1). Due to the large number of pixel pairs
that goes into the calculation of the variance function the relative error is
typically 10-3 and therefore negligible.
The variance function is shown in Fig. 5 for the full
velocity field in a
log-log plot.
The best fit of the variance function to a
power law is found to have
![]() and this is also shown in
Fig. 5.
For comparison, Miesch et al. (1999) obtained values of
and this is also shown in
Fig. 5.
For comparison, Miesch et al. (1999) obtained values of
![]() between 0.33 and 1.05 for several molecular clouds at scales
larger than
between 0.33 and 1.05 for several molecular clouds at scales
larger than
![]() AU while Ossenkopf & Mac Low (2002) obtained
AU while Ossenkopf & Mac Low (2002) obtained
![]() for the Polaris Flare at scales larger than 2000 AU. It
is noteworthy that our
value of
for the Polaris Flare at scales larger than 2000 AU. It
is noteworthy that our
value of
![]() is significantly lower than the
Kolmogorov value of 0.67. We also note that the variance function is closely related to the Larson relationship such that the exponent of the variance function should be of the order of twice the Larson exponent. This is approximately satisfied here.
is significantly lower than the
Kolmogorov value of 0.67. We also note that the variance function is closely related to the Larson relationship such that the exponent of the variance function should be of the order of twice the Larson exponent. This is approximately satisfied here.
The variance function in Fig. 5 in fact deviates significantly from a single power law, again underlining the non-Kolmogorov nature of the gas dynamics. This is particularly apparent through a positive deviation around 800 AU and a negative deviation around 100-200 AU. The curvature of the structure function may suggest the presence of a multi-fractal medium. At all events, several power laws operating in different ranges would appear necessary to fit the behaviour of the variance function.
![\begin{figure}
\par {\includegraphics[width=8cm]{3439fig5.ps} }
\end{figure}](/articles/aa/full/2006/02/aa3439-05/Timg94.gif) |
Figure 5: The variance function for the full velocity field. A power law form with exponent 0.53 is overlaid. The inset displays the variance function of the filtered velocity image compared to the variance function of the full field. |
| Open with DEXTER | |
The physical meaning attached to
![]() in Fig. 5 is
that it approximately represents all energies in eddies below any scale L(Davidson 2004). The deviation from a power law in
Fig. 5 below
in Fig. 5 is
that it approximately represents all energies in eddies below any scale L(Davidson 2004). The deviation from a power law in
Fig. 5 below
![]() 2000 AU therefore represents more energy at lower scales and
implies that there is an excess of material in
motion at 2000 AU and below. This scale suggests that the excess arises from outflow events associated with star
formation which result in energy injection at scales below 2000 AU. This feature is apparent from the data presented in Paper I and in Nissen et al. (2005).
Conversely the material appears to suffer less velocity dispersion at
scales below 300 AU. Thus material associated with these smaller scales appears to have dissipated some of its turbulent energy at larger scales. We speculate that these smaller less turbulent scales may be associated with protostellar nebulae or perhaps evaporating discs around protostars.
In earlier work, purely on the basis of spatially resolved
imaging (Vannier et al. 2001; Lacombe et al. 2004), a range of preferred scale sizes lying between 700 AU and 1100 AU was identified in Peak 2. In those cases and in the present case we suggest that the
breaks in power laws are directly linked to scales associated with
star formation.
2000 AU therefore represents more energy at lower scales and
implies that there is an excess of material in
motion at 2000 AU and below. This scale suggests that the excess arises from outflow events associated with star
formation which result in energy injection at scales below 2000 AU. This feature is apparent from the data presented in Paper I and in Nissen et al. (2005).
Conversely the material appears to suffer less velocity dispersion at
scales below 300 AU. Thus material associated with these smaller scales appears to have dissipated some of its turbulent energy at larger scales. We speculate that these smaller less turbulent scales may be associated with protostellar nebulae or perhaps evaporating discs around protostars.
In earlier work, purely on the basis of spatially resolved
imaging (Vannier et al. 2001; Lacombe et al. 2004), a range of preferred scale sizes lying between 700 AU and 1100 AU was identified in Peak 2. In those cases and in the present case we suggest that the
breaks in power laws are directly linked to scales associated with
star formation.
The inset in
Fig. 5 shows the effect of the removal of the large scale
gradient on the variance function. The variance function of the
filtered velocity image is identical
to the variance function of the full field for scales smaller than
half the size of the
filter (![]() 3000 AU) above which the function flattens. It is clear that the
filter has no effect on very small scales
and that the removal of the large scale velocity structure causes
the variance function to be systematically smaller on larger
scales. This effect of the
filtering has also been noted by Miesch et al. (1999) and is most likely an artefact due to the finite size of the map (Ossenkopf & Mac Low 2002).
3000 AU) above which the function flattens. It is clear that the
filter has no effect on very small scales
and that the removal of the large scale velocity structure causes
the variance function to be systematically smaller on larger
scales. This effect of the
filtering has also been noted by Miesch et al. (1999) and is most likely an artefact due to the finite size of the map (Ossenkopf & Mac Low 2002).
![\begin{figure}
\par {\includegraphics[width=8cm]{3439fig6.ps} }
\end{figure}](/articles/aa/full/2006/02/aa3439-05/Timg96.gif) |
Figure 6: The kurtosis function, Eq. (9), for the full velocity field (solid line). Theoretical predictions for 3 different Reynolds numbers from Eggers & Wang (1998) are shown for comparison. |
| Open with DEXTER | |
Turning now to the kurtosis function, the kurtosis is a measure of the degree of correlation in the motion at a certain scale relative to overall motions seen in the map. A velocity field with no spatial correlations would display a Gaussian shape. As mentioned above, a Gaussian has a kurtosis of 3. Thus values of kurtosis exceeding 3 indicate the strength of velocity correlation at specific lags. From simulations Ossenkopf & Mac Low (2002) found that kurtosis values above 3 can only be verified if the map has a scale considerably larger than the lag. As the lag approaches the size of the map, the value of the kurtosis tends to approach the Gaussian value of 3. This arises because the map cannot of course contain larger scales than the size of the map itself. Thus a kurtosis value around 3 is always expected at scales approaching the size of the map and provides no useful information on the velocity correlations at that scale.
Looking specifically at filamentary structure, Lis et al. (1998) found
non-Gaussian wings of velocity difference PDFs at small scales
evolving into Gaussians at larger scales, without quoting values of
kurtosis.
Miesch et al. (1999) found kurtosis values between 10 and 30 at the
smallest lags (
![]() AU), with the
required Gaussian value of 3 at large lags of the order of the map size
(
AU), with the
required Gaussian value of 3 at large lags of the order of the map size
(
![]() AU). Similar behaviour was found by Ossenkopf & Mac Low (2002).
The kurtosis function derived from our present data is shown in
Fig. 6 as a continuous line. The kurtosis values approach 30 at small lags
(100 AU)
and decrease gradually until reaching the value of 3 at
large lags. The shape of the
kurtosis function shows some similarity to those presented in
Miesch et al. (1999). However a much more striking comparison may be found
with results of a model of multifractal processes in Eggers & Wang (1998). In Eggers & Wang (1998) the kurtosis, called flatness in that work, is
constant out to some lag beyond which the kurtosis decreases with
increasing lag. The shape of the kurtosis was found by
Eggers & Wang (1998) to depend on the Reynolds
number, where
AU). Similar behaviour was found by Ossenkopf & Mac Low (2002).
The kurtosis function derived from our present data is shown in
Fig. 6 as a continuous line. The kurtosis values approach 30 at small lags
(100 AU)
and decrease gradually until reaching the value of 3 at
large lags. The shape of the
kurtosis function shows some similarity to those presented in
Miesch et al. (1999). However a much more striking comparison may be found
with results of a model of multifractal processes in Eggers & Wang (1998). In Eggers & Wang (1998) the kurtosis, called flatness in that work, is
constant out to some lag beyond which the kurtosis decreases with
increasing lag. The shape of the kurtosis was found by
Eggers & Wang (1998) to depend on the Reynolds
number, where
![]() marks a transition from a convex
shape to a concave shape. The shape remains essentially unchanged for
higher Reynolds numbers.
marks a transition from a convex
shape to a concave shape. The shape remains essentially unchanged for
higher Reynolds numbers.
In order to compare with results in Eggers & Wang (1998)
we make an estimate of the Reynolds number of the flows in OMC1.
The Reynolds number is given by
![]() ,
where u and l are
the typical velocity and length scale, respectively, associated with
the gas flows. The dynamical viscosity,
,
where u and l are
the typical velocity and length scale, respectively, associated with
the gas flows. The dynamical viscosity, ![]() ,
can be approximated by
,
can be approximated by
![]() ,
where
,
where ![]() is the mean-free-path of the
particles and
is the mean-free-path of the
particles and
![]() is the rms thermal velocity
(kT/
is the rms thermal velocity
(kT/![]() m
m![]() )1/2 (Frisch 1995). Thus,
)1/2 (Frisch 1995). Thus,
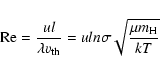 |
(10) |
The Eggers & Wang (1998) description of turbulent processes is ad hoc in the
sense that it does not result from detailed high resolution three
dimensional
MHD simulations. Instead some reasonable assumptions are made concerning
the
cascade of turbulent energy, assuming it to be a stochastic process,
isotropic and homogeneous in space, with certain additional properties
which are briefly summarized below.
Once one assumes that the turbulence is isotropic and homogeneous, the turbulence in the Fourier domain is represented by a spectrum which
is a function of a single variable r, corresponding to a size of
turbulent eddies.
The approach of Eggers & Wang (1998) is to impose a recipe for the cascade
of energy from larger to smaller scales. The recipe states that energy
at a given scale r is transferred only to a scale r/2.
The amount of energy transferred, or more precisely the ratio
s of the velocity amplitudes between scale r and r/2 in equilibrium,
is given by a probability distribution :
Equation (11) states that the probability p is high (![]() )
for the
ratio of velocities to be relatively small (s=s1), which
corresponds to a low efficiency of
energy cascade from one scale to the next. However there remains a probability
of
)
for the
ratio of velocities to be relatively small (s=s1), which
corresponds to a low efficiency of
energy cascade from one scale to the next. However there remains a probability
of ![]() that there is efficient cascading, s=s2.
Starting from some chosen outer scale, this recipe allows for a very quick
calculation of the energy at any given smaller scale by multiplying
the probabilities for every cascade step lying between these two
scales and producing the appropriate PDF semi-analytically. Hence the
term multiplicative turbulence. The
viscous cut-off of the turbulence is implemented through stopping the
further cascading of energy if the Reynolds number at a given scale
falls below a set value. The velocity fluctuation spectrum is replaced below that scale by an exponentially decaying tail.
that there is efficient cascading, s=s2.
Starting from some chosen outer scale, this recipe allows for a very quick
calculation of the energy at any given smaller scale by multiplying
the probabilities for every cascade step lying between these two
scales and producing the appropriate PDF semi-analytically. Hence the
term multiplicative turbulence. The
viscous cut-off of the turbulence is implemented through stopping the
further cascading of energy if the Reynolds number at a given scale
falls below a set value. The velocity fluctuation spectrum is replaced below that scale by an exponentially decaying tail.
We show in Fig. 6 a comparison between our observed
kurtosis and that presented in Eggers & Wang (1998) for Reynolds numbers
between
![]() and
and
![]() ,
the highest which Eggers & Wang (1998) show, noting once more that the form of the kurtosis function appears to be independent of
Reynolds number above
,
the highest which Eggers & Wang (1998) show, noting once more that the form of the kurtosis function appears to be independent of
Reynolds number above
![]() .
The lower Reynolds number cases
are shown purely for comparison. The similarity of the kurtosis
function between that for our data and that of Eggers & Wang (1998)
suggests that the model of a multifractal, multiplicative turbulent medium on which Eggers & Wang (1998) is based may capture some of the physics of the turbulence in
the hot component of the gas in OMC1.
.
The lower Reynolds number cases
are shown purely for comparison. The similarity of the kurtosis
function between that for our data and that of Eggers & Wang (1998)
suggests that the model of a multifractal, multiplicative turbulent medium on which Eggers & Wang (1998) is based may capture some of the physics of the turbulence in
the hot component of the gas in OMC1.
The high spatial resolution of the data allows the analysis of individual clumps of shocked gas with the same statistical methods as above. First, the dimensions of individual clumps must be defined and the following algorithm is used to identify the extent of any clump. The data are smoothed by a 9 by 9 pixel boxcar, in order that random fluctuations become unimportant. A clump is defined as a region which encompasses all pixels surrounding a local brightness maximum where the emission is situated on a continuously decreasing slope from the maximum brightness. Thus when we move in any direction starting from the pixel of maximum brightness and encounter a pixel with higher brightness than the preceding pixel, we define this as the boundary of the clump in this direction. As a further constraint we only use pixels with a brightness larger than 20% of the local brightness maximum. This avoids clumps becoming unrealistically large in the outer regions with low brightness and few brightness maxima. The 20% restriction has no effect in bright congested regions such as Peak 1 and 2. In passing, we note that we cannot rule out that some clumps so identified are the result of chance superpositions of two or more isolated clumps in the same line-of-sight. We have ignored this possibility.
With the above definition, we have delineated 170 clumps. These are in most part essentially the same features as analyzed in Nissen et al. (2005). The number of pixels in each clump ranges from 841 to 18 026, which corresponds to sizes of clumps between approximately 500 and 2200 AU. Due to the small size of the clumps, the earlier discussion concerning the removal of the large scale gradient is irrelevant here, since filtering does not affect the velocity field over such restricted regions.
![\begin{figure}
\par {\includegraphics[width=8.5cm,clip]{3439fig7.ps} }
\end{figure}](/articles/aa/full/2006/02/aa3439-05/Timg115.gif) |
Figure 7: PDFs of eight representative clumps. a), b), c) and d) are multi-modal, e) and f) are stretched exponential, g) and h) are Gaussian. Positions are shown in Figs. 8, 10, 11. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=12cm]{3439fig8.eps}\end{figure}](/articles/aa/full/2006/02/aa3439-05/Timg116.gif) |
Figure 8:
Position of clumps with bi- or multimodal PDF (blue),
stretched exponential PDF (green) and Gaussian PDF (red). The underlying grey background represents the spatial extent of velocity integrated H2 emission at 2.121 |
| Open with DEXTER | |
The spatial distribution of clumps with Gaussian PDFs, stretched exponential
PDFs and bi- or multimodal PDFs is shown in Fig. 8.
Clumps with Gaussian PDFs are found in all regions of the observed
field, except in the central region around BN-IRc2, with essentially
the same distribution as clumps with non-Gaussian
PDFs. That is,
there is no tendency for clumps with Gaussian PDFs, for example, to group together in small
areas. Thus it seems that the turbulence dominating the BN-KL nebula
can simultaneously produce both Gaussian and non-Gaussian PDFs in clumps
with sizes
of
![]() AU, and that the clumps with Gaussian and non-Gaussian PDFs are
intermingled. However there appears to be some mechanism that inhibits the
formation of clumps with Gaussian PDFs in the outflow region around
BN-IRc2.
AU, and that the clumps with Gaussian and non-Gaussian PDFs are
intermingled. However there appears to be some mechanism that inhibits the
formation of clumps with Gaussian PDFs in the outflow region around
BN-IRc2.
In connection with the above, Gaussian PDFs would of course arise if the velocity data had a significant noise contribution. However it turns out that
this is not the case save perhaps in 3 of the 27 clumps mentioned above.
For six of the 27 clumps with Gaussian
PDFs, the 1![]() uncertainty on the velocities
(Eq. (1)) exceeds the
half-width (one standard deviation) of the Gaussian PDF in 1% or more of the
total number of pixels. The numbers of pixels are 1%, 4%, 5%, 28%, 32% and 54% of the totals. In the latter three of these six clumps the velocity
distribution could be
dominated by uncertainties in the velocities and these data may
therefore be spurious, in the sense that the Gaussian character may be
over-emphasized by noise.
uncertainty on the velocities
(Eq. (1)) exceeds the
half-width (one standard deviation) of the Gaussian PDF in 1% or more of the
total number of pixels. The numbers of pixels are 1%, 4%, 5%, 28%, 32% and 54% of the totals. In the latter three of these six clumps the velocity
distribution could be
dominated by uncertainties in the velocities and these data may
therefore be spurious, in the sense that the Gaussian character may be
over-emphasized by noise.
The variance function of the
velocity field has also been
calculated for each clump, using Eq. (8). Most of the variance functions
appear to be well approximated
by power laws with a few exceptions, but the value of the scaling exponent ![]() varies between essentially zero, that is, a flat distribution, and 1.61. The variance functions are
shown in Fig. 9 for the eight representative clumps shown in Fig. 7.
varies between essentially zero, that is, a flat distribution, and 1.61. The variance functions are
shown in Fig. 9 for the eight representative clumps shown in Fig. 7.
![\begin{figure}
\par {\includegraphics[width=8.5cm]{3439fig9.ps} }
\end{figure}](/articles/aa/full/2006/02/aa3439-05/Timg118.gif) |
Figure 9: The variance function for the eight individual clumps shown in Fig. 7. Power law fits are overlaid and the value of the exponent is given. |
| Open with DEXTER | |
The
errors in the variance functions have been calculated in the same way as for the full
region in Sect. 4.4. The magnitude of the errors
depend on the brightness (see Eq. (1)) and the physical
size of the clump, where size is the dominating parameter. Thus the smaller clumps have the larger errors, but even the smallest clumps have relative errors of no more than 10%. Two of the clumps in
Fig. 9 have relative errors of 10% which is of the
same order as the size of the symbols in Fig. 9. Thus the errors have
been omitted in Fig. 9. Errors in values of ![]() arise from lack of precision of the power law fit, rather than from
random errors in the variance. Typical errors in
arise from lack of precision of the power law fit, rather than from
random errors in the variance. Typical errors in ![]() are
are ![]() 0.01. Clumps with
Gaussian PDFs show
0.01. Clumps with
Gaussian PDFs show
![]() including or excluding the 3
clumps with significant noise contributions (see Sect. 5.1).
Clumps with
non-Gaussian PDFs cover the whole range of
including or excluding the 3
clumps with significant noise contributions (see Sect. 5.1).
Clumps with
non-Gaussian PDFs cover the whole range of
![]() .
.
![\begin{figure}
\par\includegraphics[width=12cm]{3439fi10.eps}\end{figure}](/articles/aa/full/2006/02/aa3439-05/Timg121.gif) |
Figure 10:
Clumps with the variance function scaling exponent
|
| Open with DEXTER | |
A high value of ![]() represents more ordered structure in the velocity
field and large velocity gradients within the clump. This
suggests the presence of ordered shock structure. Figure 10 shows the spatial distribution of clumps with
represents more ordered structure in the velocity
field and large velocity gradients within the clump. This
suggests the presence of ordered shock structure. Figure 10 shows the spatial distribution of clumps with
![]() ,
that is, clumps with the highest degree of order in the velocity field. The
less ordered clumps with
,
that is, clumps with the highest degree of order in the velocity field. The
less ordered clumps with
![]() ,
the Kolmogorov
value, are shown in Fig. 11. Examination of Figs. 10 and 11 shows that the
value of
,
the Kolmogorov
value, are shown in Fig. 11. Examination of Figs. 10 and 11 shows that the
value of ![]() does not correlate with brightness, that is, high
does not correlate with brightness, that is, high ![]() can occur equally for strong and weak emission clumps. Furthermore, in
Peaks 1 and 2 - but not in the central region around BN-IRc2, see
below - clumps with
high
can occur equally for strong and weak emission clumps. Furthermore, in
Peaks 1 and 2 - but not in the central region around BN-IRc2, see
below - clumps with
high ![]() may be found mixed with clumps with low
may be found mixed with clumps with low ![]() in the same
spatial region. A theory of star formation including turbulence,
self-gravity, bipolar outflows, etc. should thus be able to reproduce
such a range of exponents of the variance function
within a limited physical region.
in the same
spatial region. A theory of star formation including turbulence,
self-gravity, bipolar outflows, etc. should thus be able to reproduce
such a range of exponents of the variance function
within a limited physical region.
The majority of clumps with ![]() less than the Kolmogorov value of
0.67 resides in Peaks 1 and 2 as seen in Figs. 10 and 11. The major part of these corresponds to clumps with measured velocities which display no clear
structure and whose relative velocities within any clump do not exceed 5 km s-1 (Nissen et al. 2005), accordingly giving low values of the exponent. We suggest that some of these regions may arise from
photodissociation regions (PDRs) involving an irregular surface
containing a variety of lines of sight, illuminated by
less than the Kolmogorov value of
0.67 resides in Peaks 1 and 2 as seen in Figs. 10 and 11. The major part of these corresponds to clumps with measured velocities which display no clear
structure and whose relative velocities within any clump do not exceed 5 km s-1 (Nissen et al. 2005), accordingly giving low values of the exponent. We suggest that some of these regions may arise from
photodissociation regions (PDRs) involving an irregular surface
containing a variety of lines of sight, illuminated by
![]() Ori-C, in a model essentially as described in Field et al. (1994) for the PDR NGC 2023. This would be
consistent with
a region lacking regular structure. However some low
Ori-C, in a model essentially as described in Field et al. (1994) for the PDR NGC 2023. This would be
consistent with
a region lacking regular structure. However some low ![]() clumps
are very bright and cannot be reconciled with a PDR excitation model. These are likely to be shocks travelling across the line of sight.
clumps
are very bright and cannot be reconciled with a PDR excitation model. These are likely to be shocks travelling across the line of sight.
![\begin{figure}
\par\includegraphics[width=12cm]{3439fi11.eps}\end{figure}](/articles/aa/full/2006/02/aa3439-05/Timg123.gif) |
Figure 11:
Clumps with the variance function scaling exponent
|
| Open with DEXTER | |
Many clumps with high ![]() (Fig. 10) are situated
in the vicinity of
the BN-IRc2 complex in the central region. Moving away from
BN-IRc2, their occurrence becomes progressively less. Some of the high
(Fig. 10) are situated
in the vicinity of
the BN-IRc2 complex in the central region. Moving away from
BN-IRc2, their occurrence becomes progressively less. Some of the high
![]() clumps possess morphologies which resemble bow
shocks
(e.g. at (-18
clumps possess morphologies which resemble bow
shocks
(e.g. at (-18
![]() ,
0
,
0
![]() )
and (-21
)
and (-21
![]() ,
-7
,
-7
![]() ), see
Fig. 10)
and are part of the blue-shifted lobe of a bipolar outflow from
radio source I, itself associated with a massive
O-star
(Nissen et al. 2005; Greenhill et al. 2004b,a; Doeleman et al. 1999; Menten & Reid 1995; Shuping et al. 2004).
Other high
), see
Fig. 10)
and are part of the blue-shifted lobe of a bipolar outflow from
radio source I, itself associated with a massive
O-star
(Nissen et al. 2005; Greenhill et al. 2004b,a; Doeleman et al. 1999; Menten & Reid 1995; Shuping et al. 2004).
Other high ![]() clumps
correspond to protostellar candidates identified in
Paper I and arise from outflows created internally in the
clumps e.g. at
(-30
clumps
correspond to protostellar candidates identified in
Paper I and arise from outflows created internally in the
clumps e.g. at
(-30
![]() ,35
,35
![]() )
and (-10
)
and (-10
![]() ,15
,15
![]() ), marked A and B in
Fig. 10.
), marked A and B in
Fig. 10.
In contrast to regions of high ![]() ,
regions of low
,
regions of low ![]() are
notably absent around BN-IRc2 and in the vicinity of source I, and
tend to congregate where regions of high
are
notably absent around BN-IRc2 and in the vicinity of source I, and
tend to congregate where regions of high ![]() are scarce. Our view of turbulent motion, based on models of turbulence,
like that for example of Eggers & Wang (1998), deals only with spatial
scales and not directions. Thus we tend to consider only isotropic
turbulence. However in the central region between Peaks 1 and 2, and also
to the south-west of BN, the outflow from source I imposes a strong constraint on the radial motion of clumps in that region, where as mentioned clumps show a strong blue-shift. Motion
is evidently not isotropic here. We suggest that high values of
are scarce. Our view of turbulent motion, based on models of turbulence,
like that for example of Eggers & Wang (1998), deals only with spatial
scales and not directions. Thus we tend to consider only isotropic
turbulence. However in the central region between Peaks 1 and 2, and also
to the south-west of BN, the outflow from source I imposes a strong constraint on the radial motion of clumps in that region, where as mentioned clumps show a strong blue-shift. Motion
is evidently not isotropic here. We suggest that high values of
![]() arise in this region because effects of turbulence in the radial
direction are effectively swamped in the variance function
by large blue-shifted motions and the turbulence tends to 2D rather than
isotropic 3D. As we move away from the region of the blue-shifted outflow,
low
arise in this region because effects of turbulence in the radial
direction are effectively swamped in the variance function
by large blue-shifted motions and the turbulence tends to 2D rather than
isotropic 3D. As we move away from the region of the blue-shifted outflow,
low ![]() clumps are once more encountered (see Fig.
11). It is an interesting challenge to theory to test if
imposition of a strong outflow has the effects that we observe here on
values of
clumps are once more encountered (see Fig.
11). It is an interesting challenge to theory to test if
imposition of a strong outflow has the effects that we observe here on
values of ![]() ,
as a check on our interpretation. Models should
also demonstrate the absence of Gaussian PDFs.
,
as a check on our interpretation. Models should
also demonstrate the absence of Gaussian PDFs.
We now consider high ![]() regions outside the blue-shifted outflow
zone, that is, those which are well-mixed with regions of low
regions outside the blue-shifted outflow
zone, that is, those which are well-mixed with regions of low ![]() .
The formation and evolution of protostellar objects involve periods where
a high degree of order in the velocity field surrounding the protostar
is expected. A bipolar outflow encountering the circumstellar envelope
would for example shock-excite the gas while creating an organized
velocity field, with accompanying high
.
The formation and evolution of protostellar objects involve periods where
a high degree of order in the velocity field surrounding the protostar
is expected. A bipolar outflow encountering the circumstellar envelope
would for example shock-excite the gas while creating an organized
velocity field, with accompanying high ![]() .
The detection of clumps with
high values of
.
The detection of clumps with
high values of ![]() could therefore
potentially allow an independent method of identifying early
protostellar objects in the Class 0/1 phase. This method may prove of value with the advent of very high spatial resolution radio maps with the Atacama Large Millimetre Array.
could therefore
potentially allow an independent method of identifying early
protostellar objects in the Class 0/1 phase. This method may prove of value with the advent of very high spatial resolution radio maps with the Atacama Large Millimetre Array.
The fraction of gas studied in the present work is highly excited and very dense and quite distinct from gas whose statistical properties have been studied in earlier work. The latter refers to much larger scales and to much cooler, lower density and relatively quiescent gas. Nevertheless we have found that the hot dense gas in OMC1 nicely follows the general trends observed in earlier studies, down to the smallest, densest scales investigated here.
Our major conclusions from the statistical analysis of flows of H2 in OMC1 may be outlined as follows:
1. The size-linewidth relation of Larson (1981)
is recovered at the small scales investigated here. The scaling
exponent is
![]() ,
which agrees with the
average value of
,
which agrees with the
average value of
![]() that Caselli & Myers (1995) found in
Orion at scales
0.03-1 pc, using CO as an indicator (and which did not in fact include OMC1).
that Caselli & Myers (1995) found in
Orion at scales
0.03-1 pc, using CO as an indicator (and which did not in fact include OMC1).
2. We find that the outflow, shown elsewhere (Nissen et al. 2005) to originate from a young and deeply buried O-star, between Peaks 1 and 2, generates structure which also follows the Larson relationship. Thus quite different environments preserve the Larson relationship. The velocity dispersion is however higher for any given size of object than elsewhere in the field and the exponent is significantly smaller than in the full region.
3. If we use velocity filtered data, removing the largest scales which appear as an apparent gradient of velocity, the Larson relationship breaks down. We conclude that the large scale motions are an inherent part of the turbulent cascade and should therefore not be removed from the data. Large scale injection of turbulent energy is the dominant process and outflows from massive star(s) in the IRc2 complex may contribute a substantial part of the driving of the turbulence at the scale of 0.1 pc.
4. The probability distribution function (PDF) of velocities is best fitted by an exponential or a weakly stretched exponential and departs strongly from Gaussian. This suggests that the turbulence in the region studied here is characterized by intermittency.
5. The variance function of the velocity differences is not well represented by a single power
law. A multifractal model is implied. The best fit scaling
component is
![]() ,
significantly lower than the Kolmogorov
value of 0.67, underlining the non-Kolmogorov nature of the turbulence.
,
significantly lower than the Kolmogorov
value of 0.67, underlining the non-Kolmogorov nature of the turbulence.
6. The behaviour of the variance function shows that there is a preferred scale size in the medium below 2000 AU reflecting the presence of protostellar
zones of this dimension and below. There is also clear evidence of
less turbulent structure below ![]() 300 AU, perhaps representing a
population of protostellar disks which have expelled part of their
turbulent energy.
300 AU, perhaps representing a
population of protostellar disks which have expelled part of their
turbulent energy.
7. As further evidence of the multifractal nature of the medium, the kurtosis function of the velocity differences closely resembles that of the multifractal model of Eggers & Wang (1998) for high Reynolds numbers.
8. Analysis of 170 individual clumps with sizes between 500 and 2200 AU opens a window on a regime of scales that has never before been explored using statistical techniques. Studies at these scales reveal considerable diversity of velocity PDFs, with some Gaussian, some showing evidence of intermittency and many with complex structure, reflecting multiple outflows. Variance functions are approximately power laws, with exponents varying between zero and 1.61. There is no spatial association between high and low exponent clumps nor is there any association between Gaussian PDFs and high or low exponents.
9. To emphasize the last point, clumps with a variety of forms of the PDF and different values of the scaling exponent of the variance function are found in the same spatial region and in the whole region covered by the observations.
10. An outflow region associated with a deeply embedded O-star between Peaks 1 and 2 shows markedly different statistical characteristics from Peaks 1 and 2. Clumps in the vicinity of the BN-IRc2 complex typically show high scaling exponents in the variance function. This may be due to the action of the energetic outflow imposed on intrinsic turbulent motion within individual clumps. At all events high and low exponent clumps are spatially segregated in this zone, with low exponent clumps found only at the edges.
11. The outflow region apart, our results suggest that analysis using variance functions could be a useful way in which to establish the presence of early star-forming regions.
The above results constitute a challenge for numerical simulations of turbulence in star forming regions. To our knowledge the resolution of any present numerical simulation is substantially lower than the resolution of these observations, but advances in computer technology will soon allow simulations to reach the scales encountered here. A self-consistent theory of star formation including self-gravity and MHD turbulence should be able to reproduce the features outlined in this paper. Thus the size-linewidth relation, the probability distribution function of peak velocities and the variance and the kurtosis of velocity differences as a function of lag form a dataset which models of star-forming regions should aim to reproduce.
Acknowledgements
The authors would like to thank Dr. Wang for supplying us with numerical values for inclusion in Fig. 6. D.F. and M.G. would like to acknowledge the support of the Aarhus Centre for Atomic Physics (ACAP), funded by the Danish Basic Research Foundation and the Instrument Centre for Danish Astrophysics (IDA), funded by the Danish Natural Science Research Council. DF would also like to thank the Observatoire Paris-Meudon for support during the period in which this work was performed. J.L.L. would like to acknowledge the support of the PCMI National Program funded by the CNRS. We would also like to thank the Directors and Staff of the CFHT for making possible the observations reported in this paper. We should also like to acknowledge the helpful comments made by the referee.