A&A 445, 423-439 (2006)
DOI: 10.1051/0004-6361:20042223
J. Fliri1,![]() - A.
Riffeser1,2,
- A.
Riffeser1,2,![]() - S. Seitz 1 - R.
Bender1,2
- S. Seitz 1 - R.
Bender1,2
1 - Universitätssternwarte München, Scheinerstrasse 1,
81679 München, Germany
2 - Max-Planck-Institut für Extraterrestrische
Physik, Giessenbachstrasse, 85748 Garching, Germany
Received 21 October 2004 / Accepted 24 August 2005
Abstract
In this paper we present the WeCAPP catalogue
of variable stars found in the bulge of M 31. Observations
in the WeCAPP microlensing survey (optical R and I bands)
for a period of three years (2000-2003)
resulted in a database with unprecedented time coverage for an
extragalactic variable star study. We detected 23781 variable sources
in a
![]() field centered on the nucleus of
M 31. The catalogue of variable stars contains the positions, the
periods, and the variation amplitudes in the R and I bands. We
classified the variables according to their position in the R-band
period-amplitude
plane. Three groups can be distinguished; while the first two groups
can be mainly associated with Cepheid-like variables (population I
Cepheids in group I; type II Cepheids and RV Tauri stars in group II),
the third one consists of Long Period Variables (LPVs). We detected 37
RV Tauri stars and 11 RV Tauri candidates, which makes this catalogue
one of the largest
collections of this class of stars to date. The classification scheme
is supported by Fourier decomposition of the light curves. Our data
shows a correlation of the low-order Fourier coefficients
field centered on the nucleus of
M 31. The catalogue of variable stars contains the positions, the
periods, and the variation amplitudes in the R and I bands. We
classified the variables according to their position in the R-band
period-amplitude
plane. Three groups can be distinguished; while the first two groups
can be mainly associated with Cepheid-like variables (population I
Cepheids in group I; type II Cepheids and RV Tauri stars in group II),
the third one consists of Long Period Variables (LPVs). We detected 37
RV Tauri stars and 11 RV Tauri candidates, which makes this catalogue
one of the largest
collections of this class of stars to date. The classification scheme
is supported by Fourier decomposition of the light curves. Our data
shows a correlation of the low-order Fourier coefficients ![]() with
with ![]() for classical
Cepheids, as well as for type II Cepheids and RV Tauri stars.
Correlating our sample of variable stars with X-ray based
catalogues of Kaaret (2002, ApJ, 578, 114) and Kong et al. (2002, ApJ, 577, 738) results in 23 and 31
coincidences, 8 and 12 of which are M 31 globular clusters. The number density
of detected variables is clearly not symmetric, which has to be
included in the calculations of the expected microlensing event rate
towards M 31. This asymmetry is due to the enhanced extinction in the
spiral arms superimposed on the bulge of M 31, which reduces the number
of sources to about 60%, if compared to areas of equivalent bulge
brightness without enhanced extinction present.
for classical
Cepheids, as well as for type II Cepheids and RV Tauri stars.
Correlating our sample of variable stars with X-ray based
catalogues of Kaaret (2002, ApJ, 578, 114) and Kong et al. (2002, ApJ, 577, 738) results in 23 and 31
coincidences, 8 and 12 of which are M 31 globular clusters. The number density
of detected variables is clearly not symmetric, which has to be
included in the calculations of the expected microlensing event rate
towards M 31. This asymmetry is due to the enhanced extinction in the
spiral arms superimposed on the bulge of M 31, which reduces the number
of sources to about 60%, if compared to areas of equivalent bulge
brightness without enhanced extinction present.
Key words: galaxies: individual: M 31 - cosmology: dark matter - stars: variables: general - stars: variables: Cepheids - X-rays: stars
In the past decade the microlensing surveys of the galactic bulge and the Magellanic Clouds (LMC and SMC) have greatly extended our knowledge of variable stars. As the observations of these experiments usually cover a long time span with good time sampling, the resulting data sets are perfectly suited for the study of many different types of variable sources. Hence, lots of the progress in this field has resulted from the work of collaborations like MACHO (e.g., Alcock et al. 1998,1995), EROS (e.g., Beaulieu et al. 1995; Derue et al. 2001), OGLE (e.g., Wray et al. 2004; Cieslinski et al. 2003) or MOA (e.g., Noda et al. 2002; 2004). The list of identified variable stars in the Galaxy and the Magellanic Clouds was enlarged in numerous publications, which not only improved on the number statistics, but has also helped to understand the physical processes dominating these stars better.
M 31 has been surveyed for variable sources since the 1920s, starting with the pioneering work of Edwin Hubble. With plates taken at the newly available Mount Wilson telescope, Hubble succeeded in resolving Cepheid variables in the outer parts of M 31. Using the already established period-luminosity relation, Hubble (1922) was able to determine the distance to M 31 to 300 kpc (the difference to the actual value of 780 kpc (Stanek & Garnavich 1998) is mainly due to an erroneous calibration of the zero-point of the PL-relation and a missing reddening correction) and in this way to reveal the extragalactic nature of the "Andromeda Nebula''. Baade & Swope (1965,1963) continued the work on variable stars in M 31 and detected over 400 variables, among them Cepheids and novae. Looking at the relations between period, luminosity, amplitude, and frequency, they found that these Cepheids resemble the ones in the Milky Way, but seem to be different from those in the Small Magellanic Cloud. More recently, the DIRECT project (Kaluzny et al. 1998) performed a comprehensive variable star study in M 31 with the main goal being to reduce the uncertainties in its distance determination. In course of the survey, the DIRECT collaboration identified and examined Cepheids and Detached Eclipsing Binaries in five fields of the M 31 disk, which was published in a series of papers. Unfortunately, the data of a 6th field of the bulge of M 31, which in part overlaps with our surveyed area, remained unpublished.
During past years Andromeda was a preferred target for
a new kind of microlensing experiment. M 31 has the advantage
of offering the possibility to distinguish between
lensing by dark halo objects (Machos) and lensing by stars in M 31
(a contribution called "self-lensing'') in a statistical way, using
the near-far asymmetry of the microlensing event rate. As the disk
of M 31 is highly inclined (![]() ,
Stanek & Garnavich 1998)
one expects more Macho events towards the
far side of the M 31 disk than towards the near side.
On the other hand, self-lensing events should not show this signature.
Detecting
an asymmetry in the event rates would thus help to distinguish
between both kinds of events. Several "pixellensing'' surveys -
AGAPE (Ansari et al. 1997),
POINT-AGAPE (Auriere et al. 2001), WeCAPP (Riffeser et al. 2001),
MEGA (de Jong et al. 2004), SLOTT/AGAPE (Calchi Novati et al. 2002) -
therefore observed the bulge and parts of the disk of M 31
fairly continuously, and also generated catalogues of variable
sources as a by-product of
these experiments. The work presented in this paper thus overlaps
with the work resulting from the AGAPE (Ansari et al. 2004) and POINT-AGAPE
(An et al. 2004) data sets.
,
Stanek & Garnavich 1998)
one expects more Macho events towards the
far side of the M 31 disk than towards the near side.
On the other hand, self-lensing events should not show this signature.
Detecting
an asymmetry in the event rates would thus help to distinguish
between both kinds of events. Several "pixellensing'' surveys -
AGAPE (Ansari et al. 1997),
POINT-AGAPE (Auriere et al. 2001), WeCAPP (Riffeser et al. 2001),
MEGA (de Jong et al. 2004), SLOTT/AGAPE (Calchi Novati et al. 2002) -
therefore observed the bulge and parts of the disk of M 31
fairly continuously, and also generated catalogues of variable
sources as a by-product of
these experiments. The work presented in this paper thus overlaps
with the work resulting from the AGAPE (Ansari et al. 2004) and POINT-AGAPE
(An et al. 2004) data sets.
In contrast to classical microlensing surveys, pixellensing
experiments monitor the variation in the surface brightness of a nearby
galaxy rather than the variation in the luminosities of resolved
stars. Two methods were developed and implemented to overcome the
problem of crowding: the super-pixel method (Baillon et al. 1993,
used by the AGAPE and
POINT-AGAPE collaborations) and difference imaging (Tomaney & Crotts 1996; Alard & Lupton 1998),
which we used to extract and measure the variable sources.
The principle of difference imaging is straightforward: positionally
and photometrically aligned
images of two different epochs are subtracted from one another, and if
a source changes its luminosity between the two epochs, it shows
up as a point source in the difference image. All blended flux
cancels out and contributes only to the noise level in the difference
image. The success of difference imaging strongly depends on the quality of
the matching of the point-spread-functions (PSFs) between the two
images. In our implementation, the residuals in the difference images
reach the theoretical Poisson noise limit (see Sect. 2.3).
As the Poisson noise of the M 31 surface brightness is the limiting
factor for the detection of the variable sources, we stacked all
images of one night and generate difference images from these
co-added images. Due to this daily stacking scheme, we
were not sensitive to variations and to periods smaller than 1.3 days,
and focus therefore on longer period variables, namely Cepheids,
RV Tauri stars, and Long Period Variables (LPVs), i.e. Miras and
semi-regular variables. The catalogue is completed by eclipsing
binaries and by variables showing eruptive or irregular
variations. The ![]() Scuti and RR Lyrae stars show variation
amplitudes below our detection limit and will therefore be missed in
this study.
Scuti and RR Lyrae stars show variation
amplitudes below our detection limit and will therefore be missed in
this study.
The paper is organized as follows. In Sect. 2 we give an overview of the survey, the observations, and data reduction. Section 3 deals with source detection and the derivation of possible periods of the variables. In Sects. 4 and 5, we show the different groups of variable sources detected in the survey. The catalogue of variable stars is presented in Sect. 6 and is correlated with X-ray selected catalogues in Sect. 7. While Sect. 8 summarizes the paper, the appendix deals with the accuracy of the derived periods.
The data presented here result from three years of observing the
central part of M 31 by the WeCAPP project. We obtained data from the
0.8 m telescope at Wendelstein Observatory (Germany) and from the
1.23 m telescope at Calar Alto Observatory (Spain). At Wendelstein
with its field of view (FOV) of
![]() ,
we
selected a field (F1 in the following) along the minor axis of M 31,
which contains the area with the highest expected rate of
pixellensing events (see also Fig. 1 for the location of
F1). Observations of this field were accompanied by images of F3, the
opposite field along the NW minor axis, taken with a sparser time
sampling. The Calar Alto field covered
,
we
selected a field (F1 in the following) along the minor axis of M 31,
which contains the area with the highest expected rate of
pixellensing events (see also Fig. 1 for the location of
F1). Observations of this field were accompanied by images of F3, the
opposite field along the NW minor axis, taken with a sparser time
sampling. The Calar Alto field covered
![]() centered on the nucleus of M 31. Two quadrants of the
field coincided with the maximal lensing field F1 and the opposite
field F3. Due to these simultaneous observations, we reached a very good
time sampling when M 31 was observable. Since summer 2002 we
have been mosaicing fields F1 to F4 solely with the Wendelstein telescope.
A composite image (V-, R-, and I-band) of fields F1 to F4 taken at
Calar Alto Observatory during the campaign 2000/2001 is shown in
Fig. 1. The epochs with data taken for the four fields are
shown in Fig. 2.
centered on the nucleus of M 31. Two quadrants of the
field coincided with the maximal lensing field F1 and the opposite
field F3. Due to these simultaneous observations, we reached a very good
time sampling when M 31 was observable. Since summer 2002 we
have been mosaicing fields F1 to F4 solely with the Wendelstein telescope.
A composite image (V-, R-, and I-band) of fields F1 to F4 taken at
Calar Alto Observatory during the campaign 2000/2001 is shown in
Fig. 1. The epochs with data taken for the four fields are
shown in Fig. 2.
![\begin{figure}
\par\includegraphics[width=8.8cm]{2223f001.eps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg31.gif) |
Figure 1:
V-, R-, and I-band composite image of
the observed fields F1 to F4, taken at Calar Alto Observatory during
the campaign 2000/2001. The black lines mark the positions of fields
F1 to F4. The identified variable sources lie
within RA(2000): [00h43m25.0s, 00h41m59.9s] and Dec(2000):
[41d08
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.8cm]{2223f002.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg32.gif) |
Figure 2: Distribution of the observations for the four fields. During the first two campaigns, we reached a very dense time sampling of the observations. Note that the third and fourth campaigns were restricted to Wendelstein Observatory only. |
| Open with DEXTER | |
Table 1:
Properties of the CCD cameras used during WeCAPP at
Wendelstein (We) and Calar Alto (CA) Observatories. Both
CCDs have a pixel size of
![]() .
.
![\begin{figure}
\par\includegraphics[width=8.8cm]{2223f003.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg46.gif) |
Figure 3: Floating chart of the WeCAPP reduction pipeline mupipe. The reduction package includes full error propagation for each pixel through all reduction steps. In this way, all data points are properly taken into account in the search for variable sources. The reduction pipeline returns light curves for each pixel in the frame, representing the temporal change of the flux present inside the PSF centered on the particular pixel. |
| Open with DEXTER | |
A floating chart of the reduction pipeline is shown in
Fig. 3. In the last step, mupipe returns roughly
![]() pixel light curves together with appropriate errors,
with each of the light curves representing the time variability of the flux
present inside the PSF centered on the particular pixel. The
extraction of intrinsic variable sources from these pixel light curves
is presented in the next section.
pixel light curves together with appropriate errors,
with each of the light curves representing the time variability of the flux
present inside the PSF centered on the particular pixel. The
extraction of intrinsic variable sources from these pixel light curves
is presented in the next section.
For the selection of the intrinsic variable sources, we used the
R-band data from the Calar Alto campaigns 2000/2001 and 2001/2002 to
create a
![]() variation frame. To get rid of systematic
effects induced by the different seeing conditions of each frame we
used the following approach. We selected a stacked image with roughly the
median seeing of the 2000/2001 campaign (about 1.5
variation frame. To get rid of systematic
effects induced by the different seeing conditions of each frame we
used the following approach. We selected a stacked image with roughly the
median seeing of the 2000/2001 campaign (about 1.5
![]() )
as the master
frame and matched the PSF of each stacked frame with a smaller PSF to
the one of the master frame. In this way we ended up with difference
images for 113 epochs (i.e. 48% of the epochs with R-band data
obtained at Calar Alto), which were then used to detect the
variable sources. For each of the light curves extracted from the
PSF1.5 difference images, we calculated the reduced
)
as the master
frame and matched the PSF of each stacked frame with a smaller PSF to
the one of the master frame. In this way we ended up with difference
images for 113 epochs (i.e. 48% of the epochs with R-band data
obtained at Calar Alto), which were then used to detect the
variable sources. For each of the light curves extracted from the
PSF1.5 difference images, we calculated the reduced
![]() deviation from a constant (i.e. zero) baseline fit. The errors
entering these calculations were the errors propagated by
mupipe. The results were written into a
deviation from a constant (i.e. zero) baseline fit. The errors
entering these calculations were the errors propagated by
mupipe. The results were written into a
![]() -frame of the
field. The mode of the
-frame of the
field. The mode of the
![]() -frame is 1.02, which shows the
accuracy of the propagated errors.
Each value
-frame is 1.02, which shows the
accuracy of the propagated errors.
Each value ![]() 1.15 is connected to a non-constant, i.e. variable, source
at the 99.99% confidence level.
To avoid contamination of the M 31 sample with foreground objects, we
set all pixels in a radius of 5 pixels around the positions of bright
foreground stars to zero before detecting the variable sources in the
1.15 is connected to a non-constant, i.e. variable, source
at the 99.99% confidence level.
To avoid contamination of the M 31 sample with foreground objects, we
set all pixels in a radius of 5 pixels around the positions of bright
foreground stars to zero before detecting the variable sources in the
![]() -frame.
-frame.
![\begin{figure}
\par\includegraphics[width=7.8cm]{2223f004.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg48.gif) |
Figure 4:
Extract (
|
| Open with DEXTER | |
The algorithm extracts the power in the first sine and cosine terms for a set of equally spaced frequencies and also yields the significance of the detected peaks in the power spectrum. The Lomb normalized periodogram for N measured data points hj=h(tj), j=1,...,N, taken at epochs tj, is defined by
where
![]() is the angular frequency for
period P, mean
is the angular frequency for
period P, mean ![]() ,
variance
,
variance ![]() ,
and
constant
,
and
constant ![]() are defined as follows
are defined as follows
| (5) |
![\begin{figure}
\par\includegraphics[width=8.8cm,angle=0]{2223f005.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg60.gif) |
Figure 5:
Two examples of power spectra
|
| Open with DEXTER | |
The significance level P(>z) of a peak with amplitude
z in the power spectrum is given by
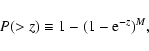 |
(6) |
We used the algorithm taken from the Numerical
Recipes (Press et al. 1988). Small modifications in the code allowed us to
search for the different maxima in the power spectrum. The positions
and values of the peaks are returned and can be used for further study
of the light curves. In this implementation, the significance P(>z)is approximated for small values of P(>z) by
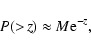 |
(7) |
| |
Figure 6: Histogram of the number of epochs of the level A sources in the R-band (black curve) and I-band (grey curve, red curve in the online version). For sources located in field F1, we usually got data points in the R-band on more than 400 epochs. |
| Open with DEXTER | |
As first cut we demanded that the light curve comprises at least 40 data points in both filters. All sources which did not pass this criterion we removed from the sample. This reduced the number of variables under inspection to 25 316 and defined the level A sample. In Fig. 6 we show the histogram of the number of epochs for these sources in the R-band (black curve) and I-band (red curve). The lowest number peaks represent the time sampling present in fields F2 and F4, followed by the peak corresponding to field F3. As F2 and F4 were observed with comparable frequency, both fields contributed to the lowest number peak. The last peak, with usually more than 400 epochs in the R-band, is related to field F1.
As the Lomb algorithm assumes that all data points have the same error (see Eqs. (1) and (3)), data points with big error bars or outliers can spoil the period-finding process and yield spurious periods. To avoid this, we first eliminated in each light curve ten data points with the biggest errors and, in a second step, five data points with the highest as well as five data points with the lowest values. In doing so, we ensure that we have at least 20 data points in both filters to look for a periodic signal.
We then checked the R-band and I-band light curves separately for periodicities. As the color of variable stars usually changes during a cycle, combing the two data sets would not result in accurate determinations of the period of the sources. Finally we obtained 25 316 variables with determined periods (of any significance level) in both bands.
We regard those periods as real that are the same in both bands
inside tight boundaries reflecting the error of the period
determination. For periods PR <215 days, we took the theoretical
error (see Eq. (A.2)) resulting from
![]() as limit,
while from 215 days onwards we chose a more conservative constant limit of
30 days, which was increased to 60 days for PR>400 days. This
criterion defined the level B sample (20 311 objects).
as limit,
while from 215 days onwards we chose a more conservative constant limit of
30 days, which was increased to 60 days for PR>400 days. This
criterion defined the level B sample (20 311 objects).
As the final cut we selected all those variables from level B which showed
a significance level of the period determination of P(>z) <10-10 in R or I and which had a determined R-band period
![]() days. This final cut reduced the number of sources to
19 551 and defined the level C sample with well-determined
periods. The remaining sources in level B were inspected visually and
assigned to the group of regular, irregular, long-variation (period
could not be determined because of an incomplete cycle) or
miscellaneous variables in the final catalogue, or were rejected from
the sample as spurious detections. Finally, all sources of the level
C sample were added automatically to the final catalogue.
days. This final cut reduced the number of sources to
19 551 and defined the level C sample with well-determined
periods. The remaining sources in level B were inspected visually and
assigned to the group of regular, irregular, long-variation (period
could not be determined because of an incomplete cycle) or
miscellaneous variables in the final catalogue, or were rejected from
the sample as spurious detections. Finally, all sources of the level
C sample were added automatically to the final catalogue.
For the variables which showed deviant periods in R and I, we proceeded as follows. If the significance level of one of the deviant periods was better than 10-15 and at the same time better than the significance in the other band by a factor of 1010, we chose the period in the first band and add the variable to the final catalogue. If this was not the case, we inspected the light curve visually and decided if one of the periods was the real one, or if the variation was of an irregular nature. In this step we also rejected the last spurious detections from the sample and the true variables were added to the final catalogue.
![\begin{figure}
\par\includegraphics[width=8.1cm]{2223f07a.ps}\par\includegraphics[width=8.1cm]{2223f07b.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg68.gif) |
Figure 7: Top panel: histogram of the periods of the 31 eclipsing binary candidates. The 4 (semi-) detached systems populate the low period area up to a period of 7 days, whereas the candidate contact systems generally have longer periods. Bottom panel: binned R-band light curve of a semi-detached system in the phase representation. The system has a R-band period of 7.0791 days. |
| Open with DEXTER | |
Selecting all light curves with a reasonable signal detection efficiency (SDE, Kovacs et al. 2002) SDE >6, periods P>1.30 days and rejecting periods between 1.95 days and 2.05 days (to avoid to pick up aliasing periods) together resulted in an additional sample of 155 light curves. Visual inspection of the folded light curves finally yielded 3 additional candidates for (semi-) detached eclipsing binary systems.
In Fig. 7 we show the distribution of periods of the 31 EB candidates in the upper panel. The 4 (semi-) detached systems populate the low period area up to a period of 7 days, whereas the candidate contact systems generally have longer periods. In the bottom panel, we show the binned R-band light curve of a semi-detached system in the phase representation. The system was detected using the Lomb algorithm and has a R-band period of 7.0791 days.
By summing up all variables in 100![]() 100 pixel [
100 pixel [
![]() ]
bins, we calculated the number density of variable
sources. In the resulting density map
(Fig. 9), the spiral arms are clearly visible. A
comparison of the number densities at equivalent positions in the M 31
bulge - one in the dust lane of the spiral arms, the other in the
opposite hemisphere - shows a reduction to about 60% compared to the
part with no strong extinction.
]
bins, we calculated the number density of variable
sources. In the resulting density map
(Fig. 9), the spiral arms are clearly visible. A
comparison of the number densities at equivalent positions in the M 31
bulge - one in the dust lane of the spiral arms, the other in the
opposite hemisphere - shows a reduction to about 60% compared to the
part with no strong extinction.
| |
Figure 8: Number counts of sources of the catalogue as function of the distance to the center of M 31. Black: all sources. Blue: sources in the northern hemisphere of M 31. Red: sources in the southern hemisphere of M 31. The asymmetry of the detected sources is clearly visible and is due to the enhanced disk-extinction in the northern part. The low number of sources near the center is due to incompleteness induced by crowding and saturated parts in the frames. |
| Open with DEXTER | |
To examine this subject further, we compared the number density map (see Fig. 9) with an extinction map of our field. In Fig. 10 we plot the positions of the sources on top of the R-band extinction map, which we derived from the V- and R-band frames taken by the LGS survey in the following way:
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f009.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg70.gif) |
Figure 9:
Number density of variable sources by
summing up all variables in
|
| Open with DEXTER | |
We started from the relation between the color excess E(V-R) and the
extinction AR in the R-band (
![]() ,
see
Binney & Merrifield 1988)
,
see
Binney & Merrifield 1988)
| AR = a E(V-R). | (8) |
![\begin{displaymath}M_{R,r}-M_{R,0}= a ~~ \Big[\big(M_{V,r}-M_{R,r})-(M_{V,0} - M_{R,0}\big)\Big].
\end{displaymath}](/articles/aa/full/2006/02/aa2223-04/img72.gif) |
(9) |
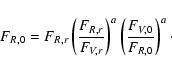 |
(10) |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f010.eps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg75.gif) |
Figure 10: R-band extinction map of the M 31 field. White areas correspond to high extinction values. The extinction in the R-band was derived using the V- and R-band images taken from the LGS survey (Massey et al. 2001). Overplotted are the positions of the catalogue variables (blue dots). In the central regions, the extinction map could not be calculated due to saturation in the original LGS frames. |
| Open with DEXTER | |
Using this assumption,
we finally obtain a relation for FR,0
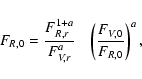 |
(11) |
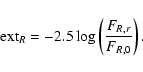 |
(12) |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f011.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg80.gif) |
Figure 11:
Theoretically expected number densities of
LPVs according to Renzini (1998) calculated with the small bulge
decomposition of Kent (1989). The field is centered on the nucleus
of M 31; North is on top, and East is on the left of the diagram. The
WeCAPP field for which we calculated the number density in
Fig. 9 is shown by the grey rectangle (blue
rectangle in the online version). Contour levels are 1,
2, 3, 4 and
|
| Open with DEXTER | |
Finally we compared the number densities of sources present in our
catalogue with theoretical predictions. According to Renzini (1998),
the number of LPVs per integrated 105 bolometric luminosities is
equal to 0.5. Renzini (1998) uses a slightly older (15 Gyr) and
less metal-rich (1 ![]() )
bulge when compared to the model used for
calculating the extinction frame. With the small bulge
decomposition of Kent (1989) and under the assumption that the LPVs
are present in the bulge only, we derived the expected number densities
of LPVs and show it in Fig. 11. Agreement with the
detected number densities is good in the outer parts of the
field. Towards the center, we suffer from incompleteness due to
enhanced noise, on the one hand, and crowding of the sources, on the
other.
)
bulge when compared to the model used for
calculating the extinction frame. With the small bulge
decomposition of Kent (1989) and under the assumption that the LPVs
are present in the bulge only, we derived the expected number densities
of LPVs and show it in Fig. 11. Agreement with the
detected number densities is good in the outer parts of the
field. Towards the center, we suffer from incompleteness due to
enhanced noise, on the one hand, and crowding of the sources, on the
other.
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f012.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg81.gif) |
Figure 12:
Period-amplitude relation in the R-band
for the catalogue sources (eclipsing binaries, irregular,
long-variation, and miscellaneous variables excluded). The amplitudes
were transformed into magnitudes using the R-band fluxes of Vega. Note
that these magnitudes only reflect the flux difference and are not the
real variation magnitude of a single star. Three populations are visible
in this diagram. The black lines show the defining relations
(from left to right) for group I (population I Cepheids: black dots),
group II (type II Cepheids: blue dots; RV Tauri stars: red dots; RV
Tauri candidates: open magenta circles; SR variables: green dots), and
group III (LPVs). For the RV Tauri stars and candidates, we use the
single or fundamental period (minimum to minimum). The sources in
group III are color-coded according to the significance of the
I-band period as returned by the Lomb algorithm (low significance:
black
|
| Open with DEXTER | |
Figure 12 shows the relation between the logarithm of
the period and the logarithm of the amplitude
![]() (i.e. the
variation magnitude as measured in the frame) for the sources of the
final catalogue. Three different groups can be distinguished in this
diagram:
(i.e. the
variation magnitude as measured in the frame) for the sources of the
final catalogue. Three different groups can be distinguished in this
diagram:
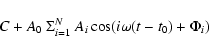 |
(13) |
Simon & Lee (1981) were the first to calculate amplitude ratios of
the form
Rij=Ai/Aj and phase differences
![]() of the parameters of the different harmonics.
Since for classical Cepheids both definitions show a progression with the
period, as well as a correlation among one another, Fourier analysis
proved to be an excellent diagnostic for examining the pulsation properties
of these stars. Fourier analysis therefore was widely used in the past
to examine Cepheids (e.g., Simon & Moffett 1986; Alcock et al. 1999), particularly
to distinguish between fundamental and first overtone pulsators
(e.g., Beaulieu et al. 1995; Antonello & Poretti 1986).
of the parameters of the different harmonics.
Since for classical Cepheids both definitions show a progression with the
period, as well as a correlation among one another, Fourier analysis
proved to be an excellent diagnostic for examining the pulsation properties
of these stars. Fourier analysis therefore was widely used in the past
to examine Cepheids (e.g., Simon & Moffett 1986; Alcock et al. 1999), particularly
to distinguish between fundamental and first overtone pulsators
(e.g., Beaulieu et al. 1995; Antonello & Poretti 1986).
We detected 33 population I Cepheids in our sample. To check whether
our classification is correct and if there are first overtone
pulsators (s-Cepheids) amongst the detected Cepheids, we fitted
truncated Fourier series (see Sect. 4.3.2) to the light
curves of group I. Figure 13 shows the characteristic
progression of the Fourier parameters with the period of the light
curve for the classical Cepheids: as the amplitude ratio R21between the first and second harmonic drops the corresponding phase
difference shows a mild rise. The amplitude ratio R21 declines
until a period of about 10 days is reached, and then starts to rise
again. Due to suppression of the second harmonic, the Cepheid light
curves in the vicinity of this period look quite sinusoidal.
Figure 13 shows that the minimum of R21 is
connected to a dramatic change of ![]() .
It is generally
believed that this change is connected to the resonance between the
fundamental mode and the second overtone
.
It is generally
believed that this change is connected to the resonance between the
fundamental mode and the second overtone
![]() (e.g.,
Simon & Moffett 1986).
(e.g.,
Simon & Moffett 1986).
![\begin{figure}
\par\includegraphics[width=8.8cm,angle=0]{2223f13a.ps}\par\includegraphics[width=8.8cm,angle=0]{2223f13b.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg90.gif) |
Figure 13:
Amplitude ratio
R21=A2/A1 ( upper
panel) and phase difference
|
| Open with DEXTER | |
First overtone pulsators can be detected using the amplitude ratio
R21, as s-Cepheids show lower values than their fundamental
mode counterparts. Following Beaulieu et al. (1995) we demanded
R21<0.3for P < 3 days and
R21<0.2 for
![]() days for the
Cepheids to be classified as first overtone pulsators. Using this
criterion we identified 2 first overtone pulsators in our sample. One
source with a R21 value close to the border with the s-Cepheids
fell off the fundamental mode sequence in the phase difference
diagram. Following Beaulieu et al. (1995), we classify this source as
an intermediate Cepheid.
days for the
Cepheids to be classified as first overtone pulsators. Using this
criterion we identified 2 first overtone pulsators in our sample. One
source with a R21 value close to the border with the s-Cepheids
fell off the fundamental mode sequence in the phase difference
diagram. Following Beaulieu et al. (1995), we classify this source as
an intermediate Cepheid.
One source is clearly separated from the Cepheid relation in the
period-amplitude plane (see Fig. 12). This variable
shows Cepheid-like variations that are modulated by a period of
208 days in R. The modulation is most likely due to another variable
source inside the PSF. Fourier decomposition of the R-band data
shows that the source has two excited periods, 1.7330 days and 2.3515
days, besides the subdominant modulation of the light curve. In
Fig. 14 we show the power spectrum of this source.
The two periods would classify the source as a beat Cepheid, the first
one detected in M 31. Beat Cepheids are a rare sub-class of Cepheids in
which two pulsation modes are excited simultaneously. The ratio of the
two periods
![]() makes it likely that we
see a fundamental mode / first overtone (F/1H) pulsator, if the
Cepheid hypothesis for this source is confirmed. For F/1H beat
Cepheids, the first overtone should be the dominant mode, which is
fulfilled for our candidate. Interestingly, the position in the
makes it likely that we
see a fundamental mode / first overtone (F/1H) pulsator, if the
Cepheid hypothesis for this source is confirmed. For F/1H beat
Cepheids, the first overtone should be the dominant mode, which is
fulfilled for our candidate. Interestingly, the position in the
![]() diagram would place this beat Cepheid on a
sequence defined by the SMC beat Cepheids of Beaulieu et al. (1997), well
above the relations for the LMC and the Galaxy. This would point to a
Cepheid in M 31 of approximately the same metal content by mass as the
SMC beat Cepheids. The position of this object coincides with
a resolved source in our reference image, one which is classified as a star
(261 262) in the Haiman et al. (1994) catalogue and which also correlates with
an X-ray source in the Kong et al. (2002) catalogue. As the X-ray hardness
ratio of this source points to a soft spectrum consistent with
stellar X-ray emission, it is classified as a possible foreground star
in the Kong et al. (2002) catalogue (J004301.8+411726, see also
Table 4). Future investigations will show if these correlations
are real or coincidental.
diagram would place this beat Cepheid on a
sequence defined by the SMC beat Cepheids of Beaulieu et al. (1997), well
above the relations for the LMC and the Galaxy. This would point to a
Cepheid in M 31 of approximately the same metal content by mass as the
SMC beat Cepheids. The position of this object coincides with
a resolved source in our reference image, one which is classified as a star
(261 262) in the Haiman et al. (1994) catalogue and which also correlates with
an X-ray source in the Kong et al. (2002) catalogue. As the X-ray hardness
ratio of this source points to a soft spectrum consistent with
stellar X-ray emission, it is classified as a possible foreground star
in the Kong et al. (2002) catalogue (J004301.8+411726, see also
Table 4). Future investigations will show if these correlations
are real or coincidental.
| |
Figure 14: Power spectrum of the beat Cepheid candidate in the R-band. The two peaks in the spectrum correspond to periods of 1.7330 days and 2.3515 days. |
| Open with DEXTER | |
In addition to the beat Cepheid, there is another peculiar source in group I that remains unclassified at this stage. It shows two periods of 6.9489 and 20.4960 days. We will investigate that object further, together with the beat Cepheid candidate, and also present a more detailed description of the Fourier parameters of group I stars in a future publication.
![\begin{figure}
\par\includegraphics[width=8.8cm,angle=0]{2223f015.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg96.gif) |
Figure 15:
Phase differences
|
| Open with DEXTER | |
We detected 37 RV Tauri stars and 11 RV Tauri candidates, which makes
this catalogue one of the biggest collections of RV Tauris to
date. The light curves show the typical alternation of deep and
shallow minima, the second maximum being fainter than the first one,
although for a few sources this latter difference is rather marginal.
The light curve shape can be divided into two groups, one resembling
the "flat-topped'' Cepheid II shape (see
Fig. 22), the other showing sinusoidal variations.
To avoid misclassification of the sinusoidal light curves of RV
Tauri stars with the not-too-different light curves of ![]() -Lyrae
eclipsing binaries, we extracted the phase difference between the
second and the fourth harmonic from Fourier fits to the light
curves. According to Szymanski et al. (2001) these two phases should be
strongly coupled for sinusoidal contact systems, yielding
-Lyrae
eclipsing binaries, we extracted the phase difference between the
second and the fourth harmonic from Fourier fits to the light
curves. According to Szymanski et al. (2001) these two phases should be
strongly coupled for sinusoidal contact systems, yielding
![]() (M. Szymanski, priv. comm.). For pulsating
stars, the correlation is much weaker. Five of our RV Tauri candidates
with sinusoidal light curves have a
(M. Szymanski, priv. comm.). For pulsating
stars, the correlation is much weaker. Five of our RV Tauri candidates
with sinusoidal light curves have a
![]() within
1-
within
1-![]() compatible with 0 (or equivalently 2
compatible with 0 (or equivalently 2![]() )
and another 6 lie
within 3-
)
and another 6 lie
within 3-![]() .
We classified all 11 RV Tauris whose
.
We classified all 11 RV Tauris whose
![]() values are within 3-
values are within 3-![]() compatible with 0 as RV Tauri candidates,
and the remaining 37 sources as RV Tauri stars.
compatible with 0 as RV Tauri candidates,
and the remaining 37 sources as RV Tauri stars.
Using the fundamental period (minimum to minimum) for the Fourier
extension of the RV Tauri sources yields relatively bad fits and
subsequently more uncertain Fourier parameters. We therefore used the
formal period in the analysis, which yields a more appropriate
description of the data, better fits, and more reliable Fourier
parameters. In Fig. 15 we show a "phase-phase''
diagram as a further result of the Fourier analysis of the RV Tauri
and candidate RV Tauri light curves. The phase differences ![]() and
and ![]() correlate for the RV Tauri light curves (red dots),
showing that these sources form a homogeneous group of stars.
The RV Tauri candidates (magenta open circles) also follow the relation
that supports the RV Tauri nature of these stars. Furthermore we show
the detected type II Cepheids as blue dots in this figure. The
sequences of RV Tauri stars and type II Cepheids overlap, making the
RV Tauri sequence an extension of the Cepheid sequence at higher
periods. This supports the close connection between RV Tauri stars and
type II Cepheids. In fact, Alcock et al. (1998) show that a single
period-luminosity-color relationship describes both the type II
Cepheids and RV Tauri stars in the LMC. We show the phase parameters
for the stars presented in this study as green dots in Fig. 15. For
this purpose we re-analyzed the light curves taken from the MACHO project
database
correlate for the RV Tauri light curves (red dots),
showing that these sources form a homogeneous group of stars.
The RV Tauri candidates (magenta open circles) also follow the relation
that supports the RV Tauri nature of these stars. Furthermore we show
the detected type II Cepheids as blue dots in this figure. The
sequences of RV Tauri stars and type II Cepheids overlap, making the
RV Tauri sequence an extension of the Cepheid sequence at higher
periods. This supports the close connection between RV Tauri stars and
type II Cepheids. In fact, Alcock et al. (1998) show that a single
period-luminosity-color relationship describes both the type II
Cepheids and RV Tauri stars in the LMC. We show the phase parameters
for the stars presented in this study as green dots in Fig. 15. For
this purpose we re-analyzed the light curves taken from the MACHO project
database![]() and
used the formal period to derive the Fourier parameters. Two stars
with an uncertain classification were rejected from the analysis. The
LMC variables lie on the sequence of the WeCAPP RV Tauri and Cepheid
II stars, supporting our classification of the variables in
group II. However, as we are not able to resolve the RV Tauri
stars due to the high surface brightness of the central parts of M 31
in the analyzed data set, we cannot finally prove the assignment
of these stars as RV Tauri by placing the sources on a color-magnitude
diagram.
and
used the formal period to derive the Fourier parameters. Two stars
with an uncertain classification were rejected from the analysis. The
LMC variables lie on the sequence of the WeCAPP RV Tauri and Cepheid
II stars, supporting our classification of the variables in
group II. However, as we are not able to resolve the RV Tauri
stars due to the high surface brightness of the central parts of M 31
in the analyzed data set, we cannot finally prove the assignment
of these stars as RV Tauri by placing the sources on a color-magnitude
diagram.
The period range of the 93 type II Cepheids extends to periods longer than the approximate limit of about 20 days, as proposed by Alcock et al. (1998). There is still the possibility that some of these long-period Cepheids are in reality RV Tauri stars, since noise in the light curves can prevent us from detecting the alternation of deep and shallow maxima as required for assigning of the variable as a RV Tauri candidate or star. The majority of the light curves of this type of variable have a "flat-topped'' shape (Kwee 1967) with relatively long and flat maxima. As already mentioned, the light curves of type II Cepheids show progression of the phase differences and occupy distinct places in Fourier space. We will discuss the Fourier parameters of the Cepheid-like variables in group I and II more thoroughly in a future publication. The sample of type II Cepheids outnumbers the sample of population I Cepheids by about a factor of three. As the type II Cepheids trace the old bulge population, this is not unexpected, even when taking their smaller brightness compared to population I Cepheids (at the same period) into account. The population I Cepheids, more massive and younger than the type II Cepheids, are typical members of the M 31 disk population, which is superimposed on the M 31 bulge.
The third constituent of the group II sources are small-period semi-regular variables that contribute from periods of about 16 days onwards. The Fourier analysis of the light curves shows no correlations of the amplitude ratios or phase differences with period. Phase-phase diagrams also do not reveal a correlation of the phase parameters.
| |
Figure 16: Histogram of the periods of the Cepheid variables in group I. |
| Open with DEXTER | |
| |
Figure 17: Histogram of the periods of variables belonging to group II. We show the distributions for type II Cepheids (blue line), RV Tauri stars (red line), RV Tauri candidates (magenta line), and the semi-regular stars (green line). For the RV Tauri stars and candidates, we use the single or fundamental period (minimum to minimum). |
| Open with DEXTER | |
In Fig. 16 we give the period distribution of the population I Cepheids, whereas Fig. 17 shows the distribution of periods for variables belonging to group II. In red, magenta, blue, and green we present the distribution for the RV Tauri stars, RV Tauri candidates, type II Cepheids, and semi-regular variables.
LPVs are a very promising tool for answering various astrophysical questions. They follow tight period-luminosity relations in the near-IR (especially the K-band) (Wood 2000; Feast et al. 2002,1989), which makes them excellent galactic and extragalactic distance estimators. They are furthermore good indicators of the parent population to which they belong, as a dependence exists of the luminosity (hence, period) of Miras on the age. Longer period Miras should have higher mass progenitors and therefore belong to a younger population. LPVs are historically separated into two main groups: i) Miras with regular variations, periods between 80 and 1000 days, and an amplitude of the variation in the V-band of more than 2.5 mag; ii) semi-regulars (SR) with less regular variations, smaller periods, and a V-band variation smaller than 2.5 mag. Semi-regulars are divided in two groups, SRas with more regular variations and SRbs with less regular variations.
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f018.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg105.gif) |
Figure 18:
Distribution of the periods of LPVs in the
bulge of M 31 detected by the WeCAPP project. Top: class i - regular
and semi-regular variables (significance level P(>z) < 10-20in R or I). Bottom: class ii - irregular variables (significance
level P(>z) |
| Open with DEXTER | |
Recently Lebzelter et al. (2002) proposed a new classification scheme that is less dependent on this kind of artificial division and used it for the AGAPEROS survey of variable red stars towards the Magellanic Clouds. Their classification is based on the regularity of the variation alone, thereby providing three classes of stars: i) LPVs with regular variation; ii) LPVs with semi-regular variation; iii) LPVs with irregular variation. No cuts in amplitude were applied, therefore class i contains members of the classical Mira group, as well as members of the SRa type of objects.
We modified this classification scheme for our purposes and defined a significance cut of P(> z)=10-20 according to the period-finding algorithm in R or I for the division of our sample of LPVs in classes i (regular and semi-regular) and ii (irregular). Class ii coincides with the class of irregular stars introduced in Sect. 4. Because of the non-linear dependence of the significance on the S/N of the light curve (see discussion below), we abandoned inventing an automatic cut for the division into semi-regular and regular variations. The cut at 10-20 is somewhat subjective, as stars with semi-regular variations, but low S/N light curves are classified as irregular, since the low S/N prevents the period being determined with better significance. On the other hand, this cut ensures that most of the irregular light curves are classified in the right way. The histograms of the periods for the irregular and the regular/semi-regular sample of LPVs are shown in Fig. 18. The irregular variables show on average smaller "periods'' than the group of regular or semi-regular variables. Note, that this statement is of qualitative nature only, as the periods for these sources are not well-determined.
![\begin{figure}
\par\includegraphics[width=8cm,angle=0]{2223f19a.ps}\hspace*{3.5mm}
\includegraphics[width=8cm,angle=0]{2223f19b.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg106.gif) |
Figure 19: Left panel: variation color R-I shown as a function of the R-band variation magnitude. The sources of groups I and II are shown as big closed circles, the sources of group III as small closed circles. The color coding is the same as in Fig. 12, i.e. the LPVs are again color-coded according to the significance of the I-band period. The sources in groups I and II as a whole show bluer variations than the LPVs in group III. The significance of the I-band period rises for brighter R variation magnitudes and redder variation colors. This is a result of the higher S/N of the I-band light curves, but can in part also be attributed to the enhanced regularity of the light curves. Right panel: this figure shows the variation color R-I as function of the period of the variable sources. Note that due to the normalization to the fluxes of Vega in the particular systems, this R-I color should not be mistaken with the color of the variation amplitudes of the sources. Nevertheless, some trends are visible in this diagram: as the variation of the LPVs gets redder with increasing period, the I-band periods become more significant, reflecting the rising S/N in I due to higher R-Ivalues and a rising regularity of the light curves. |
| Open with DEXTER | |
We color-coded the LPVs in Fig. 12 according to the significance P(>z) of the I-band period. The slope of the variation magnitude-period relation changes from slightly positive for the low significance tail (black dots) to negative for the sources with intermediate and high significant periods (green and red dots). The same trend can be seen in the left panel of Fig. 19, which shows the variation color R-I as a function of the R-band variation magnitude. The significance of the I-band period rises for brighter R variation magnitudes and redder variation colors. The differences in the significance of the LPV I-band periods, therefore, is a result of the different S/N of the I-band light curves (rising S/N in I due to higher R-I values), but can in part also be attributed to different stages of regularity in the light curves. The right panel of Fig. 19 finally shows the variation color R-I as function of the period of the variable sources. The variation of the LPVs gets redder with increasing period, and at the same time shows more significant periods.
Group II comprises 93 type II Cepheids, 37 RV Tauri stars, 11 RV Tauri candidates, and 193 low period semi-regular variables. Group III consists of 4287 irregular and 18 974 regular/semi-regular variables. The 82 presumably group III members show variations on longer timescales than the survey length. The positions on the R-band period-amplitude plane of the 31 eclipsing binary candidates coincide with the positions of groups I and II. Finally we detected 39 miscellaneous variables, among them 16 novae and 15 R Coronae Borealis candidates.
The full catalog is available in electronic form at the CDS. We give the
name, the position in the WCS, the periods (if available) derived from
the R- and I-band data, the amplitudes of the variation
![]() and
and
![]() ,
and provide classification according to
Sects. 4 and 5: DC (classical or
,
and provide classification according to
Sects. 4 and 5: DC (classical or
![]() -Cepheids), SC (s-Cepheids), BC (beat Cepheids), IC
(intermediate Cepheids), W (type II Cepheids), RV (RV Tauri stars),
rv (RV Tauri candidates), S (regular or and semi-regular variations),
and I (irregular variables). We also mark the identified Novae (N),
eclipsing binary candidates (E), RCB candidates (RCB), and other
miscellaneous variables (M). As an illustration of its contents, in
Table 2 we list the entries 100-120 in the catalogue. In
Figs. 20 to 28 we show typical light curves
for each of the groups.
-Cepheids), SC (s-Cepheids), BC (beat Cepheids), IC
(intermediate Cepheids), W (type II Cepheids), RV (RV Tauri stars),
rv (RV Tauri candidates), S (regular or and semi-regular variations),
and I (irregular variables). We also mark the identified Novae (N),
eclipsing binary candidates (E), RCB candidates (RCB), and other
miscellaneous variables (M). As an illustration of its contents, in
Table 2 we list the entries 100-120 in the catalogue. In
Figs. 20 to 28 we show typical light curves
for each of the groups.
We found 23 coincidences with the Kaaret (2002) catalogue when using
a search radius of 1
![]() .
To estimate how many coincidences we
expected by chance, we followed the approach proposed by
Hornschemeier et al. (2001). We shifted one of the catalogues to be compared
(in our case we shifted the catalogues taken from the literature) by
20
.
To estimate how many coincidences we
expected by chance, we followed the approach proposed by
Hornschemeier et al. (2001). We shifted one of the catalogues to be compared
(in our case we shifted the catalogues taken from the literature) by
20
![]() in north-east, south-east, south-west, and north-west
directions, and checked for coincidences between these mock catalogues
and our catalogue. By averaging these numbers, we got the expected
number of coincidences by chance.
in north-east, south-east, south-west, and north-west
directions, and checked for coincidences between these mock catalogues
and our catalogue. By averaging these numbers, we got the expected
number of coincidences by chance.
By applying a search radius of 1
![]() ,
the number of false
coincidences with the Kaaret (2002) catalogue becomes 12. This
high level of false coincidences (about 50%) results from the high
number density of the variable star catalogue. Nevertheless, the
false detections rate suggests that about 11 of the coincidences
should be real. This is supported by the fact that 6 of the
coincident sources have an entry in the 2 MASS catalogue
(Cutri et al. 2000), and 8 of the Kaaret-WeCAPP sources are identified as
globular clusters (4 of them with a 2MASS entry, Kaaret 2002).
Furthermore, we found that 13 of the sources have coincident
counterparts in the Kong et al. (2002) catalogue as well (see below). In
Table 3 we give the positions of all 23 coincidences,
and we give the 2MASS name also for sources with entries in the 2MASS catalogue.
Two of the Kaaret-WeCAPP sources with 2MASS fluxes (WeCAPP_V8946
and WeCAPP_V10578) have no globular cluster (gc) counterpart
Kaaret (2002). While V8946 coincides with a gc-candidate
identified by Wirth, Smarr, & Bruno (1985), a gc-counterpart for WeCAPP_V10578 is
completely unknown. Another two of the WeCAPP-Kaaret sources
(V16322 and V10431) have been identified as optical novae showing supersoft
X-ray emission (Pietsch et al. 2005).
,
the number of false
coincidences with the Kaaret (2002) catalogue becomes 12. This
high level of false coincidences (about 50%) results from the high
number density of the variable star catalogue. Nevertheless, the
false detections rate suggests that about 11 of the coincidences
should be real. This is supported by the fact that 6 of the
coincident sources have an entry in the 2 MASS catalogue
(Cutri et al. 2000), and 8 of the Kaaret-WeCAPP sources are identified as
globular clusters (4 of them with a 2MASS entry, Kaaret 2002).
Furthermore, we found that 13 of the sources have coincident
counterparts in the Kong et al. (2002) catalogue as well (see below). In
Table 3 we give the positions of all 23 coincidences,
and we give the 2MASS name also for sources with entries in the 2MASS catalogue.
Two of the Kaaret-WeCAPP sources with 2MASS fluxes (WeCAPP_V8946
and WeCAPP_V10578) have no globular cluster (gc) counterpart
Kaaret (2002). While V8946 coincides with a gc-candidate
identified by Wirth, Smarr, & Bruno (1985), a gc-counterpart for WeCAPP_V10578 is
completely unknown. Another two of the WeCAPP-Kaaret sources
(V16322 and V10431) have been identified as optical novae showing supersoft
X-ray emission (Pietsch et al. 2005).
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f020.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg107.gif) |
Figure 20:
Light curve of a |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f021.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg108.gif) |
Figure 21: Light curve of a long period type II Cepheid (group II) in the R-band ( top panels) and the I-band ( bottom panels). |
| Open with DEXTER | |
The Kong et al. (2002) catalogue contains 31 coincidences with our
variable star catalogue when applying a 1
![]() search radius. As
we expect 17 coincidences by chance, about 14 of the coincidences
should be real. As mentioned above, 13 of the sources are also
coincident with the Kaaret (2002) catalogue. According to
Kong et al. (2002), 12 of the sources have a globular cluster counterpart
(3
search radius. As
we expect 17 coincidences by chance, about 14 of the coincidences
should be real. As mentioned above, 13 of the sources are also
coincident with the Kaaret (2002) catalogue. According to
Kong et al. (2002), 12 of the sources have a globular cluster counterpart
(3
![]() search radius), and 22 of the coincidences are variable
in the X-rays at the 3-
search radius), and 22 of the coincidences are variable
in the X-rays at the 3-![]() level. We show the positions and
identifiers of all 31 coincidences in Table 4.
level. We show the positions and
identifiers of all 31 coincidences in Table 4.
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f022.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg109.gif) |
Figure 22: Light curve of a RV Tauri star (group II) in the R-band ( top panels) and the I-band ( bottom panels). We show the light curves convolved with the formal periods (deep minimum to deep minimum). The double wave light curve with alternating deep and shallow minima is nicely uncovered. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f023.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg110.gif) |
Figure 23: Light curve of a low period semi-regular variable (group II) in the R-band ( top panels) and the I-band ( bottom panels). |
| Open with DEXTER | |
The GCVS (Durlevich et al. 1996) comprises 250 entries within our field of
view, most of them of nova type. Of there 161 (6) were classified as
novae, along with 53 as novae of fast type (NA), 9 (2) of slow type
(NB), and (2) of very slow type (NC). Furthermore the GCVS reports 1
SNIa remnant in our field, 1 (1) LC type (irregular variable
supergiant), 3 (1) semi-regular variables (SR), 3 ![]() -Cepheids,
(1) SDOR variable, 2 (1+2) irregular variables, and 1 unstudied (S:
classification) variable. The numbers in brackets give additional
candidates for the particular variable star group with questionable
classifications according to the GCVS.
-Cepheids,
(1) SDOR variable, 2 (1+2) irregular variables, and 1 unstudied (S:
classification) variable. The numbers in brackets give additional
candidates for the particular variable star group with questionable
classifications according to the GCVS.
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f024.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg111.gif) |
Figure 24: Light curve of an LPV with regular variation (group III) in the R-band ( top panels) and the I-band ( bottom panels). As illustration of the agreement of the data taken with different telescopes, we show the data collected at Calar Alto as grey dots (red dots in the online version) and data taken at Wendelstein as black dots. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f025.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg112.gif) |
Figure 25: Light curve of a LPV (group III) with changing variation amplitudes from cycle to cycle. Top panels: R-band. Bottom panels: I-band. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f026.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg113.gif) |
Figure 26: Light curve of an irregular LPV (group III). Top panel:R-band. Bottom panel: I-band. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f027.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg114.gif) |
Figure 27: Light curve of a R Coronae Borealis candidate (miscellaneous variables). Top panel: R-band. Bottom panel: I-band. These rare carbon-rich stars show unpredictable and frequent fading of light in optical wavebands, most probably due to dust grains ejected from the stellar photosphere. For a review of these RCB stars see Clayton (1996). |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=7.5cm,angle=0]{2223f028.ps}
\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg115.gif) |
Figure 28: Light curve of a nova (miscellaneous variables). Top panel: R-band. Bottom panel: I-band. A paper concerning the characteristics of all detected novae is in preparation. |
| Open with DEXTER | |
The crowding of the WeCAPP sources demands that we keep the search
radius at 1
![]() ,
even when comparing with the GCVS, whose
accuracy is well below this value. We found 27 coincidences; the number
of false detections (21) suggests, however, that most of the
coincidences are not real. As 23 of them are classified as
novae in the GCVS, we only show the 4 coincidences that we regard as
real in Table 5. Note, that we do not match the positions
of all three
,
even when comparing with the GCVS, whose
accuracy is well below this value. We found 27 coincidences; the number
of false detections (21) suggests, however, that most of the
coincidences are not real. As 23 of them are classified as
novae in the GCVS, we only show the 4 coincidences that we regard as
real in Table 5. Note, that we do not match the positions
of all three ![]() -Cepheids found in the GCVS inside our field. The
GCVS Cepheid V0934 has a position difference of 2.1
-Cepheids found in the GCVS inside our field. The
GCVS Cepheid V0934 has a position difference of 2.1
![]() when
compared to our position, and GCVS Cepheid V0811 is off by
10.2
when
compared to our position, and GCVS Cepheid V0811 is off by
10.2
![]() .
Because of these in part large uncertainties in the
positions of the GCVS, we are not trying to match the two remaining
semi-regulars, given their smaller variation amplitude.
.
Because of these in part large uncertainties in the
positions of the GCVS, we are not trying to match the two remaining
semi-regulars, given their smaller variation amplitude.
The distribution of the detected variable sources shows an asymmetry due to the enhanced extinction in the spiral arms projected on the M 31 bulge. Assuming that the non-variable stars in the bulge behave in the same way as the variable counterparts, this asymmetry enlarges the expected asymmetry in the microlensing signal resulting from the high inclination of M 31. Theoretical calculations, therefore, have to take a modified distribution of sources (or the distribution of the extinction present in a given band) into account.
The catalogue containing regular, semi-regular and irregular LPVs, Cepheids, RV Tauri stars, eclipsing binary, and R Coronae Borealis candidates enlightens the rich population of variable sources in M 31, which can then be exploited for various astrophysical questions. Two more papers dealing with the Fourier parameters for the Cepheid-like stars and the WeCAPP nova catalogue are in preparation. A fraction of the nova catalogue has already been correlated with supersoft X-ray sources (SSSs) in M 31, showing that classical novae constitute the major class of SSSs in M 31 (Pietsch et al. 2005).
Recently it was proposed that sequence E, first detected by
Wood (1999) in the MACHO data towards the LMC bar, is populated by
ellipsoidal red giants (Soszynski et al. 2004). Wood (1999) found five
distinct period-luminosity sequences, of which three could be
attributed to different evolutionary phases and pulsation modes. For
two of them, sequences D and E, it was suggested that they are
populated by contact binaries and by semi-detached binaries with an invisible
companion. Analyzing the data of the LMC ellipsoidal candidates from
the OGLE web archive![]() and
accounting for the distance modulus of M 31 proves that these sources
are below the detection limit of our survey. Therefore, we cannot put
any constraints on a possible population of ellipsoidal red giants in
M 31. The more detailed examination of the group III LPVs will be subject to
future work. Until now we have measured the dominant period in these stars
that are known to show multi-periodic phenomena. Future work will
include extraction of the sub-dominant periods and
distribution of the ratio of the different periods. Furthermore, the
distribution and possible correlations of the Fourier parameters for
these stars is an interesting and, until now, unexamined problem which we
can address with this data set.
and
accounting for the distance modulus of M 31 proves that these sources
are below the detection limit of our survey. Therefore, we cannot put
any constraints on a possible population of ellipsoidal red giants in
M 31. The more detailed examination of the group III LPVs will be subject to
future work. Until now we have measured the dominant period in these stars
that are known to show multi-periodic phenomena. Future work will
include extraction of the sub-dominant periods and
distribution of the ratio of the different periods. Furthermore, the
distribution and possible correlations of the Fourier parameters for
these stars is an interesting and, until now, unexamined problem which we
can address with this data set.
Acknowledgements
The authors thank the referee Jean-Philippe Beaulieu for his comments, which improved the manuscript considerably. We would like to thank the observers and staff at Wendelstein Observatory, Otto Bärnbantner, Christoph Riess, Heinz Barwig, Claus Gössl, and Wolfgang Mitsch, and all the staff at Calar Alto Observatory for their extensive support during the observing runs of this project. JF thanks Armin Gabasch and Ulrich Hopp for stimulating discussions. This work was supported by the Sonderforschungsbereich 375-95 Astro-Particle-Physics of the Deutsche Forschungsgemeinschaft.
Table 2:
Extract from the WeCAPP catalogue of
variable stars. We give the identification, the right ascension and
declination, the assigned period and its significance s (
![]() un-significant,
un-significant,
![]() highly
significant) in R and I, the amplitude of variation in both bands,
and finally a classification according to the scheme presented in
Sects. 4 and 5. The variation amplitudes
highly
significant) in R and I, the amplitude of variation in both bands,
and finally a classification according to the scheme presented in
Sects. 4 and 5. The variation amplitudes
![]() and
and
![]() are given in units of [10-5 Jy].
are given in units of [10-5 Jy].
Table 3:
Coincidences between the WeCAPP catalogue
of variable stars and the X-ray selected catalogue of point sources by
Kaaret (2002). A search radius of 1
![]() was used. We give the
identifier and WCS coordinates for the WeCAPP sources, and the
identifier for the Kaaret (2002) sources. For sources coincident
with the 2MASS catalogue Cutri et al. (2000), we give the 2MASS identifier
also. We also show the difference
was used. We give the
identifier and WCS coordinates for the WeCAPP sources, and the
identifier for the Kaaret (2002) sources. For sources coincident
with the 2MASS catalogue Cutri et al. (2000), we give the 2MASS identifier
also. We also show the difference ![]() r of the matching of both catalogues
for each of the correlated sources.
r of the matching of both catalogues
for each of the correlated sources.
Table 4:
Coincidences between the WeCAPP catalogue of
variable stars and the X-ray selected catalogue of point sources by
Kong et al. (2002). A search radius of 1
![]() was used. We give the
identifier and WCS coordinates for the WeCAPP sources, and the
identifier and IAU name for the Kong et al. (2002) sources.
We also show the difference
was used. We give the
identifier and WCS coordinates for the WeCAPP sources, and the
identifier and IAU name for the Kong et al. (2002) sources.
We also show the difference ![]() r
of the matching of both catalogues for each of the correlated sources.
Symbols in the last row are taken from Kong et al. (2002), and they mark
globular cluster counterparts (g, search radius 3
r
of the matching of both catalogues for each of the correlated sources.
Symbols in the last row are taken from Kong et al. (2002), and they mark
globular cluster counterparts (g, search radius 3
![]() ), X-ray
variable sources (v), and X-ray transients (t).
), X-ray
variable sources (v), and X-ray transients (t).
Table 5:
Coincidences between the WeCAPP catalogue of
variable stars and the General Catalogue of Variable Stars (GCVS,
Durlevich et al. 1996). A search radius of 1
![]() was used. We give the
identifier, WCS coordinates and a classification for the WeCAPP
sources, and the identifier and a classification according to the
GCVS. We also the
difference
was used. We give the
identifier, WCS coordinates and a classification for the WeCAPP
sources, and the identifier and a classification according to the
GCVS. We also the
difference ![]() r of the matching of both catalogues
for each of the correlated sources.
r of the matching of both catalogues
for each of the correlated sources.
A quantitative way to describe the effects of the time sampling of
observations on the power spectrum is given by the window function
![]() .
.
![]() is defined as the Fourier transform of the sampling
function s(t), where s(ti) is of constant value in case of
observations taking place at times ti, and s(ti) is zero otherwise:
is defined as the Fourier transform of the sampling
function s(t), where s(ti) is of constant value in case of
observations taking place at times ti, and s(ti) is zero otherwise:
The strong power in periods around 450 days (at
![]() days-1) is clearly visible, whereas
no "aliasing'' problem is expected at small periods (high frequencies).
The full width half
maximum
days-1) is clearly visible, whereas
no "aliasing'' problem is expected at small periods (high frequencies).
The full width half
maximum
![]() of the main peak of the window function
of the main peak of the window function
![]() determines the theoretical error in the period calculation
determines the theoretical error in the period calculation
| |
Figure A.1:
The window
function |
| |
Figure A.2:
Window function |
![\begin{figure}
\par\mbox{\includegraphics[width=8.8cm,angle=0]{2223fa3a.ps}\hspace*{3mm}
\includegraphics[width=8.8cm,angle=0]{2223fa3b.ps} }\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg138.gif) |
Figure A.3: Left panel: leakage function for the sampling given in the survey for different periodic signals. The function shows how a signal which is located at zero offset leaks into neighboring frequencies. We calculated this function for a signal according to Eq. (A.4) and periods of 5, 10, 20, 50, 100, 200, 250, 300 (cyan curve), 400, 450, 500, 550, 600, and 700 days (black curves, if not mentioned otherwise). The power in the second peak is high for periods of 400 (blue curve), 450 (magenta curve), and 500 days (red curve). In this period regime, the power in the second peak can exceed the power in the first peak (at zero frequency difference) resulting in an aliasing of periods. The aliasing decreases for periods of 550 (green curve) and 600 days (yellow curve), and vanishes for even longer periods. The aliasing is also evident in the Monte-Carlo simulation of the survey. Right panel: leakage function in the period representation for the sampling given in the survey for different periodic signals. For periods between 350 and about 550 days, the power in the second peak can exceed the power in the first peak (at zero period difference) resulting in a possible aliasing of periods. The resulting displacement of the true period can be read from the x-axis. |
In the right panel of Fig. A.3 we show the leakage function in the period representation. For periods between about 350 and 550 days the power in the second peak in the Fourier spectrum can exceed the power in the first peak, which means that the derived period is offset from the real one by the position of the second peak.
![\begin{figure}
\par\includegraphics[width=6.3cm,clip]{2223fa04.eps}\end{figure}](/articles/aa/full/2006/02/aa2223-04/Timg139.gif) |
Figure B.1: Result of simulations for decreasing S/N of the light curves from the upper left to the lower right corner. The mean magnitude of the source changes in steps of one magnitude from MR=-1 mag in the upper left corner to MR=2 mag in the lower right corner. Red dots show the accuracy of the period determination for light curves with an amplitude AR= 2.0 mag; blue dots correspond to AR= 1.0 mag; and black dots have AR= 0.5 mag. The apparent horizontal lines at large periods result from the finite frequency resolution of the period-finding algorithm. Above a threshold in S/N, the accuracy of the period determination seems independent of the particular S/N of the light curves. In this regime only periods longer than 500 days have a large false detection probability. Below the threshold the accuracy breaks down very rapidly, independent of the period. In magenta we show the theoretical expected errors of the period determination according to Eq. (A.3). |
We also tested the accuracy of the period determination with
Monte Carlo simulations of the survey. We analyzed
the accuracy for different mean magnitudes and amplitudes at a fixed
position, thus fixed noise contributions of the galaxy and the sky.
We chose the mean magnitude MR of the variable to be
MR=-1,0,1,2 mag and shift them to a distance of M 31. For each of
these mean magnitudes, we changed the amplitude AR of the variation
from 0.5 mag to 2 mag. The background (surface brightness of the
galaxy + sky contribution) was set to
Mbg,R=19 mag per area of the
PSF. In each run we simulated 105 light curves according to