A&A 445, 43-49 (2006)
DOI: 10.1051/0004-6361:20053557

Probing dark matter caustics with weak lensing

R. Gavazzi1,3 - R. Mohayaee2 - B. Fort2


1 - Laboratoire d'Astrophysique, OMP, UMR 5572, 14 Av. Edouard Belin, 31400 Toulouse, France
2 - Institut d'Astrophysique de Paris, UMR7095 CNRS, Université Pierre & Marie Curie, 98bis Bd. Arago, 75014 Paris, France
3 - Oxford University, Astrophysics, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK

Received 2 June 2005 / Accepted 18 August 2005

Abstract
Caustics are high-density structures that form in collisionless media. Under self-gravity, cold dark matter flows focus onto caustics which are yet to be resolved in numerical simulations and observed in the real world. If detected, caustics would provide strong evidence for dark matter and would rule out alternative models such as those with modified dynamics. Here, we demonstrate how they might be observed in weak lensing data. We evaluate the shear distortion and show that its radial profile is marked by a characteristic sawtooth pattern due to the caustics in dark matter haloes that form by selfsimilar accretion. We discuss the observational complications, mainly due to the poor knowledge of the virial radii of the haloes and demonstrate that a superposition of about 600 cluster-size haloes would give a signal-to-noise ratio which is sufficiently large for the detection of caustics with ground-based observations. This number is reduced to 200 for space-based observations. These bounds can be easily achieved by the ongoing wide field optical surveys such as CFHTLS and the future space-based projects SNAP and DUNE which have to be accompanied by an X-ray follow-up of the selected clusters for a precise determination of their virial radius.

Key words: cosmology: dark matter - cosmology: gravitational lensing

1 Introduction

The nature of dark matter, which constitutes about $30\%$ of the mass of the Universe, remains largely unknown. Results from cosmic microwave background explorers and large-scale galaxy surveys suggest that dark matter is cold with little velocity dispersion (e.g. Spergel et al. 2003; Tegmark et al. 2004). If so, then its evolution is mainly governed by its self-gravity and expressed by Jeans-Vlassov-Poisson equations. The collisionless nature of dark matter predicts the formation of multi-stream regions bounded by very high density manifolds known as caustics.

In a cold dark matter Universe, caustics can form on large scales of many megaparsecs, manifesting in the filamentary structure of galaxy distribution (Shandarin & Zeldovich 1989) and also at smaller scales of a few parsecs or kiloparsecs in dark matter haloes. This is well illustrated in some pionering numerical works (Melott & Shandarin 1989). Due to their abundance, the rich observational and numerical data and their high density contrasts, haloes are likely areas for the caustics.

Analytic models for the formation and evolution of dark matter haloes are still rare and most works are based on the selfsimilar accretion model (Gott 1975; Gunn 1977; Fillmore & Goldreich 1984; Bertschinger 1985). In this model, first proposed to explain the rotation curve of galaxies, haloes form by temporally self-similar collapse of dark matter shells onto an initially over-dense perturbation. Dark matter shells initially expand until they reach their turnaround radii where they separate from the background expansion and collapse. After collapse they re-bounce and collapse again and the density profile settles asymptotically into a power-law which is convolved with singular spikes, namely with caustics.

In the following we shall refer to such caustics as "outer caustics''. They are suggestive of the sharp stellar shells observed around giant ellipticals which can arise in the merger of galaxies (Fort et al. 1986; Quinn 1984; Malin & Carter 1980). The main observational difference between the merger and selfsimilar spherical infall is that the former predicts that the caustics are interleaved with the caustic radii alternating on opposite sides of the galaxy and the latter predicts concentric spherical shells.

The spherically symmetric model has been extended to consider infalling matter with angular momentum and calculated the properties of an additional kind of "inner caustics'' with torus-like topology (Sikivie 1998,1999). Such accretion with angular momentum is more relevant for galaxy-size haloes than for clusters of galaxies dominated by radial infall.

Here, we focus on the outer caustics of cluster-size haloes and argue that they can be reasonably approximated by selfsimilar infall models. In the original version of this model, dark matter is absolutely cold, i.e. with zero velocity dispersion, and caustics are infinitely thin concentric spherical shells with diverging densities. However, realistically, dark matter has a small velocity dispersion and these shells have finite thicknesses. The thicknesses of the caustics would however remain very small (due to the coldness of dark matter) and thus they would contain very little mass in spite of their significant density. Various characteristics of the caustics such as their density profile, their thickness and their approximate maximum density for a low velocity dispersion dark matter medium have been recently evaluated (Mohayaee & Shandarin 2005, hereafter MS05).

Detection of dark matter caustics remains a challenging problem both for 3-dimensional numerical simulations and for observations. Dark matter annihilation in the caustics has already been studied (see e.g. Mohayaee & Shandarin 2005; Sikivie et al. 1997; Pieri & Branchini 2005; Hogan 2001). Since the flux of the annihilation products, e.g. $\gamma$-rays or antiproton flux, depends on the square of the local density[*], caustics with their sharply-peaked densities would be the likely places for significant emissivity. Such kind of observations are promising for the eventual detection of dark matter in the caustics. However, the major problem with dark matter detection through gamma-ray emission is the severe background contamination of the signal and the low signal-to-noise ratio of present day observations.

It has been shown that rotation curves of galaxies might be sensitive to the presence of inner caustics and claimed a marginal detection based on an ensemble average over 32 rotation curves (Kinney & Sikivie 2000). Inner caustic rings are located in the plane of the disk and are likely to modify rotation curves more efficiently than outer caustics with spherical symmetry. Moreover, rotation curves only probe the dark matter potential of galactic haloes where a large amount of tracers (gas or stars) is available. Therefore, outer caustics which are located well beyond the observable tracers cannot leave a detectable imprint on rotation curves.

Gravitational lensing provides a promising alternative tool. Since lensing probes the projected density profile with no regards to the nature or dynamical state of the deflecting mass, it should be sensitive to the caustics. The lensing properties of dark matter caustics and particularly their efficiency in magnifying and/or producing multiple images of background sources has already been investigated (Charmousis et al. 2003).

Inner caustics may be dense enough to produce substantial magnification and small separation multiple images as in micro-lensing by compact objects. High magnification events due to such caustics may explain the anomaly in flux ratios observed in multiply-imaged quasars which are hardly reproduced by a smooth halo or even subhalos (see e.g. Kochanek & Dalal 2004; Dalal & Kochanek 2002).

Conversely, it has been found that outer caustics are inefficient in magnifying distant sources and would yield at most a few percent net magnification or shear (Charmousis et al. 2003). As we shall detail below, the selfsimilarity of dark matter accretion implies that outer caustics occur at the same radius provided physical radii are properly rescaled by the halo mass. Hence the tiny lensing signal of caustics could show up statistically by averaging over many rescaled haloes. Such a statistical approch is much more complicate for the lensing-based detection of inner caustic rings because of the random orientation of rings (or angular momenta).

In this work, we consider the lensing properties of the outer caustics only and we propose the weak-lensing effect as a potential way to detect caustics. We demonstrate that the caustics will produce sharp variations in the projected surface mass density around haloes. Depending on the height and width of caustics, gravitationally-distorted background galaxies will experience local variations of shear.

If the aforementioned universal property of haloes is fullfilled, then the rapid progress in X-ray and lensing observations of cluster of galaxies may offer one possibility to observe dark matter caustics. Deep and wide surveys such as CFHTLS will cover fields of view of a few hundreed square degrees and will provide us with a useful material for the detection of dark matter caustics through the capability of mass to coherently stretch the image of the background galaxies. They will provide us with a large enough number of galaxy clusters[*] to achieve the required level of signal-to-noise ratio. Wide field spatial surveys will be even more powerful for the investigation of the lensing properties of dark matter haloes and their associated caustics. An important requirement for the detection of caustics is the measurement of virial radii of the clusters which can be provided by X-rays (e.g.  Arnaud et al. 2005).

Throughout this paper, we assume an Einstein-de Sitter Universe but our results should be qualitatively similar in a concordance $\Lambda$CDM model. The role of dark energy becomes important at low redshifts ($\sim$0.2) which we expect to occur well after the formation of the typical dark matter haloes we consider here. Furthermore, once a particle turns around and collapses, it separates from the background expansion and its subsequent motion should not be affected by the $\Lambda$ term.

The paper is organized as follows. We review the three-dimensional and projected properties of self-similar haloes and caustics in Sect. 2. We derive the lensing signal for a single halo, compare it to the noise level of fiducial observations and estimate the number of haloes required to achieve a significant signal-to-noise ratio in Sect. 3, where we also examine the ability of weak lensing to constrain the velocity dispersion of dark matter particles. We summarize, discuss the prospectives for future works and conclude in Sect. 4.

  
2 Dark matter caustics

2.1 Tri-dimensional key equations

Table 1: The non-dimensional times ($\xi _k$), positions ($\lambda _k$), thicknesses ( $\Delta r_k$), maximum densities ( $\rho _{\rm max}$) of the first ten caustics, the halo density itself ( $\rho _{\rm halo}$) at the positions of these caustics and other parameters used in expressions (3), (5)-(7). The present velocity dispersion is that for neutralinos which is about 0.03 cm s-1. It is worth emphasizing that the thicknesses of the caustics do not depend on the halo parameters but only on the velocity dispersion of dark matter [see expression (6)]. It is instructive to compare the last two columns, which show that for a cluster-size halo with $r_{\rm vir}\sim 1$ Mpc, the caustic density can be many orders of magnitude higher than the halo density itself.

In an Einstein-de Sitter Universe a spherical overdensity expands and then turns around to collapse. After collapse and at late times, the fluid motion becomes selfsimilar: its form remains unchanged when its length is re-scaled in terms of the radius of the shell that is currently at the "turn around'' and is falling onto the galaxy for the first time. Physically, selfsimilarity arises because gravity is scale-free and because mass shells outside the initial overdensity are also bound and turn around at successively later times. Self-similar solutions give power-law density profiles whose exact scaling properties depend on the central boundary conditions and on whether the fluid is collisionless or collisional (Gott 1975; Gunn 1977; Fillmore & Goldreich 1984; Bertschinger 1985). The density profile obeys a power-law on the scale of the halo which provides an explanation of the flattening of the rotation curves of the galaxies. However, on smaller scales the density profile contains many spikes (i.e. caustics) of infinite density. The position and the time of formation of these caustics are among the many properties that have been studied in the selfsimilar infall model (Bertschinger 1985).

In the presence of a small velocity dispersion the maximum density and thickness of the caustic shells and their density profiles have been evaluated in the framework of a selfsimilar collapse model (MS05).

The global halo density profile, asymptotically reached in this process, is well-approximated by

 \begin{displaymath} \frac{\rho_{\rm halo}(\lambda)}{\rho_{\rm H}} \sim \frac{8.4~\lambda^{-9/4}}{(1+\lambda^{3/4})^2} , \end{displaymath} (1)

where $\lambda=r/r_{\rm ta}$ with $r_{\rm ta}$ the present turnaround radius of the halo and $\rho_{\rm H}=3H^2/8\pi G$ the background density. The turnaround radius can be easily computed using the virial radius. Within the virial radius, $r_{\rm vir}=r_{200}$, the mean density, $\rho_{\rm vir}$, is, by definition, 200 times the background density. Thus, using the density profile (1), we obtain the following relationship between the turnaround and the virial radii: $r_{\rm ta}\sim~ 4~r_{\rm vir}$.

For a perfectly cold dark matter medium, the density profile close to a caustic at $\lambda _k$ is (Bertschinger 1985)

 \begin{displaymath} \frac{\rho_0(\lambda)}{\rho_{\rm H}}= \frac{G_k}{\sqrt{\lambda_k-\lambda}} ; \qquad\qquad \sigma=0, \end{displaymath} (2)

with

 \begin{displaymath}G_k=\frac{\pi^2}{4\sqrt{-2\lambda_k''~}}~\frac{{\rm e}^{-2 \xi_k/3}}{\lambda_k^2 } , \end{displaymath} (3)

where the values of the various quantities $\xi _k$, $\lambda _k$, $\lambda_k''$(and $\Lambda_k$ which will appear in the coming expression (6)) are given in Table 1 (see MS05 for a detailed description of these parameters).


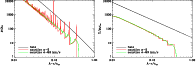  \begin{figure} \par\mbox{\resizebox{8.5cm}{!}{\includegraphics{3557fig1.eps}} \resizebox{8.5cm}{!}{\includegraphics{3557fig2.eps}} } \end{figure} Figure 1: Left panel: in units of the background density, $\rho _{\rm H}$, we show the 3D density profile for the halo (black), for the caustics in a perfectly cold medium (red) and for the caustics smoothed out by a warm/hot dark matter with velocity dispersion $\sigma=60~ {\rm km~ s}^{-1}$ (green). Red spikes are all singular with infinite density and limited here to finite values because of finite resolution. Right panel: the same colour-coding for the projected 2D density profiles in units of $\rho _{\rm H} r_{\rm ta}$. When projected, caustic peaks are smoother and look like a flight of stairs. Therefore, we expect low lensing magnifications close to the caustics (see Sect. 3).
Open with DEXTER

When the temperature of particles is not strictly zero and the velocity of particles is distributed according to the distribution function f(v), caustic positions are shifted by a small value  $\delta\lambda$ and the caustic density is modified as (MS05):

\begin{displaymath}\rho_\sigma(\lambda)= \int {\rm d}v~ \rho_0~[\lambda - \delta\lambda(v)]~ f(v) ; \qquad \sigma\not=0. \end{displaymath} (4)

In this work, we choose a top-hat velocity distribution function (MS05). Then, the density close to the kth caustic in the halo is given by

 \begin{displaymath} \frac{\rho_\sigma(\lambda)}{\rho_{\rm H}} = \frac{G_k}{\Delt... ..., \\ 0 &{\rm ~~for~}\lambda> \lambda_k^+ , \end{array}\right. \end{displaymath} (5)

where $\lambda_k^-=\lambda_k-\Delta_k$ and $\lambda_k^+=\lambda_k+\Delta_k$and the thickness of the kth caustic, $\Delta_k$, in nondimensional coordinate is given by

 \begin{displaymath}r_{\rm ita}~ \Delta_k=\Delta r_k={(3\pi)^{2/3}\over 4} {\rm e}^{5\xi_k/9}~\vert\Lambda_k\vert~~ t~\sigma(t) \end{displaymath} (6)

and $r_{\rm ita}$ is the initial turnaround radius and $\sigma(t)$is the value of the velocity dispersion of dark matter particles at time twhich is that at decoupling re-scaled by the expansion factor[*]. The standard spherical collapse model yields a relation  $r_{\rm ita}=2 r_{\rm vir}$ for a constant overdensity (see e.g. chapter 5.10 of Padmanabhan 2002). However, the real value of the initial turnaround radius would be lower due to the continuous accretion by the halo. Thus the physical thickness of the caustic, $\Delta r_k$, depends only on its position in the halo and the nature of dark matter.

The maximum density at each caustic position can also be approximated by the expression (see Table 1 and also MS05)

 \begin{displaymath} \rho_{\rm max}={2~G_k {\rm e}^{-5\xi_k/18}\over (3\pi)^{1/3}... ...bda_k~}}~~ \sqrt{r_{\rm ta}\over t~~\sigma(t)}~~ \rho_{\rm H}. \end{displaymath} (7)

Expressions (5)-(7) provide us with a sufficient basis for the evaluation of magnification and shear due to dark matter caustics. Although in the rest of this work we directly integrate expression (5) and never use (7), values for the latter are given in Table 1 to demonstrate the density contrast of each caustic with respect to its host halo.

Although the selfsimilar model might seem naive, it provides a good approximation for outer caustics in galaxy-cluster haloes which are not significantly disrupted by merger and substructures and to a good approximation are spherical. Furthermore, fluctuations caused by large scale structure would already be averaged out in the statistical evaluation of the shear.

  
2.2 Projected densities

Since we are concerned with the lensing properties of caustics, we have to calculate the projected density profile for the caustics and for the halo. The Abel integral relates the 3-dimensional density ($\rho$) and the 2-dimensional density profiles ($\Sigma$) by

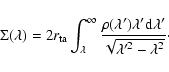\begin{displaymath}\Sigma(\lambda)= 2 r_{\rm ta} \int_{\lambda}^\infty \frac{\rh... ...) \lambda' {\rm d}\lambda'}{\sqrt{\lambda'^2-\lambda^2}}\cdot \end{displaymath} (8)

We numerically integrate the above expression, for the density profiles (2) and (5). The halo surface mass density can be evaluated analytically if we neglect the $(1+\lambda^{3/4})^2$ term in Eq. (1), i.e. at small scales $\lambda\ll 1$, yielding the approximate projected halo profile

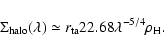\begin{displaymath}\Sigma_{\rm halo}(\lambda) \simeq r_{\rm ta} 22.68 \lambda^{-5/4}\rho_{\rm H}. \end{displaymath} (9)

Let us define the mean projected density enclosed by the cylinder of radius $\lambda$:

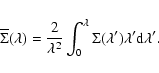\begin{displaymath}\overline{\Sigma}(\lambda)= \frac{2}{\lambda^2} \int_{0}^\lambda \Sigma(\lambda') \lambda'{\rm d}\lambda' . \end{displaymath} (10)

Thus, under the hypothesis of small $\lambda$, the mean projected density for the halo component is $\overline{\Sigma}_{\rm halo}(\lambda)= \frac{8}{3} \Sigma(\lambda)$.

Figure 1 shows the 3D (left) and 2D (right) density profiles for the halo and the caustics. We consider the case of a perfectly cold dark matter with very peaked caustics and the case in which they are smoothed out by a finite velocity dispersion $\sigma \sim 60 ~ {\rm km~ s}^{-1}$. This value is very high for most cold dark matter models but its extremity illustrates well the peak dilution and shows that caustics survive a large thermal softening. When considering the projected density, instead of spikes we rather see stairs that come from the analytic $1/\!\sqrt{r_k-r}$ singularity of caustics. Consequently even with singular caustics, the projected density profile is not peaked. The implications for lensing are discussed in the next section.

  
3 Weak lensing

3.1 General equations

The fundamental quantity for gravitational lensing is the lens potential  $\psi(\vec{\theta})$ at the angular position  $\vec{\theta}$ which is related to the surface mass density $\Sigma(\vec{\theta})$ projected into the lens plane through:

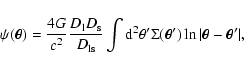\begin{displaymath}\psi(\vec{\theta}) = \frac{4 G}{c^2} \frac{D_{\rm l} D_{\rm s... ...igma(\vec{\theta}') \ln\vert \vec{\theta}-\vec{\theta}'\vert , \end{displaymath} (11)

where $D_{\rm l}$, $D_{\rm s}$ and $D_{\rm ls}$ are angular distances to the lens, to the source and between the lens and the source respectively. The deflection angle  $\vec{\alpha}=\vec{\nabla}\psi$ relates a point in the source plane  $\vec{\beta}$ to its image(s) in the image plane  $\vec{\theta}$ through the lens equation $\vec{\beta}=\vec{\theta}-\vec{\alpha}(\vec{\theta})$. The local relation between  $\vec{\beta}$ and $\vec{\theta}$ is the Jacobian matrix $A_{ij}=\partial \beta_i/\partial \theta_j$:

 \begin{displaymath} A_{ij} = \delta_{ij} - \psi_{,ij} = \left(\begin{array}{cc}... ...amma_2 \\ -\gamma_2 & 1-\kappa+\gamma_1 \end{array}\right), \end{displaymath} (12)

with the convergence $\kappa(\vec{\theta})=\Sigma(\vec{\theta})/\Sigma_{\rm crit}$ directly related to the surface mass density via the critical density

 \begin{displaymath} \Sigma_{\rm crit}= \frac{c^2}{4 \pi G}\frac{D_{\rm ls}}{D_{\rm l}D_{\rm s}}, \end{displaymath} (13)

and the 2-component shear $\gamma=\gamma_1+i \gamma_2$ in complex notation. The convergence satisfies the Poisson equation $\Delta \psi = 2 \kappa$. In the weak lensing regime ( $\gamma \ll 1$), an elliptical object in the source plane with complex ellipticity $e_{\rm s}$ is mapped into an elliptical image with a different ellipticity  $e = e_{\rm s} + \gamma$. We refer the reader to the reviews of Mellier (1999) and Bartelmann & Schneider (2001) for detailed accounts of weak lensing.

For a circularly symmetric lens, $\gamma$ is oriented tangentially to the lens center and its amplitude at radius r is $\gamma(r)=(\overline{\Sigma}(r)-\Sigma(r))/\Sigma_{\rm crit}$. Since sources are randomly oriented, the tangential component of the observed galaxies is an unbiased estimator of $\gamma$. When averaging the estimate of $\gamma$ within an aperture of solid angle $\Omega$, containing $N=\Omega n$ galaxies (n is the number density of sources), the noise dispersion of $\gamma$ is $\sigma_\gamma=\frac{\sigma_{\rm e}}{\sqrt{N}}$ where $\sigma_{\rm e}\sim0.3$ is the intrinsic dispersion of source ellipticities (along one component).

3.2 Shear measurement

In order to be consistent with our calculations of Sect. 2.2, we define a pseudo-shear: $\Gamma(\lambda)=(\overline{\Sigma}-\Sigma)/\rho_{\rm H} r_{\rm ta}$and the corresponding noise level $\Gamma_N=\Sigma_{\rm crit}\sigma_\gamma / \rho_{\rm H} r_{\rm ta}$. For an EdS cosmology, and considering an annulus of inner and outer radii $\lambda_1$ and $\lambda_2$ respectively, it is straightforward to write $\Gamma_N$ in this useful form:

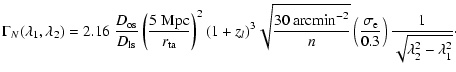$\displaystyle \Gamma_N(\lambda_1,\lambda_2)= 2.16~ \frac{D_{\rm os}}{D_{\rm ls}... ...\frac{\sigma_{\rm e}}{0.3}\right) \frac{1}{\sqrt{\lambda_2^2-\lambda_1^2}}\cdot$     (14)

This expression seems to indicate that the noise level will be lower for nearby haloes. However, it hides the fact that low redshift haloes require a very wide sky coverage for the outermost caustics ($\sim$ $r_{\rm ta}/3$) to fit the field of view of the observation. Consequently, intermediate redshift haloes ( $z\sim0.2{-}0.5$) are the most interesting targets. In addition, nearby (and thus large angular scale) clusters suffer from noise due to large-scale structure (LSS) fluctuation integrated along the line-of-sight and unrelated to the halo we are considering (Hoekstra 2003). For scales $\la $15 arcmin, the smearing of the shear profile by LSS is minimised.

Figure 2 shows $\Gamma$ as a function of $\lambda$ for the same values of the thermal velocity dispersions $\sigma=0~ {\rm km~ s}^{-1}$ and $\sigma=60~ {\rm km~ s}^{-1}$. Comparing these curves, one can see that the sawtooth patterns due to caustics survive significantly high temperatures. Next, we consider the noise level for a fiducial halo at redshift $z_{\rm l}=0.3$and a turnaround radius $r_{\rm ta}=5~ {\rm Mpc}$ which is a typical value for clusters (upper green "binned'' curve). With a single halo the detection of caustics is impossible. If we are able to stack the signal from a few tens of clusters (lower blue-binned curve), the noise level will be low enough to be sensitive to caustics as a whole. However, we would detect a smooth contribution which is indistinguishable from the halo itself.

Sawtooth patterns cannot be confused with the effect of substructures since the contribution of the latter would be averaged out over the azimuthal angle (most outer caustics have spherical symmetry) and once rescaled, caustics always appear at the same place within haloes. This is not the case for substructures which can appear at any radius inside the host halo.


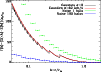  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{3557fig3.eps}} \end{figure} Figure 2: $\Gamma (\lambda )$ contribution of caustics for two values of $\sigma $: cold medium $\sigma =0$ (black curve) and warm medium $\sigma \sim 60$ km s-1 (red curve). The green (resp. blue) "binned'' curve is the noise level for one (resp. 100 stacked) halo(es).
Open with DEXTER

Consequently, the right way to probe the existence of caustics is to measure the $\Gamma$ signal in excess/default relative to the extreme value of $\sigma $, e.g. $\sigma\ga 300 ~ {\rm km~ s}^{-1}$ as taken here. For this purpose, one needs $\ga$100 stacked clusters. With the corresponding noise level, it would be possible to test the thermal smoothing of caustics and put constraints on $\sigma $. However, the sensitivity is poor and only upper limits can be put on $\sigma $ with a realistic number of haloes. For instance with N=200 (resp. 500) clusters, we could achieve a limit $\sigma < 170~ {\rm km~ s}^{-1}$ (resp.  $40~ {\rm km~ s}^{-1}$) at a $95.4\%$ confidence level.

When considering galaxies instead of clusters with turnaround radii about 10 times smaller, the number of haloes required to achieve the same detection level is 104 times higher. So using a few 105 galaxies between $z\sim 0.1{-}0.5$ would yield the same results.

This required level of signal can easily be achieved with a wide and moderately deep survey like the ongoing CFHTLS. Typically, a square-degree field of view will contain a few such cluster-size haloes with $r_{\rm ta}\sim 5~ {\rm Mpc}$, a few thousand elliptical galaxies with $r_{\rm ta}\sim 1~ {\rm Mpc}$ and tens of thousands of spiral galaxies with $r_{\rm ta}\sim 500~ {\rm kpc}$. The total coverage of the CFHTLS wide survey is 170 square degree and will contain a large enough number of clusters/galaxies. Furthermore the wide fields of view are well-suited to measure shear up to the outermost caustic of clusters ( $1~ {\rm Mpc}=5\hbox{$^\prime$ }$ at z=0.3 and $4\hbox{$^\prime$ }$ at z=0.5).

Spatial observations provide an improvement on shear measurements: (i) the intrinsic dispersion in source ellipticities is lowered  $\sigma_{\rm e}\sim0.2$ and (ii) the density of sources is increased $n\sim50$ arcmin-2. Hence the total number of haloes required to achieve the same detection level can be lowered by a factor of three. Future wide spatial surveys like SNAP or DUNE will provide the required sky coverage.

3.3 Halo-stacking issues

So far, we have considered the observational difficulties encountered by the dispersion in intrinsinc source ellipticities. However, practical complications such as the difficult signal stacking process should also be overcome before a detection of the caustics can be achieved. To do so, high-precision measurements of the location of the center and the turnaround radius of each halo are required. Otherwise, imperfect alignment/rescaling would tend to blur the caustics spikes and reduce the sensitivity. The center of a well-relaxed cluster coincides within one arc-second with the center of the halo. Hence the only scaling factor is the turnaround radius that can be related to the virial radius (see the sentence following expression (1)).


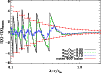  \begin{figure} \par\resizebox{8.8cm}{!}{\includegraphics{3557fig4.eps}} \end{figure} Figure 3: Difference between the $\Gamma (\lambda )$ contribution of cold caustics and the smooth component. We illustrate the blurring effect of an imperfect knowledge of the turnaround radius of stacked haloes. The solid black line, dashed green line and dot-dashed blue line correspond to zero, 3% and 10% uncertainties, respectively. As in Fig. 2, the binned curve represents the noise level achieved with 600 stacked haloes. The convolution effect of error in the assumed/measured value of $r_{\rm ta}$ is important and a significant detection of caustics requires well-determined turnaround radii ( $\protect\la$ a few percent relative accuracy). The very small scale oscillations in the plot are numerical artifacts and ideally the only sawtooth patterns are those due to caustics.
Open with DEXTER

Figure 3 shows the blurring of caustics due to an imperfect knowledge of the turnaround radius of each stacked halo. We consider a dispersion around the true value of 3% and 10%. To properly detect caustics, one needs a precise estimate of  $r_{\rm ta}$. Provided dark matter is cold enough, $\sigma\la$ a few $~ {\rm km~ s}^{-1}$, which is a realistic prescription, a reasonable number of stacked haloes, $\sim$600, can overcome the loss of a few percents of relative precision caused by the errors in the determination of the turnaround radius.

Consequently the number of haloes necessary for detection needs to be increased in order to achieve the necessary level of signal-to-noise ratio. Moreover, additional external information for the determination of  $r_{\rm ta}$ such as X-rays or dynamical observations in addition to weak lensing data are indispensable for a convincing detection of caustics. The present-day state-of-the-art X-ray estimates for the scale radius is $\la $$10\%$ for nearby clusters (z<0.2) (Arnaud et al. 2005; Pointecouteau et al. 2005) and it seems that a similar precision can be reached at higher redshifts (0.4<z<0.7) (Kotov & Vikhlinin 2005). In addition shear, which is used for caustic detection, also provides constraints on the halo density profile. The virial radius of some clusters presenting strong and weak lensing features can be measured with good accuracy ( $\Delta r_{200}/r_{200} \la 3$%) (Gavazzi 2005; Broadhurst et al. 2005). Consequently, future large cluster samples with X-rays and lensing data of present-day quality will provide us with the necessary precision to probe dark matter caustics.

  
4 Discussion and conclusion

Although the Liouville theorem claims that singularities will survive, they are likely to develop a complex topology in the course of evolution of structures under self-gravity. It is not clear to what degree the merging processes and substructures will smear out the caustics or complicate their geometries. Here, we have considered the outer caustics of cluster-size haloes which are expected to have suffered far less from mergers and due to their relatively large separations are unlikely to have been washed away by the dispersive-like effect of the substructures. These caustics are the ones that contribute most to the lensing signal for the following reasons. Their amplitude relative to the background smooth halo component is more important as compared to the inner caustics. The inner caustics smear most from thermalisation and imperfect stacking and finally, the noise level increases toward the center of haloes thus giving more weight to the outer caustics. Hence, we have focused on caustics of cluster-size haloes and have argued that they can be reasonably approximated by a selfsimilar spherical accretion model, though the triaxiality of haloes is well established in numerical simulations (Jing & Suto 2002). However, caustic patterns should exist in triaxial matter distributions. The singularities will have the same elliptical symmetry and may be properly stacked from one halo to another by choosing a subsample of apparently circular projected haloes or by using the shear azimuthal variations to constrain the halo ellipticity. We expect this effect to be comparable to the uncertainty in the halo scaling radius (either turnaround or virial).

We have shown that the existence of dark matter caustics could be probed by properly stacking the weak lensing signal of a reasonable number of haloes. The main observational limitation is perhaps the precise estimation of the turnaround radius, $r_{\rm ta}$, of superimposed haloes but we have shown that the loss of a few percent relative accuracy in the determination of  $r_{\rm ta}$ (or asphericity) can be compensated for by stacking about 600 haloes.

Although the sensitivity is low, a detection of caustics provides an upper bound for the temperature of dark matter, thus excluding hot dark matter models. The sensitivity is not sufficient to distinguish between various cold dark matter candidates (like axions or neutralinos) since for most of the corresponding velocity dispersions, the shear signal would be similar.

However, a detection of caustics would be a strong argument for the existence of cold dark matter since alternative models like MOND could not explain such density singularities and at most could serve in place of a smooth halo (namely provide an equivalent effective gravitational potential).

Putting constraints on the velocity dispersion of dark matter is a challenging topic in modern cosmology since it offers the possibility to pin-down an actual physical parameter of dark matter. In this paper, we investigated the possibility of such a measurement with the weak lensing effect of dark matter caustics. The implicit observational hypothesis is that we can have a selfsimilar geometrical description of the caustic shell distribution which depends on a single characteristic scaling parameter: i.e. the virial radius.

Wide field surveys such as the ongoing CFHTLS accompanied by X-ray observations can provide the required statistics for a successful detection of caustics. The number of haloes required to be superimposed will be lowered by a further factor of 3 for future space-based experiments like SNAP or DUNE.

Here, we have used the first and most common caustic singularity, that for which the density profile falls with inverse square-root of the distance from the caustic. Caustics of higher-order singularities can also appear in collisionless media and have already been classified (Arnold 1986). It remains a challenging task to generalize our work to haloes with non-vanishing eccentricity where higher-rank caustics would occur and to examine if they can modify the magnification properties of the lensed images and account for anomalous image flux ratios.

Acknowledgements

Special thanks go to Sergei Shandarin for an ongoing collaboration on dark matter caustics. We also thank Francis Bernardeau, Ed Bertschinger, Monique Arnaud, Gary Mamon and Etienne Pointecouteau for many helpful discussions and comments. R.G. is supported at Toulouse from a CNRS postdoc contract #1019 and at Oxford by a grant from the Leverhulme Trust. R.M. is supported by European Gravitational Observatory grant at the school of astronomy, university of Cardiff, UK.

References

 
Copyright ESO 2005