A&A 445, 243-272 (2006)
DOI: 10.1051/0004-6361:20053088
P. Weltevrede1 - R. T. Edwards1,3 - B. W. Stappers2,1
1 - Astronomical Institute "Anton Pannekoek'',
University of Amsterdam,
Kruislaan 403, 1098 SJ Amsterdam, The Netherlands
2 -
Stichting ASTRON, Postbus 2, 7990 AA Dwingeloo, The Netherlands
3 -
CSIRO Australia Telescope National Facility, PO Box 76, Epping NSW 1710, Australia
Received 18 March 2005 / Accepted 3 July 2005
Abstract
We present the results of a systematic, unbiased search for
subpulse modulation of 187pulsars performed with the
Westerbork Synthesis Radio Telescope (WSRT) in the Netherlands at an
observing wavelength of 21 cm. Using new observations and archival
WSRT data we have increased the list of pulsars that show the drifting
subpulse phenomenon by 42, indicating that at least one in
three pulsars exhibits this phenomenon. The real fraction of pulsars
that show the drifting phenomenon is likely to be larger than 55%. The majority of the analysed pulsars show subpulse modulation
(170), of which the majority were not previously
known to show subpulse modulation and 30show clear
systematic drifting. The large number of new drifters we have found
allows us, for the first time, to do meaningful statistics on the
drifting phenomenon. We find that the drifting phenomenon is
correlated with the pulsar age such that drifting is more likely to
occur in older pulsars. Pulsars that drift more coherently seem to be
older and have a lower modulation index. There is no significant
correlation found between P3 and other pulsar parameters (such as
the pulsar age), as has been reported in the past. There is no
significant preference of drift direction and the drift direction is
not found to be correlated with pulsar parameters.
None of the four complexity parameters predicted by different emission
models are shown to be inconsistent with the set of
modulation indices of our sample of pulsars. Therefore none of the
models can be ruled out based on our observations. We also present
results on some interesting new individual sources like a pulsar that
shows similar subpulse modulation in both the main- and interpulse and
six pulsars with opposite drift senses in different components.
Key words: stars: pulsars: general
Despite the fact that explaining the emission mechanism of radio
pulsars has proved very difficult, we have very detailed knowledge
about the emission mechanism from observations. We know from the very
high observed brightness temperatures that the radio emission must be
coherent, we know what kind of magnetic field strengths are involved
and even the orientation of the magnetic axis, rotation axis and the
line of sight can be derived from observations. Furthermore if one can
detect single pulses one can see that the pulses of some pulsars
consist of subpulses and for some pulsars these subpulses drift in
successive pulses in an organized fashion through the pulse window
(Drake & Craft 1968; Sutton et al. 1970). If one plots a so-called "pulse-stack'', a
plot in which successive pulses are displayed on top of one another,
the drifting phenomenon causes the subpulses to form "drift bands''
(an example is shown in the left panel of
Fig. 1). This complex, but highly regular intensity
modulation in time is known in great detail for only a small number of
well studied pulsars.
![\begin{figure}
\par\includegraphics[angle=270,width=6cm,clip]{3088f1a.ps}\includ...
...088a69.ps}\includegraphics[angle=270,width=3.5cm,clip]{3088a145.ps}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg10.gif) |
Figure 1: The left panel shows a pulse-stack of one hundred successive pulses of PSR B1819-22. Two successive drift bands are vertically separated by P3 and horizontally by P2. The products of our analysis are shown for three pulsars. The top panel shows the integrated pulse profile (solid line), the longitude-resolved modulation index (solid line with error bars) and the longitude-resolved standard deviation (open circles). Below this panel the LRFS is shown with on its horizontal axis the pulse longitude in degrees, which is also the scale for the abscissa of the plot above. Below the LRFS the 2DFS is plotted and the power in the 2DFS is vertically integrated between the dashed lines, producing the bottom plots. Both the LRFS and 2DFS are horizontally integrated, producing the side-panels of the spectra. See the main text for further details about the plots. |
| Open with DEXTER | |
Because the properties of the subpulses are most likely determined by the emission mechanism, we learn about the physics of the emission mechanism by studying them. That drifting is linked to the emission mechanism is suggested by the fact that drifting is affected by "nulls'' (e.g. Janssen & van Leeuwen 2004; Taylor & Huguenin 1971; van Leeuwen et al. 2002), where nulling is the phenomenon whereby the emission mechanism is switched off for a number of successive pulses. Another complex phenomenon is drift mode changes where the drift rate switches between a number of discrete values. For some pulsars there are observationally determined rules describing which drift mode changes are allowed from which drift mode (e.g. Redman et al. 2005; Wright & Fowler 1981). It has been found that the nulls of PSR B2303+30 are confined to a particular drift mode (Redman et al. 2005), which further strengthens the link between drifting and the emission mechanism.
Another characteristic feature of the emission mechanism is that when one averages the individual pulses, the resulting pulse profile is remarkably stable over time (Helfand et al. 1975). Explaining the various shapes of the pulse profiles of different pulsars and their dependence on observing frequency has proven to be very complicated, so not surprisingly an explanation that is fully consistent with the overwhelmingly detailed complex behavior of individual (sub)pulses, the nulling phenomenon and the polarization of individual pulses (e.g. Edwards 2004) seems to be far away. In this paper we describe trends of the subpulse modulation we find for a large sample of pulsars. By doing this we determine observationally what the important physical parameters are for subpulse modulation, which could help in formulating an emission model that is fully consistent with the observations.
There are a few types of models that attempt to explain the drifting
phenomenon. The most well known is the sparking gap model
(Ruderman & Sutherland 1975), which has been extended by many authors
(e.g. Gil et al. 2003; Gil & Sendyk 2000; Qiao et al. 2004; Cheng & Ruderman 1980; Filippenko & Radhakrishnan 1982) making it the most
developed model for explaining the drifting phenomenon. These models
explain the drifting phenomenon by the generation of the radio
emission via a rotating "carousel'' of discharges which circulate
around the magnetic axis due to an
![]() drift. In the carousel model it is expected that all pulsars should
have some sort of circulation time. For PSR B0943+10
(Asgekar & Deshpande 2001; Deshpande & Rankin 1999,2001) and possibly PSR B0834+06 (Asgekar & Deshpande 2005)
a tertiary subpulse modulation feature has been detected from the
fluctuation properties and viewing geometry. This periodicity has been
interpreted as related to the carousel modulation period (i.e. the
circulation time
drift. In the carousel model it is expected that all pulsars should
have some sort of circulation time. For PSR B0943+10
(Asgekar & Deshpande 2001; Deshpande & Rankin 1999,2001) and possibly PSR B0834+06 (Asgekar & Deshpande 2005)
a tertiary subpulse modulation feature has been detected from the
fluctuation properties and viewing geometry. This periodicity has been
interpreted as related to the carousel modulation period (i.e. the
circulation time ![]() ), supporting the interpretation of the
drifting subpulses being caused by a rotating carousel of
sub-beams. The circulation times of these pulsars, as well as the more
indirectly derived circulation times of PSR B0809+74
(van Leeuwen et al. 2003) and PSR B0826-34 (Gupta et al. 2004) are
consistent with the sparking gap model (Gil et al. 2003). A different
geometry of the polar cap of PSR B0826-34 is proposed by
Esamdin et al. (2005). In their interpretation the carousel changes drift
direction, something what would be inconsistent with the sparking gap
model.
), supporting the interpretation of the
drifting subpulses being caused by a rotating carousel of
sub-beams. The circulation times of these pulsars, as well as the more
indirectly derived circulation times of PSR B0809+74
(van Leeuwen et al. 2003) and PSR B0826-34 (Gupta et al. 2004) are
consistent with the sparking gap model (Gil et al. 2003). A different
geometry of the polar cap of PSR B0826-34 is proposed by
Esamdin et al. (2005). In their interpretation the carousel changes drift
direction, something what would be inconsistent with the sparking gap
model.
These models still have problems, like explaining the subpulse phase steps which are observed for some pulsars. Two clear examples of pulsars that show subpulse phase steps are PSR B0320+39 and PSR B0809+74 as found by Edwards et al. (2003) and Edwards & Stappers (2003b). We find that the new drifter PSR B2255+58 also shows a phase step.
Non-radial pulsations of neutron stars were originally proposed as the
origin of the radio pulses of pulsars (Ruderman 1968) and later as a
possible origin of the drifting subpulses (Drake & Craft 1968). Recently
this idea was revised by Clemens & Rosen (2004). This model gives a natural
explanation for observed subpulse phase steps, nulls and mode
changes. This model can be tested, although there are many
complications, by exploring average beam geometries. Although this
model can explain phase steps, it cannot explain the curvature of the
drift bands of many pulsars (see Sect. 4.5 for
details). In this model it is also difficult to explain pulsars with
opposite drift senses in different components, because drifting is a
simply a beat between the pulse period and the pulsation
time. Bi-drifting is recently observed for PSR J0815+09
(McLaughlin et al. 2004). In this paper we show a number of other pulsars
with opposite drift senses in different components![]() . For PSR B1839-04 we observe that the two
components have mirrored drift bands (i.e. the components drift in
phase) like PSR J0815+09, something we do not know for the other
pulsars. In the sparking gap model bi-drifting can be explained if
these pulsars have both an inner annular gap and an inner core gap
(Qiao et al. 2004).
. For PSR B1839-04 we observe that the two
components have mirrored drift bands (i.e. the components drift in
phase) like PSR J0815+09, something we do not know for the other
pulsars. In the sparking gap model bi-drifting can be explained if
these pulsars have both an inner annular gap and an inner core gap
(Qiao et al. 2004).
A feedback model is proposed by Wright (2003) as a natural mechanism for both the sometimes regular and sometimes chaotic appearance of subpulse patterns. In this model the outer magnetosphere interacts with the polar cap and the observed dependency of conal type on pulse period (Rankin 1993a) and angle between the rotation and magnetic axis (Rankin 1990) follows naturally.
Up to now most observational literature on the drifting phenomenon has been focused on describing individual very interesting drifting subpulse pulsars. The focus of this paper will not only be the individual systems, but also the properties common to the pulsars that show drifting, an approach started by Backus (1981), Ashworth (1982) and Rankin (1986). In the work of Backus (1981) 20 pulsars were studied for their subpulse behavior at 430 MHz and 9 were observed to be drifting. In the work of Ashworth (1982) the single pulse properties of nine new drifters are described and the properties common to 28 drifters in a sample of 52 pulsars are analysed. This sample consists of both their own results and a few previously published results. Most observations were obtained at or near 400 MHz, but some at higher frequencies.
In the work of Rankin (1986) all the, then published, single pulse properties are combined and described in the light of her empirical theory. Because understanding the drifting phenomenon is considered important for unraveling the mysteries of the emission mechanism of radio pulsars, we decided that it was time to start this more general and extensive observational program on the drifting phenomenon.
The main goals of this unbiased search for pulsar subpulse modulation is to determine what percentage of the pulsars show the drifting phenomenon and to find out if these drifters share some physical properties. As a bonus of this observational program new individually interesting drifting subpulse systems are found. In this paper we focus on the 21 cm observations and in a subsequent paper we will focus on lower frequency observations and the frequency dependence of the subpulse modulation properties of radio pulsars.
The list of pulsars which show the drifting phenomenon is slowly expanding in time as more sufficiently bright pulsars are found by surveys (e.g. Lewandowski et al. 2004), but we have successfully chosen a different approach to expand this list much more rapidly. The reason that we have found so many new drifting subpulse systems is twofold: we have analyzed a large sample of pulsars of which many were not known to show this phenomenon, and we used a sensitive detection method. Previous studies of drifting subpulses often used tracking of individual subpulses through time, an analysis method that requires a high signal-to-noise (S/N) ratio because it requires the detection of single pulses. This automatically implies that this kind of analysis can only be carried out on a limited number of pulsars. Analyzing the integrated Two-Dimensional Fluctuation Spectrum (2DFS; Edwards & Stappers 2002) and the Longitude-Resolved Fluctuation Spectrum (LRFS; Backer 1970) allows us to detect drifting subpulses even when the S/N is too low to see single pulses. This method was already successfully used with archival Westerbork Synthesis Radio Telescope (WSRT) data by Edwards & Stappers (2003a) to find drifting subpulses in millisecond pulsars.
By using the technique described above combined with the high sensitivity of the WSRT we have analyzed a large sample of 187 pulsars. An important aspect when calculating the statistics of drifting is that one has to be as unbiased as possible, so we have selected our sample of pulsars based only on the predicted S/N in a reasonable observing time. While this sample is obviously still luminosity biased, it is not biased towards well-studied pulsars, pulse profile morphology or any particular pulsar characteristics as were previous studies (e.g. Ashworth 1982; Backus 1981; Rankin 1986 and references therein). Moreover, all the conclusions in this paper are based on observations at a single frequency.
The paper is organized such that we start by explaining the technical details of the observations and data analysis. After that the details of the individual detections are described and in Table 2 all the details of our measurements can be found. After the individual detections the statistics of the drifting phenomenon are discussed followed by the summary and conclusions. In Appendix A are the plots for all the pulsars in our source list. They can also be found in Appendix B, but there they are ordered by appearance in the text.
All the analyzed observations were collected with the WSRT in the
Netherlands. The telescope is located at a latitude of 52
![]() 9
in the north, meaning that not all pulsars are visible for the WSRT.
Only catalogued
9
in the north, meaning that not all pulsars are visible for the WSRT.
Only catalogued![]() pulsars with a
declination (J2000) above -
pulsars with a
declination (J2000) above -
![]() were included in our source
list.
were included in our source
list.
This list of pulsars that are visible to the WSRT was sorted on the
observation duration required to achieve a signal-to-noise (S/N) ratio
of 130. Of this list we selected the first 191pulsars, which required observations of less then half an hour in
duration. The S/N ratio of a pulsar observation can be predicted with
the following equation (Dewey et al. 1985)
All observations were conducted with the 21 cm backend at WSRT, which
has the following receiver system parameters: ![]() ,
G=1.2K/Jy,
,
G=1.2K/Jy,
![]() K,
K,
![]() K (which is the
average of the entire sky),
K (which is the
average of the entire sky),
![]() MHz and
MHz and
![]() .
It is
required that the pulsars have an integrated pulse profile with a
predicted S/N ratio of 130, so the required observation duration in seconds is
.
It is
required that the pulsars have an integrated pulse profile with a
predicted S/N ratio of 130, so the required observation duration in seconds is
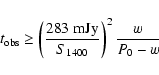 |
(2) |
The sensitivity to detect drifting subpulses not only depends on the S/N ratio of the observation, but also on obtaining a large number of pulses. This is because the observation should contain enough drift bands to be able to identify the drifting phenomenon. Our second requirement on the minimum observation length was therefore that the observations should contain at least one thousand pulses, so some pulsars had to be observed for longer than was required to get a S/N ratio of 130. To make sure that the statistics on the drifting phenomenon is not biased by the pulse period, it is important to include these long period pulsars in the source list.
Archival data was used if available and the sample of pulsars was completed with new observations. The best WSRT data available was chosen, so for a number of pulsars the data greatly exceed the minimum S/N and the number of pulses requirement. This does not bias our sample of observations toward well-studied pulsars, because all the observations are long enough to provide a good chance to detect the drifting phenomenon. We have observations of all the sources except the millisecond pulsar B1821-24, because of the high time resolution required and the associated data storage problems. The observations of PSR B1823-13, B1834-06 and J1835-1020 failed, and therefore are not included in this paper.
All the observations presented in this paper were made at an observation wavelength of 21 cm spread out over the last five years. The signals of all fourteen 25-m dishes of the WSRT were added together by taking into account the relative time delays between them and processed by the PuMa pulsar backend (Voûte et al. 2002). In order to reduce the effects of interference, badly affected frequency channels were excluded. The frequency channels were then added together in an offline procedure after dedispersing them by using previously published dispersion measures.
To study the single pulse behavior of pulsars one usually converts the one-dimensional de-dispersed time series into a two-dimensional pulse longitude versus pulse number array (pulse-stack). An example is shown in the left panel of Fig. 1, where one hundred successive pulses are plotted on top of one other. The pulse number is plotted vertically and the time within the pulses (i.e. the pulse longitude) horizontally. The off-pulse region is used to remove the baseline from the pulsar signal, making the average noise level zero.
To correct for the pulse longitude shift of successive pulses
the TEMPO software package![]() was used.
Because the pulse period (P0) of the pulsar is not exactly equal to
an integer number of time sample intervals, each pulse (as it appears
in the binned sequence) is effectively shifted by a constant amount
modulo one bin. This induces, as noted by Vivekanand et al. (1998), a periodic
longitude shift of successive pulses. Following Edwards & Stappers (2003a), we have
compensated for this longitude shift of each pulse, and thereby
avoiding artificial features appearing in the spectra that are
derived from the pulse-stacks. All pulse longitudes in this paper
have an arbitrary offset because absolute alignment was not necessary
for our analysis.
was used.
Because the pulse period (P0) of the pulsar is not exactly equal to
an integer number of time sample intervals, each pulse (as it appears
in the binned sequence) is effectively shifted by a constant amount
modulo one bin. This induces, as noted by Vivekanand et al. (1998), a periodic
longitude shift of successive pulses. Following Edwards & Stappers (2003a), we have
compensated for this longitude shift of each pulse, and thereby
avoiding artificial features appearing in the spectra that are
derived from the pulse-stacks. All pulse longitudes in this paper
have an arbitrary offset because absolute alignment was not necessary
for our analysis.
In the left panel of Fig. 1 one can see a sequence of 100 pulses of one of the new drifters we have found which clearly shows the drifting phenomenon. Drifting means that the subpulses drift in longitude from pulse to pulse and thereby the pulsar emission shows diagonal intensity bands in the pulse-stack (drift bands). The drift bands are characterized by two numbers: the horizontal separation between them in pulse longitude (P2) and the vertical separation in pulse periods (P3). The drift bands of this pulsar are clearly seen by eye in the pulse-stack and the values P2and P3 could in principle be measured directly, but in many cases of the newly discovered drifters the drift bands are not visible to the eye. To be able to detect the drifting phenomenon in as many pulsars as possible, all the pulse-stacks were analyzed in a systematic way as described in the next two subsections.
In Fig. 1 the products of our method of analysis are shown for three pulsars and in this section it is explained how these plots are generated from the pulse-stack and how one can interpret them.
The first thing that is produced from the pulse-stack is the
integrated pulse profile. This is simply done by vertically
integrating the pulse-stack, i.e. adding the bins with the same pulse
longitude in the successive pulses:
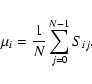 |
(3) |
The first basic method to find out if there is subpulse modulation is
to calculate the longitude-resolved variance
![]()
The detection of a modulation index does not give information about
whether the subpulse modulation occurs in a systematic or a disordered
fashion. The first step in detecting a regular intensity variation is
to calculate the Longitude Resolved Fluctuation Spectrum (LRFS;
Backer 1970). The pulse-stack is divided into blocks of 512
successive pulses![]() and the Discrete Fourier Transform (DFT) was performed on these
blocks to calculate the LRFS (for details of the analysis we refer to
Edwards & Stappers 2002,2003a). The fluctuation power spectra of the different
blocks were then averaged to obtain the final spectrum.
and the Discrete Fourier Transform (DFT) was performed on these
blocks to calculate the LRFS (for details of the analysis we refer to
Edwards & Stappers 2002,2003a). The fluctuation power spectra of the different
blocks were then averaged to obtain the final spectrum.
In Fig. 1 the LRFS of the three pulsars are shown below the pulse profile plots. The units of the vertical axis are in cycles per period (cpp), which corresponds to P0/P3 in the case of drifting (where P3 is the vertical drift band separation). The horizontal axis is the pulse longitude in degrees, which is aligned with the plot above. The power in the LRFS is horizontally integrated, producing the side panel. If the emission of the pulsar is modulated with a period P3, then a distinct region of the LRFS will show an excess of power (i.e. a feature) in the corresponding pulse longitude range. The LRFS can be used to see at which pulse longitudes the pulsar shows subpulse modulation and with which periodicities. The grayscale in the LRFS corresponds to the power spectral density. Under Parseval's theorem, the summed LRFS is identical to Eq. (4) (Edwards & Stappers 2003a), so integrating the LRFS vertically gives the longitude resolved variance (the open dots in the plot above the LRFS).
The detection of a modulation index suggests that there is subpulse
modulation and by analyzing the LRFS it can be determined if this
modulation is disordered or (quasi-)periodic. However from the
LRFS one cannot determine if the subpulses are drifting over a certain
longitude range, because to calculate the LRFS only DFTs along
vertical lines in the pulse-stack are performed. To determine if the
subpulses are drifting, the Two-Dimensional Fluctuation Spectrum
(2DFS; Edwards & Stappers 2002) is calculated. The procedure is similar to
calculating the LRFS, but now we select one or more pulse longitude
ranges between which the DFT is not only calculated along vertical
lines, but along lines with various slopes. The effect is that the
pulse longitude information that we had in the LRFS is lost, but we
gain the sensitivity to detect periodic subpulse modulation in the
horizontal direction (i.e. if there also exists a preferred P2value). Following the same procedure used while calculating the LRFS,
the pulse-stack is divided in blocks of 512 successive
pulses![]() and the spectra of the
different blocks were then averaged to obtain the final spectra.
and the spectra of the
different blocks were then averaged to obtain the final spectra.
In Fig. 1 the 2DFS is plotted below the LRFS. The vertical axis has the same units as the LRFS, but now the units of the horizontal axis are also cycles per period, which corresponds to P0/P2 in the case of drifting (where P2 is the horizontal drift band separation in time units). The power in the 2DFS is horizontally and (between the dashed lines) vertically integrated, producing the side and bottom panels in Fig. 1. These panels are only produced to make it easier to see by eye what the structure of the feature is.
From the pulse-stack in Fig. 1 one can see that two
successive drift bands of PSR B1819-22 are vertically separated by
![]() and horizontally by
and horizontally by
![]() .
Instead of measuring drifting directly from the pulse-stack, we use
the 2DFS. From both the 2DFS and LRFS of this pulsar we see that there
are multiple drift features. This is because PSR B1819-22 is a drift
mode changer (i.e. the drift bands have different slopes in different
parts of the observation). We note that only one drift mode is seen in
the short stretch of pulses shown in the pulse-stack in
Fig. 1. For PSR B1819-22 one can see the main
feature in the LRFS around 0.056 cpp, which corresponds to the P3value we see in the plotted pulse-stack. In the 2DFS of this pulsar we
see the main feature at the same vertical position as in the LRFS
(corresponding to the same P3 value) and because the feature is
offset from the vertical axis we know that the subpulses drift. From
the horizontal position of the feature in the 2DFS we see that
.
Instead of measuring drifting directly from the pulse-stack, we use
the 2DFS. From both the 2DFS and LRFS of this pulsar we see that there
are multiple drift features. This is because PSR B1819-22 is a drift
mode changer (i.e. the drift bands have different slopes in different
parts of the observation). We note that only one drift mode is seen in
the short stretch of pulses shown in the pulse-stack in
Fig. 1. For PSR B1819-22 one can see the main
feature in the LRFS around 0.056 cpp, which corresponds to the P3value we see in the plotted pulse-stack. In the 2DFS of this pulsar we
see the main feature at the same vertical position as in the LRFS
(corresponding to the same P3 value) and because the feature is
offset from the vertical axis we know that the subpulses drift. From
the horizontal position of the feature in the 2DFS we see that
![]() ,
which corresponds well with the P2measured directly from the pulse-stack shown.
,
which corresponds well with the P2measured directly from the pulse-stack shown.
In this paper we use the convention that P3 is always a positive number and P2 can be either positive or negative. A negative value of P2 means that the subpulses appear earlier in successive pulses, which is called negative drifting in the literature. The tabulated signs of P2 in this paper therefore correspond to the drift direction, such that a positive sign corresponds to positive drifting. To comply with this convention, all the plotted 2DFSs in this paper are in fact flipped about the vertical axis compared with the definition of the 2DFS in Edwards & Stappers (2002).
To reduce the effect of interference on the LRFS and 2DFS the spectrum
of the off-pulse noise was subtracted from the LRFS and 2DFS if a
large enough off-pulse longitude interval was available. Interference
will in general not be perfectly removed by this procedure, however
any artificial features produced by interference can easily be
identified because it will not be confined to a specific pulse
longitude range. In Fig. 1 the spectra of PSR
B2043-04 shows interference with a
![]() .
In the
spectra as shown in Appendices A and B,
the channels containing interference are set to zero, thereby
improving the visual contrast of the plots.
.
In the
spectra as shown in Appendices A and B,
the channels containing interference are set to zero, thereby
improving the visual contrast of the plots.
In this paper the modulation index is not directly derived from the
pulse-stack (Eqs. (4) and (5)),
but from the LRFS. This is done by vertically integrating the LRFS,
which gives the longitude resolved variance
(Eq. (4)). The advantage of this method is that by
excluding the lowest frequency bin the effect of interstellar
scintillation (which at this observing frequency has typical low
frequencies) can be removed from the modulation index (for details of
the analysis we refer to Edwards & Stappers 2002,2003a). After exclusion of the
lowest frequency bins the variance is overestimated by
![]() ,
where
,
where
![]() is the modulation
index induced by the scintillation (see Eqs. (20)-(22) of
Edwards & Stappers 2004). The longitude resolved modulation index and standard
deviation are corrected accordingly.
is the modulation
index induced by the scintillation (see Eqs. (20)-(22) of
Edwards & Stappers 2004). The longitude resolved modulation index and standard
deviation are corrected accordingly.
If a feature is seen in the 2DFS and we make sure it is not associated with interference, P2 and P3 can be measured and its significance determined. The drift feature will always be smeared out over a region in the 2DFS. This could be because there is not one fixed value of the drift rate throughout the observation due to random slope variations of the drift bands, drift mode changes or nulling. But the feature is also broadened if the drifting is not linear (i.e. subpulse phase steps or swings) and because of subpulse amplitude windowing (Edwards & Stappers 2002).
Because of all these effects it is impossible to fit one
specific mathematical function to all the detected features, so it is
more practical to calculate the centroid of a rectangular region in
the 2DFS containing the feature. The advantage of this procedure is
that no particular shape of the feature has to be assumed. The
centroids are defined as:
| (6) |
Because the analyzed pulse sequences are sometimes relatively short, there is the possibility that the occasional occurrence of strong (sub)pulses are dominating the spectra and therefore lead to misleading conclusions. To estimate what kind of "random'' fluctuation features one can expect from a given pulse sequence, we have randomized the order of the pulses and then passed this new pulse-stack through our software to determine the magnitude of any features which could be attributed to strong (sub)pulses. Any actual drifting will lose coherence in this process and thus we can use the randomized results when estimating the significance of drift features when there is no well defined P3.
For most pulsars there is power along the vertical axis in the 2DFS. Therefore the centroid of a larger region around a drift feature usually results in a centroid located closer to the vertical axis, hence in a larger absolute value of P2. In most cases this causes the uncertainty on P2 to be asymmetric around its most likely value and therefore it is useful to tabulate the uncertainty in both signs.
If the centroid of the feature in the 2DFS is significantly offset
from the vertical axis, it means that
![]() and that drifting
can be associated with the feature (i.e. there exists a preferred
drift direction of the subpulses from pulse to pulse). Drifters are
defined in this paper as pulsars which have at least one feature in
its 2DFS which show a significant finite P2. It must be noted that
drift bands are often very non-linear and therefore the magnitude of P2 is probably of little meaning. Also not only an offset from the
vertical axis indicates drifting, but any asymmetry about the vertical
axis indicates drifting-like behavior. Any frequency dependence along
the vertical axis indicates structured subpulse modulation, either
quasi-periodic or as a low frequency excess. Pulsars with a low
frequency excess show an excess of power in their spectra toward long
frequencies (i.e. the spectra are "red'').
and that drifting
can be associated with the feature (i.e. there exists a preferred
drift direction of the subpulses from pulse to pulse). Drifters are
defined in this paper as pulsars which have at least one feature in
its 2DFS which show a significant finite P2. It must be noted that
drift bands are often very non-linear and therefore the magnitude of P2 is probably of little meaning. Also not only an offset from the
vertical axis indicates drifting, but any asymmetry about the vertical
axis indicates drifting-like behavior. Any frequency dependence along
the vertical axis indicates structured subpulse modulation, either
quasi-periodic or as a low frequency excess. Pulsars with a low
frequency excess show an excess of power in their spectra toward long
frequencies (i.e. the spectra are "red'').
The drifters are classified into three classes and an example of each
class is shown in Fig. 1. One can see that PSR B2043-04 has a vertically narrow drift feature in its spectra,
meaning that P3 has a stable and fixed value throughout the
observation. We will call these pulsars the coherent drifters class (class Coh in Table 2). The criterion used for
this class is that the drift feature has a vertical extension smaller
than 0.05 cpp. The pulsars that show a vertical, broad, diffuse
drift feature are divided into two classes, depending on whether the
feature is clearly separated from the alias borders (P0/P3=0and
P0/P3=0.5). In Table 2 the pulsars in
class Dif are clearly separated from the alias border and the pulsars
in class Dif![]() not.
In Fig. 1 PSR B1819-22 is a diffuse (Dif) drifter
and PSR B2148+63 is a Dif
not.
In Fig. 1 PSR B1819-22 is a diffuse (Dif) drifter
and PSR B2148+63 is a Dif![]() drifter.
drifter.
Besides the drifters there is also a class of pulsars which show longitude stationary subpulse modulation (class Lon in Table 2). These pulsars show subpulse modulation with a P3 value, but without a finite P2 value. Because it is not clear if these pulsars should be counted as drifters or as non-drifters, they are excluded from the statistics.
For many pulsars we find that the magnitude of P2 exceeds the pulse width. This means in the case of regular drifting that in a single pulse only one subpulse is visible and that the drifting will manifest itself more as an amplitude modulation rather than as a phase modulation. An illustrative example of a regular drifter with a large P2 is PSR B0834+06 (Asgekar & Deshpande 2005). Whether the drifting manifests itself more as an amplitude modulation or as a phase modulation will largely depend on the viewing geometry. Also the presence of pulse sequences without organized drifting, longitude stationary subpulse modulation or drift reversals will result in a large P2 value.
The calculation of the 2DFS is an averaging process. This is what makes it a powerful tool to detect drifting subulses in low S/N observations, but at the same time this implies that different pulse-stacks can produce similar 2DFS. For instance a feature that is split and shows a horizontal separation can be caused by drift reversals, but also by subpulse phase steps or swings (see Edwards et al. 2003 for a pulse sequence of PSR B0320+39 and the resulting 2DFS). Note also that with only the LRFS it is impossible to identify complex drift behavior like drift reversals or subpulse phase steps.
The details of each observation can be found in Table 2, including the classification we made, the measured P2 and P3 values, the modulation index and the detection threshold for the modulation index. The P2 and P3values are average values during the observation. Especially when the pulsar is a drift mode changer, a different observation may lead to different values for P2 and P3. The plots of all the pulsars can be found in Appendix A. For some of the pulsars the 2DFS for two different pulse longitude ranges are shown if useful. The plots of these pulsars come after the plots of the pulsars with only one 2DFS plot. The same plots can also be found in Appendix B, but there they are ordered by appearance in the text instead of ordered by name.
As can be seen from Fig. 1, the subpulses of PSR
B1819-22 appear to drift toward the leading part of the pulse
profile. In the sparking gap model (e.g. Ruderman & Sutherland 1975), every
subpulse is associated with one emission entity close to the surface
of the star. These entities (the sparks) move around the magnetic
axis, causing the subpulses to drift through the pulse window. Because
the emission entities are only sampled once per rotation period of the
star, it is very difficult to determine if the subpulses in one drift
band correspond to the same emission entity for successive pulses. For
instance for PSR B1819-22 we do not know if the emission entities
drift slowly toward the leading part of the pulse profile (not
aliased) or faster toward the trailing part of the pulse profile
(aliased).
![\begin{figure}
\par\mbox{\rotatebox{270}{\resizebox{0.42\vsize}{!}{\includegraph...
...resizebox{0.42\vsize}{!}{\includegraphics[angle=0]{3088f2c.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg43.gif) |
Figure 2: A section of the pulse-stacks and the derived spectra of the two artificially generated pulse sequences to illustrate possible effects of pulsars that constantly change their alias order. The drifting in the left pulse-stack constantly crosses the P3=2P0 alias border and the right pulse-stack constantly changes its apparent drift direction via longitude stationary subpulse modulation. For the explanation of the plots we refer to Fig. 1 and the main text. |
| Open with DEXTER | |
The physical conditions of the pulsar probably determines what the
physical drift rate of the emission entities are, rather than the
observed (possibly aliased) drift rate. This could already be a
serious problem if one wants to correlate physical parameters of
pulsars to the observed drift rate of coherent drifters, for which we
at least know they stay in the same alias mode. If a feature in the
2DFS is not clearly separated from the alias borders, the power in
that feature could consist of drift bands in different alias modes
(i.e. the apparent drift direction could be changing constantly during
the observation). In that case the measured value of P3 using the
centroid of the feature is related to the true drift rate of the
emission entities in a complicated way, depending on what fraction of
the time the pulsar spends in which alias mode. Therefore it is
expected that it will be very hard to find a correlation between
physical pulsar parameters and the P3 values of the pulsars in the
Dif![]() class, so it will be useful to classify the pulsars
depending on whether the features in the 2DFS are clearly separated
from the alias borders. Inspection of the pulse-stacks with strong
enough single pulses reveals that some of the pulsars in the
Dif
class, so it will be useful to classify the pulsars
depending on whether the features in the 2DFS are clearly separated
from the alias borders. Inspection of the pulse-stacks with strong
enough single pulses reveals that some of the pulsars in the
Dif![]() class change their drift direction during the
observation. This is further evidence to indicate the value of
considering the Dif and Dif
class change their drift direction during the
observation. This is further evidence to indicate the value of
considering the Dif and Dif![]() classes separately.
classes separately.
To illustrate this we have artificially generated two pulse sequences of a pulsar that has a variable rotation period of the emission entities in two different scenarios (see Fig. 2). In both scenarios the emission entities are simulated to drift from the trailing to the leading edge of the pulse profile with a variable drift rate. In the left sequence the vertical drift band separation P3 is close to 2P0 and in the right sequence the P3 period is much larger. In the left sequence the subpulses around the first pulse appear to drift toward the leading edge of the pulse profile. As time increases, we speed up the rotation of the emission entities, which causes P3 to become smaller. Around pulse number 15 the Nyquist border P3=2P0 is reached and the drift pattern becomes a check-board like pattern. As time further increases the emission entities are still speeding up, causing clear drift bands to reappear with an opposite apparent drift direction (around pulse 25). After this the rotation of the emission entities is gradually slowed down to the initial value, causing the drift bands to change apparent drift direction again around pulse 50. The same cycle is repeated for the next pulses. In this simulation the carousel rotation period is set to vary with about 40% around its mean value.
The resulting spectra of this pulse sequence are also shown in Fig. 2. The LRFS shows that the subpulse modulation is extended toward the P3=2P0 alias border and the 2DFS shows a feature that is split by the vertical axis, because there are two apparent drift directions in the pulse sequence. As can be seen in the bottom panel, there is more power in the left peak. This corresponds to more power being associated with negative drifting (drifting toward the leading edge of the pulse profile). This is also directly visible in the pulse-stack. A good example of a known pulsar that shows this kind of drift behavior is PSR B2303+30 (e.g. Redman et al. 2005) and its 2DFS (see Fig. A.15) indeed shows a very clear double peaked feature.
![\begin{figure}
\par\rotatebox{270}{\resizebox{!}{0.49\hsize}{\includegraphics[an...
...}{\resizebox{!}{0.49\hsize}{\includegraphics[angle=0]{3088f3b.ps}}}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg44.gif) |
Figure 3: This figure shows the spectra of the well known drifter PSR B0809+74 ( left) as well as the results from the same data after putting the pulses in a random order ( right). |
| Open with DEXTER | |
In the second scenario of Fig. 2 the pulse-stack shows
drift bands with a much larger P3. Because of possible aliasing
this does not directly imply that the emission entities are rotating
slower. In fact, we have chosen the entities to rotate faster than in
the first scenario. This causes the driftbands to be aliased and the
drift bands appear to drift in the opposite direction to the emission
entities (which again are simulated to drift toward the leading edge
of the pulse profile). As time increases the rotation of the emission
entities is sped up. Because of aliasing the drift rate appears to
decrease until around pulse 25 the drifting has become longitude
stationary (
![]() ). The emission entities are now rotating so
fast that in one pulse period they exactly reappear at the pulse
longitude of another drift band. When the rotation period of the
emission entities is speeded up even further, the drift bands change
their apparent drift direction again as can be seen around pulse
50. Now the rotation period of the emission entities is slowed down
until around pulse 100 the initial conditions are reached again. After
this the same cycle is repeated. A clear example of a known pulsar
that shows this kind of drift reversals is PSR B0826-34
(Esamdin et al. 2005; Gupta et al. 2004).
). The emission entities are now rotating so
fast that in one pulse period they exactly reappear at the pulse
longitude of another drift band. When the rotation period of the
emission entities is speeded up even further, the drift bands change
their apparent drift direction again as can be seen around pulse
50. Now the rotation period of the emission entities is slowed down
until around pulse 100 the initial conditions are reached again. After
this the same cycle is repeated. A clear example of a known pulsar
that shows this kind of drift reversals is PSR B0826-34
(Esamdin et al. 2005; Gupta et al. 2004).
The LRFS of this sequence shows that the subpulse modulation is extended toward the horizontal axis and the 2DFS shows again a feature that is split by the vertical axis. As can be seen in the bottom panel, there is more power in the right peak, which corresponds to more power associated with positive drifting. In the pulse-stack there are indeed more drift bands that drift toward the trailing edge of the pulse profile than in the opposite direction.
In the left panel of Fig. 3 the spectra of the well known regular drifter PSR B0809+74 are shown. The drift feature in the 2DFS shows a clear horizontal structure caused by the non linear drift bands of PSR B0809+74 at this observing frequency (Edwards & Stappers 2003b; Wolszczan et al. 1981; Prószynski & Wolszczan 1986). If drift bands are not straight, there is no one unique value of P2 that is associated with the drifting and therefore the drift feature in the 2DFS will be more complex than just one peak. This makes P2 an ill-defined parameter. However this is no shortcoming of the 2DFS, it is a shortcoming of the whole concept of P2 under curved driftbands. In this paper P2 is just a rough measure of the presence of drift, its direction and the magnitude of the slope in a overall mean sense only.
If the drift bands are non linear, the subpulses will have a pulse longitude dependent spacing. This pulse longitude dependent spacing is described by the so-called "modulation phase profile'' or "phase envelope'' (Edwards & Stappers 2002).
For most drifters the vertical drift band separation P3 is a much better defined parameter than the horizontal separation P2, e.g. the drift feature in the 2DFS of PSR B0809+74 (left panel of Fig. 3) is much sharper in the vertical direction than in the horizontal direction. There is however the possibility that single pulses show regular spaced subpulses, while there is no memory for where the subpulses appear in successive pulses. In that case there is a P2 value, but P3 is undefined. One can simulate such a scenario by putting the pulses of a regular drifter in a random order. This is done for PSR B0809+74 in the right panel of Fig. 3.
One can see, first of all, that the longitude-resolved standard
deviation and modulation index are independent of the ordering of the
pulses, as expected from Eqs. (4) and (5). Secondly, the spectra no longer show any
vertical structure. This indicates that, as expected, P3 has become
undefined. The 2DFS is symmetric about the vertical axis, so there is
no longer a preferred drift direction. The horizontal subpulse
separation is however still visible in the 2DFS as two vertical bands
at ![]() 37 cpp, the same horizontal position as the largest peak in
the 2DFS in the left panel of Fig. 3.
37 cpp, the same horizontal position as the largest peak in
the 2DFS in the left panel of Fig. 3.
We have found two pulsars that show this kind of features: PSRs B2217+47 and B0144+59. In the carousel model this phenomenon could be explained by a highly variable circulation time that causes the alias order to change constantly. However there is no evidence that this phenomenon is related to the same origin as the drifting subpulses, as it only shows that the subpulses appear quasiperiodic.
B0149-16: the 2DFS of this pulsar (Fig. A.1)
shows a weak drift feature.
B0609+37: almost all power in the 2DFS of this pulsar is in a
well confined drifting feature (Fig. A.2), meaning that the
subpulse drifting is very organized and stable.
B0621-04: a strong and very coherent
![]() feature is seen in the LRFS and 2DFS of this pulsar
(Fig. A.2), which is also seen in other observations.
The feature is significantly offset from the vertical axis, so this
pulsar shows very stable drifting subpulses. Only the 2DFS of the
trailing peak is plotted.
feature is seen in the LRFS and 2DFS of this pulsar
(Fig. A.2), which is also seen in other observations.
The feature is significantly offset from the vertical axis, so this
pulsar shows very stable drifting subpulses. Only the 2DFS of the
trailing peak is plotted.
J1650-1654: this pulsar shows a very clear drift feature in
its 2DFS (Fig. A.5). The feature seems to show some
vertical structure, which could be because of drift rate
variations. The feature also seems to show some horizontal structure
like PSR B0818-13, which could indicate that the drift bands are
curved or show a phase step. This would be consistent with the minimum
in the modulation index in the middle of the pulse profile. However
this observation is too short to state if this effect is due to a
systematic drift rate change across the pulse profile or due to random
variations.
B1702-19: the pulse profile of this pulsar shows an interpulse
(Biggs et al. 1988). The main pulse shows a drift feature and the 2DFS
of the interpulse shows a feature with the same P3 value
(Fig. A.20), but no significant offset from the vertical
axis could be detected for this feature. This is not the only pulsar
to show correlations in emission properties between the main- and
interpulse. PSR B1822-09 exhibits an anti-correlation between the
intensity in the main- and the interpulse (e.g. Fowler et al. 1981; Fowler & Wright 1982) and
also a correlation in the subpulse modulation
(e.g. Gil et al. 1994). That pulsar also shows drifting in the
main pulse in the "B''-mode and longitude stationary subpulse
modulation in both the main- and interpulse in the "Q''-mode with the
same P3. Also PSR B1055-52 is known to show a main
pulse-interpulse correlation. For that pulsar a correlation between
the intensity of the main and interpulse has been found by
Biggs (1990). However PSR B1702-19 is the first pulsar that shows
a correlation between the drifting subpulses in the main pulse and
the subpulse modulation in the interpulse.
B1717-29: a very narrow drift feature is seen in both the
LRFS and the 2DFS of this pulsar (Fig. A.5). Because the
very low S/N of this observation it was impossible to measure a
significant modulation index using the whole P3 range of the
LRFS. By only using the frequencies in the LRFS that contains the
drift feature it was possible to significantly determine the
modulation index corresponding to the drift feature. This drifting is
confirmed in another observation.
B1839-04: both components of the pulse profile of this pulsar
are drifting (Fig. A.21). The drift bands are clearly
visible in the pulse-stack to the eye and both components have an
opposite drift sense. The slope of the drift bands in the two
components are mirrored and the drift bands of the two components are
also roughly in phase. So when a drift band is visible in one
component, it is also visible (although mirrored) in the other
component. This "bi-drifting'' subpulse behavior is also observed for
PSR J0815+09, which also has opposite drift senses in different
components (McLaughlin et al. 2004). This "bi-drifting'' could be a sign
that these pulsars have both an inner annular gap and an inner core
gap (Qiao et al. 2004), but also "double imaging'' could be
responsible (Edwards et al. 2003). Note also that the second harmonic of
the drift feature is visible in the 2DFS of especially the trailing component.
B1841-04: this pulsar has a weak, definite drift feature
in its 2DFS (Fig. A.9), which is also visible in the LRFS.
B1844-04: there is a weak detection of a narrow drift feature
in the 2DFS of this pulsar, which is also visible in the LRFS
(Fig. A.10).
J1901-0906: the trailing component of this pulsar shows a
clear and narrow drift feature in its 2DFS, which is not detected in
the leading component (Fig. A.21). The 2DFS of the leading
component has a drift feature with a different P3 which is also
present in the right component (
![]() ,
,
![]() ). The drifting can be seen by eye in the
pulse-stack. The different measured P3 values in the two
components could indicate that this pulsar is a drift mode changer.
). The drifting can be seen by eye in the
pulse-stack. The different measured P3 values in the two
components could indicate that this pulsar is a drift mode changer.
B2000+40: although this observation is contaminated by
interference, clear drifting is detected in the leading component. The
rest of the pulse profile (mostly in the trailing component) is also
drifting (Fig. A.22). The feature in the leading component
shows horizontal structure which could be caused by drift reversals or
more likely by a subpulse phase jump or swing.
B2043-04: this pulsar has a very clear and narrow drifting
component in its 2DFS (Fig. A.14). The feature is
perhaps extended toward the alias border, but this
is not significant. Almost all power in the 2DFS is in the drift
feature.
These pulsars show a drift feature over an extended P3 range
(larger than 0.05 cpp). If the drift feature is clearly separated from
both alias borders (
P0/P3 = 0 and
P0/P3=0.5), the pulsar is
classified as Dif. If it is not, the pulsar is classified as
Dif![]() in Table 2. In this section the pulsars
in the latter class are indicated with an asterisk next to their
name. Not all drift features in the spectra have peaks which are
offset from the vertical axis, but they must be asymmetric about the
vertical axis.
in Table 2. In this section the pulsars
in the latter class are indicated with an asterisk next to their
name. Not all drift features in the spectra have peaks which are
offset from the vertical axis, but they must be asymmetric about the
vertical axis.
B0031-07: this pulsar shows a broad drifting feature in its
2DFS (Fig. A.1). Three drift modes have been found for this
pulsar by Huguenin et al. (1970) at 145 and 400 MHz. In our observation most
power in the 2DFS is due to the "A''-mode drift (P3=12P0). The
slope of the drift bands change from band to band
(e.g. Vivekanand & Joshi 1997), causing the feature to extend vertically in the
2DFS. The "B''-mode drift (P3=6P0) is also visible in our
observation, but there is no feature corresponding to "C''-mode drift
(P3=4P0). This is consistent with the multifrequency study of
Smits et al. (2005).
B0301+19![]() :
the trailing component shows a broad drift feature in
its 2DFS (Fig. A.17), but no drifting is detected in the
leading component. This pulsar is observed to have straight drift
bands in both components of the pulse-stack (Schönhardt & Sieber 1973 at 430 MHz). The feature in the trailing component is reported to be broader
than in the leading component (Backer et al. 1975, also at 430 MHz),
probably because drifting subpulses appear more erratic in the
trailing component. The feature we see is also broad and may even
be extended to the alias border.
:
the trailing component shows a broad drift feature in
its 2DFS (Fig. A.17), but no drifting is detected in the
leading component. This pulsar is observed to have straight drift
bands in both components of the pulse-stack (Schönhardt & Sieber 1973 at 430 MHz). The feature in the trailing component is reported to be broader
than in the leading component (Backer et al. 1975, also at 430 MHz),
probably because drifting subpulses appear more erratic in the
trailing component. The feature we see is also broad and may even
be extended to the alias border.
B0329+54![]() :
the power in the LRFS of this pulsar peaks toward
1/P3=0, as reported by Taylor & Huguenin (1971) for low frequencies
(Fig. A.17). Drifting is detected in four of the five
components. The third component (the right part of the central peak)
has a broad drift feature and the subpulses have a positive drift
sense, something that is also reported by Taylor et al. (1975) at 400 MHz.
Besides these known features we find that the first component (left
peak) and the fourth component (the bump between the central and
trailing peak) are also drifting with a positive drift senses:
:
the power in the LRFS of this pulsar peaks toward
1/P3=0, as reported by Taylor & Huguenin (1971) for low frequencies
(Fig. A.17). Drifting is detected in four of the five
components. The third component (the right part of the central peak)
has a broad drift feature and the subpulses have a positive drift
sense, something that is also reported by Taylor et al. (1975) at 400 MHz.
Besides these known features we find that the first component (left
peak) and the fourth component (the bump between the central and
trailing peak) are also drifting with a positive drift senses:
![]() and
and
![]() and
and
![]() and
and ![]() respectively. The second component (the
left part of the central peak) has an opposite drift sense:
respectively. The second component (the
left part of the central peak) has an opposite drift sense:
![]() and
and
![]() .
The last component
shows no significant drifting. The 2DFS of the second and third
component are shown in Fig. A.17. The difference between
the values of P3 in the different components seems not to be
significant.
.
The last component
shows no significant drifting. The 2DFS of the second and third
component are shown in Fig. A.17. The difference between
the values of P3 in the different components seems not to be
significant.
B0628-28![]() :
sporadic drifting with a positive drift sense has
been reported for this pulsar by Ashworth (1982) at 400 MHz, but the
P2 and P3 values could not be measured. The positive drift sense
is confirmed in our observation as a clear excess of power in the right
half of the 2DFS (Fig. A.3). The feature in the 2DFS is not
separated from either alias borders. Most power in both the LRFS and
2DFS is in the lower half.
:
sporadic drifting with a positive drift sense has
been reported for this pulsar by Ashworth (1982) at 400 MHz, but the
P2 and P3 values could not be measured. The positive drift sense
is confirmed in our observation as a clear excess of power in the right
half of the 2DFS (Fig. A.3). The feature in the 2DFS is not
separated from either alias borders. Most power in both the LRFS and
2DFS is in the lower half.
B0751+32![]() :
the 2DFS of the leading component of the pulse
profile of this pulsar
:
the 2DFS of the leading component of the pulse
profile of this pulsar![]() shows drifting
over the whole P3 range with a negative P2 value
(Fig. A.19). This can clearly be seen in the bottom plot,
which shows an excess of power in the left half. This confirms the
drifting as reported by Backus (1981) at 430 MHz. Both components also
show a strong
shows drifting
over the whole P3 range with a negative P2 value
(Fig. A.19). This can clearly be seen in the bottom plot,
which shows an excess of power in the left half. This confirms the
drifting as reported by Backus (1981) at 430 MHz. Both components also
show a strong
![]() feature. This feature shows negative
drifting in the leading component, but no significant drifting in the
trailing component.
feature. This feature shows negative
drifting in the leading component, but no significant drifting in the
trailing component.
B0823+26![]() :
only the pulse longitude range of the main pulse is
shown in Fig. A.3 and the 2DFS of the main pulse shows a
clear broad drift feature. Backer (1973) found that at 606 MHz this
pulsar shows drifting in bursts, but the drift direction is different
for different bursts. In our observation there seems to exist a clear
preferred subpulse drift direction, so this pulsar is classified
as a drifter.
:
only the pulse longitude range of the main pulse is
shown in Fig. A.3 and the 2DFS of the main pulse shows a
clear broad drift feature. Backer (1973) found that at 606 MHz this
pulsar shows drifting in bursts, but the drift direction is different
for different bursts. In our observation there seems to exist a clear
preferred subpulse drift direction, so this pulsar is classified
as a drifter.
B0834+06![]() :
the 2DFS of both components have a weak drift feature
at the alias border (Fig. A.19). This confirms the drifting
detected by Sutton et al. (1970) at low frequencies. The circulation time of
this pulsar (
:
the 2DFS of both components have a weak drift feature
at the alias border (Fig. A.19). This confirms the drifting
detected by Sutton et al. (1970) at low frequencies. The circulation time of
this pulsar (![]() )
has been measured by Asgekar & Deshpande (2005).
)
has been measured by Asgekar & Deshpande (2005).
B1133+16![]() :
the 2DFS of both components of this pulsar
(Fig. A.19) show a very broad drifting feature with the
same drift sign consistent with other data we have analyzed. The
trailing component shows also a long period drift feature (
:
the 2DFS of both components of this pulsar
(Fig. A.19) show a very broad drifting feature with the
same drift sign consistent with other data we have analyzed. The
trailing component shows also a long period drift feature (
![]() and
and
![]() ). This drifting is
consistent with the drifting found by Nowakowski (1996) at 430 and 1418 MHz
and by Taylor et al. (1975); Backer (1973) at low frequencies.
). This drifting is
consistent with the drifting found by Nowakowski (1996) at 430 and 1418 MHz
and by Taylor et al. (1975); Backer (1973) at low frequencies.
B1237+25![]() :
the 2DFS of the outer components of the pulse profile
are clearly drifting with opposite drift sign (they are plotted in
Fig. A.20). The 2DFS of the three inner components (which
are not plotted) all show drifting with a positive drift sense (except
the middle one which does not show significant drifting). The values
are
:
the 2DFS of the outer components of the pulse profile
are clearly drifting with opposite drift sign (they are plotted in
Fig. A.20). The 2DFS of the three inner components (which
are not plotted) all show drifting with a positive drift sense (except
the middle one which does not show significant drifting). The values
are
![]() ,
,
![]() and
and
![]() ,
,
![]() respectively. This drifting is
consistent with Prószynski & Wolszczan (1986) at 408 and 1420 MHz.
respectively. This drifting is
consistent with Prószynski & Wolszczan (1986) at 408 and 1420 MHz.
J1518+4904: this millisecond pulsar![]() has a clear broad
drift feature (Fig. A.4). This pulsar was already known
to be a drifter (Edwards & Stappers 2003a at 1390 MHz), showing that
drifting is not an phenomenon exclusive to slow pulsars.
has a clear broad
drift feature (Fig. A.4). This pulsar was already known
to be a drifter (Edwards & Stappers 2003a at 1390 MHz), showing that
drifting is not an phenomenon exclusive to slow pulsars.
B1642-03![]() :
drifting is observed to occur in bursts in this
pulsar with both drift senses (Taylor & Huguenin 1971 at 400 MHz) and
also Taylor et al. (1975) report that there is no preferred drift sense at
400 MHz. The 2DFS of our observation (Fig. A.4) reveals a
broad drift feature with a preferred drift sense, so this pulsar
is classified as a drifter. The alias border seems to be crossed on
both sides, because the feature is extended over the whole P3 range
and seems double peaked.
:
drifting is observed to occur in bursts in this
pulsar with both drift senses (Taylor & Huguenin 1971 at 400 MHz) and
also Taylor et al. (1975) report that there is no preferred drift sense at
400 MHz. The 2DFS of our observation (Fig. A.4) reveals a
broad drift feature with a preferred drift sense, so this pulsar
is classified as a drifter. The alias border seems to be crossed on
both sides, because the feature is extended over the whole P3 range
and seems double peaked.
B1822-09![]() :
for this pulsar a correlation in the subpulse
modulation between the main- and interpulse has been found (see the
text of the coherent drifter PSR B1702-19 for details). There are no
features in the spectra of our observation of the the interpulse and
therefore the interpulse is not plotted in Fig. A.21. There
is drifting detected in the trailing component of the main pulse, but
it is not clear what exact range in the 2DFS shows drifting causing
the large uncertainty on the P3 value. The observation is
consistent with the "B''-mode drift found by Fowler et al. (1981) at 1620 MHz
with a
:
for this pulsar a correlation in the subpulse
modulation between the main- and interpulse has been found (see the
text of the coherent drifter PSR B1702-19 for details). There are no
features in the spectra of our observation of the the interpulse and
therefore the interpulse is not plotted in Fig. A.21. There
is drifting detected in the trailing component of the main pulse, but
it is not clear what exact range in the 2DFS shows drifting causing
the large uncertainty on the P3 value. The observation is
consistent with the "B''-mode drift found by Fowler et al. (1981) at 1620 MHz
with a
![]() .
There is also a feature at 0.02 cpp, which
could be related to the
.
There is also a feature at 0.02 cpp, which
could be related to the
![]() "Q''-mode drift found by
Fowler et al. (1981). Contrary to their results, in our observation there is
no evidence that this feature is drifting. This could be because our
observation was much shorter.
"Q''-mode drift found by
Fowler et al. (1981). Contrary to their results, in our observation there is
no evidence that this feature is drifting. This could be because our
observation was much shorter.
B1845-01![]() :
the 2DFS of this pulsar (Fig. A.10) shows a
broad drifting feature confirming the detection of drifting in this
pulsar by Hankins & Wolszczan (1987) at 1414 MHz.
:
the 2DFS of this pulsar (Fig. A.10) shows a
broad drifting feature confirming the detection of drifting in this
pulsar by Hankins & Wolszczan (1987) at 1414 MHz.
B1919+21: both components of this pulsar are clearly drifting and
almost all power in the 2DFS is in the drift feature
(Fig. A.22). The feature of the leading component shows
horizontal structure. The centroid of the whole feature in the leading
component gives
![]() with the same P3 value. The
reason for this horizontal structure in the drift feature is, like PSR
B0809+74, that there is a subpulse phase step in the drift bands. This
observation confirms the reported phase step by Prószynski & Wolszczan (1986) seen
at 1420 MHz.
with the same P3 value. The
reason for this horizontal structure in the drift feature is, like PSR
B0809+74, that there is a subpulse phase step in the drift bands. This
observation confirms the reported phase step by Prószynski & Wolszczan (1986) seen
at 1420 MHz.
B1929+10![]() :
the LRFS peaks at low frequencies
(Fig. A.13), comparable to what was found by Nowakowski et al. (1982)
at 0.43, 1.7 and 2.7 GHz. Oster et al. (1977) suggested, using 430 MHz
data, that this pulsar drifts. The 2DFS of our observation shows two
broad features with opposite drift sense with two different P3values. The most clear drift feature is between the dashed lines and
the other feature is directly above this feature up to
:
the LRFS peaks at low frequencies
(Fig. A.13), comparable to what was found by Nowakowski et al. (1982)
at 0.43, 1.7 and 2.7 GHz. Oster et al. (1977) suggested, using 430 MHz
data, that this pulsar drifts. The 2DFS of our observation shows two
broad features with opposite drift sense with two different P3values. The most clear drift feature is between the dashed lines and
the other feature is directly above this feature up to
![]() .
Also Backer (1973) has seen two features in the LRFS of this
pulsar at 606 MHz and the short period feature appeared to have a
negative drift and the long period fluctuations appeared to be
longitude stationary. A negative drift sense is detected for the short
period feature, but the long period feature shows a positive
drift. Both drift features are arising from the leading half of the
pulse profile. An explanation for the observed behavior is that this
pulsar is a drift mode changer showing different P3 values
with opposite drift senses. There is also an indication for a
.
Also Backer (1973) has seen two features in the LRFS of this
pulsar at 606 MHz and the short period feature appeared to have a
negative drift and the long period fluctuations appeared to be
longitude stationary. A negative drift sense is detected for the short
period feature, but the long period feature shows a positive
drift. Both drift features are arising from the leading half of the
pulse profile. An explanation for the observed behavior is that this
pulsar is a drift mode changer showing different P3 values
with opposite drift senses. There is also an indication for a
![]() modulation. There is a strong very narrow spike around
P3=5P0, which could be caused by a few strong pulses.
modulation. There is a strong very narrow spike around
P3=5P0, which could be caused by a few strong pulses.
B1933+16![]() :
this pulsar shows subpulse modulation over the
whole P3 range (Fig. A.13). It was found by Backer (1973)
that there is no preferred subpulse drift sense at 430 MHz, however
regular drifting with
:
this pulsar shows subpulse modulation over the
whole P3 range (Fig. A.13). It was found by Backer (1973)
that there is no preferred subpulse drift sense at 430 MHz, however
regular drifting with
![]() has been reported by
Oster et al. (1977) at 430 MHz. We can confirm that there is preferred
positive drifting in a broad feature near the P3=2P0 alias border.
has been reported by
Oster et al. (1977) at 430 MHz. We can confirm that there is preferred
positive drifting in a broad feature near the P3=2P0 alias border.
B1944+17![]() :
this pulsar shows a clear broad drift feature in the
2DFS (Fig. A.13) and the drifting can clearly be seen by eye
in the pulse-stack. The feature is broad because this pulsar shows
drift mode changes (Deich et al. 1986 at both 430 and 1420 MHz). The
P3=13P0 "A''-mode drift and the
P3=6.4P0 "B''-mode drift are
visible in the 2DFS at 0.075 and 0.16 cpp respectively. We see also
evidence for a feature in a different alias mode, although much weaker
than the main feature (
:
this pulsar shows a clear broad drift feature in the
2DFS (Fig. A.13) and the drifting can clearly be seen by eye
in the pulse-stack. The feature is broad because this pulsar shows
drift mode changes (Deich et al. 1986 at both 430 and 1420 MHz). The
P3=13P0 "A''-mode drift and the
P3=6.4P0 "B''-mode drift are
visible in the 2DFS at 0.075 and 0.16 cpp respectively. We see also
evidence for a feature in a different alias mode, although much weaker
than the main feature (
![]() cpp and
cpp and
![]() ). It could be that the zero drift "C''-mode
(Deich et al. 1986) is a drift mode for which the drift sense is
changing continuously.
). It could be that the zero drift "C''-mode
(Deich et al. 1986) is a drift mode for which the drift sense is
changing continuously.
B2016+28![]() :
the 2DFS of the trailing part of the pulse profile
shows a very broad drifting feature (Fig. A.22), which is
caused by drift mode changes (e.g. Oster et al. 1977 at both 430 and
1720 MHz). The leading part of the pulse profile shows the same broad
drift feature, but also a much stronger slow drift mode. This slow
drift mode is probably also seen in the trailing part of the pulse
profile, but less pronounced. The drift bands can be seen by eye in
the pulse-stack.
:
the 2DFS of the trailing part of the pulse profile
shows a very broad drifting feature (Fig. A.22), which is
caused by drift mode changes (e.g. Oster et al. 1977 at both 430 and
1720 MHz). The leading part of the pulse profile shows the same broad
drift feature, but also a much stronger slow drift mode. This slow
drift mode is probably also seen in the trailing part of the pulse
profile, but less pronounced. The drift bands can be seen by eye in
the pulse-stack.
B2020+28![]() :
the LRFS shows a strong even-odd modulation, similar
to the 1.4 GHz observation of Nowakowski et al. (1982). At 430 MHz Backer et al. (1975)
found that both components show an even-odd modulation, but no
systematic drift direction was detected in the leading component. In
our observation the 2DFS of both components of this pulsar contains a
broad drifting feature with opposite drift sense close to the alias
border (Fig. A.23). There is no evidence that the feature
extends over the alias border, although the feature is not
clearly separated from the alias border.
:
the LRFS shows a strong even-odd modulation, similar
to the 1.4 GHz observation of Nowakowski et al. (1982). At 430 MHz Backer et al. (1975)
found that both components show an even-odd modulation, but no
systematic drift direction was detected in the leading component. In
our observation the 2DFS of both components of this pulsar contains a
broad drifting feature with opposite drift sense close to the alias
border (Fig. A.23). There is no evidence that the feature
extends over the alias border, although the feature is not
clearly separated from the alias border.
B2021+51![]() :
this pulsar is clearly drifting
(Fig. A.14), consistent with e.g. Oster et al. (1977) at 1720
MHz. The drifting is detectable over the whole P3 range. The P2and P3 values that are given in Table 2 are for the region
in the 2DFS between the dashed lines. The centroid of the whole 2DFS
gives
:
this pulsar is clearly drifting
(Fig. A.14), consistent with e.g. Oster et al. (1977) at 1720
MHz. The drifting is detectable over the whole P3 range. The P2and P3 values that are given in Table 2 are for the region
in the 2DFS between the dashed lines. The centroid of the whole 2DFS
gives
![]() and
and
![]() .
It is clear
that the drift rate changes by a large factor during the observation,
which was also observed by Oster et al. (1977). It was suggested by
Oster et al. (1977) that maybe the apparent drift direction changes
sporadically. In our observation there is no clear evidence that the
alias mode is changing.
.
It is clear
that the drift rate changes by a large factor during the observation,
which was also observed by Oster et al. (1977). It was suggested by
Oster et al. (1977) that maybe the apparent drift direction changes
sporadically. In our observation there is no clear evidence that the
alias mode is changing.
B2044+15![]() :
this observation is contaminated by
interference, however the 2DFS of the trailing component of the pulse
profile convincingly shows a broad drifting feature. Only the 2DFS of
the trailing component shows features and is plotted in
Fig. A.14. Our observation confirms the drifting found by
Backus (1981) at 430 MHz.
:
this observation is contaminated by
interference, however the 2DFS of the trailing component of the pulse
profile convincingly shows a broad drifting feature. Only the 2DFS of
the trailing component shows features and is plotted in
Fig. A.14. Our observation confirms the drifting found by
Backus (1981) at 430 MHz.
B0037+56![]() :
the 2DFS of this pulsar
:
the 2DFS of this pulsar![]() shows a clear drift feature (Fig. A.1) which appears to
be extended over the alias border. The drift bands are visible
to the eye in the pulse-stack and the apparent change of drift sense
is also visible. There is also a P3=2P0 modulation present.
shows a clear drift feature (Fig. A.1) which appears to
be extended over the alias border. The drift bands are visible
to the eye in the pulse-stack and the apparent change of drift sense
is also visible. There is also a P3=2P0 modulation present.
B0052+51: the trailing component of this pulsar has a broad
drift feature in its 2DFS (Fig. A.17). There is a hint of
drifting with an opposite drift sign in the first component, but this
is not significant. The spectra also show a
![]() modulation.
modulation.
B0136+57![]() :
the drift feature is only detected in the leading part
of the pulse profile and it appears that the feature extends to
the horizontal axis (Fig. A.1).
:
the drift feature is only detected in the leading part
of the pulse profile and it appears that the feature extends to
the horizontal axis (Fig. A.1).
B0138+59![]() :
the drift feature in the 2DFS is broad and close to
the horizontal axis (Fig. A.1). The drift feature
is confirmed in a second observation we made.
:
the drift feature in the 2DFS is broad and close to
the horizontal axis (Fig. A.1). The drift feature
is confirmed in a second observation we made.
B0450+55![]() :
most of the power of the 2DFS is in the drifting
feature (Fig. A.18) and the drift bands are visible to the
eye in the pulse-stack. The drift feature is extended to both
alias borders. The leading component of this pulsar shows drifting in
the opposite direction.
:
most of the power of the 2DFS is in the drifting
feature (Fig. A.18) and the drift bands are visible to the
eye in the pulse-stack. The drift feature is extended to both
alias borders. The leading component of this pulsar shows drifting in
the opposite direction.
B0523+11: this pulsar has a weak drift feature in the 2DFS of
the trailing component (Fig. A.18). In the 2DFS of the
leading component there is also a feature with the same P3 value,
but in that feature there is no significant offset from the vertical
axis measured. This means significant drifting is detected in the
trailing component, and longitude stationary subpulse modulation with
the same P3 value in the leading component. No drifting has been
found at 430 MHz by Backus (1981), but our observation shows that this
pulsar is a drifter.
B0525+21![]() :
subpulse modulation without apparent drift as
well as some correlation between the subpulses of the two components
of the pulse profile has been detected for this pulsar by Backer (1973)
at 318 MHz and Taylor et al. (1975) at 400 MHz. We find that the two
components show broad features to which opposite drift senses can be
associated (Fig. A.18). The features are possibly extended
toward the P3=2P0 alias border.
:
subpulse modulation without apparent drift as
well as some correlation between the subpulses of the two components
of the pulse profile has been detected for this pulsar by Backer (1973)
at 318 MHz and Taylor et al. (1975) at 400 MHz. We find that the two
components show broad features to which opposite drift senses can be
associated (Fig. A.18). The features are possibly extended
toward the P3=2P0 alias border.
B0919+06![]() :
the power in the 2DFS is over the whole P3range is measured to be significantly offset from the vertical axis
(Fig. A.3). The power in the 2DFS peaks toward the
horizontal axis and especially this low frequency excess is offset
from the vertical axis. This can clearly be seen in the bottom plot
whichshows a "shoulder'' at the left side of the peak. No drifting has
been reported for this pulsar by Backus (1981) at 430 MHz.
:
the power in the 2DFS is over the whole P3range is measured to be significantly offset from the vertical axis
(Fig. A.3). The power in the 2DFS peaks toward the
horizontal axis and especially this low frequency excess is offset
from the vertical axis. This can clearly be seen in the bottom plot
whichshows a "shoulder'' at the left side of the peak. No drifting has
been reported for this pulsar by Backus (1981) at 430 MHz.
B1039-19: both components of this pulsar show a clear,
broad drift feature in its 2DFS with the same drift sense
(Fig. A.19).
B1508+55![]() :
the subpulse modulation of this pulsar has been found
to be unorganized and without a preferred drift sense or a particular
P3 value (Taylor & Huguenin 1971 at 147 MHz). In the 2DFS of our
observation there is a broad drift feature present
(Fig. A.4), which is offset from the vertical axis
over the whole P3 range.
:
the subpulse modulation of this pulsar has been found
to be unorganized and without a preferred drift sense or a particular
P3 value (Taylor & Huguenin 1971 at 147 MHz). In the 2DFS of our
observation there is a broad drift feature present
(Fig. A.4), which is offset from the vertical axis
over the whole P3 range.
B1604-00![]() :
there are very broad features in both parts of the
pulse profile and both components are drifting with the same drift
sense (Fig. A.20).
:
there are very broad features in both parts of the
pulse profile and both components are drifting with the same drift
sense (Fig. A.20).
B1738-08![]() :
the 2DFS of both halves of the pulse profile have a
broad drift feature with the same drift sense
(Fig. A.20). In the trailing component there is maybe also a
second weak drift feature present with
:
the 2DFS of both halves of the pulse profile have a
broad drift feature with the same drift sense
(Fig. A.20). In the trailing component there is maybe also a
second weak drift feature present with
![]() and the same drift
sense. The average P3 values appear to be significantly different
in the two components, which could be because of different drift mode
changes in the two components. The drifting can be seen by eye in
the pulse-stack.
and the same drift
sense. The average P3 values appear to be significantly different
in the two components, which could be because of different drift mode
changes in the two components. The drifting can be seen by eye in
the pulse-stack.
B1753+52: the trailing part of the pulse profile shows a broad
drift feature in its 2DFS (second 2DFS in Fig. A.21)
and the rest of the pulse profile (first 2DFS) probably has the
same drift sense.
B1819-22: the 2DFS of this pulsar very clearly shows a
drift feature (Fig. A.7), which is broadened by mode
changes. A part of the pulse-stack is shown in Fig. 1. A full single pulse analysis will follow in a
later paper.
J1830-1135![]() :
the 2DFS of this pulsar with a very long pulse
period (6.2 s) shows a drift feature at the P3=2 P0 alias
border at +100 cpp, which is possibly double peaked
(Fig. A.8).
:
the 2DFS of this pulsar with a very long pulse
period (6.2 s) shows a drift feature at the P3=2 P0 alias
border at +100 cpp, which is possibly double peaked
(Fig. A.8).
B1857-26: the components at both edges of the pulse profile
are drifting with the same drift sense, which can be seen in
Fig. A.21 as an excess of power in the 2DFS at positive
P2 values. The drift bands are sometimes visible to the eye in the
pulse-stack. The center part of the pulse profile does not show
drifting in its 2DFS and is therefore not plotted. This pulsar is
known to be a nuller (Ritchings 1976; Biggs 1992), but no drifting is
reported in the literature.
B1900+01![]() :
drifting is clearly seen over the whole P3 range of
the 2DFS and the top part of the 2DFS is double peaked
(Fig. A.11). The alias mode of this
pulsar probably changes during the observation.
:
drifting is clearly seen over the whole P3 range of
the 2DFS and the top part of the 2DFS is double peaked
(Fig. A.11). The alias mode of this
pulsar probably changes during the observation.
B1911-04![]() :
the low frequency modulation, which is generated in
the trailing part of the pulse profile, is double peaked
(Fig. A.12). This could indicate the presence of a
subpulse phase jump or swing or that the drift sense changes
constantly during the observation. There seems to exist a preferred drift
sense.
:
the low frequency modulation, which is generated in
the trailing part of the pulse profile, is double peaked
(Fig. A.12). This could indicate the presence of a
subpulse phase jump or swing or that the drift sense changes
constantly during the observation. There seems to exist a preferred drift
sense.
B1917+00![]() :
this pulsar shows a broad drifting component in
its 2DFS, which is visible in the bottom plot as an excess of power at
positive P2 (Fig. A.12). According to Rankin (1986) a much
longer
:
this pulsar shows a broad drifting component in
its 2DFS, which is visible in the bottom plot as an excess of power at
positive P2 (Fig. A.12). According to Rankin (1986) a much
longer
![]() value without a measured P2 was reported in a
preprint by L.A. Nowakowski and T.H. Hankins, but to the best of our
knowledge the paper was never published.
value without a measured P2 was reported in a
preprint by L.A. Nowakowski and T.H. Hankins, but to the best of our
knowledge the paper was never published.
B1952+29![]() :
the drifting in both components of this pulsar is
clearly visible to the eye in the pulse-stack and in the 2DFS
(Fig. A.22). The drift sense is the same for both
components.
:
the drifting in both components of this pulsar is
clearly visible to the eye in the pulse-stack and in the 2DFS
(Fig. A.22). The drift sense is the same for both
components.
B1953+50![]() :
this pulsar shows a very clear broad drifting feature
in its 2DFS (Fig. A.13) at low frequencies (right peak at
P2=70 cpp).
:
this pulsar shows a very clear broad drifting feature
in its 2DFS (Fig. A.13) at low frequencies (right peak at
P2=70 cpp).
B2053+36![]() :
this pulsar has a broad drift feature in its
2DFS at low frequencies which is double peaked (Fig. A.14).
This could indicate that the drift sense is changing constantly during
the observation, which is supported by the fact that the feature is
extended towards zero frequencies. However also a subpulse phase jump
or swing could produce the double peaked feature. Subpulse modulation
without a drift sense has been reported for this pulsar at 430 MHz by
Backus (1981).
:
this pulsar has a broad drift feature in its
2DFS at low frequencies which is double peaked (Fig. A.14).
This could indicate that the drift sense is changing constantly during
the observation, which is supported by the fact that the feature is
extended towards zero frequencies. However also a subpulse phase jump
or swing could produce the double peaked feature. Subpulse modulation
without a drift sense has been reported for this pulsar at 430 MHz by
Backus (1981).
B2110+27![]() :
this pulsar shows drifting over the whole P3range in its 2DFS (Fig. A.15). The lower part of the 2DFS is
clearly double peaked, which could suggest that the alias mode is
constantly changing during the observation. The upper part of the 2DFS
is not convincingly double peaked. In the pulse-stack drifting is
visible to the eye. The drift bands are probably distorted by nulls,
causing the drift feature in the 2DFS to be extended over the whole
P3 range. Short sequences of drift bands with negative drifting and
a
:
this pulsar shows drifting over the whole P3range in its 2DFS (Fig. A.15). The lower part of the 2DFS is
clearly double peaked, which could suggest that the alias mode is
constantly changing during the observation. The upper part of the 2DFS
is not convincingly double peaked. In the pulse-stack drifting is
visible to the eye. The drift bands are probably distorted by nulls,
causing the drift feature in the 2DFS to be extended over the whole
P3 range. Short sequences of drift bands with negative drifting and
a
![]() can be seen in the pulse-stack as well as some single
drift bands with an opposite drift. A few apparent drift reversals are
visible in the sequence, although nulling makes it difficult to
identify them.
can be seen in the pulse-stack as well as some single
drift bands with an opposite drift. A few apparent drift reversals are
visible in the sequence, although nulling makes it difficult to
identify them.
B2111+46: it has been reported that this pulsar shows subpulse
drift with a positive and negative drift sense, but without either
dominating (Taylor et al. 1975 at 400 MHz). We also see subpulse
modulation over the whole P3 range without a preferred drift
direction in the middle and trailing components, but there is some
systematic drift in the leading component of this pulsar
(Fig. A.23).
B2148+63![]() :
the 2DFS of this pulsar shows broad, triple, well
separated features (Fig. A.15). The values of P2 and
P3 in Table 2 are for the feature as a whole. The centroids of
the individual peaks give
:
the 2DFS of this pulsar shows broad, triple, well
separated features (Fig. A.15). The values of P2 and
P3 in Table 2 are for the feature as a whole. The centroids of
the individual peaks give
![]() ,
,
![]() and
and
![]() ,
,
![]() .
The most likely interpretation of the 2DFS is that the apparent
drift direction is constantly changing via its P3=2P0 alias border
(see Fig. 2 for the expected 2DFS in this scenario). All
other interpretations seems unlikely, because the feature is clearly
extended toward the P3=2P0 alias border, both sides of the feature
are separated from the vertical axis, this separation is the same on
both sides and one side of the feature contains more power. The latter
indicates that negative drifting dominates in this pulsar.
.
The most likely interpretation of the 2DFS is that the apparent
drift direction is constantly changing via its P3=2P0 alias border
(see Fig. 2 for the expected 2DFS in this scenario). All
other interpretations seems unlikely, because the feature is clearly
extended toward the P3=2P0 alias border, both sides of the feature
are separated from the vertical axis, this separation is the same on
both sides and one side of the feature contains more power. The latter
indicates that negative drifting dominates in this pulsar.
B2154+40![]() :
this pulsar shows a very broad drift feature in the
2DFS of the leading component of the pulse profile, but no
significant drift is detected in the trailing component
(Fig. A.23). The feature is probably extended toward the
alias border.
:
this pulsar shows a very broad drift feature in the
2DFS of the leading component of the pulse profile, but no
significant drift is detected in the trailing component
(Fig. A.23). The feature is probably extended toward the
alias border.
B2255+58: the very clear drift feature in the 2DFS of this
pulsar (Fig. A.15) shows horizontal structure (like
observed for instance for PSR B0809+74 and PSR B0320+39). From
the modulation phase profile it follows that the drift bands make a
subpulse phase step of about
![]() in the middle of the pulse
profile. The longitude resolved modulation index shows a minimum at
the position of the subpulse phase step, as is also observed for PSR
B0809+74 and PSR B0320+39. The phase step in the drift bands can be
seen by eye in the pulse-stack.
in the middle of the pulse
profile. The longitude resolved modulation index shows a minimum at
the position of the subpulse phase step, as is also observed for PSR
B0809+74 and PSR B0320+39. The phase step in the drift bands can be
seen by eye in the pulse-stack.
B2324+60![]() :
this pulsar shows a broad drift feature in its 2DFS at
the alias border (Fig. A.16) and some drift bands can be
seen in the pulse-stack. There is also a strong
:
this pulsar shows a broad drift feature in its 2DFS at
the alias border (Fig. A.16) and some drift bands can be
seen in the pulse-stack. There is also a strong
![]() feature detected.
feature detected.
J2346-0609![]() :
the 2DFS of the trailing component of the pulse
profile has a drift feature close to the alias border
(Fig. A.24). The feature is not clear enough to state if
the drift feature crosses the alias border during the
observation. The spectra also show some low frequency modulation,
especially in the leading component.
:
the 2DFS of the trailing component of the pulse
profile has a drift feature close to the alias border
(Fig. A.24). The feature is not clear enough to state if
the drift feature crosses the alias border during the
observation. The spectra also show some low frequency modulation,
especially in the leading component.
B2351+61![]() :
the 2DFS of this pulsar is double peaked at low
frequencies (Fig. A.16), which could indicate that the
drift direction may constantly change during the observation. Also the
presence of a subpulse phase step or swing could produce this
feature. The centroid is significantly offset from zero, so there
exists a preferred drift sense during the observation.
:
the 2DFS of this pulsar is double peaked at low
frequencies (Fig. A.16), which could indicate that the
drift direction may constantly change during the observation. Also the
presence of a subpulse phase step or swing could produce this
feature. The centroid is significantly offset from zero, so there
exists a preferred drift sense during the observation.
B0402+61: the 2DFS of the trailing component of this pulsar
shows a broad feature without a preferred drift direction
(Fig. A.18). The
2DFS and LRFS of the leading component is featureless.
B1846-06: the 2DFS of this pulsar shows a broad feature with a
positive value for P2 (Fig. A.10). The same drift sense
seems to be detected at low frequencies in the 2DFS.
B1937-26: there is no significant preferred drift sense detected
in the 2DFS of this pulsar (Fig. A.13), but there seems
to be a broad double peaked feature at the alias border.
B1946+35: the LRFS and 2DFS shows a strong low frequency feature in
both components of this pulsar (Fig. A.22). No significant
offset from the vertical axis has been detected in the 2DFS.
B2011+38: the broad feature in the 2DFS of this pulsar may have
a preferred negative value for P2 (Fig. A.14). The 2DFS
and LRFS of this pulsar increases towards low frequencies and peaks at
![]() .
.
B2106+44: the 2DFS and LRFS of this pulsar peaks towards
low frequencies and seems to have a positive value for P2(Fig. A.15).
B0540+23: sporadic bursts of both positive and negative
drift have been reported by Ashworth (1982) at 400 MHz and by
Nowakowski (1991) at 430 MHz. No preferred drift direction is detected
in the 2DFS of this pulsar (Fig. A.2), but in the
pulse-stack short drift bands are seen with different drift senses
confirming the previous reported drifting. Because this pulsar does
not show a preferred drift direction in our observation, this pulsar
is not classified as a drifter in our paper.
B0611+22: our observation does not show any features in the 2DFS
of this pulsar (Fig. A.2), something that has also been
reported by Backer et al. (1975) at 430 MHz. Drifting with
P3=50-100P0 has been reported by Ferguson & Boriakoff (1980) at 430 MHz, who
have analyzed successive integrated pulse profiles. It is not clear if
this kind of drifting is related to subpulse drifting, because in
their analysis the subpulses are not directly measured.
B0656+14: the modulation index of this pulsar shows a sharp peak
at the leading edge of the pulse profile (Fig. A.3), which
is caused by a very bright subpulse. A full investigation of this
phenomenon will be published in a upcoming paper. A preferred
negative drift sense has been reported by Backus (1981) at 430 MHz. We
do not see a preferred drift sense, but there is low frequency
modulation.
B0820+02: positive drifting has been reported by Backus (1981) at
430 MHz. Our observation probably lacks the S/N to confirm this
(Fig. A.3)
B0950+08: drifting has been reported for this pulsar
(e.g. Backer 1973 and Wolszczan 1980) with a variable
![]() .
This drifting is not visible in the 2DFS of our
observation (Fig. A.4), but subpulse modulation is
seen over the whole P3 range without a preferred drift sense. The
interpulse has no measured modulation and is not plotted. The
observing frequency of Backer (1973) was 430 MHz, so it could be that
the drifting of this pulsar is only visible at low observing
frequencies. The observing frequency of Wolszczan (1980) is not mentioned
in their paper.
.
This drifting is not visible in the 2DFS of our
observation (Fig. A.4), but subpulse modulation is
seen over the whole P3 range without a preferred drift sense. The
interpulse has no measured modulation and is not plotted. The
observing frequency of Backer (1973) was 430 MHz, so it could be that
the drifting of this pulsar is only visible at low observing
frequencies. The observing frequency of Wolszczan (1980) is not mentioned
in their paper.
B1112+50: this pulsar is known to show nulling and pulse profile
mode switching and in one of these modes drifting subpulses are
reported (e.g. Wright et al. 1986 at 1412 MHz). There is no clear drift
feature detected in the 2DFS of our observation, but subpulse
modulation is seen over the whole P3 range
(Fig. A.19).
B1612+07: negative subpulse drift has been reported by
Backus (1981) at 430 MHz for this
pulsar![]() . The 2DFS of our observation is
featureless (Fig. A.4), which could be because a too low
S/N.
. The 2DFS of our observation is
featureless (Fig. A.4), which could be because a too low
S/N.
B1918+19: this pulsar is shown to be a drifter with at least
four drift modes at 430 MHz (Hankins & Wolszczan 1987). There are no features in
the 2DFS of our observation (Fig. A.12), which could be
because a too low S/N.
B2315+21: drifting with a negative drift sense has been reported
for this pulsar at 430 MHz by Backus (1981). Our spectra
(Fig. A.16) do not show any sign of drifting, what could be
because a too low S/N.
A modulation index could be derived from the observations of the following pulsars and their spectra show an excess of power toward the horizontal axis (i.e. a "red'' feature). This means that there is some correlation between successive pulses, but no quasiperiodicity.
| B0011+47 | B0355+54 | B0740-28 | B0756-15 |
| B1706-16 | B1754-24 | B1800-21 | B1804-08 |
| J1808-0813 | B1821-19 | B1826-17 | B1839+56 |
| B1905+39 | B1907+10 | B1914+13 | B1924+16 |
| B2323+63 | B2327-20 |
B1804-08: the 2DFS of this pulsar possably shows a broad
drift feature which is generated primarily by the trailing component
of the pulse profile (Fig. A.6), but after randomizing
the order of the pulses this feature turned out to be not
significant.
B1924+16: the 2DFS of this pulsar shows a hint of a broad
drifting feature (Fig. A.13), but scrambling the pulse
stack showed that this drifting is not significantly detected.
B0144+59:
two vertical bands are detected in the 2DFS of the trailing component
(best visible in the bottom plot of Fig. A.17). This bands
may also be present (although weakly) in the middle component. A
![]() (160 cpp) subpulse separation can be
associated with this feature, but no particular P3 value. This
indicates that there is a quasiperiodic intensity modulation in the
pulses with a period of about 1.3 ms, but there is no correlation in
the positions of the subpulses from pulse to pulse. The same features
are seen in another observation we made of this pulsar. We see the
same kind of phenomenon (a bit more clear) for PSR B2217+47. The
leading component does not show any features and is therefore not
plotted. The spectra shown are calculated using transforms of only 32 pulses in order to reduce the resolution. This makes it more easy to
see the features by eye.
(160 cpp) subpulse separation can be
associated with this feature, but no particular P3 value. This
indicates that there is a quasiperiodic intensity modulation in the
pulses with a period of about 1.3 ms, but there is no correlation in
the positions of the subpulses from pulse to pulse. The same features
are seen in another observation we made of this pulsar. We see the
same kind of phenomenon (a bit more clear) for PSR B2217+47. The
leading component does not show any features and is therefore not
plotted. The spectra shown are calculated using transforms of only 32 pulses in order to reduce the resolution. This makes it more easy to
see the features by eye.
B0531+21: both the 2DFS of the main and interpulse of the
Crab pulsar does not show any sign of drifting (Fig. A.18).
A very large modulation index measured is measured (m=5), which
is caused by its giant pulses (Staelin & Reifenstein 1968).
B0626+24: the 2DFS of this pulsar shows subpulse modulation over
the whole P3 range (Fig. A.2). Subpulse modulation
without a drift sense has been reported by Backus (1981) at 430 MHz.
J1022+1001: this millisecond pulsar is known to show subpulse
modulation (Edwards & Stappers 2003a). The power in the 2DFS of the trailing
component peaks toward P3=2P0 (Fig. A.4), consistent
with the analysis of Edwards & Stappers (2003a) at 1380 MHz (we have used the same
data). The 2DFS shown in the figure is that of the trailing
component.
B1541+09: this pulsar (Fig. A.4) is observed to have
a low frequency excess and exhibits mode changes and organized, but
short, drifts in both directions (Nowakowski 1996 at 430 MHz).
J1713+0747: this pulsar shows subpulse modulation
(Edwards & Stappers 2003a at 1190 and 1700 MHz), but the quality of our
observation is too poor to confirm this (Fig. A.5).
B1736-29: the interpulse of this pulsars is not plotted, because
no features are detected in its spectra and no modulation index has
been measured (Fig. A.5).
B1737+13: this pulsar shows a clear
P3=11-14P0 longitude
stationary subpulse modulation, but no drifting has been detected
(Rankin et al. 1988 at 1412 MHz). No features appear in the spectra of
our observation (Fig. A.5). No drifting has been detected
for this pulsar by Backus (1981) at 430 MHz.
B1749-28: this pulsar shows flat featureless spectra
(Fig. A.6). A flat featureless fluctuation spectrum has
also been observed for this pulsar at a lower observing frequency
by Taylor & Huguenin (1971).
B1818-04: the power in the 2DFS is
possibly double peaked (Fig. A.7). This could be
because of the presence of a subpulse phase step or swing or because
of drift reversals. It has been reported that the subpulse modulation
is not well organized (Taylor & Huguenin 1971 and Taylor et al. 1975 both at 400 MHz).
B1839+09: subpulse modulation without any drift sense has been
detected by Backus (1981) at 430 MHz. No features appear in the spectra
of our observation (Fig. A.9).
B1842-04: when we first analyzed the spectra of this
pulsar, an extremely bright and surprisingly sharp longitude
stationary
P3=3.00P0 subpulse modulation feature appeared. Folding
the data with a three times longer pulse period revealed that the
pulse period of this pulsar, as reported by Clifton et al. (1992), is wrong by
a factor three. It turns out that the correct pulse period of this
pulsar has appeared in the literature (Hobbs et al. 2004) without
a comment about this discrepancy. Private communication with G. Hobbs
revealed that this deviation is first discovered, although apparently not
reported in the literature, by the Parkes multibeam survey. Using the
correct pulse period the spectra are featureless
(Fig. A.10).
B1842+14: subpulse modulation without a drift sense has been
detected by Backus (1981) at 430 MHz. The spectra of our observation is
featureless (Fig. A.10).
J1850+0026: the shown 2DFS of this pulsar
(Fig. A.10) is of the trailing peak.
B2022+50: the interpulse of this pulsar (which also does not
show any features in its spectum) is not plotted
(Fig. A.14).
J2145-0750: weak quasi-periodicities around 0.22 and 0.45 cpp are visible in the LRFS and 2DFS of the leading component of this
millisecond pulsar (Fig. A.15), as has been reported by
Edwards & Stappers (2003a) at 860 and 1380 MHz. We have used the same 21 cm data as
has been used by Edwards & Stappers (2003a).
B2217+47: there is no preferred drift sense detected in the
feature in the 2DFS of this pulsar (Fig. A.15), which would
confirm the observation of Taylor & Huguenin 1971 at 147 MHz. However the 2DFS
shows two vertical bands smeared over the whole P3 range.
This modulation is primarily generated in the right part of the pulse
profile. The interpretation is, like for PSR B0144+59, that
there is a quasiperiodic intensity modulation in the pulses with a
period of about 2.5 ms, but there is no correlation in the positions
of the subpulses from pulse to pulse.
| J0134-2937 | B1254-10 | J1730-2304 | B1744-24A |
| J1757-2223 | B1758-23 | J1812-2102 | B1821-11 |
| B1821+05 | J1828-1101 | B1832-06 | J1852-2610 |
| J1852+0305 | B1903+07 | B1915+13 | B1916+14 |
| B1937+21 |
B1821+05: subpulse modulation without a drift sense has been
reported by Backus (1981) at 430 MHz. No features are seen in the 2DFS
(Fig. A.8) and no modulation index could be measured for
this pulsar. This is probably because of the low S/N of our
observation.
B1915+13: no features are seen in the spectra of this pulsar by
Backer et al. (1975) at 430 MHz. In our observation there are also no features
(Fig. A.12), which could be because of the low S/N of our
observation.
B1937+21: the spectra of this pulsar are featureless and
there is no modulation index measured. Only the 2DFS of the main pulse
is plotted in Fig. A.13.
The selection of our sample of pulsars is based only on the predicted S/N in a reasonable observing time. While this sample is luminosity biased, it is not biased on pulsar type or any particular pulsar characteristics. This allows us, first of all, to address the very basic question: what fraction of the pulsars show the drifting phenomenon?
Of the 187analyzed pulsars 68pulsars show the drifting phenomenon, indicating that at least one in three pulsars drift. This is however a lower limit for a number of reasons. First of all, not all the observations have the expected S/N. This could be because of interference during the observation, interstellar scintillation, digitization effects, or because the flux or pulse width for some pulsars was wrong in the database used. The latter was confirmed by measuring the pulse with directly from our own observation. Also there are 6pulsars which show longitude stationary subpulse modulation. Longitude stationary subpulse modulation could indicate that there is drifting, but without a preferred drift sense and therefore it could be related to the same phenomenon.
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{3088f4.ps}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg89.gif) |
Figure 4: The fraction of pulsars we observe to show the drifting phenomenon (solid line) and the number of pulsars (dashed line) versus the measured S/N ratio of the observation. The root-mean-square (rms) is calculated as an estimate for the error (if the bin contains more than one observation). The dotted line is a fit for the S/N dependence of the chance to detect drifting subpulses. |
| Open with DEXTER | |
Because many pulsars in our sample were found to be drifting, the sensitivity of our method to detect drifting could be checked. The S/N of the observations is determined by comparing the root-mean-square (rms) of the off-pulse region of the pulse profile with the power in the pulse. The width of the pulse was automatically determined by trying different pulse-widths and maximizing the resulting S/N. In Fig. 4 the fraction of pulsars that show the drifting phenomenon is plotted versus the S/N ratio of the observation. One can see that the probability of detecting drifting is higher for observations with a higher S/N. The method used is also working for observations with a low S/N, but not in all cases. This could be because, in order to detect drifting in observations with a low S/N, the fraction of pulse energy that is in the drifting subpulses should be high. Also the fraction of time the pulsar shows drifting subpulses during the observation should be high and the drifting must be reasonably coherent.
To make the statistics more independent of the S/N ratio of the
observations, we will do the statistics for the observations with a
![]() .
For 106pulsars in our sample this criterion
is met. By excluding observations with a low S/N a bias toward
long period pulsars (which are observed longer to get enough pulses)
and well studied pulsars (for which long archival data was available)
may be introduced. Therefore all the statistics are checked including
the low S/N observations.
.
For 106pulsars in our sample this criterion
is met. By excluding observations with a low S/N a bias toward
long period pulsars (which are observed longer to get enough pulses)
and well studied pulsars (for which long archival data was available)
may be introduced. Therefore all the statistics are checked including
the low S/N observations.
Besides the S/N of the observations, the amount of scatter-broadening could also influence the probability to detect drifting subpulses. If the amount of scatter broadening is wider than the subpulse separation P2, then the sensitivity to detect drifting subpulses will be severely diminished. There are a number of pulsars in our sample that seem to show scatter broadening. It is however difficult to distinguish between a pulse profile that is scatter broadened and a profile which has an intrinsic exponential tail like shape. Most pulsars that probably show scatter broadening have a S/N below the threshold value of 100, so they are therefore excluded from the statistical analysis (PSRs B1758-23, B1817-13, B1822-14, J1828-1101, B1832-06 and B1849+00). There is only one pulsar that seems to show scatter broadening and has a S/N above the threshold value (PSR B1815-14). Because the low number of pulsars that are scatter broadened, it seems very likely that their influence on the statistics can be neglected. Scatter broadening will be more of an issue for our subsequent paper, which will focus on a lower frequency study of the subpulse modulation properties of radio pulsars.
Of the pulsars with high enough S/N observations, 57 are detected to be drifters (54%) and 5pulsars show longitude stationary subpulse modulation (5%). From Fig. 4 it is clear that the real drift percentage could even be higher than 54%. This number is consistent with Ashworth (1982) and Backus (1981), who found about the same number based on a smaller sample of pulsars. There are many reasons why drifting is not expected to be detected for all pulsars. For instance for some pulsars the line of sight cuts the magnetic pole centrally and therefore longitude stationary subpulse modulation is expected. Also, refractive distortion in the pulsar magnetosphere (e.g. Petrova 2000; Fussell & Luo 2004; Weltevrede et al. 2003) or nulling will disrupt the drift bands, making it difficult or even impossible to detect drifting. A P3=50-100P0 has been reported by Ferguson & Boriakoff (1980) for PSR B0611+22, indicating that the P3 value for some pulsars could be very large. In that case longer observations are needed to detect this drifting and distinguishing it from interstellar scintillation could become a problem. Some pulsars are known to show organized drifting subpulses in bursts. In that case some of our observations could be too short to contain enough drift bands to detect the drifting.
With a lower limit of one in two it is clear that drifting is at the
very least a common phenomenon for radio pulsars. This implies that
the physical conditions required for the emission mechanism of radio
pulsars to work cannot be very different than the physical conditions
required for the drifting mechanism. Therefore it could well be that
the drifting phenomenon is an intrinsic property of the emission
mechanism, although for some pulsars it is difficult or even
impossible to detect.
![\begin{figure}
\par\includegraphics[angle=270,width=12.4cm,clip]{3088f5.ps}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg92.gif) |
Figure 5:
The |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=270,width=7.6cm,clip]{3088f6a.ps}\hspace*{10mm}%
\includegraphics[angle=270,width=7.6cm,clip]{3088f6b.ps}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg93.gif) |
Figure 6:
The left panel shows the histogram of
the characteristic ages of the analyzed pulsars with a
|
| Open with DEXTER | |
The unbiased sample of pulsars not only allows us to determine what
fraction of the pulsars show the drifting phenomenon, but also to
correlate the drifting phenomenon with other pulsar parameters. Two
directly measurable and therefore important physical parameters of the
pulsar are the pulse period and its time derivative (spin-down
parameter). From the position of a pulsar in the ![]() diagram
and assuming magnetic dipole breaking, an estimate of the age and the
magnetic field strength can be obtained. Therefore it is useful to try
to correlate the drifting phenomenon with the position of the pulsars
in the
diagram
and assuming magnetic dipole breaking, an estimate of the age and the
magnetic field strength can be obtained. Therefore it is useful to try
to correlate the drifting phenomenon with the position of the pulsars
in the ![]() diagram (Fig. 5). All the analyzed
pulsars with a measured
diagram (Fig. 5). All the analyzed
pulsars with a measured ![]() are in this diagram
are in this diagram![]() and the coherent
drifters, diffuse drifters and pulsars showing longitude stationary
subpulse modulation are plotted with different symbols to identify any
trends between position and classification of the pulsars. To make the
plot more readable the millisecond pulsars are not plotted.
and the coherent
drifters, diffuse drifters and pulsars showing longitude stationary
subpulse modulation are plotted with different symbols to identify any
trends between position and classification of the pulsars. To make the
plot more readable the millisecond pulsars are not plotted.
The ![]() diagram reveals that the pulsars that show the
drifting phenomenon are more likely to be found closer to the death
line
and this is more pronounced for the coherent drifters. This suggests
that the population of pulsars that show the drifting phenomenon is on
average older (the pulsar age is defined as
diagram reveals that the pulsars that show the
drifting phenomenon are more likely to be found closer to the death
line
and this is more pronounced for the coherent drifters. This suggests
that the population of pulsars that show the drifting phenomenon is on
average older (the pulsar age is defined as
![]() )
than the population of pulsars that do not show drifting. This
confirms the result of Ashworth (1982), who also found that drifters are
on average older. Moreover it seems that drifting is more coherent for
older pulsars. This trend is more visible in the pulsar age histograms
(left panel of Fig. 6), where the nondrifters, the
coherent drifters and all the drifters (both coherent and diffuse) are
plotted separately. This correlation seems to suggest an evolutionary
trend that the subpulse
modulation is disordered for the youngest
pulsars and gets more and more organized into drifting subpulses as
the pulsar ages.
)
than the population of pulsars that do not show drifting. This
confirms the result of Ashworth (1982), who also found that drifters are
on average older. Moreover it seems that drifting is more coherent for
older pulsars. This trend is more visible in the pulsar age histograms
(left panel of Fig. 6), where the nondrifters, the
coherent drifters and all the drifters (both coherent and diffuse) are
plotted separately. This correlation seems to suggest an evolutionary
trend that the subpulse
modulation is disordered for the youngest
pulsars and gets more and more organized into drifting subpulses as
the pulsar ages.
The significance of this trend can be determined with the Kolmogorov-Smirnov test (KS-test), which tells us how likely it is that two distributions are statistically different. It follows that the age distribution of the drifters is only 0.03% likely to be the same as the age distribution of pulsars not showing the drifting phenomenon. Thus the drifters and nondrifters have significantly different age distributions. The KS-test is also used to find out if the coherent drifters have a separate age distribution. It follows that the coherent drifters are only 0.4%and 8%likely to have the same age distribution as the nondrifting and the diffuse drifting pulsars respectively. Therefore the pulsars which drift coherently are likely to have a separate age distribution. Although likely, the difference in the age distribution of the coherent drifters is not detected to be significantly different from the drifters. Nevertheless it is intriguing to think that drifting becomes more and more coherent for pulsars with a higher age. A larger sample of pulsars is needed to check whether this is significant. The same trend is found when the low S/N observations are included in our sample. In that case the drifters and coherent drifters are respectively 0.03%and 0.1%likely to have the same age distribution as the nondrifters, confirming the assertion that the drifters and non-drifters have different age distributions.
The S/N of the observations used in the left panel of Fig. 6 may be different in each of the age bins, thereby introducing a "S/N versus age'' bias. To correct for this effect, for each distribution and for each age bin the median of the S/N of the observations was calculated. This median S/N was used to estimate what the chance was of detecting drifting (the dotted line in Fig. 4). The distributions of the drifters and coherent drifters were divided by this chance (because a low S/N implies that there was only a low chance of detecting drifting) and the distribution of the non drifters was divided by one minus this chance (because a low S/N implies a high chance of not detecting drifting). This gives the "S/N versus age bias'' corrected age distributions (right panel of Fig. 6). As one can see this correction does not lead to a qualitatively different result.
![\begin{figure}
\par\includegraphics[angle=270,width=8.4cm,clip]{3088f7.ps}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg95.gif) |
Figure 7:
The surface magnetic field strength
histogram of the pulsars which do not show the drifting phenomenon
(solid line), those which do show the drifting phenomenon (dashed
line) and those which drift coherently (dotted line).
Only observations with a
|
| Open with DEXTER | |
A possible explanation for the age dependence of the drifting phenomenon is that the drift bands are more distorted for younger pulsars. One mechanism to distort the drift bands isnulling (e.g. Janssen & van Leeuwen 2004; Taylor & Huguenin 1971; van Leeuwen et al. 2002) and the fraction of time that pulsars spend in their nulling state (the nulling fraction) is known to be correlated with the pulsar age. However it has been found by Ritchings (1976) that the nulling fraction is on average higher for older pulsars, which is confirmed in later studies (e.g. Biggs 1992; Li & Wang 1995). Although the correlation with other pulsar parameters seems to be stronger, these studies prove that nulling cannot explain this correlation.
Another possible scenario is that the alignment of the magnetic dipole
axis with the rotation axis has something to do with the observed
trend. Observations seem to show that the angle ![]() between the
magnetic axis and the rotation axis is on average smaller for older
pulsars (e.g. Tauris & Manchester 1998), indicating that the magnetic axis and
the rotation axis becomes more aligned or anti-aligned for older
pulsars. This angle is likely to be an important physical parameter in
the mechanism that drives the drifting phenomenon (for instance the
classical Ruderman & Sutherland 1975 model can only be applied for an
anti-parallel magnetic axis). In this scenario as the pulsar gets
older, the rotation axis and the magnetic axis grows more aligned,
which makes the drifting mechanism more effective or regular. This
trend is also consistent with the fact that pulsars with a regular
drift pattern tend to have small values for
between the
magnetic axis and the rotation axis is on average smaller for older
pulsars (e.g. Tauris & Manchester 1998), indicating that the magnetic axis and
the rotation axis becomes more aligned or anti-aligned for older
pulsars. This angle is likely to be an important physical parameter in
the mechanism that drives the drifting phenomenon (for instance the
classical Ruderman & Sutherland 1975 model can only be applied for an
anti-parallel magnetic axis). In this scenario as the pulsar gets
older, the rotation axis and the magnetic axis grows more aligned,
which makes the drifting mechanism more effective or regular. This
trend is also consistent with the fact that pulsars with a regular
drift pattern tend to have small values for ![]() (Rankin 1993b; Wright 2003). However, we have found that the interpulse
pulsar PSR B1702-19 is a coherent drifter, suggesting that
coherent drifters can have a large
(Rankin 1993b; Wright 2003). However, we have found that the interpulse
pulsar PSR B1702-19 is a coherent drifter, suggesting that
coherent drifters can have a large ![]() (an
(an ![]() value of
value of
![]() and
and
![]() have been found by Rankin 1993b and
Lyne & Manchester 1988 respectively). Also the pulse morphology seems to
evolve when the pulsar ages (Rankin 1983; Beskin et al. 1984), such that
core single stars are on average younger than pulsars with more
complex profiles. This could make drifting subpulses more likely to
be detected in older pulsars. In the non-radial pulsations model this
trend can also be explained, because the appearance of narrow drifting
subpulses is favored in pulsars with an aligned magnetic axis
(Clemens & Rosen 2004).
have been found by Rankin 1993b and
Lyne & Manchester 1988 respectively). Also the pulse morphology seems to
evolve when the pulsar ages (Rankin 1983; Beskin et al. 1984), such that
core single stars are on average younger than pulsars with more
complex profiles. This could make drifting subpulses more likely to
be detected in older pulsars. In the non-radial pulsations model this
trend can also be explained, because the appearance of narrow drifting
subpulses is favored in pulsars with an aligned magnetic axis
(Clemens & Rosen 2004).
An estimate for the component of the surface magnetic field of
pulsars perpendicular to the rotation axis can be directly derived
from the position of the pulsar in the ![]() diagram
(
diagram
(
![]() Gauss). The histograms of the
magnetic field strengths of the three different groups of pulsars
(Fig. 7) do not show a clear trend, which is confirmed by
the KS-test.
It follows that the magnetic field strength distribution of the
nondrifters has a chance of
Gauss). The histograms of the
magnetic field strengths of the three different groups of pulsars
(Fig. 7) do not show a clear trend, which is confirmed by
the KS-test.
It follows that the magnetic field strength distribution of the
nondrifters has a chance of ![]() 20%and
20%and
![]() 50%to be statistically the same as the
distributions of all the drifters (both the coherent and diffuse
drifters) and the coherent drifters respectively. This means that the
magnetic field strength distributions are not significantly
different. If the low S/N pulsars are included, the magnetic field
distributions are more likely to be the same than to be different.
50%to be statistically the same as the
distributions of all the drifters (both the coherent and diffuse
drifters) and the coherent drifters respectively. This means that the
magnetic field strength distributions are not significantly
different. If the low S/N pulsars are included, the magnetic field
distributions are more likely to be the same than to be different.
It seems that the drifting phenomenon is only weakly correlated with, or even independent of magnetic field strength. This is consistent with the large fraction of pulsars that are found to show the drifting phenomenon, because the drifting phenomenon is too common to require very special physical conditions.
The drifting phenomenon is a form of subpulse modulation, so the longitude-resolved modulation index mi(Eq. (5)) is an obvious parameter to try to correlate with the drifting phenomenon. Because the longitude-resolved modulation index can vary a lot with pulse longitude, as can be seen in the figures in Appendix A, it is a somewhat arbitrary what one should call the modulation index. The longitude-resolved modulation index of many pulsars do show a minimum in the middle of the pulse profile where the total intensity is relatively high. This means that if the S/N of an observation increases, the average modulation index will also increase. This is because then the modulation index can be measured at pulse longitudes farther away from the peak intensity of the pulse profile where the longitude-resolved modulation index tends to be higher. We have therefore chosen the modulation index m to be the longitude-resolved modulation index mi at the pulse longitude bin i where mi has its minimum value. This definition should make the modulation index a more S/N independent number than for instance the average of the longitude-resolved modulation index. The same definition is used by Jenet & Gil (2003) to measure the modulation index.
Modulation index histograms are shown in Fig. 8. Readily
apparent is the trend that pulsars that show the drifting phenomenon
more coherently have on average a lower modulation index. There seems
to be no significant difference in the modulation index of the pulsars
that do and do not show the drifting phenomenon. The significance of
this trend is also checked with the KS-test and the modulation index
distribution of the drifters is ![]() 50%as likely to be the
same as the distribution of the nondrifting pulsars. The coherent
drifting distribution is only 6%and 5%likely
to be the same as the nondrifters and the diffuse drifting
distributions respectively. These numbers are too high to state that
the modulation index distribution of the coherent drifters are
significantly different.
50%as likely to be the
same as the distribution of the nondrifting pulsars. The coherent
drifting distribution is only 6%and 5%likely
to be the same as the nondrifters and the diffuse drifting
distributions respectively. These numbers are too high to state that
the modulation index distribution of the coherent drifters are
significantly different.
While the trend seen in Fig. 8 is not shown to be statistically significant, it is intriguing and a larger sample of pulsars is needed to determine its true significance. If the correlation is proven to be significant it would indicate that pulsars that show coherently drifting subpulses have on average a lower modulation index. Although this trend may appear counterintuitive because drifting subpulses imply subpulse modulation, it can be explained.
From the summation in Eq. (4) (and demonstrated in
Fig. 3) it follows that the modulation index is
independent of whether the subpulses appear randomly or organized and
from Eq. (5) it follows that the modulation
index is even independent of the drift band separation P3 in the
case of a coherent drifter. However, if the number of subpulses per
pulse is large, the subpulses could possibly overlap causing the
intensity to change less from pulse to pulse resulting in a lower
modulation index (Jenet & Gil 2003). It must be noted that since sparks
cannot physically overlap on the polar cap, this only works if there
is significant broadening in the mapping from polar cap to the
radiation beam pattern. Another parameter influencing the modulation
index is the width of the subpulse intensity distribution. If the
subpulses have a narrow subpulse intensity distribution, e.g. the
subpulses have more equal intensities, the modulation index will also
be lower. A clear example of this effect is the huge measured
modulation index of PSR B0531+21 (m=5), caused by its giant pulses
(Staelin & Reifenstein 1968).
![\begin{figure}
\par\includegraphics[angle=270,width=7.8cm,clip]{3088f8.ps}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg101.gif) |
Figure 8:
The modulation index distribution of the
pulsars that do not show the drifting phenomenon (solid line), that do
show the drifting phenomenon (dashed line)
and of the pulsars that drift coherently (dotted line).
Observations with a
|
| Open with DEXTER | |
To explain the trend that pulsars that show the drifting phenomenon coherently have on average a lower modulation index, these pulsars must either have on average more subpulses per pulse or the subpulse intensity distribution must be more narrow. In the sparking gap model it seems reasonable that the subpulses of the coherent drifters have more equal intensities. Coherent drifting could indicate that the electrodynamical conditions in the sparking gap are stable, which could be the reason why the subpulses have on average more equal intensities. Also the presence of subpulse phase steps results in a minimum in the longitude resolved modulation index (Edwards & Stappers 2003b; Edwards et al. 2003). This effect can be seen in the longitude resolved modulation index of PSR B0320+39, PSR B0809+74, PSR B1919+21 and the new drifter PSR B2255+58. Also PSR B0818-13 shows a minimum in its longitude resolved modulation index at the position of its subpulse phase swing. It is argued by Edwards et al. (2003) that the local reduction of the modulation index accompanied by a rapid swing in the modulation phase profile are the result of interference between two superposed drifting subpulse signals that are out of phase. It is not unlikely that interference can only occur if the drifting is coherent, which could explained the trend.
It should also be noted that the modulation index of a purely sinusoidal
subpulse signal results in a modulation index of
![]() .
Subpulse patterns with different waveforms or drift band
shapes will generally have larger modulation indices. Many pulsars
have a modulation index which is significantly lower than this
value. This implies that the pulsar emission has both a subpulse
signal and a non-varying component, which could indicate the presence
of superposed out of phase subpulse signals.
.
Subpulse patterns with different waveforms or drift band
shapes will generally have larger modulation indices. Many pulsars
have a modulation index which is significantly lower than this
value. This implies that the pulsar emission has both a subpulse
signal and a non-varying component, which could indicate the presence
of superposed out of phase subpulse signals.
Another explanation for this trend would be that refraction is perhaps more dominant for pulsars that do not show coherently drifting subpulses. The pulse morphology could well be influenced by refractive properties of the pulsar magnetosphere (Petrova 2000; Fussell & Luo 2004; Lyubarskii & Petrova 1998; Weltevrede et al. 2003), so it could be that for some pulsars the organized drifting subpulses are more refractively distorted than for others. For those pulsars the coherent drifting is distorted in this scenario, causing the subpulses to appear more disordered in the pulse window. Moreover it is expected that the intensities of the individual subpulses varies more because of lensing (e.g. Petrova 2000; Fussell & Luo 2004) and possible focusing of the radio emission (Weltevrede et al. 2003), causing the modulation index to be higher in those pulsars.
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{3088f9.ps}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg103.gif) |
Figure 9:
The average modulation index versus pulsar age
histogram for the pulsars showing the drifting phenomenon (dashed
line) and all the pulsars with a measured modulation index (solid
line). The rms is calculated as an estimate for the error (if the bin
contains more than one pulsar). Pulsars with a
|
| Open with DEXTER | |
If a correlation between the drifting phenomenon and both the pulsar age and the modulation index exist, there could also be a correlation between pulsar age and modulation index. The modulation index versus pulsar age histogram is plotted in Fig. 9 and it is clear that no significant correlation is found, indicating that the modulation index is the same for pulsars with different ages. This seems to suggest that a high pulsar age and a low modulation index are two independent factors affecting the likelihood that a pulsar will exhibit coherently drifting subpulses.
![\begin{figure}
\par\includegraphics[angle=270,width=11.7cm,clip]{3088f10.ps}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg104.gif) |
Figure 10: The modulation index for all analyzed pulsars which have a measured modulation index (except PSR B0531+21) versus the four complexity parameters as described in the text. |
| Open with DEXTER | |
The modulation index of core type emission is observed by Weisberg et al. (1986) to be in general lower than that of conal type of emission. This is also a consequence of the Gil & Sendyk (2000) model. In the sparking gap model, the drifting phenomenon is associated with conal emission and therefore expected to be seen in pulsars with an on average higher modulation index. The modulation index distributions of the drifters and nondrifters are likely to be the same, so drifting phenomenon appears not to be an exclusively conal phenomenon (as suggested by Rankin 1986). If well organized coherent drifting is an exclusively conal phenomenon, it is expected that coherent drifters have an on average a higher modulation index, exactly opposite to the observed trend.
Also, if drifting is an exclusively conal phenomenon, no drifting is
expected for pulsars classified as "core single stars''. Although
this may be true for many cases there are some exceptions. The
interpulse of PSR B1702-19 is classified as a core single star
(Rankin 1990 and references therein) and shows a clear and narrow P3 feature. The diffuse drifter B2255+58 is another good example of
a drifter that is classified as a core single star. Most of the core
single stars that show drifting are diffuse Dif![]() drifters (PSR
B0136+57, B0823+26, B1642-03, B1900+01, B1911-04, B1953+50 and
B2053+36). The coherent drifter PSR B1844-04 has been classified as
a core single or a triple profile. This means that it is questionable
if the lack of of ordered subpulse modulation is a useful criterion to
identify core emission (as suggested by Rankin 1986). The
classification can be frequency dependent, so core single pulsars at
low frequencies could show conal emission at higher frequencies. The
many core single stars that appear to be drifting stresses the
importance of being unbiased on pulsar type when studying the drifting
phenomenon.
drifters (PSR
B0136+57, B0823+26, B1642-03, B1900+01, B1911-04, B1953+50 and
B2053+36). The coherent drifter PSR B1844-04 has been classified as
a core single or a triple profile. This means that it is questionable
if the lack of of ordered subpulse modulation is a useful criterion to
identify core emission (as suggested by Rankin 1986). The
classification can be frequency dependent, so core single pulsars at
low frequencies could show conal emission at higher frequencies. The
many core single stars that appear to be drifting stresses the
importance of being unbiased on pulsar type when studying the drifting
phenomenon.
In the framework of the sparking gap model (e.g. Gil et al. 2003; Gil & Sendyk 2000; Ruderman & Sutherland 1975) the subpulses are generated (indirectly) by discharges in the polar gap (i.e. sparks). Each individual spark should emit nearly steady, unmodulated radiation, so the modulation of the pulsar emission is due to the changing positions of the subpulses in the pulse window and the number of visible sparks in different pulses. The more sparks there are visible in the pulse window, the less the intensity will change from pulse to pulse because the subpulses could overlap. The number of sparks that fits on the polar cap is quantified by the complexity parameter (Gil & Sendyk 2000) and therefore one expects an anti-correlation between the modulation index m (which is a measure for how much the intensity varies from pulse to pulse) and this complexity parameter (Jenet & Gil 2003). As noted in the previous subsection, this only works if there is significant broadening in the mapping from polar cap to the radiation beam pattern.
The complexity parameter is a function of the pulse period and its
derivative and its precise form depends on the model one assumes for
the pulsar emission. By correlating the modulation index of a sample
of pulsars with various complexity parameters as predicted by
different emission models one could try to distinguish which model
best fits the data (Jenet & Gil 2003). We have correlated the
modulation indices in our sample of pulsars with the complexity
parameter of four different emission models as derived by Jenet & Gil (2003)
and Gil & Sendyk (2000):
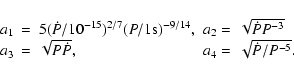 |
(7) |
Physically, a1 is proportional to the polar cap radius rpdivided by the gap height h as predicted in the sparking gap model
and is therefore a measure for the number of sparks across the polar
cap. The parameter a2 is proportional to the acceleration
parameter, which is the surface magnetic field strength ![]() divided by P2. This acceleration parameter is proportional to total
current outflow from the polar cap, and roughly to the circulation
time of the sparks expressed in pulse periods. The acceleration
parameter is also proportional to the square root of the spin down
energy loss rate. Finally a3 and a4 are proportional to
respectively the magnetic field strength at the surface and at the
light cylinder.
divided by P2. This acceleration parameter is proportional to total
current outflow from the polar cap, and roughly to the circulation
time of the sparks expressed in pulse periods. The acceleration
parameter is also proportional to the square root of the spin down
energy loss rate. Finally a3 and a4 are proportional to
respectively the magnetic field strength at the surface and at the
light cylinder.
According to Jenet & Gil (2003) the anti-correlation between the modulation index and the complexity parameter will be masked by viewing angle issues in conal emission, so one might get better results by including only pulsars that are known to emit core emission. Because, as discussed in Sect. 4.3, it is not clear how drifting subpulses relate to the morphological classification of the pulsar, all pulsars with a measured modulation index are included in our sample. The modulation index is chosen to be the minimum in the longitude-resolved modulation index (like in Jenet & Gil 2003), which should give the best estimate for the modulation index of the core emission if present in the pulse profile.
The modulation index versus the four complexity parameters plots are shown in Fig. 10. To find out if there exist an (anti-)correlation without fitting a specific function to the data a rank-order correlation is used. This means that the rank of the values among all the other values is used rather than the values itself. This implies that the correlation coefficient is identical for the set of points (xi, yi) and (F(xi), G(yi)), as long as the functions F and G are monotonic functions. This means that for instance, because a2 is proportional to the square root of the spin down energy loss rate, the correlation coefficient of a2 and the modulation index will be same as the correlation coefficient of the the spin down energy loss rate and the modulation index.
Following Jenet & Gil (2003) we have used the Spearman rank-ordered
correlation coefficient ![]() and its significance parameter
and its significance parameter ![]() (Press et al. 1992). A problem arises when one wants to include the
uncertainties of the data points, because then the rank of the values
is not uniquely defined anymore. As one can see in
Fig. 10, the errorbars are overlapping each other, so
they should be included in the analysis. The significance parameter
(Press et al. 1992). A problem arises when one wants to include the
uncertainties of the data points, because then the rank of the values
is not uniquely defined anymore. As one can see in
Fig. 10, the errorbars are overlapping each other, so
they should be included in the analysis. The significance parameter ![]() does not include the uncertainties on the data points and is
therefore not directly usable to estimate the significance of
does not include the uncertainties on the data points and is
therefore not directly usable to estimate the significance of ![]() .
.
To include the uncertainties in the analysis we have used a Monte
Carlo approach. The data points are replaced with Gaussian
distributions with a width corresponding to the 1-![]() uncertainties of the measurements. In each integration step a point is
randomly picked from these distributions. Instead of calculating
uncertainties of the measurements. In each integration step a point is
randomly picked from these distributions. Instead of calculating ![]() and
and ![]() directly from the data points, we calculate them
for the randomly choosen points. So for each integration step we
randomly select a set of points for which we get a
directly from the data points, we calculate them
for the randomly choosen points. So for each integration step we
randomly select a set of points for which we get a ![]() and
and ![]() .
The probability distribution
.
The probability distribution ![]() is calculated by
averaging the Gaussian distributions centered around the calculated
values of
is calculated by
averaging the Gaussian distributions centered around the calculated
values of ![]() with a 1-
with a 1-![]() width
width ![]() .
The calculated
probablility distributions are plotted in Fig. 11. The
position of the peak of the probability distribution corresponds to
the most likely value of the correlation coefficient and the
1-
.
The calculated
probablility distributions are plotted in Fig. 11. The
position of the peak of the probability distribution corresponds to
the most likely value of the correlation coefficient and the
1-![]() width of the peak is a measure for the significance of the
correlation coefficient.
width of the peak is a measure for the significance of the
correlation coefficient.
The results of this analysis are tabulated in Table 1. Based on a sample of 12 pulsars, Jenet & Gil (2003) concluded that the sparking gap model (a1) showed the highest anti-correlation and that the surface magnetohydrodynamic wave instabilities (a3) is unlikely. Also in this enlarged sample, a3shows the least evidence for an anti-correlation (it is even more likely that the modulation index is positively correlated with a3). The strongest anti-correlations are found for a2 and a4, which corresponds respectively to continuous current outflow instabilities and outer magnetospheric instabilities. However, none of the correlations are significantly inconsistent with an anti-correlation, and therefore none of the models can be ruled out based on these observations.
One can also see that the modulation index is uncorrelated with the
age of the pulsar, which is consistent with
Fig. 9. There is a hint that the modulation index is
weakly correlated with the pulse period and the surface magnetic field
strength ![]() .
.
The value of P3 is observed to be independent of the observing frequency (Izvekova et al. 1993), but the value of P2 could vary a little (e.g. Edwards & Stappers 2003a). Moreover observations show that measuring a value for P2 can be far from trivial (e.g. Edwards & Stappers 2003b) and it is only a meaningful parameter if the drift bands are linear. This means that correlating P3 with other pulsar parameters is the most direct way to find out if the drift rate depends on any physical parameters of the pulsar. The strongest correlation is expected to be found when P2 is constant for different pulsars. Such a correlation would be a very important observational restriction on pulsar emission models.
![\begin{figure}
\par\includegraphics[angle=270,width=8.4cm,clip]{3088f11.ps}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg108.gif) |
Figure 11:
The probability functions |
| Open with DEXTER | |
Table 1: The correlation coefficients and their significance as derived from Fig. 11.
Table 2:
The details of all the analysed pulsars. The classification of the pulsar in the second column, where "Coh'' is a coherent drifter, "Dif'' and "Dif![]() '' are diffuse drifters with or without drift features which are clearly separated from the alias borders and "Lon'' are pulsars showing longitude stationary subpulse modulation. The next columns are the pulse period, its dimensionless time derivative, the number of pulses in the observation, the signal to noise ratio, the minimum in the longitude resolved modulation index, the minimum detectable modulation index, the horizontal and vertical driftband separation and the figure number.
'' are diffuse drifters with or without drift features which are clearly separated from the alias borders and "Lon'' are pulsars showing longitude stationary subpulse modulation. The next columns are the pulse period, its dimensionless time derivative, the number of pulses in the observation, the signal to noise ratio, the minimum in the longitude resolved modulation index, the minimum detectable modulation index, the horizontal and vertical driftband separation and the figure number.
![\begin{figure}
\par\includegraphics[angle=270,width=8.2cm,clip]{3088f12.ps}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg578.gif) |
Figure 12:
The measured value of the vertical drift
band separation P3 versus the pulsar age
of all the pulsars showing the drifting phenomenon. The coherent
drifters are the filled circles, the Dif drifters (with drift feature
clearly separated from the alias borders) are the open circles and the
Dif |
| Open with DEXTER | |
A significant correlation between P3 and the pulsar age has been
reported in the past (Wolszczan 1980; Rankin 1986; Ashworth 1982). As one can
see in Fig. 12 there is no clear correlation present in our
data, which is confirmed by ![]() -fitting. The figure looks
qualitatively the same as Fig. 4 of Rankin (1986), although she only
plots "conal P3 values''. As discussed in Sect. 4.3, it is not clear if one should make this
distinction.
-fitting. The figure looks
qualitatively the same as Fig. 4 of Rankin (1986), although she only
plots "conal P3 values''. As discussed in Sect. 4.3, it is not clear if one should make this
distinction.
There is no correlation found between P3 and the magnetic field strength, contrary to what was reported by Wolszczan (1980) and Ashworth (1982). Also there seems to be no correlation between P3 and the pulse period (consistent with Wolszczan 1980, contrary to the tendency reported by Backer 1973). The evidence for a pulsar subpopulation located close to the P3=2P0 Nyquist limit (Rankin 1986; Wright 2003) also seems to be weak.
In a sparking gap model one would expect that the spark-associated
plasma columns drift because of an
![]() drift, which depends on both the pulse period and its derivative
(e.g. Gil & Sendyk 2000; Ruderman & Sutherland 1975). The absence of any correlation between P3 and a physical pulsar parameter is difficult to explain in this
model, unless many pulsars in our sample are aliased. If a pulsar is
aliased a higher
drift, which depends on both the pulse period and its derivative
(e.g. Gil & Sendyk 2000; Ruderman & Sutherland 1975). The absence of any correlation between P3 and a physical pulsar parameter is difficult to explain in this
model, unless many pulsars in our sample are aliased. If a pulsar is
aliased a higher
![]() drift can result in a
lower P3 value and visa versa, making P3 not a direct measure of
the
drift can result in a
lower P3 value and visa versa, making P3 not a direct measure of
the
![]() drift. In the plot a distinction is
therefore made between the coherent drifters, the diffuse Dif
drifters and the Dif
drift. In the plot a distinction is
therefore made between the coherent drifters, the diffuse Dif
drifters and the Dif![]() drifters (the latter are probably more
likely to be aliased), but this separation does not reveal a
significant correlation. Also if P2 is highly variable from pulsars
to pulsar, any correlation with P3 is expected to be weaker.
drifters (the latter are probably more
likely to be aliased), but this separation does not reveal a
significant correlation. Also if P2 is highly variable from pulsars
to pulsar, any correlation with P3 is expected to be weaker.
There are a number of pulsars found that show evidence for drift
reversals. This kind of behavior is known for PSR B2303+30 which shows
drift reversals around P3=2P0 (Redman et al. 2005). This is confirmed
in the 2DFS of our observation and two other other pulsars that very
clearly show the same kind of behavior in its 2DFS are found: PSR
B2148+63 and PSR B2310+42. Another pulsar that is known to show drift
reversals is PSR B0826-34 (Gupta et al. 2004; Esamdin et al. 2005). This pulsar
continuously changes the apparent drift direction via longitude
stationary subpulse modulation. There are a few more pulsars found
which possibly show the same kind of subpulse behavior: PSRs B0037+56,
B1642-03, B1944+17, B2110+27, B2351+61. The evidence for drift
reversals is less clear than for the afore mentioned
![]() pulsars. If pulsars are proven to show drift reversals via longitude
stationary subpulse modulation and one believes that the physical
drift direction of the emission entities cannot change drift
direction, it would imply that the the drifting in both drift
directions is aliased.
pulsars. If pulsars are proven to show drift reversals via longitude
stationary subpulse modulation and one believes that the physical
drift direction of the emission entities cannot change drift
direction, it would imply that the the drifting in both drift
directions is aliased.
A correlation between the drift direction and the pulsar spin-down was reported by Ritchings & Lyne (1975), such that a high spin-down is correlated with positive drifting. The same trend was also found by Ashworth (1982) and Backus (1981), although its significance was less. In our sample there is no significant correlation between the drift direction and the pulsar spin-down. Also there is no significant difference between the number of positive and negative drifters.
The value of P3 is a much better defined parameter than P2if the drift bands are non linear. Although this makes it difficult to find any correlations with P2, the fact that the drift bands can be non linear is very interesting by itself. The drift bands of for instance PSR B0809+74 (Edwards & Stappers 2003b; Wolszczan et al. 1981; Prószynski & Wolszczan 1986) and PSR B0320+39 (Edwards & Stappers 2003b; Edwards et al. 2003) show subpulse phase steps and we find that the new drifter PSR B2255+58 also shows a phase step. Although the carousel model predicts curved drift bands under certain geometries, it cannot explain sharp discontinuities of this type. A way out could be that the observed discontinuities are caused by local irregularities of the magnetic field (Wolszczan et al. 1981).
It is argued by Edwards et al. (2003) that the local reduction of the modulation index accompanied by a rapid swing in the modulation phase profile are the result of interference between two superposed drifting subpulse signals that are out of phase. In the non-radial pulsations model subpulse phase steps could be explained (Clemens & Rosen 2004), but it has trouble explaining how the modulation phase profile can be anything but piecewise linear. Visually curved drift bands are expected by applying subpulse amplitude windowing (pulse longitude dependent subpulse intensities), as pointed out by Clemens & Rosen 2004. However it is observed that the phase profile of, for example, PSR B0818-13 makes a swing in the middle of the pulse profile. The phase profile is not sensitive for subpulse amplitude windowing and therefore the subpulse phase swing cannot be explained by the non-radial pulsations model.
Subpulse modulation is shown to be very common for radio pulsars. Of the 187analyzed pulsars 170 are shown to exhibit subpulse modulation. The measured upper limits on the modulation index of many of the pulsars that do not have a measured modulation index were high, indicating that pulsars without any subpulse modulation are probably rare. The number of pulsars that are known to show the drifting phenomenon is significantly expanded by 42. Our sample of pulsars is not biased on pulsar type or any particular pulsar characteristics, which allows us to do meaningful statistics on the drifting phenomenon.
As the drifting phenomenon is thought to be exclusively a conal phenomenon, the modulation index of the drifters is expected to be on average higher than the modulation index of the nondrifters. The absence of such a correlation (and possible opposite trend for the coherent drifters) seems to suggest that drifting is not exclusively related to conal emission. Furthermore a number of pulsars classified as core single stars are found to show drifting, which stresses the importance to be unbiased on pulsar type when studying the drifting phenomenon.
Of the 187analyzed pulsars 68are shown to exhibit the drifting phenomenon (of which 30drift coherently or have drift features clearly separated from the alias borders), which means that at least one in three pulsars show drifting. If the observations that had little chance of detecting the drifting phenomenon because of an insufficient S/N are ignored, it is shown that at least some 55% of the pulsars drift. This implies that the physical conditions required for the drifting mechanism to work cannot be very different than the required physical conditions for the emission mechanism of radio pulsars, which is consistent with the absence of a strong correlation between the drifting phenomenon and the magnetic field strength. It could well be that the drifting phenomenon is an intrinsic property of the emission mechanism, although drifting could in some cases be very difficult or even impossible to detect.
The set of modulation indices of our sample of pulsars is not shown to be inconsistent with four complexity parameters as derived for different emission models. Therefore none of the models can be ruled out based on the present observations. Other correlations are found which should be explained by emission models. The population of pulsars that show the drifting phenomenon are on average older than the population of pulsars that do not show drifting and it seems that drifting is more coherent for older pulsars.
Although significant correlations between P3 and the pulsar age,
the magnetic field strength and the pulse period have been reported
previously, we find no such correlations in our enlarged sample. In a
sparking gap model one would expect that the subpulses drift because
of an
![]() drift, which depends on both the
pulse period and its derivative.
The absence of a correlation between P3 and any physical pulsar
parameter is difficult to explain in such a model, unless many pulsars
in our sample are aliased or if P2 is highly variable from
pulsar to pulsar.
drift, which depends on both the
pulse period and its derivative.
The absence of a correlation between P3 and any physical pulsar
parameter is difficult to explain in such a model, unless many pulsars
in our sample are aliased or if P2 is highly variable from
pulsar to pulsar.
No significant correlation is found between the modulation index and the pulsar age. This seems to suggest that a high pulsar age and a low modulation index are two independent factors for pulsars that affect the likelihood of them exhibiting coherently drifting subpulses. The evolutionary trend found seems to suggest that the mechanism that generates the drifting subpulses gets more and more stable as the pulsar ages, which could be because the magnetic axis and the rotation axis becomes more aligned for older pulsars.
The presence of subpulse phase steps results in a minimum in the longitude resolved modulation index. If subpulse phase steps are exclusively (or at least more likely) to occur in pulsars with coherently drifting subpulses, the modulation index of coherent drifters is expected to be on average lower. This is indeed the trend the we observe. It is argued by Edwards et al. (2003) that the local reduction of the modulation index accompanied by a rapid swing in the phase angle are the result of interference between two superposed drifting subpulse signals that are out of phase. It is not unlikely that interference can only occur if the drifting is coherent. Many pulsars are shown to have a modulation index which is significantly lower than what is expected for a purely sinusoidal subpulse signal. This implies the presence of a non-varying component in the pulsar signal, which could be caused by superposed out of phase subpulse signals.
Another possible scenario to explain the trend is that coherent drifting indicates that the electrodynamical conditions in the sparking gap are stable, which could cause the subpulses to have more equal intensities. Another explanation for this trend would be that refraction in the magnetosphere is stronger for pulsars that do not show the drifting phenomenon coherently. In that scenario the organized drifting subpulses are refracted in the magnetosphere, causing the coherent drifting to be distorted. Furthermore it is expected that refraction would cause the subpulses to appear more disordered in the pulse window and that the intensity distribution of the subpulses becomes broadened because of lensing and possible focusing of the radio emission.
Acknowledgements
The authors are grateful for the comments of the referee of this manuscript, which have led to many improvements in this paper. We are also thankful for the valuable comments and suggestions of Geoff Wright and Joanna Rankin and we would like to thank the staff of the WSRT for their support with scheduling and assisting with the observations. The Westerbork Synthesis Radio Telescope is operated by the ASTRON (Netherlands Foundation for Research in Astronomy) with support from the Netherlands Foundation for Scientific Research NWO.
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...270}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a10.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg581.gif) |
Figure A.1: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...270}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a20.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg582.gif) |
Figure A.2: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...270}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a30.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg583.gif) |
Figure A.3: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...270}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a40.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg584.gif) |
Figure A.4: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...270}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a50.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg585.gif) |
Figure A.5: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...270}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a60.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg586.gif) |
Figure A.6: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...270}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a70.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg587.gif) |
Figure A.7: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...270}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a80.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg588.gif) |
Figure A.8: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...270}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a90.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg589.gif) |
Figure A.9: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a100.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg590.gif) |
Figure A.10: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a110.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg591.gif) |
Figure A.11: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a120.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg592.gif) |
Figure A.12: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a130.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg593.gif) |
Figure A.13: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a140.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg594.gif) |
Figure A.14: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a150.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg595.gif) |
Figure A.15: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...x{270}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a156.ps}}}
\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg596.gif) |
Figure A.16: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS is the 2DFSs plotted. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}
\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a161.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg597.gif) |
Figure A.17: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS are two 2DFSs plotted of different pulse longitude ranges. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a166.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg598.gif) |
Figure A.18: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS are two 2DFSs plotted of different pulse longitude ranges. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a171.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg599.gif) |
Figure A.19: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS are two 2DFSs plotted of different pulse longitude ranges. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a176.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg600.gif) |
Figure A.20: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS are two 2DFSs plotted of different pulse longitude ranges. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a181.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg601.gif) |
Figure A.21: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS are two 2DFSs plotted of different pulse longitude ranges. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a186.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg602.gif) |
Figure A.22: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS are two 2DFSs plotted of different pulse longitude ranges. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
![\begin{figure}\mbox{\rotatebox{270}{\resizebox{12cm}{!}{\includegraphics[angle=0...
...70}{\resizebox{12cm}{!}{\includegraphics[angle=0]{3088a191.ps}}} }\end{figure}](/articles/aa/full/2006/01/aa3088-05/Timg603.gif) |
Figure A.23: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS are two 2DFSs plotted of different pulse longitude ranges. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |
| |
Figure A.24: The integrated pulse profile (solid line) and the modulation index (solid points) are shown in the top plot, which is aligned with the LRFS. Below the LRFS are two 2DFSs plotted of different pulse longitude ranges. The integrated power of the spectra are shown the side- and bottom-panels of the spectra. See the main text and Fig. 1 for further details about the plots. |