A&A 444, 505-519 (2005)
DOI: 10.1051/0004-6361:20052896
S. Orlando1 - G. Peres2 - F. Reale2 - F. Bocchino1 - R. Rosner3,4 - T. Plewa3,4 - A. Siegel3,4
1 - INAF - Osservatorio Astronomico di Palermo "G.S.
Vaiana'', Piazza del Parlamento 1, 90134 Palermo, Italy
2 -
Dip. di Scienze Fisiche & Astronomiche, Univ. di
Palermo, Piazza del Parlamento 1, 90134 Palermo,
Italy
3 -
Dept. of Astronomy and Astrophysics,
University of Chicago,
5640 S. Ellis Avenue, Chicago, IL 60637, USA
4 -
Center for Astrophysical Thermonuclear Flashes,
University of Chicago,
5640 S. Ellis Avenue, Chicago, IL 60637, USA
Received 17 February 2005 / Accepted 29 July 2005
Abstract
We model the hydrodynamic interaction of a shock wave of
an evolved supernova remnant with a small interstellar gas cloud
like the ones observed in the Cygnus loop and in the Vela SNR. We
investigate the interplay between radiative cooling and thermal
conduction during cloud evolution and their effect on the mass and
energy exchange between the cloud and the surrounding medium. Through
the study of two cases characterized by different Mach numbers of
the primary shock (
![]() and 50, corresponding to a post-shock
temperature
and 50, corresponding to a post-shock
temperature
![]() K and
K and ![]()
![]() K, respectively), we explore two very different physical regimes:
for
K, respectively), we explore two very different physical regimes:
for
![]() ,
the radiative losses dominate the evolution of the
shocked cloud which fragments into cold, dense, and compact filaments
surrounded by a hot corona which is ablated by the thermal conduction;
instead, for
,
the radiative losses dominate the evolution of the
shocked cloud which fragments into cold, dense, and compact filaments
surrounded by a hot corona which is ablated by the thermal conduction;
instead, for
![]() ,
the thermal conduction dominates the
evolution of the shocked cloud, which evaporates in a few dynamical
time-scales. In both cases we find that the thermal conduction is
very effective in suppressing the hydrodynamic instabilities that
would develop at the cloud boundaries.
,
the thermal conduction dominates the
evolution of the shocked cloud, which evaporates in a few dynamical
time-scales. In both cases we find that the thermal conduction is
very effective in suppressing the hydrodynamic instabilities that
would develop at the cloud boundaries.
Key words: hydrodynamics - shock waves - ISM: clouds - ISM: supernova remnants
One of the primary reasons for the great morphological complexity of the shells of supernova remnants (SNRs) is the inhomogeneity of the interstellar medium (ISM) where they propagate (e.g. Hester 1987). Optical, UV and X-ray observations of SNRs show that the SN-generated shock waves travel through and interact with the denser clouds they encounter (e.g. Bocchino et al. 2000; Levenson et al. 2002; Patnaude et al. 2002; Nichols & Slavin 2004; Levenson & Graham 2005; Miceli et al. 2005), generating transmitted and reflected (bow) shocks, which, in turn, interact with each other (e.g. McKee & Cowie 1975; White & Long 1991; Poludnenko et al. 2002). Knowledge of how the SNR shocks interact with the inhomogeneous ISM and interstellar clouds is very important for the study of the interstellar gas dynamics itself, for our understanding of the emission of this process, and for the detailed analysis of the mass distribution of the plasma in the Galaxy, energy exchanges, and the chemical composition and evolution of the ISM.
The overall evolution of the shock-cloud interaction has been studied analytically by a number of authors (e.g. McKee & Cowie 1975; Heathcote & Brand 1983; McKee et al. 1987). However, the complex nature of the phenomenon, involving the non-linear interaction among thermally conducting supersonic flows, radiative losses, magnetic fields, non-equilibrium ionization effects, etc., and the comprehension of the details of the mass and energy exchange between the cloud and the inter-cloud medium have required numerical simulations.
The first numerical studies of this problem showed that hydrodynamic
Kelvin-Helmholtz (KH) and Rayleigh-Taylor (RT) instabilities develop at
the interface between the cloud and the post-shock ambient medium due
to the shear motions around the cloud and to the density gradients at
the cloud boundary (Woodward 1976;
Bedogni & Woodward 1990). Klein et al. (1994) (hereafter
KMC94) studied extensively the interaction of a strong shock with a
single, non-radiative cloud with 2-D calculations. They explored the
parameter space defined by the Mach number ![]() and the initial
density contrast cloud/surrounding medium
and the initial
density contrast cloud/surrounding medium ![]() ,
and showed that the
cloud is ultimately destroyed within a few dynamical time-scales by the
hydrodynamic instabilities (see also Poludnenko et al. 2002 for
the interaction of a strong shock with a system of clouds).
,
and showed that the
cloud is ultimately destroyed within a few dynamical time-scales by the
hydrodynamic instabilities (see also Poludnenko et al. 2002 for
the interaction of a strong shock with a system of clouds).
The first 3-D calculations of the shock-cloud interaction showed a richer structure of the hydrodynamic instabilities (Stone & Norman 1992; Xu & Stone 1995). The 3-D calculations do not invalidate any of the conclusions drawn from the 2-D calculations; however, they showed that the cloud breaks in all directions and that the turbulent mixing of the cloud and the interstellar medium is complete, with the formation of macroscopic vortex filaments. The details of the cloud mass mixing, therefore, may be different if computed in 2- or 3-D.
The interaction of the shock with a radiative cloud has been only
recently analyzed in detail (Mellema et al. 2002;
Fragile et al. 2004). 2-D calculations have shown large
differences from the non-radiative case: the compressed radiating cloud
breaks up into numerous dense and cold fragments. The cooling processes
can be highly efficient already for moderate cloud densities (
![]() 1 cm-3) and shock Mach number (
1 cm-3) and shock Mach number (
![]() 20). 2-D calculations of the
interaction between magnetized shocks and radiative clouds
(Fragile et al. 2005) showed that the magnetic field may
increase the efficiency of the radiative cooling, acting as a
confinement mechanism ultimately driven by the interstellar flow and
local field stretching.
20). 2-D calculations of the
interaction between magnetized shocks and radiative clouds
(Fragile et al. 2005) showed that the magnetic field may
increase the efficiency of the radiative cooling, acting as a
confinement mechanism ultimately driven by the interstellar flow and
local field stretching.
The interaction of a strong shock with a thermally conducting and radiative cloud has been less studied so far. Vieser & Hensler (2000) and Hensler & Vieser (2002) investigated the effect of the heat conduction in the context, different from that of this paper, of a giant self-gravitating cloud moving subsonically (i.e. in the absence of shock waves) through an hot diluted medium; they showed that the thermal conduction suppresses the hydrodynamic instabilities leading to cloud disruption, so that the cloud is stabilized and survives. However, a detailed and systematic analysis of the competition of the radiative losses and the thermal conduction in the evolution and in the energy exchanges of the shock-cloud system is still missing. Nevertheless, this competition may be important in determining both the local and the global dynamics of the shocked cloud. In particular, the radiative losses may induce thermal instabilities, and lead to the cloud fragmentation in cold and dense cloudlets (Mellema et al. 2002; Fragile et al. 2004). The thermal conduction may instead act to save the cloud (KMC94) and, therefore, to reduce the mixing of cloud material with the ambient medium, through the suppression of the hydrodynamic instabilities. In addition, the thermal conduction leads to the heating and evaporation of the shocked cloud, reducing the radiative cooling.
In spite of the extensive literature on this subject, several aspects of the shock-cloud interaction remain unexplored: how do the effects of radiative losses and thermal conduction combine on the interaction and subsequent evolution of unmagnetized shocked clouds? How and under which physical conditions can the magnetic fields suppress the thermal conduction during the cloud evolution? To what extent do the complex dynamics of the shock-cloud interaction induce deviations from the equilibrium of ionization of the cloud medium? What observational features (e.g. morphological, spectral) in the optical, UV, and X-ray bands are tracers of the physical processes at work and can, thus, provide accurate diagnostics of shocked cloud plasma?
To answer these questions, we have started a new project devoted to study the shock-cloud interaction through detailed and extensive numerical modeling. The project aims at overcoming some of the limitations found in the previous analogous studies and crucial for the accurate interpretation of the high resolution multi-wavelength observations of middle-aged SNR shell available with the last-generation instruments. In the present paper, the detailed numerical study focuses specifically on the interplay between the radiative losses and the thermal conduction, the latter including both the classical and the free-streaming regime (Cowie & McKee 1977). Our approach is to consider two examples of shock-cloud interaction, with different shock Mach numbers, as test cases in which one or the other of the two processes plays a dominant role. For each of these cases, we identify the effects of the thermal conduction and of the radiative losses on the dynamics, by comparing models calculated with these physical processes turned "on'' or "off''. We perform 2-D hydrodynamic simulations and also 3-D simulations, where necessary.
In future papers, we plan to analyze the deviations from the equilibrium of ionization during the shock-cloud dynamics and the observable properties of the shocked clouds, including spectra synthesized at different evolutionary phases.
The paper is organized as follows: Sect. 2 describes the numerical setup and the characteristic physical parameters of the problem; in Sect. 3 we investigate the role played by the thermal conduction and by the radiative losses in the dynamics of the shocked cloud and how such a role changes under different physical conditions; in Sect. 4 we summarize the results and draw our conclusions.
We study the impact of a shock wave on an isolated unmagnetized
spherical cloud. The cloud is assumed to be small compared to the
curvature radius of the shock. These assumptions and the adopted
parameters of the shock wave are characteristic of a SNR forward shock
overruning a small interstellar cloud![]() . We assume that the fluid is fully ionized, and may be
regarded as a perfect gas (with a ratio of specific heats
. We assume that the fluid is fully ionized, and may be
regarded as a perfect gas (with a ratio of specific heats
![]() ).
).
We consider a numerical model based on the solution of the Euler
equations, taking into account the effects of the radiative losses from
an optically thin plasma and of the thermal conduction (including the
effects of heat flux saturation):
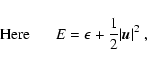
is the total gas energy (internal energy, ![]() ,
and kinetic energy),
t is the time,
,
and kinetic energy),
t is the time,
![]() is the mass density,
is the mass density,
![]() is the mean atomic mass (assuming cosmic abundances),
is the mean atomic mass (assuming cosmic abundances), ![]() is the
mass of the hydrogen atom,
is the
mass of the hydrogen atom, ![]() is the hydrogen number density,
is the hydrogen number density,
![]() is the electron number density, u is the gas velocity,
T is the temperature, q is the conductive flux, and
is the electron number density, u is the gas velocity,
T is the temperature, q is the conductive flux, and
![]() represents the radiative losses per unit emission measure
represents the radiative losses per unit emission measure![]() (e.g. Raymond & Smith 1977; Mewe et al. 1985;
Kaastra & Mewe 2000). We use the ideal gas law,
(e.g. Raymond & Smith 1977; Mewe et al. 1985;
Kaastra & Mewe 2000). We use the ideal gas law,
![]() .
.
To allow for a smooth transition between the classical and saturated
conduction regime, we followed Dalton & Balbus (1993) and defined
the conductive flux as
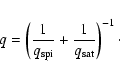 |
(2) |
Here
![]() represents the classical conductive flux
(Spitzer 1962)
represents the classical conductive flux
(Spitzer 1962)
where the thermal conductivity is
![]() erg s-1 K-1 cm-1. The saturated flux,
erg s-1 K-1 cm-1. The saturated flux,
![]() ,
is (Cowie & McKee 1977)
,
is (Cowie & McKee 1977)
where ![]() is the isothermal sound speed, and
is the isothermal sound speed, and ![]() is a number
of the order of unity. We set
is a number
of the order of unity. We set
![]() according to the values
suggested for a fully ionized cosmic gas:
according to the values
suggested for a fully ionized cosmic gas:
![]() (Giuliani 1984; Borkowski et al. 1989;
Fadeyev et al. 2002, and references therein); we assumed
that electron and ion temperatures are equal
(Giuliani 1984; Borkowski et al. 1989;
Fadeyev et al. 2002, and references therein); we assumed
that electron and ion temperatures are equal![]() .
.
In order to trace the motion of the cloud material, we consider a
passive tracer associated with the cloud. To this end, we add the
equation
to the standard set of hydrodynamic equations.
![]() is the mass
fraction of the cloud inside the computational cell. The cloud material
is initialized with
is the mass
fraction of the cloud inside the computational cell. The cloud material
is initialized with
![]() ,
while
,
while
![]() in the
ambient medium. During the shock-cloud evolution, the cloud and the
ambient medium mix together, leading to regions with
in the
ambient medium. During the shock-cloud evolution, the cloud and the
ambient medium mix together, leading to regions with
![]() .
At any time t the density of cloud material in a fluid cell is
given by
.
At any time t the density of cloud material in a fluid cell is
given by
![]() .
.
The calculations described in this paper were performed using the FLASH code (Fryxell et al. 2000). FLASH is an adaptive mesh refinement multiphysics code. For the present application, the code has been extended by additional computational modules to handle the radiative losses and the thermal conduction in the formulation of Spitzer (1962). The hydrodynamic equations are solved using the FLASH implementation of the PPM algorithm (Colella & Woodward 1984). The thermal conduction is treated using an operator-splitting method with respect to the hydrodynamic evolution: the heat flux is calculated with a finite difference explicit formula and then added to the energy fluxes generated by PPM (see Appendix A for more details and for the tests to validate the algorithm). The code was designed to make efficient use of massively parallel computers using the message-passing interface (MPI) for interprocessor communications.
The initial configuration of our numerical model is schematically shown
in Fig. 1. It consists of an unperturbed ambient medium with a
spherical cloud in pressure equilibrium with its surrounding; a planar
shock moves toward the cloud and starts to interact with it.
The unperturbed medium is assumed to be isothermal (
![]() K) and homogeneous with hydrogen number density
K) and homogeneous with hydrogen number density
![]() cm-3 (see Table 1). The cloud has radius
cm-3 (see Table 1). The cloud has radius
![]() pc and density
pc and density
![]() (
(
![]() cm-3 for density contrast
cm-3 for density contrast ![]() ); its temperature is
determined by pressure balance across the cloud boundary.
); its temperature is
determined by pressure balance across the cloud boundary.
| Temperature | Density | Velocity | |
| ISM | 104 K | 0.1 cm-3 | 0.0 |
| Cloud | 103 K | 1.0 cm-3 | 0.0 |
| Post-shock medium: | |||
| - Mach 30 shock |
|
0.4 cm-3 | 250 km s-1 |
| - Mach 50 shock |
|
0.4 cm-3 | 430 km s-1 |
The post-shock initial conditions of the ambient medium are given by
the strong shock limit (Zel'dovich & Raizer 1966). The post-shock density and
velocity are, respectively,
Here
![]() is the shock speed,
is the shock speed, ![]() is the shock
Mach number and
is the shock
Mach number and
![]() is the sound speed in the interstellar
medium. The post-shock ion temperature is
is the sound speed in the interstellar
medium. The post-shock ion temperature is
where ![]() is the Boltzmann constant. For the
is the Boltzmann constant. For the
![]() case
(shock speed
case
(shock speed
![]() km s-1),
km s-1),
![]() km s-1 and
km s-1 and
![]() K; for the
K; for the
![]() case (shock speed
case (shock speed
![]() km s-1),
km s-1),
![]() km s-1 and
km s-1 and
![]() K.
K.
In the 3-D simulations, we solve the hydrodynamic equations in
one quadrant of the whole spatial domain (indicated by a dark patch
covering the top portion of the volume shown in Fig. 1). The
coordinate system is oriented in such a way that the shock front lies
in the (x,y) plane and moves in z-direction which points through
the cloud center. The cloud is initially centered at
(x,y,z) = (0,0,0)and the computational domain extends ![]() 2 pc in both the x and ydirections, and
2 pc in both the x and ydirections, and ![]() 6 pc in the z direction. At
6 pc in the z direction. At
![]() the variables have been set to the post-shock values while we allowed for
free outflow at
the variables have been set to the post-shock values while we allowed for
free outflow at
![]() and along
and along
![]() and
and
![]() .
Both planes cutting through the center of the cloud along
.
Both planes cutting through the center of the cloud along
![]() and
and
![]() have been treated as impenetrable walls.
Our assumption of four-fold symmetry in 3-D simulations, aimed
at reducing computational cost, leads to a long-wavelength cut-off of
the perturbation spectrum experienced by the model object. For example,
long-wavelength modes participating in the development of instabilities
in the plane parallel to the shock front are not represented in our
model. However, we expect that such particular instabilities are not
likely to dominate the evolution of the system essentially due to lack of
asymmetry (a spherically symmetric cloud, planar shock-wave) and relatively
weak waves developing in that plane.
have been treated as impenetrable walls.
Our assumption of four-fold symmetry in 3-D simulations, aimed
at reducing computational cost, leads to a long-wavelength cut-off of
the perturbation spectrum experienced by the model object. For example,
long-wavelength modes participating in the development of instabilities
in the plane parallel to the shock front are not represented in our
model. However, we expect that such particular instabilities are not
likely to dominate the evolution of the system essentially due to lack of
asymmetry (a spherically symmetric cloud, planar shock-wave) and relatively
weak waves developing in that plane.
Our 2-D models considered a slab corresponding to the (x,z) plane of
the 3-D simulations. The 2-D domain has been extended to ![]() pc because in some 2-D simulations the cloud expands faster. We use
reflecting boundary conditions at
pc because in some 2-D simulations the cloud expands faster. We use
reflecting boundary conditions at
![]() ,
consistent with the
adopted symmetry; a constant inflow is imposed at the lower boundary
with free outflow elsewhere.
,
consistent with the
adopted symmetry; a constant inflow is imposed at the lower boundary
with free outflow elsewhere.
At the coarsest resolution, the adaptive mesh algorithm used in the
FLASH code uniformly covers the 3-D computational domain with a mesh
of
![]() blocks (
blocks (![]() blocks in the 2-D cases). All
the blocks used in the computation have 83 cells (82 in the 2-D
cases). We allow for 5 levels of refinement, with resolution increasing
twice at each refinement level. The default refinement criterion adopted
follows the changes in density and temperature (Löhner 1987). This
grid configuration yields an effective resolution of
blocks in the 2-D cases). All
the blocks used in the computation have 83 cells (82 in the 2-D
cases). We allow for 5 levels of refinement, with resolution increasing
twice at each refinement level. The default refinement criterion adopted
follows the changes in density and temperature (Löhner 1987). This
grid configuration yields an effective resolution of ![]()
![]() pc at the finest level corresponding to
pc at the finest level corresponding to ![]() 132 zones
per cloud radius.
132 zones
per cloud radius.
A number of useful dynamical time-scales can be calculated analytically in order to estimate the relative importance of various physical effects. In our discussion we focus on the cloud crushing time, time-scales characteristic of hydrodynamic instabilities, thermal conduction and radiative cooling.
The cloud-crushing time (KMC94), i.e. the characteristic time for the
transmitted shock to cross the cloud, is generally defined as
Here
![]() is the velocity of the shock
transmitted into the cloud (McKee & Cowie 1975, KMC94) and
is the velocity of the shock
transmitted into the cloud (McKee & Cowie 1975, KMC94) and
![]() is a parameter of the order of 1 (see Appendix B for a
detailed evaluation of
is a parameter of the order of 1 (see Appendix B for a
detailed evaluation of ![]() ). For the conditions considered here and
). For the conditions considered here and
![]() ,
the cloud crushing time varies between
,
the cloud crushing time varies between
![]() yr for
yr for
![]() shock and
shock and
![]() yr for
yr for
![]() shock.
shock.
The cloud can be subject to both KH and RT instabilities. The KH and RT
growth times can be expressed in terms of
![]() (KMC94):
(KMC94):
 |
(9) |
Here
![]() is the wave-number of the perturbation. KMC94
showed that the most disruptive wavelengths are those corresponding to
is the wave-number of the perturbation. KMC94
showed that the most disruptive wavelengths are those corresponding to
![]() .
If not suppressed, these instabilities
are responsible for cloud break-up on time-scales comparable with
.
If not suppressed, these instabilities
are responsible for cloud break-up on time-scales comparable with
![]() ,
eventually leading to efficient mixing of the cloud
material with its surrounding and to the final cloud destruction (see
also Xu & Stone 1995; Poludnenko et al. 2002).
,
eventually leading to efficient mixing of the cloud
material with its surrounding and to the final cloud destruction (see
also Xu & Stone 1995; Poludnenko et al. 2002).
One of the processes capable of delaying or suppressing destructive
action of hydrodynamic instabilities is thermal conduction. Thermal
conduction smoothes the temperature and density gradients and, therefore,
lowers the efficiency of the KH and RT instabilities. The characteristic
time-scale for the conduction is
where l is a characteristic length of temperature variation. If
![]() ,
thermal gradients on scales below
l are diffused on time-scales shorter than
,
thermal gradients on scales below
l are diffused on time-scales shorter than
![]() .
.
The radiative cooling may also be able to slow down the growth of
hydrodynamic instabilities. The cooling leads to the formation of
thin dense sheets in the shocked cloud regions (e.g.
Falle 1975; Falle 1981). This is
the opposite behavior to the diffusive action of the thermal conduction
and of the KH and RT instabilities. The cooling time for the shocked
gas is
where, for temperatures characteristic of our models (
![]() K), we have approximated the cooling function as
K), we have approximated the cooling function as
![]() erg s-1 cm3(Raymond et al. 1976; Raymond & Smith 1977).
erg s-1 cm3(Raymond et al. 1976; Raymond & Smith 1977).
The thermal conduction and the radiative losses are competing effects:
the former leads to the heating and evaporation of the cloud, while the
latter to the cooling and condensation of the cloud fragments. The
radiative losses dominate over the effects of the thermal conduction,
whenever the cooling time-scale is shorter than the conduction
time-scale:
Note that by setting instead the equality sign into Eq. (12), we derive the Field length scale (Begelman & McKee 1990), i.e. the maximum scale on which the conduction dominates the radiative cooling.
Figure 2 shows the relationship between the different
time-scales![]() as
a function of the density contrast
as
a function of the density contrast ![]() and of the shock Mach number
and of the shock Mach number
![]() ,
for a cloud of 1 pc radius. For density contrasts above the
dotted line, structures of 1 pc (or below) are subject to the
thermal conduction over a time-scale shorter than
,
for a cloud of 1 pc radius. For density contrasts above the
dotted line, structures of 1 pc (or below) are subject to the
thermal conduction over a time-scale shorter than
![]() ;
for density contrasts above the dashed line, the shocked cloud
material is subject to the radiative losses over a time-scale shorter
than
;
for density contrasts above the dashed line, the shocked cloud
material is subject to the radiative losses over a time-scale shorter
than
![]() ;
the solid line divides the (left) region
dominated by the radiative cooling from the (right) region dominated by
the thermal conduction. In Appendix B, we derive the cooling
time-scale behind the shock transmitted into the cloud,
;
the solid line divides the (left) region
dominated by the radiative cooling from the (right) region dominated by
the thermal conduction. In Appendix B, we derive the cooling
time-scale behind the shock transmitted into the cloud,
![]() ,
and the thermal conduction time-scale in the shocked
ambient medium,
,
and the thermal conduction time-scale in the shocked
ambient medium,
![]() ,
expressed in terms of
,
expressed in terms of
![]() and
and ![]() .
.
Figure 2 shows that, in a
![]() case,
case,
![]() and,
therefore, we expect that the shock transmitted into the cloud is
strongly radiative and that its evolution is dominated by the energy
losses on time-scales shorter than the cloud crushing time. On the other
hand, the thermal conduction dominates over the radiative losses in a
and,
therefore, we expect that the shock transmitted into the cloud is
strongly radiative and that its evolution is dominated by the energy
losses on time-scales shorter than the cloud crushing time. On the other
hand, the thermal conduction dominates over the radiative losses in a
![]() case; the cloud is expected to evaporate on a time-scale
comparable with
case; the cloud is expected to evaporate on a time-scale
comparable with
![]() (since this case is located close to
the dotted line;
(since this case is located close to
the dotted line;
![]() ).
).
Ferrara & Shchekinov (1993) pointed out that the conductive fronts
do not induce relevant dynamical effects if
![]() is much
shorter than the dynamical response time of the system, which can be
approximated as the sound crossing time of the cloud:
is much
shorter than the dynamical response time of the system, which can be
approximated as the sound crossing time of the cloud:
![]() .
From Eq. (10), it is easy to show that
.
From Eq. (10), it is easy to show that
 |
(13) |
Considering the hydrogen number density of the shocked cloud
![]() cm-3,
cm-3,
![]() pc, and a length scale l = 1 pc, the
conductive time-scale is shorter than the dynamical time-scale for
pc, and a length scale l = 1 pc, the
conductive time-scale is shorter than the dynamical time-scale for
![]() K. In the cases considered here, however, the temperatures
are lower and the evolution of conductive fronts is expected to influence
gas dynamics. In the saturated regime, the thermal conduction time scale
becomes even longer, strengthening the above argument.
K. In the cases considered here, however, the temperatures
are lower and the evolution of conductive fronts is expected to influence
gas dynamics. In the saturated regime, the thermal conduction time scale
becomes even longer, strengthening the above argument.
The saturated heat flux (Eq. (4)) provides a lower limit on the
conduction time-scale:
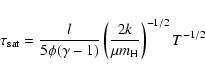 |
(14) |
and an upper limit on the propagation velocity of the conduction front:
In the case of strong shocks subject to heat transfer, a thermal precursor
develops if the propagation velocity of the conduction front is larger
than the shock speed w (Zel'dovich & Raizer 1966). By combining Eqs. (6),
(7), and (15), the condition for
![]() reads
reads
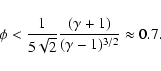 |
(16) |
Since we use
![]() ,
typical of a fully ionized cosmic gas, in all
the simulations (see Sect. 2.1),
,
typical of a fully ionized cosmic gas, in all
the simulations (see Sect. 2.1),
![]() and no
thermal precursor develops. Our choice turns out to be consistent with the
fact that no precursor is observed in young and middle aged SNRs.
and no
thermal precursor develops. Our choice turns out to be consistent with the
fact that no precursor is observed in young and middle aged SNRs.
We consider two examples of shock-cloud interaction with different
Mach number (
![]() and
and
![]() ), to analyze the dynamics
when either the heat conduction or the radiation plays a dominant role.
The effects of the thermal conduction and of the radiation in the
shock-cloud interaction are also investigated by comparing these models
with other models without conduction and radiation.
), to analyze the dynamics
when either the heat conduction or the radiation plays a dominant role.
The effects of the thermal conduction and of the radiation in the
shock-cloud interaction are also investigated by comparing these models
with other models without conduction and radiation.
The models neglecting both thermal conduction and radiation have been computed in a 3-D Cartesian coordinate system (x,y,z), in order to describe well the hydrodynamic instabilities at the boundaries of the shocked cloud (e.g. Xu & Stone 1995). On the other hand, the heat conduction is known to damp rapidly the hydrodynamic instabilities; therefore, a 2-D cylindrical coordinate system (r,z)is enough to describe the shock-cloud interaction including the thermal conduction: indeed we anticipate that, in the latter case, there are no complex instabilities to follow.
KMC94 showed that the purely hydrodynamic shock-cloud problem (without
thermal conduction and radiation) is independent of the Mach number of
the shock (the so-called Mach-scaling) and invariant under the scaling
where t is the time, ![]() the Mach number, u the gas velocity,
and T the temperature, with distance, density, and pre-shock pressure
left unchanged, and provided that
the Mach number, u the gas velocity,
and T the temperature, with distance, density, and pre-shock pressure
left unchanged, and provided that
![]() .
Therefore, only one
simulation without thermal conduction and radiation is required for our
purposes and the results are representative of all the cases examined,
provided that
.
Therefore, only one
simulation without thermal conduction and radiation is required for our
purposes and the results are representative of all the cases examined,
provided that
![]() .
.
We run two 3-D simulations with different spatial resolution to check if the adopted resolution is sufficient to capture the basic cloud evolution over the time interval considered. Both simulations have a spatial resolution higher than previously obtained in 3-D in the shock-cloud problems: they have more than 100 zones per cloud radius, following the prediction of KMC94 and Mac Low et al. (1994) that this is the minimum spatial resolution for adequate description of all physical quantities. A summary of all the simulations in this paper is given in Table 2.
| Run | Geometry | Res.a | therm. cond. | ||
| & rad. losses | |||||
| HY1 | 3-D cart. (x,y,z) | 105 | 50 | 10 | no |
| HY2 | 3-D cart. (x,y,z) | 132 | 50 | 10 | no |
| HTR30 | 2-D cyl. (r,z) | 132 | 30 | 10 | yes |
| HTR50 | 2-D cyl. (r,z) | 132 | 50 | 10 | yes |
We first briefly describe the relevant aspects of the shock-cloud interaction without thermal conduction and radiative losses. We then investigate the effects of both physical processes on the dynamics by comparing the above models with other models that take full account of conduction and radiation.
![\begin{figure}
\par\includegraphics[width=15.4cm,clip]{fig3_aa2896-05.eps} %
\end{figure}](/articles/aa/full/2005/47/aa2896-05/Timg107.gif) |
Figure 3:
3-D visualizations of the mass density evolution during the
shock-cloud interaction at selected times in units of
|
We simulate the impact of the Mach 50 shock on the cloud: as discussed
above, the case of the
![]() shock can be derived, through simple
scaling, from the
shock can be derived, through simple
scaling, from the
![]() case and, therefore, no specific
simulation is required.
case and, therefore, no specific
simulation is required.
The evolution of the
![]() shock-cloud interaction is illustrated
for the highest resolution simulation (run HY2 with a resolution of
shock-cloud interaction is illustrated
for the highest resolution simulation (run HY2 with a resolution of
![]() 132 zones per cloud radius) in the 3-D visualizations of Fig.
3. As in previous 2-D and 3-D studies (KMC94,
Xu & Stone 1995, and references therein), we divide the
early shock-cloud interaction into four stages:
132 zones per cloud radius) in the 3-D visualizations of Fig.
3. As in previous 2-D and 3-D studies (KMC94,
Xu & Stone 1995, and references therein), we divide the
early shock-cloud interaction into four stages:
Figures 4 and 5 show the evolution of the mass density and of the temperature, respectively, in a 2-D section of the (x,z) plane in the simulations HY2 (left half panels) and HTR50 (right half panels).
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{fig5_aa2896-05.eps} \end{figure}](/articles/aa/full/2005/47/aa2896-05/Timg116.gif) |
Figure 5: As in Fig. 4 for the plasma temperature distribution (MK). |
During the first two stages (
![]() ), the whole front
face of the cloud, overrun by the shock and prone to hydrodynamic
instabilities, is strongly diffused and the shocked cloud material is
quickly heated. The cloud stripping, present in HY2, is masked by the
evaporation process as well. A transition region from the inner part of
the cloud to the ambient medium gradually grows during the evolution,
after the expansion of the cloud. In such a region, the density and
temperature gradients vary very smoothly in the radial direction. As we
will discuss below in more detail, the reflected shock in HTR50 is
slightly stronger and cooler than in HY2 as some fraction of its
thermal energy is conducted into the evolving cloud boundary and some
fraction of the cloud material is mixed in the surrounding medium.
During the third stage (
), the whole front
face of the cloud, overrun by the shock and prone to hydrodynamic
instabilities, is strongly diffused and the shocked cloud material is
quickly heated. The cloud stripping, present in HY2, is masked by the
evaporation process as well. A transition region from the inner part of
the cloud to the ambient medium gradually grows during the evolution,
after the expansion of the cloud. In such a region, the density and
temperature gradients vary very smoothly in the radial direction. As we
will discuss below in more detail, the reflected shock in HTR50 is
slightly stronger and cooler than in HY2 as some fraction of its
thermal energy is conducted into the evolving cloud boundary and some
fraction of the cloud material is mixed in the surrounding medium.
During the third stage (
![]() ), the
cloud is progressively heated up to the temperature of the surrounding
medium. After
), the
cloud is progressively heated up to the temperature of the surrounding
medium. After ![]()
![]() the cloud has density contrast
the cloud has density contrast
![]() with respect to the surrounding medium.
Note that, although the density and the temperature of the cloud are
indistinguishable from those of the surrounding medium at the end of
the simulation, the cloud material is not fractioned in small cloudlets
as in HY2 (see the contour enclosing the cloud material).
with respect to the surrounding medium.
Note that, although the density and the temperature of the cloud are
indistinguishable from those of the surrounding medium at the end of
the simulation, the cloud material is not fractioned in small cloudlets
as in HY2 (see the contour enclosing the cloud material).
Figures 4 and 5 also show that the thermal conduction
influences the propagation speed of the shocks generated during the
evolution: the shock transmitted into the cloud is faster and the
reflected bow shock is slower than those generated in HY2. In addition,
we note that the self-reflected part of the primary shock is slower in
HTR50 than in HY2. These results can be understood looking at
Fig. 6, which show the mass density and temperature profiles
along the symmetry axis, z, in HY2 and HTR50. In HTR50 we see the
progressive heating of the shocked cloud material and its evaporation
in the surrounding medium (see panels at
![]() and
and
![]() ), driven by the thermal conduction. As a result, the
material behind the transmitted shock in HTR50 is at higher temperature
and at lower density than that in HY2.
Since the propagation velocity of a shock depends on the
temperature of the post-shock plasma (see Eqs. (6) and
(7); Zel'dovich & Raizer 1966), the transmitted shock in HTR50 is faster
than that in HY2. On the other hand, the material behind the reflected
shock in HTR50 is cooler than that in HY2 because a fraction of its
thermal energy has been conducted into the cloud, and denser than that
in HY2 because a fraction of the cloud material has evaporated into the
surrounding shocked medium (see Fig. 6). As a consequence, the
reflected shock in HTR50 is slower than that in HY2. Analogous
considerations explain why the self-interacting primary shock in HTR50
is slower than that in HY2.
), driven by the thermal conduction. As a result, the
material behind the transmitted shock in HTR50 is at higher temperature
and at lower density than that in HY2.
Since the propagation velocity of a shock depends on the
temperature of the post-shock plasma (see Eqs. (6) and
(7); Zel'dovich & Raizer 1966), the transmitted shock in HTR50 is faster
than that in HY2. On the other hand, the material behind the reflected
shock in HTR50 is cooler than that in HY2 because a fraction of its
thermal energy has been conducted into the cloud, and denser than that
in HY2 because a fraction of the cloud material has evaporated into the
surrounding shocked medium (see Fig. 6). As a consequence, the
reflected shock in HTR50 is slower than that in HY2. Analogous
considerations explain why the self-interacting primary shock in HTR50
is slower than that in HY2.
We compare the evolution of the shock-cloud interaction derived in simulation HTR30 with that derived in HY2, after scaling the velocity and temperature distributions derived in the latter, according to the transformations shown in Eq. (17). Figures 7 and 8 compare the evolution of the density and temperature distribution, respectively, in these two runs.
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{fig7_aa2896-05.eps} %
\end{figure}](/articles/aa/full/2005/47/aa2896-05/Timg123.gif) |
Figure 7: As Fig. 4 for the Mach 30 case. Note that the velocity field calculated in the run HY2 has been scaled by the factor 3/5, according to the Mach scaling (see Eq. (17)). The velocity arrows scale linearly with respect to the reference velocity shown in the upper left panel and corresponding to 300 km s-1. The contour encloses the cloud material. |
![\begin{figure}
\par\includegraphics[width=15.8cm,clip]{fig8_aa2896-05.eps} %
\end{figure}](/articles/aa/full/2005/47/aa2896-05/Timg124.gif) |
Figure 8: As Fig. 5 for the Mach 30 case. The velocity field and the temperature distribution calculated in the run HY2 have been scaled by the factor 3/5 and (3/5)2, respectively, according to the Mach scaling (see Eq. (17)). |
Just as in the simulation with
![]() ,
during the first two stages
(
,
during the first two stages
(
![]() ), the thermal conduction limits the development
of the dynamical instabilities. On the other hand, for
), the thermal conduction limits the development
of the dynamical instabilities. On the other hand, for
![]() ,
the shocked cloud evolves in a dense and cold structure: the strong
cooling in the post-shock cloud region results in the rapid
accumulation of the cooled material in a thin dense shell
(Falle 1981) as well as in the substantial weakening
of the transmitted shock. The shell forms very quickly (at
,
the shocked cloud evolves in a dense and cold structure: the strong
cooling in the post-shock cloud region results in the rapid
accumulation of the cooled material in a thin dense shell
(Falle 1981) as well as in the substantial weakening
of the transmitted shock. The shell forms very quickly (at
![]() it is already there) in agreement with the cooling
time
it is already there) in agreement with the cooling
time
![]() (see Appendix B). On the other hand, a diluted outer part of the cloud
starts to develop a hot corona surrounding the dense shell and
characterized by particle density
(see Appendix B). On the other hand, a diluted outer part of the cloud
starts to develop a hot corona surrounding the dense shell and
characterized by particle density
![]() cm-3 and
cm-3 and
![]() K. From Eq. (12) and from the above
values of the density and the temperature, we derive that the evolution
of this corona is dominated by the thermal conduction. At
K. From Eq. (12) and from the above
values of the density and the temperature, we derive that the evolution
of this corona is dominated by the thermal conduction. At
![]() ,
the shock propagating in the ISM has enveloped the cloud, focused
behind it, and started to enter from the rear: it forms, therefore, its
own dense shell and a transient ring-like shell configuration forms in
the time interval
,
the shock propagating in the ISM has enveloped the cloud, focused
behind it, and started to enter from the rear: it forms, therefore, its
own dense shell and a transient ring-like shell configuration forms in
the time interval
![]() .
During the
following phases (
.
During the
following phases (
![]() ), the cooling-dominated cloud
material fragments into dense, cold, and compact filaments which
survive until the end of our simulation, whereas the hot corona
gradually evaporates under the effect of the thermal conduction.
The strong cooling leads to cool and dense material accumulating along
the symmetry axis in Figs. 7 and 8. Note that the
details of the plasma cooling to such low temperatures depend, however,
on the cooling function adopted in our computations which is appropriate
to temperatures
), the cooling-dominated cloud
material fragments into dense, cold, and compact filaments which
survive until the end of our simulation, whereas the hot corona
gradually evaporates under the effect of the thermal conduction.
The strong cooling leads to cool and dense material accumulating along
the symmetry axis in Figs. 7 and 8. Note that the
details of the plasma cooling to such low temperatures depend, however,
on the cooling function adopted in our computations which is appropriate
to temperatures
![]() K, and on the numerical resolution
which affect the peak density and hence the cooling efficiency of the gas.
K, and on the numerical resolution
which affect the peak density and hence the cooling efficiency of the gas.
The tracer defined in Eq. (5) and the Eq. (12)
allow us to investigate further the efficiency of the radiative losses.
We first identify zones consisting of the original cloud material by
more than 90%. We then quantify the mass fraction of this material
(
![]() where
where
![]() is the cloud mass at the beginning
of the interaction) dominated by the radiative losses and the mass
fraction dominated by the thermal conduction as a function of time,
applying Eq. (12) in each of those zones (see Fig.
9). We find that the thermal collapse starts at
is the cloud mass at the beginning
of the interaction) dominated by the radiative losses and the mass
fraction dominated by the thermal conduction as a function of time,
applying Eq. (12) in each of those zones (see Fig.
9). We find that the thermal collapse starts at
![]() ,
in agreement with our previous results (see also
Appendix B). The cooling process is very efficient throughout
the cloud and
,
in agreement with our previous results (see also
Appendix B). The cooling process is very efficient throughout
the cloud and ![]() 80% of the initial cloud material is subject to
radiative cooling at
80% of the initial cloud material is subject to
radiative cooling at
![]() .
On the other hand, as
mentioned above, not all of the cloud is dominated by radiative
losses:
.
On the other hand, as
mentioned above, not all of the cloud is dominated by radiative
losses: ![]() 10% of the initial cloud mass forms the hot thermally
conducting corona located around the cooling-dominated region. The
remaining 10% of the initial cloud mass is mixed together with the
ambient medium. During the shock-cloud interaction, the hot corona
expands and gradually evaporates under the effect of thermal conduction,
whereas the cold core collapses and fragments in cloudlets under the
effect of radiation.
10% of the initial cloud mass forms the hot thermally
conducting corona located around the cooling-dominated region. The
remaining 10% of the initial cloud mass is mixed together with the
ambient medium. During the shock-cloud interaction, the hot corona
expands and gradually evaporates under the effect of thermal conduction,
whereas the cold core collapses and fragments in cloudlets under the
effect of radiation.
In order to study quantitatively the global evolution of the gas cloud,
we consider several diagnostic variables. Equation (5) allows us
to trace the cloud material in the ambient gas. We use such a tracer to
identify zones whose content is the original cloud material by more
than 90%; then we define the cloud mass,
![]() ,
as the total mass
in these zones, and the cloud volume,
,
as the total mass
in these zones, and the cloud volume,
![]() ,
as the total volume
occupied by these zones, namely:
,
as the total volume
occupied by these zones, namely:
where the integral is done on zones with
![]() .
.
Following Xu & Stone (1995), we study the mixing of the cloud
material with the ambient gas, defining the mixing fraction,
![]() ,
as
,
as
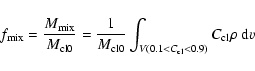 |
(19) |
where
![]() is the cloud mass in zones which contain more than
10% and less than 90% of the cloud material (the integral is over
zones with
is the cloud mass in zones which contain more than
10% and less than 90% of the cloud material (the integral is over
zones with
![]() )
and
)
and
![]() is the cloud
mass at the beginning of the interaction.
is the cloud
mass at the beginning of the interaction.
The cloud mass and volume in Eq. (18) allow us to derive
an average particle density of the cloud as
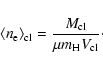 |
(20) |
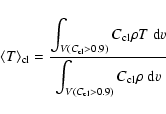 |
(21) |
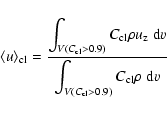 |
(22) |
where, again, we integrate on zones with
![]() and uz is the velocity component in the z-direction.
and uz is the velocity component in the z-direction.
Figure 10 plots the evolution of the global quantities for all
the simulations of Table 2: the normalized cloud mass
![]() ,
the normalized cloud volume,
,
the normalized cloud volume,
![]() (where
(where
![]() is the initial cloud volume), the mixing fraction,
is the initial cloud volume), the mixing fraction,
![]() ,
the average cloud density normalized to the density of the
shocked ambient gas,
,
the average cloud density normalized to the density of the
shocked ambient gas,
![]() ,
the average mass-weighted cloud temperature normalized to the temperature
of the shocked ambient gas,
,
the average mass-weighted cloud temperature normalized to the temperature
of the shocked ambient gas,
![]() ,
and the average mass-weighted z-component of the cloud velocity relative
to the shocked ambient gas,
,
and the average mass-weighted z-component of the cloud velocity relative
to the shocked ambient gas,
![]() .
.
The dashed and the solid lines in Fig. 10 mark the results
for the simulations without both thermal conduction and radiation
(runs HY1 and HY2). The discrepancies between the 3-D low- and
high-resolution results are very small, indicating that both our
3-D simulations have enough resolution to capture the dominant
dynamical effects present in the evolution, as predicted by KMC94 and
Mac Low et al. (1994). Figure 10 also shows that, when the
thermal conduction and the radiation are negligible, the mass loss rate of
the cloud becomes significant after one
![]() (i.e. after the
hydrodynamic instabilities have fully developed at the cloud boundary)
and
(i.e. after the
hydrodynamic instabilities have fully developed at the cloud boundary)
and ![]() 50% of the cloud mass is contained in mixed zones at
50% of the cloud mass is contained in mixed zones at
![]() .
During the first two stages (
.
During the first two stages (
![]() ),
the cloud is progressively compressed: its volume decreases down to 30%
of the initial value, its average density and temperature increase up
to 3 cm-3 (
),
the cloud is progressively compressed: its volume decreases down to 30%
of the initial value, its average density and temperature increase up
to 3 cm-3 (![]()
![]() )
and
)
and
![]() K (
K (![]()
![]() ), respectively. During the third phase (
), respectively. During the third phase (
![]() ),
),
![]() re-expands back to 50% of
the initial volume, leading to a decrease of both
re-expands back to 50% of
the initial volume, leading to a decrease of both
![]() and
and
![]() to
to ![]() 2 cm-3(
2 cm-3(![]()
![]() )
and
)
and ![]()
![]() K (
K (
![]() ),
respectively. In the last phase, the cloud is first
slightly compressed (at
),
respectively. In the last phase, the cloud is first
slightly compressed (at
![]() )
by
the interaction with the "Mach disk'' formed during the reflection of
the primary shock at the symmetry axis, and both
)
by
the interaction with the "Mach disk'' formed during the reflection of
the primary shock at the symmetry axis, and both
![]() and
and
![]() increase; then the
average cloud density slightly decreases, while
increase; then the
average cloud density slightly decreases, while
![]() continues to increase and
continues to increase and
![]() to decrease, because of the
mixing of the cloud material with the ambient medium. During the whole
evolution, the cloud is continuously accelerated: the average cloud
velocity increases up to
to decrease, because of the
mixing of the cloud material with the ambient medium. During the whole
evolution, the cloud is continuously accelerated: the average cloud
velocity increases up to ![]()
![]() at
at
![]() .
.
The dotted lines of Fig. 10 mark the results for HTR50. The
mass loss rate of the cloud in this case is almost constant during the
whole simulation (
![]() ), while in HY2 (and HY1) it
becomes significant only after
), while in HY2 (and HY1) it
becomes significant only after ![]()
![]() .
This different
behavior is due to the different mechanism of cloud mass loss: in
HTR50 the mass loss comes from the cloud evaporation driven by the
thermal conduction, whereas in HY2 the hydrodynamic instabilities
ablate the cloud after
.
This different
behavior is due to the different mechanism of cloud mass loss: in
HTR50 the mass loss comes from the cloud evaporation driven by the
thermal conduction, whereas in HY2 the hydrodynamic instabilities
ablate the cloud after ![]()
![]() (see Sect.
2.3). During the first two stages (
(see Sect.
2.3). During the first two stages (
![]() ),
therefore, the mass loss rate in HTR50 is more efficient than that in
HY2 and, at
),
therefore, the mass loss rate in HTR50 is more efficient than that in
HY2 and, at
![]() ,
,
![]() 5% of the cloud mass has
been already mixed with the ambient medium (
5% of the cloud mass has
been already mixed with the ambient medium (![]() 0% in run HY2). On
the other hand, during the third and fourth stages, in HTR50 the mass
loss rate is less efficient than that in HY2 and, at
0% in run HY2). On
the other hand, during the third and fourth stages, in HTR50 the mass
loss rate is less efficient than that in HY2 and, at
![]() ,
only
,
only ![]() 10% of the cloud mass is contained in mixed zones
(
10% of the cloud mass is contained in mixed zones
(![]() 50% in run HY2).
50% in run HY2).
![\begin{figure}
\par\includegraphics[width=7.8cm,clip]{2896fig8.ps}\end{figure}](/articles/aa/full/2005/47/aa2896-05/Timg168.gif) |
Figure 9: Mass fraction of the initial cloud material dominated by the radiative losses (dashed line) or by the thermal conduction (dotted line) in run HTR30. |
![\begin{figure}
\par\includegraphics[width=12cm,clip]{2896fig9.ps} \end{figure}](/articles/aa/full/2005/47/aa2896-05/Timg169.gif) |
Figure 10: Evolution of the global properties of the gas cloud defined in Sect. 3.4 for runs HY1 and HY2 which neglect the thermal conduction and the radiation (dashed and solid lines), and for runs HTR50 and HTR30, which instead include the thermal conduction and the radiation (dotted and dash-dotted lines). |
In HTR50, during the first stage (
![]() ), the cloud is
compressed, the volume slightly decreases down to 80% of the initial
value and the average density of the cloud slightly increases up to
), the cloud is
compressed, the volume slightly decreases down to 80% of the initial
value and the average density of the cloud slightly increases up to
![]() 1.2 cm-3 (
1.2 cm-3 (![]()
![]() ). During this phase the
cloud is heated efficiently by the thermal conduction and its average
temperature increases rapidly to
). During this phase the
cloud is heated efficiently by the thermal conduction and its average
temperature increases rapidly to
![]() K (
K (![]()
![]() ). As a consequence, the pressure inside the cloud
increases and, at
). As a consequence, the pressure inside the cloud
increases and, at
![]() ,
the cloud expands again,
earlier than in HY2 (
,
the cloud expands again,
earlier than in HY2 (
![]() )
until
)
until
![]() :
:
![]() increases by a factor 2.5 of the
initial volume,
increases by a factor 2.5 of the
initial volume,
![]() gradually
decreases to 0.3-0.4 cm-3, namely the mass density of the
surrounding ambient medium (
gradually
decreases to 0.3-0.4 cm-3, namely the mass density of the
surrounding ambient medium (
![]() ). During this phase, the average cloud temperature,
). During this phase, the average cloud temperature,
![]() ,
keeps increasing up to
,
keeps increasing up to
![]() K
(
K
(![]()
![]() ).
).
In the last phase (
![]() ), the cloud volume is almost
constant;
), the cloud volume is almost
constant;
![]() slightly decreases down
to
slightly decreases down
to ![]() 0.32 cm-3 (
0.32 cm-3 (![]()
![]() ), while
), while
![]() keeps increasing up to
keeps increasing up to ![]()
![]() K (
K (![]()
![]() ), because of the thermal conduction. During the whole
evolution, the cloud is continuously accelerated up to
), because of the thermal conduction. During the whole
evolution, the cloud is continuously accelerated up to ![]()
![]() ,
i.e. more than in HY2, because the cloud has a larger
volume and offers, therefore, a larger surface to the pressure of the
shock front.
,
i.e. more than in HY2, because the cloud has a larger
volume and offers, therefore, a larger surface to the pressure of the
shock front.
The dot-dashed lines mark the results for
![]() (HTR30). In this
case, the trend of the cloud mass loss rate is similar to the one in
HTR50, indicating that the mass loss is again driven by the thermal
conduction rather than by hydrodynamic instabilities. In fact, although
the radiative losses are dominant in HTR30, a small fraction of the
cloud forms a hot corona (in which the thermal conduction is the
dominant process) around the cooling-dominated portion of the cloud
(see Sect. 3.3.2). Since the mass exchange between the cloud and
the ambient medium occurs at the cloud boundary coincident with the
boundary of the corona, the mass loss rate is again regulated by the
thermal conduction.
(HTR30). In this
case, the trend of the cloud mass loss rate is similar to the one in
HTR50, indicating that the mass loss is again driven by the thermal
conduction rather than by hydrodynamic instabilities. In fact, although
the radiative losses are dominant in HTR30, a small fraction of the
cloud forms a hot corona (in which the thermal conduction is the
dominant process) around the cooling-dominated portion of the cloud
(see Sect. 3.3.2). Since the mass exchange between the cloud and
the ambient medium occurs at the cloud boundary coincident with the
boundary of the corona, the mass loss rate is again regulated by the
thermal conduction.
During the first stage (
![]() ), the evolution of the
cloud is similar to that of the other simulations: the cloud is
compressed, rapidly heated up to
), the evolution of the
cloud is similar to that of the other simulations: the cloud is
compressed, rapidly heated up to
![]() K (
K (![]()
![]() )
due both to the shock compression and to the thermal conduction,
and accelerated up to
)
due both to the shock compression and to the thermal conduction,
and accelerated up to
![]() .
At
.
At
![]() ,
the transmitted shock becomes strongly radiative (see Sect.
2.3). At variance with the other simulations, there is no
re-expansion phase in run HTR30 and the cloud volume decreases down to
20% of the initial value by the end of the simulation. The average
density of the cloud has increased by a factor 5, at
,
the transmitted shock becomes strongly radiative (see Sect.
2.3). At variance with the other simulations, there is no
re-expansion phase in run HTR30 and the cloud volume decreases down to
20% of the initial value by the end of the simulation. The average
density of the cloud has increased by a factor 5, at
![]() .
In spite of the cloud compression, during this phase
the average cloud temperature decreases due to the efficient radiative
cooling and, at
.
In spite of the cloud compression, during this phase
the average cloud temperature decreases due to the efficient radiative
cooling and, at
![]() ,
,
![]() K (
K (![]()
![]() ). The cloud is
first accelerated up to
). The cloud is
first accelerated up to
![]() at
at
![]() ,
and
thereafter
,
and
thereafter
![]() ranges between 0.2 and 0.4
ranges between 0.2 and 0.4
![]() ,
because the cloud collapses and offers therefore a
smaller surface to the pressure of the shock front.
,
because the cloud collapses and offers therefore a
smaller surface to the pressure of the shock front.
Note that the emergence of a dense and cold interstellar gas phase (as
in the
![]() case) or the evaporation of the whole cloud (as in
the
case) or the evaporation of the whole cloud (as in
the
![]() case), besides the shock Mach number, also depends
on the density and dimensions of the cloud. For instance, we expect that a
higher initial cloud density would lead to stronger radiative losses
and, therefore, to enhance their role in the evolution of the
shock-cloud interaction: cooling-dominated regions may exist even at
high temperatures, in appropriate physical conditions. As shown in
Fig. 2, the evolution of the shocked cloud may be dominated
by the radiative losses even in the
case), besides the shock Mach number, also depends
on the density and dimensions of the cloud. For instance, we expect that a
higher initial cloud density would lead to stronger radiative losses
and, therefore, to enhance their role in the evolution of the
shock-cloud interaction: cooling-dominated regions may exist even at
high temperatures, in appropriate physical conditions. As shown in
Fig. 2, the evolution of the shocked cloud may be dominated
by the radiative losses even in the
![]() shock case if the
cloud has a density contrast
shock case if the
cloud has a density contrast ![]() (corresponding to a particle
density
(corresponding to a particle
density
![]() cm-3). As for the cloud dimensions, we
expect that, for moderate cloud densities (
cm-3). As for the cloud dimensions, we
expect that, for moderate cloud densities (
![]() cm-3) and moderate shock Mach number (
cm-3) and moderate shock Mach number (
![]() ), the
cooling processes would be efficient preferentially in large clouds
with dimensions larger than the Field length scale, l, while small
clouds with dimensions <l are likely to be ablated by the thermal
conduction in few
), the
cooling processes would be efficient preferentially in large clouds
with dimensions larger than the Field length scale, l, while small
clouds with dimensions <l are likely to be ablated by the thermal
conduction in few
![]() .
.
To study the pure hydrodynamic evolution with high accuracy, we considered
adiabatic 3-D simulations without thermal conduction and radiative losses;
the spatial resolution of these simulations is the highest ever obtained
in 3-D shock-cloud interaction simulations. Such a resolution allowed us
to describe appropriately the hydrodynamic instabilities developing at
the cloud boundaries (they are resolved down to 0.0076 pc in HY2) and,
therefore, to evaluate accurately the mass exchange between the cloud
and the ambient medium. According to previous results (e.g. KMC94),
we found that the SNR shock triggers the development of hydrodynamic
instabilities at the cloud boundaries, which destroy the cloud after
several
![]() .
In this case, the cloud mass loss rate is very
efficient, i.e.
.
In this case, the cloud mass loss rate is very
efficient, i.e. ![]() 50% of the initial cloud mass is mixed with
the ambient medium at
50% of the initial cloud mass is mixed with
the ambient medium at
![]() .
.
We then compared the above models to other models accounting for both
the thermal conduction and the radiative losses. Since the hydrodynamic
instabilities are efficiently suppressed by the thermal conduction, the
evolution can be accurately described with 2-D simulations. The thermal
conduction plays a dominant role in the evolution of moderately over-dense
parsec-size clouds crushed by a 50 Mach shock (post-shock temperature
![]() K), since
K), since
![]() for structures smaller than
for structures smaller than ![]() 0.8 pc
(see Appendix B), i.e. over a distance comparable to the size of
the crushed cloud (see also the location of HTR50 in Fig. 2).
The main effect of the thermal conduction is to smooth out the temperature
and density inhomogeneities. The hydrodynamic instabilities responsible
of the cloud destruction are therefore strongly suppressed, and the
cloud becomes more stable and survives for a longer time. At the cloud
boundary, the temperature and density gradients (very steep in the model
without thermal conduction) are reduced, building up a broad transition
region from the inner portion of the cloud to the ambient medium. During
evolution, the cloud expands and gradually evaporates. The cloud does
not fragment into cloudlets. The mass loss of the
cloud is driven by the thermal conduction and is less efficient than in
the presence of hydrodynamic instabilities.
0.8 pc
(see Appendix B), i.e. over a distance comparable to the size of
the crushed cloud (see also the location of HTR50 in Fig. 2).
The main effect of the thermal conduction is to smooth out the temperature
and density inhomogeneities. The hydrodynamic instabilities responsible
of the cloud destruction are therefore strongly suppressed, and the
cloud becomes more stable and survives for a longer time. At the cloud
boundary, the temperature and density gradients (very steep in the model
without thermal conduction) are reduced, building up a broad transition
region from the inner portion of the cloud to the ambient medium. During
evolution, the cloud expands and gradually evaporates. The cloud does
not fragment into cloudlets. The mass loss of the
cloud is driven by the thermal conduction and is less efficient than in
the presence of hydrodynamic instabilities.
The radiative losses play a crucial role for the
![]() case
(post-shock temperature
case
(post-shock temperature
![]() K) since, for the
conditions of the shocked cloud gas,
K) since, for the
conditions of the shocked cloud gas,
![]() for structures larger than
for structures larger than ![]() 0.3 pc (see Appendix B and the location of HTR30 in Fig.
2). The different structure of the shock transmitted into the
cloud leads to the formation of dense and cold gas there. On the other
hand, Eq. (12) suggests that the thermal conduction is effective
in suppressing hydrodynamic instabilities on sub-parsec scales. The
shocked cloud evolves into a dense and cold core - unaffected by
heat conduction - surrounded by a hot and diluted corona, where the
conducted heat exceeds the cooling. The core ultimately fragments
into dense, cold and compact filaments, consistent with previous
works (Mellema et al. 2002; Fragile et al. 2004).
The corona, instead, expands, and evaporates under the effect of the
thermal conduction. This is the main mechanism of mass loss of the cloud
in this case. The complete evaporation of the corona leaves a "naked''
fragmented core collapsing under the effect of the radiation. The cloud
keeps its identity as long as the corona surrounds the whole fragmented
core.
0.3 pc (see Appendix B and the location of HTR30 in Fig.
2). The different structure of the shock transmitted into the
cloud leads to the formation of dense and cold gas there. On the other
hand, Eq. (12) suggests that the thermal conduction is effective
in suppressing hydrodynamic instabilities on sub-parsec scales. The
shocked cloud evolves into a dense and cold core - unaffected by
heat conduction - surrounded by a hot and diluted corona, where the
conducted heat exceeds the cooling. The core ultimately fragments
into dense, cold and compact filaments, consistent with previous
works (Mellema et al. 2002; Fragile et al. 2004).
The corona, instead, expands, and evaporates under the effect of the
thermal conduction. This is the main mechanism of mass loss of the cloud
in this case. The complete evaporation of the corona leaves a "naked''
fragmented core collapsing under the effect of the radiation. The cloud
keeps its identity as long as the corona surrounds the whole fragmented
core.
Note that some details of the simulations depend on the choice of the
parameters. For instance, the formation of the dense and cold core or
the evaporation of the whole cloud depends also on the density and
dimensions of the cloud. However, the two complementary cases
![]() and
and
![]() that we present here are representative of regimes
in which either the radiative losses or the thermal conduction play a
dominant role.
that we present here are representative of regimes
in which either the radiative losses or the thermal conduction play a
dominant role.
The results presented here are important for the study of middle-aged
X-ray SNR shells whose morphology is affected by ISM inhomogeneities. The
examples include the Cygnus Loop (e.g. Patnaude et al. 2002
on the detection of an isolated ISM cloud in the South-East part of
the shell), the Vela SNR (e.g. Miceli et al. 2005, on the XMM-Newton
observation of an ISM feature in the northern part of the remnant) and
G272.2-3.2 (e.g. Egger et al. 1996; on the multi-wavelength
observation of an ISM cloud hit by the shock). In other cases,
the unfavorable location of the system in the
![]() plane
(Fig. 2) or the cloud destruction by SN progenitor wind may
lead to difficulties in the detection of observable effects of shock
interactions with clouds.
plane
(Fig. 2) or the cloud destruction by SN progenitor wind may
lead to difficulties in the detection of observable effects of shock
interactions with clouds.
Future steps in this project include: the study of the deviations from equilibrium ionization occurring during the complex shock-cloud interaction; the synthesis, from the numerical simulations, of spatially and spectrally resolved X-ray observations with the latest instruments (e.g. Chandra, XMM-Newton, Astro-E2), amenable to direct comparison with SNR observations made with the same instruments; proper account for an ambient magnetic field along with its effect on thermal conduction and on radiative losses.
Acknowledgements
S.O. acknowledges the hospitality of the Flash Center at the University of Chicago, where part of the present work was carried out. We thank the anonymous referee for his/her useful comments on the manuscript. This work is supported in part by the U.S. Department of Energy under Grant No. B523820 to the Center of Astrophysical Thermonuclear Flashes at the University of Chicago (USA). The software used in this work was in part developed by the Center of Astrophysical Themonuclear Flashes. The 3-D simulations were performed on the IBM/Sp4 machine at CINECA (Bologna, Italy) and the 2-D simulations on the Compaq cluster at the SCAN (Sistema di Calcolo per l'Astrofisica Numerica) facility of the INAF - Osservatorio Astronomico di Palermo. This work was supported in part by Ministero dell'Istruzione, dell'Università e della Ricerca and by Istituto Nazionale di Astrofisica.
The thermal conduction is added to the FLASH code using an
operator-splitting method with respect to the hydrodynamic evolution:
the heat losses (or gains) due to the thermal conduction are added as
a source term to the energy equation. The heat flux in the formulation
of Spitzer (1962) is calculated by explicit finite difference as:
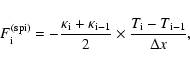 |
(A.1) |
where
![]() and
and ![]() are the Spitzer's thermal
conductivity and the plasma temperature, respectively, at the ith
grid point and
are the Spitzer's thermal
conductivity and the plasma temperature, respectively, at the ith
grid point and ![]() is the cell size. Analogously, the saturated
heat flux is:
is the cell size. Analogously, the saturated
heat flux is:
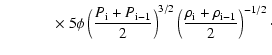 |
(A.2) | ||
where ![]() and
and
![]() are the plasma pressure and mass
density, respectively, at the ith grid point. The total heat flux,
including saturation effects, is:
are the plasma pressure and mass
density, respectively, at the ith grid point. The total heat flux,
including saturation effects, is:
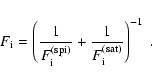 |
(A.3) |
The heat flux is then added to the energy flux generated by the PPM module. This addition is done before any of the zones are updated in the hydrodynamic step. This grants conservation, since the total flux (including the thermal flux) will be corrected during the flux conservation step.
Since the thermal conduction is solved explicitly, a time-step limiter
is required to avoid numerical instability. Stability is guaranteed for
![]() ,
where D is the diffusion coefficient,
related to the conductivity,
,
where D is the diffusion coefficient,
related to the conductivity, ![]() ,
and to the specific heat at constant
volume, cv, by
,
and to the specific heat at constant
volume, cv, by
![]() .
.
We have verified the FLASH code conduction module using test problems with known analytic solutions. The test case we considered is the propagation of a plane conduction front in a uniform, high temperature plasma, with negligible saturation effects (cf. Reale 1995). Since the test includes the plasma hydrodynamics, the propagation of the conduction front is slightly complicated by the presence of the plasma dynamics. The presence of a thermal front causes also a strong pressure wave which eventually drives significant plasma motion in the same direction as the conduction front. However, as we show below, the mean propagation speed of the conduction is much higher than the mean plasma sound speed and the much faster front can be considered propagating as a pure conduction front.
In the case of a plane, pure conduction, front an analytic solution is
available as a self-similar solution (Zel'dovich & Raizer 1966). Defining the
dimensionless parameter
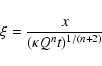 |
(A.4) |
where Q is the integral of T over the whole space, n = 5/2, and
![]() (typical of coronal plasma) in our case,
the solution is given by
(typical of coronal plasma) in our case,
the solution is given by
where
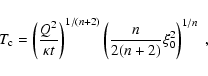 |
(A.6) |
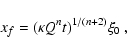 |
(A.7) |
![\begin{displaymath}\xi_0 = \left[\frac{(n+2)^{1+n} ~2^{1-n}}{n\pi^{n/2}}
\left(\frac{\Gamma(1/2+1/n)}{\Gamma(1/n)}\right)^n\right]^{1/(n+2)}
\end{displaymath}](/articles/aa/full/2005/47/aa2896-05/img222.gif) |
(A.8) |
and ![]() is the gamma function.
is the gamma function.
In our test, we took as the initial condition the analytic solution at
t = 0.1 s for a plasma with a particle density of 109 cm-3and
![]() K cm, so that the maximum initial
temperature is at
K cm, so that the maximum initial
temperature is at
![]() K. Reflecting boundary conditions
have been assumed at the left boundary and outflow boundary conditions
(zero-gradient) at the right boundary.
K. Reflecting boundary conditions
have been assumed at the left boundary and outflow boundary conditions
(zero-gradient) at the right boundary.
In our test simulations, the conduction front propagates through ![]()
![]() cm in 3 s with a mean propagation speed
cm in 3 s with a mean propagation speed ![]() 700 km s-1,
i.e. much larger than the mean plasma sound speed (for
700 km s-1,
i.e. much larger than the mean plasma sound speed (for
![]() K,
K,
![]() km s-1). The front, therefore, propagates almost as
a pure conduction front and we can compare the numerical solution with
the analytic solution (Eq. (A.5)). Figure A.1 compares the
temperature distributions computed numerically and analytically, and shows
a good agreement between them. We expect a departure from the analytic
solution as soon as the conduction speed (which is
km s-1). The front, therefore, propagates almost as
a pure conduction front and we can compare the numerical solution with
the analytic solution (Eq. (A.5)). Figure A.1 compares the
temperature distributions computed numerically and analytically, and shows
a good agreement between them. We expect a departure from the analytic
solution as soon as the conduction speed (which is ![]() T5/2)
is significantly reduced at lower temperatures and approaches the plasma
local sound speed (
T5/2)
is significantly reduced at lower temperatures and approaches the plasma
local sound speed (![]() T1/2), as it happens at later times
when the front temperature is reduced significantly from the initial high
value. We checked that the local plasma bulk velocity increases with time,
although remaining well below the sound speed; also the density begins to
change significantly only at late times, when a density front is forming,
as a consequence of the pressure front.
T1/2), as it happens at later times
when the front temperature is reduced significantly from the initial high
value. We checked that the local plasma bulk velocity increases with time,
although remaining well below the sound speed; also the density begins to
change significantly only at late times, when a density front is forming,
as a consequence of the pressure front.
The effect of the thermal conduction on the dynamics of the shock-cloud
interaction is evaluated by comparing the time-scale for conduction in
the shocked ambient medium with the cloud crushing time. In particular,
using Eqs. (8) and (10), we derive the condition:
We use Eqs. (6) and (7) to express
![]() and
and
![]() as
as
Substituting Eqs. (B.2) into (B.1)
where
![]() and
and
![]() are the temperature and the density
of the shocked cloud, respectively. We use the relation
(e.g. KMC94; McKee & Cowie 1975)
are the temperature and the density
of the shocked cloud, respectively. We use the relation
(e.g. KMC94; McKee & Cowie 1975)
and Eqs. (6) and (7) to express
![]() and
and
![]() as:
as:
Substituting Eqs. (B.6) into (B.4) and using Eqs. (B.2)
![\begin{displaymath}\left(\frac{[\tau_{\rm rad}]_{\rm cl}}{[\tau_{\rm cond}]_{\rm...
..._{\rm
ism}^2}{n_{\rm ism}}~ \frac{{\cal M}^4}{\chi^{5/4} l} >1
\end{displaymath}](/articles/aa/full/2005/47/aa2896-05/img242.gif) |
(B.8) |
 |
(B.9) |
the numerical factor ![]() is 1 at the shock and decreases behind the
shock and
is 1 at the shock and decreases behind the
shock and
![]() is the ratio of specific heat in the cloud
material. Setting
is the ratio of specific heat in the cloud
material. Setting
![]() and
and
![]() ,
the above
expression reduces to
,
the above
expression reduces to ![]() .
Substituting F into Eq. (B.5)
.
Substituting F into Eq. (B.5)
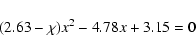 |
(B.10) |
where
![]() .
The above equation has the solution
.
The above equation has the solution
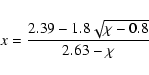 |
(B.11) |
leading to
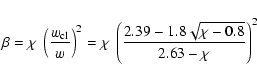 |
(B.12) |
which ranges between 1 and 2.5 for
![]() .
.
For the cases considered in this paper, ![]() and
and
![]() .
From Eq. (B.3), the thermal conduction time-scale is shorter
than the cloud crushing time on scales below
.
From Eq. (B.3), the thermal conduction time-scale is shorter
than the cloud crushing time on scales below
![]() pc in the
pc in the
![]() shock case and
shock case and
![]() pc in the
pc in the
![]() case:
thermal gradients smaller than that will be diffused on time-scales
shorter than
case:
thermal gradients smaller than that will be diffused on time-scales
shorter than
![]() .
These numbers suggest that hydrodynamic
instabilities, which in our problem develop on sub-parsec scales and
on time-scales shorter than the cloud crushing time, are suppressed by
thermal conduction in both the cases considered. In addition, our
estimate suggests that, in the
.
These numbers suggest that hydrodynamic
instabilities, which in our problem develop on sub-parsec scales and
on time-scales shorter than the cloud crushing time, are suppressed by
thermal conduction in both the cases considered. In addition, our
estimate suggests that, in the
![]() shock case, the cloud itself,
has a radius comparable to the characteristic length-scale l and,
therefore, is likely to "evaporate'' due to the thermal conduction on
time-scale of the order of
shock case, the cloud itself,
has a radius comparable to the characteristic length-scale l and,
therefore, is likely to "evaporate'' due to the thermal conduction on
time-scale of the order of
![]() .
.
From Eq. (B.7), in the
![]() shock case,
shock case,
![]() ,
indicating that the shock
transmitted into the cloud is regulated by the energy losses on
time-scales of the order of
,
indicating that the shock
transmitted into the cloud is regulated by the energy losses on
time-scales of the order of
![]() ,
i.e. the time-scale on
which we focused on our simulations. On the other hand, in the
,
i.e. the time-scale on
which we focused on our simulations. On the other hand, in the
![]() shock case
shock case
![]() 0.4, indicating that the transmitted shock is strongly radiative and its
evolution is regulated by the energy losses on time scales shorter than
the cloud crushing time.
0.4, indicating that the transmitted shock is strongly radiative and its
evolution is regulated by the energy losses on time scales shorter than
the cloud crushing time.