A&A 444, 201-211 (2005)
DOI: 10.1051/0004-6361:20053399
R. Baptista1 -
L. Morales-Rueda2 -
E. T. Harlaftis3,![]() -
T. R. Marsh4 -
D. Steeghs5
-
T. R. Marsh4 -
D. Steeghs5
1 - Departamento de Física, Universidade Federal de Santa
Catarina, Campus Trindade, 88040-900, Florianópolis, SC, Brazil
2 -
Department of Astrophysics, Radboud University Nijmegen, 6500 GL
Nijmegen, The Netherlands
3 -
Institute of Space Applications and Remote Sensing, National
Observatory of Athens, PO Box 20048, Athens 118 10, Greece
4 -
Department of Physics, University of Warwick, Coventry CV4 7AL, UK
5 -
High Energy Astrophysics Division, Center for Astrophysics, MS-67,
60 Garden Street, Cambridge, MA 02138, US
Received 11 May 2005 / Accepted 1 July 2005
Abstract
We report the analysis of time-resolved spectroscopy of IP Pegasi in
outburst with eclipse mapping techniques to investigate the location
and geometry of the observed spiral structures. We were able to obtain
an improved view of the spiral structures with the aid of light curves
extracted in velocity bins matching the observed range of velocities
of the spiral arms combined with a double default map tailored for
reconstruction of asymmetric structures.
Two-armed spiral structures are clearly seen in all eclipse maps.
The arms are located at different distances from the disc centre.
The "blue'' arm is farther out in the disc (
![]() )
than the "red'' arm (
)
than the "red'' arm (
![]() ).
There is evidence that the velocity of the emitting gas along the
spiral pattern is lower than the Keplerian velocity for the same disc
radius. The discrepancy is smaller in the outer arm (measured velocities
10-15 per cent lower than Keplerian) and is more significant in the
inner arm (observed velocities up to 40 per cent lower than Keplerian).
We measured the opening angle of the spirals from the azimuthal
intensity distribution of the eclipse maps to be
).
There is evidence that the velocity of the emitting gas along the
spiral pattern is lower than the Keplerian velocity for the same disc
radius. The discrepancy is smaller in the outer arm (measured velocities
10-15 per cent lower than Keplerian) and is more significant in the
inner arm (observed velocities up to 40 per cent lower than Keplerian).
We measured the opening angle of the spirals from the azimuthal
intensity distribution of the eclipse maps to be
![]() .
A comparison with similar measurements on data at different outburst
stages reveals that the opening angle of the spiral arms in IP Peg
decreases while the outbursting accretion disc cools and shrinks,
in agreement with the expected evolution of a tidally driven spiral wave.
The sub-Keplerian velocities along the spiral pattern and the clear
correlation between the opening angle of the spirals and the outburst
stage favors the interpretation of these asymmetric structures
as tidally-induced spiral shocks.
.
A comparison with similar measurements on data at different outburst
stages reveals that the opening angle of the spiral arms in IP Peg
decreases while the outbursting accretion disc cools and shrinks,
in agreement with the expected evolution of a tidally driven spiral wave.
The sub-Keplerian velocities along the spiral pattern and the clear
correlation between the opening angle of the spirals and the outburst
stage favors the interpretation of these asymmetric structures
as tidally-induced spiral shocks.
Key words: stars: novae, cataclysmic variables - stars: individual: IP Pegasi - accretion, accretion disks - shock waves - line: formation - techniques: spectroscopic
IP Pegasi is a dwarf nova, a compact binary in which a late-type star
overfills its Roche lobe and transfers matter to a companion white dwarf
via an accretion disc. It shows recurrent outbursts (every 70-100 days)
in which the disc expands and brightens by 2-3 mag during 10-12 days
as a consequence of a sudden increase in mass accretion through
the disc. In the quiescent, low-mass accretion state, the white
dwarf and the bright spot (formed by the impact of the infalling gas
stream with the outer edge of the disc) dominate the light from the
binary at optical and ultraviolet wavelengths, whereas during outburst
the hot and large disc is the dominant source of light.
The binary is seen at a high inclination angle (
![]() ), which
leads to deep eclipses in the light curve every 3.8 h when the
white dwarf, accretion disc and bright spot are occulted by the mass-donor
star. This allows the emission from the different light sources to be
distinguished and spatially resolved studies to be performed,
making IP Peg an ideal laboratory for the study of accretion physics.
In particular, it is well suited for the application of indirect imaging
techniques to resolve the disc emission both in position (eclipse mapping,
Horne 1985) and velocity (Doppler tomography, Marsh & Horne 1988).
), which
leads to deep eclipses in the light curve every 3.8 h when the
white dwarf, accretion disc and bright spot are occulted by the mass-donor
star. This allows the emission from the different light sources to be
distinguished and spatially resolved studies to be performed,
making IP Peg an ideal laboratory for the study of accretion physics.
In particular, it is well suited for the application of indirect imaging
techniques to resolve the disc emission both in position (eclipse mapping,
Horne 1985) and velocity (Doppler tomography, Marsh & Horne 1988).
Additional attention has been drawn to IP Peg after the discovery of a two-armed spiral structure in its accretion disc during outburst (Steeghs et al. 1997). These spiral structures were seen in different outbursts and at different outburst stages - from the end of the rise and maximum (Steeghs et al. 1997; Harlaftis et al. 1999; Baptista et al. 2000) through the decline stages (Morales-Rueda et al. 2000; Baptista et al. 2002) and possibly also at the very late decline (Saito et al. 2005). They are believed to be raised by tides from the mass-donor star on the outer accretion disc when it expands during outburst (see review by Steeghs 2001).
Spiral shocks in accretion discs were predicted theoretically and
advocated as an alternative mechanism for the removal of angular
momentum required for the disc gas to accrete (Sawada et al. 1986).
Numerical hydrodynamic simulations suggest that strong spiral shocks
are formed in hot accretion discs (e.g., Sato et al. 2003, and references
therein) and that the opening angle of the spirals (the angle formed by
the shock front and the azimuthal direction of the disc gas flow)
depends on the disc temperature: the cooler the disc, the more tightly
wound the spiral pattern is. Godon et al. (1998) argued that wide open
spirals could only form in accretion discs much hotter (
![]() )
than those of dwarf novae. Steeghs & Stehle (1999) remarked
that the disc radius is also important in determining the shape of the
spirals and that wide open spiral arms such as those observed in
IP Peg could be raised at the much lower temperatures found in
accretion discs of outbursting dwarf novae (
)
than those of dwarf novae. Steeghs & Stehle (1999) remarked
that the disc radius is also important in determining the shape of the
spirals and that wide open spiral arms such as those observed in
IP Peg could be raised at the much lower temperatures found in
accretion discs of outbursting dwarf novae (
![]() )
if
the disc is large - as expected for outbursting discs.
)
if
the disc is large - as expected for outbursting discs.
In a previous paper (Harlaftis et al. 2004) we investigated the ability of the eclipse mapping method to recover spiral structures and we set the observational requirements for a successful reconstruction. We also showed how the detection of spiral arms with eclipse mapping is improved with a proper extraction of velocity-resolved eclipse light curves to avoid contamination by light sources other than the spiral arms. In this follow up paper we reanalyze the spectroscopic data of Morales-Rueda et al. (2000) with eclipse mapping techniques to investigate the spatial properties of the observed two-armed spiral structure.
This paper is organized as follows. The details of the analysis are presented in Sect. 2 while the results are presented and discussed in Sect. 3. Section 4 compares the orientation of the spiral arms from this study with those from the previous analysis of Baptista et al. (2000, hereafter BHS) and Baptista et al. (2002, hereafter BHT) to infer the changes in the opening angle of the spiral arms with outburst stage, and discusses the implications of our results for the interpretation of the observed spiral structures in terms of irradiation of tidally-thickened outer disc regions by a hot inner disc. The conclusions are summarized in Sect. 5. The Appendix discusses the changes implemented in the eclipse mapping method in order to allow an improved reconstruction of asymmetric structures such as spiral arms in accretion discs.
Time-resolved spectrophotometry of IP Pegasi was secured with the
Intermediate Dispersion Spectrograph on the 2.5 m Isaac Newton
Telescope, at La Palma, during the nights of 1994 October 30 and 31.
The observations were made 5 and 6 days after the onset of an
outburst, when the star was at the maximum brightness plateau phase
of the 12-14 day long outburst (Morales-Rueda et al. 2000, see
their Fig. 1). A total of 164 blue spectra (
![]() )
was obtained at a time resolution of 220 s and a
spectral resolution of 100 km s-1 at H
)
was obtained at a time resolution of 220 s and a
spectral resolution of 100 km s-1 at H![]() .
The reader is
referred to Morales-Rueda et al. (2000) for a detailed description of
the data set and of the reduction procedures.
.
The reader is
referred to Morales-Rueda et al. (2000) for a detailed description of
the data set and of the reduction procedures.
![\begin{figure}
\par\includegraphics[angle=-90,scale=0.42]{3399fig1.eps}\end{figure}](/articles/aa/full/2005/46/aa3399-05/Timg21.gif) |
Figure 1:
Top: zoomed trailed spectrogram of the H |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[angle=-90,width=14cm]{3399fig2.eps}\end{figure}](/articles/aa/full/2005/46/aa3399-05/Timg22.gif) |
Figure 2:
Extracted core ( left panels) and spiral ( right panels) light
curves for He II and H |
| Open with DEXTER | |
The spectra were phase-folded according to the linear ephemeris
of Wolf et al. (1993),
The upper panel of Fig. 1 shows a zoomed trailed spectrogram
of H![]() during eclipse (phase range -0.1 to +0.1 cycles) on
the first night of observations. The lower panel shows the resulting
line profile integrated over the eclipse phase range.
The emission lines of IP Peg in outburst have contributions from the
spiral arms as well as the irradiated face of the secondary star
(Harlaftis 1999) and possibly another low-velocity emission component
(Harlaftis et al. 1999; Steeghs et al. 1996). The signature of the
two-armed spiral structure appears in Fig. 1
as the two bright arcs running from positive, high velocities
(
during eclipse (phase range -0.1 to +0.1 cycles) on
the first night of observations. The lower panel shows the resulting
line profile integrated over the eclipse phase range.
The emission lines of IP Peg in outburst have contributions from the
spiral arms as well as the irradiated face of the secondary star
(Harlaftis 1999) and possibly another low-velocity emission component
(Harlaftis et al. 1999; Steeghs et al. 1996). The signature of the
two-armed spiral structure appears in Fig. 1
as the two bright arcs running from positive, high velocities
(
![]() )
before mid-eclipse to negative, high
velocities after phase zero. The observed change in line profile during
eclipse indicates that the "red'' spiral arm is being eclipsed at
about the same phase (
)
before mid-eclipse to negative, high
velocities after phase zero. The observed change in line profile during
eclipse indicates that the "red'' spiral arm is being eclipsed at
about the same phase (
![]() cycles) at which the "blue''
arm starts reappearing from eclipse. The low-velocity emission is
seen as the faint line-emission component changing from blue to red shifts
(at
cycles) at which the "blue''
arm starts reappearing from eclipse. The low-velocity emission is
seen as the faint line-emission component changing from blue to red shifts
(at
![]() )
around mid-eclipse.
)
around mid-eclipse.
Because the spiral arms and the other emission components contribute to the line profile at different Doppler velocities, it is possible to separate the contribution of these distinct light sources by a proper extraction of velocity-resolved eclipse light curves. For example, BHT performed velocity-resolved eclipse mapping to separate the HeI emission from each of the spiral arms in IP Peg. Harlaftis et al. (2004) discussed how dilution by other light sources reduces the ability of the eclipse mapping method to reconstruct spiral structures in accretion discs. They also showed how the detection of spiral arms may be improved with the aid of velocity-resolved light curves. Here we use this technique as an useful tool to minimize the contribution of the low-velocity gas to the light curve and to optimize the detection of the spiral arms in line eclipse maps.
Figure 1 shows the choice of the velocity-resolved passbands
used to separate the contribution of the spirals from that of
low-velocity gas in the emission lines of IP Peg.
Two light curves were extracted for each line, one covering the low
velocity range (-400 to
![]() )
and one matching the
observed velocity range of the spiral arms (-1000 to -400 plus
+400 to
)
and one matching the
observed velocity range of the spiral arms (-1000 to -400 plus
+400 to
![]() for all lines except He I 4472, for
which we use the narrower ranges -900 to -400 plus +400 to
for all lines except He I 4472, for
which we use the narrower ranges -900 to -400 plus +400 to
![]() to avoid contamination by the Mg II
to avoid contamination by the Mg II
![]() Å line). The low-velocity range light curve will be
hereafter referred to as the "core'' light curve, while the higher
velocity range curve will be referred to as the "spiral'' light curve.
Core and spiral light curves were extracted for H
Å line). The low-velocity range light curve will be
hereafter referred to as the "core'' light curve, while the higher
velocity range curve will be referred to as the "spiral'' light curve.
Core and spiral light curves were extracted for H![]() ,
H
,
H![]() ,
He II 4686, He I 4472 and the Bowen blend at
,
He II 4686, He I 4472 and the Bowen blend at
![]() Å.
Å.
![\begin{figure}
\par\includegraphics[width=14cm]{3399fig3.eps}\end{figure}](/articles/aa/full/2005/46/aa3399-05/Timg35.gif) |
Figure 3:
Left: data trailed spectrograms (linear greyscale) and
corresponding Doppler maps (logarithmic greyscale) for H |
| Open with DEXTER | |
Four orbital cycles were observed. The orbital modulation and the shape of the eclipse are consistent from one night to the other (see Fig. 5 of Morales-Rueda et al. 2000), indicating that the disc brightness distribution is relatively stable over that time scale. We therefore combined the 4 light curves to produce median light curves at a phase resolution of 0.01 cycles for all lines. The error bars were computed from the absolute deviation with respect to the median in each phase bin. The resulting light curves are shown in Fig. 2.
The He II and Bowen blend core light curves show a narrow, deep and
reasonably well centered eclipse indicating that the low-velocity
emission in these lines arise from a region close to the white dwarf
at disc centre. A possible interpretation would be that this
line component is produced in a collimated, hot wind from the inner
disc, in which most of the velocity is directed away from the orbital
plane giving rise to small Doppler shifts.
The Balmer and He I core light curves show the very broad, asymmetric
and phase offset eclipse seen in Harlaftis et al. (2004, see their
Figs. 7 and 8). The eclipse is too wide to be caused by occultation
of the accretion disc by the secondary star. The shape of this eclipse
is possibly produced by self-occultation
of an asymmetric brightness distribution in the irradiated face of
the secondary star or by occultation of an emission source at a
different position in the binary (e.g., Steeghs et al. 1996).
On the other hand, all spiral light curves show the orbital modulation
and asymmetric eclipse shape characteristics of the emission from a
two-armed spiral structure in the accretion disc (e.g., BHS, Steeghs
& Stehle 1999). Two separate brightness sources are eclipsed in
sequence. The first one is eclipsed at
![]() cycle
and the second one at
cycle
and the second one at
![]() cycle;
they reappear from eclipse at phases
cycle;
they reappear from eclipse at phases
![]() cycle and
cycle and
![]() cycle, respectively (see Fig. 3 for
a zoomed view of the light curves around eclipse).
Hence, our choice of passband successfully framed the emission from
the spiral arms in the spiral light curves
cycle, respectively (see Fig. 3 for
a zoomed view of the light curves around eclipse).
Hence, our choice of passband successfully framed the emission from
the spiral arms in the spiral light curves![]() .
.
Morales-Rueda et al. (2000) found that the eclipses of the emission lines were significantly shifted towards negative phases. The +0.008 cycle offset applied to the data (Sect. 2.1) eliminates the phase offset of the continuum light curve and reduces the discrepancy for the line light curves. Figure 2 shows that the remaining phase offset is caused by asymmetries in the brightness distribution of the low-velocity line emitting gas (core light curves). There is no phase offset in the spiral light curves. Therefore, the shifted eclipses seen in the full-line light curves are not an evidence of unequal brightnesses in the two arms, as claimed by Smak (2001).
In the remainder of this paper we concentrate on the analysis of the spiral light curves. Our eclipse mapping code (Baptista & Steiner 1993) assumes that any brightness change in the light curve is caused by occultation of disc regions by the secondary star. Therefore, the out-of-eclipse orbital modulation of the spiral light curves was removed by fitting a spline function to the regions of the light curve excluding the eclipse, dividing the light curve by the fitted spline, and scaling the result to the flux level of the spline function at phase zero (e.g., BHS). This procedure allows the removal of orbital modulations with only minor effects of the eclipse shape itself.
The eclipse maps are flat square arrays of
![]() pixels and
side 2 RL1 centered on the white dwarf, where RL1 is the
distance from disc centre to the inner Lagrangian point. The adopted
eclipse geometry is
pixels and
side 2 RL1 centered on the white dwarf, where RL1 is the
distance from disc centre to the inner Lagrangian point. The adopted
eclipse geometry is
![]() and q=0.5 (Wood & Crawford 1986),
which ensures that the white dwarf is at the centre of the map.
The reconstructions were obtained using a double default function
with
and q=0.5 (Wood & Crawford 1986),
which ensures that the white dwarf is at the centre of the map.
The reconstructions were obtained using a double default function
with
![]() (see Appendix).
(see Appendix).
The statistical uncertainties of the eclipse maps were computed with a Monte Carlo procedure (e.g., Rutten et al. 1992). For each line light curve, we create a set of 20 artificial light curves in which the flux at each phase is varied around the true value according to a Gaussian distribution with standard deviation equals to the uncertainty at that point. These light curves are fitted with the eclipse mapping code to generate a set of randomized eclipse maps. These are combined to produce an average map and a map of the standard deviations with respect to the average. A map of the statistical significance (or the inverse of the relative error) is obtained by dividing the true eclipse map by the map of the standard deviations.
The resulting eclipse maps are shown in Fig. 3 in a logarithmic
grey-scale. For completeness, the data trailed spectrograms and the
computed Doppler maps of the corresponding lines (Morales-Rueda et al.
2000) are shown in the left two columns. Doppler maps for the H![]() and Bowen blend lines (not shown in Morales-Rueda et al. 2000) are also
included. The Doppler maps and trailed spectrograms correspond to the
data of the first night of observations, except for the Bowen blend map.
In this case the data of the two nights were combined and the spectra
around eclipse excluded from the analysis in order to produce a single
Doppler map of better signal-to-noise ratio.
The Doppler maps of Fig. 3 are shown rotated 90 degrees
clockwise with respect to their usual presentation (e.g., Morales-Rueda
et al. 2000) in order to display the spiral arms in a similar
orientation as in the eclipse maps. The blue spiral arm appears
closer to the secondary star in the lower right side of the Doppler map.
We shall remark that the coordinate frames of the Doppler and eclipse
maps are very different: the inner, low-velocity side of a spiral
arm in the Doppler map is related to the outer side of the
corresponding structure in the eclipse map.
and Bowen blend lines (not shown in Morales-Rueda et al. 2000) are also
included. The Doppler maps and trailed spectrograms correspond to the
data of the first night of observations, except for the Bowen blend map.
In this case the data of the two nights were combined and the spectra
around eclipse excluded from the analysis in order to produce a single
Doppler map of better signal-to-noise ratio.
The Doppler maps of Fig. 3 are shown rotated 90 degrees
clockwise with respect to their usual presentation (e.g., Morales-Rueda
et al. 2000) in order to display the spiral arms in a similar
orientation as in the eclipse maps. The blue spiral arm appears
closer to the secondary star in the lower right side of the Doppler map.
We shall remark that the coordinate frames of the Doppler and eclipse
maps are very different: the inner, low-velocity side of a spiral
arm in the Doppler map is related to the outer side of the
corresponding structure in the eclipse map.
The advantage of using velocity-resolved light curves matched to the observed velocity range of the spirals becomes clear when we compare our eclipse maps with those obtained from light curves over the full line width (BHS; Harlaftis et al. 2004). BHS needed to compute the asymmetric part of their eclipse maps in order to see clearly the spiral structures, whereas the significant dilution by other line emitting sources hampered the detection of the spiral arms in the Balmer and He I full-line eclipse maps of Harlaftis et al. (2004). Here, the spiral structures are conspicuous in the eclipse maps without the need of further data processing.
The double-stepped bulges in the eclipse shapes map into two asymmetric
structures corresponding to the two-armed spiral structure seen in the
Doppler maps. The solid contour line overploted on each eclipse map
depicts the 3-![]() confidence level region as derived from the map
of the statistical significance in each case (Sect. 2.2). The
two-armed spiral structure is at or above the 3-
confidence level region as derived from the map
of the statistical significance in each case (Sect. 2.2). The
two-armed spiral structure is at or above the 3-![]() confidence
level in all line maps. We will hereafter refer to these structures
as to the "blue'' and "red'' spiral arms.
They are located at different distances from disc centre.
The red spiral arm is seen in the upper side of the eclipse map, at
radii of
confidence
level in all line maps. We will hereafter refer to these structures
as to the "blue'' and "red'' spiral arms.
They are located at different distances from disc centre.
The red spiral arm is seen in the upper side of the eclipse map, at
radii of
![]() .
The blue arm is seen in the lower right
side of the map, at radii of
.
The blue arm is seen in the lower right
side of the map, at radii of
![]() .
This is in
agreement with the Doppler tomography, which indicates smaller
velocities for the blue spiral arm (
.
This is in
agreement with the Doppler tomography, which indicates smaller
velocities for the blue spiral arm (
![]() )
than
for the red spiral arm (
)
than
for the red spiral arm (
![]() )
(Morales-Rueda
et al. 2000). The red arm is brighter than the blue arm in the Bowen
blend, whereas the opposite holds for H
)
(Morales-Rueda
et al. 2000). The red arm is brighter than the blue arm in the Bowen
blend, whereas the opposite holds for H![]() .
The two arms have
comparable brightness in the other lines. This is also in line with
the results from the Doppler tomography.
.
The two arms have
comparable brightness in the other lines. This is also in line with
the results from the Doppler tomography.
To further investigate the properties of the asymmetric arcs we
divided the eclipse map into azimuthal slices (i.e., "slices of pizza'')
and computed the radius at which the intensity is a maximum for each
azimuth. A corresponding Keplerian velocity is obtained from the
radius of maximum intensity assuming that
![]() and
and
![]() for IP Peg (Marsh & Horne 1990).
This exercise allows us to trace the distribution of the spiral
structures in radius and azimuth (BHS).
for IP Peg (Marsh & Horne 1990).
This exercise allows us to trace the distribution of the spiral
structures in radius and azimuth (BHS).
Figure 4 shows the azimuthal intensity distribution ![]() ,
radius
,
radius
![]() and corresponding Keplerian velocity at maximum
intensity
and corresponding Keplerian velocity at maximum
intensity
![]() .
Azimuths are expressed in terms of
orbital phase. These are measured from the line joining both stars
and increase clockwise for the eclipse maps of Fig. 3.
The uncertainties in
.
Azimuths are expressed in terms of
orbital phase. These are measured from the line joining both stars
and increase clockwise for the eclipse maps of Fig. 3.
The uncertainties in ![]() ,
,
![]() and
and
![]() are derived from the Monte Carlo simulations (see Sect. 2.2).
Dotted lines in Fig. 4 depict the 1-
are derived from the Monte Carlo simulations (see Sect. 2.2).
Dotted lines in Fig. 4 depict the 1-![]() limits in these
distributions.
limits in these
distributions.
![\begin{figure}
\par\includegraphics[angle=-90,width=13.5cm]{3399fig4.eps}\end{figure}](/articles/aa/full/2005/46/aa3399-05/Timg51.gif) |
Figure 4:
The dependency with binary phase of the maximum intensity
(lowermost panels), radius and corresponding Keplerian velocity at
maximum intensity (second and third rows of panels from the bottom)
as derived from the line eclipse maps.
Dotted lines depict the
|
| Open with DEXTER | |
The two-armed asymmetric structures in the eclipse maps lead to a
double-humped shape in the azimuthal intensity distribution. The valleys
in the azimuthal intensity distribution trace the region in between the
spirals, where
![]() is meaningless. Accordingly, the
distributions of
is meaningless. Accordingly, the
distributions of
![]() and
and
![]() are cut-off in
the phase range where the intensity drops below 10 per cent of the peak
intensity. The maximum intensity along the outer, blue arm occurs at
a radius of
are cut-off in
the phase range where the intensity drops below 10 per cent of the peak
intensity. The maximum intensity along the outer, blue arm occurs at
a radius of
![]() ,
whereas that of the inner, red arm is at
,
whereas that of the inner, red arm is at
![]() .
The position (and velocity) of
the blue arm is more precisely measured than that of the red arm.
The location, radial and azimuthal range of the spiral arms are the
same for all lines - from the low-excitation Balmer lines to the high
excitation He II and Bowen blend lines - within the uncertainties.
.
The position (and velocity) of
the blue arm is more precisely measured than that of the red arm.
The location, radial and azimuthal range of the spiral arms are the
same for all lines - from the low-excitation Balmer lines to the high
excitation He II and Bowen blend lines - within the uncertainties.
A similar procedure was applied to the Doppler maps of Fig. 3 to compute the observed velocity at the maximum intensity as a function of orbital phase. The results are plotted as solid grey lines in the velocity panels of Fig. 4. The results for the Bowen blend line are less reliable than for the other lines as the corresponding Doppler map is quite noisy (Fig. 3). We shall regard the results of the following analysis for this line as merely illustrative.
The upper panels of Fig. 4 show the ratio of the observed velocity (Doppler map) to the Keplerian velocity at the same radius (eclipse map). A horizontal dashed line in each panel depicts the reference unity velocity ratio. This comparison indicates that the velocity of the emitting gas along the spiral arms is generally lower than the Keplerian velocity at that radius. The difference is small for the blue arm, which shows velocities 10-15 per cent lower than Keplerian. However, the discrepancy is large for the red arm, with differences reaching up to 40 per cent. This indicates that the velocity field along the spiral arms is not Keplerian, in agreement with the results of BHS. This result seems in line with the interpretation of these asymmetric structures as caused by tidally-induced spiral shocks, because the heated (and emitting) post-shock gas is expected to move at velocities lower than the Keplerian velocity of the non-shocked disc orbiting gas at the same radius.
Nevertheless, hydrodynamical simulations by Steeghs & Stehle (1999) suggest that the departures from a Keplerian flow along the spiral pattern increase with radius, and that one should expect the velocity discrepancy to be larger for the outer, blue arm - just the opposite of what is observed. The larger velocity discrepancy (and possibly also the smaller distance with respect to disc centre) of the red arm may be a consequence of its interaction with the infalling gas stream. In this regard, the hydrodynamical simulations by Bisikalo et al. (1998) and Makita et al. (2000) show that the gas stream may penetrate the disc, forming a bow shock that interacts and mixes with the red arm to enhance emission along a spiral pattern close to the disc centre.
The shape of the azimuthal intensity distribution and the position of maxima/minima intensities are defined by the opening angle of the spiral arms (see the Appendix). For a fixed orientation of the spiral arms (as expected for tidally-induced spirals), the azimuth (binary phase) of maximum/minimum intensity increases as the opening angle of the spiral decreases. We performed simulations with artificial brightness distributions containing spiral arms to calibrate this relation. These are described in the Appendix. It is therefore possible to infer the opening angle of the spiral arms from the measured binary phase of minimum in the intensity distribution of Fig. 4.
We fitted a parabola to the lower portion of the ![]() distribution
to find an average orbital phase of minimum of
distribution
to find an average orbital phase of minimum of
![]() cycles.
From this measurement, we estimate the opening angle of the spiral arms
in our data to be
cycles.
From this measurement, we estimate the opening angle of the spiral arms
in our data to be
![]() .
We performed similar analysis with the maximum intensity distributions
of BHS and BHT to find opening angles of
.
We performed similar analysis with the maximum intensity distributions
of BHS and BHT to find opening angles of
![]() and
and
![]() ,
respectively. Our data were collected 5-6 days
after the onset of the 1994 October outburst. Those of BHS and BHT
were obtained, respectively, 3 and 9 days after the start of the
corresponding outbursts.
,
respectively. Our data were collected 5-6 days
after the onset of the 1994 October outburst. Those of BHS and BHT
were obtained, respectively, 3 and 9 days after the start of the
corresponding outbursts.
Figure 5 shows the evolution of the measured opening angle of
the spiral arms in IP Peg with the time from the start of the outburst.
![\begin{figure}
\par\includegraphics[angle=-90,width=8cm,clip]{3399fig5.eps}\end{figure}](/articles/aa/full/2005/46/aa3399-05/Timg57.gif) |
Figure 5: The measured opening angle of the spiral arms in IP Peg as a function of outburst stage. |
| Open with DEXTER | |
The spiral structures seen in IP Peg and a few other outbursting dwarf novae have usually been interpreted as an observational confirmation of tidally induced spiral shocks in accretion discs (Steeghs 2001, and references therein). Smak (2001), and Ogilvie (2002) proposed that these spiral structures are not evidence of spiral shocks, but are caused by irradiation of tidally thickened sectors of the outer disc by the hot, inner disc regions.
Smak's (2001) model predicts that the blue arm is systematically brighter
than the red arm. There is no observational support for this claim.
Our analysis of 5 different emission lines show that the ratio of the
brightness of the two arms is line-dependent and probably also time
dependent. For example, both arms have comparable brightness in the
He II
![]() Doppler tomogram of the first night of observations,
whereas the blue arm appears stronger than the red arm in the Doppler
tomogram of the same line in the second night of observations (see
Fig. 4 of Morales-Rueda et al. 2000). Our data show no clear evidence
that one arm is systematically brighter than the other one.
Doppler tomogram of the first night of observations,
whereas the blue arm appears stronger than the red arm in the Doppler
tomogram of the same line in the second night of observations (see
Fig. 4 of Morales-Rueda et al. 2000). Our data show no clear evidence
that one arm is systematically brighter than the other one.
Our results may be used to set further constraints on both interpretations.
First, the eclipse mapping procedure projects any emission produced at
height z above the disc back along the inclined line of sight to the
point where it pierces the disc plane, at a distance ![]() away
from the secondary star with respect to its true position (Baptista
et al. 1995). Conversely, if the spiral structures are produced in
vertically-extended disc regions, their true positions would be at a
distance
away
from the secondary star with respect to its true position (Baptista
et al. 1995). Conversely, if the spiral structures are produced in
vertically-extended disc regions, their true positions would be at a
distance ![]() towards the secondary star.
For the high inclination of IP Peg, even a small vertical height
towards the secondary star.
For the high inclination of IP Peg, even a small vertical height
![]() moves the spiral arms by
moves the spiral arms by
![]() towards the secondary star with respect
to their positions in the eclipse maps. This displacement is enough
to shift both arms to the front side of the disc (the disc hemisphere
closest to the secondary star).
However, the effects raised by the tides from the secondary star are
point-symmetric with respect to the white dwarf, for both the shocks
and the irradiation interpretations (Steeghs & Stehle 1999; Makita
et al. 2000; Smak 2001; Ogilvie 2002). It would be hard to explain
the resulting highly asymmetric geometrical configuration within the
framework of tides induced by the secondary star.
towards the secondary star with respect
to their positions in the eclipse maps. This displacement is enough
to shift both arms to the front side of the disc (the disc hemisphere
closest to the secondary star).
However, the effects raised by the tides from the secondary star are
point-symmetric with respect to the white dwarf, for both the shocks
and the irradiation interpretations (Steeghs & Stehle 1999; Makita
et al. 2000; Smak 2001; Ogilvie 2002). It would be hard to explain
the resulting highly asymmetric geometrical configuration within the
framework of tides induced by the secondary star.
In order to avoid completely braking the point-symmetry of the
arms with respect to the white dwarf, they must be at heights lower
than
![]() .
But this is of the order of (or even lower than) the expected thickness
of the accretion disc at the radial position of the
arms
.
But this is of the order of (or even lower than) the expected thickness
of the accretion disc at the radial position of the
arms![]() .
Thus, our results suggest that the site of the line emission along the
spirals cannot be too far above the orbital plane. There is no evidence
of a measurable disc thickening effect.
.
Thus, our results suggest that the site of the line emission along the
spirals cannot be too far above the orbital plane. There is no evidence
of a measurable disc thickening effect.
Second, a consequence of the irradiation model is that mainly the side of the thickened disc regions facing the hot inner disc would be irradiated. When the thickened disc structure is viewed from a highly inclined line of sight towards the secondary star (i.e., around eclipse) the illuminated red arm would be seen mostly face-on, but the blue arm would suffer self-occultation (or would be seen with a much lower effective area). Thus, in the irradiation model one expects that the red arm appears systematically (and possibly significantly) brighter than the blue arm around eclipse (and this brightness difference would be transported to any eclipse map). Eclipse mapping results offer no support for this prediction.
Finally, while sub-Keplerian velocities along the spiral pattern are expected in the spiral shock model, there is no immediate explanation for them in the irradiation model.
Therefore, the combined results from the Doppler tomograms and eclipse maps seem to favour the spiral shock interpretation of the observed asymmetric structures.
We reanalyzed time-resolved spectroscopy of IP Pegasi in outburst with eclipse mapping techniques in order to investigate the location and geometry of the observed spiral structures. We were able to obtain an improved view of the spiral arms with the aid of light curves extracted in velocity bins matching the observed range of velocities of the spiral arms and a double default map tailored for reconstruction of asymmetric structures.
Two-armed spiral structures are clearly seen in all eclipse maps.
The arms are located at different distances from the disc centre.
The "blue'' arm is farther out in the disc (
![]() )
than the "red'' arm (
)
than the "red'' arm (
![]() ). The observed
difference in radius is significant at the 3-
). The observed
difference in radius is significant at the 3-![]() level.
The "red'' arm is stronger in the Bowen blend, whereas the "blue''
arm is stronger in H
level.
The "red'' arm is stronger in the Bowen blend, whereas the "blue''
arm is stronger in H![]() .
The two arms have comparable brightnesses
in the other lines. The brightness ratios derived from the eclipse maps
and Doppler tomograms are consistent with each other.
.
The two arms have comparable brightnesses
in the other lines. The brightness ratios derived from the eclipse maps
and Doppler tomograms are consistent with each other.
There is evidence that the velocity of the emitting gas along the spiral pattern is lower than the Keplerian velocity for the same disc radius. The discrepancy is lower in the "blue'', outer arm - with the measured Doppler velocities being typically 10-15 per cent lower than Keplerian - but is more significant in the "red'', inner arm - where the observed velocities can be 40 per cent lower than the Keplerian velocities.
It is possible to measure the opening angle ![]() of the spirals from
the azimuthal intensity distribution of the eclipse maps. For the data
of this paper we measure
of the spirals from
the azimuthal intensity distribution of the eclipse maps. For the data
of this paper we measure
![]() .
We performed a similar
analysis with the data of BHS and BHT to find opening angles of
.
We performed a similar
analysis with the data of BHS and BHT to find opening angles of
![]() and
and
![]() ,
respectively.
The difference between the measured opening angle of the spirals in
these three cases is statistically significant at the 3-
,
respectively.
The difference between the measured opening angle of the spirals in
these three cases is statistically significant at the 3-![]() confidence level.
There is clear evidence that the opening angle of the spiral arms in
IP Peg decreases towards the later stages of the outburst while the
accretion disc cools and shrinks. This fits nicely into the expected
evolution of a tidally driven spiral wave and it is supported by
hydrodynamical simulations of accretion discs.
confidence level.
There is clear evidence that the opening angle of the spiral arms in
IP Peg decreases towards the later stages of the outburst while the
accretion disc cools and shrinks. This fits nicely into the expected
evolution of a tidally driven spiral wave and it is supported by
hydrodynamical simulations of accretion discs.
The sub-Keplerian velocities along the spiral pattern and the clear correlation between the opening angle of the spirals and the outburst stage favors the interpretation of these asymmetric structures as tidally-induced spiral shocks.
It would be crucial to confirm these results with further time-lapse, combined Doppler tomography and eclipse mapping of emission lines of IP Peg along the same outburst cycle.
Acknowledgements
We dedicate this paper to the memory of our colleague and dear friend Emilios Harlaftis. The INT Telescope is operated on the Island of La Palma by the Isaac Newton Group in the Spanish Observatory del Roque de los Muchachos of the Instituto de Astrofisica de Canarias. This work was partially supported by CNPq/Brazil through the research grant 62.0053/01-1 - PADCT III/Milenio. R.B. acknowledges financial support from CNPq/Brazil through grants 300.354/96-7 and 301.442/2004-5. L.M.R. was supported by a PPARC post-doctoral grant and by NWO-VIDI grant 639.042.201 to P. J. Groot during the course of this research. T.R.M. acknowledges the support of a PPARC Senior Research Fellowship. DS acknowledges a Smithsonian Astrophysical Observatory Clay Fellowship.
The default map defines the point-spread-function of the reconstructed eclipse map. The original default map of Horne (1985) blurs any asymmetric point-like source into a ring at the same disc radius and is well suited to recover the radial profile of broad and fairly symmetrical disc brightness distributions.
The limited azimuthal smearing default (Rutten et al. 1992; Baptista
et al. 1996) added the capability to recover azimuthal information
about asymmetrically located light sources such as the bright spot
at the disc rim.
Nevertheless, it was not designed for reconstructions of highly
asymmetric light sources such as the spiral structures seen in the
accretion disc of IP Peg in outburst.
The azimuthal smearing default map blurs the spiral pattern into a
``butterfly''-shaped structure (Harlaftis et al. 2004). It is possible
to use these maps to define the range of radii and azimuths covered by
the spirals, but it is not possible to trace the spiral pattern -
i.e., to measure the spiral opening angle ![]() .
.
Harlaftis et al. (2004) suggest the use of a default map which steers the eclipse mapping solution towards a spiral shape in order to improve the reconstruction of spiral structures in IP Peg. The idea is to minimize the azimuthal blur effect, allowing to trace the observed spiral arms.
We followed this idea and created a spiral default map,
which blurs the intensity of each point source in the eclipse
map along a spiral pattern in the disc. The first problem with this
approach is that the spiral default map introduces an extra, ad hoc
parameter, namely, the opening angle of the spiral pattern ![]() .
Since the opening angle is not known in advance (on the contrary, this
is one of the quantities we wish to measure from the eclipse map),
a plausible approach would be to make reconstructions for a set of
values of
.
Since the opening angle is not known in advance (on the contrary, this
is one of the quantities we wish to measure from the eclipse map),
a plausible approach would be to make reconstructions for a set of
values of ![]() and try to determine which map is the correct one.
and try to determine which map is the correct one.
In order to test the ability of the eclipse mapping method in
recovering the proper value of ![]() using the spiral default map,
we created artificial maps with two-armed logarithmic spiral patterns
for different values of
using the spiral default map,
we created artificial maps with two-armed logarithmic spiral patterns
for different values of ![]() .
The spirals have a radial width of
.
The spirals have a radial width of
![]() and a radial range between 0.2-0.6 RL1 with a
brightness cut off
and a radial range between 0.2-0.6 RL1 with a
brightness cut off
![]() law. The trace of
the spirals is defined by,
law. The trace of
the spirals is defined by,
We simulated the eclipse of the artificial maps using the geometry of
IP Peg (
![]() and q=0.5, Wood & Crawford 1986) to create light
curves with added Gaussian noise and obtained reconstructions using
spiral default maps for a set of
and q=0.5, Wood & Crawford 1986) to create light
curves with added Gaussian noise and obtained reconstructions using
spiral default maps for a set of ![]() values.
These simulations show that there is no correlation between the map
with the correct
values.
These simulations show that there is no correlation between the map
with the correct
![]() and the map of highest entropy in a
sequence of reconstructions with a range of values of
and the map of highest entropy in a
sequence of reconstructions with a range of values of ![]() .
We further tried to see if one could recover the correct value
.
We further tried to see if one could recover the correct value
![]() by using a spiral default map with a fixed, arbitrary
value
by using a spiral default map with a fixed, arbitrary
value ![]() .
In all cases the asymmetric arcs in the reconstruction are steered
towards
.
In all cases the asymmetric arcs in the reconstruction are steered
towards ![]() instead of towards
instead of towards
![]() .
The conclusion is that using a spiral default map is not useful in
investigating spiral structures in eclipse maps, unless we know in
advance the opening angle of the spirals.
.
The conclusion is that using a spiral default map is not useful in
investigating spiral structures in eclipse maps, unless we know in
advance the opening angle of the spirals.
With the usual default map of limited azimuthal smearing, the
ability to trace the spiral pattern is hampered by the azimuthal
smearing effect, which is responsible for the "butterfly'' shape
of the reconstructed spiral arms (Harlaftis et al. 2004).
For an azimuthal gaussian blur width of
![]() ,
all
point sources in the eclipse map will be azimuthally smeared by
,
all
point sources in the eclipse map will be azimuthally smeared by
![]() .
An obvious way to minimize the azimuthal smearing effect
and improve the reconstruction of asymmetric structures would be to
reduce
.
An obvious way to minimize the azimuthal smearing effect
and improve the reconstruction of asymmetric structures would be to
reduce
![]() .
This corresponds to relaxing the fundamental
constraint that the disc brightness distribution has to be the most
axi-symmetric as possible. However, eclipse maps obtained with
lower values of
.
This corresponds to relaxing the fundamental
constraint that the disc brightness distribution has to be the most
axi-symmetric as possible. However, eclipse maps obtained with
lower values of
![]() start to show criss-crossed arcs
at the position of bright compact sources. The reason it that, without
the axi-symmetry constraint, the intensity of a compact source is
distributed along the arcs that outline the shadow of the secondary
star at the corresponding ingress/egress phases (e.g., Horne 1985).
The need to avoid this physically unreasonable mapping is what prompted
Horne (1985) to propose the default map with azimuthal smearing.
start to show criss-crossed arcs
at the position of bright compact sources. The reason it that, without
the axi-symmetry constraint, the intensity of a compact source is
distributed along the arcs that outline the shadow of the secondary
star at the corresponding ingress/egress phases (e.g., Horne 1985).
The need to avoid this physically unreasonable mapping is what prompted
Horne (1985) to propose the default map with azimuthal smearing.
A default map which tries to avoid building structure along the
ingress/egress arcs of the secondary star would be particularly
interesting for the reconstruction of asymmetric sources, because
in this case
![]() could be reduced without the above undesired
side effect. The approach of multiple default maps of Spruit (1994)
is very useful in this regard.
could be reduced without the above undesired
side effect. The approach of multiple default maps of Spruit (1994)
is very useful in this regard.
![\begin{figure}\par\includegraphics[width=8.5cm]{3399apf1.eps}\end{figure}](/articles/aa/full/2005/46/aa3399-05/Timg78.gif) |
Figure A.1:
Comparison of reconstructions obtained with the standard
eclipse mapping (single default map) and the double-default eclipse
mapping. The top panel shows the original map with two spiral arms of
opening angle
|
![\begin{figure}
\par\includegraphics[width=13cm,clip]{3399apf2.eps}\end{figure}](/articles/aa/full/2005/46/aa3399-05/Timg79.gif) |
Figure A.2:
Sequence of brightness distributions with spiral arms of
different opening angles. Left panel: simulated noisy light curves
(
|
Following the prescription of Spruit (1994), the concept of the default
function D(j) can be generalized to the case of multiple functions
by,
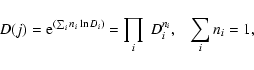 |
(A.2) |
Here we implement a default function consisting of two default maps:
a standard default map of limited azimuthal smearing
![]() with a
positive index n, and a default map of criss-crossed arcs
with a
positive index n, and a default map of criss-crossed arcs
![]() with a negative exponent (1-n),
with a negative exponent (1-n),
![\begin{displaymath}D(j) = [D_{\rm az}(j)]^n \times [D_{\rm criss}(j)]^{(1-n)} , \;\;\; n>1
.
\end{displaymath}](/articles/aa/full/2005/46/aa3399-05/img83.gif) |
(A.3) |
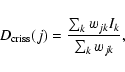 |
(A.4) |
![\begin{displaymath}w_{jk} = \exp\left[ - \frac{1}{2} \left(
\frac{ \phi_{\rm i}...
...{\rm e}(j) - \phi_{\rm e}(k) }{\Delta\phi} \right)^2 \right] ,
\end{displaymath}](/articles/aa/full/2005/46/aa3399-05/img85.gif) |
(A.5) |
This double-default function is tailored for reconstructions of asymmetric
brightness distributions. It yields no perceptible improvement in
the quality of reconstructions of broad, fairly symmetric brightness
distributions found in usual eclipse mapping applications.
However, it does make a difference for reconstructions of spiral arms.
Figure A.1 compares a reconstruction of a brightness distribution
with two spiral arms as obtained with the standard single default map
of limited azimuthal smearing with that obtained with the double default
map.
The two reconstructions were obtained with
![]() .
Because of the reduced
.
Because of the reduced
![]() value, a criss-crossed structure
develops in the reconstruction with the single default map. It can be
seen as a bright arc running across the upper left spiral arm. This
arc outlines the shadow of the secondary star at the mid-ingress phase
of that spiral arm. This artifact is largely suppressed in the
reconstruction with the double default map. Furthermore, the
"butterfly'' shape of the reconstruction with the single default map
is replaced by a better defined trace of the spirals in the
reconstruction with the double default map.
value, a criss-crossed structure
develops in the reconstruction with the single default map. It can be
seen as a bright arc running across the upper left spiral arm. This
arc outlines the shadow of the secondary star at the mid-ingress phase
of that spiral arm. This artifact is largely suppressed in the
reconstruction with the double default map. Furthermore, the
"butterfly'' shape of the reconstruction with the single default map
is replaced by a better defined trace of the spirals in the
reconstruction with the double default map.
Figure A.2 shows the performance of the double-default eclipse mapping for the reconstruction of two-armed spiral brightness distributions at different opening angles. The left hand panels display the data and model light curves. It is seen that the shape of the eclipse changes significantly as the opening angle of the spirals is reduced. Original and reconstructed maps are shown in the middle two columns. The right-hand panels show the distributions of the maximum intensity in the map as a function of binary phase (or azimuth, see BHS). The distribution of the original map is shown as a dashed gray line while that of the reconstruction is indicated by a solid line. Vertical dotted lines mark the azimuths of minimum intensity in each case. Orbital phases are measured with respect to the inner Lagrangian point L1 and increase clockwise.
![\begin{figure}
\par\includegraphics[width=8.3cm]{3399apf3.eps}\end{figure}](/articles/aa/full/2005/46/aa3399-05/Timg91.gif) |
Figure A.3:
Reconstruction of a brightness distribution with spiral arms of
|
Wide open spirals (
![]() )
produce narrow, well defined maxima
and minima in the azimuthal intensity distribution. The corresponding
eclipse maps show well defined and separated asymmetric arcs with a
reasonably good reconstruction of the shape, radial and azimuthal range
of the spirals. As the opening angle is reduced, the maxima of the
azimuthal intensity distribution become broader while the minima become
narrower. Because of the winding up of the spiral arms, both maxima
and minima intensities move towards higher orbital phases in a monotonic,
fairly linear way. The shape of the azimuthal distribution and the
position of maxima/minima intensities are defined by the opening angle
of the spiral arms. Thus, it is possible to estimate the opening angle
of the spirals by measuring the position of maxima/minima intensity in
the azimuthal distribution.
)
produce narrow, well defined maxima
and minima in the azimuthal intensity distribution. The corresponding
eclipse maps show well defined and separated asymmetric arcs with a
reasonably good reconstruction of the shape, radial and azimuthal range
of the spirals. As the opening angle is reduced, the maxima of the
azimuthal intensity distribution become broader while the minima become
narrower. Because of the winding up of the spiral arms, both maxima
and minima intensities move towards higher orbital phases in a monotonic,
fairly linear way. The shape of the azimuthal distribution and the
position of maxima/minima intensities are defined by the opening angle
of the spiral arms. Thus, it is possible to estimate the opening angle
of the spirals by measuring the position of maxima/minima intensity in
the azimuthal distribution.
The maxima of the azimuthal intensity distribution are affected by
noise in the light curve and by residual criss-crossed arc effect and
are less reliably recovered in the reconstructions.
On the other hand, the minima of the azimuthal intensity distribution
trace the region in between the spirals. Because there is essentially
no flux at these azimuths, their positions are less prone to be distorted
by noise. Also, the minima become narrower as the opening angle
decreases and are, therefore, easier to measure in the limit of low
![]() 's. We therefore choose to measure the opening angle of the
spirals from the azimuths of minimum intensity.
's. We therefore choose to measure the opening angle of the
spirals from the azimuths of minimum intensity.
For small opening angles the two spiral arms become so tightly wound
that they start to overlap in azimuth. Because of the (reduced, but
still present) azimuthal smearing effect, they become indistinguishable
in the reconstructions and it is no longer possible to use the azimuthal
intensity distribution to estimate the opening angle of the spirals.
For the simulations presented in Fig. A.2, this occurs at
![]() .
The minimum opening angle that is possible
to measure depend on the radial extension of the spiral arms.
If the spiral pattern does not extend as far inside the disc as those
in Fig. A.2 it is possible to measure
.
The minimum opening angle that is possible
to measure depend on the radial extension of the spiral arms.
If the spiral pattern does not extend as far inside the disc as those
in Fig. A.2 it is possible to measure ![]() for spirals with
smaller opening angles than the limit of the above example.
This is illustrated in Fig. A.3, which shows the results for
a two-armed spiral pattern distribution with
for spirals with
smaller opening angles than the limit of the above example.
This is illustrated in Fig. A.3, which shows the results for
a two-armed spiral pattern distribution with
![]() and a reduced
radial range of
and a reduced
radial range of
![]() .
The azimuthal intensity distribution
is easily recovered in this case, allowing a precise measurement of the
azimuth of minimum intensity. The reconstructed brightness distribution
is similar to those of the IP Peg eclipse maps of BHT.
.
The azimuthal intensity distribution
is easily recovered in this case, allowing a precise measurement of the
azimuth of minimum intensity. The reconstructed brightness distribution
is similar to those of the IP Peg eclipse maps of BHT.
From our simulations we find the following empirical relation between
the spiral opening angle ![]() and the observed orbital phase of minimum
intensity
and the observed orbital phase of minimum
intensity
![]() ,
,
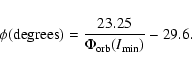 |
(A.6) |