A&A 444, 1-13 (2005)
DOI: 10.1051/0004-6361:20052657
B. Fuchs - C. Dettbarn - T. Tsuchiya![]()
Astronomisches Rechen-Institut am Zentrum für Astronomie der Universität Heidelberg, Mönchhofstrasse 12-14, 69120 Heidelberg, Germany
Received 7 January 2005 / Accepted 4 July 2005
Abstract
Non-linear effects in the dynamical evolution of a shearing sheet made of
stars are studied. First the implications of hitherto neglected
non-linearities of the Boltzmann equation for the dynamical evolution of
the shearing sheet are investigated. Using a formalism developed
previously on the basis of the linearized Boltzmann equation it is
demonstrated that the inclusion of the non-linear term leads to a
feedback cycle for swing amplified density waves in the unbounded
shearing sheet. Such a feedback is unique to star disks and is not known for
gas disks. In order to present concrete examples of the non-linear feedback
cycle a SCF code was developed and numerical simulations of the dynamical
evolution of the shearing sheet are performed. The numerical results
seem to confirm the theoretical predictions. The evolution of the
shearing sheet resembles closely and might actually explain the recurrent
spiral instabilities found in large-scale numerical simulations of the
dynamical evolution of galactic disks.
Key words: galaxies: kinematics and dynamics - galaxies: spiral
The shearing sheet (Goldreich & Lynden-Bell 1965; Julian & Toomre 1966) model has been developed as a tool to study the dynamics of
galactic disks and is particularly well suited to theoretically describe
the dynamical mechanisms responsible for the formation of spiral arms.
For simplicity, the model describes only the dynamics of a
patch of a galactic disk. It is assumed to be infinitesimally thin and
its radial size is assumed to be much smaller than the disk. Polar
coordinates can be therefore converted to pseudo-Cartesian
coordinates and the velocity field of the differential rotation of the
disk can be approximated by a linear shear flow. These simplifications
allow an analytical treatment of the problem, which helps to clarify
the underlying physical processes operating in the disk. In the previous
papers of this series (Fuchs 2001a,b, 2004, 2005) we have studied various
aspects of the dynamics of spiral density waves in a shearing sheet of
stars based on the linearized Boltzmann equation.
In the present paper we study non-linear effects in the dynamical
evolution of the shearing sheet. In particular, we investigate the role of the
hitherto neglected non-linear term of the Boltzmann equation. The principal
result is that the non-linearity leads to a feedback cycle for swing
amplification of spiral density waves. Recurrent spiral instabilities,
which lead to an ever changing appearance of the disk, have been
reported by Sellwood & Carlberg (1984) and Sellwood (1989) from their
numerical simulations of the dynamical evolution of self gravitating,
differentially rotating disks. Toomre (1990) and Toomre & Kalnajs (1991) have
argued that these recurrent spiral density waves are essentially due to swing
amplified (Toomre 1981) random fluctuations of the surface density of the disks.
Sellwood (1989), on the other hand, points out that contrary to expectation the
spiral instabilities stay at the same level of activity in the experiments,
if the particle number is increased and thus the particle noise is reduced.
Moreover, Sellwood & Carlberg (1984) have shown that, once the cycles
of recurrent transient spiral density waves have established themselves in
their simulations, the leading density wavelets which are then swing amplified
are extremely unlikely due to chance alignments
of the stars, because the amplitudes of these leading wavelets are too large.
They consider the recurrent spirals not to be unconnected random events
arising from swing amplified random noise. Sellwood (2000) puts
forward the notion of a feedback mechanism for spiral instabilities, which is
related to fine structure of the distribution function of stars in phase space
carved in by transient spiral density waves, which can then in turn incite
density waves again. As a concrete example
Sellwood (1989) and Sellwood & Kahn (1991)
have developed the concept of recurring groove instabilities.
These rely on fairly sharp boundaries of the dynamically active parts of the
self gravitating disks, because they are initiated by edge modes (Toomre 1981).
The groove instabilities develop then as rigidly rotating spiral modes of the
disk![]() and
seed fresh grooves through particle wave resonance at their Lindblad
resonances. However, Sellwood & Carlberg (1984) have shown in detail
that the spiral structures seen in their numerical simulations are transient
swing amplified shearing density waves exactly of the kind found in the
infinite shearing sheet model. They demonstrate not only that the spiral arms
shear from leading to trailing orientation, but also that the density
waves grow preferentially with azimuthal wave numbers predicted by the shearing
sheet model, which has become widely known
as the Toomre (1981) "X=2'' prescription. Exactly the same was found by
Fuchs & von Linden (1998) in their numerical simulations of the dynamical
evolution of a self gravitating disk made of stars and interstellar gas. Toomre (1990) has argued convincingly that the spiral arms of Sc galaxies are such
transient shearing density waves. One
of the deeper reasons for this success of the infinite shearing sheet model in
describing spiral density waves realistically is the rapid convergence of the
Poisson integral in self gravitating disks (Julian & Toomre 1966). Consider,
for example, the potential of a sinusoidal density perturbation
and
seed fresh grooves through particle wave resonance at their Lindblad
resonances. However, Sellwood & Carlberg (1984) have shown in detail
that the spiral structures seen in their numerical simulations are transient
swing amplified shearing density waves exactly of the kind found in the
infinite shearing sheet model. They demonstrate not only that the spiral arms
shear from leading to trailing orientation, but also that the density
waves grow preferentially with azimuthal wave numbers predicted by the shearing
sheet model, which has become widely known
as the Toomre (1981) "X=2'' prescription. Exactly the same was found by
Fuchs & von Linden (1998) in their numerical simulations of the dynamical
evolution of a self gravitating disk made of stars and interstellar gas. Toomre (1990) has argued convincingly that the spiral arms of Sc galaxies are such
transient shearing density waves. One
of the deeper reasons for this success of the infinite shearing sheet model in
describing spiral density waves realistically is the rapid convergence of the
Poisson integral in self gravitating disks (Julian & Toomre 1966). Consider,
for example, the potential of a sinusoidal density perturbation
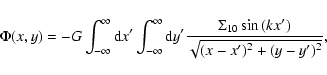 |
(1) |
| |
= | ||
| = | (2) |
It is the aim of the present paper to demonstrate on the basis of the infinite shearing sheet model that a feedback cycle of swing amplified density waves is indeed theoretically expected. In the next section a formal derivation is presented, while in the third section we describe numerical SCF simulations of the dynamical evolution of the shearing sheet and illustrate the feedback cycle with concrete examples. The SCF simulations are directly compared with N-body simulations of the dynamical evolution of the shearing sheet by Toomre (1990), Toomre & Kalnajs (1991) and Chiueh & Tseng (2000).
Non-linear interaction of density waves has been previously studied by Tagger et al. (1987) and Sygnet et al. (1988). These authors considered, however, the interaction of rigidly rotating, slowly growing spiral modes, which do not develop in the unbounded shearing sheet. A preliminary report on the work presented here was given in Fuchs (1991).
The time evolution of the distribution function of stars in phase space, f, is determined by the collisionless Boltzmann equation
![\begin{displaymath}\frac{\partial f}{\partial t} + \left[f, H\right] = 0~,
\end{displaymath}](/articles/aa/full/2005/46/aa2657-05/img20.gif) |
(3) |
| (4) |
![\begin{displaymath}\frac{\partial \delta f}{\partial t} + \left[f_{\rm {0}} , \d...
... \delta f , H_{\rm {0}} \right] = - [\delta f, \delta
\Phi]~,
\end{displaymath}](/articles/aa/full/2005/46/aa2657-05/img26.gif) |
(5) |
The non-linear Poisson bracket has the explicit form
![$\displaystyle [\delta f, \delta \Phi] =
\frac{\partial \delta f}{\partial w_1}
...
...{\partial \delta f}
{\partial J_2} \frac{\partial \delta \Phi}{\partial w_2} ~,$](/articles/aa/full/2005/46/aa2657-05/img27.gif) |
(6) |
![\begin{displaymath}\delta f = \sum_{l_1} \int {\rm d} l_2 f_{\rm {\bf l}} ({\vec J})
{\rm e}^{{\rm i}[l_1 w_1 + l_2 w_2]}~.
\end{displaymath}](/articles/aa/full/2005/46/aa2657-05/img28.gif) |
(7) |
![\begin{displaymath}\delta \Phi = \int {\rm d} k_{x}\int {\rm d} k_{y} \Phi_{\rm {\bf k}}
{\rm e}^{{\rm i}[ k_{x} x + k_{y} y]}
\end{displaymath}](/articles/aa/full/2005/46/aa2657-05/img29.gif) |
(8) |
![$\displaystyle {\rm exp}~{\rm i}[k_{x}x+ k_{y} y] =
{\rm exp}~{\rm i} \Big( k_{x...
...pa}}\sin{w_1}
+ k_{y} w_2 - k_{y} \frac{\sqrt{2 \kappa J_1}}{2 B}\cos{w_1}\Big)$](/articles/aa/full/2005/46/aa2657-05/img30.gif) |
(9) |
| |
|||
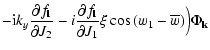 |
|||
| (10) |
The Boltzmann Eq. (5) can be viewed as a linear partial differential
equation for ![]() with the two inhomogeneous terms
with the two inhomogeneous terms
![]() and
and
![]() ,
respectively.
Formally it can be solved for each inhomogeneity separately and both
solutions can be then combined as the final solution
,
respectively.
Formally it can be solved for each inhomogeneity separately and both
solutions can be then combined as the final solution
| (11) |
![\begin{displaymath}\frac{\partial \delta f_1}{\partial t} + [\delta f_1,H_0] =
- [f_0,\delta \Phi]
\end{displaymath}](/articles/aa/full/2005/46/aa2657-05/img45.gif) |
(12) |
![\begin{displaymath}\frac{\partial \delta f_2}{\partial t} + [\delta f_2,H_0] =
- [\delta f,\delta \Phi]
\end{displaymath}](/articles/aa/full/2005/46/aa2657-05/img46.gif) |
(13) |
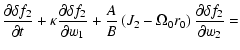 |
|||
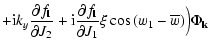 |
|||
| (14) |
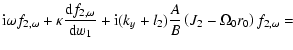 |
|||
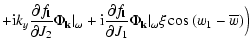 |
|||
| (15) |
| |
![$\displaystyle = \frac{{\rm e}^{{\rm i}[\pi \eta +l_1 w_1]}}{2i\sin{\pi \eta}}
\...
...\Bigg[\omega t +(k_{y} + l_2) w_2 + k_{x}\frac{J_2 - \Omega_0 r_0}
{-2B}\Bigg]}$](/articles/aa/full/2005/46/aa2657-05/img60.gif) |
||
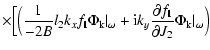 |
|||
![$\displaystyle \times
\int_{-2\pi}^0 {\rm d}w_1' \exp{{\rm i} [(l_1+\eta)w_1' +\xi \sin{(w_1'+w_1-\overline{w})}]}$](/articles/aa/full/2005/46/aa2657-05/img62.gif) |
|||
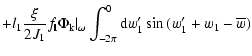 |
|||
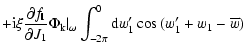 |
|||
| (16) |
Even in the linear case the spatial pattern of the disk response is
different to that of the imprinted potential perturbation
(cf. Eq. (10) of Paper I). In particular, through the dependence on
![]() and thus on the
and thus on the
![]() variable there is a further dependence
of the disk response on the x coordinate. This means that the
disk response to a Fourier component of the potential
is not a Fourier component of the general disk
response. Kalnajs (1971) has shown a way to overcome this difficulty by
integrating the disk response over all wave numbers and then Fourier
transforming this with respect to the spatial x and y coordinates
again. The result is integrated over velocity space in order to obtain the
surface density of the disk response and inserted into the Poisson equation
whose lhs is also Fourier transformed,
variable there is a further dependence
of the disk response on the x coordinate. This means that the
disk response to a Fourier component of the potential
is not a Fourier component of the general disk
response. Kalnajs (1971) has shown a way to overcome this difficulty by
integrating the disk response over all wave numbers and then Fourier
transforming this with respect to the spatial x and y coordinates
again. The result is integrated over velocity space in order to obtain the
surface density of the disk response and inserted into the Poisson equation
whose lhs is also Fourier transformed,
| |
![$\displaystyle \!\!\int^{+\infty}_{-\infty} {\rm d}z
\int^{+\infty}_{-\infty} {\rm d}x \int^{+\infty}_{-\infty} {\rm d}y
{\rm e}^{-{\rm i} [k'_{x} x + k'_{y} y ]}$](/articles/aa/full/2005/46/aa2657-05/img72.gif) |
||
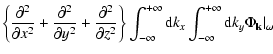 |
|||
![$\displaystyle = \frac{4\pi G}{\left(2\pi\right)^{\rm {2}}} \int^{+\infty}_{-\in...
... d}x
\int^{+\infty}_{-\infty}{\rm d}y {\rm e}^{-{\rm i} [k'_{x} x + k'_{y} y ]}$](/articles/aa/full/2005/46/aa2657-05/img76.gif) |
|||
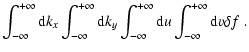 |
(17) |
| |
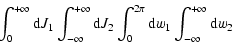 |
||
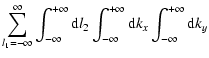 |
|||
![$\displaystyle \times \frac{{\rm e}^{{\rm i}\left [\pi \eta +l_1 w_1\right ]}}
{...
...left[\omega t +(k_{y} + l_2) w_2 + k_{x}\frac{J_2 - \Omega_0 r_0}
{-2B}\right]}$](/articles/aa/full/2005/46/aa2657-05/img82.gif) |
|||
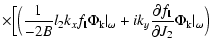 |
|||
![$\displaystyle \times
\int_{-2\pi}^0 {\rm d}w_1' \exp{{\rm i} [(l_1+\eta)w_1' +\xi \sin{(w_1'+w_1-\overline{w})}]}$](/articles/aa/full/2005/46/aa2657-05/img62.gif) |
|||
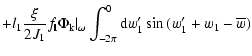 |
|||
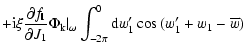 |
|||
| (18) |
![\begin{displaymath}\frac{1}{2\pi}\int^{+\infty}_{-\infty}{\rm d}w_{\rm {2}} {\rm...
... k'_{y} ] w_2} =
\delta\left(k_{{y}} + l_2 - k'_{{y}}\right).
\end{displaymath}](/articles/aa/full/2005/46/aa2657-05/img89.gif) |
(19) |
It was shown in Paper I that the solution of the linearized Boltzmann
Eq. (12) leads, upon inserting it into the Fourier transformed Poisson
Eq. (17), to the Volterra integral equation (
k'y > 0)
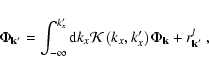 |
(20) |
| |
= | 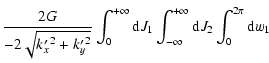 |
|
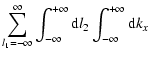 |
|||
![$\displaystyle \times \frac{{\rm e}^{{\rm i}[\pi \eta +l_1 w_1]}}
{2{\rm i}\sin{...
...ta}}
\exp{{\rm i}[\omega t +k'_{y} w_2 + k_{x}\frac{J_2 - \Omega_0 r_0}
{-2B}]}$](/articles/aa/full/2005/46/aa2657-05/img98.gif) |
|||
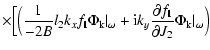 |
|||
![$\displaystyle \times
\int_{-2\pi}^0 {\rm d}w_1' \exp{{\rm i} [(l_1+\eta)w_1' +\xi \sin{(w_1'+w_1-\overline{w})}]}$](/articles/aa/full/2005/46/aa2657-05/img62.gif) |
|||
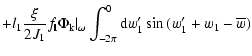 |
|||
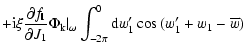 |
|||
| (21) |
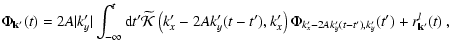 |
(22) |
![$\displaystyle \int_{-\infty +i\nu}^{\infty +i\nu} {\rm d}\omega {\rm e}^{{\rm i...
..._0r_0)k'_{y})t + \eta w'_1]}
\frac{{\rm e}^{{\rm i}\pi \eta}}{\sin{(\pi \eta)}}$](/articles/aa/full/2005/46/aa2657-05/img102.gif) |
(23) |
 |
(24) |
| |
= | 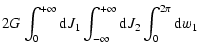 |
|
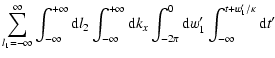 |
|||
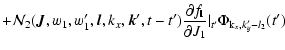 |
|||
![$\displaystyle +
\mathcal{N}_3({\vec J},w_1,w'_1,{\vec l},k_{x},{\vec k'},t-t')
...
...{\rm {\bf l}}}{\partial J_2}\vert _{t'}\Phi_{{\rm k}_{x},k'_{y}-l_2}(t')\Big]~,$](/articles/aa/full/2005/46/aa2657-05/img111.gif) |
(25) |
The Volterra Eq. (22) augmented by
![]() reveals
clearly the role of the non-linear term of the Boltzmann equation in the
dynamical evolution of the shearing sheet.
reveals
clearly the role of the non-linear term of the Boltzmann equation in the
dynamical evolution of the shearing sheet.
In Fig. 1 the linear evolution of a density wave, calculated neglecting the
non-linear part of Eq. (22), is illustrated. The density wave is
initialized as
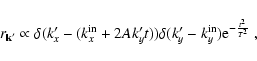 |
(26) |
| |
Figure 1:
Linear swing amplification of a density wave in the shearing sheet.
The wave is initialized as a delta like impulse in wave number space with an
initial wave vector
|
| Open with DEXTER | |
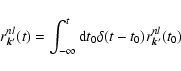 |
(27) |
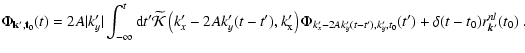 |
(28) |
| |
= | 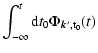 |
|
| = | 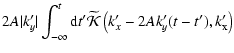 |
||
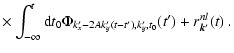 |
(29) |
The feedback cycle described here is of course an effect depending quadratically on the magnitude of the perturbations of the sheet. Thus, if the amplitudes of the density waves are at very low levels, the efficiency of the swing amplification mechanism might not be sufficient to sustain the cycle and it will die out eventually.
In the previous section we have developed the theoretical concept of a feedback cycle for density waves in the shearing sheet mitigated by the non-linear coupling of the waves. In order to demonstrate concrete examples of this effect we have run numerical simulations of the dynamical evolution of the shearing sheet.
The SCF method relies on a complete set of pairwise basis functions into which
the density of the particles and the gravitational potential are simultaneously
expanded. Each of the pairwise basis functions solve the Poisson
equation. For the shearing sheet these are simply Fourier transforms,
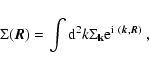 |
(30) |
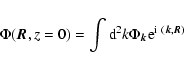 |
(31) |
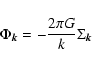 |
(32) |
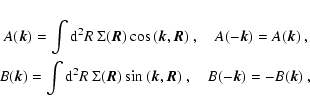
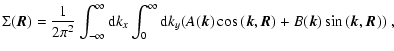 |
(33) |
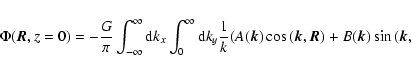
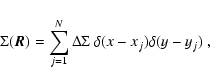 |
(34) |
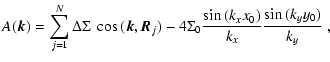 |
|||
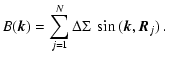 |
(35) |
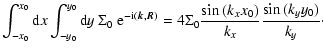 |
(36) |
We have discussed in the introduction that the reason for the success of the
infinite shearing sheet model describing spiral density waves realistically is
the rapid convergence of the Poisson integral in self gravitating disks and that
the "effective range'' of gravity of the
density waves is only of the order
![]() .
Thus, if the size of
the simulated sheet is chosen large enough, it should behave like an infinite
shearing sheet.
Next the wave numbers are discretized with bin widths
.
Thus, if the size of
the simulated sheet is chosen large enough, it should behave like an infinite
shearing sheet.
Next the wave numbers are discretized with bin widths
![]() and
and
![]() ,
respectively. Discretizing Eqs. (33) accordingly we
obtain for the planar components of the gradient of the gravitational potential
,
respectively. Discretizing Eqs. (33) accordingly we
obtain for the planar components of the gradient of the gravitational potential
![$\displaystyle -\nabla \Phi ({\vec R}_{j}, z=0) = \sum_{k_{x,n}}\Delta
{k_{x}}\s...
...vec k}_{n},{\vec R}_{j})}
+B({\vec k}_{n}) \cos{({\vec k}_{n},{\vec R}_{j})}]~,$](/articles/aa/full/2005/46/aa2657-05/img143.gif) |
(37) |
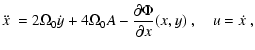 |
|||
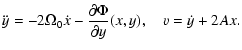 |
(38) |
The basic dynamics of the shearing sheet is characterized by Oort's constants
![]() ,
,
![]() ,
the epicyclic
frequency of the particle orbits
,
the epicyclic
frequency of the particle orbits
![]() ,
the
epicyclic ratio of the velocity dispersions of the particles
,
the
epicyclic ratio of the velocity dispersions of the particles
![]() ,
the critical wave number
,
the critical wave number
![]() and the critical wave length
and the critical wave length
![]() ,
and finally the Toomre stability
parameter
,
and finally the Toomre stability
parameter
![]() .
We introduce
dimensionless model units in the following way. The length unit is
.
We introduce
dimensionless model units in the following way. The length unit is
![]() and accordingly the wave number unit
and accordingly the wave number unit
![]() .
We set
.
We set
![]() which implies
which implies
![]() .
The
time unit is then the epicyclic period
.
The
time unit is then the epicyclic period
![]() .
Moreover we assume a flat
rotation curve,
.
Moreover we assume a flat
rotation curve,
![]() so that
so that
![]() and
and
![]() .
The radial velocity
dispersion is given by
.
The radial velocity
dispersion is given by
![]() and the epicyclic ratio
is
and the epicyclic ratio
is
![]() .
In all the simulations presented here we have
used the following parameters:
.
In all the simulations presented here we have
used the following parameters:
number of particles N = 32768
size x0=10, y0 =
![]() = 14.1
= 14.1
time step 0.03125
bin size of wave numbers
![]() = 0.0625
= 0.0625
64 bins in kx ranging from -4 to 4
32 bins in ky ranging from 0 to 4
Q=1.2
![\begin{figure}
\par\includegraphics[width=5.1cm,clip]{2657fig2.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg168.gif) |
Figure 2:
Initial set up of the 32 768 particles in the simulation of the
shearing sheet. The y-axis points into the direction of the shear flow.
The size is
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16cm,clip]{2657fig3.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg169.gif) |
Figure 3: Dynamical evolution of the shearing sheet. Snapshots of particle positions are shown for t = 0.5, 1, ... 3.5, and 4, respectively. The y-axis is oriented in the direction of the shear flow. The size of each frame is the same as in Fig. 2. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8cm,clip]{2657fig4.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg172.gif) |
Figure 4:
The rise of
|
| Open with DEXTER | |
The SCF simulations shown in Fig. 5 look very similar to the
direct N-body simulations of the dynamical evolution of the shearing sheet by
Toomre (1990) and Toomre & Kalnajs (1991). In these simulations an artificial
friction force acting on the particles in the sheet is included in order to
overcome the disk heating problem. Toomre & Kalnajs (1991) explain the
"hotch-potch of swirling density waves'' as the collective response of the
shearing sheet to each of its individual members by polarization
clouds around each particle. Instead of this quasi-linear concept we prefer to
interpret our simulations in terms of the feedback cycle described in Sect. 2. The SCF simulations illustrated in Fig. 5 resemble closely
the direct N-body simulations of Chiueh & Tseng (2000, their run a). Disk
heating effects are apparently controlled there by the choice the softening
length.
![\begin{figure}
\par\includegraphics[width=16.2cm,clip]{2657fig5.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg180.gif) |
Figure 5: Same as Fig. 3, but the shearing sheet is dynamically cooled by accretion of particles during the simulation. |
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=8.2cm,clip]{2657fig6.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg181.gif) |
Figure 6: Same as Fig. 4, but the shearing sheet is dynamically cooled by accretion of particles during the simulation. |
| Open with DEXTER | |
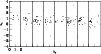 |
Figure 7:
Peaks of positive
|
| Open with DEXTER | |
 |
Figure 8:
Power spectrum
|
| Open with DEXTER | |
The numerically simulated shearing sheet is subjected to a "strong'' external
potential perturbation of the form considered in Sect. 2.5,
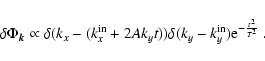 |
(39) |
The shearing sheet is now subjected to two independent impulsive external
potential perturbations of the form given in Eq. (39) with initial wave
vectors
![]() and
and
![]() ,
respectively. As shown in
Figs. 10 and 11 both perturbations evolve like the single perturbation in the
previous section.
However, further density waves appear with circumferential wave numbers
ky as predicted by the sum rule given in Eq. (19). We
interpret these new density waves, which are delayed relative to the imposed
perturbations, as examples of the onset of the non-linear feedback cycle
predicted theoretically in Sect. (2). In Fig. 10 an example is shown which
started with the initial wave vectors
,
respectively. As shown in
Figs. 10 and 11 both perturbations evolve like the single perturbation in the
previous section.
However, further density waves appear with circumferential wave numbers
ky as predicted by the sum rule given in Eq. (19). We
interpret these new density waves, which are delayed relative to the imposed
perturbations, as examples of the onset of the non-linear feedback cycle
predicted theoretically in Sect. (2). In Fig. 10 an example is shown which
started with the initial wave vectors
![]() and
and
![]() ,
respectively. At time t=0.88 there appears a new weak feature at about
,
respectively. At time t=0.88 there appears a new weak feature at about
![]() .
This then couples back with the first
externally triggered wave leading to a strong wave at time t = 1.13 with
.
This then couples back with the first
externally triggered wave leading to a strong wave at time t = 1.13 with
![]() ,
which travels behind the second externally
triggered wave. The example in Fig. 11 started with initial wave vectors
,
which travels behind the second externally
triggered wave. The example in Fig. 11 started with initial wave vectors
![]() and
and
![]() ,
respectively. At time t=0.5 a new weak feature
appears at about
,
respectively. At time t=0.5 a new weak feature
appears at about
![]() .
After the second
externally triggered wave was wrapped up very tightly, so that it
travelled out of the frames shown in Fig. 11, there appears at time t = 1.13
a new strong wave at
.
After the second
externally triggered wave was wrapped up very tightly, so that it
travelled out of the frames shown in Fig. 11, there appears at time t = 1.13
a new strong wave at
![]() .
Non-linear coupling
of density waves with different wave numbers, which led to recurrent density
wave activity, has already been noted by Chiueh & Tseng (2000) in their
simulations, although no detailed explanation was offered. They also find the
decline of the amplitudes of density waves at given ky wave number
which they ascribe to Landau damping. However, since density waves in the
shearing sheet swing around with the shear flow, there is effectively no
relative streaming of disk particles relative to the waves (cf. Fig. 3 of
Toomre 1981), which would lead to Landau damping (Lynden-Bell & Kalnajs 1972).
Thus in our view hardly any Landau damping is to be expected. The
density waves die out, because the density contrast is wiped out by the
epicyclic motions of the stars, when the density wave crests are wrapped up
tightly by the shear (Julian & Toomre 1966; Fuchs 2001a).
.
Non-linear coupling
of density waves with different wave numbers, which led to recurrent density
wave activity, has already been noted by Chiueh & Tseng (2000) in their
simulations, although no detailed explanation was offered. They also find the
decline of the amplitudes of density waves at given ky wave number
which they ascribe to Landau damping. However, since density waves in the
shearing sheet swing around with the shear flow, there is effectively no
relative streaming of disk particles relative to the waves (cf. Fig. 3 of
Toomre 1981), which would lead to Landau damping (Lynden-Bell & Kalnajs 1972).
Thus in our view hardly any Landau damping is to be expected. The
density waves die out, because the density contrast is wiped out by the
epicyclic motions of the stars, when the density wave crests are wrapped up
tightly by the shear (Julian & Toomre 1966; Fuchs 2001a).
The aim of this paper is to study non-linear effects in the dynamical evolution of an unbounded shearing sheet made of stars, which models a patch of a galactic disk. We have analyzed these effects both theoretically and by numerical simulations.
First we have investigated theoretically the implication of the non-linear
term of the Boltzmann equation for the dynamical evolution of the shearing
sheet. The non-linear term is expressed in
terms of Fourier expansions of the perturbations of the distribution function of
the stars in phase space and the gravitational potential of the sheet,
respectively, and the Boltzmann equation augmented by this term is formally
solved. It is shown that this further term can be viewed formally as an
inhomogeneity of the fundamental Volterra integral equation which describes the
dynamical evolution of the shearing
sheet. The inhomogeneity is given by combinations of the Fourier coefficients
of the perturbations of the distribution function and the gravitational
potential of the sheet, sampled over the past history of the evolution of the
sheet. This leads to a feedback cycle for swing amplified density waves. It is
quite different from the effect of non-linearities of the hydrodynamical or
Jeans equations, which have been used alternatively to describe the dynamics
of the shearing sheet or galactic disks.
![\begin{figure}
\par\includegraphics[width=16.1cm,clip]{2657fig9.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg197.gif) |
Figure 9:
Response of the shearing sheet to an external impulsive potential
perturbation with an initial wave vector
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.1cm,clip]{2657fi10.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg199.gif) |
Figure 10:
Response of the shearing sheet to two external impulsive potential
perturbations with initial wave vectors
|
| Open with DEXTER | |
![\begin{figure}
\par\includegraphics[width=16.3cm,clip]{2657fi11.ps} %
\end{figure}](/articles/aa/full/2005/46/aa2657-05/Timg201.gif) |
Figure 11:
Same as Fig. 10, but with two external impulsive potential
perturbations with initial wave vectors
(kx, ky) = (-2, 0.5)
|
| Open with DEXTER | |
In order to present concrete examples of the non-linear feedback cycle we have developed a self-consistent field code and have run numerical simulations of the dynamical evolution of the shearing sheet. The SCF method is based on a set of pairwise basis functions into which the surface density and the gravitational potential of the shearing sheet are expanded. Each of the pairwise basis functions solve the Poisson equation. In the case of the shearing sheet these are simply Fourier transforms. The equations of motion of the particles in the shearing sheet are the epicyclic equations of motion, which describe the motion of the particles in the unperturbed sheet, augmented by the forces due to the fluctuations of the sheet. In the simulations the shearing sheet turned out to be prone to rapid dynamical heating. Thus it was necessary to cool the sheet dynamically by adding mass continously to the sheet during the simulations. We have shown that the live shearing sheet responds to impulsive external potential perturbations by developing shearing density waves. In particular, by applying simultaneous multiple perturbations we have demonstrated the appearance of non-linearly induced shearing density waves, exactly as theoretically predicted.
The feedback cycle found here might well account for the hitherto unexplained recurrent shearing spiral instabilities seen in the large scale numerical simulations of the dynamical evolution of galactic disks.
Acknowledgements
We are indebted to the anonymous referee for comments that helped to improve the paper. B.F. thanks E. Sedlmayr and H. Völk for their encouragement to pursue non-linear studies. T.T. acknowledges support by a grant from the Alexander-von-Humboldt foundation.
| (A.1) |
| u(t0+h) | = | ||
| = | |||
| = | ![$\displaystyle u_0 + f(u,x) h + \frac{1}{2}h^2 \left[
\left(f \cdot \frac{\parti...
...partial u}\right)f
+\left(g \cdot \frac{\partial }{\partial x} \right)f
\right]$](/articles/aa/full/2005/46/aa2657-05/img205.gif) |
(A.2) | |
| +O(h3) , |
| x(t0+h) | = | ||
| = | |||
| = | ![$\displaystyle x_0 + g(u,x) h + \frac{1}{2}h^2 \left[
\left( f \cdot \frac{\part...
...partial u}\right)g +
\left( g \cdot \frac{\partial}{\partial x}\right)g
\right]$](/articles/aa/full/2005/46/aa2657-05/img208.gif) |
||
| + O(h3) . | (A.3) |
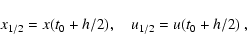 |
(A.4) |
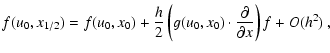 |
|||
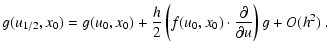 |
(A.5) |
| u(t0+h) | = | u0 + h f(u0,x1/2) | |
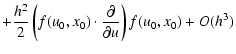 |
|||
| = | u0 + h f(u0,x1/2) | ||
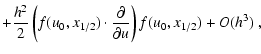 |
|||
| x(t0+h) = x0 + h g(u1/2,x0) | |||
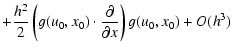 |
|||
| = | x0 + h g(u1/2,x0) | ||
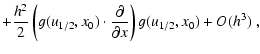 |
(A.6) |
| u1/2 | = | u-1/2 + h f(u-1/2,x0) | |
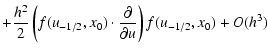 |
|||
| x1 | = | x0 + h g(u1/2,x0) | |
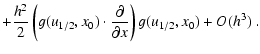 |
(A.7) |
| |
= | ||
| = | 2 B u + fy | ||
| = | u | ||
| = | v -2 A x . | (A.8) |
| u1/2 | = | ||
| v1/2 | = | ||
| x1 | = | x0 + h u1/2 + O(h3) | |
| y1 | = | y0 + h(v1/2 - 2A x0) - h2 A u1/2 + O(h3) . | (A.9) |